Modeled source apportionment of black carbon particles coated with a light-scattering shell

The Aethalometer model has been used widely for estimating the contributions of fossil fuel emissions and biomass burning to equivalent black carbon (eBC). The calculation is based on measured absorption Ångström exponents (α_abs). The interpretation of α_abs is ambiguous since it is well known that it not only depends on the dominant absorber but also on the size and internal structure of the particles, core size, and shell thickness. In this work the uncertainties of the Aethalometer-model-derived apparent fractions of absorption by eBC from fossil fuel and biomass burning are evaluated with a core–shell Mie model. Biomass-burning fractions (BB(%)) were calculated for pure and coated single BC particles for lognormal unimodal and bimodal size distributions of BC cores coated with ammonium sulfate, a scattering-only material. BB(%) was very seldom 0 % even though BC was the only absorbing material in the simulations. The shape of size distribution plays an important role. Narrow size distributions result in higher α_abs and BB(%) values than wide size distributions. The sensitivity of α_abs and BB(%) to variations in shell volume fractions is the highest for accumulation-mode particles. This is important because that is where the largest aerosol mass is. For the interpretation of absorption Ångström exponents it would be very good to measure BC size distributions and shell thicknesses together with the wavelength dependency of absorption.

1 Introduction

Incomplete combustion of organic fuels results in emission of light-absorbing carbon (LAC) particles that contain both black carbon (BC) and brown carbon (BrC). BrC is light-absorbing organic matter in atmospheric aerosols of various origins, e.g., soil humics, humic-like substances (HULIS), tarry materials from combustion, and bioaerosols (Andreae and Gelenscer, 2006; Laskin et al., 2015). BrC can significantly absorb solar radiation in the ultraviolet–visible (UV–Vis) wavelength range (λ≈ 300–800 nm). The radiative effects of BC and BrC vary in time during atmospheric aging. For many combustion sources the absorbance in fresh emission is almost completely caused by BC particles, but during atmospheric transport they often get coated with some light-scattering compounds, for instance ammonium sulfate or light-absorbing organic carbon, BrC. For some sources (e.g., biomass burning) BrC may contribute substantially to light absorption already in the directly emitted aerosols and either increase or decrease during aging. Thus, BrC is highly time-dependent as its composition and absorption properties change during atmospheric oxidation processes (Laskin et al., 2015).

The absorption coefficient σ_ap is approximately proportional to the power function ${\mathit{\lambda }}^{-{\mathit{\alpha }}_{\mathrm{abs}}}$, where λ is the wavelength and α_abs is the absorption Ångström exponent. α_abs is generally used to distinguish aerosol types: for pure BC particles α_abs≈ 1, while for other light-absorbing aerosols (BrC, soil dust) it is clearly > 1 (e.g., Kirchstetter et al., 2004; Bond and Bergstrom, 2006; Bergstrom et al., 2007; Moosmüller et al., 2011; Kirchstetter and Thatcher, 2012; Lack et al., 2012; Bond et al., 2013; Saleh et al., 2013; Laskin et al., 2015; Valenzuela et al., 2015; Devi et al., 2016). The method has been used not only for in situ absorption measurements but also for interpreting absorption coefficients retrieved from remote sensing measurements, such as the Aerosol Robotic Network (AERONET; e.g., Russell et al., 2010; Arola et al., 2011; Chung et al., 2012; Cazorla et al., 2013; Feng et al., 2013; Schuster et al., 2016; Wang et al., 2016).

One of the instruments used for measuring black carbon concentrations is the Aethalometer that collects aerosol on a filter tape, measures changes in light attenuation in the wavelength range of 370–950 nm, and calculates the equivalent black carbon (eBC) concentrations. The data are used also to calculate α_abs and to estimate the contributions of fossil fuel emissions and biomass burning to eBC. The Aethalometer model (Sandradewi et al., 2008a) is probably the most widely used method for this, and it is even calculated automatically in the new Aethalometer model AE33. It is there assumed that the absorption Ångström exponents are α_ff = 1 and α_bb = 2 for eBC from fossil fuel and biomass burning, respectively. These are the default settings in the AE33, but also different α_ff and α_bb values have been used (Sandradewi et al., 2008b; Herich et al., 2011; Fuller et al., 2014; Harrison et al., 2013; Healy et al., 2017; Zotter et al., 2017; Helin et al., 2018)

The interpretation of α_abs is ambiguous since it not only depends on the dominant absorber but also on the size and internal structure of the particles, core size, and shell thickness. For instance, for pure BC particles, α_abs may be < 1 and BC particles coated with non-absorbing material may have α_abs in the range from < 1 to ∼ 1.7 (e.g., Gyawali et al., 2009; Lack and Cappa, 2010; Lack and Langridge, 2013; Schuster et al., 2016; Liu et al., 2018; Chylek et al., 2019; Zhang et al., 2020). The present paper may be considered an extension to the abovementioned analyses since they did not explicitly analyze the effects on the Aethalometer model.

The aim of this study is to estimate uncertainties of the Aethalometer-model-derived fractions of absorption by eBC from fossil fuel and biomass burning when spherical BC cores are coated by some non-absorbing material. To state this more clearly, it is assumed that there is only one type of BC particles that can be called fossil fuel BC in the Aethalometer model terminology. Consequently, any deviations from biomass-burning fraction of BB % = 0 indicate uncertainty in the source appointment. Biomass-burning fractions were calculated for pure and coated single particles for lognormal unimodal and bimodal size distributions. The work is based on modeling only; no measurement data are used.

2 Methods

The BC cores were assumed to be coated with an ammonium sulfate shell by using two approaches. It was assumed (1) that the shell thickness is the same for all particles in a size distribution (Fig. 1a) and (2) that the core volume fraction is the same for all particles in a size distribution (Fig. 1b). The core volume fraction was calculated from

$$\begin{array}{}\text{(1)}& f_{\mathrm{c}}={\displaystyle \frac{V_{\mathrm{core}}}{V_{\mathrm{p}}}}={\left({\displaystyle \frac{D_{\mathrm{core}}}{D_{\mathrm{p}}}}\right)}^{\mathrm{3}}={\left({\displaystyle \frac{D_{\mathrm{core}}}{D_{\mathrm{core}}+\mathrm{2}s}}\right)}^{\mathrm{3}},\end{array}$$

where V_p is the particle volume, V_core is the BC core volume, D_p is the particle diameter (= D_core+2s), D_core is the BC core diameter, and s is the shell thickness. The shell volume fraction was then calculated from $f_{\mathrm{s}}=\mathrm{1}-f_{\mathrm{c}}$. The ratio of the coated particle diameter to the core diameter is an often used metric for presenting the coating of particles. R, f_c, and f_s can be calculated from each other as

$$\begin{array}{}\text{(2)}& R={\displaystyle \frac{D_{\mathrm{p}}}{D_{\mathrm{core}}}}={\left({\displaystyle \frac{\mathrm{1}}{f_{\mathrm{c}}}}\right)}^{\mathrm{1}/\mathrm{3}}={\left({\displaystyle \frac{\mathrm{1}}{\mathrm{1}-f_{\mathrm{s}}}}\right)}^{\mathrm{1}/\mathrm{3}}.\end{array}$$

The number-weighted D_p-to-D_core ratio is calculated from

$$\begin{array}{}\text{(3)}& R_{N\left(D_{\mathrm{p}}\right)}={\displaystyle \frac{\sum N_i{R}_i}{N_{\mathrm{tot}}}}={\displaystyle \frac{\sum N_i\left(D_{\mathrm{p},i}/D_{\mathrm{core},\mathrm{i}}\right)}{N_{\mathrm{tot}}}},\end{array}$$

where N_i and R_i are the number concentration and D_p-to-D_core ratio of the particle diameter D_p,i, respectively. If f_s is independent of particle size – which is the assumption used in some of the simulations below – Eq. (3) simplifies to $R_{N\left(D_{\mathrm{p}}\right)}$ = R.

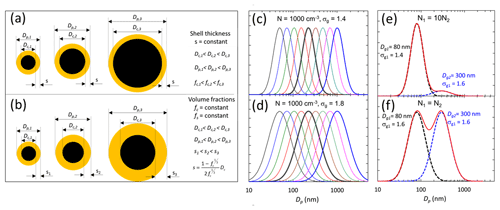
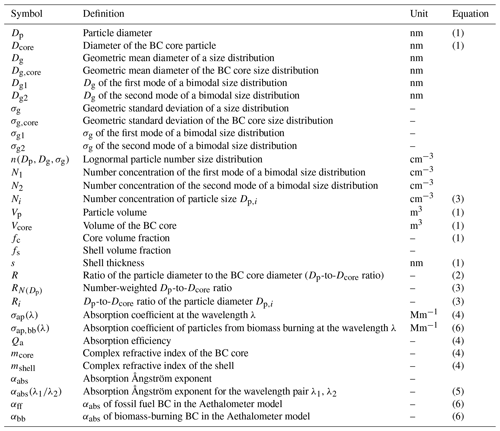
Figure 1 Examples of particles and size distributions used in the simulations: (a) particles with a BC core coated with a constant shell thickness s, (b) particles with constant BC core and shell volume fractions f_c and f_s, (c) unimodal narrow size distributions with the geometric standard deviation of σ_g = 1.4, (d) unimodal wide size distributions with σ_g = 1.8, (e) bimodal size distributions with a dominating Aitken mode, and (f) bimodal size distributions with equal-sized Aitken and accumulation modes.

Lognormal size distributions $n(D_{\mathrm{p}},D_{\mathrm{g}},{\mathit{\sigma }}_{\mathrm{g}})$ were generated, where D_p is the particle diameter, D_g is the geometric mean diameter, and σ_g is the geometric standard deviation. The D_p range was 3 nm–10 µm. For the unimodal size distributions the D_g range was 50 nm–1 µm, and σ_g was given three values: 1.4, 1.6, and 1.8 (Fig. 1c and d). Bimodal size distributions were also generated. For the small-particle mode the geometric mean diameter D_g1 range was 50–100 nm, and the large-particle mode D_g2 range was 100–500 nm. In addition to varying the geometric mean diameters, the ratios of the number of particles in the two modes were also varied. Two cases were used for this: (1) N₁=10N₂, σ_g1=1.4, σ_g2=1.6 (Fig. 1e) and (2) N₁=N₂, σ_g1=1.6, σ_g2=1.6 (Fig. 1f).

Absorption coefficients were calculated from

$$\begin{array}{}\text{(4)}& {\mathit{\sigma }}_{\mathrm{ap}}\left(\mathit{\lambda }\right)=\int Q_{\mathrm{a}}\left(\mathit{\lambda },D_{\mathrm{p}},m_{\mathrm{core}},m_{\mathrm{shell}},s\right){\displaystyle \frac{\mathit{\pi }}{\mathrm{4}}}{D}_{\mathrm{p}}^{\mathrm{2}}n\left(D_{\mathrm{p}}\right)\mathrm{d}{D}_{\mathrm{p}},\end{array}$$

where Q_a is the absorption efficiency that is a function of the wavelength λ, D_p, the complex refractive indices of the core and shell, m_core and m_shell , respectively, and the shell thickness s. Q_a was calculated using the N-Mie Fortran code written and described in detail by Voshchinnikov and Mathis (1999). The code is based on the recursive algorithm of Wu and Wang (1991). The code calculates the extinction, scattering, and absorption efficiency factors for n-layered spheres. The complex refractive indices were $m_{\mathrm{core}}=\mathrm{1.85}+\mathrm{0.71}i$ (BC as in Lack and Cappa, 2010) and $m_{\mathrm{shell}}=\mathrm{1.52}+\mathrm{0}i$ (ammonium sulfate) for the core and shell, respectively. Absorption coefficients were calculated for the Aethalometer wavelengths λ = 470 and 950 nm, and α_abs was calculated from

$$\begin{array}{}\text{(5)}& {\mathit{\alpha }}_{\mathrm{abs}}(\mathrm{470}/\mathrm{950})=-{\displaystyle \frac{\ln \left({\mathit{\sigma }}_{\mathrm{ap}}(\mathit{\lambda }=\mathrm{470}\mathrm{nm})/{\mathit{\sigma }}_{\mathrm{ap}}(\mathit{\lambda }=\mathrm{950}\mathrm{nm})\right)}{\ln \left(\mathrm{470}/\mathrm{950}\right)}}.\end{array}$$

The wavelengths 470 and 950 nm were used as they are used also in the AE33 automatic source apportionment. In analyses of aerosol optical depth data from AERONET, α_abs is often calculated for the wavelength pair 440 and 870 nm (Russell et al., 2010; Schuster et al., 2016). To evaluate the applicability of the simulations of the present work to AERONET data analyses, σ_ap was calculated also for these wavelengths, and the respective α_abs was calculated from them. There are size-dependent differences between ${\mathit{\alpha }}_{\mathrm{abs}}(\mathrm{470}/\mathrm{950})$ and ${\mathit{\alpha }}_{\mathrm{abs}}(\mathrm{440}/\mathrm{870})$, but they are not big (see Figs. S1 and S2 in the Supplement), so it may safely be concluded that the results to be presented below are valid also for the AERONET data.

Table 1 Nomenclature.

For the absorption due to particles from wood burning or biomass burning, Zotter et al. (2017) give the equation

$$\begin{array}{}\text{(6)}& {\mathit{\sigma }}_{\mathrm{ap},\mathrm{bb}}\left({\mathit{\lambda }}_{\mathrm{2}}\right)={\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{ap}}\left({\mathit{\lambda }}_{\mathrm{1}}\right)-{\mathit{\sigma }}_{\mathrm{ap}}\left({\mathit{\lambda }}_{\mathrm{2}}\right){\left(\frac{{\mathit{\lambda }}_{\mathrm{1}}}{{\mathit{\lambda }}_{\mathrm{2}}}\right)}^{-{\mathit{\alpha }}_{\mathrm{ff}}}}{{\left(\frac{{\mathit{\lambda }}_{\mathrm{1}}}{{\mathit{\lambda }}_{\mathrm{2}}}\right)}^{-{\mathit{\alpha }}_{\mathrm{bb}}}-{\left(\frac{{\mathit{\lambda }}_{\mathrm{1}}}{{\mathit{\lambda }}_{\mathrm{2}}}\right)}^{-{\mathit{\alpha }}_{\mathrm{ff}}}}},\end{array}$$

where α_ff and α_bb are the α_abs of fossil fuel and biomass-burning BC in the Aethalometer model. Noting that ${\mathit{\sigma }}_{\mathrm{ap}}\left({\mathit{\lambda }}_{\mathrm{1}}\right)={\mathit{\sigma }}_{\mathrm{ap}}\left({\mathit{\lambda }}_{\mathrm{2}}\right){\left({\mathit{\lambda }}_{\mathrm{1}}/{\mathit{\lambda }}_{\mathrm{2}}\right)}^{-{\mathit{\alpha }}_{\mathrm{abs}}}$, the fraction of absorption due to biomass burning is

$$\begin{array}{}\text{(7)}& \begin{array}{rl}\mathrm{BB}\left(\mathit{\%}\right)& =\mathrm{100}\mathit{\%}{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{ap},\mathrm{bb}}\left({\mathit{\lambda }}_{\mathrm{2}}\right)}{{\mathit{\sigma }}_{\mathrm{ap}}\left({\mathit{\lambda }}_{\mathrm{2}}\right)}}\\ & =\mathrm{100}\mathit{\%}{\displaystyle \frac{{\left(\frac{{\mathit{\lambda }}_{\mathrm{1}}}{{\mathit{\lambda }}_{\mathrm{2}}}\right)}^{-{\mathit{\alpha }}_{\mathrm{abs}}}-{\left(\frac{{\mathit{\lambda }}_{\mathrm{1}}}{{\mathit{\lambda }}_{\mathrm{2}}}\right)}^{-{\mathit{\alpha }}_{\mathrm{ff}}}}{{\left(\frac{{\mathit{\lambda }}_{\mathrm{1}}}{{\mathit{\lambda }}_{\mathrm{2}}}\right)}^{-{\mathit{\alpha }}_{\mathrm{bb}}}-{\left(\frac{{\mathit{\lambda }}_{\mathrm{1}}}{{\mathit{\lambda }}_{\mathrm{2}}}\right)}^{-{\mathit{\alpha }}_{\mathrm{ff}}}}}\end{array},\end{array}$$

so that BB% depends on the Ångström exponents α_abs, α_ff, and α_bb. Two settings for the constants were used: the one presented in the AE33 manual, α_ff = 1 and α_bb = 2; and the one presented by Zotter et al. (2017), α_ff = 0.9 and α_bb = 1.68. The symbols and their definitions are presented in Table 1.

3 Results and discussion

3.1 Single particles

The absorption Ångström exponent α_abs and the fraction of biomass-burning BC for single coated particles are shown in Fig. 2. The dashed lines in Fig. 2a, c, and e show the core diameter D_core of particles that have the same diameter D_p at all shell thicknesses. In Fig. 2b, d, and f the dashed lines show the particle diameter D_p and f_s of particles that have the same D_core at all shell volume fractions f_s in the range f_s ≤ 99 %. The dependence of α_abs on core and shell is presented twice. This is apparently superfluous, but they are visualizations that complement each other.

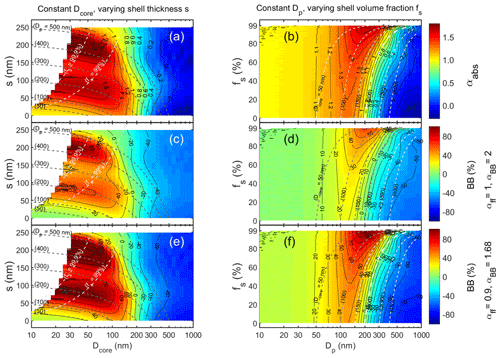
Figure 2 Absorption Ångström exponent (α_abs) and the fraction of biomass-burning BC calculated from it for single coated particles (a, c, e) as a function of BC core diameter (D_core) and shell thickness (s) and (b, d, f) as a function of particle diameter (D_p = D_core+2s) and shell volume fraction f_s in the range f_s ≤ 99 %. In panels (a), (c), and (e), the dark dashed lines show the D_core and s of particles that have the same D_p – written in parentheses – at all shell thicknesses, and the light dashed lines show the shell thicknesses that correspond to f_s = 99 % and 99.9 %. In panels (b), (d), and (f), the dashed lines show the D_p and f_s of particles that have the same D_core – written in parentheses – at all shell volume fractions. The color bars are common for panels (a) and (b), (c) and (d), and (e) and (f).

The first approach (Fig. 2a, c, and e) shows that when D_core < ∼ 150 nm and s > ∼ 25–50 nm the absorption Ångström exponent α_abs > 1.4. The respective BB fractions are larger than about 40 % or 60 % for the Aethalometer model parameters of α_ff = 1, α_bb = 2 (pair 1) and α_ff = 0.9, α_bb = 1.68 (pair 2), respectively. Figure 2a also shows that for D_core < ∼ 100 nm there are two maxima of the α_abs when the shell grows thicker. In the second maximum, α_abs > ∼ 1.6. As a result the BB fractions would be > 60 % and even > 100 % for the two Aethalometer model parameter pairs. When D_core is in the range of ∼ 170–200 nm, α_abs ≈ 1 and α_abs decreases with a growing s. For larger core diameters the absorption Ångström exponent is even smaller. When D_core > 200 nm, α_abs < 1 and even negative for D_core > ∼ 360 nm. Further, when D_core > 200 nm, α_abs does not grow essentially at all as a function of s.

The visualization of α_abs as a function of shell volume fraction f_s and particle full diameter D_p (Fig. 2b) shows some other features. When D_p < 50 nm, α_abs varies in the range of 1.0–1.1, and it does not depend on f_s, but in the D_p range of about 100–300 nm α_abs depends strongly on f_s. When D_p ≈ 500 nm, α_abs < 1 for almost all shell volume fractions, up to f_s ∼ 99 %. For larger particles α_abs is close to 0 at all shell volume fractions.

The visualization also shows that the α_abs value of 1, usually considered an indication of BC, is not a result of an unambiguous D_core−s (Fig. 2a) or D_p−f_s (Fig. 2b) combination.

3.2 Unimodal BC core size distributions, same coating thickness for all sizes

For single particles α_abs depends clearly on both the core size and the shell thickness. However, in real atmospheric studies the wavelength dependency of absorption by particle size distributions is measured. Here these were first modeled by assuming that pure BC particle size distributions get coated with ammonium sulfate layers so that the shell thickness is independent of particle size as visualized in Fig. 1a. For example, the shell thickness on a 50 nm BC particle would be the same as on a 200 nm particle, which means the shell volume fractions are not the same. The BC core geometric mean diameter (D_g,core) was varied from 50 to 200 nm at 10 nm intervals. The geometric standard deviations of the size distributions were σ_g = 1.4, σ_g = 1.6, and σ_g = 1.8, representing narrow, average, and wide size distributions. The shell thickness s varied from 0 to 250 nm at 1 nm intervals. Absorption coefficient and subsequently α_abs was calculated for the full size distribution 3–2500 nm.

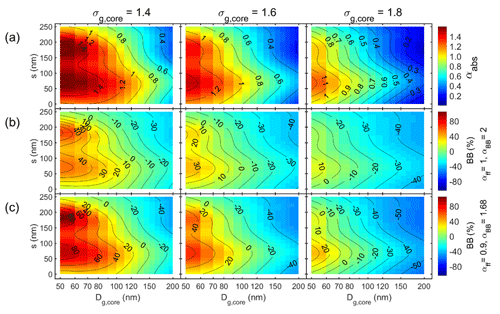
Figure 3 Unimodal particle size distributions with a size-independent shell thickness (s) for three widths of the core size distributions: σ_g,core = 1.4, 1.6, and 1.8. (a) Absorption Ångström exponent (α_abs) and the fraction of biomass-burning BC (BB(%)) calculated from it with the Aethalometer model constants of (b) α_ff = 1 and α_bb = 2 and (c) α_ff = 0.9 and α_bb = 1.68 vs. the geometric mean diameter of the core (D_g,core).

The results are first shown as a function of D_g,core and shell thickness s for the three size distribution widths (Fig. 3). There are both similarities and differences compared with the corresponding relationships of single particles (Fig. 2). For example, for single particles α_abs ≈ 1 at D_core ≈ 180 nm for shell thicknesses s ≈ 0–70 nm as shown by the almost vertical α_abs = 1 isoline in Fig. 2a, whereas for the size distributions with σ_g,core > 1 the respective isoline is a strong function of both s and σ_g,core (Fig. 3a). At all widths of the size distribution, α_abs increases with increasing shell thickness and then starts decreasing. For small core sizes (D_g,core < ∼ 80 nm) α_abs also has a second maximum when the size distribution is narrow. The width of the size distribution has a clear effect on the α_abs: for all core sizes and shell thicknesses α_abs decreases with increasing σ_g,core.

Both for single particles and size distributions the first maximum of α_abs is the smaller the larger the D_g,core and σ_g,core are (Fig. 4a). The first maximum is reached at shell thickness s ≈ 70 ± 5 nm for all size distribution widths although for single particles the variability of the shell thickness corresponding to the first maximum is larger (Fig. 4b). The first maximum α_abs results in apparent BB fractions of up to ∼ 100 % for single particles and in the range from 0 % to ∼ 80 % for the size distributions, and again the BB(%) is smaller the larger the D_g,core and σ_g are (Fig. 4c and d).

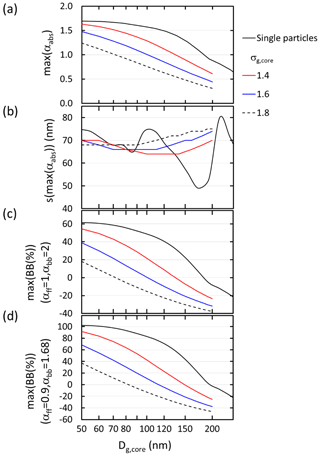
Figure 4 Size distribution dependence of the first maximum of α_abs when a size-independent shell grows on a BC core: (a) the first maximum value of α_abs, (b) the shell thickness at the maximum α_abs, (c) maximum biomass-burning fraction with the Aethalometer model constants α_ff = 1 and α_bb= 2, and (d) maximum biomass-burning fraction with the Aethalometer model constants α_ff = 0.9 and α_bb = 1.68 as a function of the BC core geometric mean diameter (D_g,core) and geometric standard deviation (σ_g,core).

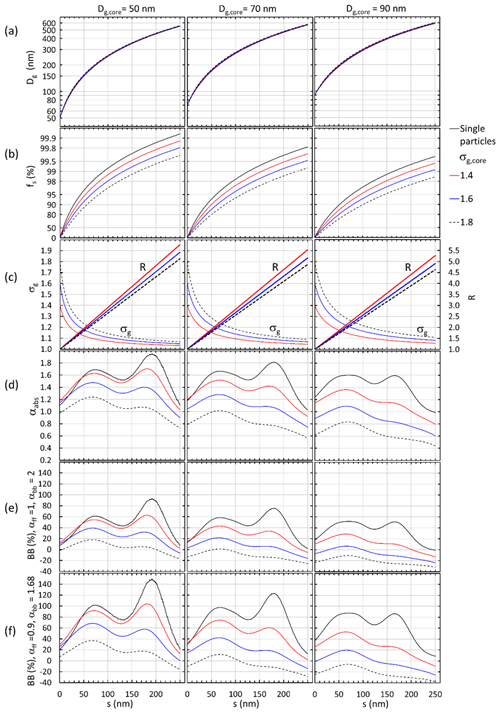
Figure 5 Examples of the growth of a non-size-dependent scattering shell on BC core size distributions with $D_{\mathrm{g},\mathrm{core}}=\mathrm{50}$, 70, and 90 nm and on single BC particles. (a) Geometric mean diameter, (b) shell volume fraction, (c) geometric standard deviation and D_p-to-D_core ratio (R), (d) absorption Ångström exponent, (e) BB(%) with the Aethalometer model constants α_ff = 1 and α_bb = 2, and (d) biomass-burning fraction with the Aethalometer model constants α_ff = 0.9 and α_bb = 1.68 as a function shell thickness s.

This approach is further followed by plotting the parameters as a function of shell thickness for three different BC core diameters, 50, 70, and 90 nm of single particles and core size distributions with the geometric standard deviations of σ_g,core = 1.4, 1.6, and 1.8 (Fig. 5). This analysis can be considered a description of what may happen to the size distribution, α_abs, and the apparent BB(%) during condensational growth on fresh small BC cores if the growing shell thickness were independent of the core diameter, even if this is unrealistic. The shell volume fraction f_s increases to > 99.9 % when the shell thickness grows from s = 0 to 250 nm on single 50 nm particles but to lower fractions for the wider size distributions and larger core sizes so that for D_g,core = 90 m and σ_g = 1.8, f_s ≈ 98 % even with s = 250 nm (Fig. 5a). The geometric mean diameter D_g of the whole size distribution grows to ∼ 600 nm when the shell thickness grows to 250 nm, with minimal differences between the original widths (Fig. 5b). The width of the size distribution, i.e., σ_g, decreases fast to < 1.2 (Fig. 4c). Such values correspond to very narrow size distributions, which are not really observed in the real atmosphere.

The number-weighted D_p-to-D_core ratio $R_{N\left(D_{\mathrm{p}}\right)}$, Eq. (3), was calculated for the size range 90–600 nm to present the numbers comparable with papers that present shell-to-core ratios of refractory BC (rBC) obtained from SP2 measurements. For instance, Kondo et al. (2011) measured urban air of Tokyo and obtained the median R = 1.1 with a range up to about 1.3, the mean D_g = 64 ± 6 nm, and σ_g = 1.66 ± 0.12. Moteki et al. (2007) conducted SP2 measurements in an aircraft in urban plumes on the Japanese coast. They fitted the data with lognormal size distributions with mass median diameters (MMDs) of 190 and 210 nm and σ_g of 1.55 and 1.45 for fresh and aged rBC, respectively. The fresh rBC was thinly coated with R < 2 and the aged rBC thickly coated with R ∼ 2. The MMD and σ_g values yield D_g = 107 and 139 nm. Shiraiwa et al. (2008) measured the mixing state and size distribution of BC aerosol with an SP2 at a remote island (Fukue) in Japan. They observed that the BC number median diameters were in the range of 120–140 nm in every air mass type, and the median shell $/$ core diameter ratio (R) in different air masses varied in the range of 1.2–1.6. However, they also observed that the fraction of R values in the range 2–3.5 was not negligible either (Fig. 9 of Shiraiwa et al., 2008). Such values correspond to the range where α_abs first grows to > 1.6 for the narrow (σ_g,core = 1.4) BC core size distribution that has the smallest geometric mean size (D_g,core = 50 nm) but to lower values for the wider size distributions that have larger D_g,core (Fig. 5c and d). The first maximum is reached at shell thicknesses of s ≈ 70 nm that correspond to R ≈ 2 and shell volume fractions of f_s ≈ 90 ± 8 % (Fig. 5b). Schwarz et al. (2008) reported statistics of rBC mass size distributions in urban aerosol: f_s = 9 ± 6 %, s = 20 ± 10 nm, MMD = 170 nm, and σ_g of 1.71, which yields D_g = 72 nm; in biomass-burning emissions: $f_{\mathrm{s}}=\mathrm{70}\pm \mathrm{9}$ %, s = 65 ± 12 nm, MMD = 210 nm, and σ_g = 1.43, which yields D_g = 143 nm; and in background continental aerosol: f_s = 46 ± 3 %, s = 48 ± 14 nm, MMD = 210 nm, and σ_g=1.55, which yields D_g = 118 nm.

The referenced studies show that the s, R, and f_s values are in the range observed in ambient measurements studies. What is not realistic in atmospheric aerosol is the width of the size distribution, which soon decreases to σ_g < 1.2 (Fig. 5c).

After reaching the first maximum, α_abs decreases, and for single particles and the narrowest core size distributions it starts growing again and reaches a second maximum at shell thicknesses of s ≈ 170 nm, which corresponds to R > 4 and f_s > 98 %. Such s and R values are not in the range observed in the abovementioned studies, nor are the low geometric standard deviations of σ_g < 1.1 realistic, so the second maximum can be considered as a theoretical value only. For size distributions with D_g,core > 70 nm there is no second maximum of α_abs.

As α_abs increases and decreases, it is clear that this applies to BB(%) as well (Fig. 5d–e). For the smallest core sizes (D_g,core = 50 nm) and the narrowest size distributions (σ_g,core = 1.4), the first maximum BB(%) may be as high as ∼ 90 % when the values of α_ff = 0.9 and α_bb = 1.68 are used in Eq. (7) but lower, ∼ 50 %, when the values of α_ff = 1 and α_bb = 2 are used. For the wider core size distributions the BB(%) fractions are lower. For the widest core size distributions (σ_g,core = 1.8) clearly positive BB(%) values are reached only for the smallest core sizes.

Figure 5 can also be considered a proxy for a time series of the development of α_abs and derived BB(%) after emission of BC particles and their growth by condensation of non-absorbing compounds. A similar development – α_abs values increase to > 1.3 and decrease to < 0.9 during a several-day-long pollution episode during which the D_g of the whole size distribution grew possibly by condensation – was observed at the Station for Observing Regional Processes of the Earth System (SORPES) in Nanjing, China (Fig. 9 of Shen et al., 2018). There was no SP2 available for the core–shell structure measurements in that study, so it cannot really be proven that the observed α_abs development was due to condensational growth even though it seems a good explanation and is qualitatively in line with Fig. 5.

3.3 Unimodal size distributions with the same BC core fraction for all sizes

The second approach is to assume that the BC core fraction – or equivalently the shell volume fraction – is the same for all sizes, which means that the shell thickness increases with size as was visualized in Fig. 1b. This can be considered to be a result of aging of BC by not only condensational growth but also by cloud processing. The latter would lead to thick shells on particles activated into cloud droplets that would absorb for instance SO₂ and NH₃ and that would not rain but later get back into the aerosol phase by evaporation of cloud water. The constant volume fraction is not realistic but neither is the constant shell thickness. Both can be considered to be approximations.

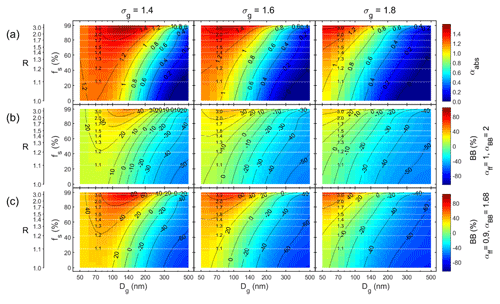
Figure 6 Unimodal particle size distributions with size-independent shell volume fractions f_s and three widths of the size distributions: σ_g = 1.4, 1.6, and 1.8. (a) Absorption Ångström exponent (α_abs) and the fraction of biomass-burning BC (BB(%)) calculated from it with the Aethalometer model constants of (b) α_ff = 1 and α_bb = 2 and (c) α_ff = 0.9 and α_bb = 1.68 vs. the geometric mean diameter of the whole size distribution (D_g). The white horizontal grid lines show constant D_p-to-D_core ratios (=R).

In this approach the geometric standard deviations of the whole size distributions were set to σ_g = 1.4, 1.6, and 1.8, and the shell volume fractions f_s were set to vary from 0 % to 99 %. The resulting α_abs and BB(%) are presented as a function of D_g, f_s, and σ_g (Fig. 6). They are comparable with the analogous plots for single particles, i.e., σ_g = 1.0 (Fig. 2b, d, and f). Note that from Eq. (2) it follows that the assumption of a constant f_s means that also the D_p-to-D_core ratio R is constant and that the f_s range of 0 % to 99 % corresponds to the R range of 1 to 4.6. Figure 6 therefore has two y axes: one showing the f_s and the other the corresponding R values.

Several observations can be made from Fig. 6. One of them is that the isoline of α_abs = 1 grows with growing D_g for each of the size distribution widths (σ_g) but decreases with growing σ_g. Another is that the wider the size distribution is, the lower the α_abs and BB(%) are at any given shell volume fraction. The third one is that for all three widths α_abs and BB(%) grows when f_s grows but that the growth is not uniformly distributed over the f_s vs. D_g space.

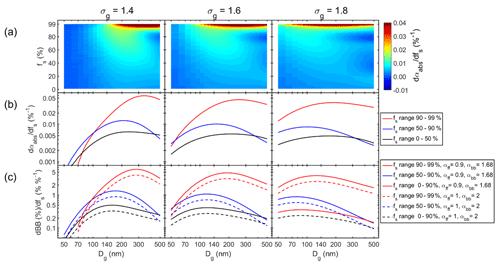
Figure 7 Size-dependent sensitivity of α_abs and BB(%) to variations of the shell volume fraction f_s. (a) α_abs sensitivity in the whole f_s range of 1 %–99 %, (b) average α_abs sensitivity in three f_s ranges, and (c) average BB(%) sensitivities in three f_s ranges.

The last observation leads to calculations of size-dependent sensitivities of α_abs to variations in f_s. The sensitivity was calculated as $\mathrm{d}{\mathit{\alpha }}_{\mathrm{abs}}/\mathrm{d}{f}_{\mathrm{s}}$, and its unit is %⁻¹. Figure 7a shows the sensitivities in the whole f_s range of 1 %–99 % as a function of D_g for the three size distribution widths. The sensitivity depends clearly on both D_g and σ_g of the size distribution, and it also varies with f_s. It is very clear that α_abs is most sensitive to f_s variations when D_g of the size distribution is in the accumulation-mode sizes of 100–200 nm. The sensitivity grows fairly steadily with growing f_s until it increases very strongly for f_s > 90 % – which equals R > 2.

Another step for visualizing the sensitivities was taken by calculating size-dependent average sensitivities of α_abs and BB(%) in three f_s ranges: f_s = 0 %–50 %, 50 %–90 %, and 90 %–99 % (Fig. 7b and c).

According to Eq. (2) the f_s ranges correspond to the R ranges of 1–1.3, 1.3–2.2, and 2.2–4.6. The lines in Fig. 7b and c can be used for a rough estimate on a possible effect on α_abs and BB(%). For instance, if D_g≈ 140 nm, σ_g = 1.4, and f_s ≈ 50 %–90 % , an increase in f_s from 50 % to 51 % leads to an α_abs increase of ∼ 0.01 and consequently to a BB(%) increase of ∼ 1 % when Aethalometer model constants of α_ff = 0.9 and α_bb = 1.68 are used.

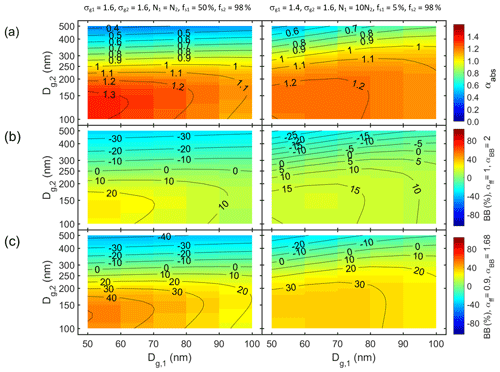
Figure 8 Bimodal particle size distributions with size-independent shell volume fractions f_s in two modes as a function of geometric mean diameters of mode 1 (D_g1) and mode 2 (D_g2). (a) Absorption Ångström exponent (α_abs) and the fraction of biomass-burning BC (BB(%)) calculated from it with the Aethalometer model constants of (b) α_ff = 1 and α_bb = 2 and (c) α_ff = 0.9 and α_bb = 1.68. The widths, the relative number of particles in the two modes, and the shell volume fractions of the two modes: σ_g1 = 1.6, σ_g2 = 1.6, N₁ = N₂, f_s1 = 50 %, and f_s2 = 98 % on the left column and σ_g1 = 1.4, σ_g2 = 1.6, N₁ = 10N₂, f_s1 = 5 %, and f_s2 = 98 % on the right column.

3.4 Bimodal size distributions with the same BC core fraction for all sizes in the mode

Finally, bimodal size distributions are examined briefly. The size distributions consist of two externally mixed modes that have different shell volume fractions. In both modes the shell volume fractions are size-independent as in Fig. 1b. Mode 1 is an Aitken mode with the geometric mean diameter D_g1 in the range 50–100 nm. There are two different settings for the Aitken mode: in the first case its number concentration is 10 times larger than that of the accumulation mode, i.e., N₁ = 10N₂; it consists of almost pure fresh BC particles with f_s1 = 5 % (R ≈ 1.02); and it is narrow, σ_g1 = 1.4. In the second setting the number concentrations of the Aitken and accumulation mode are equal (N₁ = N₂); the Aitken mode is aged so that f_s1 = 50 % (R ≈ 1.3); and it is wider, σ_g1 = 1.6. Mode 2 is an accumulation mode with the geometric mean diameter D_g2 in the range 100–500 nm, σ_g2 = 1.6, and it is very aged, with f_s2 = 98 % (R ≈ 3.7). The accumulation mode could be the result of cloud processing as explained above.

The results show that α_abs is more sensitive to variations of the accumulation mode than of the Aitken mode (Fig. 8a). For instance, if D_g2 < 250 nm, α_abs > 1 at all D_g,1 values. Also, if D_g,1 = 60 nm and D_g2 varies in the whole range of 100–500 nm, α_abs varies in the range of ∼ 0.4–1.3. When the Aitken mode dominates the number concentration (N₁ = 10N₂) with the fresh BC particles, the maximum α_abs ≈ 1.2 at D_g1≈ 60 nm and D_g2≈ 140 nm is smaller than when the two modes have an equal amount of particles. In the latter case the maximum α_abs > 1.3. When the Aitken mode with f_s = 5 % dominates the number concentration, the whole size distribution moves to the region that is less sensitive to f_s variations as discussed above in Sect. 3.3. It is worth noting also that the maximum α_abs and BB(%) values (Fig. 8b and c) are smaller than derived from the unimodal size distributions (Sect. 3.3).

4 Summary and conclusions

The purpose of this study is not to claim that all Aethalometer model results are wrong but that they have higher uncertainties than have been discussed in the literature. It is clear that there are BrC particles that have absorption Ångström exponents clearly larger than 1, as shown in a very large number of publications. However, the size of light-absorbing particles and their coating even by purely scattering material clearly affect the wavelength dependence of absorption and thus have the potential to affect the Aethalometer model results. Since the wavelength dependency is used for source apportionment, these effects have the potential to result in contributions of wood-burning or fossil fuel emissions that are tens of percent too high or low.

There are some important results. In the modeling, α_abs equals 1 or 0.9 in very rare cases, and thus BB(%) was very seldom 0 % even though one type of BC was the only absorbing material in the simulations. The shape of size distribution plays an important role. Narrow size distributions result in higher α_abs and BB(%) values than wide size distributions. The sensitivity of α_abs and BB(%) to variations in shell volume fractions is the highest for accumulation-mode particles. This is important because that is where the largest aerosol mass is.

The goal of the paper was not to find out whether some pair of α_ff and α_bb is better than the other. Two well-known α_ff and α_bb pairs were used and shown how large the uncertainties may become just for these two pairs even if BC particles were coated by purely scattering material. The goal was not at all to find a good pair. On the contrary, the study shows that no constant values are good since in the real atmosphere BC particle size distributions are not constant, neither their mean diameter nor the coating of the particles. They all vary dynamically in the atmosphere. The study shows that any constant values will undoubtedly lead to large uncertainties of both the BB and FF fractions if no information on the size of the core or the thickness of the shell is available, even if purely scattering material is coating BC cores. As a conclusion, for the interpretation of absorption Ångström exponents it would be very important to measure BC size distributions and shell thicknesses together with the wavelength dependency of absorption.

There are obvious limitations in this study. A core–shell Mie model was used only so the work is limited to spherical particles. Fresh BC particles are usually agglomerates. There are studies that show that during aging processes these agglomerate may collapse and become closer to spherical particles, so Mie modeling probably agrees better for aged than fresh BC particles. Further, even if particles were spherical, how well can they be modeled with a Mie code when they are collected on filters? Or does light absorption then follow the spectral absorbance of the bulk materials?

This question could in principle be answered by generating spherical BC particles, coating them in an aging chamber with some non-absorbing material – for instance ammonium sulfate, and measuring both light absorption at multiple wavelengths with an Aethalometer and BC core size distributions and shell thicknesses with an SP2. If α_abs increases up to some maximum value as a function of shell thickness and then starts decreasing like in the simulations above, then the process agrees with the growth of a size-independent coating. Or if α_abs increases steadily then it suggests that the growth is size-dependent and possibly with a size-independent shell volume fraction growth rate. If these effects are observed then the uncertainties discussed in this work should be taken seriously.

On the other hand, if none of these effects were observed and the absorption Ångström exponents of the collected particles were ≈ 1 regardless of core size and shell thickness, it would be safe to say that the Aethalometer measures the absorption spectra of the bulk materials and that the Aethalometer model yields correct results. The truth is probably somewhere between these extremes: when the filter tape is still relatively clean the particles can be modeled even with a Mie code, and for heavily loaded filters α_abs is that of bulk material. This could and should also be tested experimentally.