the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Improved method of estimating temperatures at meteor peak heights
Alexander Kozlovsky
Thomas Ulich
Ilkka Virtanen
Mark Lester
Bernd Kaifler
For 2 decades, meteor radars have been routinely used to monitor atmospheric temperature around 90 km altitude. A common method, based on a temperature gradient model, is to use the height dependence of meteor decay time to obtain a height-averaged temperature in the peak meteor region. Traditionally this is done by fitting a linear regression model in the scattered plot of and height, where τ is the half-amplitude decay time of the received signal. However, this method was found to be consistently biasing the slope estimate. The consequence of such a bias is that it produces a systematic offset in the estimated temperature, thus requiring calibration with other co-located measurements. The main reason for such a biasing effect is thought to be due to the failure of the classical regression model to take into account the measurement error in τ and the observed height. This is further complicated by the presence of various geophysical effects in the data, as well as observational limitation in the measuring instruments. To incorporate various error terms in the statistical model, an appropriate regression analysis for these data is the errors-in-variables model. An initial estimate of the slope parameter is obtained by assuming symmetric error variances in normalised height and . This solution is found to be a good prior estimate for the core of this bivariate distribution. Further improvement is achieved by defining density contours of this bivariate distribution and restricting the data selection process within higher contour levels. With this solution, meteor radar temperatures can be obtained independently without needing any external calibration procedure. When compared with co-located lidar measurements, the systematic offset in the estimated temperature is shown to have reduced to 5 % or better on average.
- Article
(2992 KB) - Full-text XML
- BibTeX
- EndNote
As meteoroids enter the Earth's atmosphere, they produce ionised trails which can be detected as back-scattered radio signals by interferometric radars. After the trail has been formed, the ionisation begins to dissipate by various processes, such as ambipolar diffusion, eddy diffusion, or electron loss due to recombination and attachment depending on the height of ablation. The rate at which the echo power decreases is also determined by the combined effect of electron line density of the trail, ambient pressure and temperature.
If the electron line density of the trail is less than 2.4×1014 electrons m−1, the trail is called “underdense”, meaning each electron in the trail scatters independently (e.g. Bronshten, 1983, p. 356). The decay of underdense trails is thought to be mainly due to ambipolar diffusion at a height range of 85–95 km, where the majority of the meteors ablate (Jones, 1975). In the weak scattering limit the backscattered amplitude of the radio signal from an underdense trail decays with time (t) as
where λr is the radar wavelength, and Da is the ambipolar diffusion coefficient (Kaiser, 1953). This coefficient depends on the ambient pressure (P) and temperature (T) of the neutral gas (Chilson et al., 1996) and can be estimated from the half-amplitude decay time (τ) as
Kamb in Eq. (2) is a constant related to the ionic constituent of the plasma in the trail (Hocking et al., 1997). The pressure at a given height (h) is
where m is the mass of a typical atmospheric molecule, g is the acceleration of gravity, k is the Boltzmann constant and z is an axis along the vertical. Substituting the equation for pressure in Eq. (2) and differentiating Eq. (4) provides the height profile of the decay time:
where Ψ is a constant. Equation (5) states that the height profile of decay time is a function of both temperature and temperature gradient under the assumption of ambipolar diffusion for underdense meteor trails. In practice, most trail echoes are received at a small altitude range referred to as the region of peak meteor occurrence (Hocking, 1999). Hence a height-averaged temperature gradient near the peak height can be used to estimate the mean temperature (T0) at the peak height by fitting a linear function (Hocking, 1999). A linear approximation of Eq. (5) is
where β is the slope of the scattered plot of and height, and T0 is the average temperature of the atmosphere at the height of peak meteor occurrence. A typical scattered plot of height and shows significant variation in the measured data along both abscissa and ordinate (Fig. 1). Traditionally, the slope (β) is estimated using the ordinary least-squares (OLS) method with as the independent variable. The justification of using as an independent variable is that the measurement errors in τ are smaller than those in heights (Hocking et al., 1997). While the pulse length and angular resolution, etc. of the radar introduces intrinsic measurement errors in heights, much of the variation in decay time is due to various geophysical effects that persist at all altitudes. At higher altitude, the collision frequency with neutrals is reduced, and the diffusion is inhibited in a direction orthogonal to the geomagnetic field (Jones, 1991; Robson, 2001). This anisotropic diffusion causes an increase in the duration of meteor radar echoes as compared to ambipolar diffusion, whereas at lower altitude, decay time tends to decrease due to additional effect of electron loss by recombination and attachment (Younger et al., 2008). In addition, other geophysical factors, such as meteor fragmentation, turbulence within trail, chemical composition of the meteors or the temperature variation due to passage of tides and gravity waves, can contribute to the measurements of decay time and heights at all altitudes (Hocking, 2004).
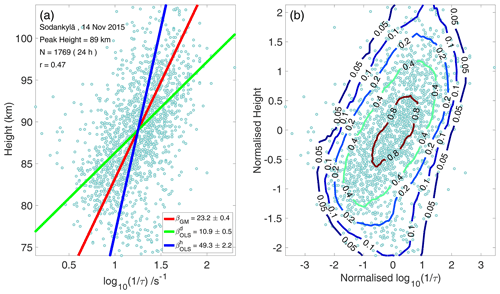
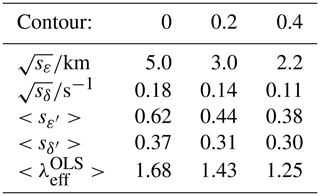
Figure 1(a) Typical scatter plot of and height. The lines correspond to best-fit models using different regression methods described in the text. The green and blue line corresponds to the ordinary least-squares method (OLS), with and height as independent variables respectively. The red line corresponds to the geometric mean (GM) of and . (b) The bivariate distribution of the data. The measured height and are converted to dimension-free coordinates using Eq. (18). The relative density contours are obtained by counting the number of detections in a circle of unit area relative to the detection density at the height of peak meteor occurrences at the centre.
Temperature estimation from meteor radar (MR) data requires obtaining the best-fit regression line in the scattered plot of and height. However, the pioneer work done by Hocking (1999) to implement this method using ordinary least-squares fitting showed a clear systematic offset between the MR temperature and co-located lidar measurements, indicating that the estimated slope was not determined correctly. To correct for this offset, a common practice is to calibrate the meteor radar temperatures using temperatures from lidar, OH spectrometer, satellite or rocket climatology. Hocking et al. (2001b) provided a statistical comparison technique (SCT) to calibrate the biased slope estimate as
or
where sδ and sε are the error variances of the (log of) diffusion coefficient (or decay time) and height respectively, sd and sh are data variances of and of height respectively and and are slope coefficients when diffusion coefficient or height is treated as an independent variable respectively in the OLS regression analysis. The calibrated slope, βSCT, is traditionally obtained by arbitrarily choosing sδ or sε that gives the best temperature estimates of MR as compared to optical or satellite data (e.g. Holdsworth et al., 2006; Hocking et al., 2007; Kim et al., 2012). A severe shortcoming of such a calibration procedure is that the calibration factors (sδ and sε) in the parentheses of Eq. (7) or Eq. (8) are dependent on the data selection criteria (e.g. limiting heights, decay time or zenith angle to a certain range). Moreover, the outcome of any such calibration routine will depend on the location of the MR and the choice of the calibration instrument. From a pure statistical context, the arbitrary choice of calibration parameters makes the estimated temperature also an arbitrary quantity, thereby making it impossible to draw any reasonable statistical inferences.
In practice, the ordinary least-squares method will not be valid for MR data since neither the height nor the decay time can be predetermined as an independent variable, and both variables are subject to intrinsic measurement errors and various geophysical effects. The reasons for such a bias, and thus the need for calibration, are discussed on theoretical and experimental grounds in Sect. 3.1. In addition, a statistical procedure to estimate sδ and sε using SCT calibration is formulated and presented in Sect. 3.1. An alternative method that includes measurement errors in the regression model is introduced in Sect. 3.2. This analysis does not require an absolute knowledge of sδ or sε, but only the relative value is needed. As an alternative to SCT calibration, in Sect. 4, an independent slope estimation is obtained using the errors-in-variables model. A comparison study of the estimated MR temperatures with co-located lidar temperatures is discussed to validate the method.
The All-Sky Interferometric Meteor Radar (SKiYMET) at Sodankylä Geophysical Observatory (SGO; 67∘22′ N, 26∘38′ E; Finland) has been routinely monitoring daily meteor-height averaged temperatures and wind velocity since December 2008 (Kozlovsky et al., 2016). The radar operates at a transmission power of 15 kW and frequency of 36.9 MHz, with a transmitting antenna which has a broad radiation pattern designed to illuminate a large expanse of the sky. The meteor trails are detected within a circle of 300 km diameter around SGO. The phase differences in the five-antennae receiving array allow for the determination of the azimuth, elevation, range, and line-of-sight Doppler velocity of the meteor trails. The 2144 Hz pulse repetition frequency of MR transmission introduces a range ambiguity of 70 km, and the built-in analysis software therefore assumes meteor trails are within the height of 70 to 110 km for unambiguous detections. Uncertainty in the height is ±1 km (or better for large zenith angle), which is determined by the 2 km range resolution. In addition, the half-time (τ) of the received signal is calculated from the width of the autocorrelation function. A detailed description of the algorithm of the SKiYMET signal processing software is outlined in Hocking et al. (2001a).
SGO is located at the corrected geomagnetic latitude of 64.1∘, which is statistically a region of the auroral oval. Hence the radar frequently detects non-meteor targets during substorms associated with ionospheric plasma waves generated due to Farley–Buneman instability (Kelley, 2009). The Doppler velocity of such echoes can be more than a few hundreds of metres per second, which are mostly detected at low elevation (Lukianova et al., 2018). For the Sodankylä radar, Kozlovsky and Lester (2015) identified ground echoes modulated by the ionosphere during pulsating auroras. These targets have near-zero Doppler velocities and are also observed at low elevation. Furthermore, the SKiYMET system detects both underdense and overdense echoes as valid meteors. However, more than 95 % of detections are underdense (Hocking et al., 2001b). The percentage of overdense trails may be larger during some meteor trails such as Geminids or Quadrantids, and this leads to underestimation of temperatures (Kozlovsky et al., 2016). This artefact in temperature was found to be reduced for Sodankylä radar for a zenith angle of less than 50∘. The initial data selection criteria is kept to a bare minimum, such that all heights and decay times are included, as long as they are unambiguous detections above a 40∘ elevation angle with Doppler radial velocity in the range ±100 m s−1. Subsequently, to improve the temperature estimation, we used a contour selection process; i.e. the data outside a certain contour in the normalised height– distribution were rejected (Fig. 1b).
For temperature estimation we considered daily data for a 6-month period from October 2015 to March 2016 since simultaneous lidar measurements were available during this time. The Compact Rayleigh Autonomous Lidar (CORAL) provided vertical profiles of the atmospheric temperature at 27–98 km over Sodankylä as part of the GW-LCYCLE-II (Gravity Wave Life Cycle Experiment) campaign in winter 2015/2016 (Reichert et al., 2019). The median number of daily meteor detections in this data set is 1652, with a minimum of 410 meteor detections on 4 October 2015 and a maximum of 3456 detections during the Geminids meteor shower on 14 December 2015.
The Mass Spectrometer–Incoherent Scatter or MSIS90 (Hedin, 1991) model temperatures are used to generate a temperature gradient model near the peak heights. Model temperatures are computed for each date at intervals of 6 h between 85 and 95 km. A third-degree polynomial fit is carried out to obtain the height profiles at 06:00, 12:00, 18:00 and 24:00 UT. For each time interval, the gradient at the respective meteor peak height, as well as at 1 km above and below the peak height, is estimated. These 12 values are then used to obtain the mean and standard deviation of the temperature gradient for each day near the peak height, which varies in the range 89±1 km. The daily meteor detections, the peak heights and the corresponding temperature gradient model values are shown in Fig. 2. The standard deviation of the MSIS model values corresponds to roughly of the order of 0.7 K km−1.
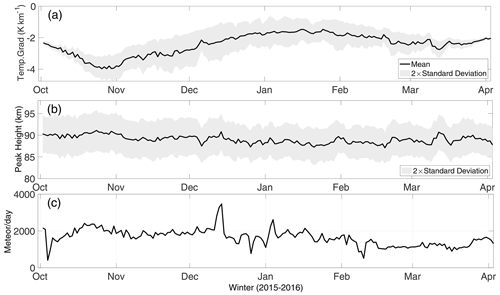
Figure 2(a) Temperature gradient model derived from MSIS90. (b) Peak meteor heights for the data used in this work and (c) the daily meteor detection for zenith angle less than 50∘ and velocity in the range ±100 m s−1.
Our reasons for choosing the MSIS temperature gradient are twofold. Firstly, MSIS data are easily accessible from the online version, which guarantees reproducibility of this work independent of location. Secondly, even if the temperature gradient term in Eq. (6) is ignored, the resulting offset in the estimated temperature is on average 10 % (Hocking, 1999) or less. Hence an approximate estimate is sufficient for the main objective of this paper. However, the actual temperature gradient in the atmosphere may be slightly different from these model values, which can contribute to the biasing effect in the estimated temperatures. Any such possibility and its effect on the estimated temperatures is addressed in the subsequent section.
3.1 Estimation of error variances in decay time and height
In the following text we use the notation and formulation in Gillard and Iles (2005). The observables, and height, are represented as di and hi respectively and the corresponding unobserved true values as ξi and ηi respectively, where the index i represents the ith meteor detection. For consistency we also assume that is presented in abscissa, and height is in the ordinate in the respective scattered plot (as shown in Fig. 1). Suppose we are assuming a linear relation in variables ξi and ηi as
Due to measurement errors and various geophysical processes, the true values ξi and ηi will be subject to random errors, and hence the observable di and hi will have scatter around the linear model in Eq. (9):
and
where δi and εi are errors in the measured and height respectively and are assumed to be mutually uncorrelated, have zero mean and be independent of the suffix i. This implies that the measurement error variances, sδ and sε, are constant with respect to the suffix i. Classical regression analysis or ordinary least-squares (OLS) treats di as an independent variable without intrinsic errors (or, di=ξi) and then minimises the sum of squared residuals along the ordinate. The slope from the OLS method can be represented in terms of the covariance (Cov) and variance (Var) as (e.g. Smith, 2009; Keles, 2018)
where is the OLS slope estimated by considering as an independent variable, and r is the Pearson product-moment correlation coefficient between d and h. Likewise, by reversing the arguments above, it is trivial to show that the reciprocal value of the OLS slope estimate with height as an independent variable is (e.g. Smith, 2009)
To see the effect of errors in the independent variable on the OLS slope estimate, e.g. for , Eqs. (10) and (11) are used in Eq. (12):
Since δi, εi and ξi are mutually independent, Eq. (14) simplifies to
where ζ is known as the attenuation or regression dilution bias. Since variances are always positive by definition, Eq. (15) shows that in the presence of measurement error in the so-called independent variable (in abscissa), the OLS slope estimate () will always be smaller than the unbiased slope β. Likewise, is greater than β if there is error in the measured height (specific example presented in Fig. 1a). By substituting , Eq. (15) can be rearranged as
Equation (16) is a well known identity in statistical literature (e.g. Carroll and Ruppert, 1996; Frost and Thompson, 2000), that was re-derived by Hocking et al. (2001b) in Eq. (7) in the context of SCT correction. Equation (16) reveals that an absolute knowledge of error variances, sδ ( or sε), is required to obtain the bias-corrected slope (β) if we choose OLS fitting for the slope estimate. A common practice is to calibrate the biased slope with optical or satellite data by arbitrarily choosing a value of sδ or sε (e.g. Holdsworth et al., 2006; Hocking et al., 2007; Kim et al., 2012). In the remaining part of this section, we demonstrate how to obtain an average value of the error variances in these data following a revised calibration procedure.
For each 24 h of the data set, we performed two OLS fittings to estimate and by using Eqs. (12) and (13). The corresponding biased temperatures, and respectively, are estimated using Eq. (6). Experimental values of the parameters sδ and sε can be obtained by comparing these estimated biased temperatures with the co-located lidar temperatures (Tlidar) as the reference values. Using Eqs. (7) and (8), and noting that the slope is proportional to the estimated temperatures from Eq. (6), we obtain
where and are MR temperatures estimated using OLS fitting with and height as an independent variable respectively. Furthermore, if the measurements are normalised with the mean and standard deviation (SD) as
then , and the OLS estimate of the ratio of the measurement error variance is (from Eqs. 17 and 18)
where the error variances, and , are in the dimension-free system defined by Eq. (18). In essence, is a measure of all sources of errors in the normalised heights and decay times that cause the real data to deviate from the idealised physical model of Eq. (6), thereby producing a typical scatter as seen in Fig. 1.
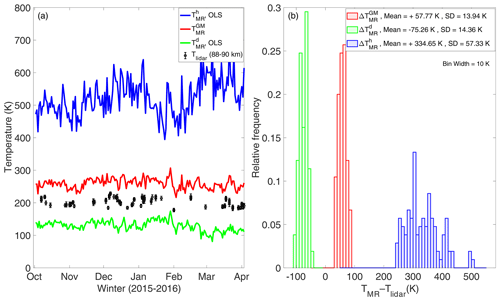
Figure 3(a) Temperature estimated in OLS method using (green) and height (blue) as an independent variable. Also shown are (red) the temperatures obtained using the geometric mean (GM) fitting and the lidar temperatures (in black). (b) The offset between the lidar (Tlidar) temperatures and the estimated MR temperatures (TMR) using OLS fitting and GM fitting (without contour selection).
, sδ and sε were estimated by Eqs. (17) and (19) using 24 h of MR data and co-located lidar temperatures at 88, 89 and 90 km for the dates for which lidar data were available. The biasing effect on the OLS estimate of MR temperatures with and height as an independent variable respectively are presented in Fig. 3 (green and blue lines and histogram). As expected from Eq. (7) or Eq. (8), a mean offset of −75 and +335 K occurs depending on whether or height respectively is considered as an independent variable. In practice, the magnitude of these biases is related to the total errors in heights and from Eq. (17), which was not taken into account by the OLS regression model in Eqs. (12) and (13). Furthermore, the relative density contour lines for each data point is obtained by counting the number of detections in a circle of unit area in the normalised height– plane relative to the number of detections in unit area at the peak meteor region (Fig. 1b). In addition, all the error estimates from the SCT method are obtained at contour levels 0, 0.2 and 0.4, and the results are presented in Table 1. Several key features of these data are reflected in Table 1. Despite the data transformation via Eq. (18), the average error variances for the height data are more than those for the data in these coordinates. This asymmetry in the error variances implies that the bivariate distribution is slightly skewed away from a perfectly normal distribution along the y direction. However, this effect of asymmetric error variances is less pronounced near the core of this distribution. This implies that the parameter is closer to 1 near the core of this distribution and further away from 1 near the tail of the distribution. The data near the outer contour area are subject to larger parameter estimation error due to observational limitation. For example, the zenith-angle-dependent error in height can easily skew the distribution in this direction. On the other hand, natural geophysical variability in these data contributes significantly at all altitudes. As seen in Table 1, the average error in height for contour levels 0, 0.2 and 0.4 are 5.0, 3.0 and 2.2 km respectively. This error is significantly higher than what is expected from purely parameter estimation error (for zenith angle less than 50∘, the error in height is 1 km or less), indicating that geophysical variability dominates the total error variance in these data at all altitudes. The average error variances estimated at the contour level 0.2 (Table 1) correlate very well with the values reported in Hocking (2004) and Holdsworth et al. (2006). Hocking (2004) estimated △(height) =3.25 km using a numerical model for a pulse length equivalent to 2 km and a meteor at an altitude of 90 km and zenith angle 50∘. Likewise, their estimation of was based on simulation studies for meteors below 95 km and confirmed that “decay times' variability” arise due to 27 % variability in Kamb and 8 % variability in temperatures over the meteor region. The argument for choosing 95 km as the maximum height is that above this altitude, meteor decay rates are substantially affected by processes other than ambipolar diffusion. Holdsworth et al. (2006, p. 5) applied similar data rejection criteria and found out that is required to calibrate the slope if is used as an independent variable in the OLS regression model. Likewise, Thorsen et al. (1997) performed the comparison between the parameter estimation error and the geophysical variability for estimating the mean wind field in the middle atmosphere and found that the geophysical variability dominated at all heights.
It is worth noting that instead of directly using the individual observation between biased MR temperatures and lidar measurements from Eq. (17), we have used the statistical mean of differences for calibration. This is because lidar data are not available for all days during the 6 months of data used in this work. Moreover, both MR and lidar data have their own intrinsic errors and technical differences in the observation time and volume of sky. MR temperatures are daily averages over 24 h of observation, whereas lidar data are just the nightly mean profile. The lidar probes a small volume limited to the diameter of the lidar beam, while the radar illuminates a large part of the sky. For a single observation, the lidar may see the phase structure of large-scale gravity waves, while the MR averages over the gravity wave structure due to different spatial resolutions. As a result, the radar averages over gravity waves with horizontal wavelengths smaller than few hundred kilometres. On the other hand, the lidar may resolve these gravity waves if the runtime is shorter than the period of these waves. As gravity wave amplitudes can be up to 10–15 K at these altitudes (Reichert et al., 2019), we cannot expect perfect agreement between radar and lidar temperature due to geophysical variation which shows up differently in the two data sets as a result of the different observational volumes.
While such calibration routine may prevent large offsets in the estimated temperatures, the day-to-day variation in these error variances due to natural geophysical processes will persistently introduce artefacts in the estimated temperatures. Moreover, due to the continually changing atmospheric dynamic, these calibration parameters need to be updated at time intervals. This in turn requires availability of optical or satellite data throughout the year for the given location. In all generality, it is desirable to avoid any kind of calibration process and instead formulate an independent estimate of temperatures using MR data alone. As an alternative to the OLS method, errors-in-variables (EIV) regression analysis provides a way to incorporate the error variances in both height and data, thereby reducing the biasing effect in the estimated slope parameter.
3.2 Errors-in-variables (EIV) model: GM solution
For fitting a straight line model, such as
to a set of N data points (xi, yi) measured with errors, the corresponding χ2 merit function is (Press et al., 1992, p. 660)
where σyi and σxi are the standard deviation of the ith data point, and the weighted sum in the denominator of Eq. (21) can be interpreted as the weighted error of the ith data point. The regression coefficients, a and b, can be found by minimising the merit function with respect to these coefficients following any suitable numerical root-finding routine. However, under the assumption of symmetric error variances, it is possible to derive an analytic solution for the regression coefficients. This solution, when the data are appropriately normalised, leads to a slope estimate which is both scale-invariant and symmetric with respect to the data.
Application of Eq. (21) to physics data requires that all measured variables are dimensionally consistent so that χ2 is dimension-free. Moreover, the analysis in this section requires that the measurements are presented in an appropriate dimension-free system. This facilitates the direct comparison between different parameters, such as the measured variables or the associated error variances. By applying the coordinate transformation introduced in Eqs. (18) to (9), we therefore intend to solve the simplified bivariate linear system of equations,
where ηi′, ξi′ and βW are dimension-free. For the specific choice of normalisation by Eq. (18), the intercept (αW) is always zero in the transformed coordinate system. The merit function in Eq. (21) can be further simplified by invoking a homoscedastic standard weighting model (Macdonald and Thompson, 1992). This error model assumes that the error variances are independent of data point, thereby simplifying the merit function as (Macdonald and Thompson, 1992; Lolli and Gasperini, 2012)
where and are constant error variances of the measured and heights respectively in the normalised (or, dimension-free) coordinate system, and λ is the ratio
The χ2 minimisation of Eq. (23) with respect to βW leads to the analytic expression (Carroll and Ruppert, 1996; Smith, 2009; Lolli and Gasperini, 2012) for the EIV slope parameter in terms of the variances (, ) and covariances () of the measured variables,
or
since from Eq. (18). And the covariance () is computed using the standard definition,
Equation (26) can be solved if a prior knowledge of λ is available, which in turn requires a precise estimate of all sources of errors in the measured data. In the more practical case for unknown λ, we need to initiate a good starting estimate. Using the calibration procedure described by Eqs. (17) and (18), the mean values of and are found to be 0.62±0.04 and 0.37±0.06 respectively (without any contour selection: Table 1). Since the EIV estimate of the slope requires only the ratio between and , a good choice of this starting value is λ=1. Furthermore, for , there is a simple geometric interpretation of the merit function in Eq. (23). This solution corresponds to minimising the Euclidean or orthogonal distance between the fitted line and the measured data. The residual function to be minimised with respect to the regression coefficients is
since βW=1 when λ=1 from Eq. (26). Following Eq. (22), we therefore have our first estimate of β in the scattered plot of and heights,
Equation (29) is commonly referred to as a reduced major axis (RMA) solution in statistics literature (Smith, 2009). In practice, this is just the geometric mean (GM) of the two OLS estimates, and , as can be seen by combining Eqs. (12) and (13):
The GM solution in Eq. (30) has the unique feature that this is the only case of EIV estimate which is both scale-invariant and symmetric in the variables (e.g. Ricker, 1984; Smith, 2009). While these properties do not necessarily imply that the GM solution is the correct solution (discussed below), this first estimate reflects the nature of the biasing effect in the estimated slope in relation to the data selection process. A specific example of GM fitting is presented in Fig. 1a. The standard error in the OLS and GM slope estimate reported in Fig. 1a is from Vicente de Julián-Ortiz et al. (2010). Due to the relatively low detections with Sodankylä radar (Fig. 2c), the 2σ error in the estimated temperature using the GM solution is found to be significantly higher (13 K on average at contour level 0). This 13 K of noise level in the temperature can be reduced by a factor of or if a 3 or 5 d running mean of temperature is estimated with this radar. However, to test the robustness of the proposed method, this paper has estimated the daily averaged temperatures.
The systematic offset between MR temperature and co-located lidar temperature as a result of using Eq. (30) is reflected in Fig. 3a (red curve) and b (red histogram). Each of these temperatures are then compared with lidar temperatures at 88, 89 and 90 km for the dates when lidar data are available. The intrinsic noise in the lidar temperature is about 5–10 K (Reichert et al., 2019), which implies no temperature gradient is observed between 88 and 91 km in these data. Figure 3b (red histogram) reveals that the MR temperatures are overestimated by a mean value of +58 K for the case of the GM solution.
When compared to the temperature gradient model derived from optical, satellite and rocket climatology (e.g. Holdsworth et al., 2006), it can be easily argued that our MSIS-derived gradient model (Fig. 2a) is more negative than expected. If these values are shifted by a constant positive offset of +1 K km−1, the absolute value of the estimated temperatures will increase by 10 K (Singer et al., 2004). This will further increase the offset between lidar and MR temperature, thereby shifting the histogram (in red) in Fig. 3b further to the right.
On the other hand, lidar temperatures are usually obtained during the night-time, which can lead to a systematic offset due to day–night differences or tidal variations. As discussed by Hocking et al. (2004), the day–night temperature difference at these altitudes is of the order of 3–4 K. This is significantly less than the standard errors in these temperatures, which is on average 6 K at contour level 0. Hence we expect the day–night difference in Sodankylä MR temperatures to be insignificant during the winter period. Moreover, any attempt to estimate MR temperatures using only night-time data has the adverse effect of reducing the accuracy in the estimated temperatures due to data loss. While no specific studies of tidal variation have been made for this location, the data from other sites (e.g. Hocking and Hocking, 2002; Stober et al., 2008) show that the temperature variation due to tidal activity is typically less than 10 K. We can therefore rule out the possibility of an offset in the MSIS gradient model or tidal effects as the primary cause for the +58 K offset seen in Fig. 3b (red histogram).
Ricker (1984) emphasised that the biasing in GM solution is conditional upon the value of the correlation coefficient (r) between the variables, while Kimura (1992) demonstrated that this solution will be an overestimate in the case of low r values. For the data set used in this work, we found that the correlation between and height is typically 0.50±0.05, thereby indicating the presence of significant natural variation in the measurements. Furthermore, Jolicoeur (1990) used error modelling to conclude that r must be more than 0.6 for the GM solution to be acceptable. In fact, we have observed that if we restrict our data selection process by excluding all data beyond the density contour 0.2 (Fig. 1b), this increases the r to be typically around 0.66±0.06, with the consequence of reduced biasing in the GM solution. Such a contour selection process essentially removes the erroneous data at higher and lower altitudes from the tail of the distribution, whereby the assumption of equal error variances (i.e. ) is achieved in the normalised coordinates (Table 1). In other words, the validity of GM solution is conditional upon how close the parameter λ is to 1 for a given data selection process.
The convergence of λ towards 1 near the core of this bivariate distribution is evident from Table 1. This is demonstrated in Fig. 4a, where we have estimated the GM slope at various contour levels between 0 and 0.7. In addition, Fig. 4b reflects the asymptotic behaviour of GM solution at higher contour levels in normalised coordinates. For these data, beyond the contour level 0.4, any change in slope at higher contour level is within the 2σ error limit. This error in the slope corresponds to an average 2σ error of 11 K in the estimated temperatures at contour level 0.4. In addition, the estimated temperatures can be biased due to small variation of λ from 1 on a day-by-day basis. For example, If the true value of λ is 1.25, the GM slope will be overestimated by 4 % (from Eq. 26 for the date 14 November 2015). For a typical winter temperature of 200 K at 90 km, a 4 % offset translates to overestimation of temperatures by 8 K. In principle, this bias can be further reduced by selecting a higher contour level than 0.4, with the consequence of increased noise level in the estimated temperatures. For these data, the contour level 0.4 is found to provide an optimum condition such that a maximum of 25 % uncertainty in the parameter λ leads to 4 % bias in temperature, which, in turn, is comparable to the standard error in the temperature from regression analysis.
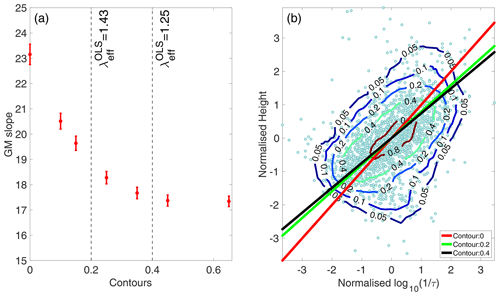
Figure 4GM solution at different contour levels in (a) original coordinate and in (b) normalised coordinate for the date 14 November 2015. The vertical dashed lines in (a) correspond to the average value of λ obtained from SCT calibration at contour level 0.2 and 0.4 respectively for winter 2015–2016. The error bar in (a) corresponds to 2σ error .
We have applied the GM slope estimate at contour level 0.4 to the MR data from the period October 2015 to March 2016. This is presented in Fig. 5, along with the data from co-located lidar observations. The differences between MR temperatures and lidar are shown in Fig. 6a for altitudes near peak meteor counts. The mean difference between lidar and MR temperatures is +12 K, which is expected due to the variation in the true value of λ from 1. The root-mean-square (rms) difference is about 21 K. This difference is partly due the intrinsic errors of 5–10 K in lidar temperature and partly due to the statistical noise in the estimated MR temperatures.
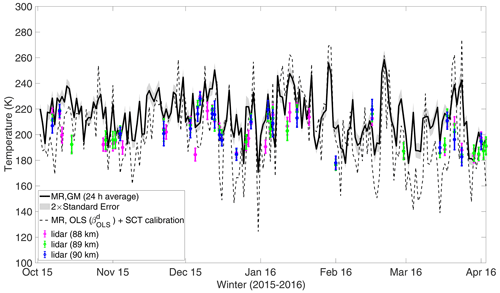
Figure 5Comparison of the bias-corrected MR temperatures with lidar data for the winter 2015–2016. The solid line corresponds to the temperature estimated using the GM solution at contour level 0.4. The dashed line corresponds to the SCT-calibrated temperatures using the co-located lidar measurements. The OLS estimates are obtained with as an independent variable. The errors in lidar temperatures are 5–10 K, and the 2σ error (grey shade) of the temperature from EIV analysis is on average 11 K. The differences between lidar and MR temperatures are presented in Fig. 6.
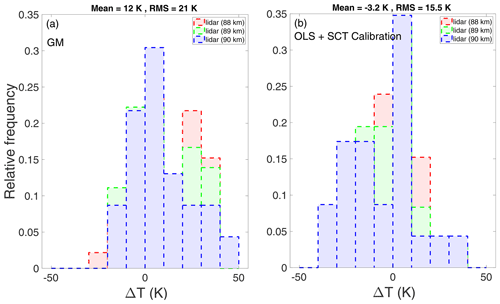
Figure 6Difference between MR temperatures and lidar data for (a) the GM solution at contour level 0.4 and (b) SCT calibration applied to OLS estimate of . MR temperatures are shown in Fig. 5.
For direct comparison with the results above, we have also estimated the MR temperatures using the revised SCT calibration procedure described in Sect. 3.1. For this we have estimated the OLS slope () and used (Table 1) to obtain the calibrated temperatures from Eqs. (16) and (6). These calibrated temperatures are presented in Fig. 5. The histogram in Fig. 6b shows the differences between lidar data and the SCT-calibrated MR temperatures. The mean difference between the MR and lidar temperatures is again about −3 K, thereby showing that the biasing effect has been properly corrected by this calibration procedure. The rms difference is 15 K. Although the temperature estimated from the GM solution is slightly biased as compared to that estimated using SCT calibration, the presence of artefacts in the latter is clearly visible in Fig. 5. As evident from Fig. 7, the GM solution based on contour selection improves the temperature estimation significantly as compared to the traditional use of the OLS regression analysis.
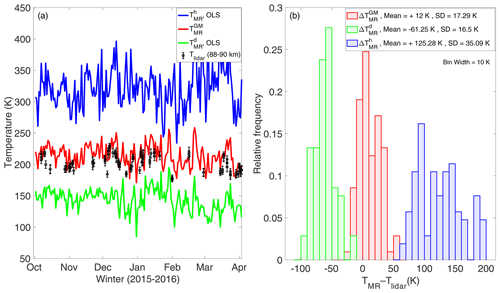
Figure 7(a) Improved temperature estimation using the GM solution (red) as compared to OLS estimates (blue and green) at contour level 0.4. (b) Reduced mean offset between MR and lidar temperature for GM slope estimate (red) as compared to OLS estimate (green and blue).
The EIV analysis does not distinguish between the measurement error and natural geophysical variability (e.g. Sprent, 1990, p. 13). In other words, the error variances, and , consist of both measurement errors and the natural geophysical variation. The effective value of λ in a normalised coordinate may vary on a day-by-day basis and may be radar-dependent. For example, meteor trails can get modified by wind effects, ion composition, meteor fragmentation and strong ionospheric currents, as well as temperature and pressure fluctuations, on various spatial and temporal scales (Hocking, 2004; Younger et al., 2014). Despite the contour selection process, asymmetric effects of geophysical variation may have increased the effective variance of hi′, leading to overestimates in the GM solution (Gillard and Iles, 2005). Due to the high-latitude location of Sodankylä radar, the geomagnetic effect above 95 km can contribute to the systematic bias. Below 85 km, the decay of meteor radar echoes may deviate slightly from diffusion-only evolution (Lee et al., 2013), thereby requiring a better physical model that does not assume the linearity of Eq. (6). Assessing the contribution of geophysical variability at various altitudes would require carefully designed replicates of observations as well as long-term comparison of MR temperatures with other co-located instruments. In other words, the case for λ≠1 needs to be handled with careful modelling of errors by taking into account the dominant effect of geophysical variability in these data. This remains a subject of future research.
The biasing effect in MR temperature has been a pressing issue for the last 2 decades. Attempts have been made in the past to correct the slope in the scattered plot of and height, usually either by direct calibration with optical or satellite data or by an arbitrary choice of data rejection criteria to exclude parts of measurements. This paper has addressed the underlying reasons for such a biasing effect, which is mainly due to the presence of various error terms. We have reviewed the conventional calibration procedure (1) and then provided an alternative method (2) for estimating MR temperature that does not require any calibration. We have applied both of these methods to the MR data from winter 2015–2016 and assessed the quality of the estimated MR temperature using co-located lidar measurements. The key points from each of these two aspects of the paper are given below.
-
This paper has reviewed the statistical comparison technique (SCT), originally proposed by Hocking et al. (2001b), within the context of MR temperature calibration. We have extended the theoretical basis of the SCT method to obtain an estimate of error variances of and height using co-located lidar measurements. No significant offset was seen in the calibrated MR temperature, even without applying any outlier rejection criteria. But artefacts introduced due to the difference in measurement techniques between MR and lidar were clearly visible in the estimated temperatures.
-
As an alternative method, we have applied the errors-in-variables (EIV) regression analysis to estimate the slope in the scattered plot of and height. The model error in EIV analysis takes into account the total errors variances in both abscissa and ordinate. It is observed that the geophysical variability dominates at all altitudes as compared to measurement errors and is the key factor in addressing the biasing effect. Moreover, any asymmetry in the error variance is minimal near the meteor peak region. This allows for an independent estimate of weighted-averaged atmospheric temperatures at 90 km using a suitable contour selection procedure. The temperatures estimated using this method show very good agreement with co-located lidar measurement and with reduced systematic offset as compared to the traditional least-squares analysis.
Data used in the paper are available at https://www.sgo.fi/pub/AMT_2020_ESarkar/ (last access: 13 April 2021, Sarkar et al., 2021, emranul.sarkar@oulu.fi). The MSIS model data were obtained from https://ccmc.gsfc.nasa.gov/modelweb/atmos/nrlmsise00.html (last access: 17 May 2021, Hedin, 1991, https://doi.org/10.1029/90JA02125). The lidar data are available at https://halo-db.pa.op.dlr.de/mission/109 (last access: 17 May 2021, DLR, 2021).
ES developed the method, carried out all data analysis and wrote the manuscript. The idea was suggested by AK, who also supervised this work. TU prepared the script for reading the raw data files from the radar and supervises the doctoral thesis of ES. IV co-supervises the doctoral thesis of ES and made suggestions. BK provided the lidar data. ML supported the MR operation at the Sodankylä. All the authors contributed to proofreading the manuscript.
The author declares that there is no conflict of interest.
Emranul Sarkar thanks the University of Oulu's Kvantum Institute for their support. We thank the anonymous referees for providing helpful suggestions to improve this paper.
Ilkka Virtanen has been supported by the Academy of Finland (project no. 301542). Bernd Kaifler has been supported by the German Research Foundation (DFG), research unit Multiscale Dynamics of Gravity Waves (MS-GWaves; grant no. RA 1400/6-1). Mark Lester has been supported by the Science and Technologies Facilities Council (STFC; grant no. ST/S000429/1).
This paper was edited by Jorge Luis Chau and reviewed by two anonymous referees.
Bronshten, V. A.: Physics of meteoric phenomena, Dordrecht, Kluwer, Holland, https://doi.org/10.1007/978-94-009-7222-3, 1983. a
Carroll, R. and Ruppert, D.: The use and misuse of orthogonal regression in linear errors-in-variables models, The American Statistician, 50, 1–6, https://doi.org/10.1080/00031305.1996.10473533, 1996. a, b
Chilson, P. B., Czechowsky, P., and Schmidt, G.: A comparison of ambipolar diffusion coefficients in meteor trains using VHF radar and UV lidar, Geophys. Res. Lett., 23, 2745–2748, https://doi.org/10.1029/96GL02577, 1996. a
DLR (German Aerospace Center): Lidar data, HALO database [data sets], available at: https://halo-db.pa.op.dlr.de/mission/109, last access: 17 May 2021. a
Frost, C. and Thompson, S. G.: Correcting for regression dilution bias: comparison of methods for a single predictor variable, J. R. Stat. Soc. A Stat., 163, 173–189, https://doi.org/10.1111/1467-985X.00164, 2000. a
Gillard, J. W. and Iles, T. C.: Method of moments estimation in linear regression with errors in both variables, Cardiff University School of Mathematics Technical paper, Cardiff, Wales, UK, 3–43, 2005. a, b
Hedin, A. E.: Extension of the MSIS thermosphere model into the middle and lower atmosphere, J. Geophys. Res., 96, 1159–1172, https://doi.org/10.1029/90JA02125, 1991 (data available at: https://ccmc.gsfc.nasa.gov/modelweb/atmos/nrlmsise00.html, last access: 17 May 2021). a, b
Hocking, W. K.: Temperatures using radar-meteor decay times, Geophys. Res. Lett., 26, 3297–3300, https://doi.org/10.1029/1999GL003618, 1999. a, b, c, d
Hocking, W. K.: Radar meteor decay rate variability and atmospheric consequences, Ann. Geophys., 22, 3805–3814, https://doi.org/10.5194/angeo-22-3805-2004, 2004. a, b, c, d
Hocking, W. K. and Hocking, A.: Temperature tides determined with meteor radar, Ann. Geophys., 20, 1447–1467, https://doi.org/10.5194/angeo-20-1447-2002, 2002. a
Hocking, W. K., Thayaparan, T., and Jones, J.: Meteor decay times and their use in determining a diagnostic mesospheric temperature-pressure parameter: Methodology and one year of data, Geophys. Res. Lett., 24, 2977–2980, https://doi.org/10.1029/97GL03048, 1997. a, b
Hocking, W. K., Fuller, B., and Vandepeer, B.: Real-time determination of meteor-related parameters utilizing modern digital technology, J. Atmos. Sol.-Terr. Phy., 63, 155–169, https://doi.org/10.1016/S1364-6826(00)00138-3, 2001a. a
Hocking, W. K., Thayaparan, T., and Franke, S. J.: Method for statistical comparison of geophysical data by multiple instruments which have differing accuracies, Adv. Space Res., 27, 1089–1098, https://doi.org/10.1016/S0273-1177(01)00143-0, 2001b. a, b, c, d
Hocking, W. K., Singer, W., Bremer, J., Mitchell, N., Batista, P., Clemesha, B., and Donner, M.: Meteor radar temperatures at multiple sites derived with SKiYMET radars and compared to OH, rocket and lidar measurements, J. Atmos. Sol.-Terr. Phy., 66, 585–593, https://doi.org/10.1016/j.jastp.2004.01.011, 2004. a
Hocking, W. K., Argall, P. S., Lowe, R. P., Sica, R. J., and Ellinor, H.: Height-dependent meteor temperatures and comparisons with lidar and OH measurements, Can. J. Phys., 85, 173–187, https://doi.org/10.1139/p07-038, 2007. a, b
Holdsworth, D. A., Morris, R. J., Murphy, D. J., Reid, I. M., Burns, G. B., and French, W. J. R.: Antarctic mesospheric temperature estimation using the Davis mesosphere-stratosphere-troposphere radar, J. Geophys. Res., 111, D05108, https://doi.org/10.1029/2005JD006589, 2006. a, b, c, d, e
Jolicoeur, P.: Bivariate allometry: interval estimation of the slopes of the ordinary and standardized normal major axes and structural relationship, J. Theor. Biol., 144, 275–285, https://doi.org/10.1016/S0022-5193(05)80326-1, 1990. a
Jones, J.: On the decay of underdense radio meteor echoes, Mon. Not. R. Astron. Soc., 173, 637–647, https://doi.org/10.1093/mnras/173.3.637, 1975. a
Jones, W.: Theory of diffusion of meteor trains in the geomagnetic field, Planet. Space Sci., 39, 1283–1288, https://doi.org/10.1016/0032-0633(91)90042-9, 1991. a
Kaiser, T.: Radio echo studies of meteor ionization, Adv. Phys., 2, 495–544, https://doi.org/10.1080/00018735300101282, 1953. a
Keles, T.: Comparison of Classical Least Squares and Orthogonal Regression in Measurement Error Models, International Online Journal of Educational Sciences, 10, 204–219, https://doi.org/10.15345/iojes.2018.02.0103.014, 2018. a
Kelley, M. C.: The Earth's Ionosphere: Plasma Physics and Electrodynamics, 2nd edn., Academic Press (Elsevier), San Diego, CA USA, ISBN 978-0-12-088425-4, 2009. a
Kim, J.-H., Kim, Y. H., Jee, G., and Lee, C.: Mesospheric temperature estimation from meteor decay times of weak and strong meteor trails, J. Atmos. Sol.-Terr. Phy., 89, 18–26, https://doi.org/10.1016/j.jastp.2012.07.003, 2012. a, b
Kimura, D. K.: Symmetry and scale dependence in functional relationship regression, Syst. Biol., 41, 233–241, https://doi.org/10.1093/sysbio/41.2.233, 1992. a
Kozlovsky, A. and Lester, M.: On the VHF radar echoes in the region of midnight aurora: Signs of ground echoes modulated by the ionosphere, J. Geophys. Res.-Space, 120, 2099–2109, https://doi.org/10.1002/2014JA020715, 2015. a
Kozlovsky, A., Lukianova, R., Shalimov, S., and Lester, M.: Mesospheric temperature estimation from meteor decay times during Geminids meteor shower, J. Geophys. Res.-Space, 121, 1669–1679, https://doi.org/10.1002/2015JA022222, 2016. a, b
Lee, C. S., Younger, J. P., Reid, I. M., Kim, Y. H., and Kim, J.-H.: The effect of recombination and attachment on meteor radar diffusion coefficient profiles, J. Geophys. Res.-Atmos., 118, 3037–3043, https://doi.org/10.1002/jgrd.50315, 2013. a
Lolli, B. and Gasperini, P.: A comparison among general orthogonal regression methods applied to earthquake magnitude conversions, Geophys. J. Int., 190, 1135–1151, https://doi.org/10.1111/j.1365-246X.2012.05530.x, 2012. a, b
Lukianova, R., Kozlovsky, A., and Lester, M.: Recognition of meteor showers from the heights of ionization trails, J. Geophys. Res.-Space, 123, 7067–7076, https://doi.org/10.1029/2018JA025706, 2018. a
Macdonald, J. R. and Thompson, W. J.: Least-squares fitting when both variables contain errors: Pitfalls and possibilities, Am. J. Phys., 60, 66–73, https://doi.org/10.1119/1.17046, 1992. a, b
Press, W. H., Teukolsky, S. A., Flannery, B. P., and Vetterling, W. T.: Numerical recipes in Fortran 77: volume 1, volume 1 of Fortran numerical recipes: the art of scientific computing, Cambridge University Press, Cambridge, ISBN 0-521-43064-X, 1992. a
Reichert, R., Kaifler, B., Kaifler, N., Rapp, M., Pautet, P.-D., Taylor, M. J., Kozlovsky, A., Lester, M., and Kivi, R.: Retrieval of intrinsic mesospheric gravity wave parameters using lidar and airglow temperature and meteor radar wind data, Atmos. Meas. Tech., 12, 5997–6015, https://doi.org/10.5194/amt-12-5997-2019, 2019. a, b, c
Ricker, W. E.: Computation and uses of central trend lines, Can. J. Zool., 62, 1897–1905, https://doi.org/10.1139/z84-279, 1984. a, b
Robson, R. E.: Dispersion of meteor trails in the geomagnetic field, Phys. Rev. E, 63, 026404, https://doi.org/10.1103/PhysRevE.63.026404, 2001. a
Sarkar, E., Kozlovsky, A., Ulich, T., Virtannen, I., Lester, M., and Kaifler, B.: Improved method of estimating temperatures at meteor peak heights, Sodankylä Geophysical Observatory (SGO) [data set], available at: https://www.sgo.fi/pub/AMT_2020_ESarkar/, last access: 13 April 2021. a
Singer, W., Bremer, J., Weiß, J., Hocking, W. K., Höffner, J., Donner, M., and Espy, P.: Meteor radar observations at middle and Arctic latitudes Part 1: mean temperatures, J. Atmos. Sol.-Terr. Phy., 66, 607–616, https://doi.org/10.1016/j.jastp.2004.01.012, 2004. a
Smith, R. J.: Use and misuse of the reduced major axis for line-fitting, Am. J. Phys. Anthropol., 140, 476–486, https://doi.org/10.1002/ajpa.21090, 2009. a, b, c, d, e
Sprent, P.: Some history of functional and structural relationships, in: Statistical analysis of measurement error models and applications (contempory mathematics 112), edited by: Brown, P.J. and Fuller, W. A., American Mathematical Society, Providence, RI, 3–15, 1990. a
Stober, G., Jacobi, C., Fröhlich, K., and Oberheide, J.: Meteor radar temperatures over Collm (51.3∘ N, 13∘ E), Adv. Space Res., 42, 1253–1258, https://doi.org/10.1016/j.asr.2007.10.018, 2008. a
Thorsen, D., Franke, S. J., and Kudeki, E.: A new approach to MF radar interferometry for estimating mean winds and momentum flux, Radio Sci., 32, 707–726, https://doi.org/10.1029/96RS03422, 1997. a
Vicente de Julián-Ortiz, J., Pogliani, L., and Besalu, E.: Two-variable linear regression: modeling with orthogonal least-squares analysis, J. Chem. Educ., 87, 994–995, https://doi.org/10.1021/ed100307z, 2010. a
Younger, J. P., Reid, I. M., Vincent, R. A., and Holdsworth, D. A.: Modeling and observing the effect of aerosols on meteor radar measurements of the atmosphere, Geophys. Res. Lett., 35, L15812, https://doi.org/10.1029/2008GL033763, 2008. a
Younger, J. P., Reid, I. M., and Vincent, R. A.: The diffusion of multiple ionic species in meteor trails, J. Atmos. Sol.-Terr. Phy., 118, 119–123, https://doi.org/10.1016/j.jastp.2013.10.007, 2014. a