the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Modeling the dynamic behavior of a droplet evaporation device for the delivery of isotopically calibrated low-humidity water vapor
Erik Kerstel
A model is presented that gives a quantitative description of the dynamic behavior of a low-humidity water vapor generator in terms of water vapor concentration (humidity) and isotope ratios. The generator is based on the evaporation of a nanoliter-sized droplet produced at the end of a syringe needle by balancing the inlet water flow and the evaporation of water from the droplet surface into a dry-air stream. The humidity level is adjusted by changing the speed of the high-precision syringe pump and, if needed, the dry-air flow. The generator was developed specifically for use with laser-based water isotope analyzers in Antarctica, and it was recently described in Leroy-Dos Santos et al. (2021). Apart from operating parameters such as temperature, pressure, and water and dry-air flows, the model has as “free” input parameters: water isotope fractionation factors and the evaporation rate. We show that the experimental data constrain these parameters to physically realistic values that are in reasonable to good agreement with available literature values. With the advent of new ultraprecise isotope ratio spectrometers, the approach used here may permit the measurement of not only the evaporation rate but also the effective fractionation factors and isotopologue-dependent diffusivity ratios, in the evaporation of small droplets.
- Article
(1027 KB) - Full-text XML
- Companion paper
- BibTeX
- EndNote
Water is arguably the most important molecule in Earth's atmosphere. The large enthalpy change associated with the evaporation and condensation of water causes it to dominate the global redistribution of energy by tropospheric transport of latent heat. Water vapor is also the most important greenhouse gas. The natural atmospheric greenhouse effect warms Earth’s surface by 33 K to hospitable temperatures of 15 ∘C on average. About 75 % of this temperature increase is generated by water vapor and clouds, as a feedback effect driven by the non-condensable greenhouse agents – foremost carbon dioxide (Lacis et al., 2010). This feedback effect, in turn, is a superposition of a multitude of large and (especially as clouds are involved) complex individual processes that partially cancel each other. Due to this complexity, water, in the form of water vapor as well as liquid- and crystal-phase water inside clouds, is by far the largest unknown in current climate models (IPCC, 2013). Atmospheric data of relevant tracers, which may help to disentangle and quantify the many relevant processes, are desperately needed. Of these, the isotopic composition of water (in particular the and ratios, in addition to and the derived quantities of deuterium excess and 17O excess) is arguably the best candidate, as all processes in which water is involved are isotope dependent. Therefore, water isotope ratios enable the identification of different moist air masses and the observation of their mixing; they also reflect the evaporation and condensation history of the moist air in question. In the journal Nature, the climate researcher Gavin Schmidt actually called the water isotopes “the most super-duper fantastic thing ever” (Tollefson, 2008).
It is also no overstatement to say that laser-based isotope analyzers have revolutionized the field of water isotope ratio instrumentation, which, until not so long ago, was dominated by isotope ratio mass spectrometers (e.g., Kerstel, 2004; Kerstel and Gianfrani, 2008). In particular, laser instruments have enabled continuous measurements of low-humidity atmospheric air in airborne and Antarctic field settings (see, among others, Iannone et al., 2009b, 2010; Moyer et al., 2013; Steen-Larsen et al., 2014; Casado et al., 2016; Ritter et al., 2016; Bréant et al., 2019). In order to calibrate such instruments against international standard and reference materials that are all in liquid form, it is necessary to bring these into the vapor phase without causing fractionation (or alternatively with well-controlled, quantitative fractionation) while also controlling the level of humidity (the volume mixing ratio). Several solutions have been proposed and developed into prototypes and commercial instruments, but few are capable of delivering a stable supply at low humidity levels (Iannone et al., 2009a; Sturm and Knohl, 2010; Gkinis et al., 2010; Tremoy et al., 2011). One approach is that of the instrument developed in our laboratory (and first reported in Landsberg et al., 2014), based on nanoliter (nL) sized droplet evaporation, with the specific aim of calibrating laser-based isotope ratio (, , and in water) analyzers deployed in Antarctica. This prototype instrument has undergone significant engineering developments in order to improve its performance and robustness, as reported in Leroy-Dos Santos et al. (2021).
The current paper describes a theoretical model of the droplet evaporation that was developed to quantitatively describe the operation of the device. The model is presented here in detail and subsequently applied to data collected with the original prototype, as this device allowed us to easily modify some crucial parameters (such as the velocity of the air in the evaporation chamber) and, as it was equipped with two instead of one syringe pump, enabled rapid switching between two independently prepared humid air flows. It also showed nonideal behavior that was eliminated in the final version but that enabled a more extensive test of the model. Finally, whereas it was deemed sufficient for the new instrument to be passively temperature stabilized to 20±1 ∘C, the prototype instrument had its evaporation chamber actively stabilized at 35.0±0.1 ∘C.
The theoretical understanding of the dynamic behavior has enabled the identification of the droplet evaporation device as an independent tool to investigate isotope fractionation factors involved in liquid–vapor transitions as well as isotope fractionation occurring during the process of evaporation of cloud water droplets. The same is true for the determination of the evaporation rate of nanoliter- and microliter-sized droplets, which has been the subject of a large body of research, starting with the fundamental work of Maxwell (2003) and Langmuir (1918) and continuing more recently in the fields of drying, painting and patterning technologies, dehumidification, cooling technologies, desalination, and DNA synthesis, among others.
Here, the dynamic behavior of the water vapor concentration (humidity) and isotope ratios of a low humidity level generator (LHLG) is modeled, such as the one described in the companion paper by Leroy-Dos Santos et al. (2021). Water isotope ratios are generally expressed in terms of the so-called “delta-value”: , the relative deviation of the abundance ratio of the rare isotope x in reservoir w with respect to the same ratio in the international standard material Vienna Standard Mean Ocean Water (VSMOW) (IAEA, 2017). In our case the relevant abundance ratios are and . Although the model can just as well be applied to the 17O isotope ratio, which is also measured by the laser spectrometer, these measurements were not considered here (in fact, δ17O qualitatively tracks δ18O very closely). Note that the isotope abundance ratios are exceedingly small numbers that can, in practice, be replaced by the corresponding molecular abundance ratios (Kerstel, 2004): ‰ and ‰ (IAEA, 2006).
The LHLG instrument uses a commercial high-precision syringe pump system (Harvard 11 Pico Plus Elite) to push in the plunger of a small-volume syringe. The needle of the syringe punctures the septum of a small evaporation chamber in which a steady air flow at a controlled pressure of 1 bar is maintained around the needle tip. Water being pushed through the syringe needle will start to form a droplet at the tip of the needle, provided that the water flow is high enough to overcome the evaporation from the exposed water surface inside the needle. Initially, as the water cap or droplet is still small, the evaporation rate from its surface into the surrounding dry-air flow is smaller than the rate of water supply and the droplet continues to grow. As the droplet grows in size, its surface area increases and so will the rate of evaporation. Once steady state is reached, the evaporation of water from the surface of the droplet at the end of the syringe is exactly matched in quantity and isotopic composition by the supply of the standard water through the syringe needle.
Considering the isotopic composition of the evaporated water, it is clear that, at the very beginning, the isotopic composition of the meniscus (the droplet cap) equals that of the bulk water in the syringe. Moreover, in steady state, the isotopic composition of the vapor is identical to that in the syringe reservoir, due to conservation of mass. In the transient regime, however, the isotopic fractionation occurring at the surface liquid-to-gas phase boundary implies an enrichment of the surface layer that first needs to diffuse inward. Thus, one expects to see a depleted vapor phase (relative to the reservoir liquid) as long as the droplet is growing. Inversely, if the water flow is reduced and the droplet shrinks, a temporary enrichment of the vapor is expected.
In order to model these dynamics quantitatively and, thus, understand which factors control the magnitude of the transient signals, a pinned, sessile droplet is considered, with the shape of a partial sphere, as shown in Fig. 1.
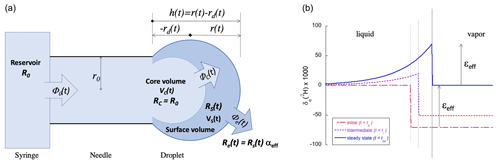
Figure 1(a) Schematic representation of the ideal spherical droplet formed at the end of the syringe needle tip, illustrating the different reservoirs with volumes V, water fluxes Φ, and isotope ratios R involved in the model. As and , it follows that . (b) The isotope ratio profile over the liquid to vapor boundary (left to right, with the thin vertical lines representing the growing water surface) at three instants in time if the water flux Φ0 from the syringe (with δ0=0) follows a step function with Φ0(t)=0 for t<t0 and with for t>t0. The isotope fractionation is taken to be ‰ for δ2H. While the droplet is growing, δe<δ0. Eventually, at t=t∞, the incoming water flux Φ0 equals the evaporated water flux Φe and δe=δ0.
For completeness, it is assumed that only a fraction f of the droplet volume (a boundary layer) becomes enriched. It will later be shown that the best model results are obtained by assuming that the entire droplet becomes enriched (f=1, see Sect. 3.1) – an observation that is further supported by considerations involving the relative speeds of isotopic diffusion and the water flow (Sect. 4.1). Figure 1b shows the radial isotope concentration profile inside the droplet and the neighboring vapor following a step function in the flow rate from zero to some fixed value at t=t0. The actual form of the profile is not important for the model and could just as well be approximated by a square profile. Thus, four different bodies of water can be distinguished:
-
The first is the syringe reservoir with a constant isotope ratio R0 and an outgoing water flux equal to Φ0(t) determined by the syringe pump speed.
-
The second is the core volume of the droplet with an isotope ratio Rc=R0 and a time-dependent volume Vc(t). The water flux from the core to the surface layer of the droplet is given by Φc(t). Only in steady state is Φc=Φ0.
-
The third is a fraction f () of the total droplet volume Vd(t) that will become enriched in the heavy isotope, Vs(t), with isotope ratio Rs(t):
-
The last is the evaporated water flux Φe(t), leaving the droplet with isotope ratio . Here, the relevant isotope fractionation factor is that between the vapor- and liquid-phase water: .
A last essential part of the model is the assumption that the evaporation flux is proportional to the exposed surface area of the droplet:
Figure 1 gives a schematic representation of our model, indicating the relevant water volumes and inter-volume fluxes as well as the isotope ratios R of each volume. Solving the model ab initio is not difficult and will be shown to give a qualitatively and quantitatively satisfactory description of the dynamics under realistic conditions.
The free input parameters to the model are (a) the fraction f of the droplet that becomes enriched, (b) the effective liquid-to-vapor fractionation factor αeff, and (c) the evaporation rate ke. The initial estimates of these parameters were obtained from previous studies by Cappa et al. (2003) and Luz et al. (2009) for αeff and from Walton (2004) and Sefiane et al. (2009) for ke. The values of these parameters that provide the best fit to the experimental data are subsequently rationalized in Sect. 4.1, 4.3, and 4.4.
The first task is to model the evaporated total water flux Φe(t) as a function of a variable input water flux Φ0(t), driven by variations in the syringe pump speed. For this, the mass balance equation for the noncompressible fluid is written out in discrete time with time step dt:
The evaporation flux Φe(t) is a function of the droplet size through Eq. (2). For simplicity, the droplet at the tip of the needle is modeled as a partial sphere, a spherical cap. The surface area of the spherical-cap-shaped droplet is given by the following equation (see Fig. 1):
where r is the radius of curvature of the cap, h is the cap height (), and 2r0 is the inner diameter of the needle, all as defined in Fig. 1. The volume of the droplet is equally a function of h:
As(t) and, thus, Φe(t) can then be expressed in terms of Vd by inversion of Eq. (5), with h(Vd) being obtained as the only real root of the cubic equation, giving
where
and
The above already permits the expression of both the droplet size (e.g., in terms of the droplet radius ) and the evaporative water flux Φe(t) as a function of Vd(t) as well as the subsequent calculation of both as function of the time-dependent input water flux Φ0(t) by numerical integration of Eq. (3).
Going one step further, a second mass balance equation is included in the model to account for the rare isotopologues (in this case, either 2H16O1H or 1H18O1H). First, the rare isotope fluxes (identified by *) are expressed in terms of the total fluxes and the isotope ratio of the reservoir in question. For the three relevant fluxes, this results in the following (see Fig. 1):
Recall that Rw is the ratio of the abundance of the rare to the most abundant water isotope in the reservoir w (w=0, c, s, e for the syringe and needle, the core of the droplet, the droplet surface layer, and the evaporated water, respectively). Thus, the factors (1+Rw) in Eqs. (9), (10), and (11) account for the conversion from the isotope abundance ratio to the isotope concentration. Finally, the fractionation factor between the (evaporated) vapor-phase water and the liquid αeff≈1 (ϵeff≪1), making the approximation formed in Eq. (11) a very good one.
Equations similar to Eqs. (9), (10), and (11) hold for the different water reservoir volumes, allowing us to write the following for the volume of the isotopically enriched evaporating surface layer:
Substituting
and using the definition
then yields
where the approximation for from Eq. (11) has been used.
The isotope ratio in the enriched fraction f of the droplet volume (using Eq. 1 and an appropriate value of f) can now be calculated by integration of Eq. (15) while evaluating Eq. (1) to Eq. (4) at each time step. The isotope ratio of the evaporated water is then obtained as
with
and
The above model has been programmed in Mathcad (PTC Mathcad, 2020) and used to simulate data that were recorded with a high-precision, low-humidity water isotope spectrometer, named HiFI, described in Landsberg (2014) and Landsberg et al. (2014). As we are specifically interested in the dynamic behavior of the water vapor source that feeds the spectrometer, it is necessary to take the response time of the spectrometer into account. This response is typically described by a double or even triple exponential. At humidity levels of several thousand parts per million by volume (ppmv), the initial (fast) response time of the bare spectrometer was determined to be in the range of 1 to 2 s for both the water concentration and the isotope ratios, with a second, slower exponential response of the order of 15 s. However, in the configuration of this study and at the lower water concentrations of a few hundred parts per million by volume, the response time is significantly longer, especially for the δ2H isotope ratio. These response times were measured using the previously mentioned prototype humidity source (see Sect. 1), a predecessor of the isotopic humidity generator described in Leroy-Dos Santos et al. (2021), which was equipped with two independent syringe pumps, enabling rapid switching between two different water sources using a two-position, four-port valve (Vici Valco EUDA-4UWE) just before the spectrometer (Landsberg, 2014). The humidified air stream was sent either to the spectrometer or to a waste pump. The isotope response was determined by switching between two very different water standards, assuring a high signal-to-noise ratio of the measurements while keeping the concentration constant at about 600 ppmv. The standard waters used were working standards of the Groningen Center for Isotope Research (CIO), known as GS-48 (δ18O ‰, δ2H ‰) and BEW-2 (δ18O =795 ‰, δ2H =5983 ‰). It is noted that, despite careful storage, these absolute isotopic compositions can no longer be guaranteed with the precision specified by the CIO, as the standards had previously been used for other experiments. For all measurements shown here, the water isotope analyzer was calibrated with respect to the same water (GS-48) used for the evaporation measurements, resulting in relative isotope deviations (δ-values) equal to zero under steady-state conditions. Therefore, the absolute isotope ratios are not relevant. In any case, the drift of the standards was estimated to be less than 1 ‰ for δ2H and less than 0.2 ‰ for δ18O (due to possible Rayleigh distillation).
The instrument isotope response curves are shown in Fig. 2, and the double exponential fit parameters are summarized in Table 1. Whereas the total water vapor concentration and δ18O show practically the same time response, δ2H is about twice as slow, due to different time constants for the surface adsorption processes. Although at much higher humidity, Steen-Larsen et al. (2014) observed a qualitatively similar behavior. In the following sections, the time response of the spectrometer is taken into account, by convolution of the simulated response of the humidity generator with the calculated impulse response of the spectrometer that corresponds to the step response of Fig. 2, before comparison to the corresponding experimental data.
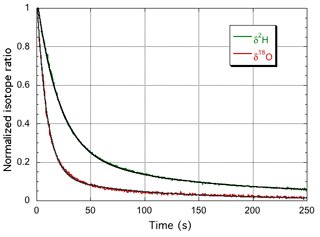
Figure 2The normalized response curves of the spectrometer for switching between the GS-48 and BEW-2 isotope standards, both prepared as a mixture of ∼600 ppmv water vapor in dry air. The experimental data are fit with a double exponential, yielding 9.2 and 20.7 s for the fast decay times for δ18O (red curve) and δ2H (green curve), respectively. It is noted that the update frequency of the water isotope spectrometer is 2 Hz (Landsberg et al., 2014).
Table 1Parameters of the double exponential fit to the measured instrument response for δ18O and δ2H. The water vapor concentration is observed to closely follow the δ18O behavior and was modeled with the δ18O parameters.
3.1 Humidity and isotope step responses
The model detailed in Sect. 2 was first used to simulate the dynamic behavior of the combination of the LHLG and the HiFI isotope analyzer, while the LHLG was programmed to generate small humidity steps of about 200 ppmv around an absolute value of roughly 400 ppmv. The simulated water vapor concentration response was fit to the experimental data by adjusting the evaporation rate ke, the only free parameter in this case (see the top panel of Fig. 3). The rationale for the values of ke determined in this study will be discussed in Sect. 4.4. Having fixed the evaporation rate at an optimal value of ke=3 µm s−1, the next step is to confirm that the isotope responses are modeled correctly, considering that both the δ2H and δ18O simulated responses also depend on the fraction f of the droplet volume that becomes enriched, as well as the effective liquid-to-vapor fractionation factor αeff. As it can be expected that the entire droplet becomes enriched in the heavy isotopologues, the logical starting point is the assumption that f=1. As we will see shortly, this choice is validated by the experimental observations. It will subsequently be rationalized by theoretical considerations in Sect. 4.1.
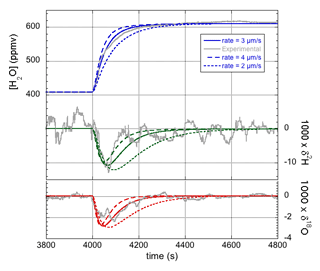
Figure 3Experimental data (gray curves) and model simulations of the humidity (blue traces; top) and isotope response curves (green for δ2H and red for δ18O; bottom) for three different values of the evaporation rate ke. The best fit is obtained for ke≈3 µm s−1, whereas a higher (lower) value results in a simulated dynamic response that is too fast (slow) compared with the measured response.
Regarding the fractionation factors, at the very low relative humidity of the experiment (h≈0.01), the effective fractionation factors αeff can be written as the product of a diffusion fractionation factor αdiff and an equilibrium fractionation factor αeq (Cappa et al., 2003). Moreover, the diffusion fractionation factor can be related to the ratio of the molecular diffusivities (Stewart, 1975), such that one may write
As before, the label x refers to the rare isotope or isotopologue (2H and 18O or 2H16O1H and ), and a refers to the abundant isotope or isotopologue (1H and 16O or ). Thus, the effective fractionation factors for 2H16O1H and are not independent but are determined by the single parameter n. The exponent n in Eq. (19) equals unity in the case of laminar flow and equals zero in the case of fully turbulent flow. The equilibrium fractionation factors were accurately determined by Horita and Wesolowski (1994), and their values at 35 ∘C – the temperature of the evaporation chamber – are used here. The diffusivities were determined by Cappa et al. (2003) and more recently by Luz et al. (2009). The more recent values are used here, but the difference is minimal for our purpose (Cappa et al., 2003, predict only slightly lower values of αeff in the laminar limit of n=1). Table 2 gives the values of the effective liquid-to-vapor fractionation factors for three different values of the flow parameter n, and Fig. 4 shows the corresponding model simulations compared to experimental data. The δ18O simulation shows a larger effect of changing n than the δ2H simulation. In contrast, changing the values of f has the same relative effect on both simulations (not shown in Fig. 4). With n=0.43 and f=1, a good fit to both isotope response curves is obtained. Thus, one may also conclude that the data support the theoretical finding (Sect. 4.1) that f=1. A good observer will have noted the difference in magnitude and noise level of the δ2H and δ18O responses shown in Figs. 3 and 4. Both are easily explained by noting that the isotopic fractionation is larger for 2H than for 18O, while the signal-to-noise ratio of the deuterium feature detected by the infrared spectrometer is concurrently significantly lower than that of , which, in turn, is directly related to the lower abundance of 2H16O1H with respect to 1H18O1H in the natural water sample.
Table 2Effective fractionation factors as a function of the flow parameter n. For n=0, the fractionation factors are equal to the equilibrium values at 35 ∘C, as determined by Horita and Wesolowski (1994).
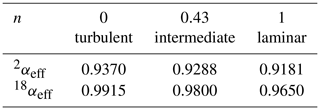
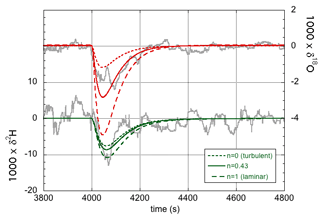
Figure 4Experimental data (gray curves) and model simulations of the isotope response curves (green for δ2H and red for δ18O) for three different values of the flow parameter n. n=0 (dotted lines) corresponds to the turbulent flow limit, whereas n=1 (dashed lines) corresponds to the limit of laminar flow. For n=0.43 (solid lines), a good fit is obtained for both isotopes.
3.2 Dynamic response under nonideal conditions
The LHLG prototype was modified immediately following the experiments presented in the previous section. Notably, it was deemed that the bore of the aluminum injector chamber that accepts the syringe's needle was too narrow. With an internal diameter of only 2 mm, careful guidance of the needle and precise positioning of the syringe was needed to avoid occasional contact of the droplet with the chamber wall. This also limited the maximum droplet size and, therewith, the volume mixing ratio (humidity level) that could be attained to roughly 1000 ppmv. The injection chamber was therefore replaced by a stainless-steel sample cylinder with a volume of 75 mL and a Sulfinert hydrophobic coating (Restek 304L-HDF4-75). Because the flow velocity is now significantly lower, the coating serves to minimize the memory effect due to surface adsorption of water molecules. In addition, a section of polytetrafluoroethylene (PTFE) tubing was added between the syringe (Hamilton 84853) and the removable needle to make the alignment more easily manageable. This initially gave rise to unexpected results that were attributed to the appearance of small air bubbles in the water injection line. These problems were later resolved by reengineering the LHLG as described in Leroy-Dos Santos et al. (2021). These “useless” results that otherwise might have been discarded are reported here anyway because they nicely demonstrate the ability of the model to simulate the behavior of this nonideal instrument; thus, they validate the model under a different operating regime.
During similar experiments to those reported in Sect. 3.1, recording the response of the LHLG following small steps in the flow of injected water, relatively large sinusoidal oscillations were observed with a period that matched the revolution speed of the lead screw of the precision pump. It is proposed that these oscillations become prominently visible when small imperfections in the lead screw combine with small air bubbles present in the water injection line, possibly amplified by viscous resistance of the liquid inside the water line and needle. Whatever the precise underlying mechanics, a sinusoidal variation of the water flow was modeled with a period equal to one revolution of the screw drive. The amplitude and phase of the (possibly amplified) lead screw imperfection was chosen to yield a simulation that best matched the observed amplitude of the oscillations. The only other parameter that needed adjustment was the evaporation rate. A value of ke=1 µm s−1 was found to produce a simulation that best matched the water vapor concentration response when the pump was switched between different water flow rates, as seen in Fig. 5a. The lower evaporation is due to the lower flow velocity of the air around the droplet (see Sect. 4.4).
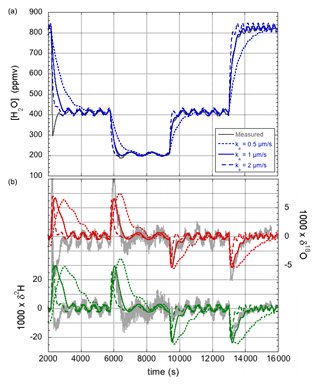
Figure 5Humidity (a) and isotope responses (b) of the modified LHLG subject to stepwise changes in the water flow rate. The best fit (blue for the humidity response, green for δ2H, and red for δ18O) to the experimental data (gray curves) is obtained for an evaporation rate of ke=1 µm s−1. The overshoot in the first measured downward humidity transition and the corresponding inverted isotope response are most likely due to an air bubble in the water line.
The corresponding response of the isotope ratios is shown in Fig. 5b. It may be clear that the correspondence between simulation and experiment is (already) satisfactory, considering that no further parameter adjustments were made. The simulation will be further refined in Sect. 4.3.
4.1 Droplet isotopic enrichment
Here, support is provided for the observation of an enrichment in the heavy isotopologues of the entire droplet and not just in a surface layer of limited thickness. Referring to Fig. 4 (for which n=0.43, i.e., 18αeff=0.98, and f=1), in principle the same amplitude of the modeled response can be obtained by assuming fully laminar flow (n=1) and assuming that a much smaller fraction of the droplet becomes enriched in the heavy isotopes. However, this gives a less satisfactory fit to the data, as shown in Fig. 6. Notably, the response simulated with n=1 (i.e., 18αeff=0.9650) and f=0.5 reached the same maximum amplitude, but it is clearly narrower than the experimental curve. Importantly, this is also not what is predicted based on the speed of isotopic diffusion in the droplet.
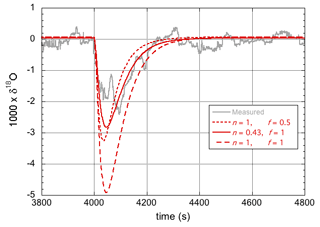
Figure 6Experimental data and model simulations of the 18O response curves for two different values of αeff and two different values of f.
To see that f is equal to unity in the present experiment, I consider that the enrichment occurring at the surface of the droplet will diffuse inwards, resulting in an isotope gradient inside the droplet with a characteristic diffusion length given by Bird et al. (2006):
where D is the diffusion coefficient and t is time. Differentiation of Eq. (20) yields the velocity of the diffusion front:
The diffusion coefficients of HDO and H18OH in water measured by Horita and Cole have been reported to be and m2 s−1, respectively (Horita and Cole, 2004). This shows that diffusion over lengths comparable to the size of a typical droplet (0.1 mm) takes place on a timescale of the order of 1 s. Thus, it is likely that the entire droplet becomes isotopically enriched, rather than just a surface layer: f=1.
4.2 Back diffusion
The question arises as to whether the diffusion is strong enough to allow the isotopic enrichment to propagate all the way to the syringe reservoir. To answer this question, the diffusion velocity of Eq. (21) is compared to the flow velocity inside the syringe needle:
where Φ0 is the water flux through the syringe needle, and A0 is the needle's internal cross-sectional area. After a characteristic time te, the diffusion velocity will have become smaller than the flow velocity, at which point in time the diffusion front does not further penetrate into the needle. This characteristic time equals
With typical values for the prototype instrument (an inner diameter of 464 µm for the 26-gauge needle and a low water flux of about 100 nL min−1), the flow velocity inside the needle is about 0.6 mm min−1, such that te≈25 s. Equation (20) then shows that the enrichment propagates about 0.5 mm into the 51 mm long needle. Moreover, at the given flow rate, it takes about 600 s to arrive at the typical droplet size of 10 µL. In this case, the isotopic diffusion into the needle stops before steady state is reached. Even at the lowest water flow rates of about 0.1 nL min−1, the diffusion can be stopped well within the length of the needle (if necessary by reducing the needle inner diameter). Thus, it is unlikely that the isotopic composition of the syringe reservoir would change due to back diffusion of heavier isotopologues. This was also confirmed experimentally by bringing the same liquid standard material into the vapor phase with both the LHLG and a commercial humidity generator (Picarro SDM) at time intervals of 1 month and not observing any difference between the measurements (within a measurement precision of 0.2 ‰ and 1 ‰ for δ18O and δ2H, respectively) (Leroy-Dos Santos et al., 2021).
4.3 Fractionation factors
The effect of the precise values of the 2H16O1H- and -isotopologue effective fractionation factors on the simulations has already been discussed to some extent in Sect. 3.1, where it was found that the best match with experiment is obtained by assuming fractionation factors that correspond to an intermediate case between laminar and turbulent flow (characterized by n=0.43). This can be rationalized by estimating the Reynolds number for the flow around the water droplet, . In the previous formula, ρ≈1.25 kg m−3 is the density of the air flowing around the needle and droplet; v=1.6 m s−1 is the velocity of the air around the droplet inside the narrow-bore chamber (inner diameter 2 mm), given the air flow of 300 mL min−1 (standard temperature and pressure); L≈0.5 mm is the diameter of the droplet; and μ=18.3 µPa s−1 is the dynamic viscosity of air at 35 ∘C. With these values, Re≈60. This contrasts with a value of v≈0.007 m s−1 and Re≈0.2 for the case of the approximately 30 mm internal diameter steel cylinder used in the modified instrument. Therefore, the latter case should be much closer to the limit of fully laminar flow. The simulations in Fig. 5 were consequently repeated – but now with the fractionation factors for n=1 (see Table 2). The new simulations are shown in Fig. 7.
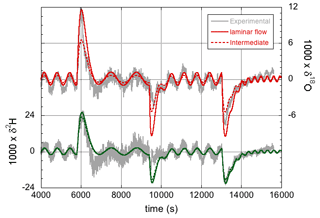
Figure 7The isotope response of the modified LHLG subject to stepwise changes in the water flow rate. Improved simulations (compared with those in Fig. 5) are obtained with ke=1 µm s−1 and effective fractionation factors for the limiting case of fully laminar flow.
Whereas the differences for 2H are minor, the effect of the larger 18O fractionation (i.e., the smaller liquid-to-vapor fractionation factor, which is smaller than unity) in the laminar flow regime is clearly visible, and it arguably provides a slightly better fit to the data, primarily during the water vapor concentration changes, as can be seen in Fig. 7. It should be noted, however, that in the regions of oscillatory behavior in between the concentration steps, the fit could also have been nudged by adjusting the amplitude of the lead screw modulation. Still, the results of Sect. 3.2 are just as well (or better) described (than shown in Fig. 5) by assuming fully laminar flow.
4.4 Evaporation rate
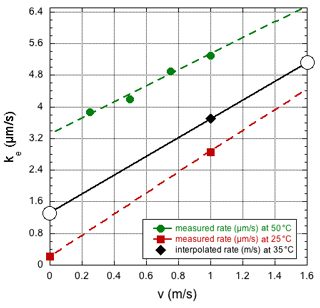
The two experiments discussed here in Sect. 3.1 and 3.2 required rather different evaporation rates to simulate the data with our model, ke≈3 and 1 µm s−1, respectively. The difference is clearly related to the different Reynolds numbers or, more directly, the different dry-air flow velocities of 1.6 and 0.007 m s−1. In fact, the values are in reasonable agreement with the results reported by Walton (2004). Although his measurements were recorded at only a small number of air temperatures and flow velocities, values applicable to our situation can be estimated by linear extrapolation of the observed rates as a function of flow velocity, and fitting a (weakly) quadratic dependence on the temperature to the data collected at a fixed flow velocity of 1 m s−1. In Fig. 8, selected data from Walton (2004) are presented along with the estimated values for our case. Thus, one predicts a rate of 5.2 µm s−1 at a flow velocity v=1.6 m s−1 and a rate of 1.3 µm s−1 at a flow velocity v=0 m s−1, which are higher than the experimental values found here. So far, it has been assumed that the droplet is at the same temperature as the evaporation chamber, but it cannot be excluded that the actual droplet temperature is lower, especially in the high-velocity case. However, the study by Sefiane et al. (2009) measured an evaporation rate at 22 ∘C and 1 bar, corresponding to ∼4 µm s−1, which is very close to the value extrapolated from the data of Walton (2004) at 25 ∘C. It is noted that the observation of a slightly lower evaporation rate than that found by Walton (2004) or Sefiane et al. (2009) is in agreement with the experimental sessile droplet, as it sits on the beveled tip of the syringe needle (Landsberg, 2014; Leroy-Dos Santos et al., 2021), having a somewhat smaller surface-to-volume ratio than the one that is modeled. It should also be mentioned that it is unlikely that the difference with the observations by Walton (2004) or Sefiane et al. (2009) are due to an underestimation of the spectrometer humidity response time, as it is difficult to imagine a response time of the water vapor concentration that is slower than that of the isotope ratios.
It has been shown that the dynamic behavior of a humidity generator based on droplet evaporation can be accurately modeled. Confrontation with experimental data of the water vapor concentration and two isotopic ratios as a function of the injected water flow enables the determination of physically realistic values of the droplet evaporation rate and the liquid-to-vapor isotope fractionation factors. However, the signal-to-noise ratio of the water isotope analyzer at the very low humidity levels investigated is not quite sufficient to make very precise determinations of the fractionation factors. However, recent developments in ultraprecise and ultrasensitive isotope measurements (e.g., Stoltmann, 2017; Kassi et al., 2018) will enable one to deliver more precise values by at least an order of magnitude. What may appear as a bit of a quixotic study of evaporating water droplets may, thus, in fact permit the measurement of not only the evaporation rate but also the effective fractionation factors and therewith also isotopologue-dependent diffusivity ratios, in the evaporation of small sessile droplets. Apart from this potentially new application, it is highly satisfactory to be able to accurately simulate the dynamic behavior of the LHLG with few free parameters and under rather different operating conditions.
Please contact the author if you wish to obtain a copy of the Mathcad code.
All relevant data are presented here in graphical format. Underlying data (both experimental and simulated) can be obtained in tabulated format from the author.
The author declares that there is no conflict of interest.
I am indebted to past and present colleagues and students. In particular, Janek Landsberg was instrumental in building the prototype humidity generator, with valuable contributions from Daniele Romanini and Samir Kassi. Janek Landsberg and Marine Favier recorded some of the experimental data shown here. Amaelle Landais, Andreas Zahn, and David Walton provided valuable feedback on the paper, as did an anonymous reviewer.
This paper was edited by Marc von Hobe and reviewed by David Walton and one anonymous referee.
Bird, R. B., Stewart, W. E., and Lightfoot, E. N.: Transport Phenomena, revised 2nd edn., John Wiley & Sons, New York, N.Y., 2006. a
Bréant, C., Leroy Dos Santos, C., Agosta, C., Casado, M., Fourré, E., Goursaud, S., Masson-Delmotte, V., Favier, V., Cattani, O., Prié, F., Golly, B., Orsi, A., Martinerie, P., and Landais, A.: Coastal water vapor isotopic composition driven by katabatic wind variability in summer at Dumont d'Urville, coastal East Antarctica, Earth Planet. Sc. Lett., 514, 37–47, https://doi.org/10.1016/j.epsl.2019.03.004, 2019. a
Cappa, C. D., Hendricks, M. B., DePaolo, D. J., and Cohen, R. C.: Isotopic fractionation of water during evaporation, J. Geophys. Res., 108, 4525, https://doi.org/10.1029/2003JD003597, 2003. a, b, c, d
Casado, M., Landais, A., Masson-Delmotte, V., Genthon, C., Kerstel, E., Kassi, S., Arnaud, L., Picard, G., Prie, F., Cattani, O., Steen-Larsen, H.-C., Vignon, E., and Cermak, P.: Continuous measurements of isotopic composition of water vapour on the East Antarctic Plateau, Atmos. Chem. Phys., 16, 8521–8538, https://doi.org/10.5194/acp-16-8521-2016, 2016. a
Gkinis, V., Popp, T. J., Johnsen, S. J., and Blunier, T.: A continuous stream flash evaporator for the calibration of an IR cavity ring-down spectrometer for the isotopic analysis of water, Isot. Environ. Healt. S., 46, 463–475, https://doi.org/10.1080/10256016.2010.538052, 2010. a
Horita, J. and Cole, D. R.: Stable isotope partitioning in aqueous and hydrothermal systems to elevated temperatures, in: Aqueous Systems at Elevated Temperatures and Pressures, edited by: Palmer, D. A., Fernández-Prini, R., and Harvey, A. H., chap. 9, 277–319, https://doi.org/10.1016/B978-012544461-3/50010-7, 2004. a
Horita, J. and Wesolowski, D. J.: Liquid-vapor fractionation of oxygen and hydrogen isotopes of water from the freezing to the critical temperature, Geochim. Cosmochim. Ac., 58, 3425–3437, 1994. a, b
IAEA: Reference Sheet for International Measurement Standards: VSMOW-SLAP, Department of Nuclear Sciences and Applications IAEA Environment Laboratories, Vienna, Tech. rep., VSMOW-SLAP-1Dec2006, available at: https://nucleus.iaea.org/rpst/documents/vsmow_slap.pdf (last access: 9 June 2021), 2006. a
IAEA: Reference Sheet for VSMOW2 and SLAP2 International Measurement Standards, Department of Nuclear Sciences and Applications IAEA Environment Laboratories, Vienna, Tech. rep., RS_VSMOW2_SLAP2_rev1/2017-07-11, available at: https://nucleus.iaea.org/rpst/documents/vsmow_slap.pdf (last access: 9 June 2021), 2017. a
Iannone, R. Q., Kassi, S., Jost, H.-J., Chenevier, M., Romanini, D., Meijer, H. A. J., Dhaniyala, S., Snels, M., and Kerstel, E.: Development and airborne operation of a compact water isotope ratio infrared spectrometer, Isot. Environ. Healt. S., 45, 303–320, https://doi.org/10.1080/10256010903172715, 2009a. a
Iannone, R. Q., Romanini, D., Kassi, S., Meijer, H. A. J., and Kerstel, E. R. T.: A Microdrop Generator for the Calibration of a Water Vapor Isotope Ratio Spectrometer, J. Atmos. Ocean. Tech., 26, 1275–1288, https://doi.org/10.1175/2008JTECHA1218.1, 2009b. a
Iannone, R. Q., Romanini, D., Cattani, O., Meijer, H. A. J., and Kerstel, E.: Water isotope ratio (δ2H and δ18O) measurements in atmospheric moisture using an optical feedback cavity enhanced absorption laser spectrometer, J. Geophys. Res., 115, D10111, https://doi.org/10.1029/2009JD012895, 2010. a
IPCC: Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, in: Climate Change 2013: The Physical Science Basis, edited by: Stocker, T., Qin, D., Plattner, G.-K., Tignor, M., Allen, S., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P., Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, available at: https://www.ipcc.ch/report/ar5/wg1/ (last access: 9 June 2021), 2013. a
Kassi, S., Stoltmann, T., Casado, M., Daëron, M., and Campargue, A.: Lamb dip CRDS of highly saturated transitions of water near 1.4 µm, J. Chem. Phys., 148, 054201, https://doi.org/10.1063/1.5010957, 2018. a
Kerstel, E.: Isotope ratio infrared spectrometry., in: Handbook of stable isotope analytical techniques, edited by De Groot, P. A., vol. 1, chap. 34, pp. 759–787, Elsevier (Amsterdam), 2004. a, b
Kerstel, E. and Gianfrani, L.: Advances in laser-based isotope ratio measurements: selected applications, Appl. Phys. B, 92, 439–449, https://doi.org/10.1007/s00340-008-3128-x, 2008. a
Lacis, A. A., Schmidt, G. A., Rind, D., and Ruedy, R. A.: Atmospheric CO2: Principal Control Knob Governing Earth's Temperature, Science, 330, 356–359, https://doi.org/10.1126/science.1190653, 2010. a
Landsberg, J.: Development of a water vapor isotope ratio infrared spectrometer and application to measure atmospheric water in Antarctica, PhD thesis, Université Grenoble Alpes, France, 2014. a, b, c
Landsberg, J., Romanini, D., and Kerstel, E.: Very high finesse optical-feedback cavity-enhanced absorption spectrometer for low concentration water vapor isotope analyses, Opt. Lett., 39, 1795–1798, https://doi.org/10.1364/OL39.001795, 2014. a, b, c
Langmuir, I.: The Evaporation of Small Spheres, Phys. Rev., 12, 368, https://doi.org/10.1103/PhysRev.12.368, 1918. a
Leroy-Dos Santos, C., Casado, M., Prié, F., Jossoud, O., Kerstel, E., Farradèche, M., Kassi, S., Fourré, E., and Landais, A.: A dedicated robust instrument for water vapor generation at low humidity for use with a laser water isotope analyzer in cold and dry polar regions, Atmos. Meas. Tech., 14, 2907–2918, https://doi.org/10.5194/amt-14-2907-2021, 2021. a, b, c, d, e, f, g
Luz, B., Barkan, E., Yam, R., and Shemesh, A.: Fractionation of oxygen and hydrogen isotopes in evaporating water, Geochim. Cosmochim. Ac., 73, 6697–6703, https://doi.org/10.1016/j.gca.2009.08.008, 2009. a, b
Maxwell, J. C.: On the Dynamical Theory of Gases, in: Kinetic Theory of Gases: An Anthology of Classic Papers With Historical Commentary, edited by: Brush, S. G., Imperial College Press, History of Modern Physical Sciences, 1, 197–261, https://doi.org/10.1142/9781848161337_0014, 2003. a
Moyer, E. J., Sarkozy, L., Lamb, K., Clouser, Stutz, E., Kühnreich, B., Landsberg, F., Habig, J. C., Hiranuma, N., Wagner, S., Ebert, V., Kerstel, E., Möhler, O., and Saathoff, H.: Applications of Absorption Spectroscopy for Water Isotopic Measurements in Cold Clouds, Mineral. Mag., 77, 1797, available at: https://pubs.geoscienceworld.org/minmag/article-pdf/77/5/1661/2920758/gsminmag.77.5.13-M.pdf (last access: 9 June 2021), 2013. a
PTC Mathcad: MathCAD: Math software for engineering calculations, available at: https://www.mathcad.com/en, last access: 30 September 2020. a
Ritter, F., Steen-Larsen, H. C., Werner, M., Masson-Delmotte, V., Orsi, A., Behrens, M., Birnbaum, G., Freitag, J., Risi, C., and Kipfstuhl, S.: Isotopic exchange on the diurnal scale between near-surface snow and lower atmospheric water vapor at Kohnen station, East Antarctica, The Cryosphere, 10, 1647–1663, https://doi.org/10.5194/tc-10-1647-2016, 2016. a
Sefiane, K., Wilson, S. K., David, S., Dunn, G. J., and Duffy, B. R.: On the effect of the atmosphere on the evaporation of sessile droplets of water, Phys. Fluids, 21, 062101, https://doi.org/10.1063/1.3131062, 2009. a, b, c, d
Steen-Larsen, H. C., Masson-Delmotte, V., Hirabayashi, M., Winkler, R., Satow, K., Prié, F., Bayou, N., Brun, E., Cuffey, K. M., Dahl-Jensen, D., Dumont, M., Guillevic, M., Kipfstuhl, S., Landais, A., Popp, T., Risi, C., Steffen, K., Stenni, B., and Sveinbjörnsdottír, A. E.: What controls the isotopic composition of Greenland surface snow?, Clim. Past, 10, 377–392, https://doi.org/10.5194/cp-10-377-2014, 2014. a
Steen-Larsen, H. C., Sveinbjörnsdottir, A. E., Peters, A. J., Masson-Delmotte, V., Guishard, M. P., Hsiao, G., Jouzel, J., Noone, D., Warren, J. K., and White, J. W. C.: Climatic controls on water vapor deuterium excess in the marine boundary layer of the North Atlantic based on 500 days of in situ, continuous measurements, Atmos. Chem. Phys., 14, 7741–7756, https://doi.org/10.5194/acp-14-7741-2014, 2014. a
Stewart, M. K.: Stable isotope fractionation due to evaporation and isotopic exchange of falling waterdrops: Applications to atmospheric processes and evaporation of lakes, J. Geophys. Res., 80, 1133–1146, https://doi.org/10.1029/JC080i009p01133, 1975. a
Stoltmann, T.: Development and applications of a laser spectrometer dedicated to the measurement of isotopic anomalies in carbon dioxide, PhD thesis, Universite Grenoble Alpes, France, 2017. a
Sturm, P. and Knohl, A.: Water vapor δ2H and δ18O measurements using off-axis integrated cavity output spectroscopy, Atmos. Meas. Tech., 3, 67–77, https://doi.org/10.5194/amt-3-67-2010, 2010. a
Tollefson, J.: Vapour spies to reveal climate clues, Nature, 455, 714–714, https://doi.org/10.1038/455714a, 2008. a
Tremoy, G., Vimeux, F., Cattani, O., Mayaki, S., Souley, I., and Favreau, G.: Measurements of water vapor isotope ratios with wavelength-scanned cavity ring-down spectroscopy technology: new insights and important caveats for deuterium excess measurements in tropical areas in comparison with isotope-ratio mass spectrometry, Rapid Commun. Mass Sp., 25, 3469–3480, 2011. a
Walton, D. E.: The Evaporation of Water Droplets. A Single Droplet Drying Experiment, Dry. Technol., 22, 431–456, https://doi.org/10.1081/DRT-120029992, 2004. a, b, c, d, e, f, g