the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The Berkeley Environmental Air-quality and CO2 Network: field calibrations of sensor temperature dependence and assessment of network scale CO2 accuracy
Erin R. Delaria
Jinsol Kim
Helen L. Fitzmaurice
Catherine Newman
Paul J. Wooldridge
Kevin Worthington
The majority of global anthropogenic CO2 emissions originate in cities. We have proposed that dense networks are a strategy for tracking changes to the processes contributing to urban CO2 emissions and suggested that a network with ∼ 2 km measurement spacing and ∼ 1 ppm node-to-node precision would be effective at constraining point, line, and area sources within cities. Here, we report on an assessment of the accuracy of the Berkeley Environmental Air-quality and CO2 Network (BEACO2N) CO2 measurements over several years of deployment. We describe a new procedure for improving network accuracy that accounts for and corrects the temperature-dependent zero offset of the Vaisala CarboCap GMP343 CO2 sensors used. With this correction we show that a total error of 1.6 ppm or less can be achieved for networks that have a calibrated reference location and 3.6 ppm for networks without a calibrated reference.
- Article
(9305 KB) - Full-text XML
-
Supplement
(3775 KB) - BibTeX
- EndNote
The atmosphere has warmed approximately 1 ± 0.2 ∘C since pre-industrial times, which is unequivocally due to anthropogenic emissions of CO2 and other greenhouse gases (GHGs) (IPCC, 2021). Global initiatives are needed to limit warming to 1.5 ∘C by achieving net zero GHG emissions by 2050 and a 45 % emissions decline from 2010 levels by 2030 (Rogelj et al., 2021). As over 70 % of global anthropogenic CO2 emissions originate from cities (United Nations, 2011), effective CO2 monitoring strategies in urban regions are needed to assess progress toward emissions commitments.
Monitoring trends in CO2 emissions by tracking ambient CO2 in urban environments is challenging because of the large diversity of emissions sources, complex spatial and temporal patterns of emission rates, varied topography, and the effects of meteorology on the observed concentrations (e.g., Vardoulakis et al., 2003; Lateb et al., 2016). As a result, most cities rely exclusively on economics and social data and do not check whether their reported emissions match the observed CO2 enhancements in the air over their city. To date, most efforts to assess CO2 emissions from cities have relied upon a small number of high-cost CO2 instruments that provide precise and accurate representations of regional signals. Other approaches include use of correlations between CO2 and other gases, measurements of 14C in annual grasses, and use of satellite column CO2 observations such as from OCO-2 (e.g., Pataki et al., 2003, 2006; Riley et al., 2008; Thompson et al., 2009; Kort et al., 2013; Andrews et al., 2014; Fu et al., 2019; Ye et al., 2020). Most of these efforts have used as a target metric an annual average of fossil fuel-related CO2 emissions from an entire city (e.g., McKain et al., 2012; Kort et al., 2013; Bréon et al., 2015; Verhulst et al., 2017). Simultaneous measurements of CO and 14CO2 have also provided information about sector-specific emission sources (Turnbull et al., 2015). Other methods of evaluating urban emissions have relied on emissions inventories (e.g., Gurney et al., 2009; Gately et al., 2013, 2017). These emissions inventories are frequently applied to inverse modeling approaches in combination with either short-term mobile measurements or a small number of long-term measurement sites to extract regional emissions (e.g., Brondfield et al., 2012; Sargent et al., 2018; Nathan et al., 2018; Turnbull et al., 2019). Several studies have also combined a network of CO2 observations with inverse modeling approaches to evaluate the accuracy of emissions inventories and CO2 sources (e.g., Lauvaux et al., 2016, 2020).
We are pursuing a distinct approach aimed at process-level understanding of the components of an urban emissions inventory. To do so, we are developing tools for the deployment of spatially dense networks of CO2 measurements, in combination with gases and aerosols that are co-emitted and that affect air quality. The result is an ability to map emissions with ∼ 1 km or “neighborhood scale” fidelity. The Berkeley Environmental Air-quality and CO2 Network (BEACO2N) (Turner et al., 2020; Kim et al., 2018; Shusterman et al., 2018, 2016; Turner et al., 2016) is our platform for research and development of tools for dense networks. New deployments in Glasgow, Scotland and Los Angeles, California are bringing new collaborators and experience in different cities to the project. BEACO2N has been operating since 2012 in the San Francisco Bay area and consists of over 70 nodes separated by approximately 2 km (Fig. 1). The nodes incorporate commercially available, low-cost sensors for measuring CO, NO, NO2, O3, particulates, and CO2.
Figure 1Map of all Bay Area BEACO2N sites (small red dots), BEACO2N sites discussed in this work (large blue dots), and the Richmond Field Station (star).
Turner et al. (2016) assessed the performance of a hypothetical BEACO2N-like observing system coupled to an inverse model and demonstrated that a random measurement uncertainty of 1 ppm between nodes was adequate to meaningfully constrain CO2 emissions from a point, line, or area source of 147, 45, and 9 t C h−1, respectively. With a 1 ppm mismatch error, weekly CO2 emissions in the San Francisco Bay area could be estimated to within 5 % error. In this paper we describe advances in our approach to maintaining stable, multiyear comparability among BEACO2N nodes in a city and evaluate the accuracy achieved with these new procedures. Our emphasis in the revised approach to sensor accuracy is on tracking and correcting the temperature dependence of the Vaisala CarboCap GMP343 CO2 instruments. We present the development and evaluation of the methods using observations from the San Francisco Bay Area BEACO2N deployment and then apply these ideas to the BEACO2N network in Houston, Texas.
The efficacy of a network of a large number of low-cost nondispersive infrared (NDIR) CO2 sensors to evaluate CO2 emissions has been previously discussed (Shusterman et al., 2016; Turner et al., 2016; Martin et al., 2017; Shusterman et al., 2018; Müller et al., 2020). Martin et al. (2017) showed that after correcting six SenseAir K30 carbon dioxide NDIR sensors (with off-the-shelf reported errors of 5–20 ppm) for environmental variables, the median root mean square error could be reduced to below 2 ppm, making the sensors potentially useful for ambient air-quality monitoring. Recently, Müller et al. (2020) evaluated the potential applications of a low-cost CO2 NDIR sensor network for resolving site-specific CO2 signals in Switzerland. The calibration method of Müller et al. (2020) involved laboratory chamber calibrations of over 300 low-cost NDIR CO2 sensors and ambient colocation with a reference instrument prior to deployment, as well as regular monitoring and drift correction during a 2-year deployment period. Shusterman et al. (2016) developed an in situ method for calibrating and correcting for individual instrument biases and temporal drifts of the Vaisala CarboCap GMP343 CO2 instruments deployed in the BEACO2N nodes. Using this method, Shusterman et al. (2018) demonstrated that the BEACO2N network could provide highly sensitive detection of changes to traffic emissions at a scale relevant to policy concerns. Shusterman et al. (2018) also illustrated the efficacy of the BEACO2N network in showing both regional CO2 emissions and local CO2 enhancements at the scale of a single neighborhood. In an analysis of the BEACO2N observations for 6 weeks before and after the COVID-19 shutdown, Turner et al. (2020) showed that a 25 % change in emissions is easily derived by an inverse model and that hourly variations in emissions can be inferred.
The use of a large number of low-cost CO2 sensors introduces challenges regarding accuracy and inconsistent behavior between instruments that often requires labor-intensive regular calibration, data correction and filtering, and validation with comparison to a smaller number of frequently calibrated high-accuracy instruments. In particular, the low-cost NDIR absorption sensor used in each BEACO2N node (Vaisala CarboCap GMP343) is susceptible to temporal drift and fluctuations due to environmental variables that present challenges to achieving a goal of 1 ppm network error (van Leeuwen, 2010; Shusterman et al., 2016). Correction of the Vaisala CarboCap GMP343 instruments (Vaisala, hereafter) for changes in pressure, temperature, and humidity is required for accurate measurements (Vaisala, 2013). The typical correction for pressure and temperature accounts for changes in the number density of CO2 according to the ideal gas law (van Leeuwen, 2010; Vaisala, 2013; Shusterman et al., 2016). The humidity effect on measured CO2 is accounted for by considering the dilution effect of water vapor according to Dalton's law of partial pressures (van Leeuwen, 2010; Vaisala, 2013; Shusterman et al., 2016). However, even after accounting for these factors, reported corrected CO2 concentrations for the Vaisala instrument have been observed to exhibit a strong temperature dependence of up to 1 ppm ∘C−1 (van Leeuwen, 2010). Using a laboratory calibration procedure, van Leeuwen (2010) found that a linear correction was necessary to account for the residual temperature dependence. However, correcting for the temperature dependence using lab calibrations is labor intensive, as the temperature dependence is unique for each Vaisala sensor. Regular laboratory temperature calibration would also be required to account for temporal variations in the temperature correction as sensors age. For a high-density urban network like BEACO2N, this would require substantial time investment by trained personnel. The associated high labor costs defeat the purpose of using low-cost sensors. In situ field calibration of the Vaisala sensors thus presents a more attractive method for correcting for the temperature dependence of the CO2 measurements.
2.1 BEACO2N network
The Berkeley Environmental Air-quality and CO2 Network (BEACO2N) Bay Area deployment currently consists of 73 nodes spaced at ∼ 2 km intervals with locations in Alameda, San Francisco, Contra Costa, Sonoma, Sacramento, and Solano counties. A full description of a BEACO2N node can be found in Kim et al. (2018). Briefly, each node contains a nondispersive infrared Vaisala CarboCap GMP343 CO2 sensor, along with a Shinyei PPD42NS nephelometric particulate matter sensor and several Alphasense electrochemical sensors for measuring CO, NO, NO2, and O3 (CO-B4, NO-B4, either NO2-B42F or NO2-B43F, and either Ox-B421 or Ox-B431). The most recent version adds a Plantower PMS 5003 aerosol sensor. Sensors are assembled into compact, weatherproof enclosures with air flow through the enclosure provided by two 30 mm fans. Data are compiled with a Raspberry Pi microprocessor and an Adafruit Metro Mini microcontroller. Data are acquired every 5 or 10 s and are transferred to a central server via an Ethernet or Wi-Fi connection. Observations are posted on the BEACO2N website within a few hours of measurement time (http://beacon.berkeley.edu, last access: 14 June 2021).
The Vaisala CarboCap GMP343 instrument uses pulsed light from a filament lamp, which is reflected and refocused on an IR detector located behind a Fabry-Perot Interferometer (FPI). The FPI is electrically tuned so that its passband corresponds to either the absorption wavelength of CO2 or a reference band (Vaisala, 2013). The calibration procedure for the Vaisala CarboCap GMP343 CO2 sensor is as outlined in Shusterman et al. (2016, 2018). Briefly, deployed Vaisala sensors operate with the internal relative humidity (RH), temperature, and pressure compensation set to “off” and the oxygen correction set to “on”, with oxygen input as 20.95 %. A post hoc multiplicative scale factor is applied to convert the raw CO2 outputs to the mole fraction of CO2 that would be measured if the observed air parcel were dried and brought to standard temperature and pressure (STP) ([CO2]STP). Raw CO2 data are adjusted using temperature (T) measured by the internal thermometer of the Vaisala. Water vapor pressure () and air pressure (Ptot) are obtained from the pressure and dew point temperature measured inside each node enclosure by a Bosch Sensortec Adafruit BME280 sensor. The [CO2]STP is then adjusted to account for temporal drift in the instrument “zero” by comparing the background signal of the Vaisala CO2 measurement at each node to a reference Picarro G2301 system, located at the Richmond Field Station in Richmond, CA (Fig. 1). A moving 3-week window of the 10th percentile of Vaisala CarboCap CO2 data (Vaisala[CO2]10 %) is generated and compared with the 10th percentile of the reference Picarro instrument (Picarro[CO2]10 %). The difference between Vaisala[CO2]10 % and Picarro[CO2]10 % is used to define the offset of the Vaisala instrument . A linear correlation between and time is generated and used to calculate the drift-corrected CO2 data, (Eqs. 1–2):
where mt is the temporal drift (ppm d−1) and b is a constant atemporal bias.
2.2 Picarro reference instrument
A “supersite” with reference grade instruments is operated within the BEACO2N Bay Area network to provide a reference for the network calibration. Instruments are installed within a temperature-controlled instrument shelter at the U.C. Berkeley Richmond Field Station. Measurements include basic meteorology, NOx (Thermo 42CTL with a molybdenum NO2 to NO converter), O3 (Teledyne/API T400), CO2, CH4, and CO (Picarro G2401 cavity ring down analyzer). Air is sampled through Teflon tubes mounted to a small tower affixed to the trailer roof, for a combined height of 6 meters above the ground. The colocated BEACO2N node is attached outside of the trailer to the same tower.
The NOx and Picarro analyzer calibrations are checked against reference gases every 2 to 3 weeks. The reference gas cylinders for NOx, CO, and CH4 are Certified Standard grade from Praxair, and for CO2 are from the NOAA Global Monitoring Laboratory (two levels: 403.61 and 687.47 ppm). The Picarro checks are made by flowing the sequence of references gases into a tee at the inlet of the instrument for 15 min per step. The sequence of steps is performed twice during a check. The flow rate is set to be larger than the instrument sample flow (0.4 L min−1) to overflow the inlet. The O3 analyzer is checked against a photometric calibrator (Teledyne/API 703E).
2.3 Identification of a temperature-dependent error in Vaisala measurements
There exists an additional temperature dependence among the Vaisala CarboCap GMP343 instruments that varies between instruments. The temperature dependence was first identified from observations of CO2 diurnal cycles at certain Bay Area BEACO2N sites that were out of phase or larger in magnitude than the diurnal cycles at nearby nodes or measured by the Picarro. The presence of a temperature dependence in suspect Vaisala instruments was confirmed by examining the relationship between temperature in the node and the difference between baseline CO2 signals measured by the Vaisala and the Picarro reference instrument.
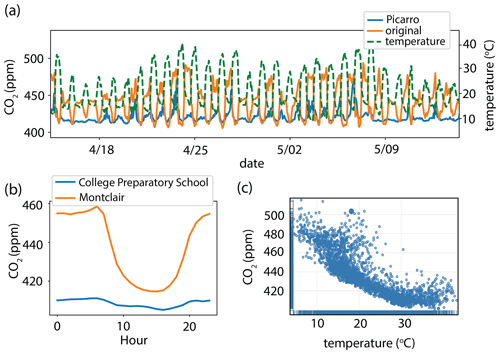
Diurnal cycles of urban CO2 typically exhibit a daily maximum at night or mid-morning (depending on influence from traffic emissions) due to mixing in a shallow nighttime planetary boundary layer (PBL), and reach a minimum during the day as PBL height increases and vegetation takes up CO2 (Idso et al., 2002; Coutts et al., 2007; Turnbull et al., 2015; Shusterman et al., 2016). The presence of an additional temperature dependence in the Vaisala CO2 instrument is particularly pronounced and obvious in the measurements obtained with the sensor located at the East Bay Municipal Utility District (EBMUD) BEACO2N site during 2020 (Fig. 2). The magnitude of the diurnal cycle at EBMUD is larger and out of phase with the Picarro reference instrument (Fig. 2a). The result of this temperature dependence at EBMUD (Fig. 2c) is a diurnal cycle that peaks midday (Fig. 2b). Figure 2b compares the CO2 diurnal cycle at EBMUD with the nearby urban site Laney College (Fig. 1). In contrast to EBMUD, Laney College exhibits a daily maximum at mid-morning–a pattern more consistent with typical urban CO2 behavior (Idso et al., 2002; Coutts et al., 2007; Turnbull et al., 2015; Shusterman et al., 2016).
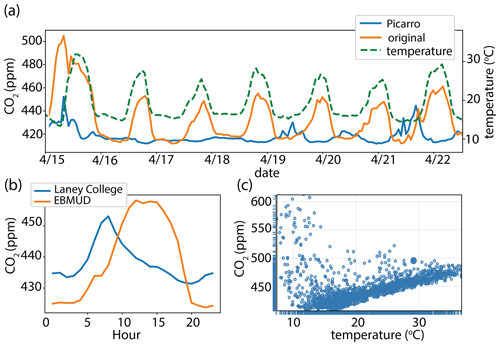
Figure 2(a) CO2 mixing ratios from April 2020 at EBMUD and measured with a Picarro instrument at the Richmond Field Station supersite. (b) EBMUD 2020 diurnal cycle compared with Laney College. (c) Temperature dependence of the CO2 signal at EBMUD.
The Vaisala temperature dependence varies in magnitude and sign. Figure 3 shows the CO2 mixing ratios and temperature dependence at the Montclair Elementary School site. Compared to the Picarro instrument, this site also demonstrates higher amplitude diurnal cycles (Fig. 3a), but these diurnal cycles are in phase with the reference instrument. Unlike EBMUD, the Montclair site exhibits a negative temperature dependence (Fig. 3c). Figure 3b shows the diurnal cycles at Montclair and the nearby node located at College Preparatory School (CPS). The comparison of these two sites suggests there may indeed be an amplification of the diurnal cycle at Montclair caused by a negative temperature dependence of the Vaisala instrument.
2.4 Temperature correction method
The goal of our approach to accounting for the temperature dependence of the Vaisala instruments is to rely exclusively on the network itself and, if available, supplementary reference instruments, such as a Picarro, for derivation of correction factors to null sensor temperature dependence.
The method we developed builds on our method for accounting for drift in the instrument zero. To derive a temperature factor, we use hourly averaged [CO2]STP and node measurements of temperature (T). It is important to note that a major factor contributing to the temperature inside the node is whether the node is placed in the sun or shade. As a result, direct correlation with meteorological temperature measured outside the node is not strong. For a moving three-week window, at each hour (h), the lowest 10th percentile of [CO2]STP within ±1 ∘C of T(h) is calculated. A running array of temperature-based 10th percentile data is created for both the Picarro supersite at the Richmond Field Station and each Vaisala instrument using the temperature (T) of the Vaisala instrument. The Vaisala temperature is assumed to be the temperature that the instrument is responding to. is then calculated, where
A linear regression for against T provides a slope (mT) and intercept (bT) for a moving three-week time window. We considered the possibility that the instrument response to temperature could be a zero shift and/or a change in the response to CO2. We were able to achieve similar results assuming the temperature effect is entirely due to one or the other of these possibilities. As there is already substantial drift in the instrument zero, we proceed under the assumption that the effect can be entirely attributed to the temperature dependence of the instrument zero. The median of mT (medmT)is calculated for the deployment period of the Vaisala sensor to determine the temperature-corrected offset and CO2 mixing ratios of Vaisala CO2 measurements, based on an additive error correction (Eqs. 4–5). When it is observed that either the offset bias, the temperature-dependent slope, or the time-dependent drift in the instrument zero shifts dramatically during a deployment period, the deployment is manually separated into different periods that are calibrated separately. The occurrence and magnitude of this varies between instruments (0–3 times during a two-year-long deployment), and is typically identified by routine checks for agreement between neighboring sensors. Shifts in the offset bias, the temperature-dependent slope, or the time-dependent drift appear as sudden or gradual offsets in mixing ratios measured by a sensor and its neighbors. Typical identified shifts in the offset bias, the temperature-dependent slope, or the time-dependent drift are on the order of 10 ppm, 0.5 ppm ∘C−1, and 0.1 ppm d−1, respectively:
An example calibration, demonstrating mT and over time at EBMUD 2020, is shown in Fig. S1 in the Supplement. Following calculation of the temperature-corrected offset, the temporal drift slope and intercept of this corrected offset are calculated and corrected using the methods described above, resulting in the generation of the temperature- and drift-corrected CO2 offset .
The final temperature- and drift-corrected CO2 is then calculated as
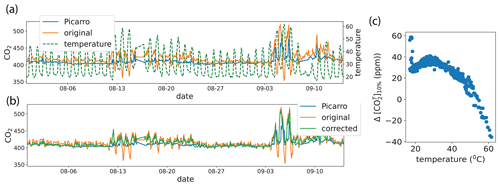
Figure 4(a) CO2 mixing ratios measured by the Picarro instrument at the Richmond Field Station (blue solid), uncorrected CO2 measured at Elsa Widenmann Elementary School (orange solid), and node temperature measured at Elsa (green dashed). (b) CO2 mixing ratios at Elsa Widenmann Elementary School with no temperature correction (green), temperature correction applied (green) and measured with a Picarro instrument at the Richmond Field Station (blue). (c) Temperature dependence at Elsa Widenmann Elementary School of .
The majority of the BEACO2N nodes examined demonstrated a strong linear relationship between and node temperature. However, the node at Elsa Widenmann Elementary School appeared to show a strong negative temperature dependence only on particularly warm days (Fig. 4a, c). The temperature dependence of for this node better fit a quadratic than a linear relationship. To account for nodes with a nonlinear temperature dependence, in cases where a quadratic fit improves the R2 of the fit by more than 0.2, the and are calculated via Eqs. (7)–(8):
where and are the first and second terms of the quadratic fit of against T.
We attempted to determine a relationship between Vaisala sensor age and temperature-dependence slope, but mT was only weakly correlated with sensor age (r≈0.3). We did, however find some evidence that older sensors had a larger likelihood of having a larger temperature dependence. For sensors less than 3 years since their initial deployment, 90 % had mT<1 ppm ∘C−1 and 64 % had mT<0.5 ppm ∘C−1. For sensors older than 3 years, 75 % had mT<1 ppm ∘C−1. and 47 % had mT<0.5 ppm ∘C−1.
Figures 5b, e, and 4c show the temperature dependence of nodes located at EBMUD, Montclair, and Elsa Widenmann, respectively. Figures 5a, d, and 4b show a comparison of the data at EBMUD, Montclair, and Elsa, respectively, with and without adjustment for a temperature-dependent zero offset. With the application of the temperature correction, the magnitudes of the diurnal cycles are reduced and demonstrate much better agreement in amplitude and phase with the Picarro instrument. The resulting diurnal cycle at EMBUD shows a much more typical diurnal cycle for an urban site, with a maximum occurring at mid-morning (Fig. 5c). At Montclair, the magnitude of the diurnal cycle is reduced, reaching a maximum of ∼ 430 ppm CO2 during the early morning, and a minimum of ∼ 412 ppm CO2 during midday–a pattern much more aligned with the diurnal cycle exhibited at CPS (Figs. 3b, 5c).
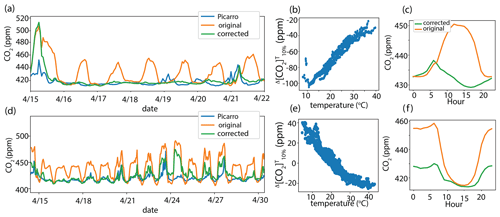
Figure 5CO2 mixing ratios at (a) EBMUD and (d) Montclair with no temperature correction (orange), temperature correction applied (green), and measured with a Picarro instrument at the Richmond Field Station supersite (blue). Temperature dependence of at (b) EBMUD and (e) Montclair. Diurnal cycle with and without temperature correction at (c) EBMUD and (f) Montclair.
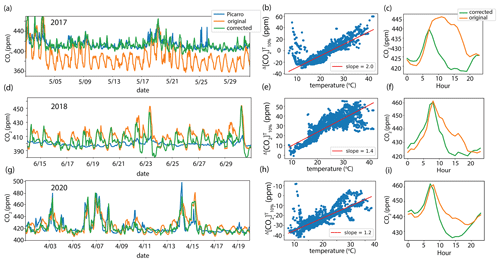
Figure 6Data from 2017 are in top panels, 2018 are in middle panels, 2020 are in bottom panels. (a) CO2 mixing ratios at Laney College with no temperature correction (green), temperature correction applied (blue), and measured with a Picarro instrument at the Richmond Field Station supersite (2018 and 2020) or with the Exploratorium Buoy (2017). (b) Temperature dependence at Laney College of . (c) Laney College diurnal CO2 cycle with (green) and without (orange) temperature correction.
Following confirmation of the effectiveness of the temperature correction method on the sensors deployed at EBMUD in 2020 (EBMUD 2020, hereafter sensors will be referred to with the name and site year) and Montclair 2018, we examined the temperature-corrected CO2 data at the Laney College BEACO2N site during the spring (March–June) of three different years when different Vaisala CarboCap GMP343 instruments were deployed. Given the hypothesis that the observed temperature dependence is due to temperature-dependent errors in the Vaisala CO2 signal, a successful calibration should be sensor specific, rather than site specific. Figure 6b demonstrates the varying temperature dependence during three different years with different instrument deployments. Each deployment has a distinct offset and slope of vs. temperature. During all deployment years, the temperature correction results in better agreement between the reference instruments and the Vaisala data (e.g., 14 April 2020), while preserving local signals (e.g., 15 June 2018) (Fig. 6a). The correction is also effective for the data record before deployment of the Picarro reference instrument in August 2017, when the Exploratorium CO2 Buoy, located in the San Francisco Bay, was used as a reference instrument (Fig. 6a). The correction of the CO2 diurnal cycle at Laney College is most notable during 2017, although midday levels of CO2 are reduced in the corrected data for 2018 and 2020 as well (Fig. 6c).
The temperature correction method was further validated by examining neighboring sites in two regions of the Bay Area during and before periods of high CO2 during September 2020 northern California fires. The Richmond sites of Washington Elementary School, Nystrom Elementary School, Dejean Middle School, and Peres Elementary and the Vallejo sites of Beverly Hills Elementary School, Mare Island Health and Fitness Academy, Grace Patterson Elementary School, and Highland Elementary School were compared. The resulting temperature-dependent percent differences of CO2 between adjacent sites are reduced to approximately 0 %–2 % from 1 %–5 % (Figs. S3, S6). Temperature corrections also result in better agreement in CO2 mixing ratios between adjacent sites in Richmond (Figs. 7 and S2) and in Vallejo (Figs. S4, S5). The results were identical when a multiplicative correction term, rather than additive, was considered (e.g., if the temperature effect was assumed to be on the CO2 signal magnitude rather than entirely on the instrument zero).
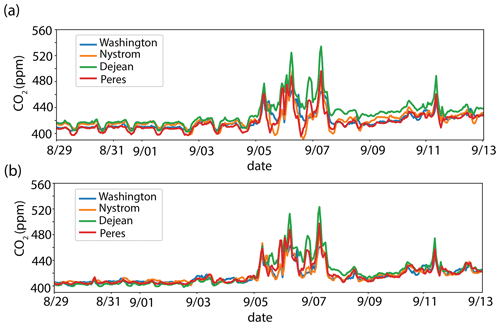
Figure 7CO2 mixing ratios during and before 2020 September wildfires at four adjacent sites in Richmond without (a) and with (b) temperature correction.
Comparison of nearest-neighbor sites
To assess the improvement in the network precision following application of the temperature-dependence correction, we combined observations from the entire Bay Area network using data from all of 2020. All sites with available data for more than one month of 2020 were included. Nearest neighbor pairs of each site were identified, where nearest neighbors to an individual site were considered as the closest BEACO2N sites within a 2 km radius of the site. There are 53 unique nearest neighbor pairs.
For each nearest neighbor pair X and Y, an array of the fractional differences between sites was calculated as: . This was done using both the measurements before and after correction for temperature-dependent instrument zero . Figure 8a and d show the fractional differences of each nearest neighbor pair as a histogram calculated using and , respectively. Most nearest neighbor site pairs exhibit a distribution of fractional differences centered close to zero, with both positive and negative tails (Fig. 8a, d). The temperature correction results in a clear improvement of agreement between nearest neighboring sites, with the mean of the absolute value of the average fractional differences of all nearest neighbor pairs decreasing by a factor of 2 from 0.025 to 0.013. For , this represents an average difference of 6.5 ppm at [CO2]=500 ppm. Figure 8b and e express the fractional differences of nearest neighbor pairs as a single distribution calculated using and , respectively. Fit to a Lorentz distribution, the mean and scale parameter of the distribution of nearest neighbor pairs using is 0.0026 and 0.014, respectively, without accounting for temperature dependence and there is a substantial narrowing of the distribution, resulting in a mean and scale parameter of 0.005 and 0.007, respectively, after accounting for the effect of a temperature-dependent offset.
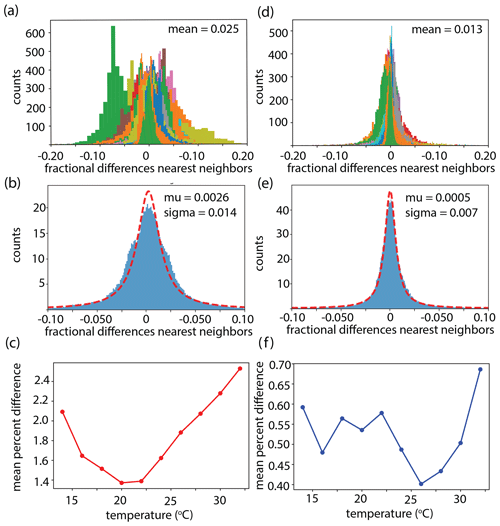
Figure 8Histogram of the fractional differences between nearest neighbors sites (a) without and (d) with the temperature correction applied. Different colors represent different pairs of neighboring sites. Histogram of the fractional differences between all aggregated nearest neighboring sites (b) without and (e) with the temperature correction applied fit to a Lorentz distribution. Network mean of the percent difference for each nearest neighbor pair averaged by 2 ∘C bins (c) without and (f) with temperature correction applied.
Further analysis was performed to confirm that the temperature correction method eliminates any temperature-dependent disagreement between nearest neighboring sites. The nearest neighbor fractional differences of CO2 data were separated into 2 ∘C temperature bins. For each temperature bin, the absolute value of the mean fractional difference between each nearest neighbor pair, using either or , was calculated. We then averaged the mean fractional difference in each temperature bin over all nearest neighbor pairs. A plot of the resulting network mean percent difference vs. temperature is shown in Fig. 8c and f, using and data, respectively. In the original data, the mean percent differences were greatest at both high and low temperatures. In the temperature-corrected data, there is no clear dependence of nearest neighbor mean percent differences on temperature. The mean percent difference at all temperatures is also reduced.
Turner et al. (2016) suggested that a mismatch error of ∼ 1 ppm CO2 would be compatible with relevant constraints on point, line, and area CO2 sources of 147, 45, and 9 t C h−1, respectively. Minimizing the network measurement error to close to 1 ppm is desirable, as at this measurement uncertainty, the error in emissions estimates from inverse modeling becomes dominated by model uncertainties (Turner et al., 2016). Assessing network error in the field is, however, a complex problem. We approach the problem by exploring differences between adjacent nodes, which should be an upper limit to the uncertainty. Although the site-to-site variation is strongly influenced by local emissions sources, there are also strong correlations with changes in urban-, synoptic-, and global-scale CO2 signals that are spatially coherent across pairs of adjacent nodes. Variances between adjacent nodes are due to a combination of true site-specific signals and instrument biases. It is therefore difficult to know the minimum variance in adjacent nodes for a hypothetical “perfect” measurement. For nearest neighbor sites, the majority of the CO2 signal should show near-zero difference, representing the background signal. In the observation record we would also expect moments when either site in a pair has a larger signal, driven by local emission sources and meteorology. Sites closer to the highway also typically have larger CO2 signals (Shusterman et al., 2018). In the following section we describe a procedure for evaluating network error and summarize the improvements following inclusion of the temperature correction described above.
4.1 Site variance and correlation length scales
To evaluate the network error, a semivariogram of γnn vs. distance was constructed for (Fig. 9). Using data from all sites with more than three days of available data during the summer of 2020, we calculated the semivariance between CO2 measurements at each BEACO2N node, i, and all other sites in the Bay Area network (Eq. 9)
Summer months were chosen because the average and diurnal variability of CO2 mixing ratios are reduced, meaning that measured site variances are relatively more influenced by instrument error, rather than by “true” atmospheric variance, than in the winter. In Fig. 9 the square root of the semivariance is plotted against the distance separating the BEACO2N nodes and fitted with an exponential model. The Picarro reference instrument at the Richmond Field Station was included in this analysis.
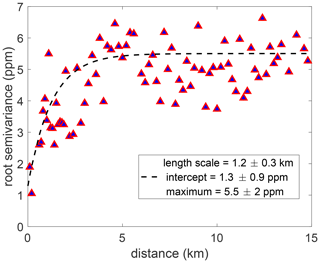
Figure 9Semivariogram of BEACO2N sites for data with temperature correction applied. Data are averaged by 0.1 km bins. Plot includes data from the Picarro instrument at Richmond Field Station.
Using the root semivariance as a correlation metric, in temperature-corrected data, the e-folding length scale for variation is 1.2 ± 0.3 km (1.7 ± 0.7 km using semivariance as a correlation metric, not shown), supporting the BEACO2N hypothesis that 2 km node spacing in a dense network will capture important elements of local variability. The temperature-correction results in a maximum root semivariance of 5.5 ± 2 ppm (reduced from 8 ppm in the uncorrected data). Extrapolated to a distance of zero, the temperature correction method has a predicted root semivariance of 1.3 ± 0.9 ppm, representing the network error. This analysis suggests that the temperature correction method provides a meaningful reduction of network measurement uncertainties toward our desired ∼ 1 ppm network error.
Length scales for correlations (r2) between sites calculated by Shusterman et al. (2018) during the summer 2017 were larger than the 1.2 km length scale identified here for root semivariance (1.7 km for semivariance). To more directly compare, we also performed the method of Shusterman et al. (2018) on the temperature-corrected CO2 data for the summer of 2020. We examined the correlation of CO2 concentrations for every pairing of Bay Area sites during this period for all hours, during the day, and during the night (Fig. S7). The e-folding distance for the decay of r2 correlation coefficients was 2.8 km for all times, 3.7 km during the day, and 2.8 km at night. This is in good agreement with the length scales of 2.9 km at all times, 3.6 km during the day, and 2.2 km at night found by Shusterman et al. (2018). The base-line correlation for sites separated by more than 20 km was found to be 0.46, larger than the correlation background of ∼0.3 of Shusterman et al. (2018). The temperature correction does not affect the characteristic length scale of BEACO2N sites, but improves the overall base-line correlations and variances.
4.2 Contribution of instrument error to site variance
We can represent the network instrument error also by examining the sources contributing to the semivariance between nearest neighboring sites. The semivariance (γnn) of nearest neighboring sites can be expected to have contributions from both “true” variations in emissions and meteorology and erroneous differences caused by instrument error. “True” variations in emissions and meteorology are reflected in temporal changes in CO2 concentrations due to emissions plumes and changes in wind speed and direction. Here we used temporal changes in CO2 concentrations at a certain site as a proxy for “true” atmospheric variations in CO2. To estimate the portion of the semivariance resulting from atmospheric phenomena, an analogous quantity for the hourly variations in CO2 was calculated for each site according to Eq. (10):
where N is the number of hours of data and [CO2]h , and [CO2]h+1 are the measured mixing ratios of CO2 at each hour and 1 h later, respectively. The individual instrument error was then calculated as:
The resulting upper-bound instrument error from the median of individual instrument errors for the Bay Area network is 2.5 ± 0.5 ppm. (This estimate for nontemperature corrected data is 4.5 ± 0.9 ppm). We consider this an upper bound because hourly variations in the CO2 signal reflects the atmospheric changes at an individual site, which may not match with the atmospheric changes at the nearest neighbor sites. Variations in emissions or wind velocity may result in larger “true” differences between a site and its nearest neighbor than are represented by the site's hourly variability.
To reduce the influence from short-term atmospheric variations, the network error was also estimated using an individual site's root mean squared error (RMSEi) as a metric for “true” atmospheric variation (Eq. 12) and a “paired” RMSE (RMSEpaired) using the mean CO2 signal of its nearest neighbor site () as a measure of total variation (Eq. 13). The site error was then calculated according to Eq. 14:
The resulting network instrument errors were between 0.5 and 4 ppm, with a median of 1.6 ± 0.4 ppm, in good agreement with the error calculated from the semivariogram fit. Based on these analyses, we estimate the network error of the Bay Area BEACO2N network to be less than 1.6 ppm, close to our goal of 1 ppm network error.
The BEACO2N network has recently been extended to several other cities, and will further expand to additional locations in coming years. Currently, locations where BEACO2N nodes are deployed (in addition to the Bay Area) are Houston (19 nodes, network start November 2017), Glasgow in collaboration with the University of Strathclyde (> 20 nodes, network start May 2021), New York City (8 nodes, network start April 2018), and Los Angeles, in collaboration with the University of Southern California (12 nodes, network start May 2021). The goal of the network is to be self-calibrated, as not all locations at which the nodes will be deployed have a highly precise and frequently calibrated reference instrument. As such, an alternative method of obtaining a reference for the determination of drift, offset, and temperature dependence is needed.
We find that the network median [CO2]STP can be used as a reference. To begin, we define the network median as the median [CO2]STP of sites having a temperature-dependent slope (mT) less than 1 ppm ∘C−1. is used as a “reference site” from which temperature-based 10th percentile data is calculated for the determination of :
5.1 Bay Area tests
We observe good agreement between the Picarro reference instrument during 2020 and (Fig. 10). The mean percent difference considering all 2020 data is 0.46 %, representing an accuracy error of 2 ppm at 420 ppm CO2 (Fig. 10d). We also do not see evidence of a temperature-dependent offset between the Picarro reference instrument and .
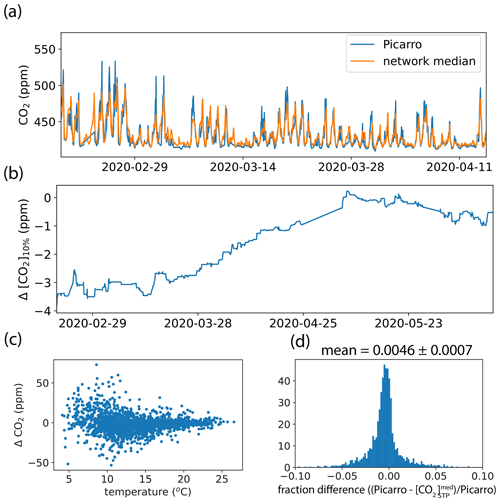
Figure 10(a) CO2 mixing ratios measured by the Picarro instrument at the Richmond Field Station (blue) and the median CO2 of all Bay Area nodes having a temperature-dependent slope less than an absolute value of 1 ppm ∘C−1 (orange). (b) The difference in the tenth percentile of CO2 mixing ratios measured by the Picarro instrument and the network median plotted versus date and (c) versus temperature. (d) Histogram of the fractional differences between Picarro CO2 mixing ratios and the network median. Data for (c) and (d) include all of 2020.
The precision of the Bay Area network is negligibly affected when the network median is used as the reference, with the mean of the absolute value of the average fractional differences of all nearest neighbor pairs equal to 0.015 ± 0.008 (compared to 0.013 ± 0.007 with the Picarro as reference) (Fig. S8). The resulting maximum root semivariance is 5.5 ± 2 ppm and extrapolated root semivariance at 0 km separation is 0.8 ± 0.9 ppm, respectively, approximately equal to the values calculated when the Picarro is used as a reference. The network accuracy is however, more appreciably altered. Figure 11 shows the fractional difference between determined using the Picarro and as a reference at each site. The resulting mean percent difference is 0.51 ± 0.02 %, representing a network accuracy error of 2 ppm at 420 ppm CO2. This accuracy error is mainly driven by small differences in the offsets (2 ppm on average) and mT (0.2 ppm ∘C−1 on average, see Supplement) between calculated using the Picarro and as a reference. These results suggest that the network precision can be expected to remain near 1 ppm CO2 with the use of as a reference, but additional accuracy error of 2 ppm may be introduced. The influence of a sea breeze in the Bay Area makes the median tenth percentile CO2 measured by Bay Area nodes a regional background. Although the median tenth percentile of other inland sensor networks may not represent a regional background, it can be expected to represent the overall network regional average baseline.
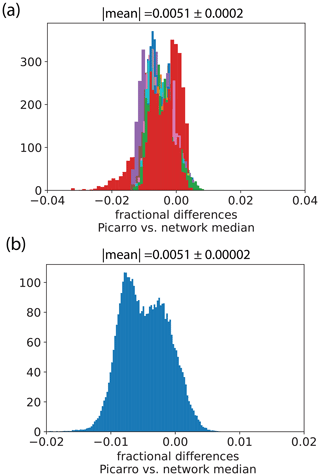
Figure 11(a) Histogram of the fractional differences between sites with temperature-corrected CO2 calculated using the Picarro instrument and the Bay Area network median as a reference. Different colors represent different sites. The mean indicated is the average of the absolute values of each neighboring pair's mean fractional difference. (b) Histogram of the aggregated fractional differences between sites with temperature-corrected CO2 calculated using the Picarro instrument and the Bay Area network median as a reference. The mean and error indicated are the mean and 95 % confidence interval of the distribution.
Analysis of the Bay Area network was performed on the 36 nodes with sufficient data availability for 2020. However, the newly established networks have fewer nodes than in the Bay Area. To use as a reference, we must have sufficient nodes from which to calculate the network median. To evaluate this, for n=1–26, a random subset of n Bay Area nodes was selected 100 times. For each of the 100 random subsets of n nodes, the mean fraction difference was calculated between the network median CO2 and the median calculated using the subset. The average and standard error of the 100 mean fraction differences was then calculated. The results of this analysis are presented in Fig. 12. We suggest that a minimum of 7 nodes with mT less than 1 ppm ∘C−1 is required for the accuracy error to be lower than 2 %. For less than 1 % error, at least 12 nodes are required.
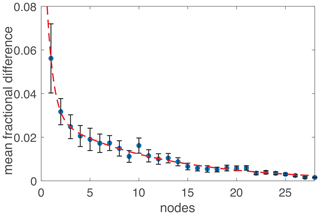
Figure 12Fractional difference between the Bay Area network median calculated from all Bay Area sites and the network median calculated from a subset of between one and 26 nodes. A random subset of n=1–26 nodes were selected to calculate the mean fractional difference between the network median CO2 and the median calculated using the subset. This was repeated 100 times for each of n=1–26 nodes. The reported fractional difference and error bars are the average and 95 % confidence interval of the mean fractional difference from the 100 random samples.
5.2 Houston
Data from the Houston network were subsequently calibrated using as a reference for determining temperature dependence, drift, and offset. Temperature dependence calibration of each site in the Houston network was performed twice. All sites were first included in and sites with mT greater than 1 ppm ∘C−1 were identified. These sites were then excluded from and each site was recalibrated. Histograms of the fraction differences between nearest neighbor sites are shown in Fig. 13. The average mean percent difference between nearest neighbors was 2 ± 1 %. Though considerably larger than the differences between nearest neighbors in the Bay Area network, it is not immediately clear whether this difference is caused by greater precision error in Houston or differing meteorology and CO2 sources that cause greater differences between CO2 mixing ratios at adjacent sites. We attempted to perform a similar instrumental error analysis, but there are currently insufficient overlapping CO2 data in Houston for uncertainty analysis. However, we do not have reason to expect the instrument errors would be any larger in the Houston network.
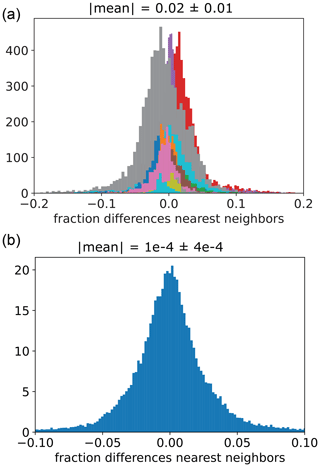
Figure 13(a) Histogram of the fractional differences between nearest neighbors sites in the Houston network with the temperature correction applied using the network median as a reference. Different colors represent different pairs of neighboring sites. The mean indicated is the average of the absolute values of each neighboring pair’s mean fractional difference. The error is the associated 95 % confidence interval. (b) Histogram of the fractional differences between all aggregated nearest neighbors sites with the temperature correction applied. The mean and error indicated are the mean and 95 % confidence interval, respectively, of the distribution.
We have assessed the accuracy of the BEACO2N network following in situ calibration of the temperature-dependence in Vaisala CO2 sensors. We report meaningful reductions in network uncertainties following application of a temperature-dependence correction, and a resulting network instrument error of 1.6 ppm CO2 or less.
A method for correcting Vaisala instrument temperature dependence in BEACO2N has been established and evaluated using sites across the San Francisco Bay Area network. The method corrects observations from individual instruments so that they exhibit a temperature dependence in their lowest temperature-based 10th percentile of CO2 data that is equivalent to that of a reference site, thus correcting erroneous instrument temperature dependence while preserving true diurnal cycles and local signals. This field calibration of temperature dependence can be entirely internal to the network and does not necessarily require a reference instrument, although the addition of a reference instrument provides greater network accuracy. The implementation of the temperature correction method produces more reasonable diurnal cycles, diurnal cycles that are maintained for sites influenced by similar emissions sources, and better agreement between adjacent sites. We additionally describe methods for characterizing network scale uncertainties and site-to-site biases. The average variation between adjacent sites was found to be 1.3 % following implementation of temperature correction (compared to 2.5 % prior to the correction). The temperature correction greatly improves the precision of CO2 measurements in the BEACO2N network.
We show that the network precision can be maintained at 1.3 % even in locations without a high-cost reference instrument, using the network median as a reference, provided that there are at least 12 sites with small temperature dependencies. This has important implications for the expansion of BEACO2N to additional cities globally, as well as for other dense low-cost CO2 networks. However, without a reference instrument, the network accuracy error increases relative to a network that utilizes a reference instrument by 2 ppm.
The data used for this study are publicly available at http://beacon.berkeley.edu (Cohen Research, 2021). Raw data can be given upon request.
The supplement related to this article is available online at: https://doi.org/10.5194/amt-14-5487-2021-supplement.
JK, HLF, CN, and PJW collected the data used in this analysis. ERD composed the manuscript and designed and executed the analysis in consultation with JK and KW. KW also aided with data processing and implementation of the temperature calibration method. JK and RCC provided additional manuscript feedback and RCC supervised the project.
Ronald C. Cohen is associate editor of Atmospheric Measurement Techniques.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We also thank Alexander J. Turner for his input and former members of the BEACO2N project for establishing the network: Alexis A. Shusterman, Virginia Teige, and Kaitlyn Lieschke.
This research has been supported by the Koret Foundation and University of California, Berkeley.
This paper was edited by William R. Simpson and reviewed by two anonymous referees.
Andrews, A. E., Kofler, J. D., Trudeau, M. E., Williams, J. C., Neff, D. H., Masarie, K. A., Chao, D. Y., Kitzis, D. R., Novelli, P. C., Zhao, C. L., Dlugokencky, E. J., Lang, P. M., Crotwell, M. J., Fischer, M. L., Parker, M. J., Lee, J. T., Baumann, D. D., Desai, A. R., Stanier, C. O., De Wekker, S. F. J., Wolfe, D. E., Munger, J. W., and Tans, P. P.: CO2, CO, and CH4 measurements from tall towers in the NOAA Earth System Research Laboratory's Global Greenhouse Gas Reference Network: instrumentation, uncertainty analysis, and recommendations for future high-accuracy greenhouse gas monitoring efforts, Atmos. Meas. Tech., 7, 647–687, https://doi.org/10.5194/amt-7-647-2014, 2014. a
Bréon, F. M., Broquet, G., Puygrenier, V., Chevallier, F., Xueref-Remy, I., Ramonet, M., Dieudonné, E., Lopez, M., Schmidt, M., Perrussel, O., and Ciais, P.: An attempt at estimating Paris area CO2 emissions from atmospheric concentration measurements, Atmos. Chem. Phys., 15, 1707–1724, https://doi.org/10.5194/acp-15-1707-2015, 2015. a
Brondfield, M. N., Hutyra, L. R., Gately, C. K., Raciti, S. M., and Peterson, S. A.: Modeling and validation of on-road CO2 emissions inventories at the urban regional scale, Environ. Pollut., 170, 113–123, https://doi.org/10.1016/j.envpol.2012.06.003, 2012. a
Cohen Research: Berkeley Environmental Air-quality & CO2 Network (BEACO2N), University of California Berkeley, available at: http://beacon.berkeley.edu, last access: 9 August 2021. a
Coutts, A. M., Beringer, J., and Tapper, N. J.: Characteristics influencing the variability of urban CO2 fluxes in Melbourne, Australia, Atmos. Environ., 41, 51–62, https://doi.org/10.1016/j.atmosenv.2006.08.030, 2007. a, b
Fu, P., Xie, Y., Moore, C. E., Myint, S. W., and Bernacchi, C. J.: A Comparative Analysis of Anthropogenic CO2 Emissions at City Level Using OCO-2 Observations: A Global Perspective, Earth Future, 7, 1058–1070, https://doi.org/10.1029/2019EF001282, 2019. a
Gately, C. K., Hutyra, L. R., Wing, I. S., and Brondfield, M. N.: A Bottom up Approach to on-Road CO2 Emissions Estimates: Improved Spatial Accuracy and Applications for Regional Planning, Environ. Sci. Technol., 47, 2423–2430, https://doi.org/10.1021/es304238v, 2013. a
Gately, C. K., Hutyra, L. R., Peterson, S., and Sue Wing, I.: Urban emissions hotspots: Quantifying vehicle congestion and air pollution using mobile phone GPS data, Environ. Pollut., 229, 496–504, https://doi.org/10.1016/j.envpol.2017.05.091, 2017. a
Gurney, K. R., Mendoza, D. L., Zhou, Y., Fischer, M. L., Miller, C. C., Geethakumar, S., and de la Rue du Can, S.: High Resolution Fossil Fuel Combustion CO2 Emission Fluxes for the United States, Environ. Sci. Technol., 43, 5535–5541, https://doi.org/10.1021/es900806c, 2009. a
Idso, S. B., Idso, C. D., and Balling, R. C.: Seasonal and diurnal variations of near-surface atmospheric CO2 concentration within a residential sector of the urban CO2 dome of Phoenix, AZ, USA, Atmos. Environ., 36, 1655–1660, https://doi.org/10.1016/S1352-2310(02)00159-0, 2002. a, b
IPCC: Summary for Policymakers, in: Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S. L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M. I., Huang, M., Leitzell, K., Lonnoy, E., Matthews, J. B. R., Maycock, T. K., Waterfield, T., Yelekçi, O., Yu, R., and Zhou, B., Cambridge University Press, in press, 2021. a
Kim, J., Shusterman, A. A., Lieschke, K. J., Newman, C., and Cohen, R. C.: The BErkeley Atmospheric CO2 Observation Network: field calibration and evaluation of low-cost air quality sensors, Atmos. Meas. Tech., 11, 1937–1946, https://doi.org/10.5194/amt-11-1937-2018, 2018. a, b
Kort, E. A., Angevine, W. M., Duren, R., and Miller, C. E.: Surface observations for monitoring urban fossil fuel CO2 emissions: Minimum site location requirements for the Los Angeles megacity, J. Geophys. Res.-Atmos., 118, 1577–1584, https://doi.org/10.1002/jgrd.50135, 2013. a, b
Lateb, M., Meroney, R., Yataghene, M., Fellouah, H., Saleh, F., and Boufadel, M.: On the use of numerical modelling for near-field pollutant dispersion in urban environments – A review, Environ. Pollut., 208, 271–283, https://doi.org/10.1016/j.envpol.2015.07.039, 2016. a
Lauvaux, T., Miles, N. L., Deng, A., Richardson, S. J., Cambaliza, M. O., Davis, K. J., Gaudet, B., Gurney, K. R., Huang, J., O'Keefe, D., Song, Y., Karion, A., Oda, T., Patarasuk, R., Razlivanov, I., Sarmiento, D., Shepson, P., Sweeney, C., Turnbull, J., and Wu, K.: High-resolution atmospheric inversion of urban CO2 emissions during the dormant season of the Indianapolis Flux Experiment (INFLUX), J. Geophys. Res.-Atmos., 121, 5213–5236, https://doi.org/10.1002/2015JD024473, 2016. a
Lauvaux, T., Gurney, K. R., Miles, N. L., Davis, K. J., Richardson, S. J., Deng, A., Nathan, B. J., Oda, T., Wang, J. A., Hutyra, L., and Turnbull, J.: Policy-Relevant Assessment of Urban CO2 Emissions, Environ. Sci. Technol., 54, 10237–10245, https://doi.org/10.1021/acs.est.0c00343, 2020. a
Martin, C. R., Zeng, N., Karion, A., Dickerson, R. R., Ren, X., Turpie, B. N., and Weber, K. J.: Evaluation and environmental correction of ambient CO2 measurements from a low-cost NDIR sensor, Atmos. Meas. Tech., 10, 2383–2395, https://doi.org/10.5194/amt-10-2383-2017, 2017. a, b
McKain, K., Wofsy, S. C., Nehrkorn, T., Eluszkiewicz, J., Ehleringer, J. R., and Stephens, B. B.: Assessment of ground-based atmospheric observations for verification of greenhouse gas emissions from an urban region, P. Natl. Acad. Sci. USA, 109, 8423–8428, https://doi.org/10.1073/pnas.1116645109, 2012. a
Müller, M., Graf, P., Meyer, J., Pentina, A., Brunner, D., Perez-Cruz, F., Hüglin, C., and Emmenegger, L.: Integration and calibration of non-dispersive infrared (NDIR) CO2 low-cost sensors and their operation in a sensor network covering Switzerland, Atmos. Meas. Tech., 13, 3815–3834, https://doi.org/10.5194/amt-13-3815-2020, 2020. a, b, c
Nathan, B. J., Lauvaux, T., Turnbull, J. C., Richardson, S. J., Miles, N. L., and Gurney, K. R.: Source Sector Attribution of CO2 Emissions Using an Urban CO CO2 Bayesian Inversion System, J. Geophys. Res.-Atmos., 123, 13611–13621, https://doi.org/10.1029/2018JD029231, 2018. a
Pataki, D. E., Bowling, D. R., and Ehleringer, J. R.: Seasonal cycle of carbon dioxide and its isotopic composition in an urban atmosphere: Anthropogenic and biogenic effects, J. Geophys. Res.-Atmos., 108, 4735, https://doi.org/10.1029/2003JD003865, 2003. a
Pataki, D. E., Bowling, D. R., Ehleringer, J. R., and Zobitz, J. M.: High resolution atmospheric monitoring of urban carbon dioxide sources, Geophys. Res. Lett., 33, L03813, https://doi.org/10.1029/2005GL024822, 2006. a
Riley, W. J., Hsueh, D. Y., Randerson, J. T., Fischer, M. L., Hatch, J. G., Pataki, D. E., Wang, W., and Goulden, M. L.: Where do fossil fuel carbon dioxide emissions from California go? An analysis based on radiocarbon observations and an atmospheric transport model, J. Geophys. Res.-Biogeo., 113, G04002, https://doi.org/10.1029/2007JG000625, 2008. a
Rogelj, J., Shindell, D., Jiang, K., Fifita, S., Forster, P., Ginzburg, V., Handa, C., Kheshgi, H., Kobayashi, S., Kriegler, E., Mundaca, L., Séférian, R., and Vilariño, M. V.: Mitigation Pathways Compatible with 1.5 ∘C in the Context of Sustainable Development, in: Global Warming of 1.5 ∘C. An IPCC Special Report on the impacts of global warming of 1.5 ∘C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty, edited by: Masson-Delmotte, V., Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P. R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., Connors, S., Matthews, J. B. R., Chen, Y., Zhou, X., Gomis, M. I., Lonnoy, E., Maycock, T., Tignor, M., and Waterfield, T., in press, 2021. a
Sargent, M., Barrera, Y., Nehrkorn, T., Hutyra, L. R., Gately, C. K., Jones, T., McKain, K., Sweeney, C., Hegarty, J., Hardiman, B., Wang, J. A., and Wofsy, S. C.: Anthropogenic and biogenic CO2 fluxes in the Boston urban region, P. Natl. Acad. Sci. USA, 115, 7491–7496, https://doi.org/10.1073/pnas.1803715115, 2018. a
Shusterman, A. A., Teige, V. E., Turner, A. J., Newman, C., Kim, J., and Cohen, R. C.: The BErkeley Atmospheric CO2 Observation Network: initial evaluation, Atmos. Chem. Phys., 16, 13449–13463, https://doi.org/10.5194/acp-16-13449-2016, 2016. a, b, c, d, e, f, g, h, i
Shusterman, A. A., Kim, J., Lieschke, K. J., Newman, C., Wooldridge, P. J., and Cohen, R. C.: Observing local CO2 sources using low-cost, near-surface urban monitors, Atmos. Chem. Phys., 18, 13773–13785, https://doi.org/10.5194/acp-18-13773-2018, 2018. a, b, c, d, e, f, g, h, i, j
Thompson, R. L., Manning, A. C., Gloor, E., Schultz, U., Seifert, T., Hänsel, F., Jordan, A., and Heimann, M.: In-situ measurements of oxygen, carbon monoxide and greenhouse gases from Ochsenkopf tall tower in Germany, Atmos. Meas. Tech., 2, 573–591, https://doi.org/10.5194/amt-2-573-2009, 2009. a
Turnbull, J. C., Sweeney, C., Karion, A., Newberger, T., Lehman, S. J., Tans, P. P., Davis, K. J., Lauvaux, T., Miles, N. L., Richardson, S. J., Cambaliza, M. O., Shepson, P. B., Gurney, K., Patarasuk, R., and Razlivanov, I.: Toward quantification and source sector identification of fossil fuel CO2 emissions from an urban area: Results from the INFLUX experiment, J. Geophys. Res.-Atmos., 120, 292–312, https://doi.org/10.1002/2014JD022555, 2015. a, b, c
Turnbull, J. C., Karion, A., Davis, K. J., Lauvaux, T., Miles, N. L., Richardson, S. J., Sweeney, C., McKain, K., Lehman, S. J., Gurney, K. R., Patarasuk, R., Liang, J., Shepson, P. B., Heimburger, A., Harvey, R., and Whetstone, J.: Synthesis of Urban CO2 Emission Estimates from Multiple Methods from the Indianapolis Flux Project (INFLUX), Environ. Sci. Technol., 53, 287–295, https://doi.org/10.1021/acs.est.8b05552, 2019. a
Turner, A. J., Shusterman, A. A., McDonald, B. C., Teige, V., Harley, R. A., and Cohen, R. C.: Network design for quantifying urban CO2 emissions: assessing trade-offs between precision and network density, Atmos. Chem. Phys., 16, 13465–13475, https://doi.org/10.5194/acp-16-13465-2016, 2016. a, b, c, d, e
Turner, A. J., Kim, J., Fitzmaurice, H., Newman, C., Worthington, K., Chan, K., Wooldridge, P. J., Köehler, P., Frankenberg, C., and Cohen, R. C.: Observed Impacts of COVID-19 on Urban CO2 Emissions, Geophys. Res. Lett., 47, e2020GL090037, https://doi.org/10.1029/2020GL090037, 2020. a, b
United Nations, Human Settlement Programme: Hot Cities: Battle Ground for Climate Change, Washington, DC, USA, 2011. a
Vaisala: Vaisala CARBOCAP Carbon Dioxide Probe GMP343 User's Guide, Vaisala Oyj, Helsinki, Finland, 2013. a, b, c, d
van Leeuwen, C.: Improved Operation of the Vaisala Carbocap GMP343 for the School CO2-Web, University of Groningen, Groningen, the Netherlands, 2010. a, b, c, d, e
Vardoulakis, S., Fisher, B. E., Pericleous, K., and Gonzalez-Flesca, N.: Modelling air quality in street canyons: a review, Atmos. Environ., 37, 155–182, https://doi.org/10.1016/S1352-2310(02)00857-9, 2003. a
Verhulst, K. R., Karion, A., Kim, J., Salameh, P. K., Keeling, R. F., Newman, S., Miller, J., Sloop, C., Pongetti, T., Rao, P., Wong, C., Hopkins, F. M., Yadav, V., Weiss, R. F., Duren, R. M., and Miller, C. E.: Carbon dioxide and methane measurements from the Los Angeles Megacity Carbon Project – Part 1: calibration, urban enhancements, and uncertainty estimates, Atmos. Chem. Phys., 17, 8313–8341, https://doi.org/10.5194/acp-17-8313-2017, 2017. a
Ye, X., Lauvaux, T., Kort, E. A., Oda, T., Feng, S., Lin, J. C., Yang, E. G., and Wu, D.: Constraining Fossil Fuel CO2 Emissions From Urban Area Using OCO-2 Observations of Total Column CO2, J. Geophys. Res.-Atmos., 125, e2019JD030528, https://doi.org/10.1029/2019JD030528, 2020. a
- Abstract
- Introduction
- Development of a CO2 field calibration method for Vaisala temperature dependence
- Evaluation of calibration
- Assessment of the network error
- Application to other city networks
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Development of a CO2 field calibration method for Vaisala temperature dependence
- Evaluation of calibration
- Assessment of the network error
- Application to other city networks
- Conclusions
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement