ALADIN laser frequency stability and its impact on the Aeolus wind error

The acquisition of atmospheric wind profiles on a global scale was realized by the launch of the Aeolus satellite, carrying the unique Atmospheric LAser Doppler INstrument (ALADIN), the first Doppler wind lidar in space. One major component of ALADIN is its high-power, ultraviolet (UV) laser transmitter, which is based on an injection-seeded, frequency-tripled Nd:YAG laser and fulfills a set of demanding requirements in terms of pulse energy, pulse length, repetition rate, and spatial and spectral beam properties. In particular, the frequency stability of the laser emission is an essential parameter which determines the performance of the lidar instrument as the Doppler frequency shifts to be detected are on the order of 10⁸ smaller than the frequency of the emitted UV light. This article reports the assessment of the ALADIN laser frequency stability and its influence on the quality of the Aeolus wind data. Excellent frequency stability with pulse-to-pulse variations of about 10 MHz (root mean square) is evident for over more than 2 years of operations in space despite the permanent occurrence of short periods with significantly enhanced frequency noise (> 30 MHz). The latter were found to coincide with specific rotation speeds of the satellite's reaction wheels, suggesting that the root cause are micro-vibrations that deteriorate the laser stability on timescales of a few tens of seconds. Analysis of the Aeolus wind error with respect to European Centre for Medium-Range Weather Forecasts (ECMWF) model winds shows that the temporally degraded frequency stability of the ALADIN laser transmitter has only a minor influence on the wind data quality on a global scale, which is primarily due to the small percentage of wind measurements for which the frequency fluctuations are considerably enhanced. Hence, although the Mie wind bias is increased by 0.3 m s⁻¹ at times when the frequency stability is worse than 20 MHz, the small contribution of 4 % from all Mie wind results renders this effect insignificant (< 0.1 m s⁻¹) when all winds are considered. The impact on the Rayleigh wind bias is negligible even at high frequency noise. Similar results are demonstrated for the apparent speed of the ground returns that are measured with the Mie and Rayleigh channel of the ALADIN receiver. Here, the application of a frequency stability threshold that filters out wind observations with variations larger than 20 or 10 MHz improves the accuracy of the Mie and Rayleigh ground velocities by only 0.05 and 0.10 m s⁻¹, respectively, however at the expense of useful ground data.

1 Introduction

The launch of the ESA's Aeolus mission in August 2018 was an influential event in the history of spaceborne active remote sensing (Stith et al., 2018; Kanitz et al., 2019; Parrinello et al., 2020). Since then, the first Doppler wind lidar in space has offered the acquisition of global wind profiles from the ground up to the lower stratosphere, which helps to fill observation gaps in the global wind data coverage, particularly over the oceans, poles, tropics, and the Southern Hemisphere (Stoffelen et al., 2020). In this manner, the lack of wind data on a global scale, which represented a major deficiency in the Global Observing System (GOS) (Baker et al., 2014; Andersson, 2018; NAS, 2018), was mitigated, thus contributing to the improvement of the accuracy of numerical weather prediction (NWP) (Straume et al., 2020). On 9 January 2020, the operational assimilation of the Aeolus wind data started at the European Centre for Medium-Range Weather Forecasts (ECMWF), followed by the German, French, and British weather services (Deutscher Wetterdienst, DWD; Météo France; and Met Office) in May, June and December 2020, respectively. Recent assessments of the significance of the Aeolus data for NWP have demonstrated a statistically positive impact, especially in the tropics and at the poles, thus providing a useful contribution to the GOS (Rennie and Isaksen, 2020; Rennie et al., 2021; Martin et al., 2021). This was made possible by the identification of and correction for large systematic errors which had strongly degraded the wind data quality in the initial phase of the mission (Kanitz et al., 2020; Reitebuch et al., 2020). Firstly, dark current signal anomalies on single (“hot”) pixels of the Aeolus detectors which had led to wind errors of up to 4 m s⁻¹ were recognized and successfully accounted for by the implementation of dedicated calibration instrument modes (Weiler et al., 2021a). Secondly, biases that were found to be closely correlated with small variations in the temperature distribution across the primary telescope mirror (Rennie and Isaksen, 2020; Weiler et al., 2021b) were corrected.

Apart from these two major issues, the performance of Aeolus and particularly the precision of the Rayleigh wind results are impaired by the lower-than-expected atmospheric return signal levels, which deviated from end-to-end simulations by a factor of 2.0 to 2.5 already shortly after launch (Reitebuch et al., 2020). The situation was aggravated by a progressive decrease in emit energy of the laser transmitter during the first year of operation. Consequently, a switchover to the redundant laser onboard Aeolus was performed in summer of 2019. The second laser showed higher emit energy at a significantly lower decrease rate (Lux et al., 2020a) so that as of September 2021 it provides more than 70 mJ of pulse energy.

A common characteristic of both lasers is the occurrence of periods with significantly increased frequency fluctuations that were not observed in the same manner during on-ground tests. The laser frequency stability is a crucial parameter for the Aeolus mission and many Doppler wind lidar instruments in general given the fact that a wind speed of 1 m s⁻¹ introduces Doppler frequency shifts of only a few megahertz at the operating ultraviolet (UV) wavelength of the laser. Hence, the frequency fluctuations have to be on the same order to ensure sufficiently low wind errors. Frequency-stable laser emission is also essential for other space lidar technologies that rely on high-spectral-resolution lidar (HSRL) or differential absorption lidar (DIAL). These techniques will be applied in the upcoming space missions EarthCARE (Earth Clouds, Aerosols and Radiation Explorer) (Illingworth et al., 2015), ACDL (Aerosol and Carbon Detection Lidar) (Liu et al., 2019) and MERLIN (Methane Remote Sensing Lidar Mission) (Ehret et al., 2017), which are scheduled for launch within the next 5 years. However, it should be mentioned that not all Doppler lidar and HSRL techniques require high frequency stability, especially if the referencing to the outgoing signal is performed on a pulse-by-pulse basis (Baidar et al., 2018; Tucker et al., 2018; Bruneau and Pelon, 2021).

In this context of frequency stability, the topic of micro-vibrations and their influence on the stability of spaceborne lasers is highly relevant. Micro-vibrations are defined as vibrations at frequencies greater than ≈ 1 Hz which cannot be effectively compensated for by the spacecraft attitude and orbit control system (AOCS) (Toyoshima, 2010). They are generated from mechanically moving devices on a satellite and can propagate along the structural panels, thus disturbing the satellite payload and causing spacecraft pointing instability (Dennehy and Alvarez-Salazar, 2018). Current research is primarily focused on the latter effect, especially with regard to optical communication (Chen et al., 2019). However, micro-vibrations can also materialize as translational accelerations which disturb the optical path difference in interferometers and highly sensitive accelerometers in gravimetry missions. The detrimental impact of micro-vibrations on the frequency stability performance of space lidar instruments has not been investigated in detail so far. With regard to Aeolus the main susceptibility to micro-vibrations is related to the alteration of the laser cavity length, which leads to frequency fluctuations in the emitted light. For other space lidar missions – like ICESat, employing the Geoscience Laser Altimeter System (GLAS) (Abshire et al., 2005); ICESat-2, which operates the Advanced Topographic Laser Altimeter System (ATLAS) (Martino et al., 2019); or CALIPSO, deploying the Cloud–Aerosol Lidar with Orthogonal Polarization (CALIOP) (Winker et al., 2006), the requirements in terms of the laser spectral properties are less stringent than for Aeolus, and, hence, micro-vibrations play only a minor role for the stability of the laser. Regarding the Gravity Recovery and Climate Experiment (GRACE) follow-on mission, the sensitivity of the laser ranging interferometer instrument at frequencies greater than 0.2 Hz is limited by the frequency stability of the laser which was assessed by ground tests prior to the launch in 2018 (Abich et al., 2019). Precise quantification of the frequency stability is a challenging task and only possible for Aeolus thanks to its unprecedented spectrometers that enable assessment of this parameter in orbit. For these reasons, literature on laser frequency stability of space lasers and its impact on the data quality of the retrieved products is rather scarce and more related to the preparation of future space missions (Hovis et al., 2008).

This research article aims to provide a comprehensive overview of the frequency stability of the Aeolus laser transmitters and to explore its influence on the quality of the Aeolus wind data. After a short description of the ALADIN instrument and measurement principle (Sect. 2.1), the results from on-ground tests of the laser spectral properties are recapitulated (Sect. 2.2). In Sect. 2.3, the utilization of the Mie receiver channel for the assessment of the laser frequency stability is explained, followed by an introduction of the periods that were analyzed for the present study (Sect. 2.4). Section 3 comprises the results of the analysis, starting with a presentation of the ALADIN laser frequency stability over 1 selected week of the mission (Sect. 3.1). Section 3.2 then elaborates on the correlation of this parameter with the geolocation of the satellite, leading to the detrimental influence of the reaction wheels on the spectral characteristics of the laser (Sect. 3.3) and the identification of micro-vibrations as the most likely root cause (Sect. 3.4). The fourth section addresses the question of to what extent the Aeolus data quality is diminished by the temporally increased frequency noise. After a short assessment regarding the number of affected data in different phases of the mission, the impact of the degraded frequency stability on the accuracy and precision of the wind results (Sect. 4.1) as well as on the ground velocities (Sect. 4.2) is evaluated. Finally, a summary and conclusion of the study are provided in Sect. 5 together with an outlook on possible improvements in future space lidar missions.

2 Methods and datasets

This section provides a brief description of the ALADIN instrument and its operating principle. After summarizing the results from on-ground tests of the laser frequency stability, the approach to assess the frequency stability in orbit by using the Mie channel is explained. Afterwards, the periods of the Aeolus mission that were selected for analysis are presented in the context of the overall performance of the ALADIN laser transmitters over the course of the 2 years after launch in 2018.

2.1 ALADIN configuration and measurement principle

The direct-detection Doppler wind lidar ALADIN onboard Aeolus is composed of a pulsed, frequency-stabilized UV laser transmitter, transmit–receive optics (TRO), a 1.5 m diameter Cassegrain-type telescope, and a dual-channel receiver which is sensitive to both molecular and particle backscatter from clouds and aerosols (ESA, 2008; Stoffelen et al., 2005; Reitebuch, 2012; Reitebuch et al., 2018). A schematic diagram of the instrument is illustrated in Fig. 1.

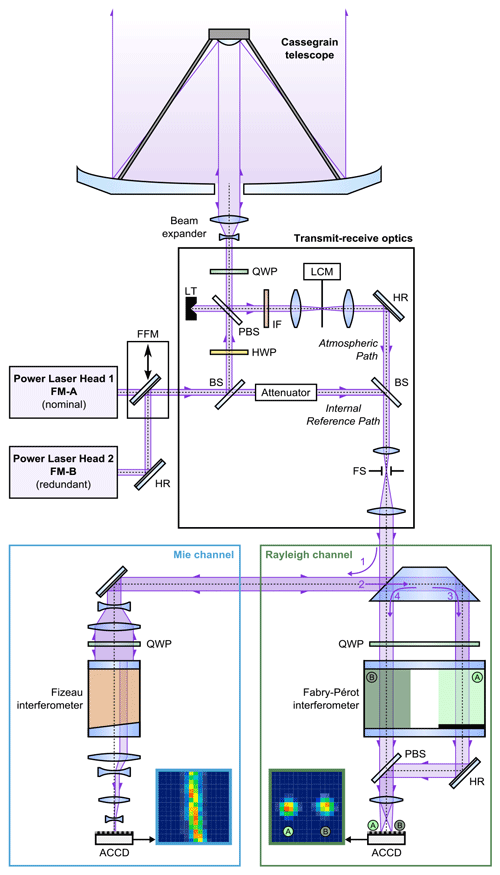
Figure 1 Schematic of the direct-detection Doppler wind lidar ALADIN on board Aeolus. The instrument consists of two fully redundant, switchable UV laser transmitters (FM-A, FM-B), a Cassegrain telescope, transmit–receive optics (TRO) and a dual-channel receiver. The latter is composed of a Fizeau interferometer and sequential Fabry–Pérot interferometers for analyzing the Doppler frequency shift from particulate and molecular backscatter signals, respectively. HR: highly reflective mirror; FFM: flip-flop mechanism; BS: beam splitter; PBS: polarizing beam splitter; HWP: half-wave plate; QWP: quarter-wave plate; IF: interference filter; LT: light trap; LCM: laser chopper mechanism; FS: field stop; ACCD: accumulation charge coupled device. Numbers indicate the sequential light path in the receiver.

A flip-flop mechanism provides the ability to switch between the two fully redundant laser transmitters, referred to as flight models A and B (FM-A, FM-B). Both lasers are realized as diode-pumped Nd:YAG lasers in a master oscillator power amplifier configuration that are frequency-tripled to 354.8 nm emission wavelength (ESA, 2008; Cosentino et al., 2012, 2017; Lux et al., 2020a). A nonplanar Nd:YAG ring laser, frequency-locked to an ultra-low-expansion cavity, provides narrowband seed radiation that is fiber-coupled into the folded cavity of the 80 cm long Q-switched master oscillator (MO). The MO cavity length is actively controlled by means of a piezo actuator in order to find the optimal condition for single longitudinal mode operation for each laser pulse (Cosentino et al., 2017). The cavity control scheme is based on the ramp-hold-fire technique (Henderson et al., 1986), which involves the detection of cavity resonances of the injected seed radiation while sweeping the cavity length and firing the Q-switch at the detected resonance position of the piezo actuator. The actual implementation of this technique in the ALADIN MO is capable of achieving a cavity control length of better than a few nanometers. However, it has the drawback of a delay in the millisecond regime between the detection of the cavity resonance and the laser pulse emission (Trespiti et al., 2017).

The infrared (IR) single longitudinal mode output pulses from the MO (energy: 5 to 10 mJ; full width at half maximum (FWHM) pulse duration: 20 ns; pulse repetition frequency: 50.5 Hz) are amplified in a double-pass pre-amplifier and subsequent single-pass power amplifier, which are each realized by side-pumped and conductively cooled Nd:YAG zigzag slabs. The amplification stage boosts the energy of the IR pulses to more than 250 mJ, before they are guided to the harmonic generation stage of the laser. The latter comprises a set of nonlinear lithium triborate (LBO) crystals to generate UV output pulses with a conversion efficiency of about 25 %, resulting in an in-flight emit energy in excess of 60 mJ.

The UV beam from one of the two switchable laser transmitters is then directed to the telescope, which is used in a monostatic configuration; i.e., signal emission and reception are realized via the same primary and secondary mirror. A small portion (0.5 %) of the beam is separated at a beam splitter (BS) within the TRO configuration and, after being attenuated, guided to the instrument field stop (FS) and receiver channels. This portion is referred to as the internal reference path (INT) signal and serves the determination of the frequency of the outgoing beam as well as the calibration of the frequency-dependent transmission of the receiver spectrometers. The INT signal is thus essential for the wind measurement principle of ALADIN, which relies on detecting frequency differences between the emitted laser pulses and those backscattered from the atmospheric particles and molecules moving with the ambient wind. The frequency shift Δf_Doppler in the backscattered signal that is introduced by virtue of the Doppler effect is proportional to the wind speed v_LOS along the laser beam line of sight (LOS) according to $\mathrm{\Delta }{f}_{\mathrm{Doppler}}=\mathrm{2}{f}_{\mathrm{0}}{v}_{\mathrm{LOS}}/c$, where c is the speed of light, and f₀ is the frequency of the emitted light. The atmospheric return signal collected by the telescope enters the TRO, where it passes through a laser chopper mechanism (LCM) before being spatially overlapped with the INT beam by another beam splitter. Due to the long travel time of the atmospheric return of a few milliseconds, the detection is temporally separated from the INT signal.

The ALADIN receiver consists of two complementary channels which individually derive the Doppler frequency shift from the narrowband (FWHM ≈ 50 MHz) Mie backscatter from particles like clouds and aerosols on the one hand and from the broadband (FWHM ≈ 3.8 GHz at 355 nm and 293 K) Rayleigh–Brillouin backscatter from molecules on the other hand. The Mie channel is realized by a Fizeau interferometer and relies on the fringe-imaging technique (McKay, 2002), where a linear interference pattern (fringe) is vertically imaged onto the detector. The spatial location of the fringe changes approximately linearly with frequency of the incident light so that a Doppler frequency shift manifests as a spatial displacement of the fringe centroid position. Derivation of the Doppler shift from the broadband Rayleigh–Brillouin backscatter spectrum is achieved by two sequential Fabry–Pérot interferometers (FPIs) that are utilized for applying the double-edge technique (Chanin et al., 1989; Garnier and Chanin, 1992; Flesia and Korb, 1999). The two FPIs act as bandpass filters with adequate width and spacing that are symmetrically placed around the frequency of the emitted laser pulse. Measurement of the contrast between the signals transmitted through the two filters allows for accurately determining the frequency shift between the emitted and backscattered laser pulse.

The Mie and Rayleigh signals are finally detected by two accumulation charge-coupled devices (ACCDs) with an array size of 16 pixels × 16 pixels in the imaging zone of the ACCD. The electronic charges of all 16 rows in the image zone are then binned together to one row. For the wind profile, this row is transferred to a memory zone. The latter can store 25 rows, each representing one vertical range gate of the measured wind profile. It is important to note that the atmospheric signals from 18 successive laser pulses are accumulated already on board the spacecraft to so-called “measurements” (duration 0.4 s). Since February 2019, P=19 laser pulses are emitted per measurement interval, from which one is lost due to the readout of the ACCD (P−1 setting). Post-processing on the ground can sum the signals from 30 measurements, i.e., 540 laser pulses, and form one “observation” (duration 12 s). In contrast to the atmospheric return, the INT signal is acquired for each single pulse and stored directly as one row in the memory zone.

According to the above equation for the Doppler frequency shift, a LOS wind speed of 1 m s⁻¹ translates to a frequency shift of 5.63 MHz (at f₀ = 844.75 THz; all subsequent frequency stability values given at this UV frequency). Therefore, in order to measure wind speeds with an accuracy of 1 m s⁻¹, the required relative accuracy of the frequency measurement is on the order of 10⁻⁸, which poses stringent requirements on the frequency stability of the laser transmitter. This is especially true as the atmospheric backscatter from multiple outgoing laser pulses are accumulated on the ACCD prior to digitization and data downlink. This implies that a pulse-to-pulse normalization of the return signal frequency with the internal reference frequency is not possible. Instead, the determined frequency of the pulses averaged over one measurement is affected by inhomogeneous cirrus or broken clouds as only a subset of the 18 pulses may be detected in the atmospheric path. As a result, large frequency variations on the measurement level (over periods of 0.4 s) in combination with atmospheric inhomogeneities result in significant wind errors that are then vertically correlated below the (cloud) bin that filters out some of the emitted pulses (Marksteiner et al., 2015). The same holds true for ground return signals from pulses within one measurement that are reflected off a surface with varying albedo so that the different weighting of the return signals in the accumulation of the pulses results in an error in the determined ground velocity.

2.2 On-ground assessment of the laser frequency stability

Measurement of the ALADIN laser absolute frequency and its temporal stability was done during pre-flight tests under vacuum conditions by means of an external wavelength meter (High Finesse WSU10) that was calibrated using a helium neon laser (Mondin and Bravetti, 2017). The experimental setup was provided by the German Aerospace Center (DLR) and represents an integral part of the diagnostics for determining the spectral properties of the ALADIN Airborne Demonstrator (A2D) (Lemmerz et al., 2017). Using it for characterization of the ALADIN laser, it was found that the laser frequency stability was well within the specification requirement, which states that the root mean square (RMS) variation in the frequency stability over 14 s should be below 7 MHz. The 14 s time period was chosen to ensure an adequate signal-to-noise ratio (SNR) over one Aeolus observation (12 s). In addition, sensitivity tests with a thermal cycle of ±0.2 ^∘C were carried out for about 4 h: one at ambient temperature, one with the laser interface at +35 ^∘C and two at −2.5 ^∘C. For all four thermal cycles, the absolute laser frequency varied by less than 25 MHz (peak to peak), demonstrating a good stability also over medium timescales as thermal variations over 1 week in orbit were expected to be even below 0.2 ^∘C. However, the test also revealed that operation in a vibrational environment, in this case introduced by vacuum pumps and a chiller, led to a degraded laser frequency stability with pulse-to-pulse fluctuations above 30 MHz RMS (Mondin and Bravetti, 2017). Further pre-flight test results are discussed in the context of micro-vibrations in Sect. 3.4.

2.3 Utilization of the Mie channel as a wavelength meter in orbit

An external wavelength meter is not available in space. However, the spectrometer data gained from the Fizeau interferometer of the Mie channel can be exploited for deriving the spectral properties of the narrowband laser emission. For this purpose, the INT signal that is usually analyzed after accumulation of multiple pulses on the measurement level and contained in the L1A Aeolus data product (Reitebuch et al., 2018) is evaluated for each individual pulse. As stated above, the Mie channel response is represented by the centroid position of the fringe that is imaged onto the Mie detector and then integrated over the 16 lines of the ACCD. Figure 2 shows the vertically summed ACCD counts over the 16 horizontal pixels for one laser pulse. The fringe centroid position is calculated by a Nelder–Mead downhill simplex algorithm (Nelder and Mead, 1965) to optimize a Lorentzian line shape fit of the signal distribution (Reitebuch et al., 2018). In this manner, the Mie response is derived with high accuracy. Conversion of the Mie response into relative laser frequency is based on dedicated in-flight calibrations of the Mie channel from which a sensitivity of ≈100 MHz per pixel was determined. The accuracy of the “inherent wavemeter” on board Aeolus is estimated to be 1 MHz. It is mainly limited by the shot-noise-limited signal-to-noise ratio (SNR) of the Mie signal and the FWHM of the Fizeau interference fringe (≈ 1.3 pixels). This could be demonstrated with A2D laboratory measurements comparing the spectrometer response from the ALADIN pre-development model Fizeau interferometer and parallel wavemeter measurements using the A2D UV laser (Lux et al., 2019). Hence, frequency fluctuations in the internal path signal can be measured as variations in the calculated Mie response on a pulse-to-pulse basis, which allows for assessing the frequency stability of the Aeolus laser transmitter over short- and long-term timescales.

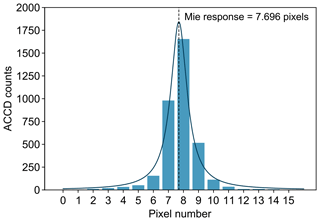
Figure 2 Internal reference path Mie signal for one laser pulse (24 November 2020, 0:23:47 UTC). After vertical integration of imaged fringe on the Mie ACCD (see also Fig. 1), the signal is distributed over 16 pixels (blue bars). A Nelder–Mead downhill simplex algorithm is applied to determine the centroid position from a Lorentzian line shape fit (dark-blue line).

2.4 Analyzed periods of in-orbit Aeolus datasets

The laser frequency stability was analyzed for different periods of the Aeolus mission. Since the satellite is circling around the Earth with an orbit repeat cycle of 1 week, it was decided to study the performance over selected 7 d periods. This approach was also motivated by the observed correlation between the frequency stability and the satellite's geolocation (see Sect. 3.2). After 1 week the maximum coverage of the globe is reached, and the operation timeline, particularly the attitude control sequence of the platform, approximately repeats. In total, 5 weeks between December 2018, when the mission was still in the commissioning phase after its launch on 22 August 2018, and October 2020 were chosen for investigation, as listed in Table 1. The table contains information on the operated laser transmitter as well as on the MO output energy (IR), the laser emit energy (UV) and the laser frequency stability, which is discussed later in the text. The energy values represent the respective mean values and standard deviations from laser internal photodiode readings. It should be noted that the IR energy reported by the MO photodiode of the FM-A is considered inaccurate. Here, Q-switch discharges influence the energy monitoring as they result in IR radiation with the wrong polarization that is circulating in the MO. This light is partially incident on the MO photodiode, thus corrupting the energy measurement. As can be seen from the table, the UV emit energy of FM-A decreased significantly between December 2018 and May 2019. The degradation of the laser performance was traced back to a progressive misalignment of the MO (Lux et al., 2020a) and led to the decision to switch to the second laser FM-B. This was necessary to ensure a sufficient SNR of the backscatter return and thus a low random error in the wind observations. The FM-B not only delivered a higher initial energy after switch-on in late June 2019 (67 mJ compared to 65 mJ after FM-A switch-on) but also has been showing a much slower power degradation. After an initial drop by 6 mJ between July 2019 and October 2019, the UV emit energy has decreased by less than 0.08 mJ per week. Thanks to an optimization of the laser cold-plate temperatures in March 2020, which increased the UV energy by about 4 mJ, the energy has remained above 60 mJ as of the writing of this paper. Despite the better overall performance compared to the FM-A, the FM-B behavior was observed to be more affected by orbital and seasonal temperature variations in the satellite platform that were transferred to the laser optical bench. As a consequence, laser anomalies associated with larger energy variations of about ±1 mJ occurred on both shorter- (hours) and longer-term timescales (weeks to months).

Table 1 Overview of the periods that were studied in terms of the laser frequency stability. The active laser transmitter operated in the respective period (FM-A or FM-B) and the corresponding master oscillator IR output energy and UV emit energy (as reported by the laser internal photodiodes) are provided. Note that the reading of the MO photodiode for FM-A is considered inaccurate (see text). The frequency stability is given as the mean of the standard deviations from all wind observations of the respective week.​​​​​​​

The periods listed in Table 1 are chosen such that they represent different phases of the mission: the early FM-A phase in December 2018, when the instrument parameters had settled after launch, but the degradation of the MO was already ongoing; the late FM-A phase in May 2019, when the degradation had progressed; the early FM-B phase in October, after completed thermalization of the second laser; and later FM-B periods in August and September/October 2020, after optimization of the laser cold-plate temperatures. The latter two periods were also chosen to identify the variability in the frequency stability performance decoupled from the power performance of the laser, which was stable in summer and autumn 2020 and free of temperature-related laser anomalies as stated above.

3 Results

The frequency stability of the ALADIN laser is first presented with one example, namely the week in October 2019, to illustrate the main temporal characteristics of the spectral behavior as well as the relation to the geolocation of the satellite. This leads to the correlation of the laser frequency stability with platform parameters, particularly the reaction wheel speeds, which is elaborated on subsequently. This correlation is additionally analyzed for the FM-A period in May 2019 to allow for a comparison between the two flight model lasers. The section concludes with a discussion of micro-vibrations as the root cause of the frequency noise.

3.1 Frequency stability of the ALADIN laser transmitters

Figure 3a depicts a typical time series of the laser frequency on the pulse-to-pulse level over about one orbit that was measured for FM-B on 14 October 2019 between 01:27 and 02:57 UTC. The plot contains the calculated Mie responses from 243 000 pulses distributed over 450 observations of 12 s each. The mean Mie response is 7.25 pixels, corresponding to a fringe centroid position close to the center of the ACCD, as shown in Fig. 2. The response variations are converted into relative frequency fluctuations considering the sensitivity of the Mie channel of ≈ 100 MHz per pixel, whereby the mean response value was identified as a reference frequency. An important parameter is the standard deviation of the relative frequency over one observation (540 pulses, 12 s), which is referred to as σ_f(N=540) in the following. This quantity describes the frequency stability within those periods that are considered for Rayleigh wind retrieval on the observation scale. The mean of the standard deviations from all observations of the 90 min period accounts for 8.4 MHz, which is comparable to the performance during on-ground tests (Sect. 2.2) and only slightly above requirements (7 MHz). However, it is worse than the in-flight performance of the A2D (< 4 MHz RMS) during airborne operations, which is characterized by a very similar laser design (Lemmerz et al., 2017; Lux et al., 2020b) but using a more agile ramp-fire technique to actively control the MO cavity length. The lower frequency stability can be ascribed to the fact that the time series also exhibits numerous sporadic periods at which much higher frequency fluctuations occur. During these periods, which last from a few seconds to several minutes, the variations increase to more than 20 MHz, with peak-to-peak variations of up to 150 MHz (see Fig. 3b). Despite the periods of increased frequency jitter, the stability of less than 10 MHz is unrivalled by any spaceborne high-power laser so far. It should also be noted that frequency variations of 3 MHz (corresponding to 1 MHz of the IR output of the MO) require a cavity length stabilization of only 3 nm within one oscillator free spectral range of 532 nm or 180 MHz, considering the 80 cm resonator length.

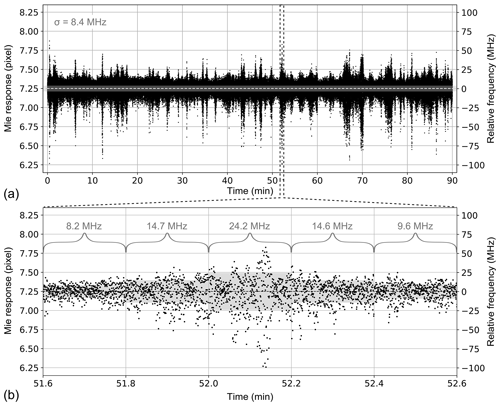
Figure 3 ALADIN laser frequency stability: (a) time series of the laser frequency fluctuations over about one orbit (14 October 2019, 01:27 to 02:57 UTC), as measured from the Mie channel of the receiver; (b) close-up of a selected period showing the frequency variations over five observations. The given values denote σ_f(N=540) as defined in the text. The standard deviations are also indicated as gray-shaded areas.

It should be pointed out that, apart from laser frequency variations caused by cavity length changes, the measured Mie response can, in principle, also be altered by angular variations in the laser beam incident on the Fizeau interferometer. In order to estimate the contribution of angular variations, a potential correlation of the Mie response with the far-field beam position was investigated. For this purpose, the horizontal position of the two spots from the internal reference signal that are imaged onto the Rayleigh ACCD (see also Fig. 1) was analyzed during periods of enhanced noise. The studies showed a small spot motion correlated with the Mie response, which is most likely due to the influence of the Fizeau reflection that is promoted by the sequential configuration of the two receiver channels. The change in spot position was in line with the motion that was observed at times when the laser frequency was deliberately tuned, e.g., during instrument calibrations. This result strongly suggested that the contribution of angular variations to the Mie response fluctuations is negligible and that variations in the internal path Mie response are largely due to changes in the laser frequency.

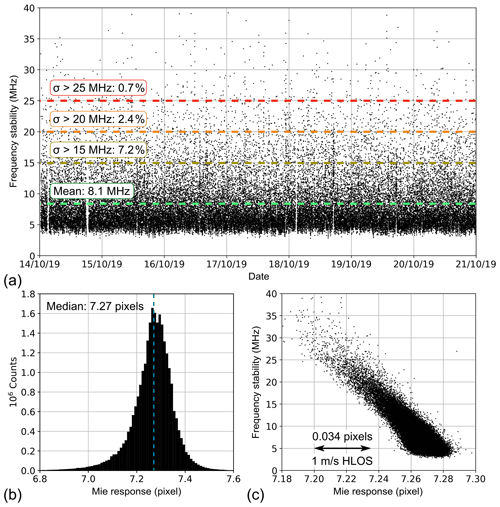
Figure 4 (a) Time series of the laser frequency stability over 1 week from 14 to 21 October 2019, i.e., during FM-B operation. The data points represent σ_f(N=540). Data gaps are due to calibrations or orbit maintenance. The horizontal lines indicate mean over all observations of 8.1 MHz (green) as well as thresholds to indicate the percentage of observations for which the frequency stability is worse than 15 MHz (yellow), 20 MHz (orange) and 25 MHz (red). (b) Probability density distribution of the Mie internal reference response for the dataset in October 2019. (c) Relationship between the laser frequency stability in terms of σ_f(N=540) and the mean Mie internal reference response per observation. A response shift by 0.034 pixels translates to a frequency shift by about 3.4 MHz, corresponding to a HLOS wind speed change of 1 m s⁻¹, assuming a constant response of the atmospheric or ground return signal.

Analysis of the entire week from 14 to 21 October 2019 reveals a mean frequency stability of 8.1 MHz over the 49 209 observations, as depicted in Fig. 4a, where the standard deviation is plotted for each observation of the regarded period. Data gaps in the timeline are due to special operations that are regularly performed in each week, such as instrument spectral registration (ISR; Reitebuch et al., 2018), the so-called down under dark experiment (Weiler et al., 2021a) or orbit correction maneuvers. The figure also illustrates the percentage of observations that are affected by enhanced frequency fluctuations. While the frequency stability is better than 15 MHz for the vast majority of observations (about 93 %), it is worse than 20 MHz for 2.4 % and even worse than 25 MHz for almost 1 % of the observations. However, there are also a considerable number of observation periods (19 %) for which the frequency stability is better than 5 MHz, i.e., comparable to the A2D laser performance.

To estimate the potential impact of the enhanced fluctuations on the wind accuracy, the following calculation is performed. According to the above equation for the Doppler shift, a frequency difference of 10 MHz is introduced by a LOS wind speed of about 1.8 m s⁻¹. Taking into account the off-nadir angle of Aeolus of 37^∘ at the location of the measurement track, this translates to a horizontal LOS (HLOS) wind speed of 1.8 m s⁻¹ $/\sin \left(\mathrm{37}{}^{\circ }\right)$ ≈ 3.0 m s⁻¹. Consequently, wind errors of several meters per second are potentially caused when only a small subset of emitted pulses from one observation (with σ = 10 MHz) is backscattered from the atmosphere or the ground and contributes to the return signal in the wind retrieval.

Interestingly, the distribution of measured Mie responses (see Fig. 4b) indicates that the frequency fluctuations are not symmetrically distributed. Instead, the frequency tends to jump to lower values (i.e., lower responses). This behavior is also visible in Fig. 3, where the largest departures from the mean are negative. As a result, the higher the standard deviation over one particular observation is, the larger the negative shift in the respective mean from the mean over all observations will be. This relationship is shown in Fig. 4c and can most likely be traced back to disturbances of the active stabilization of the MO cavity length during the periods of enhanced frequency jitter, which results in frequency jumps preferentially in one direction. For instance, such jumps occur when the interference signal produced by the seed laser circulating in the MO features parasitic peaks that are erroneously detected as MO cavity resonances. A similar behavior was observed for the A2D in a highly vibrational environment or in the case of imperfect alignment of the MO.

3.2 Correlation with the satellite's geolocation

The enhanced frequency fluctuations in the laser transmitter were detected very early in the mission and attributed to potential vibrations introduced by the satellite platform, which affects the MO cavity length (Lux et al., 2020a). However, a correlation to platform parameters, particularly the rotation velocity of the satellite's reaction wheels, was not found initially. This was mainly due to the fact that only short timelines were analyzed, typically covering only several minutes to hours, as shown in Fig. 3. Since the platform parameters vary slowly over the orbit, a relationship to the fast changes in the laser frequency stability within several seconds was considered unlikely.

During the first year of operation, the assessment of the frequency stability was then focused on the weekly instrument response calibrations (IRCs; Reitebuch et al., 2018). IRCs are required to determine the relationship between the Doppler frequency shift in the backscattered light, i.e., the wind speed, and the response of the Rayleigh and Mie spectrometers. The procedure involves a frequency scan over 1 GHz in steps of 25 MHz to simulate well-defined Doppler shifts in the atmospheric backscatter within the limits of the laser frequency stability. During the IRC, which takes about 16 min (two observations (12 s) for each of the 40 frequency steps), the contribution of (real) wind related to molecular or particular motion along the instruments' LOS is virtually eliminated by rotating the satellite by an angle of 35^∘. This results in nadir pointing of the instrument and, in the case of negligible vertical wind, vanishing LOS wind speed. The IRCs are preferably carried out over regions with high surface albedo in the UV spectral region, e.g., over ice, to ensure strong return signals and, in turn, high SNR. This is particularly important for the Mie response calibration, which relies on measuring the spectrometer response from the ground return to be then used for the retrieval of atmospheric winds.

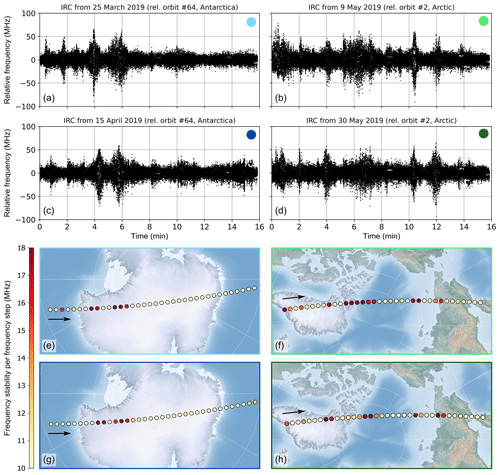
Figure 5 Time series of the laser frequency fluctuations over periods of selected IRCs over Antarctica (a, c) and the Arctic (b, d) together with the corresponding geolocations of the individual frequency steps in panels (e)–(h). Each dot corresponds to one frequency step (24 s), whereby the color coding describes the standard deviation of the relative frequency on the pulse-to-pulse level within this period (σ_f(N=1080)).

The laser frequency stability was studied for each of the 60 IRCs conducted between 7 September 2018 and 9 December 2019, most of them over Antarctica, while IRCs no. 31 to no. 43 were performed over the Arctic. Here, it was found that the frequency stability was degraded during the IRCs compared to operation in nominal wind velocity mode (WVM). While it was on the order of 8 to 10 MHz in WVM, the mean stability over the 16 min IRC period accounted for 12 to 14 MHz when the satellite was pointing nadir, suggesting an influence of the platform attitude on the laser. This conclusion was strengthened by the circumstance that the laser temperatures and energies were strongly varying during the nadir and off-nadir slews before and after the IRC, respectively. Moreover, these orbit maneuvers involved thruster firings, which also caused increased frequency noise during the slews before and after the weekly IRC, thus pointing to mechanical disturbances as the root cause. Furthermore, the frequency stability was shown to be significantly better over Antarctica ((11.6 ± 1.7) MHz) than over the Arctic ((15.2 ± 2.1) MHz), although the IRC procedure was the same over both locations. Finally, it was noticed that the progression of the relative laser frequency featured recurring temporal patterns for those IRCs that were carried out over the same locations in subsequent weeks. For instance, an accumulation of periods with increased frequency jitter was observed at the beginning of the time series for the Antarctica IRCs, whereas numerous high-noise periods, distributed over the entire procedure, were evident for the Arctic IRCs. Figure 5 depicts the laser frequency variations over selected IRC periods over the two different geolocations, clearly demonstrating the reproducibility of the jitter patterns for the weekly IRCs.

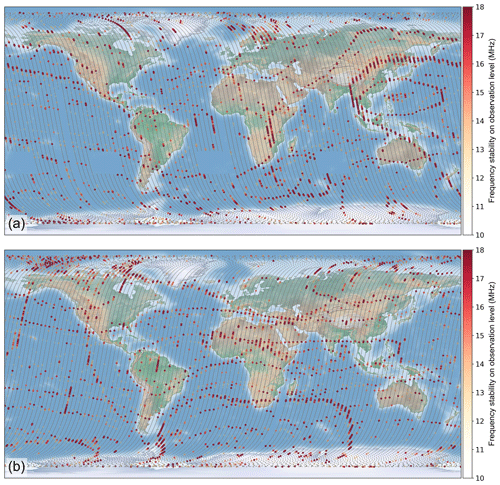
Figure 6 Geolocation of wind observations with enhanced frequency noise for (a) ascending and (b) descending orbits. The plot contains the data from the week between 14 October 2019 (00:00 UTC) and 21 October 2019 (00:00 UTC) (see also Fig. 4). Each dot corresponds to one observation (12 s), whereby the color coding describes the σ_f(N=540). Note that the opacity of the dots also scales with the frequency stability so that observations with σ < 10 MHz are not visible.

Following these observations, the laser frequency stability was studied over 1-week periods to review the influence of the satellite's geolocation (see Sect. 2.4). The performance from the week between 14 and 21 October 2019 (Fig. 4a), based on the Mie response data from more than 27 million laser pulses, is illustrated in Fig. 6. Each dot in the two maps represents one observation, whereby the color and opacity indicate the frequency stability in terms of σ_f(N=540). The analysis revealed that the enhanced frequency noise does not occur randomly but is correlated with the location of the satellite over the Earth's surface. More strikingly, different linear and circular structures are evident for ascending and descending orbits, which makes clear that the frequency stability depends not only on the geolocation but also on the satellite's orientation along the orbit. For ascending orbits those observations with enhanced frequency fluctuations are accumulated in several bands wrapping around the globe, most prominently around East Asia and the Pacific Ocean. In contrast, multiple narrow latitudinal bands and a circular structure over the South Atlantic and southern Indian Ocean are apparent for descending orbits.

The geolocational patterns were found to be reproducible for the investigated FM-B periods with only slight variations (< 200 km). This is especially true for the linear and circular structures that are formed by neighboring orbits, i.e., with large temporal distance. In contrast, continuous phases of enhanced frequency noise over several observations which manifest as orange and red lines along one orbit, e.g., in northern Canada or over northern Europe in Fig. 6a, were evident at different geolocations for the weeks in August 2020 and September/October 2020.

Similar correlation of the laser frequency stability with the satellite position was also obvious for the periods in December 2018 and May 2019 when FM-A was operated. However, the geolocational patterns for ascending and descending orbits markedly differed from those of the FM-B periods, suggesting that the mechanism introducing the enhanced frequency noise acts differently on the two laser transmitters, potentially due to the different locations in the payload. The underlying reason for the observed dependence on geolocation could be traced back to the reaction wheels of the satellite, as is explained in the following section.

3.3 Influence of the reaction wheels

Precise three-axis attitude control of the Aeolus satellite is accomplished by a set of reaction wheels (RWs) which rotate at different speeds, thereby causing the spacecraft to counter-rotate proportionately through the conservation of angular momentum. Due to external disturbances, mainly aerodynamic drag, the total angular momentum is periodically modified so that magnetorquers are additionally required to generate an effective external torque. Otherwise the wheel speed would gradually increase in time and reach saturation (Markley and Crassidis, 2014). The attitude and orbit control system of Aeolus additionally consists of thrusters which allow for larger torque to be exerted on the spacecraft.

A sketch illustrating the orientation of the reaction wheels within the spacecraft is shown in Fig. 7. The reaction wheel assemblies (RWAs) are mounted on the spacecraft such that they form a tetrahedron whose axis of symmetry lies along the +Z axis, i.e., the line-of-sight direction of the telescope. Hence, the normal vectors of the four wheels span a plane parallel to the X–Y plane (Fig. 7b) in which the two lasers (including the respective MO axes) are located. Each wheel is canted such that the angle between its spin axis and each spacecraft axis is 54.74^∘. The reaction wheels were manufactured by Stork Product Engineering B.V. in 2005 (design later transferred to Moog Bradford) and have a capacity of 40 Nm s and maximum torque of 0.2 Nm. These wheels consist of a rotating inertial mass driven by a brushless DC motor (Bradford space, 2021) and supported by oil-lubricated bearings. The wheels are all mounted on isolation suspensions to reduce micro-vibrations.

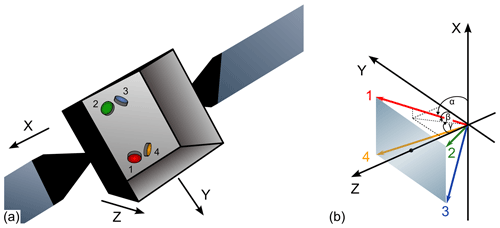
Figure 7 (a) Orientation of the four reaction wheels with respect to the spacecraft body. (b) Alignment of the reaction wheel spin axes with respect to the spacecraft body. The axes of the four wheels are oriented such that $\left|\mathit{\alpha }\right|=\left|\mathit{\beta }\right|=\left|\mathit{\gamma }\right|=\mathrm{54.74}$^∘.

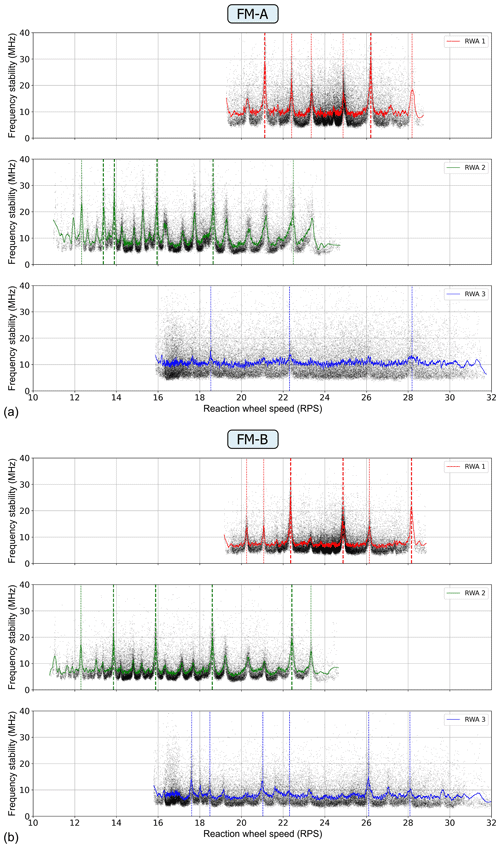
Figure 8 Correlation between the laser frequency stability and the speeds of the three active reaction wheels: the plots in panel (a) are based on data from the FM-A laser for the period between 13 and 20 May 2019, while the plots in panel (b) show the correlation for the FM-B laser in the period between 14 and 21 October 2019. The colored lines result from a Savitzky–Golay smoothing with a window size of 201 and polynomial order of two.

Based on the dataset from the week in October 2019, the frequency stability on the observation level, as depicted in Fig. 6, was correlated with the rotational speed of the three active reaction wheels on board Aeolus (RWA 4 serves as a backup). The same procedure was performed for the FM-A period in May 2019 (see Table 1). The resulting six correlation plots, which can also be considered to be spectra in terms of the wheel rotation frequency (rotations per second, RPS), are shown in Fig. 8. Note that the plot includes data from both ascending and descending orbits and that RWA 1 and RWA 3 rotate counterclockwise, while RWA 2 rotates clockwise. For the sake of better comparability of the three spectra, the absolute wheel speeds are plotted in the figure, and the negative sign for the wheel speeds of RWA 1 and RWA 3 was omitted. The six spectra exhibit pronounced peaks which demonstrate that the laser frequency fluctuations are enhanced at specific rotational speeds of the reaction wheels. Thus, the latter are subsequently referred to as critical wheel speeds or critical frequencies.

For both periods, i.e., operated lasers, the frequency stability is primarily influenced by RWA 1 and RWA 2, which show a multitude of critical wheel speeds with comparable strength in their common operating range between 19 and 24 RPS. In contrast, the correlation of the frequency stability with the speed of RWA 3 is rather poor, especially for FM-A, which can be attributed to being located farther away from RWA 3 than FM-B. For RWA 1 and RWA 2 a stronger correlation to their nearby FM-A rather than to FM-B, located on the opposite side of the instrument, is not possible to demonstrate. Since the performances of FM-A and FM-B are compared for different periods of operation, and these units showed very different behavior in terms of laser performance, degradation and susceptibility to temperature variations, it is difficult to judge if one reaction wheel has a greater disturbing effect on one laser or another due to being located closer by.

The center frequencies and $\mathrm{1}/e^{\mathrm{2}}$ widths of the strongest peaks were determined from Gaussian fits and are provided in Tables 2 and 3 for FM-A and FM-B, respectively. From a comparison of the two tables, it can be concluded that the same set of critical wheel speeds appears for both lasers, however with different relative strength. Furthermore, the critical frequencies are consistent among the three wheels. For instance, all wheels feature the same critical frequency of around (22.4 ± 0.1) RPS. Since the three wheels span different speed ranges, only a subset of critical speeds is identified for each wheel. By combining the information obtained from all spectra, the following seven reaction wheel speeds were identified to be most critical regarding the frequency stability of both lasers (sign neglected): ω₁ ≈ 13.9 RPS, ω₂ ≈ 15.9 RPS, ω₃ ≈ 18.6 RPS, ω₄ ≈ 22.4 RPS, ω₅ ≈ 24.9 RPS, ω₆ ≈ 26.2 RPS and ω₇ ≈ 28.2 RPS. These frequencies are printed in bold italics in Tables 2 and 3.

Table 2 Critical wheel speeds for the analyzed period between 13 and 20 May 2019 (FM-A period), as derived from the correlation with the frequency stability depicted in Fig. 8a. The values represent the center frequency and $\mathrm{1}/e^{\mathrm{2}}$ width from Gaussian fits applied to the six most pronounced peaks. The strongest peaks for each reaction wheel are indicated in bold type, while those frequencies which are critical for both lasers are additionally printed in italics.

Table 3 Same as Table 2 but for the analyzed period between 14 and 21 October 2019 (FM-B period).

The variability in the center frequency of the common critical wheel speeds is on the order of 0.1 RPS, which is comparable to the average width of the fitted peaks. Note that the individual wheel speeds are known with an accuracy of about 0.01 RPS. The fact that the peaks are relatively narrow explains the rather short duration of the high-noise periods of several tens of seconds as the critical wheel speeds are usually passed on these timescales. Analysis of the other three periods listed in Table 1 yields that the center frequencies and widths of the peaks are constant over time for each laser.  Interestingly,  the  peak  heights  in the  spectra for the  early  FM-A period in December 2018 are lower compared to the May 2019 period plotted in Fig. 8a. This is due to the better overall performance of FM-A, particularly the better MO alignment, at the beginning of the mission (see also Table 1) so that the laser was less prone to external perturbations. Consequently, the frequency stability was less degraded at the critical wheel speeds, which manifests in smaller peaks in the spectra.

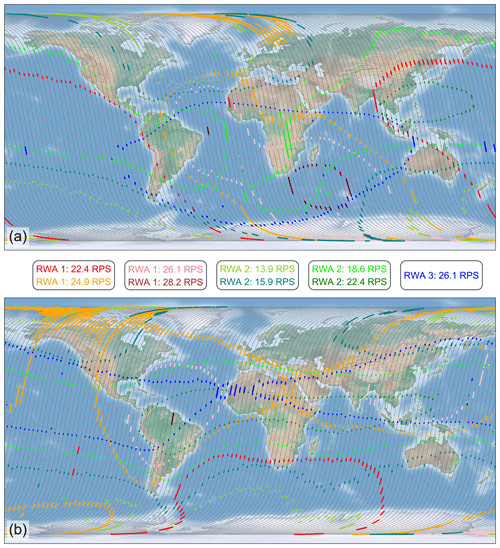
Figure 9 Geolocation of the most critical frequencies of the three active reaction wheels for (a) ascending and (b) descending orbits. The plot contains the data from the week between 14 October 2019 (00:00 UTC) and 21 October 2019 (00:00 UTC) (see also Fig. 6 for the corresponding frequency stability). Each dot corresponds to one observation (12 s), for which one of the wheels operates at one of the critical wheel speeds as listed in bold type in Table 3.

Steering of the satellite pointing by means of the reaction wheel speeds involves regular and repeated patterns over the 1-week orbit repeat cycle, which differ only slightly depending on the elapsed time since the last orbit correction maneuver. The global occurrence of the most critical wheel speeds during the analyzed week in October 2019 is illustrated in Fig. 9. The two maps show those observations during ascending (panel a) and descending orbits (panel b), for which one of the wheels operates at one of the critical frequencies that are printed in bold type in Table 3. Comparison of the geolocational patterns with those of the laser frequency stability (Fig. 6) underlines the strong correlation between the reaction wheel speeds and the laser frequency noise. For instance, the manifestation of high noise along a linear structure that extends from South and North America across the Pacific Ocean to East Asia for ascending orbits can be traced back to the influence of RWA 1 operating at the critical frequency of ω₄ ≈ 22.4 RPS. The enhanced noise which is observed in the north polar regions, on the other hand, is primarily related to RWA 2 rotating at a speed of ω₅ ≈ 24.9 RPS. It should be pointed out that the sequence of operating speeds for each wheel slightly changes from week to week depending on the actual orbit position of the Aeolus spacecraft. Consequently, the areas which experience high frequency noise have been shifting by a few hundreds of kilometers over the course of the mission.

The occurrence of critical frequencies from different wheels along the orbit suggests that the three wheels act independently on the laser. This hypothesis was confirmed by further analysis, which revealed that enhanced noise is observed almost every time when one of the wheels rotates at a critical speed, regardless of the speed of the other two wheels. Hence, there is no entanglement of the critical frequencies, even though the speeds of the wheels are related among each other. Additional studies also showed that the frequency stability is not correlated with the wheel acceleration.

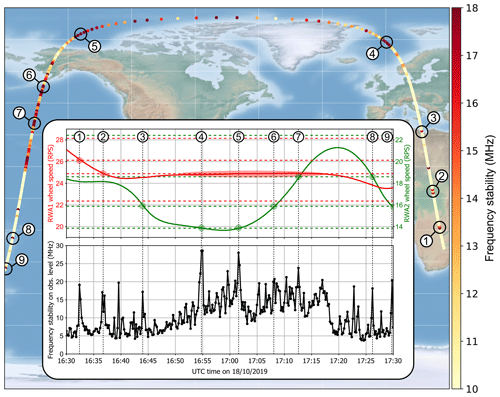
Figure 10 Geolocation of observations with enhanced laser frequency variations and their relation with the reaction wheel speeds of RWA 1 and RWA 2 in the period from 16:30 to 17:30 UTC on 18 October 2019. Each dot on the map corresponds to one observation, whereby the color coding describes the frequency stability in terms of σ_f(N=540). The inset depicts the temporal evolution of the RWA 1 (red) and RWA 2 (green) wheel speeds in the top panel together with the frequency stability per observation. Dashed horizontal lines in the top panel indicate the most critical wheel speeds that were determined for the analyzed week in October 2019 (see Table 3). Additional peaks in the frequency stability are related to other critical frequencies which are not listed in Table 3 but visible in Fig. 8.

The impact of the reaction wheel speeds on the laser frequency stability is finally demonstrated at an example scene, which clearly illustrates the origination of the geolocation patterns. Figure 10 shows a map with the color-coded frequency stability per observation (dots on the map) for the period between 16:30 and 17:30 UTC on 18 October 2019. Within this hour the satellite crossed Africa and Europe on an ascending orbit and passed the north pole before flying over Alaska and the Pacific on a descending orbit. The inset of the figure depicts the temporal evolution of the wheel speeds of RWA 1 (red) and RWA 2 (green), which are most relevant regarding the laser frequency stability, as stated above. The timeline of the latter is plotted below. The critical speeds of RWA 1 and RWA 2 that were identified from the correlation plots in Fig. 8b are indicated by dashed horizontal lines of the respective color in the top panel of the inset. The nine marked spots indicate events when the wheels rotated at their critical speeds. As can be seen from the figure, such events are correlated with enhanced frequency variations that result in standard deviations of more than 15 MHz. The frequency noise was especially high in the period between 16:50 and 17:15 UTC, when the wheel speed of RWA 1 remained very close to ω₅ ≈ 24.9 RPS, hence leading to a plateau of increased jitter with additional spikes at times when RWA2 rotated at ω₁ ≈ 13.9 RPS or ω₃ ≈ 18.6 RPS.

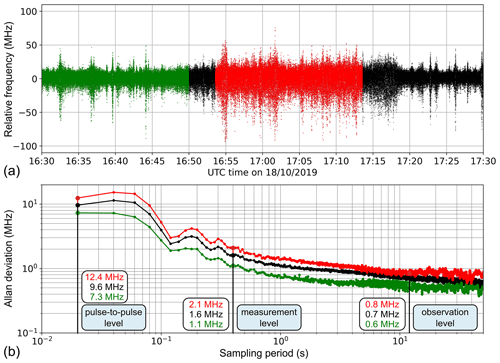
Figure 11 Laser frequency stability on the pulse-to-pulse level for the period from 16:30 to 17:30 UTC on 18 October 2019 (see also Fig. 10). (a) Time series of the relative frequency. From the overall 1 h period, two intervals of 20 min with good (green) and poor frequency stability (red) were selected for further analysis. Panel (b) represents the Allan deviation calculated for the selected time series in the upper panel. The dashed vertical lines indicate sampling periods relevant for the wind retrieval (pulse-to-pulse level: 0.02 s; measurement level: 0.4 s; observation level: 12 s).

As shown in this example, the existence of critical wheel speeds explains the enhanced frequency jitter in the following situations.

• Over longer periods, i.e., along orbits. That is the case when the speed reaches a local maximum or minimum that lies close to one of the critical values and results in a longer-term perturbation of the laser over several minutes.

• At isolated points in time forming the linear and circular patterns around the globe. That is the case when the speed quickly crosses a critical value so that only very few consecutive observations are affected. Such events occur at different geolocations for ascending and descending orbits but are largely reproducible from week to week.

The laser frequency fluctuations for the presented scene are additionally shown on the pulse-to-pulse level in Fig. 11a together with the Allan deviation calculated for three selected time series. The Allan deviation (Allan, 1966) is a statistical means to determine the frequency stability over a wide range of averaging times, which allows the identification of different types of noise sources and drift components which affect the stability on different timescales. While the black data points represent the entire 1 h period, the green and red data points correspond to 20 min subperiods with comparatively low and high frequency noise, respectively. The Allan deviation provides further information on the frequency stability on those timescales that are relevant for the wind retrieval. Apart from the observation level (12 s, 540 pulses) the frequency variations on the measurement level (0.4 s, 18 pulses; see Sect. 2.1) are crucial for the wind data quality. This is due to the fact that the signal data from individual measurements are classified into “clear” and “cloudy” bins by using estimates of the backscatter ratio before the on-ground accumulation to so-called groups in the L2B processor (Rennie et al., 2020). This grouping algorithm enables the distinction between measurements that are better analyzed with the Rayleigh or Mie spectrometer, respectively, and hence to minimize the effect of crosstalk between the two receiver channels that is detrimental to the wind data quality. In particular, Mie wind results are usually provided on timescales shorter than 12 s as they require fewer measurement bins to achieve a given level of precision compared to the Rayleigh winds, with the typical levels of backscatter, e.g., from clouds (Rennie et al., 2020).

For the low-noise period, the Allan deviation on the measurement level (0.4 s sampling period) is 1.1 MHz, which is about 50 % better than for the entire 1 h period (1.6 MHz) and almost 2 times better compared to the high-noise period (2.1 MHz). The differences are less pronounced when sampling on the pulse-to-pulse or observation levels is regarded. This underlines that the enhanced frequency fluctuations typically occur in the second regime (see also Fig. 3b) so that the mean laser frequency varies strongly from one measurement to the other. On longer timescales, the enhanced noise has a minor impact on the mean frequency; i.e., the variation is smaller from observation to observation. As a result, the Allan deviation on the observation level is around (0.7 ± 0.1) MHz, almost independent of the occurrence of enhanced noise periods.

Although the root cause of the enhanced frequency noise is understood to be introduced by the reaction wheels, there is an apparent correlation with other platform parameters. In particular, a link to the data obtained from the magnetometer on board Aeolus was discovered. A thorough investigation revealed a strong influence from the magnetic fields generated by the platform magnetorquers, which serve the regulation of the reaction wheel speeds. Due to the complex coupling between magnetorquer currents and reaction wheel speeds, there is an indirect relationship between the critical wheel speeds, i.e., the frequency stability, and the magnetometer data via the superimposed magnetic fields of the magnetorquers and the Earth.

3.4 Micro-vibrations as the root cause for increased frequency jitter

The observation of critical speeds of the reaction wheels that give rise to enhanced frequency noise strongly suggests that micro-vibrations are the root cause of the degraded laser frequency stability in orbit. This hypothesis is further strengthened by the fact that the frequency noise levels also increase during periods of heavy thruster firings, e.g., during orbit maneuvers and wheel speed set point changes before and after IRCs (see Sect. 3.2).

When the thrusters are not used, the dominating micro-vibrations occurring in the satellite are a result of its structure responding to disturbing forces and moments generated by the reaction wheels. These disturbances result mainly from static and dynamic imbalances of the flying wheel, bearing imperfections, and the structural modes of the wheel assembly and are exerted on the satellite structure as a combination of harmonics, each with a frequency being a constant multiple of the wheel speed. Typically, these disturbances become most intense at the wheel speeds at which the critical harmonics excite the structural modes of the wheel assembly. Please refer to Le (2017) for a detailed characterization and study of the mechanical disturbances generated by reaction wheels of the class of those embarked on Aeolus.

For Aeolus the reaction wheels were mounted on micro-vibration isolation suspensions, which filter the generated disturbance forces and moments. Such suspension was found to reduce the disturbances by more than 1 order of magnitude at the most critical frequencies, while the amplifications occurring at the lower frequency due to the suspension modes are minimized by the presence of viscoelastic elastomeric mounts.

The on-ground micro-vibration verification activities were quite extensive within the Aeolus project. These included disturbing the laser transmitter with representative mechanical excitation spectra, thus identifying susceptibility in the 400 to 600 Hz frequency band as well as around 250 Hz. Moreover, micro-vibration tests were performed at the satellite level, first with the aim of characterizing the micro-vibration environment throughout the satellite. This was achieved by operating the reaction wheels all over their operational speed range and having the satellite mounted on doughnut-shaped cushions to isolate it from external disturbances (Lecrenier et al., 2015). The tests demonstrated that, despite the fact that the peak of disturbances from the reaction wheels coincided with the most susceptible frequencies of the lasers, the vibration levels were lower than the danger levels previously attributed to them thanks to the isolation suspension. The margins observed between the micro-vibration levels measured during the full-satellite test and the danger levels characterized during the preceding laser tests were considered large enough to cover the mechanical changes that occur when passing from the ground to the orbital environment. Due to the different support boundary conditions of the satellite and the effects of gravity and air, the structural damping and natural frequencies of the satellite structure are expected to differ in orbit from their characterization on the ground. Moreover, a worsening of the disturbance signature of the reaction wheels as a result of their exposure to the vibrations of the satellite-level tests and the launch environment is also commonly observed.

These margins were finally confirmed by an in situ test during the thermal vacuum campaign with the flight model of the spacecraft. This included operation of the laser whilst the wheels were running at speeds previously identified as critical and after wheel power-off. The Mie and Rayleigh frequency response data from these tests clearly showed significant peaks at several harmonic frequencies (roughly 4.5, 10, 13, 16, 18.5, 21.5, 23, 24, 24.5 RPS) when the wheels were operating. In fact, the pulse-to-pulse frequency stability varied along the thermal plateau more strongly than during the dedicated reaction wheel test. Unfortunately, due to programmatic constraints, no tests were ever run with the spacecraft mounted in an isolated configuration from the ground and with flight-representative time-varying speed profiles whilst operating the laser to check its frequency stability.

4 Impact of the frequency fluctuations on the data quality

After having identified the root cause of the temporally degraded frequency stability in orbit, the question is to what extent the Aeolus wind data quality are diminished during the periods of enhanced frequency noise. Before answering this question, it is meaningful to consider how often these periods occur and how long they last. For this purpose, the percentage of observations for which the frequency stability is significantly worse in comparison to the overall performance over a certain period can be regarded. This information is summarized in Table 4 for the 5 selected weeks of the mission that were already introduced in Sect. 2.4 as being representative of different periods of the Aeolus mission.

Table 4 Laser frequency stability during different phases of the Aeolus mission. The table provides the standard deviation of the relative frequency at the pulse-to-pulse level (mean over all observations from 1 week) as well as the percentage of observations (%obs) for which σ_f(N=540) is above 15, 20 and 25 MHz, respectively. FM-A was operating during the first two selected periods, while FM-B was operating in the other 3 weeks. See also the time series of the frequency stability for the week in October 2019 in Fig. 4.

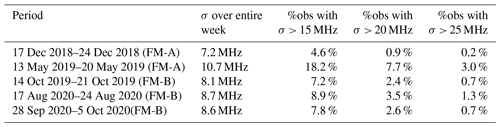
The table provides the standard deviation over the entire week and the portion of observations for which σ_f(N=540) is above 15, 20 and 25 MHz. The data for the week in October 2019 are also visualized in Fig. 4a. The worst performance was evident at the end of the FM-A period in May 2019, when the MO was already strongly misaligned. Consequently, the frequency stability calculated over the whole week was 10.7 MHz, while nearly one-fifth of all observations showed frequency variation larger than 15 MHz. This corresponds to an increase by a factor of 4 compared to the early FM-A phase in December 2018, when less than 5 % of all observations were affected by enhanced noise of that order. Regarding extreme cases, i.e., when the standard deviation exceeded 25 MHz, the percentage has even multiplied by 15, from 0.2 % to 3.0 %, over the course of the FM-A period. In contrast, the performance of FM-B is rather stable, with the frequency stability ranging between 8 and 9 MHz and about 1 % of observations with σ > 25 MHz. As of October 2020, nearly 8 % of all observations showed frequency fluctuations above 15 MHz, and for less than 3 % the standard deviation was above 20 MHz.

In the following two sections, the influence of the frequency stability on the systematic and random error is assessed for the Mie and Rayleigh wind results as well as for the respective ground velocities. While the latter study is performed on the observation level (540 pulses), the impact on the wind results is discussed on the measurement level (18 pulses) for the reasons related to the wind retrieval processing that were explained at the end of Sect. 3.3.

4.1 Accuracy and precision of the Aeolus Rayleigh and Mie winds

The wind error assessment is based on the data from 2 weeks of FM-B operation in August and September/October 2020, as listed in Tables 1 and 4. These datasets already include the correction for the influence of the temperature variations across the primary telescope mirror on the wind results (M1 correction), which was implemented prior to the operational assimilation of the Aeolus wind data in NWP by various weather services (Rennie and Isaksen, 2020; Weiler et al., 2021b). The Rayleigh and Mie wind observations were extracted from the L2C product, which, in addition to a copy of the Aeolus L2B product, includes ECMWF model winds (analysis and background) provided on the same horizontal and vertical grid. Using the background model winds as the reference, the wind speed differences between observation and background (O–B) can be interpreted as the wind errors.

The L2B/C wind data are provided on a different temporal grid as the L1A data used for the calculation of the Mie responses and corresponding frequency fluctuations. This is due to the classification of measurement bins into “clear” and “cloudy” bins (Sect. 3.3), which results in so-called groups of varying horizontal length. Consequently, for investigating the influence of the frequency stability on the wind accuracy and precision, an adaptation of the different temporal grids of the L1A/B and L2B/C products has to be performed. Moreover, it has to be considered that each wind profile measured within a certain period of time generally comprises multiple wind results from the adjacent vertical bins to be compared with the respective frequency stability within the regarded time interval. Finally, only reliable wind results with low estimated error should enter the statistics. The estimated wind error is included in the L2B/C product and, in the case of the Rayleigh channel, is derived from the SNR and the pressure and temperature sensitivity of the Rayleigh responses (Rennie et al., 2020). For the Mie channel, it is primarily linked to the SNR. The estimated error also considers the impact of the solar background on the wind accuracy, which is mainly relevant for the Rayleigh winds. In the analysis presented here, estimated error thresholds of 8 m s⁻¹ for the Rayleigh and 4 m s⁻¹ for the Mie channel were used as airborne validation campaigns have demonstrated that these values ensure small departures of the Aeolus winds from high-accuracy wind lidar measurements (Witschas et al., 2020).

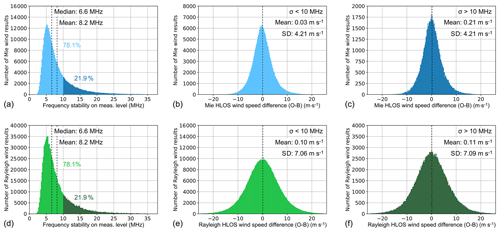
Figure 12 (a) Histogram of the laser frequency stability on the measurement level for those measurements that yielded valid Mie winds during the period from 17 to 24 August 2020 (bin size: 0.2 MHz). The probability density functions of the wind speed difference with respect to the ECMWF model background (O–B) are shown in panels (b) and (c) for measurements with a frequency stability better and worse than 10 MHz, respectively (bin size: 0.2 m s⁻¹). The bottom panels depict the corresponding statistics for the Rayleigh wind data.

The results of the statistical analysis for one of the two studied periods are shown in Fig. 12. Here, panel (a) depicts a histogram of the laser frequency stability on the measurement level, i.e., calculated as the standard deviation over 18 pulses within 0.4 s, i.e., σ_f(N=18). After interpolation of the frequency stability data onto the temporal grid of the Mie wind data, the former could be filtered for those measurements within the week from 17 to 24 August 2020 that yielded valid Mie winds. From the nearly 350 000 Mie (cloudy) wind results, more than 78 % were obtained at a frequency stability of better than 10 MHz on the measurement level, as indicated by the light-blue area in the histogram. Regarding the Rayleigh (clear) winds, the percentage is identical, although the number of wind data is about 2.8 times larger (≈ 990 000 winds) compared to the Mie channel due to the usually larger data coverage. The median of the laser frequency stability is 6.6 MHz for the two data subsets, while the mean values both account for 8.2 MHz, which is comparable to the frequency stability on the observation level for the August 2020 period stated in Table 4. Although the frequency stability is comparable for the two different processor timescales when the mean over large datasets is considered, the fluctuations are significantly higher on the measurement level (> 30 MHz) than on the observation level in rare cases when the peak of a short high-noise period falls within one measurement.

In a next step, the Mie and Rayleigh wind results were separated into those for which the frequency stability was better or worse than 10 MHz on the measurement level. The resulting probability density functions (PDFs) of the (O–B) horizontal line-of-sight (HLOS) wind speed differences are provided in the middle and right columns of Fig. 12. Due to the much smaller number of wind results for σ > 10 MHz (≈ 22 %), the distribution is a bit noisier than for σ < 10 MHz. Nevertheless, nearly Gaussian distributions are evident for the two subsets, both for the Mie and Rayleigh channel. The mean of the Mie distribution, or bias, of the “high-noise” case is slightly larger ((0.214 ± 0.015) m s⁻¹) than that of the “low-noise” case ((0.030 ± 0.008) m s⁻¹). Hence, when only considering winds from the week in August 2020 for which the frequency stability was worse than 10 MHz on the measurement level, the bias differs by about 0.18 m s⁻¹ from the mean (O–B) wind difference over all winds for which σ < 10 MHz. When the wind data are further restricted to σ > 20 MHz, the change in bias increases to 0.31 m s⁻¹ (not shown).

The widths of the two distributions, however, are identical (standard deviation: 4.21 m s⁻¹), showing that the frequency stability has no significant influence on the random error. The same is true for the Rayleigh winds whose PDFs are depicted in Fig. 12e and f. Here, the differences in the bias and random error for σ < 10 MHz and σ > 10 MHz are below 0.04 m s⁻¹. Thus, it can be concluded that the accuracy of the Rayleigh winds is less affected by the enhanced frequency noise than that of the Mie winds and that the influence on the random wind error is negligible for both channels.

The same analysis was performed for the week between 28 September and 5 October 2020 and yielded similar results. Here, the percentage of Mie and Rayleigh wind results for which the frequency stability on the measurement level is better than 10 MHz is 78.6 % and 78.9 %, respectively. The Mie bias increases from (0.079 ± 0.008) m s⁻¹ for σ < 10 MHz to (0.187 ± 0.016) m s⁻¹ for σ > 10 MHz, while the Rayleigh bias differs by only 0.02 m s⁻¹. The respective random errors are 4.22 and 4.28 m s⁻¹ for the Mie and 7.16 and 7.17 m s⁻¹ for the Rayleigh channel, respectively.

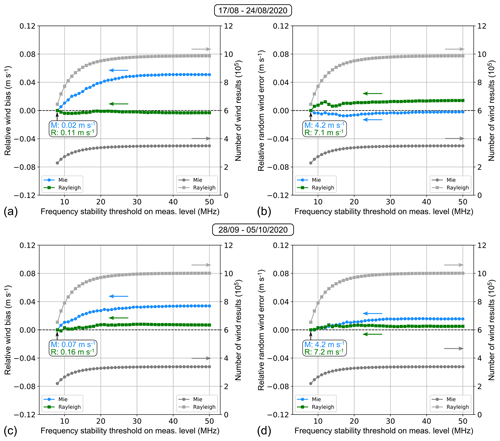
Figure 13 Wind bias (a) and random error (b) of the Mie (blue dots) and the Rayleigh channel (green squares) with respect to the ECMWF model background (O–B) depending on a frequency stability threshold for the period between 17 and 24 August 2020. The bias and random errors were subtracted by the respective values obtained for a threshold of 8 MHz for the sake of comparability (see reference values in the boxes). The number of Mie and Rayleigh wind results for which the frequency stability is below the threshold are shown with light-gray dots and dark-gray squares, respectively. Panels (c) and (d) show the corresponding data for the week between 28 September and 5 October 2020.

In order to further evaluate the impact of the laser frequency noise on the Aeolus wind data quality, a variable frequency stability threshold was applied, and the bias and random error with respect to the ECMWF model background were calculated for those winds that were measured during periods with frequency fluctuations below the threshold. The statistical results are depicted in Fig. 13. The mean Mie and Rayleigh wind biases are plotted in the left column, while the respective random errors for the 2 investigated weeks in August and September/October 2020 are shown on the right. Both values are presented relative to the statistical parameters that are obtained for a threshold of 8 MHz as this allows for a direct comparison of the two different datasets regardless of the absolute values, which differ among the analyzed periods and receiver channels due to other error contributions. The reference bias and random error values are indicated in the round boxes. A frequency stability of 8 MHz was chosen as a reference threshold since this value is close to the mean stability over the entire week and thus represents the average conditions in terms of laser frequency noise. The plots additionally present the number of winds that entered the statistics depending on the applied threshold. As can be seen from the figure, the number of wind results increases considerably when the threshold is relaxed from 8 to 15 MHz, whereas only few results are added at even higher thresholds. Overall, the number of Rayleigh (≈ 1 000 000) and Mie winds (≈ 350 000) is comparable for the two periods. Regarding the bias, a noticeable impact of the frequency stability is only evident for the Mie winds, as seen before. Here, the bias increases by up to 0.05 m s⁻¹ when wind data from high-noise periods are included in the statistics. For the Rayleigh winds, the bias change is negligible (< 0.01 m s⁻¹). The same holds true for the random errors in both channels, which change by less than 0.02 m s⁻¹ when the frequency stability threshold is relaxed from 8 MHz to more than 20 MHz.

In conclusion, the temporally degraded frequency stability of the ALADIN laser transmitter has only marginal influence on the wind data quality on a global scale. This is primarily due to the small percentage of measurements for which the frequency fluctuations are considerably enhanced. The biggest impact is observed for the Mie wind bias, which is increased by more than 0.3 m s⁻¹ when considering only those phases with strong variations (> 20 MHz) on the measurement level. However, as these winds represent only about 4 % of all wind results from the studied weeks, the effect is hardly noticeable in the statistics derived from the entire global dataset. Nevertheless, this study helps to identify an optimal threshold for a quality control (QC) that filters out measurements for which the frequency noise is considerably enhanced. The according QC parameter, which describes the frequency stability in terms of the standard deviation on the measurement level, is already included in the L1B product.

Since wind observations with enhanced frequency jitter occur over specific geolocations (see Fig. 6), it is interesting to study whether the wind data are significantly degraded in such affected locations. For this purpose, several areas where one or multiple critical reaction wheel speeds regularly occur, i.e., in East Asia or central Africa, were analyzed with regard to the deviations from Aeolus observations from ECMWF model winds (O–B). This preliminary study revealed that, although the percentage of measurements with frequency stability worse than 15 MHz is increased by a factor of 2 to 3 compared to the global percentage, the change in wind bias and random error is below 0.5 m s⁻¹. However, as the number of wind results is drastically decreased by the restriction to rather small geographical boxes, these results lack statistical significance. Hence, additional studies using longer periods of wind data are required to verify this small influence on the wind data quality on a local scale. Furthermore, as outlined in the end of Sect. 2.1, the impact of enhanced frequency noise is most pronounced in cases when only a small subset of the emitted pulses is detected in the atmospheric path, i.e., in heterogenous atmospheric scenes (Marksteiner et al., 2015). Therefore, proper extraction of such scenes, e.g., broken cloud conditions, is advisable prior to the statistical analysis. Nonetheless, the current study has provided a strong hint that the laser frequency stability is not a major contributor to the systematic and random errors in the Aeolus wind product for the SNR cases analyzed.

4.2 Influence on the Rayleigh and Mie ground velocities

Analogous to the approach presented in the previous section, the correlation between the laser frequency stability and the apparent velocity of the ground returns was investigated. Ground return signals are generally crucial for airborne and spaceborne radar and lidar systems that rely on the Doppler effect as they can be exploited for identifying systematic errors that are, for instance, caused by improper knowledge of the platform attitude or variations in the instrument's alignment (Bosart et al., 2002; Kavaya et al., 2014; Chouza et al., 2016). For the Aeolus mission, the ground surface could be used as a zero wind reference, which allows for the estimation of unknown wind biases from the measured ground velocities. This method, however, requires precise differentiation between atmospheric and ground return signals in order to prevent erroneous ground velocities (also referred to as zero wind calibration, or ZWC, values), which is particularly challenging due to ALADIN's coarse vertical resolution of several hundred meters. The ground detection scheme and its limitations are very similar for ALADIN and the A2D and are explained in detail in Weiler (2017) and Lux et al. (2018).

The ground velocities, obtained separately for the Rayleigh and Mie channel, are contained in the AUX_ZWC product, which is generated by the Aeolus L1B processor. The same 2 weeks in 2020 as in the previous section were studied. However, in contrast to the wind results, the ground velocities which are part of the L1B baseline 10 data are not bias-corrected using the M1 telescope mirror temperatures as for the L2B product so that they show rather large deviations from the “ideal value” of 0 m s⁻¹ (Rayleigh: −18 m s⁻¹; Mie: −2 m s⁻¹). Hence, the analysis relies on relative changes in the ground velocities depending on the frequency stability, while the influence of attitude control mispointing on this parameter can be neglected. Moreover, in contrast to the multitude of Rayleigh and Mie wind results, which are available from multiple range gates and all over the globe, ground return signals that are strong enough to be utilized for a potential ZWC of the Aeolus data are rare. Given the susceptibility to atmospheric contamination, i.e., the detrimental impact of the broadband atmospheric return signal on the narrowband ground return signal, only ground velocities that were measured from surfaces with high albedo in the UV spectral range are considered valid, which drastically limits the number of available ZWC values. The useful signal thresholds applied in the L1B processor are 1000 ACCD counts and 1200 ACCD counts for the Mie and Rayleigh channel, respectively. For this reason, the ZWC data from the 2 weeks were combined in order to obtain meaningful statistics. Since only data from high-albedo regions, i.e., Antarctica, Arctic and sea ice and snow-covered land areas, entered the statistics, solely the frequency stability over these locations plays a role in the analysis. Here, the precision of the ground returns is impaired by blowing snow that leads to a narrowband Mie return with a potentially non-vanishing Doppler shift, thus acting as another source of random errors on the ground returns. Since the ice coverage was comparable in the 2 weeks in 2020, the studied locations and thus the influence of the wheel speeds on the respective frequency fluctuations were similar for the individual periods that contributed nearly the same number of ground velocity values (≈ 4000) to the combined dataset. Note also that the ZWC data are provided only on the observation level (12 s = 540 pulses) as there is no differentiation between clear and cloudy bins. Consequently, the ground velocities are correlated with the laser frequency variations on the observation level.

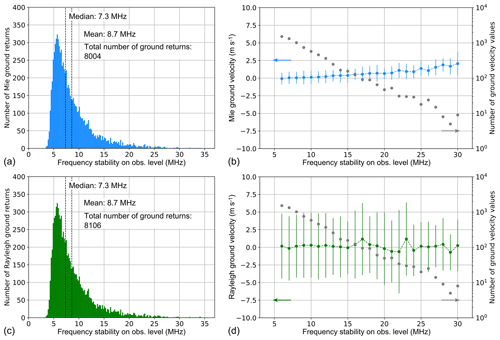
Figure 14 Histograms of the laser frequency stability on the observation level for those observations that yielded valid Mie ground returns during the combined periods from 17 to 24 August 2020 and from 28 September to 5 October 2020. (b) Mean Mie ground velocity in dependence on the frequency stability. The ground velocities were subtracted by the mean over all values for which the frequency stability is better than 8 MHz for the sake of comparability. A data point plotted versus a frequency stability of k represents the mean over all ground velocities for which the stability is in the interval between (k−1) MHz and k MHz, while the error bar represents the corresponding standard deviation. The number of ground velocity values within each interval is shown in gray. The bottom panels (c) and (d) depict the corresponding statistics for the Rayleigh ground returns.

Analogous to Fig. 12a and d, histograms of the laser frequency stability on the observation level are depicted in Fig. 14a and c for those observations that yielded valid Mie and Rayleigh ground velocities, respectively. The number of ZWC values is very similar for the two channels (≈ 4000), suggesting that almost the same observations, i.e., geographical locations, were considered in the statistical analysis. This also explains the agreement of the median and mean frequency stability on the observation level, which account for 7.3 and 8.7 MHz, respectively. The fact that these values are slightly higher than those on the measurement level presented in the previous section is most likely due to the restriction to polar regions, where critical wheel speeds are overrepresented (see Fig. 9). The influence of the frequency noise on the Mie and Rayleigh ground velocities is displayed in Fig. 14b and d, where the respective mean ground velocities are plotted against the frequency stability, which was subdivided into bins of 1 MHz. Here, a data point plotted versus a frequency stability of k MHz represents the mean over those ground velocities that fall in the interval between (k−1) MHz and k MHz. The velocities were subtracted by the mean over all ZWC values for which the frequency stability is better than 8 MHz to exclude the large bias contributions that are different for the two receiver channels. The error bar represents the corresponding standard deviation per bin. In addition, the number of ground velocities per interval that entered the statistics is plotted in gray.

Like for the wind results, the number of ZWC values strongly decreases when considering only those observations for which the frequency stability is considerably degraded. The portion of ground velocities with frequency stability worse than 15 MHz is as low as 8.2 % for both channels. In accordance with the findings in Sect. 4.1, there is no significant influence of the enhanced frequency noise on the Rayleigh channel, whereas the determined Mie ground velocities change almost linearly with the frequency stability. When regarding only observations with 29 MHz < σ < 30 MHz (rightmost dot in Fig. 14b), the ground velocity is about 2.1 m s⁻¹ higher than for those observations with 5 MHz < σ < 6 MHz. However, it should also be noted that only nine ZWC values contributed to this last data point, resulting in large uncertainty (standard deviation: 1.7 m s⁻¹) and thus small statistical significance.

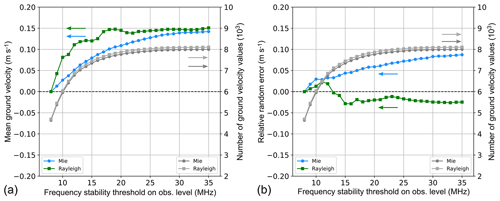
Figure 15 Mean ground velocity (a) and relative random error (b) of the Mie (blue dots) and Rayleigh channel (green squares) depending on a frequency stability threshold for the combined periods from 17 to 24 August 2020 and from 28 September to 5 October 2020. The data were subtracted by the respective values obtained for a threshold of 8 MHz for the sake of comparability. The number of ground velocity values for which the frequency stability is below the threshold is shown in gray.

The mean ZWC values are additionally calculated for a varying frequency stability threshold, analogous to Fig. 13, in order to consider the different weighting of the observations with low and high frequency noise. The results are plotted in Fig. 15 for the Mie and Rayleigh channel for both the mean and the standard deviation of the ground velocities of the respective data subset after applying the threshold. Here, a similarly weak dependency is evident for the Mie and Rayleigh channels, where the mean ZWC values (relative to the 8 MHz threshold) increase to 0.15 m s⁻¹ as the threshold is relaxed to 30 MHz. The random errors are even less affected and change by less than 0.10 m s⁻¹ depending on the applied frequency stability threshold.

From these results it can be concluded that, like for the atmospheric winds, the enhanced frequency noise has only minor influence on the Mie and Rayleigh ground velocities. Although the impact is slightly larger, it is still hardly noticeable in the statistics derived from the complete ZWC dataset and certainly represents a smaller issue than, e.g., blowing snow affecting the Mie and Rayleigh responses. Nevertheless, the approximately linear relationship between the frequency stability and the Mie mean ZWC value with a slope of about 0.08 m s⁻¹ MHz⁻¹ (Fig. 14b) demonstrates that a more severe degradation of the stability would lead to a significant change in the Mie ground velocities. Hence, assuming frequency fluctuations of 50 MHz on the observation level, the corresponding Mie ZWC values would deviate by more than 3 m s⁻¹. Depending on the contribution of those high-noise observations to the entire dataset, the frequency noise can, in principle, drastically deteriorate the ZWC accuracy. This is especially true if there are only a few valid measurements per observation in the case of broken ground or cloud detection. Therefore, application of an appropriate QC threshold, as stated in the previous section, is recommended for the processing of ground velocities as well.

5 Summary, conclusions and outlook

The Doppler wind lidar ALADIN on board Aeolus has set new technological standards in the field of spaceborne remote sensing. In particular, the design and performance of the frequency-stabilized UV laser transmitter is unprecedented for a space laser. By the end of 2020, the two ALADIN lasers had accumulated around 3.5 billion high-energy laser pulses in 27 months of operation. The present study has shown that the frequency stability of the emitted pulses is better than 10 MHz, except for the late FM-A period in spring 2019, most probably because of the advanced misalignment of its master oscillator. The excellent stability is achieved despite the permanent occurrence of short periods during which the frequency fluctuations are considerably enhanced to 30 MHz RMS on the observation level (12 s), 50 MHz RMS on the measurement level (0.4 s), and even up to 150 MHz peak to peak on the pulse-to-pulse level.

The investigation of the frequency stability during instrument response calibrations has revealed that it is correlated with the satellite's geolocation. This correlation entails a clustering of observations with enhanced frequency variations in specific regions of the Earth, forming linear and circular structures around the globe. The patterns differ for ascending and descending orbits and the two flight model lasers but are stable over the mission lifetime.

The underlying reason for the dependency on geolocation is the existence of critical rotation speeds of the satellite's reaction wheels, which suggests that micro-vibrations are the root cause for the deterioration of the laser stability on timescales of a few tens of seconds. This hypothesis is supported by the fact that the laser stability is also degraded during thruster firings of the satellite, which introduce high vibration levels also at the location of the power laser head. The identified detrimental frequencies of the reaction wheels range between 14 and 28 RPS and are consistent among the three active wheels, although the relative impact on the two lasers is different. Owing to the dependency of the reaction wheel speeds on the magnetorquer control authority and the strong influence of the latter on the magnetometer readings, there is an indirect link and hence decent correlation between the frequency stability and the magnetic field measured by the onboard magnetometer.

In the context of the enhanced frequency noise, the Aeolus wind error with respect to ECMWF model background winds was studied, pointing out that the temporally degraded stability of the ALADIN laser transmitter has only marginal influence on the global wind data quality. For 2 studied weeks in 2020, the Mie wind bias is increased by 0.3 m s⁻¹ during phases with strong variations (> 20 MHz) on the measurement level. Considering the small portion of such wind measurements (≈ 4 %) during a repeat cycle of 1 week, the influence on the accuracy of the Mie winds acquired over the entire globe is well below 0.1 m s⁻¹. However, a more noticeable contribution of the high frequency noise to the Mie wind bias is expected in regions where the reaction wheels are run at the critical speeds, although further studies are necessary for verification. The Rayleigh wind results are hardly affected, most likely because other noise contributors dominate, such as photon shot noise and fluctuations in the incidence angle on the spectrometers. Concerning the ground velocities, collected in areas with high surface albedo, a similarly small impact of the laser frequency stability was determined. The mean ground return velocity derived from the Mie spectrometer changes linearly with the frequency stability on the observation level by about 0.08 m s⁻¹ MHz⁻¹, whereas the Rayleigh ground velocities are nearly independent of the frequency noise over the investigated range.

Despite the small effect on the wind data, application of a QC in the Aeolus processor could be foreseen for the Mie winds to filter out measurements during which the frequency stability is worse than 20 MHz. The same threshold is suggested for the processing of the Mie and Rayleigh ground velocities as this will slightly improve the accuracy of the ground velocity values, while their number is not considerably reduced. These QC approaches become more important if the atmospheric return SNR is further decreasing within the mission lifetime as this will increase the share of Mie wind results among the overall Aeolus wind observations. For the Rayleigh winds, a QC based on the frequency stability is not considered useful since the error is largely dominated by shot noise. Hence, the discarding of any measurements, even with poor frequency stability, will rather diminish the Rayleigh wind precision given that it is primarily limited by shot noise.

Concerning the use of Aeolus data on smaller geographical scales, e.g., for its validation by on-ground or airborne instruments, the geolocational dependence of the laser frequency stability should be considered. Regions where the reaction wheels repeatedly rotate at their critical frequencies suffer from enhanced frequency noise during every overpass along Aeolus' ascending or descending orbit. Consequently, the percentage of wind observations with degraded stability is considerably higher than on a global scale and is expected to have a stronger impact on the wind accuracy, especially for the Mie channel.

With a view to future space lidar missions, particularly those which have strict requirements in terms of the laser frequency stability like EarthCARE, ACDL, MERLIN or Aeolus follow-on missions, several lessons learned are derived from the current study: first, the cavity control scheme of the laser transmitter plays an important role in ensuring a sufficiently short dead time of the feedback loop and in turn in filtering out vibration frequencies of several hundreds of hertz, which potentially deteriorate the laser stability. A modified ramp-delay-fire technique that was developed for the A2D (Lemmerz et al., 2017) allows for fast responses in the microsecond regime, thus providing high frequency stability (< 4 MHz RMS) even in harsh vibration environments. Referencing on a pulse-by-pulse basis, as performed in other wind lidar instruments (Baidar et al., 2018; Tucker et al., 2018; Bruneau and Pelon, 2021), would relax the requirements in terms of frequency stability. This could, for instance, be realized with avalanche photodiodes (APDs) working in real counting mode. There are studies ongoing with APDs in analog mode offering very low dark noise.

Second, although the on-ground micro-vibration tests led to the important implementation of isolation suspensions which effectively attenuated the micro-vibration levels by about 1 order of magnitude, the tests did not clearly reveal the existence of the critical reaction wheel speeds, which would affect the performance in a measurable way. This is mainly due to the too short operation of the wheels at their critical speeds, which did not allow for sufficient statistics of the acquired laser data depending on wheel speed. Therefore, extended tests with the spacecraft mounted in an isolated configuration and with flight-representative time-varying reaction wheel speeds whilst operating the laser are recommended. Moreover, it is proposed to use an appropriate number of accelerometers at different locations of the laser bench during such tests to properly characterize the impact of micro-vibrations on the laser behavior, particularly the frequency stability. Finally, a higher temporal resolution of the laser housekeeping telemetry data than currently available for Aeolus (0.25 Hz) with a focus on cavity control parameters is advisable to better evaluate the laser performance both on the ground and in space.

Furthermore, it is considered that the installation of accelerometers in the instrument flight model and the acquisition of micro-vibration measurements in orbit, even resulting in modest numbers of data, are extremely beneficial. These not only will allow a more definitive identification of the spacecraft elements responsible for deviations in scientific measurements but will also provide a reference for correlation of mechanical models representing orbital conditions.

Passive suspensions provide a well-proven solution for the mitigation of micro-vibrations generated by reaction wheels in orbit. With their simple configuration, they have low mass, consume no electrical power and require no computational resources. However, inherent to their mechanical architecture, they produce a non-negligible amplification of the disturbances at the frequencies of the suspension modes. Also, extreme isolation at high frequencies, which can be required by some applications, is often compromised by the presence of spurious mechanical modes whose effects in orbit are difficult to predict. As an alternative, active closed-loop vibration isolation systems based on sensing and counteracting the mechanical disturbances arising in the spacecraft show great promise in overcoming the limitations of passive systems. These can be implemented at the level of the source (Preda et al., 2018) and/or the payload (Sanfedino et al., 2021) and can significantly mitigate the micro-vibration environment in Aeolus follow-on and other future space lidar missions.