Comparison of mid-latitude single- and mixed-phase cloud optical depth from co-located infrared spectrometer and backscatter lidar measurements

The long-wave downwelling spectral radiance measurements performed by means of the Far-Infrared Radiation Mobile Observation System (FIRMOS) spectrometer at the summit of the Zugspitze (German Alps) in the winter 2018/19 allowed the retrieval of the optical and micro-physical properties of ice and mixed clouds, showing a good agreement of the statistical relationship between the ice water path and the ice optical depth with the ones from previous works. In this paper the optical depths retrieved from FIRMOS are initially compared with selected cases calculated from backscattering light detection and ranging (lidar) data by using a transmittance method. Then, in order to compare the whole FIRMOS dataset, the power-law relationship between backscattering and extinction is used to apply the Klett method and automatize the routine. Minimizing the root mean square differences, the exponent k of the power-law relationship is assessed to be 0.85 with a variability in the range of 0.60–1.10 for ice clouds and 0.50 with a variability within 0.30–0.70 for mixed clouds.

1 Introduction

The assessment of cloud radiative properties, particularly of cirrus and mixed clouds, is a paramount objective in improving the accuracy of general circulation models (GCMs) (Lubin et al., 1998), and it represents an outstanding problem for the remote sensing and radiative transfer communities. To date, there is still a lack of measurements of long-wave spectral properties of cirrus clouds, despite the fact that they represent one of the key component of the Earth radiation budget (ERB) (Cox et al., 2010; Kiehl and Trenberth, 1997). As a consequence, the uncertainties in the parameterization of their radiation properties are still large (Yang et al., 2015).

Clouds with temperature between 0 and −38 ^∘C, where particles can be either frozen or liquid, represent the so-called mixed-phase clouds, and their degree of glaciation depicts one of the largest uncertainties in climate prediction as stated by Costa et al. (2017); there are in fact many gaps that still remain in the experimental and theoretical description of this type of cloud (Korolev et al., 2017). Within this temperature regime, clouds can occur as liquid only (supercooled water) as well as in the mixed phase, in which ice crystals coexist with water droplets, and also as purely ice. Mixed-phase clouds are very common in polar regions, both in the Arctic (Turner, 2003) and Antarctica (Cossich et al., 2021), but they can also be widely found at mid-latitudes, so much so that Costa et al. (2017) show that out of 16 measurement flights of the COALESC (Combined Observation of the Atmospheric boundary Layer to study the Evolution of StratoCumulus) campaign performed with aircraft at mid-latitudes, 14 observations provided the presence of clouds in the mixed-phase regime.

Ice and mixed-phase clouds exert a very strong effect on the spectral radiance in the mid-infrared and far-infrared (MIR and FIR) portion, between 100–1600 cm⁻¹ (6–100 µm), since they modulate the incoming solar radiation in the short waves and the outgoing thermal emission in the long waves coming from the ground and lower atmosphere. For this reason, our knowledge about the cloud radiative properties has to be improved starting by increasing satellite, ground and in situ observations.

In September 2019 Far-infrared Outgoing Radiation Understanding and Monitoring (FORUM) was selected by the European Space Agency (ESA) as the ninth Earth Explorer (EE-9), with the purpose of studying the FIR portion of Earth's top-of-atmosphere (TOA) emission spectrum, below 667 cm⁻¹ (wavelengths above 15 µm) (Palchetti et al., 2020b). The FORUM measurement will cover the broad band 100–1600 cm⁻¹ with a spectral resolution of 0.5 cm⁻¹ (full width at half maximum), opening the capability to improve the knowledge of the FIR spectral properties of water vapour and cirrus clouds, whose radiative effect depends on their optical and micro-physical properties, such as the particle effective sizes and crystal habits.

During the so-called Phase A (feasibility study) of the satellite development, the Far-Infrared Radiation Mobile Observation System (FIRMOS) project was started with the aim of deploying a prototype of the FORUM spectrometer to perform field spectral measurements of the atmospheric downwelling long-wave radiation (DLR) with ground-based observations. Spectral measurements of DLR, up to the FIR region, are already successfully exploited to retrieve cloud properties, in particular cirrus clouds, at mid-latitudes (Palchetti et al., 2016; Maestri et al., 2014) and in polar regions (Di Natale et al., 2017; Maesh et al., 2001; Turner, 2003; Garrett and Zhao, 2013; Rowe et al., 2019). DLR measurements are, in general, very important since, while they provide the complementary part of the TOA spectral radiance, they also form a very useful basis to test the retrieval algorithms for future satellite applications, such as FORUM.

In this paper, the cloud optical and micro-physical properties are simultaneously retrieved, together with the thermodynamic phase (ice, water or mixed) using FIRMOS measurements. The resulting optical depths are in accordance with those obtained from selected measurements of a co-located backscatter lidar. Finally, the relationship between the retrieved optical depth and the ice water path is shown and compared with the results presented in previous works.

FIRMOS and lidar observations and the data analysis methodology are described in Sect. 2; the results are presented and discussed in Sect. 3, and the conclusions are drawn in Sect. 4.

2 Observations and methodology

The FIRMOS spectrometer was deployed from December 2018 to February 2019 to perform systematic measurements of the long-wave downwelling spectral radiance emitted by the atmosphere (Palchetti et al., 2020b) at the Alpine observatory on the summit of the Zugspitze (47.421^∘ N, 10.986^∘ E) in the south of Germany, at 2962 m a.s.l. (Palchetti et al., 2021). The instrument acquires spectra in the broad band between 100–1000 cm⁻¹ with an unapodized spectral resolution of 0.3 cm⁻¹ every 8 min. A backscatter stratospheric aerosol lidar operating in semi-automatic mode at a wavelength of 532 nm was located at the Environmental Research Station Schneefernerhaus on the south slope of the mountain, 300 m below (2675 m a.s.l.) and 680 m southwest of the summit; it operated with a frequency of one profile every 4–10 min with an integration time of 1 min and a vertical resolution of 7.5 m.

2.1 Spectral measurements and retrieval of cloud parameters

The retrieval of atmospheric state and cloud parameters is performed by exploiting the band between 200–1000 cm⁻¹ (10–50 µm), which provides the most relevant information about water vapour, temperature and cloud properties. The atmospheric window between 820–980 cm⁻¹ and the microwindows below 600 cm⁻¹ provide a high signal coming from the clouds; the band falling in the region 200–600 cm⁻¹ provides information about the water vapour profile, and the CO₂ band between 600–750 cm⁻¹ gives us information about the atmospheric temperature. The Simultaneous Atmospheric and Clouds Retrieval (SACR) algorithm (Di Natale et al., 2020b), which includes a forward and a retrieval model based on the optimal estimation (OE) approach, is used to retrieve simultaneously the cloud optical and micro-physical properties, such as the effective diameter of the ice particles and water droplets and the optical depth and the ice fraction, together with the atmospheric profiles of water vapour and temperature. A similar analysis was already performed by Turner and Eloranta (2008) to retrieve the optical depths of ice and water components in mixed-phase clouds from the data collected during the Mixed-Phase Arctic Cloud Experiment (M-PACE) at the Atmospheric Radiation Measurement (ARM) North Slope of Alaska (NSA) climate research facility in Barrow by using spectrally resolved infrared radiance observations from the Atmospheric Emitted Radiance Interferometer (AERI) and ones from a high-spectral-resolution lidar (HSRL).

The effective diameter (D_ei) of the ice crystals is defined following Yang et al. (2005):

$$\begin{array}{}\text{(1)}& D_{\mathrm{ei}}={\displaystyle \frac{\mathrm{3}}{\mathrm{2}}}{\displaystyle \frac{\sum _{h=\mathrm{1}}^N\underset{L_{\min }}{\overset{L_{\max }}{\int }}{f}_{\mathrm{h}}\left(L\right)V_{\mathrm{h}}\left(L\right)n\left(L\right)dL}{\sum _{h=\mathrm{1}}^N\underset{L_{\min }}{\overset{L_{\max }}{\int }}{f}_{\mathrm{h}}\left(L\right)A_{\mathrm{h}}\left(L\right)n\left(L\right)dL}},\end{array}$$

where L is the maximum length of the ice crystals; n(L) is the particle size distribution; V_h and A_h represent the particle volume and the projected area, respectively; the subscript h denotes the habit index and f_h indicates the habit fraction defined such that $\sum _{h=\mathrm{1}}^N{f}_{\mathrm{h}}=\mathrm{1}$ at each particle length L; and N is the total number of habits. For water droplets, assuming the spherical shape, the optical properties are derived from Mie theory, and Eq. (1) reduces to the effective diameter D_ew:

$$\begin{array}{}\text{(2)}& D_{\mathrm{ew}}=\mathrm{2}{\displaystyle \frac{\underset{r_{\min }}{\overset{r_{\max }}{\int }}{R}^{\mathrm{3}}n\left(R\right)dR}{\underset{r_{\min }}{\overset{r_{\max }}{\int }}{R}^{\mathrm{2}}n\left(R\right)dR}},\end{array}$$

where R is the radius of the droplets. The particle size distribution is modelled with a gamma size distribution for both ice and water as performed by Turner (2005).

The issue of the treatment of mixed-phase clouds is simplified by assuming that mixed-phase clouds are composed of a uniform mixture of spherical water droplets and ice crystals, which in turn are modelled as a mixture of different habits. This assumption is made since no depolarization measurements to discriminate the vertical distribution of thermodynamic phase were available. However, in order to take into account the multiple-scattering effect at different heights and the layers' inhomogeneity, the normalized raw lidar signal is used to modulate the internal distribution of optical depth (OD) within the cloud (Di Natale et al., 2020a). The different behaviour of the ice and water refractive index below 1000 cm⁻¹ (Turner, 2005) is exploited to discriminate the solid and liquid component from the infrared spectrum.

The total ice fraction (γ) is defined as the ratio between the ice water path (IWP) and the total water path (TWP) (Yang et al., 2003) as follows:

$$\begin{array}{}\text{(3)}& \mathit{\gamma }={\displaystyle \frac{\mathrm{IWP}}{\mathrm{TWP}}},\end{array}$$

where TWP is the sum of the ice and liquid component. γ is fitted together with D_ei, D_ew and the optical depth at the visible wavelength ($\mathrm{OD}={\mathrm{OD}}^{\mathrm{ice}}+{\mathrm{OD}}^{\mathrm{wat}}$). This latter parameter is related to the optical depth in the FIR band at the wavenumber ν (OD_FIR,ν) by the equation

$$\begin{array}{}\text{(4)}& {\mathrm{OD}}_{\mathrm{FIR},\mathit{\nu }}=\mathrm{OD}{\displaystyle \frac{{〈Q_{\mathrm{e}}〉}_{\mathrm{FIR},\mathit{\nu }}}{〈Q_{\mathrm{e}}〉}},\end{array}$$

where Q_e is the extinction efficiency. These parameters, together with the absorption efficiency, the single-scattering albedo, and the asymmetry factor for ice and water, are mixed up in the radiative transfer solution as described in Yang et al. (2003).

The instrument line shape (ILS) of the FIRMOS spectroradiometer is also fitted, in the same way with the REFIR-PAD spectroradiometer operating in Antarctica at Dome C (Palchetti et al., 2015; Bianchini et al., 2019), as a linear combination of a sinc function, which generally contributes with more than 90 %, and a sinc² function, which allows us to take into account the self-apodization due to the finite internal solid angle Ω of the instrument. The resulting ILS is expressed as follows:

$$\begin{array}{}\text{(5)}& {\mathrm{ILS}}_{\mathit{\nu }}\left(\mathrm{\Omega }\right)={\mathit{\alpha }}_{\mathit{\nu }}\left(\mathrm{\Omega }\right)\cdot \mathrm{sinc}\left({\displaystyle \frac{\mathit{\nu }}{\mathrm{\Delta }\mathit{\nu }}}\right)+\left(\mathrm{1}-{\mathit{\alpha }}_{\mathit{\nu }}\left(\mathrm{\Omega }\right)\right)\cdot {\mathrm{sinc}}^{\mathrm{2}}\left({\displaystyle \frac{\mathit{\nu }}{\mathrm{2}\mathrm{\Delta }\mathit{\nu }}}\right),\end{array}$$

where Δν is the spectral resolution (equal to 0.3 cm⁻¹) and ν represents the wavenumber. The α coefficient depends on Ω as shown in Bianchini et al. (2019). Ω is also fitted together with a frequency scale shift β, which takes into account both the shift due to the finite aperture given by $\mathit{\nu }\left(\mathrm{1}-\frac{\mathrm{\Omega }}{\mathrm{4}\mathit{\pi }}\right)$ (Davis et al., 2001) and the effect due to the instability of the reference laser, as follows (Palchetti et al., 2016):

$$\begin{array}{}\text{(6)}& {\mathit{\nu }}^{\prime }=(\mathrm{1}+\mathit{\beta })\cdot \mathit{\nu }.\end{array}$$

On average values equal to 0.001 sr and $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ are found for Ω and β. The state vector used in the retrieval is then given by

$$\begin{array}{}\text{(7)}& \mathit{x}=\left(D_{\mathrm{ei}},D_{\mathrm{ew}},\mathit{\gamma },\mathrm{OD},\mathit{U},\mathit{T},\mathrm{\Omega },\mathit{\beta }\right),\end{array}$$

where U and T represent the vectors of water vapour and temperature profiles' fitted levels. The levels are taken at 2.962 (corresponding to the ground), 3.3, 3.9, 4.4, 5 and 7 km for water vapour and 2.962, 2.966, 3.2, 3.4, 3.7, 4.4 and 7 km for temperature. This choice comes from sensitivity studies; particularly the very first level of temperature is introduced in order to take into account the strong variability just above the instrument. The routine minimizes the cost function given by

$$\begin{array}{}\text{(8)}& {\mathit{\chi }}^{\mathrm{2}}=(\mathit{y}-\mathit{F}(\mathit{x}\left){)}^T{\mathbf{S}}_y^{-\mathrm{1}}\right(\mathit{y}-\mathit{F}\left(\mathit{x}\right))+{\left(\mathit{x}-{\mathit{x}}_{\mathrm{a}}\right)}^T{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\left(\mathit{x}-{\mathit{x}}_{\mathrm{a}}\right),\end{array}$$

where y, F and x_a indicate the vectors of the measurements and the forward model and the vector containing the a priori parameters, respectively. S_y denotes the variance–covariance matrices (VCMs) of the measurements and contains the noise, which is considered uncorrelated and is given by the sum of the square of the noise-equivalent-to-signal ratio (NESR) and the calibration error. The S_a matrix represents the VCM of the a priori estimate x_a, and it is composed of the VCM a priori for clouds, atmospheric profiles and instrumental coefficients. The OE approach minimizes the cost function in Eq. (8) through the iterative formula given by (Rodgers, 2000)

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{\mathit{x}}_{i+\mathrm{1}}=& {\mathit{x}}_i+{\left[{\mathbf{K}}_i^T{\mathbf{S}}_y^{-\mathrm{1}}{\mathbf{K}}_i+{\mathit{\lambda }}_i{\mathbf{D}}_i+{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\right]}^{-\mathrm{1}}\\ & \left[{\mathbf{K}}_i^T{\mathbf{S}}_y^{-\mathrm{1}}\left(\mathit{y}-\mathbf{F}\left({\mathit{x}}_i\right)\right)-{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\left({\mathit{x}}_i-{\mathit{x}}_{\mathrm{a}}\right)\right],\end{array}\end{array}$$

where λ_i denotes the Levenberg–Marquardt damping factor at the iteration i, K_i represents the Jacobian matrix of F and D_i is a diagonal matrix which is described in detail in Di Natale et al. (2020b). The error in the retrieved parameters can be calculated when the convergence is reached, when variations on χ² are less than 1 ‰, through the formula (Rodgers, 2000)

$$\begin{array}{}\text{(10)}& {\mathbf{S}}_x={\left({\mathbf{K}}^T{\mathbf{S}}_y^{-\mathrm{1}}\mathbf{K}+{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\right)}^{-\mathrm{1}}.\end{array}$$

The cloud top and bottom heights (CTH and CBH) are fixed in the radiative transfer calculations and are inferred from the lidar backscattering signal interpolated at the FIRMOS acquisition times. The optical properties of cirrus clouds are tabulated for different crystal habits in specific databases (Yang et al., 2013). In this work a mixture of different habits typical of mid-latitudes is used in Eq. (1), as discussed in previous works (King et al., 2004). According to this, for ice crystal lengths lower than 70 µm the habit distribution is composed of 50 % bullet rosettes, 25 % plates and 25 % hollow columns, while for crystal lengths greater than 70 µm the habit distribution is given by 30 % aggregates, 30 % bullet rosettes, 20 % plates and 20 % hollow columns.

As an example of the retrieval, Fig. 1 shows a comparison of a FIRMOS spectrum (black) detected during the passage of a cirrus cloud at 7.5 km of altitude on 6 February 2019 and the simulated spectrum (red). The fit procedure is initialized with the CBH and CTH derived from the lidar range-corrected signal (RCS) detected by the backscatter lidar (in black in the left panel of Fig. 2) and the a priori profiles (in red in the central and right panels of Fig. 2) of water vapour and temperature provided by the National Centers for Environmental Prediction (NCEP), with error bars assumed equal to 50 % and 0.1 %, respectively, and assuming correlation lengths equal to 2 km. Regarding the clouds, first guesses and a priori values are taken from previous studies with the error equal to 100 % in order to avoid over-constraining of the retrieval procedure. Anyway, in the case that the cloud bottom temperature goes down below −35 ^∘C, γ is automatically set to 0.95 with a stringent a priori error of 0.05, since at this temperature the coexistence of liquid water is very unlikely. The reduced χ² turns out to be 1.18, and an effective diameter of (28.9±4.5) µm and ice OD equal to (0.42±0.04) are provided. A comparison of the radiance differences (green) is also reported in the lower panel of Fig. 1 together with the instrumental noise (black). In Fig. 2 the retrieved profiles (in blue) with the bars of the retrieval errors given by Eq. (10) are also reported.

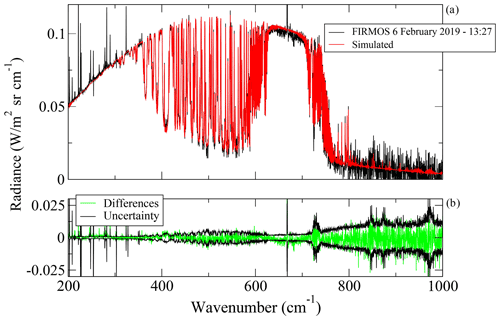
Figure 1 (a) The comparison of the FIRMOS measurement (black) in the presence of a cirrus cloud at 7.5 km on 6 February 2019 at 13:27 UTC with the simulated spectrum (red) at the last fit iteration. (b) The differences (green) between the measurement and simulation in comparison with the instrumental uncertainty (black).

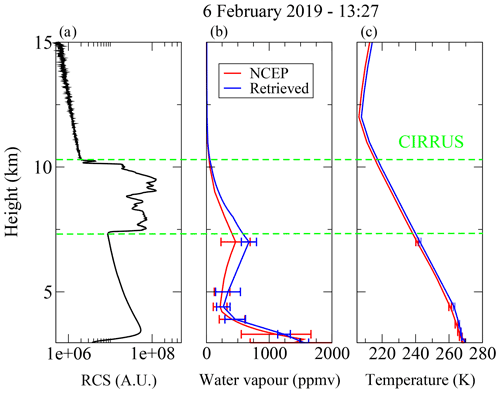
Figure 2 (a) The lidar range-corrected signal (RCS) as a function of the height above the ground corresponding to the measurement of Fig. 1. (b, c) The NCEP profiles (red curves) of the water vapour volume mixing ratio (vmr) and temperature together with the ones retrieved from FIRMOS data (blue curves).

From all FIRMOS measurements a dataset of 245 spectra between 22 January and 7 February 2019 is selected within the time range of the acquired lidar measurements. From the analysis of these spectra 174 were ice clouds (γ≥0.8) and 71 mixed clouds ($\mathrm{0.2}<\mathit{\gamma }<\mathrm{0.8}$) (Turner, 2003). We also required the condition that in the case of γ<0.2, the constraint $|\mathit{\gamma }-\mathrm{0.2}|<\mathrm{\Delta }\mathit{\gamma }$, with Δγ retrieval error, must be met in order to avoid any misclassification. All retrievals converge with a reduced χ² lower than 2, confirming the good quality of the retrieval. In Fig. 3 the scatter plots of OD versus the IWP and liquid water path (LWP) (left panels), the effective diameters of ice crystals and water droplets (central panels), and the ice fraction and the cloud temperature (right panel) are reported for ice (black) and mixed (green) clouds. The IWP is derived from the retrieved parameters by using the following equation (Yang et al., 2005):

$$\begin{array}{}\text{(11)}& {\mathrm{OD}}_{\mathrm{FIR},\mathit{\nu }}^{\mathrm{ice}}={\displaystyle \frac{\mathrm{3}\cdot \mathrm{IWP}}{D_{\mathrm{ei}}{\mathit{\rho }}_{\mathrm{i}}}}{\displaystyle \frac{{〈Q_{\mathrm{ei}}〉}_{\mathrm{FIR},\mathit{\nu }}}{\mathrm{2}}},\end{array}$$

which comes from Eq. (4) for the ice-only case, where Q_e can be considered constant and equal to 2 at visible wavelengths because of the large size parameter ($\frac{\mathit{\pi }{D}_{\mathrm{e}}}{\mathit{\lambda }}$), ρ_i=917 kg m⁻³ is the density of the pure ice, and ${\mathrm{OD}}_{\mathrm{FIR}}^{\mathrm{ice}}$ is referred to the ice component. From the comparison with Eq. (4), the OD^ice at visible wavelengths depends on the IWP and D_ei. The LWP can be derived since Eq. (11) is also valid for the water case by replacing the parameters for ice with the analogue ones for water and using ρ_w=1000 kg m⁻³. The retrieved ODs are found ranging between 0.01 and 1 for ice clouds and mostly between 0.1 and 10 for mixed clouds. The effective diameters mostly range between 10 and 40 µm for ice particles and between 2 and 10 µm for water droplets. The average values of OD^ice, OD^wat, D_ei and D_ew are found to be equal to 0.13, 0.77, 19 and 6.7 µm, respectively. The cloud temperature is found to be lower than 240 K for ice clouds and mostly in the range below 220 K, corresponding to cirrus clouds above 8 km of height. The mixed clouds are warmer with temperature above 240 K, and they occur at lower heights, below 6 km.

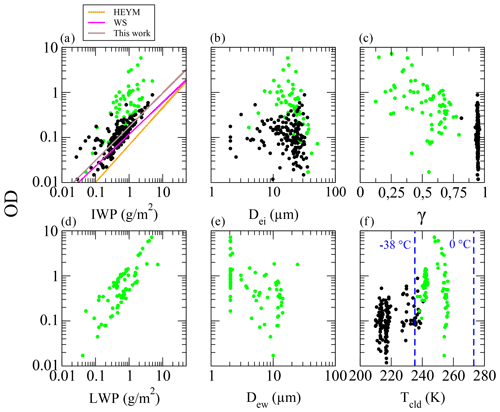
Figure 3 (a, d) The scatter plot of OD vs. the ice water path (IWP) and liquid water path (LWP) for ice (black) and mixed (green) clouds. The solid brown, orange and magenta lines represent the power-law fit obtained in this work and in the previous works of Heymsfield et al. (2003) and Wang and Sassen (2002), denoted as HEYM and WS, respectively. (b, e) The OD vs. effective diameters of ice crystals (D_ei) and water droplets (D_ew). (c, f) The same scatter plot of OD vs. the ice fraction (γ) and cloud temperature (T_cld).

Following previous works (Heymsfield et al., 2003), a power law in the form $\mathrm{OD}=a\cdot {\mathrm{IWP}}^b$ is used to fit the retrieved data of the IWP and OD for ice clouds. From FIRMOS measurements the fit result provides the coefficients $a=(\mathrm{0.173}\pm \mathrm{0.005})$ and $b=(\mathrm{0.748}\pm \mathrm{0.028})$. The fitted curve is reported in Fig. 3 (in brown). This is close to those found in other works (Heymsfield et al., 2003) (in orange) and, particularly, is in very good agreement with those found by Wang and Sassen (2002) (in magenta) for mid-latitude cirrus clouds.

2.2 Lidar OD measurements and comparison with the retrieved values from FIRMOS

The optical depths of thin cirrus clouds are retrieved from backscatter profiles of the Zugspitze aerosol lidar by using the transmittance method introduced by previous works (Young, 1995; Chen et al., 2002; Giannakaki et al., 2007). This instrument (Höveler et al., 2016) transmits laser pulses at 10 W and 100 Hz, and it is commonly used for measurements of the stratospheric aerosol load within NDACC (Network for the Detection of Atmospheric Composition Change). The cirrus OD is directly retrieved from the weakening of the lidar return P by the cirrus itself. This is principally performed by, firstly, linearizing of the lidar logarithmic range-corrected signal (LRCS) S=ln (Pz²); detecting the bottom and top of the cirrus layer; defining two altitude intervals close to the cirrus with pure Rayleigh backscatter, one below the cirrus and one above (typically 1 km); and calculating a best-fit line by least squares for the lidar signal in the two intervals. Finally, the OD is given by half of the difference between the two fit lines at the upper edge of the cirrus since the light detected by the lidar passes the cirrus twice. This method is suitable for cirrus layers which are optically thin (OD < 1) and which exhibit a significant extinction with respect to a reasonable signal-to-noise ratio of the lidar signal. At typical altitudes for cirrus in the winter season (8–10 km) this means an OD larger than roughly 0.01. Other further preconditions are sufficiently low aerosol or cloud interference and a fairly stable temperature gradient in the two intervals where the fit lines are calculated. Under appropriate conditions, directly determining the transmittance from the lidar signal weakening avoids the use of uncertain a priori knowledge. Particularly, as already mentioned, ice crystals of cirrus clouds exhibit a large variety of shapes and, thus, a large range of ratios between backscatter and extinction. As an example, in the upper panel of Fig. 4 a comparison is shown of the ODs retrieved from the lidar data through the transmittance method (black) and those retrieved from FIRMOS data with SACR (red) obtained on 6 February 2019 by using the mentioned mixture of ice crystal habits typical of mid-latitudes. The results are in good agreement except for a few cases. These differences are motivated by the fact that the two instruments were not exactly co-located, but instead the lidar was measuring at a horizontal distance of 600 m from the FIRMOS spectrometer and 300 m lower. Moreover, the lidar has beam divergence much smaller than the FIRMOS field of view, which is equal to 22.4 mrad. This means that the FIRMOS signal comes from a wide portion of the observed source. This effect means that the horizontal inhomogeneity of the cloud does not contribute to the lidar signal unlike the spectrometer. In order to check whether the habit choice affects the OD retrieval, in the lower panel of Fig. 4 a comparison of the ODs retrieved from FIRMOS by assuming different pristine habits, namely aggregates, bullet rosettes, hollow columns and plates, is also plotted in addition to those obtained by assuming the mid-latitude mixture (in black). The lower panel of Fig. 4 shows that the differences between the retrieved ODs are within the error bars so it can be stated that the retrieval from FIRMOS measurements provides the cloud optical depth regardless of the habit choice used for the retrieval.

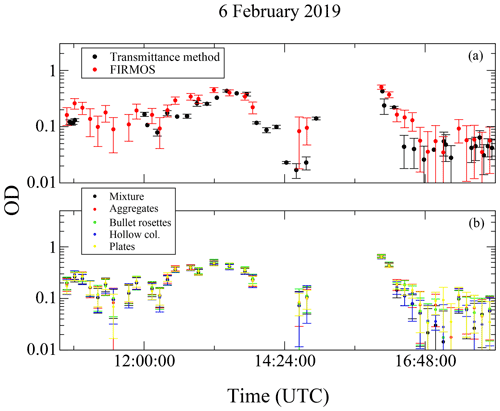
Figure 4 (a) Comparison of the ODs retrieved from FIRMOS data (in red) on 6 February 2019 and those obtained through the transmittance method (in black). (b) The retrieved ODs from FIRMOS by assuming the mixture (black) and different ice crystals habits (red, green, blue and yellow).

The transmittance method approach to retrieve the ODs from lidar measurements takes a long time if the analysis must be performed over a large dataset, since it cannot be automatized, and it is not suitable for retrieving OD > 1. For this reason the applicability of the Klett method, which can be automatized and, thus, more suitable to analysing large datasets, is also investigated.

2.3 OD retrieval by using the Klett method

The retrieval of the OD can be performed by using the Klett inversion method (Klett, 1981, 1985) from the lidar backscattering signal P as a function of the altitude z. Since only one lidar equation and two unknowns, the backscatter (β) and the extinction (σ), are involved in this problem, the relationship that binds them has to be assumed. A common solution is to assume a power-law relationship with exponent k as follows:

$$\begin{array}{}\text{(12)}& \mathit{\beta }\left(z\right)=C\cdot \mathit{\sigma }(z{)}^k,\end{array}$$

with C constant and k depending on the laser frequency, the aerosol composition and the inhomogeneity of the layers, particularly the variability in the aerosol size distribution, the particles' shape and the mixing with the air, and it also contains the multiple-scattering effect implicitly (Del Guasta et al., 1993; Elouragini, 1995). The coefficient k generally ranges in the interval of 0.67–1.00 (Klett, 1981; Elouragini, 1995), but it can also assume higher and lower values (Takamura and Sasano, 1987; Klett, 1985). Solving the lidar equation by using Eq. (12), the cloud extinction profile (σ_c(z)) is calculated as a function of the height z as follows:

$$\begin{array}{}\text{(13)}& {\mathit{\sigma }}_{\mathrm{c}}\left(z\right)={\displaystyle \frac{\exp \left[\frac{S\left(z\right)-S_{\mathrm{r}}}{k}\right]}{{\mathit{\sigma }}_{\mathrm{r}}^{-\mathrm{1}}+\frac{\mathrm{2}}{k}\underset{z}{\overset{z_{\mathrm{r}}}{\int }}\exp \left[\frac{S\left(z^{\prime }\right)-S_{\mathrm{r}}}{k}\right]\mathrm{d}{z}^{\prime }}}-{\mathit{\sigma }}_{\mathrm{m}}\left(z\right),\end{array}$$

where S(z)=ln (P(z)z²) represents the LRCS; σ_m(z) is the molecular extinction derived from the atmospheric profiles; S_r and σ_r denote the LRCS and the extinction at a reference height z_r fixed at 500 m above the CTH, respectively, in which the backscattering contribution is totally due to the molecules. From the extinction the optical depth is obtained as the integral over the cloud thickness:

$$\begin{array}{}\text{(14)}& \mathrm{OD}=\underset{\mathrm{CBH}}{\overset{\mathrm{CTH}}{\int }}{\mathit{\sigma }}_{\mathrm{c}}\left(z\right)\mathrm{d}z.\end{array}$$

3 Results and discussion

The assumption of Eq. (12) implies that the power-law exponent k must be known; otherwise it must be fitted. As already mentioned, this parameter depends on the optical properties of aerosols in the air (Chan, 2010), which in turn are related to the thermodynamic phase and the shape of the particles. Accurate knowledge of the particle shape can only be assumed for the liquid phase, in which case the particles are described in term of spheres; otherwise a complex mixture of different crystal habits must be considered. Anyway, as already shown, the retrieved OD from these measurements does not strongly depend on the habit distribution. For this reason, a possible estimate of k can be obtained by comparing the ODs derived from the lidar data (named OD_lidar) by using Eq. (13) and those retrieved from FIRMOS spectra (named OD_FIRMOS). This can be carried out since the applicability of the Klett method allows us to automatize the calculation of OD_lidar and to exploit the whole dataset. The best value of k is chosen by taking the minimum of the root mean square (rms) of the differences between FIRMOS and lidar ODs as in previous works (Chan, 2010). Some cases in which the lidar signal variations do not correspond to a proportional variation in the FIRMOS spectra were excluded from the comparison, since this indicates that the scenario observed by the two instruments is totally different because of the non-perfect co-location.

Figure 5 shows the variation of the rms as a function of k. As k depends on the cloud homogeneity, it is not constant for all scenarios. Thus, it is reasonable to provide a value at the minimum of the rms and a range of variability. The minimum of the rms corresponds to k being equal to 0.85 for ice clouds, which is in accordance with the theoretical range of 0.67–1.00, and to 0.50 for mixed clouds. The correlation index at the minimum turns out to be 0.67 and 0.78 for ice and mixed clouds, respectively, as reported in Fig. 5. The range of variability of the k parameter is estimated as shown in Fig. 6 by using the extreme values corresponding to the blue and green curves that include most of the scenarios. In the case of ice clouds, the range of variability is $\mathrm{0.60}\le k\le \mathrm{1.10}$, as deducible from the upper panel of Fig. 6. For mixed clouds the range of variability is $\mathrm{0.30}\le k\le \mathrm{0.70}$, as shown in the lower panel of the same figure. The differences in the ice cloud scenarios below number 10 and between 139 and 150 (upper panel) are probably due to an inhomogeneity in the cloudy scene observed by FIRMOS and the lidar, such as the presence of occasional and scattered cirrus clouds during these measurements. The high OD values (up to 6) of mixed clouds in the first two scenarios (lower panel) are not reproducible with the Klett approach, since in this case the high liquid water optical depths likely fully attenuate the lidar signal.

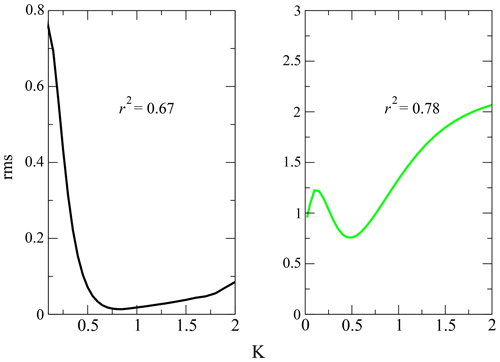
Figure 5 Plots of the curves of the root mean square (rms) differences between the optical depths retrieved from FIRMOS and the lidar as a function of the power-law exponent k for the ice (black) and mixed (green) clouds. r² denotes the correlation index.

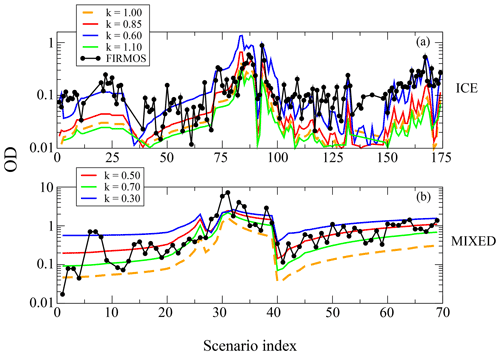
Figure 6 (a, b) The comparison of ice and mixed-cloud ODs retrieved from FIRMOS (black dots) with those obtained with the Klett approach from lidar measurements. The red lines indicate the retrieved OD by using the k of the best fit, while the green and the blue lines show the variability. The dashed orange lines show the result for k=1 which is the typical value assumed in other studies.

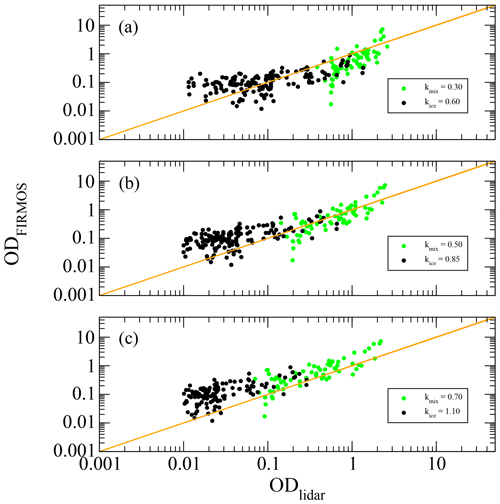
Figure 7 (b) The scatter plot between the optical depths retrieved from FIRMOS and the backscattering lidar for k equal to the value at the minimum as plotted in Fig. 5. (a, c) The same comparison for values of k larger and lower than the minimum, respectively. The black and green colours indicate the ice and mixed clouds as reported in Figs. 3 and 5.

The scatter plot of OD_lidar versus OD_FIRMOS is reported in Fig. 7 for different values of k and for all the types of cloud. The scatter plot obtained for the k values minimizing the rms is shown in the central panel. The upper and lower panels show the scatter plots for values of k lower and greater than the minimum, respectively, corresponding to the estimated variability. Once the k value is estimated, this approach allows us to rapidly calculate the ODs and the corresponding variability by applying the Klett method to the lidar measurements, using a simple algorithm.

4 Conclusions

In this work the spectral DLR measurements performed by means of the Far-Infrared Radiation Mobile Observation System (FIRMOS) spectrometer installed in the winter 2018/19 (between December 2018 and February 2019) at the Alpine observatory on the summit of the Zugspitze (Germany) were used to determine the power-law exponent k of the extinction–backscatter relationship (Eq. 12) for ice and mixed-phase clouds. The SACR routine, based on an optimal estimation approach, was used with FIRMOS spectral radiances to calculate cloud optical and micro-physical properties, such as the effective diameters of ice crystals and water droplets and the optical depth, together with the ice fraction and the atmospheric profiles. The different behaviour of the ice and water refractive index below 1000 cm⁻¹ was exploited to retrieve the ice fraction by modelling cloud as an homogenous mixture of ice crystals and water droplets, since measurements of depolarization were not available. The single-scattering properties of ice crystals were taken from specific databases provided by Yang et al. (2013), and the average values are obtained by assuming a mixture of habits typical of mid-latitudes. A statistical parameterization between the IWP and the OD in the form $\mathrm{OD}=a\cdot {\mathrm{IWP}}^b$ was used to fit data, and coefficients a and b were found to be in accordance with those derived from previous works.

The simultaneous availability of a backscatter lidar, co-located near the Zugspitze summit, allows us to constrain the cloud geometrical properties for simulating the radiative transfer in the presence of clouds. The backscattering signal was used to modulate the cloud vertical distribution of the optical depth and take into account the multiple-scattering effect of the different layers. These data also allowed us to validate the retrieved optical depth from FIRMOS spectra with those obtained from lidar data by applying a transmittance method. Since a power law between the backscatter and the extinction coefficients is commonly assumed to invert the lidar equation, the procedure to estimate the best values of the exponent k of this relationship is presented and discussed. This approach mainly consists in the minimization of the root mean square (rms) differences between the ODs retrieved from FIRMOS spectra and those obtained from lidar measurements by using the Klett method. In such a way, it was found that for cirrus clouds k varies in the interval of 0.60–1.10, providing a variability of 0.25 with respect to the best value at the minimum of the rms differences equal to 0.85, while for mixed clouds k varies in the range 0.30–0.70, with a variability of 0.20 with respect to the best value equal to 0.50. The assessment of k represents useful information for the application of the Klett method to lidar measurements. This approach opens the possibility of retrieving the cloud ODs from large datasets of lidar measurements, which can be used to determine the climatology of this parameter.