Triple-frequency radar retrieval of microphysical properties of snow

An algorithm based on triple-frequency (X, Ka, W) radar measurements that retrieves the size, water content and degree of riming of ice clouds is presented. This study exploits the potential of multi-frequency radar measurements to provide information on bulk snow density that should underpin better estimates of the snow characteristic size and content within the radar volume. The algorithm is based on Bayes' rule with riming parameterised by the “fill-in” model. The radar reflectivities are simulated with a range of scattering models corresponding to realistic snowflake shapes. The algorithm is tested on multi-frequency radar data collected during the ESA-funded Radar Snow Experiment For Future Precipitation Mission. During this campaign, in situ microphysical probes were mounted on the same aeroplane as the radars. This nearly perfectly co-located dataset of the remote and in situ measurements gives an opportunity to derive a combined multi-instrument estimate of snow microphysical properties that is used for a rigorous validation of the radar retrieval. Results suggest that the triple-frequency retrieval performs well in estimating ice water content (IWC) and mean mass-weighted diameters obtaining root-mean-square errors of 0.13 and 0.15, respectively, for log ₁₀IWC and log ₁₀D_m. The retrieval of the degree of riming is more challenging, and only the algorithm that uses Doppler information obtains results that are highly correlated with the in situ data.

1 Introduction

Quantifying snowfall rates is essential for understanding the water cycle in middle and high altitudes. Solid-phase precipitation affects many aspects of human life. On the one hand, it can represent a hazard to several public services (e.g: transport, energy distribution networks) as well as private properties; on the other hand, snow accumulation and its eventual runoff is important for hydroelectric power generation and water resource management (Skofronick-Jackson et al., 2019). Snow cover plays a very important role in the climate system, modifying the global and regional energy budget due to its high scattering albedo. Despite the undeniable importance of precipitation in the solid phase, there is large discrepancy between different snowfall accumulation estimates (Mroz et al., 2021b), which reflects a high degree of uncertainty in these products.

To reduce the uncertainties related to the snow modelling, observational data are needed, but these are still rare due to their cost and the remoteness of high-latitude regions where most of the snowfall occurs. Moreover, in situ measurements on the ground are affected by problems like under-catch and wind-blown snow biases (Fassnacht, 2004), and they are only representative of the environment around the data collection site. Radar measurements offer better spatial and temporal coverage, but their interpretation is subject to errors/uncertainties that follow from the assumptions made about the scattering properties of the targets in the radar volume; those depend on the snow particle size, density, shape and structure (e.g. Kuo et al., 2016; Eriksson et al., 2018). Because different frequency radars respond differently to the microphysical properties of snow (once their wavelengths become comparable with the size of snow aggregates), multi-frequency algorithms were recognised as a potential tool for solid-phase precipitation studies (Hogan et al., 2000; Kneifel et al., 2011). Over the years, the availability of data from complex multi-frequency Doppler radar systems has fostered the development of algorithms based on dual-frequency reflectivity (e.g. Matrosov, 1998), triple-frequency reflectivity (e.g. Leinonen et al., 2018; Tridon et al., 2019; Battaglia et al., 2020b), dual-frequency reflectivity and Doppler measurements (e.g. Mason et al., 2018), and even full Doppler spectral information (e.g. Mroz et al., 2021a). An increase in the number of observables included in the inversion schemes went hand in hand with an increase in the number of retrieved microphysical parameters. For instance, the most recent algorithms aim at quantifying the ice water content, the characteristic size and the bulk density of snow in the radar volume.

This study presents an algorithm for estimating the following microphysical snow properties: mean mass-weighted diameter, ice water content and degree of riming. The retrieval utilises triple-frequency radar measurements and is based on Bayes' rule. It does not assume any functional form of the particle size distribution, but it is based on several datasets collected during historical airborne campaigns. More detail on the methodology can be found in Sect. 2. Validation of the retrieval, with nearly perfectly co-located in situ and remote sensing measurements, is presented in Sect. 3. Additionally, we compare the results for different combinations of radar observables. Conclusions are drawn in Sect. 4.

2 Methodology

2.1 Theoretical basis

The equivalent reflectivity factor for a radar operating at the wavelength λ is given by

$$\begin{array}{}\text{(1)}& Z_{\mathrm{e}}={\displaystyle \frac{{\mathit{\lambda }}^{\mathrm{2}}}{{\mathit{\pi }}^{\mathrm{5}}|K_{\mathrm{w}}{|}^{\mathrm{2}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\mathit{\sigma }}_{\mathrm{b}}\left(D\right)N\left(D\right)\mathrm{d}D,\end{array}$$

where σ_b is the backscattering cross-section of the particle, D is its diameter, N is the particle size distribution (PSD) and K_w is the dielectric factor of liquid water at a reference temperature and frequency. Note that the PSD is a positive function only over a limited set of particle sizes, so the effective integration limits are finite. In this study, it is assumed that $|K_{\mathrm{w}}{|}^{\mathrm{2}}=\mathrm{0.93}$, which is a good approximation for standard temperatures and frequencies below the Ka-band. The reflectivity is usually expressed in mm⁶ m⁻³ or, due to its high variability, in logarithmic units of dBZ=10log ₁₀ (mm⁶ m⁻³). The radar signal, regardless of its frequency, is attenuated along the beam propagation path. This effect is ignored in this study, due to the relatively short path through the ice cloud and thus negligible extinction even at the most affected W-band (Protat et al., 2019). In fact, the distance to the nearest range gate from which the data are collected is so short that the attenuation correction would be smaller than the uncertainty in the measurements themselves. In the case of longer distances, attenuation corrections must be performed (e.g. Kalogeras and Battaglia, 2021) before our algorithm can be applied.

Due to a large variety of particle size distributions (PSDs) found in nature, no explicit analytical formula that approximates their shape is used. Instead, the radar simulations used in this study are based on the binned PSD measurements collected by optical instruments during different in situ airborne campaigns. In addition to radar reflectivity simulations, selected microphysical properties are prescribed to each PSD in the dataset. These properties include the ice water content (IWC), the mean mass-weighted snow diameter (D_m) and the degree of riming (α), which is defined below. The size of snowflakes is defined in terms of the diameter of the smallest circumscribing sphere. The database constructed in this way defines a statistical mapping between microphysical properties of ice PSDs $[D_{\mathrm{m}},\text{IWC},\mathit{\alpha }]$ and radar reflectivities at the frequencies of interest.

The mass of the snowflakes is modelled using the parameterisation of Morrison and Grabowski (2008). In this scheme, riming is modelled by “filling-in” the interstices between ice crystal branches by super-cooled liquid droplets (Heymsfield, 1982). The mass of unrimed aggregates follows the power-law relationship:

$$\begin{array}{}\text{(2)}& m_{\text{ag}}\left(D\right)={\mathit{\alpha }}_{\text{ag}}{D}^{{\mathit{\beta }}_{\text{ag}}},\end{array}$$

where α_ag and β_ag are the parameters of the fit, and the physical quantities are in SI units. We assume α_ag=0.015 and β_ag=2.05, which agrees well with in situ observations (Leroy et al., 2016) and the simulations of aggregates (Leinonen and Szyrmer, 2015). For sizes where the power-law formula would exceed the mass of solid ice spheres, the latter is used.

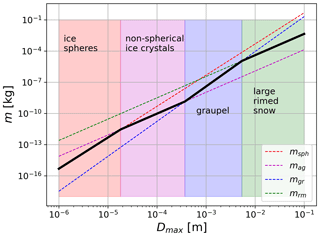
Figure 1 Mass–size parameterisation of Morrison and Grabowski (2008) for rimed aggregates. The different colours correspond to the size ranges where a specific power-law formula is used: red for small solid ice spheres, magenta for non-spherical ice crystals, blue for fully rimed snow and green for aggregates that are not completely filled with rime.

The mass parameterisation for particles that underwent a riming process is more complex. The range of ice sizes is divided into four domains: small ice spheres, dense non-spherical ice crystals, graupel (fully rimed aggregates) and large partially rimed snowflakes as it is shown in Fig. 1. The first two groups are the same as those described for unrimed snow flakes, but their specific relationship between mass and size is only applicable up to a certain size. The transition between dense non-spherical ice crystals and graupel (gr) occurs at the size where their masses are equal. For diameters exceeding this critical point, the mass of particle is given by

$$\begin{array}{}\text{(3)}& m_{\text{gr}}\left(D\right)={\mathit{\alpha }}_{\text{gr}}{D}^{{\mathit{\beta }}_{\text{gr}}},\end{array}$$

where α_gr and β_gr are the m–D parameters specific for graupel (α_gr=469 and β_gr=3.36; Leinonen and Szyrmer, 2015). As a consequence of the filling-in conceptual model, this relation applies to particles that are small enough to be fully filled with rime. For larger sizes, the exponent (β) of the mass–size relation remains the same as for unrimed aggregates (β_ag=2.05), and only the prefactor (α) increases:

$$\begin{array}{}\text{(4)}& m_{\text{rm}}\left(D\right)={\mathit{\alpha }}_{\text{rm}}{D}^{{\mathit{\beta }}_{\text{sn}}}.\end{array}$$

Again, the changeover between graupel and partially rimed aggregates occurs where their masses become equal, which provides a continuous transition in the m–D formula. The larger the α_rm, the larger the mass of rimed particles and the size where the transformation occurs. With this approach, the density of ice particles is completely determined by α_rm, and this parameter is used to describe the degree of riming.

2.2 Scattering model

To simulate radar reflectivity, the backscattering cross-section of all the particles within the radar volume must be known (see Eq. 1). This is straightforward for rain drops since their shape can be precisely simulated (Ekelund et al., 2020a), but it is more complicated for snow due to the variety of snowflake types, sizes, possible arrangements of the ice crystals within a single aggregate and is some cases a certain degree of riming (Kneifel et al., 2020). For wavelengths much larger than the size of snow, the “soft” sphere approximation provides a good approximation of the scattering properties (Kuo et al., 2016). However, when a diameter of a snowflake is comparable to or larger than the wavelength, the scattering calculations need to account for all the aforementioned properties of the ice particle (Tyynela et al., 2011). In this study, we use a combination of three publicly available scattering data sets: the ARTS database of Eriksson et al. (2018), the OpenSSP database of Kuo et al. (2016) and the rimed snowflakes simulations of Leinonen and Szyrmer (2015). The fist two data sets cover a variety of snowflake types and sizes populating our database up to 13 mm in diameter. The data set of Leinonen and Szyrmer (2015) complements the other two by covering a much larger range of snow densities and larger sizes (D < 25 mm).

Despite the fact that the formation of certain types of snow is determined by the atmospheric conditions, ice particles observed by the radar could be transported there, which makes it very difficult to reliably simulate measurements tailored to a given snow type. Therefore, we treat all the snowflake types as equally possible, and the backscattering properties are given as a function of their mass and size only; i.e. $(m,D)\mapsto {\mathit{\sigma }}_{\mathrm{b}}$. The function σ_b is constructed by grouping all the snow particles from the scattering data sets by their mass and size using logarithmically spaced bins along two dimensions. Then, in each bin, a mean mass-squared-normalised backscattering cross-section is computed by averaging ${\mathit{\sigma }}_{\mathrm{b}}(D_{\mathrm{i}},m_{\mathrm{i}})/m_{\mathrm{i}}^{\mathrm{2}}$ of individual particles in the bin. Because in the Rayleigh scattering regime σ_b is proportional to m² (Hogan et al., 2012), the introduced normalisation reduces variability of the averaged variable within the bin, and it prevents biases toward large masses that would contribute the most to the mean otherwise. The final estimate of σ_b in each bin is given by

$$\begin{array}{}\text{(5)}& {\mathit{\sigma }}_{\mathrm{b}}(m,D)=m^{\mathrm{2}}\cdot {\text{mean}}_{i\in \text{bin}}\left({\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{b}}(m_{\mathrm{i}},D_{\mathrm{i}})}{m_{\mathrm{i}}^{\mathrm{2}}}}\right).\end{array}$$

For an arbitrary value of m and D, one needs to interpolate between the mean normalised backscattering values and multiply by mass squared. For sampling points outside the convex hull defined by the range of sizes and masses within our dataset, the soft sphere approximation is used.

Based on this approach, to simulate the radar reflectivity at a given wavelength, λ, and for an arbitrary particle size distribution, N(D), it is sufficient to determine the degree of snow riming (α_rm in the previous section). Once α_rm is set, the relation between the snowflake mass and size is unambiguously determined, which allows for calculations of the backscattering cross-sectional area, and the equivalent radar reflectivity value follows from Eq. (1).

2.3 Inversion scheme

The previous section described how to simulate radar reflectivity for a given PSD and a degree of riming. This section focuses on the inverse problem; i.e. given a set of radar measurements, how does one estimate the properties of the observed PSD. This study focuses on the triple-frequency observations that, due to limited information content, prevent a size-resolved retrieval of the PSD. Therefore, the inversion scheme presented here aims at estimating only bulk properties of snow in the radar volume. These properties include: mean mass-weighted diameter (D_m), ice water content (IWC) and a degree of riming (α_rm). All of these parameters are positive; thus, for practical reasons it is more convenient to retrieve their logarithms; thus, the state vector is given by

$$\begin{array}{}\text{(6)}& \mathit{x}=[{\log }_{\mathrm{10}}{D}_{\mathrm{m}},{\log }_{\mathrm{10}}\text{IWC},{\log }_{\mathrm{10}}{\mathit{\alpha }}_{\text{rm}}{]}^{\mathrm{T}}.\end{array}$$

The observation vector is formed from the reflectivity at the smallest frequency and the dual-frequency ratios (DWRs), i.e. the differences between reflectivities at different bands in dBZ:

$$\begin{array}{}\text{(7)}& \mathit{y}=[Z_{\mathrm{X}},{\text{DWR}}_{\mathrm{X}-\text{Ka}},{\text{DWR}}_{\text{Ka}-\mathrm{W}}{]}^{\mathrm{T}}.\end{array}$$

There are several advantages to exploiting the DWR–DWR space. First, the DWRs are independent of the IWC (see Eq. 1) of the observed PSD, because its dependence cancels out once the difference (quotient in the linear units) of the different bands is taken. This simplifies the inversion scheme because it introduces some degree of orthogonality in the observation space. Secondly, previous studies (Kneifel et al., 2011, 2015) have shown that the DWR–DWR data have a potential to discriminate between different degrees of riming on top of the sizing capabilities. For the uncertainty in the radar measurements, 1 dB random error at all the frequency bands is assumed. Because the radar measurement errors are uncorrelated, the error covariance matrix of the observation vector y is

$$\begin{array}{}\text{(8)}& \mathbf{COV}=\left[\begin{array}{ccc}\mathrm{1}& -\mathrm{1}& \mathrm{0}\\ -\mathrm{1}& \mathrm{2}& -\mathrm{1}\\ \mathrm{0}& -\mathrm{1}& \mathrm{2}\end{array}\right].\end{array}$$

The retrieval scheme adopted for this study is based on Bayesian theory and aims at estimating the expected value of the state x for a given measurement y:

$$\begin{array}{}\text{(9)}& E\left(\mathit{x}\mathrm{|}\mathit{y}\right)=\underset{\mathrm{X}}{\int }\mathit{x}p\left(\mathit{x}\mathrm{|}\mathit{y}\right)\mathrm{d}\mathit{x},\end{array}$$

where p(x|y) denotes the conditional probability of x subject to y being observed. To estimate p(x|y), a dataset of in situ PSD measurements is used. All the PSD measurements are aggregated over 5 s. At a typical aeroplane speed of 150 m s⁻¹ it is equivalent of approx. 8 min integration for the ground-based instrument (for unrimed snowfall that sediments at approx. 1.5 m s⁻¹). This mitigates the problem of undercatch of large snowflakes that are the most uncommon in the sampling volumes. This database is constructed from the measurements collected during MC3E (Jensen et al., 2016), IPHEx (Erlingis et al., 2018), OLYMPEX (Houze et al., 2017) and HAIC/HIWC (Leroy et al., 2015) field campaigns where approximately 0.25 million PSD measurements were taken in total. The HAIC/HIWC campaign was selected to complement NASA-led campaigns to add high ice water content (IWC) measurements. Unlike the other campaigns where the water content was measured with the Nevzorov probe, the HIWC used an isokinetic evaporator specifically designed for high-IWC measurements. The measurements of IWC are used as complementary information to the PSD data, which allows us to estimate the degree of riming by matching the measured IWC with the one simulated from the PSD for different values of α_rm. This procedure establishes a PSD-specific relationship between the mass and size of the observed snowflakes so that the mass-weighted mean diameter (D_m) can be estimated, and it is included in the in situ training dataset. For each PSD, the radar reflectivities at X-, Ka- and W-band are simulated using the scattering model described in Sect. 2.2. Then, for any hypothetical measurement y, the probability that the PSD resembles this measurement is computed as

$$\begin{array}{}\text{(10)}& p\left({\mathit{x}}^i\mathrm{|}\mathit{y}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }\sqrt{\text{det}\left(\mathbf{COV}\right)}}}\exp \left[-\mathrm{0.5}\left(\mathit{\delta }{\mathit{y}}_{\mathrm{i}}{)}^{\mathrm{T}}{\mathbf{COV}}^{-\mathrm{1}}\right(\mathit{\delta }{\mathit{y}}_{\mathrm{i}})\right],\end{array}$$

where δyⁱ is the difference between the hypothetical and the simulated measurement corresponding to the ith element in the in situ database:

$$\begin{array}{}\text{(11)}& \begin{array}{rl}\mathit{\delta }{\mathit{y}}_{\mathrm{i}}=& \mathit{y}-{\mathit{y}}_{\mathrm{i}}=[Z_{\mathrm{X}}-Z_{\mathrm{X}}^i,{\text{DWR}}_{\mathrm{X}-\text{Ka}}-{\text{DWR}}_{\mathrm{X}-\text{Ka}}^i,\\ & {\text{DWR}}_{\text{Ka}-\mathrm{W}}-{\text{DWR}}_{\text{Ka}-\mathrm{W}}^i{]}^{\mathrm{T}}.\end{array}\end{array}$$

By expressing Eq. (9) in a discrete form, the expected value of x subject to y being observed is given by

$$\begin{array}{}\text{(12)}& E\left(\mathit{x}\mathrm{|}\mathit{y}\right)={\displaystyle \frac{{\sum }_i{\mathit{x}}^{i}p\left({\mathit{x}}^i\mathrm{|}\mathit{y}\right)}{{\sum }_{i}p\left({\mathit{x}}^i\mathrm{|}\mathit{y}\right)}}.\end{array}$$

Theoretical uncertainty in the retrieval is estimated as a weighted standard deviation of the state vectors for a given measurement:

$$\begin{array}{}\text{(13)}& \text{Var}\left(\mathit{x}\mathrm{|}\mathit{y}\right)={\displaystyle \frac{{\sum }_{\mathrm{i}}\left({\mathit{x}}^i{)}^{\mathrm{2}}p\right({\mathit{x}}^i\mathrm{|}\mathit{y})}{{\sum }_{\mathrm{i}}p\left({\mathit{x}}^i\mathrm{|}\mathit{y}\right)}}-E(\mathit{x}\mathrm{|}\mathit{y}{)}^{\mathrm{2}}.\end{array}$$

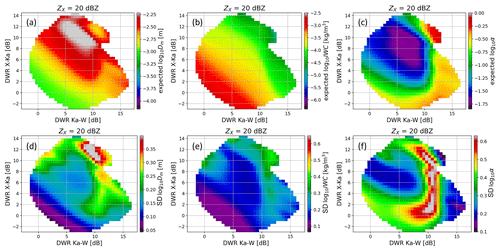
Figure 2 (a–c) The expected values of log ₁₀D_m, log ₁₀IWC and log ₁₀α_rm in the DWR_X−Ka–DWR_Ka−W space for Z_X = 20 dBZ. (d–f) Uncertainties in the quantities presented in the top row (see the colour bar captions). The inverse model is derived from the in situ airborne PSD measurements during the MC3E, IPHEx, OLYMPEX and HAIC/HIWC campaigns.

The retrieval presented here is based purely on the database of in situ measurements and does not assume any analytical form of the PSD. Moreover, the radar simulations are based on the scattering properties of realistic snowflakes. An example of this inverse mapping for Z_X = 20 dBZ is presented in Fig. 2. The characteristics of the retrieval are in line with the previous studies (Kneifel et al., 2015), e.g. low-density snow usually occurs for ${\text{DWR}}_{\text{Ka}-\mathrm{W}}<\mathrm{10}$ dB and DWR_X−Ka > 4 dB, whereas heavily rimed particles occupy regions with low DWR_X−Ka or DWR_Ka−W > 12 dB. The mean mass-weighted snow diameter tends to increase with the DWR values, and the largest sizes are observed for low-density aggregates. Although the DWRs do not depend on the IWC, it is evident from the plot that, for the same reflectivity, low DWRs correspond to higher ice loads. This shows a compensating effect between D_m and IWC: to get the same reflectivity value for small particles, the IWC has to be large and vice versa.

The estimates of the uncertainty reveal limited capabilities of the triple-frequency retrievals to accurately quantify bulk ice density except for the signatures of extreme aggregation or strong riming mentioned before. The transition between these two distinct regimes is characterised by very large uncertainty in log ₁₀α_rm that reaches 0.65 (more than a factor of 4) for Z_X = 20 dBZ. The other two state variables are much better constrained by the measurements; however, an elevated uncertainty is also observed for the transition region between heavy riming and aggregation domains.

The methodology presented in this section can be also applied to an arbitrary set of measurements. In particular, a single-frequency retrieval can be constructed and compared to the multi frequency one. We perform this exercise with an X-band retrieval that is validated in the next section. We also test a retrieval where triple-frequency reflectivity data are supplemented by mean Doppler velocity measurements.

3 Application and validation

3.1 SnowRadExp dataset

The Radar Snow Experiment For Future Precipitation Mission (RadSnowExp; Wolde et al., 2019) research flights were conducted in mid-latitudes and near the Arctic Circle (Iqaluit, NU, Canada, 63^∘ N), during the autumn of 2018, covering a wide geographical region and microphysical conditions. The flights focused on sampling precipitation systems where large aggregates and rimed particles were present in order to optimise the triple-frequency analyses. Multi-frequency radar observations were obtained from nadir- and zenith-looking antennas of the NRC (National Research Council Canada) airborne W- and X-band (NAWX) radars (Wolde and Pazmany, 2005) and the University of Wyoming's Ka-band Precipitation Radar (KPR; Haimov et al., 2018). The NAWX antennas are housed inside an unpressurised blister radome mounted on the right side of the aircraft fuselage, and the KPR radar was installed on the left wing-tip pylon. Although the three radars are on the same platform and almost co-located, mismatched radar beamwidths and differences in vertical resolutions and radar data dwell times required additional processing steps to provide the best possible matching of the radar volumes to reduce the DWR estimation errors (Nguyen et al., 2021). In addition to the radars, the NRC Convair-580 aircraft was equipped with a wide array of state-of-the-art in situ sensors for measurements of aircraft and atmospheric state parameters and cloud microphysical properties. Bulk liquid water content (LWC) and total water content (TWC) were measured simultaneously with single-particle size distribution, ranging from small cloud droplets to large precipitation hydrometeors. In this work, cloud particle size distribution was composed using a combination of data from several single-particle probes: fast cloud droplet probe (FCDP, 2–50 µm, SPEC Inc.), two-dimensional stereo probe (2DS, 10–1200 µm, SPEC Inc.), and a vertically oriented high-volume precipitation spectrometer version 3 probe (HVPS3, 150–19200 µm, SPEC Inc.) or precipitation imaging probe (PIP, 100–6400 µm, DMT). TWC and LWC were measured by the Nevzorov, a constant-temperature hot-wire probe (Korolev et al., 1998). We estimate the accuracy of the Nevzorov data during RadSnowExp to be of the order of 0.05 g m⁻³.

3.2 Validation data

The data collected during the SnowRadExp campaign offer an unprecedented opportunity to validate the triple-frequency radar snow retrieval since the remote measurements are well co-located with the in situ observations of snow microphysics. Having said that, a gap between the probes and the first radar range gate of approximately 100 m can introduce some uncertainty in the validation process due to the vertical gradients in the snow microphysics and therefore in the reflectivity. For some parts of the validation flight, the difference between the radar return below and above the plane can reach 10 dB. In such a situation it is difficult to decide which measurement resembles best the microphysics at the flight level.

To address the collocation issue, an Optimal Estimation (OE) framework (Rodgers, 2000) is used to provide the most likely estimate of the state variables. The only variable that is estimated here is a degree of riming (log ₁₀α_rm), while it is assumed that the PSD measured by the optical probe is errorless. The a priori estimate of log ₁₀α_rm is based on the in situ dataset described in Sect. 2.3, where the mean value of −1.31 and the standard deviation of 0.43 are observed. The measurement vector is composed of log ₁₀IWC as it is measured by the Nevzorov probe and the average of the reflectivity above and below the aircraft at X, Ka and W bands. The corresponding uncertainties in the measurements are 0.05 g m⁻³ and one-half of the difference between the radar measurements. In case the reflectivity difference between both sides of the plane is within 2 dB, we set the uncertainty in the measurement to 1 dB to account for random errors in the radar observation. The forward model to simulate the IWC and the radar reflectivity at the frequencies of interest is the one described in the Methodology section.

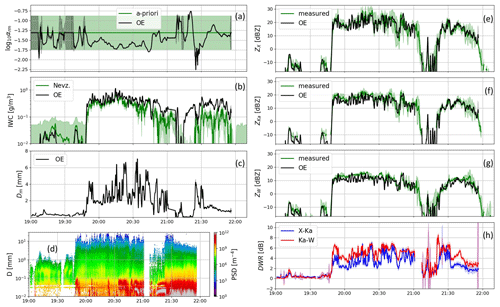
Figure 3 The estimates of the microphysical properties of snow and the radar reflectivity at the flight level. Panel (a) shows the retrieved degree of riming in black and its prior estimate in green. The retrieval is based on the data from triple-frequency radar, Nevzorov probe and PSD measurements. Panel (b) depicts the estimated IWC (black) and Nevzorov probe data (green). Panel (c) depicts the estimated mean mass-weighted diameter of snow. Panel (d) depicts the PSD data collected by the optical array probe. Panels (e–g) show the reflectivity at the X-, Ka- and W-band, respectively. The reflectivity measured above and below the aeroplane is shown as edges of the green shaded areas; the black line represents the estimated value at flight level after assimilation of radar and on-board in situ instrument data. Panel (h) depicts the optimal estimates of the DWRs. Shading in all panels represents the uncertainty in each estimate.

Figure 3a depicts the results of the OE retrieval for a flight leg. The black line with shading represents the retrieved value of log ₁₀α_rm and its estimated standard deviation, respectively. The remaining panels show the other microphysical properties (on the left) and the radar reflectivities (on the right) with their associated uncertainties estimated by propagating the errors in α_rm. For the first half of the flight (until 20:45 UTC), the optimally estimated IWC is in agreement with the Nevzorov probe data, but later it tends to be higher than the in situ instrument reports. This discrepancy mainly occurs where the measured IWC is relatively low, and so the associated uncertainty is large. The estimates of the reflectivity at all the considered frequency bands are in agreement with the measurements (see blue and red lines in Fig. 3), and the estimate of their uncertainty is within 1 dB for the most of the flight.

3.3 Validation of the snow microphysical retrieval

The optimally estimated radar measurements and the microphysical data described in the previous subsection are used for the validation of the microphysical retrieval. First, the triple-frequency radar reflectivity at the in situ flight level is used to form the measurement vector (see Eq. 7). Then, the expected value of the state vector is estimated using the methodology presented in Sect. 2.3. Finally, the retrieval results are evaluated against the microphysical properties of snow determined using the optimal estimation framework (see Sect. 3.2). These validation data serve as an in situ “truth”. An analogous analysis is repeated for two other retrievals: one that is based on single-frequency X-band radar reflectivity only and another one based on triple-frequency reflectivity data with the addition of the mean Doppler velocity at the X-band. Note that the Doppler velocities as well as the radar reflectivity values at the flight level are not directly measured. They are estimated from the radar measurements below and above the aeroplane and in situ probe data using the data assimilation technique that exploits the radar simulator described in Sect. 3.2. Their uncertainties are estimated by propagating the errors in the state vector, x (Eq. 6).

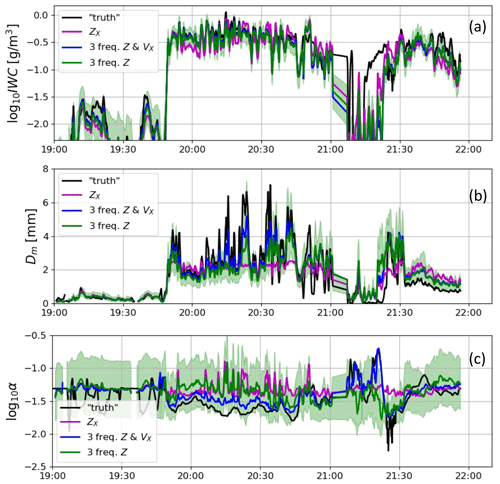
Figure 4 The results of different microphysical retrieval along the validation flight. The black line, denoted as truth, shows the microphysical properties of snow derived in Sect. 3.2 using the optimal estimation framework that combines information provided by the PSD measurements, Nevzorov probe and radar data together. The green, blue and magenta lines correspond to the retrievals based on the triple-frequency reflectivity, triple-frequency reflectivity with the mean Doppler velocity at the X-band and the algorithm based on the X-band reflectivity only, respectively. The green shading shows the uncertainty in the triple-frequency retrieval.

The results of the three retrievals in comparison to the in situ truth along the flight are shown in Fig. 4. At first glance, all the retrievals perform well in estimating IWC; nevertheless, multi-frequency algorithms show some advantages in certain parts of the flight. The retrieval of the mean mass-weighted diameter shows more differences between the algorithms. Clearly, the single-frequency algorithm struggles in retrieving large snow sizes (D_m > 2.5 mm). This indicates that the radar reflectivity at the X-band is correlated more with the water content than with the size when large snowflakes are present in the radar volume. The retrieval based on triple-frequency reflectivity performs better in estimating D_m, but it is not as close to the truth as the algorithm that uses the Doppler information. This improved size estimation capability is the result of additional information on ice density provided by the velocity of particles.

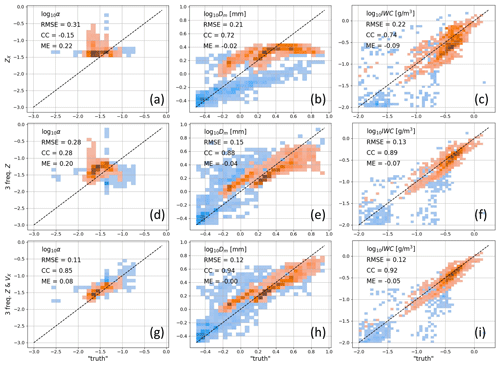
Figure 5 Histograms of in situ measurements (x axis) collected during the RadSnowExp campaign and the retrieved (y axis) microphysical parameters. Different columns correspond to different microphysical properties, i.e. log ₁₀α_rm, log ₁₀D_m and log ₁₀IWC. The rows correspond to different combination of radar measurements: single-frequency reflectivity, triple-frequency reflectivity and triple-frequency reflectivity with Doppler data. The blue pixels represent the data along the whole flight, while the red ones represent measurements where Z_X > −20 dBZ, DWR_X−Ka > 1 dB, DWR_Ka−W > 1 dB and the IWC is at least 70 % of the total water content. The bulk statistics shown in the top left corner of each panel correspond to the red pixels.

A more quantitative retrieval evaluation is presented in Fig. 5. The bulk retrieval statistics are displayed in the top left corner of each panel. These statistics were produced for the validation points where Z_X > −20 dBZ, DWR_X−Ka > 1 dB and DWR_Ka−W > 1 dB. These conditions were imposed to show the difference between the triple-frequency algorithm and the single-frequency one. For negligible DWRs, the multi-frequency information is reduced to one frequency, and the difference between the algorithms disappears. As an additional constraint, we require that the IWC is at least 70 % of the total water content, which removes points where D_m estimates are negatively biased by an abundant number of small liquid drops in the PSD data.

Out of all the microphysical parameters, the one that is the most difficult to retrieve is the degree of riming. The single-frequency retrieval is uncorrelated with the in situ data, which indicates the minimal information content on the snow density of these measurements, at least in the range of the observed reflectivity values (−20 < Z_X < 30 dBZ). The triple-frequency radar reflectivity observations contain more information about the density of ice. This is reflected in a positive but still low Pearson correlation coefficient (CC) of 0.28. The triple-frequency radar measurements are not enough to constrain the inverse model enough to estimate this parameter with high accuracy. This has been already suggested by the uncertainty estimates of this parameter presented in Fig. 2f. The DWR–DWR space separates well the extreme signatures of riming and aggregation, but the intermediate values of log ₁₀α_rm cluster around DWR_Ka−W of 10 dB which results in high uncertainty in this parameter. These results confirm the findings of Mason et al. (2019), who showed that it is very challenging to disentangle the effects associated with changes of the PSD and of the snow density just looking at DWR–DWR plots. Therefore, we recommend caution when interpreting DWR–DWR data. The best retrieval of the degree of riming is achieved when reliable mean Doppler velocity estimates are available. In this case, the correlation between the truth and the retrieved values increases to 0.85, and the root-mean-square error (RMSE) drops by a factor of 3 compared to the reflectivity-only-based algorithm.

The accuracy ranking of the retrievals of D_m and IWC is identical to that for α_rm. The single-frequency retrieval gets the lowest score, the second place goes to the triple-frequency one and the triple-frequency Doppler algorithm performs the best. All the retrievals of D_m are strongly correlated with the in situ data. Clearly, the algorithm based on X-band reflectivity underestimates the highest end of the snow sizes. The triple-frequency one also tends to underestimate the large sizes, but the underestimate is smaller as it is shown by the reduced RMSE value. The underestimate is not as systematic as for the single-frequency retrieval, but the validation data are more scattered for large values, which reflects uncertainties in the algorithm. There is an additional improvement in the accuracy of the D_m retrieval if Doppler measurements are included. These observations facilitate the estimation of the ice density and thus reduce the uncertainty in the characteristic size of snow. The bimodal clustering of the validation points for D_m results from overestimating the size of small snowflakes (log ₁₀D_m < 0.2) by all the presented algorithms. These sizes correspond to PSDs measured after 21:30 UTC, and they are characterised by a very high concentration of particles smaller than 0.1 mm. Such small ice crystals do not generate any DWR signal, but their concentration is large enough to produce D_m smaller than expected from the global statistics. This pinpoints the shortcomings of the dual- and multi-frequency radar-based approaches; i.e. their sizing capabilities are limited to the parts of the PSD where at least one of the frequency bands is in the non-Rayleigh regime. An unusual concentration of small ice crystals for a given D_m can affect the accuracy of the estimate. The retrievals of IWC show very similar bulk statistics as the one for D_m. None of the algorithms seem to be affected by a systematic bias with larger uncertainties for the single-frequency algorithm.

4 Conclusions

A methodology to estimate some important bulk microphysical properties of snow is presented and evaluated using in situ airborne data. The retrieval algorithm is based on the Bayes theorem, where the expected values of the microphysical properties for a given set of the radar measurements are estimated from a dataset of airborne in situ flights and corresponding radar reflectivity simulations. In this study, we focus on the triple-frequency reflectivity retrieval. The capabilities of the algorithm are tested with the data collected during the SnowRadExp campaign in Canada. Advantages and limitations of the retrieval are shown by contrasting the performance of the algorithm with two possible alternatives: the algorithm based on X-band reflectivity only and the retrieval where triple-frequency reflectivity data are complemented by the mean Doppler velocity information.

The evaluation results indicate that the single-frequency (X-band only) algorithm can be effectively used to estimate the ice water content in the radar volume but, not unexpectedly, with uncertainties larger than for multi-frequency approaches. The estimate of the mean mass-weighted diameter saturates at around 3 mm, which results in a negative bias for larger sizes. This demonstrates that the size of snow and the radar reflectivity are not well correlated in the presence of large snowflakes. In stratiform precipitation conditions, which were sampled during the flight used for validation, single-frequency radar measurements do not constrain the retrieval of the ice density which tend to oscillate around the global mean statistics.

The main advantage of triple-frequency approaches over single-frequency approaches is their capability to better represent the in situ estimates of the mean mass-weighted diameter, especially for the characteristic sizes greater than 3 mm. Moreover, they are characterised by higher accuracy of the IWC estimates (0.22 vs. 0.13 root-mean-square error of log ₁₀IWC). In contrast to the single-reflectivity algorithm, the multi-frequency one presents some skill in retrieving the degree of riming of the observed snow. However these abilities are limited to only cases with extreme aggregation or riming. Intermediate regimes are very difficult to distinguish from the signatures in the DWR–DWR space that can be produced either by varying the shape of the particle size distribution or the ice density. This ambiguity results in high uncertainty in the estimates of the degree of riming and low correlation coefficient (0.3) between the in situ data and the retrieval.

The triple-frequency reflectivity retrieval that also ingests Doppler information performs the best out of all the analysed algorithms. In stratiform conditions, it retrieves accurately the degree of riming reaching a root-mean-square error of log ₁₀α_rm of 0.11. The retrieved degree of riming is strongly correlated with the validation data (CC = 0.85). This capability helps in further improvements in the estimates of the size and water content of the observed snow PSD.

The analysis presented here takes advantage of a validation dataset that is estimated via optimally matching the in situ measurements of the water content measured by the Nevzorov probe, the PSD measurements collected by optical array probes and the remote sensing data from triple-frequency radars. This unique dataset provides an unprecedented opportunity to validate multi-frequency radar retrievals of the snow microphysics. The application of the methodology is restricted to one flight only and should be applied to long-term observations in order to produce more statistically significant results. Future studies could also consider the inclusion of radars in the G-band (Lamer et al., 2021) and assess their impact on the retrieval of smaller particles.

Note that the radar observations at the flight level used for the retrieval were not directly measured by the radar. They were simulated using the same forward model as for the in situ PSD dataset. This has two consequences. First, this approach is the equivalent of assuming that the forward model is error free; i.e. the scattering properties of snow depend only on its size and mass, and snow riming can be parameterised with one continuous parameter only. Secondly, the vector of observables used for validation is also free of the random errors that affect real measurements. In particular, the Doppler measurements are assumed to be unaffected by the vertical air motion that can substantially alter real data. Although this approach results in the error estimates presented here being underestimated, it shows capabilities and limitations of different radar setups when no assumption on the PSD shape is made, which is the goal of this paper.

A key finding of the study is that the Doppler capability is essential to estimate the density of snow in the radar volume, which remains the biggest challenge in the accurate quantification of the ice-phase precipitation. Based on these findings, we strongly recommend considering Doppler capabilities for future space-borne radar missions (Battaglia et al., 2020a) aimed at characterising solid-phase precipitation.