The polarimetric characteristics of dust with irregular shapes: evaluation of the spheroid model for single particles

In the atmosphere, the dust shapes are various, and a single model is difficult to represent the complex shapes of dust. We proposed a tunable model to represent dust with various shapes. Two tunable parameters were used to represent the effects of the erosion degree and binding forces from the mass center, respectively. Thus, the model can represent various dust shapes by adjusting the tunable parameters. To evaluate the applicability of the single spheroid model in calculating the optical properties of single dust with irregular shapes, the aspect ratios of spheroids were retrieved by best fitting the phase function of dust with irregular shapes. In this work, the optical properties and polarimetric characteristics of irregular dust with a diameter range of 0.2–2.0 µm were investigated. Our findings show that the dust shapes have a substantial impact on the scattering matrix, and sometimes the sign of elements of the scattering matrix could be modified by changing the tunable parameters. The applicability of the spheroid model is significantly affected by the erosion degree and binding forces, and substantial deviations could be observed when the dust diameter is in the range of 0.8–2.0 µm. The F₁₁ relative differences of approximately 100 % between dust with irregular shapes and best-fitted spheroids could be observed in certain scattering angles. The maximum differences in other elements between irregular dust particles and best-fitted spheroids can reach approximately 0.3–0.8. Besides, the signs of $F_{\mathrm{12}}/F_{\mathrm{11}}$, $F_{\mathrm{33}}/F_{\mathrm{11}}$, $F_{\mathrm{34}}/F_{\mathrm{11}}$ and $F_{\mathrm{44}}/F_{\mathrm{11}}$ can be modified from negative to positive at some scattering angles if substituting the irregular dust with best-fitted spheroids. As the binding force is small, the deviation of extinction or scattering cross-section generally increases with the erosion degree, and the relative differences between dust with irregular shapes and spheroids can reach approximately 30 % when the erosion degree is large, while the differences are mitigated with the binding force increasing. Besides, with the binding force increasing, the aspect ratio is closer to 1:1. The deviations of the spheroid model in estimating the polarized light were also investigated using the successive-order-of-scattering (SOS) vector radiative transfer (VRT) model. With a diameter (d_p) of 0.2 µm, the relative difference of normalized radiance does not exceed 3 %, and the absolute values of the deviation of the polarized bidirectional reflectance factor (PBRF) and the ratio of radiance to polarized intensity (DoLP) are below 0.005 and 0.02, respectively. However, with the particle size increasing, the difference becomes much more substantial. The relative difference of the normalized radiance can exceed 10 %, and the deviations of the PBRF and DoLP can vary in the ranges of −0.015 to 0.025 and −0.05 to 0.15, respectively. Thus, the single spheroid model may lead to non-negligible deviations for estimating the polarimetric characteristics of single dust particles with more complex shapes. In this work, only the optical properties of single particles were considered. In the future, the applicability of an ensemble of spheroidal particles for reproducing the scattering properties and polarimetric characteristics of an ensemble of irregularly shaped dust particles should be further investigated.

1 Introduction

Dust particles, as a main atmospheric aerosol in the Earth system, play an important role in climate forcing (IPCC, 2014; Textor et al., 2006). Dust can directly absorb and scatter solar radiation, thereby modifying the radiation balance (Huang et al., 2009; Ge et al., 2010; Li et al., 2016). Dust particles can also indirectly affect the Earth’s climate, as they can serve as highly effective cloud condensation nuclei (CCN) and ice nuclei (IN), and thus modify cloud lifetimes, albedo and microphysical properties (Li et al., 2010; Seigel et al., 2013). Besides, as an important aerosol in the atmosphere, dust is one of the main sources of PM_2.5 and PM₁₀ (Kuo and Shen, 2010), and it can significantly affect the air quality. Thus, the monitoring of dust in the atmosphere can improve the understanding of the drivers of climate change and air quality.

Remote sensing, as an effective tool for monitoring Earth, has been applied to retrieve the aerosol properties (Kokhanovsky et al., 2007; Dubovik et al., 2006; Zhang et al., 2020; Si et al., 2021). Ground-based and satellite measurements are the main remote sensing techniques to derive aerosol particle properties. Ground-based remote sensing, such as the AERONET (AErosol RObotic NETwork) project (Holben et al., 1998), mainly inverts the aerosol properties based on the optical measurements from the sun-sky-lunar spectral photometer (Dubovik et al., 2002; Z. Q. Li et al., 2018; Sinyuk et al., 2020), and it can provide relatively accurate estimations. However, ground-based remote sensing has difficulties with covering the global range. Satellite remote sensing allows us to see a much larger area than ground-based remote sensing, so it can provide regional or global measurements. However, satellite remote sensing may provide inaccurate estimates due to the poor understanding of aerosol optical properties. The traditional satellite aerosol retrieval algorithms mainly derive the aerosol properties through the total atmospheric column along with surface characteristics based on radiation fluxes, while due to surface perturbations it is difficult to estimate the contribution of different components.

Polarization is more sensitive to the atmosphere and less disturbed by surfaces than radiation (Dubovik et al., 2019; Z. Li et al., 2018). Thus, previous studies have applied polarimetric remote sensing to monitor atmospheric aerosols (Dubovik et al., 2019; Hasekamp et al., 2011; Dubovik et al., 2011; Xu et al., 2016). Both traditional remote sensing and polarimetric remote sensing require a forward model for radiative transfer calculations, and we need to provide the optical properties of aerosols as input for the radiative transfer model. The ensemble-averaged extinction cross-section, single-scattering albedo and phase matrix are the most important aerosol optical parameters for radiative transfer calculations (Mishchenko et al., 2002; Liu and Mishchenko, 2005; Heidinger et al., 2006). In remote sensing based on the radiative fluxes, for efficient calculations, most radiative transfer calculations ignore the polarized components, so the phase matrix is simplified as a phase function (Lenoble et al., 2007). However, the full calculations require to use of the vector radiative transfer, which requires the complete phase matrix of aerosols (Spurr, 2006; Cai et al., 2006).

In most remote sensing algorithms, aerosol shapes were commonly assumed to be spherical, and the optical properties can be calculated using Mie theory. However, transmission electron microscopy (TEM) and scanning electron microscope (SEM) images have shown that most aerosols exhibit distinct non-spherical shapes (Lindqvist et al., 2014; Woodward et al., 2015; Chou et al., 2008; Luo et al., 2021a, b, 2018a, b). The spheroid model, as one of the most simplified non-spherical models, has been used to model the optical properties of dust (e.g., Dubovik et al., 2006). Compared to the spherical model, the aspect ratio of the particle needs to be determined. However, in the atmosphere, the dust exhibits much more complex shapes than spheroids (Lindqvist et al., 2014; Woodward et al., 2015; Chou et al., 2008; Lin et al., 2018), and the spheroid model has difficulties with simultaneously best fitting all the elements of the phase matrix (Lindqvist et al., 2014). The first element of the phase matrix (phase function) is most important for radiation calculations. Mishchenko et al. (1997) have used the spheroids to model the phase function of dust. Even though dust particles are not perfect spheroids, the spheroids can provide reasonable estimations for the phase functions with a wide aspect ratio distribution (Mishchenko et al., 1997). Kocifaj et al. (2008) have retrieved the aspect ratio based on the phase function and extinction coefficient simultaneously. Li et al. (2019) have shown that the polarimetric characteristics calculated by assuming the microscope-measured aspect ratios are distinct from those using the inversion-based aspect ratios. Nevertheless, spheroids are used as a model for reproducing the optical properties of dust; thus, their aspect ratio is not necessarily a microphysical property of the particles. It is still unclear whether the spheroids that best fit the phase function can represent other elements of the scattering matrix and the polarization. Thus, it is desirable to know the applicability of spheroids in reproducing the other elements of the scattering matrix and the polarization.

Some modeling work has been conducted to investigate the optical properties of more irregular dust, and they have shown that the optical properties of dust are significantly affected by their shapes (Yang et al., 2007; Lindqvist et al., 2014; Bi et al., 2010; Liu et al., 2013; Escobar-Cerezo et al., 2017; Zubko, 2013; Kanngießer and Kahnert, 2021; Kemppinen et al., 2015a; Kahnert, 2015; Gasteiger et al., 2011). However, in applications, we are more curious about whether the optical properties can be reproduced by a simplified model. Even though an ensemble of irregularly shaped dust particles exists in the atmosphere, the optical properties may be reproduced by an ensemble of spheroidal particles with a wide aspect ratio distribution. As a first step, we are mainly focused on answering the following questions:

• Could the single spheroid with a best-fitted aspect ratio reproduce the single-scattering properties of a single dust particle with more complex shapes?

• Could the single spheroid with a best-fitted aspect ratio reproduce the polarimetric characteristics of a single dust particle with more complex shapes?

• How do the dust shapes affect the scattering properties and polarimetric characteristics?

In the atmosphere, the dust shapes are various, and a single model is difficult to represent the complex shapes of dust, so we need to develop dust models which can represent various shapes. In principle, in order to reproduce the scattering properties of dust, ensembles of spheroidal particles should be used (i.e., with a distribution of sizes and aspect ratios). However, as a first step towards exploring the applicability of spheroidal shapes for reproducing the scattering properties of dust, we just consider single particles in this work, and further investigations for ensembles of dust particles should be investigated in the future. To answer the above questions, we proposed a tunable model to represent the dust with various morphologies, and the scattering properties were calculated using discrete dipole approximation (DDA) methods. Then, we retrieved the aspect ratio that best fits the phase function of dust with complex morphologies using the spheroid model, and the scattering matrices of dust with complex morphologies and best-fitted spheroids were compared. Besides, the radiance and polarization were calculated using a vector radiative transfer (VRT) code based on plane-parallel successive order of scattering (SOS), and the capabilities of spheroids for representing the radiance and polarization of irregular dust were evaluated.

2 Method

2.1 Modeling of dust with irregular shapes

To model the dust with irregular shapes, we proposed a model based on the physical process. To evaluate the applicability of spheroids as dust turns more irregular, we assumed that the ideal dust particles are spheroids, but they could become more irregular in the atmosphere. We assumed that the evolution of dust shapes is mainly affected by two factors. On the one hand, the dust could be eroded under the effects of external forces, such as wind, water, etc. Due to erosion forces acting on the particles, part of the dust mass would be lost in the form of dust granules leaving the particle surface. However, the binding force from the particle center of mass could constrain this loss. We have generated various dust shapes based on the above mechanisms.

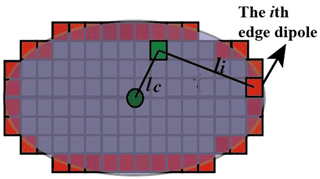
Figure 1 shows the generation of irregular dust. Firstly, we generated spheroids with different aspect ratios, and they were discretized into numerous dipoles. Then, the dipoles were gradually lost under the erosion of external force. From physical points, the surface of the dust is more easily eroded, and the mass close to the surface may be lost easier. To reflect the erosion by an external force, we first identified the edge dipoles (close to the surface) occupied by the dust and then decide if a selected dipole is lost based on a parameter:

$$\begin{array}{}\text{(1)}& J={\displaystyle \frac{\mathrm{1}}{N_{\mathrm{s}}}}\sum _{i=\mathrm{1}}^{N_{\mathrm{e}}}{\displaystyle \frac{R_n}{{\left(l_i+{\mathrm{10}}^{-\mathrm{9}}\right)}^{\mathrm{2}}}}-{\displaystyle \frac{R}{{l_{\mathrm{0}}}^{\mathrm{2}}}},\end{array}$$

where the first item on the right-hand side of the formula reflects the effects of external force. l_i represents the distance from the selected dipole to the ith edge dipoles, and larger $\mathrm{1}/l_i^{\mathrm{2}}$ denotes a larger external force. Here 10⁻⁹ was used to prevent a zero denominator. Previous studies have simulated the surface roughness by randomly adding or subtracting dipoles in random surface locations (Kemppinen et al., 2015b; Veghte et al., 2015). We adopted similar methods in this work. We used a random parameter R_n, which represents the randomness of external force, to simulate the roughness of the surface. R_n varies from 0 to 1. However, the roughness of the dust surface is also probably at smaller scales than the dipole size, which was not considered in this work. N_e represents the number of edge dipoles. In this work, as there are too many edge dipoles, to speed up the calculation, we randomly selected $\mathrm{1}/\mathrm{5}$ of the edge dipoles. The second part reflects the binding force from the center of mass. l₀ represents the distance from the center of the selected dipole to the mass center of the dust, and larger $\mathrm{1}/l_{\mathrm{0}}^{\mathrm{2}}$ denotes a larger binding force. R is a tunable parameter to represent the magnitude of the binding force. Larger R may lead to more spherical dust shapes. The dipoles with larger J indicate that the dipoles were affected by a larger external force or a smaller binding force. Thus, the dipoles with larger J are lost easier.

Figure 1 The generation of irregular dust.

We first sort the J value of the dipoles occupied by the dust, and the dipoles with larger J are lost easier. With the erosion, the mass of the dust is gradually lost. We define a parameter to represent the ratio of the lost volume to the original dust volume:

$$\begin{array}{}\text{(2)}& f={\displaystyle \frac{V_{\mathrm{Lost}}}{V_{\mathrm{0}}}},\end{array}$$

where V₀ represents the volume of the original spheroids, and V_Lost denotes the volume lost in the erosion process. As shown in Fig. 2, with a larger R, dust particles eroded under external forces are easier to become more spherical when the binding force is large. In our algorithm, the R and f are two tunable parameters to reflect the effects of the binding force and erosion degree, respectively, and various dust shapes could be generated by adjusting these two parameters. In this work, to evaluate the applicability of spheroids, the ideal shapes are assumed as spheroids. However, in the atmosphere, faceted dust particles were also observed in the atmosphere (Gasteiger et al., 2011), and these particles should also be investigated in the future.

Figure 2 The typical morphologies of simulated dust.

2.2 Calculation of the single-scattering properties of dust

The normalized scattering matrix, extinction cross-section (C_ext) and scattering cross-section (C_sca) are the key parameters of the single-scattering properties of aerosols (Mishchenko et al., 2002; Liu and Mishchenko, 2005). All the calculations assume that dust particles are randomly oriented particles (Mishchenko and Yurkin, 2017), and the possibility of each particle direction was assumed to be identical. For rotationally symmetric, randomly oriented particles, the normalized Stokes scattering matrix has six independent elements (Paton, 1958; Mishchenko et al., 2002):

$$\begin{array}{}\text{(3)}& F\left(\mathit{\theta }\right)=\left[\begin{array}{cccc}{F}_{\mathrm{11}}\left(\mathit{\theta }\right)& F_{\mathrm{12}}\left(\mathit{\theta }\right)& \mathrm{0}& \mathrm{0}\\ F_{\mathrm{12}}\left(\mathit{\theta }\right)& F_{\mathrm{22}}\left(\mathit{\theta }\right)& \mathrm{0}& \mathrm{0}\\ \mathrm{0}& \mathrm{0}& F_{\mathrm{33}}\left(\mathit{\theta }\right)& F_{\mathrm{34}}\left(\mathit{\theta }\right)\\ \mathrm{0}& \mathrm{0}& -F_{\mathrm{34}}\left(\mathit{\theta }\right)& F_{\mathrm{44}}\left(\mathit{\theta }\right)\end{array}\right].\end{array}$$

The first element of the scattering matrix F₁₁(θ) is the phase function and satisfies:

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\underset{\mathrm{0}}{\overset{\mathit{\pi }}{\int }}{F}_{\mathrm{11}}\left(\mathit{\theta }\right)\sin \left(\mathit{\theta }\right)d\mathit{\theta }=\mathrm{1}.\end{array}$$

In this work, we mainly focus on the polarization of the dust particles, so the vector radiative transfer equations need to be considered, and the complete Stokes scattering matrix was inputted into the radiative transfer equations. The real part of the dust was assumed to be 1.52 based on the study by van Beelen et al. (2014) and Dey et al. (2006). The imaginary parts of dust refractive indices (k) can generally vary in a relatively wide range. Petzold et al. (2009) have shown that k ranges from 0.0003 to 0.0017 at 700 nm, and Wagner et al. (2012) further showed that k can range from 0.0023 to 0.0051 at 655 nm. Dey et al. (2006) and van Beelen et al. (2014) observed a relatively large k of approximately 0.005, which corresponds to either dust mixtures with more absorbing particles. In this work, we used a relatively large k of 0.005 (van Beelen et al., 2014; Dey et al., 2006), while we consider a range of 0.0007–0.1 for sensitivity analysis. In this work, the polarimetric characteristics of dust with irregular shapes were investigated at a wavelength (λ) of 670 nm, which is a typical polarimetric band in polarimetric instruments or satellites, such as POLDER-1/ADEOS I, POLDER-3/PARASOL, MAI/TG-2, CAPI/TanSat and DPC/GF-5.

The T-matrix method has great advantages in calculating the optical properties of symmetrical particles (Mishchenko et al., 1996; Kahnert, 2013). In this work, the T-matrix code developed by Mishchenko and Travis (1998) was used to calculate the single-scattering properties of spheroids. However, for dust with more complex shapes, such as the dust models proposed in Sect. 2.1, the T-matrix code of Mishchenko and Travis (1998) is inapplicable. The discrete dipole approximation (DDA) method can calculate the optical properties of particles with arbitrary shapes, and it was used to calculate the single-scattering properties of the irregular dust particles (Gasteiger et al., 2011). In this work, a widely used DDA code, DDSCAT version 7.3, was applied (Draine and Flatau, 2008, 1994), and the first element of the scattering matrix was normalized to satisfy Eq. (4). We assumed that the dust particles are randomly oriented, so we average the DDA calculations over $\mathrm{12}\times \mathrm{7}\times \mathrm{12}=\mathrm{1008}$ directions, which can achieve relatively accurate results (Dong et al., 2015; Kahnert, 2017; Luo et al., 2019, 2021b). For accurate calculations, the dipole spacing (d) satisfies $\mathrm{2}\mathit{\pi }\left|m\right|d/\mathit{\lambda }<\mathrm{0.5}$, where m is the refractive index of dust.

As shown in Fig. S1 in the Supplement, the difference of the scattering matrix of spherical particles calculated using DDSCAT is below 1 %, which is much smaller than the difference caused by the dust shapes. Thus, the accuracy of DDSCAT is acceptable.

2.3 Retrieval of the aspect ratio of irregular dust

In this work, we attempt to find spheroids that best fit the phase function of irregular dust particles. Firstly, the scattering matrix of dust with irregular shapes was calculated using DDSCAT; then the spheroid model was used to retrieve the aspect ratio by minimizing the following function:

$$\begin{array}{}\text{(5)}& D=|{\mathit{F}}_{\mathbf{11}\mathit{\_}\mathit{I}\mathit{r}\mathit{r}\mathit{e}\mathit{g}\mathit{u}\mathit{l}\mathit{a}\mathit{r}}-{\mathit{F}}_{\mathbf{11}\mathit{\_}\mathit{s}\mathit{p}\mathit{h}\mathit{e}\mathit{r}\mathit{o}\mathit{i}\mathit{d}}{|}^{\mathrm{2}},\end{array}$$

where F_{11_Irregular} and F_{11_spheroid} are the phase function of dust with complex shapes and best-fitted spheroids, respectively. By minimizing D, we can find the aspect ratios that best fit the phase function of dust with irregular shapes.

2.4 Radiative transfer calculation

A successive-order-of-scattering (SOS) vector radiative transfer (VRT) code was employed to calculate the radiance and polarization (Lenoble et al., 2007). The C_ext, C_sca and scattering matrix of dust with different shapes were inputted to the SOS model. The polarized light can be characterized by the Stokes vector $[I,Q,U,V]$. The normalized radiance (I) was widely used to represent the characteristics of bidirectional reflectance. Given the cosine value of the solar zenith angle (μ₀) and the extraterrestrial solar irradiance (F₀), the normalized I can be calculated using (Lenoble et al., 2007; Zhai et al., 2013):

$$\begin{array}{}\text{(6)}& \text{Normalized\_I}={\displaystyle \frac{\mathit{\pi }I}{{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}}}}.\end{array}$$

Similar to the radiance, the polarized bidirectional reflectance factor (PBRF) was also investigated. PBRF is defined as the normalized polarized intensity, can be expressed as the following (Zhai et al., 2013; Zhang et al., 2021):

$$\begin{array}{}\text{(7)}& \text{PBRF}={\displaystyle \frac{\mathit{\pi }\sqrt{Q^{\mathrm{2}}+U^{\mathrm{2}}}}{{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}}}}.\end{array}$$

Note that here we do not consider the circular polarization (V) as V is commonly small enough.

Another important parameter (DoLP), which characterizes the ratio of radiance to polarized intensity, was also used in polarimetric remote sensing. DoLP is defined as the following (Li et al., 2019; Zhang et al., 2021):

$$\begin{array}{}\text{(8)}& \text{DoLP}={\displaystyle \frac{\mathit{\pi }\sqrt{Q^{\mathrm{2}}+U^{\mathrm{2}}}}{I}}.\end{array}$$

Table 1 shows the input parameters adopted in this work for radiative transfer calculations.

Li et al., 2019Z. Q. Li et al., 2018(Lin et al., 2018)

Table 1 Input parameters for radiative transfer calculation.

3 Results

3.1 Single-scattering properties of single dust particles with irregular shapes

3.1.1 Effects of dust shapes

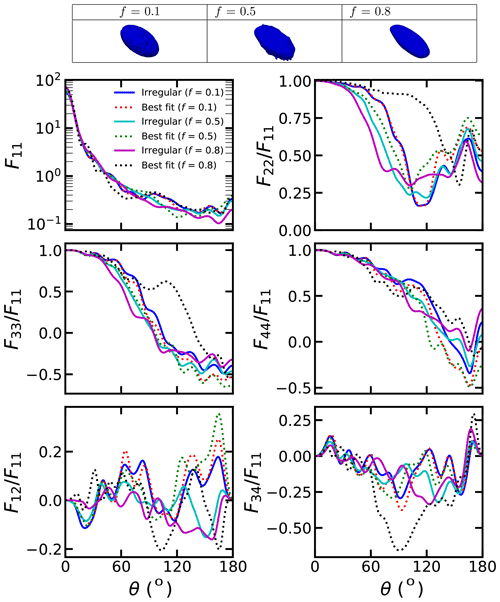
The scattering matrices of dust with different irregular shapes and the corresponding spheroids that best fit the phase function are shown in Figs. 3–4 and S2. When the particle size is small (d_p=0.2 µm), the changes of the F₁₁, F₃₃, F₄₄, F₁₂ and F₃₄ are relatively small with the particle shape varying. However, with the particle size increasing, the effects of particle shapes on the scattering matrix become more significant. Fixing the original aspect ratio to 2:1 and the parameter R to 0, with the erosion of the external force (increasing f), the phase function exhibits larger forward scattering and smaller backward scattering. With the f varying, obvious variations are observed from 150 to 180^∘ scattering angles. The $F_{\mathrm{22}}/F_{\mathrm{11}}$ is also significantly affected by varying f. Fixing R to 0, larger f generally leads to smaller $F_{\mathrm{22}}/F_{\mathrm{11}}$. The erosion of the external force would also lead to sizable variations in $F_{\mathrm{33}}/F_{\mathrm{11}}$, $F_{\mathrm{44}}/F_{\mathrm{11}}$, $F_{\mathrm{12}}/F_{\mathrm{11}}$ and $F_{\mathrm{34}}/F_{\mathrm{11}}$. Specifically, the signs of $F_{\mathrm{33}}/F_{\mathrm{11}}$, $F_{\mathrm{44}}/F_{\mathrm{11}}$, $F_{\mathrm{12}}/F_{\mathrm{11}}$ and $F_{\mathrm{34}}/F_{\mathrm{11}}$ could be modified with the variation of f in specific scattering angle ranges.

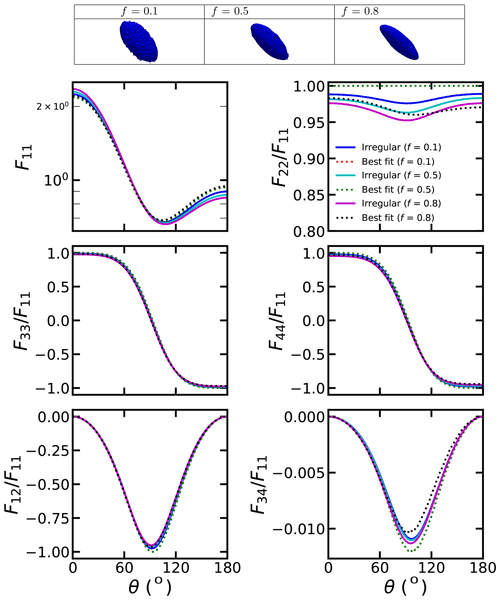
Figure 3 The scattering matrix of dust with irregular shapes, where the aspect ratio is 2:1 and d_p=0.2 µm.

Figure 4 Similar to Fig. 3 but for d_p=2.0 µm.

Figure 5 Similar to Fig. 4 but for an aspect ratio of 1:1.

From the comparisons of Figs. 4–6, we can see how the aspect ratio of the original dust affect the impacts of f. When R=0, the binding force from the center of the dust is small, so the shapes of the dust become more irregular with the increase of the erosion degree, and $F_{\mathrm{22}}/F_{\mathrm{11}}$ becomes smaller. On the other hand, with a larger R, the large binding force would constrain the dust shape, and the dust becomes more spherical with the mass loss, so $F_{\mathrm{22}}/F_{\mathrm{11}}$ becomes closer to 1. Generally, the effects of f on the scattering matrix are significantly affected by original aspect ratios. Modifying the aspect ratio, the $F_{\mathrm{33}}/F_{\mathrm{11}}$, $F_{\mathrm{44}}/F_{\mathrm{11}}$ and $F_{\mathrm{12}}/F_{\mathrm{11}}$ values of dust with different f could exhibit rather different trends with the scattering angles. From Figs. 4–7, we can see the comparison of the scattering matrix of dust with different binding forces (R). With an aspect ratio of 2:1, the phase function exhibits smaller backward scattering with increasing f when R=0, while the opposite phenomenon was observed for R=1. Besides, the $F_{\mathrm{22}}/F_{\mathrm{11}}$ decreases with the increase of f when R=0, and the opposite phenomenon was also observed for R=1.

Figure 6 Similar to Fig. 4 but for an aspect ratio of 1:2.

Figure 7 Similar to Fig. 4 but for R=1.

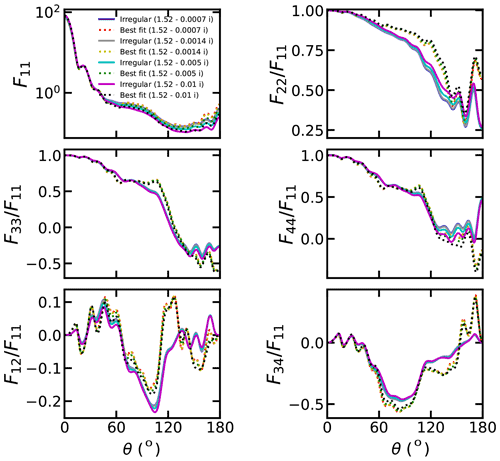
The imaginary parts of refractive indices of dust particles can vary in a relatively wide range. Figure 8 shows the effects of the imaginary parts of refractive indices (k) on the scattering matrix. The imaginary part of the refractive index has non-negligible impacts on the scattering matrix. With larger k, smaller F₁₁ values are observed at backscattering angles. The relative differences in F₁₁ between cases of m=1.52–0.01i and m=1.52–0.0007i can exceed 60 % at backward angles. Besides, larger $F_{\mathrm{22}}/F_{\mathrm{11}}$ values were observed for larger k. Compared to spheroids, the scattering matrices of dust with irregular shapes seem more sensitive to the imaginary parts of refractive indices.

Figure 8 Similar to Fig. 4 but for different refractive indices, where f=0.5.

3.1.2 The differences in single-scattering properties between irregular dust and best-fitted spheroids

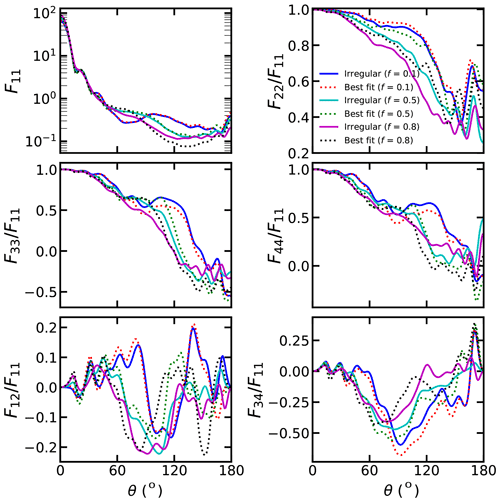
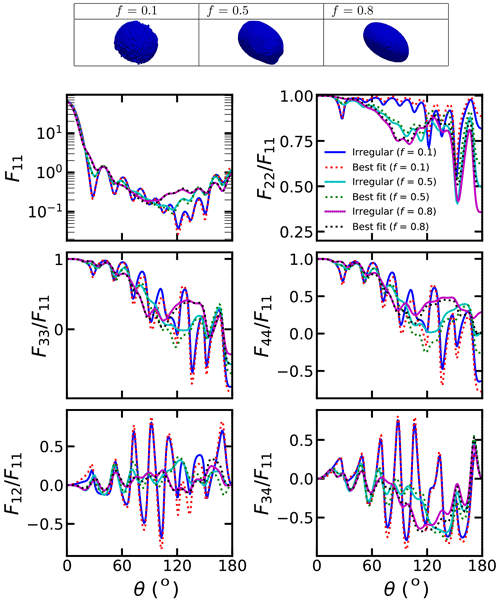
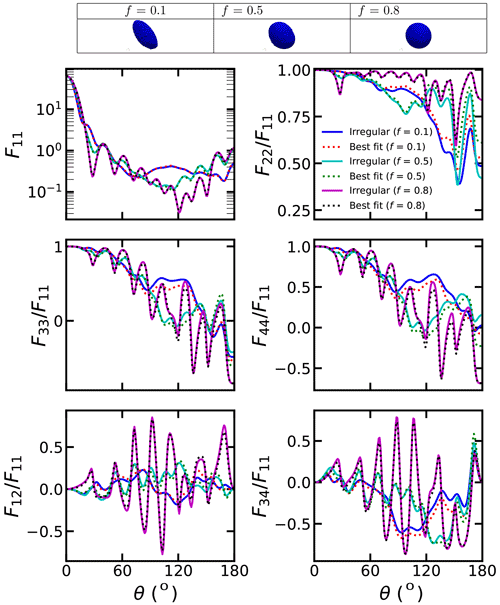
From Figs. 3–7, we can also see the comparison of the phase matrix of dust with irregular shapes and best-fitted spheroids. As shown in Fig. 3, when the particle size is small, the differences between the scattering matrix of dust with irregular shapes and those fitted using the spheroids are not substantial. As shown in Fig. S3, the absolute F₁₁ relative differences between irregular dust particles and the best-fitted spheroids do not exceed 12 %, and the differences in other elements do not exceed 0.05. Thus, single spheroidal particles can provide a reasonable estimation for small single dust particles. However, we can see some small differences. With an original aspect ratio of 2:1 and an R of 0, the spheroid model would underestimate the forward scattering and overestimate the backward scattering of F₁₁.

With a large particle size, the scattering matrix differences between dust with irregular shapes and best-fitted spheroids become rather obvious. Figures S4–S5 show that the absolute F₁₁ relative differences between the irregular dust and the best-fitted spheroids can exceed 75 % at backward angles. Besides, the $F_{\mathrm{22}}/F_{\mathrm{11}}$ of dust with irregular shapes deviates substantially from those of spheroids, and the differences in $F_{\mathrm{22}}/F_{\mathrm{11}}$ between irregular dust particles and the best-fitted spheroids can reach approximately 0.3. The $F_{\mathrm{33}}/F_{\mathrm{11}}$ and $F_{\mathrm{44}}/F_{\mathrm{11}}$ differences between irregular dust particles and the best-fitted spheroids are also substantial, which can reach approximately 0.3 and 0.35, respectively (see Fig. S5). For the $F_{\mathrm{12}}/F_{\mathrm{11}}$ and $F_{\mathrm{34}}/F_{\mathrm{11}}$, the sign can even be modified from negative to positive at some scattering angles if substituting the irregular dust with best-fitted spheroids. As shown in Fig. S4, the absolute $F_{\mathrm{12}}/F_{\mathrm{11}}$ and $F_{\mathrm{34}}/F_{\mathrm{11}}$ differences of exceeding 0.5 can be observed.

Figures 4–6 show similar results but for different original aspect ratios. The original aspect ratio has a significant impact on the applicability of spheroids. With an original aspect ratio of 1:1, spheroids fit the scattering matrix of irregular dust relatively well compared to those with other aspect ratios. As shown in Fig. S6, with an original aspect ratio of 1:1, the absolute F₁₁ relative differences between irregular dust particles and the best-fitted spheroids are below 30 %, and the differences for other elements are also below 0.3. However, the fits of spheroids are relatively bad for the dust with original aspect ratios of 2:1 and 1:2 compared to those with an original aspect ratio of 1:1. As shown in Fig. S7, the absolute F₁₁ relative differences of approximately 100 % between irregular dust particles and the best-fitted spheroids are observed when the original aspect ratio is 1:2. The differences in other elements are also significantly larger than those with original aspect ratio of 1:1. Specifically, the absolute values of the differences in $F_{\mathrm{22}}/F_{\mathrm{11}}$, $F_{\mathrm{33}}/F_{\mathrm{11}}$ and $F_{\mathrm{34}}/F_{\mathrm{11}}$ between the irregular dust particles and best-fitted spheroids could exceed 0.6, 0.8 and 0.6, respectively, when the original aspect ratio is 1:2. The reason may be that the mass of spherical particles is lost relatively uniformly, and the overall structure can be well represented by a spheroid.

Figures 4 and 7 show how the binding force from the mass center affects the applicability of spheroids. As shown in Fig. 4, when the binding force is small (R=0), the scattering matrix differences between dust with irregular shapes and best-fitted dust become substantial as f increases to 0.8. As shown in Fig. S5, the absolute F₁₁ relative differences of exceeding 40 % were observed, and the differences for other elements can exceed 0.3. Notably, the $F_{\mathrm{44}}/F_{\mathrm{11}}$ differences of exceeding 0.5 were observed at backward angles. However, as R increases to 1, the difference turns much smaller (see Figs. 7 and S8). As shown in Fig. S8, the absolute F₁₁ relative differences are generally below 15 % when R=1. This can be explained from physical points. When the binding force is small, the mass of the dust is lost uniformly with the erosion, so the shapes can be very different from spheroids. However, with a large binding force, the mass loss is constrained by the mass center, so the erosion is relatively uniform, and the shapes after erosion are close to spheroids.

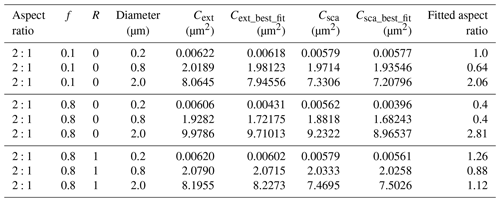
Table 2 shows the scattering or extinction cross-sections of dust with irregular shapes. Fixing the aspect ratio to 2:1, with f and R varying, the variations of C_ext and C_sca are not substantial, and they are under 3 %. However, the C_ext and C_sca of best-fitted spheroids decrease substantially with the f increasing. Fixing the aspect ratio to 2:1 and R to 0, as f increases from 0.1 to 0.8, the C_ext and C_sca of best-fitted spheroids decrease by approximately 30 %. When the f is small, the deviation of C_ext and C_sca between the irregular dust and best-fitted spheroids are not substantial, while the difference increases as f increases. When the aspect ratio is 2:1, f=0.8, R=0 and d_p=0.2 µm, the relative difference of C_ext and C_sca can reach approximately 30 %. However, the differences are mitigated when R increases, as the large binding force constrains the dust shape becoming more complex, and the aspect ratio is closer to 1:1.

Table 2 The scattering or extinction cross-section of dust with irregular shapes.

Figure 8 also compares the scattering matrix of dust with irregular shapes and best-fitted spheroids for different k. Generally, the scattering matrix shows similar angular distributions for different k for both dust with irregular shapes and best-fitted spheroids. However, the scattering matrix differences between dust with irregular shapes and best-fitted spheroids are affected by the k. As shown in Fig. S9, the relative ΔF₁₁ can deviate approximately 18 % at certain scattering angles when modifying k from 0.007 to 0.01. In this work, we mainly consider a typical wavelength of 0.67 µm. As shown in Fig. S10, the dust scattering matrix of dust with irregular shapes and best-fitted spheroids varies in different wavelengths.

3.2 The skylight polarization of dust with irregular shapes

3.2.1 Effects of irregular shapes

To investigate the effects of dust shape on the polarized remote sensing signal, the normalized radiance (I), PBRF and DoLP were calculated. Figures 9–11 show the effects of the erosion degree on the polarized remote sensing signal. In the plots, the backscattering direction is on the meridian plane with a zenith angle of 60^∘ and a relative azimuth of 180^∘. As shown in Fig. 9, the differences in normalized radiance (I), PBRF and DoLP between the erosion fraction (f) of 0.1 and 0.8 are not substantial. Fixing d_p to 0.2 µm, with f increasing, the variation of I, PBRF and DoLP are not substantial. Besides, the trends of I, PBRF and DoLP with the relative azimuth angles and zenith angles are similar.

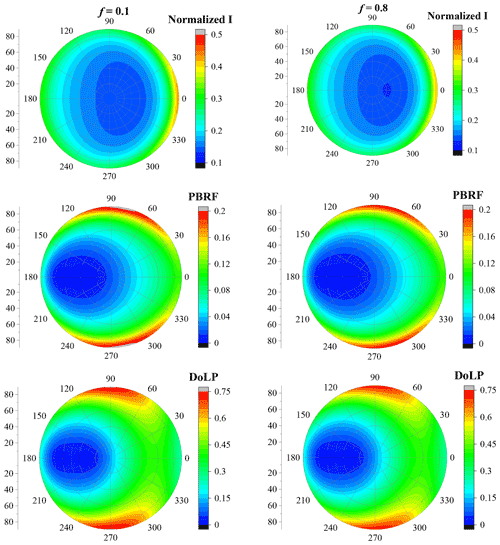
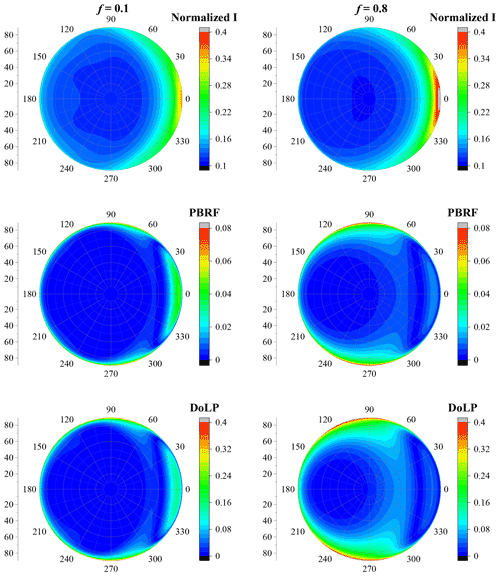
Figure 9 The polarimetric characteristics of dust with irregular shapes, where the aspect ratio is 2:1, d_p=0.2 µm and R=0.

Figure 10 Similar to Fig. 9 but for d_p=0.8 µm.

Figure 11 Similar to Fig. 9 but for d_p=2.0 µm.

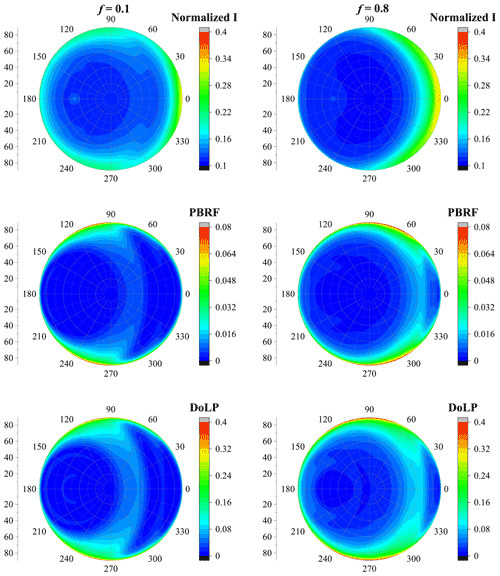
Nevertheless, with the particle size increasing, the erosion degree has more obvious impacts on the normalized radiance (I), PBRF and DoLP. Figures 10–11 show similar results as Fig. 9 but for dust with a d_p of 0.8 and 2.0 µm, respectively. Unlike dust with a d_p of 0.2 µm, when the particle size increases to 0.8 and 2.0 µm, the erosion fraction has a significant impact on I, PBRF and DoLP. The effects of f are significantly related to the particle size. Fixing d_p to 0.8 µm, when f increases from 0.1 to 0.8, the normalized radiance exhibits a slightly decrease at backward-scattering angles, and obvious increase is observed at forward-scattering angles. The similar phenomenon was observed at d_p of 2.0 µm.

With a d_p of 0.8 µm, with increasing f, PBRF decreases at forward-scattering angles but increases when the relative azimuth angle ranges from approximately 0 to 90^∘ and when the zenith angle is around 45^∘, as well as when both the relative azimuth angles and the zenith angle range from 60 to 90^∘. However, when d_p is 2.0 µm, PBRF decreases when the relative azimuth angle is around 105^∘ and when the zenith angle is around 90^∘, as well as when the zenith angle is around 20^∘ and when the relative azimuth angle ranges from approximately 0 to 135^∘. Besides, with a d_p of 2.0 µm, PBRF increases when the relative azimuth angle is around 60^∘ and when the zenith angle is around 90^∘, as well as when the relative azimuth angle ranges from approximately 0 to 60^∘ and when the zenith angle is around 65^∘, which is rather different from the angular distribution of dust with a d_p of 0.8 µm.

The effects of f on DoLP are also significantly related to d_p. When d_p is 0.8 µm, DoLP decreases at forward-scattering angles but increases when the relative azimuth angle ranges from approximately 0 to 120^∘ and when the zenith angle is around 40^∘, as well as when both relative azimuth angles and zenith angle range from 60 to 90^∘. However, with a d_p of 2.0 µm, when modifying f from 0.1 to 0.8, a slight decrease in DoLP is found when the relative azimuth angle ranges from 0 to 60^∘ and when the zenith angle is around 30^∘. Besides, fixing d_p to 2.0 µm, as f increases from 0.1 to 0.8, an obvious increase in DoLP is observed when the zenith angle ranges from 60 to 90^∘ and when the relative azimuth angle is around 60^∘. Also, DoLP increases when the zenith angle is around 60^∘ and when the relative azimuth angle ranges from approximately 0 to 60^∘ with f increasing from 0.1 to 0.8. Figures 9–11 also show that the polarized light signal is rather sensitive to the particle size, which agrees with the findings of previous studies.

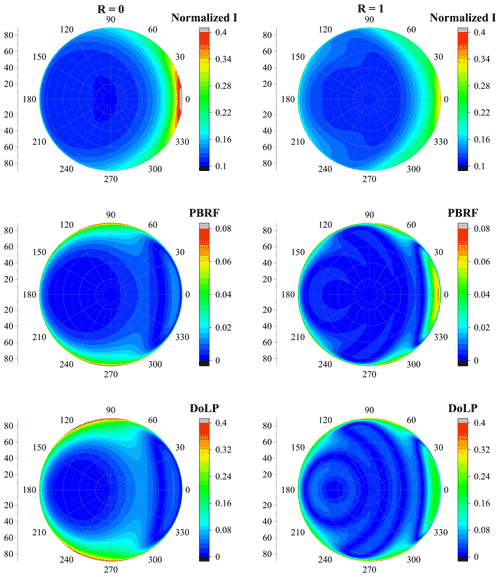
Figure 12 compares normalized radiance, PBRF and DoLP of dust with different binding forces. With an original aspect ratio of 2:1, as R increases from 0 to 1, the dust shape can become more spherical with the erosion. It could be seen from Fig. 12 that I, PBRF and DoLP are significantly affected by the binding force. Fixing the original aspect ratio to 2:1 and the particle diameter to 2.0 µm, with R increasing from 0 to 1, a slight decrease in the normalized radiance is observed at backward-scattering angles, and an obvious increase in the normalized radiance is observed in the forward-scattering angles. Modifying R from 0 to 1, PBRF shows an obvious increase at backward-scattering angles, and a slight decrease was observed when both relative azimuth angles and zenith angles are approximately 90^∘. As R varies from 0 to 1, DoLP increases significantly at forward-scattering angles and decreases when relative azimuth angles range from 90 to 120^∘ and when zenith angles are 70 to 90^∘. Besides, DoLP also decreases when relative azimuth angles range from 0 to 90^∘ and when zenith angles are 30 to 50^∘. Thus, the angular distributions of normalized radiance, PBRF and DoLP are significantly affected by the dust shape and particle size. Besides, as shown in Figs. S11–S13, with the increase of aerosol optical depth (AOD), the normalized radiance increases at backward-scattering angles. The normalized radiance decreases substantially with the increasing surface albedo, while DoLP shows a little increase with the increase of surface albedo. The normalized radiance, PBRF and DoLP show a little decrease with increasing k. However, similar angular distributions of normalized radiance, PBRF and DoLP could be found for different AOD, surface albedo and imaginary parts of the refractive index of dust. Thus, the modifications of AOD, surface albedo and imaginary parts of the refractive index of dust should not significantly affect the main conclusion of this work.

Figure 12 The polarimetric characteristics of dust with irregular shapes, where the aspect ratio is 2:1, d_p=0.8 µm, f=0.8.

3.2.2 The differences between dust with irregular shapes and spheroids

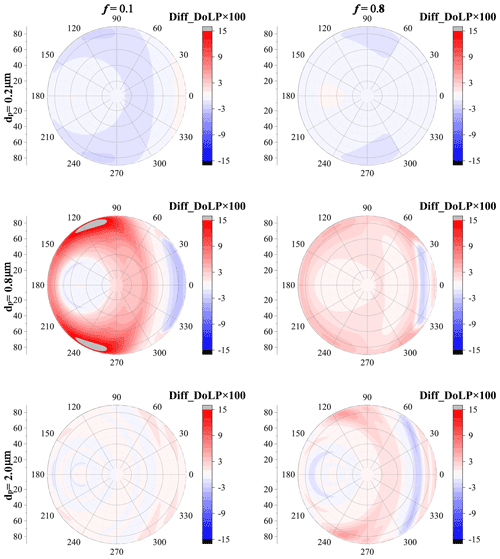
Figure 13 shows the difference of normalized I between the dust with irregular shapes and best-fitted spheroids. As both the particle size and erosion degree are small, the relative differences between the dust with irregular shapes and best-fitted spheroids are not substantial, and the absolute value is below 3 % when f=0.1. However, even with a small particle size, as f increases to 0.8, the relative differences are rather more obvious, which range from approximately −6 % to 5 %. With a d_p of 0.2 µm, the best-fitted spheroids underestimate the normalized radiance at backward-scattering angles and overestimate the normalized radiance at forward angles.

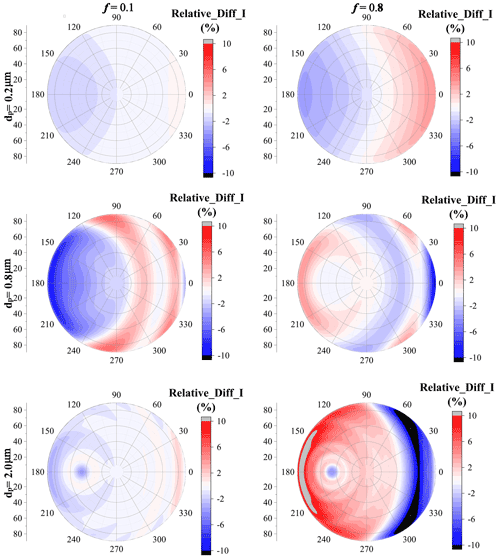
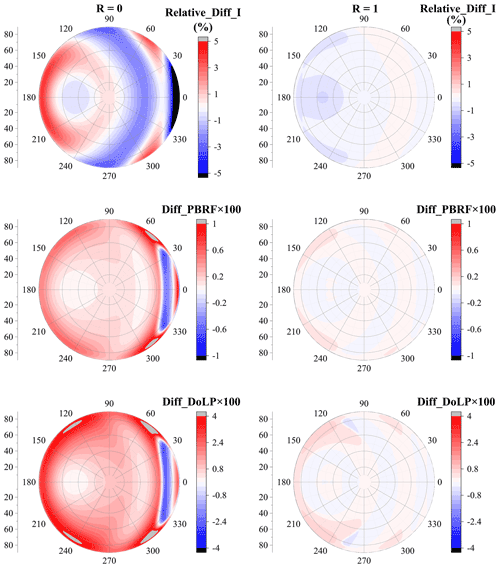
Figure 13 The relative difference of normalized radiance between dust with irregular shapes and best-fitted spheroids, where the aspect ratio is 2:1 and R=0.

As the particle diameter increases to 0.8 µm, the relative difference of normalized radiance between the dust with irregular shapes and best-fitted spheroids becomes more obvious, and the relative difference in radiance can vary in the range of −10 to 10. Unlike dust with a d_p of 0.2 µm, when d_p=0.8 µm, the differences between irregular dust and best-fitted spheroids l are significantly affected by the erosion degree (i.e., f). When f=0.1, the spheroid model underestimates the radiance at backward-scattering angles but overestimates the radiance when the zenith angles range from 10 to 85^∘ and when relative azimuth angles range from 0 to 120^∘. Nevertheless, with an f of 0.8, the spheroid model would overestimate the radiance at backward-scattering angles, and underestimate the radiance at forward angles.

As d_p further increases to 2.0 µm, the angular distribution of the radiance difference between the dust with irregular shapes and best-fitted spheroids is further modified. Although the difference in radiance decreases compared to that for dust with a d_p of 0.8 µm when f=0.1, as f increase to 0.8, the absolute value of the relative difference in radiance can exceed 10 %. Besides, the angular distributions of the difference also vary significantly with modifying f. Fixing d_p to 2.0 µm, the spheroid model overestimates the radiance at forward-scattering angles, while it underestimates the radiance at backward-scattering angles when f=0.1, and an opposite phenomenon is observed when f=0.8.

The spheroid model can also provide inaccurate estimations for PBRF. As shown in Fig. 14, with a small particle size (d_p=0.2 µm), the difference of PBRF between the dust with irregular shapes and best-fitted spheroids is not substantial, and the maximum absolute value is below approximately 0.005. For dust with a d_p of 0.2 µm, the spheroid model generally underestimates the PBRF at backward-scattering angles while overestimating the PBRF at forward-scattering angles. As d_p increases to 0.8 µm, the PBRF differences between dust with irregular shapes and best-fitted spheroids become rather obvious, and the difference varies from approximately −0.015 to 0.025. Unlike dust with a d_p of 0.2 µm, when d_p increases to 0.8 µm, the spheroid model generally overestimates the PBRF at backward-scattering angles but overestimates the PBRF when the zenith angles range from 70 to 80^∘ and when relative azimuth angles range from approximately 0 to 30^∘. As d_p further increases to 2.0 µm, the maximum absolute value of the PBRF difference shows decreases, and the difference varies in the range of approximately −0.015 to 0.015. When f=0.1, the spheroid model generally overestimates the PBRF, but the spheroid model would underestimate the PBRF when the zenith angles are around 70^∘ and when relative azimuth angles range from 0 to 60^∘.

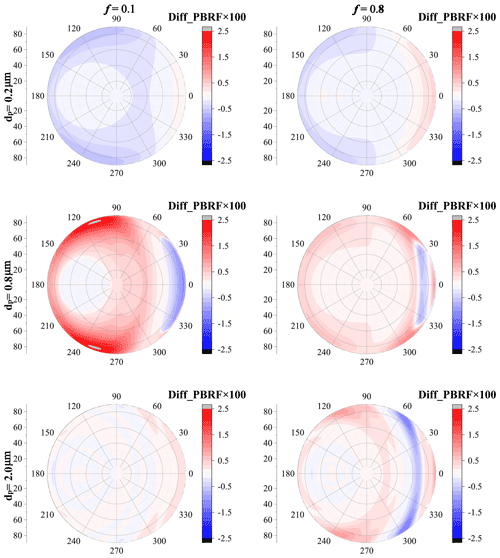
Figure 14 The difference of PBRF between dust with irregular shapes and best-fitted spheroids, where the aspect ratio is 2:1 and R=0.

Figure 15 shows the comparison of DoLP between dust with irregular shapes and best-fitted spheroids. Similar to normalized radiance and PBRF, the DoLP differences between dust with irregular shapes and best-fitted spheroids are not substantial when d_p=0.2 µm, and the absolute value of the difference does not exceed 0.02. As d_p increases to 0.8 µm, the difference between the spheroid model and dust with irregular shapes becomes rather obvious, and the difference varies from approximately −0.05 to 0.15. Besides, with a d_p of 0.8 µm, the PBRF difference generally exhibits similar angular distributions for f=0.1 and f=0.8. The spheroid model generally overestimates the DoLP at backward-scattering angles. As d_p increases to 2.0 µm, the difference decreases, and it varies from approximately −0.03 to 0.05. Besides, the angular distributions of DoLP are also different when f varies. The spheroid model generally overestimates DoLP when f=0.1, while some underestimations are found when the zenith angles are around 65^∘ and when relative azimuth angles range from approximately 0 to 30^∘.

Figure 15 Similar to Fig. 14 but for DoLP.

Figure 16 compares the deviations of spheroids for estimating the normalized radiance, PBRF and DoLP of dust with different binding forces. The binding forces have a significant impact on the deviations. Fixing d_p to 0.8 µm, original aspect ratio to 2:1 and f to 0.8, with R increasing from 0 to 1, the absolute values of deviations of radiance, PBRF and DoLP decrease substantially. When R=0, the relative difference of radiance varies from −6 % to 5 %, while it varies in the range of approximately −1.5 % to 1 % when R = 1. As R increases from 0 to 1, the PBRF differences change from the range of approximately −0.008 to 0.01 to approximately −0.0005 to 0.002, and the DoLP differences change from approximately −0.03 to 0.04 to approximately −0.008 to 0.008. The physical points can explain why the difference decreases with R increasing. With larger R, the binding force from the mass center increases, which can constrain the shape from becoming more complex, so the dust shape is close to the spheroid. As shown in Figs. S14–S16, the differences in polarimetric characteristics between dust with irregular shapes and best-fitted spheroids share similar angular distributions for different aerosol optical depth (AOD), surface albedo and imaginary parts of the refractive index, and the modifications of AOD, surface albedo and imaginary parts of the refractive index should not modify the main conclusions.

Figure 16 The difference of polarimetric characteristics between dust with irregular shapes and best-fitted spheroids, where the aspect ratio is 2:1, f=0.8 and d_p=0.8 µm.

4 Summary and conclusions

Spheroidal shapes are commonly used to reproduce the scattering properties of dust, although their applicability is still unclear. To calculate the scattering properties of dust, we proposed a tunable model to represent dust with various shapes. We assumed that the dust shapes are mainly affected by two factors: (1) the dust shape can vary with erosion by external force, which can lead to loss of mass, and (2) the binding force from the center of mass can prevent the loss of dust mass. We proposed an algorithm with two tunable parameters to simulate the effects of these two factors, and various complex dust shapes were generated. As we used tunable parameters to represent various dust shapes, our model is helpful for the parameterization of the optical properties of dust with different shapes (but not for faceted dust particles). To evaluate the capability of spheroids to reproduce the single dust particle scattering properties, we used single spheroidal particles that fit well with the phase function of single dust particles with irregular shapes, and then we investigated their capability to reproduce all the elements of the scattering matrix.

The single-scattering properties of single dust particles with irregular shapes were investigated. We found that both the erosion of external force and binding force from the mass center can have a significant impact on the dust shapes, so they significantly affect the single-scattering properties of dust. Besides, the applicability of the best-fitted spheroids in estimating the scattering matrix was evaluated. With a small particle size, the differences in the scattering matrix between best-fitted spheroids are not substantial. With a diameter of 0.2 µm, the absolute F₁₁ relative differences between irregular dust particles and the best-fitted spheroids do not exceed 12 %, and the differences in other elements do not exceed 0.05. However, with the particle size increasing, a F₁₁ relative difference of approximately 100 % could be observed in certain scattering angles. The maximum differences in other elements between irregular dust particles and best-fitted spheroids can reach approximately 0.3–0.8. Besides, the signs of $F_{\mathrm{12}}/F_{\mathrm{11}}$, $F_{\mathrm{33}}/F_{\mathrm{11}}$, $F_{\mathrm{34}}/F_{\mathrm{11}}$ and $F_{\mathrm{44}}/F_{\mathrm{11}}$ can be modified from negative to positive at some scattering angles if substituting the irregular dust with best-fitted spheroids. The signs of $F_{\mathrm{12}}/F_{\mathrm{11}}$ and $F_{\mathrm{34}}/F_{\mathrm{11}}$ can be modified from negative to positive at some scattering angles if substituting the irregular dust with best-fitted spheroids. Our findings also show that the binding force can affect the applicability of spheroids. Generally, with larger binding forces, the dust shapes are constrained from becoming more complex, and the spheroid model could provide relatively reasonable estimations. As the binding force is small, the deviation of extinction or scattering cross-section generally increases with the erosion degree, and the relative difference can reach approximately 30 % when the erosion degree is large, while the deviation is mitigated with the binding force increasing. Besides, when increasing R, the retrieved aspect ratio is closer to 1:1, and the particles become more spherical.

To see how the dust shapes affect the polarimetric remote sensing, we have calculated the normalized radiance, PBRF and DoLP of dust using the SOS model. Our findings show that dust shapes have a relatively unobvious impact on the normalized radiance, PBRF or DoLP when the particle size is small, while the effects become rather obvious as the particle size increases. Our findings show that both the erosion degree and the binding force can significantly affect the angular distribution of normalized radiance, PBRF and DoLP. The differences between irregular dust particles and best-fitted spheroids were also investigated. When the particle size is small, the spheroid model can provide good estimations. With a d_p of 0.2 µm, the relative difference of normalized radiance between irregular dust and best-fitted spheroids does not exceed 3 %, and the absolute values of the differences in PBRF and DoLP are below 0.005 and 0.02, respectively. With the particle size increasing, the difference becomes much more substantial. The relative difference of normalized radiance can exceed 10 %, and the deviation of PBRF and DoLP can vary in the ranges of −0.015 to 0.025 and −0.05 to 0.15, respectively. Thus, the use of the spheroid model in the component retrievals based on polarized light should consider the effects of more complex dust shapes. In this work, only the optical properties of single particles were considered, and the radiative transfer calculations were also performed using the optical properties of single particles for theoretical analysis. In the future, the applicability of an ensemble of spheroidal particles for reproducing the scattering properties and polarimetric characteristics of an ensemble of irregularly shaped dust particles should be further investigated.