Sensitivity analysis of attenuation in convective rainfall at X-band frequency using the mountain reference technique

The RadAlp experiment aims at improving quantitative precipitation estimation (QPE) in the Alps thanks to X-band polarimetric radars and in situ measurements deployed in the region of Grenoble, France. In this article, we revisit the physics of propagation and attenuation of microwaves in rain. We first derive four attenuation–reflectivity (AZ) algorithms constrained, or not, by path-integrated attenuations (PIAs) estimated from the decrease in the return of selected mountain targets when it rains compared to their dry weather levels (the so-called mountain reference technique – MRT). We also consider one simple polarimetric algorithm based on the profile of the total differential phase shift between the radar and the mountain targets. The central idea of the work is to implement these five algorithms all together in the framework of a generalized sensitivity analysis in order to establish useful parameterizations for attenuation correction. The parameter structure and the inherent mathematical ambiguity of the system of equations makes it necessary to organize the optimization procedure in a nested way. The core of the procedure consists of (i) exploring with classical sampling techniques the space of the parameters allowed to be variable from one target to the other and from one time step to the next, (ii) computing a cost function (CF) quantifying the proximity of the simulated profiles and (iii) selecting parameters sets for which a given CF threshold is exceeded. This core is activated for a series of values of parameters supposed to be fixed, e.g., the radar calibration error for a given event. The sensitivity analysis is performed for a set of three convective events using the 0^∘ elevation plan position indicator (PPI) measurements of the Météo-France weather radar located on top of the Moucherotte mountain (altitude of 1901 m a.s.l. – above sea level). It allows the estimation of critical parameters for radar QPE using radar data alone. In addition to the radar calibration error, this includes the time series of radome attenuation and estimations of the coefficients of the power law models relating the specific attenuation and the reflectivity (A–Z relationship) on the one hand and the specific attenuation and the specific differential phase shift (A–K_dp relationship) on the other hand. It is noteworthy that the A–Z and A–K_dp relationships obtained are consistent with those derived from concomitant drop size distribution measurements at ground level, in particular with a slightly non-linear A–K_dp relationship (A=0.28 $K_{\mathrm{dp}}^{\mathrm{1.1}})$. X-Band radome attenuations as high as 15 dB were estimated, leading to the recommendation of avoiding the use of radomes for remote sensing of precipitation at such a frequency.

1 Introduction

Estimation of atmospheric precipitation is important in a high mountain region such as the Alps for the assessment and management of water and snow resources (drinking water, hydropower production, agriculture and tourism), as well as for the prediction of natural hazards associated with intense precipitation and snowpack melting. In complement with in situ rain gauge networks and snowpack monitoring systems, remote sensing, using ground-based weather radar systems, has a high potential that needs to be exploited but also several limitations that need to be surpassed. A first dilemma is related to the choice of the altitude of the radar set-up, with a compromise to be found between maximizing the visibility of the radar system(s) at the regional scale and increasing the representativeness of the measurements made in altitude compared to precipitation reaching the ground, especially during cold periods. A second dilemma is the well-known detection/resolution versus attenuation compromise, which is acute for weather radar frequencies. S-band and C-band frequencies (around 3 and 5 GHz, respectively) are traditionally preferred in continental-wide weather radar networks (Serafin and Wilson, 2000; Saxion et al., 2011; Saltikoff et al., 2019), for their appropriate precipitation detection capability and their moderate sensitivity to attenuation. In Europe, MeteoSwiss has the longest-standing experience in operating such a C-band weather radar network in high mountain regions (Joss and Lee, 1995; Germann et al., 2006; Sideris et al., 2014; Foresti et al., 2018). Implementation of radars operating at the X-band frequency (∼9–10 GHz) has also been proposed in the last few decades for research and operational applications at local scales, e.g., for precipitation monitoring in urban areas and/or in mountainous regions (Delrieu et al., 1997; McLaughlin et al., 2009; Scipion et al., 2013; Lengfeld et al., 2014, to name just a few). The renewed interest in the X-band frequency, known for a long time to be prone to attenuation (e.g. Hitschfeld and Bordan, 1954), is based on the promises of polarimetric techniques (e.g. Bringi and Chandrasekar, 2001; Ryzhkov et al., 2005) for attenuation correction (Testud et al., 2000; Matrosov and Clark, 2002; Matrosov et al., 2005, 2009; Koffi et al., 2014; Ryzhkov et al., 2014). Météo-France has chosen to complement the coverage of its operational radar network ARAMIS (Application Radar à la Météorologie Infra-Synoptique) in the Alps by means of X-band polarimetric radars. A first set of three radars was installed in southern Alps within the RHyTMME project (Risques Hydrométéorologiques en Territoires de Montagnes et Méditerranéens) in the period 2008–2013 (Westrelin et al., 2012; Yu et al., 2018). An additional radar (Mont Moucherotte radar; MOUC radar, hereinafter) was installed in 2014 on top of the Moucherotte mountain (1901 m) that oversees the valley of Grenoble. The RadAlp experiment (Khanal et al., 2019; Delrieu et al., 2020) is a contribution to research aimed at improving quantitative precipitation estimation (QPE) based on the Météo-France MOUC radar, complemented by a suite of sensors installed on the Grenoble valley floor at the Institute for Geosciences and Environmental research (IGE; 210 m a.s.l. – above sea level). This includes the IGE research X-band polarimetric radar named XPORT, a K-band micro rain radar (MRR) and in situ sensors (disdrometers and rain gauges).

The present article aims to show that mountain returns can be useful for the parameterization of QPE algorithms for weather radar systems operating at attenuating frequencies in mountainous regions. It is part of a series of contributions devoted to the surface reference technique proposed for spaceborne radar configuration (Meneghini et al., 1983; Marzoug and Amayenc, 1994; more recently, Meneghini et al., 2020) and its transposition to ground-based radar configurations with the mountain reference technique (Delrieu et al., 1997, 2020; Serrar et al., 2000). Figures 1 and 2 illustrate our point. Figure 1 shows a map of dry weather mountain returns of the MOUC radar. The configuration of the radars operated in the RadAlp experiment is recalled in the insert; note that only the MOUC radar data are used in the current study. The measurements are taken at an elevation angle of 0^∘, which corresponds to the lowest plan position indicator (PPI) of the volume-scanning strategy of the MOUC radar. The reflectivity data are averaged over a 4 h period; one PPI is performed at the 0^∘ elevation angle every 5 min. We have selected 22 mountain targets corresponding to compact groups of gates in successive radials (3–6 typically; the radial spacing is 0.5^∘) and ranges (5–10 gates; the gate extent is 240 m), presenting a majority of dry weather reflectivity values greater than 45 dBZ. The paths between the radar and the targets are free of beam blockages and present as few noisy gates (due to side lobes) as possible. In addition to the reflectivity map, the top graphs of Fig. 2 display the co-polar correlation (ρ_hv) and the total differential phase shift (Ψ_dp) maps at 15:00 UTC on 21 July 2017, before the convective event that occurred on that day between 15:30 and 18:00 UTC. The Ψ_dp map is essentially noisy at that time, and the red colour in the ρ_hv map, corresponding to values close to 1, highlights some small rain cells, in particular one to the south of the radar domain close to target 22 (Grand Veymont mountain). The middle row maps correspond to the occurrence of intense precipitation over the city of Grenoble at 16:05 UTC. A peak of 40 mm h⁻¹ in 10 min was recorded at that time by the rain gauge located on top of the IGE building. The Ψ_dp map displays marked increasing radial profiles in the northeasterly (NE) direction. The ρ_hv map allows a good delimitation of the whole rain pattern and clearly shows the dominance of the mountain returns over the rain returns for most of the Belledonne and Taillefer targets. The most striking observation on the reflectivity map is the dramatic decrease in the mountain returns of targets 1–10 in the NE sector, which results, without doubt, from the rain cell falling over the city of Grenoble at that time. This is a clear example of what will be termed as an along-path attenuation hereinafter. In the bottom row of Fig. 2, which corresponds to the measurements made at 17:00 UTC, one can observe a similar strong along-path attenuation in the NE direction in the Ψ_dp map, associated with a second 40 mm h⁻¹ rain rate peak at the IGE site (see eventually the hyetograph in Delrieu et al., 2020; their Fig. 2). But more impressive is the general decrease in returns from all the mountain targets, associated with a rain cell occurring at the radar site. This is an example of so-called on-site attenuation, related to the formation of a water film on the radome, combined with along-path attenuation in the immediate vicinity of the radar site.

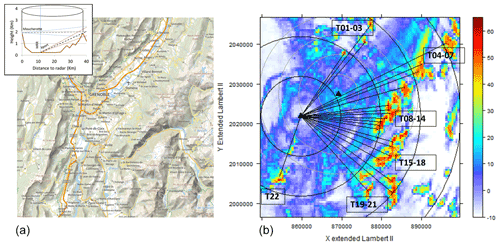
Figure 1 (a) The 50×50 km² map of the region of Grenoble, France (from Geoportail, Institut Géographique National). (b) Dry weather reflectivity map of the X-band weather radar located on top of the Moucherotte mountain (1901 m a.s.l.) in the Vercors Massif. The radar is marked with a black triangle, and circular range markers are spaced by 10 km. The Cartesian map has a resolution of 500 m. The measurements were taken at an elevation angle of 0^∘ during dry weather conditions before the 21 July 2017 event. The radial lines indicate the azimuths and ranges of the 22 mountain targets used for the MRT implementation. Targets 1–3 are located in the Chartreuse Massif, targets 4–14 in the Belledonne Massif, targets 15–21 in the Taillefer Massif and target 22 in the Vercors Massif. In the background, the second black triangle indicates the IGE site at the bottom of the valley (210 m a.s.l.). The grey circles with 5 km spacing indicate the coverage of the XPORT X-band polarimetric radar, whose measurements were used in the present study only for the detection of the melting layer.

The article is organized as follows. In the theoretical part (Sect. 2), we find it useful to revisit in some detail the physics of propagation and attenuation of microwaves in rain. We derive (Sect. 2.2) four attenuation–reflectivity (AZ) algorithms constrained or not by path-integrated attenuations (PIAs) estimated from the decrease in the return of selected mountain targets when it rains, compared to their dry weather levels. We also consider a simple polarimetric algorithm based on the profile of the total differential phase shift between the radar and the mountain targets (Sect. 2.3). The structure and interdependencies of the parameters are discussed in Sect. 2.4. This leads to the description of the principles of the generalized sensitivity analysis proposed for studying the physical model at hand (Sect. 3.1). The results obtained are illustrated and discussed, item by item, in Sect. 3.2.1–3.2.5. Concluding remarks and future work are presented in Sect. 4.

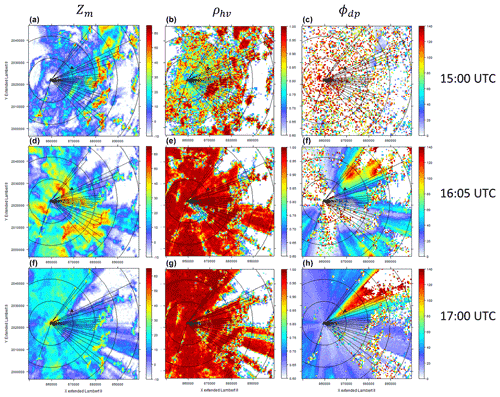
Figure 2 Examples of 0^∘ elevation PPIs of measured reflectivity (a, d, f), co-polar correlation coefficient (b, e, g) and total differential phase shift (c, f, h) taken before (a, b, c) and at two moments with intense precipitation (d–h) during the 21 July 2017 convective event. As in Fig. 1, the circular range markers of the Moucherotte mountain radar are spaced by 10 km.

2 Theory

2.1 Basic definitions and notations

Let us express the radar returned power profile P(r) (mW) as follows:

$$\begin{array}{}\text{(2.1)}& P\left(r\right)=(C/r^{\mathrm{2}})Z\left(r\right)\mathrm{AF}\left(r\right),\end{array}$$

where Z(r) (mm⁶ m⁻³) is the true reflectivity profile, AF (r) (–) is the attenuation factor at range r (km), and C is the radar constant. We suppose the measured reflectivity profile Z_m(r) to depend both on the attenuation and on a possible radar calibration error denoted dC as follows:

$$\begin{array}{}\text{(2.2)}& Z_{\mathrm{m}}\left(r\right)=P\left(r\right)r^{\mathrm{2}}/C=Z\left(r\right)\mathrm{AF}\left(r\right)dC\end{array}$$

In addition to the running range r, let us consider the range r₀ corresponding to the blind range of the radar system, which is eventually extended to the range where the reflectivity measurements start to be free of spurious detections due, e.g., to side lobes.

The attenuation factor AF(r) is expressed as the product of two terms in the following:

$$\begin{array}{}\text{(2.3)}& \mathrm{AF}\left(r\right)=\mathrm{AF}\left(r_{\mathrm{0}}\right)\mathrm{AF}(r_{\mathrm{0}},r),\end{array}$$

where AF(r₀) is the on-site attenuation factor which, as discussed in the introduction, may result from two main sources, i.e. attenuation due to a water film on the radome and along-path attenuation due to precipitation falling between the radar site and range r₀.

As a classical formulation (e.g. Marzoug and Amayenc, 1994), we express the two-way attenuation factor as a function of the specific attenuation profile A(r) (dB km⁻¹) through the following equation:

$$\begin{array}{}\text{(2.4)}& \mathrm{AF}\left(r\right)=\mathrm{AF}\left(r_{\mathrm{0}}\right)\exp \left(-\mathrm{0.46}\underset{r_{\mathrm{0}}}{\overset{r}{\int }}A\left(s\right)\mathrm{d}s\right).\end{array}$$

Furthermore, we have to introduce relationships between the radar measurable variables (specific attenuation and reflectivity) and the variable of interest for QPE, i.e. the rain rate R (mm h⁻¹), which are assumed to be of power type with the following notations:

$$\begin{array}{}\text{(2.5)}& {\displaystyle }A=a_{AZ}{Z}^{b_{AZ}},\text{(2.6)}& {\displaystyle }R=a_{RA}{A}^{b_{RA}},\text{(2.7)}& {\displaystyle }R=a_{RZ}{Z}^{b_{RZ}}.\end{array}$$

The order used for the variables in Eqs. (2.5)–(2.7) is meaningful, since the specific attenuation profile is derived from the measured reflectivity profile, while the rain rate profile can be derived in a second step either from the specific attenuation profile or from the corrected reflectivity profile. Due to the well-known lower variability of the R–A relationship compared to the R–Z relationship, Eq. (2.6) is preferred to Eq. (2.7) for the estimation of the rain rate profiles (Ryzhkov et al., 2014).

Let us now consider another particular range, denoted as r_m, where estimates of the attenuation factor may be available. We use the following notation:

$$\begin{array}{}\text{(2.8)}& {\mathrm{AF}}_{\mathrm{m}}\left(r_{\mathrm{m}}\right)=\mathrm{AF}\left(r_{\mathrm{m}}\right)d{\mathrm{AF}}_{\mathrm{m}},\end{array}$$

where AF(r_m) is the true attenuation factor at range r_m, and the term dAF_m represents a multiplicative error term. As illustrated in the introduction, such direct estimates of the attenuation factor can be obtained in mountainous regions using the mountain reference technique (MRT).

We frequently use hereinafter the notion of path-integrated attenuation (PIA), in units of decibels (hereafter dB), defined as follows:

$$\begin{array}{}\text{(2.9)}& \mathrm{PIA}\left(r\right)=-\mathrm{10}\log \left(\mathrm{AF}\left(r\right)\right).\end{array}$$

Note that, since AF(r) is comprised between 1 (no attenuation) and 0 (full attenuation), the PIA subsequently takes values in the range of 0 (no attenuation) up to +∞ (full attenuation). The PIAs at ranges r₀ and r_m are denoted as PIA₀ and PIA_m, respectively, in the following.

2.2 Formulation of the attenuation–reflectivity algorithms

The following mathematical developments are inspired by the works on rain-profiling algorithms in satellite measurement configuration (e.g. Meneghini et al., 1983; Marzoug and Amayenc, 1994). The attenuation–reflectivity algorithms (AZ algorithms) proposed in this section rely on two basic equations. The first one is the analytical solution of Eq. (2.4), when the power law model (Eq. 2.5) is supposed to represent perfectly the A–Z relationship. By taking the derivative of ${\mathrm{AF}}^{b_{AZ}}(r_{\mathrm{0}},r)$ with respect to range r, one obtains the following:

$$\begin{array}{}\text{(2.10)}& \begin{array}{rl}\mathrm{d}({\mathrm{AF}}^{b_{AZ}}& \left(r_{\mathrm{0}},r\right))/\mathrm{d}r={\mathrm{AF}}^{b_{AZ}}(r_{\mathrm{0}},r)\\ & \left(-\mathrm{0.46}{a}_{AZ}{b}_{AZ}Z(r{)}^{b_{AZ}}\right).\end{array}\end{array}$$

Substitution of the true reflectivity by the measured reflectivity through Eq. (2.2) and integration between r₀ and r yields the following:

$${\mathrm{AF}}^{b_{\mathrm{AZ}}}\left(r_{\mathrm{0}},r\right)=\mathrm{1}-\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ(r_{\mathrm{0}},r)/(\mathrm{AF}\left(r_{\mathrm{0}}\right)dC{)}^{b_{AZ}},$$

with

$$\begin{array}{}\text{(2.11)}& SZ\left(r_{\mathrm{0}},r\right)=\underset{r_{\mathrm{0}}}{\overset{r}{\int }}{Z}_{\mathrm{m}}{\left(s\right)}^{b_{AZ}}\mathrm{d}s.\end{array}$$

The second equation is obtained by integrating Eq. (2.10) up to range r_m and by introducing the attenuation factor estimate available at this range, yielding the following:

$$\begin{array}{}\text{(2.12)}& \begin{array}{rl}& {\left(\mathrm{AF}\left(r_{\mathrm{m}}\right)/\mathrm{AF}\left(r_{\mathrm{0}}\right)\right)}^{b_{AZ}}\\ & +\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ(r_{\mathrm{0}},r_{\mathrm{m}})/{\left(\mathrm{AF}\left(r_{\mathrm{0}}\right)dC\right)}^{b_{AZ}}=\mathrm{1}.\end{array}\end{array}$$

We develop, in Appendix A, four formulations of attenuation corrections for a supposedly homogeneous precipitation type, i.e. we assume the a_AZ and b_AZ coefficients to be constant along the propagation path. Each formulation filters out one of the four parameters PIA_m, dC, a_AZ and PIA₀, respectively. Note that, due to the mathematical expression of the intervening equations, there is no possibility to filter out the b_AZ parameter, which will be assumed to be constant, close to a value of 0.8 at the X-band (Ryzhkov et al., 2014), and to present a low sensitivity in the system of equations. The resulting expressions of the reflectivity and specific attenuation corrected profiles are listed hereafter.

2.2.1 AZhb algorithm (independent of PIA_m)

$$\begin{array}{}\text{(2.13)}& \begin{array}{rl}& Z_{AZ\mathrm{hb}}\left(r\right)=Z_{\mathrm{m}}\left(r\right)/\\ & {\left[\left(\mathrm{AF}\right(r_{\mathrm{0}})dC{)}^{b_{AZ}}-\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ(r_{\mathrm{0}},r)\right]}^{\mathrm{1}/b_{AZ}}\end{array}\end{array}$$

$$\begin{array}{}\text{(2.14)}& \begin{array}{rl}& A_{AZ\mathrm{hb}}\left(r\right)=a_{AZ}{Z}_{\mathrm{m}}^{b_{AZ}}\left(r\right)/\\ & \left[\left(\mathrm{AF}\right(r_{\mathrm{0}})dC{)}^{b_{AZ}}-\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ(r_{\mathrm{0}},r)\right].\end{array}\end{array}$$

This formulation is equivalent to the solution proposed early by Hitschfeld and Bordan (1954), hence the proposed name AZhb. It can be termed as a forward algorithm since only the measured reflectivities between the range r₀ and the running range r are used for the correction at range r. The minus sign between the two terms of the denominator indicates that the denominator is not prevented from tending towards 0 when the SZ cumulative term increases. This solution is subsequently known to be unstable and highly sensitive to calibration error, inadequate values of the A–Z relationship coefficients and on-site attenuation.

2.2.2 AZC algorithm (independent of dC)

$$\begin{array}{}\text{(2.15)}& \begin{array}{r}{Z}_{AZC}\left(r\right)\\ & =Z_{\mathrm{m}}\left(r\right){\left[\mathrm{AF}(r_{\mathrm{0}}{)}^{b_{AZ}}-\mathrm{AF}(r_m{)}^{b_{AZ}}\right]}^{\mathrm{1}/b_{AZ}}/\\ & \left\{\mathrm{0.46}{a}_{AZ}{b}_{AZ}\left[\mathrm{AF}\left(r_{\mathrm{0}}{)}^{b_{AZ}}SZ\right(r,r_{\mathrm{m}})\right.\right.\\ & {\left.\left.+\mathrm{AF}\left(r_{\mathrm{m}}{)}^{b_{AZ}}SZ\right(r_{\mathrm{0}},r)\right]\right\}}^{\mathrm{1}/b_{AZ}}\end{array}\end{array}$$

$$\begin{array}{}\text{(2.16)}& \begin{array}{r}{A}_{AZC}\left(r\right)\\ & =Z_{\mathrm{m}}(r{)}^{b_{AZ}}\left[\mathrm{AF}({\mathrm{r}}_{\mathrm{0}}{)}^{b_{AZ}}-\mathrm{AF}(r_{\mathrm{m}}{)}^{b_{AZ}}\right]\\ & /\left\{\mathrm{0.46}{b}_{AZ}\left[\mathrm{AF}\left(r_{\mathrm{0}}{)}^{b_{AZ}}SZ\right(r,r_{\mathrm{m}})\right.\right.\\ & \left.\left.+\mathrm{AF}\left(r_{\mathrm{m}}{)}^{b_{AZ}}SZ\right(r_{\mathrm{0}},r)\right]\right\}.\end{array}\end{array}$$

In addition to its independence with respect to dC, it is interesting to note that the specific attenuation profile provided by the AZC algorithm does not depend on the a_AZ parameter. This parameter is, however, present in the expression of the reflectivity profile.

2.2.3 AZα algorithm (independent of a_AZ)

$$\begin{array}{}\text{(2.17)}& \begin{array}{r}{Z}_{AZ\mathit{\alpha }}\left(r\right)\\ & =Z_{\mathrm{m}}\left(r\right)SZ(r_{\mathrm{0}},r_{\mathrm{m}}{)}^{\mathrm{1}/b_{AZ}}/\\ & \left\{dC\left[\mathrm{AF}\left(r_{\mathrm{0}}{)}^{b_{AZ}}SZ\right(r,r_{\mathrm{m}})\right.\right.\\ & {\left.\left.+\mathrm{AF}\left(r_{\mathrm{m}}{)}^{b_{AZ}}SZ\right(r_{\mathrm{0}},r)\right]\right\}}^{\mathrm{1}/b_{AZ}}\end{array}\end{array}$$

$$\begin{array}{}\text{(2.18)}& \begin{array}{r}{A}_{AZ\mathit{\alpha }}\left(r\right)\\ & =Z_{\mathrm{m}}(r{)}^{b_{AZ}}\left[\mathrm{AF}(r_{\mathrm{0}}{)}^{b_{AZ}}-\mathrm{AF}(r_{\mathrm{m}}{)}^{b_{AZ}}\right]/\\ & \left\{\mathrm{0.46}{b}_{AZ}\left[\mathrm{AF}\left(r_{\mathrm{0}}{)}^{b_{AZ}}SZ\right(r,r_{\mathrm{m}})\right.\right.\\ & \left.\left.+\mathrm{AF}\left(r_{\mathrm{m}}{)}^{b_{AZ}}SZ\right(r_{\mathrm{0}},r)\right]\right\}.\end{array}\end{array}$$

We note that the specific attenuation profiles provided by the AZC and AZα algorithms are identical. Moreover, they do not depend on the a_AZ and dC parameters. This is a priori a very interesting property of these algorithms, exploited in particular by Testud et al. (2000) and Ryzhkov et al. (2014). However, the reflectivity profiles provided by the two algorithms are different, and in particular, the reflectivity profile of the AZα algorithm depends on dC, while the reflectivity profile of the AZC algorithm depends on a_AZ.

2.2.4 AZ0 algorithm (independent of PIA₀)

$$\begin{array}{}\text{(2.19)}& \begin{array}{rl}& Z_{AZ\mathrm{0}}\left(r\right)=Z_{\mathrm{m}}\left(r\right)/\\ & {\left\{\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ(r,r_{\mathrm{m}})+\left(\mathrm{AF}\right(r_{\mathrm{m}})dC{)}^{b_{AZ}}\right\}}^{\mathrm{1}/b_{AZ}}\end{array}\end{array}$$

$$\begin{array}{}\text{(2.20)}& \begin{array}{rl}& A_{AZ\mathrm{0}}\left(r\right)=a_{AZ}{Z}_{\mathrm{m}}(r{)}^{b_{AZ}}/\\ & \left\{\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ(r,r_{\mathrm{m}})+{\left(\mathrm{AF}\left(r_{\mathrm{m}}\right)dC\right)}^{b_{AZ}}\right\}.\end{array}\end{array}$$

The AZ0 algorithm has the simplest mathematical expressions among the three algorithms using the PIA constraint. It looks like a backward algorithm, since the reflectivity and the specific attenuation profiles estimated at the running range r depend only on the measured reflectivities between ranges r and r_m, while the AZC and AZα algorithms make use of the entire measured reflectivity profile between r₀ and r_m for the estimations at range r.

The plus (+) signs in the denominators of Eqs. (2.15)–(2.20) are indicators of the inherent stability of the three algorithms using the PIA constraint, unlike the AZhb algorithm.

2.3 Formulation of a polarimetric algorithm

In addition to the AZ algorithms, we consider a PIA profile, denoted as PIA_Φdp(r₀,r), derived from the profile of the total differential phase shift on propagation, denoted as Φ_dp(r₀,r) (^∘) in the following:

$$\begin{array}{}\text{(2.21)}& {\mathrm{\Phi }}_{\mathrm{dp}}(r_{\mathrm{0}},r)=\mathrm{2}\underset{r_{\mathrm{0}}}{\overset{r}{\int }}{K}_{\mathrm{dp}}\left(s\right)\mathrm{d}s,\end{array}$$

where K_dp is the specific differential phase shift on propagation (^∘ km⁻¹). Assuming a power law relationship between the specific attenuation and the specific differential phase shift on propagation, with the following:

$$\begin{array}{}\text{(2.22)}& A=a_{AK}{K}_{\mathrm{dp}}^{b_{AK}}.\end{array}$$

We obtain the following:

$$\begin{array}{}\text{(2.23)}& {\mathrm{PIA}}_{\mathrm{\Phi }\mathrm{dp}}({\mathrm{r}}_{\mathrm{0}},r)=\mathrm{2}{a}_{AK}\underset{r_{\mathrm{0}}}{\overset{r}{\int }}{K}_{\mathrm{dp}}^{b_{AK}}\left(s\right)\mathrm{d}s.\end{array}$$

This polarimetry-derived PIA profile can be compared to the PIA profiles obtained by integrating the AZ specific attenuation profiles given by Eqs. (2.14), (2.16), (2.18, which is identical to 2.16) and (2.20) between r₀ and r.

2.4 Analysis of the parameters of the considered physical model

Equations (2.11), (2.12), (2.9) and (2.23) form a system of equations with seven parameters (or unknowns), namely the coefficients of the A–Z relationship (a_AZ, b_AZ), the coefficients of the A–K_dp relationship (a_AK, b_AK), the radar calibration error (dC), the on-site attenuation (PIA₀) and the path-integrated attenuation at range r_m (PIA_m). We focus in this article on the idea of constraining this system of equations with the PIAs derived from the mountain reference technique. The question of the R–A transformation is beyond the scope of the present study.

From a physical point of view, the parameters dC, PIA₀ and PIA_m are mutually independent and a priori independent of the coefficients of the Z–A–K_dp power law models.

We will assume the radar calibration error to be constant for a given precipitation event, with possible variations from one event to the next.

Regarding on-site attenuation, Frasier et al. (2013) made a synthesis of previous theoretical and empirical studies and provided an empirical model based on the comparison of the measurements of two X-band radar systems in the French southern Alps, where one is equipped with a radome, and the other one is without a radome. From this article, we take into account a dependence of PIA₀ on the measured reflectivity in the vicinity of the radar site, denoted as Z₀. Based on Fig. 5 in Frasier et al. (2013), we have fitted a coarse power law model for X-band radome attenuation on their experimental data, yielding ${\mathrm{PIA}}_{\mathrm{0}}^{\ast }=\mathrm{0.0126}{Z}_{\mathrm{0}}^{\mathrm{1.6}}$, with ${\mathrm{PIA}}_{\mathrm{0}}^{\ast }$ in decibels and Z₀ in decibels relative to 1 mm⁶ m⁻³ (hereafter dBZ). Based on their Fig. 6, which shows important variations between the theoretical and empirical results proposed in the literature, we have defined a large range of lower and upper limits for the PIA₀ draws conditioned on Z₀ via the ${\mathrm{PIA}}_{\mathrm{0}}^{\ast }$ model (see Table 1). With n=5, the crude model proposed yields upper limits of the PIA₀ sampling range of 4.8, 9.2, 14.6 and 20.8 dB for Z₀ values of 20, 30, 40 and 50 dBZ, respectively. In the following simulations, PIA₀ will be allowed to vary from one target to the next, i.e. in different directions, and from one time step to the next.

Table 1 Values and ranges of the variation in the attenuation model parameters in the sensitivity analysis.

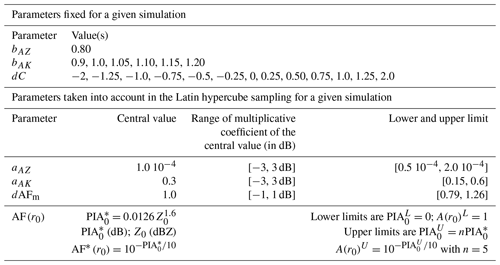
The accuracy of the MRT-derived PIA_m was studied in Delrieu et al. (1999a) by comparing MRT estimates with direct measurements obtained with a receiving antenna set up in the mountain range. They showed (i) that selecting strong mountain returns (typically greater than 45–50 dBZ) allows one to mitigate the impact of precipitation falling over the target (negative bias), (ii) that a refined estimation of the so-called dry weather baseline is required to account for the possible modification of backscattering properties of the mountain surfaces before and after the event and (iii) that the time variability in the dry weather returns defines the minimum detectable PIA. These elements were accounted for in the present study by selecting strong mountain targets, studying their dry weather time variability (see also Delrieu et al., 2020) and subsequently defining the range of variation in the dAF_m multiplicative error (Table 1).

The prefactors and exponents of the Z–A–K_dp power law models are mutually dependent, since they are determined by the shape, density and size distributions of the hydrometeors and their electromagnetic properties, which are largely driven by their solid versus liquid composition. These coefficients may vary considerably from one precipitation type to another. In addition, even for a given precipitation type, the actual Z–A–K_dp values present an inherent variability with respect to the power law models, associated with the greater or lesser proximity of the particle size distribution (PSD) moments associated to each particular variable. As a further complexity, when, for a given propagation path, various types of hydrometeors are successively encountered (e.g. rain, melting precipitation and snow), it would be desirable to apply the appropriate coefficients for the different precipitation types, provided one is able to determine them. As a major simplification in the present work, we will be considering a homogeneous precipitation type (convective rainfall). Because of the mathematical form of the equations at hand, and the likely mutual dependence of the exponent and prefactor of each power law model, we will assume the exponents of the A–Z and the A–K_dp relationships to be constant for all the considered events, while the prefactors will be allowed to vary for each single target and time step.

There have been several studies deriving A–Z and A–K_dp relationships at the X-band using different approaches, including model calculations and also the direct use of observational data (e.g. Bringi and Chandrasakar, 2001; Gorgucci and Chadrasakar, 2005; Park et al., 2005; Schneebeli and Berne, 2012; Matrosov et al. 2014; Yu et al., 2018). Estimations of these coefficients and their ranges in variation were obtained in our study by processing the drop size distribution (DSD) data collected with a Parsivel² disdrometer located at the IGE site. The dataset includes 337 rainy days during the period April 2017–March 2020. The raw DSD measurements have a time resolution of 1 min. They are binned into 32 diameter classes with increasing sizes from 0.125 mm up to 6 mm. Various filters have been applied to discard anomalous data and, in particular, to detect non-liquid precipitation, thanks to the falling speed spectra. The volumetric concentration spectra have been computed at a 5 min resolution. DSD spectra with 5 min rain rate less than 0.1 mm h⁻¹ were discarded from the analysis. A dataset of about 14 600 DSD spectra was thus obtained, corresponding to all types of precipitation occurring in liquid phase in the Grenoble valley. As for the scattering model, we used the CANTMAT version 1.2 software programme that was developed at Colorado State University by C. Tang and V. N. Bringi. The CANTMAT software uses the T-matrix formulation to compute radar observables such as horizontal reflectivity, vertical reflectivity, differential reflectivity, co-polar cross-correlation, specific attenuation, specific phase shift, etc., as a function of the DSD, the radar frequency, air temperature, oblateness models and canting models for the raindrops, as well as the incidence angle of the electromagnetic waves. The results presented herein were computed for the X-band frequency, a temperature of 10 ^∘C, the Beard and Chung (1987) oblateness model, a standard deviation of the canting angle of 10^∘ and an incidence angle of 0^∘ (horizontal scanning, as for the MOUC radar data).

Figure 3 illustrates the fittings of the A–Z relationships that can be obtained from a classical logarithm of a base 10 transformation of the two variables. One can note that the scatterplot is well conditioned for deriving a power law model in the sense that it does not present any particular curvature. The least square regressions of A over Z and of Z over A, as well as the least rectangle regression, are displayed to illustrate the impact of the regression technique on the model coefficients. Note that the least rectangle fit should be preferred, since, for these calculations based on DSD data, the two variables can be considered to be on an equal footing. The determination coefficient is high, and the three regressions performed subsequently give parameter sets close to each other. From the fittings in Fig. 3, we have chosen b_AZ=0.8 as a fixed value for this exponent and $a_{AZ}={\mathrm{1.010}}^{-\mathrm{4}}$ as the central value for the sampling of the prefactor in the following sensitivity analysis. Although the scatter of the points around the power law model suggests a possible range of variation of [−5, 5 dB] for the DSD-derived values, we have limited this range to [−3, 3 dB] in our simulations on the basis of the much bigger resolution volume of the radar and the assumption that the prefactor is constant throughout the reflectivity profile (Table 1).

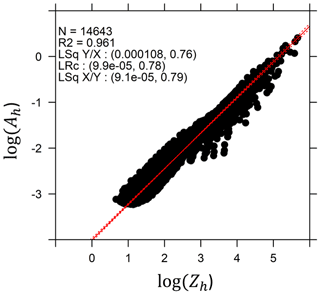
Figure 3 Results of the fitting of DSD-derived power law models for the horizontal specific attenuation A_h (dB km⁻¹) as a function of the horizontal reflectivity Z_h (mm⁶ m⁻³), using a classical logarithmic of base 10 transformation of the two variables. In the insert, the number of points N, the square of the correlation coefficient (R²) of the logarithmic regression, the prefactors and exponents of the resulting least square regressions of the variable in ordinate versus the variable in abscissa (Lsq $Y/X$) and vice versa (Lsq $X/Y$), as well as the least rectangle regression (LRc), which considers the two variables on an equal footing, are shown.

Figure 4 gives the results obtained for the A–K_dp relationship. It can be seen that the scatterplot of the logarithmic of base 10 transformed variables (Fig. 4a) presents a significant curvature. Due to the important weight given to low and medium values in the regressions, the fitted power law models are clearly unsatisfactory for the highest values, which are of interest in the present study since they correspond to convective precipitation. We have therefore tested two other fitting techniques based on the natural values of the two variables (Fig. 4b). A linear fit with a zero-forced intercept yields A_h=0.32 K_dp, which is consistent with linear relationships proposed in the literature in similar climatological contexts; however, these are with a somewhat higher value of the multiplicative coefficient (e.g. 0.245 in Schneebeli and Berne (2012) and 0.276 in Yu et al. 2018). However, we note that this linear fit is not satisfactory with a significant underestimation of the A_h values for K_dp>3 ^∘ km⁻¹. The fitting of a non-linear power law model (NLPL) proves to be more satisfactory with $A_{\mathrm{h}}=\mathrm{0.30}{K}_{\mathrm{dp}}^{\mathrm{1.1}}$. Since the exponents estimated with the log-transformed data are close to 0.9, we have decided to perform several simulations with fixed values of b_AK in the range [0.9–1.2] (see Table 1). Regarding the prefactor a_AK, we have considered a central value of 0.3 and a range of variation of [−3, 3 dB], with minimum and maximum values of 0.15 and 0.6, respectively.

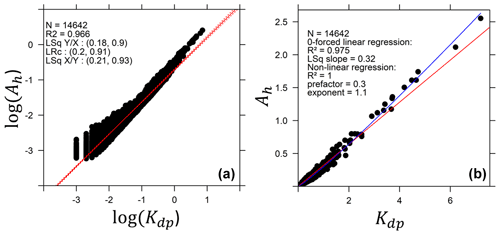
Figure 4 Fitting of DSD-derived power law models for the horizontal specific attenuation A_h (dB km⁻¹) as a function of the specific differential phase shift on propagation K_dp (^∘ km⁻¹) (a) using a classical logarithmic of base 10 transformation of the two variables (same comments as in Fig. 3 for this graph) and (b) using natural values of the two variables. The red line in panel (b) is the zero-forced linear regression with a slope equal to 0.32, and the blue curve is the non-linear fit of a power law model with a prefactor of 0.30 and an exponent of 1.1.

Additional tests have been performed, including, for instance, the influence of the air/hydrometeor temperature, the precipitation type (e.g. stratiform versus convective rainfall) and the DSD integration time step. Concerning the last factor, we have compared the results obtained for the 2 and 5 min time steps, and we have found no significant influence on the coefficients of the power law models, while the R² values were significantly downgraded for the 2 min time step (not shown here for the sake of conciseness). As for the precipitation type, we carried out a rough classification of the 337 events into stratiform and convective types by considering an event as convective if a rain rate threshold of 10 mm h⁻¹ was exceeded for at least one 5 min time step during the event. As one would expect from the scatterplots in Figs. 3 and 4, significant differences appeared between the stratiform and convective A–K_dp relationships, whereas the A–Z relationships were almost identical. This is an argument for keeping the exponent b_AZ constant in our simulation procedure. Regarding the sensitivity on temperature, one possible extension of the present work could be to consider the temperature time series available for each event at the IGE site in the scattering calculations. This would most likely result in an increase in the variability of the A–Z and A–K_dp relationships. As a classical concern, one may, however, wonder how the average temperature in the radar resolution volume could be estimated (Ryzhkov et al., 2014). We chose herein to rely on the ability of the simulation procedure to deviate from the central values of the parameters and their ranges of variation defined in Table 1 to be large enough.

3 Sensitivity analysis

3.1 Principle

The parameter structure analysed in Sect. 2.4 led us to organize the sensitivity analysis procedure in a nested way.

For all the considered rain events, we assume the exponents of the A–Z and A–K_dp relationships to be constant. For each event, we assume the radar calibration error to be constant. A simulation is performed for each combination of the b_AZ, b_AK and dC values listed in Table 1, i.e. $\mathrm{1}\times \mathrm{6}\times \mathrm{13}=\mathrm{78}$ simulations.

For each mountain target and each time step, the simulation core is implemented as follows.

The Z_m(r) and Φ_dp(r) profiles between the radar and the mountain target are preprocessed. For each of the successive radials composing the target, this includes the determination of gates affected by clutter in the region of the mountain target and along the propagation path. This is done by considering both dry weather mean values exceeding various thresholds (25 dBZ for significant clutter; 45 dBZ for a gate belonging to the mountain target) and by using the profile of the co-polar correlation coefficient (ρ_hv) (Delrieu et al., 2020). The median Z_m(r) and Φ_dp(r) profiles over the series of radials are then computed. The MRT PIA_m is evaluated as being the difference in the Z_m mean values between the dry weather baseline and the current time step, with the mean being taken over by all the gates composing the target. The r₀ value is estimated as the range of the first gate for which four successive values (corresponding to a range extent of 960 m) exceed a ρ_hv value of 0.95. This last value is set as a threshold between precipitation and clutter/no precipitation (from the statistics presented in Khanal et al., 2019). The Z₀ value is computed as the product of $\mathrm{1}/dC$ (correction for the radar calibration error) and the mean reflectivity of the selected four successive gates if they are located within the first 2 km range; otherwise, the Z₀ value is set to 0. The reader is referred to Khanal et al. (2022) for the most recent description of the fairly sophisticated procedure used for the Φ_dp(r) regularization based on the total differential phase shift profiles Ψ_dp(r) for all the radials associated with a given target. Note that a target is selected at a given time step for the following steps of the simulation if PIA_m> 1 dB and if a good quality index of the Φ_dp(r) regularization is obtained (Khanal et al., 2022).

The Latin hypercube sampling (LHS) technique (https://cran.r-project.org/web/packages/lhs/index.html, last access: 19 May 2022) is then used to generate N parameter sets (with N = 1000 in the following) filling uniformly the parameter space composed of the following four parameters: the prefactors a_AZ and a_AK, the on-site attenuation factor AF(r₀) and the multiplicative error dAF_m (Eq. 2.8) on the MRT attenuation factor. The central values and intervals of variation in these four parameters are listed in Table 1. It is noteworthy that the random draws are made on the decibel-transformed (db-transformed) ranges of parameters so that there are as many values below and above the central value, e.g., as many values between 0.15 and 0.3, on the one hand, and between 0.3 and 0.6, on the other hand, for the a_AK parameter.

After discarding unphysical parameter sets (e.g. those for which PIA₀>PIA_m), the five algorithms are implemented for all the remaining sets. A cost function (CF) is evaluated in order to measure the convergence/proximity of the simulated profiles for each parameter set. Several formulations of the cost function were tested, and we propose the following one hereinafter, which was found to be appropriate:

$$\begin{array}{}\text{(3.1)}& \begin{array}{r}\mathrm{CF}=\mathrm{Mean}\left(R^{\mathrm{2}}\right({\mathrm{PIA}}_{AZ\mathrm{hb}}(r_{\mathrm{0}},r),{\mathrm{PIA}}_{AZC}(r_{\mathrm{0}},r)),\\ R^{\mathrm{2}}\left({\mathrm{PIA}}_{AZ\mathrm{hb}}\right(r_{\mathrm{0}},r),{\mathrm{PIA}}_{AZ\mathrm{0}}(r_{\mathrm{0}},r\left)\right),\\ R^{\mathrm{2}}\left({\mathrm{PIA}}_{AZ\mathrm{hb}}\right(r_{\mathrm{0}},r),{\mathrm{PIA}}_{\mathrm{\Phi }\mathrm{dp}}(r_{\mathrm{0}},r\left)\right),\\ R^{\mathrm{2}}\left({\mathrm{PIA}}_{AZC}\right(r_{\mathrm{0}},r),{\mathrm{PIA}}_{AZ\mathrm{0}}(r_{\mathrm{0}},r\left)\right),\\ R^{\mathrm{2}}\left({\mathrm{PIA}}_{AZC}\right(r_{\mathrm{0}},r),{\mathrm{PIA}}_{\mathrm{\Phi }\mathrm{dp}}(r_{\mathrm{0}},r\left)\right),\\ R^{\mathrm{2}}\left({\mathrm{PIA}}_{AZ\mathrm{0}}\right(r_{\mathrm{0}},r),{\mathrm{PIA}}_{\mathrm{\Phi }\mathrm{dp}}(r_{\mathrm{0}},r\left)\right)),\end{array}\end{array}$$

where “Mean” stands for the mean value of something, and R² is the determination coefficient between the two profiles indicated between parentheses. The profiles considered in this expression of the cost function are the PIA profiles between ranges r₀ and r. Since the specific attenuation profiles are identical for the AZC and AZα formulations (Eqs. 2.16 and 2.18), only the PIA profile of the first is considered in Eq. (3.1). Due to the inherent instability of the AZhb algorithm, we consider the first three R² terms in the computation of the CF value only if PIA_m < 10 dB. Indeed, this 10 dB value proved to be about the maximum PIA that this algorithm is able to deal with, even with an almost perfect parameterization (Delrieu et al., 1999b). The last three terms of the CF are measuring the proximity of the three PIA-constrained algorithms. In the following, we have selected CF_th=0.8 as the satisfaction threshold, i.e. the CF value to be exceeded to consider a given parameter set as being optimal.

The acronym OPS will be used to denote the optimal parameter set hereinafter. The number of optimal parameter sets (NOPSs) can be computed for a given target and time step and summed up for all the targets and time steps of an event and for a series of events to yield a measure of the overall quality of a simulation for given fixed parameters (b_AZ, b_AK and dC) and randomly drawn parameters (a_AZ, a_AK, AF(r₀) and dAF_m) for each single target/time step using the Latin hypercube sampling (LHS) technique. We recognize that the choice of the cost function (Eq. 3.1) and the satisfaction threshold CF_th are essentially subjective. This choice relies on the experience gained in the implementation of the simulation framework. The following three elements can be mentioned on this subject: (i) accounting for the AZhb algorithm in the CF for low to moderate PIAs less than 10 dB proved to be a good option owing to the strong sensitivity of this algorithm on the calibration error; (ii) adding the polarimetric algorithm and the corresponding R² terms in the CF allowed us to dramatically reduce the mathematical ambiguity (i.e. the fact that several combinations of parameters, including non-physical values, may lead to the convergence of the solutions of the different algorithms) of the physical model at hand; and (iii) several satisfaction thresholds were tested with low sensitivity on the results in terms of the quantiles of the statistical distributions of the estimated parameters.

3.2 Results

3.2.1 Illustration for a given target and time step

Figure 5 gives an example of result of the core procedure for target 13 (T13) on 21 July 2017 16:05 UTC. For this case, with a MRT PIA of 25.9 dB at a range of about 20 km, we obtain ${\mathrm{\Phi }}_{\mathrm{dp}}(r_{\mathrm{0}},r_{\mathrm{m}})=\mathrm{71.5}$^∘ and Z₀= 9.5 dBZ. The optimal set of fixed parameters for the considered event is $d{C}^{\ast }=\mathrm{0.5}$ dB, b_AZ=0.8 and $b_{AK}^{\ast }=\mathrm{1.1}$ (see the next sub-sections). Since, for the best OPS, all the profiles overlap perfectly, the results presented in Fig. 5 correspond actually to a near-optimal set so that one can see some differences between the solutions of the different algorithms. The set of LHS parameters for this specific target/time step is ${\mathrm{PIA}}_{\mathrm{0}}^{\ast }=\mathrm{0.46}$ dB, $a_{AZ}^{\ast }={\mathrm{1.0110}}^{-\mathrm{4}}$, $a_{AK}^{\ast }=\mathrm{0.34}$ and $d{\mathrm{AF}}_{\mathrm{m}}^{\ast }=\mathrm{0.99}$. The CF value is 0.925, while the one obtained with the best OPS is 0.981. Note that 55 parameter sets overpassed the CF threshold value of 0.8 for this example, i.e. NOPS = 55 for this target and time step. For this good (though not the best) OPS, the reflectivity profiles (Fig. 5a) call for the following comments. We have here a clear example of the inherent instability of the AZhb algorithm, which blows up at a range of about 7 km for this parameterization. One should remember that this algorithm is not accounted for in the CF computation for such high PIAs, as explained when commenting on Eq. (3.1). The three other AZ algorithms give rather similar results. As a general behaviour (and in particular whatever the value of the on-site attenuation), we note that the optimal parameterizations lead to the convergence of the AZC and AZ0 algorithms near the radar and to the convergence of the AZα and AZ0 algorithms at the other end of the profile. Figure 5b gives the solutions obtained in terms of specific attenuation profiles. The AZhb profile is not drawn in this figure. As shown in Sect. 2.2, the AZα and AZC solutions are identical (represented in red) and slightly different at a long range from the AZ0 solution. The comparison of the corrected and uncorrected profiles clearly shows in this example the dramatic impact of attenuation with regard to both the underestimation of the first precipitation cell and the non-detection of the second one. Figure 5c displays the raw and processed Φ_dp profiles. For such a strong attenuation case, one can see that the raw profile has little noise and no significant bumps that could signify a differential phase shift on backscattering (δ_hv) contamination (Trömel et al., 2013). Finally, Fig. 5d allows a comparison of the PIA profiles derived from the AZC–AZα algorithms (identical solutions), the AZ0 algorithm and from the Φ_dp profile. Although there are some differences, the overall consistency between the three profiles is good.

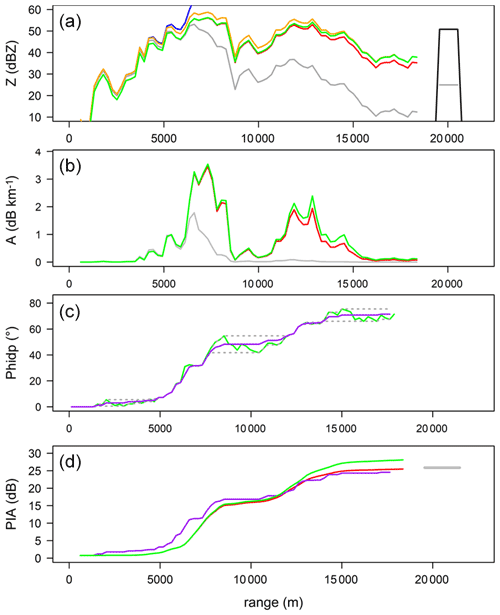
Figure 5 Implementation of the five algorithms (blue – AZhb; red – AZC; orange – AZα; green – AZ0; purple – PIA_ϕdp) for mountain target T13 during the 21 July 2017 convective event at 16:00 UTC using a near-optimal parameter set (see text for details). The results are displayed in terms of profiles of (a) reflectivity, (b) specific attenuation, (c) differential phase shift on propagation and (d) path-integrated attenuation. The grey profile in panel (a) is the measured reflectivity profile; the black and grey horizontal lines at range 20 km represent the mean dry weather baseline and current reflectivities, respectively, of the mountain target. The resulting measured PIA value of 25.2 dB is reported in grey in panel (d). The grey profile in panel (b) is derived from the measured reflectivity profile by using Eq. (2.5). The purple line in panel (c) is the raw total differential phase shift profile, and the grey dotted curves are the envelope curves used in the regularization procedure (Delrieu et al., 2020; Khanal et al., 2022).

3.2.2 Time series of optimal parameter values

Figure 6 presents the time series of quantiles of the distributions of the input variables and the estimated optimal parameters obtained for the best simulation of the 21 July 2017 convective event. The sampling strategy making use of Z₀ (see Table 1) is considered for PIA₀. We will come back, in Sect. 3.2.5, to the relationship between PIA₀ (Fig. 6c) and Z₀ (Fig. 6a). The medians of PIA_m and Φ_dp(r₀,r_m) (Fig. 6b) give an indication on the evolution of the storm which was intense between 15:30 and 17:00 UTC, with medians of about 20 dB and 60^∘, respectively. The interquartile ranges of these two variables are quite large, as a result of both the variation in the radar target distances (from 15 up to 40 km) and the precipitation variability as a function of the azimuth, illustrated in Figs. 1 and 2. The time evolution of the storm intensity is also visible on the NOPS time series (Fig. 6f), with multiplicative factors in the range of 5 to 10 between the period 16:00–17:00 and the period 17:00–18:00 UTC. Although, for a given target, there is an increasing trend of NOPS when PIA_m increases (not shown for the sake of conciseness); this is also related to the higher number of targets reached (i.e. targets with PIA_m values greater than 1 dB) between 16:00 and 17:00 UTC. The time series of the prefactors a_AK (Fig. 6d) and a_AZ (Fig. 6e) have a similar behaviour with rather stable median values that are close to the central values of the sampling intervals derived from the analysis of the DSD data (Sect. 2.4; Table 1). This is reassuring as to the relevance for radar data processing of these DSD-derived relationships deduced from in situ microphysical measurements and scattering models. We note, however, that the interquartile ranges are quite large, especially those of the a_AZ parameter. This is an indication that the mathematical ambiguity (Haddad et al., 1995) of the system of equations at hand remains important. It is noteworthy to mention that the ambiguity of the AZ algorithms alone is much larger (e.g. with larger interquartile ranges for the a_AZ parameter). Introducing the polarimetric algorithm and the associated constraints on the coefficients of the A–K_dp relationship allowed it to reduce dramatically (not shown for the sake of conciseness).

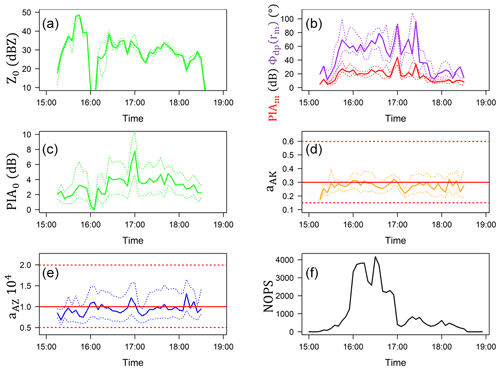
Figure 6 Time series of the input variables and optimal parameters for the best simulation obtained for the 21 July 2017 convective event. The optimal set of fixed parameters for this event is dC = 0.5 dB, b_AZ=0.80 and b_AK=1.1. For each of the three considered input variables (a) Z₀, (b) PIA_m (red) and Φ_dp(r₀r_m) (purple) are displayed the median (continuous line) and the 25 % and 75 % quantiles (dotted lines) of their distributions over the 22 mountain targets. A similar representation is proposed for the LHS optimal parameters (c) PIA₀, (d) a_AK and (e) a_AZ, except that the distributions are established over all optimal parameters of all targets. In panels (d) and (e), the dotted horizontal lines materialize the lower and upper limits consider in the LHS of the considered parameter. The time series of the number of optimal parameter sets (NOPSs) cumulated over all the 22 targets is displayed in panel (f).

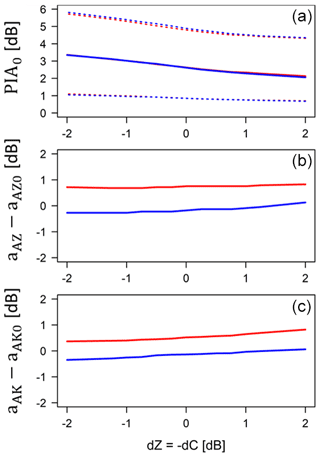
Figure 7 Evolution of the medians of the distributions of on-site attenuation (a), prefactor of the A–Z relationship (b) and prefactor of the A–K_dp relationship (c) estimated for the 21 July 2017 event as a function of the calibration error. The variable dZ, equal to dC, is used to represent the dBZ value to be added to the measured reflectivities for correcting the calibration error. The prefactors, expressed in dB, are calculated with respect to the central values of their intervals of variation as follows: $a_{AZ\mathrm{0}}=\mathrm{10}\log \left({\mathrm{1.010}}^{-\mathrm{4}}\right)$ and a_AK0=10 log(0.3) (Table 1). As in Fig. 4b, the red curves correspond to b_AK=1, and the blue curves to b_AK=1.1. The dotted red and blue curves in the top graphs represent the 25 % and 75 % quantiles of the distributions of PIA₀.

Figure 7 presents additional results for the 21 July 2017 event with the evolution of the medians at the event timescale of estimated PIA₀ (Fig. 7a), the prefactor of the A–Z relationship (Fig. 7b) and the prefactor of the A–K_dp relationship (Fig. 7c) as a function of the calibration error, for two values of the b_AK exponent (1.0 and 1.1). For convenience, the variable dZ = − dC is used in Fig. 7 to represent the dBZ value to be added to the measured reflectivities for correcting the calibration error. We note that the calibration error has a significant impact on the median and interquartile range of PIA₀, with, logically, stronger on-site attenuations for negative dZ values. The prefactors, expressed in dB relative to the central values in Fig. 7, show a slighter and opposite trend to increase as dZ increases. We also note the marked influence of the b_AK exponent on the two prefactors, with an offset of about 0.9 and 0.65 dB on the medians of a_AZ and a_AK, respectively, for dZ = 0.

Figure 8 Evolution of the total number of optimal parameter sets (NOPSs) as a function of the radar calibration error for three convective events separately (dotted blue curves) and all together (solid blue curve). The other fixed parameters for these simulations are b_AZ=0.8 and b_AK=1.1.

3.2.3 Estimating the radar calibration error

In order to increase the robustness of the results, the simulation procedure was performed for three convective events that occurred successively during summer 2017. Table 2 presents some characteristic features of these events. For all of them the melting layer (ML) altitude, determined with the 25^∘ elevation XPORT radar data by using the procedure developed in Khanal et al. (2019), was situated well above the altitude of the Moucherotte mountain radar; hence, there is no ML contamination of the considered radar data. The first two events were rather intense and similar in terms of total rain amount and maximum rain rate at the IGE site and in terms of the PIA_m statistics based on the 22 mountain targets. The third one was a bit less intense. To our knowledge, there was no occurrence of hail reported in the area of interest for these three events.

Table 2 Some characteristics of the three convective events considered in this study. The melting layer (ML) detection was performed with the 25^∘ elevation angle measurements of the XPORT radar, using the algorithm described in Khanal et al. (2019). The total rain amount and the maximum rain rate are recorded at the rain gauge available at the IGE site at the bottom of the Grenoble valley. The PIA_m statistics are derived from the MRT by considering all the 22 mountain targets and the 0^∘ elevation data of the Moucherotte mountain radar.

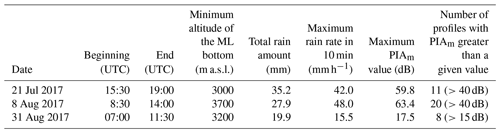
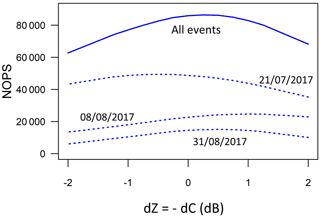
We propose to consider the total NOPSs obtained for a given simulation and for a given event as a quality criterion to judge the relevance of a set of fixed parameters (dC, b_AZ and b_AK). Figure 8 shows the NOPS evolution for the three events separately and all together as a function of the fixed values of dC, with the other fixed parameters being b_AZ=0.8 and b_AK=1.1 in this figure. We note that the various curves are rather flat near their optimum values. The overall sensitivity to the calibration error is clear, however, in the considered [−2, 2 dB] range, e.g., with a ratio of the maximum to the minimum NOPS values of 1.4 for the all-events curve. Although the global results tend to indicate an almost perfect calibration of the measured reflectivities (optimal dZ value $-d{Z}^{\ast }$ in the following – of 0.25 dBZ), one can note that the dZ^∗ values vary from one event to the next with −0.5 dBZ for the 21 July 2017 event, 1.0 dBZ for the 8 August 2018 event and 0.5 dBZ for the 31 August 2017 event. We find it difficult to know whether such variations in the electronic calibration of the radar from one event to the next are physically realistic. By eliminating the data from time steps with significant on-site attenuation, we checked that on-site attenuation could not be held responsible for these dZ^∗ variations.

3.2.4 Linearity of the A–K_dp relationship

Similarly, Fig. 9 shows the evolution of the NOPS criterion computed for the three events all together as a function of the dZ and b_AK (Table 1) values. We note a slight superiority of the simulations with b_AK in the range [1.05–1.15] compared to the one with b_AK=1.0 in terms of the NOPS maximum value. This observation is also valid for each of the three events separately (not shown for clarity in plotting). The simulation with b_AK=0.9 is clearly below the other ones. For b_AK=1.1 and for the optimal dZ value of each event, the log-transformed distribution of a_AK computed over the three events is nearly symmetrical, with an average value of 0.28 and an interquartile range of about [−1, 1 dB]. Hence, we obtain in this study quite a remarkable agreement between the radar and DSD-derived A–K_dp relationships, with $A=\mathrm{0.28}{K}_{\mathrm{dp}}^{\mathrm{1.1}}$ and $A=\mathrm{0.30}{K}_{\mathrm{dp}}^{\mathrm{1.1}}$, respectively. Similarly, the optimal A–Z relationship derived from the simulation exercise is very close to the one obtained by the DSD measurements (Fig. 3) with $A={\mathrm{1.0710}}^{-\mathrm{4}}{Z}^{\mathrm{0.80}}$.

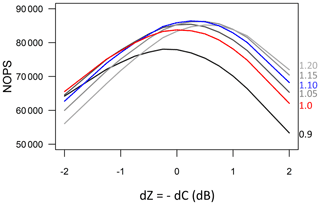
Figure 9 Evolution of the total number of optimal parameter sets (NOPSs) computed for the three convective events all together as a function of dZ for various values of the exponent of the A–K_dp relationship listed on the right-hand side of the figure. As in Figs. 4b and 7, the red curve corresponds to b_AK=1.0 and the blue curve to b_AK=1.1.

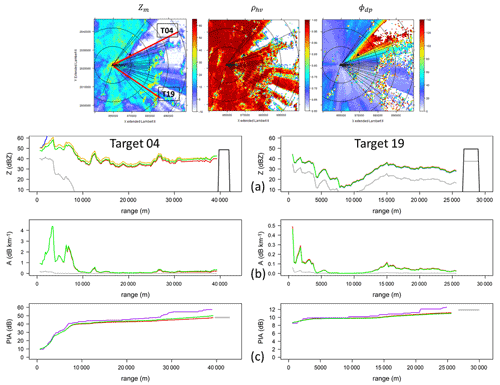
Figure 10 Implementation of the five algorithms with sets of optimal parameters (blue – AZhb; red – AZC; orange – AZα; green – AZ0; purple – PIA_ϕdp) on 21 July 2017 at 17:00 UTC for mountain target T04, with both along-path and on-site attenuation (left), and for mountain target T19 with on-site attenuation mainly (right). The results are displayed in terms of profiles of (a) reflectivity, (b) specific attenuation and (c) path-integrated attenuation. In the upper images, the PPIs of the measured reflectivity (with the indication of the position of the two targets in red) are displayed together with the co-polar correlation coefficient and the raw total differential phase shift.

3.2.5 Radome attenuation

Coming back to Fig. 6, we remind the reader that the sampling strategy making use of Z₀ was considered for the random drawing of PIA₀ values in the simulation. One has to remark that such close-range reflectivity measurements are actually affected by radome attenuation. This may explain why estimated PIA₀ values are higher for the time step at 17:00 UTC than for time steps between 15:30 and 15:55, while Z₀ values are about 10 dBZ higher in the latter period. The relevance of the Z₀ variable for detection and quantification of on-site attenuation remains limited for a radar equipped with a radome.

Figure 10 gives two examples of the core procedure implementation in the case of severe on-site attenuation that occurred on 21 July 2017 at 17:00 UTC (Fig. 2; bottom graphs). The constraint on the maximum value for the PIA₀ sampling as a function of Z₀ was relaxed in these calculations, with a maximum PIA₀ limit set to 30 dB, whatever Z₀. The mountain returns from target 04 (T04) allow us to quantify both on-site attenuation and along-path attenuation due to precipitation falling over the city of Grenoble (NE sector) at that time (left-hand side example). At this range of about 40 km, we obtain PIA_m=47.9 dB and ${\mathrm{\Phi }}_{\mathrm{dp}}(r_{\mathrm{0}},r_{\mathrm{m}})=\mathrm{129.9}$^∘. The mountain returns from target 19 (T19) located in the southeastern sector (right-hand side) seem to be essentially affected by the precipitation conditions at the radar site. At this range of about 27 km, we obtain PIA_m=11.9 dB and ${\mathrm{\Phi }}_{\mathrm{dp}}(r_{\mathrm{0}},r_{\mathrm{m}})=\mathrm{12.2}$^∘. This yields ${\mathrm{PIA}}_{\mathrm{m}}/{\mathrm{\Phi }}_{\mathrm{dp}}(r_{\mathrm{0}},r_{\mathrm{m}})$ ratios of 0.37 and 0.97 dB ^∘−1 for the two targets, respectively. These values are clearly (especially the second one) well above the range of expected values for the slope of a supposedly linear A–K_dp relationship. In addition to the generalized decrease in the mountain returns visible in Fig. 2, this is an indication of a large on-site attenuation effect. The dC-corrected Z₀ values computed in the directions of the two targets are significantly different with 38.9 and 28.6 dBZ, respectively. One can observe the very good convergence of all the AZ algorithms in both cases. In particular for T19, all the AZ reflectivity profiles, including the AZhb one, are perfectly matched. The agreement is also very good between the PIA profiles of the AZ algorithms and the one of the polarimetric algorithm, except for a very slight stall of PIA_Φdp(r) at a range of about 30 km for T04, likely due to disturbances associated with side-lobe effects (visible on the ρ_hv PPI on top of Fig. 10).

For the two OPS considered in Fig. 10, one obtains PIA₀ values of 10.1 and 10.8 dB. By considering the PIA₀ statistical distribution calculated over the optimal parameter sets of all the targets for the considered time step, one obtains a symmetrical distribution with a slightly higher mean value of 12.6 dB and a rather large interquartile range of 4.5 dB. The mean value increases somehow (13.5 dB) and the interquartile range decreases to 3.2 dB if the PIA₀ distribution is computed for targets 9–22 only, i.e. for targets with reduced along-path attenuation. It is worth noting that such statistics are not improved (e.g. interquartile range reduced) if one considers a more stringent satisfaction criterion (e.g. CF_th=0.9 instead of CF_th=0.8).

4 Discussion and future work

In this article, we have started to implement a simulation framework to study the interactions between X-band microwaves and hydrometeors in a mountainous context. Emphasis was placed on the attenuation problem, which is known to be severe for the frequency under consideration and essentially impossible to correct unless estimates of total attenuation are available at a distance from the radar. The RadAlp experiment allows us to obtain direct PIA estimates from the mountain reference technique in some specific directions and indirect estimates from the processing of the profiles of total differential phase shift available for each radial. Although the polarimetric technique is a priori much more convenient to apply and has interesting characteristics (independence on radar calibration, on-site attenuation and partial beam blockages), it suffers from several limitations, including (i) the fact that the Ψ_dp profile is noisy for light precipitation, (ii) the possible contaminations by the differential phase shift on backscatter δ_hv, (iii) the possible impact of non-uniform beam filling and (iv) the need to specify the relationship between the specific attenuation and the specific differential phase shift which depends on hydrometeor types, temperature and so on. In a similar way to the satellite configuration (e.g. the possibility to use the surface reference technique in addition to the dual-frequency measurements at Ka and Ku bands for processing the radar data of the Global Precipitation Measurement (GPM) core platform; Meneghini et al., 2020), we have proposed taking advantage of all the MRT and polarimetric measurements available to perform a generalized sensitivity analysis of the physical model of interest. In the simple case of convective precipitation (i.e. without the contamination of the radar data by snow or melting precipitation), we have obtained interesting results regarding the estimation of radar calibration error, radome attenuation and the A–Z and A–K_dp relationships. We note that, for the estimated optimal radar calibration error, the A–Z and A–K_dp relationships derived from radar data are consistent with those derived from concomitant drop size distribution measurements at ground level, in particular with a slightly non-linear A–K_dp relationship ($A=\mathrm{0.28}{K}_{\mathrm{dp}}^{\mathrm{1.1}})$. This is reassuring regarding the relevance of the use of microphysical data and scattering models for the parameterization of radar data processing. We have deliberately left aside the question of the specific attenuation–rain rate conversion in this article. An interesting validation exercise to be performed consists of using the DSD-derived A–R relationship for the conversion of the estimated specific attenuation profiles. The resulting radar rain rate estimates will be compared with the rain gauge measurements available. Another outcome of the study is the quantification of X-band radome attenuation. Values as high as 15 dB were estimated, leading to the recommendation of avoiding the use of radomes for remote sensing of precipitation at such a frequency. As an alternative, it would be desirable to develop specific sensors to detect/quantify the presence of water on the radome wall (Mancini et al., 2018). As a next step, we plan to extend the procedure to stratiform events with MOUC radar measurements made at times within or above the melting layer. The multi-angle, multi-frequency, polarimetric measurements of the valley-based radars will be critical in this respect for the characterization of the ML from below (Khanal et al., 2019, 2022), the parameterization of Z–A–K_dp–R relationships for different hydrometeor types and the mitigation of the mathematical ambiguity of the physical model of interest.

Appendix A: Formulation of the attenuation–reflectivity algorithms

A1 AZhb algorithm (independent of PIA_m)

This formulation is based on Eq. (2.11) only. In other words, it does not make use of PIA_m. By combining Eqs. (2.11), (2.2) and (2.3), one obtains a corrected reflectivity profile through the following equation:

$$\begin{array}{}\text{(A1)}& \begin{array}{rl}{Z}_{AZ\mathrm{hb}}\left(r\right)& =Z_{\mathrm{m}}\left(r\right)/\\ & {\left[\left(\mathrm{AF}\right(r_{\mathrm{0}})dC{)}^{b_{AZ}}-\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ(r_{\mathrm{0}},r)\right]}^{\mathrm{1}/b_{AZ}}.\end{array}\end{array}$$

The specific attenuation profile follows from the use of the A–Z power law model as follows (Eq. 2.5):

$$\begin{array}{}\text{(A2)}& \begin{array}{rl}{A}_{AZ\mathrm{hb}}\left(r\right)& =a_{AZ}{Z}_{\mathrm{m}}^{b_{AZ}}\left(r\right)/\\ & \left[\left(\mathrm{AF}\right(r_{\mathrm{0}})dC{)}^{b_{AZ}}-\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ(r_{\mathrm{0}},r)\right].\end{array}\end{array}$$

A2 AZC algorithm (independent of dC)

The attenuation constraint (Eq. 2.1.2.) is used to express dC as follows:

$$\begin{array}{}\text{(A3)}& \begin{array}{rl}dC=& \left[\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ\left(r_{\mathrm{0}},r_{\mathrm{m}}\right)/\left(\mathrm{AF}(r_{\mathrm{0}}{)}^{b_{AZ}}\right.\right.\\ & {\left.\left.-\mathrm{AF}(r_{\mathrm{m}}{)}^{b_{AZ}}\right)\right]}^{\mathrm{1}/b_{AZ}},\end{array}\end{array}$$

which is introduced in Eq. (2.11) to yield the following:

$$\begin{array}{}\text{(A4)}& \begin{array}{rl}& {\mathrm{AF}}_{\mathrm{AZC}}^{b_{AZ}}(r_{\mathrm{0}},r)\\ & =\left[\mathrm{AF}\left(r_{\mathrm{0}}{)}^{b_{AZ}}SZ\right(r,r_{\mathrm{m}})+\mathrm{AF}(r_{\mathrm{m}}{)}^{b_{AZ}}SZ(r_{\mathrm{0}},r)\right]\\ & /\mathrm{AF}\left(r_{\mathrm{0}}{)}^{b_{AZ}}SZ\right(r_{\mathrm{0}},r_{\mathrm{m}}).\end{array}\end{array}$$

The corrected reflectivity profile is then derived from Eqs. (2.2), (2.3), (A.3) and (A.4) to read as follows:

$$\begin{array}{}\text{(A5)}& \begin{array}{rl}& Z_{AZC}\left(r\right)=Z_{\mathrm{m}}\left(r\right){\left[\mathrm{AF}(r_{\mathrm{0}}{)}^{b_{AZ}}-\mathrm{AF}(r_{\mathrm{m}}{)}^{b_{AZ}}\right]}^{\mathrm{1}/b_{AZ}}\\ & /\left\{\mathrm{0.46}{a}_{AZ}{b}_{AZ}\left[\mathrm{AF}\left(r_{\mathrm{0}}{)}^{b_{AZ}}SZ\right(r,r_{\mathrm{m}})+\mathrm{AF}(r_{\mathrm{m}}{)}^{b_{AZ}}\right.\right.\\ & SZ(r_{\mathrm{0}},r)]{\mathit{\}}}^{\mathrm{1}/b_{AZ}}.\end{array}\end{array}$$

Note that, in the previous derivations, the expression of dC given by Eq. (A.3) is used twice. It is used first in the expression of ${\mathrm{AF}}_{AZC}^{b_{AZ}}(r_{\mathrm{0}},r)$ from Eq. (2.11) and then in the substitution of dC in Eq. (2.2).

The specific attenuation profile follows from the use of the A–Z relationship Eq. (2.5):

$$\begin{array}{}\text{(A6)}& \begin{array}{rl}& A_{AZC}\left(r\right)=Z_{\mathrm{m}}(r{)}^{b_{AZ}}\left[\mathrm{AF}(r_{\mathrm{0}}{)}^{b_{AZ}}-\mathrm{AF}(r_{\mathrm{m}}{)}^{b_{AZ}}\right]\\ & /\left\{\mathrm{0.46}{b}_{AZ}\left[\mathrm{AF}\left(r_{\mathrm{0}}{)}^{b_{AZ}}SZ\right(r,r_{\mathrm{m}})+\mathrm{AF}(r_{\mathrm{m}}{)}^{b_{AZ}}\right.\right.\\ & SZ(r_{\mathrm{0}},r)\left]\mathit{\right\}}.\end{array}\end{array}$$

A3 AZα algorithm (independent of a_AZ)

The attenuation constraint (Eq. 2.12) is used to express a_AZ as follows:

$$\begin{array}{}\text{(A7)}& \begin{array}{rl}{a}_{AZ}=& \left[d{C}^{b_{AZ}}\left(\mathrm{AF}\right(r_{\mathrm{0}}{)}^{b_{AZ}}-\mathrm{AF}\left(r_{\mathrm{m}}{)}^{b_{AZ}}\right)\right]/\\ & \left[\mathrm{0.46}{b}_{AZ}SZ(r_{\mathrm{0}},r_{\mathrm{m}})\right],\end{array}\end{array}$$

which can be introduced in Eq. (2.11) to yield the following:

$$\begin{array}{}\text{(A8)}& \begin{array}{rl}& {\mathrm{AF}}_{AZ\mathit{\alpha }}^{b_{AZ}}(r_{\mathrm{0}},r)=\left[\mathrm{AF}\left(r_{\mathrm{0}}{)}^{b_{AZ}}SZ\right(r,r_{\mathrm{m}})\right.\\ & \left.+\mathrm{AF}\left(r_{\mathrm{m}}{)}^{b_{AZ}}SZ\right(r_{\mathrm{0}},r)\right]/\mathrm{AF}\left(r_{\mathrm{0}}{)}^{b_{AZ}}SZ\right(r_{\mathrm{0}},r_{\mathrm{m}}).\end{array}\end{array}$$

Equation (A.8) is actually identical to the ${\mathrm{AF}}_{AZC}^{b_{AZ}}(r_{\mathrm{0}},r)$ expression (A.4). From Eqs. (A.8), (2.2) and (2.3), the resulting corrected reflectivity profile can be expressed as follows:

$$\begin{array}{}\text{(A9)}& \begin{array}{rl}& Z_{AZ\mathit{\alpha }}\left(r\right)=Z_{\mathrm{m}}\left(r\right)SZ(r_{\mathrm{0}},r_{\mathrm{m}}{)}^{\mathrm{1}/b_{AZ}}/\left\{dC\left[\mathrm{AF}(r_{\mathrm{0}}{)}^{b_{AZ}}\right.\right.\\ & {\left.\left.SZ(r,r_{\mathrm{m}})+\mathrm{AF}\left(r_{\mathrm{m}}{)}^{b_{AZ}}SZ\right(r_{\mathrm{0}},r)\right]\right\}}^{\mathrm{1}/b_{AZ}}.\end{array}\end{array}$$

One can note that Z_AZα(r) is different from Z_AZC(r) (Eq. A.5) and that it depends on dC.

Next, it can be verified, by using Eqs. (A.9), (2.5) and (A.7) (a second time, for the necessary substitution of a_AZ), that the AZα specific attenuation profile is identical to the AZC specific attenuation profile given by Eq. (A.6) with the following:

$$\begin{array}{}\text{(A10)}& \begin{array}{rl}& A_{AZ\mathit{\alpha }}\left(r\right)=Z_{\mathrm{m}}(r{)}^{b_{AZ}}\left[\mathrm{AF}(r_{\mathrm{0}}{)}^{b_{AZ}}-\mathrm{AF}(r_{\mathrm{m}}{)}^{b_{AZ}}\right]/\\ & \left\{\mathrm{0.46}{b}_{AZ}\left[\mathrm{AF}\left(r_{\mathrm{0}}{)}^{b_{AZ}}SZ\right(r,r_{\mathrm{m}})+\mathrm{AF}(r_{\mathrm{m}}{)}^{b_{AZ}}\right.\right.\\ & SZ(r_{\mathrm{0}},r)\left]\mathit{\right\}}.\end{array}\end{array}$$

A4 AZ0 algorithm (independent of PIA₀)

The attenuation constraint (Eq. 2.12) is used to express $\mathrm{AF}(r_{\mathrm{0}}{)}^{b_{AZ}}$ as follows:

$$\begin{array}{}\text{(A11)}& \begin{array}{rl}& \mathrm{AF}(r_{\mathrm{0}}{)}^{b_{AZ}}=\left[\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ\right(r_{\mathrm{0}},r_{\mathrm{m}})\\ & \left.+{\left(\mathrm{AF}\left(r_{\mathrm{m}}\right)dC\right)}^{b_{AZ}}\right]/d{C}^{b_{AZ}},\end{array}\end{array}$$

which can be introduced in Eq. (2.11) to yield the following:

$$\begin{array}{}\text{(A12)}& \begin{array}{rl}& {\mathrm{AF}}_{AZ\mathrm{0}}^{b_{AZ}}(r_{\mathrm{0}},r)=\mathit{\left\{}\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ\right(r,{\mathrm{r}}_{\mathrm{m}})\\ & \left.+\mathrm{AF}(r_{\mathrm{m}}{)}^{b_{AZ}}d{C}^{b_{AZ}}\right\}/\mathit{\left\{}\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ\right(r_{\mathrm{0}},r_{\mathrm{m}})\\ & \left.+\left(\mathrm{AF}\right(r_{\mathrm{m}})dC{)}^{b_{AZ}}\right\}.\end{array}\end{array}$$

The resulting corrected reflectivity profile is as follows:

$$\begin{array}{}\text{(A13)}& \begin{array}{rl}& Z_{AZ\mathrm{0}}\left(r\right)=Z_{\mathrm{m}}\left(r\right)/\mathit{\left\{}\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ\right(r,r_{\mathrm{m}})\\ & {\left.+\left(\mathrm{AF}\right(r_{\mathrm{m}})dC{)}^{b_{AZ}}\right\}}^{\mathrm{1}/b_{AZ}}.\end{array}\end{array}$$

And the specific attenuation profile is as follows:

$$\begin{array}{}\text{(A14)}& \begin{array}{rl}& A_{AZ\mathrm{0}}\left(r\right)=a_{AZ}{Z}_{\mathrm{m}}(r{)}^{b_{AZ}}/\mathit{\left\{}\mathrm{0.46}{a}_{AZ}{b}_{AZ}SZ\right(r,r_{\mathrm{m}})\\ & \left.+\left(\mathrm{AF}\right(r_{\mathrm{m}})dC{)}^{b_{AZ}}\right\}.\end{array}\end{array}$$