the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Effective uncertainty quantification for multi-angle polarimetric aerosol remote sensing over ocean
Kirk Knobelspiesse
Bryan A. Franz
Peng-Wang Zhai
Andrew M. Sayer
Amir Ibrahim
Brian Cairns
Otto Hasekamp
Yongxiang Hu
Vanderlei Martins
P. Jeremy Werdell
Xiaoguang Xu
Multi-angle polarimetric (MAP) measurements can enable detailed characterization of aerosol microphysical and optical properties and improve atmospheric correction in ocean color remote sensing. Advanced retrieval algorithms have been developed to obtain multiple geophysical parameters in the atmosphere–ocean system. Theoretical pixel-wise retrieval uncertainties based on error propagation have been used to quantify retrieval performance and determine the quality of data products. However, standard error propagation techniques in high-dimensional retrievals may not always represent true retrieval errors well due to issues such as local minima and the nonlinear dependence of the forward model on the retrieved parameters near the solution. In this work, we analyze these theoretical uncertainty estimates and validate them using a flexible Monte Carlo approach. The Fast Multi-Angular Polarimetric Ocean coLor (FastMAPOL) retrieval algorithm, based on efficient neural network forward models, is used to conduct the retrievals and uncertainty quantification on both synthetic HARP2 (Hyper-Angular Rainbow Polarimeter 2) and AirHARP (airborne version of HARP2) datasets. In addition, for practical application of the uncertainty evaluation technique in operational data processing, we use the automatic differentiation method to calculate derivatives analytically based on the neural network models. Both the speed and accuracy associated with uncertainty quantification for MAP retrievals are addressed in this study. Pixel-wise retrieval uncertainties are further evaluated for the real AirHARP field campaign data. The uncertainty quantification methods and results can be used to evaluate the quality of data products, as well as guide MAP algorithm development for current and future satellite systems such as NASA’s Plankton, Aerosol, Cloud, ocean Ecosystem (PACE) mission.
Satellite remote sensing has revolutionized Earth observation capabilities and plays a significant role in studying atmosphere, ocean, and land systems. Remote sensing techniques have advanced rapidly to provide highly accurate geophysical property retrievals by utilizing the rich information content of observations at multiple spectral bands, viewing angles, and polarization states. Multi-angle polarimeters (MAPs) are particularly well suited to characterize aerosol microphysical properties (Mishchenko and Travis, 1997; Chowdhary et al., 2001; Hasekamp and Landgraf, 2007; Knobelspiesse et al., 2012). Improved aerosol characterization helps reduce uncertainties in aerosol radiative forcing estimates and thereby advances our understanding of Earth’s climate (Bender, 2020; IPCC, 2022). Furthermore, better quantification of the aerosol path radiance in the atmosphere reduces error in the retrieval of spectral water-leaving radiances from ocean color remote sensing systems (Mobley et al., 2016; Mobley, 2022), which is important for the study of aquatic phytoplankton dynamics, marine ecosystems, and the global carbon cycle (Frouin et al., 2019; Groom et al., 2019).
Joint aerosol and ocean color retrieval algorithms have been developed for a variety of spaceborne and airborne MAPs such as the Polarization and Directionality of the Earth’s Reflectances (POLDER) instruments (Hasekamp et al., 2011; Dubovik et al., 2011, 2014; Li et al., 2019; Hasekamp et al., 2019b; Chen et al., 2020), the Airborne Multiangle SpectroPolarimetric Imager (AirMSPI; Xu et al., 2016, 2019), the Spectropolarimeter for Planetary EXploration (SPEX) airborne (Fu and Hasekamp, 2018; Fu et al., 2020; Fan et al., 2019), SPEXone (spaceborne version of SPEX airborne; Hasekamp et al., 2019b), the Research Scanning Polarimeter (RSP; Chowdhary et al., 2005; Wu et al., 2015; Stamnes et al., 2018; Gao et al., 2018, 2019, 2020), the Directional Polarimetric Camera (DPC)/GaoFen-5 (Wang et al., 2014; Li et al., 2018), Airborne Hyper-Angular Rainbow Polarimeter (AirHARP; Puthukkudy et al., 2020; Gao et al., 2021a, b), and HARP2 (the spaceborne version of AirHARP; Gao et al., 2021b). The algorithms typically follow iterative optimization approaches utilizing a vector radiative transfer forward model and simultaneously retrieve a suite of geophysical parameters. A thorough review of MAP instruments and retrieval algorithms can be found in Dubovik et al. (2019).
Uncertainty quantification is an integral part of retrieval algorithm development. The uncertainties of the retrieved products (hereafter “retrieval uncertainties”) are key to understanding retrieval performance, gauging whether the algorithm provides results of useful quality, and guiding where further efforts for improvement are best focused. In this study, we define retrieval error as the difference between the retrieval results and truth (whether synthetic data or external reference data), and we define retrieval uncertainty as the standard deviation (1σ) confidence interval around the retrieval solution (assuming a Gaussian distribution). Broadly, two methods are commonly used to determine retrieval uncertainties (see Sayer et al., 2020, for a review in the context of aerosol remote sensing).
-
Propagated (hereafter “theoretical”) uncertainty. Based on Bayesian theory, the uncertainty in observations and forward models as well as a priori assumption (hereafter “input uncertainty model”) can be mapped to the domain of retrieved parameters based on sensitivities derived from radiative transfer modeling (e.g., Rodgers, 2000). Pixel-wise uncertainties can be conveniently determined from an optimization algorithm based on its Jacobian matrix, which represents the measurement sensitivity with respect to the retrieval parameters.
However, theoretical uncertainties derived from these techniques often represent a best-case scenario as they rely on several assumptions (discussed by Povey and Grainger, 2015): (a) the input uncertainty model is sufficient, (b) the retrievals converge to their global minimum, and (c) the forward model is linear with respect to the retrieval parameters near the solution. Evaluating these assumptions for a given sensor and algorithm is therefore important. For MAP measurements, theoretical uncertainties have been widely used for aerosol and cloud retrieval algorithms for sensors, such as POLDER (Hasekamp et al., 2011; Dubovik et al., 2011), RSP (Knobelspiesse et al., 2012), ground-based AERONET photo-polarimetric measurements (Xu and Wang, 2015; Xu et al., 2015), and general polarimetric instrument concept studies (Hasekamp and Landgraf, 2007; Knobelspiesse et al., 2012).
-
Truth-based (hereafter “real”) uncertainty. Retrieval errors are evaluated by comparing retrieval results with reference data taken as a truth and used to draw general inference about retrieval uncertainties under various conditions. The real uncertainty does not require the same assumptions as error propagation but requires the existence of “truth” data of high and known confidence, which may be unavailable for some geophysical parameters. Additionally, the truth data and matchup process have their own uncertainties which must be considered. In the absence of independent external truth, simulated retrievals are a useful tool. For MAP measurements, real uncertainties have been discussed for aerosols over ocean, land, and cloud by comparing retrievals with synthetic data and in situ measurements, such as for POLDER (Hasekamp et al., 2011; Dubovik et al., 2011; Chen et al., 2020), RSP (Chowdhary et al., 2012; Stamnes et al., 2018; Gao et al., 2019; Fu et al., 2020), AirMSPI (Xu et al., 2016), SPEX Airborne (Fu et al., 2020), SPEXone (Hasekamp et al., 2019a), AirHARP (Puthukkudy et al., 2020; Gao et al., 2021a, b), and HARP2 (Gao et al., 2021b).
In short, theoretical uncertainties provide pixel-wise estimates of performance for every parameter, while real uncertainties provide a more complete assessment of performance, but with limitations due to the availability of high-quality reference data. The two are a natural complement as ground-truth data or simulated retrievals provide an avenue to evaluate theoretical uncertainties in a statistical sense. A statistical (not one-to-one) comparison is necessary because a retrieval with associated uncertainty represents a range of plausible values of a geophysical quantity, whereas an individual reference truth has a definite value. Several approaches have been proposed to address the question of whether the distribution of observed retrieval errors is consistent with the distribution as expected from the theoretical uncertainty (Hasekamp and Landgraf, 2005; Sayer et al., 2020). For example, Hasekamp and Landgraf (2005) found the retrieval errors normalized by theoretical uncertainties from polarimetric retrievals can reproduce the general features of a Gaussian distribution, which was then used to discuss the impact of local minima and non-linearity around the truth. Sayer et al. (2020) illustrated a framework for aerosol retrievals based on normalized error distributions to quantitatively compare the real and theoretical uncertainties. Meanwhile, Monte Carlo methods based on random sampling (Kalos and Whitlock, 2008) have been widely used to generate random error samples and used for analyzing their uncertainties (see Zhang, 2021, for a survey) with applications to assess uncertainties of ocean bio-optical algorithms (McKinna et al., 2019). Monte Carlo methods are flexible and robust given sufficient sampling but have not been well explored for MAP retrieval uncertainty studies.
In this paper, we discuss theoretical uncertainties from MAP retrievals over a coupled atmosphere and ocean system, and then we propose a flexible framework to validate these theoretical uncertainties against real uncertainties. The following topics will be addressed in this work.
-
Performance. How well do theoretical uncertainties represent real retrieval uncertainties for both aerosol properties and the ocean color signal?
This will be assessed not just for properties retrieved directly from the MAP data, but also derived properties such as aerosol optical depth (AOD), single scattering albedo (SSA), and various aspects of the derived water-leaving signals. To quantify the performance in this study, random errors are sampled from theoretical pixel-wise uncertainties using a Monte Carlo method, and results are compared with the real errors.
-
Speed. How can uncertainty estimation be made sufficiently fast to be practical in operational data processing?
Uncertainty evaluation often requires Jacobian matrix and derivative calculations, which can be computationally expensive. To achieve optimal speed within the framework of this work, all Jacobian matrix and derivatives are evaluated analytically using automatic differentiation based on neural networks.
-
Input uncertainty model. How representative is the algorithm’s input uncertainty model?
The input uncertainty model includes two main components: (a) measurement uncertainties, which are mostly characterized by instrument calibration uncertainties, and (b) forward model uncertainties, which refer to whether the forward model can sufficiently describe the measurements.
This work focuses on the first two topics. The third topic has been partially addressed using an adaptive angular screening approach, described in Gao et al. (2021b), to automatically remove MAP angles where the input uncertainty model is insufficient to describe forward model uncertainty due to contamination by cirrus clouds and other anomalies (Gao et al., 2021b). Noise correlation in the uncertainty model may impact retrieval results, though it is often ignored as assumed in this study (Knobelspiesse et al., 2012). We study both theoretical and real uncertainties based on retrievals from synthetic AirHARP and HARP2 measurements, as well as AirHARP field measurement. This work provides a general approach to understand and evaluate pixel-wise uncertainties of high-dimensional retrieval problems and can guide further uncertainty studies and algorithm development when more advanced instruments with high angular and spectral resolutions are available. Our primary focus is on these instruments due to HARP2’s inclusion in NASA’s upcoming Plankton, Aerosol, Cloud, ocean Ecosystem (PACE) mission (Werdell et al., 2019), but the analysis is useful for future MAP missions, such as NASA’s Multi-Angle Imager for Aerosols (MAIA) (Diner et al., 2018) and Atmosphere Observing System (AOS) missions (https://aos.gsfc.nasa.gov/, last access: 18 August 2022), and the Multi-view Multi-channel Multi-polarization Imager (3MI) that will fly on ESA’s MetOp-SG mission (Marbach et al., 2015; Fougnie et al., 2018). Section 2 of this paper describes the FastMAPOL retrieval algorithm used in the study, Sect. 3 discusses the methodology in the retrieval uncertainty evaluation, Sect. 4 quantified the performance of retrieval uncertainties based on synthetic AirHARP and HARP2 data, Sect. 5 applied the pixel-wise uncertainties on the retrievals from AirHARP field measurements, and Sect. 6 provides discussions and conclusions.
The FastMAPOL algorithm (Gao et al., 2021a) uses neural network forward models of a coupled atmosphere–ocean system and has been used to perform retrievals on synthetic and observed AirHARP measurements (Gao et al., 2021a) and synthetic HARP2 measurements (Gao et al., 2021b). In this section, we will first introduce the MAP measurements from the PACE mission and then review key components of the retrieval algorithm.
2.1 HARP MAP measurement
PACE will carry three instruments that are expected to advance our characterization of the atmosphere, ocean, and land states (Werdell et al., 2019; Remer et al., 2019a, b; Frouin et al., 2019). The main instrument on PACE is a hyperspectral scanning radiometer named the Ocean Color Instrument (OCI). There are two MAP instruments on PACE. The first is SPEXone, contributed by a consortium of organizations in the Netherlands including SRON (Netherlands Institute for Space Research) and Airbus Defence and Space Netherlands, which will perform multi-angle measurements at five along-track viewing angles of 0, ±20, and ±58∘, with a narrow cross-track nadir surface swath of 100 km and a continuous spectral range spanning 385–770 nm at resolutions of 2–3 nm for intensity and 10–40 nm for polarization (van Amerongen et al., 2019; Rietjens et al., 2019; Hasekamp et al., 2019a). The second is HARP2, contributed by UMBC (University of Maryland, Baltimore County), a wide field-of-view imager that measures the total and polarized radiances at 440, 550, 670, and 870 nm, with a nadir-view swath of 1556 km (Martins et al., 2018). The 670 nm band will measure 60 viewing angles compared to the other bands' 10 angles. AirHARP is the airborne version of HARP2 and measures the same number of viewing angles at 670 nm but 20 viewing angles at the other three bands. Note that, for the HARP instruments, the view angles observed by different spectral bands are close but not identical.
The total measured reflectance (ρt(λ)) and degree of linear polarization (DoLP; Pt(λ)) are taken as input to the FastMAPOL retrieval algorithm, defined as
where Lt, Qt, and Ut are the first three Stokes parameters; F0 is the extraterrestrial solar irradiance; and μ0 is the cosine of the solar zenith angle. We adopt instrument calibration uncertainties of 3 % in reflectance for both AirHARP and HARP2, 0.01 in DoLP for AirHARP, and 0.005 in DoLP for HARP2 (McBride et al., 2019; Puthukkudy et al., 2020; Gao et al., 2021a, b).
2.2 Neural network radiative transfer forward model
Vector radiative transfer models (VRTMs) are used to simulate the reflectance and polarization over a coupled atmosphere and ocean system (Zhai et al., 2009, 2010). However, it is computationally time consuming to call a VRTM within a retrieval scheme, and the large number of retrieval parameters mean that creating a lookup table of results in reasonable size, as is common for retrievals with a small number of parameters, is prohibitive. Therefore, to achieve high speed and accuracy for retrievals, Gao et al. (2021a) trained several feed-forward neural network (NN) models with synthetic data generated by the VRTM developed by Zhai et al. (2009, 2010, 2022). NNs for reflectance (ρt) and DoLP (Pt) are trained individually, both with an input layer with 15 parameters, followed by three hidden layers with 1024, 256, and 128 nodes and a final output layer with 4 nodes to represent the four HARP bands. Details of the forward model and the NN training process are provided by Gao et al. (2021a).
The atmospheric model for the airborne measurements consists of a combination of aerosols and air molecules from surface to 2 km, an aerosol-free molecular layer (i.e., Rayleigh scattering) above that, and (for the airborne AirHARP instrument) an additional aerosol-free layer above the aircraft altitude. A total of 15 geophysical parameters, shown in Table 1, are used as inputs to the forward model. The solar and viewing geometries are represented by the solar and viewing zenith angles (θ0 and θv) and a relative azimuth angle (ϕv). The aerosol complex refractive index for both fine and coarse modes is assumed to be spectrally flat, represented by four parameters, including both real (mr,f and mr,c) and imaginary (mi,f and mi,c) parts. In this work, we only consider weakly absorbing aerosols with mi<0.03. It will be a subject of future studies on how the theoretical uncertainties represents the real uncertainties for more complex aerosol models, following the approach discussed in this study.
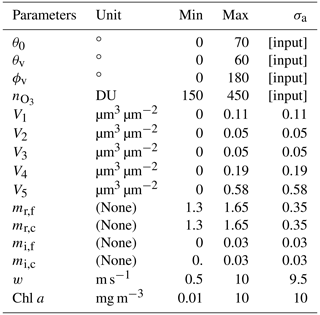
Table 1Parameters used to train the FastMAPOL forward model as described in Sect. 2.2. The minimum (min) and maximum (max) values of each parameter are also shown. The a priori uncertainties (σa) are estimated as the difference between the max and min values for the study in Sect. 3, except the four parameters as indicated, which are assumed as known input.
The aerosol size distribution is assumed as a combination of five lognormally distributed aerosol sub-modes, each with prescribed mean radii and variances; the five volume densities (Vi) are free parameters (Dubovik et al., 2006; Xu et al., 2016). The five-mode approach is found to provide good retrievals for most aerosol parameters (Fu and Hasekamp, 2018). The combined aerosol fine mode consists of the three smaller sub-modes, and the coarse mode consists of the two larger sub-modes. Therefore, the fine-mode volume fraction (fvf) is defined as
Ozone absorption is quantified by the ozone column density (); absorption by other gaseous species is minimal in HARP’s spectral bands and is therefore neglected. Ocean surface roughness is represented by the isotropic Cox and Munk (1954) model parameterized by wind speed (m s−1). Strong sunglint is excluded here by removing view angles within 40∘ of the specular reflection direction due to the challenges to represent the sunglint signals from ACEPOL field campaign using the isotropic Cox and Munk model (Gao et al., 2020, 2021a). We only consider open-ocean waters modeled as a uniform layer with bio-optical properties parameterized as a function of chlorophyll a concentration (Chl a) (Gao et al., 2019). Complex bio-optical properties for coastal waters require additional parameters in the bio-optical model (Gao et al., 2018), which require additional NN trainings that will be pursued in a future study.
NN uncertainties σNN are < 1 % for reflectance and < 0.003 for DoLP for all HARP bands, which are much smaller than the measurement uncertainties (Sect. 2.1). To achieve high NN accuracy, numerical uncertainty on the radiative transfer simulations used to train the NN has an uncertainty σRT much smaller than σNN (Gao et al., 2021a). The forward calculation of aerosol optical depth (AOD) and single scattering albedo (SSA) from aerosol size and refractive index is also performed using NNs based on simulations using the numerical code based on the Lorenz–Mie theory (Mishchenko et al., 2002). In addition, the spectral ocean color remote sensing reflectance (Rrs(λ)) is derived based on the retrieved aerosol properties through atmospheric correction, a procedure to derive ocean color signals by removing the contributions with atmosphere and ocean surface from the top-of-atmosphere (TOA) measurements (Mobley et al., 2016; Mobley, 2022). The atmospheric correction and other associated procedures have been implemented using NNs by Gao et al. (2021a) with more details provided in Appendix A. The atmospheric correction method also provides a convenient way to derive ocean color signals from other sensors, such as PACE OCI, using the MAP retrieved aerosol properties. Note that NN method has also been used to directly link Rayleigh-corrected TOA radiances with normalized remote sensing reflectance by Fan et al. (2021).
2.3 Cost function and input uncertainty model
The optimal values of retrieval parameters are obtained using a maximum likelihood approach by minimizing the difference between the measurements and the forward model fit represented by a cost function (Rodgers, 2000):
where m is a vector including measurements from all angles and bands (both total reflectance and DoLP; Eqs. 1 and 2) and F(x) is the forward-modeled observations described in the previous section. The state vector x includes the 11 parameters retrieved as summarized in Table 1. N is the total number of measurements. The input uncertainty model is characterized by the error covariance matrix Sϵ representing the combined measurement and forward model uncertainty. In this work, we assume uncorrelated uncertainty, and therefore Sϵ is a diagonal matrix. The diagonal elements (σϵ) include contributions from instrumental σins, neural network σNN, and VRTM σRT, assuming no correlations between these uncertainty sources:
As discussed in Sect. 1, an adaptive data screening method is used to remove the real measurements which cannot be fitted well by the forward model (Gao et al., 2021b). In this way, the impact of forward model uncertainties can be reduced. We do not consider additional forward model uncertainties in this study.
The subspace trust-region interior reflective (STIR) algorithm is employed to conduct non-linear least-square minimization of the cost function (Branch et al., 1999). Its implementation in the Python package SciPy is used in this study (Virtanen et al., 2020). STIR is based on the Levenberg–Marquardt algorithm combined with an interior method and reflective boundary technique (Branch et al., 1999). The interior method ensures that the retrieval parameters are searched strictly within the interior of the feasible region as specified in Table 1, while the reflection technique can significantly reduce the number of iterations in the minimization process.
3.1 Pixel-wise retrieval uncertainty quantification
The propagated (theoretical) pixel-wise uncertainty quantification is based upon a Bayesian approach which assumes Gaussian distributions of input uncertainty (including measurements, forward model, and a priori) and output (retrieval) uncertainty (Rodgers, 2000). These represent the 1 standard deviation (1σ) uncertainty on the retrieved state and are determined by mapping the measurement and forward model uncertainties into retrieval parameter space,
where S is the retrieval uncertainty covariance matrix, Sϵ is the error covariance matrix as in Eq. (4) which includes contributions from measurement and forward model as shown in Eq. (5), K is the Jacobian matrix, and Sa is the a priori uncertainty covariance matrix. FastMAPOL does not use explicit a priori information on the cost function. However, each retrieval parameter has a range of acceptable values (Table 1) which are imposed by the STIR optimization algorithm; therefore, these parameter ranges work as implicit prior constraints. To capture the impact of these constraints, we assume Sa is diagonal and take the permitted range of each state parameter as an assumed a prior uncertainty as listed in Table 1. This is an approximation to the Rodgers (2000) formalism and serves to stop the retrieval uncertainty exceeding the physically plausible range (though in most cases it has little numerical effect). The Jacobian matrix, K, expresses the sensitivity of the forward model to changes in the retrieval parameters, which is defined as
where indices i and j represent the different measurements and the retrieved parameters, respectively. The finite-difference method is often used to compute the Jacobian matrix, but it is time-consuming due to the many retrieval parameters used to calculate the derivatives. In our previous work (Gao et al., 2021b), we implemented an analytical approach based on neural networks, which is extended here with significant speed improvement as discussed in Sect. 3.3.
The 1σ uncertainties on each retrieved parameter are simply the square roots of the diagonal elements of S. For quantities b that are not directly contained in x but can be calculated from it, such as AOD or SSA, their uncertainty (Δb) can be expressed as
The additional derivatives of b with respect to state parameters are necessary to compute Δb. Automatic differentiation is used to calculate both the Jacobian matrix and the derivatives defined in Eq. (8) for AOD and SSA, as well as water-leaving signals involving atmospheric corrections. More details are discussed in Appendix A.
Other Bayesian inference methods exist that are capable of deriving retrieval uncertainties without explicitly computing the Jacobian matrix or requiring that uncertainties be Gaussian. For example, Knobelspiesse et al. (2021) applied the Generalized Nonlinear Retrieval Analysis (GENRA, Vukicevic et al., 2010) method on simulated MISR data to access the retrieval uncertainties of multiple retrieval parameters. However, such methods often require a large number of computationally expensive forward model calculations and are less practical for high-dimensional problems such as this. Thus, the more computationally efficient Jacobian-based approach is the main focus of this work.
3.2 Retrieval uncertainty performance evaluation
Verifying theoretical uncertainty estimates is necessary because real retrieval performance depends on other factors. A key factor is how well the inversions converge to the global minimum of the cost function instead of a false convergence to a local minimum. This is not captured by Eq. (6). Several factors can lead to false convergence to local minima, e.g.,
-
accuracy of the forward model and Jacobian matrix;
-
tolerance for iterative optimization, which may impact how early the iterative parameter updates stop;
-
the possibility that retrievals may get stuck at parameter boundaries, if not adequately treated in the inversion algorithm;
-
the possibility that the input uncertainty model may be insufficient, leading to inappropriate weights of different measurements in the cost function; and
-
false convergence from non-monotonic cost functions due to insufficient information in the measurements.
To evaluate the performance of the uncertainty quantification using error propagation, we can compare theoretical uncertainty with the uncertainties calculated by comparing the final retrieval results with reference truth values. Two useful metrics, the mean absolute error (MAE) and the root mean square error (RMSE) between the truth (Ti) and retrievals (Ri), are defined as
where M is the total number of retrieval cases. For a Gaussian distribution, RMSE and MAE are related as
MAE is more robust to outliers than RMSE, so comparing the two can be informative as to whether the overall error distribution is close to Gaussian. MAE has also been shown to be less dependent on the number of cases considered than RMSE (Willmott and Matsuura, 2005). Over a large ensemble of cases, the overall error distribution is not necessarily expected to be Gaussian because it may be drawn from a large number of different atmospheric/oceanic states, each with a different magnitude of uncertainty.
Chlorophyll a concentration (Chl a) varies across several orders of magnitude and plays an important role to determine Rrs and their the uncertainties (McKinna et al., 2019). As recommended by Seegers et al. (2018), we use a log-transformed metric:
where
MAE(log ) indicates the averaged ratio between the retrieval and truth values in such a way that a value of 1.2 indicates that the retrievals exceed truth by 20 %. To compare with the theoretical uncertainty for Chl a requires that its retrieval uncertainty must be transformed to a log 10 scale as follows:
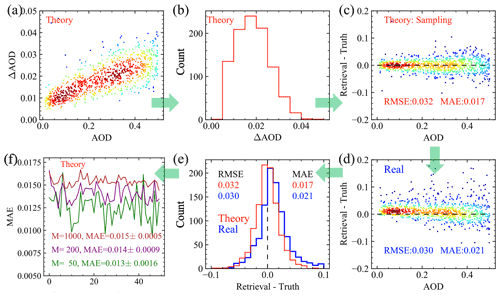
Figure 1Demonstration of the procedures to compare theoretical and real uncertainties. (a) Theoretical uncertainties of AOD retrievals over 1000 synthetic HARP2 measurements; (b) histogram of panel (a); (c) the retrieval error sampled from panel (a); (d) the retrieval error derived from the difference between the real retrieval results and truth data; (e) the histogram for the retrieval errors in both panel (c) and (d); (f) the MAE for 50 sets of random theoretical errors considering a total number of cases of 50, 200, and 1000.
Direct comparison of theoretical uncertainties and real errors is difficult because the former is a measure of the estimated dispersion of the retrieval in terms of a distribution of 1σ uncertainties, and the latter is a distribution of retrieval errors indicating the difference between real retrieval results and the truth reference data that relate specifically to observational conditions available at the time of collection. To effectively compare the theoretical uncertainties and real errors, we propose a sampling-based method, Monte Carlo error propagation (MCEP), which samples random retrieval errors from the theoretical uncertainties and therefore enables comparisons on the same retrieval error domains. This method is demonstrated in Fig. 1 using 1000 synthetic retrievals of AOD at 550 nm from HARP2 data. The synthetic datasets are generated with random draws from a uniform distribution of AOD values from 0.01 to 0.5. The selection of a uniform AOD distribution is to ensure the same number of cases are considered in each sub-interval for later statistical discussion. Detailed information on the synthetic data is provided in the next section. This choice of synthetic data is to explore the dependency of retrieval uncertainties with respect to AOD. To represent the overall retrieval performance of actual PACE data, synthetic or real HARP2 data with realistic statistical distributions will be studied in the future.
The goal is to generate a statistical distribution of the retrieval error (defined as the difference between retrieval and truth) for both theoretical and real uncertainties and to develop proper metrics for comparison based on the distribution. Steps involved in MCEP are listed below using the example in Fig. 1.
-
Conduct retrievals and compute theoretical retrieval uncertainties according to the error propagation method discussed in Sect. 3.1. Here AOD is derived from the directly retrieved refractive indices and volume densities shown in Table 1, and ΔAOD is thereby calculated from Eq. (8) for each individual retrieval. Figure 1a shows the theoretical AOD uncertainties evaluated for 1000 cases with its histogram shown in Fig. 1b.
-
Generate a distribution of random theoretical errors. This is done by taking the theoretical uncertainty for each retrieval and generating a random number from a Gaussian distribution with a zero mean and a standard deviation equal to the theoretical uncertainty (i.e., individual points from Fig. 1a). This random number will be the theoretical retrieval error for the corresponding theoretical retrieval uncertainty. These sampled random errors are shown in Fig. 1c.
-
The real retrieval errors, shown in Fig. 1d, are calculated as the difference between the retrieval results and truth data. Figure 1c and d showed similar dependency on the AOD.
-
The histograms for the error data in Fig. 1c and d are compared in Fig. 1e, which shows directly comparable statistical distributions. These distributions can be analyzed using metrics such as RMSE and MAE in Eqs. (10) and (11).
-
Evaluate the variations of the uncertainty metrics derived from step 4: (1) generate multiple sets of random theoretical errors following step 2; (2) compute the metrics for each set of errors; and (3) compute 1σ uncertainties of the metrics. This uncertainty depends on the number of cases used within each set and, therefore, can also be used to approximate the uncertainty of the metrics evaluated from real errors due to the same number of cases (M) used in Eqs. (9) and (10). The MAE results for M equal to 50, 200, and 1000 over 50 sets of theoretical random errors are shown in Fig. 1f.
The MCEP method enables direct comparison of error distributions between theoretical uncertainties and real retrievals, which therefore provide additional flexibility in analyzing their statistics. For the example in Fig. 1e, the peak of real retrieval errors is ∼0.01, suggesting that the retrievals tend to overestimate total AOD. The sampling method used in step (2) of MCEP does not assume any particular statistical distribution of the AOD values and their theoretical uncertainties. The random sampled error distribution, similar to the real errors, is more peaked than a Gaussian distribution, with ratios between RMSE and MAE of and for the real and theoretical errors, respectively. The larger ratios (compared to 1.25 for a Gaussian, Eq. 11) confirm that both distributions have a narrower peak and longer tails (therefore larger RMSE values) than a Gaussian distribution. To evaluate the retrieval uncertainties quantitatively and reduce the influence of outliers, in later studies, we focus on MAE evaluated from the random errors as shown in Fig. 1e. Since the MCEP method is directly based on the statistical distribution, metrics other than MAE and RMSE can also be derived. For example, the method proposed by Sayer et al. (2020), which computes the 68th percentile from absolute normalized error distributions, can be applied on the random error samples in the MCEP method as a metric to evaluate 1σ uncertainties for both real and theoretical errors.
Furthermore, following step 5 in MCEP, we can analyze the uncertainties of MAE with respect to a set of random errors. MAE values for 50 sets of random theoretical errors are computed as shown in Fig. 1f. The relative standard deviation of these MAE values is about 3 % when all 1000 cases are used. The relative uncertainties increase to 7 % and 12 % when the number of cases are reduced to 200 and 50. Therefore, for discussion in the next section with a smaller number of cases considered, it is useful to understand how much the MAE varies. A similar approach can be applied to comparisons with high-quality in situ measurements. The same challenge is that the metrics such as RMSE and MAE may suffer from larger statistical variations if only a smaller number of retrieval cases are available.
To evaluate the retrieval capability of the FastMAPOL algorithm on the HARP instruments, we conducted studies on synthetic AirHARP and HARP2 data and then derived the pixel-wise retrieval uncertainties. The theoretical uncertainties are then compared with real uncertainties, and their difference is quantified using the MCEP methodology discussed in Sect. 3. The real uncertainties are derived from the retrieval results based on synthetic data which include impacts from local minima in the cost functions as summarized in Sect. 3.2; however, these synthetic data studies do not address the potential impacts of modeling errors in the forward model. To evaluate the assumption in the forward model, comparison with in situ measurements is required in future studies.
4.1 Synthetic data
We performed radiative transfer simulations to generate 1000 synthetic sets of measurement using the coupled atmosphere–ocean VRTM (Zhai et al., 2009, 2010, 2022) discussed in Sect. 2. A fixed solar zenith angle of 50∘ is used to approximate the solar zenith angle from the AirHARP measurements in the ACEPOL field campaign discussed in the next section. The other input parameters in Table 1 are sampled uniformly within their ranges, except aerosol volume densities and Chl a. Aerosol volume densities are determined by AOD at 550 nm, which is sampled uniformly over the range [0.01, 0.5], and fine-mode volume fraction, which is sampled uniformly within [0, 1]. Chl a is randomly sampled with a log-uniform distribution. Although ozone density is randomly sampled to generate synthetic data, it is assumed as known input to the retrieval algorithm.
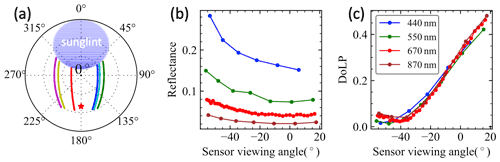
Figure 2(a) Random viewing geometry with different examples indicated by different colors in the polar plot of zenith angles (radial direction) and azimuth angles. The red star symbol indicates the anti-solar direction at a zenith angle of 50∘ and azimuth angle of 180∘. The blue oval shape indicates the sunglint region removed in this study. (b, c) Example synthetic HARP2 data with added random noise for reflectance and DoLP. The sensor viewing angle indicates the viewing zenith angle in the along-track direction, with a positive angle indicating forward-looking directions and a negative sign indicating the angle viewing backward (within the azimuthal angle between 90 and 270∘).
Realistic HARP-like viewing geometries are constructed as discussed in Gao et al. (2021b), which represents a simplified PACE orbit geometry with some examples in Fig. 2a. The number of viewing angles at each band is based on AirHARP and HARP2 characteristics (Sect. 2.1).
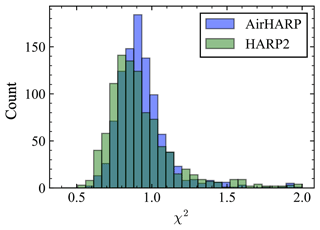
Random noise is added to the 1000 sets of synthetic AirHARP and HARP2 measurements, and then the FastMAPOL retrieval algorithm is applied to them. The synthetic data are computed directly using the vector radiative transfer model, but the NN forward model is used in the retrieval algorithm to achieve maximum efficiency. In this way the contribution of the NN uncertainties is captured both in the simulation and the uncertainty model as shown in Eq. (5). The retrieval cost function values (χ2) at convergence (Eq. 4) are shown for both sensors in Fig. 3; the mean χ2 values for both cases are approximately 1.0, but with the most probable χ2 values being 0.8 for HARP2 and 0.9 for AirHARP, which suggests slight overfitting of the data in general. To reduce the impact of outliers, we choose a maximum χ2 value of 1.5 in this study as shown in Fig. 3, which corresponds to a success rate of 96 % for AirHARP cases and 93 % for HARP2 cases.
4.2 Pixel-wise retrieval uncertainties quantification
We apply the method discussed in Sect. 3 to compare theoretical and real uncertainties. An example of spectral AOD and Rrs for one retrieval is shown in Fig. 4 with the retrieval uncertainties as a function of wavelength. Here, total AOD uncertainty is the combination of fine-mode and coarse-mode uncertainties. The absolute Rrs uncertainties at 440 and 550 nm are larger than at 670 and 870 nm, as are the retrieval errors. However, the Rrs percentage errors generally increase with the wavelength due to the decrease of the Rrs magnitudes.
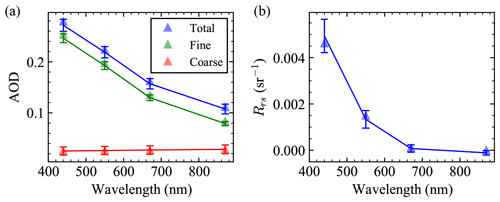
Figure 4Example of AOD (solid line) and Rrs spectra retrieved from one case of synthetic HARP2 measurements as shown in Fig. 2b and c with retrieval uncertainties indicated by the error bar. The triangles indicate truth values. Chl a for this case is 0.1 mg m−3.
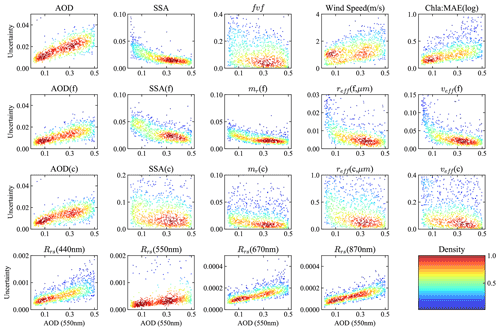
Figure 5Theoretical retrieval uncertainties estimated from error propagation plotted against the AOD at 550 nm (horizontal axis) for AOD, SSA, fine-mode volume fraction (fvf), refractive index (mr), effective radius (reff) and variance (veff), wind speed, Chl a in log 10 scale, and remote sensing reflectance (Rrs). Synthetic HARP2 measurements are used in these retrievals. Colors indicate the relative density of the dots in the plot.
For more general atmosphere and ocean conditions, Fig. 5 shows dependence of the retrieval uncertainties on AOD at 550 nm for retrieved and derived parameters from synthetic HARP2 measurements. In general, increasing AOD is associated with increasing AOD uncertainty. The uncertainty of ocean parameters also increases with AOD, which is expected because the atmosphere is an obstruction to the oceanic signal. Increasing AOD does, however, decrease the uncertainty of retrieved and derived aerosol properties. These changes are not always a linear function of AOD. The larger spread of coarse-mode properties (particularly SSA) than fine-mode results indicates less sensitivity to coarse-mode aerosol property retrievals.
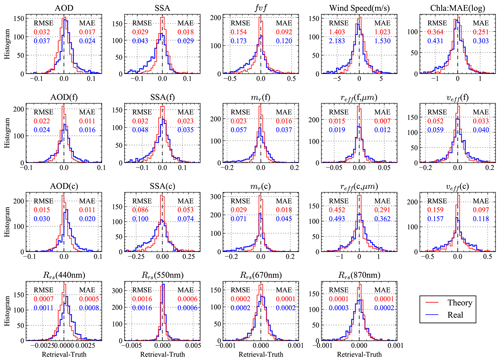
Figure 6Histograms of the theoretical and real retrieval errors evaluated using the MCEP method in Sect. 3.2 for the same cases as in Fig. 5.
Following the methodology proposed in Sect. 3.2, the statistical distributions of the retrieval errors are shown in Fig. 6, derived from the theoretical retrieval uncertainties in Fig. 5. Most histograms show a distribution with a well-centered peak and similar width and shape between the theoretical and real uncertainties. The mean value indicates the bias of the distribution. The AOD error distribution has a slightly longer tail in the positive side, resulting in a mean difference of 0.011 for both total and coarse-mode AOD; the mean value difference for fine-mode AOD is negligible (0.001) (also discussed in Fig. 4). These results suggest that the source of the bias in total AOD is due to the impacts from coarse-mode retrievals. Similar to AOD, most distributions in Fig. 6 are narrower than a Gaussian distribution with longer tails, and the ratios of RMSE and MAE from both theoretical and real uncertainty results are mostly between 1.3 and 2. The histogram of the wind speed error over the ensemble seems to be closer to Gaussian. SSA has a relatively larger negative tail mean values of −0.02, −0.01, and −0.04 for total, coarse-mode, and fine-mode SSA. Refractive index differences also show a larger negative tail indicating a trend of slightly underestimating the refractive index, which leads to a mean value of −0.01 and −0.03 for the fine- and coarse-mode real refractive indices. However, the most probable errors for refractive index are well centered around zeros.
4.3 Evaluating the performance of pixel-wise retrieval uncertainty
To quantify theoretical and real uncertainties, Fig. 7 shows MAE for AirHARP and HARP2 averaged as a function of AOD at 550 nm, based on the error distributions shown in Fig. 6. The uncertainties of the total, fine- and coarse-mode AOD increase as AOD increases, though the ratio of AOD uncertainty to AOD shows a decreasing trend. As in Fig. 5, uncertainties of aerosol microphysical properties (SSA, refractive index, effective radius, and variance) decrease as AOD increases, which is consistent with Gao et al. (2021a). The uncertainty for Chl a is represented in terms of MAE(log ) as defined in Eq. (12) with a value between 1 and 3, which also depends upon the magnitude of Chl a as discussed in Gao et al. (2021a). The uncertainty of Rrs increases almost linearly with AOD. At 440 nm, the uncertainty increases from 0.0004 to 0.0012, while for 550 nm, the uncertainty increases from 0.0002 to 0.0007. Note that the accuracy of the atmospheric correction used to derive Rrs also depends upon the number of viewing angles used for aerosol retrievals (Gao et al., 2021b).
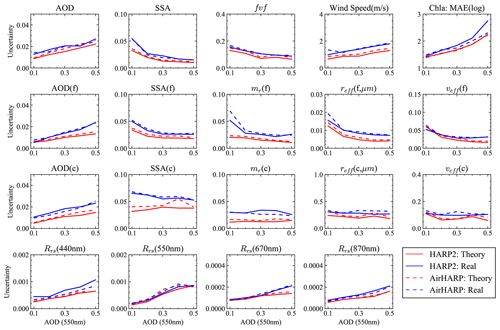
Figure 7The retrieval uncertainties represented by MAE averaged within several ranges of AOD at 550 nm, including [0.01, 0.1], [0.1, 0.2], [0.2, 0.3], [0.3, 0.4], and [0.4, 0.5]. The horizontal axes indicate the maximum AOD used in the corresponding AOD range. Results for both HARP2 and AirHARP are shown. Chl a in terms of MAE(log ) as defined in Eq. (12) is used.
The retrieval uncertainties for synthetic HARP2 and AirHARP datasets are close to each other for most retrieval cases as shown in Fig. 7. Gao et al. (2021b) demonstrated that HARP2 has a smaller retrieval uncertainty than AirHARP when the same number of viewing angles are used due to HARP2's smaller DoLP calibration uncertainty. However, this is partially compensated for by AirHARP’s higher number of view angles, resulting in similar retrieval uncertainties for the two sensors in Fig. 7. Note that the uncertainty correlation between angles may also impact the retrieval performance, which is not included in this study.
4.4 Averaged retrieval uncertainty
To understand the accuracy of the MAE as derived above for each AOD range (each with around 200 cases), we generated multiple sets of random theoretical errors following step 5 in Sect. 3.2 and compared the averaged MAE with the MAE derived from real errors as shown in Fig. 8. Most relationships are linear and close to the one-to-one line, indicating that the retrieval is skillful at determining magnitudes as well as which retrievals are better-constrained than others. The exception is coarse-mode aerosol properties, which tend to cluster together due to less dependency on the total AOD as shown in Fig. 7. The 1σ uncertainties of the MAE for theoretical uncertainties are also shown in Fig. 8 as the horizontal error bar for both HARP2 and AirHARP. Ten sets of random errors are found to be sufficient to evaluate the uncertainties for MAE. We found that MAE varied within approximately 10 % of its mean value in most cases, except for coarse-mode properties, wind speed, and Rrs at 550 nm, which can reach up to 15 %. The same values are used to estimate the uncertainties of the real errors due to the impact of the number of cases. Therefore, the MCEP method can assess the impact of the number of cases for comparison with in situ measurement in future studies, where satellite/ground matchup availability can vary dramatically depending on the location of in situ site (Sayer et al., 2020).
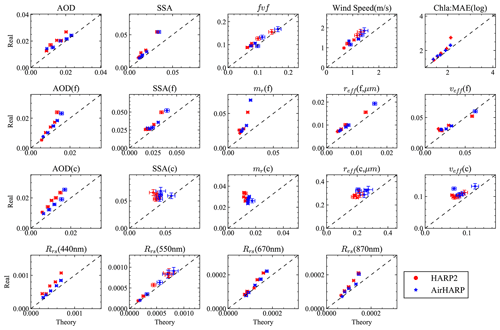
Figure 8Comparing the averaged MAE derived from theoretical and real uncertainties for both HARP2 and AirHARP. The error bars indicate the 1σ uncertainties of the MAE based on the average of 10 sets of random theoretical errors as discussed in MCEP method in Sect. 3.2. The same error bar is used for the real uncertainties as an approximation.
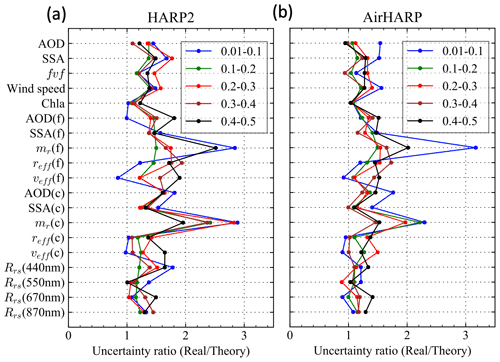
Ratios between the averaged MAEs for the real and theoretical uncertainties over five AOD intervals from Fig. 8 are shown in Fig. 9. The ratios are mostly in the range 1–1.5, indicating that the theoretical uncertainties work well to represent the real retrieval uncertainties in most cases but are generally underestimates. The largest ratios are for fine- and coarse-mode aerosol refractive indices, especially at small aerosol loading, probably due to the lack of information and therefore more impact of local minima and initial values (Hasekamp and Landgraf, 2005). Parameters with large gaps between real and theoretical uncertainties also indicate where retrieval algorithms can be further improved, for instance, by including additional a priori constraints, such as smoothness in refractive index spectra and size distribution, as well as temporal and spatial variations of the retrieval parameters. Various constraints in the framework of multi-term least-square method are summarized by Dubovik et al. (2021). A similar uncertainty quantification methodology can be applied to validate the retrieval performance of future space-borne sensors such as HARP2 measurements from PACE, with more realistic parameter distributions.
The pixel-wise theoretical uncertainties achieve a reasonably good performance to represent real retrievals as discussed in the last two sections. Their performances on various retrieved geophysical properties are quantified by comparing with the real retrieval errors. Based on these results, in this section, we will use the theoretical uncertainties to analyze the retrieval results from AirHARP field measurements from the Aerosol Characterization from Polarimeter and Lidar (ACEPOL) field campaign conducted from October to November of 2017, where the NASA’s ER-2 aircraft carried four MAPs – AirHARP, AirMSPI, SPEX airborne, and RSP – and two lidar sensors – HSRL-2 (Burton et al., 2015) and CPL (the Cloud Physics Lidar) (McGill et al., 2002) – and flew over a variety of scenes at a high altitude of approximately 20 km (Knobelspiesse et al., 2020). Several MAP aerosol retrievals from ACEPOL measurements have been reported (Fu et al., 2020; Puthukkudy et al., 2020; Gao et al., 2020; Hannadige et al., 2021; Gao et al., 2021a).
There are a total of five AirHARP ocean scenes available in ACEPOL. Three scenes on 23 October 2017 (Scenes 1, 2, and 3) have been discussed by Gao et al. (2021a, b). This study further analyzes the retrieval uncertainties on Scenes 2 and 3 and adds two additional scenes from 27 October (Scene 4) and 7 November (Scene 5). The adaptive data screening method (Gao et al., 2021b) was applied on all these scenes to mask out viewing angles contaminated by cirrus clouds, ocean surface floating objects, or other irregularities that could not be represented adequately by the current forward model.
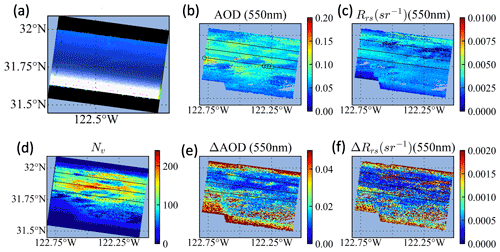
Figure 10(a) RGB image for Scene 2 on 23 October 2017. Retrieval results are shown for (b) AOD and (c) Rrs, respectively; retrieval uncertainties for these are shown in panels (e) and (f), respectively. (d) The number of total observations used in retrievals. The HSRL AODs at 532 nm are indicated in panel (b). More detailed analysis on AOD and its uncertainties over the three solid lines are discussed in Fig. 11.
Figure 10 shows retrieval results for Scene 2, with AOD and Rrs (both at 550 nm) in Fig. 10b and c and their retrieval uncertainties shown in Fig. 10e and f, respectively. The retrieved AOD and Rrs are reasonably smooth, varying mostly in the ranges 0.07–0.1 and 0.003–0.004 respectively. Figure 10d shows the total number of observations used in the retrieval, which decreases toward the bottom of the image due to sunglint as shown in Fig. 10a. A smaller number of measurements is also available at the top edge of the image due to the sensor geometry, which also results in larger AOD and Rrs uncertainties. There are several patches elsewhere with fewer measurements due to the removal of cirrus-cloud-contaminated angles (Gao et al., 2021b). Most pixels have at least 100 suitable measurements; the largest number of observations available is 228. A larger number of measurements is generally associated with lower uncertainties for both AOD and Rrs. Patches with small Rrs values in the upper right portion of Fig. 10c also have larger uncertainties in Fig. 10f. Retrieval uncertainties can be used as a flexible quality flag for each pixel, which is more effective than relying solely on the number of measurements or the cost function values only, as uncertainty estimates are specific to each retrieved parameter.
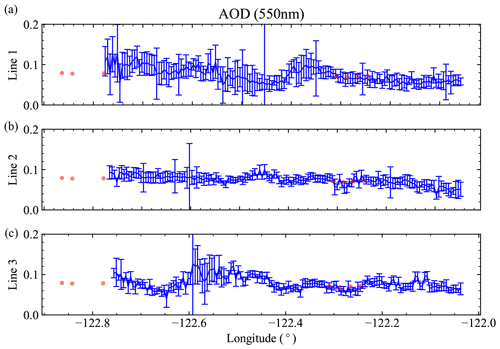
Figure 11 shows the retrieved AOD at 550 nm and its uncertainties along the three black lines in Fig. 10a. Line 1 contains the pixels closest to the HSRL track. Due to the impact of cirrus clouds, only a few HSRL pixels are available, but they agree with the retrieval results within the estimated uncertainties. The regions with cirrus cloud angles removed by the adaptive data screening approach also show larger uncertainties (the left portion of line 1 and the peak in line 3 near −122.6∘ longitude). The measurements in line 2 are less impacted by cirrus clouds with an average of 155 observations per retrieval, compared to 91 and 120 for lines 1 and 3 respectively. The χ2 map (shown in Gao et al., 2021b) shows that excluding the cirrus-contaminated angles makes retrieval cost function more spatially uniform across the scene. The mean χ2 values along the three lines are 1.54, 1.25, and 1.34; since these χ2 values are still larger than 1, there may be additional relevant uncertainties not captured in the input uncertainty model that require future investigation.
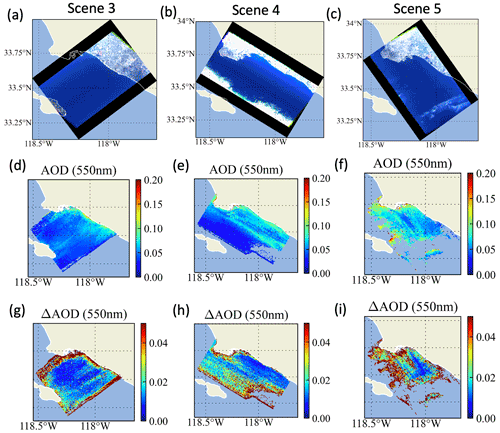
Figure 12Three AirHARP scenes on 23 October, 27 October, and 7 November 2017, which are in different flight directions but over the same region. The RBG images are shown in panels (a), (b), and (c); the retrieved AODs at 550 nm are shown in panels (d), (e), and (f); and their uncertainties are shown in panels (g), (h), and (i).
Equivalent results for the other three scenes (3, 4, 5) are shown in Fig. 12. The most probable χ2 are 1.2, 1.4, and 0.8 respectively. For Scene 3, the retrieved AOD values are mostly around 0.05 but increase up to 0.1 near the coast as shown in Fig. 12d. The retrieval uncertainties as shown in Fig. 12h are typically around 0.01 but exceed 0.05 near the coast and the edge of the image. For retrieval uncertainties larger than 0.05, the average number of measurements is less than 22, but for those with uncertainties under 0.05, an average of 80 measurements were available. Scene 4 is similar, although with sunglint in the lower portion of the image and larger associated uncertainties. For Scene 5 in Fig. 12, many pixels in the left and lower half of the image are impacted by the cirrus clouds, often leaving few suitable angles and leading to AOD uncertainty larger than 0.05 (the brown color shown in Fig. 12i). The central region with the smallest AOD uncertainties less than 0.01 correspond to pixels with 161 or more observations.
Quantifying the uncertainties associated with remote sensing retrievals is key to understanding retrieval performance and gauging the quality and utility of the retrieval results. Retrieval uncertainties depend on the spectral, angular, radiometric, and polarimetric characteristics of the instrument. Increasing dimensionality and accuracy of measurements benefits retrievals but also introduces new challenges in the inversion of geophysical properties and estimation of retrieval uncertainties.
This study discussed and applied a practical, efficient way to estimate theoretical uncertainties for aerosol and ocean data products retrieved by FastMAPOL from synthetic AirHARP and HARP2 measurements, as well as field AirHARP measurements from the ACEPOL field campaign. Theoretical retrieval uncertainties for aerosol and ocean color properties are discussed. The speed with which the uncertainties can be computed is optimized using analytical derivatives based on automatic differentiations. To validate how well the retrieval uncertainties represent real retrievals, we provided a flexible Monte Carlo error propagation (MCEP) method to compare the retrieval uncertainties from error propagation with errors from synthetic retrievals. More discussions are as follows.
-
Using MCEP, statistical distributions can be compared to understand their properties and develop proper metrics for comparison. The real and theoretical retrieval uncertainties for multiple retrieval parameters are compared directly by their error histograms sampled from the Monte Carlo method based on the synthetic data retrievals. The ratios of the statistical metrics such as MAE for theoretical and real errors are computed and compared. These ratios provide a tool to quantify the overall performance of the retrieval uncertainty. The ratios are mostly 1–1.5 with respect to different AOD ranges, which suggests that the FastMAPOL retrieval algorithm performs well as it approaches the optimal uncertainties predicted from error propagation. The larger ratios observed for aerosol refractive indices suggest a need to improve constraints on and/or test for proper convergence of those parameters, especially for cases with small AODs. Future studies of synthetic data with realistic statistics are needed to further evaluate the overall performance of the retrieval algorithm.
-
Synthetic data are only one piece of the evaluation and are limited because they use the same underlying forward model as the retrieval. Future comparison of retrieval results with in situ measurements is desirable to provide a more complete assessment. However, what is available at present for AirHARP is sparse in volume, as AirHARP data are only available for a few field campaigns and PACE has not yet launched. Notably, there is no avenue to validate all retrieved products at once. The MCEP method and others (e.g., Hasekamp and Landgraf, 2005; Sayer et al., 2020) can also be used to compare uncertainty estimates with the in situ measurements. Furthermore, the MCEP method provides a flexible framework to evaluate the uncertainties associated with the number of cases used in the statistical comparison, which can often be sparse for in situ data. Use of in situ data, however, also involves additional measurement and co-location uncertainties not included in the input uncertainty model (e.g., Virtanen et al., 2018; Sayer, 2020). Additionally, they may reveal assumptions in the forward model that are insufficient. For example, for coastal waters, we may need a more complete and realistic ocean bio-optical model as demonstrated by Gao et al. (2019). The parameterization of aerosol size bins and refractive index spectral shape may also need refinement.
-
The Monte Carlo method has been used widely for uncertainty quantification due to its flexibility and robustness (e.g., Andrieu et al., 2003). In this work, the theoretical retrieval uncertainties are still computed through the error propagation method. However, to validate the theoretical uncertainties, we need to compare with reference truth data, which are often limited by their sample size, especially for in situ measurements. It is important to consider the impacts of sample size and the statistical distribution on the robustness of metrics used in the analysis. In this study, we chose a Monte Carlo method to randomly sample errors from theoretical uncertainties, which provides a direct bridge to compare with the real retrieval errors. The current MCEP method generates random errors from the theoretical uncertainties derived through error propagation in step 2; another approach is to generate random errors directly from the error covariance matrix in Eq. (4) and then propagate them through Eq. (6). The latter would be more flexible to deal with more general measurement uncertainty statistics but more computationally expensive due to the large number of measurements present in MAP retrievals. Our MCEP method can be further developed to understand the impact of a priori constraints, broader statistical types of measurement errors, for better validation and understanding of retrieval uncertainties.
-
Retrieval initialization and convergence can be important. Gao et al. (2020) discussed the impact of initial values by conducting hundreds of retrievals using random initial values and found the RMSE of the retrieval results produced a value similar to the error propagation results reported by Knobelspiesse et al. (2012). As discussed in Sect. 5, the cost function may not always converge to the values expected from χ2 distribution, and large values are often observed as shown by Wu et al. (2015) and Gao et al. (2020, 2021a). This may be due to the impacts of anomalies not captured by the forward model (such as, here, cirrus clouds) or modeled but not quantified adequately in the input uncertainty model for measurements plus forward models. Theoretical error propagation can give inaccurate results in these cases. It would be practical to remove such anomalous measurements from the retrieval, as in the adaptive data screening method by Gao et al. (2021b). Fewer suitable measurements tend to lead to larger retrieval uncertainty, although this is arguably preferable (considering data coverage) to discarding the whole retrieval based on a high-cost function. In these situations, the theoretical uncertainty estimate may guide whether a retrieval is useful for a particular application on a per-parameter basis.
This work provides a general framework to understand the uncertainties from the retrieval algorithm and provides a bridge from theoretical uncertainty toward future evaluation using in situ measurements. More complex input uncertainty model, such as the one including uncertainty correlations between the multi-angle measurements, can be evaluated based on this framework. Although based on synthetic and airborne measurements, the methods on uncertainty quantification are flexible and can be applied to existing and future satellite missions such as NASA’s PACE mission with advanced multi-angle polarimetric instruments.
Fast speed to compute retrieval uncertainties is useful for operational processing and analyzing satellite data. Although the error propagation method used in this study is already very efficient, it is still challenging to achieve a speed complementary to the retrievals due to the requirement to compute Jacobian matrix and multiple additional derivatives for parameters not directly retrieved as shown in Eq. (8). Such parameters in this study include aerosol properties such as AOD, SSA, aerosol effective radius, and Rrs. Derivatives of aerosol properties can be either computed from an analytical function (e.g., effective size) or based on single scattering calculations (e.g., AOD, SSA), such as using Lorenz–Mie theory (Grainger et al., 2004; Spurr et al., 2012) or the T-Matrix method (Xu and Davis, 2011; Spurr et al., 2012; Sun et al., 2021). However, uncertainties for Rrs are more challenging to quantify as they require additional radiative transfer simulations to conduct atmospheric and bidirectional reflectance distribution function (BRDF) corrections. Following Mobley et al. (2016), Rrs is defined as
where ρt is the reflectance measured by the sensor as defined in Eq. (1), and is the reflectance with contributions only from the atmosphere and ocean surface. CBRDF is a BRDF correction that adjusts the water-leaving signal from an arbitrary viewing and solar geometry to the sun at zenith and nadir viewing direction. Td and tu are direct and diffuse transmittance.
Gao et al. (2021b) reported that using the automatic differentiation method to compute Jacobians resulted in a factor of 5 to 10 times speedup in retrievals compared to numerical calculations using finite difference; therefore, it provided a feasible approach to accelerate retrieval uncertainty calculation. In this study, we use automatic differentiation to calculate analytical Jacobians and other derivatives for AOD, SSA, , and the combined factor of based on the NNs developed by Gao et al. (2021a). The mathematical formulation for automatic differentiation summarized in Gao et al. (2021b) can be generalized for all the feed-forward neural networks used in our study. Specifically, the derivatives of Rrs with respect to a retrieval parameter xi are
where N1 and N2 represent the NNs for and . The uncertainty of Rrs is calculated by combining Eq. (A2) with Eq. (8). Note that the retrieval uncertainties in Rrs discussed in this study only include the contribution from atmospheric correction and BRDF correction as shown in Eq. (A2), which do not include uncertainties in ρt. These results can demonstrate the accuracy when HARP retrieved aerosol properties are applied to instruments with higher accuracy in ρt such as OCI to assist their atmospheric correction (Gao et al., 2020; Hannadige et al., 2021).
The AirHARP and HSRL-2 data used in this study are available from the ACEPOL data portal (https://doi.org/10.5067/SUBORBITAL/ACEPOL2017/DATA001, ACEPOL Science Team, 2017). The AirHARP L2 data product and their uncertainty files are available upon request from the corresponding author.
MG, KK, BAF, and PWZ formulated the original concept. MG developed the algorithm and generated the scientific data. PWZ developed the radiative transfer code used in the simulations. KK, AMS, AI, YH, and OH advised on the uncertainty models. KK, PWZ, AMS, BC, and OH advised on the aerosol products. BAF, AI, and PJW advised on the ocean color products. VM and XX provided and advised on the HARP data. MG wrote the manuscript draft. All authors provided critical feedback and edited the manuscript.
At least one of the (co-)authors is a member of the editorial board of Atmospheric Measurement Techniques. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors would like to thank the ACEPOL teams for conducting the field campaign, thank the HARP and HSRL teams and PIs for providing the data, and thank the NASA Ocean Biology Processing Group (OBPG) system team for supporting the high-performance computing (HPC).
Meng Gao, Kirk Knobelspiesse, Bryan A. Franz, Andre M. Sayer, Amir Ibrahim, Brian Cairns, and P. Jeremy Werdell have been supported by the NASA PACE project. Peng-Wang Zhai and Yongxiang Hu have been supported by NASA (grant no. 80NSSC20M0227). The ACEPOL campaign has been supported by the NASA Radiation Sciences Program, with funding from NASA (ACE and CALIPSO missions) and SRON. Part of this work has been funded by the NWO/NSO project ACEPOL (project no. ALWGO/16-09).
This paper was edited by Piet Stammes and reviewed by Feng Xu and two anonymous referees.
ACEPOL Science Team: Aerosol Characterization from Polarimeter and Lidar Campaign, NASA Langley Atmospheric Science Data Center DAAC [data set], https://doi.org/10.5067/SUBORBITAL/ACEPOL2017/DATA001 2017. a
Andrieu, C., de Freitas, N., Doucet, A., and Jordan, M. I.: An Introduction to MCMC for Machine Learning, Mach. Learn., 50, 5–43, https://doi.org/10.1023/A:1020281327116, 2003. a
Bender, F. A.-M.: Aerosol Forcing: Still Uncertain, Still Relevant, AGU Advances, 1, e2019AV000128, https://doi.org/10.1029/2019AV000128, 2020. a
Branch, M. A., Coleman, T. F., and Li, Y.: A Subspace, Interior, and Conjugate Gradient Method for Large-Scale Bound-Constrained Minimization Problems, SIAM J. Sci. Comput., 21, 1–23, https://doi.org/10.1137/S1064827595289108, 1999. a, b
Burton, S. P., Hair, J. W., Kahnert, M., Ferrare, R. A., Hostetler, C. A., Cook, A. L., Harper, D. B., Berkoff, T. A., Seaman, S. T., Collins, J. E., Fenn, M. A., and Rogers, R. R.: Observations of the spectral dependence of linear particle depolarization ratio of aerosols using NASA Langley airborne High Spectral Resolution Lidar, Atmos. Chem. Phys., 15, 13453–13473, https://doi.org/10.5194/acp-15-13453-2015, 2015. a
Chen, C., Dubovik, O., Fuertes, D., Litvinov, P., Lapyonok, T., Lopatin, A., Ducos, F., Derimian, Y., Herman, M., Tanré, D., Remer, L. A., Lyapustin, A., Sayer, A. M., Levy, R. C., Hsu, N. C., Descloitres, J., Li, L., Torres, B., Karol, Y., Herrera, M., Herreras, M., Aspetsberger, M., Wanzenboeck, M., Bindreiter, L., Marth, D., Hangler, A., and Federspiel, C.: Validation of GRASP algorithm product from POLDER/PARASOL data and assessment of multi-angular polarimetry potential for aerosol monitoring, Earth Syst. Sci. Data, 12, 3573–3620, https://doi.org/10.5194/essd-12-3573-2020, 2020. a, b
Chowdhary, J., Cairns, B., Mishchenko, M., and Travis, L.: Retrieval of aerosol properties over the ocean using multispectral and multiangle Photopolarimetric measurements from the Research Scanning Polarimeter, Geophys. Res. Lett., 28, 243–246, https://doi.org/10.1029/2000GL011783, 2001. a
Chowdhary, J., Cairns, B., Mishchenko, M. I., Hobbs, P. V., Cota, G. F., Redemann, J., Rutledge, K., Holben, B. N., and Russell, E.: Retrieval of Aerosol Scattering and Absorption Properties from Photopolarimetric Observations over the Ocean during the CLAMS Experiment, J. Atmos. Sci., 62, 1093–1117, https://doi.org/10.1175/JAS3389.1, 2005. a
Chowdhary, J., Cairns, B., Waquet, F., Knobelspiesse, K., Ottaviani, M., Redemann, J., Travis, L., and Mishchenko, M.: Sensitivity of multiangle, multispectral polarimetric remote sensing over open oceans to water-leaving radiance: Analyses of RSP data acquired during the MILAGRO campaign, Remote Sens. Environ., 118, 284–308, 2012. a
Cox, C. and Munk, W.: Measurement of the Roughness of the Sea Surface from Photographs of the Sun's Glitter, J. Opt. Soc. Am., 44, 838–850, 1954. a
Diner, D. J., Boland, S. W., Brauer, M., Bruegge, C., Burke, K. A., Chipman, R., Girolamo, L. D., Garay, M. J., Hasheminassab, S., Hyer, E., Jerrett, M., Jovanovic, V., Kalashnikova, O. V., Liu, Y., Lyapustin, A. I., Martin, R. V., Nastan, A., Ostro, B. D., Ritz, B., Schwartz, J., Wang, J., and Xu, F.: Advances in multiangle satellite remote sensing of speciated airborne particulate matter and association with adverse health effects: from MISR to MAIA, J. Appl. Remote Sens., 12, 1–22, https://doi.org/10.1117/1.JRS.12.042603, 2018. a
Dubovik, O., Sinyuk, A., Lapyonok, T., Holben, B. N., Mishchenko, M., Yang, P., Eck, T. F., Volten, H., Muñoz, O., Veihelmann, B., van der Zande, W. J., Leon, J.-F., Sorokin, M., and Slutsker, I.: Application of spheroid models to account for aerosol particle nonsphericity in remote sensing of desert dust, J. Geophys. Res.-Atmos., 111, D11208, https://doi.org/10.1029/2005JD006619, 2006. a
Dubovik, O., Herman, M., Holdak, A., Lapyonok, T., Tanré, D., Deuzé, J. L., Ducos, F., Sinyuk, A., and Lopatin, A.: Statistically optimized inversion algorithm for enhanced retrieval of aerosol properties from spectral multi-angle polarimetric satellite observations, Atmos. Meas. Tech., 4, 975–1018, https://doi.org/10.5194/amt-4-975-2011, 2011. a, b, c
Dubovik, O., Lapyonok, T., Litvinov, P., Herman, M., Fuertes, D., Ducos, F., Lopatin, A., Chaikovsky, A., Torres, B., Derimian, Y., Huang, X., Aspetsberger, M., and Federspiel, C.: GRASP: a versatile algorithm for characterizing the atmosphere, SPIE Newsroom, https://doi.org/10.1117/2.1201408.005558, 2014. a
Dubovik, O., Li, Z., Mishchenko, M. I., Tanré, D., Karol, Y., Bojkov, B., Cairns, B., Diner, D. J., Espinosa, W. R., Goloub, P., Gu, X., Hasekamp, O., Hong, J., Hou, W., Knobelspiesse, K. D., Landgraf, J., Li, L., Litvinov, P., Liu, Y., Lopatin, A., Marbach, T., Maring, H., Martins, V., Meijer, Y., Milinevsky, G., Mukai, S., Parol, F., Qiao, Y., Remer, L., Rietjens, J., Sano, I., Stammes, P., Stamnes, S., Sun, X., Tabary, P., Travis, L. D., Waquet, F., Xu, F., Yan, C., and Yin, D.: Polarimetric remote sensing of atmospheric aerosols: Instruments, methodologies, results, and perspectives, J. Quant. Spectrosc. Ra., 224, 474–511, https://doi.org/10.1016/j.jqsrt.2018.11.024, 2019. a
Dubovik, O., Fuertes, D., Litvinov, P., Lopatin, A., Lapyonok, T., Doubovik, I., Xu, F., Ducos, F., Chen, C., Torres, B., Derimian, Y., Li, L., Herreras-Giralda, M., Herrera, M., Karol, Y., Matar, C., Schuster, G. L., Espinosa, R., Puthukkudy, A., Li, Z., Fischer, J., Preusker, R., Cuesta, J., Kreuter, A., Cede, A., Aspetsberger, M., Marth, D., Bindreiter, L., Hangler, A., Lanzinger, V., Holter, C., and Federspiel, C.: A Comprehensive Description of Multi-Term LSM for Applying Multiple a Priori Constraints in Problems of Atmospheric Remote Sensing: GRASP Algorithm, Concept, and Applications, Front. Remote Sens., 2, 23, https://doi.org/10.3389/frsen.2021.706851, 2021. a
Fan, C., Fu, G., Di Noia, A., Smit, M., Rietjens, J. H., A. Ferrare, R., Burton, S., Li, Z., and P. Hasekamp, O.: Use of A Neural Network-Based Ocean Body Radiative Transfer Model for Aerosol Retrievals from Multi-Angle Polarimetric Measurements, Remote Sens., 11, 2877, https://doi.org/10.3390/rs11232877, 2019. a
Fan, Y., Li, W., Chen, N., Ahn, J.-H., Park, Y.-J., Kratzer, S., Schroeder, T., Ishizaka, J., Chang, R., and Stamnes, K.: OC-SMART: A machine learning based data analysis platform for satellite ocean color sensors, Remote Sens. Environ., 253, 112236, https://doi.org/10.1016/j.rse.2020.112236, 2021. a
Fougnie, B., Marbach, T., Lacan, A., Lang, R., Schlüssel, P., Poli, G., Munro, R., and Couto, A. B.: The multi-viewing multi-channel multi-polarisation imager – Overview of the 3MI polarimetric mission for aerosol and cloud characterization, J. Quant. Spectrosc. Ra., 219, 23–32, https://doi.org/10.1016/j.jqsrt.2018.07.008, 2018. a
Frouin, R. J., Franz, B. A., Ibrahim, A., Knobelspiesse, K., Ahmad, Z., Cairns, B., Chowdhary, J., Dierssen, H. M., Tan, J., Dubovik, O., Huang, X., Davis, A. B., Kalashnikova, O., Thompson, D. R., Remer, L. A., Boss, E., Coddington, O., Deschamps, P.-Y., Gao, B.-C., Gross, L., Hasekamp, O., Omar, A., Pelletier, B., Ramon, D., Steinmetz, F., and Zhai, P.-W.: Atmospheric Correction of Satellite Ocean-Color Imagery During the PACE Era, Front. Earth Sci., 7, 145, https://doi.org/10.3389/feart.2019.00145, 2019. a, b
Fu, G. and Hasekamp, O.: Retrieval of aerosol microphysical and optical properties over land using a multimode approach, Atmos. Meas. Tech., 11, 6627–6650, https://doi.org/10.5194/amt-11-6627-2018, 2018. a, b
Fu, G., Hasekamp, O., Rietjens, J., Smit, M., Di Noia, A., Cairns, B., Wasilewski, A., Diner, D., Seidel, F., Xu, F., Knobelspiesse, K., Gao, M., da Silva, A., Burton, S., Hostetler, C., Hair, J., and Ferrare, R.: Aerosol retrievals from different polarimeters during the ACEPOL campaign using a common retrieval algorithm, Atmos. Meas. Tech., 13, 553–573, https://doi.org/10.5194/amt-13-553-2020, 2020. a, b, c, d
Gao, M., Zhai, P.-W., Franz, B., Hu, Y., Knobelspiesse, K., Werdell, P. J., Ibrahim, A., Xu, F., and Cairns, B.: Retrieval of aerosol properties and water-leaving reflectance from multi-angular polarimetric measurements over coastal waters, Opt. Express, 26, 8968–8989, https://doi.org/10.1364/OE.26.008968, 2018. a, b
Gao, M., Zhai, P.-W., Franz, B. A., Hu, Y., Knobelspiesse, K., Werdell, P. J., Ibrahim, A., Cairns, B., and Chase, A.: Inversion of multiangular polarimetric measurements over open and coastal ocean waters: a joint retrieval algorithm for aerosol and water-leaving radiance properties, Atmos. Meas. Tech., 12, 3921–3941, https://doi.org/10.5194/amt-12-3921-2019, 2019. a, b, c, d
Gao, M., Zhai, P.-W., Franz, B. A., Knobelspiesse, K., Ibrahim, A., Cairns, B., Craig, S. E., Fu, G., Hasekamp, O., Hu, Y., and Werdell, P. J.: Inversion of multiangular polarimetric measurements from the ACEPOL campaign: an application of improving aerosol property and hyperspectral ocean color retrievals, Atmos. Meas. Tech., 13, 3939–3956, https://doi.org/10.5194/amt-13-3939-2020, 2020. a, b, c, d, e, f
Gao, M., Franz, B. A., Knobelspiesse, K., Zhai, P.-W., Martins, V., Burton, S., Cairns, B., Ferrare, R., Gales, J., Hasekamp, O., Hu, Y., Ibrahim, A., McBride, B., Puthukkudy, A., Werdell, P. J., and Xu, X.: Efficient multi-angle polarimetric inversion of aerosols and ocean color powered by a deep neural network forward model, Atmos. Meas. Tech., 14, 4083–4110, https://doi.org/10.5194/amt-14-4083-2021, 2021a. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p
Gao, M., Knobelspiesse, K., Franz, B. A., Zhai, P.-W., Martins, V., Burton, S. P., Cairns, B., Ferrare, R., Fenn, M. A., Hasekamp, O., Hu, Y., Ibrahim, A., Sayer, A. M., Werdell, P. J., and Xu, X.: Adaptive Data Screening for Multi-Angle Polarimetric Aerosol and Ocean Color Remote Sensing Accelerated by Deep Learning, Front. Remote Sens., 2, 46, https://doi.org/10.3389/frsen.2021.757832, 2021b. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t
Grainger, R. G., Lucas, J., Thomas, G. E., and Ewen, G. B. L.: Calculation of Mie derivatives, Appl. Opt., 43, 5386–5393, https://doi.org/10.1364/AO.43.005386, 2004. a
Groom, S., Sathyendranath, S., Ban, Y., Bernard, S., Brewin, R., Brotas, V., Brockmann, C., Chauhan, P., Choi, J.-k., Chuprin, A., Ciavatta, S., Cipollini, P., Donlon, C., Franz, B., He, X., Hirata, T., Jackson, T., Kampel, M., Krasemann, H., Lavender, S., Pardo-Martinez, S., Mélin, F., Platt, T., Santoleri, R., Skakala, J., Schaeffer, B., Smith, M., Steinmetz, F., Valente, A., and Wang, M.: Satellite Ocean Colour: Current Status and Future Perspective, Front. Mar. Sci., 6, 485, https://doi.org/10.3389/fmars.2019.00485, 2019. a
Hannadige, N. K., Zhai, P.-W., Gao, M., Franz, B. A., Hu, Y., Knobelspiesse, K., Werdell, P. J., Ibrahim, A., Cairns, B., and Hasekamp, O. P.: Atmospheric correction over the ocean for hyperspectral radiometers using multi-angle polarimetric retrievals, Opt. Express, 29, 4504–4522, https://doi.org/10.1364/OE.408467, 2021. a, b
Hasekamp, O. P. and Landgraf, J.: Linearization of vector radiative transfer with respect to aerosol properties and its use in satellite remote sensing, J. Geophys. Res.-Atmos., 110, D04203, https://doi.org/10.1029/2004JD005260, 2005. a, b, c, d
Hasekamp, O. P. and Landgraf, J.: Retrieval of aerosol properties over land surfaces: capabilities of multiple-viewing-angle intensity and polarization measurements, Appl. Opt., 46, 3332–3344, https://doi.org/10.1364/AO.46.003332, 2007. a, b
Hasekamp, O. P., Litvinov, P., and Butz, A.: Aerosol properties over the ocean from PARASOL multiangle photopolarimetric measurements, J. Geophys. Res.-Oceans, 116, D14204, https://doi.org/10.1029/2010JD015469, 2011. a, b, c
Hasekamp, O. P., Fu, G., Rusli, S. P., Wu, L., Noia, A. D., aan de Brugh, J., Landgraf, J., Smit, J. M., Rietjens, J., and van Amerongen, A.: Aerosol measurements by SPEXone on the NASA PACE mission: expected retrieval capabilities, J. Quant. Spectrosc. Ra., 227, 170–184, https://doi.org/10.1016/j.jqsrt.2019.02.006, 2019a. a, b
Hasekamp, O. P., Gryspeerdt, E., and Quaas, J.: Analysis of polarimetric satellite measurements suggests stronger cooling due to aerosol-cloud interactions, Nat. Commun., 10, 5405, https://doi.org/10.1038/s41467-019-13372-2, 2019b. a, b
IPCC: Climate Change 2022: Impacts, Adaptation, and Vulnerability. Contribution of WorkingGroup II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Pörtner, H.-O., Roberts, D., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegría, A., Craig, M., Langsdorf, S., Löschke, S., Möller, V., Okem, A., and Rama, B., Cambridge University Press, in press, 2022. a
Kalos, M. H. and Whitlock, P. A.: Monte carlo methods, John Wiley & Sons, https://doi.org/10.1002/9783527626212, 2008. a
Knobelspiesse, K., Cairns, B., Mishchenko, M., Chowdhary, J., Tsigaridis, K., van Diedenhoven, B., Martin, W., Ottaviani, M., and Alexandrov, M.: Analysis of fine-mode aerosol retrieval capabilities by different passive remote sensing instrument designs, Opt. Express, 20, 21457–21484, https://doi.org/10.1364/OE.20.021457, 2012. a, b, c, d, e
Knobelspiesse, K., Barbosa, H. M. J., Bradley, C., Bruegge, C., Cairns, B., Chen, G., Chowdhary, J., Cook, A., Di Noia, A., van Diedenhoven, B., Diner, D. J., Ferrare, R., Fu, G., Gao, M., Garay, M., Hair, J., Harper, D., van Harten, G., Hasekamp, O., Helmlinger, M., Hostetler, C., Kalashnikova, O., Kupchock, A., Longo De Freitas, K., Maring, H., Martins, J. V., McBride, B., McGill, M., Norlin, K., Puthukkudy, A., Rheingans, B., Rietjens, J., Seidel, F. C., da Silva, A., Smit, M., Stamnes, S., Tan, Q., Val, S., Wasilewski, A., Xu, F., Xu, X., and Yorks, J.: The Aerosol Characterization from Polarimeter and Lidar (ACEPOL) airborne field campaign, Earth Syst. Sci. Data, 12, 2183–2208, https://doi.org/10.5194/essd-12-2183-2020, 2020. a
Knobelspiesse, K., Ibrahim, A., Franz, B., Bailey, S., Levy, R., Ahmad, Z., Gales, J., Gao, M., Garay, M., Anderson, S., and Kalashnikova, O.: Analysis of simultaneous aerosol and ocean glint retrieval using multi-angle observations, Atmos. Meas. Tech., 14, 3233–3252, https://doi.org/10.5194/amt-14-3233-2021, 2021. a
Li, L., Dubovik, O., Derimian, Y., Schuster, G. L., Lapyonok, T., Litvinov, P., Ducos, F., Fuertes, D., Chen, C., Li, Z., Lopatin, A., Torres, B., and Che, H.: Retrieval of aerosol components directly from satellite and ground-based measurements, Atmos. Chem. Phys., 19, 13409–13443, https://doi.org/10.5194/acp-19-13409-2019, 2019. a
Li, Z., Hou, W., Hong, J., Zheng, F., Luo, D., Wang, J., Gu, X., and Qiao, Y.: Directional Polarimetric Camera (DPC): Monitoring aerosol spectral optical properties over land from satellite observation, J. Quant. Spectrosc. Ra., 218, 21–37, https://doi.org/10.1016/j.jqsrt.2018.07.003, 2018. a
Marbach, T., Riedi, J., Lacan, A., and Schlüssel, P.: The 3MI mission: multi-viewing-channel-polarisation imager of the EUMETSAT polar system: second generation (EPS-SG) dedicated to aerosol and cloud monitoring, in: Polarization Science and Remote Sensing VII, edited by: Shaw, J. A. and LeMaster, D. A., International Society for Optics and Photonics, SPIE, 9613, 271–278, https://doi.org/10.1117/12.2186978, 2015. a
Martins, J. V., Fernandez-Borda, R., McBride, B., Remer, L., and Barbosa, H. M. J.: The HARP hyperangular imaging polarimeter and the need for small satellite payloads with high science payoff for earth science remote sensing, in: IGARSS 2018 – Int. Geosci. Remote Se., Valencia, Spain, 22–27 July 2018, 6304–6307, https://doi.org/10.1109/IGARSS.2018.8518823, 2018. a
McBride, B. A., Martins, J., Puthukuddy, A., Xu, X., Borda, R. F., Barbosa, H. M. J., Hasekamp, O., and Remer, L. A.: The Hyper-Angular Rainbow Polarimeter-2 (HARP-2): A wide FOV polarimetric imager for high resolution spatial and angular characterization of cloud and aerosol microphysics, in: Proceedings of the 70th International Astronautical Congress, Washington, DC, USA, 21–25 October 2019, IAC-19–B1.2.7, https://iafastro.directory/iac/archive/browse/IAC-19/B1/2/52335/ (last access: 18 August 2022), 2019. a
McGill, M., Hlavka, D., Hart, W., Scott, V. S., Spinhirne, J., and Schmid, B.: Cloud Physics Lidar: instrument description and initial measurement results, Appl. Opt., 41, 3725–3734, https://doi.org/10.1364/AO.41.003725, 2002. a
McKinna, L. I. W., Cetinić, I., Chase, A. P., and Werdell, P. J.: Approach for Propagating Radiometric Data Uncertainties Through NASA Ocean Color Algorithms, Front. Earth Sci., 7, 176, https://doi.org/10.3389/feart.2019.00176, 2019. a, b
Mishchenko, M. I. and Travis, L. D.: Satellite retrieval of aerosol properties over the ocean using polarization as well as intensity of reflected sunlight, J. Geophys. Res.-Atmos., 102, 16989–17013, https://doi.org/10.1029/96JD02425, 1997. a
Mishchenko, M. I., Travis, L. D., and Lacis, A. A.: Scattering, Absorption, and Emission of Light by Small Particles, Cambridge University Press, Cambridge, UK, ISBN 9780521782524, 2002. a
Mobley, C. D.: The Oceanic Optics Book, International Ocean Colour Coordinating Group (IOCCG), Dartmouth, NS, Canada, https://doi.org/10.25607/OBP-1710, 2022. a, b
Mobley, C. D., Werdell, J., Franz, B., Ahmad, Z., and Bailey, S.: Atmospheric Correction for Satellite Ocean Color Radiometry, National Aeronautics and Space Administration, Washington, DC, USA, https://oceancolor.gsfc.nasa.gov/docs/technical/NASA-TM-2016-217551.pdf (last access: 18 August 2022), 2016. a, b, c
Povey, A. C. and Grainger, R. G.: Known and unknown unknowns: uncertainty estimation in satellite remote sensing, Atmos. Meas. Tech., 8, 4699–4718, https://doi.org/10.5194/amt-8-4699-2015, 2015. a
Puthukkudy, A., Martins, J. V., Remer, L. A., Xu, X., Dubovik, O., Litvinov, P., McBride, B., Burton, S., and Barbosa, H. M. J.: Retrieval of aerosol properties from Airborne Hyper-Angular Rainbow Polarimeter (AirHARP) observations during ACEPOL 2017, Atmos. Meas. Tech., 13, 5207–5236, https://doi.org/10.5194/amt-13-5207-2020, 2020. a, b, c, d
Remer, L. A., Davis, A. B., Mattoo, S., Levy, R. C., Kalashnikova, O. V., Coddington, O., Chowdhary, J., Knobelspiesse, K., Xu, X., Ahmad, Z., Boss, E., Cairns, B., Dierssen, H. M., Diner, D. J., Franz, B., Frouin, R., Gao, B.-C., Ibrahim, A., Martins, J. V., Omar, A. H., Torres, O., Xu, F., and Zhai, P.-W.: Retrieving Aerosol Characteristics From the PACE Mission, Part 1: Ocean Color Instrument, Front. Earth Sci., 7, 152, https://doi.org/10.3389/feart.2019.00152, 2019a. a
Remer, L. A., Knobelspiesse, K., Zhai, P.-W., Xu, F., Kalashnikova, O. V., Chowdhary, J., Hasekamp, O., Dubovik, O., Wu, L., Ahmad, Z., Boss, E., Cairns, B., Coddington, O., Davis, A. B., Dierssen, H. M., Diner, D. J., Franz, B., Frouin, R., Gao, B.-C., Ibrahim, A., Levy, R. C., Martins, J. V., Omar, A. H., and Torres, O.: Retrieving Aerosol Characteristics From the PACE Mission, Part 2: Multi-Angle and Polarimetry, Front. Environ. Sci., 7, 94, https://doi.org/10.3389/fenvs.2019.00094, 2019b. a
Rietjens, J., Campo, J., Chanumolu, A., Smit, M., Nalla, R., Fernandez, C., Dingjan, J., van Amerongen, A., and Hasekamp, O.: Expected performance and error analysis for SPEXone, a multi-angle channeled spectropolarimeter for the NASA PACE mission, in: Polarization Science and Remote Sensing IX, edited by: Craven, J. M., Shaw, J. A., and Snik, F., International Society for Optics and Photonics, SPIE, 11132, 34–47, https://doi.org/10.1117/12.2530729, 2019. a
Rodgers, C.: Inverse Methods for Atmospheric Sounding: Theory and Practice, World Scientific Publishing, Singapore, https://doi.org/10.1142/3171, 2000. a, b, c, d
Sayer, A. M.: How Long Is Too Long? Variogram Analysis of AERONET Data to Aid Aerosol Validation and Intercomparison Studies, Earth Space Sci., 7, e2020EA001290, https://doi.org/10.1029/2020EA001290, 2020. a
Sayer, A. M., Govaerts, Y., Kolmonen, P., Lipponen, A., Luffarelli, M., Mielonen, T., Patadia, F., Popp, T., Povey, A. C., Stebel, K., and Witek, M. L.: A review and framework for the evaluation of pixel-level uncertainty estimates in satellite aerosol remote sensing, Atmos. Meas. Tech., 13, 373–404, https://doi.org/10.5194/amt-13-373-2020, 2020. a, b, c, d, e, f
Seegers, B. N., Stumpf, R. P., Schaeffer, B. A., Loftin, K. A., and Werdell, P. J.: Performance metrics for the assessment of satellite data products: an ocean color case study, Opt. Express, 26, 7404–7422, https://doi.org/10.1364/OE.26.007404, 2018. a
Spurr, R., Wang, J., Zeng, J., and Mishchenko, M.: Linearized T-matrix and Mie scattering computations, J. Quant. Spectrosc. Ra., 113, 425–439, https://doi.org/10.1016/j.jqsrt.2011.11.014, 2012. a, b
Stamnes, S., Hostetler, C., Ferrare, R., Burton, S., Liu, X., Hair, J., Hu, Y., Wasilewski, A., Martin, W., van Diedenhoven, B., Chowdhary, J., Cetinić, I., Berg, L. K., Stamnes, K., and Cairns, B.: Simultaneous polarimeter retrievals of microphysical aerosol and ocean color parameters from the “MAPP” algorithm with comparison to high-spectral-resolution lidar aerosol and ocean products, Appl. Opt., 57, 2394–2413, https://doi.org/10.1364/AO.57.002394, 2018. a, b
Sun, B., Gao, C., Bi, L., and Spurr, R.: Analytical Jacobians of single scattering optical properties using the invariant imbedding T-matrix method, Opt. Express, 29, 9635–9669, https://doi.org/10.1364/OE.421886, 2021. a
van Amerongen, A., Rietjens, J., Campo, J., Dogan, E., Dingjan, J., Nalla, R., Caron, J., and Hasekamp, O.: SPEXone: a compact multi-angle polarimeter, in: International Conference on Space Optics – ICSO 2018, Chania, Greece, 9–12 October 2018, edited by: Sodnik, Z., Karafolas, N., and Cugny, B., International Society for Optics and Photonics, SPIE, 11180, 223–236, https://doi.org/10.1117/12.2535940, 2019. a
Virtanen, P., Gommers, R., Oliphant, T. E., Haberland, M., Reddy, T., Cournapeau, D., Burovski, E., Peterson, P., Weckesser, W., Bright, J., van der Walt, S. J., Brett, M., Wilson, J., Millman, K. J., Mayorov, N., Nelson, A. R. J., Jones, E., Kern, R., Larson, E., Carey, C. J., Polat, I., Feng, Y., Moore, E. W., VanderPlas, J., Laxalde, D., Perktold, J., Cimrman, R., Henriksen, I., Quintero, E. A., Harris, C. R., Archibald, A. M., Ribeiro, A. H., Pedregosa, F., van Mulbregt, P., and SciPy 1.0 Contributors: SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 17, 261–272, https://doi.org/10.1038/s41592-019-0686-2, 2020. a
Virtanen, T. H., Kolmonen, P., Sogacheva, L., Rodríguez, E., Saponaro, G., and de Leeuw, G.: Collocation mismatch uncertainties in satellite aerosol retrieval validation, Atmos. Meas. Tech., 11, 925–938, https://doi.org/10.5194/amt-11-925-2018, 2018. a
Vukicevic, T., Coddington, O., and Pilewskie, P.: Characterizing the retrieval of cloud properties from optical remote sensing, J. Geophys. Res.-Atmos., 115, D20211, https://doi.org/10.1029/2009JD012830, 2010. a
Wang, J., Xu, X., Ding, S., Zeng, J., Spurr, R., Liu, X., Chance, K., and Mishchenko, M.: A numerical testbed for remote sensing of aerosols, and its demonstration for evaluating retrieval synergy from a geostationary satellite constellation of GEO-CAPE and GOES-R, J. Quant. Spectrosc. Ra., 146, 510–528, https://doi.org/10.1016/j.jqsrt.2014.03.020, 2014. a
Werdell, P. J., Behrenfeld, M. J., Bontempi, P. S., Boss, E., Cairns, B., Davis, G. T., Franz, B. A., Gliese, U. B., Gorman, E. T., Hasekamp, O., Knobelspiesse, K. D., Mannino, A., Martins, J. V., McClain, C. R., Meister, G., and Remer, L. A.: The Plankton, Aerosol, Cloud, Ocean Ecosystem Mission: Status, Science, Advances, B. Am. Meteorol. Soc., 100, 1775–1794, https://doi.org/10.1175/BAMS-D-18-0056.1, 2019. a, b
Willmott, C. J. and Matsuura, K.: Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance, Clim. Res., 30, 79–82, http://www.jstor.org/stable/24869236 (last access: 18 August 2022), 2005. a
Wu, L., Hasekamp, O., van Diedenhoven, B., and Cairns, B.: Aerosol retrieval from multiangle, multispectral photopolarimetric measurements: importance of spectral range and angular resolution, Atmos. Meas. Tech., 8, 2625–2638, https://doi.org/10.5194/amt-8-2625-2015, 2015. a, b
Xu, F. and Davis, A. B.: Derivatives of light scattering properties of a nonspherical particle computed with the T-matrix method, Opt. Lett., 36, 4464–4466, https://doi.org/10.1364/OL.36.004464, 2011. a
Xu, F., Dubovik, O., Zhai, P.-W., Diner, D. J., Kalashnikova, O. V., Seidel, F. C., Litvinov, P., Bovchaliuk, A., Garay, M. J., van Harten, G., and Davis, A. B.: Joint retrieval of aerosol and water-leaving radiance from multispectral, multiangular and polarimetric measurements over ocean, Atmos. Meas. Tech., 9, 2877–2907, https://doi.org/10.5194/amt-9-2877-2016, 2016. a, b, c
Xu, F., Diner, D. J., Dubovik, O., and Schechner, Y.: A Correlated Multi-Pixel Inversion Approach for Aerosol Remote Sensing, Remote Sens., 11, 746, https://doi.org/10.3390/rs11070746, 2019. a
Xu, X. and Wang, J.: Retrieval of aerosol microphysical properties from AERONET photopolarimetric measurements: 1. Information content analysis, J. Geophys. Res.-Atmos., 120, 7059–7078, https://doi.org/10.1002/2015JD023108, 2015. a
Xu, X., Wang, J., Zeng, J., Spurr, R., Liu, X., Dubovik, O., Li, L., Li, Z., Mishchenko, M. I., Siniuk, A., and Holben, B. N.: Retrieval of aerosol microphysical properties from AERONET photopolarimetric measurements: 2. A new research algorithm and case demonstration, J. Geophys. Res.-Atmos., 120, 7079–7098, https://doi.org/10.1002/2015JD023113, 2015. a
Zhai, P.-W., Hu, Y., Trepte, C. R., and Lucker, P. L.: A vector radiative transfer model for coupled atmosphere and ocean systems based on successive order of scattering method, Opt. Express, 17, 2057–2079, 2009. a, b, c
Zhai, P.-W., Hu, Y., Chowdhary, J., Trepte, C. R., Lucker, P. L., and Josset, D. B.: A vector radiative transfer model for coupled atmosphere and ocean systems with a rough interface, J. Quant. Spectrosc. Ra., 111, 1025–1040, 2010. a, b, c
Zhai, P.-W., Gao, M., Franz, B. A., Werdell, P. J., Ibrahim, A., Hu, Y., and Chowdhary, J.: A Radiative Transfer Simulator for PACE: Theory and Applications, Front. Remote Sens., 3, 840188, https://doi.org/10.3389/frsen.2022.840188, 2022. a, b
Zhang, J.: Modern Monte Carlo methods for efficient uncertainty quantification and propagation: A survey, Computation. Stat., 13, e1539, https://doi.org/10.1002/wics.1539, 2021. a
- Abstract
- Introduction
- FastMAPOL aerosol and ocean color retrieval algorithm
- Uncertainty quantification for MAP retrievals
- Retrieval uncertainties from synthetic AirHARP and HARP2 measurements
- Retrieval uncertainties from AirHARP field measurements
- Discussions and conclusions
- Appendix A: Speed improvement using automatic differentiation
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- FastMAPOL aerosol and ocean color retrieval algorithm
- Uncertainty quantification for MAP retrievals
- Retrieval uncertainties from synthetic AirHARP and HARP2 measurements
- Retrieval uncertainties from AirHARP field measurements
- Discussions and conclusions
- Appendix A: Speed improvement using automatic differentiation
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References