Calibration of radar differential reflectivity using quasi-vertical profiles

Accurate precipitation estimation with weather radars is essential for hydrological and meteorological applications. The differential reflectivity (Z_DR) is a crucial weather radar measurement that helps to improve quantitative precipitation estimates using polarimetric weather radars. However, a system bias between the horizontal and vertical channels generated by the radar produces an offset in Z_DR. Existing methods to calibrate Z_DR measurements rely on the intrinsic values of the Z_DR of natural targets (e.g. drizzle or dry snow) collected at high elevation angles (e.g. higher than 40^∘ or even at 90^∘), in which Z_DR values close to 0 dB are expected. However, not all weather radar systems can scan at such high elevation angles or point the antenna vertically to collect precipitation measurements passing overhead. Therefore, there is a need to develop new methods to calibrate Z_DR measurements using lower-elevation scans. In this work, we present and analyse a novel method for correcting and monitoring the Z_DR offset using quasi-vertical profiles computed from scans collected at 9^∘ elevations. The method is applied to radar data collected through 1 year of precipitation events by two operational C-band polarimetric weather radars in the UK. The proposed method shows a relative error of 0.1 dB when evaluated against the traditional approach based on Z_DR measurements collected at 90^∘ elevations. Additionally, the method is independently assessed using disdrometers located near the radar sites. The results showed a reasonable agreement between disdrometer-derived and radar-calibrated Z_DR measurements.

1 Introduction

Conventional weather radars transmit signals in the microwave frequency range that are backscattered towards the radar antenna when precipitation particles (also known as hydrometeors, including raindrops, snow, melting snow, hail, graupel) lie along the path of the radar beam. The signal backscattered by hydrometeors is related to the radar reflectivity Z that can be converted to an estimation of rainfall rate R using a power-law equation Z=aR^b. Dual-polarisation weather radars measure the radar reflectivity at horizontal Z_H and vertical Z_V polarisations, and the ratio between both of them is known as the differential reflectivity Z_DR. Z_DR was proposed to improve radar rainfall estimation because raindrops are distorted into oblate spheroids as they fall to the ground (Pruppacher and Beard, 1970; Seliga and Bringi, 1976). Small raindrops give Z_DR values close to zero, whereas larger raindrops give Z_DR>0. The differential reflectivity (Z_DR) plays a crucial role in quantitative precipitation estimation (QPE) algorithms using polarimetric weather radars. Its relation with the orientation, shape and size of the hydrometeors improves not only the accuracy of radar QPE algorithms (Bringi et al., 2011; Cifelli et al., 2011; Giangrande and Ryzhkov, 2008; Ryzhkov et al., 2005b; Vulpiani et al., 2009) but also the classification of hydrometeors (Al-Sakka et al., 2013; Besic et al., 2016; Park et al., 2009; Straka et al., 2000).

However, to incorporate Z_DR as a valid input for radar QPE, it is necessary to ensure that it is properly calibrated. Ryzhkov et al. (2005a) showed that an accuracy of 0.2 dB in the differential reflectivity calibration is desirable for practical applications of polarimetric weather radar data, as this value generates uncertainty in the rain estimates close to 18 %. However, several factors introduce a bias into Z_DR, e.g. (a) the presence of cross-polar radiation (Zrnić et al., 2010); (b) errors in the transmitter and the receiver chain (or both) (Zrnic et al., 2006), or (c) an overall system bias due to the ratio of power transmitted to the horizontal and vertical polarisations (Bringi and Chandrasekar, 2001).

Several calibration procedures have been proposed to correct the overall system bias (or offset) in Z_DR depending on the radar scanning strategy. For radars capable of performing measurements at a 90^∘ elevation angle (herein referred to as birdbath scans), the most accepted calibration procedure is based on radar observations of raindrops as the antenna rotates about the vertical; non-zero values of Z_DR present under these conditions can be set as the Z_DR offset. This method was introduced by Gorgucci et al. (1999) and has been further explored and validated on several radar campaigns; e.g. Bechini et al. (2002) used vertical profiles (VPs) generated from data collected by a weather radar located in Italy to estimate both the Z_DR offset and the error in the radar reflectivity (Z_H). They analysed the standard deviation of Z_DR taken at vertical incident and concluded that the accuracy of this method is close to 0.1 dB. Similarly, Gourley et al. (2009) estimated the Z_DR offset using birdbath scans collected by a C-band radar, and their results demonstrated its impact on the absolute calibration of Z_H; Louf et al. (2019) used polarimetric birdbath scans measured by a C-band radar located in Australia to validate a new approach for calibrating and monitoring Z_H using ground clutter and satellite data. Frech and Hubbert (2020) used data collected from the radar network operated by the German Meteorological Service to monitor the Z_DR calibration. Their method relies on range-averaged values of Z_DR collected in light rain and detected using thresholds on polarimetric variables like the co-polar correlation coefficient or the coherent power to target an accuracy of Z_DR of around ±0.1 dB. More recently, Ferrone and Berne (2021) expanded the birdbath method by estimating the offset based on interpolated Z_DR values taken from rain, snow or ice regions, the main advantage of this method being its applicability when rain regions are not available to estimate the Z_DR offset.

However, some weather radar networks are unable to perform birdbath scans due to mechanical constraints. So several procedures have been proposed to overcome this restriction and correct the Z_DR offset. Ryzhkov et al. (2005a) presented a method based on the Z_DR values of dry snow collected at elevation angles between 40 and 60^∘. They linked these values to the Z_DR offset, achieving an accuracy of 0.2 dB. Giangrande and Ryzhkov (2005) expanded this method for scans affected by the presence of partial beam blockage and explored its relation with the Z_DR offset, stating that this method achieves an accuracy of 0.3 dB when applied to large data sets. Bechini et al. (2008) proposed a method to quantify the Z_DR offset by probing the differential reflectivity while increasing the elevation angle but remaining below the melting layer (ML). Then these data are compared with theoretical profiles of Z_DR to estimate the Z_DR offset. Although it is possible to achieve high accuracy by applying this method (∼0.1 dB), thousands of profiles are needed to generate profiles suitable for the comparison process.

Another well-known technique to calibrate Z_DR relies on sun measurements. It is based on the detection of solar spike echoes as this type of radiation has equal power at both horizontal and vertical polarisations (Gourley et al., 2006), hence generating measurements of Z_DR close to 0 dB. The sun-radiation detection method has been further investigated in several works; e.g. Gourley et al. (2006) compared both the birdbath scans and sun-radiation detection methods using C-band polarimetric data, determining that higher accuracy is achieved when using the former. An online variation of the solar-radiation detection method that does not require the operational scanning strategy to be stopped was introduced by Holleman et al. (2010). It is based on other works conceived to monitor the absolute radar calibration, like the methods introduced by Darlington et al. (2003) and Huuskonen and Holleman (2007). This online method enables monitoring the calibration of Z_DR and also the analysis of the correlation between horizontal and vertical channels. Later, Huuskonen et al. (2016) expanded this method based on data collected from the Finnish radar network, adding quality control to the solar signals and achieving accuracy of Z_DR below 0.05 dB. Chu et al. (2019) also used the sun-radiation detection method and concluded that an accurate calibration depends on the availability of radar data taken at sunrise/sunset, among other considerations. It is worth noting that the offset detected by the solar method must be taken with care as it is related to the receiver chain only, whereas the offset computed from birdbath scans includes both the transmitter and the receiver chain (Huuskonen et al., 2016).

Some other alternative techniques have been proposed to complement the operational calibration and monitoring of Z_DR. Bringi et al. (2006) estimated the Z_DR offset using range–height–indicator (RHI) scans collected by a C-band polarimetric radar located in Japan. They probed Z_DR in ice regions (i.e. at high altitudes) where values of 0 dB are expected and set the mean values of the observed data as the Z_DR offset. Richardson et al. (2017) proposed the use of turbulent eddies to monitor the differential reflectivity as the nature of such scatters results in values of Z_DR close to 0 dB. Additionally, Ryzhkov et al. (2016) proposed the application of the quasi-vertical profile (QVP) approach to monitor the calibration of Z_DR using a similar rationale to that in Ryzhkov et al. (2005a). This approach is explored by Griffin et al. (2020) and Kumjian et al. (2016), in which previously offset-corrected QVPs of Z_DR are used to describe processes like the ML and ice aggregation/riming. Although the QVPs are a valuable tool for monitoring the temporal evolution of precipitation and the microphysics of precipitation, there is little research using QVPs in rain to estimate the Z_DR offset. Most of the Z_DR calibration methods described above (except for the method that relies on sun measurements) rely on higher-elevation scans. There is a need to develop alternative methods that can be used when only lower-elevation scans are available.

This study presents an operational method to correct the Z_DR offset that can be implemented using QVPs of polarimetric variables. The method is based on QVPs generated from scans with elevation angles of 9^∘ and collected during light rain. These scans are usually available in operational radar scanning strategies deployed in radar networks worldwide, thus becoming an excellent option for radar networks not capable of collecting measurements at vertical incidence. The C-band polarimetric weather radars developed by the UK Met Office (UKMO) can perform measurements at vertical incidence, allowing a thorough comparison of the performance of both methods. Additionally, we explore the temporal variation in the Z_DR offset using long-term observations collected by two operational weather radars. The calibrated Z_DR measurements are further compared with measurements from independent disdrometer observations located near the radar sites. The paper is organised as follows. In Sect. 2, we define the radar and disdrometer data sets used in this work. The two different methods used to calibrate the radar Z_DR are described in Sect. 3. In Sect. 4, we examine the performance of the proposed method using long-term data sets collected by two weather radars and several disdrometers. We discuss the methods and results in Sect. 5. Finally, we summarise the findings of this work in Sect. 6.

2 Data sets

2.1 Radar data sets

The raw polarimetric radar data sets were obtained from two C-band weather radars that are part of the UKMO operational weather radar network. The Chenies radar site is located at Hertfordshire, near London, the United Kingdom (Met Office, 2013), and the Dean Hill radar site is located at Wiltshire, near Salisbury, the United Kingdom (Met Office, 2021). Both radars transmit and receive signals at horizontal and vertical polarisations simultaneously, generating plan position indicator (PPI) products at various pulse lengths and revolutions per minute (RPM) and covering several elevation angles. The PPI products include measurements of reflectivity (Z_H), differential reflectivity (Z_DR), the correlation coefficient (ρ_HV), the differential propagation phase (Φ_DP) and radial velocity (V) collected throughout 2018 to carry out a long-term analysis of the Z_DR calibration; such products and their processing are described next.

The birdbath scans are sampled with the radar antenna pointing vertically (i.e. 90^∘ elevation angle) while at the same time the antenna rotates around its axis (from 0 to 360^∘ in azimuth). The scans have a temporal resolution of 10 min, 75 m of gate resolution and a maximum range (equivalent to height for vertical scans) of 12 km. These products are used to build vertical profiles (VPs) of polarimetric variables and monitor the Z_DR calibration. The VPs are generated by averaging raw polarimetric data taken from 360 vertical rays following the procedure suggested by Bechini et al. (2002); however, the first kilometre in height is discarded to minimise the risk of side-lobe contamination and the presence of other artefacts that could affect the Z_DR calibration. Also, the VPs are used as input for a ML detection algorithm to distinguish the precipitation in the liquid phase, as described in Sanchez-Rivas and Rico-Ramirez (2021). These VPs will be used to compute the true Z_DR calibration offset, which will be used to validate the proposed algorithm. Note that this Z_DR offset is not error-free but provides a reliable benchmark to validate our algorithm.

PPI scans at a 9^∘ elevation angle are collected every 10 min and sampled in short-pulse (SP) mode (pulse length equal to 500 µs), with a gate resolution of 600 m and a maximum range of 115 km. These scans are processed to generate QVPs of polarimetric variables following the procedure suggested by Ryzhkov et al. (2016), averaging azimuthally the polarimetric variables and generating one QVP of each polarimetric variable per PPI scan. As above, these data are also used to detect the ML. These QVPs will be used to calibrate and monitor Z_DR using lower-elevation scans.

PPI scans at 0.5, 1.0 and 2.0^∘ elevation angles are collected every 5 min and sampled in long-pulse (LP) mode (pulse length equal to 2000 µs), covering a range of 250 km and with the same gate resolution as above. These low elevation angles are used to compare the offset-corrected radar Z_DR with Z_DR values derived from disdrometer data. A fuzzy-logic classifier is applied using the methodology proposed by Rico-Ramirez and Cluckie (2008) to remove non-meteorological echoes. Once the differential reflectivity has been calibrated, corrections for attenuation in Z_H and Z_DR are applied following the methods described by Rico-Ramirez (2012) and Bringi et al. (2001), respectively.

It is important that the UK Met Office continuously monitors the quality of the radar reflectivity (Harrison et al., 2012, 2017); hence no Z_H calibration process is required.

The location and other relevant technical details of the radars are provided in Fig. 1 and in Tables 1 and 2.

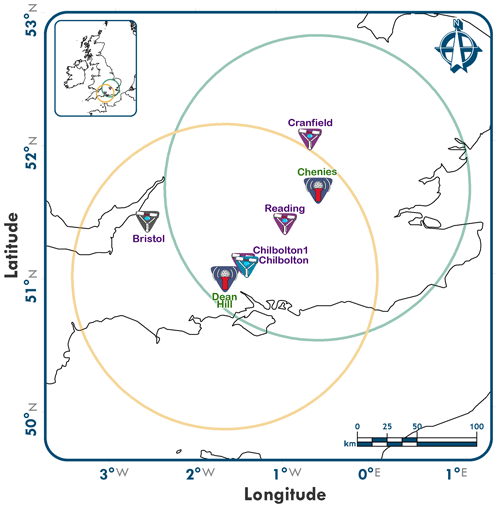
Figure 1 Location of the radars (Chenies and Dean Hill) and disdrometers (Bristol, Chilbolton, Cranfield and Reading). The circles represent the coverage of each radar at a distance of 115 km (maximum coverage of the radars operating at short pulse lengths).

Table 1 Polarimetric radar characteristics.

Note that PRF denotes pulse repetition frequency, RPM denotes revolutions per minute, SP denotes short pulse and LP denotes long pulse.

2.2 Disdrometer data sets

In this study, disdrometer data are used for verifying the consistency of the radar differential reflectivity measurements as the disdrometers are instruments that measure the drop size distribution (DSD) of precipitation. Several disdrometer data sets were collected from different projects with locations neighbouring the radar sites and matching time periods. These include disdrometers from the Chilbolton Facility for Atmospheric and Radio Research (CFARR), the Disdrometer Verification Network (DiVeN), and the University of Bristol (UoB) (see locations in Fig. 1 and Table 2).

CFARR operates a Joss–Waldvogel impact disdrometer (model RD-69) located at Chilbolton, Hampshire, southern England, that has provided continuous DSD data since 2003. The disdrometer converts the vertical momentum of a falling drop into signals whose amplitude depends on the diameter of the impacting drop. This device provides drop counts every 10 s over 127 bins ranging from 0.3 to 5 mm, with a sampling area of approximately 50 cm² (Science and Technology Facilities Council et al., 2003). This instrument does not measure the fall velocity of precipitation particles, and therefore the device does not provide a hydrometeor classification. For this work, data were available from January to July 2018.

DiVeN was deployed in 2017, and the disdrometer network includes several Thies laser precipitation monitors in the UK that provide information on the quantity, intensity and type of precipitation (Pickering et al., 2019). The Thies disdrometer measures the diameters and fall velocities of the hydrometeors and categorises hydrometeors into different classes (drizzle, drizzle/rain, rain, ice, snow, wet ice, wet snow, graupel, wet graupel and hail). The disdrometer provides the number of drops recorded every minute over a matrix covering 20 diameter and 22 velocity classes. The diameters range from 0.125 to 8 mm; the velocities range from 0.0 to 20.0 m s⁻¹, and the sampling area of the instrument is approximately 45.6 cm² (Natural Environment Research Council et al., 2019). For this work, we selected three disdrometers operating near the radar sites, one at Chilbolton, Hampshire (herein Chilbolton1); one at Reading, Berkshire; and one at Cranfield, Bedfordshire, all located in England. Data were collected for precipitation events throughout 2018.

The UoB operates several Parsivel² disdrometers, one of them located at Bristol, southwest England. This laser disdrometer measures the drop size distribution (DSD) and categorises the precipitation particles into several classes (drizzle, drizzle/rain, rain, rain/snow, snow, sleet, hail). The instrument provides the number of drops recorded every minute over a matrix covering 32 diameter and 32 velocity classes. The particle size includes 32 bins ranging from 0.2 to 25 mm, and the particle speed includes 32 bins ranging from 0.2 to 20 m s⁻¹) (OTT HydroMet, 2016). The sampling area of this instrument is approximately 50 cm². Data were collected for precipitation events throughout 2018.

Table 2 Summary of radars (RAD) and disdrometers (DIS).

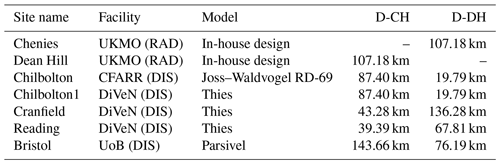
Note that D-CH denotes distance to the Chenies radar site and D-DH distance to the Dean Hill radar site.

Processing of disdrometer data

The raindrop size distribution (DSD) can be computed from the disdrometer data by (Ji et al., 2019)

$$\begin{array}{}\text{(1)}& N_t\left(D_i\right)={\displaystyle \frac{n_i\left(t\right)}{A\cdot \mathrm{\Delta }t\cdot V_i\cdot \mathrm{\Delta }{D}_i}},\end{array}$$

where D_i is the drop diameter (mm), n_i is the number of drops counted during the sampling interval Δt (s) at the ith bin size, A (m²) is the sampling area of the disdrometer, V_i (m s⁻¹) is the terminal velocity of the raindrops at the ith bin size and ΔD_i (mm) is the ith bin width diameter interval. The sampling interval Δt was fixed to 60 s to ensure there are a sufficient number of measurements to compute a reliable DSD, which is also consistent with previous studies (Bringi et al., 2011; Ji et al., 2019). The terminal velocity of raindrops was computed by (Atlas et al., 1973)

$$\begin{array}{}\text{(2)}& V\left(D\right)=\mathrm{9.65}-\mathrm{10.3}\exp (-\mathrm{0.6}{D}_i),\end{array}$$

where D is in millimetres and V is in m s⁻¹. The disdrometers measure the DSDs with a 1 min sampling interval. The Thies and Parsivel disdrometers measure the terminal velocity of raindrops to classify precipitation particles based on the velocity–diameter relationships. Only those measurements classified as liquid rain were used in this analysis. The DSDs were fitted to a normalised gamma drop size distribution using the procedure given in Bringi et al. (2003), where the normalised gamma DSD is given by

$$\begin{array}{}\text{(3)}& N\left(D\right)=N_{w}f\left(\mathit{\mu }\right){\left({\displaystyle \frac{D}{D_{\mathrm{m}}}}\right)}^{\mathit{\mu }}\exp \left[-(\mathrm{4}+\mathit{\mu }){\displaystyle \frac{D}{D_{\mathrm{m}}}}\right].\end{array}$$

Here f(μ) is given by

$$\begin{array}{}\text{(4)}& f\left(\mathit{\mu }\right)={\displaystyle \frac{\mathrm{6}}{{\mathrm{4}}^{\mathrm{4}}}}{\displaystyle \frac{(\mathit{\mu }+\mathrm{4}{)}^{\mathit{\mu }+\mathrm{4}}}{\mathrm{\Gamma }(\mathit{\mu }+\mathrm{4})}},\end{array}$$

where N_w (m⁻³ mm⁻¹) represents the normalised intercept parameter, D_m (mm) is the mass-weighted mean diameter and μ is the shape of the distribution. D_m is related to D₀ (median volume diameter) for a gamma DSD by (Bringi et al., 2003)

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{D_{\mathrm{0}}}{D_{\mathrm{m}}}}={\displaystyle \frac{\mathrm{3.67}+\mathit{\mu }}{\mathrm{4}+\mathit{\mu }}}.\end{array}$$

From the above analysis, the parameters N_w, D₀ (or D_m) and μ were retrieved for each 1 min measured DSD. Then Eq. (3) was used to compute the theoretical DSD, which was used as input to a T-matrix scattering model developed by Mishchenko (2000) and adapted to compute all the different polarimetric weather radar measurements, including Z_H and Z_DR, which are both used in this analysis. The scattering simulations were performed using the following assumptions: (i) the raindrop shape model from Thurai et al. (2007) (their Eq. (2) for D>1.5 mm, their Eq. (3) for $\mathrm{0.7}\le D\le \mathrm{1.5}$ mm, spherical raindrops otherwise); (ii) no canting angle distribution; (iii) maximum diameter for the integration fixed to 3D₀; (iv) temperature of 10 ^∘C, radar wavelength of 5.3 cm and elevation angle of 0^∘.

3 Methods

3.1 Offset detection and monitoring of Z_DR using vertical profiles (VPs)

The overall system bias (or offset) in Z_DR can be estimated using VPs taken in light-rain events, as described in the literature review. The VPs represent averaged observations of the 360 vertical rays, reducing the variance in Z_DR caused by the symmetry axis and the variety of shapes of the raindrops. Then the premise of this method is to use VPs related to light rain, where a deviation from 0 dB in the rain region of the VPs can be set as the Z_DR offset. An in-depth discussion on the selection of this natural target to detect the Z_DR offset is provided in Sect. 5.

The offset on Z_DR can be detected and corrected by an automated operational procedure as follows.

1. It is necessary to detect the rain region on the VPs; this can be achieved by implementing the ML detection algorithm proposed by Sanchez-Rivas and Rico-Ramirez (2021) and then setting the ML bottom as a boundary. Values on the VPs below the bottom of the ML are likely related to precipitation in the liquid phase.

2. Once the rain region is identified on the VPs, thresholds related to light rain are set, and only VPs containing two or more consecutive bins of Z_DR having corresponding values of 5 dBZ $<Z_{\mathrm{H}}<\mathrm{30}$ dBZ and ρ_HV>0.98 are kept for further calculations.

3. The Z_DR offset is calculated for each VP related to light rain using the following expression:

   $$\begin{array}{}\text{(6)}& Z_{\mathrm{DR}}^{{\mathrm{O}}_{\mathrm{VP}}}={\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n{Z}_{{\mathrm{DR}}_i},\end{array}$$

   where i represents a valid bin along the VP, n the number of valid bins below the melting layer and avoiding clutter echoes, $Z_{\mathrm{DR}}^{{\mathrm{O}}_{\mathrm{VP}}}$ the offset calculated from the vertical profile, and $Z_{{\mathrm{DR}}_i}$ the bins of Z_DR below the ML. Note that n includes bins from different azimuths. If $Z_{\mathrm{DR}}^{{\mathrm{O}}_{\mathrm{VP}}}$ is different from 0 dB, then Z_DR needs to be calibrated.

4. Finally, Z_DR PPI measurements at different elevation angles can be corrected by subtracting the offset computed in Eq. (6) to the original Z_DR measurements using

   $$\begin{array}{}\text{(7)}& Z_{\mathrm{DR}}^{\mathrm{Oc}}=Z_{\mathrm{DR}}^{\mathrm{m}}-Z_{\mathrm{DR}}^{{\mathrm{O}}_{\mathrm{VP}}},\end{array}$$

   where $Z_{\mathrm{DR}}^{\mathrm{Oc}}$ is the offset-corrected differential reflectivity, $Z_{\mathrm{DR}}^{\mathrm{m}}$ is the differential reflectivity measured by the radar and $Z_{\mathrm{DR}}^{{\mathrm{O}}_{\mathrm{VP}}}$ is the offset calculated from the vertical profiles.

3.2 Offset detection and monitoring of Z_DR using quasi-vertical profiles (QVPs)

The QVPs of polarimetric variables provide insight into the evolution and structure of rain events through time, thus enabling monitoring the calibration of the radar variables. Hence, we propose a method to estimate the Z_DR offset that can be applied to QVPs generated from lower-elevation scans with elevation angles of around 9^∘ collected during light-rain events. The proposed method is based on the following rationale.

• a.

  The rain region within the QVPs of Z_DR is mostly uniform when the profiles are generated from data collected in light rain and near the radar as this region represents averaged observations of small oblate raindrops. Figure 2 portrays the radar coverage of two PPI scans at different elevation angles recorded by one of the radars. It can be seen that birdbath scans (and subsequent VPs) capture uniformly the rain region (between 1 and 2.5 km in height) developed above the radar (Fig. 2a). Similarly, the rain region below the bright band (located at 2.5 km in height) is mostly homogeneous for this particular PPI with an angle elevation of 9^∘ (Fig. 2b).

• b.

  The intrinsic value of Z_DR for angles below 90^∘ and collected in light rain is larger than zero, and it is elevation-dependent, as demonstrated by Bringi and Chandrasekar (2001) and formulated by Ryzhkov et al. (2005a) as

  $$\begin{array}{}\text{(8)}& Z_{\mathrm{dr}}\left(\mathit{\theta }\right)\approx {\displaystyle \frac{Z_{\mathrm{dr}}\left(\mathrm{0}\right)}{{\left[Z_{\mathrm{dr}}^{\mathrm{1}/\mathrm{2}}\left(\mathrm{0}\right){\sin }^{\mathrm{2}}\mathit{\theta }+{\cos }^{\mathrm{2}}\mathit{\theta }\right]}^{\mathrm{2}}}},\end{array}$$

  where Z_dr(0) and Z_dr(θ) represent the differential reflectivity at a linear scale at elevation angles of 0^∘ and θ^∘, respectively. Figure 3 displays the theoretical variation in Z_DR with elevation angle. It can be seen that the difference in Z_DR values between an elevation below 10^∘ and the elevation of 0^∘ is negligible. In fact using Eq. (8) for $\mathit{\theta }=\mathrm{10}{}^{\circ }$ results in Z_dr values very close to each other; that is

  $$\begin{array}{}\text{(9)}& Z_{\mathrm{dr}}(\mathit{\theta }=\mathrm{10}{}^{\circ })\approx \mathrm{0.968}{Z}_{\mathrm{dr}}(\mathit{\theta }=\mathrm{0}{}^{\circ })\left[\mathrm{dB}\right].\end{array}$$

  Hence, Z_DR radar measurements collected at elevation angles below 10^∘ are similar to those collected at lower elevation angles, and so they do not add additional uncertainty to the offset correction method. However, Fig. 3 also shows that Z_DR values for lower elevation angles have a wide range of values (e.g. between 0 and 2 dB in this figure) compared with elevation angles of 90^∘ in which Z_DR values close to zero are expected. This represents a challenge for our approach, and therefore we have to constrain the Z_dr measurements used to compute the offset into a narrow band as explained next.

• c.

  We simulated a wide range of DSDs using the range of parameters described in Bringi and Chandrasekar (2001) expected in real storm events using the following parameter ranges:

  $$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathrm{10}}^{\mathrm{3}}\le N_w\le {\mathrm{10}}^{\mathrm{5}}\left[\mathrm{mm}{\mathrm{m}}^{-\mathrm{3}}\right],\\ {\displaystyle }& {\displaystyle }\mathrm{0.5}\le D_{\mathrm{0}}\le \mathrm{2.5}\left[\mathrm{mm}\right],\\ {\displaystyle }& {\displaystyle }-\mathrm{1}\le \mathit{\mu }\le \mathrm{5}\\ {\displaystyle }& {\displaystyle }R\le \mathrm{300}\left[\mathrm{mm}{\mathrm{h}}^{-\mathrm{1}}\right].\end{array}$$

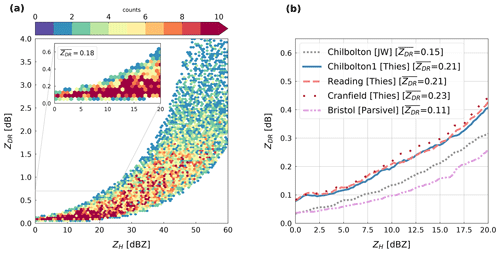
  We randomly generated 10 000 sets of DSD parameters (N_w, D₀ and μ) uniformly distributed within the ranges defined above. Then we use Eq. (3) to simulate the DSDs, which are used as input to a T-matrix scattering model to compute Z_H and Z_DR. The scattering simulations are performed using the same assumptions described in the section “Processing of disdrometer data”. The results of these simulation are shown in Fig. 4a, which depicts the theoretical variation in Z_DR versus Z_H, which is consistent with previous studies (Bechini et al., 2008; Bringi et al., 2006; Giangrande and Ryzhkov, 2005; Ryzhkov et al., 2005a). Figure 4a shows that Z_DR increases with Z_H and also that Z_DR has a wide range of values for a given value of Z_H. However, the expected range of Z_DR measurements in light rain (e.g. for Z_H<20 dBZ) becomes narrow and gives Z_DR<0.6 dB (see zoomed-in region in Fig. 4a).

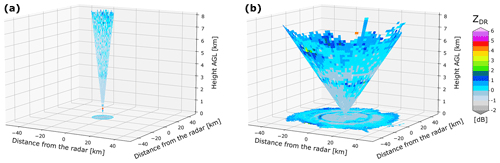
Figure 2 Representation of the radar conical coverage using (a) a birdbath scan, useful for building VPs, and (b) a 9^∘ PPI scan, used to generate QVPs.

Based on the premises described above, we propose an operational method to compute and correct the Z_DR offset using QVPs as described below.

1. As in the VP method, the rain region is identified in the QVPs using a ML detection algorithm to set the ML bottom as a boundary. Values below this height are likely related to precipitation in the liquid phase. Additionally, a maximum height limit of 3 km is set to this ML bottom boundary to reduce the range effects inherent to the generation process of the QVPs. The maximum height limit of 3 km seems to work well in the UK, but it might need to be adjusted in other regions.

2. Using the theoretical variation in Z_H and Z_DR given in Fig. 4a, we compute the mean dependencies but limited to a narrow range related to light rain ($\mathrm{0}<Z_{\mathrm{H}}<\mathrm{20}$ dBZ), as shown in the zoomed-in box in Fig. 4a. This yields a mean value of $\stackrel{\mathrm{‾}}{Z_{\mathrm{DR}}}=\mathrm{0.18}$ dB, which is set as the intrinsic value of Z_DR in light rain at ground level for lower-elevation scans. This value is compared to Z_H−Z_DR values computed from disdrometer measurements (see Fig. 4b), confirming the good agreement between theoretical and measured Z_DR values.

3. Various thresholds are set to detect QVPs related to light rain and discard bins within the QVPs related to mixed-phase precipitation. Thus, only QVPs containing three or more consecutive bins of Z_DR with corresponding values of 0 dBZ $<Z_{\mathrm{H}}<\mathrm{20}$ dBZ and ρ_HV>0.985 on the QVPs of Z_H and ρ_HV, respectively, are kept for further calculations. Note that the threshold set for Z_H is the same as the range selected in the DSD simulations, whereas the threshold set for ρ_HV is more strict than in the method based on VPs in order to discard bins within the QVPs not related to light rain.

4. The average value of Z_DR is computed, calculating one value per QVP related to light rain:

   $$\begin{array}{}\text{(10)}& Z_{\mathrm{DR}}^{{\mathrm{O}}_{\mathrm{QVP}}}=\left({\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n{Z}_{{\mathrm{DR}}_i}\right)-\mathrm{0.18}\mathrm{dB}.\end{array}$$

5. Finally, Z_DR measurements can be corrected by

   $$\begin{array}{}\text{(11)}& Z_{\mathrm{DR}}^{\mathrm{Oc}}=Z_{\mathrm{DR}}^{\mathrm{m}}-Z_{\mathrm{DR}}^{{\mathrm{O}}_{\mathrm{QVP}}},\end{array}$$

   where $Z_{\mathrm{DR}}^{\mathrm{Oc}}$ is the offset-corrected differential reflectivity, $Z_{\mathrm{DR}}^{\mathrm{m}}$ is the differential reflectivity measured by the radar and $Z_{\mathrm{DR}}^{{\mathrm{O}}_{\mathrm{QVP}}}$ is the offset calculated from the QVPs.

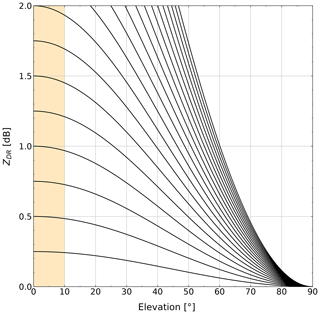
Figure 3 Theoretical dependencies of Z_DR at different elevation angles. Highlighted area shows the small variation in Z_DR for elevation angles below 10^∘.

Figure 4 (a) Simulated Z_H−Z_DR dependencies expected in real storm events; (b) Z_H−Z_DR dependencies measured by several types of disdrometers at different locations.

4 Long-term monitoring of the Z_DR calibration

We processed the radar data sets collected by two operational weather radars throughout 1 year of precipitation events to generate VPs and QVPs of polarimetric variables as described in Sect. 2.1. Then we applied both Z_DR offset-correction methods to the generated VPs and QVPs to compare the results of the Z_DR calibration.

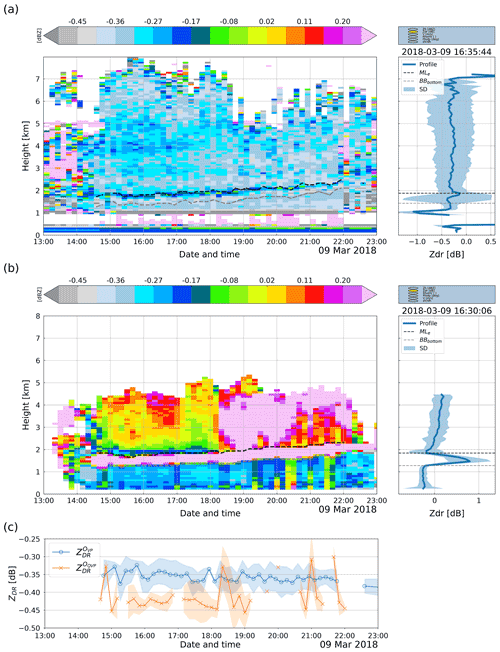
Figure 5 Rain event recorded by the UKMO Chenies radar on 9 May 2018. Panel (a) shows a collection of Z_DR VPs in a height-versus-time plot along with the melting level (ML_e) and the bottom of the melting layer (BB_bottom). Its right panel depicts a single VP and its standard deviation (SD). Panel (b) shows the same as in (a) but using QVPs of Z_DR. Panel (c) shows the Z_DR offset computed using VPs (blue line, circle markers) and QVPs (orange line, cross markers); the filled areas represent the computed standard deviation for each data point.

We present a rain event recorded in southern England by the Chenies radar to exemplify the above-mentioned processes. In Fig. 5a, the left panel shows VPs (each one representing the mean value of 360 rays) of Z_DR in a height-versus-time (HTI) plot related to a rain event. In contrast, the right panel shows a single VP taken from the same event. Note that the first kilometre of the VPs is contaminated with spurious echoes; hence all bins below this height were discarded from the analysis. The HTI plot shows that the values of Z_DR deviate from 0 dB in the rain medium, i.e. below the bottom of the bright band (BB_bottom); thus Z_DR needs to be calibrated. The single VP plot enables an in-depth analysis of the profile characteristics. For example, it can be seen that Z_DR values within the rain region (below 1.5 km in height) are close to −0.35 dB and also that its standard deviation (SD) remains relatively steady. But this changes in the ML, where the VP turns noisy and produces a higher standard deviation. However, dry aggregated snow signatures are visible above 2 km in height (at the top of the melting layer), where the Z_DR values are similar to those observed for liquid precipitation (∼0.37 dB), confirming the reliability of dry snow in detecting the Z_DR offset. These characteristics are consistent throughout the entire event.

On the other hand, Fig. 5b shows QVPs of Z_DR values generated from data related to the event described above. It can be seen that there are clear signatures of the melting layer within the QVPs that are useful to classify the hydrometeors' phase. The single QVP plot shows that the standard deviation of the averaged values used to generate the QVP is smaller in the rain region (below 1.35 km) compared to the standard deviation observed within and above the ML. Moreover, the signatures of dry snow are not clearly visible, and the values observed for rain particles differ from those seen at the top of the ML, thus hampering using dry snow as the calibration target for our data sets. After applying the proposed method, the averaged value of Z_DR in the rain region is −0.26 dB, which, along with the computed intrinsic value of Z_DR (0.18 dB), results in an offset of −0.44 dB, which is close to the offset calculated using the VP method (−0.35 dB).

Figure 5c shows the temporal variation in the Z_DR offset for both VP $\left(Z_{\mathrm{DR}}^{{\mathrm{O}}_{\mathrm{VP}}}\right)$ and QVP $\left(Z_{\mathrm{DR}}^{{\mathrm{O}}_{\mathrm{QVP}}}\right)$ methods. For this precipitation event, the differences between methods are around 0.1 dB. Still, it is worth mentioning that $Z_{\mathrm{DR}}^{{\mathrm{O}}_{\mathrm{VP}}}$ exhibits values that remain relatively constant during this event, whereas the values of $Z_{\mathrm{DR}}^{{\mathrm{O}}_{\mathrm{QVP}}}$ show greater variation and are not altogether far from $Z_{\mathrm{DR}}^{{\mathrm{O}}_{\mathrm{VP}}}$. It is also important for this event that the number of valid VPs is larger than the number of QVPs classified as valid according to the proposed constraints described in the method. A discussion on the selection of the natural targets to detect the Z_DR offset and the performance of the proposed method is provided in Sect. 5.

4.1 Validation of the QVP-based approach using birdbath scans

The QVP-based approach will be assessed by comparing its results with the “true offset” computed from the VP-based method since it is widely accepted and has been proven effective, as described in the literature review. Therefore, it is essential to highlight that the errors in the Z_DR calibration based on QVPs are relative to the traditional method. Additionally, both methods will be compared to independent measurements provided by the disdrometers.

Figure 6 shows the temporal variation in the Z_DR offset for the two radar data sets used in this work. For the Chenies radar data set (Fig. 6a), it can be seen that the offset in Z_DR computed using the birdbath method fluctuates between −0.2 and −0.7 dB during most of the year. During February 2018, filters were installed at the Chenies radar, introducing a variation into the radar calibration that can be observed at this period (Timothy Darlington, Met Office, personal communication, 2021). The proposed method based on QVPs proves to be effective as the Z_DR offset values are similar to those calculated using VPs. For the Dean Hill radar data sets, the Z_DR offset varies in a broader range, but as above, the computed offset is similar in both methods. Similarly, an upgrade implemented on the Dean Hill radar during October 2018 modified the Z_DR calibration (Timothy Darlington, Met Office, personal communication, 2021), changing from −0.2 to 0.5 dB at around this time of the year. However, a few points throughout the entire year exhibit more significant differences. This shows that some profiles may surpass the constraints set to reject QVPs that do not meet the light-rain criteria. Averaging the entire radar domain plays a key role here, as mixed-phase precipitation can affect the QVPs (see Discussion in Sect. 5). Additionally, Fig. 6 shows two particular rain events (zoomed-in boxes in this figure) for a deeper visualisation of the calibration methods, where it can be seen that both methods produce similar results.

Figure 6 also shows that the number of profiles detected by each method is different. The VP-based method detects a larger number of profiles that meet the criteria of light rain, especially for the Dean Hill radar data set. For this radar data set, the number of valid profiles detected by the QVP-based approach represents 47 % of the profiles detected by the VP-based method. This difference is not that big for the Chenies radar data set, as the number of profiles detected by the QVP-based method represents the 78 % of profiles detected by the VP-based method. Although this is a limitation of the method, this ensures that only those QVPs due to light rain and with high ρ_HV values are used for the estimation of the Z_DR offset. In this case, we use the last valid QVP-based Z_DR offset, which is then compared to the Z_DR offset computed by the VP-based method.

Finally, we observed an overall relative error in the Z_DR offset using QVPs of ±0.1 dB compared to the method based on VPs. This increases the confidence in using the proposed method based on QVPs.

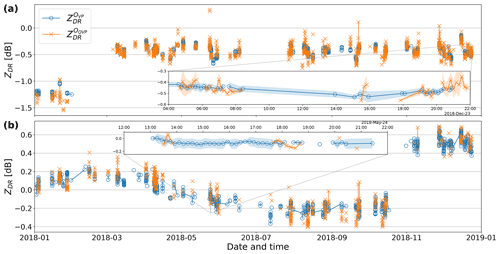
Figure 6 Temporal variation in the Z_DR offset on two weather radars during 1 year of rain events. The top panel shows the variation on the Chenies radar site, whilst the bottom panel depicts the offset variation at the Dean Hill radar site. The case of a rain event on 9 March 2018 is zoomed in on in both panels for an in-depth examination. The date is indicated in the format year-month.

We evaluate the outputs of each method for the two different radar sites using metrics like the correlation coefficient (r), the mean absolute error (MAE) and the root mean squared error (RMSE). To effectively assess the performance of the QVP-based approach and its temporal variation, each computed offset value is stored as the radar Z_DR offset until a new one is detected; e.g. in Fig. 6b, for the case on 24 May 2018, the VP-based method yields a constant offset value of around −0.15 dB between 13:05 and 18:05 Greenwich mean time (GMT – this time zone applies throughout), whereas the QVP-based method only detected a handful of valid QVPs for the same time period. However, the offset is similar at those points in time, with differences of around ±0.1 dB. It is worth mentioning that this is a warm-rain event, and only a few QVPs meet the criteria set for detecting light rain.

Figure 7 shows a comparison of the Z_DR offset estimated by both methods for both radars for the entire year. The results show that the Z_DR offset for the Chenies radar was between −0.7 and −0.1 dB, with a small number of events showing an offset of around −1.3 dB. For the Dean Hill radar, the Z_DR offset was between −0.4 and 0.6 dB. The figure shows a good correlation between the outputs of both methods, where the relative performance of the QVP-based method is in good agreement (±0.1 dB) with the true offset computed from birdbath scans (VP-based method).

Figure 7 Comparison of Z_DR offsets computed with QVPs and VPs. The scatter density plot shown in (a) provides metrics for evaluating the methods applied to the Chenies radar data set, whereas (b) shows the same as in (a) but for the Dean Hill radar data set.

4.2 Differential reflectivity comparison using radar and disdrometers

Several validation procedures of the proposed method for correcting the Z_DR offset were performed utilising the disdrometer data sets described in Sect. 2.2. The fitted normalised gamma DSDs allows the estimation of the reflectivity and the differential reflectivity at ground level, enabling the validation of the QVP-based method.

First, we compare the radar-calibrated Z_DR measurements by the two approaches described in the previous sections at the disdrometer locations. Only individual radar bins exactly over the corresponding disdrometers locations are considered for comparison. Based on the distance between the radars and the disdrometers, we link the Cranfield and Reading disdrometers to the Chenies radar, whereas the Chilbolton1 disdrometer will be compared to the Dean Hill radar. The disdrometer located at Bristol was not used in this analysis because it is too far from both radar sites. In addition, we use the hydrometeor classification produced by the Thies disdrometers to evaluate the radar measurements related to liquid precipitation, as these disdrometers provide information about the rain type and intensity. This classification is helpful to discard DSDs related to snow or hail.

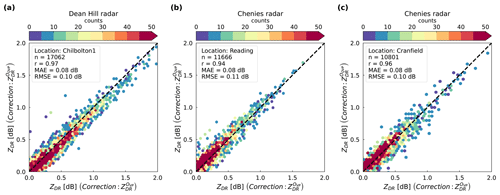
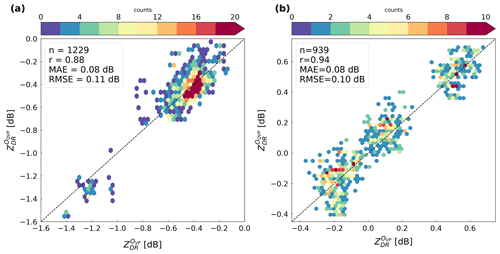
Figure 8 Scatterplots between calibrated Z_DR measurements using VPs and QVPs. Each plot represents radar Z_DR measurements at different locations and filtered using precipitation and intensity classifiers gathered from disdrometers.

Figure 8 shows the scatterplots using both methods to calibrate Z_DR measurements at disdrometer locations. For the Chenies radar data, we applied Eqs. (7) and (11) to correct the Z_DR offset in PPI scans taken at a 0.5^∘ elevation angle, whilst for the Dean Hill data, we applied the same equations to correct the Z_DR offset but on PPI scans taken at a 2^∘ elevation angle as lower elevations are beam-blocked or contaminated with ground clutter. The proposed approach based on QVPs proves effective as an accuracy of ∼0.1 dB is achieved in all analysed cases when comparing the Z_DR measurements calibrated using QVPs against Z_DR measurements calibrated using the traditional method based on VPs.

In addition, we compare the polarimetric variables measured by the radar with the variables derived from disdrometer DSDs. We discard data not related to liquid precipitation by using the classifiers available on the disdrometer data sets and using only radar data with corresponding values of ρ_HV≥0.98. As described in Sect. 2.1, algorithms for removing non-meteorological echoes and for correcting the signal attenuation are applied to radar data sets when appropriate. Regarding the disdrometer data sets, we applied a moving-average filter (window size of 5) to reduce data fluctuations due to the finer time resolution of the disdrometer data (1 min) compared to the radar data sets (5 min). Furthermore, to include data collected by the CFARR Chilbolton disdrometer (model Joss–Waldvogel, not capable of classifying the rain type), we used the classification from the Thies disdrometer (Chilbolton1) to discard data from the former not related to rain, as these two disdrometers are close to each other (just a few metres apart).

Figure 9 shows the comparison between calibrated Z_DR radar measurements and Z_DR derived from disdrometer observations collected throughout 1 year of precipitation events. The Z_DR measurements shown in Fig. 9a were calibrated with VPs, whereas the Z_DR measurements shown in Fig. 9b were calibrated with QVPs. The results show comparable errors using either of the Z_DR calibration methods, confirming the good performance of the proposed method (the MAE and RMSE are below 0.3 dB and 0.4, respectively, in all disdrometer sites for both calibration methods). Although these errors are more significant than the errors shown in Fig. 8, these are also due to additional factors such as sampling errors (e.g. comparing point disdrometer observations with areal radar measurements), variations in Z_DR measurements aloft (e.g. comparing radar observations aloft with ground disdrometer observations), timing errors (e.g. disdrometer measurements are integrated over time each minute, whereas radar observations are taken in a few seconds every 5 min) and uncertainty in the estimation of Z_DR from DSD measurements. As mentioned above, scans taken at different elevation angles are used on each radar to capture the precipitation occurring above the disdrometer, adding some uncertainty to the interpretation of these results.

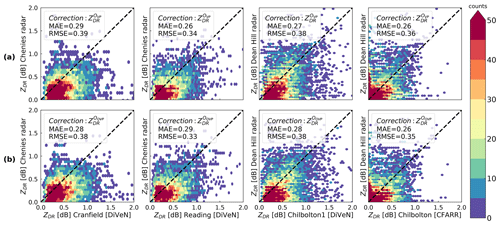
Figure 9 Scatterplots between radar and disdrometer Z_DR measurements at several locations: panel (a) shows scatter density plots of Z_DR offset-corrected using VPs at two different radar sites versus Z_DR derived from disdrometer data; panel (b) shows the same as in (a), but the radar Z_DR measurements are calibrated applying the QVP-based method.

4.2.1 Case study – 24 May 2018

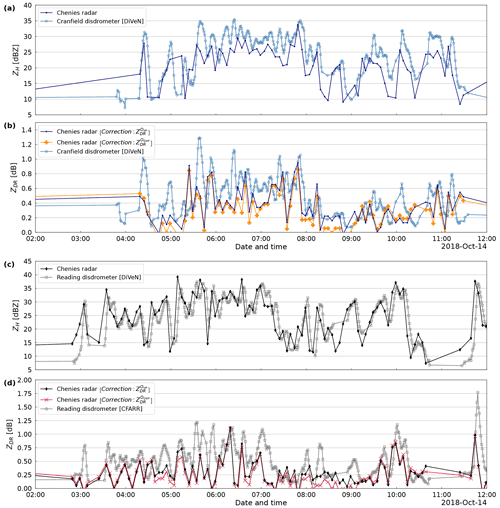
Figure 10 portrays a rain event recorded by the Dean Hill radar at an elevation angle of 2^∘ and data from two disdrometers located at the same location (Chilbolton Observatory). The top panel shows a good agreement between the radar reflectivity and the reflectivity derived from disdrometer DSDs as there is a similar trend in all data sets. Overall, the correlation of Z_H for the whole year of data between the radar data set and the two disdrometers is ≥0.80 (graph not shown). On the other hand, the bottom panel of Fig. 10 illustrates the calibrated Z_DR measurements by both methods and the Z_DR measurements derived from disdrometer observations. It can be seen that the Z_DR measurements calibrated with the proposed QVP-based method are in good agreement with the Z_DR measurements calibrated with scans collected at vertical incidence as a maximum difference of ±0.1 dB is observed. Both methods are consistent with the data derived from the two disdrometers located at the Chilbolton Observatory.

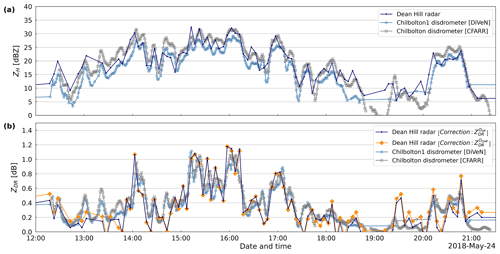
Figure 10 Time series of disdrometer and radar data related to a precipitation event registered in southern England: (a) reflectivity (Z_H) simulated from disdrometer DSD data at two nearby locations and Z_H measured by the C-band Dean Hill weather radar at an angle elevation of 2^∘; (b) differential reflectivity (Z_DR) measured by the Dean Hill radar and offset-corrected using two different approaches and Z_DR simulated from two disdrometers.

4.2.2 Case study – 14 October 2018

Figure 11 shows data collected by the Chenies radar at an elevation angle of 0.5^∘ and data from two disdrometers (Cranfield and Reading) located at different locations. As above, Z_H values are similar on the three devices. Figure 11a shows that the radar tends to underestimate the reflectivity, with differences of the order of 5–10 dBZ between the radar data and the Cranfield disdrometer, especially at times between 05:30 and 08:00. For this site, the correlation of Z_H for the whole year of data between the radar data set and the disdrometers is acceptable (r≈0.7) considering the distance between devices (graph not shown). Consequently, the Z_DR measured by the radar is in general smaller compared to the Z_DR derived from the Cranfield disdrometer (see Fig. 11b). However, it is important that both Z_DR calibration methods yield similar trends in both VP- and QVP-based methods, where maximum differences of 0.2 dB are observed for a short period of time, between 08:30 and 08:45.

On the other hand, Fig. 11c and d show data measured by the Chenies radar and the Reading disdrometer. It can be seen that there is an excellent agreement between devices for both Z_H and Z_DR. It is important that Z_DR values corrected using the proposed method based on QVPs exhibit almost the same pattern compared to the Z_DR values corrected using the VP-based method.

Figure 11 Time series of disdrometer and radar measurements. Panels (a) and (c) show the reflectivity, whereas panels (b) and (d) show the differential reflectivity.

5 Discussion

This work reviews the use of QVPs of polarimetric radar measurements to estimate and monitor the overall system bias (or offset) in the differential reflectivity. Although several sources of error affect this variable, we focused on detecting and correcting the overall system bias. It is important to calibrate Z_DR measurements as this variable is a crucial input to hydrometeor classification methods (Al-Sakka et al., 2013; Park et al., 2009), attenuation correction schemes (Bringi et al., 2011; Gou et al., 2019) or QPE algorithms (Chandrasekar and Bringi, 1988; Cifelli et al., 2011; Giangrande and Ryzhkov, 2008; Ryzhkov et al., 2005b; Vulpiani et al., 2009). Ryzhkov et al. (2005a) demonstrated that keeping the bias below ±0.2 dB generates accurate and reliable radar products.

Previous works have developed methods to compute the Z_DR offset using different targets, like light rain (Bechini et al., 2008; Gorgucci et al., 1999), dry snow (Ferrone and Berne, 2021; Ryzhkov et al., 2005a), ice (Bringi et al., 2006), sun spikes (Chu et al., 2019; Holleman et al., 2010) or turbulent eddies (Richardson et al., 2017). Most of these methods are based on measurements taken at high elevation angles that reduce the intrinsic variability in Z_DR. However, mechanical restrictions may prevent some radars from scanning at such high elevation angles; therefore, we evaluate a new approach to compute and correct the offset in radar Z_DR measurements based on QVPs of polarimetric variables built from PPI scans taken at lower elevation angles of around 9^∘. The proposed method is an alternative method to calibrate Z_DR measurements, but the traditional method based on VPs should be used instead if these vertical scans are available. As described in Sect. 3.2, we set light rain as the target to compute the Z_DR offset, using QVPs mainly to reduce the variability in Z_DR. Regarding the selection of this natural target, it is worth saying that we also explored the use of dry snow to derive the Z_DR offset. Dry aggregated snow can be found 1 or 2 km above the melting layer in stratiform clouds (Brandes and Ikeda, 2004; Ryzhkov et al., 2005a). Ryzhkov et al. (2005a) explored high-elevation-angle scans (∼ 40–60^∘) and observed that dry aggregated snow yields distinctive polarimetric signatures, i.e. values of Z_DR close to 0 dB, demonstrating that this target can be used to detect the Z_DR offset. Consequently, we analysed hundreds of polarimetric profiles (both VPs and QVPs data sets) and found that such a signature of dry snow is only observable on the VPs in our data set. This effect can be seen in Fig. 5a, where similar values of Z_DR can be seen on both light rain (below the melting layer bottom) and dry snow (above the melting layer top). Conversely, in the QVP data set (obtained at lower elevation angles of 9^∘), we observed that values of Z_DR in the rain medium were not consistent with those observed aloft, as shown in Fig. 5b. This lack of clear signatures of dry snow on QVPs is probably related to the beam broadening and non-uniform beam-filling effects, expected when the QVPs intercept the ML and regions above 9^∘ elevations. As shown in the right panel of Fig. 5b, the standard deviation (blue area) increases within and above the ML due to the presence of mixed-phase particles, hence complicating the estimation of the Z_DR offset using such meteorological targets. This is the reason why we could not use QVPs built from relatively low elevation angle scans (<10^∘) and set dry snow as the target to derive the Z_DR offset.

But using QVPs in light-rain events for detecting the Z_DR offset also presents several risks. First, it is important that there is an inherent variability in Z_DR in light rain. This is shown in Fig. 4a, where it can be seen that the variability in Z_DR increases with larger values of Z_H. Thus, we propose a constraint to reduce the variability in Z_DR; i.e. $\mathrm{0}<Z_{\mathrm{H}}<\mathrm{20}$. This range is a compromise to avoid having significant variations on Z_DR but still keep enough QVPs related to light rain in the analysis and enable the reliable detection of the Z_DR offset. In addition, the inherent averaging process in the QVP construction may wash out some key microphysical processes within the precipitation events. Thus, we proposed several constraints to minimise these effects. For example, we imposed a limit of 3 km in height within the QVPs to apply our method: as shown in Fig. 2b, the coverage of the PPI scans at a 9^∘ elevation angle captures a mostly uniform volume in the rain region (below 2.5 km). For this elevation angle and a height of 3 km, the base diameter of the cone is around 37 km. Hence we consider that the azimuthal averaging procedure to generate the QVPs below this height reduces deviations in Z_DR and enables proper monitoring of the calibration of this variable. Additionally, we define thresholds to discard values within QVPs not related to light rain; e.g. Fig. 5b shows a collection of QVPs related to a rain event. Most of the QVPs show a constant value of Z_DR below the ML, whilst outlier values can be discarded by checking their corresponding values on the QVPs of Z_H and ρ_HV (plots not shown). This figure also shows that the values of Z_DR above the rain region are loosely correlated to the Z_DR offset, hence hampering the use of meteorological targets like snow or ice. It is clear that dry snow has lower natural Z_DR variability compared to light rain when using high tilts (40–60^∘). However, this variability increases at lower elevations, and the QVPs are affected by this issue. This is why we restricted the height within the QVPs along with thresholds in ρ_HV in an effort to keep the variability at a minimum.

It is worth mentioning that setting the boundaries of the melting layer correctly within the QVPs is a critical step towards detecting reliable values of the Z_DR offset, as this enables the identification of echoes related to liquid precipitation. Allabakash et al. (2019), Griffin et al. (2020), Lukach et al. (2021) and Sanchez-Rivas and Rico-Ramirez (2021) demonstrated that heights of the ML top and bottom could be accurately estimated using QVPs. We consider that QVPs without ML signatures are filtered by this requirement, thus reducing the uncertainty of using QVPs of polarimetric variables that do not depict light stratiform rain.

To validate the proposed approach, we implemented an operational procedure to detect the Z_DR offset using light-rain measurements taken at vertical incidence. This method was proposed initially by Gorgucci et al. (1999), and it is a boilerplate practice that has been tested on several radar campaigns and has confirmed its reliability by keeping the Z_DR offset below 0.2 dB (Bechini et al., 2002; Frech and Hubbert, 2020; Gourley et al., 2009; Louf et al., 2019). Figures 6 and 7 show the good agreement between both methods: the proposed method based on QVPs shows maximum differences of 0.1 dB compared to the method based on VPs. A few data points exhibit larger variation, but this is mainly caused by vague polarimetric signatures of the ML (no peaks within the polarimetric profiles, especially on those generated from ρ_HV measurements), misleading the ML detection algorithm and, thus, the classification of the particles in the liquid phase. The good performance of the method based on QVPs is also confirmed in Fig. 8, where we evaluated data classified by the disdrometers as related to light to moderate rain rates, and the differences between both Z_DR calibration methods remain around 0.1 dB.

Figures 9–11 show a comparison between radar and disdrometer data. It is important to keep in mind that there is some uncertainty in the interpretation of these results, such as (i) the spatial distribution of radar measurements and the well-known discrepancy when comparing it to a fixed-point location, (ii) the impact of the signal attenuation in Z_H and Z_DR, (iii) the distance between the radars and the disdrometers, (iv) the use of PPI scans collected at higher elevation containing issues related to beam blockage or clutter contamination, and (v) the different temporal resolution of each device. However, the errors (MAE and RMSE) between Z_DR measured by the radar and Z_DR derived from disdrometers are below 0.4 dB in all cases, which is acceptable considering the factors mentioned above but also that this analysis includes 1 year of data related to precipitation events. Furthermore, we compared the disdrometer-derived Z_DR measurements with radar Z_DR measurements but without applying the offset correction procedure, and we observed bigger discrepancies between data sets, reaching differences of the order of 1 dB (plots not shown).

Finally, the case studies shown in Figs. 10 and 11 confirm the good performance of the proposed method to correct the Z_DR offset. These events, related to moderate to intense rain events, exhibit differences below ±0.2 dB. These results are in good agreement with the required accuracy established by Ryzhkov et al. (2005a) to generate reliable quantitative precipitation estimates using polarimetric weather radar data.

6 Conclusions

In this work, we have evaluated different methods for monitoring the calibration of the radar differential reflectivity (Z_DR). We explored the use of vertical profiles to calibrate the radar differential reflectivity. Light rain or dry snow are excellent targets to detect the Z_DR offset, and we consider that these methods must be used when possible. However, some radar systems cannot perform scans at such high elevation angles. Thus, we proposed a novel, operational method to calibrate Z_DR using QVPs of polarimetric variables built from low-elevation scans. This method has the main advantage of not depending on scans taken at vertical incidence or high elevation angles. However, it relies on detecting QVPs depicting stratiform light-rain events (common in the UK), but it may not be suitable for places where heavy-rain events are recurrent. Moreover, we are not suggesting that our approach should replace the well-known Z_DR calibration method based on birdbath scans.

In addition, we carried out several trials using other meteorological targets like dry snow, but the results were inconclusive. Targeting areas above the melting layer exacerbate the beam broadening and non-uniform beam-filling problems as the range increases. These circumstances complicate using dry snow or other solid-phase targets to detect the Z_DR offset on QVPs built from relatively low elevation scans. Thus, we selected the use of light rain, but we proposed several constraints to minimise the variability in Z_DR in this media. Future work may implement a previous hydrometeor classification on the QVPs to improve this method. The proposed method is based on a reference Z_DR value expected at ground level derived from a wide range of DSDs using a range of parameters expected in real storm events. This value (0.18 dB) was computed using constraints related to light rain using Z_H. Additionally, we compared this theoretical Z_DR value to real data derived from disdrometer observations, observing consistency between data.

We applied both methods to precipitation events collected by two C-band weather radars for the whole year of 2018. The proposed method to detect the offset in Z_DR using QVPs was compared against the true offset computed from VPs. We observed a good agreement between both methods, as the MAE and the RMSE are within ±0.1 dB. However, we are aware that this is a relative evaluation; thus, we also implemented evaluation methods using disdrometer measurements. We compared radar Z_DR measurements with Z_DR measurements derived from disdrometer observations, obtaining a good agreement between the various data sets. This long-term evaluation of our method includes different types of precipitation events, ranging from light to heavy rain. We consider that this evaluation process demonstrates the efficacy of the proposed constraints to filter unsuitable QVPs. The proposed method using QVPs generated from PPIs proved to be effective for calibrating and monitoring the radar differential reflectivity as our results are close to those produced by the traditional method that uses birdbath scans.