A new hot-stage microscopy technique for measuring temperature-dependent viscosities of aerosol particles and its application to farnesene secondary organic aerosol

The viscosity of secondary organic aerosol (SOA) is needed to improve predictions of air quality, climate, and atmospheric chemistry. Many techniques have been developed to measure the viscosity of micrometer-sized materials at room temperature; however, few techniques are able to measure viscosity as a function of temperature for these small sample sizes. SOA in the troposphere experience a wide range of temperatures, so measurement of viscosity as a function of temperature is needed. To address this need, a new method was developed based on hot-stage microscopy combined with fluid dynamics simulations. The current method can be used to determine viscosities in the range of roughly 10⁴ to 10⁸ Pa s at temperatures greater than room temperature. Higher viscosities may be measured if experiments are carried out over multiple days. To validate our technique, the viscosities of 1,3,5-tris(1-naphthyl)benzene and phenolphthalein dimethyl ether were measured and compared with values reported in the literature. Good agreement was found between our measurements and literature data. As an application to SOA, the viscosity as a function of temperature for lab-generated farnesene SOA material was measured, giving values ranging from 3.1×10⁶ Pa s at 51 ^∘C to 2.6×10⁴ Pa s at 67 ^∘C. We fit the temperature-dependent data to the Vogel–Fulcher–Tammann (VFT) equation and obtained a fragility parameter for the material of 7.29±0.03, which is very similar to the fragility parameter of 7 reported for α-pinene SOA by Petters and Kasparoglu (2020). These results demonstrate that the viscosity as a function of temperature can be measured for lab-generated SOA material using our hot-stage microscopy method.

1 Introduction

Secondary organic aerosol (SOA) is formed in the atmosphere by the oxidation of volatile and intermediate volatile organic compounds followed by gas-to-particle partitioning of oxidation products (Hallquist et al., 2009; Jimenez et al., 2009). SOA can also be formed by condensed-phase reactions (Ervens et al., 2011; McNeill, 2015). SOA is a major contributor to respirable particulate matter in urban environments, which leads to negative health effects (Lelieveld et al., 2015; Nel, 2005; Pope and Dockery, 2006; Shiraiwa et al., 2017a). SOA also influences climate directly by scattering and absorbing incoming solar radiation as well as indirectly by acting as cloud condensation nuclei and ice-nucleating particles (Masson-Delmotte et al., 2021; Myhre et al., 2013).

Recent work has shown that predictions of the size and mass of SOA can be sensitive to diffusion rates in SOA (Han et al., 2019; Kim et al., 2019; Shiraiwa et al., 2011, 2013; Shiraiwa and Seinfeld, 2012; Vander Wall et al., 2020; Ye et al., 2018; Yli-Juuti et al., 2017; Zaveri et al., 2014, 2018, 2022; Zhang et al., 2019a). Diffusion rates within SOA influence heterogeneous chemistry and condensed-phase photochemistry (Alpert et al., 2021; Dalton and Nizkorodov, 2021; Fitzgerald et al., 2016; Gržinić et al., 2015; Li and Knopf, 2021; Li et al., 2021; Marshall et al., 2016; Schmedding et al., 2020; Shiraiwa et al., 2011; Steimer et al., 2014) and the long-range transport of pollutants (Friedman et al., 2014; Keyte et al., 2013; Mu et al., 2018; Shrivastava et al., 2017; Zelenyuk et al., 2012). Water uptake, and hence ice-nucleating properties of SOA, depend on diffusion rates (Fowler et al., 2020; Ignatius et al., 2016; Ladino et al., 2014; Lata et al., 2021; Lee et al., 2020; Murray et al., 2010; Tumminello et al., 2021). Diffusion rates can also influence crystallization rates within SOA-containing particles (Bodsworth et al., 2010; Fard et al., 2017; Ji et al., 2017; Murray, 2008). As a result, measurements of diffusion rates within SOA as a function of key atmospheric variables, namely relative humidity (RH) and temperature (Porter et al., 2021), are needed. Alternatively, measuring the viscosity of SOA as a function of RH and temperature can be used together with the Stokes–Einstein relation or the fractional Stokes–Einstein relation to calculate diffusion rates within SOA (Evoy et al., 2019, 2020, 2021; Ingram et al., 2021; Price et al., 2016).

Measurement of the viscosity of SOA is challenging due to the exceedingly small amount of SOA material (typically in the microgram range) that can be collected from the atmosphere or environmental chambers in a reasonable amount of time. Nevertheless, several techniques have been developed to measure the viscosity of SOA as a function of relative humidity (RH) at ambient temperatures (Reid et al., 2018). In addition, atomic force microscopy (AFM) techniques have recently been developed for probing the RH-dependent phase state of aerosols (Lee et al., 2020; Lee and Tivanski, 2021; Madawala et al., 2021). Although some of these methods could be extended to different temperatures by making modifications to the techniques (e.g. Logozzo and Preston, 2022), only three methods have been developed and used to measure the viscosity of SOA as a function of temperature. One such method is a dimer relaxation technique to measure viscosities of SOA in the range of 5×10⁵ to 2×10⁷ Pa s at temperatures ranging from −15 to 80 ^∘C (Champion et al., 2019; Petters et al., 2019). This technique has the advantage that the viscosity of the SOA is determined without collecting the material on substrates. On the other hand, this technique is limited to relatively high aerosol number concentrations. Järvinen et al. (2016) used light scattering techniques to measure viscosities of SOA at ∼10⁷ Pa s and for temperatures between −38 and 10 ^∘C (Järvinen et al., 2016). Similar to the dimer relaxation technique, the viscosity of the SOA is determined without collecting the material. Qin et al. (2021) coupled AFM to a temperature-controlled sample module to measure the viscosities in the range of $\sim {\mathrm{10}}^{-\mathrm{3}}$ to 10⁻¹ Pa s at temperatures between 15 and 95 ^∘C for organic particles collected on substrates (Qin et al., 2021). Although SOA in the atmosphere is frequently $>{\mathrm{10}}^{-\mathrm{1}}$ Pa s (Maclean et al., 2021a; Shiraiwa et al., 2017b), at this point, the temperature-dependent AFM technique has only been used to probe particles with viscosities $\le {\mathrm{10}}^{-\mathrm{1}}$ Pa s.

Hot-stage microscopy (HSM) has been used previously to measure the temperature-dependent viscosity of relatively large amounts of samples (>70 mg needed for sample preparation) (Garcia-Valles et al., 2013; Pascual et al., 2001, 2005; Scholze, 1962). In this method, the material of interest, in the form of a powder, is pressed into a cube or cylinder with a length scale on the order of ∼3000 µm. The cube or cylinder is then heated at a fixed rate and viewed with an optical microscope. From images recorded during heating, several characteristic temperatures are determined including the temperature of first shrinkage, the temperature of maximum shrinkage, and the temperature for half-ball formation. Viscosities are then estimated for these characteristic temperatures by comparison with characteristic temperatures of laboratory standards having well-known viscosities. For this procedure to be accurate, the material of interest must have a similar surface tension, contact angle, and slip length (a measure of resistance to flow at a solid substrate) as the laboratory standards. Note that this procedure will not work with SOA due to the small amount of SOA material that can be collected on a reasonable timescale. In addition, SOA can have a wide range of properties (and hence surface tensions, contact angles, and slip lengths), so what to use as an appropriate laboratory standard is unclear.

In the following, we develop a new methodology for measuring the viscosity of SOA material as a function of temperature, building on the HSM technique discussed above. In our method, many SOA particles are coalesced into one larger particle with an area-equivalent diameter of ∼60 to 190 µm and placed on a hot stage coupled to an optical microscope. The temperature of the hot stage is then increased rapidly to a temperature of interest and held at this temperature for an extended time. Images of the particles are recorded as a function of time at this fixed temperature. If the temperature is hot enough, the shape of the particles changes to reduce the overall surface energy of the system. Fluid dynamic simulations are then used to determine the viscosity of the material from the change in the shape of the particles during the observation time at the fixed temperature. The fluid dynamics simulations explicitly account for the surface tension, contact angle, and slip length of the material. The technique can be used to measure the viscosity of small amounts of SOA material (<1 mg of material is needed for sample preparation). The viscosity measurements described here can be made on SOA material collected on substrates, and as result they do not have to be made at the same location or time as SOA generation or collection. The methodology presented here is complementary to the dimer relaxation, light scattering, and AFM techniques discussed above for measuring temperature-dependent viscosities of SOA material. Our new methodology also uses inexpensive equipment that is available in many laboratories.

To validate our HSM technique, the viscosities of 1,3,5-tris(1-naphthyl)benzene (TαNB) (Fig. 1a) and phenolphthalein dimethyl ether (PDE) (Fig. 1b) were measured as a function of temperature and the results were compared to literature values. TαNB and PDE were chosen for the validation measurements since these materials readily form an amorphous solid at room temperature (a prerequisite for our measurements), and the temperature-dependent viscosity of this material has been reported in the literature (Plazek et al., 1999; Stickel et al., 1996). We show that the viscosities determined with our new methodology are consistent with the viscosities reported in the literature for TαNB and PDE.

Figure 1 Chemical structures of (a) 1,3,5-tris(1-naphthyl)benzene, (b) phenolphthalein dimethyl ether, and (c) farnesene.

As the first application of our new methodology, the temperature-dependent viscosity of SOA material generated from the photooxidation of farnesene was measured. Farnesene (Fig. 1c), an acyclic sesquiterpene, can be a significant component of biogenic volatile organic compounds (VOCs) emitted to the atmosphere from trees, shrubs, grasslands, and crops (Bouvier-Brown et al., 2009; Geron and Arnts, 2010; Helmig et al., 2006; Li and Xie, 2014; Ylisirniö et al., 2020). Plants have increased emission rates of farnesene and other sesquiterpenes under periods of insect herbivory, heat, and drought stress, which is projected to increase due to climate change, making farnesene an interesting VOC to study (Faiola et al., 2019; Mentel et al., 2013). Previous work has shown that farnesene reacts with atmospheric oxidants such as ozone (O₃), hydroxyl radicals (OH), and nitrate radicals (NO₃) to form SOA with a high yield (Jaoui et al., 2013). Acyclic terpenes, such as farnesene, tend to break down into smaller products during O₃ oxidation but not OH or NO₃ oxidation. As a result, SOA yields from plants can depend strongly on the prevailing oxidant (Faiola et al., 2019). The viscosity of SOA generated from a mixture of VOCs including farnesene has been studied at room temperature (Smith et al., 2021), but the viscosity of SOA generated from only farnesene has not been studied at room temperature or as a function of temperature.

In addition to measuring the temperature-dependent viscosities of farnesene SOA material, we also determined the chemical composition of the farnesene SOA using high-resolution mass spectrometry. The measured viscosity was then compared with predictions based on the chemical composition coupled with the parameterization presented in DeRieux et al. (2018). The DeRieux et al. (2018) parameterization has often been used to predict the viscosity and glass transition temperatures of SOA (DeRieux et al., 2018; Ditto et al., 2019; Gervasi et al., 2020; Maclean et al., 2021b; Pratap et al., 2018; Riva et al., 2019; Schum et al., 2018; Slade et al., 2019; Tikkanen et al., 2020; Wolf et al., 2019; Zhang et al., 2019a, b), but the accuracy of this parameterization for predicting the viscosity of SOA has not been previously tested for SOA produced from acyclic terpenes.

2 Materials and methods

2.1 Generation of amorphous solid particles

To be compatible with our new technique, the material must have the following properties: (1) the material must be amorphous (i.e. non-crystalline), (2) the material must have a viscosity greater than approximately 10⁸ Pa s at room temperature so the material does not flow significantly on a timescale of hours at room temperature, (3) the material must be in the form of particles with dimensions ∼ 20–300 µm, and (4) the particles must be in a non-equilibrium geometry at the start of the experiments. Below is a description of how we generated particles with these properties for TαNB, PDE, and farnesene SOA material.

When purchased, 1,3,5-tris(1-naphthyl)benzene (TRC Canada) and phenolphthalein dimethyl ether (Polymer Source) were in a crystalline state. To generate amorphous solid particles of TαNB and PDE with the properties discussed above, the following procedure was used: first some of the crystalline material was placed on a glass slide, and the temperature of the slide was increased to a temperature above the melting point of the crystalline material (TαNB: mp = 184–186 ^∘C; PDE: mp = 100 ^∘C). After the crystalline material had melted, the temperature was rapidly decreased (∼2 ^∘C s⁻¹) to room temperature, resulting in the formation of a glassy material (Magill and Plazek, 1967; Plazek and Magill, 1966; Stickel et al., 1996). The glassy material was then scraped off the slide with a razor blade, forming amorphous solid particles in a non-equilibrium geometry (i.e. jagged geometry) with area-equivalent diameters ranging from ∼60 to 190 µm. The formation of a glass state was verified by showing that the material flowed at a temperature significantly lower than the melting temperature of the crystalline material (see below).

Farnesene SOA particles were generated by photooxidation of farnesene in a 5 m³ environmental chamber operated in batch mode at 50 % RH and room temperature (21–23 ^∘C), similar to previous work (Smith et al., 2021). A farnesene isomer mixture (Sigma-Aldrich, product no.: W383902) was injected into the chamber (8 µL) and a proton-transfer-reaction time-of-flight mass spectrometer (PTR-ToF-MS; Ionicon model 8000) with H₃O⁺ as the reagent ion was used to confirm the completeness of injection of the farnesene precursor into the chamber by monitoring $m/z$ 205 (protonated farnesene). The initial mixing ratio of farnesene was ∼160 ppb for all experiments. Next, H₂O₂ (45 µL of 30 wt % H₂O₂ in water) was added to the chamber through a heated inlet (50 ^∘C), resulting in 2 ppm of H₂O₂ in the chamber. Photooxidation was initiated by turning on a bank of UV-B lights, which led to the production of OH radicals by photodissociation of H₂O₂ (Smith et al., 2021).

No seeds were used during SOA generation to avoid interference with viscosity measurements. Particle size and number concentration were measured using a scanning mobility particle sizer (SMPS; TSI differential mobility analyzer model 3080 and CPC model 3775). During photooxidation, the mass concentration of SOA in the chamber reached approximately 500 µg m⁻³. After SOA was generated, the UV-B lights were turned off, and SOA particles were collected onto hydrophobic glass substrates placed on stage 9 of a non-rotating micro-orifice uniform deposit impactor (MOUDI) operated at 30 L min⁻¹ with all the remaining MOUDI stages removed as discussed elsewhere (Smith et al., 2021). Hydrophobic glass slides were generated by coating plain glass slides with FluoroPel 800 (Cytonix USA). Samples were collected for 3 h. This method of collection resulted in droplets with spherical cap geometries and diameters of ∼30 to 250 µm, formed by the aggregation of smaller SOA particles on the hydrophobic glass substrates. These droplets are not expected to contain crystalline material, since SOA consists of hundreds of different compounds, and the concentration of any given compound is not expected to be high enough for crystallization (Marcolli et al., 2004). Furthermore, optical images of SOA particles are consistent with a non-crystalline state for the SOA. After collection, samples were placed in protective plastic enclosures, sealed with a vacuum food sealer, and stored in a freezer at −20 ^∘C until analysis (except for 24 h transit time when the samples had to be shipped to other participating laboratories on ice at 0 ^∘C). To prepare the sample for the viscosity measurements, some of the SOA material was scraped off the slide using a razor blade, resulting in amorphous solid particles with non-equilibrium geometries and area-equivalent diameters of ∼80 to 170 µm.

2.2 Hot-stage microscope

After the amorphous solid particles were generated, one or more of the particles was attached to the flat end of an ultra-fine tungsten needle (Roboz Surgical Instruments Co.) by bringing the end in contact with the amorphous particles. This needle was then placed in the HSM apparatus for the viscosity measurements. The HSM apparatus consists of a temperature control stage (HC321Gi, INSTEC) mounted above an optical transmission microscope (Zeiss Axio Observer) (Fig. 2a). The needle was held in place using an aluminum needle holder (Fig. 2b), and the needle was situated so that the flat end of the needle hung over the edge of the viewing window for imaging. This configuration enabled a side view of the solid amorphous particles during heating.

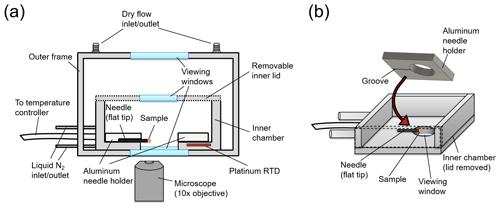
Figure 2 Schematic of the hot-stage microscopy apparatus, where panel (a) is a cross-section of the whole apparatus and panel (b) shows a perspective view of the inner chamber of the temperature control stage.

The temperature of the hot stage was controlled by offsetting hot and cold inputs. The cold input was supplied by a liquid nitrogen flow around the walls of the inner chamber and the hot input was supplied by electrical heaters connected to a temperature controller box (mk2000, INSTEC). The temperature of the hot stage was measured with a platinum resistance temperature detector (RTD) (Fig. 2a). The temperature offset between the RTD reading and the flat end of the needle was determined by measuring the melting point of a range of substances (diphenyl ether, 1-octadecanol, glutaric acid, pimelic acid, vanillyl mandelic acid, and cholesterol) placed on the flat end of the needle and by comparing the measurements with melting temperatures reported in the literature for these substances. The temperature ramp used when measuring the melting points was 0.1 ^∘C min⁻¹ and images from the melting point experiments were analyzed with the Zen Microscopy software (Zeiss). From the melting point experiments, a calibration curve was generated (Fig. S1 in the Supplement). This calibration curve was used to determine the temperature offset for the viscosity measurements.

2.3 Viscosity measurements

In a typical experiment used to determine the viscosity of particles, the temperature control stage was first purged with nitrogen. For the farnesene SOA experiments, the samples were purged with nitrogen for at least 75 min before heating, since farnesene SOA is hygroscopic. The viscosity results were not strongly sensitive to conditioning times between 75 and 200 min (Fig. S2). If the farnesene SOA material did not reach equilibrium after purging (i.e. it still contained some water), the viscosities reported here should be regarded as lower limits to the viscosity of dry farnesene SOA, since water acts as a plasticizer (i.e. decreases the viscosity of highly viscous material). After purging the cell with nitrogen, the temperature of the cell was increased at a rate of ∼2 ^∘C s⁻¹ to an experimental temperature, T_exp. During heating, images were recorded as a function of time. Due to the fast ramp rate, the temperature slightly overshot the desired T_exp in each experiment and then oscillated around T_exp, with the oscillations decreasing with time (e.g. Fig. 3). The start of the experiment (i.e. t=0) was defined as the first image captured after the temperature oscillation was <2 ^∘C.

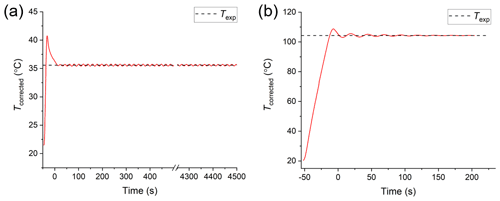
Figure 3 Temperature profiles from hot-stage microscopy experiments. Beginning at room temperature (prior to t=0), the temperature ramps at ∼2 ^∘C s⁻¹ to the experimental temperature (T_exp; black dashed line). The start of the experiment (t=0) begins once the temperature oscillations about T_exp are <2 ^∘C. The profile in panel (a) is an example of the minimum temperature used (35.6 ^∘C) and in panel (b) is an example of the maximum (104.3 ^∘C).

At the start of the viscosity measurements, the amorphous solid particles were non-spherical (e.g. Figs. 4–6a, c). If the temperature used in the experiment (T_exp) was hot enough, the material began to flow to minimize the surface energy of the system. To relate the flow of the particle to the particle's viscosity, a quantitative measure of the shape change was needed.

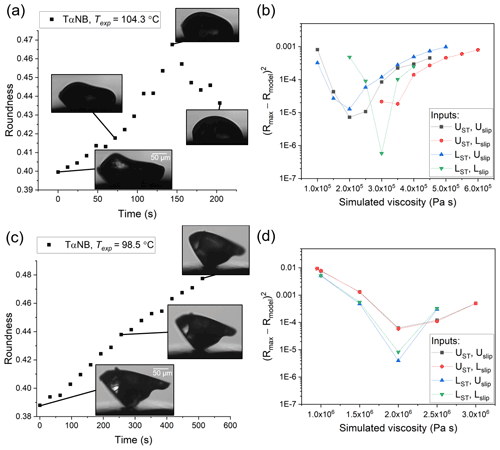
Figure 4 Hot-stage microscopy experiments with TαNB. Roundness as a function of time at (a) 104.3 ^∘C and (c) 98.5 ^∘C. The squared difference between observed and simulated roundness as a function of simulated viscosity for the two sample TαNB experiments, where panel (b) corresponds to panel (a) and panel (d) to panel (c). The simulation that best reproduces the observation corresponds to the minimum sum of squared difference. The different colors correspond to different input combinations of surface tension and slip length used in the simulations, where U_ST, U_slip, L_ST, and L_slip correspond to the upper limit of surface tension, the upper limit of slip length, the lower limit of surface tension, and the lower limit of slip length, respectively.

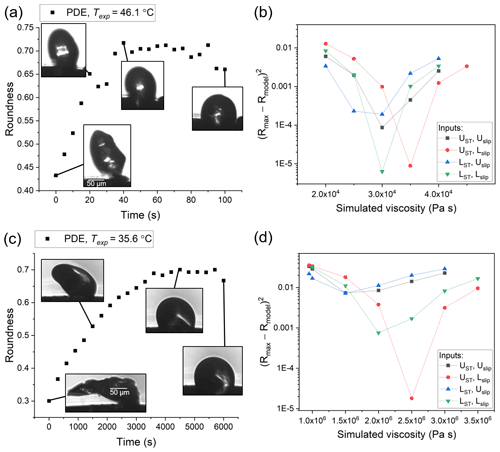
Figure 5 Hot-stage microscopy experiments with PDE. Roundness as a function of time at (a) 46.1 ^∘C and (c) 35.6 ^∘C. The squared difference between observed and simulated roundness as a function of simulated viscosity for the two sample experiments, where panel (b) corresponds to panel (a) and panel (d) to panel (c). The simulation that best reproduces the observation corresponds to the minimum sum of squared difference. The different colors correspond to different input combinations of surface tension and slip length used in the simulations, where U_ST, U_slip, L_ST, and L_slip correspond to the upper limit of surface tension, the upper limit of slip length, the lower limit of surface tension, and the lower limit of slip length, respectively.

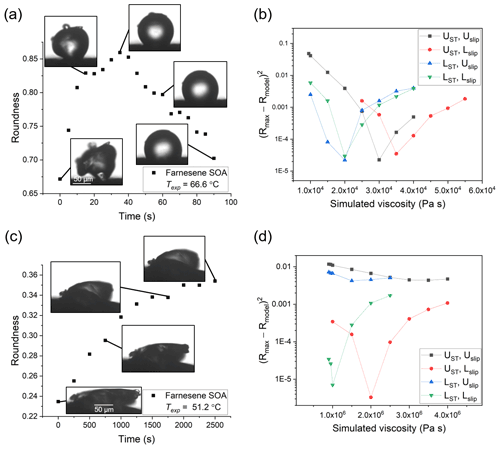
Figure 6 Hot-stage microscopy experiments with farnesene SOA material. Roundness as a function of time at (a) 66.6 ^∘C and (c) 51.2 ^∘C. The squared difference between observed and simulated roundness as a function of simulated viscosity for the two sample experiments, where panel (b) corresponds to panel (a) and panel (d) to panel (c). The simulation that best reproduces the observation corresponds to the minimum sum of squared difference. The different colors correspond to different input combinations of surface tension and slip length used in the simulations, where U_ST, U_slip, L_ST, and L_slip correspond to the upper limit of surface tension, the upper limit of slip length, the lower limit of surface tension, and the lower limit of slip length, respectively.

To quantify the shape change we used roundness, which is a measure of how close the shape is to a circle (a roundness value of 1 indicates a perfect circle). Roundness was calculated with the following equation:

$$\begin{array}{}\text{(1)}& \text{roundness}={\displaystyle \frac{\mathrm{4}A}{\mathit{\pi }{\left(L_{\mathrm{Feret},\max }\right)}^{\mathrm{2}}}},\end{array}$$

where A is the projected area of the particle and L_Feret,max is the maximum Feret length of the 2-D projection, which is defined as the maximum distance between two parallel tangential planes to the projected 2-D geometry. The image analysis software ImageJ was used to process the images recorded during the experiments. The silhouette of the needle was removed from the images, and the images were subsequently binarized. The threshold for binarization was calculated using the default ImageJ settings in all but a few cases. In the few exceptions, the default threshold method was clearly not capturing the particle's shape, so the “Mean” threshold method was used instead. For a different microscope set-up with different lighting, a different threshold method may be more accurate than the one chosen here. The roundness was then determined from the sequence of binary images using an image analysis script. This script measures the roundness of binary images by differentiating between black and white pixels and then calculating the area and L_Feret,max. The area is calculated by counting the number of black pixels. The L_Feret,max is determined by mapping the black pixels on the perimeter of the object and subsequently finding the maximum distance between two diametrically opposed points on the convex hull that encloses the object. One limitation of this approach is that the focus and lighting during image capture can vary across experiments. However, experiments were only analyzed if a majority of the particle was in focus during the experiments, so any uncertainty due to variability in lighting and focus is very likely to be negligible. Note, in these experiments, the effect of gravity on the shape of the particles is expected to be negligible because the force due to gravity (F_g) acting on the particle is much smaller than the surface tension force (F_ST) acting on the particle (Sect. S3 in the Supplement).

In HSM experiments with TαNB, PDE, and farnesene SOA material, if the temperature was hot enough for the substance to flow, the roundness of the particles first increased to minimize the surface area of the particle and then decreased as the material spread on the surface (e.g. Figs. 4–6a, c). From the images, we determined the maximum roundness (R_max) and the time necessary to reach R_max, defined here as the experimental flow time, τ_exp,flow. The τ_exp,flow and R_max values were then used in the fluid dynamics simulations discussed below to determine the viscosity. In some cases with TαNB and PDE, crystallization occurred before the maximum roundness was observed. In these experiments, τ_exp,flow was assigned as the time just before crystallization was observed and the roundness at τ_exp,flow was assigned R_max.

2.4 Fluid dynamics simulations

To extract viscosity values from the experiments, the physics software COMSOL Multiphysics (v5.4) was used. The Microphysics Module within COMSOL was used along with a two-phase laminar flow and moving mesh. Only the 2-D silhouette of the particle could be imaged; the 3-D morphology of the particles was not known. Therefore, a 2-D model was used to represent particle shape in the simulations which has the added benefit of reduced simulation times. Sensitivity tests show that viscosities determined with a 2-D model are similar to viscosities determined with a 3-D model (see Sect. 3.3). The initial 2-D geometry used in the simulations was the same as the projected geometry observed in the HSM experiments. To obtain the same initial 2-D geometry, the initial projected geometry captured during the HSM experiment was binarized and imported into COMSOL. For the simulations, slip length, surface tension, and contact angles were needed. For slip lengths and surface tensions, conservative upper and lower limits were estimated based on literature values (Table 1). For contact angles, 37.5, 50.5, and 29.9^∘ were used for TαNB, PDE, and farnesene SOA material, respectively, based on measurements (see Sect. 2.5).

Table 1 Input values of surface tension and slip length used in fluid dynamics simulations.

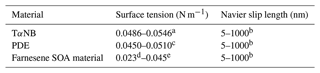
^a The surface tension of TαNB was reported to be 0.0516 N m⁻¹, based on the ACD/Labs Percepta Platform-PhysChem Module retrieved from ChemSpider. The upper and lower limits correspond to the reported uncertainty of ±0.0030 N m⁻¹.
^b The range of values for Navier slip length is based on values reported in the literature (Baudry et al., 2001; Bhushan et al., 2009; Cho et al., 2004; Churaev et al., 1984; Cottin-Bizonne et al., 2002, 2005; Craig et al., 2001; Jing and Bhushan, 2013; Joseph and Tabeling, 2005; Mcbride and Law, 2009; Tretheway and Meinhart, 2002; Vinogradova et al., 2009; Zhu et al., 2012).
^c The surface tension of PDE was reported to be 0.0480 N m⁻¹, based on the ACD/Labs Percepta Platform-PhysChem Module retrieved from ChemSpider. The upper and lower limits correspond to the reported uncertainty of ±0.0030 N m⁻¹.
^d The lower limit for the surface tension of farnesene SOA material was the lower uncertainty of the ACD/Labs value for farnesene retrieved from ChemSpider.
^e The upper limit for the surface tension of farnesene SOA material is an upper limit to surface tensions reported in the literature for water + SOA solutions and common SOA functional groups such as alcohols, organic acids, esters, and ketones (Demond and Lindner, 1993; Gorkowski et al., 2020; Gray Bé et al., 2017; Hritz et al., 2016).

The time used in the simulations, τ_model, was set to τ_exp,flow. The output of a simulation was a binary 2-D image of the final geometry at τ_model. The roundness of the final 2-D geometry, R_model, was then calculated with the same MATLAB script as used for the images recorded during HSM experiments (see above). R_model was then compared to R_max by calculating the squared difference between R_model and R_max. The viscosity in the simulation was then varied, and the squared difference between R_model and R_max was determined as a function of the viscosity. This procedure was repeated using upper and lower limits for the surface tension and upper and lower limits for the slip length, resulting in four plots of the squared difference between R_model and R_max as a function of viscosity for each experiment (e.g. Figs. 4–6b, d). From each plot, the viscosity that gave the smallest squared difference between R_model and R_max was identified, resulting in four viscosities for each experiment. The largest and smallest viscosities from these four minima were assigned as the upper and lower limits for the experiment. This whole process was then repeated for several experiments. The upper limit was assigned as the average of the upper limit values from replicate experiments summed with the standard error of the mean. The lower limit was assigned as the average of the lower limit values subtracted by the standard error of the mean.

2.5 Contact angle measurements

For the fluid dynamics simulations discussed above, the contact angle between the material studied and the substrate was needed. To determine these contact angles, the material was heated to the point where it had completely liquefied, flowed, and reached an equilibrium geometry on the flat end of the ultra-fine needle (e.g. Fig. S3). The equilibrium contact angle between the material and the flat end of an ultra-fine tungsten needle was then measured directly from captured images using the ImageJ angle tool. Based on at least five measurements, the average contact angles for TαNB, PDE, and farnesene SOA material were 37.5±4.0, 50.5±5.4, and 29.9±4.3^∘, respectively, where the uncertainties are twice the standard error of the mean. The simulations described above used the average contact angles determined with this approach. However, changing the contact angle in the simulations by ±2σ only changed the viscosity in the simulations by 5 % of an order of magnitude at most, which was considered small compared to the uncertainties in the reported viscosities.

2.6 Measurements of the chemical composition of farnesene SOA using mass spectrometry

To determine the chemical composition of the SOA, the SOA was generated in the environmental chamber using the same procedure as discussed above and then collected onto aluminum foil, followed by extraction in 1:1 ($v/v$) liquid chromatography–mass spectrometry (LCMS) grade acetonitrile and water. The chemical composition of the extracted SOA was obtained in positive and negative ionization mode using ultra-performance liquid chromatography–photodiode array detection–electrospray ionization–high-resolution mass spectrometry (UPLC-PDA-ESI-HRMS). A Vanquish Horizon UPLC (Thermo Scientific) was equipped with a Luna 1.6 µm Omega Polar C18 (150×2.1 mm column). Solvents A and B used during liquid chromatography were high-performance liquid chromatography (HPLC) grade acetonitrile (containing 0.1 % $v/v$ formic acid) and water (also with 0.1 % $v/v$ formic acid), respectively. A Q-Exactive Plus Orbitrap mass spectrometer (Thermo Scientific) with a mass resolving power of $\sim \mathrm{1.4}\times {\mathrm{10}}^{\mathrm{5}}$ at $m/z$ 200 was used, and data were acquired from $m/z$ 50 to $m/z$ 750. The ESI source parameters were set to a spray voltage of +3.5 kV in positive mode and −2.5 kV in negative mode, the capillary temperature was 320 ^∘C, and the S-lens ion funnel radiofrequency (RF) level was 50. In addition to the samples, a solvent blank was prepared following the same procedure above but using a clean aluminum foil substrate without analyte. The analysis procedure of the mass spectrometry data has been described in detail previously (Maclean et al., 2021a; Smith et al., 2021). Briefly, the peaks were integrated and extracted from the mass spectra from 2 to 16 min corresponding to SOA elution in the chromatogram, and peaks containing 13C isotopes were removed. All peaks were assigned to the formulas C_xH_yO_z with an accuracy of $m/z$ 0.0005 units while containing the assignments to closed-shell ions with even nominal masses and constraining $\mathrm{H}/\mathrm{C}$ to 0.30–2.25 and $\mathrm{O}/\mathrm{C}$ to 0.00–2.30. Masses were only considered if they were 3 times more abundant in the sample compared to the blank. The assigned ion formulas were corrected for the ionization mechanism, and all the HRMS results below are reported as formulas of neutral SOA compounds. The assumed ionization mechanisms were the formation of adducts with H⁺ or Na⁺ for positive ions and deprotonation for negative ions.

2.7 Predictions of the temperature-dependent viscosity of farnesene SOA using the chemical composition

The temperature-dependent viscosity of farnesene SOA was predicted from the chemical composition of farnesene SOA using the method in DeRieux et al. (2018). First, the T_g of each compound identified in the HRMS was determined using Eq. (2), which relates the number of C, H, and O in a compound, i, to its T_g (DeRieux et al., 2018):

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{T}_{\mathrm{g},i}=& \left(n_{\mathrm{C}}^{\mathrm{0}}-\ln \left(n_{\mathrm{C}}\right)\right)b_{\mathrm{C}}+\ln \left(n_{\mathrm{H}}\right)b_{\mathrm{H}}\\ & +\ln \left(n_{\mathrm{C}}\right)\ln \left(n_{\mathrm{H}}\right)b_{\mathrm{CH}}\\ & +\ln \left(n_{\mathrm{O}}\right)b_{\mathrm{O}}+\ln \left(n_{\mathrm{C}}\right)\ln \left(n_{\mathrm{O}}\right)b_{\mathrm{CO}},\end{array}\end{array}$$

where n_C, n_H, and n_O are the number of carbon, hydrogen, and oxygen, respectively. The coefficients $n_{\mathrm{C}}^{\mathrm{0}}$, b_C, b_H, b_CH, b_O, and b_CO were 12.13, 10.95, −41.82, 21.61, 118.96, and −24.38, respectively, for CHO-containing compounds.

Next, the T_g of the overall SOA (for dry conditions) was calculated using the Gordan–Taylor equation (Gordan and Taylor, 1952) with an assumed Gordan–Taylor constant (k_GT) of 1:

$$\begin{array}{}\text{(3)}& T_{\mathrm{g},\mathrm{org}}={\sum }_i{w}_i{T}_{\mathrm{g},i},\end{array}$$

where w_i is the mass fraction of component i. The w_i values were assumed to be proportional to the relative abundance (I_i) in the combined mass spectra, that is,

$$\begin{array}{}\text{(4)}& w_i=I_i.\end{array}$$

As described previously, this assumption is a limitation of these viscosity predictions (DeRieux et al., 2018; Song et al., 2019). The Vogel–Fulcher–Tammann equation was used to describe the temperature dependence of viscosity (Fulcher, 1925):

$$\begin{array}{}\text{(5)}& {\log }_{\mathrm{10}}\mathit{\eta }=A+\mathrm{0.434}{\displaystyle \frac{D_{\mathrm{f}}{T}_{\mathrm{0}}}{T-T_{\mathrm{0}}}},\end{array}$$

where η is viscosity, T is temperature, D_f is the fragility parameter, T₀ is the Vogel temperature, and $A=-\mathrm{5}$ (Angell, 1991). We assumed D_f=10, as done previously (Gervasi et al., 2020; Maclean et al., 2021a, b; Shiraiwa et al., 2017b). The Vogel temperature, T₀, was determined from Eq. (6) below, which is derived from Eq. (5), assuming the viscosity is 10¹² Pa s at T=T_g (Angell, 1991, 2002):

$$\begin{array}{}\text{(6)}& T_{\mathrm{0}}={\displaystyle \frac{\mathrm{39.17}{T}_{\mathrm{g}}}{D_{\mathrm{f}}+\mathrm{39.17}}},\end{array}$$

where T_g was obtained from Eq. (3) and D_f was set to 10. Once T₀ was calculated, a Vogel–Fulcher–Tammann (VFT) curve was constructed using Eq. (5).

3 Results and discussion

3.1 Measured viscosities of TαNB and PDE

The viscosity of TαNB was measured at 98.5 and 104.3 ^∘C, and the viscosity of PDE was measured at 35.6, 40.9, and 46.6 ^∘C. At each temperature, the experimental flow time, τ_exp,flow, and maximum roundness, R_max, was determined for at least two different particles (Tables S1 and S2 in the Supplement). On average, the τ_exp,flow value decreased as temperature increased, as expected. The 2-D fluid dynamics simulations (Sect. 2.4) were used to convert τ_exp,flow and R_max values to viscosities. Upper and lower limits for the viscosities were determined from each experiment and combined to give an overall upper and lower limit to the viscosity of the material (Fig. 7). The viscosity midpoints for TαNB at 98.5 and 104.3 ^∘C were 1.1×10⁶ and 2.8×10⁵ Pa s, respectively. The viscosity midpoints for PDE at 35.6, 40.9, and 46.6 ^∘C were 8.2×10⁶, 2.4×10⁵, and 3.5×10⁴ Pa s, respectively. For reference, the room temperature viscosities of tar pitch and lard are 10⁸ and 10³ Pa s, respectively. For TαNB, the viscosity decreased by a factor of ∼4 for a 5.8 ^∘C increase in temperature. For PDE, the viscosity decreased by roughly 2.5 orders of magnitude for a ∼11.0 ^∘C increase in temperature.

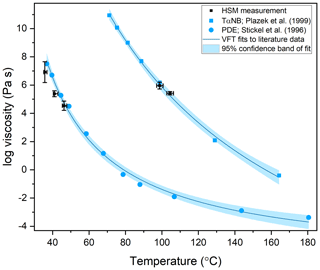
Figure 7 The viscosity of TαNB and PDE as a function of temperature. The blue squares are measurements of TαNB from Plazek et al. (1999), and the blue circles are measurements of PDE from Stickel et al. (1996). The blue trend lines are a Vogel–Fulcher–Tammann (VFT) fit to the literature data sets, with the light blue area corresponding to the 95 % confidence band of the fits. The black data points are the midpoint of the upper and lower limits measured with the hot-stage microscopy (HSM) technique. The y-error bars correspond to the calculated upper and lower limits of viscosity from at least two separate experiments. The temperature uncertainty (x error) is a propagation of the uncertainty in the temperature control stage calibration and the largest temperature oscillation during the experiment. Note that for PDE, the x-error bars are asymmetric because the largest temperature oscillation was always toward hotter temperatures.

The measured viscosities of TαNB and PDE were compared to literature values from Plazek et al. (1999) and Stickel et al. (1996) by applying VFT fits to their data, indicated by the blue lines in Fig. 7, with the light blue shading representing the 95 % confidence intervals of the fits. The viscosity measured using our HSM method agrees with the literature values, within the uncertainty of our measurements and the VFT fit to their data, suggesting our approach is valid for determining temperature-dependent viscosities of small samples (<1 mg of material).

The temperature ranges over which we reported viscosities for TαNB and PDE were quite narrow (temperature ranges of 5.8 and 11.0 ^∘C, respectively). The upper limit of the temperature range in our experiments is limited by flow becoming so fast that R_max is reached before the temperature has stabilized (oscillations <2 ^∘C) at T_exp. At T_exp=104.3 ^∘C, R_max is reached in ∼1 min, so the upper-temperature range in our experiments for TαNB is likely only a few degrees warmer. Similarly, for PDE at T_exp=46.6 ^∘C, R_max was reached in <45 s. The lower limit of the temperature ranges for TαNB and PDE experiments was restricted, in part because crystallization became dominant at colder temperatures. However, wider temperature ranges should be possible for other amorphous materials where crystallization does not occur.

3.2 Measured viscosity of farnesene SOA material

The viscosity of farnesene SOA material was determined at temperatures of 51.2, 61.5, and 66.6 ^∘C. For each experiment, τ_exp,flow, R_max, and the upper and lower limits to the viscosities were determined using the observed projected geometry and 2-D fluid dynamics simulations (Table S3). On average, τ_exp,flow increased with colder temperature: as the temperature decreased by ∼15 ^∘C, τ_exp,flow increased by ∼2 orders of magnitude. At T_exp=66.6 ^∘C, the temperature was near the upper limit of the measurable temperature range, since τ_exp,flow was ∼30 s at this temperature. It could be possible to do experiments a couple of degrees warmer, but soon the flow will be so fast that R_max is reached before the temperature stabilizes (oscillations <2 ^∘C) at T_exp. On the lower end, we chose T_exp=51.2 ^∘C for the practical purpose of keeping τ_exp,flow less than a few hours. In principle, the τ_exp,flow in our experiments could be as long as multiple days.

The viscosity midpoints determined from the fluid dynamics simulations for farnesene SOA at T_exp= 51.2, 61.5, and 66.6 ^∘C were 3.1×10⁶, 1.1×10⁵, and 2.6×10⁴ Pa s, respectively (Fig. 8). These viscosities fall between the viscosities of tar pitch (viscosity =10⁸ Pa s) and lard (viscosity =10³ Pa s).

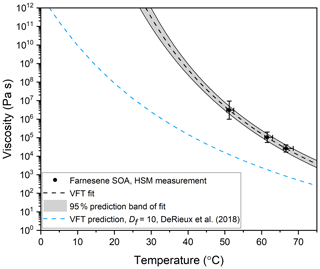
Figure 8 Viscosity as a function of temperature for farnesene SOA material. The black data points represent the midpoint of the upper and lower limits of viscosity, measured with hot-stage microscopy (HSM). The y-error bars correspond to the calculated upper and lower limits of viscosity from at least two separate experiments. The temperature uncertainty (x error) is a propagation of the uncertainty in the temperature control stage calibration and the largest temperature oscillation during the experiment. Note that the x-error bars are asymmetric because the largest temperature oscillation was always toward hotter temperatures. The black dotted line is a VFT fit to the HSM measurements, with the grey area representing the 95 % prediction band of the fit. In the VFT fit, D_f and T₀ were left as free parameters, while A was fixed at −5. This fit was extrapolated to 10¹² Pa s, yielding a T_g of 302 K. The blue dashed line is the prediction using the method in DeRieux et al. (2018) with HRMS data and of D_f=10, which yields a T_g of 275 K.

3.3 Sensitivity to the geometry assumed in the fluid dynamics simulations

All the viscosity results discussed above were determined using fluid dynamic simulations and a 2-D model to describe the HSM experiments. A 2-D model was used to minimize computation time and because the actual 3-D morphology of the particles was not known. To test if the simulated viscosities were sensitive to the assumed morphology (2-D vs. 3-D), we compared simulations with both 2-D and 3-D geometries for a few experimental conditions. To create a 3-D geometry, the 2-D geometry was expanded into 3-D by using the “extrude” function in COMSOL (e.g. Fig. S4). To determine the extrude depth, we used the conservation of mass. Specifically, we assumed the depth of the extrusion was equal to the particle volume (V) divided by the initial 2-D area (A_i). A_i was measured directly using ImageJ. V was determined from images of the particles after they had flowed and reached an equilibrium geometry, assuming a spherical cap geometry. The difference in simulated viscosity between the 2-D and 3-D simulations was minor (Table S4). Specifically, for TαNB, the upper and lower limits of viscosity calculated using the 3-D geometry fell within the upper and lower limits of the 2-D geometry. For farnesene SOA material, the upper and lower limits of viscosity were equivalent for 2-D and 3-D. Based on the 2-D vs. 3-D results for both TαNB and farnesene SOA material, 2-D simulations were deemed adequate, since there were only minor variations in simulated viscosity and there was a significant amount of saved computation time (∼5 s for each 2-D simulation compared to ∼ 7–45 min for each 3-D simulation).

3.4 Predicted viscosities of farnesene SOA based on chemical composition

The combined mass spectra for farnesene photooxidation SOA in positive and negative mode are shown as a function of neutral mass and normalized to the largest peak in each mode (Fig. S5). The chemical composition of the SOA is discussed in Sect. S7, including a summary of compounds that have been previously identified in the literature (Table S5). Based on the HRMS data and Eq. (3), the glass transition temperature for farnesene SOA was predicted to be T_g=275 K. This value, together with Eqs. (5) and (6), was used to predict the viscosity of farnesene SOA (blue dashed curve in Fig. 8). Assuming a D_f value of 10, as done previously, the predicted viscosities were ∼ 1–2 orders of magnitude less than the measured viscosities. This level of disagreement is not surprising considering the uncertainties in the parameterization and the uncertainty in the composition of the SOA material. For example, as shown by Angell (1997), and discussed in Gervasi et al. (2020), the D_f value for organics is typically in the range of ∼ 5–30 (Angell, 1997; Gervasi et al., 2020). Furthermore, in-source fragmentation may have occurred for farnesene SOA during the UPLC-PDA-ESI-HRMS analysis. In-source fragmentation could lead to smaller molecular-weight compounds seen in the mass spectra <250 Da and the presence of compounds containing less than 10 carbons (Fig. S6). These lower molecular-weight compounds would lead to lower calculated glass transition temperatures and therefore contribute to an overall lower predicted viscosity than the experimentally determined viscosity values. Future studies are needed in order to confirm if this phenomenon is happening for farnesene SOA.

An alternative approach for interpreting temperature-dependent viscosity data used by Rothfuss and Petters (2017) and Marsh et al. (2018) involves fitting the VFT equation to the temperature-dependent viscosity data to estimate D_f, T₀, and T_g values for the material (Marsh et al., 2018; Rothfuss and Petters, 2017). In Fig. 8 we follow this approach. The VFT equation was fit to the experimental data with D_f and T₀ as free parameters, and A fixed at −5 as done previously. Using this approach, we get a D_f value of 7.29±0.03, a T₀ value of 254.4±0.3 K, and a T_g value of $\mathrm{301.7}\begin{array}{c}+\mathrm{1.4}\\ -\mathrm{1.7}\end{array}$ K. The D_f value is very similar to the D_f value of 7 reported for α-pinene SOA by Petters and Kasparoglu (2020) from temperature-dependent viscosity data (Petters and Kasparoglu, 2020). The T_g value is ∼27 K higher than predicted with the DeRieux et al. (2018) model. However, better closure is not expected due to the uncertainties in the chemical composition of the SOA (see discussion above) and the uncertainties in T_g values (±21 K) predicted by DeRieux et al. (2018).

4 Conclusions

We have presented the details of a new hot-stage microscopy technique for measuring the temperature-dependent viscosity of samples with small sizes (<1 mg of material). Highly viscous samples were stuck to a flat-tipped needle, heated in a temperature control stage, and imaged with a microscope. When the temperature was increased, the particles flowed to minimize their surface energy. The viscosity was extracted from these images by modelling the flow using fluid dynamics simulations. The current method can be used to provide viscosities in the range of roughly 10⁴ to 10⁸ Pa s at temperatures greater than room temperature. Higher viscosities may be measured if experiments are carried out over multiple days. The technique was validated by reproducing the viscosity of two literature standards: TαNB and PDE. The viscosity of TαNB was measured at temperatures of 98.5 and 104.3 ^∘C, while the viscosity of PDE was measured at temperatures of 35.6, 40.9, and 46.6 ^∘C. As an application to the study of atmospheric aerosols, the viscosity of farnesene SOA material was measured at 51.2, 61.5, and 66.6 ^∘C. The viscosity of farnesene SOA material increased by ∼2 orders of magnitude as the temperature decreased by ∼15 ^∘C. We compared our measurements here to the predicted viscosity using HRMS measurements with the DeRieux et al. (2018) parameterization. Using the previously used value of D_f=10, the parameterization underpredicted our measurements by ∼ 1–2 orders of magnitude. Considering the uncertainties in composition and uncertainties in the parameterization, this level of disagreement is not surprising. We fit the temperature-dependent data to the VFT equation and obtain a fragility parameter for the material of 7.29±0.03, which is very similar to the fragility parameter of 7 reported for α-pinene SOA by Petters and Kasparoglu (2020). This study illustrates that our new experimental approach for measuring viscosities as a function of temperature provides important data for testing methods used for predicting viscosities of SOA in the atmosphere.