Influence of CO₂ adsorption on cylinders and fractionation of CO₂ and air during the preparation of a standard mixture

We evaluated carbon dioxide (CO₂) adsorption on the internal surface of the cylinder and the fractionation of CO₂ and air during the preparation of standard mixtures with atmospheric CO₂ level through multistep dilution. The CO₂ molar fractions in the standard mixtures deviated from the gravimetric values by $-\mathrm{0.207}\pm \mathrm{0.060}$ µmol mol⁻¹ on average, which is larger than the compatibility goal (0.1 µmol mol⁻¹) recommended by the World Meteorological Organization. The deviation was consistent with those calculated using two fractionation factors: one was estimated by the mother–daughter transfer experiment in which CO₂–air mixtures were transferred from a mother cylinder to an evacuated daughter cylinder, and another was computed by applying the Rayleigh model to the change in CO₂ molar fractions in a source gas as its pressure was depleted from 11.5 to 1.1 MPa. The mother–daughter transfer experiments showed that the deviation was caused by the fractionation of CO₂ and air during the transfer of the source gas (CO₂–air mixture with a higher CO₂ molar fraction than that in the prepared gas mixture). The CO₂ fractionation was less significant when the transfer speed decreased to less than 3 L min⁻¹, indicating that thermal diffusion mainly caused the fractionation. The CO₂ adsorption on the internal cylinder surface was experimentally evaluated by emitting a CO₂–air mixture from a cylinder. When the cylinder pressure was reduced from 11.0 to 0.1 MPa, the CO₂ molar fractions in the mixture exiting the cylinder increased by 0.16±0.04 µmol mol⁻¹. By applying the Langmuir adsorption–desorption model to the measured data, the amount of CO₂ adsorbed on the internal surfaces of a 10 L aluminum cylinder when preparing a standard mixture with atmospheric CO₂ level was estimated to be 0.027±0.004 µmol mol⁻¹ at 11.0 MPa.

1 Introduction

Carbon dioxide (CO₂) is an important greenhouse gas that significantly contributes to the radiative force of the atmosphere. Numerous laboratories have systematically measured atmospheric CO₂ to better understand its sources and sinks. The measurements are typically performed using analyzers calibrated based on the CO₂ scale of the World Meteorological Organization (WMO). The WMO has recommended a compatibility goal of 0.1 µmol mol⁻¹ for CO₂ measurements in the Northern Hemisphere (WMO, 2020) to address small but globally significant gradients over large spatial scales. The WMO CO₂ scale has been determined using only standard gas mixtures prepared via manometry. Thus, the scale must be validated using other methods such as gravimetry. However, the scale of standard mixtures prepared by gravimetry is not consistent among respective laboratories (Tsuboi et al., 2017; Flores et al., 2019), preventing the validation of the WMO CO₂ scale.

Recently, CO₂ has been shown to adsorb on the internal surface of a high-pressure cylinder and desorb from the surface as the internal pressure decreases (Langenfelds et al., 2005; Leuenberger et al., 2015; Brewer et al., 2018; Schibig et al., 2018; Hall et al., 2019). The amount of CO₂ adsorbed on the internal surface of a cylinder was determined using a “decanting” experiment to continuously measure the CO₂ molar fraction of a CO₂–air mixture exiting the cylinder. For example, Leuenberger et al. (2015) estimated the amount of CO₂, expressed as a fraction of the total gas in a cylinder, to be 0.028 µmol mol⁻¹ at 6 MPa by applying the Langmuir model (Langmuir, 1918) to the results as 30 L aluminum cylinders were emptied from 6.0 to 0.1 MPa. Schibig et al. (2018) also estimated the amount of CO₂ to be 0.0165±0.0016 µmol mol⁻¹ at 15.0 MPa as 29.5 L aluminum cylinders were emptied from 15.0 to 0.1 MPa. These values slightly deviate from the gravimetrically assigned CO₂ molar fractions in standard mixtures. However, Miller et al. (2015) conducted a series of “mother–daughter” experiments in which they transferred half of a CO₂–air mixture from a “mother” cylinder into an evacuated “daughter” cylinder. They reported that CO₂ molar fractions in the mother cylinders were 0.02 %–0.03 % higher than those in the daughter cylinders. The values were greater than the adsorbed CO₂ amounts estimated by the decanting experiments. According to Hall et al. (2019), CO₂ molar fractions in the mother and daughter cylinders after the experiment were 0.06 µmol mol⁻¹ higher and 0.10–0.13 µmol mol⁻¹ lower than the CO₂ molar fractions in the mother cylinders before the transfer. The increased and decreased amounts were 5 to 10 times larger than the adsorbed amounts estimated by the decanting experiments. They proposed that the detected CO₂ change was due to thermal fractionation rather than CO₂ adsorption on the internal cylinder surface. Langenfelds et al. (2005) also assumed diffusive fractionation due to pressure diffusion, thermal diffusion, and effusion, which changed the CO₂ molar fraction observed in CO₂–air mixtures due to gas handling. If the CO₂ changes are caused by a kinetic process, such as diffusive fractionation, the fractionation factor is constant regardless of the CO₂ molar fraction. In gravimetry, standard mixtures with atmospheric CO₂ levels are prepared by multistep dilution, which involves diluting pure CO₂ with air two or three times. Each dilution step is accomplished by transferring a source gas from a mother cylinder into an evacuated daughter cylinder and pressurizing it with the dilution gas (air). The fractionation of CO₂ and air (nitrogen, oxygen, argon, and impurities other than CO₂) likely occurs in the second and third dilution steps because a CO₂–air mixture with a higher CO₂ molar fraction than that of the prepared standard mixture is used as the source gas. The fractionation process decreases the CO₂ molar fraction of the source gas transferred into the daughter cylinder, which increases the CO₂ molar fraction of the remaining source gas in the mother cylinder. This can deteriorate the reproducibility of the assigned CO₂ molar fractions because CO₂ molar fractions in the prepared standard mixtures are influenced by the decrease and increase in CO₂ in the transferred gas mixture and the remaining source gas, respectively. To avoid fractionation in each dilution step, one method is to gravimetrically prepare standard mixtures by one-step dilution to mix pure CO₂ and air directly as there is no process to transfer a CO₂–air mixture into another cylinder (Hall et al., 2019). Tohjima et al. (2006) gravimetrically prepared standard mixtures by one-step dilution. However, they did not discuss the fractionation and adsorption that occurred during the multistep dilution process.

To accurately determine the CO₂ molar fraction, the adsorption and fractionation effects on the preparation of standard mixtures with atmospheric CO₂ levels must be revealed. Therefore, in this study, we evaluated the systematic error of the CO₂ molar fraction in standard mixtures prepared by multistep dilution. CO₂ adsorption and fractionation depend on the type and size of a cylinder (Leuenberger et al., 2015). The evaluation was performed using 10 L aluminum cylinders commonly used for the preparation of gravimetric standard mixtures because previous studies evaluated CO₂ adsorption as well as CO₂ and air fractionation using 29.5 L aluminum and 50 L steel cylinders. Based on decanting experiments, we evaluated the amount of CO₂ adsorbed on the internal surface of a 10 L aluminum cylinder. The fractionation of CO₂ and air in the transfer of CO₂–air mixtures was then evaluated based on mother–daughter experiments, and the fractionation factor in the transfer of a source gas was estimated based on the results. Finally, we demonstrated that standard mixtures gravimetrically prepared by three-step dilution had a systematic error of CO₂ molar fractions by comparing them with the standard mixtures prepared by one-step dilution.

2 Methods

2.1 Decanting and mother–daughter experiments

Decanting and mother–daughter experiments were conducted to estimate CO₂ adsorption on the internal cylinder surface and the fractionation of CO₂ and air during the transfer of the CO₂–air mixture. Decanting experiments were performed using 10 L aluminum cylinders (Luxfer Gas Cylinders, UK) with a brass diaphragm valve (G-55, Hamai Industries Limited, Japan). The cylinders were evacuated to $\sim {\mathrm{10}}^{-\mathrm{4}}$ Pa using a turbo molecular pump and pressurized to 11.0 MPa using CO₂–air mixtures with CO₂ molar fractions ranging from 350 to 450 µmol mol⁻¹. The CO₂–air mixtures were decanted using single-stage regulators (Torr 1300, Nissan Tanaka Co., Japan) attached to the cylinders from 11.0 to 0.1 MPa at total flow rates of 80, 150, and 300 mL min⁻¹. After flowing through the regulator, the mixture was divided in two ways by T-pieces. The branched flow was controlled using two mass flow controllers (SEC-Z512MGX 100 SCCM, and 1SLM, Horiba STEC Co., Ltd., Japan); one was introduced as a sample gas into a Picarro G2301 (Picarro, Inc., USA) at a flow rate of 80 mL min⁻¹, and the other was exhausted to the surroundings at rates of 0, 70, and 220 mL min⁻¹. An absolute pressure gauge of flush diaphragm type (PPA-33X, KELLER AG, Switzerland) attached to the regulator was used to measure the pressures in the cylinders. The output obtained from the Picarro G2301 was linearly calibrated using one standard mixture containing atmospheric CO₂ levels with a standard uncertainty of less than 0.1 µmol mol⁻¹ as the signal was assumed to be zero when the CO₂ molar fraction was zero. After calibrating the Picarro G2301 for 20 min, the CO₂ in the decanting flow was measured for 100 min. The decanting flow was stopped while the Picarro G2301 was calibrated using the standard mixture.

The mother–daughter experiment was performed using 10 or 48 L aluminum cylinders (Luxfer Gas Cylinders, UK) with a brass diaphragm valve. These cylinders were filled with CO₂–air mixtures with CO₂ molar fractions ranging from 380 to 460 µmol mol⁻¹ and 3.2 to 13.9 MPa; some of these mixtures were purchased from a gas supplier (Japan Fine Products, Japan), while others were prepared in our laboratory. CO₂–air mixtures were prepared using pure CO₂ and purified air, which was obtained by removing CO₂, CH₄, CO, and H₂O, among others, from ambient air. In this experiment, the cylinders containing the mixtures were referred to as the mother cylinders, while the receiving cylinders into which the mixture was transferred were referred to as the daughter cylinders. The mixtures in the mother cylinders with vertical or horizontal placements were transferred into the evacuated daughter cylinders with a vertical placement through a manifold made of a $\mathrm{1}/\mathrm{4}$ in. o.d. stainless-steel line, diaphragm valves (FUDDF-716G, Fujikin Incorporated, Japan), and an absolute pressure gauge, as shown in Fig. 1a. The sheet, diaphragm, and body of the valve were made of polychlorotrifluoroethylene (PCTFE), nickel–cobalt alloy, and stainless steel, respectively. The mother and daughter cylinders were connected, and then the manifold was evacuated to $\sim {\mathrm{10}}^{-\mathrm{4}}$ Pa by a turbo molecular pump after all diaphragm valves opened (A1–A4 or a1–a6). The valve of the mother cylinder opened after the valves of A3 or a3 closed, and then the mixture was released from the mother cylinder to the daughter cylinder by opening the valve of the daughter cylinder. The transfer speed was controlled by the degree of valve opening and calculated from the transfer time and volume. The valves of the mother and daughter cylinders were closed immediately after the transfer volume reached the desired level, which was confirmed by monitoring the weight of the daughter cylinder using a load-cell-type balance (BW22KH, SHIMADZU Corporation, Japan), as shown in Fig. 1a. The transfer time and the pressure of the daughter cylinders were measured using a clock and the absolute pressure gauge, respectively. The transfer volume was computed using the inner volume and the pressure of the daughter cylinder. The molar CO₂ fractions in the mother cylinders were measured using the Picarro G2301 before starting each experiment, and after each experiment, those in the mother and daughter cylinders were measured for several hours to half a day after the mixtures were transferred. The Picarro G2301 was calibrated using standard mixtures with atmospheric CO₂ levels before and after each transfer experiment. We also measured $\mathit{\delta }{(}^{\mathrm{29}}{\mathrm{N}}_{\mathrm{2}}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}})$, $\mathit{\delta }{(}^{\mathrm{34}}{\mathrm{O}}_{\mathrm{2}}{/}^{\mathrm{32}}{\mathrm{O}}_{\mathrm{2}})$, $\mathit{\delta }{(}^{\mathrm{32}}{\mathrm{O}}_{\mathrm{2}}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}})$, $\mathit{\delta }{(}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}})$, and $\mathit{\delta }{(}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{36}}\mathrm{Ar})$ in the mother and daughter cylinders using a mass spectrometer (Delta-V, Thermo Fisher Scientific Inc., USA) to clarify the mechanism(s) of diffusive fractionation during the mother–daughter experiment based on the relationship between the measured elemental and isotopic ratios (e.g., Langenfelds et al., 2003; Ishidoya et al., 2013). The details of the technique were provided by Ishidoya and Murayama (2014). The value of $\mathit{\delta }({\mathrm{CO}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}})$ was calculated using the ratio of ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}$ obtained from Eq. (1), assuming that minor components except for CO₂ can be ignored $({\mathrm{N}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}}+\mathrm{Ar}+{\mathrm{CO}}_{\mathrm{2}}=\mathrm{1})$:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\mathrm{CO}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}=& {\displaystyle \frac{{\mathrm{CO}}_{\mathrm{2}}}{{\mathrm{N}}_{\mathrm{2}}}}\times {\displaystyle \frac{\mathrm{1}-{\mathrm{CO}}_{\mathrm{2}}}{\mathrm{1}-{\mathrm{CO}}_{\mathrm{2}}}}={\displaystyle \frac{{\mathrm{CO}}_{\mathrm{2}}}{{\mathrm{N}}_{\mathrm{2}}}}\times {\displaystyle \frac{{\mathrm{N}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}}+\mathrm{Ar}}{\mathrm{1}-{\mathrm{CO}}_{\mathrm{2}}}}\\ & ={\displaystyle \frac{{\mathrm{CO}}_{\mathrm{2}}}{\mathrm{1}-{\mathrm{CO}}_{\mathrm{2}}}}\times \left(\mathrm{1}+{\displaystyle \frac{{\mathrm{O}}_{\mathrm{2}}}{{\mathrm{N}}_{\mathrm{2}}}}+{\displaystyle \frac{\mathrm{Ar}}{{\mathrm{N}}_{\mathrm{2}}}}\right),\end{array}\end{array}$$

where CO₂ molar fractions measured with the Picarro G2301 were used. The ratios of ${\mathrm{O}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}$ and $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$ were computed using the values measured by the mass spectrometer (Aoki et al., 2019).

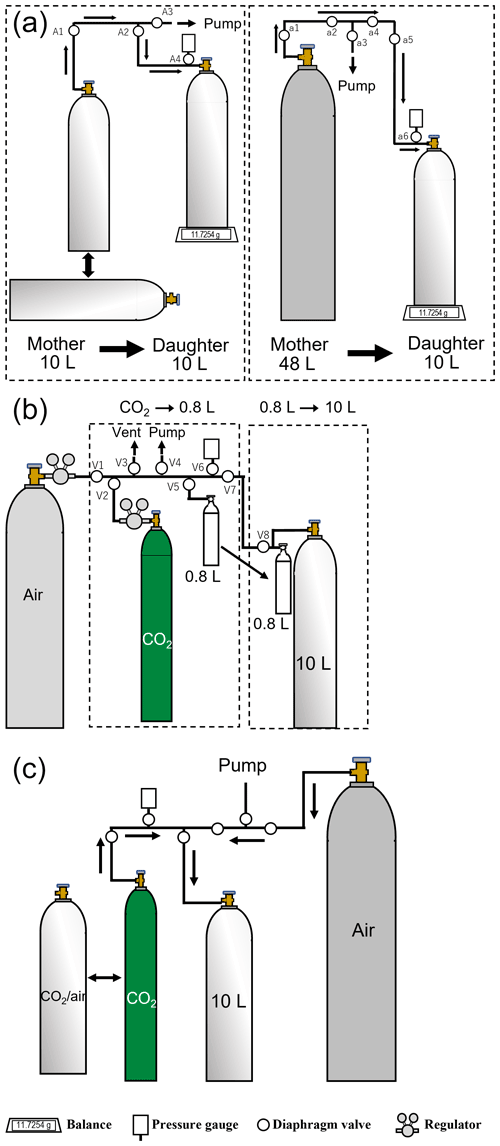
Figure 1 (a) Schematic of the manifold used to transfer the CO₂–air mixture from a mother cylinder to a daughter cylinder in a mother–daughter experiment, (b) the manifold used to transfer pure CO₂ to a 0.8 L aluminum cylinder and from a 0.8 L aluminum cylinder to a 10 L aluminum cylinder for preparing a standard mixture via one-step dilution, and (c) the manifold used to transfer the source gas (pure CO₂ or a CO₂–air mixture) and the dilution gas (purified air).

2.2 Preparation of standard mixtures

2.2.1 Starting materials

Standard mixtures were gravimetrically prepared using one-step and three-step dilution in accordance with ISO 6142-1:2015 (International Organization for Standardization, 2015b). Pure CO₂ (>99.998 %, Nippon Ekitan Corp., Japan) and purified air (G1-grade, <0.1 µmol mol⁻¹ for CO, CO₂, THC, <0.01 µmol mol⁻¹ for NO_x, SO₂, $<-\mathrm{80}$^∘ for H₂O; Japan Fine Products, Japan) were used as a source gas. The purity of CO₂ and the N₂ molar fraction in the air were determined using a subtraction method in which the sum of the molar fractions of impurities was subtracted from 1 (ISO 19229:2015; International Organization for Standardization, 2015a). Impurities in the source gases were identified and quantified using five analyzers. A gas chromatograph with a thermal conductivity detector (GC-TCD) was used to analyze N₂, O₂, CH₄, and H₂ in pure CO₂. Ar in the air was analyzed using GC-TCD with an oxygen absorber. A paramagnetic oxygen analyzer was used to quantify O₂ in the air. A Fourier-transform infrared spectrometer was used to detect trace amounts of CO₂, CH₄, and CO in the air. A capacitance-type moisture sensor was used to measure H₂O in pure CO₂, and a cavity ring-down moisture analyzer was used to measure H₂O in the air.

2.2.2 Balances and weighing sequence

A 0.8 L aluminum cylinder and a 10 L aluminum cylinder were used to prepare standard mixtures with atmospheric CO₂ levels using one-step dilution, while a 10 L cylinder was used for three-step dilution. The two types of cylinders were weighed using two different balances (mass comparators). One is AX2005 (Mettler Toledo, Switzerland) with a resolution of 0.01 mg and a maximum load of 2 kg used for weighing the 0.8 L cylinder. Another is XP26003L (Mettler Toledo, Switzerland) with a resolution of 1 mg and a maximum load of 26 kg (Matsumoto et al., 2004; Aoki et al., 2019) used for weighing the 10 L cylinder. The mass measurement of each cylinder, which was performed in a weighing room controlled at 26±0.5 ^∘C with a relative humidity of 48±1 %, was conducted with respect to a nearly identical reference cylinder to reduce any influence exerted by zero-point drifts, sensitivity issues associated with the mass comparator, changes in buoyancy acting on the cylinder, or adsorption effects on the cylinder surface because of the presence of water vapor (Alink and van der Veen, 2000; Milton et al., 2011). This was performed based on several consecutive weighing operations in the ABBA sequence, where “A” and “B” denote the reference and the sample, respectively. The process of loading and unloading the cylinders was automated, and one complete cycle of the ABBA sequence took 5 min. The mass difference, which was calculated by subtracting the reference cylinder from the sample cylinder readings, provided the mass reading recorded from the weighing system. Aoki et al. (2019) reported that the mass reading deviates because of temperature differences between the sample and the surrounding air. In this study, the mass measurement was performed for the sample and the surrounding areas at the same temperature to reduce the deviation.

2.2.3 One-step dilution process

Standard mixtures were gravimetrically prepared by mixing pure CO₂ and air using stainless-steel manifolds (Fig. 1b and c), as shown in Fig. 2a. The pure CO₂ cylinder and the 0.8 L aluminum cylinder were connected at the position of valve 2 (V2) and valve 5 (V5) to the stainless-steel manifold (Fig. 1b), the internal surface of which was electropolished. The 0.8 L aluminum cylinder was evacuated to $\sim \mathrm{5.0}\times {\mathrm{10}}^{-\mathrm{5}}$ Pa via the manifold by opening V2, V4, V5, and V6. Pure CO₂ was added to the 0.8 L aluminum cylinder after closing V4. Furthermore, we connected the 0.8 L cylinder and the evacuated 10 L cylinder at the position of V8 and then evacuated the manifold to $\sim \mathrm{5.0}\times {\mathrm{10}}^{-\mathrm{5}}$ Pa by opening V4, V7, and V8. The 0.8 L cylinder was moved from V5 to V8 to reduce the dead volume when pure CO₂ was transferred to the 10 L cylinder. The valves of the 0.8 and 10 L cylinders were opened after closing V8, allowing pure CO₂ to flow into the 10 L cylinder. Both cylinder valves were closed, and then the remaining CO₂ in the manifold was transferred into the 10 L cylinder by alternating the pressurization–expansion operation that pressurized the manifold to ∼1.5 MPa with air and opening the valve of the 10 L cylinder. The 10 L cylinder was connected to another manifold, shown in Fig. 1c, after CO₂ was completely transferred into the cylinder by repeating this pressurization–expansion process 300 times. The manifold was evacuated to $\sim \mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{4}}$ Pa, and then the cylinder was further pressurized to ∼10.0 MPa with air using the manifold. The CO₂ mass filled into the 10 L cylinder was determined by weighing the 0.8 L cylinder before and after pure CO₂ was transferred, whereas the mass of the air was calculated by subtracting the CO₂ mass from the difference in the 10 L cylinder mass before and after transferring pure CO₂ and air into the 10 L cylinder.

Figure 2 (a) Preparation of standard mixtures with the atmospheric CO₂ level via one-step dilution. (b) Preparation of third gas mixtures with the atmospheric CO₂ level via three-step dilution.

2.2.4 Three-step dilution process

Figure 2b shows that the standard mixtures were gravimetrically prepared in the 10 L cylinders by diluting pure CO₂ with air three times using the manifold shown in Fig. 1c. The details of the preparation technique were described by Matsumoto et al. (2004, 2008) and Aoki et al. (2019). In the first dilution step, a gas mixture with a CO₂ molar fraction of 65 000 µmol mol⁻¹, referred to as the first gas mixture, was prepared from pure CO₂ and air. Pure CO₂ was transferred into the 10 L cylinder that was evacuated to $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{4}}$ Pa and then pressurized to 10.0 MPa with air using the manifold shown in Fig. 1c. The masses of pure CO₂ and air were approximately 110 and 1100 g, respectively. In the second step, a gas mixture with a CO₂ molar fraction of 5000 µmol mol⁻¹, referred to as the second gas mixture, was prepared from the first gas mixture and air. The first gas mixture was transferred into the 10 L cylinder evacuated to $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{4}}$ Pa and then pressurized to 10.0 MPa by air. The masses of the first gas mixture and air were approximately 100 and 1200 g, respectively. In the third step, a gas mixture with the atmospheric CO₂ level, referred to as the third gas mixture, was gravimetrically prepared from the second gas mixture and air. The second gas mixture was transferred into the 10 L cylinder evacuated to $\mathrm{1.5}\times {\mathrm{10}}^{-\mathrm{4}}$ Pa and then pressurized to 10.0 MPa with air. The masses of the second gas mixture and air were approximately 100 and 1200 g, respectively. The masses of pure CO₂, CO₂–air mixture, and air used as source gases were determined by weighing the cylinder before and after filling each source gas.

2.2.5 Analysis of standard mixtures

The gravimetrically prepared standard mixtures (third gas mixtures) were measured using the Picarro G2301 equipped with a multiport valve (Valco Instruments Co. Inc., USA) for gas introduction and a mass flow controller (SEC-N112, 100SCCM, Horiba STEC, Co., Ltd, Japan). The output of the Picarro G2301 was calibrated using the standard mixtures prepared by one-step dilution. CO₂ molar fractions in the third gas mixtures were calculated from the calibration line obtained by applying the Deming least-square fit to the measured data. In the calibration, two series of standard mixtures were used. One series was composed of four standard mixtures with a molar fraction range from 390 to 430 µmol mol⁻¹, and another series was composed of five standard mixtures with a molar fraction range from 390 to 420 µmol mol⁻¹.

3 Results and discussion

3.1 Adsorption and fractionation of CO₂–air mixtures

As described in the Introduction, the adsorption of CO₂ on the internal cylinder surface causes a small deviation of the gravimetrically assigned CO₂ molar fraction. Furthermore, the transfer of the CO₂–air mixture changed CO₂ molar fractions by about 0.10 µmol mol⁻¹. The transfer of source gases impacts the CO₂ molar fractions more strongly compared to the deviation in the adsorption process. Therefore, we estimated the amount of CO₂ adsorbed on the internal surface of a 10 L aluminum cylinder and then evaluated the fractionation amount caused by the transfer of CO₂–air mixtures used as source gases in the evacuated cylinders.

3.1.1 Amount of CO₂ adsorbed on the internal cylinder surface

By applying the Langmuir adsorption–desorption model to the results of decanting experiments, it is possible to determine the amount of CO₂ adsorbed on the internal cylinder surface (Leuenberger et al., 2015; Schibig et al., 2018; Hall et al., 2019). In this method, the amount of CO₂ adsorbed on the internal surfaces at the initial pressure of the decanting experiment is expressed as the molar fraction. For example, Schibig et al. (2018) performed a decanting experiment by emptying 29.5 L aluminum cylinders at low (300 mL min⁻¹) and high (5 L min⁻¹) flow rates, thereby identifying the CO₂ adsorbed amount to be molar fractions of 0.0165±0.0016 and 0.043±0.008 µmol mol⁻¹ at 15.0 MPa, respectively. Leuenberger et al. (2015) also performed the decanting experiment by emptying 30 L aluminum cylinders at a low flow rate of 250 mL min⁻¹ and a high flow rate of 5 L min⁻¹ and estimated a molar fraction of 0.028 µmol mol⁻¹ at 6.0 MPa and 0.047 µmol mol⁻¹ at 9.0 MPa. The low-flow decanting experiments indicated that less CO₂ was adsorbed on the internal surfaces of cylinders compared to the high-flow decanting experiments. The enrichment of CO₂ molar fraction detected in the high-flow decanting experiment was related to thermal diffusion and fractionation in the cylinder. A low-flow decanting experiment is suitable for evaluating the amount of CO₂ adsorbed on the internal cylinder surface in the case of 29.5 and 30 L aluminum cylinders (Schibig et al., 2018; Leuenberger et al., 2015). It is not known whether this applies to 10 L aluminum cylinders. Therefore, we investigated the optimum flow rate to evaluate the adsorbed amount by measuring the CO₂ molar fraction in a gas mixture exiting the 10 L cylinder at low flow rates of 80, 150, and 300 mL min⁻¹ as the pressure decreased from 11.0 to 0.1 MPa. The deviations in CO₂ molar fractions from the initial values against relative cylinder pressure ($P/P_{\mathrm{0}}$) at different flow rates are shown in Fig. 3a, where P is the actual pressure of the cylinder (MPa), and P₀ is the initial pressure of the cylinder (MPa) before the decanting experiment. The CO₂ in the gas mixture increased by 0.16±0.04 µmol mol⁻¹ as the cylinder pressure decreased from 11.0 to 0.1 MPa. Unless otherwise noted, the numbers following the symbol ± represent the standard deviations. The increase in CO₂ molar fraction is the same for flow rates of 80, 150, and 300 mL min⁻¹, indicating that the contribution of thermal fractionation is negligible at a flow rate of 300 mL min⁻¹ or less. The amount adsorbed on the internal cylinder surface ($X_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{ad}}$) was calculated using the following equation based on the Langmuir model, derived by Leuenberger et al. (2015) (Fig. 3b):

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{X}_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{meas}}=& X_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{ad}}\cdot ({\displaystyle \frac{K\cdot \left(P-P_{\mathrm{0}}\right)}{\mathrm{1}+K\cdot P}}+\left(\mathrm{1}+K\cdot P_{\mathrm{0}}\right)\\ & \cdot \ln \left({\displaystyle \frac{P_{\mathrm{0}}\cdot \left(\mathrm{1}+K\cdot P\right)}{P\cdot \left(\mathrm{1}+K\cdot P_{\mathrm{0}}\right)}}\right))+X_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{initial}},\end{array}\end{array}$$

where $X_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{ad}}$ is the CO₂ molar fraction multiplied by the occupied adsorption sites at pressure P₀, $X_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{meas}}$ is the measured molar fraction, $X_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{initial}}$ is the CO₂ molar fraction measured in the cylinder at pressure P₀, K is the ratio of the adsorption rate constant to the desorption rate constant (its unit is MPa⁻¹), and $X_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{ad}}$ and K were obtained from the least-square fit to the results. These experiments were performed seven times, and the average of $X_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{ad}}$ was 0.027±0.004 µmol mol⁻¹, corresponding to 0.030 mL standard temperature and pressure (STP) (1.2 µmol or 7.3×10¹⁷ molecules). There was no difference in the values of $X_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{ad}}$ for the CO₂ range from 350 to 450 µmol mol⁻¹. The ratio of the adsorption of CO₂ to the total CO₂ in the cylinder was 0.008±0.001 % in units of moles. The inner diameter of 0.16 m, length of 0.56 m, and internal surface area are roughly calculated to be 0.32 m². The occupied area of CO₂ adsorbed on the internal surface was estimated to be 0.06 m², assuming a molecule diameter of 0.34 nm, which corresponds to approximately 20 % of the inner area by a monolayer of adsorbed CO₂ molecules. The CO₂ molar fractions in the third gas mixtures gravimetrically determined in the following section were computed considering the adsorbed amount in the third dilution step because the adsorption of CO₂ causes a small deviation in the CO₂ molar fraction in the cylinder. However, the amount was neglected in the case of the first and second gas mixtures because the CO₂ molar fraction was significantly higher than the atmospheric CO₂ level (10 and 100 times or more, respectively). In the Langmuir model, the increase rate of the amount adsorbed on the internal surface decreases with the increased molar fraction of CO₂. The adsorbed amount is lower than the adsorption ratio of 0.008±0.001 % in the case of the first and second gas mixtures with a high CO₂ molar fraction.

3.1.2 Mother–daughter experiment

The fractionation of CO₂ and air results from the diffusive fractionation process based on three types of diffusion, i.e., pressure diffusion, thermal diffusion, and effusion, as described by Langenfelds et al. (2005) and Moore (1962). Pressure diffusion is driven by a pressure gradient. The diffusion causes heavier molecules to be preferentially accumulated in the region of higher pressure. Thermal diffusion is driven by a temperature gradient. Heavier molecules are preferentially accumulated in the colder region. Effusion is known as Knudsen diffusion. Gas molecules escaping from a pressurized vessel through a tiny orifice are subject to molecular effusion. However, effusion was negligible in our mother–daughter experiments since Knudsen diffusion occurs when the size of the orifice is small compared to the mean free path among molecular collisions. On the other hand, temperature decreases of 2–8 K for the mother cylinders were observed during our mother–daughter experiments. This may allow the fractionation of CO₂ and air by the adsorption process because fractionation is caused by the increase in the amount of CO₂ adsorbed on the internal surface upon the cooling of the mother cylinder in the transfer of the gas mixture. Leuenberger et al. (2015) identified the temperature dependence of the amount of CO₂ adsorbed on the internal surface of an aluminum cylinder to be in the range from −0.0002 to −0.0003 $\mathrm{\mu }\mathrm{mol}{\mathrm{mol}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}$. This corresponds to a decrease in the range of 0.0004–0.0024 µmol mol⁻¹ for CO₂ molar fractions in the mixtures transferred from the mother cylinder, which is significantly lower than the changes in CO₂ molar fractions in the transfer of CO₂–air mixtures detected by Hall et al. (2019).

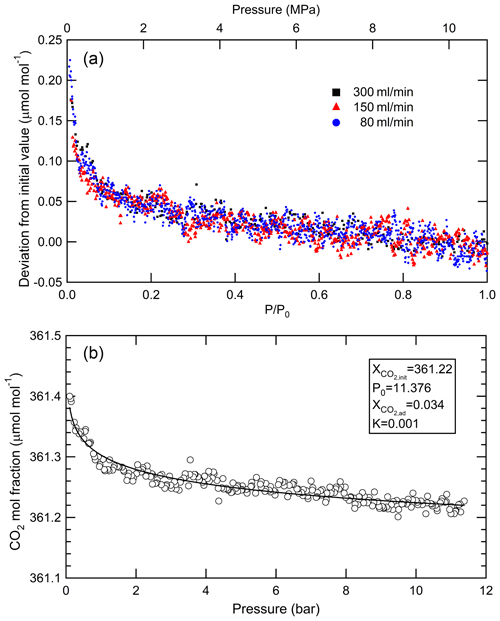
Figure 3 (a) Change in the CO₂ molar fractions from the initial values of the CO₂–air mixtures with the atmospheric CO₂ level against relative pressure as the cylinder was emptied at flow rates of 80, 150, and 300 mL min⁻¹ from 11.0 to 0.1 MPa. (b) Typical results obtained by applying the Langmuir model to the change in CO₂ molar fraction from the initial value of the CO₂–air mixture as the cylinder was emptied from 11.0 to 0.1 MPa.

Mother–daughter experiments of gas mixtures with atmospheric CO₂ levels were performed in 15 sets using 48 and 10 L aluminum cylinders as mother cylinders and 10 L aluminum cylinders as daughter cylinders: three sets were performed using the horizontal placement of mother cylinders, and 12 sets were performed using the vertical mother cylinder placement. All transfers with the horizontal placement increased the CO₂ molar fractions in the daughter cylinders, as shown in Fig. 4, while all transfers with the vertical placement decreased the CO₂ molar fractions in the daughter cylinders. The experiments with the vertical mother cylinder and the horizontal mother cylinder inversely deviated the CO₂ molar fractions. The difference in the deviations indicated that fractionations occurred in the mother cylinders rather than in the transfer line and manifold since the pressure and thermal gradient in the mixtures in the transfer line and manifold are determined regardless of the mother cylinder placement type. The mother cylinder placement type does not change the direction of the pressure gradient even if it changes the magnitude of the pressure gradient in the mother cylinder. The deviation in CO₂ molar fraction was the opposite, suggesting that the fractionation of CO₂ and air was caused based on thermal diffusion rather than pressure diffusion. The source gas used for the preparation of standard mixtures is transferred into a vertical receiving cylinder from a vertical mother cylinder. Experiments using the mother cylinders with the vertical placement were conducted at different mother cylinder pressures, transferred gas amounts, and transfer speeds corresponding to the transfer conditions of the source gas to understand the contribution of fractionation to the CO₂ molar fraction.

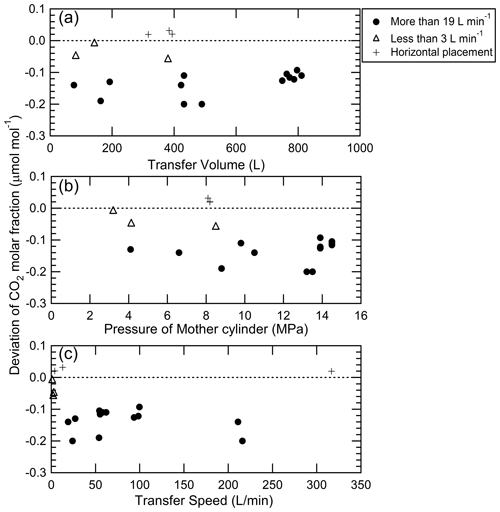
Figure 4 Deviations of CO₂ molar fractions in daughter cylinders from initial values against (a) transfer volume, (b) mother cylinder pressure, and (c) transfer speed when the CO₂–air mixtures with the atmospheric CO₂ level were transferred from the mother cylinder to the daughter cylinder. The closed circles represent the results measured at a transfer speed of more than 19 L min⁻¹, while the open triangles represent the results measured at a transfer speed of less than 3 L min⁻¹. These results were obtained using the vertical mother cylinders; the plus signs represent the results obtained using the horizontal mother cylinders.

The mother–daughter experimental results performed with the vertical mother cylinder placement are summarized in Table 1. Here, the CO₂ molar fractions in the daughter cylinders were corrected by the amount of CO₂ absorbed on the internal surface based on the value of 0.027±0.004 µmol mol⁻¹ determined by the decanting experiment. The dependence of the CO₂ molar fractions in the daughter cylinders relative to the transfer volume, cylinder pressure, and transfer speed is shown in Fig. 4. The closed circles in Fig. 4 represent transfer speeds more than 19 L min⁻¹, whereas the open triangles represent transfer speeds less than 3 L min⁻¹. All CO₂ molar fractions in the mixtures transferred into the daughter cylinders decreased compared to the CO₂ molar fraction before the transfer of the mixtures, as shown in Fig. 4. The decrease in the CO₂ molar fractions of the mixtures in the daughter cylinders was 0.122±0.040 µmol mol⁻¹ on average at a transfer speed of more than 19 L min⁻¹, whereas the decrease in the CO₂ molar fractions in the daughter cylinders from the initial values became significantly small at 0.036±0.027 µmol mol⁻¹ (0.008±0.006 %) on average when the mixtures were transferred at an extremely slow transfer speed of less than 3 L min⁻¹. The decreased values at the transfer speed of more than 19 L min⁻¹ agree with previous values of 0.10 and 0.13 µmol mol⁻¹ reported by Hall et al. (2019), who reported that the decrease could be related to thermal diffusion. Correspondingly, the remaining mixtures in all vertical mother cylinders provided higher CO₂ molar fractions than those before the mixture transfer, contrary to the daughter cylinders. The deviated CO₂ amount (n) in units of moles was computed from the change in the CO₂ molar fraction ($c_{{\mathrm{CO}}_{\mathrm{2}}}$) to evaluate the mass balance of CO₂ corresponding to the increase and decrease in CO₂ molar fractions. The deviated CO₂ amount is determined from the initial value before the transfer of the mixture, as well as the cylinder volume (V) and pressure (p) in the daughter cylinder using the ideal gas law: $n=c_{{\mathrm{CO}}_{\mathrm{2}}}\times p\times V/(R\times T)$, where R and T represent the gas constant (0.082057 L atm K⁻¹ mol⁻¹) and gas temperature (298 K), respectively. The mass balance between the increase and decrease was consistent within uncertainties in each experiment (Table 1), indicating that the changes in CO₂ were caused by diffusive fractionation rather than CO₂ adsorption.

Table 1 Results of the mother–daughter experiment using 10 and 48 L aluminum cylinders performed using the vertical placement of the mother cylinder. CO₂–air mixtures with the atmospheric CO₂ level were transferred from 10 or 48 L aluminum cylinders (mother) to 10 L aluminum cylinders (daughter) at various mother cylinder pressures, transfer volumes, and transfer speeds.

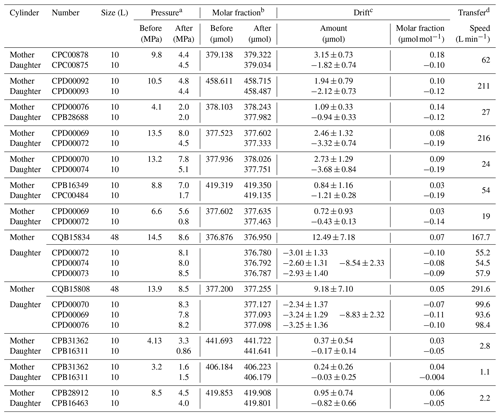
^a Pressures were measured using the pressure gauge attached to the regulator.
^b CO₂ molar fractions in mother and daughter cylinders were measured after several hours to half a day of transferring the mixtures. These values have a measurement uncertainty of 0.030 µmol mol⁻¹.
^c The change in the amount of substance (n) for CO₂ was computed from the change in the amount of CO₂ molar fraction ($c_{{\mathrm{CO}}_{\mathrm{2}}}$), the cylinder volume (V), and the pressure (p) in the daughter cylinder using the ideal gas law: $n=c_{{\mathrm{CO}}_{\mathrm{2}}}\times p\times V/(R\times T)$. The numbers following the symbol ± denote the standard uncertainties calculated based on the measurement uncertainty.
^d Transfer speeds were roughly computed by dividing the transfer volume by the transfer time.

As shown in Fig. 4, the CO₂ decrease does not depend on the transfer volume and initial pressure of the mother cylinder, but it becomes significantly smaller for flow rates below 19 L min⁻¹. The amount of CO₂ molar fraction decrease was constant regardless of the transfer volume, indicating that the fractionation factor did not change during the transfer. The decreased CO₂ amounts due to transfer speed also support the idea that the fractionation is caused by thermal diffusion because the transfer speed determines the thermal gradient. Source gases generally transfer into daughter cylinders at transfer speeds of more than 19 L min⁻¹. Therefore, CO₂ molar fractions in standard mixtures with the atmospheric CO₂ level are influenced by the fractionation in the transfer of the source gas, but it may be significantly suppressed by the transfer of the mixture at a lower transfer speed. However, it is difficult to transfer source gases at the transfer speed presented in this experiment because the speed is much lower than the transfer speed in the preparation of the standard mixtures. We must develop a technique to control the transfer speed of the source gas.

The fractionation factor (α) in the transfer of a source gas was estimated from the results of the transfer speed of more than 19 L min⁻¹. The CO₂ molar fraction in the gas mixture in the cylinder (X_out) is modified by the fractionation factor as follows:

$$\begin{array}{}\text{(3)}& X_{\mathrm{out}}=\mathit{\alpha }{X}_{\mathrm{0}},\end{array}$$

where X₀ is the initial CO₂ molar fraction. The fractionation factor (α) was estimated to be $X_{\mathrm{out}}/X_{\mathrm{0}}=\mathrm{0.99968}\pm \mathrm{0.00010}$ using only the values with transfer speeds of more than 19 L min mol⁻¹ in Table 1. If a standard mixture with a CO₂ molar fraction of 400 µmol mol⁻¹ is prepared by three-step dilution, the CO₂ molar fraction in the standard mixture is predicted to decrease by 0.252±0.082 µmol mol⁻¹ by the fractionation effect in the second and third dilution steps. Additionally, the CO₂ molar fraction in a source gas (X) can be expressed using pressure (P) and the initial pressure (P₀) of the source gas by the Rayleigh fractionation model.

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{X}{X_{\mathrm{0}}}}={\left({\displaystyle \frac{P}{P_{\mathrm{0}}}}\right)}^{\mathit{\alpha }-\mathrm{1}}\end{array}$$

According to Eq. (4), the CO₂ molar fraction in the source gas is estimated to be 1.00076±0.00024 against the initial value with a decrease in pressure from 11.0 to 1.0 MPa. This value corresponds to an increase of 0.30±0.09 µmol mol⁻¹ in a standard mixture with a CO₂ molar fraction of 400 µmol mol⁻¹ prepared from the source gas.

We also measured different molecular pairs, ${}^{\mathrm{32}}{\mathrm{O}}_{\mathrm{2}}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}}$, ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}}$, and ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}$, and the same molecular pairs, ${}^{\mathrm{29}}{\mathrm{N}}_{\mathrm{2}}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}}$, ${}^{\mathrm{34}}{\mathrm{O}}_{\mathrm{2}}{/}^{\mathrm{32}}{\mathrm{O}}_{\mathrm{2}}$, and ${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{36}}\mathrm{Ar}$, to confirm if the fractionating process discussed above occurred by the transfer of the mixture. The relationship of the deviations of $\mathit{\delta }{(}^{\mathrm{32}}{\mathrm{O}}_{\mathrm{2}}{/}^{\mathrm{28}}\mathrm{N}{)}_{\mathrm{2}}$, $\mathit{\delta }{(}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}})$, $\mathit{\delta }({\mathrm{CO}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}})$, $\mathit{\delta }{(}^{\mathrm{34}}{\mathrm{O}}_{\mathrm{2}}{/}^{\mathrm{32}}{\mathrm{O}}_{\mathrm{2}})$, and $\mathit{\delta }{(}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{36}}\mathrm{Ar})$ with the deviations of $\mathit{\delta }{(}^{\mathrm{29}}{\mathrm{N}}_{\mathrm{2}}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}})$ in the daughter cylinders relative to their mother cylinders is shown in Fig. 5. The closed circles represent the values obtained from the mother–daughter experiment using 10 and 48 L cylinders. The dotted lines represent the theoretical value of thermal diffusion, which was calculated using the equations provided by Langenfelds et al. (2005). The solid lines represent the deviations due to thermal diffusion experimentally estimated by Ishidoya et al. (2013, 2014). The deviation of molecular pairs in the daughter cylinders relative to their mother cylinders occurred not only between different molecular pairs, $\mathit{\delta }{(}^{\mathrm{32}}{\mathrm{O}}_{\mathrm{2}}{/}^{\mathrm{28}}\mathrm{N}{)}_{\mathrm{2}}$, $\mathit{\delta }{(}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}})$, and $\mathit{\delta }({\mathrm{CO}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}})$, but also the same molecular pairs, $\mathit{\delta }{(}^{\mathrm{29}}{\mathrm{N}}_{\mathrm{2}}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}})$, $\mathit{\delta }{(}^{\mathrm{34}}{\mathrm{O}}_{\mathrm{2}}{/}^{\mathrm{32}}{\mathrm{O}}_{\mathrm{2}})$, and $\mathit{\delta }{(}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{36}}\mathrm{Ar})$, suggesting that the deviation corresponded to the mass number of the molecules. The relationship of the deviations was close to the experimental thermal diffusion, supporting the idea that the fractionation occurs due to thermal diffusion. The deviations of $\mathit{\delta }({\mathrm{CO}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}})$ were more than the values expected from theoretical and experimental thermal diffusions because the deviation of the experimental thermal diffusion for $\mathit{\delta }({\mathrm{CO}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}})$ had larger uncertainty than those of the other species. The values of $\mathit{\delta }{(}^{\mathrm{32}}{\mathrm{O}}_{\mathrm{2}}{/}^{\mathrm{28}}\mathrm{N}{)}_{\mathrm{2}}$ and $\mathit{\delta }{(}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}})$ also scattered more than their uncertainties. Further studies are needed to understand the fractionation mechanism(s) in detail.

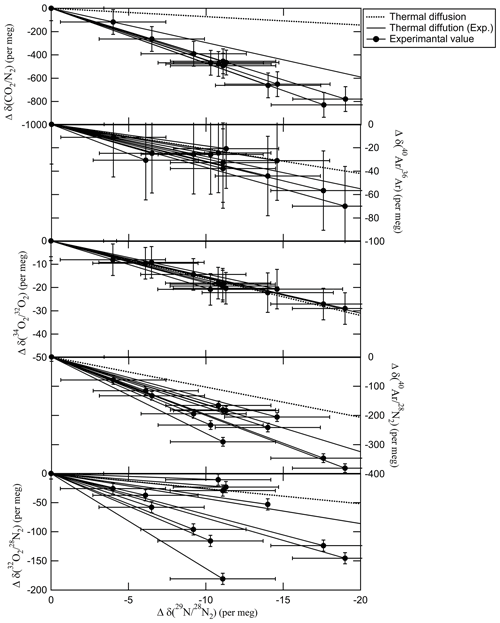
Figure 5 Relationship between the deviations of $\mathit{\delta }{(}^{\mathrm{44}}{\mathrm{CO}}_{\mathrm{2}}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}})$, $\mathit{\delta }{(}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{36}}\mathrm{Ar})$, $\mathit{\delta }{(}^{\mathrm{34}}{\mathrm{O}}_{\mathrm{2}}{/}^{\mathrm{32}}{\mathrm{O}}_{\mathrm{2}})$, $\mathit{\delta }{(}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}})$, and $\mathit{\delta }{(}^{\mathrm{32}}{\mathrm{O}}_{\mathrm{2}}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}})$ and the deviations of $\mathit{\delta }{(}^{\mathrm{29}}{\mathrm{N}}_{\mathrm{2}}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}})$ in the daughter cylinders relative to their mother cylinders after the CO₂–air mixtures with the atmospheric CO₂ level were transferred from the mother cylinder to the daughter cylinder. The error bar indicates the expanded uncertainty of the deviations. The dotted line represents the theoretical value of thermal diffusion (Langenfelds et al., 2005). The solid lines represent the deviations due to thermal diffusion experimentally estimated by Ishidoya et al. (2013, 2014).

3.2 Comparison between one-step dilution and three-step dilution

In the previous section, we determined the fractionation factor in the transfer of a source gas to be 0.99968±0.00010. This indicates that the CO₂ molar fraction in the gravimetrically prepared standard mixture with the atmospheric CO₂ level has a systematic error resulting from the fractionation in the second and third dilution steps. Two types of experiments were conducted to confirm the systematic error. One evaluated the fractionation in the second and third dilution steps based on the increase in CO₂ molar fractions in the first and second gas mixtures. Another evaluated the deviations of CO₂ molar fractions from the gravimetric values by measuring the third gas mixtures based on standard mixtures prepared by one-step dilution, which can avoid fractionation.

Two series of standard mixtures were prepared by one-step dilution to determine CO₂ molar fractions in the third gas mixtures used in the two experiments. The CO₂ molar fractions were corrected based on the adsorption of CO₂ to the internal surface using an $X_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{ad}}$ of 0.027±0.004 µmol mol⁻¹. Four standard mixtures were prepared as the first series to evaluate the fractionation in the second and third dilution steps, and the CO₂ molar fractions were 390.687±0.077, 402.253±0.078, 415.452±0.080, and 426.602±0.082 µmol mol⁻¹. Five standard mixtures were prepared as the second series to demonstrate the deviations of CO₂ molar fractions in the third gas mixtures, where the CO₂ molar fractions were 390.599±0.078, 399.807±0.094, 402.724±0.094, 406.021±0.094, and 419.618±0.098 µmol mol⁻¹. The numbers following the symbol ± denote expanded uncertainty mainly associated with the masses of source gases, CO₂, and air. The molar mass of air also contributes to the uncertainty of the CO₂ molar fraction because the composition of the air is different among individual cylinders purchased from the same gas manufacturer. For example, O₂ molar fractions of the air that our laboratory uses range from 208 000 to 209 600 µmol mol⁻¹. This difference causes the CO₂ molar fraction to deviate by 0.09 µmol mol⁻¹. Therefore, the molar fractions of N₂, O₂, and Ar in the air used in this experiment were determined based on the standard mixtures composed of N₂, O₂, Ar, and CO₂. Ar molar fractions were determined in the range of 9300 to 9360 µmol mol⁻¹ using GC-TCD, and their largest standard uncertainty was 6 µmol mol⁻¹, whereas O₂ molar fractions were determined in the range of 208 804 to 209 276 µmol mol⁻¹ using the paramagnetic O₂ analyzer, and their largest standard uncertainty was 6 µmol mol⁻¹ (Aoki and Shimosaka, 2019). N₂ molar fractions in the air were calculated by subtracting the Ar and O₂ molar fractions from 1. The first and second series were measured using the Picarro G2301, as shown in Fig. 6a. The line represents the Deming least-square fit to the data. The residuals from the line are shown in Fig. 6b. The error bar is expressed as the expanded uncertainty of the gravimetric values. The residual ranged from −0.014 to 0.008 µmol mol⁻¹ for the first series and from −0.057 to 0.054 µmol mol⁻¹ for the second series. The residuals were within the expanded uncertainties.

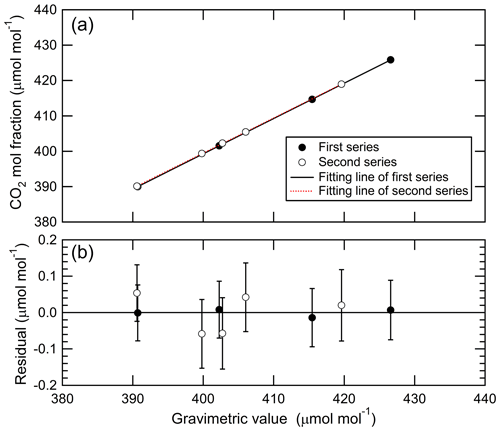
Figure 6 (a) Relationship between the measured CO₂ molar fractions and the gravimetric values for two series of standard mixtures prepared via one-step dilution. (b) Residuals from the Deming least-square fit shown in panel (a).

To evaluate the increase in CO₂ molar fraction in the second gas mixture as the source gas, six reference mixtures (third gas mixtures) with a molar fraction of approximately 400 µmol mol⁻¹ were prepared from a common second gas mixture, which had a gravimetric value of 5022.46±0.18 µmol mol⁻¹ for CO₂ in the process shown in Fig. 7a. The number following the symbol ± denotes the expanded uncertainty. The pressures of the second gas mixture used for the preparation of the third gas mixtures were 11.5, 9.7, 8.05, 4.2, 2.75, and 1.1 MPa. The increase in CO₂ molar fractions in the second gas mixture was evaluated by measuring the third gas mixtures using the Picarro G2301 based on the first series because it is directly reflected in the third gas mixtures, which were prepared from the second gas mixtures. The decrease amounts of the CO₂ molar fractions in the second gas mixture transferred into the daughter cylinder are the same for all third gas mixtures because the effects on the transferred mixtures act similarly. The relationship between the deviations from the gravimetric values in the third gas mixtures and the pressure of the second gas mixture is shown in Fig. 8a. The vertical axis is expressed as the deviation values found by subtracting the measured values from the gravimetric values for the third standard mixtures. The error bars represent the expanded uncertainties calculated by combining the standard uncertainty of the measurement with that of the gravimetric values for the standard mixtures prepared by three-step dilution. The known negative offset from the gravimetric value caused by the fractionation process in the gas transfer during the third gas mixture preparation is observed for the third gas mixture at 11.5 MPa. By decreasing the pressure of the second gas mixture to 1.1 MPa, the CO₂ in the third gas mixture increased by 0.25±0.10 µmol mol⁻¹, which agrees with the increased value of 0.30±0.10 µmol mol⁻¹ predicted from Eq. (4) using the fractionation factor of 0.99968±0.00010 determined in Sect. 3.1. However, we estimated the fractionation factor in the third dilution step by applying the Rayleigh fractionation model (Eq. 4) to the increase in the CO₂ mole fraction with the decrease in inner pressure, as shown by the solid line in Fig. 8a. The estimated fractionation factor was 0.99975±0.00004, which is consistent with the fractionation factor of 0.99968±0.00010 estimated in Sect. 3.1. This consistency indicates that the fractionation detected in the mother–daughter experiment also occurs in source gas transfer during the preparation of the third gas mixtures.

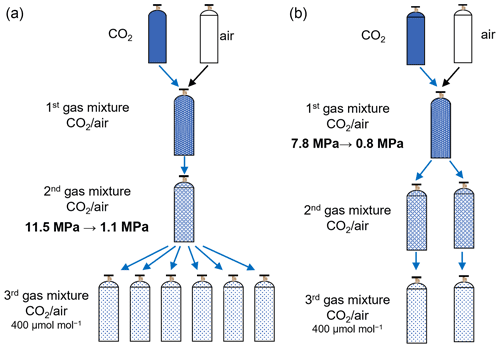
Figure 7 (a) Preparation of third gas mixtures with the atmospheric CO₂ level via three-step dilution to evaluate the fractionation in the third and (b) second dilution steps.

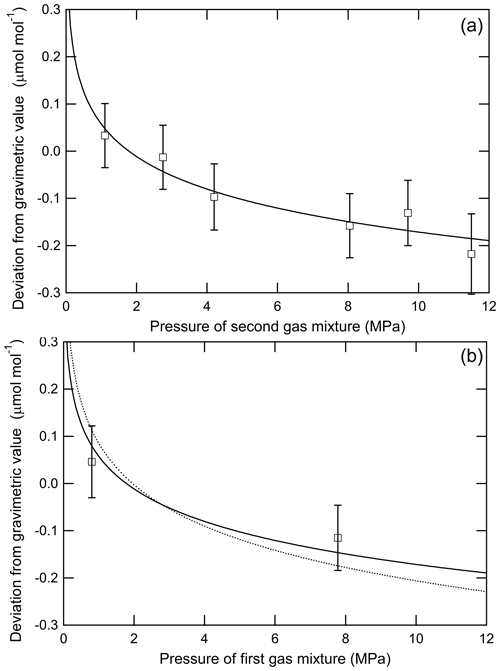
Figure 8 (a) Deviations of the measured CO₂ molar fractions from the gravimetric values against the pressure of the second gas mixture. CO₂ molar fractions determined based on the standard mixtures prepared via one-step dilution. The solid line represents the Rayleigh model fit for the plots. (b) Deviations of the measured CO₂ molar fractions from the gravimetric values against the pressure of the first gas mixture. The CO₂ molar fractions determined based on the standard mixtures prepared via one-step dilution. The solid and dotted lines represent the Rayleigh model fit based on fractionation factors of 0.99975±0.00004 and 0.99968±0.00010, respectively.

The fractionation of CO₂ and air likely occurs in the second dilution step in which the first gas mixture composed of CO₂ and air was transferred to the evacuated cylinder. We evaluated the fractionation based on the change in the deviations from the gravimetric values in the third gas mixtures prepared using the process shown in Fig. 7b. Two types of third gas mixtures with a CO₂ molar fraction of approximately 400 µmol mol⁻¹ were prepared from two types of second gas mixtures, which were prepared using a common first gas mixture having a CO₂ molar fraction of 65164.9±1.9 µmol mol⁻¹. The second gas mixtures had CO₂ molar fractions of 5022.46±0.18 and 4824.67±0.35 µmol mol⁻¹, which were prepared from the first gas mixture at a pressure of 7.8 and 0.8 MPa, respectively. The second gas mixtures were used only for the preparation of the third gas mixtures. The number following the symbol ± denotes the expanded uncertainty. The CO₂ molar fractions in the third gas mixtures were determined using the Picarro G2301, which is based on the first series. The contribution of the fractionation of CO₂ in the daughter cylinder was canceled because the effects on the transferred mixtures act similarly as described in the previous paragraph. The relationship between the deviations in the measured values from the corresponding gravimetric values and the pressure of the first gas mixture is shown in Fig. 8b. The solid and dotted lines in Fig. 8b represent the Rayleigh model line, which was calculated based on the fractionation factor of 0.99975±0.00004 and 0.99968±0.00010. The error bars represent the expanded uncertainties calculated based on the combination of the standard uncertainty of the measurement with that of the gravimetric values for the third gas mixtures. The deviations increased by 0.16±0.10 µmol mol⁻¹ as the pressure decreased from 7.8 to 0.8 MPa. Both lines agree with the deviations within the uncertainties. The fractionation factor in the second dilution step is equivalent to the fractionation factor in the third dilution step, indicating that fractionation occurs regardless of the CO₂ molar fraction of the source gas.

Finally, we demonstrated that the CO₂ molar fraction in the third gas mixture deviated from its gravimetric value according to the fractionation factors described above. In this demonstration, four third gas mixtures with atmospheric CO₂ levels were newly prepared by three-step dilution. The increase in CO₂ molar fractions in the first and second gas mixtures was corrected based on the decrease in their pressures from the initial values. The decrease in CO₂ molar fractions by the adsorption of CO₂ for the third gas mixtures was corrected based on the $X_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{ad}}$ of 0.027±0.004 µmol mol⁻¹. These corrections allow for extracting only the deviations from gravimetric values caused by fractionation in the transfer of the first and second gas mixtures. The CO₂ molar fractions in the third gas mixtures were measured using the Picarro G2301 based on the second series. Figure 9 shows the measured results. The measured values of CO₂ molar fractions were calculated based on the calibration line obtained by applying the Deming least-square fit to the measured values. The error bars represent the expanded uncertainties of the gravimetric values. The deviations were $-\mathrm{0.207}\pm \mathrm{0.060}$ µmol mol⁻¹ on average. The deviation dropped between $-\mathrm{0.252}\pm \mathrm{0.082}$ and $-\mathrm{0.200}\pm \mathrm{0.032}$ µmol mol⁻¹ when calculated using the fractionation factor of 0.99968±0.00010 and 0.99975±0.00004, respectively, and it was consistent with both values within their uncertainty. This indicates that the fractionation of CO₂ and air occurs according to our estimated fractionation factor in each dilution process.

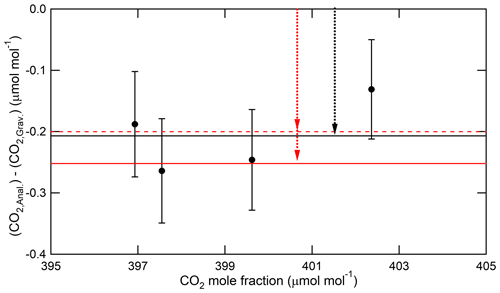
Figure 9 Deviations of the measured values from the gravimetric values of CO₂ molar fractions in the standard mixtures (third gas mixtures) prepared via three-step dilution. The measured values were calculated from the calibration line obtained by applying the Deming least-square fit to the measured data. The black line represents the average value of the deviations. The red solid and dotted lines represent the values calculated using fractionation factors of 0.99968±0.00010 and 0.99975±0.00004, respectively. The red and black arrows represent the deviation of CO₂ molar fraction in the third gas mixtures according to the fractionation of CO₂ and air.

4 Conclusion

CO₂ adsorption on the internal cylinder surface and the fractionation of CO₂ and air were used to evaluate systematic deviations in CO₂ molar fraction during the preparation of standard mixtures with the atmospheric CO₂ level. Decanting experiments were performed to evaluate the amount of CO₂ adsorbed on the internal surface of a 10 L aluminum cylinder during the preparation of CO₂–air mixtures with the atmospheric CO₂ level. The amount of adsorbed CO₂ was determined to be 0.027±0.004 µmol mol⁻¹ at 11.0 MPa, resulting in a small deviation in the gravimetric value. The mother–daughter experiments were performed to understand the fractionation of CO₂ and air when the CO₂–air mixture used was transferred into an evacuated cylinder as a source gas. The CO₂ molar fractions in the mother and daughter cylinders increased and decreased, respectively, indicating that fractionation not only decreases the CO₂ molar fraction in the prepared standard mixture but also increases it in the remaining source gas. The decrease in the CO₂ molar fractions in the daughter cylinders was constant regardless of the transfer volume, the initial pressure of the mother cylinder, and the transfer speeds at flow rates exceeding 19 L min⁻¹ used in the preparation of the standard mixtures. This indicates that the degree of fractionation during source gas transfer is constant. We demonstrated that CO₂ molar fractions in standard mixtures prepared by three-step dilution decreased by $-\mathrm{0.207}\pm \mathrm{0.060}$ µmol mol⁻¹ from the gravimetric values because of source gas fractionation, which is greater than the compatibility goal of 0.1 µmol mol⁻¹. The decrease was between the values calculated using fractionation factors of 0.99975±0.00004 and 0.99968±0.00010; one was estimated using the mother–daughter transfer experiments, and another was computed by applying the Rayleigh model to the increase in CO₂ molar fractions in the source gas. Fractionation at different stages of multistep dilution can result in a CO₂ increase, as well as a CO₂ decrease in the final gas mixture. This affects the reproducibility and accuracy of CO₂ molar fractions in standard gases determined by gravimetry. CO₂ molar fractions in standard mixtures prepared by multistep dilution involve systematic error because of the fractionation of CO₂ and air. Therefore, the effects of fractionation must be considered when gravimetrically determining CO₂ molar fractions in standard mixtures prepared by multistep dilution.