Simultaneous retrieval of aerosol and ocean properties from PACE HARP2 with uncertainty assessment using cascading neural network radiative transfer models

The University of Maryland, Baltimore County (UMBC) Hyper-Angular Rainbow Polarimeter (HARP2) will be on board NASA's Plankton, Aerosol, Cloud, ocean Ecosystem (PACE) mission, scheduled for launch in January 2024. In this study we systematically evaluate the retrievability and uncertainty of aerosol and ocean parameters from HARP2 multi-angle polarimeter (MAP) measurements. To reduce the computational demand of MAP-based retrievals and maximize data processing throughput, we developed improved neural network (NN) forward models for spaceborne HARP2 measurements over a coupled atmosphere and ocean system within the FastMAPOL retrieval algorithm. To this end, a cascading retrieval scheme is implemented in FastMAPOL, which leverages a series of NN models of varying size, speed, and accuracy to optimize performance. Two sets of NN models are used for reflectance and polarization, respectively. A full day of global synthetic HARP2 data was generated and used to test various retrieval parameters including aerosol microphysical and optical properties, aerosol layer height, ocean surface wind speed, and ocean chlorophyll a concentration. To assess retrieval quality, pixel-wise retrieval uncertainties were derived from error propagation and evaluated against the difference between the retrieval parameters and truth based on a Monte Carlo method. We found that the fine-mode aerosol properties can be retrieved well from the HARP2 data, though the coarse-mode aerosol properties are more uncertain. Larger uncertainties are associated with a reduced number of available viewing angles, which typically occur near the scan edge of the HARP2 instrument. Results of the performance assessment demonstrate that the algorithm is a viable approach for operational application to HARP2 data after the PACE launch.

1 Introduction

Satellite remote sensing has greatly enhanced our understanding of the Earth's environment, including the characterization of atmospheric aerosols and surface properties (Kaufman et al., 2002; Kokhanovsky et al., 2015; Kahn, 2015; Pörtner et al., 2023). Multi-angle polarimetric (MAP) remote sensing, pioneered by the Polarization and Directionality of the Earth's Reflectances (POLDER) instrument on Advanced Earth Observing Satellites (ADEOS-I; 1996–1997 and ADEOS-II; 2002–2003) and the Polarization and Anisotropy of Reflectances for Atmospheric Sciences coupled with Observations from a Lidar (PARASOL; 2004–2013) mission (Tanré et al., 2011), has emerged as a promising approach for retrieving geophysical properties from Earth observations (Mishchenko and Travis, 1997; Hasekamp and Landgraf, 2007; Knobelspiesse et al., 2012; Lacagnina et al., 2017; Dubovik et al., 2019; Hasekamp et al., 2019b; Chen et al., 2022).

This trend is set to continue with the forthcoming launch of the National Aeronautics and Space Administration (NASA) Plankton, Aerosol, Cloud, ocean Ecosystem (PACE) mission in January 2024, featuring a hyperspectral scanning radiometer named the Ocean Color Instrument (OCI) (Meister et al., 2022) and two MAPs with high polarimetric accuracy: the University of Maryland, Baltimore County (UMBC) Hyper-Angular Rainbow Polarimeter (HARP2) (Martins et al., 2018; McBride et al., 2023) and the Netherlands Institute for Space Research (SRON) Spectro-Polarimeter for Planetary EXploration one (SPEXone) (Hasekamp et al., 2019a; Smit et al., 2019). The deployment of these instruments presents an unprecedented opportunity to enhance our understanding and representation of atmospheric and surface conditions (Remer et al., 2019a, b; Frouin et al., 2019) and bridge future MAP observations, such as the European Space Agency (ESA) Multi-viewing Multi-channel Multi-polarisation Imager (3MI) on board the MetOp-SG satellites (Fougnie et al., 2018) and NASA's Multi-Angle Imager for Aerosols (MAIA) instrument (Diner et al., 2018).

Advanced simultaneous aerosol and surface property retrieval algorithms have been developed for MAP instruments (Chowdhary et al., 2005; Waquet et al., 2009; Hasekamp et al., 2011, 2019b; Dubovik et al., 2011, 2014; Wang et al., 2014; Wu et al., 2015; Xu et al., 2016, 2021; Fu and Hasekamp, 2018; Li et al., 2018, 2019; Stamnes et al., 2018, 2023; Gao et al., 2018, 2021a, 2023; Chen et al., 2020; Fu et al., 2020; Puthukkudy et al., 2020). Most of these retrieval algorithms developed for MAP observations are based on iterative optimization approaches that utilize vector radiative transfer (RT) forward models, capable of deriving atmospheric and surface properties simultaneously. Constrained by the speed of forward model calculations, MAP retrieval algorithms are often computationally expensive, which limits their applicability for large-scale operational data production and makes it difficult to conduct comprehensive uncertainty analyses. To address the data processing challenge related to the MAP instruments, Di Noia et al. (2015) developed a neural-network-based (NN-based) retrieval algorithm that derives aerosol properties directly from groundSPEX (a ground-based version of the SPEX instrument) and RSP (Research Scanning Polarimeter; Cairns et al., 1999) measurements. These directly inverted properties were then used as initial values in a subsequent iterative optimization.

To further improve the processing efficiency and flexibility, NN-based forward models are sometimes introduced to replace the radiative transfer calculation partially or fully in the retrieval algorithms. For example, Fan et al. (2019) represented the polarimetric reflectance for an open-ocean system using an NN and applied it to SPEXone data processing by coupling it with a linearized radiative transfer atmosphere model (Hasekamp and Landgraf, 2005). The PACE HARP2 data pose a further challenge due to the large data volume, with a swath more than an order of magnitude wider than SPEXone's. Gao et al. (2021a) demonstrated that an NN-based forward model can be trained to represent the vector radiative transfer calculation on a fully coupled atmosphere and ocean system. To process HARP2 data efficiently, the FastMAPOL algorithm was developed, powered by such an NN-based radiative transfer forward model, and validated using AirHARP field campaign measurements (Gao et al., 2021a, b) and HARP2 synthetic data (Gao et al., 2021b, 2022). To facilitate data synergy from multiple PACE instruments, Stamnes et al. (2023) utilized NN-based forward models that combine spectral bands from both HARP2 and SPEXone in MAP retrievals. These recent developments build upon the successful application of NNs in non-polarimetric remote sensing (Diego and Loyola, 2004; Schroeder et al., 2007; Fan et al., 2017; Chen et al., 2018; Nanda et al., 2019; Shi et al., 2020; Ukkonen, 2022; Stegmann et al., 2022; Ibrahim et al., 2022) and achieve the high radiometric and polarimetric accuracy of modern MAPs by using a larger number of hidden layers (e.g., three layers) and nodes (usually 200–1000).

Building from these studies, this work presents a refinement of the FastMAPOL retrieval algorithm suitable for global-scale PACE HARP2 data processing. The NN forward model is further optimized based on a realistic training data set, including expected orbital satellite geometries and employing highly accurate vector radiative transfer simulations. This allows us to test the processing performance on global spaceborne data and illustrate the expected aerosol and ocean color retrieval performance of HARP2. We introduce a novel measurement-uncertainty-aware NN training via modification of its cost function, resulting in an NN accuracy more consistent with the retrieval's cost function. Additionally, we explore the trade-off between NN speed and accuracy, training different sizes of NNs based on the new cost function, and further propose a cascading retrieval scheme that leverages a series of NN models of varying size, speed, and accuracy. Initial retrievals are conducted using faster and smaller but less accurate NN models, with subsequent retrievals performed using larger and slower but more accurate NN models.

To analyze the retrieval performance and uncertainties of these products, global over-ocean HARP2 radiative transfer simulations were generated using the most accurate NN forward model. This effort is a part of the day-in-the-life (DITL) prelaunch data processing test organized by the PACE Science Data Segment (SDS). Through the global-scale data analysis based on the cascading NN scheme in FastMAPOL, we examine the retrieval uncertainties for aerosol microphysical and optical properties in both fine and coarse modes, as well as ocean surface wind speed and ocean chlorophyll a, with respect to the location, geometries, and distribution of geophysical properties. We have also included aerosol layer height (ALH) in the HARP2 retrieval products, as encouraged by the sensitivity studies conducted on RSP (Wu et al., 2016) and the HARP instrument (Xu et al., 2021). The quantification of aerosol uncertainty can greatly enhance its applicability in radiative forcing, air quality, and climate studies. Consequently, this study offers a holistic discussion on the retrieval algorithm and the resultant data products with their associated uncertainties for HARP2 in anticipation of the upcoming PACE mission.

This study presents the advancements made to the HARP2 aerosol and ocean retrieval algorithm for operational data processing, including various improvements in the radiative transfer model with more realistic representation of spaceborne measurements, effective NN training methodology, flexible NN architectures, and a cascading retrieval scheme with comprehensive uncertainty assessment. The paper is organized in four sections, including a description of the retrieval algorithm and NN forward model (Sect. 2), retrieval and uncertainty analysis of the global-scale simulations (Sect. 3), and conclusion with discussions (Sect. 4).

2 Improved FastMAPOL retrieval algorithm

This section provides an overview of the enhancements made to the FastMAPOL retrieval algorithm, with various improvements in the radiative transfer model, NN training methodologies, and retrieval schemes with cascading NN models.

2.1 Simultaneous aerosol and ocean retrieval algorithm

HARP2 measures Stokes parameters L_t, Q_t, and U_t (where the subscript t represents total measurement) at 60 viewing angles at the 660 nm band and at 10 viewing angles at the 440, 550, and 870 nm bands (Puthukkudy et al., 2020; McBride et al., 2023). The total spectral measured reflectance (ρ_t(λ)) and degree of linear polarization (DoLP or P_t(λ)) are used in the retrieval inversion, which are defined as

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathit{\rho }}_{\mathrm{t}}& {\displaystyle }={\displaystyle \frac{\mathit{\pi }{r}^{\mathrm{2}}{L}_{\mathrm{t}}}{{\mathit{\mu }}_{\mathrm{0}}{F}_{\mathrm{0}}}},\text{(2)}& {\displaystyle }{P}_{\mathrm{t}}& {\displaystyle }={\displaystyle \frac{\sqrt{Q_{\mathrm{t}}^{\mathrm{2}}+U_{\mathrm{t}}^{\mathrm{2}}}}{L_{\mathrm{t}}}},\end{array}$$

where F₀ is the extraterrestrial solar irradiance, μ₀ is the cosine of the solar zenith angle, and r is the Sun–Earth distance correction factor in astronomical units. Note that the circular polarization (Stokes parameter V_t) is not measured by HARP instruments and is often, but not always, negligible for atmospheric studies (Kawata, 1978; Gassó and Knobelspiesse, 2022).

To derive aerosol and ocean information, the retrieval algorithm minimizes the cost function χ², which quantifies the difference between the measurement and the forward model simulation (Rodgers, 2000):

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{\mathit{\chi }}^{\mathrm{2}}& \left(\mathit{x}\right)=\\ & {\displaystyle \frac{\mathrm{1}}{N}}\sum _i\left({\displaystyle \frac{\left[{\mathit{\rho }}_{\mathrm{t}}\right(i)-{\mathit{\rho }}_{\mathrm{t}}^{\mathrm{f}}(\mathit{x};i){]}^{\mathrm{2}}}{{\mathit{\sigma }}_{\mathit{\rho }}^{\mathrm{2}}\left(i\right)}}+{\displaystyle \frac{\left[P_{\mathrm{t}}\right(i)-P_{\mathrm{t}}^{\mathrm{f}}(\mathit{x};i){]}^{\mathrm{2}}}{{\mathit{\sigma }}_P^{\mathrm{2}}\left(i\right)}}\right),\end{array}\end{array}$$

where ρ_t and P_t are measurements, and ${\mathit{\rho }}_{\mathrm{t}}^{\mathrm{f}}$ and $P_{\mathrm{t}}^{\mathrm{f}}$ are the corresponding quantities computed from the forward model. The state vector x contains all retrieval parameters. The subscript i stands for the index of the measurements at different viewing angles and wavelengths, and N is the total number of measurements used in the retrieval. The total uncertainties of the reflectance and DoLP used in the algorithm are denoted as σ_ρ and σ_P; both have contributions from measurement uncertainties σ_m and forward model uncertainties σ_f. In this work, the estimated expected measurement uncertainties for HARP2 of 3 % on reflectance and 0.005 on DoLP are used (McBride et al., 2023). Note that the above assumes independence of spectral or angular correlation between uncertainties; for a more complete treatment, Eq. (3) should be represented in a matrix form using the error covariance matrix (Rodgers, 2000; Gao et al., 2023). Statistical methods such as autocorrelation analysis have been used to estimate angular correlation strength from AirHARP field measurements and may be applied to future HARP2 data (Gao et al., 2023), but at present the correlation strength is not well known, so the above form (equivalent to a diagonal covariance matrix) is used. The retrieval is an iterative procedure to minimize using the subspace trust-region interior reflective optimization approach (Branch et al., 1999) by varying the state parameters x. In this work, the forward models are based on the NN discussed in the next sections, and the Jacobian matrices, used to determine the direction to update the state parameter, are computed based on automatic differentiation (Baydin et al., 2018) as formulated for the NN forward model (Gao et al., 2021b) and implemented within the deep learning framework (Osawa et al., 2019).

2.2 Coupled atmosphere and ocean radiative transfer model

The training data for the NN forward model are generated with a PACE-tailored vector radiative transfer model using the successive orders of scattering method (Zhai et al., 2022), with much better numerical accuracy than that of the HARP instruments (Gao et al., 2021a). An improved pseudo spherical shell (IPSS) correction is considered to improve the fidelity for larger solar and viewing zenith angles (Zhai and Hu, 2022). Reflectance and DoLP are simulated at the PACE satellite altitude (676 km above the Earth's surface); viewing and solar geometries are defined at the surface as shown in Fig. 1 based on the formulas derived in Zhai and Hu (2022).

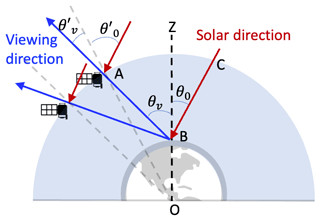
Figure 1 Spherical shell frame of the Earth system. The radiative transfer simulations are conducted according to the geometry defined at the satellite with the solar and viewing zenith angles ${\mathit{\theta }}_{\mathrm{0}}^{\prime }$ and ${\mathit{\theta }}_{\mathrm{v}}^{\prime }$ , which are converted to the geometry at the Earth's surface, with the solar and viewing zenith angles defined as θ₀ and θ_v. The solar and viewing azimuthal angles also depend on the reference frame but are not shown in the figure.

The forward radiative transfer simulations are conducted assuming a coupled atmosphere and ocean system. The atmospheric molecule distributions follow the US standard atmospheric constituent profile (Anderson et al., 1986). Absorption by oxygen, water vapor, methane, carbon dioxide, ozone, and nitrogen dioxide is considered through line-by-line calculations and integrated based on the double-k method (Duan et al., 2005; Zhai et al., 2022). The ozone density and surface pressure are assumed in the range as defined in Table 1. Near the Earth's surface, an aerosol layer is considered with a vertical number density distribution assumed as a Gaussian function (Wu et al., 2015):

$$\begin{array}{}\text{(4)}& N\left(z\right)={\displaystyle \frac{N_{\mathrm{t}}}{\mathit{\sigma }\sqrt{\mathrm{2}\mathit{\pi }}}}\exp \left(-{\displaystyle \frac{(z-z_{\mathrm{c}}{)}^{\mathrm{2}}}{\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}}}}\right),\end{array}$$

where N_t is the total aerosol column number density. z_c is defined as the aerosol layer height (ALH) in the range of 0.1 to 6 km above surface. σ is the standard deviation of the Gaussian distribution which is fixed at 2 km. The aerosol size is represented by the volume density of a combination of five lognormally distributed “submodes” similar to previous studies using the MAPOL (Gao et al., 2018) and FastMAPOL algorithms (Gao et al., 2021a). The mean radius r_i and standard deviation σ_i are fixed with values of 0.1, 0.1732, 0.3, 1.0, and 2.9 µm and 0.35, 0.35, 0.35, 0.5, and 0.5, respectively, following the work by Dubovik et al. (2011), Xu et al. (2016), and Fu et al. (2020). The first three submodes are used to represent the fine-mode aerosol, while the last two submodes are the coarse mode. Fine and coarse modes are assumed to have an independent complex refractive index with no spectral variation within the HARP spectral range. Therefore, the aerosol model includes 10 parameters: five volume densities (one for each submode), four independent parameters for the fine and coarse real and imaginary components of refractive indices, and one for ALH. Polarimetric single-scattering properties are modeled from these aerosol properties using the Lorenz–Mie code on spherical particles developed by Mishchenko et al. (2002). Note that particle non-sphericity is important for the realistic simulation of mineral dust aerosols (Dubovik et al., 2006) and will be incorporated in the next version of NN forward model following the same approach presented in this study.

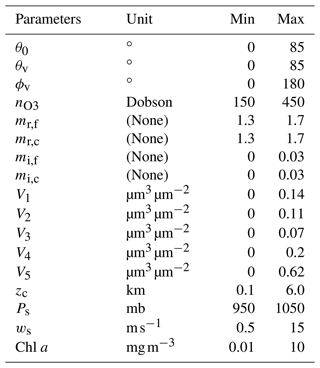
Table 1 Parameters used to represent the coupled atmosphere and ocean system in the radiative transfer simulation and NN training. θ₀ and θ_v are the solar and viewing zenith angles. ϕ_v is the relative azimuth angle. V_i denotes the five volume densities. An aerosol optical depth (AOD) range from 0.01 to 0.5 is considered and used to constrain V_i. m_r and m_i are the real and imaginary parts of the refractive index. Additional parameters include ozone column density (n_O3), aerosol layer height (z_c), surface pressure (P_s), ocean surface wind speed (w_s), and chlorophyll a concentration (Chl a). The minimum (min) and maximum (max) values determine the parameter ranges used to generate NN training data, which are also the constraints in the retrieval algorithm.

The optical model for the underlying water surface is summarized in Gao et al. (2019); briefly, it uses an open-ocean model including contributions from seawater, colored dissolved organic matter, and phytoplankton, the latter two of which are parameterized as a function of chlorophyll a concentration (Chl a; mg m⁻³). The seawater-polarized scattering properties are derived from the measured normalized Mueller matrix (Voss and Fry, 1984; Kokhanovsky, 2003). The ocean surface roughness is modeled by the isotropic Cox–Munk model with a scalar wind speed (Cox and Munk, 1954). Whitecaps are considered following the parameterization by wind speed (Koepke, 1986). While not done here, for future application to coastal waters where the open-ocean model is less valid, optimized NN models with sophisticated bio-optical models with seven (Gao et al., 2018) to three (Hannadige et al., 2023) parameters can be developed.

In summary, a total of 17 parameters are used as the input of the NN forward model as indicated in Table 1. These include the 10 aerosol parameters, as well as wind speed, ozone column density, surface pressure, and Chl a, and three geometric parameters: the solar zenith angle, viewing zenith angle, and relative azimuth angle.

2.3 NN training and performance analysis

The NN forward models (one set for reflectance and one set for DoLP) are trained following the procedures as summarized in Gao et al. (2021a) based on the radiative transfer simulations discussed in the previous section according to the parameter range as summarized in Table 1. This extends the previous work by including ALH and surface pressure as additional parameters, and the range of viewing geometries is also larger than the one used in the airborne measurement by taking advantage of the newly developed IPSS correction (Zhai and Hu, 2022) and the reference frame defined at the Earth's surface (Fig. 1). A total of 10 000 cases of radiative transfer simulations were generated with random values of the input parameters (this set is augmented as described below). A uniform distribution of aerosol optical depth (AOD) in the range between 0.01 and 0.5 is randomly sampled and used to specify volume densities following the sample strategy discussed in Gao et al. (2021a). In this study, we introduce two additional steps in the NN training to boost the NN performance:

1. Measurement-uncertainty-aware training. The NN forward models have been shown to achieve much higher accuracy than the HARP measurements using a leaky ReLU (rectified linear unit) activation function and three hidden layers (Gao et al., 2021a). However, at a low wind speed, the sunglint signal, i.e., the sunlight that reflects from the ocean surface around the specular reflection direction, can be strongly peaked, and this can dominate the mean square error (MSE) cost function used by Gao et al. (2021a) for optimization at the expense of precision in other areas. To avoid this issue, the previous study removed simulations close to the direction of specular reflection from the training data set, but the lack of data in sunglint also affected the retrieval results on wind speed and aerosol properties (Gao et al., 2021b). To enable sufficient accuracy to predict the reflection inside and outside of sunglint, we introduce the training cost function that, analogously to the retrieval cost function, normalizes the fitting residuals by the measurement uncertainty:

   $$\begin{array}{}\text{(5)}& {\displaystyle }{\mathit{\chi }}_{\text{NN},\mathit{\rho }}^{\mathrm{2}}& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{N}}\sum _i\left({\displaystyle \frac{\left[{\mathit{\rho }}_{\mathrm{t}}\right(i)-{\mathit{\rho }}_{\mathrm{t}}^{\text{NN}}(\mathit{x};i){]}^{\mathrm{2}}}{{\mathit{\sigma }}_{\mathit{\rho }}^{\mathrm{2}}\left(i\right)}}\right),\text{(6)}& {\displaystyle }{\mathit{\chi }}_{\text{NN},P}^{\mathrm{2}}& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{N}}\sum _i\left({\displaystyle \frac{\left[P_{\mathrm{t}}\right(i)-P_{\mathrm{t}}^{\text{NN}}(\mathit{x};i){]}^{\mathrm{2}}}{{\mathit{\sigma }}_P^{\mathrm{2}}\left(i\right)}}\right),\end{array}$$

   where ρ_t and P_t indicate training data, and ${\mathit{\rho }}_{\mathrm{t}}^{\text{NN}}$ and $P_{\mathrm{t}}^{\text{NN}}$ indicate the NN predictions. N in the denominator is the batch size in the training (taken as 1024 here). The same total uncertainty of σ_ρ=0.03ρ_t and σ_P=0.005 as in Eq. (3) is used here. Therefore, ${\mathit{\chi }}_{\text{NN},\mathit{\rho }}^{\mathrm{2}}$ represents the percentage error of the NN predictions, which can effectively incorporate the sunglint signals without directly impacting by its large magnitude. Since a constant value of σ_P is used, ${\mathit{\chi }}_{\text{NN},P}^{\mathrm{2}}$ is equivalent to a scaled MSE cost function. The polarization signal is better constrained within 0 and 1 for all viewing geometries, and therefore its training performance is less affected by the sunglint. This new cost function is a convenient and meaningful extension to the conventional MSE cost function applied on a set of normalized training data, especially for reflectance (e.g., Aggarwal, 2018; Fan et al., 2019; Gao et al., 2021a; Aryal et al., 2022; Stamnes et al., 2023). We found that the NN training hyperparameters (such as learning rate or batch size) reported by Gao et al. (2021a) still work well for the new cost function. The resulting training process is aware of the measurement uncertainty and therefore optimizes in a way more relevant to the retrieval's operation.

2. Training data augmentation. Generating training data from forward radiative transfer simulations is usually computationally expensive, which limits the NN training performance. However, one RT simulation can be used to generate an arbitrary number of viewing angles and increase the effective training data size, which may improve NN accuracy. This concept is equivalent to data augmentation in machine learning (Shorten and Khoshgoftaar, 2019). Gao et al. (2021a) explored it by sampling 100 sets of random viewing angles from every RT simulation. In this study, we provide a more systematic analysis of such data augmentation by sampling random sets with 100, 400, and 1000 angles, corresponding to total data sizes of 1 million, 4 million, and 10 million points, respectively, from the 10 000 RT simulations.

The NN's training performance is summarized in Fig. 2 for the feed-forward NN architecture with 17 inputs and 4 outputs and various hidden layer sizes (from two layers each with 64 nodes and 128 nodes to three layers each with 128, 256, or 512 nodes). To simplify the notation, we represent the hidden layer structure in a polynomial form; e.g., 128³ in Fig. 2 represents three hidden layers each with 128 nodes. We use 70 % of the simulated data for training (to minimize the training cost function) and the remaining 30 % for validation (to monitor the training process). Figure 2 shows that, with increasing NN hidden layer number and size, the cost functions for both training and validation data decrease, while validation cost eventually becomes larger than training cost. That suggests overfitting for the case of 1 million samples and an NN size of 128³. Introducing more training data from 4 to 10 million and an NN size up to 512³ further reduces the cost functions to convergence. More training data are generally able to reduce the difference between the training and validation cost function as compared in Fig. 2. Using 10 million total data, the reflectance NN performance stays stable, with a small training cost function value of 0.01, which suggests that the typical fitting residual between the NN and the simulation is about $\sqrt{\mathrm{0.01}}=\mathrm{0.1}$ times the measurement uncertainty, i.e., $\mathrm{0.1}\times \mathrm{3}\mathit{\%}=\mathrm{0.3}\mathit{\%}$.

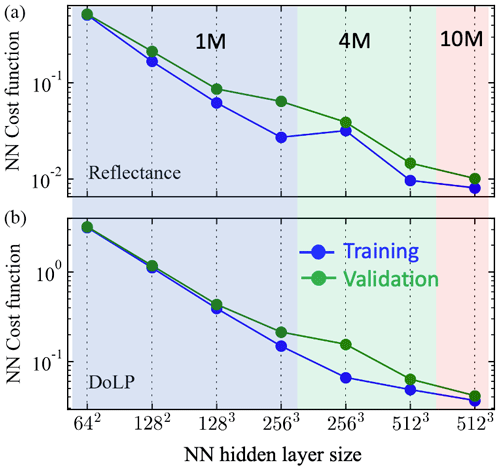
Figure 2 Training cost functions for reflectance (a) and DoLP (b) as a function of NN size. The background color indicates the number of training data used: 1 million (blue), 4 million (green), or 10 million (red). The horizontal axis indicates the size of hidden layers, as described in the text; for example, 64² indicates two hidden layers with 64 nodes at each layer. All the NN models shown here have 17 inputs and 4 outputs.

For DoLP, the NN training is more difficult because the DoLP uncertainty for HARP2 is often much smaller (0.005) than the (3 %) reflectance uncertainty. Figure 2 shows that generally a larger NN size is needed for DoLP to achieve a similar cost function value to reflectance. Using 10 million data and 512³ NN size, the cost function is about 0.04, which suggests that the NN accuracy is $\sqrt{\mathrm{0.04}}=\mathrm{0.2}$ times the measurement uncertainty, with a value of $\mathrm{0.2}\times \mathrm{0.005}=\mathrm{0.001}$. Similar accuracy for NN reflectance requires a size of 256³. An NN cost function value of 1 would indicate NN accuracy comparable to the measurement uncertainty, which would be achieved with an NN size of 64² for reflectance and 128² for DoLP.

Therefore, for the best performance of applying NN in joint retrieval algorithms, we implemented a two-level cascade scheme in FastMAPOL in which two rounds of retrievals are processed. In the first round, the NN size of 64² for reflectance and NN size of 128² for DoLP are used to efficiently find a rough solution. Then in the second (final) round the NN size of 256³ for reflectance and 512³ for DoLP are used to further fine-tune the state vector. Note that each retrieval includes multiple iterations with an order of 10 and involves the use of automatic differentiation to compute the Jacobian matrix analytically (Gao et al., 2021b). Cascading more levels could further improve the performance, but we found that two cascaded levels are sufficient for this study. By comparing the retrieval results with one and two cascading levels, we found that the retrieval uncertainties are similar to each other given the same high-accuracy NNs are used at the last level of retrievals. Therefore, the cascading algorithm will increase retrieval speed without impact retrieval accuracy. To fully test the cascade system as discussed in the next section, we used the best-accuracy NN with the largest size of 512³ to generate a set of synthetic data simulations and performed retrieval with the cascade retrieval scheme.

To further evaluate the NN uncertainty, we generated an additional 1000 independent sets of radiative transfer simulations with realistic HARP geometries as formulated in Gao et al. (2021b) and calculated the mean absolute error (MAE) and RMSE, comparing these simulations to the NN predictions. We found that the MAE is more robust to the impacts of outliers, similar to the discussion on the retrieval uncertainties (Gao et al., 2022). Based on this analysis, discussed in Appendix 1, NN uncertainties are estimated to be 0.5 % for an NN size of 512³ and 0.002 for DoLP using 512³, both similar to but slightly larger than the estimation from the training cost function. This further confirms that the new training cost function, considering measurement uncertainty, provides an intuitive way to measure the NN optimization. Note that, to ensure the high accuracy of the NN models, the RT simulations with a numerical accuracy much higher than the measurement and NN models are used to generate the training data as discussed in Gao et al. (2021a). For the application to real field measurements, the uncertainties including the NN models, RT simulations, and the measurement uncertainties need to be considered.

3 Retrieval analysis on synthetic global over-ocean HARP2 measurements

To evaluate the retrieval performance in terms of both speed and uncertainty in a realistic and representative way, we generated a day of synthetic over-ocean HARP2 measurements along PACE satellite orbits. Random errors based on estimated calibrated uncertainties are added to both the simulated reflectance and DoLP measurements. The retrieval uncertainties are evaluated through error propagation and then validated by comparing the truth and retrieval results based on the Monte Carlo approach (Gao et al., 2022). The viewing and solar geometries are based on realistic satellite orbits. This analysis is useful to understand the retrieval capability of the HARP2 data before PACE's launch.

3.1 Synthetic HARP2 L1C radiative transfer simulation

The Level-1C (L1C) file format is used to represent multi-angle measurements where different viewing directions are co-registered on the common spatial location to produce multi-angle measurements for each pixel (Lang et al., 2019). For the PACE mission, a set of common spatial grids are defined within the L1C format for all three instruments: OCI, SPEXone, and HARP2. The grids are based on the swath-based Spacecraft Oblique Cylindrical Equal Area (SOCEA) projection (Snyder, 1987) and documented in the PACE L1C document (Knobelspiesse et al., 2023). The HARP2 data processing will be performed by the PACE Science Data Segment (SDS) following the launch and instrument commissioning. The prelaunch testing of the data processing has been organized around a day in the life (DITL) that has been chosen to be 21 March 2022 (spring equinox), to ensure good daylight coverage over the majority of the world's ocean. The simulated PACE orbit for the DITL has been used to generate the sensor and solar geometry for the instrument data simulations to support the data processing tests by the SDS. The HARP2 simulations and processing results described in the following sections are based on the DITL.

The PACE L1C files are segmented in 5 min granules for daytime portions of the orbit, yielding a total of 165 granules in 15 orbits as shown in Fig. 3. The equatorial crossing time is at 13:00 LT with the satellite ascending northward. The nadir swath width is 1633 km which grows to a maximum swath width of 2380 km around 40^∘ along-track viewing zenith angle. The bin size is 5.2 km. The range of viewing zenith angle can vary from approximately −60 to 60^∘, with data collected across a time span of 6 min, during which the solar zenith angle can vary by up to 1.5^∘. Exact per-view solar geometries were used when generating the synthetic HARP2 data, which are important for reducing the impact from the measurement geometries due to satellite motions (Hioki et al., 2021).

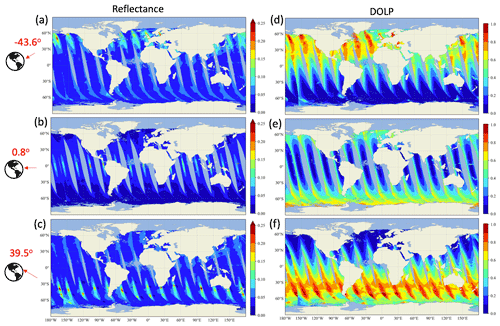
Figure 3 Global over-ocean simulation of HARP2 measurements at 550 nm for both reflectance (a–c) and DoLP (d–f), with a total of 15 orbits on the day of 21 March 2022. A total of 90 viewing angles at four HARP2 bands are generated, with three viewing angles in the along-track direction shown in the plots.

In the simulation, the surface pressure, ozone column density, surface wind speed, and speciated aerosol mass concentration vertical profiles are sampled from the NASA GMAO MERRA2 data (Gelaro et al., 2017; Randles et al., 2017; Buchard et al., 2017) along the satellite orbit to best represent the natural global-scale variability in the atmospheric state. Total column effective aerosol microphysical properties (column size and refractive index) were derived from the MERRA2 simulations of speciated aerosol mass concentration vertical profile by taking a volume-weighted average over the size bins and species in the MERRA2 data set. The aerosol size bins used in MERRA2 are different from the aerosol submodes used in the NN forward model. We have adjusted the volume density and refractive indices of the five aerosol submodes (see Table 1) to best match the aerosol representation in MERRA2. Hygroscopic growth of aerosol size is considered based on the relative humidity profile in the MERRA2 data (Castellanos et al., 2019). The total AOD in MERRA2 data is used to derive the total volume density and ensure that the same AOD will be produced based on the column effective aerosol size, refractive index, and volume density. The monthly average Chl a derived from MODIS ocean color products is used as the input to the radiative transfer simulation. Note that there are some small data gaps, most visible in the tropical Atlantic Ocean, due to the gaps in this Chl a product from heavy aerosol, cloud, or other data quality flags. However, as they are small, the retrieval performance analysis should not be significantly impacted.

The NN forward model with the maximum accuracy (512³) is used to generate the simulated L1C data for a total of 10 million pixels, each with 90 total viewing angles; examples for the HARP2 550 nm band with along-track viewing angles of −43.6, 0.8, and 39.5^∘ are shown in Fig. 3. The newly improved NN forward model can accurately represent the sunglint region, clearly recognizable from large reflectance magnitude at large viewing angles showing in the Northern (a) and Southern Hemisphere (c), as well as near the Equator (b) when looking near the nadir with a smaller reflectance magnitude. At larger viewing angles, prominent polarized signals are also shown in both the Northern (d) and Southern Hemisphere (f). DoLP generally increases with the viewing angle, until approaching the maximum value of 1 at the Brewster angle around 53^∘ at the air–water interface. The backscattering direction usually shows a minimum polarization magnitude, such as near the Equator when looking near the nadir (Fig. 3e).

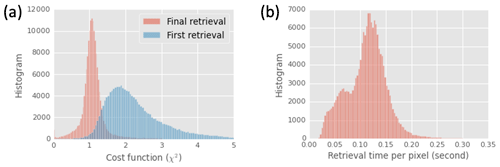
Two cascaded NN forward models for reflectance and DoLP, respectively, are used to conduct retrievals in the FastMAPOL algorithm as discussed in Sect. 2. The histogram of the cost function values for the first and final retrievals is shown in Fig. 4. The first retrieval, whose NNs have comparable uncertainty to the measurement uncertainty, produces a most probable retrieval cost function of around 2.0. After using the more accurate NN with a much smaller uncertainty, the final retrieval cost functions are mostly close to 1.0. The average total time taken for a retrieval with this two-layer cascade is 0.1 s, as shown in Fig. 4b, compared to 0.2 s for a retrieval using only the higher-accuracy NN (not shown), corresponding to roughly a 50 % speedup.

Figure 4 (a) Histogram of the cost function values (χ²) for the first retrieval using a smaller neural network (blue) and the final retrieval using the larger neural network (red) as summarized in Sect. 2. A histogram of processing time for the two-stage process is shown in (b).

3.2 Retrieval results

Initially, we conducted a retrieval analysis on a subset of data by including all the parameters as shown in Table 1 except the three geometric variables. The retrieval uncertainties for the ozone density and surface pressure are large, with an MAE of 53 DU and 24 mb and an RMSE value of 69 DU and 32 mb, respectively. As a result, instead of retrieving these two parameters, we choose to use the value directly from MERRA2 and retrieve only aerosol and ocean properties (which also results in slightly increased accuracy) when applying FastMAPOL to the L1C simulated data. Besides the directly retrieved quantities (Table 1), the aerosol optical depth (AOD) and single-scattering albedo (SSA) for both the fine and coarse modes were computed from retrieved aerosol volume densities and refractive indices using corresponding NNs trained similarly to the reflectance and DoLP but with a much smaller size of two hidden layers each with 64 nodes (Gao et al., 2021a). Total AOD is obtained as the summation of the fine- and coarse-mode AODs. Effective radius and variance are also calculated from the components' sizes and retrieved volumes.

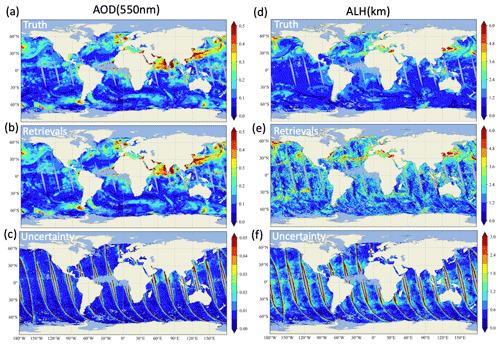
Figure 5 shows the global map of the retrieved AOD and ALH as well as the corresponding truth values and the retrieval uncertainties based on error propagation. The retrieval value and truth values are very similar to each other as shown in Fig. 5a and b for AOD. Larger uncertainties are mostly associated with the edge of the orbit, where fewer than five viewing angles per band (or total 20–30 angles) are available (see also the analysis in Hasekamp and Landgraf, 2007; Wu et al., 2015; Xu et al., 2017; Gao et al., 2021b). For real PACE data, the adaptive data screening method will be used to automatically remove the angles impacted by cirrus clouds and anomalies, and therefore the uncertainties will depend on the number of available angles associated with the location and size of those clouds (Gao et al., 2021b). Figure 5e and d show that the aerosol layer height (ALH) error has a stronger dependency on the AOD, with performance being generally better (and uncertainties smaller) where AOD is larger.

Figure 5 The retrieval results, truth, and uncertainties for AOD at 550 nm (a–c) and ALH (d–f).

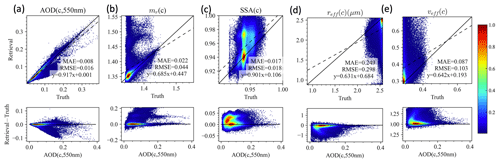
Data densities showing the correlation and difference between retrieval and truth are shown for AOD, ALH, fine-mode volume fraction (fvf), wind speed, and Chl a in Fig. 6. The retrievals perform well, with the RMSE for AOD, ALH, fvf, wind speed, and log ₁₀(Chl a) of 0.011, 0.9 km, 0.06, 1.4 m s⁻¹, and 0.19, respectively. Similar to Fig. 6, Fig. 7 shows the comparison between the retrieval results, with the truth for the fine-mode AOD at 550 nm, real part of the refractive index, single-scattering albedo, effective radius, and variance. The difference between retrieval and truth seems to strongly depend on the fine-mode aerosol loading as shown in the second row of Fig. 7. However, the retrieval becomes more challenging for the coarse mode as shown in Fig. 8 due to the much lower coarse AOD in general.

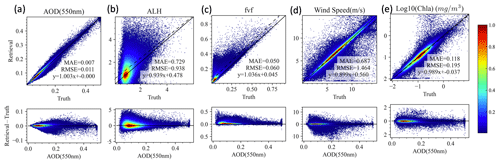
Figure 6 The comparisons of the retrieved and truth values for total AOD (550 nm), ALH, fine-mode volume fraction (fvf) wind speed, and Chl a. The top row shows heat maps (including the MAE and RMSE), while the bottom row shows the error of the corresponding upper-panel parameters as a function of the total AOD at 550 nm. The colors indicate the data density estimated by a kernel density method (Silverman, 1986).

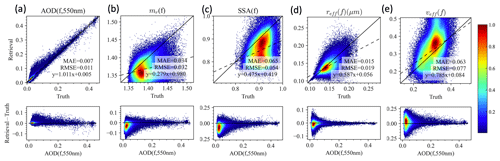
Figure 7 As in Fig. 6 except for fine-mode AOD, refractive index (m_r), SSA, effective radius (r_eff), and variance(v_eff) and the bottom row as a function of fine-mode AOD.

Figure 8 As in Fig. 7 except for coarse-mode properties instead of fine mode.

3.2.1 Uncertainty analysis

To understand the quality of the retrieval products, “theoretical retrieval uncertainties” are evaluated from the error propagation method which maps the measurement uncertainties to the retrieval domain based on the Jacobian with converged retrieval parameters (Rodgers, 2000) and accelerated using NN automatic differentiation (Gao et al., 2021b). This uncertainty can be evaluated at every pixel and therefore provide a flexible metric to evaluate retrieval quality. Examples of AOD and ALH uncertainties are shown in Fig. 6c and f. However, the real retrieval quality also depends on how well the retrieval converges, which can eventually be evaluated based on the difference between the retrieval results and the truth as shown in Figs. 6–8. To verify that the theoretical retrieval uncertainty represents actual retrieval results, we employ the Monte Carlo error propagation (MCEP) method, which generates random samples of errors based on the theoretical uncertainties. Then, the histogram of the random errors for a large volume of data can be compared with the distribution of the real error (difference between retrieval and truth) so that we can assess the difference and similarity of error distribution derived from the two methods (Gao et al., 2022).

We further group all the pixels according to their AOD values in steps of 0.01 based on the retrieval results shown in Figs. 6–8. The mean absolute error (MAE) is used to evaluate both the average theoretical and real uncertainties, with results summarized in Fig. 9. Figure 9a1 shows that both the theoretical (red lines) and the true (blue lines) absolute uncertainties of AOD increase from 0.002–0.004 to 0.015 as AOD increases from 0.01 to 0.45, which also corresponds to the reduction of relative uncertainty from 20 %–40 % to 5 %. The results agree with the analysis on synthetic HARP2 measurements with a uniform distribution of AOD (Gao et al., 2021b, 2022). Points with AOD>0.45 are excluded because there are a small number of pixels in this range so that a few outliers could affect the statistics significantly. The high-quality AOD may be useful for climate studies which usually require a goal uncertainty of less than 0.02 (Mishchenko et al., 2004; Kahn, 2015; GCOS, 2022).

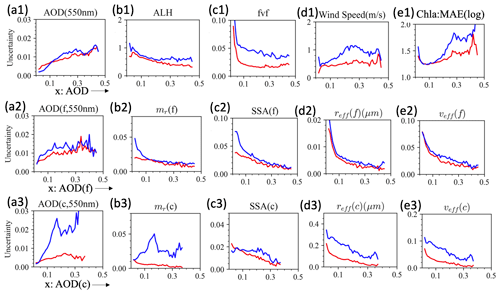
Figure 9 Comparison of theoretical (red) and real retrieval uncertainties (blue) as a function of AOD for AOD, SSA, real part of the refractive index (m_r), effective radius (r_eff) and variance (v_eff), wind speed, and Chl a. AOD, fine-mode AOD, and coarse-mode AOD values are used at the x axis from 0.01 to 0.45 with a step of 0.01.

Uncertainties of ALH decrease from 1 to 0.5 km within the range of AOD for both theoretical and real uncertainty. The retrieval uncertainty is larger than the results from the RSP instrument, using a spectral range of 410–1590 nm, where the MAE between the true the retrieval values is less than 250 m (Wu et al., 2016), probably as HARP2's shortest wavelength is 440 nm, and it has a larger polarimetric uncertainty of 0.005 compared with RSP (0.002). However, the ALH can still be useful for radiative forcing studies (e.g., Jia et al., 2022) and air quality investigations (e.g., Wang and Christopher, 2003).

Due to the wide angular range and the inclusion of sunglint signals in the NN forward model, the real wind speed accuracy is found to be much higher (1 m s⁻¹) compared to previous studies of 2–3 m s⁻¹ (Gao et al., 2022). The theoretical uncertainty has a smaller value of around 0.5 m s⁻¹, which suggests further room for retrieval improvement. The Chl a uncertainties are evaluated as the MAE of the log ₁₀(Chl a) uncertainty, as recommended by Seegers et al. (2018):

$$\begin{array}{}\text{(7)}& \begin{array}{rl}& \text{MAE(log)}={\mathrm{10}}^Y,\text{ where }\\ & Y={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N\left|{\log }_{\mathrm{10}}\right(R_i)-{\log }_{\mathrm{10}}(T_i\left)\right|,\end{array}\end{array}$$

where R_i and T_i denote the retrieval and truth values. This “multiplicative error” is a relative, dimensionless metric and takes values of 1 or more, where 1 indicates no error, 1.5 indicates a 50 % error, and so on. Figure 9e1 shows that Chl a can be retrieved accurately with a ratio of mostly less than 2.0, which suggests the potential of the MAP data for the evaluation of ocean properties. However, this will become challenging when the ocean water optical properties are more complex (Gao et al., 2019). Larger differences between the theoretical and real uncertainties are found mostly at AOD>0.2, as the ocean signal becomes increasingly obscured by the aerosols.

For the fine mode, theoretical and real uncertainties are compared in Fig. 9a2–e2. Fine-mode AOD seems to perform similarly to total AOD. The theoretical uncertainties agree with the real uncertainties when fine-mode AOD is larger than 0.1 but underestimate real uncertainties when AOD is lower. This may indicate lower sensitivity and higher instability due to the impacts of local minima in cost functions. However, the theoretical uncertainty seems to capture the real uncertainty well for effective radius and variance across the range of fine-mode AOD.

For the coarse mode, as the range of the coarse-mode imaginary refractive index in MERRA2 is limited (mostly < 0.001, probably due to the dominance of sea salt or other coarse soluble aerosols), we limited the retrieval of this parameter to a similar range. The large spread of retrieved SSA in Fig. 8c suggests the lack of sensitivity on the retrieval of the coarse-mode imaginary refractive index. The uncertainties are captured well by the theoretical uncertainties in Fig. 9c3. After launch, sensitivity studies will be required to better prescribe the coarse-mode imaginary refractive index. From the current synthetic data analysis, the real uncertainties are much higher than the theoretical uncertainties for coarse-mode properties. Low sensitivity is expected due to the low aerosol loading and lack of longer-wavelength shortwave infrared (SWIR) bands and therefore the challenges to converge to the global minimum of the cost function. The real uncertainties on coarse AOD are much larger than the fine-mode uncertainties with a value of up to 0.03, although the theoretical uncertainty for coarse-mode AOD is smaller (0.002–0.005) than the fine-mode AOD uncertainty (0.005–0.015), possibly due to the stronger constraint on the coarse-mode absorption. For PACE data, a future synergy with the SWIR bands from OCI may be used to improve the coarse-mode retrieval quality (Hasekamp et al., 2019). However, the impact of the coarse-mode aerosols in the application of atmospheric correction may be less severe due to their small overall value and weak spectral variation.

4 Discussion and conclusions

In this study we illustrated the advancements made to the FastMAPOL retrieval algorithm, including various improvements in the radiative transfer model, NN training methodology, NN architecture, and retrieval scheme.

• Radiative transfer model. We improved the radiative transfer model which is used to generate the training data for spaceborne measurement by including spherical shell correction, realistic solar and viewing geometries, and additional input parameters such as surface pressure and aerosol layer height.

• Training methodology. The NN models are trained by incorporating the measurement uncertainty model into the training cost function, which better represents sunglint signals and helps improve the NN relevance to the retrieval's operation.

• NN architecture. Flexible NN models with various numbers of hidden layers and numbers of nodes are investigated, which achieve different speeds and accuracies.

• Retrieval scheme. Two levels of NN models with increasing sizes and accuracies are used in a cascading retrieval scheme to achieve high retrieval efficiency and performance.

With the improved NN models and retrieval schemes, we also systematically investigate the retrievability of aerosol and ocean parameters and their uncertainty. The retrieval uncertainties are analyzed based on the FastMAPOL retrievals on the synthetic data sets, including the aerosol optical properties such as AOD and SSA and microphysical properties including aerosol size, refractive index, and height with more realistic statistics of the parameter values and viewing and solar geometries. For example, the overall uncertainties for AOD and wind speed are 0.01 and 1.4 m s⁻¹. The retrieval uncertainties at the pixel level are shown to depend on the number of available viewing angles and the aerosol loading. Fine-mode aerosol properties, such as the aerosol refractive index, generally show smaller retrieval uncertainties and better agreement between error propagation uncertainties and real uncertainties from simulated retrievals. Coarse-mode aerosol retrieval uncertainties are larger and not fully captured by error propagations. We also demonstrated that HARP2 measurements can be used to derive aerosol layer height with an uncertainty of 0.5 to 1.0 km depending on the aerosol loading.

Regarding the retrieval speed, in a previous version of the FastMAPOL algorithm we employed NN forward models with analytical Jacobian evaluation based on automatic differentiation, which had expedited the processing of the AirHARP data from 1 h per pixel using on-the-fly radiative transfer forward model simulations to around 0.3 s per pixel (Gao et al., 2021a, b). In this study, the processing speed of the HARP2 synthetic data is further improved to about 0.2 s per pixel by optimizing the numerical code. It is further reduced to 0.1 s using a single CPU core by applying a cascaded approach in FastMAPOL. With the newest development, the speed to process a single PACE L1C 5 min granule with an order of 400×500 pixels can be finished within 5 h in a single CPU core. As already demonstrated in our system, the whole day of synthetic data was processed within 5 h by utilizing distributed computing and running all granules parallelly. This illustrates that global-scale MAP data processing is feasible.

Furthermore, additional ocean properties can be derived from the MAP measurements and retrieval results. For example, NN models based on the retrieved aerosol and ocean parameters have been used to obtain water-leaving signals through the atmospheric and BRDF (bidirectional reflectance distribution function) corrections on real or synthetic AirHARP and HARP2 measurements (Gao et al., 2021a, 2022). Similarly, the retrieved aerosol properties can be used to assist the hyperspectral atmospheric correction as demonstrated using SPEX data as a PACE OCI proxy (Gao et al., 2019; Hannadige et al., 2021). NN methods can also be used to predict the polarimetric reflectance associated with complex water optical properties (Mukherjee et al., 2020) and instantaneous photosynthetically available radiation models within ocean bodies (Aryal et al., 2022) and derive in-water optical properties from top-of-atmosphere MAP measurements for PACE (Agagliate et al., 2023).

Therefore, based on the improved NN forward models, this study provided an efficient spaceborne MAP data processing algorithm and discussed the data product and the associated uncertainties analyzed from a global-scale synthetic HARP2 data set. For the future applications to the real satellite data after PACE launch, it would be important to ensure the forward model is appropriate for the measurements by conducting input data quality control and data screening (Gao et al., 2021b). Further evaluations on the measurement uncertainty model can be conducted by comparing it with fitting residual statistics (Gao et al., 2023). The algorithm and uncertainty analysis provide a viable way to process global HARP2 data and improve our capability to observe, understand, and protect our environment.

Appendix A: Evaluation of NN forward model uncertainty

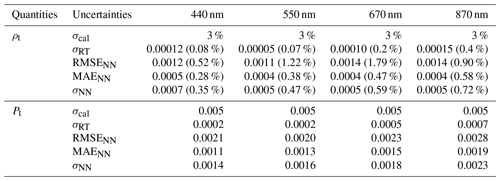
As discussed in Sect. 2, to evaluate the NN uncertainty independently, we use an additional set of 1000 simulations with realistic HARP geometries, formulated by Gao et al. (2021b). To further evaluate the accuracy of the NN, both the mean absolute error (MAE) and the root mean square error (RMSE) are computed for both reflectance and DoLP as shown in Fig. A1 and Table A1. As discussed in Gao et al. (2022), the MAE is more robust than the RMSE to outliers. We estimate the NN uncertainties using the MAE as ${\mathit{\sigma }}_{\text{NN}}=\mathit{\pi }/\mathrm{2}\times \text{MAE}$, which is equivalent to assuming the error following a Gaussian distribution (Gao et al., 2022). Note that the RMSE is slightly larger than σ_NN. The estimated errors are similar to the results obtained in Gao et al. (2021a), where 20 000 training data each sampled with 100 angles are used. Here, we decreased the training data set to 10 000 but sampled each case at 1000 angles. Note that in this study we have included the angles with sunglint, which includes many more cases in the uncertainty evaluations. To further improve the accuracy, we need to increase both the NN size and training data volume. A balance of training data volume, NN speed (smaller size), and NN accuracy (larger size, larger training data volume) is discussed in Sect. 2. NN accuracy is estimated with a value of 0.5 % for an NN size of 512³ and a value of 0.002 for DoLP using 512³; both are slightly larger than the estimation from the training cost function but on a similar scale as discussed in Sect. 2. The estimated NN uncertainties can be included in the total uncertainty model in the retrieval cost function as discussed by Gao et al. (2021a).

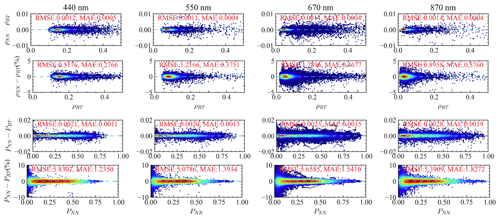
Figure A1 Comparison between the radiative transfer simulation and NN prediction: the left panel is reflectance (ρ) and the right panel is DoLP (P). The scatter plots are shown in the top panel, the absolute different in the middle panel, and the percentage difference in the bottom panel. For each plot, the data points for the 550, 660, and 870 nm bands are shifted upward by constant offsets consecutively, as indicated by the solid cyan lines.

Table A1 Comparisons of the uncertainties for reflectance (ρ) and DoLP (P) for both measurements and forward models including calibration uncertainty (σ_cal), the radiative transfer simulation uncertainty (σ_RT), and the NN uncertainty (σ_NN). The percentage values listed in the table indicate the percentage uncertainties.