the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
3D cloud masking across a broad swath using multi-angle polarimetry and deep learning
Kirk D. Knobelspiesse
Andrew M. Sayer
James Hays
Judy Hoffman
Understanding the 3D structure of clouds is of crucial importance to modeling our changing climate. Both active and passive sensors are restricted to two dimensions: as a cross-section in the active case and an image in the passive case. However, multi-angle sensor configurations contain implicit information about 3D structure, due to parallax and atmospheric path differences. Extracting that implicit information requires computationally expensive radiative transfer techniques. Machine learning, as an alternative, may be able to capture some of the complexity of a full 3D radiative transfer solution with significantly less computational expense. In this work, we develop a machine-learning model that predicts radar-based vertical cloud profiles from multi-angle polarimetric imagery. Notably, these models are trained only on center swath labels but can predict cloud profiles over the entire passive imagery swath. We compare with strong baselines and leverage the information–theoretic nature of machine learning to draw conclusions about the relative utility of various sensor configurations, including spectral channels, viewing angles, and polarimetry. Our experiments show that multi-angle sensors can recover surprisingly accurate vertical cloud profiles, with the skill strongly related to the number of viewing angles and spectral channels, with more angles yielding high performance, and with the oxygen A band strongly influencing skill. A relatively simple convolutional neural network shows nearly identical performance to the much more complicated U-Net architecture. The model also demonstrates relatively lower skill for multilayer clouds, horizontally small clouds, and low-altitude clouds over land, while being surprisingly accurate for tall cloud systems. These findings have promising implications for the utility of multi-angle sensors on Earth-observing systems, such as NASA's Plankton, Aerosol, Cloud, ocean Ecosystem (PACE) and Atmosphere Observing System (AOS), and encourage future applications of computer vision to atmospheric remote sensing.
- Article
(4676 KB) - Full-text XML
- BibTeX
- EndNote
Clouds regulate the global climate system in many important ways. Cloud radiative effects can be both warming and cooling, depending on the type and altitude of the cloud (Stephens and Webster, 1981). As the climate changes, the global cloud distribution will be affected by numerous feedback cycles, some of which are not fully understood (Ceppi et al., 2017; Gettelman and Sherwood, 2016). As a result, clouds and cloud feedbacks are among the greatest sources of uncertainty in climate sensitivity models (Pörtner et al., 2022; Meehl et al., 2020; Bony et al., 2015). Monitoring the response of global cloud distributions to a changing climate will be of utmost importance in the coming decades. Understanding the 3D structure of clouds, as well as the vertical distribution of cloud phase and thickness, is of great importance to climate modeling studies, such as the characterization of positive and negative cloud feedbacks (Rossow et al., 2022; Marchand et al., 2010).
Satellite remote sensing can help reduce these uncertainties by providing a source of consistent global data. Three satellite missions are of particular relevance to this work. One of these is Polarization and Anisotropy of Reflectances for Atmospheric Sciences coupled with Observations from a Lidar (PARASOL), a French Centre National D'études Spatiales (CNES) mission which launched in 2004 and remained operational until 2013. POLarization and Directionality of the Earth's Reflectances (POLDER) was a multi-angle polarimeter, the third of which (POLDER 3) was mounted on PARASOL. It was designed to improve understanding of clouds, aerosols, and their climate interactions (Deschamps et al., 1994; Buriez et al., 1997). POLDER data continue to provide diverse insights into aerosol properties near clouds (Waquet et al., 2013), constraints on global emissions (Chen et al., 2019), multilayer cloud identification (Desmons et al., 2017), and more. The second relevant mission is CloudSat – a NASA mission which observed the vertical distribution of clouds, aerosols, and precipitation using backscatter from its cloud-profiling radar (CPR) (Stephens et al., 2002; Im et al., 2005). From its launch in 2006 to its end-of-life in 2023, CloudSat provided diverse insights into clouds, aerosols, and precipitation (L'Ecuyer et al., 2015; Smalley et al., 2014; Haynes et al., 2009; Liu, 2008). Finally, Cloud–Aerosol Lidar and Infrared Pathfinder Satellite Observations (CALIPSO), which launched in 2006, carried an active lidar sensor and passive imagers, enabling the study of the vertical distribution of clouds and aerosols (Winker et al., 2009). All three of these satellites at one point shared an orbital constellation known as the A-Train, yielding nearly simultaneous observations of the surface (Stephens et al., 2018). CloudSat left the A-Train in 2018, followed by CALIPSO, but remained in orbit for several more years. These missions have reached their end of life now but remain an invaluable resource for preparing for the next generation of atmospheric satellites, like PACE (Plankton, Aerosol, Cloud, ocean Ecosystem) (Werdell et al., 2019).
The characterization of the vertical structure of clouds can be done from both passive and active sensors. Cloud-top height is often derived from passive thermal infrared measurements (Baum et al., 2012). These tend to provide only the top altitude of clouds in a column and struggle in multilayered cloud systems (Holz et al., 2008; Mitra et al., 2021) but have the advantage of broad spatial coverage. Active sensors, like CloudSat's CPR, have the advantage of providing a more complete vertical profile at the expense of coverage. For example, CloudSat observed a narrow cross-section of clouds at nadir, whereas POLDER's maximum swath width (across-view angles) was approximately 2200 km (Buriez et al., 1997). In addition, some passive sensors are multi-angle, allowing the use of stereoscopic methods to retrieve cloud structure.
Prior work has explored the usage of A-Train data to understand the structure of clouds, e.g., Barker et al. (2011), in which off-nadir cloud properties are estimated by nearest-neighbor matching with actively observed pixels, using the Moderate resolution Imaging Spectroradiometer (MODIS) radiances. Another approach estimates the cloud profiles from MODIS using a conditional generative adversarial network (Leinonen et al., 2019). Another work has explored the usage of POLDER data to understand the structure of clouds, using a decision tree to predict whether each pixel contains single-layer or multilayer clouds (Desmons et al., 2017). Observations from the Multi-angle Imaging SpectroRadiometer (MISR) in tandem with MODIS have been used to estimate two-layer cloud properties (Mitra et al., 2023). Airborne multi-angle platforms like the Research Scanning Polarimeter (RSP) have been used to study multilayer clouds (Sinclair et al., 2017). The estimation of vertical cloud profiles in geostationary data using machine learning has been studied (Brüning et al., 2024). This concurrent work employs a similar strategy to ours but on geostationary, single-view imagery. To our knowledge, our work is the first to estimate the full vertical cloud profiles from POLDER data.
The problem of reconstructing 3D geometry has a rich history in both remote sensing and computer vision, but the techniques used differ greatly between those fields. Whereas computer vision techniques nearly always assume a pinhole camera model, remote sensing uses a variety of different models, depending on the sensor's design. One common model for push broom sensors is the rational polynomial camera model (Gupta and Hartley, 1997; Zhang et al., 2019), which is incompatible with standard 3D reconstruction pipelines. Additionally, remote-sensing reconstruction typically operates on individual stereo pairs, rather than simultaneously reconstructing more than two views (Schönberger and Frahm, 2016). Even within the remote-sensing space, most 3D reconstruction approaches operate on relatively high-resolution imagery (on the order of several meters; e.g., Castro et al., 2020) and not on wide-swath imagery like POLDER, whose pixels are 6 km × 7 km wide (Buriez et al., 1997). Another scale-related difficulty is the difference between horizontal and vertical resolution. Many vertical cloud profiles are reported at sub-kilometer vertical resolution (Stephens et al., 2002), which may be difficult or impossible to accurately retrieve from low-resolution passive imagery like POLDER. Another example of 3D reconstruction is the MISR INteractive eXplorer project (MINX), which performs a stereo height retrieval of aerosol plumes in MISR data (Nelson et al., 2010). However, the smaller pixel size and larger parallax simplifies the determination of height. Cloud-top height retrievals were performed with the Along Track Scanning Radiometer (ATSR) sensor series (Muller et al., 2007). Both MISR and ATSR have sharper resolutions than the 6 km × 7 km pixels of POLDER (Buriez et al., 1997), with MISR at 275–1100 m (Diner et al., 1998) and with ATSR at 1 km (Muller et al., 2007).
As an alternative to stereoscopic 3D reconstruction, we elect to directly estimate the vertical cloud distribution of each location. This is accomplished with a deep-learning method, which essentially takes passive imagery as input and estimates an active sensor product as output but on the same spatial grid as the input. The model takes a flat representation of the multi-angle imagery as an input and produces a dense 3D binary cloud/no-cloud grid. The 3D masking task is known in the computer vision literature as volumetric segmentation (as opposed to image segmentation). Deep learning for volumetric segmentation is well studied, particularly within medical applications like computed tomography (Çiçek et al., 2016; Soffer et al., 2021; Ardila et al., 2019; Jnawali et al., 2018). However, these methods take a 3D input. By contrast, our method stacks the various viewpoints of the surface (as seen from different angles), as is done in 3DeepCT (Sde-Chen et al., 2021), in which deep learning is used to regress 3D liquid water content. Our motivation for stacking multiple viewpoints is “depth from disparity”, where the disparity (in appearance between viewpoints) is an indicator of the depth (distance from sensor). Another highly relevant work is VIP-CT (Ronen et al., 2022), which directly regresses the extinction coefficient of a 3D cloud field using simulated multi-angle data. Figures in this paper were generated with the matplotlib (Hunter, 2007) and seaborn (Waskom, 2021) libraries.
In order to satisfy the data requirements of a deep neural network, we synthesize POLDER data with a CloudSat product called 2B-CLDCLASS (Sassen and Wang, 2008). Both the original POLDER and CloudSat data are made available by the AERIS/ICARE Data and Services Center (see the “Code and data availability” section). The original POLDER data come from the level 1B product, whereas for CloudSat, we use a product called 2B-CLDCLASS provided by the Calxtract application from ICARE. We call the fused and re-formatted dataset the A-Train Cloud Segmentation (ATCS) Dataset due to the orbital constellation that these satellites shared. The ATCS dataset and related API are available as an archive in the SeaWiFS Bio-optical Archive and Storage System (SeaBASS) (https://seabass.gsfc.nasa.gov/archive/NASA_GSFC/ATCS/ATCS_dataset/associated, last access: 31 October 2023).
2.1 POLDER data
The POLDER level 1B data used in this study are in HDF5 format and organized by date. Each file corresponds to one PARASOL half-orbit (the daytime side). POLDER level 1 and higher products are generated on a gridded equal-area sinusoidal projection, with each pixel in this grid corresponding to approximately 6 km × 7 km on the surface (Hagolle et al., 1996). Each pixel contains the co-registered quasi-simultaneous multi-angular viewpoints. There are up to 16 viewing angles (from PARASOL's perspective) from which a point on the Earth can be observed. The maximum delay between these quasi-simultaneous observations is on the order of several minutes. See Table 1 for a description of the POLDER 3 spectral bands. See Fig. 1 for an example of nadir views in 10 POLDER 3 scenes from the test set.
2.2 2B-CLDCLASS
These files are merged with 2B-CLDCLASS data, a CloudSat product which contains CPR data, and are classified into eight cloud types (Sassen and Wang, 2008). While the eight cloud types are preserved in the ATCS dataset, this study treats cloud presence as a binary label. The CPR range extends from beneath the surface up to 25 km, the vertical resolution is 240 m, and there are 125 height bins in the data. There are few to no clouds in many of the higher-altitude bins (above 14 km) for the sampled data, which are discarded. Sub-surface bins are discarded as well. There are 59 bins in the valid range.
There are related products which combine the CloudSat radar and the CALIOP (Cloud-Aerosol Lidar with Orthogonal Polarization) lidar, such as 2B-GEOPROF-LIDAR (Mace and Zhang, 2014). When including lidar, the data contain many optically thin clouds, especially cirrus clouds, to which POLDER and many other passive sensors are often not sensitive. This caused issues when applying supervised learning; the loss function was dominated by optically thin clouds and performance on the radar-observed clouds suffered as a result. This course of study was therefore discontinued but could prove interesting for future work.
Generally, POLDER 3 and CPR are sensitive to different physics. It should be impossible for a method with access to only the shortwave information in POLDER 3 to fully capture a radar product. Some loss of information is expected, but this study aims to provide a reasonable lower bound on the degree to which POLDER 3 contains the 2B-CLDCLASS information. This goes both ways because MODIS is sensitive to some cloud features that are not detected by CloudSat and CALIOP, particularly low and optically thin clouds (Chan and Comiso, 2011; Christensen et al., 2013). POLDER 3 should also be able to detect these features, given its similar spectral sensitivity to MODIS. We focus our efforts on quantifying the passive-to-radar estimation rather than the converse in order to capture the benefits of a wide swath.
2.3 Sampling strategy
As the quantity of available data is more than sufficient to train a deep network, we make use of uniform sampling to compile the dataset. We randomly sampled half-orbit files for both PARASOL/POLDER and CloudSat/2B-CLDCLASS from every day in a predetermined date range and discarded invalid data. The date range was determined by the availability of valid data; before 27 November 2007, our data extraction process was unable to recover valid data. In December 2009, PARASOL lowered its orbit to exit the A-Train (Stephens et al., 2018), meaning POLDER 3 data were no longer quasi-simultaneous with CloudSat. Data were considered invalid under any of the following conditions: (1) any of the POLDER, 2B-CLDCLASS, or CALIPSO/CALIOP half-orbit files were missing; (2) the half-orbit file start times were off by more than 10 min (potentially indicating an incomplete record); (3) the produced records did not contain valid data for 13 or more angles in the POLDER imagery; or (4) the produced records did not contain 50 or more labeled pixels.
Standard practice in machine learning involves splitting datasets into separate sets for training, validation, and testing. Labels from the training set are used to optimize the model's parameters. The validation set is used to examine the model's performance, and its labels are held out so they cannot directly affect the model's parameters. However, hyperparameters (e.g., learning rate and how many layers in a model) are typically optimized with respect to the validation set. Neither parameters nor hyperparameters should be optimized with respect to the test set, which is the final measure of a method's efficacy. Commonly, the training set is the largest. We separately generate a training + validation (trainval) set and a test set, with the test set being approximately one-quarter the size of the trainval set. The trainval set is then split with 80 % of half-orbit files assigned to training and 20 % assigned to validation.
The trainval set has two files per day, and the test set has one file per day. For each 2B-CLDCLASS half-orbit file, we uniformly sampled random locations along the CloudSat track, attempting the alignment procedure described in the next section until acquiring enough patches, with 16 for the trainval set and 8 for the test set. The patches are 100 px × 100 px, as these have sufficient spatial context without yielding overly large file sizes. Since each pixel contains hundreds of values corresponding to various angles and spectra, increasing the patch size quickly becomes costly to storage space. Conversely, smaller patch sizes reduce spatial context, which contains useful information for the segmentation algorithm.
2.4 Alignment strategy
Alignment between POLDER and 2B-CLDCLASS data is performed with sub-pixel accuracy with respect to POLDER. The POLDER grid is a sinusoidal (equal-area) projection of the globe (Hagolle et al., 1996). Each pixel in this grid contains multi-angular sensor data, geography (latitude, longitude, and altitude), and geometry (viewing angle, solar zenith angle, and relative azimuth). The 2B-CLDCLASS data are provided temporally, with each timestamp associated with a vertical cloud profile; a latitude/longitude point on the Earth; and some metadata, such as quality flags. Although we could quantize the 2B-CLDCLASS locations to the POLDER grid, doing so would cause substantial quantization error. Instead, we compute ground distances to find nearest neighbors in the POLDER data for each 2B-CLDCLASS observation. As it would be computationally prohibitive to compute these distances between all point pairs, we first use a k-d tree (Bentley, 1975) to find the top 20 POLDER matches in latitude/longitude space for each CloudSat observation. Although the latitude/longitude grid is far from having an equal area, at sufficiently small distances, the effect of Earth's curvature on the distance ranking approaches zero. We then compute approximate ground distances from the CloudSat observation to these 20 points using the World Geodetic System 1984 (WGS 84) ellipsoid model of the Earth. From these 20 points, we select the closest ones that are found to the northeast, southeast, southwest, and northwest of the CloudSat observation. These four points are used as interpolation corners, with weights defined by their ground distances. Standard bilinear interpolation leverages the separability of the x and y components of the interpolation equation, but these corners are neither on a flat plane nor are they guaranteed to be rectangular. For these reasons, the normalized inverse distance is a more appropriate choice for the corner-weighting function.
For a pair of half-orbit files, the above defines a mapping from CloudSat observations to their corners in the POLDER grid. In order to sample patches, we compute all of the latitude intervals which would yield a 100 px north–south distance in the POLDER grid. We also compute the latitude-dependent longitude intervals which would yield a 100 px east–west distance in the POLDER grid. We uniformly sample latitude intervals and use our longitude intervals to compute an index from a 100 × 100 patch into the POLDER grid. As an additional step, we uniformly shift patches east or west by one-quarter of the patch window so that labels are not always found in the center of the patch. All patches are north-aligned; we do not perform any rotation. Only CloudSat observations which have four corners within the patch are kept. If there are fewer than 100 CloudSat observations in a patch then that patch is discarded. Additionally, occasional quantization or out-of-bound errors can cause the patch to contain fewer than 100 px × 100 px or to contain 101 px × 100 px. In these cases, we discard the patch. This process loops until sufficient patches are found for a file. Sufficient valid patches were found for every file.
We validate our alignment accuracy by computing (approximate) ground distance between the latitude and longitude values of the projected CloudSat observations and the weighted interpolation of the latitude and longitude values of the corresponding corners in the POLDER grid. The mean projection error across both the training and validation datasets is 881 m, with a maximum error of 2216 m. This is significantly less than a single pixel in the POLDER grid, which is approximately 6 km × 7 km. Sub-pixel alignment accuracy ensures that each pixel in the POLDER grid contains sensor values from the correct location.
2.5 Dataset statistics
ATCS is a large-scale dataset, enabling the training of deep neural networks. The 2B-CLDCLASS vertical cloud profiles are used as labels for the PARASOL imagery, which is used as input to the neural network. The ATCS dataset contains 20 352 labeled instances and 5032 instances in the test set, whose labels are withheld. The labeled instances are divided, with an 80 % 20 % training validation split. On average, in the labeled set, there are 116 labeled locations per 100 × 100 patch, with a standard deviation of 18, a minimum of 55, and a maximum of 171.
Data were sampled uniformly in the geographic sense, except for latitudes greater than ± 80°, which cause complications with geometric processing. There is great value in this global coverage, as cloud dynamics and appearance vary greatly by region. The difficulty of the cloud segmentation task is also strongly regionally dependent. For example, near the poles, there are high-albedo icy and snowy surfaces, which are more visually cloud-like than typical terrestrial surfaces, complicating the segmentation task (Stillinger et al., 2019).
Cloudiness also correlates strongly with altitude. There is a strong “class imbalance” between the clouds at various altitudes – a randomly sampled pixel is much more likely to contain clouds at a lower altitude than to contain clouds at the upper-altitude range, i.e., near 14 km.
Our approach is to learn a functional mapping from multi-angle imagery to per pixel vertical profiles of cloud occurrence using a deep convolutional neural network (CNN). This had two primary motivations. First, by training a model on labeled nadir pixels and applying it to unlabeled off-nadir pixels, we produce a wide-swath vertical cloud product, which has independent value. Second, the supervised learning setup allows for ablation experiments; various sensor properties (angle, spectral band, and polarization) can be omitted from the input data. The resulting change in model skill provides insights into the utility of these properties for estimation of cloud structure. The use of a neural network allows the characterization of highly non-linear relationships between these input fields and the cloud profile outputs, and deep learning outperforms shallow learning, as shown in Table 2.
Table 2Comparison of three architectures of increasing complexity. Results are reported for the test set. U-Net achieves the highest performance but has more parameters. The meaning of values in bold is the best-scoring (including ties) value in each column.

We used convolutional neural networks to incorporate spatial context, which are necessary in order to account for the parallax present in multi-angle data. Convolutions are useful for data which exhibit some form of translational invariance, meaning that some elements of appearance do not change due to translations in image space. Interestingly, convolutions are particularly suitable for satellite data, since they exhibit lower translational variance than ground-level imagery due to less perspective variation in depth. The spatial context provided by convolutional architectures can capture the apparent shift in location due to the parallax present in a cloudy scene, which is useful for the network to predict depth and vertical structure.
3.1 Representation
Instances are defined as input/output pairs, where input contains a 100 × 100 patch of multi-angle, polarimetric imagery from POLDER, as well as the pre-computed weights used for interpolation, and output contains the vertical cloud profiles from 2B-CLDCLASS. Each pixel in the input has data for up to 16 viewing angles. When data are missing for one or more viewing angles, a standard missing value of −1 is used. The median number of available viewing angles over the training and validation sets is 14, and 98 % of pixels have at least 13 available viewing angles. At each of the viewing angles, there are nine spectral bands, three of which measure linear polarization (Table 1). Linear polarization is represented as the Q and U components of the normalized Stokes' parameters (also known as S2, S3). Therefore, the channels without polarization have one value, I, while the polarization channels have three (I,Q, and U).
Raw sensor inputs must be converted into features which can be used by a neural network. Most inputs can simply be normalized before use, but some inputs must be more heavily modified. In addition to the nine intensity values, I, and the three pairs of Q,U values, there are four geometry fields, namely viewing angle, solar zenith angle, relative azimuth, and solar azimuth. We found there to be little difference from using view azimuth instead of relative azimuth. Rotations are discontinuous at 360°, which poses issues for a neural network as a small change in rotation can cause a large change in the output. We use a technique from the object recognition literature which encodes angles into binary membership in two of eight overlapping bins, as well as two in-bin floating point offsets (Mousavian et al., 2017), resulting in a vector with a length of 10. The eight overlapping intervals are [0°,90°], [45°,135°], …, [315°,45°]. The in-bin regression values are relative to the bin centers. As an example, consider the angle 100°. This occupies the second bin [45°,135°] and the third bin [90°,180°], giving it a bin membership encoding of 01100000. Its differences with the centers of the second and third bins are 10 and −35°, respectively. This yields a feature vector with a length of 10, , although the angles are converted to radians in practice. This transformation is only necessary for the azimuth angles, not the zenith angles, as zenith angles are bounded in the range [0°,90°].
There are 27 input values per view, with 6 non-polarized channels, 3 polarized channels with three values each (), a view azimuth feature with a length of 10, 1 view zenith angle, and 1 solar zenith angle. The solar azimuth feature with a length of 10 does not vary with view angle. Therefore, when using all 16 available angles, the channel depth (features per pixel) is 442. In addition, there are (non-angular) fields included for the convenience of other researchers. These values are not provided as an input to any model trained in this study and include latitude, longitude, surface altitude, and a land-or-sea flag.
Each input patch is represented as an image cube, created by stacking the multispectral and multi-angular features, as well as the geometry features described above. In line with standard practice in computer vision, each of the spectral features is normalized by subtracting their mean and dividing by their standard deviation with respect to the training set.
3.2 Architectures
Ideally, the selection of model architecture could be derived directly from the scene geometry. The receptive field of a pixel in the output of a convolutional neural network (CNN) is the extent of the input (in pixels) which can theoretically have affected it. In almost all sufficiently deep CNNs, the receptive field far exceeds the input image size. One could establish a relationship between the maximum possible disparity in pixel space due to parallax and derive a network architecture from that. There are two limitations with this approach. First, is that the model may benefit from having broader context about the scene. Second, is that the “effective receptive field” is always much smaller than the actual receptive field and is not straightforward to compute (Luo et al., 2017). For both these reasons, we instead elect to present a few reasonable architectures. We experimented with many more architectures than are presented here but found these three to be the best representatives of three different reasonable hypotheses.
3.2.1 Single-pixel network
A simple baseline approach to cloud segmentation is to independently estimate the vertical profile of cloud occurrence at each pixel. The hypothesis behind this architecture is that spatial context does not matter for this task. A multilayer perceptron (i.e., a simple neural network) predicts this vertical profile of a single pixel at a time from the sensor observations of that pixel. The single pixel model is implemented using 2D convolutions with kernel size 1 × 1. Since the kernel size is always 1 × 1, the independence of pixels is preserved (i.e., the network has no spatial context) but has the important property of keeping the same number of pixels per batch as the later experiments using 2D convolutions. Batch size would otherwise be a potentially confounding variable in any comparison between the single-pixel model and models which ingest an entire image at a time. We test a single-pixel model with three linear layers, with all but the last layer followed by batch normalization (features averaged across each batch) and a rectified linear unit (ReLU), which is defined as f(x)=x for x≥0, f(x)=0 for x<0.
3.2.2 Simple CNN
We also test a simple multilayer convolutional neural network, with the hypothesis behind this architecture being that spatial context does matter but a high depth (number of layers) does not. This model has five 3 × 3 convolutional layers. As with the single-pixel model, all but the last convolutional layer are followed by batch normalization and ReLU. Each convolutional layer includes 1 px of padding, so the image resolution stays constant during the forward pass.
3.2.3 U-Net
Finally, we implement U-Net (Ronneberger et al., 2015). The hypothesis behind this model is that both spatial context and depth are important for this task. A U-Net consists of a fixed number of down-sampling “blocks”, followed by the same number of up-sampling blocks, as well as skip connections between blocks at the same level of the spatial pyramid. The down-sampling blocks capture the typical structure of a convolutional neural network for image classification, where each subsequent layer represents a gradual trade-off of spatial resolution for increasing feature depth. U-Net also adds up-sampling blocks, which effectively do the opposite, namely decreasing the feature depth while increasing spatial resolution. This architecture is related to the commonly used encoder–decoder network. Unlike encoder–decoder networks, U-Net has skip connections which allow the preservation of spatially located features in the up-sampling path. We use five blocks in our U-Net, with the per block feature depths using the same scheme as described in Eq. (1). It is worth noting that increasing the channel depth in this way substantially affects both U-Net's parameter density and the size of the intermediate features during the forward pass. We experimented with several different schemes to decide channel depth and found this approach to be the most stable configuration for U-Net.
3.2.4 Channel depths
The number of input channels to our network is approximately 2 orders of magnitude higher than ground-level imagery; RGB imagery has three channels, but our multi-angle, multispectral images (which include a geometry encoding) have hundreds of channels. For example, the 8-angle multispectral experiments have 226 input channels.
A common choice for choosing channel depths in CNNs is to use increasing powers of two for historical reasons related to the use of pooling operators. This would result in unreasonably high feature depth, even after a few convolutional layers. Instead, we compute a scaling factor which yields a desired depth after a certain number of layers. These layer-wise feature depths ci are given by the following, where cinput is the input channel depth, coutput is the desired output channel depth, and ⌊⋅⌋ is the floor operator:
For the simple convolutional network, coutput is the number of height bins (59), and the input depth is used for the first layer's feature depth. Thus for our five-layer CNN, the per layer depths would be 226, 173, 132, 101, and 59. For the U-Net, coutput is the channel depth after the decoder half of the U-Net, which we set to be 1024. Again, for an input depth of 226, the feature depths would be 306, 414, 560, 757, and 1024. This scaling ensures a consistent rate of change in the feature depth, rounded to the nearest integer. Note that the base of the log does not matter as long as it is consistent.
3.3 Interpolation
One novel element of our network architecture is the use of interpolation during the forward pass of the model. The CloudSat labels are only available for some locations in the input images, and these locations are not quantized to the POLDER grid. Therefore, after the up-sampling blocks, the model has an interpolation layer, using the corners and corner weights described in Sect. 2.4. As a weighted average is differentiable, back-propagation can still be used to train the network. After the interpolation layer, the network has two fully connected layers. Figure 2 illustrates the forward pass, including a depiction of the interpolation process. Note the difference between this and bilinear interpolation; the bilinear interpolation is linearly separable. For accuracy, the interpolation model utilized here uses a latitude–longitude grid rather than a Cartesian grid, so the standard separability does not apply.
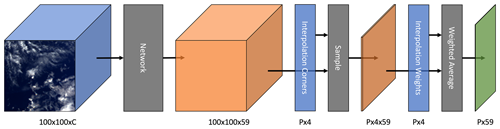
Figure 2Diagram illustrating the forward pass. The color blue denotes inputs, orange denotes intermediate tensors, and green denotes output. C denotes channel depth, and P denotes the number of labeled pixels in an instance. The model maps the input POLDER 3 imagery to predictions for each of the 59 height bins. These predictions are then interpolated and represented by the sample and weighted average blocks. Simply skipping the interpolation step allows the generation of wide-swath predictions.
The networks can be applied to data without interpolating. This is as simple as omitting the interpolation module. In Fig. 2, the 100 × 100 × 59 tensor can simply be used as the wide-swath prediction. The reduction down to a P×59 tensor is only necessary for the application of the loss function. Interpolation is slightly more complicated for U-Net, which is discussed in Appendix A.
3.4 Training procedure
In all experiments, the model is trained for 30 epochs using the Adam optimizer (Kingma and Ba, 2017) and the binary cross-entropy loss. The cross-entropy loss is theoretically well-founded; it measures how many bits would be needed to encode an event from the actual probability distribution, assuming the optimal encoding from the learned distribution. Cross-entropy also tends to converge quickly. Let σ(⋅) be the sigmoid operator, y the binary labels, and x the network's unbounded outputs (also referred to as logits). The binary cross-entropy loss is given by
We experimented with data augmentation, including random flips and rotations, but found these to significantly worsen performance, even when accounting for these changes in the geometry features. The purpose of these augmentations is to introduce symmetric and rotational invariance into the model without the need for more data. However, symmetric and rotational invariance are less important from an orbital view, and the model may benefit from memorizing the north-locked perspective inherent to the data. Therefore, we omitted data augmentation from our final experiments.
Each experiment is repeated three times for reasons discussed further in Sect. 4.2. Model checkpoints are saved every five epochs. Our implementation uses the PyTorch framework (Paszke et al., 2019). Training is performed using a single NVIDIA Tesla V100 GPU with 32 GB of memory. Training plus validation typically takes between 2 and 6 h per experiment.
We evaluate the model's performance on the test set. Some qualitative results can be seen in Fig. 3. More qualitative results are presented in Appendix B. Qualitative results suggest that the model is skillful at capturing the larger-scale structure of clouds, with worse performance for smaller cloud segments and multilayer clouds.

Figure 3Results for four instances in the test set, using the default experiment. The true cloud profiles are shown in the top row (a–d), and predictions are in the bottom row (e–h). The CALTRACK 2B-CLDCLASS file names are included at the top.
We perform a series of ablation experiments. The first experiment compares the skill of the three aforementioned architectures on the test data. In subsequent experiments, we deprive the model of various aspects of the available input data and measure the resulting effect on skill. These ablation studies reveal the impact of the viewing angles, the spectral configuration, polarimetry, and the scene geometry. The baseline “default” experiment consists of the simple convolutional model with 8 of 16 viewing angles, all available spectral channels (with polarimetry when applicable), and all geometry fields. Other experiments vary from the default experiment only in the exact ways specified in Tables 2, 3, and C1 and Figs. 4–6.
Table 3Comparison of various viewing geometries, using the simple convolutional model. The two-angle view contains only the pair of angles closest to nadir. The four-angle view adds the next innermost pair of angles, proceeding outward until all 16 angles are included. The bold values show the highest-scoring rows (including ties) in each column.
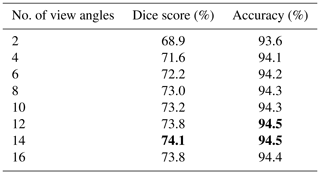
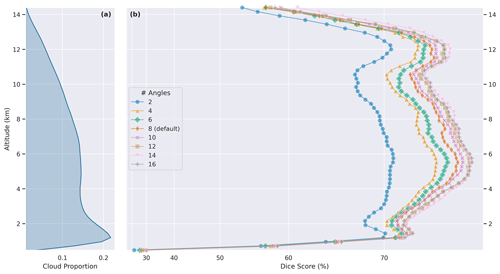
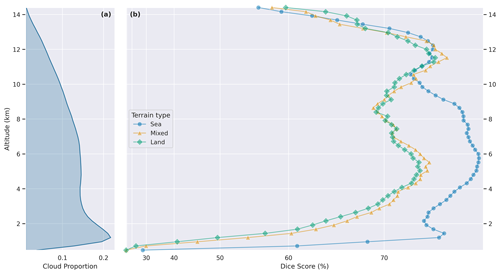
Figure 4Experiments using the simple convolutional model with different viewing geometries. Panel (a) shows the altitude-dependent proportion of pixels labeled as clouds in the dataset. Panel (b) shows the altitude-dependent Dice score of experiments with different viewing geometries. Note the significant difference between the two- and four-angle experiments, with diminishing returns with more angles.
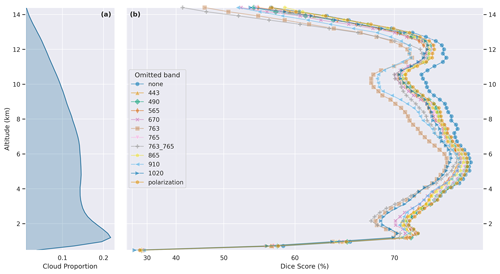
Figure 5(a) As in Fig. 4. Panel (b) shows the altitude-dependent Dice score of experiments, with various channels omitted, compared to the default labeled “none”.
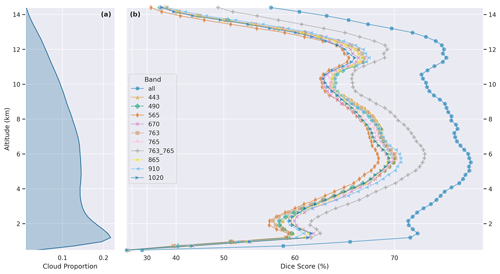
Figure 6(a) As in Fig. 4. Panel (b) shows the altitude-dependent Dice score of experiments using only one or two channels at a time compared to the default labeled “all”.
As the network is trained using the cross-entropy loss, its unbounded outputs (also known as logits) cannot directly be treated as probabilities. Within the loss function, the logits are passed into a sigmoid function to bound them within the [0,1] range. A threshold of 0.5 after the sigmoid function corresponds to a threshold of 0 before. Therefore, to evaluate the output of the network, we simply threshold the logits at 0 to convert them to a binary value, which we compare with the ground-truth cloud profiles.
4.1 Dice score
To evaluate our models, in addition to accuracy, we use the Dice score. The Dice score, originally used in an ecological context (Dice, 1945), was adopted in the medical segmentation literature as a validation metric for segmentation of MRI imagery (Zijdenbos et al., 1994). Its use has since become standard, due to its several advantages over pixel-wise accuracy metrics, including its tolerance to infrequent positive samples and that it penalizes differences in location more than differences in size. The Dice score is thus a better measure of perceptual quality than pixel-wise metrics. Let A and B be two sets representing all of the discretized locations of two respective objects. The Dice score between A and B is twice the intersection divided by the sums of the sizes of A and B. It can be contextualized in terms of the true positive (TP), false positive (FP), and false negative (FN):
We report the Dice score as a percentage. The Dice score is related to the intersection over union, also known as the Jaccard index, another metric commonly used in the segmentation literature. Both metrics have a range of [0,1], but the Dice score is strictly greater than the Jaccard index.
Notably, there is significant evidence that for many applications, the loss function, which is used to optimize the network, should be metric-specific. In segmentation, Jaccard-like loss functions often outperform their pixel-wise counterparts (such as cross-entropy) (Eelbode et al., 2020; Mohajerani and Saeedi, 2021; Wang et al., 2024). We experimented with Jaccard-like losses early in project development but observed no apparent improvement over the standard cross-entropy loss.
The Dice score generalizes to an arbitrary number of dimensions. While it is typically used for 2D data, we make use of it in both 1D and 2D contexts. The overall Dice scores presented in the tables are 2D, while the altitude-dependent Dice scores in Figs. 4, 5, 6, 8, and 11 are 1D, as they describe a single row of the time and altitude cross-section given in the 2B-CLDCLASS labels.
Alongside the Dice score, we report the bin-wise accuracy, which is the rate at which the model correctly assigns a pixel and altitude bin pair as cloudy or not cloudy. This metric is less strict than the Dice score and is less suited to labels with a strong imbalance between positives and negatives, as in our data. Our findings are therefore mostly based on the Dice score, but the inclusion of accuracy allows for easier comparison with other works.
4.2 Inter-run variability
Due to the stochastic nature of machine learning, the same experiment will yield variable results given different initializations of the network, as well as differences in the shuffled order of the training set. In this work, the inter-run variability is an important factor to consider. Repeating the U-Net experiment three times, for example, yielded validation set Dice scores of 72.8 %, 73.1 %, and 73.4 %, although the simpler architectures experience less variance. We report the maximum test set accuracy over three runs; for all runs of an experiment and for all saved model checkpoints, we use the model which yields the highest Dice score on the validation set and report its Dice score on the test set. There is little variation between the validation set and the test set metrics. U-Net, for example, has a max validation set Dice score of 73.4 %, which drops to 73.2 % on the test set.
4.3 Architecture complexity
The three architectures described in Sect. 3.2 are evaluated, with results shown in Table 2. There is a large increase in skill from the single pixel model to the simple convolutional model and a negligible increase from the simple convolutional model to the U-Net.
As the POLDER 3 data are georeferenced using the surface elevation (and not the cloud-top height), there is a parallax-induced shift when clouds are present, particularly if those clouds occur at a higher altitude. The single-pixel model, which lacks spatial context, does not have access to adjacent pixels. The simple convolutional network and the U-Net, by contrast, can leverage surrounding pixels, making use of the information contained in the parallax. Another potentially useful quality of spatial context is that it captures more information about the scene dynamics, which may be used by the model.
The results suggest that there are diminishing returns from increasing model capacity. It is unlikely, in our estimation, that larger models will achieve significantly higher performance on this dataset without changes in other aspects of the data-processing pipeline or optimization procedure.
4.4 Viewing angles
Multi-angle POLDER measurements are particularly sensitive to parallax, providing useful information on vertical cloud distribution. The impact of parallax on model skill was studied via an ablation experiment in which various viewing geometries were provided for the model. First, we started with an experiment using only the two central (closest to nadir) viewing angles. Next, we progressively added subsequent pairs of angles (in increasing zenith angle order) until all angles were included, running independent experiments on each configuration. The results are shown in Table 3, as well as Fig. 4, which captures the altitude-dependent Dice score of experiments using various numbers of angles. There is a significant improvement between two and four angles, with diminishing returns from the inclusion of more angles. There is a clear increasing trend, with 14 viewing angles achieving the best performance. The drop in performance from including the outermost pair of angles is unsurprising, as these angles contain little to no valid data in most scenes, due to the viewing geometry of POLDER 3. We elected to use eight angles as the default for other experiments, as it marked a good trade-off between performance and training time.
An important factor to consider in the evaluation of these results is the difference between the 2B-CLDCLASS vertical resolution of 240 m with the 6 km × 7 km horizontal resolution of POLDER 3. Even an extreme difference in viewing angles may not be enough to overcome the stark resolution difference. The multiple angles may aid the model to constrain the possible reflectance distribution functions attributable to a surface, helping to identify surface type and altitude, rather than being useful in the stereoscopic sense. This offers one potential explanation for the diminishing return from including more angles, but other explanations remain possible.
4.5 Spectra
We perform two ablation studies to understand the impact the nine spectral bands have on model skill. In the first, shown in Fig. 5, one or two bands can be omitted at a time, and the resulting decrease in model skill provides a measure of the unique (non-redundant) information content present in that band. In the second, shown in Fig. 6, only one or two bands can be provided at a time, and the model skill represents the bulk information content of that single band. In both studies, we include the 763 nm (oxygen A band) and 765 nm bands, as well as a combination of both 763 and 765 nm bands, as they are often jointly used to derive the oxygen pressure within an atmospheric column, which can be used to infer cloud structure (Ferlay et al., 2010). A summary of all the spectral experiments can be found in Appendix C and Table C1.
Figure 5 demonstrates the utility of various bands, with larger drops in performance suggesting that the omitted band contains uniquely useful information content. The oxygen absorption feature at 763 nm is highly correlated with model skill, consistent with the known relationship between this feature and cloud structure. The next greatest drop in skill is captured in the 910 and 1020 nm band omission experiments. The range at 910 nm is a water vapor band, which provides information on scattering and absorption interactions between clouds and vapor (Dubuisson et al., 2004). The near-infrared 1020 nm band might be useful for low-altitude clouds over the ocean, as clouds are quite bright in this wavelength, while oceans are quite dark.
4.6 Polarimetry
The importance of polarization to model skill is evaluated by comparing the default experiment to one without the polarization parameters. This is achieved by omitting the Q and U channels from the Stokes' parameterization. This caused a reduction in Dice score from 73.0 % to 72.6 %. This difference is smaller than we hypothesized. One possibility is that the Stokes' vector is not the ideal parameterization for this task. Another possibility is that the particular polarization channels in POLDER 3 have only limited unique utility for the derivation of cloud structure. Prior work has found that blue light polarization is disproportionately useful for the retrieval of aerosol layer height, especially with wavelengths of 410 nm or lower (Wu et al., 2016), but the POLDER 3 shortest-wavelength polarization band is 490 nm. The shorter-wavelength polarization information from future missions, like the Hyper-Angular Rainbow Polarimeter (HARP2) aboard PACE (Werdell et al., 2019), might prove more useful. For example, it has been shown that the polarized 440 nm band in HARP2 provides some sensitivity to aerosol altitude (Gao et al., 2023).
4.7 Cloud extent
The vertical and horizontal extent of the cloud being observed is related to the model's skill. Vertical extent is evaluated by stratifying results by two variables, namely cumulative 2B-CLDCLASS depth and distance to the top of the cloud. Cumulative depth is simply the cumulative sum of 240 m cloudy bins along each column in the 2B-CLDCLASS product (starting at the top of the atmosphere) multiplied by the vertical extent of each bin (240 m). Distance to the top of the cloud is the distance between a predicted bin and the top of the topmost cloudy bin in 2B-CLDCLASS for that column. Figure 7 illustrates the cumulative depth and top-of-cloud distance for a single instance. It is important to note the distinction between cumulative 2B-CLDCLASS depth, optical depth, and geometric depth. First, the 2B-CLDCLASS depth is more akin to geometric depth than optical depth, as the (binarized) 2B-CLDCLASS cloud-type product does not discriminate between optically thin and optically thick clouds. Still, it is not quite the same as geometric depth either as it is discretized to 240 m bins.
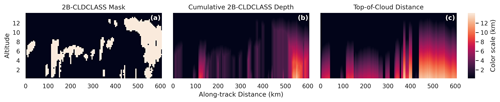
Figure 7(a) As in Fig. 3 and showing the 2B-CLDCLASS mask for a single instance. (b) Cumulative depth for each cell in the mask. (c) Top-of-cloud distance for each cell in the mask. Panels (b) and (c) differ when there are non-cloudy areas beneath the cloud.
Results on the test set are binned according to both the cumulative depth and top-of-cloud distance, and the Dice score is computed for each bin. Figure 8 shows both the proportion of data and the Dice score for bins in both variables. While performance increases with cumulative cloud depth, it decreases with top-of-cloud distance. This indicates that the model is good at identifying very tall cloud systems and struggles with identifying multilayer clouds. These findings are consistent with the qualitative examples in Appendix B.
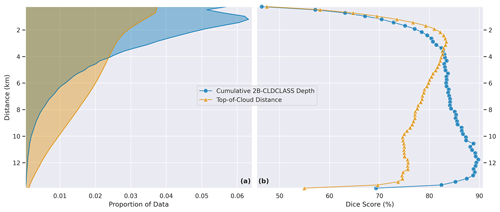
Figure 8(a) Dice score for bins by cumulative 2B-CLDCLASS depth. (b) Dice score for bins by top-of-cloud distance.
Quantifying horizontal extent is more complicated. In order to do this, we utilized a connected components algorithm (Bolelli et al., 2020) on the 2B-CLDCLASS mask. A connected component in the cloud mask can be understood as a set of cells for which every pair of cells in that set can be mutually reached via only horizontal and vertical steps without crossing a non-cloudy pixel. We then measure the horizontal extent of each component. Figure 9 shows an example of horizontal extent computed on an instance in the test set, while Fig. 10 shows the relationship between horizontal extent and model skill. Note that there are some limitations to this type of analysis. First, this only considers the along-track horizontal extent of the cloud and assumes that clouds are approximately (horizontally) circular. Clouds which are short in the along-track direction and long in the cross-track direction, or the opposite, will skew these results. A second limitation of this analysis is that clouds whose horizontal extent exceeds the extent of their corresponding instance in the ATCS dataset will be truncated. Note the sharp spike in the counts in Fig. 8, which corresponds to the most common along-track extent of instances in our dataset, a result of our 100 px × 100 px sampling size in POLDER 3 and the geometric relationship between the POLDER 3 and 2B-CLDCLASS products. The distribution of cloud horizontal extent approximates the power law relationship found in prior work (Wood and Field, 2011).
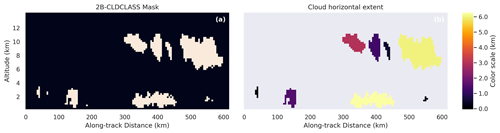
Figure 9(a) Cloud mask for an instance in the test set. (b) Corresponding cloud horizontal extent of the connected components in the cloud mask. The smallest cloud components are nearly invisible due to their low horizontal extent.
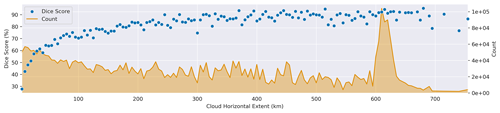
Figure 10Relationship between cloud horizontal extent, counts, and Dice score. The count indicates how many locations in the 2B-CLDCLASS product were assigned to each cloud horizontal extent bin. Dice score indicates the default model's skill over each horizontal extent bin. Note that the spike in count near 615 km corresponds to clouds that exceed the extent of their instances which are truncated.
It is clear from Fig. 10 that model skill improves as cloud horizontal extent increases. This trend is especially strong at lower horizontal extents, suggesting that the model's skill is not primarily related to parallax. This may result from the dynamics we use to train the model. Larger clouds will exert more influence on the model's supervisory signal than small clouds, even if those smaller clouds would more easily be distinguished from their background with stereo methods. Performance on only the smallest clouds (horizontal extent < 10 km) may suffer due to the limited resolution of POLDER 3. Increases in the resolution of both the passive and active sensor, such as the Atmosphere Observing System (AOS) mission, should allow a similar approach to attain higher performance on clouds with lower horizontal extent.
Stereo methods are expected to perform better on high clouds (more observable parallax) with a lower horizontal extent (distinct features). As these are two weak points of our method, an ensemble model could offer a promising avenue of study.
4.8 Terrain
Performance varies depending on terrain. Distinguishing clouds from the surface using visible or near-infrared channels is more difficult over brighter terrain and easier over the ocean, which is dark. The POLDER 3 data products contain a flag indicating whether each pixel is “Land” (100), “Sea” (0), or “Mixed” (50). This terrain flag is interpolated from the POLDER 3 grid to the 2B-CLDCLASS grid with the method described in Sect. 3.3. Any value greater than 0 and less than 100 is treated as “Mixed”. Figure 11 shows results stratified by terrain type and altitude. The gap between Land and Sea/Mixed performance is greatest at altitudes below 3 km, where parallax alone is likely insufficient to distinguish clouds from the surface, due to the limited spatial resolution of POLDER 3 data.
The results demonstrate the feasibility of estimating 3D cloud structure from passive, multi-angle imagery. The inclusion of spatial context significantly improved results, while the improvement from using a more complex model was modest (Table 2). Increasingly, extreme view angles exhibit diminishing returns (Fig. 4). It is possible that stacking the view angles in the channel dimension might not be the most effective feature representation for retrieving 3D structure. The spectral results (Figs. 5 and 6; Table C1) confirm the known utility of the oxygen A band, water vapor band, and the near-infrared for the study of clouds. Polarization only proved modestly useful for the cloud profiling task (Fig. 5 and Table C1), but this may be a limitation of the specific polarization bands available in POLDER 3 data.
Even the best experimental configuration only reaches a Dice score of 74.1 %, which is slightly lower than the average results in the segmentation literature (Eelbode et al., 2020). Seemingly, this dataset is challenging, and it is likely that there exists a limit to a model's skill. This should be unsurprising, given the nature of the labeled data; in most segmentation results, the labels come from human annotators. The human annotation process guarantees that the labels are predictable from the imagery up to the skill of the human annotator. However, our dataset is not annotated by humans but involves the fusion of two different sources of satellite data, which are sensitive to inherently different physics. This manifests in several ways. For example, one notable characteristic of the qualitative results is that all models struggle to mask the lower layer of multilayer clouds or to predict the extent of optically thick clouds. The penetration depth of clouds is quite low in the visible and near-visible spectrum. It is possible the models may not have any inputs that allow correct classification beneath cloud tops. Related to this problem is the performance drop across all models at low altitudes. Some of this skill decrease is likely due to penetration depth but may also relate to lower parallax near the surface, making it harder for the model to vertically resolve cloud location. Another phenomenon this approach may struggle to capture is optically thin clouds. As the labels are based on a cloud fraction product and not an optical depth product, there are extremely optically thin clouds present in the data. The information contained in the visible and near-visible wavelengths may not be enough to detect such clouds.
One of the most important findings of this work is the importance of spatial context. As we move into the next generation of multi-angle sensors with PACE and AOS, we can expect the resolution of these products to improve. In order to achieve the same spatial context in these higher-resolution products, the convolutional architectures will require more layers. U-Net is likely not worth the high number of parameters for POLDER 3 data, but it may be a more optimal choice for PACE and AOS. In addition to finer spatial resolution, the HARP2 polarimeter aboard PACE provides better polarimetric accuracy than POLDER 3 but lacks its absorption channels. Evaluating the impact of this trade-off on 3D cloud masking skill should yield valuable insights. The EarthCARE mission (Wehr et al., 2023) will have periodic simultaneous overpasses with PACE, and its two active instruments will enable the application of similar, partially supervised, techniques.
We designed a supervised machine-learning method to perform 3D cloud masking over a wide swath from multi-angle polarimetry and introduced a dataset to support this method. The dataset should be useful for future research in this area, as it is designed for ease-of-use in machine-learning applications. The code accompanying the dataset includes everything necessary to reproduce the results in this paper to train and validate models, generate figures, and even to create custom datasets.
By performing extensive ablations with various model inputs and hyperparameters, we analyzed the qualities of both POLDER 3 and CloudSat CPR data, as well as their relationship. Our conclusions both confirm existing knowledge and offer new insights. We found a strong relationship between the number of angles and model skill, with the 2-angle and 14-angle variations in our default experiment achieving Dice scores of 68.9 and 74.1 %, respectively, which is a 5.2 % difference – confirming the value of multi-angle sensors. The multispectral nature of the POLDER data is also strongly related to skill, with the oxygen absorption band proving particularly important. Omission of the oxygen absorption bands alone resulted in a drop in the Dice score from 73.0 to 71.0 %, and there is a 6.1 % difference in Dice score between the best-performing single-band experiment (66.9 %) and the default multiband experiment (73.0 %). Our method works well for optically thick and horizontally long clouds, unlike stereo methods, suggesting the two approaches may have some synergy. In particular, model skill was worse for clouds below 10 km altitude over land surfaces, while it was similar for land and sea surfaces above 10 km. Finally, model skill was predictably worse for multilayer clouds but surprisingly high for very tall cloud systems. Overall, results are promising and suggest the continued use of machine learning as a means to understand the relationships between various sensor modalities. Additionally, machine learning might, with further refinement, offer a useful way to retrieve 3D cloud masks from satellite data at an unprecedented scale, which would be an invaluable source of data for climate modeling.
This study constitutes an initial foray into the combined use of machine learning and multi-angle polarimetry for 3D cloud masking. Whereas its use here provided insights into the POLDER 3 sensor, other sensors have yet to be studied in such a way. The recently launched PACE mission and the upcoming AOS mission will carry multi-angle polarimeters, providing a useful test bed for this approach.
The model's supervision in this study was provided by an active radar constrained to nadir locations. The off-nadir performance of our approach has yet to be validated and would likely require cross-referencing with ground-based radar. The validation of its 2D (flattened) accuracy could be performed with other wide-swath cloud products, like the MODIS cloud mask (Ackerman et al., 2015). Having such a wide-swath 3D cloud mask product, were its accuracy sufficient, could prove useful for climate modeling.
Alternative approaches from the computer vision literature may be better suited to the stereoscopic nature of these data. 3D reconstruction pipelines such as COLMAP (Schönberger and Frahm, 2016; Schönberger et al., 2016) might be adapted for wide-swath multi-angle imagery, as has been done for high-resolution satellite imagery (Zhang et al., 2019). These would allow the estimation of 3D cloud structure without the need for radar-based supervision.
Interpolation during the forward pass is more complicated for the U-Net model, as illustrated in Fig. A1. During development, we found that the U-Net model performed better if it included fully connected layers after the interpolation module. However, these fully connected layers can still operate on the full (not interpolated) features with a shape of 100 × 100 × C. By flattening this to a 10 000 × C tensor, passing it into the fully connected layers to get a 10 000 × 59 tensor, and unflattening it to 100 × 100 × 59, the network can be applied to wide-swath data. At training time, the interpolation module is applied to the 100 × 100 × C tensor to retrieve a P × C feature, which is then passed through the fully connected layers to get a P × 59 tensor, which is then compared with the ground-truth labels in the loss function.
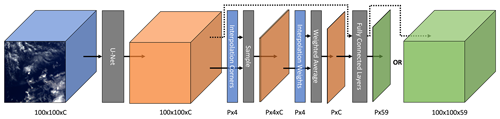
Figure A1Diagram illustrating the forward pass. The color blue denotes inputs (the shown image is from POLDER 3), orange denotes intermediate tensors, and green denotes output. C denotes channel depth, and P denotes the number of labeled pixels in an instance. The dotted line represents an alternate pathway which skips the interpolation module and is used to get wide-swath results.
The full table of spectral results (Table C1) is included here for reference. The experiments here are the same ones illustrated in Figs. 5 and 6.
Table C1Results for a variety of experimental configurations. The first section shows with and without polarization, the second section shows the effect of omitting each spectral band, and the third section shows the results when only one band is included at a time.
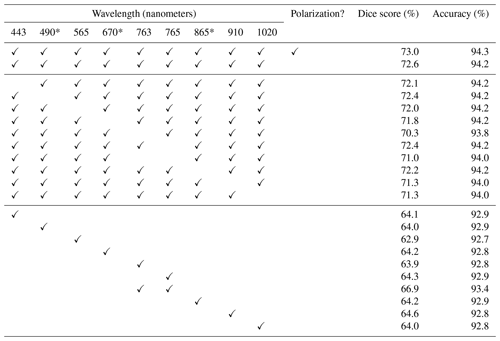
* POLDER 3 bands for which polarimetry is available.
The relationship between solar geometry and model skill was examined by stratifying the results by the POLDER 3 solar zenith and solar azimuth, with both angular dimensions divided into 5° bins. Figure D1 shows these results, including both the test set instance count and the default model's Dice score, for each bin. Most solar geometry bins are empty, due to the sun-synchronous orbit of the A-Train. Local Equator-crossing time for PARASOL was in the early afternoon during the dataset's time interval (from 2007 to 2009). Solar geometry in this dataset is mostly a function of latitude.
No strong relationship between solar geometry and model skill was found. The only notable drops in Dice score occur in bins with very little corresponding data. This means the results are less statistically significant, but it also suggests that the performance drop results from the model fitting to the dominant mode in the dataset rather than from the physical properties of observations of the rare geometries.
Both code and data will be made available prior to publication and can be retrieved using SeaBASS, which can be found at the following link: https://seabass.gsfc.nasa.gov/archive/NASA_GSFC/ATCS/ATCS_dataset/associated (last access: 31 October 2023) (https://doi.org/10.5067/SeaBASS/ATCS/DATA001, Foley, 2023).
SRF developed the code and dataset and wrote the draft. KDK, AMS, and MG guided the experiments and revised the paper. JaH and JuH advised the machine-learning-related aspect of the project.
At least one of the (co-)authors is a member of the editorial board of Atmospheric Measurement Techniques. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
We would like to acknowledge the team at ICARE for maintaining the POLDER and 2B-CLDCLASS data, as well as the CloudSat team for providing such an invaluable source of vertical cloud data. We would also like to acknowledge Jie Gong (NASA Goddard Space Flight Center) for useful discussions about the relevant data products. A significant portion of this work was performed during an internship through Science Applications International Corporation (SAIC). That internship was managed by Fred Patt (NASA Goddard Space Flight Center, SAIC), who provided valuable advice.
This paper was edited by Sebastian Schmidt and reviewed by two anonymous referees.
Ackerman, S., Frey, R., Kathleen Strabala, K., Liu, Y., Gumley, L., Baum, B., and Menzel, P.: MODIS Atmosphere L2 Cloud Mask Product, NASA MODIS Adaptive Processing System, Goddard Space Flight Center [data set], USA, https://doi.org/10.5067/MODIS/MOD35_L2.006, 2015. a
Ardila, D., Kiraly, A. P., Bharadwaj, S., Choi, B., Reicher, J. J., Peng, L., Tse, D., Etemadi, M., Ye, W., Corrado, G., Naidich, D. P., and Shetty, S.: End-to-end lung cancer screening with three-dimensional deep learning on low-dose chest computed tomography, Nat. Med., 25, 954–961, https://doi.org/10.1038/s41591-019-0447-x, 2019. a
Barker, H. W., Jerg, M. P., Wehr, T., Kato, S., Donovan, D. P., and Hogan, R. J.: A 3D cloud-construction algorithm for the EarthCARE satellite mission, Q. J. Roy. Meteor. Soc., 137, 1042–1058, https://doi.org/10.1002/qj.824, 2011. a
Baum, B. A., Menzel, W. P., Frey, R. A., Tobin, D. C., Holz, R. E., Ackerman, S. A., Heidinger, A. K., and Yang, P.: MODIS Cloud-Top Property Refinements for Collection 6, J. Appl. Meteorol. Clim., 51, 1145–1163, https://doi.org/10.1175/JAMC-D-11-0203.1, 2012. a
Bentley, J. L.: Multidimensional Binary Search Trees Used for Associative Searching, Commun. ACM, 18, 509–517, https://doi.org/10.1145/361002.361007, 1975. a
Bolelli, F., Allegretti, S., Baraldi, L., and Grana, C.: Spaghetti Labeling: Directed Acyclic Graphs for Block-Based Connected Components Labeling, IEEE T. Image Process., 29, 1999–2012, https://doi.org/10.1109/TIP.2019.2946979, 2020. a
Bony, S., Stevens, B., Frierson, D. M. W., Jakob, C., Kageyama, M., Pincus, R., Shepherd, T. G., Sherwood, S. C., Siebesma, A. P., Sobel, A. H., Watanabe, M., and Webb, M. J.: Clouds, circulation and climate sensitivity, Nat. Geosci., 8, 261–268, https://doi.org/10.1038/ngeo2398, 2015. a
Brüning, S., Niebler, S., and Tost, H.: Artificial intelligence (AI)-derived 3D cloud tomography from geostationary 2D satellite data, Atmos. Meas. Tech., 17, 961–978, https://doi.org/10.5194/amt-17-961-2024, 2024. a
Buriez, J. C., Vanbauce, C., Parol, F., Goloub, P., Herman, M., Bonnel, B., Fouquart, Y., Couvert, P., and Seze, G.: Cloud Detection and Derivation of Cloud Properties from POLDER, Int. J. Remote Sens., 18, 2785–2813, https://doi.org/10.1080/014311697217332, 1997. a, b, c, d
Castro, E., Ishida, T., Takahashi, Y., Kubota, H., Perez, G., and Marciano, J.: Determination of Cloud-top Height through Three-dimensional Cloud Reconstruction using DIWATA-1 Data, Sci. Rep.-UK, 10, 7570, https://doi.org/10.1038/s41598-020-64274-z, 2020. a
Ceppi, P., Brient, F., Zelinka, M. D., and Hartmann, D. L.: Cloud feedback mechanisms and their representation in global climate models, WIREs Clim. Change, 8, e465, https://doi.org/10.1002/wcc.465, 2017. a
Chan, M. A. and Comiso, J. C.: Cloud features detected by MODIS but not by CloudSat and CALIOP, Geophys. Res. Lett., 38, L24813, https://doi.org/10.1029/2011GL050063, 2011. a
Chen, C., Dubovik, O., Henze, D. K., Chin, M., Lapyonok, T., Schuster, G. L., Ducos, F., Fuertes, D., Litvinov, P., Li, L., Lopatin, A., Hu, Q., and Torres, B.: Constraining global aerosol emissions using POLDER/PARASOL satellite remote sensing observations, Atmos. Chem. Phys., 19, 14585–14606, https://doi.org/10.5194/acp-19-14585-2019, 2019. a
Christensen, M. W., Stephens, G. L., and Lebsock, M. D.: Exposing biases in retrieved low cloud properties from CloudSat: A guide for evaluating observations and climate data, J. Geophys. Res.-Atmos., 118, 12120–12131, https://doi.org/10.1002/2013JD020224, 2013. a
Çiçek, Ö., Abdulkadir, A., Lienkamp, S. S., Brox, T., and Ronneberger, O.: 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation, https://doi.org/10.1007/978-3-319-46723-8_49, 2016. a
Deschamps, P.-Y., Breon, F.-M., Leroy, M., Podaire, A., Bricaud, A., Buriez, J.-C., and Seze, G.: The POLDER mission: instrument characteristics and scientific objectives, IEEE T. Geosci. Remote, 32, 598–615, https://doi.org/10.1109/36.297978, 1994. a
Desmons, M., Ferlay, N., Parol, F., Riédi, J., and Thieuleux, F.: A Global Multilayer Cloud Identification with POLDER/PARASOL, J. Appl. Meteorol. Clim., 56, 1121–1139, https://doi.org/10.1175/JAMC-D-16-0159.1, 2017. a, b
Dice, L. R.: Measures of the Amount of Ecologic Association Between Species, Ecology, 26, 297–302, https://doi.org/10.2307/1932409, 1945. a
Diner, D., Beckert, J., Reilly, T., Bruegge, C., Conel, J., Kahn, R., Martonchik, J., Ackerman, T., Davies, R., Gerstl, S., Gordon, H., Muller, J.-P., Myneni, R., Sellers, P., Pinty, B., and Verstraete, M.: Multi-angle Imaging SpectroRadiometer (MISR) instrument description and experiment overview, IEEE T. Geosci. Remote, 36, 1072–1087, https://doi.org/10.1109/36.700992, 1998. a
Dubuisson, P., Dessailly, D., Vesperini, M., and Frouin, R.: Water vapor retrieval over ocean using near-infrared radiometry, J. Geophys. Res.-Atmos., 109, D19106, https://doi.org/10.1029/2004JD004516, 2004. a
Eelbode, T., Bertels, J., Berman, M., Vandermeulen, D., Maes, F., Bisschops, R., and Blaschko, M. B.: Optimization for Medical Image Segmentation: Theory and Practice When Evaluating With Dice Score or Jaccard Index, IEEE T. Med. Imaging, 39, 3679–3690, https://doi.org/10.1109/TMI.2020.3002417, 2020. a, b
Ferlay, N., Thieuleux, F., Cornet, C., Davis, A. B., Dubuisson, P., Ducos, F., Parol, F., Riédi, J., and Vanbauce, C.: Toward New Inferences about Cloud Structures from Multidirectional Measurements in the Oxygen A Band: Middle-of-Cloud Pressure and Cloud Geometrical Thickness from POLDER-3/PARASOL, J. Appl. Meteorol. Clim., 49, 2492–2507, https://doi.org/10.1175/2010JAMC2550.1, 2010. a
Foley S.: A-Train Cloud Segmentation (ATCS) Dataset, SeaBASS [data set], https://doi.org/10.5067/SeaBASS/ATCS/DATA001, 2023. a
Gao, M., Franz, B. A., Zhai, P.-W., Knobelspiesse, K., Sayer, A. M., Xu, X., Martins, J. V., Cairns, B., Castellanos, P., Fu, G., Hannadige, N., Hasekamp, O., Hu, Y., Ibrahim, A., Patt, F., Puthukkudy, A., and Werdell, P. J.: Simultaneous retrieval of aerosol and ocean properties from PACE HARP2 with uncertainty assessment using cascading neural network radiative transfer models, Atmos. Meas. Tech., 16, 5863–5881, https://doi.org/10.5194/amt-16-5863-2023, 2023. a
Gettelman, A. and Sherwood, S. C.: Processes responsible for cloud feedback, Current Climate Change Reports, 2, 179–189, 2016. a
Gupta, R. and Hartley, R.: Linear pushbroom cameras, IEEE T. Pattern Anal., 19, 963–975, https://doi.org/10.1109/34.615446, 1997. a
Hagolle, O., Guerry, A., Cunin, L., Millet, B., Perbos, J., Laherrere, J.-M., Bret-Dibat, T., and Poutier, L.: POLDER level-1 processing algorithms, Proc. SPIE, 2758, 308–319, https://doi.org/10.1117/12.243226, 1996. a, b
Haynes, J. M., L'Ecuyer, T. S., Stephens, G. L., Miller, S. D., Mitrescu, C., Wood, N. B., and Tanelli, S.: Rainfall retrieval over the ocean with spaceborne W-band radar, J. Geophys. Res.-Atmos., 114, D00A22, https://doi.org/10.1029/2008JD009973, 2009. a
Holz, R. E., Ackerman, S. A., Nagle, F. W., Frey, R., Dutcher, S., Kuehn, R. E., Vaughan, M. A., and Baum, B.: Global Moderate Resolution Imaging Spectroradiometer (MODIS) cloud detection and height evaluation using CALIOP, J. Geophys. Res.-Atmos., 113, D00A19, https://doi.org/10.1029/2008JD009837, 2008. a
Hunter, J. D.: Matplotlib: A 2D graphics environment, Comput. Sci. Eng., 9, 90–95, https://doi.org/10.1109/MCSE.2007.55, 2007. a
Im, E., Wu, C., and Durden, S.: Cloud profiling radar for the CloudSat mission, in: IEEE International Radar Conference, Arlington, VA, USA, 9–12 May 2005, IEEE, 483–486, https://doi.org/10.1109/RADAR.2005.1435874, 2005. a
Jnawali, K., Arbabshirani, M. R., Rao, N., and M. D., A. A. P.: Deep 3D convolution neural network for CT brain hemorrhage classification, in: Medical Imaging 2018: Computer-Aided Diagnosis, vol. 10575, edited by Petrick, N. and Mori, K., International Society for Optics and Photonics, SPIE, https://doi.org/10.1117/12.2293725, p. 105751C, 2018. a
Kingma, D. P. and Ba, J.: Adam: A Method for Stochastic Optimization, arXiv [preprint], https://doi.org/10.48550/arXiv.1412.6980, 30 January 2017. a
Leinonen, J., Guillaume, A., and Yuan, T.: Reconstruction of Cloud Vertical Structure With a Generative Adversarial Network, Geophys. Res. Lett., 46, 7035–7044, https://doi.org/10.1029/2019GL082532, 2019. a
Liu, G.: Deriving snow cloud characteristics from CloudSat observations, J. Geophys. Res.-Atmos., 113, D00A09, https://doi.org/10.1029/2007JD009766, 2008. a
Luo, W., Li, Y., Urtasun, R., and Zemel, R. S.: Understanding the Effective Receptive Field in Deep Convolutional Neural Networks, CoRR, arXiv [preprint], https://doi.org/10.48550/arXiv.1701.04128, 25 January 2017. a
L'Ecuyer, T. S., Beaudoing, H. K., Rodell, M., Olson, W., Lin, B., Kato, S., Clayson, C. A., Wood, E., Sheffield, J., Adler, R., Huffman, G., Bosilovich, M., Gu, G., Robertson, F., Houser, P. R., Chambers, D., Famiglietti, J. S., Fetzer, E., Liu, W. T., Gao, X., Schlosser, C. A., Clark, E., Lettenmaier, D. P., and Hilburn, K.: The Observed State of the Energy Budget in the Early Twenty-First Century, J. Climate, 28, 8319–8346, https://doi.org/10.1175/JCLI-D-14-00556.1, 2015. a
Mace, G. G. and Zhang, Q.: The CloudSat radar-lidar geometrical profile product (RL-GeoProf): Updates, improvements, and selected results, J. Geophys. Res.-Atmos., 119, 9441–9462, https://doi.org/10.1002/2013JD021374, 2014. a
Marchand, R., Ackerman, T., Smyth, M., and Rossow, W. B.: A review of cloud top height and optical depth histograms from MISR, ISCCP, and MODIS, J. Geophys. Res.-Atmos., 115, D16206, https://doi.org/10.1029/2009JD013422, 2010. a
Meehl, G. A., Senior, C. A., Eyring, V., Flato, G., Lamarque, J.-F., Stouffer, R. J., Taylor, K. E., and Schlund, M.: Context for interpreting equilibrium climate sensitivity and transient climate response from the CMIP6 Earth system models, Science Advances, 6, eaba1981, https://doi.org/10.1126/sciadv.aba1981, 2020. a
Mitra, A., Di Girolamo, L., Hong, Y., Zhan, Y., and Mueller, K. J.: Assessment and Error Analysis of Terra-MODIS and MISR Cloud-Top Heights Through Comparison With ISS-CATS Lidar, J. Geophys. Res.-Atmos., 126, e2020JD034281, https://doi.org/10.1029/2020JD034281, 2021. a
Mitra, A., Loveridge, J. R., and Di Girolamo, L.: Fusion of MISR Stereo Cloud Heights and Terra-MODIS Thermal Infrared Radiances to Estimate Two-Layered Cloud Properties, J. Geophys. Res.-Atmos., 128, e2022JD038135, https://doi.org/10.1029/2022JD038135, 2023. a
Mohajerani, S. and Saeedi, P.: Cloud and Cloud Shadow Segmentation for Remote Sensing Imagery Via Filtered Jaccard Loss Function and Parametric Augmentation, IEEE J. Sel. Top. Appl, 14, 4254–4266, https://doi.org/10.1109/JSTARS.2021.3070786, 2021. a
Mousavian, A., Anguelov, D., Flynn, J., and Kosecka, J.: 3D Bounding Box Estimation Using Deep Learning and Geometry, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), arXiv [preprint], https://doi.org/10.48550/arXiv.1612.00496, 10 April 2017. a
Muller, J., Denis, M., Dundas, R. D., Mitchell, K. L., Naud, C., and Mannstein, H.: Stereo cloud-top heights and cloud fraction retrieval from ATSR-2, Int. J. Remote Sens., 28, 1921–1938, https://doi.org/10.1080/01431160601030975, 2007. a, b
Nelson, D., Garay, M., Diner, D., and Kahn, R.: The MISR Wildfire Smoke Plume Height Project, AGU Fall Meeting Abstracts, San Francisco, CA, 13–17 December 2010. a
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., Killeen, T., Lin, Z., Gimelshein, N., Antiga, L., Desmaison, A., Köpf, A., Yang, E. Z., DeVito, Z., Raison, M., Tejani, A., Chilamkurthy, S., Steiner, B., Fang, L., Bai, J., and Chintala, S.: PyTorch: An Imperative Style, High-Performance Deep Learning Library, arXiv [preprint] [code], https://doi.org/10.48550/arXiv.1912.01703, 3 December 2019. a
Pörtner, H.-O., Roberts, D., Tignor, M., Poloczanska, E., Mintenbeck, K., Alegrıa, A., Craig, M., Langsdorf, S., Löschke, S., Möller, V., Okem, A., and Rama, B.: Climate Change 2022: Impacts, Adaptation, and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, IPCC Sixth Assessment Report, https://dx.doi.org/10.1017/9781009325844, 2022. a
Ronen, R., Holodovsky, V., and Schechner, Y. Y.: Variable Imaging Projection Cloud Scattering Tomography, IEEE T. Pattern Anal., 1–12, https://doi.org/10.1109/TPAMI.2022.3195920, 2022. a
Ronneberger, O., Fischer, P., and Brox, T.: U-Net: Convolutional Networks for Biomedical Image Segmentation, arXiv [preprint], https://doi.org/10.48550/arXiv.1505.04597, 18 May 2015. a
Rossow, W. B., Knapp, K. R., and Young, A. H.: International Satellite Cloud Climatology Project: Extending the Record, J. Climate, 35, 141–158, https://doi.org/10.1175/JCLI-D-21-0157.1, 2022. a
Sassen, K. and Wang, Z.: Classifying Clouds around the Globe with the CloudSat Radar: 1-Year of Results, Geophys. Res. Lett., 35, L04805, https://doi.org/10.1029/2007GL032591, 2008. a, b
Schönberger, J. L. and Frahm, J.-M.: Structure-From-Motion Revisited, in: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), https://doi.org/10.1109/CVPR.2016.445, 2016. a, b
Schönberger, J. L., Zheng, E., Pollefeys, M., and Frahm, J.-M.: Pixelwise View Selection for Unstructured Multi-View Stereo, in: European Conference on Computer Vision (ECCV), Springer, Cham, https://doi.org/10.1007/978-3-319-46487-9_31, 2016. a
Sde-Chen, Y., Schechner, Y. Y., Holodovsky, V., and Eytan, E.: 3DeepCT: Learning Volumetric Scattering Tomography of Clouds, in: 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021, IEEE, 5651–5662, https://doi.org/10.1109/ICCV48922.2021.00562, 2021. a
Sinclair, K., van Diedenhoven, B., Cairns, B., Yorks, J., Wasilewski, A., and McGill, M.: Remote sensing of multiple cloud layer heights using multi-angular measurements, Atmos. Meas. Tech., 10, 2361–2375, https://doi.org/10.5194/amt-10-2361-2017, 2017. a
Smalley, M., L'Ecuyer, T., Lebsock, M., and Haynes, J.: A Comparison of Precipitation Occurrence from the NCEP Stage IV QPE Product and the CloudSat Cloud Profiling Radar, J. Hydrometeorol., 15, 444–458, https://doi.org/10.1175/JHM-D-13-048.1, 2014. a
Soffer, S., Klang, E., Shimon, O., Barash, Y., Cahan, N., Greenspana, H., and Konen, E.: Deep learning for pulmonary embolism detection on computed tomography pulmonary angiogram: a systematic review and meta-analysis, Sci. Rep.-UK, 11, 15814, https://doi.org/10.1038/s41598-021-95249-3, 2021. a
Stephens, G., Winker, D., Pelon, J., Trepte, C., Vane, D., Yuhas, C., L'Ecuyer, T., and Lebsock, M.: CloudSat and CALIPSO within the A-Train: Ten Years of Actively Observing the Earth System, B. Am. Meteorol. Soc., 99, 569–581, https://doi.org/10.1175/BAMS-D-16-0324.1, 2018. a, b
Stephens, G. L. and Webster, P. J.: Clouds and Climate: Sensitivity of Simple Systems, J. Atmos. Sci., 38, 235–247, https://doi.org/10.1175/1520-0469(1981)038<0235:CACSOS>2.0.CO;2, 1981. a
Stephens, G. L., Vane, D. G., Boain, R. J., Mace, G. G., Sassen, K., Wang, Z., Illingworth, A. J., O'connor, E. J., Rossow, W. B., Durden, S. L., Miller, S. D., Austin, R. T., Benedetti, A., and Mitrescu, C.: THE CLOUDSAT MISSION AND THE A-TRAIN: A New Dimension of Space-Based Observations of Clouds and Precipitation, B. Am. Meteorol. Soc., 83, 1771–1790, https://doi.org/10.1175/BAMS-83-12-1771, 2002. a, b
Stillinger, T., Roberts, D. A., Collar, N. M., and Dozier, J.: Cloud Masking for Landsat 8 and MODIS Terra Over Snow-Covered Terrain: Error Analysis and Spectral Similarity Between Snow and Cloud, Water Resour. Res., 55, 6169–6184, https://doi.org/10.1029/2019WR024932, 2019. a
Wang, Z., Ning, X., and Blaschko, M. B.: Jaccard Metric Losses: Optimizing the Jaccard Index with Soft Labels, arXiv [preprint], https://doi.org/10.48550/arXiv.2302.05666, 20 March 2024, 2019. a
Waskom, M. L.: seaborn: statistical data visualization, Journal of Open Source Software, 6, 3021, https://doi.org/10.21105/joss.03021, 2021. a
Waquet, F., Cornet, C., Deuzé, J.-L., Dubovik, O., Ducos, F., Goloub, P., Herman, M., Lapyonok, T., Labonnote, L. C., Riedi, J., Tanré, D., Thieuleux, F., and Vanbauce, C.: Retrieval of aerosol microphysical and optical properties above liquid clouds from POLDER/PARASOL polarization measurements, Atmos. Meas. Tech., 6, 991–1016, https://doi.org/10.5194/amt-6-991-2013, 2013. a
Wehr, T., Kubota, T., Tzeremes, G., Wallace, K., Nakatsuka, H., Ohno, Y., Koopman, R., Rusli, S., Kikuchi, M., Eisinger, M., Tanaka, T., Taga, M., Deghaye, P., Tomita, E., and Bernaerts, D.: The EarthCARE mission – science and system overview, Atmos. Meas. Tech., 16, 3581–3608, https://doi.org/10.5194/amt-16-3581-2023, 2023. a
Werdell, P. J., Behrenfeld, M. J., Bontempi, P. S., Boss, E., Cairns, B., Davis, G. T., Franz, B. A., Gliese, U. B., Gorman, E. T., Hasekamp, O., Knobelspiesse, K. D., Mannino, A., Martins, J. V., McClain, C. R., Meister, G., and Remer, L. A.: The Plankton, Aerosol, Cloud, Ocean Ecosystem Mission: Status, Science, Advances, B. Am. Meteorol. Soc., 100, 1775–1794, https://doi.org/10.1175/BAMS-D-18-0056.1, 2019. a, b
Winker, D. M., Vaughan, M. A., Omar, A., Hu, Y., Powell, K. A., Liu, Z., Hunt, W. H., and Young, S. A.: Overview of the CALIPSO Mission and CALIOP Data Processing Algorithms, J. Atmos. Ocean. Tech., 26, 2310–2323, https://doi.org/10.1175/2009JTECHA1281.1, 2009. a
Wood, R. and Field, P. R.: The Distribution of Cloud Horizontal Sizes, J. Climate, 24, 4800–4816, https://doi.org/10.1175/2011JCLI4056.1, 2011. a
Wu, L., Hasekamp, O., van Diedenhoven, B., Cairns, B., Yorks, J. E., and Chowdhary, J.: Passive remote sensing of aerosol layer height using near-UV multiangle polarization measurements, Geophys. Res. Lett., 43, 8783–8790, https://doi.org/10.1002/2016GL069848, 2016. a
Zhang, K., Sun, J., and Snavely, N.: Leveraging Vision Reconstruction Pipelines for Satellite Imagery, arXiv [preprint], https://doi.org/10.48550/arXiv.1910.02989, 16 October 2019. a, b
Zijdenbos, A., Dawant, B., Margolin, R., and Palmer, A.: Morphometric analysis of white matter lesions in MR images: method and validation, IEEE T. Med. Imaging, 13, 716–724, https://doi.org/10.1109/42.363096, 1994. a
- Abstract
- Introduction
- Data
- Approach
- Results
- Discussion
- Conclusions
- Appendix A: U-Net forward pass
- Appendix B: Qualitative results
- Appendix C: Spectral results
- Appendix D: Solar geometry
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Review statement
- References
- Abstract
- Introduction
- Data
- Approach
- Results
- Discussion
- Conclusions
- Appendix A: U-Net forward pass
- Appendix B: Qualitative results
- Appendix C: Spectral results
- Appendix D: Solar geometry
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Review statement
- References