Optimization of a direct-detection UV wind lidar architecture for 3D wind reconstruction at high altitude

An architecture for a UV wind lidar dedicated to measuring vertical and lateral wind in front of an aircraft for gust load alleviation is presented. To optimize performance and robustness, it includes a fiber laser architecture and a Quadri Mach–Zehnder (QMZ) interferometer with a robust design to spectrally analyze the backscattered light. Different lidar parameters have been selected to minimize the standard deviation of wind speed measurement projected onto the laser axis, calculated through end-to-end simulations of the instrument. The optimization involves selecting an emission–reception telescope to maximize the number of collected photons backscattered between 100 and 300 m, a background filter to reduce noise from the scene, and photomultiplier tubes (PMTs) to minimize detection noise. Simulations were performed to evaluate lidar performance as a function of laser parameters. This study led to the selection of three laser architectures, a commercial solid-state laser, a design of a fiber laser, and a hybrid fiber laser, resulting in standard deviations of projected wind speed of 0.17, 0.16, and 0.09 m s⁻¹, respectively, at 10 km altitude. To reconstruct the vertical and lateral wind on the flight path, the lidar is directed along four different directions to measure four different projections of the wind. We analytically calculate (and validate through simulations) the directed angle with respect to the flight direction that minimizes the root mean square error (RMSE) between the reconstructed vertical and lateral wind components and the actual ones, assuming turbulence that follows the von Kármán turbulence model. We found that the optimum angle for an estimation at 100 m is about 50°, resulting in an improvement of about 50 % compared to an angle of 15–30° typically used in current studies.

1 Introduction

Altitude airflow velocity measurements with atmospheric lidar have various applications, including weather forecasting (Baker et al., 1995, 2014; Bruneau and Pelon, 2021; Witschas et al., 2022), determining the true air speed from aircraft (Augere et al., 2016), analyzing wind fields around high-altitude platforms (Karabulut Kurt et al., 2021), and turbulence detection for gust load alleviation (GLA) (Regan and Jutte, 2012; Fournier et al., 2021). GLA involves actively reducing the loads caused by airflow velocity on wings using actuators that modify the aerodynamic profile of the aircraft based on the direction and strength of the encountered wind. While this method is not novel and has been employed previously with detectors measuring turbulence near the aircraft structure, the use of lidar allows for measuring the wind structure in advance (referred to as feed-forward GLA), providing time for actuators to respond to the turbulence encountered. This approach has the potential to significantly enhance the performance of such a system. Implementing this method requires measuring the variation in vertical and lateral wind velocity typically 100–200 m ahead of the aircraft (in the case of the Airbus XRF1, Fournier et al., 2021, the optimal distance ahead of the aircraft is 91 m, giving the control system enough time to react). Feed-forward GLA helps reduce constraints on wing resistance during the aircraft design phase, enabling the use of longer wings or reducing wing weight to decrease aircraft fuel consumption. In addition, it will limit aircraft vibrations, particularly the effects of air pockets that can hurt passengers (Kaplan et al., 2005). For this measurement, a direct-detection UV lidar optimized for molecular scattering is the optimal choice, as the presence of molecules is guaranteed at all altitudes, and the GLA system is intended to operate throughout the entire flight. In such lidar systems, a laser beam is directed into the atmosphere, and the wind velocity projected onto the laser propagation axis is determined by analyzing the frequency shift in the backscattered light induced by molecule velocity (Doppler effect). This shift is measured using a spectral analyzer. The use of UV wavelengths maximizes the molecular signal, as Rayleigh scattering is proportional to $\mathrm{1}/{\mathit{\lambda }}^{\mathrm{4}}$, where λ is the laser wavelength. To spatially resolve the measurement, laser pulses are employed so that the signal at time t (with pulse emission at t = 0 s) corresponds to a signal reflected at range z = $ct/\mathrm{2}$, where c is the speed of light. To determine the 3D wind, the laser must be directed along multiple angles relative to the flight path to reconstruct the vertical and lateral wind components.

The spectral analyzer is a critical component for lidar performance. A first method involves measuring two signals corresponding to the backscattered light passing through two narrow bandwidth filters positioned on each side of the measured Rayleigh spectrum. Changes in the spectrum position due to molecule velocities alter the intensity ratio of the two signals (approximately linearly), allowing for the retrieval of the projected velocity (Garnier and Chanin, 1992). The primary limitation of this analyzer is that atmospheric temperature, pressure, and the presence of particles can alter the spectrum's shape, introducing biases during wind speed reconstruction. A second method involves interfering the backscattered light with itself by introducing a delay (induced by an optical path difference, OPD) between the two paths of the interferometer. In this case, the interference intensity is used to determine the phase difference between the two beams, which depends linearly on the frequency of the backscattered light. However, this intensity depends on several parameters: $I_{\mathrm{OPD}}=A\left[\mathrm{1}+M\cos \left(\mathrm{\Delta }{\mathit{\phi }}_{\mathrm{OPD}}\right)\right]$, where A=TI₀, T is the global transmission of the interferometer (i.e., the multiplication and addition of transmissions and reflections of the optics), I₀ is the intensity of the input light, M is the contrast of the interference when varying OPD, $\mathrm{\Delta }{\mathit{\phi }}_{\mathrm{OPD}}=\mathrm{\Delta }{\mathit{\phi }}_{\mathrm{0},\mathrm{OPD}}+\mathit{\delta }{\mathit{\phi }}_{\mathrm{OPD}}$ is the phase difference between the two beams, Δφ_0,OPD is the phase difference for the laser frequency, and δφ_0,OPD is the phase difference induced by the molecule velocity. The phase Δφ_0,OPD is determined by sending a sample of the laser pulse into the interferometer. To deduce the three other parameters (A, M, and δφ_OPD), measurements are performed for several OPDs separated by less than a wavelength to determine the interference oscillation pattern (i.e., cos (Δφ_OPD)). For this method, different instruments have been developed, including a Mach–Zehnder (MZ), a Quadri Mach–Zehnder (QMZ) (Bruneau, 2001), a fringe-imaging Michelson (FIM) (Cézard et al., 2009; Herbst and Vrancken, 2016), and a fringe-imaging Mach–Zehnder (FIMZ) interferometer (Bruneau, 2002). The MZ interferometer provides the lower error in the wind speed but only gives two measurements for three parameters (A, M, and δφ), so one parameter (typically M) needs to be determined independently, and the error made on this parameter introduces biases in the wind speed measurement. Additionally, to minimize errors with the MZ interferometer, the wavelength of the laser and the OPD of the interferometer need to fulfill OPD=mλ₀ (with m as an integer) (Bruneau and Pelon, 2021), requiring additional systems to lock the laser wavelength at the intersection of the two transmission curves. The QMZ, the FIM, and the FIMZ interferometers measure more than three values of OPD, allowing for the retrieval of the three parameters without any assumptions (at the cost of a factor of a $\sqrt{\mathrm{2}}$ increase in statistical error due to the desensitization of the interferometer to the backscattering ratio, Bruneau, 2001, 2002, and without requiring laser stabilization). Moreover, atmospheric parameters such as temperature, pressure, and the backscatter ratio do not produce bias. In the case of the FIM and FIMZ interferometers, the fringes need to be imaged by a set of detectors. Consequently, some signal is lost between cells of the imager, and the detectors are more expensive. On the other hand, the QMZ interferometer only needs four detectors, and each detector measures the entire signal at each output.

The second critical element is the UV laser system, which can be either diode-pumped and injection-seeded solid-state lasers (Lux et al., 2020) or microchip lasers amplified in free space (Wirth et al., 2009). This type of laser has the disadvantage of being sensitive to vibrations due to the number of free-space optics, particularly in the case of ramp-and-fire lasers, where there are piezo-monitored optics to maintain the laser cavity adapted to the injected wavelength. These challenges have led to significant developments for the DELICAT laser (Vrancken et al., 2016) (similar to WALES; Wirth et al., 2009) and AEOLUS laser (even though, in this case, the difficulty also involved the space environment; Mondin et al., 2017; Lux et al., 2021). In this regard, fiber laser systems can lead to better performance for onboard direct-detection wind lidar. Additionally, the oscillator part of fiber lasers and their fiber amplification stage have the advantage of being robust in regards to vibrations, lighter, and more cost-effective when commercialized compared to the analogous part of solid-state lasers. Moreover, fiber lasers have the advantage of offering better control of the pulse parameters (duration, cadence, timing). However, the free-space part, which includes the frequency-tripling stage and any free-space amplifier, is still just as sensitive to vibration as solid-state lasers. Advances in fiber harmonic generation may therefore lead to an all-fiber laser insensitive to vibration.

The third critical aspect concerns the method applied to measuring the vertical and lateral wind components. To reconstruct the 3D wind, a typical method consists in directing the lidar in four directions, making an angle θ with the central axis where the wind is reconstructed. This method was used for a laser anemometer (Kliebisch et al., 2023) or to perform GLA (Rabadan et al., 2010; Kikuchi et al., 2020). For GLA, the lidar can be pointed upward and downward to measure the vertical component and to the left and right to measure the lateral component (see Fig. 1). For the different cases, the angle θ is generally chosen between 15 and 30° to satisfy the condition of a quasi-homogeneous wind field, as the measurement points are close to each other and, therefore, more correlated. However, the error committed in the reconstruction of the two wind components for small angles is given by $\frac{f\left(\mathit{\delta }{V}_p\right)}{\mathrm{2}\tan \mathit{\theta }}$, where f(δV_p) is a function depending on the error δV_p induced by turbulence on the projections. The factor $\frac{\mathrm{1}}{\mathrm{2}\tan \mathit{\theta }}$ can lead to significant error amplifications (≈ 1.9–0.9 for θ = 15–30°). To our knowledge, none of the studies have optimized the angle to minimize the error in the reconstructed 3D wind in the case of turbulence.

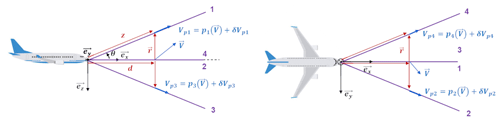
Figure 1 Measurement geometry of the reconstruction with the linear least-squares method with four axes. The lidar is located in the nose of the plane. d is the range between the lidar and the estimation point on the flight path, z is the range of the point of the projections from the lidar, and r is the displacement vector between the projections point and the estimation point.

In this article, we present a study in which we have optimized the architecture of a molecular lidar designed to measure the lateral and vertical wind in front of an aircraft for GLA applications, aiming to maximize its performance by minimizing the error in the reconstructed wind. The design includes a robust Quadri Mach–Zehnder (QMZ) interferometer, fiber laser architectures, and an optimization of the lidar angle. To optimize the lidar architecture, an end-to-end simulator was developed to determine the collected light, the signal-to-noise ratio (SNR) on the detectors, and the calculation of the error in the wind measurement projected on the lidar axis for a QMZ spectral analyzer. This simulator was used to optimize the telescope architecture, the detectors, the solar filter, and the laser parameters. Specifically, we determined lidar performance (see Tables A1 and A2 for the parameters used) based on laser parameters and derived designs for a solid-state laser, a fiber laser, and a fiber laser followed by free-space amplifiers (hybrid fiber laser). For the vertical and lateral wind reconstruction, we optimized a design where the lidar is directed along four directions (up, down, left, and right) to measure the three components of the wind vector. This involves minimizing the analytical calculations of the error in the estimation of the vertical and lateral wind components with the lidar angle. In the case of turbulence described by the von Kármán model, the error is minimized for an angle of about 50°. This improves the root mean square error (RMSE) by about 50 % compared to the typical design using an angle of 15–30°. These results were confirmed by simulations of an aircraft traveling over 8 km through turbulence described by the von Kármán model.

2 Lidar architecture optimization

Firstly, we present the architecture of the lidar and the robustified QMZ interferometer. Secondly, we present the simulator that was used for the optimization of the lidar. Thirdly, we utilize the simulator to optimize various components of the lidar, including the emission–reception telescope, the solar filter, the detectors, and the laser parameters.

2.1 Lidar architecture

The architecture of the direct-detection UV Doppler wind lidar is shown in Fig. 2a. The laser emits pulses at 355 nm for solid-state lasers and at 343 nm for fiber lasers. A beam splitter is inserted to take a sample of the laser, serving as a reference signal. The laser light passes through a beam expander that focuses the laser at long distances. A Newton telescope is used to collect the signal backscattered by molecules and particles and to focus it into a multimode fiber with a numerical aperture of 0.22. The signal goes through a solar filter to greatly reduce the light coming from the background. A fiber coupler is used to combine the collected backscattered light and the reference signal. The long fiber is employed either on the reference signal or on the backscattered signal to temporally separate the two signals at the input of the interferometer. Both signals pass through a spectral analyzer. The intensities measured by the detectors are compared for the two signals to determine δφ and to deduce the projected wind speed. It should be noted that the reference signal also allows for obtaining absolute synchronization of the measured signal.

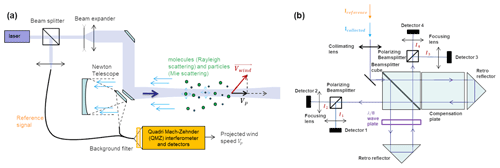
Figure 2 (a) Schematic of the monostatic architecture with separated emission–reception optics chosen for the UV Doppler wind lidar. (b) Schematic of the Quadri Mach–Zehnder.

The QMZ interferometer is shown in Fig. 2b. The signal, coming from the multimode fiber, is collimated by a converging lens and passes through a $\mathrm{50}/\mathrm{50}$ beam splitter cube, which splits the beam into two arms of different lengths. A $\mathit{\lambda }/\mathrm{8}$ wave plate on the short arm increases the OPD for horizontal polarization by $\mathit{\lambda }/\mathrm{4}$ considering the round trip, compared to vertical polarization. On the long arm, a glass plate is used to reduce beam divergence and improve the overlap of the two beams on the detector. This leads to an increase in the angular acceptance of the interferometer (Smith and Chu, 2016). The beams from both arms are combined on the $\mathrm{50}/\mathrm{50}$ beam splitter cube. The OPD of the output that has undergone an odd number of reflections is shifted by $\mathit{\lambda }/\mathrm{2}$ relative to the other. On each output, a polarizing beam splitter cube separates the horizontal and vertical polarizations. This gives four outputs with OPDs given by D₀, $D_{\mathrm{0}}+\mathit{\lambda }/\mathrm{4}$, $D_{\mathrm{0}}+\mathit{\lambda }/\mathrm{2}$, and $D_{\mathrm{0}}+\mathrm{3}\mathit{\lambda }/\mathrm{4}$ for I₁, I₂, I₃, and I₄, respectively, where D₀ is the OPD for output I₁. These outputs are focused on detectors that convert optical signals into current. The current is converted to voltage, which is then sampled and digitized into a computer. Figure 3 shows the evolution of the simulated signal at the output of the detectors, for the reference signal and the Rayleigh signal. Signal processing makes it possible to recover the phase of the interference, the frequency offset, and finally the projected wind speed.

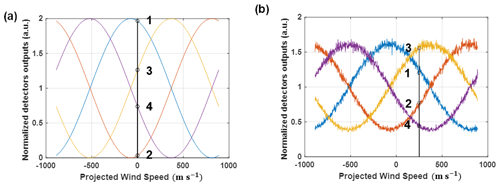
Figure 3 Signal at the detector's outputs for (a) the reference signal and (b) the Rayleigh signal. All signals are normalized by the mean value of the outputs. The black line highlights the values of the signal for the reference signal (0 m s⁻¹) and for the Rayleigh signal when the wind speed is 250 m s⁻¹ (relative wind when the plane flies at 250 m s⁻¹ at 10 km altitude). a.u. refers to “arbitrary unit”.

We have chosen an architecture that includes one $\mathrm{50}/\mathrm{50}$ beam splitter cube for the separation and recombination of the beams, along with two retroreflectors forming the two arms, to create a robust interferometer. Indeed, the QMZ interferometer is not sensitive to angular misalignment. However, simulations (Boulant et al., 2024) show that the retroreflector relative to each other needs to be positioned within about 2 µm. This is achieved using an X, Y mount on one retroreflector.

2.2 UV lidar simulator

A simulator that uses analytical formula has been developed to optimize the lidar architecture for the GLA application. It comprises three steps. The first step calculates the emission–reception overlap function, i.e., the ratio between the light entering the fiber and the light collected by the pupil. The second step assesses the SNR at the outputs of the detectors, and the third step determines the standard deviation of the wind speed to evaluate the overall lidar performance.

To calculate the overlap function, we use the method presented in the works of Cezard (2008, Sect. 3.2) and Liméry (2018, Sect. 3.3.4) . The simulator first computes the laser propagation using the Gaussian beam approximation. For each point along the laser beam, described by a distance z from the telescope and ρ from the laser axis (assuming cylindrical symmetry), the simulator determines the image of the point by the first pupil and the amount of light that enters the fiber that is $\frac{S(\mathit{\rho },z)\mathrm{2}\mathit{\pi }\mathit{\rho }\mathrm{d}\mathit{\rho }}{S_{\mathrm{pup}}\mathit{\pi }\mathit{\omega }(z{)}^{\mathrm{2}}}$, where ω(z) is the radius of the laser beam at $\mathrm{1}/e^{\mathrm{2}}$, S_pup is the surface of the first pupil, and S(ρ,z) is the surface of the pupil corresponding to the collected rays that goes to the fiber. Subsequently, for each distance from the telescope, the simulator integrates all the quantities obtained with all the points of the laser beam to calculate the ratio of the light that enters the fiber to the light collected by the pupil as the overlap function $\mathit{\gamma }\left(z\right)=\frac{\mathrm{1}}{S_{\mathrm{pup}}\mathit{\pi }\mathit{\omega }(z{)}^{\mathrm{2}}}{\int }_{\mathrm{0}}^{\mathit{\omega }\left(z\right)}S(\mathit{\rho },z)\mathrm{2}\mathit{\pi }\mathit{\rho }\mathrm{d}\mathit{\rho }$. The configuration is optimized for a given distance when the overlap function is equal to 1.

Secondly, the simulator calculates the total SNR, which is the collected light integrated over a range gate to the square root of the quadratic sum of all noise. To calculate the signal, we use the molecular backscattering and absorption coefficients determined with the evolution of the molecular density calculated using the US Standard Atmosphere model (U.S. Atmosphere, 1976). Particle backscattering and absorption are neglected at high altitudes because the concentration of particles is very low, leading to backscattering and absorption which are much lower than molecular backscattering and absorption (Vrancken et al., 2016). Then, the previously determined overlap function is used to calculate the collected signal. The total noise corresponds to the quadratic sum of the shot noise of the backscattered signal; the background noise; the speckle noise of the backscattered signal; and the detection noise, which includes the dark noise of the detector and the electronic noise (Fujii and Fukuchi, 2005, p. 488, 574 and 695). The configuration is considered to be optimized for a given average laser power (to the first order, proportional to the laser volume, this will be refined considering the different laser technology) when the noise is limited by the shot noise of the backscattered signal. Indeed, this noise can only be reduced by increasing the laser power. In this case, the SNR is proportional to the average power of the laser $\sqrt{P_{\mathrm{av}}}$.

The third step of the simulator is dedicated to calculating the standard deviation of the wind speed for the total SNR in order to assess the measurement performance. For simplicity, we utilized the analytical formula derived by Bruneau and Pelon (2003) and incorporated the contribution of speckle noise into the following formula:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}& {\mathit{\sigma }}_{v_p}^{\mathrm{2}}\\ & ={\left({\displaystyle \frac{c{\mathit{\lambda }}_{\mathrm{0}}}{\mathrm{4}\mathit{\pi }{D}_{\mathrm{0}}}}\right)}^{\mathrm{2}}{\displaystyle \frac{\mathrm{2}}{N_{\mathrm{acc}}{M}_{\mathrm{tot}}^{\mathrm{2}}{\text{SNR}}_{\mathrm{photon}}^{\mathrm{2}}}}\left(\mathrm{1}+F_{\mathrm{B}}{M}_{\mathrm{tot}}^{\mathrm{2}}{\displaystyle \frac{\sin (\mathrm{2}\mathit{\phi }{)}^{\mathrm{2}}}{\mathrm{2}}}\right)\\ & +\left({\displaystyle \frac{c{\mathit{\lambda }}_{\mathrm{0}}}{\mathrm{4}\mathit{\pi }{D}_{\mathrm{0}}}}\right){\displaystyle \frac{\mathrm{2}}{N_{\mathrm{acc}}{M}_{\mathrm{tot}}^{\mathrm{2}}{\text{SNR}}_{\mathrm{detection}}^{\mathrm{2}}}}\left(\mathrm{1}+M_{\mathrm{tot}}^{\mathrm{2}}{\displaystyle \frac{\sin (\mathrm{2}\mathit{\phi }{)}^{\mathrm{2}}}{\mathrm{2}}}\right)\\ & +{\mathit{\sigma }}_{v_p,\mathrm{speckle}}^{\mathrm{2}},\end{array}\end{array}$$

where N_acc is the accumulated lidar shot during the measurement time; M_tot is the total contrast of the interferences; SNR_photon is the SNR considering only shot noises (from backscattering signal and background signal); SNR_detection is the SNR considering only the detector and electronic noises; $F_{\mathrm{B}}=\frac{N_{\mathrm{bkg}}-N}{N_{\mathrm{bkg}}+N}$, where N_bkg is the number of background photons; and φ=Δφ_OPD for simplicity. The calculation details of ${\mathit{\sigma }}_{v_p,\mathrm{speckle}}^{\mathrm{2}}$ and some parameters are outlined in Appendix A. We verified that this analytical formula was a good estimator using Monte Carlo simulations. In these simulations, we stochastically generated the currents obtained at the detector outputs based on the statistics of the various noise sources. Subsequently, the four currents were convolved with the detector impulse response. The maximum likelihood estimator (MLE) (see paper of Cézard et al., 2009, for the principle) was then employed to retrieve the projected wind speed along the laser axis, and we assessed the error distribution across multiple simulations. Furthermore, we confirmed that the results obtained using the analytical formula closely matched the Cramér–Rao lower bound (Cézard et al., 2009) as we obtain a relative difference of 2 %.

2.3 Optimization of the lidar performance

2.3.1 Emission–reception architecture

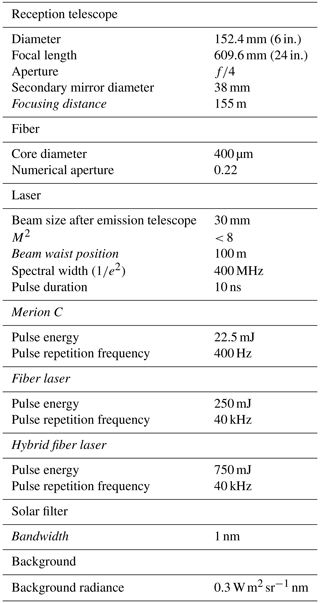
Several simulations were conducted to determine the optimal focusing distances for both the telescope and the laser, aiming to maximize the overlap function between 100 and 300 m for our optical architecture. The setup includes a telescope with a diameter of 152.4 mm, a primary mirror focal length of 609.6 mm, a second mirror obstruction diameter of 38 mm, and a fiber diameter of 400 µm. These calculations were performed considering a laser beam with a size of 30 mm upon exiting the lidar, where M², defined as the ratio of the beam divergence angle to the beam divergence angle of the perfect Gaussian beam at the same wavelength, is considered to be lower than 8, a value obtained for the commercial Merion C laser by LUMIBIRD. The optimized focusing distances were found to be 155 m for the telescope and 100 m for the laser, resulting in an overlap function γ equal to 1 across the entire range.

2.3.2 Detector

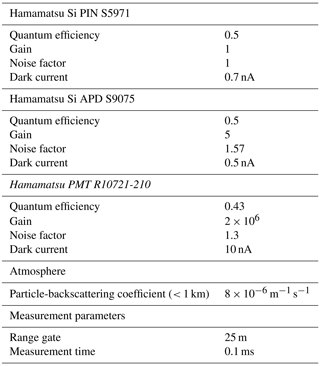
We compared the detection noise level in terms of the number of photons for the specified range gate across three types of detectors: a positive intrinsic negative (PIN) photodiode amplified with a transimpedance, an avalanche photodiode (APD), and a photomultiplier tube (PMT) (Hamamatsu S5971, 2024; Hamamatsu S9075, 2024; Hamamatsu R10721-210, 2024). Indeed, the total noise induced by the backscattered shot noise must exceed the total detection noise. Taking the definition of the excess noise factor from PMT Handbook (2017), we have $F=(\frac{{\text{SNR}}_{\mathrm{input}}}{{\text{SNR}}_{\mathrm{output}}}{)}^{\mathrm{2}}$, with ${\text{SNR}}_{\mathrm{input}}=\frac{N}{{\mathit{\sigma }}_{\mathrm{input}}}$ and ${\text{SNR}}_{\mathrm{output}}=\frac{G\mathit{\eta }N}{{\mathit{\sigma }}_{\mathrm{output}}}$, where N represents the sum of backscattered photons obtained for the four detectors, G stands for the gain of the detector, and η signifies the quantum efficiency. The noise variance induced by the backscattered shot noise at the output of the detectors will be ${\mathit{\sigma }}_{\mathrm{output}}^{\mathrm{2}}=F(G\mathit{\eta }{)}^{\mathrm{2}}{\mathit{\sigma }}_{\mathrm{input}}^{\mathrm{2}}=F(G\mathit{\eta }{)}^{\mathrm{2}}N$. This noise must exceed the detection noise, leading to the condition $N\gg \frac{\mathrm{4}{\mathit{\sigma }}_{\det }^{\mathrm{2}}}{F(G\mathit{\eta }{)}^{\mathrm{2}}}$, where ${\mathit{\sigma }}_{\det }^{\mathrm{2}}$ denotes the detection noise of a detector expressed in the number of electrons calculated for a range gate of 25 m. In order to meet the condition, we take $N>\mathrm{10}\frac{\mathrm{4}{\mathit{\sigma }}_{\det }^{\mathrm{2}}}{F(G\mathit{\eta }{)}^{\mathrm{2}}}$, with the right term corresponding to the equivalent number of photons produced by the detection noise. We found 1.1×10⁸ for the PIN photodiode, 2.8×10⁶ for the APD, and 2.9×10⁻⁵ for the PMT. Only the PMT ensures a low level of detection noise compared to the shot noise level.

2.3.3 Solar filter

The spectrally thin solar filter blocks most of the background signal (broad spectrum) that goes to the spectral analyzer but transmits the Rayleigh signal. Ideally, the filter bandwidth should encompass the spectral width of the Rayleigh signal plus and minus the maximum Doppler frequency shift (≈ 1 pm at 355 nm for a wind speed of 100 m s⁻¹). However, the smaller the desired filter bandwidth, the smaller the transmission and the more expensive the component.

To optimize the filter, we need to have photon noise of the background signal much smaller than the photon noise of the backscattered signal. We chose for the threshold $\frac{N}{N_{\mathrm{bkg}}}>\mathrm{10}$, where N_bkg is the sum of background photons of the four detectors. For this, we need

$$\begin{array}{}\text{(2)}& E_{\mathrm{P}}>BR\mathrm{\Delta }\mathit{\lambda }{z}^{\mathrm{2}},\end{array}$$

where $B=\frac{\mathrm{10}\mathit{\pi }{\text{FOV}}^{\mathrm{2}}R}{\mathrm{2}c\mathit{\beta }{T}_{\mathrm{atm}}^{\mathrm{2}}\mathit{\gamma }\left(z\right)}$, R is the background radiance, z is the range to the telescope, β is the backscatter coefficient, T_atm is the atmospheric transmission, FOV is the telescope field of view, and Δλ is the filter bandwidth (full width at half maximum). We can see that the optimized filter depends on the laser parameters.

As the minimum energy of the pulse increases with distance, in our case Eq. (1) must be fulfilled at 300 m to be fulfilled over the whole range. We also assume for the study a background radiance equal to 0.3 W m² sr⁻¹ nm. For a filter bandwidth of 1 nm, this results in a minimum laser energy per pulse of 298 µJ. This filter bandwidth is used for the rest of the simulation, as it about corresponds to the limit of the technology in terms of filter thickness.

2.3.4 Laser optimization on the ground and at 10 km altitude

To optimize the laser parameters using the simulator, simulations were performed by adjusting the average laser power and pulse repetition frequency to assess the error in the retrieved wind velocity. We neglected electrical noise by considering PMT detectors. At low altitudes (less than 1 km), we assumed a backscatter coefficient for particles of $\mathrm{8}\times {\mathrm{10}}^{-\mathrm{6}}$ ${\mathrm{m}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$. The backscatter coefficient for molecules is $\mathrm{7.2}\times {\mathrm{10}}^{-\mathrm{6}}$ ${\mathrm{m}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$ on the ground and $\mathrm{2.1}\times {\mathrm{10}}^{-\mathrm{6}}$ ${\mathrm{m}}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}$ at 10 km altitude. The simulations were performed at a distance of 150 m from the telescope on the laser axis, which corresponds to the intended 3D wind reconstruction distance of about 100 m in front of the aircraft. Additionally, we assumed a range gate of 25 m to match the GLA specifications. The measurement times were set to 0.1 s, corresponding to an integration over 25 m along the aircraft direction traveling at 250 m s⁻¹. We considered that the laser has a full width at $\mathrm{1}/e^{\mathrm{2}}$ of 400 MHz, significantly less than the spectral broadening induced by the thermal movement of the molecules (6.3 GHz for a full width at $\mathrm{1}/e^{\mathrm{2}}$; Bruneau and Pelon, 2003). For the Mie scattering, the coherence time is limited by the laser pulse duration, i.e., 10 ns. For the Rayleigh scattering, it is limited by spectral broadening due to thermal motion of the molecule, i.e., 0.63 ns for a broadening of 6.3 GHz. The simulations were conducted both on the ground and at 10 km altitude, approximately corresponding to the aircraft's cruising altitude, as the GLA must operate throughout the flight.

Figure 4a shows the evolution of the standard deviation of the projected wind speed computed on the ground with Eq. (1). The white lines give the laser parameters resulting in an error, equivalent to 3σ (where σ denotes the standard deviation), of 1 m s⁻¹ for the reconstructed vertical wind component for a lidar angle of 15 and 50°. The methodology utilized for wind calculation is elaborated in Sect. 3.1. This corresponds to a standard deviation for the projected wind speed of 0.12 m s⁻¹ for 15° and 0.35 m s⁻¹ for 50°. The magenta line denotes the threshold where the variance of the backscattered signal exceeds 10 times the background noise variance at 300 m. Beyond this threshold, the laser pulse energy diminishes, leading to an increased number of background photons compared to backscattered photons. The blue line represents the boundary where the variance of the backscattered signal surpasses 10 times the speckle variance of the backscattered signal at 100 m. Below this threshold, averaging the measurements fails to adequately average speckle patterns. Within the region delineated by these lines, the measurement is constrained by the shot noise of the backscatter, and the lidar is considered optimized. Within this range, performance is directly proportional to the average laser power (laser parameter serving as an indicator of laser size).

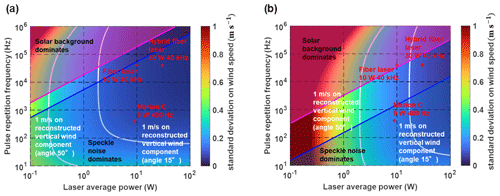
Figure 4 Standard deviation of wind speed estimation as a function of the laser average power and pulse repetition frequency at 150 m from the lidar, considering molecular scattering and particles scattering, for wind measurement (a) on the ground and (b) at 10 km altitude. The white line shows the limit of 1 m s⁻¹ on the reconstructed vertical wind component for a lidar angle of 15 and 50°.

Figure 4b shows the evolution of the standard deviation of the wind speed computed at 10 km altitude, featuring the same threshold lines as in Fig. 4a. Performance is diminished because of the absence of particles and the reduced density of molecules at this altitude, resulting in a decreased amount of backscattered signal. Additionally, the scarcity of the signal amplifies the impact of the background signal, as evidenced by the magenta line being lower than that calculated on the ground. Conversely, the speckle noise decreases because the backscattering is predominantly molecular, which is less coherent than particulate backscattering. Moreover, achieving an accuracy of 1 m s⁻¹ is more challenging at this altitude when taking a lidar angle of 15°. However, as we will see in Sect. 3, the lidar angle can be increased to 15°, and for this angle the limit on the standard deviation is 0.35 m s⁻¹, so all three lasers allow for reaching a precision of 1 m s⁻¹ for the vertical wind component.

2.3.5 Selected laser configurations

We have used Fig. 4 to select laser parameters for three laser technologies: seeded solid-state laser, fiber laser, and hybrid fiber laser.

Regarding the seeded solid-state laser, the primary challenge lies in achieving a high repetition rate to avoid being constrained by speckle noise. We have opted for the injection-seeded Merion C, commercialized by LUMIBIRD, which boasts a repetition rate of 400 Hz and delivers 22.5 mJ of energy per pulse. In this scenario, a wide bandwidth solar filter can be employed (typically ≫ 1 nm is chosen). This configuration yields a standard deviation σ_lidar of 0.11 m s⁻¹ at low altitude and 0.17 m s⁻¹ at high altitude.

The second technology is a fiber laser, made with doped and pumped fiber, emitting at 1 µm, with a frequency-tripling stage. Because of the limit in peak power due to the Brillouin effect in the fiber, we chose a high repetition rate of 40 kHz that is well adapted to the fiber laser. We estimated that the maximum average power of 10 W can be achieved with current technology, allowing for the use of a solar filter up to 0.84 nm. So with a filter of 1 nm, the projected wind speed measurement at 300 m will then be slightly affected by background noise. The results for the standard deviation σ_lidar are 0.05 m s⁻¹ at low altitude and 0.16 m s⁻¹ at high altitude.

The third configuration is the hybrid fiber laser, obtained by adding a free space amplifier at the output of the fiber laser. We estimated that the maximum average power of 30 W can be reached, which allows for the use of a solar filter up to 2.5 nm. This results in the standard deviation σ_lidar of 0.03 m s⁻¹ at low altitude and 0.09 m s⁻¹ at high altitude.

The main parameters that have been used in the simulation are summed up in Tables A1 and A2. The parameters in italics correspond to the ones that were optimized with simulations.

3 Wind reconstruction

We minimized the total error in the vertical and lateral components of the wind reconstructed using the four-axis design in the presence of turbulence. These components significantly influence lift, emphasizing the importance of accurate estimation to avoid errors when attenuating the turbulence effect in GLA applications. Firstly, we establish the expression of the instrumental-error contribution to the total error and evaluate it for the three laser designs previously established. Secondly, we define the expression of the turbulence contribution to the total error for von Kármán turbulence. Thirdly, we determine the lidar angle that minimizes the total error in the vertical component.

3.1 Lidar angle optimization with an analytical method

The first step involves establishing the contribution of instrumental error to the total error in the vertical and lateral wind components, which depends on the error in the projections used to estimate the vertical component and the lidar angle. Referring to Fig. 1, the vertical wind component is given by $v_z=\frac{V_{\mathrm{3}}-V_{\mathrm{1}}}{\mathrm{2}\sin \left(\mathit{\theta }\right)}$, where V₃ and V₁ are projections of the wind onto axes 3 and 1, respectively. The lateral component is reconstructed using the same formula, employing projections from axes 2 and 4, V₂ and V₄. These projections are affected by the lidar noise σ_lidar, evaluated in Sect. 2.3.5 for the three laser designs. If we assume that the wind is homogenous, the error is obtained from the instrumental noise given by ${\mathit{\sigma }}_{\mathrm{Vz},\mathrm{instrumental}}(d,\mathit{\theta })=\frac{\sqrt{\mathrm{2}}}{\left(\mathrm{2}\sin \left(\mathit{\theta }\right)\right)}{\mathit{\sigma }}_{\mathrm{lidar}}(d,\mathit{\theta })$. The error in the lateral component is the same due to symmetry. This error depends on d, the range of estimation along the flight path, and θ since σ_lidar depends on the range z from the lidar, where $z=d/\cos \left(\mathit{\theta }\right)$. Moreover, if we suppose that the lidar is optimized, which is the case for the hybrid fiber laser between 100 and 300 m, the predominant noise is the backscattered-signal shot noise. In this scenario, σ_lidar is proportional to the measurement range z along the lidar axis. Given that the standard deviation for the three laser configurations was calculated at 150 m, the instrumental noise at range d is ${\mathit{\sigma }}_{\mathrm{lidar}}(d,\mathit{\theta })=\frac{{\mathit{\sigma }}_{\mathrm{lidar}}\left(z_{\mathrm{0}}\right)}{z_{\mathrm{0}}}\frac{d}{\cos \left(\mathit{\theta }\right)}$. Therefore, the instrumental-error contribution to the total error in the vertical wind component is

$$\begin{array}{}\text{(3)}& {\mathit{\sigma }}_{\mathrm{Vz},\mathrm{instrumental}}(d,\mathit{\theta })={\displaystyle \frac{\sqrt{\mathrm{2}}}{\left(\mathrm{2}\sin \right(\mathit{\theta }\left)\right)}}{\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{lidar}}\left(z_{\mathrm{0}}\right)}{z_{\mathrm{0}}}}{\displaystyle \frac{d}{\cos \left(\mathit{\theta }\right)}}.\end{array}$$

We assess the error in the reconstructed vertical and lateral wind components for the three selected laser configurations. Assuming an estimation distance of d = 100 m and an angle of 15°, typically used for the lidar angle, we obtain errors of 0.32, 0.30, and 0.17 m s⁻¹ for the Merion C laser, the fiber laser, and the hybrid fiber laser, respectively. This result ensures that the 3σ error for all three designs remains below 1 m s⁻¹.

The second step involves establishing the expression of the turbulence contribution to the total error for turbulence described by the von Kármán model. This model provides expressions for power spectral densities that best match measured turbulence data (Giez et al., 2021), particularly in the inertial subrange where the energy cascade from large eddies to smaller ones occurs. The error in the vertical wind component, corresponding to the RMSE between the reconstructed component and the actual component, if we only consider the turbulence contribution, is

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& {\mathit{\sigma }}_{\mathrm{Vz},\mathrm{turbulence}}(d,\mathit{\theta })\\ & =\sqrt{\langle (V_z-V_{z\mathrm{0}}{)}^{\mathrm{2}}\rangle }\\ & =\sqrt{{\displaystyle \frac{\mathrm{2}}{\left(\mathrm{2}\sin \right(\mathit{\theta }){)}^{\mathrm{2}}}}(\langle \mathit{\delta }{V}_{p\mathrm{1}}^{\mathrm{2}}\rangle +\langle \mathit{\delta }{V}_{p\mathrm{3}}^{\mathrm{2}}\rangle -\mathrm{2}\langle \mathit{\delta }{V}_{p\mathrm{1}}\mathit{\delta }{V}_{p\mathrm{3}}\rangle )},\end{array}\end{array}$$

where V_z0 is the vertical component of the actual wind and δV_p1 and δV_p3 are the differences between the projections of the real wind and the measured projections, for axes 1 and 3, respectively (see Fig. 1). The symbols 〈 〉 account for the ensemble averaging. For von Kármán turbulence, which is homogeneous and isotropic (i.e., the statistics are independent of the coordinate rotations), the error is (calculation details in Appendix B, using the formulas presented in Wilson, 1998)

$$\begin{array}{}\text{(5)}& \begin{array}{rl}& {\mathit{\sigma }}_{\mathrm{Vz},\mathrm{turbulence}}(d,\mathit{\theta })\\ & =\sqrt{{\displaystyle \frac{D_{\mathrm{NN}}\left(\mathrm{2}r\right)}{\left(\mathrm{2}\tan \right(\mathit{\theta }){)}^{\mathrm{2}}}}+{\displaystyle \frac{\mathrm{3}{B}_{\mathrm{LL}}\left(\mathrm{0}\right)+B_{\mathrm{LL}}\left(\mathrm{2}r\right)}{\mathrm{2}}}-\mathrm{2}{B}_{\mathrm{LL}}\left(r\right)},\end{array}\end{array}$$

where r=dtan (θ) is the distance between the point on the lidar axis and the point on the flight path, B_LL is the longitudinal correlation function of the turbulence (for the wind component longitudinal to the displacement vector r), and D_NN is the structure function for the lateral component of the wind (lateral to the displacement vector r). Combining Eqs. (52), (99), and (101) of Wilson (1998), we obtain expressions for the correlation and structure functions:

$$\begin{array}{}\text{(6)}& {\displaystyle }{B}_{\mathrm{LL}}\left(r\right)={\mathit{\sigma }}_{\mathrm{S}}^{\mathrm{2}}{\displaystyle \frac{\mathrm{2}}{\mathrm{\Gamma }(\mathrm{1}/\mathrm{3})}}{\left({\displaystyle \frac{r}{\mathrm{2}l}}\right)}^{\mathrm{1}/\mathrm{3}}{K}_{\mathrm{1}/\mathrm{3}}\left({\displaystyle \frac{r}{l}}\right),\text{(7)}& {\displaystyle }{B}_{\mathrm{NN}}\left(r\right)={\mathit{\sigma }}_{\mathrm{S}}^{\mathrm{2}}{\displaystyle \frac{\mathrm{2}}{\mathrm{\Gamma }(\mathrm{1}/\mathrm{3})}}{\left({\displaystyle \frac{r}{\mathrm{2}l}}\right)}^{\mathrm{1}/\mathrm{3}}\left[K_{\mathrm{1}/\mathrm{3}}\left({\displaystyle \frac{r}{l}}\right)-\left({\displaystyle \frac{r}{\mathrm{2}l}}\right)K_{\mathrm{2}/\mathrm{3}}\left({\displaystyle \frac{r}{l}}\right)\right],\text{(8)}& {\displaystyle }{D}_{\mathrm{NN}}\left(r\right)=\mathrm{2}\left(B_{\mathrm{NN}}\left(\mathrm{0}\right)-B_{\mathrm{NN}}\left(r\right)\right),\end{array}$$

where σ_S is the standard deviation of the wind amplitude in the turbulence, l is the turbulence length scale, Γ is the gamma function, K_n is a Bessel function of the first kind, and B_NN is the lateral correlation function of the turbulence. The standard deviation of the wind amplitude is related to the spectrum energy E_v(k) of the wind field with the equation ${\int }_{\mathrm{0}}^{\mathrm{\infty }}{E}_v\left(k\right)dk=\frac{\mathrm{3}{\mathit{\sigma }}_{\mathrm{S}}^{\mathrm{2}}}{\mathrm{2}}$ (Wilson, 1998), where k represents the spatial frequency.

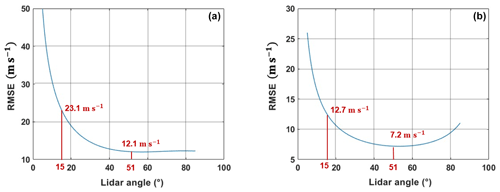
The optimization of the lidar angle was performed by minimizing the expression of the total error in the vertical wind component with respect to θ. The expression for the total error is ${\mathit{\sigma }}_{Vz}=\sqrt{{\mathit{\sigma }}_{\mathrm{Vz},\mathrm{instrumental}}(d,\mathit{\theta }{)}^{\mathrm{2}}+{\mathit{\sigma }}_{\mathrm{Vz},\mathrm{turbulence}}(d,\mathit{\theta }{)}^{\mathrm{2}}}$. This error was evaluated for a range of estimation of d = 100 m at an altitude of 10 km, using the Merion C laser, with von Kármán turbulence; l being equal to 762 m (2500 ft); and σ_S, the standard deviation of the wind amplitude, being equal to 10 m s⁻¹. Figure 5b illustrates the evolution of the total error, i.e., the RMSE between the reconstructed and actual lateral component along the flight path, as a function of the lidar angle θ. The RMSE reaches a minimum for a lidar angle of 51°. The RMSE obtained for this angle is 7.2 m s⁻¹, nearly twice as low as the RMSE of 12.7 m s⁻¹ obtained for an angle of 15°. Choosing an angle of 51° may seem counter-intuitive in case of turbulent wind; indeed the measurement points are much further apart for such an angle (2r = 240 m between the two opposite points for 50°, while 2r = 54 m for 15°). Due to this larger distance, one might assume that the measurement points are not correlated, leading to significant errors in the projections, which affect the reconstructed wind component. In fact, for the wind structure we are examining (in the inertial subrange), in a turbulent wind field like von Kármán turbulence, large eddies are much more influential than small ones. The smaller wind structures induce only a minor error in all four projections, which can be amplified for small lidar angles due to the factor $\mathrm{1}/\left(\mathrm{2}\sin \right(\mathit{\theta }){)}^{\mathrm{2}}$ in Eq. (3) when retrieving the wind component. For larger angles (above 50°), the instrumental noise becomes significant because the measurement range along the lidar axis increases.

Figure 5 RMSE between the reconstructed and actual lateral component on the flight path as a function of the lidar angle from the flight direction θ, for wind measurement at (a) low and (b) high altitude.

3.2 Optimized angle for measurements at low altitude

We study the evolution of the optimized angle for measurement on the ground. The measurement parameters remain the same: the vertical wind component is estimated at d = 100 m from the lidar using the Merion C laser. The length scale of the von Kármán turbulence at low altitude is much lower and is assumed to be equal to 100 m for this study. Additionally, we assume a turbulence strength σ_S of 10 m s⁻¹. The evolution of the RMSE at this altitude is depicted in Fig. 5a as a function of the lidar angle. We observe that the optimized angle is around 51°. However, the error is higher than at high altitude, partly due to the fact that smaller eddies have more energy. This increases the difference between the projections of the real wind and the measured projections, thereby increasing the error.

3.3 Validation with simulations of turbulence at 10 km altitude

To illustrate the improvement at 51°, reconstruction simulations of the lateral wind component with two lidar angles were conducted. The simulation utilized a simulator that calculates the 3D wind field by following the statistics of the von Kármán turbulence model, using the equations presented in the Army Research Laboratory technical report (Wilson, 1998). The 3D spectra are calculated as a function of the spatial frequency: ${\mathrm{\Phi }}_{ij}\left(k\right)=\frac{E_v\left(k\right)}{\mathrm{4}\mathit{\pi }{k}^{\mathrm{4}}}({\mathit{\delta }}_{ij}{k}^{\mathrm{2}}-k_i{k}_j)$, where the indices i and j represent the direction (x, y, or z) and δ_ij is the Kronecker delta. For von Kármán turbulence, $E_v\left(k\right)=\mathrm{1.4528}\frac{{\mathit{\sigma }}_{\mathrm{S}}^{\mathrm{2}}{k}^{\mathrm{4}}{l}^{\mathrm{5}}}{(\mathrm{1}+k^{\mathrm{2}}{l}^{\mathrm{2}}{)}^{\mathrm{17}/\mathrm{6}}}$. For each k, a 3 × 3 symmetric matrix $\mathbf{W}\left(k\right)=\left({\mathrm{\Phi }}_{ij}\right(k){)}_{i=[x,y,z],j=[x,y,z]}$ is obtained, which is factorized using a Cholesky decomposition to facilitate the generation of correlated random wind. This matrix is then multiplied by a vector of three random phases following a reduced centered normal distribution for each k. The three correlated wind components are obtained with an inverse Fourier transformation according to k. Note that the temporal evolution of the wind is not taken into account to simplify the study, assuming that the wind does not vary significantly as the plane moves through the grid. Once the winds are simulated, the plane traverses the grid with the lidar in the nose, and the wind is reconstructed in front of it with the same measurement geometry as before.

For the simulation, the wind box was taken to be equal to 8 km × 800 m × 800 m, sampled every 5 m in each direction. The turbulence length scale is taken to be equal to 762 m, the value at 10 km altitude, and we assume a turbulence with a standard deviation of the wind amplitude of 10 m s⁻¹. We considered that the plane is moving at V_aircraft = 250 m s⁻¹; that it is centered at y = 0 and z = 0, along the x axis; and that the lidar is located in the nose of the aircraft. In particular, for each measurement, we account for the plane motion during the integration time, i.e., the slight variation in the measured projected wind observed by each laser pulse. We used a simplified model for the lidar, considering, at each pulse, only one measurement on the laser axis of the projected wind speed at a range $z=d/\cos \left(\mathit{\theta }\right)$ over a range gate of 25 m. The model of the lidar measurement noise is assumed to be Gaussian, with the projected wind speed obtained on the range gate for the mean and a standard deviation corresponding to σ_lidar. For the simulation we take the one obtained for the Merion C. Once the wind components are estimated, the RMSE is estimated at each simulator run, using the mean value of the squared differences between the estimated wind component and the true wind component over the flight path over 312 values (≈ 8 km/25 m) and taking the square root of the resulting value. Figure 6 displays the results. In Fig. 6a, an example of wind simulated with the von Kármán model is depicted. In Fig. 6b, the green line, which corresponds to the vertical component retrieved using a lidar angle of 50°, is closer to the black line, which represents the real wind, than the red line, which corresponds to the vertical component reconstructed using a lidar angle of 15°. A total of 180 simulation runs have been performed, and statistics of all obtained RMSE values show a mean value of 12.7 m s⁻¹ with a 3σ error of 0.3 m s⁻¹ for the angle of 15° and a mean value of 7.2 m s⁻¹ with a 3σ error of 0.15 m s⁻¹ for the angle of 50°. This illustrates the improvement achieved with the optimized lidar angle of 50°. In addition, the result is close to the theoretical RMSE given in Fig. 5b. This shows that the motion of the plane during the integration time (i.e., 25 m) has little effect on the error in the wind reconstruction.

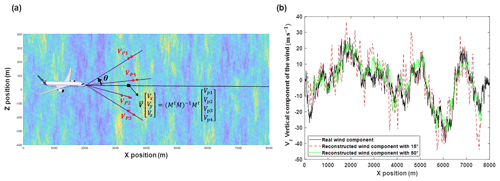
Figure 6 (a) Sample of a wind simulation (norm of the wind vector of the plane xOz (where y = 0)) and representation of the lidar measurements for the wind reconstruction ahead of a plane). (b) Evolution of the vertical wind component as a function of the position in the simulated wind volume. Shown are the actual wind component on the flight path in black and the wind component retrieved with an angle of 15° in red and with an angle of 50° in green.

4 Conclusions

A robust UV lidar architecture, including a QMZ interferometer and a fiber laser, was presented for measuring wind in the feed-forward GLA system. The end-to-end simulator was described and utilized to optimize the lidar architecture. The emission–reception configuration was optimized to ensure a complete overlap of the laser and telescope field of view between 100 and 300 m. PMTs were chosen due to their high gain, which helps limit the impact of detection noise. An optimized solar filter size was estimated for each laser configuration to mitigate the background signal. Three lasers were selected: a commercial laser, the Merion C, for initial testing, and two fiber laser models studied at ONERA (Office National d'Étude et de Recherches Aérospatiales). The error in the projected wind speed estimated at 150 m on the laser axis is 0.17 m s⁻¹ for the Merion C, 0.16 m s⁻¹ for the fiber laser, and 0.09 m s⁻¹ for the hybrid fiber laser. The simulations focused on GLA application, but the simulator can be applied to other lidar instruments performing wind measurements from space or a high-altitude platform. In particular, we previously used this simulator to calculate lidar performance for wind measurement from space using the same architecture as Aeolus but replacing the laser with a theoretical UV fiber laser and the two spectral analyzers with one QMZ interferometer (Boulant et al., 2023).

The lidar is being assembled, and the first validation will be performed soon. All the instrument characteristics (different noise levels, instrumental transmission, etc.) will be performed and compared with the simulation. In particular, the contrast with the different channel and the phase differences between channels of the QMZ interferometer will be measured and simulated to evaluate their effect on the lidar performance to refine the calculation of the performance of the system. Currently we assume a perfect interferometer with the transmission of the optics equal to 1 and an instrumental contrast of 1. This will be reevaluated in future studies with transmission and contrast measured experimentally.

A lidar angle optimization method was presented. This method evaluates the RMSE between the reconstructed vertical wind component and the actual one on the flight path for a linear least-squares method. Two contributions are considered, instrumental noise and noise induced by turbulence. The angle that minimizes the RMSE in the presence of von Kármán turbulence is approximately 50°, resulting in an RMSE that is approximately 50 % of the RMSE obtained with an angle of 15–30°. The method has been validated through simulations of turbulence and wind reconstruction. It should be noted that this method can also be applied by considering only instrumental noise. Additionally, this method demonstrates that the intuition of using a small lidar angle to maintain almost homogeneous wind field conditions between measurement points to minimize error in the vertical component is misleading. Indeed, the error between the projections on the lidar axes and those at the point of reconstruction, induced by turbulence, are amplified by the factor $\frac{\mathrm{1}}{\tan \left(\mathit{\theta }\right)}$ for a small angle. In a future work, we plan to experimentally validate the improvement of the precision of the reconstructed 3D wind with an existing heterodyne wind lidar at ONERA. The lidar will point-measure the 3D wind along a central axis using four axes evenly distributed around this central axis. The reconstructed wind will be compared with the “true” wind measured with an independent local detector (anemometer). This comparison will be performed for several angles between the four beams and the central axis to validate this calculated improvement.

The effect of refraction due to turbulence has not been taken into account in the 3D wind simulator. In the UV, the refraction is strong and the beam can be significantly deflected as it propagates through the atmosphere. This can lead to an increase in the size of the probe volume, depending on the direction of the refraction. This will be addressed in future studies. In addition, the evolution of the RMSE with multiple runs of the simulator will be performed in future work to evaluate the sensitivity of the RMSE with different turbulence levels.

The lidar angle have been optimized, but the simulator shows that for high-strength turbulence, the error in the reconstructed wind is still high (7.4 m s⁻¹ with an angle of 50°) and does not allow for reaching the GLA requirement of 1 m s⁻¹. This is the limit of the estimator with this measurement geometry. It should be noted that further reconstruction methods for decreasing the error in the reconstructed wind speed are being studied at ONERA.

Appendix A: Lidar measurement standard deviation with speckle noise

For the calculation of the speckle noise contribution of the standard deviation, we use the method described by Bruneau and Pelon (2003).

A1 Estimation of the projected wind speed from the four currents

Regarding the output of the four detectors, if we assume that the same transmission at the four outputs of the QMZ interferometer and the interferometer introduces no loss of contrast, the signals in the current are

$$\begin{array}{}\text{(A1)}& {\displaystyle }{S}_{\mathrm{1}}={\displaystyle \frac{S_{\mathrm{0}}}{\mathrm{4}}}\left(\mathrm{1}+M_{\mathrm{tot}}\cos \left(\mathit{\phi }\right)\right)+S_{\mathrm{bkg}}+S_{\mathrm{dark}},\text{(A2)}& {\displaystyle }{S}_{\mathrm{2}}={\displaystyle \frac{S_{\mathrm{0}}}{\mathrm{4}}}\left(\mathrm{1}-M_{\mathrm{tot}}\sin \left(\mathit{\phi }\right)\right)+S_{\mathrm{bkg}}+S_{\mathrm{dark}},\text{(A3)}& {\displaystyle }{S}_{\mathrm{3}}={\displaystyle \frac{S_{\mathrm{0}}}{\mathrm{4}}}\left(\mathrm{1}-M_{\mathrm{tot}}\cos \left(\mathit{\phi }\right)\right)+S_{\mathrm{bkg}}+S_{\mathrm{dark}},\text{(A4)}& {\displaystyle }{S}_{\mathrm{4}}={\displaystyle \frac{S_{\mathrm{0}}}{\mathrm{4}}}\left(\mathrm{1}+M_{\mathrm{tot}}\sin \left(\mathit{\phi }\right)\right)+S_{\mathrm{bkg}}+S_{\mathrm{dark}},\end{array}$$

where S₀ is the total current, M_tot is the contrast of the interferences due to the spectral shape of the input light, S_bkg is the signal due to the background signal, S_dark is the noise from the detector, and φ is a simpler notation of δφ_OPD. The spectrum of the incident light is from two scattering process, Rayleigh scattering and Mie scattering, so $M_{\mathrm{tot}}=\frac{\mathrm{1}}{R_{\mathit{\beta }}}{M}_m+\frac{R_{\mathit{\beta }}-\mathrm{1}}{R_{\mathit{\beta }}}{M}_p$, where R_β is the backscatter ratio, M_m is the interference contrast due to the Rayleigh spectrum, and M_p is the interference contrast due to the Mie spectrum.

Considering that the background noise and the detection noise can be estimated and subtracted from the signals, φ can be estimated by

$$\begin{array}{}\text{(A5)}& {\displaystyle }{Q}_{\mathrm{1}}={\displaystyle \frac{S_{\mathrm{1}}^{\prime }-S_{\mathrm{3}}^{\prime }}{S_{\mathrm{1}}^{\prime }+S_{\mathrm{3}}^{\prime }}}=M_{\mathrm{tot}}\cos \left(\mathit{\phi }\right),\text{(A6)}& {\displaystyle }{Q}_{\mathrm{2}}={\displaystyle \frac{S_{\mathrm{4}}^{\prime }-S_{\mathrm{2}}^{\prime }}{S_{\mathrm{4}}^{\prime }+S_{\mathrm{2}}^{\prime }}}=M_{\mathrm{tot}}\sin \left(\mathit{\phi }\right),\text{(A7)}& {\displaystyle }\mathit{\phi }=\arctan \left({\displaystyle \frac{Q_{\mathrm{2}}}{Q_{\mathrm{1}}}}\right),\end{array}$$

where $S_i^{\prime }$ indicates that background and the detection signals have been subtracted from the signal S_i. Doing the same with the reference signal (i.e., the laser light), we obtain φ₀ and the projected wind speed is estimated with

$$\begin{array}{}\text{(A8)}& v_p={\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{0}}c}{\mathrm{4}\mathit{\pi }\mathrm{\Delta }L}}(\mathit{\phi }-{\mathit{\phi }}_{\mathrm{0}}).\end{array}$$

Table A1 Summary of the parameters of the lidar and the simulation.

Parameters in italics are those deduced from simulations.

Table A2 Summary of the parameters of the lidar and the simulation.

Parameters in italics are those deduced from simulations.

A2 Standard deviation of the wind speed due to the speckle noise

Note that $Q=\frac{Q_{\mathrm{1}}}{Q_{\mathrm{2}}}$ and $S_{\mathit{\phi }}=\frac{\mathrm{4}\mathit{\pi }\mathrm{\Delta }L}{{\mathit{\lambda }}_{\mathrm{0}}c}$. The standard deviation of v_p is (neglecting the standard deviation of φ₀ because the reference signal is sufficiently high to have a good SNR)

$$\begin{array}{}\text{(A9)}& {\mathit{\sigma }}_{v_p}={\displaystyle \frac{\mathrm{1}}{S_{\mathit{\phi }}}}{\mathit{\sigma }}_{\mathit{\phi }},\end{array}$$

where σ_φ is the standard deviation of φ:

$$\begin{array}{}\text{(A10)}& \mathit{\phi }={\displaystyle \frac{\mathrm{d}\mathit{\phi }}{\mathrm{d}Q}}{\mathit{\sigma }}_Q=\cos (\mathit{\phi }{)}^{\mathrm{2}}{\mathit{\sigma }}_Q,\end{array}$$

where σ_Q is the standard deviation of Q. The variance on Q is (as Q₁ and Q₂ are uncorrelated)

$$\begin{array}{}\text{(A11)}& \text{var}\left(Q\right)=Q^{\mathrm{2}}({\displaystyle \frac{\text{var}\left(Q_{\mathrm{1}}\right)}{Q_{\mathrm{1}}^{\mathrm{2}}}}+{\displaystyle \frac{\text{var}\left(Q_{\mathrm{2}}\right)}{Q_{\mathrm{2}}^{\mathrm{2}}}}),\end{array}$$

where var(X) is the notation used for “variance of the random variable X”. We also define cov(X,Y) as the “covariance of the random variables X and Y”. Taking Eq. (A5), we have

$$\begin{array}{}\text{(A12)}& \begin{array}{rl}\text{var}\left(Q_{\mathrm{1}}\right)& =Q_{\mathrm{1}}^{\mathrm{2}}({\displaystyle \frac{\text{var}(S_{\mathrm{1}}^{\prime }-S_{\mathrm{3}}^{\prime })}{(S_{\mathrm{1}}^{\prime }-S_{\mathrm{3}}^{\prime }{)}^{\mathrm{2}}}}+{\displaystyle \frac{\text{var}(S_{\mathrm{1}}^{\prime }+S_{\mathrm{3}}^{\prime })}{(S_{\mathrm{1}}^{\prime }+S_{\mathrm{3}}^{\prime }{)}^{\mathrm{2}}}}\\ & -\mathrm{2}{\displaystyle \frac{\text{cov}(S_{\mathrm{1}}^{\prime }-S_{\mathrm{3}}^{\prime },S_{\mathrm{1}}^{\prime }+S_{\mathrm{3}}^{\prime })}{(S_{\mathrm{1}}^{\prime }-S_{\mathrm{3}}^{\prime })(S_{\mathrm{1}}^{\prime }+S_{\mathrm{3}}^{\prime })}}).\end{array}\end{array}$$

Assuming that $S_{\mathrm{1}}^{\prime }$ and $S_{\mathrm{3}}^{\prime }$ are uncorrelated, we have

$$\begin{array}{}\text{(A13)}& {\displaystyle }\text{var}(S_{\mathrm{1}}^{\prime }-S_{\mathrm{3}}^{\prime })=\text{var}(S_{\mathrm{1}}^{\prime }+S_{\mathrm{3}}^{\prime })=\text{var}\left(S_{\mathrm{1}}^{\prime }\right)+\text{var}\left(S_{\mathrm{3}}^{\prime }\right),\text{(A14)}& {\displaystyle }\text{cov}(S_{\mathrm{1}}^{\prime }-S_{\mathrm{3}}^{\prime },S_{\mathrm{1}}^{\prime }+S_{\mathrm{3}}^{\prime })=\text{var}\left(S_{\mathrm{1}}^{\prime }\right)-\text{var}\left(S_{\mathrm{3}}^{\prime }\right).\end{array}$$

The variance of Q₁ is

$$\begin{array}{}\text{(A15)}& \begin{array}{rl}\text{var}\left(Q_{\mathrm{1}}\right)& =(\mathrm{1}+Q_{\mathrm{1}}^{\mathrm{2}}){\displaystyle \frac{\text{var}\left(S_{\mathrm{1}}^{\prime }\right)+\text{var}\left(S_{\mathrm{3}}^{\prime }\right)}{(S_{\mathrm{1}}^{\prime }+S_{\mathrm{3}}^{\prime }{)}^{\mathrm{2}}}}\\ & -\mathrm{2}{Q}_{\mathrm{1}}{\displaystyle \frac{\text{var}\left(S_{\mathrm{1}}^{\prime }\right)-\text{var}\left(S_{\mathrm{3}}^{\prime }\right)}{(S_{\mathrm{1}}^{\prime }+S_{\mathrm{3}}^{\prime }{)}^{\mathrm{2}}}}.\end{array}\end{array}$$

In the case where the speckle noise dominates, we have $\text{var}\left(S_{\mathrm{1}}^{\prime }\right)=\frac{S_{\mathrm{1}m}^{\prime \mathrm{2}}}{N_m}+\frac{S_{\mathrm{1}p}^{\prime \mathrm{2}}}{N_p}$ with $S_{\mathrm{1}m}^{\prime }=\frac{S_{\mathrm{0}m}}{\mathrm{4}}(\mathrm{1}+M_m\cos (\mathit{\phi }\left)\right)$ and $S_{\mathrm{1}p}^{\prime }=\frac{S_{\mathrm{0}p}}{\mathrm{4}}(\mathrm{1}+M_p\cos (\mathit{\phi }\left)\right)$, where S_0m and S_0p are the intensities at the input of the interferometer coming from molecules and particles, respectively. The same is true for $\text{var}\left(S_{\mathrm{3}}^{\prime }\right)=\frac{S_{\mathrm{3}m}^{\prime \mathrm{2}}}{N_m}+\frac{S_{\mathrm{3}p}^{\prime \mathrm{2}}}{N_p}$ with $S_{\mathrm{3}m}^{\prime }=\frac{S_{\mathrm{0}m}}{\mathrm{4}}(\mathrm{1}-M_m\cos (\mathit{\phi }\left)\right)$ and $S_{\mathrm{3}p}^{\prime }=\frac{S_{\mathrm{0}p}}{\mathrm{4}}(\mathrm{1}-M_p\cos (\mathit{\phi }\left)\right)$. N_m and N_p are the number of speckle patterns obtained for a given range gate, linked to the size of the laser beam over the scattering volume, and the number of temporal speckles, due to the coherence of the scattered light. The number of spatial patterns is $(\frac{\mathit{\pi }{\mathit{\theta }}_{\mathrm{div}}{r}_{\mathrm{pup}}}{\mathrm{2}\mathit{\lambda }}{)}^{\mathrm{2}}$, where θ_div is the half divergence of the laser beam and r_pup is the radius of the telescope pupil (Goodman, 1975). The number of temporal speckle patterns is $\frac{\mathrm{2}\mathit{\delta }z}{c{\mathit{\tau }}_{\mathrm{coh}}}$, where δz is the range gate and τ_coh is the coherence length of the signal (Cezard, 2008). The coherence length is inversely proportional to spectrum width. Therefore, as the spectrum of the Rayleigh signal is wider than that of the Mie signal due to a larger Boltzmann distribution, where the number of time patterns will be higher for Rayleigh than for Mie.

We obtain for the variance of Q₁:

$$\begin{array}{}\text{(A16)}& {\displaystyle }\begin{array}{rl}& \text{var}\left(Q_{\mathrm{1}}\right)=(\mathrm{1}+Q_{\mathrm{1}}^{\mathrm{2}})\\ & {\displaystyle \frac{\frac{(S_{\mathrm{0}m}/\mathrm{4}{)}^{\mathrm{2}}}{N_m}\left(\mathrm{2}+\mathrm{2}{M}_m^{\mathrm{2}}\cos (\mathit{\phi }{)}^{\mathrm{2}}\right)+\frac{(S_{\mathrm{0}p}/\mathrm{4}{)}^{\mathrm{2}}}{N_p}\left(\mathrm{2}+\mathrm{2}{M}_p^{\mathrm{2}}\cos (\mathit{\phi }{)}^{\mathrm{2}}\right)}{(S_{\mathrm{0}}/\mathrm{2}{)}^{\mathrm{2}}}}\\ & -\mathrm{2}{Q}_{\mathrm{1}}{\displaystyle \frac{\frac{(S_{\mathrm{0}m}/\mathrm{4}{)}^{\mathrm{2}}}{N_m}\mathrm{4}{M}_m\cos \left(\mathit{\phi }\right)+\frac{(S_{\mathrm{0}p}/\mathrm{4}{)}^{\mathrm{2}}}{N_p}\mathrm{4}{M}_p\cos \left(\mathit{\phi }\right)}{(S_{\mathrm{0}}/\mathrm{2}{)}^{\mathrm{2}}}}.\end{array}\end{array}$$

We can see that two contributions appear in the expression: the one from the Rayleigh signal and the one from the Mie signal. In the following, we only make the calculation for the Rayleigh signal and consider the calculation to be the same for the Mie signal. If we note that Q_1m=M_mcos (φ) and Q_1p=M_pcos (φ), the variance of Q₁ is

$$\begin{array}{}\text{(A17)}& \begin{array}{rl}& \text{var}\left(Q_{\mathrm{1}}\right)\\ & ={\displaystyle \frac{\begin{array}{c}\frac{(S_{\mathrm{0}m}/\mathrm{4}{)}^{\mathrm{2}}}{N_m}(\mathrm{2}+\mathrm{2}{Q}_{\mathrm{1}m}^{\mathrm{2}})+\frac{(S_{\mathrm{0}m}/\mathrm{4}{)}^{\mathrm{2}}}{N_m}\left(\mathrm{2}{Q}_{\mathrm{1}}^{\mathrm{2}}+\mathrm{2}{Q}_{\mathrm{1}}^{\mathrm{2}}{Q}_{\mathrm{1}m}^{\mathrm{2}}\right)\\ -\mathrm{8}{Q}_{\mathrm{1}}{Q}_{\mathrm{1}m}\frac{(S_{\mathrm{0}m}/\mathrm{4}{)}^{\mathrm{2}}}{N_m}+\left(\text{Mie part}\right)\end{array}}{(S_{\mathrm{0}}/\mathrm{2}{)}^{\mathrm{2}}}}\\ & ={\left({\displaystyle \frac{S_{\mathrm{0}m}}{S_{\mathrm{0}}}}\right)}^{\mathrm{2}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{N}_m}}\left[(\mathrm{1}-Q_{\mathrm{1}}{Q}_{\mathrm{1}m}{)}^{\mathrm{2}}+(Q_{\mathrm{1}}-Q_{\mathrm{1}m}{)}^{\mathrm{2}}\right]\\ & +{\left({\displaystyle \frac{S_{\mathrm{0}p}}{S_{\mathrm{0}}}}\right)}^{\mathrm{2}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{N}_p}}\left[(\mathrm{1}-Q_{\mathrm{1}}{Q}_{\mathrm{1}p}{)}^{\mathrm{2}}+(Q_{\mathrm{1}}-Q_{\mathrm{1}p}{)}^{\mathrm{2}}\right].\end{array}\end{array}$$

For the variance of Q₂, the calculation is the same:

$$\begin{array}{}\text{(A18)}& \begin{array}{rl}& \text{var}\left(Q_{\mathrm{2}}\right)\\ & =\left({\displaystyle \frac{S_{\mathrm{0}m}}{S_{\mathrm{0}}}}{)}^{\mathrm{2}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{N}_m}}{\left[(\mathrm{1}-Q_{\mathrm{2}}{Q}_{\mathrm{2}m}{)}^{\mathrm{2}}+(Q_{\mathrm{2}}-Q_{\mathrm{2}m}\right)}^{\mathrm{2}}\right]\\ & +{\left({\displaystyle \frac{S_{\mathrm{0}p}}{S_{\mathrm{0}}}}\right)}^{\mathrm{2}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{N}_p}}\left[(\mathrm{1}-Q_{\mathrm{2}}{Q}_{\mathrm{2}p}{)}^{\mathrm{2}}+(Q_{\mathrm{2}}-Q_{\mathrm{2}p}{)}^{\mathrm{2}}\right],\end{array}\end{array}$$

where Q_2m=M_msin (φ) and Q_2p=M_psin (φ). Considering that the calculations are the same for the Rayleigh part and the Mie part of the formula, we have

$$\begin{array}{}\text{(A19)}& \begin{array}{rl}& {\displaystyle \frac{\text{var}\left(Q_{\mathrm{1}}\right)}{Q_{\mathrm{1}}^{\mathrm{2}}}}+{\displaystyle \frac{\text{var}\left(Q_{\mathrm{2}}\right)}{Q_{\mathrm{2}}^{\mathrm{2}}}}\\ & ={\left({\displaystyle \frac{S_{\mathrm{0}m}}{S_{\mathrm{0}}}}\right)}^{\mathrm{2}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{N}_m}}[{\displaystyle \frac{(\mathrm{1}-Q_{\mathrm{1}}{Q}_{\mathrm{1}m}{)}^{\mathrm{2}}+(Q_{\mathrm{1}}-Q_{\mathrm{1}m}{)}^{\mathrm{2}}}{Q_{\mathrm{1}}^{\mathrm{2}}}}\\ & +{\displaystyle \frac{(\mathrm{1}-Q_{\mathrm{2}}{Q}_{\mathrm{2}m}{)}^{\mathrm{2}}+(Q_{\mathrm{2}}-Q_{\mathrm{2}m}{)}^{\mathrm{2}}}{Q_{\mathrm{2}}^{\mathrm{2}}}}]\\ & +\left(\text{Mie part}\right)\\ & ={\left({\displaystyle \frac{S_{\mathrm{0}m}}{S_{\mathrm{0}}}}\right)}^{\mathrm{2}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{N}_m}}{\displaystyle \frac{\begin{array}{c}{M}_{\mathrm{tot}}^{\mathrm{2}}[\mathrm{1}+(M_{\mathrm{tot}}^{\mathrm{2}}{M}_m^{\mathrm{2}}-\mathrm{4}{M}_{\mathrm{tot}}{M}_m\\ +\mathrm{2}(M_{\mathrm{tot}}-M_m{)}^{\mathrm{2}})\frac{\sin (\mathrm{2}\mathit{\phi }{)}^{\mathrm{2}}}{\mathrm{4}}]\end{array}}{M_{\mathrm{tot}}^{\mathrm{4}}\cos \left(\mathit{\phi }{)}^{\mathrm{2}}\sin \right(\mathit{\phi }{)}^{\mathrm{2}}}}\\ & +\left(\text{Mie part}\right).\end{array}\end{array}$$

Finally, the variance of Q is

$$\begin{array}{}\text{(A20)}& \begin{array}{rl}& \text{var}\left(Q\right)\\ & ={\left({\displaystyle \frac{S_{\mathrm{0}m}}{S_{\mathrm{0}}}}\right)}^{\mathrm{2}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{N}_m{M}_{\mathrm{tot}}^{\mathrm{2}}\cos (\mathit{\phi }{)}^{\mathrm{2}}}}\\ & \left[\mathrm{1}+(M_{\mathrm{tot}}^{\mathrm{2}}{M}_m^{\mathrm{2}}-\mathrm{4}{M}_{\mathrm{tot}}{M}_m+\mathrm{2}(M_{\mathrm{tot}}-M_m{)}^{\mathrm{2}}){\displaystyle \frac{\sin (\mathrm{2}\mathit{\phi }{)}^{\mathrm{2}}}{\mathrm{4}}}\right]\\ & +{\left({\displaystyle \frac{S_{\mathrm{0}p}}{S_{\mathrm{0}}}}\right)}^{\mathrm{2}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{N}_p{M}_{\mathrm{tot}}^{\mathrm{2}}\cos (\mathit{\phi }{)}^{\mathrm{2}}}}\\ & \left[\mathrm{1}+(M_{\mathrm{tot}}^{\mathrm{2}}{M}_p^{\mathrm{2}}-\mathrm{4}{M}_{\mathrm{tot}}{M}_p+\mathrm{2}(M_{\mathrm{tot}}-M_p{)}^{\mathrm{2}}){\displaystyle \frac{\sin (\mathrm{2}\mathit{\phi }{)}^{\mathrm{2}}}{\mathrm{4}}}\right].\end{array}\end{array}$$

If we assume that atmospheric transmission is almost equal to 1, $\frac{S_{\mathrm{0}m}}{S_{\mathrm{0}}}\approx \frac{\mathrm{1}}{R_{\mathit{\beta }}}$ and $\frac{S_{\mathrm{0}p}}{S_{\mathrm{0}}}\approx \frac{R_{\mathit{\beta }}-\mathrm{1}}{R_{\mathit{\beta }}}$. The variance in the projected wind due to the speckle noise is

$$\begin{array}{}\text{(A21)}& \begin{array}{rl}& {\mathit{\sigma }}_{v_p}^{\mathrm{2}}\\ & ={\left({\displaystyle \frac{\mathrm{1}}{R_{\mathit{\beta }}}}\right)}^{\mathrm{2}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{N}_m{M}_{\mathrm{tot}}^{\mathrm{2}}{S}_{\mathit{\phi }}^{\mathrm{2}}}}\\ & \left[\mathrm{1}+(M_{\mathrm{tot}}^{\mathrm{2}}{M}_m^{\mathrm{2}}-\mathrm{4}{M}_{\mathrm{tot}}{M}_m+\mathrm{2}(M_{\mathrm{tot}}-M_m{)}^{\mathrm{2}}){\displaystyle \frac{\sin (\mathrm{2}\mathit{\phi }{)}^{\mathrm{2}}}{\mathrm{4}}}\right]\\ & +{\left({\displaystyle \frac{R_{\mathit{\beta }}-\mathrm{1}}{R_{\mathit{\beta }}}}\right)}^{\mathrm{2}}{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{N}_p{M}_{\mathrm{tot}}^{\mathrm{2}}{S}_{\mathit{\phi }}^{\mathrm{2}}}}\\ & \left[\mathrm{1}+(M_{\mathrm{tot}}^{\mathrm{2}}{M}_p^{\mathrm{2}}-\mathrm{4}{M}_{\mathrm{tot}}{M}_p+\mathrm{2}(M_{\mathrm{tot}}-M_p{)}^{\mathrm{2}}){\displaystyle \frac{\sin (\mathrm{2}\mathit{\phi }{)}^{\mathrm{2}}}{\mathrm{4}}}\right].\end{array}\end{array}$$

Appendix B: Expression of the mean square error (MSE) due to the turbulence

For the different winds, we will note that $\mathit{V}=(V_x,V_y,V_z)$ for the wind on the flight path at range d, ${\mathit{V}}_{\mathbf{1}}=(V_{x\mathrm{1}},V_{y\mathrm{1}},V_{z\mathrm{1}})$ for the wind located at the measurement point of axis 1, and ${\mathit{V}}_{\mathbf{3}}=(V_{x\mathrm{3}},V_{y\mathrm{3}},V_{z\mathrm{3}})$ for the wind located at the measurement point of axis 3. Then $\mathit{\delta }{V}_{p\mathrm{1}}=(V_{x\mathrm{1}}-V_x)\cos \left(\mathit{\theta }\right)-(V_{z\mathrm{1}}-V_z)\sin \left(\mathit{\theta }\right)$ and $\mathit{\delta }{V}_{p\mathrm{3}}=(V_{x\mathrm{3}}-V_x)\cos \left(\mathit{\theta }\right)+(V_{z\mathrm{3}}-V_z)\sin \left(\mathit{\theta }\right)$. The variance of δV_p1 is

$$\begin{array}{}\text{(B1)}& \begin{array}{rl}\langle \mathit{\delta }{V}_{p\mathrm{1}}^{\mathrm{2}}\rangle & =\langle (V_{x\mathrm{1}}-V_x{)}^{\mathrm{2}}\rangle \cos (\mathit{\theta }{)}^{\mathrm{2}}+\langle (V_{z\mathrm{1}}-V_z{)}^{\mathrm{2}}\rangle \sin (\mathit{\theta }{)}^{\mathrm{2}}\\ & -\mathrm{2}\sin \left(\mathit{\theta }\right)\cos \left(\mathit{\theta }\right)\langle (V_{x\mathrm{1}}-V_x)(V_{z\mathrm{1}}-V_z)\rangle ,\end{array}\end{array}$$

where 〈(V_x1−V_x)²〉 and 〈(V_z1−V_z)²〉 correspond to the lateral structure function and longitudinal structure function, respectively. The paper of Wilson (1998) gives the formula for the correlation between two wind components: $\langle V_i{V}_j\rangle \left(r\right)=\left(B_{\mathrm{LL}}\right(r)-B_{\mathrm{NN}}(r\left)\right)\frac{r_i{r}_j}{r^{\mathrm{2}}}+B_{\mathrm{NN}}\left(r\right){\mathit{\delta }}_{ij}$, where δ_ij is the Kronecker symbol and r_i and r_j are the components i and j of the displacement vector r. As r_x=0, the correlation between two wind components of different directions with one of them being equal to the x direction is equal to 0, which led to

$$\begin{array}{}\text{(B2)}& \langle \mathit{\delta }{V}_{p\mathrm{1}}^{\mathrm{2}}\rangle =D_{\mathrm{NN}}\left(r\right)\cos (\mathit{\theta }{)}^{\mathrm{2}}+D_{\mathrm{LL}}(r\left)\sin \right(\mathit{\theta }{)}^{\mathrm{2}},\end{array}$$

where $D_{\mathrm{LL}}\left(r\right)=\mathrm{2}\left(B_{\mathrm{LL}}\left(\mathrm{0}\right)-B_{\mathrm{LL}}\left(r\right)\right)$. By symmetry, $\langle \mathit{\delta }{V}_{p\mathrm{1}}^{\mathrm{2}}\rangle =\langle \mathit{\delta }{V}_{p\mathrm{3}}^{\mathrm{2}}\rangle$. For the correlation between the two differences, we have

$$\begin{array}{}\text{(B3)}& \begin{array}{rl}& \langle \mathit{\delta }{V}_{p\mathrm{1}}\mathit{\delta }{V}_{p\mathrm{3}}\rangle \\ & =\langle \left(\right(V_{x\mathrm{1}}-V_x\left)\cos \right(\mathit{\theta })-(V_{z\mathrm{1}}-V_z\left)\sin \right(\mathit{\theta }\left)\right)\\ & \left(\right(V_{x\mathrm{3}}-V_x\left)\cos \right(\mathit{\theta })+(V_{z\mathrm{3}}-V_z\left)\sin \right(\mathit{\theta }\left)\right)\rangle \\ & =\cos (\mathit{\theta }{)}^{\mathrm{2}}\langle (V_{x\mathrm{1}}-V_x\left)\right(V_{x\mathrm{3}}-V_x)\rangle \\ & -\sin (\mathit{\theta }{)}^{\mathrm{2}}\langle (V_{z\mathrm{1}}-V_z\left)\right(V_{z\mathrm{3}}-V_z)\rangle \\ & =\cos \left(\mathit{\theta }{)}^{\mathrm{2}}\right(B_{\mathrm{NN}}\left(\mathrm{2}r\right)+D_{\mathrm{NN}}\left(r\right)-B_{\mathrm{NN}}\left(\mathrm{0}\right))\\ & -\sin \left(\mathit{\theta }{)}^{\mathrm{2}}\right(B_{\mathrm{LL}}\left(\mathrm{2}r\right)+D_{\mathrm{LL}}\left(r\right)-B_{\mathrm{LL}}\left(\mathrm{0}\right)).\end{array}\end{array}$$

Here again, passage from the first line to the second line of Eq. (B3) due to the correlation between two wind components of different directions with one of them being equal to the x direction is equal to 0. Using Eqs. (B1) and (B3) in the expression of MSE${}_{T{|}_{\mathrm{turbulence}}}$, we obtain

$$\begin{array}{}\text{(B4)}& \begin{array}{rl}& {\text{MSE}}_{T{|}_{\mathrm{turbulence}}}\\ & ={\displaystyle \frac{\mathrm{2}}{{\left(\mathrm{2}\sin \left(\mathit{\theta }\right)\right)}^{\mathrm{2}}}}\left(\langle \mathit{\delta }{V}_{p\mathrm{1}}^{\mathrm{2}}\rangle +\langle \mathit{\delta }{V}_{p\mathrm{3}}^{\mathrm{2}}\rangle -\mathrm{2}\langle \mathit{\delta }{V}_{p\mathrm{1}}\mathit{\delta }{V}_{p\mathrm{3}}\rangle \right)\\ & ={\displaystyle \frac{D_{\mathrm{NN}}\left(\mathrm{2}r\right)}{{\left(\mathrm{2}\tan \left(\mathit{\theta }\right)\right)}^{\mathrm{2}}}}+{\displaystyle \frac{\mathrm{3}{B}_{\mathrm{LL}}\left(\mathrm{0}\right)+B_{\mathrm{LL}}\left(\mathrm{2}r\right)}{\mathrm{2}}}-\mathrm{2}{B}_{\mathrm{LL}}\left(r\right).\end{array}\end{array}$$