Retrieving the atmospheric concentrations of carbon dioxide and methane from the European Copernicus CO2M satellite mission using artificial neural networks

Carbon dioxide (CO₂) and methane (CH₄) are the most important anthropogenic greenhouse gases and the main drivers of climate change. Monitoring their concentrations from space helps detect and quantify anthropogenic emissions, supporting the mitigation efforts urgently needed to meet the primary objective of the Paris Agreement, adopted at the 21st Conference of the Parties to the United Nations Framework Convention on Climate Change (UNFCCC) in 2015, to limit the global average temperature increase to well below 2 °C above pre-industrial levels. In addition, satellite observations can be used to quantify natural sources and sinks, improving our understanding of the carbon cycle. Advancing these goals is one key motivation for the European Copernicus CO₂ monitoring mission CO2M. The necessary accuracy and precision requirements for the measured quantities XCO₂ and XCH₄ (the column-averaged dry-air mole fractions of CO₂ and CH₄) are demanding. According to the CO2M mission requirements, the spatial and temporal variability of the systematic errors (or spatio-temporal systematic errors) of XCO₂ and XCH₄ must not exceed 0.5 ppm and 5 ppb, respectively. The stochastic errors due to instrument noise must not exceed 0.7 ppm for XCO₂ and 10 ppb for XCH₄. Conventional so-called full-physics algorithms for retrieving XCO₂ and/or XCH₄ from satellite-based measurements of reflected solar radiation are typically computationally intensive and still usually require empirical bias corrections based on supervised machine learning methods. Here we present the retrieval algorithm Neural networks for Remote sensing of Greenhouse gases from CO2M (NRG-CO2M), which derives XCO₂ and XCH₄ from CO2M radiance measurements with minimal computational effort using artificial neural networks (ANNs). In addition, NRG-CO2M also provides estimates of both the noise-driven uncertainties and the averaging kernels of XCO₂ and XCH₄ for each sounding. Since CO2M will not be launched until 2026, our study exploits simulated measurements over land surfaces from a comprehensive observing system simulation experiment (OSSE) that includes realistic meteorology, aerosols, surface bidirectional reflectance distribution function (BRDF), solar-induced chlorophyll fluorescence (SIF), and CO₂ and CH₄ concentrations. We created a novel hybrid learning approach that combines advantages of simulation-based and measurement-based training data to ensure coverage of a wide range of XCO₂ and XCH₄ values, making the training data representative of future concentrations as well. The algorithm's postprocessing is designed to achieve a high data yield of about 80 % of all cloud-free soundings. The spatio-temporal systematic errors of XCO₂ and XCH₄ are 0.44 ppm and 2.45 ppb, respectively. The average single sounding precision is 0.41 ppm for XCO₂ and 2.74 ppb for XCH₄. Therefore, the presented retrieval method has the potential to meet the demanding CO2M mission requirements for XCO₂ and XCH₄. While the presented results are a solid proof of concept, the actual achievable quality can only be determined once NRG-CO2M is trained on real data, where it is confronted, e.g., with unknown instrument effects and systematic errors in the training truth.

1 Introduction

Carbon dioxide (CO₂) and methane (CH₄) are the most important anthropogenic greenhouse gases because they are the main drivers of climate change. Monitoring their concentrations from space is essential to identify and quantify anthropogenic emissions, thereby supporting the mitigation efforts needed to achieve the primary objective of the Paris Agreement of the United Nations Framework Convention on Climate Change (UNFCCC) to limit the global average temperature increase to well below 2 °C above pre-industrial levels (UNFCCC, 2015). In addition, satellite observations can be used to study natural sources and sinks of these gases, contributing to a better understanding of the carbon cycle and thus improving climate predictions.

Advancing these goals is the motivation for the European Copernicus CO₂ monitoring mission CO2M (Meijer et al., 2020; Lespinas et al., 2020; Sierk et al., 2021), which will serve as a central element of the monitoring and verification support (MVS) service capacity currently being developed as an integral part of the Copernicus Atmosphere Monitoring Service (CAMS). The mission involves the deployment of a constellation of three satellites, with the launch of the first CO2M satellite planned for 2026. CO2M builds on the heritage of the CarbonSat concept (Bovensmann et al., 2010; Velazco et al., 2011; Buchwitz et al., 2013; Broquet et al., 2018).

The accuracy and precision requirements for the measured quantities XCO₂ and XCH₄ (the column-averaged dry-air mole fractions of CO₂ and CH₄) are demanding, and achieving them is a major challenge. Specifically, the mission requirement document (MRD; Meijer et al., 2020) states that the systematic errors of XCO₂ and XCH₄ should not exceed a maximum spatial and temporal variability of 0.5 ppm and 5 ppb, respectively. The stochastic errors due to instrument noise should not exceed 0.7 ppm for XCO₂ and 10 ppb for XCH₄ for a reference scenario over vegetation. This is why CO2M is equipped not only with the main CO₂ imager (CO2I) instrument, comprising four imaging spectrometers, but also with the Multi-Angle Polarimeter (MAP), which helps to better account for light scattering on aerosols and the surface bidirectional reflectance distribution function (BRDF), and the Cloud Imager (CLIM), which helps to identify clouds in the field of view.

Conventional so-called full-physics algorithms for retrieving XCO₂ and/or XCH₄ (XGAS) from satellite-based measurements of reflected solar radiation in the near-infrared (NIR) and shortwave-infrared (SWIR) spectral region require accurate radiative transfer (RT) and instrument simulations, which are typically computationally expensive. Examples of such retrieval methods are described in the publications of Reuter et al. (2010, 2011, 2017a, b), Boesch and Di Noia (2023), Noël et al. (2021, 2022), Kiel et al. (2019), Guerlet et al. (2013), and Cogan et al. (2012). Three full-physics algorithms for the analysis of CO2M data are currently also being implemented in the EUMETSAT ground segment. One of these methods is the Fast atmOspheric traCe gAs retrievaL (FOCAL; Noël et al., 2024). The others are RemoTAP (Lu et al., 2022) and FUSIONAL-P, a further development of the algorithm described by Boesch and Di Noia (2023). It is anticipated that continuous analysis of the data stream from a single CO2M satellite using these three methods will require the computing power of several thousand CPU cores, and re-processing the data from two or more CO2M satellites will require several times that amount.

Despite the high computing power required, there are still a number of reasons that can lead to more or less large systematic inaccuracies in the retrieved XGAS quantities. Examples are simplifications of the RT (e.g., neglect of Raman scattering, neglect of polarization, a suboptimal number of streams, reduced accuracy of scattering phase functions, 3D effects), which are necessary to keep the computation time within acceptable limits. In addition, insufficiently characterized geophysical input parameters (e.g., spectroscopic parameters, aerosol and cloud microphysical properties, surface BRDF, all kinds of subpixel inhomogeneities) and insufficiently characterized instrument properties (e.g., inadequate stray light correction, crosstalk or sensor nonlinearity) can lead to biases.

For these reasons, currently existing full-physics retrievals typically exploit more or less complex empirical bias corrections in order to meet the demanding accuracy requirements. This applies to established methods for instruments/satellites, such as the Orbiting Carbon Observatory-2 (OCO-2; Crisp et al., 2004), the Greenhouse Gases Observing Satellite (GOSAT; Kuze et al., 2009), GOSAT-2 (Suto et al., 2021), and the Scanning Imaging Absorption Spectrometer for Atmospheric Chartography (SCIAMACHY; Burrows et al., 1995; Bovensmann et al., 1999) (Reuter et al., 2017b, a; Kiel et al., 2019; Noël et al., 2021, 2022; Boesch and Di Noia, 2023; Guerlet et al., 2013; Cogan et al., 2012; Schneising et al., 2013, 2014), and it is not unlikely that the same will apply to the CO2M XGAS retrieval algorithms currently being implemented by EUMETSAT, once they are confronted with actual measurements.

The variance of the bias correction can be of the same order of magnitude as the retrieval increment, i.e., the difference between a priori knowledge and the result (Reuter et al., 2017a; Kiel et al., 2019), implying that the bias correction contributes a non-negligible fraction of the information of the result.

Most bias correction methods are empirical and usually exploit supervised machine learning techniques. These include simple multidimensional linear regressions (Kiel et al., 2019) or more complex methods based on, e.g., random forest regressors (Noël et al., 2022; Schneising et al., 2019, 2023). For this reason, they also face the issues associated with data-driven methods, such as the need for a representative training data set including ground truth.

Consequently one motivation for this study is to try to avoid the complicated and computationally intensive step of full-physics algorithms and instead analyze the measured spectra from the outset using a data-driven method. Multilayer perceptrons (MLPs) are artificial neural networks (ANNs) that are well suited for this task and, once trained, can analyze large amounts of data with minimal computational effort. An MLP is a nonlinear function whose parameters are adjusted during training to best map the input features (e.g., spectra, meteorological profiles, observation angles) to the output target (e.g., XCO₂, XCH₄). This is called supervised learning, and it requires a representative set of input features for which one or more known output target variables exist. The principle of the method is analogous to that of linear regression, which is one of the simplest forms of supervised learning. A general introduction to MLPs can be found, e.g., in the textbook of Rojas (1996).

As is known from other regressors with many free fit parameters, MLPs tend to be good interpolators but poor extrapolators (Krasnopolsky and Schiller, 2003). This is particularly relevant because CO₂ and CH₄ increase over time, and a training data set consisting of today's measurements is not representative of the future. Furthermore, MLPs can learn from spurious correlations just as efficiently as from actual physical relationships; i.e., they can give significant weight to correlations between input and target that are not directly caused by a physical relationship but by factors such as similar seasonality (e.g., XCO₂ and solar zenith angle). However, generalized learning occurs only in the latter case, and applying the MLP to unknown scenarios leads to accurate data products only in this case. Another potential hurdle is that MLPs can be affected by uncertainties in the training target. Consequently, it is necessary to ensure that the training data set is representative of current and future conditions and that the training target is not too far from the truth.

One possible solution to obtain representative training data is to generate the training data set from simulated measurements. This simulation-based approach is followed with the nonlinear inference scheme (NLIS) algorithm developed by Crevoisier (2023) for the retrieval of midtropospheric CO₂ and CH₄ columns from Infrared Atmospheric Sounding Interferometer (IASI) and Atmospheric InfraRed Sounder (AIRS) measurements in the thermal infrared spectral region. It is also applied by Xie et al. (2024) to retrieve XCO₂ from OCO-2 measurements over east Asia. However, building the training data set from simulations does not only have advantages. For the reasons discussed above, there are usually differences between simulated and measured spectra that cannot be explained by instrument noise. As with full-physics methods, these can affect the quality of the data products and again may require empirical bias correction.

A different approach was taken by David et al. (2021), who trained an MLP to retrieve XCO₂ using actual measured OCO-2 data. This measurement-based learning has the potential advantage of virtually eliminating many of the sources of systematic errors discussed above. However, it turned out that their ANN also appeared to have learned from spurious correlations, as it was unable to detect known local increases. After modifying the ANN and its input, Bréon et al. (2022) were able to show that their ANN was now able to detect local enhancements that were not part of the training data set. However, the authors also state that their ANN is not suitable for analyzing future data due to increasing CO₂ concentrations. In addition, they emphasize that despite the promising results, it is difficult to ensure that their ANN does not learn from a spurious correlation again, especially since the reasons for the previous failure could not be fully determined.

In this paper we present the Neural networks for Remote sensing of Greenhouse gases from CO2M (NRG-CO2M) algorithm, which allows the use of actual measured spectra for training, but they are modified to cover a much larger range of XCO₂ and XCH₄ values. This type of hybrid learning combines the advantages of simulation-based and measurement-based learning. The characteristics of the actual measured spectra, including potential instrument effects, are preserved, almost any meaningful CO₂ and CH₄ concentration can be trained, and the variability of the training truth is dominated by prescribed artificial variations which can suppress learning from spurious correlations.

Nevertheless, our method also requires estimates of the true atmospheric concentrations to provide a representative training data set. These could be obtained in the same way as for empirical bias corrections (e.g., Noël et al., 2022; Schneising et al., 2023; Kiel et al., 2019) or as for the training data sets of other measurement-based ML methods (Bréon et al., 2022). Since CO2M will not be launched until 2026, for the time being our study uses simulated measurements from an extensive observing system simulation experiment (OSSE), which is a refinement of the OSSE described by Noël et al. (2024). As we are dealing with simulations, the true concentrations are known, and, similar to Noël et al. (2024), we assume that there are no systematic errors in the training truth. Obviously, such errors would have the potential to reduce the accuracy of the prediction, but a realistic estimate of the to-be-expected error patterns of the training truth is difficult and beyond the scope of this study. We do, however, allow for stochastic deviations of the training data from the true concentrations.

Section 2 describes the data sets and methods used, including the OSSE; the hybrid learning method; the transformation of the input data using principal component analysis (PCA); the method to modify the spectra; and the setup and training of the MLPs to determine XCO₂, XCH₄, and the corresponding uncertainties. Section 3 presents the results of the study, and Sect. 4 provides a summary and conclusions.

2 Data sets and methods

2.1 Observing system simulation experiment

A comprehensive observing system simulation experiment (OSSE) was performed as part of a EUMETSAT study to develop the FOCAL CO2M retrieval algorithm (Noël et al., 2024). It contains simulated CO2M radiance data for nadir-mode measurements over land, generated with the SCIATRAN RT model (Rozanov et al., 2017), taking into account realistic meteorology, surface BRDF, solar-induced chlorophyll fluorescence (SIF), aerosols, clouds, and vertical profiles of CO₂ and CH₄. The data set includes 2 years (2015 and 2020) of simulated CO2M orbit data with reduced sampling, hereafter referred to as subset data, as well as a high-resolution (HR) scene simulated with the full CO2M sampling. It is an updated and extended version of the data set of simulated CO2I measurements used by Noël et al. (2024) and is therefore only briefly described here. The data set includes 2 years of subset data instead of one, and in addition to the simulated CO2I measurements, it has been extended to also contain simulated measurements from the MAP and CLIM instruments. In addition, the spectral variation in the surface BRDF within the instrument bands is now more realistic and no longer constant.

The exact instrument characteristics of CO2M were not fully defined at the time of our study, so we used the MRD as a guide. The simulated main instrument CO2I consists of four imaging spectrometers for the wavelength ranges 405–490 nm (VIS, NO₂), 747–773 nm (NIR, O₂), 1590–1675 nm (SWIR-1, CO₂, and CH₄), and 1990–2095 nm (SWIR-2, CO₂), having spectral resolutions of 0.6, 0.12, 0.3, and 0.35 nm, respectively. In line with currently available information about CO2I, the instrument line shape functions are assumed to be Gaussian with full width at half maximum, corresponding to the respective spectral resolution.

In this study, we use CO2I data from the entire NIR band (1930 spectral features) and from the same wavelength ranges as used by Noël et al. (2024) in the SWIR-1 band (1590–1670 nm, 931 spectral features) and SWIR-2 band (1990–2090 nm, 953 spectral features). The VIS band is mainly intended for the determination of NO₂ atmospheric columns and was therefore not simulated in this study.

For the hypothetical MAP instrument, we assumed that it has seven broadband channels (MAP1–7) with center wavelengths of 410, 443, 490, 555, 670, 760, and 865 nm, within which it determines the Stokes parameters I, Q, and U for each CO2I ground pixel at 45 equidistantly distributed along-track observation angles. In reality, MAP will have a higher spatial resolution, which will be aggregated to the CO2I measurements, and its MAP6 channel will only measure intensity, but this is not taken into account in this study.

The simulated CLIM instrument has three broadband channels (CLIM1–3), the first two of which spectrally coincide with MAP5 and MAP6. The central wavelength of CLIM3 is at 1370 nm in a strong absorption band of water vapor, which makes this channel suitable for the identification of cirrus clouds. In reality, CLIM will have a much higher spatial resolution than CO2I, but this is also not taken into account in this study, so only CLIM3 provides additional information here.

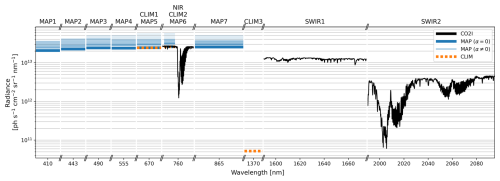
Figure 1 Simulated radiance measurements of a random CO2I sounding, including co-located MAP and CLIM radiance measurements. For MAP, the Stokes parameter I (total intensity) is shown for all simulated along-track observation angles α.

An example of the complete simulated radiance measurements of a CO2I sounding, including co-located MAP and CLIM radiance measurements, is shown in Fig. 1.

2.1.1 Subset data

CO2I will have ground pixels with a spatial resolution of approximately 2 km × 2 km and 110 ground pixels per scan line across track, and each orbit will comprise approximately 9200 daytime scan lines along track. In order to create representative training, test, and evaluation data sets, a minimum of 2 years of simulated CO2M data were desired. However, accurate RT simulations are computationally expensive, so it was not possible to simulate that many soundings in a reasonable amount of time. Consequently, we adopted a strategy of subsetting the data set by simulating only every 15th ground pixel across track and every 20th ground pixel along track. This approach reduced the computational cost by a factor of 300 while largely maintaining the spatial and temporal coverage. For the SCIATRAN RT simulations, we used pressure, temperature, specific humidity, cloud ice content, cloud water content, and cloud fraction from the ECMWF ERA5 reanalysis (Hersbach et al., 2020). Since we focus mainly on cloud-free conditions, we used static cloud microphysical properties for convenience, representing spherical water droplets with a gamma particle size distribution with an effective radius of 12 µm and fractal ice particles with an effective radius of 50 µm (Fig. 3 of Reuter et al., 2010, shows the corresponding volume scattering functions). Aerosol data were derived from CAMS' ECMWF atmospheric composition reanalysis EAC4 (Inness et al., 2019). CO₂ profiles were derived from the CAMS global CO₂ atmospheric inversion v20r2 (Chevallier et al., 2005, 2010; Chevallier, 2013), and CH₄ profiles were obtained from the CAMS global CH₄ atmospheric inversion v20r1 (Segers, 2022). Surface reflectivity was modeled using the Moderate Resolution Imaging Spectroradiometer (MODIS) BRDF and albedo model parameter data set MCD43C1 version 6.1 (Schaaf and Wang, 2021). SIF was modeled using the MODIS Normalized Difference Vegetation Index (NDVI) MYD13C version 6.12 (Didan, 2021) as a proxy, following the approach outlined by RAL (2022). The resulting data set includes approximately 2.13 million cloud-free soundings over land in 2015 and 2.15 million in 2020. In addition, the data set also includes cloudy scenes that are sampled less densely depending on the cloud optical depth (COD), in order to emulate an imperfect cloud-masking algorithm. Specifically, cloudy scenes are computed with a probability of $P_{\mathrm{COD}}=\mathrm{1}-\mathrm{COD}$ but at least 0.05. This means that optically thin clouds are likely to make it into the data set, while the probability of an optically thick cloud is only 5 %. This results in nearly half a million cloud-contaminated land scenes per year.

2.1.2 Berlin high-resolution scene

In addition to the subset data, we simulated a scene with the full CO2M sampling. It is a 3 min orbit granule with geophysical conditions of 3 July 2015, and since it includes Berlin (Germany), it is referred to as the Berlin HR scene. This scene is also used in EUMETSAT's CO2M preparation activities, and HR model data are available for it. Our SCIATRAN input for this scene is the same as for the subset data, except for pressure, temperature, specific humidity, CO₂, and CH₄, which have been provided by EUMETSAT and which are based on the CAMS “nature run” model data with a spatial resolution of about 9 km (Agustí-Panareda et al., 2022). In particular, this means that the scene includes HR CO₂ and CH₄ signals, such as XCO₂ plumes from power plants in eastern Germany, which are not resolved in the subset data. For the Berlin HR scene we simulated 43 671 soundings over land, of which 42 398 are cloud-free.

2.2 Noise

For key parts of our study (e.g., PCA and ANN training), we need data scattering within realistic uncertainties, i.e., with noise distributions reflecting the expected statistical variability. In the case of the radiometric CO2M measurements, we used the same noise models as Noël et al. (2024) and Meijer et al. (2020). Based on the study by Salstein et al. (2008), we assume that the uncertainty in the dry-air column is 2.5 ‰. We further assume that the atmospheric temperature is uncertain by 1 K, achieved by a shift in the entire profile. The atmospheric humidity is assumed to be uncertain by 10 %, achieved by profile scaling. For all observation angles, we define the uncertainty as 0.1°. The target quantities XCO₂ and XCH₄ used as training truths are assumed to have uncertainties of 1 ppm and 5 ppb, respectively, which are somewhat larger than the differences between models and ground-based measurements found by Knapp et al. (2021) and Kulawik et al. (2016) and somewhat smaller than those found by Tu et al. (2020). The uncertainty in the CO₂ and CH₄ a priori profiles is accounted for by multivariate noise computed with the same a priori error covariance matrices used by Noël et al. (2024), scaled so that the a priori XCO₂ and XCH₄ scatter around the truth with a standard deviation of 4 ppm and 20 ppb, respectively. All uncertainty specifications in this section represent 1σ values of normally distributed random variables. It should be noted that the input data for the RT simulations of the OSSE are free of noise. The main use of noise in our analyses is to generate realistically noisy training data (Sect. 2.5.2).

2.3 Modification of spectra

As discussed in Sect. 1, learning from simulated spectra can lead to biases for the same reasons as for conventional full-physics retrieval methods, namely because of inaccuracies in the RT and/or instrument simulation. This is why we prefer to learn from measured spectra. However, this approach also has some potential disadvantages: XCO₂ and XCH₄ increase over time so that today's concentrations are not representative of the future, XCO₂ and XCH₄ may have correlations to quantities such as albedo or observation geometry from which an ANN can learn as efficiently as from spectral features, and uncertainties in the training truth may exist. For these reasons, we use a method to modify measured spectra as if they include more or less of the target gases. Since CO2M was not yet operational at the time of our study, these measured spectra are simulations, i.e., the measurements of our OSSE simulated with SCIATRAN (Sect. 2.1).

An obvious way to modify a spectrum would be to use a synthetic Jacobian to simulate linear changes with respect to the geophysical state. However, due to nonlinearities of the RT, a more accurate alternative is to use the ratio of two synthetic spectra, i.e., a reference spectrum and a perturbed spectrum, for the modification. Since both the Jacobian and the ratio of the synthetic spectra depend on the geophysical state, it is necessary to first estimate it from the measurement.

In the following, we describe how we estimate the state from the measurement and generate the synthetic reference spectrum; how we perturb the state to make it representative of a wider range of conditions; how we generate the modified synthetic spectrum from it; and, finally, how we compute the modified measurement using the ratio of the synthetic spectra.

Let I_m(x) be the measured CO2I intensity, i.e., a SCIATRAN-simulated measurement of our OSSE (Sect. 2.1). It is a function of the true state x including the true atmospheric concentration profiles of CO₂ and CH₄. In reality, when working with real measurements instead of simulations, the true state is of course not known. We fit this measurement using the FOCAL retrieval as described by Noël et al. (2024) but with some adaptations, guaranteeing that the vast majority of soundings converge. Specifically, we enlarge the measurement error covariance by assuming an unrealistically large forward model uncertainty of 1 % of the continuum radiance in all four fit windows and by allowing up to 40 iterations. The fitted radiance, i.e., the synthetic reference spectrum, is $I_{\mathrm{f}}\left(\widehat{x}\right)$, where $\widehat{x}$ is the retrieved state containing the retrieved concentration profiles $\widehat{{\mathrm{CO}}_{\mathrm{2}}}$ and $\widehat{{\mathrm{CH}}_{\mathrm{4}}}$. These profiles consist of five layers, each representing the same number of dry-air particles.

It is important to note that FOCAL's RT is much simpler than the RT of SCIATRAN used to simulate the measurements so that a perfect spectral fit is usually not possible, which is likewise the case when applying FOCAL to actually measured satellite data (Noël et al., 2021, 2022; Reuter et al., 2017a). As a result, the retrieved concentrations can significantly vary from the true atmospheric state, especially in scenes with enhanced scattering due to aerosols or clouds. This is more likely to be the case than in the earlier studies by Noël et al. (2021, 2022, 2024) and Reuter et al. (2017a) because we here forced FOCAL to almost always converge, and we applied no filtering or bias correction. However, this is not an issue for our study, since we are mainly interested in relative spectral changes, and we show that it is even sufficient to use a simple non-scattering RT model that considers only gaseous absorption.

In the next step, we compute the perturbed concentration profiles $\stackrel{\mathrm{̃}}{{\mathrm{CO}}_{\mathrm{2}}}$ and $\stackrel{\mathrm{̃}}{{\mathrm{CH}}_{\mathrm{4}}}$ by adding delta profiles, which we calculate as explained as follows using the example of CO₂.

• We randomly select two five-layer CO₂ profiles of the year 2015 from the Simple cLImatological Model (SLIM) for atmospheric CO₂ or CH₄ (Noël et al., 2022) and compute the difference concentration profile ΔCO₂.

• We randomly increase or decrease ΔCO₂ in the lowermost layer according to a normal distribution with a standard deviation of 10 ppm, emulating the signal of a local source or sink.

• We compute the profile anomaly; i.e., we subtract the column average of ΔCO₂ from ΔCO₂.

• We randomly shift the entire ΔCO₂ profile according to a uniform distribution between −40 and +40 ppm.

In this way, the shape of the delta profile ΔCO₂ has large but not unrealistic variations with height, and the variation in its column average ΔXCO₂ is large enough to be representative of atmospheric growth of many years.

ΔCH₄ and ΔXCH₄ are calculated using the same method but with all variations multiplied by a factor of $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$. This means that the standard deviation of the random CH₄ perturbation in the lowermost layer becomes 50 ppb instead of 10 ppm, and the range of the uniform distribution for the random shift in the profile in the last step becomes [−200 ppb, +200 ppb] instead of [−40 ppm, +40 ppm]. Note that the perturbations of CH₄ are independent of those of CO₂.

As discussed above, the FOCAL-retrieved dry-air column averages $\widehat{{\mathrm{XCO}}_{\mathrm{2}}}$ and $\widehat{{\mathrm{XCH}}_{\mathrm{4}}}$ of our study may be significantly biased, and we here consider them to be representative of only the apparent light path. However, the corresponding climatological values ${{\mathrm{XCO}}_{\mathrm{2}}}_{\mathrm{SLIM}}$ and ${{\mathrm{XCH}}_{\mathrm{4}}}_{\mathrm{SLIM}}$ are relatively close to reality (Noël et al., 2022). Therefore, we scale the delta profiles ΔCO₂ and ΔCH₄ by a factor of $\widehat{{\mathrm{XCO}}_{\mathrm{2}}}/{{\mathrm{XCO}}_{\mathrm{2}}}_{\mathrm{SLIM}}$ and $\widehat{{\mathrm{XCH}}_{\mathrm{4}}}/{{\mathrm{XCH}}_{\mathrm{4}}}_{\mathrm{SLIM}}$, respectively, before performing the FOCAL forward run. This primarily affects scenarios with large deviations between retrieved and true concentrations.

$$\begin{array}{}\text{(1)}& {\displaystyle }\stackrel{\mathrm{̃}}{{\mathrm{CO}}_{\mathrm{2}}}=\widehat{{\mathrm{CO}}_{\mathrm{2}}}+\mathrm{\Delta }{\mathrm{CO}}_{\mathrm{2}}{\displaystyle \frac{\widehat{{\mathrm{XCO}}_{\mathrm{2}}}}{{{\mathrm{XCO}}_{\mathrm{2}}}_{\mathrm{SLIM}}}}\text{(2)}& {\displaystyle }\stackrel{\mathrm{̃}}{{\mathrm{CH}}_{\mathrm{4}}}=\widehat{{\mathrm{CH}}_{\mathrm{4}}}+\mathrm{\Delta }{\mathrm{CH}}_{\mathrm{4}}{\displaystyle \frac{\widehat{{\mathrm{XCH}}_{\mathrm{4}}}}{{{\mathrm{XCH}}_{\mathrm{4}}}_{\mathrm{SLIM}}}}\end{array}$$

These modified concentration profiles are part of the perturbed state $\stackrel{\mathrm{̃}}{x}$, which we use to perform an additional FOCAL forward run, i.e., RT and instrument simulation, in order to compute the modified synthetic spectrum $I_{\mathrm{f}}\left(\stackrel{\mathrm{̃}}{x}\right)$. This is then used to approximate what the measured radiance would look like if ΔCO₂ and ΔCH₄ were added to the true CO₂ and CH₄ profiles.

$$\begin{array}{}\text{(3)}& I_{\mathrm{m}}(x+\mathrm{\Delta }x)\approx I_{\mathrm{m}}\left(x\right){\displaystyle \frac{I_{\mathrm{f}}\left(\stackrel{\mathrm{̃}}{x}\right)}{I_{\mathrm{f}}\left(\widehat{x}\right)}}\end{array}$$

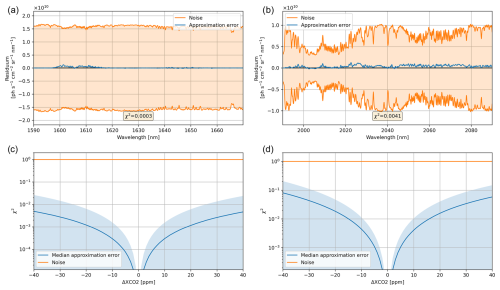
Figure 2 Spectrum of the approximation error (approximation minus SCIATRAN simulation) and instrumental noise for a typical scene and a 10 ppm shift in the CO₂ profile in the SWIR-1 (a) and SWIR-2 (b). Median (blue line) ±1σ (light blue area) of the approximation error χ² statistics for all cloud-free soundings of one orbit of subset data from 3 July 2015 as a function of the profile shift for the SWIR-1 (c) and SWIR-2 (d).

The quality of this approximation can be determined by comparing radiances approximated by Eq. (3) with corresponding SCIATRAN simulations. For this purpose, we selected one orbit of subset data of 3 July 2015, including many cloud-free scenes above Europe and Africa, and shifted the entire CO₂ profile from −40 to +40 ppm in steps of 1 ppm. Figure 2 shows an example spectrum of the approximation error in the SWIR-1 (Fig. 2a) and SWIR-2 (Fig. 2b) bands for a 10 ppm shift in the CO₂ profile. The figure shows that the approximation error, i.e., the difference between the approximation and the SCIATRAN simulation, is much smaller than the instrumental noise. As can be seen in Fig. 2c and d, the approximation error disappears for small profile shifts and steadily increases towards larger profile shifts. It is usually 1 order of magnitude larger in the SWIR-2 than in the SWIR-1. However, it is always significantly smaller than the instrumental noise. As an example, for a 10 ppm shift, the median χ² amounts to 0.0003 in the SWIR-1 and 0.0041 in the SWIR-2. This means the approximation is valid within a range much larger than the current annual growth rate, thus allowing us to generate a training data set from modified measured spectra that is also representative of atmospheric conditions several years in the future.

2.4 Principal component analysis

Atmospheric spectra, such as those measured by CO2I, contain a large amount of redundant information. In such cases, PCA is an efficient tool for dimensionality reduction without losing important information (e.g., Liu et al., 2006). It can significantly reduce the size of the training data set and improve the learning efficiency of ANNs.

We used every seventh sounding of all even weeks in the 2015 subset data set and performed a PCA on different input data sets: the NIR band, the combination of both SWIR bands, the combination of all three bands, the MAP data, and the meteorological profiles of temperature and humidity.

The choice of the number of principal components used is not trivial and is somewhat subjective. Using a large number of components ensures that no information is lost, but the dimensionality reduction is small. If only a few components are used, the dimensionality reduction is high, but important information may be lost. We found that 25 components are sufficient for the NIR band, 90 for the combined SWIR bands, 100 for the combination of all three bands, 100 for the MAP data, and 5 for the temperature and humidity profiles.

We based our choice of the number of components on calculations of the unexplained variance, the χ² of the reconstruction error, and the number of components that lead to a minimization of the denoising error. The unexplained variance is equal to 1 minus the explained variance, which is commonly used in the context of PCA (e.g., Jolliffe and Cadima, 2016). The χ² of the reconstruction error is calculated from the residual of the reconstructed and original measurements relative to the noise estimate of the measurements. The denoising error analyzes the residual between the reconstructed noisy data and the noise-free original data. It depends on the number of components used and reaches a minimum when the use of additional components would predominantly lead to fitting noise but not signal (Aires et al., 2002; Di Noia et al., 2015). The χ² of the reconstruction error and the denoising error were only determined for the radiation measurements where the noise estimates are known and reliable.

Table 1 PCA results for various input data sets: NIR band, combination of both SWIR bands, combination of all three bands, MAP data, and meteorological profiles of temperature and humidity. Input data sets used for the baseline configuration of the ANNs (see later sections) are highlighted in bold. The table lists the number of components used, the corresponding unexplained variance and the χ² of the reconstruction error, and the number of components for which the denoising error is minimal. Note: NA – not available.

As an example, for the combination of the NIR and both SWIR bands, we find that when using 100 components, the fraction of unexplained variance amounts to 4.2 × 10⁻⁹. The χ² of the reconstruction error is 1.1 × 10⁻³, which means that the instrumental noise can be expected to be about 1000 times larger than the reconstruction error. The denoising error becomes minimal when using 75 components. Selecting a significantly larger number of components can result in fitting noise, while selecting a significantly smaller number can result in loss of information. The results of all PCA studies are summarized in Table 1.

2.5 Artificial neural networks

2.5.1 Setup

In our study, we examined four different input compositions. The baseline setup is the standard setup used in this study. All other setups differ only in their details in order to study their influence on the ANN's prediction quality separately. The baseline setup exists in a variant for XCO₂ and a variant for XCH₄. For simplicity, all other input setups exist only for XCO₂.

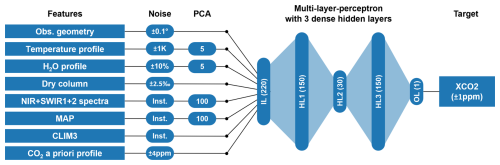
Figure 3 Baseline ANN training setup on the example of XCO₂, including the amount of noise added to the training features and to the target variable (Sect. 2.2) and the PCA components used (Sect. 2.4). When training with actual measured data in the future, the addition of noise will be omitted. Inst – noise of the instrument model, IL – input layer, HL – hidden layer, OL – output layer.

The baseline input consists of the scores of the 100 most significant principal components (PCs) of the combined NIR, SWIR-1, and SWIR-2 spectra; the scores of the 100 most significant PCs of the MAP data; the CLIM3 radiance; the scores of the five most significant PCs of the meteorological temperature and humidity profiles; the number of dry-air particles in the atmospheric column; the solar zenith angle; the satellite zenith angle; and the azimuth difference. As for conventional retrievals based on optimal estimation, the input also contains a noisy/uncertain a priori CO₂ or CH₄ profile (Sect. 2.2), which in our case consists of five atmospheric layers, each containing the same number of dry-air particles. Figure 3 illustrates the baseline ANN training setup on the example of XCO₂.

The no-MAP input differs from the baseline input only in that it does not contain MAP and CLIM data. In addition to the missing MAP data, the no-NIR input also lacks data from the NIR band. The non-scat. setup is the same as the baseline setup, except that the modified spectra used for the training data set were generated by a FOCAL variant that only considers absorption but not scattering in the atmosphere.

All results were generated using MLP regressors with three hidden layers of 150, 30, and 150 neurons. The idea behind this ANN architecture is to improve the generalization capabilities of the network by adding a so-called information bottleneck in the middle layer, which holds the information of intermediate meta-parameters. Conceptually, there are parallels to first performing a conventional retrieval and then using the set of output parameters as input to a bias correction. We used the logistic, i.e., sigmoid, activation function and trained the MLPs with the Adam stochastic optimization method (Kingma and Ba, 2014) of the scikit-learn Python library (Pedregosa et al., 2011).

2.5.2 Training and test data set

To construct a representative and realistic training data set, we use noisy input and target data (see Sect. 2.2), which we construct from the data of all even weeks of the 2015 subset data set (Sect. 2.1.1). The data of the odd weeks are mainly reserved for testing. Separating the data sets on a weekly basis ensures that seasonal variations are sampled finely enough while avoiding strong correlations between the two data sets that could occur with random sampling. It is important that the training data set contains noise, as all input and target features will of course be subject to inherent uncertainties during later training with real CO2M data. In addition, the noise supports generalized learning and suppresses overfitting. The subset data contain a small fraction of cloudy scenes (Sect. 2.1.1), which we also expect to be the case in real data due to imperfect cloud masking. In order to create a realistic data set and to make the prediction less sensitive to residual cloud contamination, we filter out only clouds with an optical thickness greater than 0.05. From each remaining sounding, we generate 10 soundings whose SWIR spectra have been modified as described in Sect. 2.3. Only these modified soundings, which have artificially increased XGAS variabilities, are the basis of our training data set.

2.5.3 Prediction of uncertainties

Interpretation of XCO₂ or XCH₄ satellite data requires appropriate uncertainty estimates. There are a number of ways to estimate the uncertainty in an ANN's prediction from the uncertainty in its input. The simplest approach is to present an existing ANN with multiple realizations of the input, modified according to its error characteristics, and then statistically analyze the predictions. However, there are more sophisticated methods, such as the use of probabilistic ANNs (Mohebali et al., 2020). Here, we use a simple but efficient method by training MLPs to predict the XGAS uncertainties σXCO₂ and σXCH₄ from the same inputs used to predict XCO₂ and XCH₄, except that no a priori information is used. More specifically, we apply the XGAS MLPs to the test data set (Sect. 2.5.2) and compute the squared prediction mismatches (prediction minus training truth) ΔXGAS² and use them as training targets for additional MLPs that predict the XGAS variances σXGAS², as suggested by Bishop (1996). The rationale behind this is that the expected value of ΔXGAS is small, enabling the variance VAR(XGAS) to be approximated by the expected value of ΔXGAS². We use data from the test period instead of the training period because the prediction mismatches ΔXGAS can be considered more realistic.

2.5.4 Column averaging kernel

In addition to reliable uncertainty estimates, the interpretation of XCO₂ or XCH₄ satellite data also requires information about the column averaging kernel (AK). The AK quantifies the retrieval's sensitivity to changes in the target gas concentration profile and is defined by

$$\begin{array}{}\text{(4)}& {\mathrm{AK}}_i={\displaystyle \frac{\mathrm{1}}{w_i}}{\displaystyle \frac{\partial \widehat{\mathrm{XGAS}}}{\partial {\mathrm{GAS}}_i^{\mathrm{t}}}},\end{array}$$

where $\widehat{\mathrm{XGAS}}$ is the retrieved XGAS, ${\mathrm{GAS}}_i^{\mathrm{t}}$ the true gas concentration in the height layer i, and w_i the relative dry-air weight of that layer; i.e., the number of dry-air particles in sub-column i divided by the total number of dry-air particles in the atmospheric column. In the context of retrieval comparison studies or surface flux inversions (e.g., Reuter et al., 2011; Bergamaschi et al., 2007; Wunch et al., 2011), 1−AK can be interpreted as the influence of or the dependence on the a priori used. While we do not have direct access to the column averaging kernel, the influence of the a priori $\partial \widehat{\mathrm{XGAS}}/\partial {\mathrm{GAS}}_i^{\mathrm{a}}$ can be easily determined numerically by predicting XGAS for perturbed a priori profiles GAS^a and approximating

$$\begin{array}{}\text{(5)}& {\mathrm{AK}}_i\approx \mathrm{1}-{\displaystyle \frac{\mathrm{1}}{w_i}}{\displaystyle \frac{\partial \widehat{\mathrm{XGAS}}}{\partial {\mathrm{GAS}}_i^{\mathrm{a}}}}.\end{array}$$

2.5.5 Postprocessing

As with conventional greenhouse gas retrieval algorithms, we filter out the least promising scenes during postprocessing. To do this, we analyzed the 2015 evaluation data set (Sect. 2.5.6) and computed a threshold for the maximum allowed predicted uncertainty (Sect. 2.5.3) that filters out 10 % of the cloud-free 2015 evaluation data. From the remaining data, we computed a threshold for the maximum allowed dependence on the a priori, which filters out another 11.11 %. In this way, the most promising 80 % of all cloud-free soundings remain after both filters. The thresholds are setup-specific and are listed in Table 2.

Table 2 Algorithm setup, postprocessing parameters, and main results generated from the evaluation subset data sets of 2015 and 2020 and from the Berlin HR scene for the baseline (bold), no-MAP, no-NIR, and non-scat. configuration.

Additionally, we used the 2015 evaluation data set to compute a setup-specific overall offset (Table 2), which we subtract from the prediction during postprocessing.

For each sounding, the a priori dependence is computed from the profile average sensitivity of the prediction to the a priori (Sect. 2.5.4). For example, if the dependence on the a priori was 5 %, then adding 1 ppm to the CO₂ a priori would increase the XCO₂ prediction by 0.05 ppm.

Similar to the dependence on the a priori, we compute the relative dependence of the prediction on the dry column. This quantity specifies how dry-column errors propagate to XGAS prediction errors. For example, if the dependence on the dry column was 5 %, then a 1 % error in the dry column would result in a 0.05 % error in the predicted XGAS. This quantity is not used directly during postprocessing but is analyzed when interpreting the results.

2.5.6 Evaluation data sets

We quantified the ANNs' prediction quality by applying them to three evaluation data sets that were not used for training: (i) the unmodified 2015 subset data set (Sect. 2.1.1), which we divided into a training and test period because it served as the basis for computing the training and test data sets (Sect. 2.3); (ii) the unmodified 2020 subset data set (Sect. 2.1.1) with geophysical conditions and greenhouse gas concentrations not seen during the training; and (iii) the Berlin HR scene (Sect. 2.1.2), also with geophysical conditions and greenhouse gas plumes that were not part of the training data set.

3 Results

For the input setups described in Sect. 2.5.1, MLPs with the properties described in the same section were trained to predict XCO₂ and the associated uncertainty. In the case of the baseline setup, MLPs were also trained to predict XCH₄ and its uncertainty. In order to analyze the prediction quality, the MLPs were applied to the evaluation data described in Sect. 2.5.6, and the prediction was compared with the truth.

Since the CO2M mission requirements are defined for cloud-free conditions, we filtered the evaluation data accordingly. Additionally, we applied the postprocessing filters described in Sect. 2.5.5. Most of the analyses were performed with noise-free input data, so the prediction errors can be considered purely systematic.

The results for the 2020 subset evaluation data and the Berlin HR scene are the most conclusive because their input is the most independent of the training data set. In the following, we focus on the results for these data sets obtained with the baseline setup. However, Table 2 summarizes the main results for the analysis of all evaluation data sets and input configurations.

3.1 Column averaging kernels

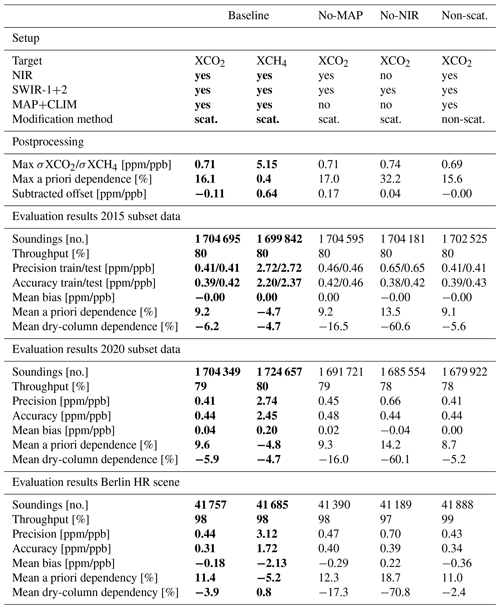
We analyzed the XCO₂ and XCH₄ AKs of the 2020 subset evaluation data set. Figure 4a shows that the XCO₂ AKs are close to optimal, i.e., close to unity, in large parts of the atmosphere. Significantly lower values are observed only in the stratosphere. The XCH₄ AKs also decrease in the stratosphere but show a slight overestimation of departures from the a priori in other layers (Fig. 4b).

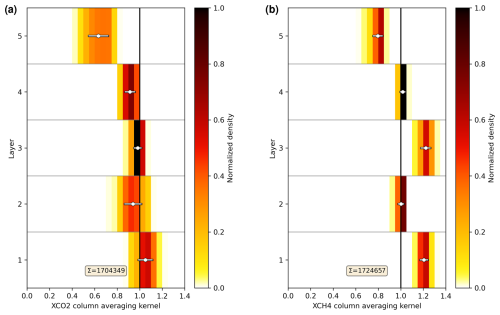
Figure 4 Normalized density distribution of the XCO₂ (a) and XCH₄ (b) column averaging kernels of all postprocessed soundings of the 2020 subset evaluation data set. Mean values and standard deviations are overlaid. The profiling splits the atmospheric column into five layers, each containing the same number of dry-air particles. Layer 1 is the closest to the surface and includes the boundary layer, and the stratosphere extends into layer 5. Σ represents the total number of soundings.

3.2 Stochastic errors

In order to determine the overall retrieval precision due to instrumental noise, we predicted XCO₂ and XCH₄ from input with and without instrumental noise and calculated the standard deviation of the difference. For the postprocessed 2020 evaluation data set and the baseline setup, it amounts to 0.41 ppm for XCO₂ and 2.74 ppb for XCH₄.

As can be seen in Table 2, these values are basically identical to those obtained for the training and test periods of the 2015 evaluation data set and similar to those obtained for the Berlin HR scene.

The stochastic XCO₂ error does not change for the non-scat. setup (Sect. 2.5.1) but increases slightly to 0.45 ppm when the MAP instrument is not used. We see a more significant increase to 0.66 ppm when also not using the NIR band.

In addition to the analysis of the overall precision, we validated the MLPs predicting the retrieval uncertainty in the individual soundings (Sect. 2.5.3). For this purpose, we defined 15 bins, each containing the same number of soundings, for the predicted XCO₂ or XCH₄ uncertainty. For each bin, we determined the average predicted uncertainty, which we compared to the actual precision in that bin.

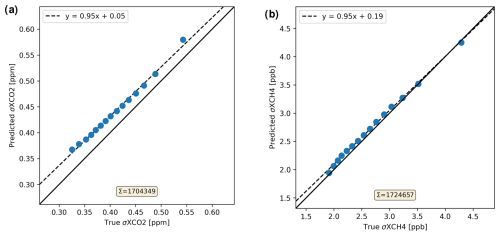
Figure 5 Comparison of the predicted and true XCO₂ (a) and XCH₄ (b) retrieval uncertainties due to instrumental noise for the postprocessed 2020 subset data. Σ represents the total number of soundings. The figure also contains the results of a linear regression.

Figure 5 shows that the XCO₂ and XCH₄ uncertainties are well predicted by the MLPs. The predicted XCH₄ uncertainties are almost accurate. The predicted XCO₂ uncertainties behave similarly but with a small offset of about 0.03 ppm.

3.3 Systematic errors

3.3.1 Overall statistics

We compute systematic errors by comparing postprocessed predicted XCO₂ and XCH₄ values with corresponding true values for noise-free input data. Figure 6 shows such a comparison for the 2020 subset data and the baseline setup.

Figure 6 Comparison of postprocessed predicted XCO₂ (a) and XCH₄ (b) with corresponding true values for noise-free 2020 subset input data. Δ represents the average prediction error (prediction minus true), σ the standard deviation of the prediction error, and Σ the total number of soundings. The figure also contains the results of a linear regression.

With 0.04 ppm for XCO₂ and 0.20 ppb for XCH₄, the mean bias (prediction minus truth) for the 2020 subset data is negligible. It is not surprising that this is also the case for the 2015 subset data, as this data set has been used to derive the postprocessing offset correction (Sect. 2.5.5). The mean bias for the Berlin HR scene is −0.18 ppm for XCO₂ and −2.13 ppb for XCH₄ (baseline setup).

Surface flux inverse modeling and emission estimation results are much more sensitive to spatially and/or temporally varying biases than to constant offsets. Therefore, we consider the standard deviation of the difference between the predicted and true values of XGAS as a measure of accuracy. For the 2020 subset data and the baseline setup it amounts to 0.44 ppm and 2.45 ppb for XCO₂ and XCH₄, respectively.

The accuracy values determined from the 2015 subset data are slightly smaller. The modification of the spectra used for the training can introduce small spectral errors (Sect. 2.3). These can erode the prediction quality the further we depart from the concentrations of the training year 2015. Additionally, we observe that the prediction accuracy is about 10 % better for the training period than for the test period.

For the Berlin HR scene and the baseline setup, we obtain an accuracy of 0.28 ppm and 1.49 ppb for XCO₂ and XCH₄, respectively.

As can be seen in Table 2, the XCO₂ accuracy depends only slightly on the setup, particularly for the subset evaluation data. At first glance, this appears to be surprising because it would imply that the NIR band and the MAP instrument have only little influence on the systematic errors, which is not necessarily the case. Our analyses of systematic errors do not consider systematic errors in the input, such as the dry column or the a priori, which will exist in reality. When removing MAP from the input, the average dependence of the XCO₂ prediction on the dry column increases from −5.9 % to −16.0 %. Additionally, removing the NIR band further increases the dry-column dependence to −60.1 % and also increases the mean a priori dependence from 9.6 % to 14.2 %. For comparison, the dry-column dependence of the FOCAL CO2M XCO₂ retrieval is 100 % by design (Noël et al., 2024), and the dry-column dependence of the operational OCO-2 XCO₂ retrieval (v11.1) is approximately 85 % (Jacobs et al., 2024).

3.3.2 Large-scale features

In order to investigate the spatial structures of the systematic errors, we generated global maps for XCO₂ (Fig. 7) and XCH₄ (Fig. 8), showing the postprocessed predicted and corresponding true values, as well as their difference for the noise-free subset input data of April and August 2020. First, the maps show a dense sampling because the postprocessing filters are designed to have a high throughput of about 80 % for all cloud-free soundings (Sect. 2.5.5).

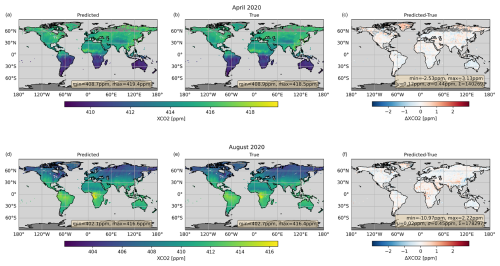
Figure 7 Global maps of postprocessed predicted XCO₂ (a, d) and the corresponding true values (b, e), as well as their difference (c, f) for noise-free subset input data of April (a–c) and August (d–f) 2020. μ represents the average prediction error (prediction minus true), σ the standard deviation of the prediction error, and Σ the total number of soundings.

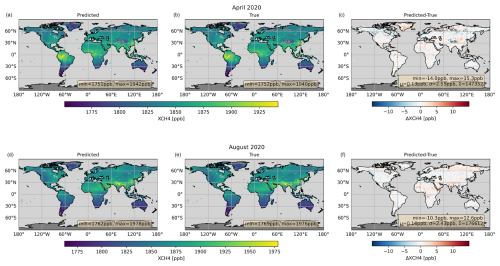
Figure 8 Global maps of postprocessed predicted XCH₄ (a, d) and the corresponding true values (b, e), as well as their difference (c, f) for noise-free subset input data of April (a–c) and August (d–f) 2020. μ represents the average prediction error (prediction minus true), σ the standard deviation of the prediction error, and Σ the total number of soundings.

The maps of the predicted and true XGAS show expected large-scale features, like low XCO₂ values in northern middle and high latitudes in August at the end of the growing season or relatively high XCH₄ values in the tropics. The differences between predicted and true XGAS values are generally much smaller than those of the large-scale features. However, the differences are not purely random and exhibit some country- to continental-scale systematic features, such as the small XCO₂ and XCH₄ high bias in Greenland in April or the small XCH₄ high bias in northern Africa in August.

There are some similarities between the XCO₂ and XCH₄ bias patterns, which may indicate that some systematic errors could cancel out in a proxy product when using, e.g., the ratio XCH₄ $/$ XCO₂ as a training target.

The global monthly average biases are small, and the corresponding standard deviations are similar to the annual averages.

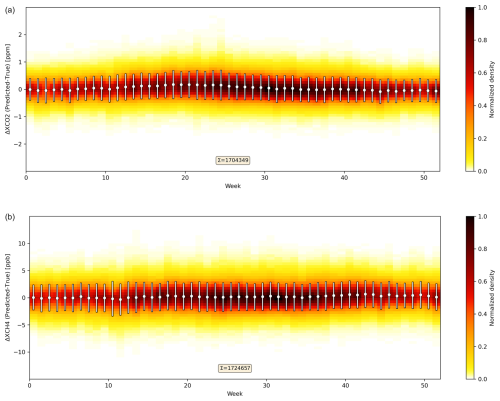
3.3.3 Seasonal cycle

Systematic errors may also have a seasonal component, e.g., due to seasonal variations in illumination conditions, albedo, or aerosols. Figure 9 shows the XGAS prediction error as a function of the week in the year 2020. According to this figure, the average systematic XCO₂ prediction error slowly drifts around zero, with the largest values of about 0.2 ppm in late (northern hemispheric) spring and the smallest values of about −0.1 ppm in autumn. The standard deviation of the XCO₂ error is larger in spring and summer (up to about 0.55 ppm) compared to autumn and winter (down to about 0.40 ppm). Various reasons can cause this behavior; e.g., sampling in summer covers a wider latitude range and, therefore, also more surface types and observation angles than in winter, and the CO₂ profiles vary more during the (northern hemispheric) growing season. The weekly average prediction error in XCH₄ has no clear seasonal cycle and is always smaller than ±1 ppb. Its standard deviation varies between about 2.2 and 3.3 ppb.

Figure 9 XCO₂ (a) and XCH₄ (b) prediction error as a function of the week for noise-free 2020 subset input data. The dots and bars represent the mean and standard deviation, respectively. Σ represents the total number of soundings.

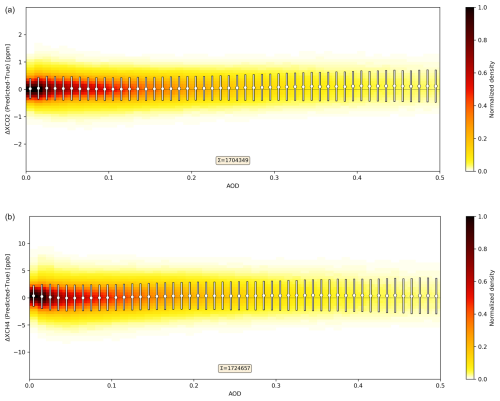
3.3.4 Aerosols

Aerosols modify the light path and can for this reason be an important source of XGAS retrieval errors. Figure 10 shows the XGAS prediction error as a function of aerosol optical depth (AOD) for noise-free 2020 subset data. As can be seen, the XCO₂ average prediction error stays close to zero up to an AOD of 0.2. For larger AODs up to 0.5, the average prediction error steadily increases to values of about 0.1 ppm. The standard deviation of the prediction error increases with AOD from about 0.35 to about 0.60 ppm. The average XCH₄ prediction error is usually below ±0.5 ppb, and its standard deviation increases from about 2.0 ppb for basically aerosol-free scenarios to about 3.2 ppb for scenarios with an AOD of up to 0.5.

Figure 10 XCO₂ (a) and XCH₄ (b) prediction error as a function of AOD for noise-free 2020 subset input data. The dots and bars represent the mean and standard deviation, respectively. Σ represents the total number of soundings.

3.3.5 Berlin HR scene

Since the AKs are close to unity in large parts of the atmosphere (Fig. 4), the prediction can be considered to be dominated by the measurement but not the a priori. In order to illustrate this, we used scene-wide constant a priori profiles instead of the true concentration profiles to analyze the Berlin HR scene. Specifically, we used the scene-wide average true CO₂ and CH₄ concentration profiles as a priori.

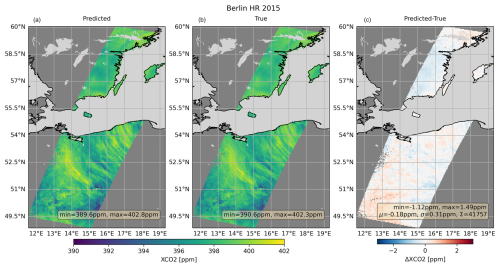
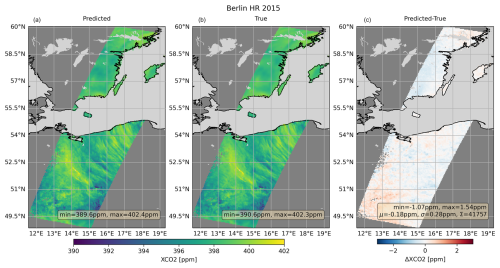
Figure 11 Postprocessed predicted XCO₂ (a) and the corresponding true values (b), as well as their difference (c) for noise-free Berlin HR input data. μ represents the average prediction error (prediction minus true), σ the standard deviation of the prediction error, and Σ the total number of soundings.

Figure 12 As Fig. 11 but for XCH₄.

Figures 11 and 12 show that the predictions reproduce the true concentrations well, even though the meteorological conditions and gas concentrations, including plumes from strong CO₂ and CH₄ sources, were not part of the training data or the a priori.

The variability of the difference structures is much smaller than the variability of the atmospheric signals. The XCO₂ prediction error has a standard deviation of 0.31 ppm and an average of −0.18 ppm. It shows no obvious correlations with the XCO₂ pattern, especially the CO₂ plumes from the coal-fired power plants Jänschwalde, Schwarze Pumpe, and Boxberg in eastern Germany.

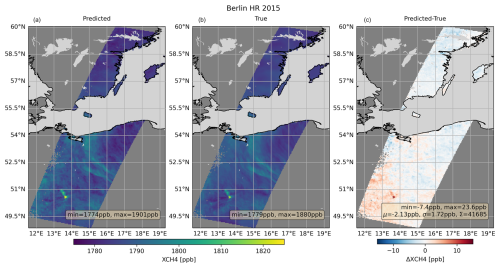
The prediction error in XCH₄ is on average −2.13 ppb and has a standard deviation of 1.72 ppb. However, the map of the XCH₄ prediction error (Fig. 12) shows an interesting feature at about 50.53° N, 13.61° E in the Czech Republic. There is a strong CH₄ plume at this position, the strength of which is obviously overestimated by the prediction.

As a reminder, the AKs describe the behavior of the retrieval in over- or underestimating differences between the true and the a priori concentrations. The plume stands out from the scene average concentrations, i.e., the a priori, at roughly 90 ppb. The XCH₄ AKs in the lowermost layer can have values of up to 1.3, which would result in an overestimation of the departure from the a priori by 30 %, i.e., 27 ppb in this case. It should be noted that this would not result in an overestimation of the emission strength, if AKs are considered appropriately.

When using the true CO₂ and CH₄ profiles as a priori, the difference maps look similar, except that there is no such overestimation of the CH₄ plume because the departure from the a priori becomes much smaller (Figs. A1 and A2).

4 Summary and conclusion

In preparation for the analysis of the large number of radiance measurements from the CO2M satellite mission, we developed the computationally efficient ANN-based algorithm NRG-CO2M to retrieve XCO₂ and XCH₄ with high accuracy and precision and high data yield.

It adapts a novel hybrid learning method that is designed to use measured spectra modified to represent a wider range of XCO₂ and XCH₄ values. The approach combines the advantages of simulation-based and measurement-based learning, preserving the characteristics of the real spectra, including instrumental effects, while allowing learning over a wide range of CO₂ and CH₄ concentrations.

It minimizes learning from spurious correlations by dominating the variability of the training data with prescribed artificial variations. However, the method still requires estimates of the true atmospheric concentrations for a representative training data set, which can be obtained similarly to methods used for empirical bias corrections.

It should be noted that the method could be applied to other instruments and applications. In addition to generating representative training data, spectra could also be modified, e.g., to study the ability of a machine learning model to predict changes in its target variable.

Since the CO2M mission will not be launched until 2026, our study is based on simulated measurements from an OSSE. These simulations assume no systematic errors in the training truth, although they do account for stochastic deviations from true concentrations.

Due to the design of the OSSE used, we have focused in this study only on soundings over land in nadir geometry, but the methods presented should be equally applicable to measurements over water surfaces and under glint conditions.

From our analyses of the 2020 subset data, we find that the systematic XCO₂ and XCH₄ errors scatter with a standard deviation of 0.44 ppm and 2.45 ppb, respectively. This compares to mission requirements for spatio-temporal systematic errors below 0.5 ppm for XCO₂ and 5 ppb for XCH₄ (MRD; Meijer et al., 2020). The average single sounding precision is 0.41 ppm for XCO₂ and 2.74 ppb for XCH₄ compared to mission requirements for stochastic errors due to instrumental noise of less than 0.7 ppm for XCO₂ and 10 ppb for XCH₄ defined for a specific vegetation scenario (MRD; Meijer et al., 2020). Therefore, we conclude that the proposed retrieval method has the potential to meet the demanding CO2M mission requirements for systematic and stochastic XCO₂ and XCH₄ errors.

Our results are qualitatively similar to those of Noël et al. (2024). They estimated the spatio-temporal systematic errors in their FOCAL setup to be 0.5 ppm for XCO₂ and 3.7 ppb for XCH₄ and the stochastic errors to be 0.5 ppm for XCO₂ and 5.0 ppb for XCH₄. However, unlike Noël et al. (2024), we did not divide the systematic error into long correlation length parts, which are relevant for the application of large-scale surface flux inversions, or short correlation length parts, which are relevant for the application of small-scale (e.g., point source) emission estimation. Our results for the Berlin HR scene illustrate how this affects estimates of the relevant systematic errors. The total systematic error in this scene comprises a variable-part scattering with a standard deviation of 0.28 ppm for XCO₂ and 1.49 ppb for XCH₄ and a scene-wide bias of −0.18 ppm for XCO₂ and −2.12 ppb for XCH₄. However, only the variable part of the systematic error is relevant for the application of small-scale (e.g., point source) emission estimation. It should also be noted that our postprocessing is designed to globally reject about 20 % of the least promising soundings compared to a rejection rate of about 37 % used by Noël et al. (2024).

We trained the ANNs with (modified) spectra from the year 2015. Consequently, it can be expected that the modification error becomes more important the further we deviate from the training year. Nevertheless, we observe that the quality of the prediction erodes only slowly because compared to 2020, the accuracy is only slightly better during the test period in 2015 (0.02 ppm for XCO₂, 0.08 ppb for XCH₄), and the precision is the same. This shows that the introduced spectrum modification method is able to efficiently improve the representativeness of the training data for future concentration years ahead.

We used a conventional XCO₂ and XCH₄ retrieval to modify the spectra used for the training data set. It is a variant of the FOCAL algorithm described by Noël et al. (2024), which takes into account scattering in the atmosphere. However, our results show that using an absorption-only retrieval for this task leads to results with essentially the same accuracy and precision.

As a test, we also trained ANNs without MAP data. This had an apparently small effect on accuracy and precision, which is not consistent with the results of Lu et al. (2022), whose retrieval method became significantly less accurate under these conditions. We can only speculate about possible reasons for this. (i) We use a different aerosol microphysical model, which is consistent with the MACC aerosol model but is less complex than the one used by Lu et al. (2022). (ii) Their CO2I-only retrieval method is fundamentally different from ours and also from FOCAL, which may result in different sensitivities to aerosol-induced biases. In this context, it should be noted that our CO2I-only results are in good agreement with those of Noël et al. (2024), suggesting that it may be possible to meet the CO2M mission requirements without using MAP. (iii) The statistics computed by Lu et al. (2022) to quantify the systematic and stochastic errors differ from those computed by us.

However, we observe that the dependence of the XCO₂ prediction on the dry column increases when MAP is not used, which may introduce systematic errors of the order of 0.1 ppm in reality when perfect knowledge of the dry column cannot be expected. Additionally, removing the NIR band further increased the dependence on the dry column but also the dependence on the a priori, making it less likely to meet the CO2M mission requirements.

It is expected that several thousand CPU cores will be required to continuously analyze the data stream from a single CO2M satellite using conventional full-physics algorithms, which are currently being implemented by EUMETSAT. In comparison, the computational requirements of the presented ANN retrievals, once trained, are negligible and can be considered to be driven by pre- and postprocessing as well as input and output operations.

However, the development of neural networks for retrieval of greenhouse gases from satellite-based measurements of reflected solar radiation in the NIR and SWIR is still in its early stages, while there is much experience with full-physics methods. This includes how they respond to instrumental effects, such as spectral artifacts or temporal changes, and machine learning strategies for bias correction. In addition, it should be noted that the results of Noël et al. (2024) suggest that 1 month of training data may be sufficient for a machine-learning-based bias correction. In contrast, we used 1 year of training data for our ANN-based approach, which can make a difference in the early phase of a satellite mission when little data are available.

In order to use NRG-CO2M to retrieve XCO₂ and XCH₄ as well as the associated uncertainties and averaging kernels from real CO2M radiance measurements, once available, the PCAs and the training of the ANNs would have to be repeated with real data. In this case, the training truth could, e.g., consist of model data confirmed by an ensemble of models, as done for NASA's OCO-2 XCO₂ bias correction (O'Dell et al., 2018), or by corresponding TCCON measurements, as done for FOCAL's GOSAT and GOSAT-2 XCO₂ bias correction (Noël et al., 2021). We expect that at least 1 full year should be used for training, although the modification of the training spectra makes them representative of a wider range of atmospheric conditions.

In the analysis of real data, several effects, detailed investigation of which is beyond the scope of this paper, may lead to somewhat degraded retrieval quality. These include unknown systematic errors in the training truth, a priori, and met profiles; non-ideal sampling of the training data set; and potential instrument or RT features that are not well approximated by our spectrum modification method. Therefore, the actual retrieval quality achievable can only be determined after NRG-CO2M has been trained on and applied to real data.

However, due to the quality achieved in the analysis of synthetic CO2M data, the proposed retrieval algorithm NRG-CO2M can be considered a promising candidate for meeting the high accuracy and precision mission requirements of CO2M while providing high data yield and negligible computational requirements, making it a valuable addition to the ensemble of conventional algorithms.

Appendix A

Figure A1 As Fig. 11 but using the true CO₂ concentration profiles as a priori instead of their scene-wide average.

Figure A2 As Fig. 12 but using the true CH₄ concentration profiles as a priori instead of their scene-wide average.