Optimal selection of satellite XCO₂ images for urban CO₂ emission monitoring

There is a growing interest in estimating urban CO₂ emission from spaceborne imagery of the CO₂ column-average dry-air mole fraction (XCO₂). Emission estimation methods have been widely tested and applied to actual or synthetic images. However, there is still a lack of objective criteria for selecting images that are worth processing. This study analyzes the performances of an automated method for estimating urban emissions as a function of the targeted cities and of the atmospheric conditions. It uses synthetic data experiments with synthetic truth and 9920 synthetic satellite images of XCO₂ over 31 of the largest cities across the world generated with a global adaptive-mesh model, the Ocean–Land–Atmosphere Model (OLAM), zoomed in at high resolution over these cities. We use a decision tree learning method applied to this ensemble of synthetic images to define criteria based on these emission and atmospheric conditions for the selection of suitable satellite images.

We show that our automated method for the emission estimation, based on a Gaussian plume model, manages to produce estimates for 92 % of the synthetic images. Our learning method identifies two criteria, the wind direction's spatial variability and the targeted city's emission budget, that discriminate images whose processing yields reasonable emission estimates from those whose processing yields large errors. Images corresponding to low spatial variability in wind direction (less than 12°) and to high urban emissions (greater than 2.1 kt CO₂ h⁻¹) account for 47 % of the images, and their processing yields relative errors in the emission estimates with a median value of −7 % and an interquartile range (IQR) of 56 %. Images corresponding to a high spatial variability in wind direction or to low urban emissions account for 53 % of our images, and their processing yield relative errors in the emission estimates with a median value of −31 % and an IQR of 99 %. Despite such efficient filtering, the accuracy of the estimates corresponding to the former group of images varies widely from city to city.

1 Introduction

Many of countries with the highest CO₂ emissions report their emissions to the United Nations Framework Convention on Climate Change (UNFCC) annually (UNFCCC, 2013). However, despite this monitoring of emissions and the commitments made by nations to reduce them, the increase in CO₂ emissions continues year after year (Friedlingstein et al., 2022). Many cities worldwide have committed to reducing their emissions, notably through joint initiatives such as the Covenant of Mayors (https://www.globalcovenantofmayors.org/, last access: 7 January 2025) or the C40 cities (https://www.c40.org/, last access: 7 January 2025). These cities compile self-reported inventories (SRIs) based on economic data to verify the effective reduction in their emissions. Gurney et al. (2021) compared SRIs of American cities to the Vulcan inventory (Gurney et al., 2020). This comparison shows large differences between the two datasets and highlights the inaccuracy in the emission estimates in most of the SRIs. Quantifying city emissions using satellite observations of CO₂ concentrations above cities could provide helpful information to decrease the uncertainty in such inventories.

Observations of the CO₂ column-average dry-air mole fraction (XCO₂) at the scale of a few square kilometers from the two current Orbiting Carbon Observatory missions (OCO-2 and OCO-3) have paved the way for quantifying emissions from large (a few kt CO₂ h⁻¹) industrial (Chevallier et al., 2022; Nassar et al., 2017; Zheng et al., 2019) and urban (Lei et al., 2021; Reuter et al., 2019; Wu et al., 2018; Ye et al., 2020) sources of CO₂. Indeed, the accuracy of the observations (less than 1 ppm (parts per million); Worden et al., 2017; Taylor et al., 2020) is of the same order of magnitude as the XCO₂ enhancements of the plumes from these sources, and their fine resolution ($\approx \mathrm{2}\times \mathrm{2}\mathrm{km}$; Eldering et al., 2017, 2019) allows them to capture detailed transects or images of the plumes. The Snapshot Area Map (SAM) mode of OCO-3 provides “snapshot” images of about 80 km×80 km over the cities and thus 2D coverage of the XCO₂ concentrations (Kiel et al., 2021), contrary to OCO-2 and to the nominal mode of OCO-3, which only sample XCO₂ over a fine swath (≈10 km). Studies have used these SAMs to evaluate transport model simulations (Kiel et al., 2021) or to calculate local ratios between mole fractions of co-emitted species (Lei et al., 2022; Wu et al., 2022). The first estimates of city emissions based on these SAMs have been presented in conferences. However, there is still a lack of systematic processing of SAMs over cities to estimate the corresponding urban emissions.

Studies such as Broquet et al. (2018), Danjou et al. (2024), Pillai et al. (2016) and Kuhlmann et al. (2020) have used synthetic data to evaluate the possibility of quantifying CO₂ urban emissions from 2D XCO₂ images, such as OCO-3 SAMs or simulated XCO₂ images from the future Copernicus Anthropogenic Carbon Dioxide Monitoring (CO2M; Sierk et al., 2021) and Global Observing SATellite for Greenhouse gases and Water cycle (GOSAT-GW; https://www.nies.go.jp/soc/doc/IWGGMS-18/O/2-6_Hiroshi_Tanimoto.pdf, last access: 7 January 2025) missions. The quantification relies on inverse modeling methods, some of which compare simulations from complex transport models to satellite observations to estimate emissions. However, Feng et al. (2016) and Lian et al. (2018) show that the Weather Research and Forecasting (WRF) model (used by Lei et al., 2021, and Ye et al., 2020, with OCO-2 data) simulates CO₂ transport poorly when the wind speed is low. Other emission estimation methods, called hereafter computationally light methods, are based on simpler transport models (Gaussian plume; Krings et al., 2011), mass balances (integrated mass enhancement method; Frankenberg et al., 2016; Varon et al., 2019) or direct flux estimation (cross-sectional method; Kuhlmann et al., 2020; Krings et al., 2011; Varon et al., 2019, 2020). Danjou et al. (2024) evaluated these methods and, again, showed that the quantification of emissions in low-wind conditions bears large errors. However, no established procedures exist to properly select the cities and the satellite images for which the estimates are most accurate.

Schuh et al. (2021) use high-resolution simulations from a single global adaptive-mesh model, the Ocean–Land–Atmosphere Model (OLAM; Walko and Avissar, 2008a, b), to rank the largest cities of the world as a function of the ratio between the average amplitude of the XCO₂ anthropogenic signals over the city and the variability in the background signal in the vicinity of the city. This classification provides insights, a priori, into the cities for which the emission estimates based on satellite images of their XCO₂ plumes will likely be the most accurate. This analysis is made possible by OLAM's ability to represent both the plumes of cities around the world at high spatial resolution and the influence of large-scale variations in CO₂ concentrations on local variations in the background of these plumes. Danjou et al. (2024) investigate a set of computationally light methods for estimating CO₂ emissions from a city using satellite images capturing most of the atmospheric CO₂ plume from this city. Their study compares existing computationally light methods and their various parameterization options at each step of the atmospheric plume detection and inversion process, using simulated satellite images (i.e., synthetic images) of XCO₂ concentration generated with a meteorological atmospheric transport model over Paris. It identifies the most suitable methods and configurations, among those tested, for the estimation of Paris CO₂ emissions. In parallel, it quantifies the impact of the various sources of uncertainties associated with each method at each step of the procedures. The error in the emission estimates is most sensitive to the meteorological conditions and more specifically to (i) the spatial variability in the wind direction and (ii) the homogeneity of the background concentration field. However, their study considers only one city, Paris, corresponding to a specific range of emissions, to a specific spatial extent and distribution of the urban emissions, to a single type of local topography, to a type of background concentration field, and to mid-latitude meteorological conditions. Therefore, there is a need to generalize these results and to re-assess the distribution of the error in the emission estimate (bias; interquartile range, IQR) and the sensitivities of this error to the spatial variability in the wind direction and in the background concentration field by applying a similar analysis to multiple cities.

Wang et al. (2018) evaluate the ability to estimate emissions from a large ensemble of urban areas (≈ 5000, whose contours are defined based on objective criteria) and power plants covering most of the global CO₂ emissions, based on synthetic XCO₂ images similar to those of the future CO2M mission, whose expected swath width is 250 km and expected resolution is around 2 km×2 km (Sierk et al., 2021). However, their quantification of the emission uncertainties does not account for the errors in atmospheric transport. Their study only addresses the sampling (swath, cloud cover loss, spatial resolution) and accuracy limitations of the XCO₂ imagery. However, the uncertainty in the shape and position of the plume (and thus the meteorology and the characteristics of the cities) can also influence the results and thus the ability to estimate the emissions of a city.

The objective of our study is to resume the series of analysis from Wang et al. (2018), Schuh et al. (2021) and Danjou et al. (2024) and deepen the evaluation of the conditions corresponding to reliable estimates of urban CO₂ emissions using satellite XCO₂ images. We aim to find thresholds for specific criteria to place bounds on the precision of our emission estimation. To do this, we use a little more than a month of simulations of local XCO₂ scenes over large cities. These simulations are generated with the global model OLAM and are evaluated by Schuh et al. (2021). We use these simulations to generate synthetic satellite images for the selected cities, and we estimate their emissions by applying one of the automated and computationally light inversion methods implemented, tested and optimized by Danjou et al. (2024). By using realistic simulations (as obtained from a global non-hydrostatic atmospheric model with a maximum resolution of a few kilometers) to derive the synthetic images and using a method independent of the model used for the simulations to estimate the emissions, we take into account realistically the uncertainty in the meteorology, atmospheric transport and background. As we are working with synthetic data, the error in the emission estimate is directly accessible by comparing the emissions estimated by the inversion method with the synthetic true emissions used in the OLAM simulations. The study of the emission estimation error for different cities and weather conditions aims to support the identification of criteria for discriminating between images, separating those whose processing yields statistically reliable estimates from those whose processing is statistically unreliable.

Such an analysis can help to identify optimal targets for satellite targeting modes, for example, for OCO-3 SAMs, or, when processing large datasets from future imagers such as CO2M, help identify the portions of the data yielding images worth processing for plume detection and inversion. In addition, our analysis can help to robustly assess the errors associated with urban emission estimates as a function of city type and atmospheric or observational conditions. At the least, this analysis is expected to support the development of tools to evaluate the reliability of the inversions.

Section 2 describes the derivation of the synthetic images and the definition of the cities' boundaries. Section 3 describes the inversion method used to make the emission estimations for the main set of analyses in this study. The results with the three other automated methods described in Danjou et al. (2024) lead to similar conclusions, and their analysis is thus summarized in Appendix B. Section 4 describes the learning method based on decision trees used to identify the best discrimination criteria. Section 5 analyses the sensitivities of the emission estimation error to the city type and atmospheric or observational conditions and presents the results of the decision tree learning method. Section 6 discusses the limitations of the analysis conducted in this study and analyzes the distribution of the discrimination criteria for cities in the world with more than 1 million inhabitants.

2 Simulations of XCO₂ images over multiple cities

Section 2.1 describes OLAM and Sect. 2.2 the configuration of the OLAM simulations used in this study. The derivation of the synthetic images from those simulations is described in Sect. 2.3. Section 2.4 details how we define the emissions zones that we target for the inversions.

2.1 OLAM

The Ocean–Land–Atmosphere Model (OLAM) is a coupled ocean–atmosphere general circulation model (Walko and Avissar, 2008a, b) with a dynamical core that has been used in the Dynamical Core Model Intercomparison Project (DCMIP; Ullrich et al., 2017). The main feature of OLAM is its hexagonal grid whose size is adaptive (see illustration in Fig. 1), which makes it possible to apply high resolution to the zones of interest (non-hydrostatic mesoscale) while maintaining a coarse mesh over the rest of the globe (hydrostatic model). The adaptive horizontal grid allows, for example, areas with complex local dynamics, such as mountainous or coastal areas, to be modeled at high spatial resolution. In our case, it allows us to realistically represent the urban plumes of a large number of cities and the underlying large-scale variations in CO₂ while maintaining a global domain and an affordable computation time. This would not be feasible if using a global model with a regular grid. Over the selected cities, the size of the mesh cells is approximately 9 km², and it is progressively enlarged until it reaches around 4×10⁴ km² (e.g., for the largest cells over the oceans).

The transport modeled between the different regions uses physical and dynamical schemes that vary according to the resolution, in particular for submesh convection. Turbulent diffusion is parameterized using the Smagorinsky model, which depends directly on the resolution of the mesh. For the submesh convection, the cumulus clouds, the precipitation and the mixing are represented with a hybrid approach combining aspects of both Grell and Dévényi (2002) and Grell and Freitas (2014).

Figure 1 Illustration of the simulated XCO₂ signal above Bengaluru on 8 August 2015 at 11:00 local time (a) and the horizontal grid used for the simulation (b). The size of the illustration ($\approx \mathrm{240}\mathrm{km}\times \mathrm{240}\mathrm{km}$) is 3 times the size of the synthetic images used in the study ($\approx \mathrm{150}\mathrm{km}\times \mathrm{150}\mathrm{km}$). The boundaries of the Bengaluru synthetic images are represented by the black line.

The model has 49 vertical levels (from 0 m a.s.l. to 37 km a.s.l.), 12 of them being in the first kilometer, which supports reliable simulations in the lower layers of the atmosphere, where the plumes are located. The vertical levels are at constant altitude and can therefore cross the surface. The fact that the levels can cross the surface helps avoid gradient errors on steep slopes that can be present in a pressure coordinate (or hybrid) grid (Ullrich et al., 2017).

2.2 Simulation of CO₂ transport

The atmospheric transport model OLAM is used to simulate the meteorological and CO₂ fields needed to build our synthetic images. Those simulations are free-running. The fluxes from the CarbonTracker 2017 global inversion system (Peters et al., 2007) are used as model input for the biogenic CO₂ surface fluxes. Anthropogenic emissions from the Open-Data Inventory for Anthropogenic Carbon dioxide (ODIAC), which is a spatialized inventory (Oda et al., 2018), are used to represent cities, industries and power plants. No temporal profile is applied to the ODIAC data, which means that the simulated anthropogenic emissions are constant over the month. From these data, the model will simulate, on its hexahedral grid, the wind, pressure, relative humidity and temperature fields (necessary for the calculation of the planetary boundary layer (PBL) height, via the calculation of the potential temperature field and the Nielsen-Gammon et al. (2008) formula) and the CO₂ concentration fields in the atmosphere. The XCO₂ fields are first calculated by the model on the hexahedral grid. The fields are then horizontally regridded to 1 km×1 km using rasterization techniques where the center of the 1 km × 1 km grid cell is mapped to the hexahedral grid average which contains it. While the mapping is not strictly mass-conserving, the errors should be relatively small. Furthermore, since this is a post hoc operation, errors do not accumulate over the length of the simulation. The simulations are performed for 31 cities. We retrieve the 2D fields of XCO₂ (i.e., vertical integration of the CO₂ profiles weighted by pressure levels) as well as the 3D fields of pressure, wind, relative humidity and temperature on the regular grid for all cities and their surroundings.

2.3 Generation of the synthetic images

The model output resolution of 1 km×1 km is comparable to that of the OCO-3 SAMs (1.25 km×2.5 km; Eldering et al., 2019) and that planned for CO2M. This resolution is finer than the finest resolution of the model's adaptive native hexagonal grid (hexagons of ≈9 km²). Therefore, the variations in the model variables (XCO₂ field, wind field, etc.) have a spatial resolution which is coarser than the 1 km×1 km resolution of the model output grid, on which the analysis will be conducted.

The simulations cover a little more than 1 month (1 August–9 September 2015 (included)), providing hourly XCO₂ fields. For each day of the simulated period, we retain the hourly fields of XCO₂ between 10:00 and 17:00 local time for our synthetic images. This simulated database corresponds to a total of 9920 images interpolated at 1 km×1 km resolution. The spatial extension of the synthetic images is restricted to a 150 km square whose axes follow the meridians and parallels and whose center is the barycenter of the targeted city (in terms of CO₂ emissions). This size is halfway between that of the OCO-3 images and the expected swath of CO2M in nadir mode. Finally, random noise of 0.7 ppm standard deviation is added to the simulated XCO₂ field to simulate the satellite data. This value corresponds to the target accuracy for a single XCO₂ measurement from the CO2M mission, similar to the current precision of XCO₂ measurements from OCO-2 (Worden et al., 2017). We do not take clouds and the corresponding loss of XCO₂ retrievals into account when generating our synthetic images.

2.4 Defining the boundaries of the cities

The first task for urban emission estimation is to define the targeted emission zone. As the aim of our quantification is ultimately to help monitor actual emission reductions, we focus on the urban area corresponding to the most significant emissions rather than the actual administrative boundaries of the city. Consequently, the definition of the targeted emission zone is made regarding the size of plumes that can be detected in a SAM and by identifying the highest-emission pixels from the spatialized inventories (using a concept similar to but a different and more straightforward approach than Wang et al., 2019). Because the typical size of a SAM is about 80 km×80 km, we set the size of the targeted emission zone at roughly the size of a 20 km radius disk. Thus, the emission zone we target occupies around 20 % of a typical SAM and 6 % of our synthetic images.

To define the boundaries of an emission zone, we first set its center at the barycenter of anthropogenic emissions within the synthetic image. We then restrict the analysis to a disk of 50 km radius around this center. The size is arbitrarily fixed at 2.5 times the 20 km long targeted emission zone radius. Within this 50 km radius disk, we select only a fraction ($\mathrm{1}/{\mathrm{2.5}}^{\mathrm{2}}$) of the pixels, keeping those for which the emissions are the highest. This fraction is explained by our choice to work with target areas of about π×20² km², i.e., $\mathrm{1}/{\mathrm{2.5}}^{\mathrm{2}}$ of the surface of the 50 km radius disk in which this selection is performed. In order to form a spatially coherent set, we extend the selected area to all pixels within 5 km of one of the pixels retained by this first selection. This enlargement allows us to avoid complex cuttings of the city and to obtain groups of pixels where emissions are statistically high. The last two steps include (i) the selection of the sole cluster of pixels located above the city center and (ii) the addition of pixels not categorized as belonging to the target area but completely surrounded by the target area. The final target area covers an area between 1333 km² (Lahore) and 2063 km² (New York), which corresponds to 6 %–9 % of the spatial coverage of our synthetic images and 20 %–33 % of the spatial coverage of most OCO-3 SAM images. We will call this targeted emission zone “the city” hereafter. More details and illustration can be found in Appendix A.

3 Inversion method

The complete description of the inversion method and the details and justifications for its specific configuration and implementation can be found in Danjou et al. (2024). We make the assumption that the configurations chosen in the framework of their study remain optimal for other cities. This assumption seems justified, as the chosen methods for each steps differ from the discarded methods based on objective criteria. This section only gives an overview of the different steps and the adaptations (compared to the reference configuration from Danjou et al., 2024) that were made in the context of this study.

The inversion method is based on the comparison of the urban plume detected in the image to a straight Gaussian plume. This comparison requires many preliminary steps. (i) The boundaries of the urban area whose emissions we want to estimate are defined. The method used here to define these boundaries is described in Sect. 2.4. (ii) The plume boundaries are defined by the pixels located above the city and those in the cone downwind of the city within an angle of 45°. The wind direction used to define the orientation of the cone is the average wind direction in the PBL over the entire image (from the OLAM simulation). Once the boundaries of the plume are known, we (iii) estimate the background concentration, i.e., the XCO₂ signal in the plume which is not generated by the city emissions. This background concentration is extrapolated from the XCO₂ values of pixels outside the plume using a Gaussian kernel. The difference between the XCO₂ concentration in the synthetic image and the estimated XCO₂ background leads to an estimate of the plume enhancement generated by the city emission. We then (iv) calculate the central axis of the plume using a degree 5 polynomial regression with the pixels in the plume, weighted by the estimated XCO₂ signal from the city. Using this central axis of the plume, we (v) delineate the area of the plume that will be used for the Gaussian plume optimization (analysis area). This area is located between 1 times the approximate radius of the city (≈20 km) and 1.5 times the approximate radius of the city (≈30 km) along the central axis of the plume (the justification for these distances is given later in the paragraph). At this stage, we have extracted the estimated XCO₂ signal from the city and we have determined the pixels that we will use for the optimization. We (vi) estimate the effective wind W, i.e., the wind driving the XCO₂ plume from the city, using the averaged wind within the PBL and within the analysis area. Finally, (vii) we estimate the emissions by inverting the following formula as defined by Krings et al. (2011):

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }{\mathrm{\Omega }}_{\mathrm{gp}}(x,y)={\displaystyle \frac{F}{\sqrt{\mathrm{2}\mathit{\pi }}\cdot \left|\mathit{W}\right|\cdot {\mathit{\sigma }}_y\left(x\right)}}{e}^{-\frac{y^{\mathrm{2}}}{\mathrm{2}\cdot {\mathit{\sigma }}_y(x{)}^{\mathrm{2}}}},\end{array}$$

where the x and y axes follow the directions parallel and perpendicular to the effective wind, F is the city emission estimate, and ΔΩ_gp is the CO₂ mass enhancement of the plume in the atmospheric column per unit area. The term σ_y(x) accounts for the horizontal extension of the source. We take ${\mathit{\sigma }}_y\left(x\right)=a\cdot (x+(\frac{r}{\mathrm{4}a}{)}^{\mathrm{1}/\mathrm{0.894}}{)}^{\mathrm{0.894}}$ as in Krings et al. (2011), where a is the Pasquill stability parameter (Pasquill, 1961) and r the city radius.

To estimate the emission budget, we perform minimization of the mean square differences between the mass per unit area simulated by the Gaussian model (ΔΩ_gp) and the “observed” mass per unit area. The observed mass per unit is calculated from the XCO₂ signal from the city derived in step (iii) using $\mathrm{\Delta }\mathrm{\Omega }(x,y)=\frac{M_{{\mathrm{CO}}_{\mathrm{2}}}}{M_{\text{dry air}}}\cdot \mathrm{\Delta }{{\mathrm{XCO}}_{\mathrm{2}}}_{\mathrm{obs}}(x,y)\times {\mathrm{10}}^{-\mathrm{6}}\times \frac{P_{\text{s, dry air}}(x,y)}{g}$, where g is the Earth's gravity (in m s⁻²), P_{s, dry air} is the dry-air surface pressure (in Pa), M_{dry air} and $M_{{\mathrm{CO}}_{\mathrm{2}}}$ are the molar mass of dry air (28.97 g mol⁻¹) and CO₂ (44.01 g mol⁻¹), and $\mathrm{\Delta }{{\mathrm{XCO}}_{\mathrm{2}}}_{\mathrm{obs}}$ is the observed plume enhancement (in ppm).

The emission budget F, the Pasquill parameter a, the city radius r and the orientation of the axis (i.e., the wind direction) are free parameters in Eq. (1) that are optimized during this minimization. The initial values are for a, the value given by the Pasquill (1961) table corresponding to the meteorological conditions at the time of the image acquisition; for the orientation of the reference frame, the direction of the average wind in the PBL (noted θ^init); and for the radius of the city, the average radius of the city (noted r^init) defined as the square root of the city surface divided by π. The choice of the initial value of the emission budget (noted F^init) is more critical. Indeed, setting an initial value close to the exact value (let alone the exact value) might artificially improve our results. Instead, we take a random number from a beta distribution (with α=1.35, β=2.5 and a scaling factor of 5) multiplied by the actual emission of the central urban area. We normalize the variables for the optimization as follows: $X={\left(\frac{F-F^{\mathrm{init}}}{F^{\mathrm{init}}},\frac{a}{\mathrm{120}},\frac{(\mathit{\theta }-{\mathit{\theta }}^{\mathrm{init}})}{\mathit{\pi }/\mathrm{4}},\frac{r-r^{\mathrm{init}}}{r^{\mathrm{init}}/\mathrm{2}}\right)}^T$. We further impose bounds on these variables during optimization (the bounds are shown without the normalization for clarity): $F\in [-F^{\mathrm{init}},+\mathrm{\infty }]$, $a\in [\mathrm{0},\mathrm{240}]$, $\mathit{\theta }\in [{\mathit{\theta }}^{\mathrm{init}}-\mathit{\pi }/\mathrm{4},{\mathit{\theta }}^{\mathrm{init}}+\mathit{\pi }/\mathrm{4}]$ and $r\in [\mathrm{0.5}\cdot r^{\mathrm{init}},\mathrm{1.5}\cdot r^{\mathrm{init}}]$. These bounds are fixed to avoid unrealistic results (e.g., detected plume direction perpendicular to the wind, high CO₂ uptake from the city).

The methods used for steps (ii) to (vii) are those defined as optimal by Danjou et al. (2024). Step (i) has been redefined in Sect. 2.4, and step (v) has been slightly adapted. We choose to make the analysis area (step v) closer (and smaller) than in their study. The new analysis area is located between the edge of the city (≈20 km) and 1.5 times the radius of the city (≈30 km) along the plume centerline, whereas it was located between the edge of the city (≈20 km) and 2 times the radius of the city (≈40 km) along the plume centerline in Danjou et al. (2024). The conclusions on the sensitivity of the inversions to the analysis area in Danjou et al. (2024) indicate that the closer the analysis area is to the city, the better the estimate.

4 Analysis of the sensitivities of the emission estimation error to observation conditions: general principles

To identify the main criteria of classification of the images based on the performances of the emission estimation, we analyze the sensitivity of the emission estimation error to the different variables characterizing the observation conditions and the inversion. Thus we can see which variables are influencing the emission estimation error the most and define criteria, based on those variables, determining whether a synthetic image is suitable for emission estimation.

We test here two types of variables: (i) predictable variables, used to determine the most favorable conditions for the inversion, which aggregate information about weather conditions and city characteristics, and (ii) diagnostic variables, used to evaluate the inversion results, which aggregate image diagnostics and inversion diagnostics. The sensitivities of the emission estimation error to the predictable variables in the first instance and to the diagnostic variables in the second instance are analyzed separately and in the same way. The two types of variables are analyzed separately as they can answer two different questions. The predictable variables can be used before the inversion to determine if an image will give a reliable emission estimate and is thus worth acquiring and inverting. The diagnostic variables are accessible only after the acquirement of the image and the inversion and can thus just give an indication of the reliability of the emission estimate. The analysis described below is therefore applied to each of the two groups.

As a starting point, we examine separately the relationship between each variable of the chosen group (predictable or diagnostic) and the error in the emission estimate. This preliminary analysis provides a first overview of the variables to which the error is sensitive. After this first step, we analyze all the relationships between the variables and the error to identify the one or two variables to which the error is most sensitive. This identification is performed using a decision tree, the depth of which determines the number of variables identified. The decision tree directly defines thresholds for these variables; following a strict interpretation of the algorithm, these thresholds can be used in a binary way to define whether a synthetic image is suitable for emission estimation. In a more general way, these thresholds can be used as an indicative criterion to evaluate the synthetic images and the corresponding urban emission estimation. These identified variables, together with their respective thresholds, can be used to indicate the level of error in an estimate obtained during an inversion.

4.1 Preliminary analysis

To quantify the sensitivity of the error in the emission estimate to a specific meteorological variable or a variable diagnosed by image processing or by inversion, we order our synthetic images according to the values of the variable. For the analysis with predictable (diagnostic) variables, we separate our set of 9920 (4259) synthetic images (see Sect. 5.2.1) thus ordered into subsets of 496 (213) synthetic images (5 % of the total number). For example, when considering the mean wind in the PBL (i.e., a predictable variable), the first subset will include 496 synthetic images corresponding to the 496 smallest values of the mean wind in the PBL. The second subset will be composed of the 496 images corresponding to the values of the mean wind in the PBL ranked between the 497th and the 992nd position. The last group of images will include 496 synthetic images corresponding to the 496 largest values of the mean wind in the PBL. We then plot the error distribution for these subsets as a function of their rank to see if a significant trend is observed.

The simulations we use are based on an inventory of anthropogenic emissions with no temporal variations. As a result, the variables related to the emissions and the shape or topographical environment of the city have no temporal variability and therefore take only 31 values. Our study of the sensitivity of the error to these variables is therefore based directly on the analysis of the error distribution as a function of the value taken by the variable of interest.

4.2 Analysis with the decision tree learning algorithm

In this study, we seek to better understand the relationship between the input variables (predictable and diagnostic variables) and the reliability of an emission estimate. For this, we train an explainable machine learning algorithm to predict the relative error in the emission estimate given some input variables (described in Sect. 4.3), like the variability in the wind direction or the emission budget, and then study which variables are determined to be relevant by the algorithm. We choose a regression decision tree for this, as they work by learning simple decision rules and therefore are highly interpretable while able to find non-linear relationships between the inputs and the target variable.

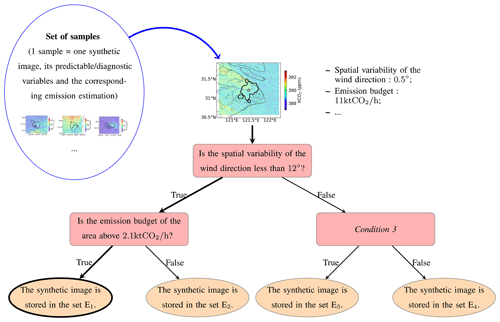
Figure 2 Illustration of how a decision tree works. The decisions (orange ellipses) and the conditions (pink rectangles) are called tree nodes. The first condition, through which the tree is entered, is called the root node; the terminal nodes (the decisions, represented by orange ellipses) are the tree leaves. Nodes that are not leaves are called internal nodes. The path followed by an individual (i.e., the conditions that have been tested for that individual) to arrive at a leaf is called a decision path. The length of a decision path is equal to the number of conditions tested on that path (i.e., the number of internal nodes traversed). The tree depth is the length of the longest decision path. The input synthetic image will follow the decision path in bold and will be classified in the bold leaf.

4.2.1 Description of the decision tree learning algorithm

A decision tree is constructed following a recursive process: at each step, the algorithm splits the data into two subsets following a binary rule applied to a single variable, finding the split that best reduces a particular loss function applied to the target variable. Each subset is split further into two until some stopping condition is reached (see Fig. 2 for illustration). This algorithm therefore splits the input space into regions, where each region corresponds to a similar value of the target variable (i.e., the error in the emission estimation in our case). We use the regression tree implementation from the scikit-learn library (Pedregosa et al., 2011) with a squared error loss and impose conditions on the algorithm to prevent overfitting (creating over-complex trees that do not generalize well): we set the maximum depth of the tree to 2 (i.e., two levels of binary splits), and we impose the condition that the leaves must contain at least 10 % of the training set. The training set (at the root node) is described in the following paragraphs.

4.2.2 Description of our method for determining the decision criteria

A simple approach is to use the total set of synthetic images (9920 synthetic images in the case of the analysis of predictable variables, ≈ 4259 synthetic images in the case of diagnostic variables) as the input set for the decision tree learning method. As the maximum depth of the tree is 2, we obtain at most four subsets (see illustration of that case in Fig. 2) and select the one with the smallest mean absolute error (MAE) in the emission estimate. This subset is considered the subset of synthetic images best suited for emission estimation, and the rest of the synthetic images are considered less well suited. We then study the distribution of the error for this set as well as the pair of criteria that led to this partition. In doing so, we have no information on the stability of the criteria and thresholds with respect to the starting set. This is problematic, especially since the city features can only take 31 values for the 9920 images, which increases the risk of overfitting.

To overcome this problem and to get an idea of the stability of the criteria, we create 100 sets of synthetic images each composed of random samples of 10 % of our total set of synthetic images. We apply the learning algorithm to each of the 100 sets. We look at the subsets corresponding to each leaf and select the one with the smallest MAE. The decision path that leads to this leaf gives us the pair of criteria that we retain. This gives us 100 pairs of criteria. We analyze the redundancy of the criteria across these 100 pairs and the stability of the threshold values of the pair with the highest occurrence. The different threshold values found for the pair with the highest occurrence are applied to determine, for each pair, a subset of synthetic images for which the emission estimates are accurate. The distribution of the criteria obtained with the 100 sets of images, as well as the error distributions of these subsets of synthetic images, is studied to determine the reliability of the criterion threshold values.

4.3 List of variables

We tested 15 predictable variables (8 characterizing the weather and 7 characterizing the city) and 10 diagnostic variables (1 being an image diagnostic and 9 being inversion diagnostics). A detailed list is provided in Table 1. Examples and justification for our choice are provided in the following.

Table 1 List of variables of interest divided by analysis group and type. The operators 〈X〉_E, σ(X)_E, q₉₀(X)_E and q₁₀(X)_E denote the mean, the standard deviation, and the ninth decile and the first decile of the variable X in the set E, respectively. The sets “a.z.”, “plume”, “$\stackrel{\mathrm{‾}}{\mathrm{plume}}$”, “city” and “synth. image” designate the set of pixels in the analysis zone, in the plume, out of the plume and above the city and all the pixels of the synthetic image, respectively. The reference frame used for the calculation of divergence, vorticity, stress, wind shear and topographic variability is the orthogonal frame with its center at the center of the city and with its horizontal axis being the mean wind direction in the PBL. ${\left(u^{\text{2D}},v^{\text{2D}}\right)}^T$ is the vertical average of the wind in the PBL, weighted by the dry-air mass.

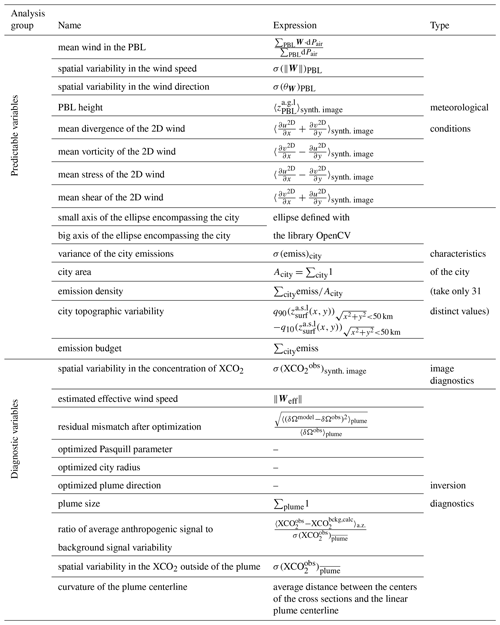
To characterize the meteorological conditions, we have, for example, retained the wind speed in the PBL and the spatial variability in the wind direction (calculated as the circular variance of the 3D wind field in the PBL at the observation time), two variables whose influence on the accuracy of the emission estimation has been highlighted in previous studies (Danjou et al., 2024; Feng et al., 2016). We have also looked at commonly used quantities characterizing the wind (divergence, vorticity, etc. of the wind in the PBL). To characterize the city properties, we looked at spatial variables (its size, the topographic variability in the surroundings, its symmetry) and variables representing the characteristics of the urban emissions (emission budget given by the inventory, emission density). In our synthetic data experiments, the analysis is based on values of the predictable variables that are extracted from the model, i.e., on the “true” values for all predictable variables. When using real satellite images (which is out of scope of this study), meteorological variables can be derived from weather products such as ERA5 (Hersbach et al., 2018). City characteristics can, as in this study, be calculated from gridded inventories such as ODIAC and from databases on urban land cover and population/socio-economic activities such as GRUMP (Center For International Earth Science Information Network-CIESIN-Columbia University et al., 2011). The analysis will then rely on estimates bearing uncertainties, which could decrease the potential to identify suitable observation conditions. We note here that during our evaluations, the thresholds given in Sect. 5.2 will be compared to crude estimates when dealing with actual satellite data, a possible source of errors in the classification.

To characterize the complexity of the background XCO₂ field in the image, we use the spatial variability in the XCO₂ concentration. This variable has been highlighted by Danjou et al. (2024) as being correlated to the error in the emission estimation. Indeed, a high variability in the background leads to an estimation of the background concentration (step iii of the inversion method) that is less accurate and thus to an error in the plume enhancement estimation and in the emission estimation. This is the only variable diagnosed directly in the image among the list of diagnostic variables investigated here. With real data, the size of the image and its spatial coverage may have an influence on the accuracy of the emission estimate. In this case, including this size in the list of diagnostic variables would make sense. However, this is not the case as we are working with synthetic data and all our images have the same size. Reproducing this variability in the coverage of real data is outside the scope of this study. The diagnostics of the inversion robustness include the size of the plume, the residual error after the optimization with the Gaussian plume, the curvature of the central axis of the plume, and the ratio between the estimated amplitude of the city signal and the variability in the signal outside the plume. Unlike predictable variables, the calculated values for the diagnosed variables are directly inferred from the observations with real data. Therefore we will not have classification errors due to this. However, the values taken by the variables might have incorrect distributions in this theoretical study. For example, the distribution we use to simulate the measurement noise in our simulations is much simpler than actual measurement errors.

5 Results

5.1 Preliminary analysis

When we apply our inversion method to our 9920 synthetic images, we obtain an emission estimate in 92 % of the cases (i.e., for 9119 synthetic images): in 8 % of the cases, the optimizer used for the minimization described in Sect. 3 does not converge. The bias (defined by the median) of the error distribution in the emission estimate is −16 % of the emissions, and the spread of this distribution (IQR) is 78 % of the emissions. Reducing the bias and spread of this distribution is essential in order to obtain usable emission estimates. Danjou et al. (2024), in their synthetic data study on the city of Paris, defined an image discrimination criterion based on the spatial variability in the wind direction, with a threshold of 7° (empirically defined). When we apply this filter, we reject 46 % of the 9119 synthetic images and obtain a much less biased distribution of the error (5 % of the emissions) and slightly less spread (64 % of the emissions). However, despite the application of this criterion, the variability in the error distribution remains large across cities. After filtering, the error distribution for the city of Lahore (largest MAE in the emission estimate) shows a bias of −21 % and a spread of 154 % of the emissions, while that for Moscow (smallest MAE in the emission estimate) shows a bias of −3 % and a spread of 26 %. This confirms that, although the criterion defined in Danjou et al. (2024) is relevant, our filtering step does not seem to be sufficient to select the synthetic images. The strong disparity in the error distributions between cities suggests that the error in the emission estimation is sensitive to the city characteristics (topography or city-specific atmospheric conditions) and/or to the city emissions (spatial distribution, magnitude, etc.)

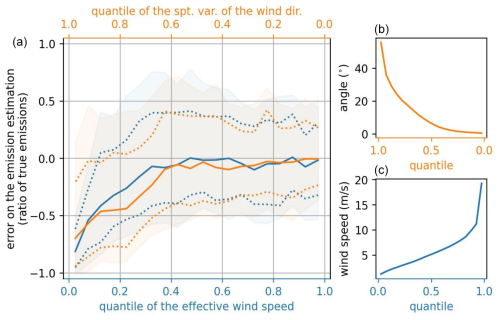
Figure 3 Sensitivity of the emission estimation error to two discriminant variables: the estimated effective wind speed (blue) and the spatial variability in the wind direction (orange). Panel (a) shows the evolution of the error distribution as a function of the quantile of the variable of interest: the solid line indicates the median, the dotted lines the first and third quartiles, and the highlighted area the quantiles at 15.9 % and 84.1 %. Panels (b) and (c) show the values taken by the variables of interest for the different quantiles. Note that the x axis is plotted in the direction of decreasing spatial variability in wind direction (i.e., inverse axis) and increasing wind speed.

Emissions are strongly underestimated when the wind is weak or when the spatial variability in the wind direction is strong (see Fig. 3). These two variables are also strongly correlated here (Spearman correlation of −0.75). The results are more accurate (lower bias and IQR) when the meteorological conditions favor the ventilation of the emitted CO₂ in a narrow and straight plume, i.e., with a high wind speed and a low variability in the wind direction, but when the emitted CO₂ accumulates above and in the vicinity of the city in a diffuse plume with high values of XCO₂ or forms a plume with a complex structure, the results of the emission estimation show an important bias (see Fig. 3).

The error in the emission estimation also shows sensitivities to other variables characterizing the observation conditions; sensitivities to the emission budget, to the ratio between the average anthropogenic signal and the variability in the background signal, or to the difference between the optimized inversion angle and the average wind direction in the PBL are also visible (see Appendix B2).

The error in estimating emissions therefore shows sensitivities, sometimes complex, to several variables, with some being related, again in complex ways. Because of those intricate sensitivities, the simple analysis conducted in this subsection is insufficient to determine the optimal set of variables and thresholds for defining the most optimal discrimination criteria for the synthetic images. This justifies the use of a more complex learning method. The supervised learning method described in Sect. 4.2 will enable us to determine the discrimination criteria more objectively, despite the covariances among the variables.

5.2 Application of the decision tree method

5.2.1 Application for predictable variables

This first analysis, using the decision tree learning method described in Sect. 4.2.1, is based on the results of the inversion of the 9119 synthetic images produced by our inversion method. We focus on the discrimination criteria given by our learning method with 100 different samples, as described in Sect. 4.2.2. For 82 of the 100 samples, the pair of criteria given by our learning method is the spatial variability in the wind direction and the emission budget, i.e., favoring large emissions and low variability in the wind direction. For the remaining 18 samples, the wind direction variability appears nine times in the criterion pair and the emission budget seven times. The other variables appearing in the pairs of criteria for the 18 samples are the spatial variability in emissions in the city (five occurrences), spatial variability in the wind speed (four occurrences), mean PBL height (two occurrences) and the length of the minor axis of ellipse (two occurrences). For six samples, the pair of criteria is in fact a singleton, indicating that one variable is significantly more important than all the remaining variables. The spatial variability, in the wind direction and the emission budget, thus stands out very strongly.

We will now study in detail the threshold values taken for the spatial variability in the wind direction and the city's emission budget for these 82 pairs of criteria. The distribution of the threshold applied to the spatial variability in the wind direction is characterized by a median of 12° and an IQR of 5°. Of the total inversions, 10 % are found between the bounds formed by the quartiles of this distribution (9 and 14°). The distribution of the threshold applied to the emission budget is characterized by a median of 2.1 kt CO₂ h⁻¹ = 5.1 Mt C yr⁻¹ and an IQR of 0.7 kt CO₂ h⁻¹. Of the total situations, 22 % fall between the bounds formed by the quartiles of this distribution (2.6 and 1.9 kt CO₂ h⁻¹). The distribution of the thresholds are therefore spread out (see Fig. 4). For a given pair of criteria among the 82 retained, the subset giving the lowest error is that formed by images whose spatial variability in wind direction is below the threshold given by the decision tree and whose emission budget is above the threshold given by the decision tree. The 82 subsets are homogeneous in terms of the median of the error distribution (−7 % [−6%, −8%]) and the IQR (55 % [52 %, 58 %]). This is less the case for the subsets' size (45 % [36 %, 52 %] of the 9119 synthetic images). For comparison, other studies such as Wang et al. (2019) or Lespinas et al. (2020) have found lower thresholds applied to the emission budget (2 and 0.5 Mt C yr⁻¹, respectively), leading to more precise estimates (uncertainties of less than 20 %). But these studies, which both follow the same formalism, include fewer sources of error in their framework (perfectly known background concentration, simplistic simulations of the urban plumes), which explains our higher threshold and uncertainties.

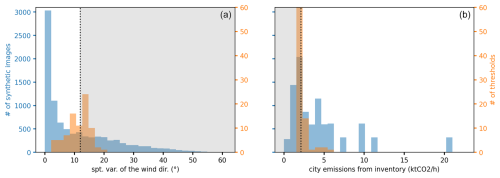
Figure 4 Distributions of the spatial variability in wind direction (a) and city emissions (b). The distribution of the criterion values is in orange, and that of the simulations is in blue. The dotted black line indicates the median threshold found and the grey area the discarded subset.

For the following analysis, we take the medians of the threshold distributions of our 82 retained pairs as the thresholds for these two criteria. The subset formed by the synthetic images respecting these two criteria is characterized by a median error in the estimated emissions of −7 % of the city's emissions and an IQR of 56 % and includes 47 % of the 9119 synthetic images. The subset formed by the synthetic images that do not respect these two criteria is characterized by a median error in the estimated emissions of −31 % of the city's emissions and an IQR of 99 % and includes 53 % of the 9119 synthetic images. The criteria therefore allow us to isolate the synthetic images that are most suitable for inversion, as the synthetic images that do not pass the criteria give highly biased estimates.

The discrimination criterion based on the spatial variability in the wind direction reduces the bias and the IQR of the error distribution, while the criterion based on the emission budget only reduces the IQR. Indeed, by applying only the discrimination criterion based on the spatial variability in the wind direction, we obtain a bias in the error of −5 % and an IQR of 68 % for the subset passing the criterion (−31 % and 99 %, respectively, for the synthetic images not passing the criterion). Applying only the discrimination criterion based on the emission budget gives us, for the subset of synthetic images passing the criterion, a bias of −16 % and an IQR of 66 % (−17 % and 110 %, respectively, for the synthetic images not passing the criterion). Thus the criterion based on the spatial variability in wind direction is a selection criterion (the synthetic images that do not pass the criterion are considered unusable), and the criterion based on the emission budget is a discrimination criterion (the synthetic images that do not pass the criterion will give a less accurate emission estimate).

Figure 5 Distribution of the error in the emission estimates (boxplot) for the synthetic images passing the selection criterion based on the spatial variability in the wind direction (> 12°). The orange bars show the number of synthetic images used. The dashed line separates the cities according to the discrimination criterion based on the city's emission budget, with, on the left, the cities passing the criterion (emissions < 2.1 kt CO₂ h⁻¹) and, on the right, the cities not passing it. The cities are ranked in descending order according to their emission budget.

5.2.2 Application for diagnostic variables

In this section, the set of synthetic images used for the analysis is the set of synthetic images (47 % of our previous set) passing the criteria regarding the spatial variability in the wind direction and regarding the emission budget defined in Sect. 5.2.1.

The pair with the highest occurrence (42 out of the 100 pairs) is the ratio of the average anthropogenic signal and the variability in the background signal to the spatial variability in the XCO₂ concentration outside the plume. For the other samples, we obtain 20 different pairs. The spatial variability in the XCO₂ concentration outside the plume is also used in the calculation of the estimated signal-to-background ratio. The two variables have a correlation of 0.34. We thus choose to reduce the tree depth to 1 and remove the ratio between the average anthropogenic signal and the variability in the background signal from our list of variables of interest. The choice of which variable to remove between the two is made based on the number of occurrences across the pairs (54 for the ratio between the average anthropogenic signal and the variability in the background signal, 77 for the XCO₂ signal variability).

In this new configuration, 72 samples out of 100 give the variability in the XCO₂ signal as a criterion. The distribution of threshold values found for this criterion has a median equal to 0.72 ppm and an IQR of 0.02 ppm. Of the synthetic images in the test set, 19 % fall within the bounds formed by the quartiles of this distribution. By taking the median of this distribution as the discrimination criterion, we obtain two subsets which contain 30 % and 70 %, respectively, of the tested set and are characterized by biases in the estimation of emissions of −6 % and −7% and IQRs of 74 % and 50 %. This discrimination criterion reduces the IQR but not the bias. However, the accuracy of this criterion is questionable: 50 % of the values taken by the signal variability outside the plume are between 0.70 (which corresponds to the measurement noise) and 0.73 ppm. A slight variation (0.01 ppm) in this separation criterion has a strong impact on the error distributions of the two subsets. Moreover, the modelization of the instrument noise (which has an important impact on the signal variability outside of the plume) is oversimplistic in our work. We therefore choose not to retain this criterion.

5.3 Study of the results by city

Of the 31 cities, 5 (Bogota, Lima, Los Angeles, Mexico City and Tehran) have more than 90 % of synthetic images that do not pass the selection criterion based on the spatial variability in wind direction. We therefore have fewer than 30 images that pass the selection criterion for these cities and choose to set them aside. All these cities are located in basins or at the foot of high mountain ranges, which explains the high spatial variability in wind direction for the vast majority of observations.

Of the remaining 26 cities, 7 have their emission budget below the threshold of the emission budget criterion (see Fig. 5) and should therefore have low-accuracy estimates. Paris is one of these cities in our simulations, with emissions of 1.8 kt CO₂ h⁻¹ for the target area. The error distribution of the emission estimate for the city of Paris has a bias of 2 % and an IQR of 83 % for the synthetic images passing the selection criterion based on the spatial variability in the wind direction (86 % of the synthetic images). These results are close to those obtained in Danjou et al. (2024) with the synthetic images of Paris generated by WRF: the distribution of the error in the emission estimate had a bias of 4 % and an IQR of 74 %, and 57 % of the synthetic images passed the criterion defined in the cited work. The IQR is larger in this study, and the number of images passing the criterion is higher. This can be explained by the fact that the criterion was stricter in Danjou et al. (2024) (< 7° compared to < 12° in this study) and that the selected months are not the same (December–April compared to August in this study).

We can see (Fig. 5) that the spread of the error in the emission estimation generally increases with decreasing emission budgets. However, this criterion alone is not sufficient to classify the cities. In particular, the bias varies considerably from one city to another, even when their emissions are similar. Only eight cities (Bengaluru, Buenos Aires, London, Moscow, Ningbo, Paris, Riyadh and Seoul) have a distribution of error in their emission estimates with a bias of less than 10 %. Our selection allowed us to roughly filter out the worst situations for estimating emissions with our method, but it has not yet allowed us to fully understand the error dependencies. We want to point out that these errors are significant, even with many images (≈320) per city and our filtering. Future studies should consider how best to use the emission estimates provided by satellite image analysis.

6 Discussion

6.1 Limitations of the study

Some potential sources of error not considered here (the complexity of measurement error, loss of data due to – among other things – cloud cover and aerosols) have already been discussed in Danjou et al. (2024) and are therefore not detailed here.

A major difference between the simulations in this study and those in Danjou et al. (2024) is the lack of temporal variability in the emissions used. In reality, the plume is generated by the emissions that occurred up to a few hours before the satellite overpass, and inventories show significant daily cycles, in particular related to traffic and industrial activity. When analyzing real data, our analysis zone may correspond to emissions that occurred, for example, 3 h before the acquisition time, and comparing the emission estimate to the emissions at the acquisition time of the synthetic image introduces an additional error. Additional uncertainties due to the emission temporal variability might affect real case studies. In practice, Danjou et al. (2024) showed that the analysis zones correspond to emissions that are very recent (less than 2 h) in most cases. Thus, carrying out this study with variable emissions should not significantly alter our results, assuming that the emissions of a given city remain similar within 2 h in the middle of the day (no morning and evening traffic rush hours). However, the issue of temporal variation in emissions arises with real data when we compare our emission estimates with inventories. For cities without hourly emission budgets (or if the comparison is made with an inventory that does not vary on an hourly basis), we will have an additional source of error, this time coming from the estimated emission budget of the inventory.

We also note here that one of the criteria is based on the city's emission budget, which may be problematic when using real data. Indeed, including an a priori value from an inventory to rank the cities means that ranking errors might result in additional uncertainties if the city's inventory estimates are incorrect.

6.2 Distribution of the discrimination criteria for the cities with more than 1 million inhabitants

This section focuses on the number of cities passing the discrimination criteria for a non-negligible part of the year. We are interested in cities with more than 1 million inhabitants in 2018, according to UNDESA (2018).

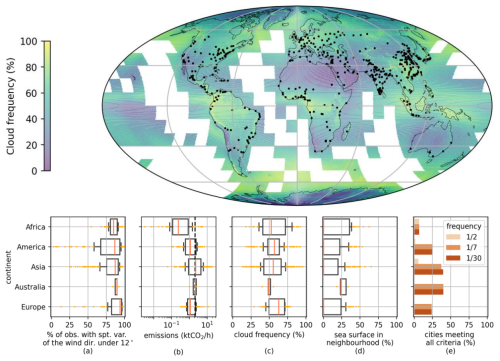
Figure 6 Average annual cloud frequency over the period 2000–2014 derived from the satellites Terra and Aqua (Wilson and Jetz, 2016) and location of cities with more than 1 million inhabitants (top panel). (a–d) Distributions for cities of different continents of the frequency of the synthetic observation with spatial variability in wind direction of less than 12° (a); of the emissions (b); of the mean annual cloud frequency (c); and of the proportion of sea surface in the neighborhood of the city (d), defined as the area within 30 km of the city. Panel (e) shows the percentage of cities per continent passing the emission budget criterion; having less than 25 % of their neighborhood covered by the sea; and for which the frequency of observations allowed a priori by the cloud cover and the threshold applied to the spatial variability in the wind direction is 1 out of 2 d (light orange), 1 d per week (orange) and 1 d per month (dark orange).

The spatial variability in wind direction is calculated as the pressure-weighted circular variance of wind in the PBL in a 150 km square centered on the city center given by UNDESA (2018). For the analysis conducted in this subsection, the meteorological data (3D wind field, pressure field, PBL height) come from the ECMWF ERA5 product (Hersbach et al., 2018) at 0.25° resolution for the year 2020. We calculate this variability for each day at 10:00, 13:00 and 16:00 local time. These different times are chosen to sample possible times of OCO-3 overpasses. For each city, we calculate the proportion of these “observations” for which the spatial variability is above 12°. We can see in Fig. 6a that for the vast majority of cities (93 %), this proportion is above 50 %. The distribution of the spatial variability in the wind direction is different from the one we have with OLAM, where more cases are rejected. An explanation may be the much lower sampling of ERA5 (around 25 km against around 3 km for OLAM in the neighborhood of the cities of interest), which smoothes the wind direction variations and thus leads to smaller values of the spatial variability in wind direction. Nevertheless, we can see that, based on this variable, the least suitable cities for emissions monitoring are located in Asia and America.

City emissions are evaluated with the ODIAC product for the year 2019 and using the definition of city boundaries defined in Sect. 2.4. Among cities with more than 1 million inhabitants, only 40 % pass this criterion (Fig. 6b).

Cloud cover is also a factor limiting the number of images that can be acquired and is not considered in this study. The database of Wilson and Jetz (2016) gives the frequency at which clouds cover a point on the globe. This dataset integrates 15 years of twice-daily remote-sensing-derived cloud observations at 1 km resolution. We are interested in the annual average of this frequency to have an order of magnitude of the days not observable due to clouds. We can see in Fig. 6c that the cloud frequency is, for most cities, between 40 % and 80 %, whatever the continent. The seasonal distributions of cloud cover and spatial variability in wind direction are not taken into account in this analysis.

Finally, the proportion of the water surface in the vicinity is also important for our measurements. The difference in reflectivity between terrestrial and aqueous surfaces results in very heterogeneous measurement quality. OCO-3 SAMs partially overlooking aqueous surfaces (e.g., coastal cities) include a large fraction of excluded pixels. For the analysis of this subsection, we define a city neighborhood as the area within 30 km of the city edge as defined with the method described in Sect. 2.4. For most cities (77 %), this proportion is less than 25 % (Fig. 6d).

To give an idea of the current ability to quantify urban CO₂ emissions using satellite imagery, we look at the distribution of cities with emissions greater than 2.1 kt CO₂ h⁻¹ and with less than 25 % sea surface in their vicinity. We add an index of how often we can measure them by multiplying the proportion of cloud-free days by the proportion of days where the spatial variability in wind direction is greater than 12°. We can see in Fig. 6e the proportion of cities per continent that pass the criteria and can be measured on average every other day, 1 d per week and 1 d per month ($\mathrm{1}/\mathrm{30}$ d). Very few African cities (4 out of 57) pass our criteria, mainly due to their low emissions. The proportion of cities passing all three criteria (emissions, sea in the vicinity, frequency of observation) does not change with the frequency threshold. Indeed, for those cities the emission budget, not the cloud cover or the spatial variability in the wind direction, is the discrimination criterion. America and Europe show similar results: most cities are rejected by our emission criterion, and the high cloud cover (often more than 50 %) does not allow for observations at least every other day. On the other hand, the number of observable cities does not increase when the threshold applied to the frequency of observation is raised from 1 d per week to 1 d per month. The observable cities in America and Europe (30 cities out of 119 and 14 cities out of 58) can provide approximately one observation per week if there are daily overpasses. Asian cities, due to higher emissions, show a higher proportion of cities passing the criteria. Very few cities (16 out of 273) are observable on average every other day. Again, the proportion of cities passing the criteria varies little between a threshold of 1 d per week and 1 d per month (101 and 109 cities out of 273, respectively). Australia stands out: only five cities have more than 1 million inhabitants. For this continent, the distribution of the variables we are interested in is fairly homogeneous, which places the cities at the limit of observability with the criteria on emissions and the proportion of sea surface in the vicinity (all the cities are coastal).

Asia and Australia stand out, with 37 % (102 cities) and 40 % (2 cities) of cities passing the criteria. Indeed, those cities, according to the ODIAC dataset, are more likely to have emissions above our threshold. They are followed by America and Europe, with 25 % of cities for both (i.e., 30 and 14 cities). Due to their lower emissions compared to other continents, African cities seem more difficult to monitor (only 7 % pass our criteria, i.e., four cities). These conclusions remain valid for satellite imagers with characteristics close to those required for CO2M (2 km×2 km resolution, 0.7 ppm) and should be revisited for future satellites with different viewing geometry or ground tracks.

6.3 Other potential criteria

Wind speed is often cited as having an impact on the magnitude of error when quantifying greenhouse gas emissions of local sources using satellite imagery (Varon et al., 2018, 2020; Nassar et al., 2022). As we have seen, using a criterion based on wind speed is relevant, as low wind speeds are often associated with high spatial variability in wind direction. These situations give rise to poorly ventilated plumes with complex structures whose corresponding emissions are difficult to calculate. This study's decision tree learning method indicates that the criterion based on spatial variability in wind direction is more accurate than a criterion based on wind speed with the set of images used here. However, this might be different when using real data. Indeed, the horizontal resolution of the weather product used here is very high around the cities of interest (≈3 km horizontally), higher than that of, for example, the ECMWF ERA5 “hourly data on pressure levels” product (≈25 km). The vertical resolution is of the same order here and in the abovementioned ERA5 product (49 and 37 vertical levels). With wind data at a resolution comparable to that of ERA5, the spatial variability in wind direction will be underestimated when the typical size of the horizontal variations is between 3 and 25 km and the accuracy of the criterion will be lower. A criterion based on wind speed might then be more relevant, as this variable is less sensitive to the resolution.

Another criterion often associated a priori with error in emission estimation is the ratio between the average anthropogenic signal and the variability in the background signal (Schuh et al., 2021). This ratio quantifies the visibility of the plume and indicates how easy it is to quantify the emissions. We have seen that the error in emission estimation shows a high sensitivity to this variable (Sect. 5.1 and Appendix B) and is apparent in our decision tree analysis for diagnostic variables (Sect. 5.2.2). However, this dependence of the error on the ratio of the average anthropogenic signal to background variability is slightly less important in our analysis than the dependence on the background variability. The relevance of the background variability as a criterion has already been discussed in Sect. 5.2.2. A priori, we might have expected the error's dependence on this ratio to be greater than its dependence on background variability. However, this dependence has already been partly filtered out by our analysis of the predictable variables, with the criterion based on the emission budget.

A last criterion often put forward is the detection limit of the satellite (or of the inversion technique), often given in terms of mass of gas emitted per unit of time, e.g., Ehret et al. (2022) and Lauvaux et al. (2022), or in terms of the signal-to-noise ratio, e.g.,  Kuhlmann et al. (2019). However, these papers focus on the detection of plumes from the measured XCO2 (or XCH4) signal. In our case, we have a priori knowledge of the location of the source and the wind direction. This allows us to define, with good precision, the plume limits (see Sect. 3) and thus to avoid a detection step. Future studies might introduce a filtering step to automatically detect plumes from unknown sources, which can significantly increase the uncertainties for such non-identified sources.

7 Conclusions

This study analyses the performance of an automatic process for estimating urban emissions from XCO₂ satellite images. This process is independent of the targeted cities: it is applied identically to all of them. The methods used are low in computation time (on the order of a minute to process an image) and flexible, which enables us to process a database of around 10 000 images with a high convergence rate (8 % of the image). This study, therefore, contributes to the development of standard and automated methods for the operational monitoring of urban emissions with satellite observations.

Our analysis, using a decision tree learning method, of the variations in the error in the emission estimation as a function of the targeted cities and atmospheric conditions shows that the spatial variabilities in the wind direction and the city's emission budget are the two main criteria, among those tested, to select the most suitable images for city emission estimates based on XCO₂ satellite imagery. This analysis with a learning method also provides precise and objective thresholds based on these criteria supporting the selection of images.

The threshold, of 12°, applied to the variability in the wind direction within the image area allows us to reduce both the bias and the spread of the distribution of the emission estimation error, which reflects the uncertainties which should be encountered when tackling actual images. The threshold of 2.1 kt CO₂ h⁻¹ applied to the emission budget reduces the spread of the error in the emission estimate. The application of these two criteria simultaneously allows us to separate the synthetic images into two sets: the first, grouping 47 % of the synthetic images, for which the distribution of the error in the estimation of emissions has a bias (median) of −7 % of the emissions and a spread (IQR) of 56 % and the second for which the distribution of the error has a bias of −31 % and a spread of 99 % of the emissions. However, parts of the subset of results from individual cities show biases in emission estimates of over 10 %, despite our filters. These significant remaining biases raise the question of the current reliability of the results obtained for a single given city. Future work should focus on determining the types of information that can be reliably derived considering the current error estimates (e.g., annual emission budget, trend detection) along with the required number of images/plumes, following Kuhlmann et al. (2019). In parallel, applying this sensitivity analysis to actual satellite data, similarly to the analysis of synthetic images used in our study (e.g., OCO-3 SAMs), would help in evaluating and to refining the criteria derived here.

This study provides objective criteria for selecting the most suitable satellite images for our urban plume inversion method. However, these criteria are derived from experiments with synthetic data, based on atmospheric model simulations and inventories. Even though the realism of these simulations and inventories has been previously evaluated against actual observations, there is a need to confirm the robustness of these criteria and of the corresponding threshold values, with applications to real satellite images. Our study, nevertheless, directly supports the interpretation of future inversion results using XCO₂ satellite images such as the OCO-3 SAMs.

Appendix A: Boundaries of the target areas

Here we give a more detailed description of the way we have defined the cities' boundaries.

1. Convert the coordinates from longitude and latitude to the metric system, using the “pyproj” Python package.

2. Set the city center as the barycenter of anthropogenic emissions within the synthetic image:

   $\left(\begin{array}{c}{x}_{\mathrm{center}}\\ y_{\mathrm{center}}\end{array}\right)=\frac{\mathrm{1}}{\sum \mathrm{inv}(x_{i,j},y_{i,j})}\cdot \left(\begin{array}{c}\sum \mathrm{inv}(x_{i,j},y_{i,j})\cdot x_{i,j}\\ \sum \mathrm{inv}(x_{i,j},y_{i,j})\cdot y_{i,j}\end{array}\right)$, with (x_i,j) and (y_i,j) being the coordinates of inventory cells encompassed by the synthetic image (or the coordinates of the pixels in the synthetic image, as synthetic-image pixels and inventory cells are the same in our case).

3. Restrict the analysis to a disk of 50 km radius around this center: $D_{\mathrm{target}}=\mathit{\left\{}\right(x_{i,j},y_{i,j})/\sqrt{(x_{i,j}-x_{\mathrm{center}}{)}^{\mathrm{2}}+(y_{i,j}-y_{\mathrm{center}}{)}^{\mathrm{2}}}<\mathrm{50}\mathrm{km}\mathit{\}}$.

4. Select the pixels for which the emissions are the highest:

   $S_{\mathrm{1}}=\mathit{\left\{}\right(x_{i,j},y_{i,j})/\mathrm{inv}(x_{i,j},y_{i,j})>\mathrm{Q}\mathrm{16}(D_{\mathrm{target}}\left)\mathrm{and}\right(x_{i,j},y_{i,j})\in D_{\mathrm{target}}\mathit{\}}$, where Q16 is the 16 % quantile ($\mathrm{1}/{\mathrm{2.5}}^{\mathrm{2}}=\mathrm{0.16}$).

5. Expand the selection by 5 pixels (i.e., 5 km) in every direction:

   $S_{\mathrm{2}}=\mathit{\left\{}\right(x_{i,j},y_{i,j})/\exists (x_{k,l},y_{k,l})\in S_{\mathrm{1}}\mathrm{and}(|k-i|<\mathrm{5}\mathrm{or}|l-j|<\mathrm{5}\left)\mathit{\right\}}$.

6. Select the sole cluster above the city center: the function label of the Python package “scipy.ndimage” is used to label the different clusters of S₂, and we keep the one that encompasses the city center.

7. Add pixels not categorized as belonging to the selected cluster but being completely surrounded by it, using the same function as above applied to pixels not labeled as the retained cluster.

The resulting boundaries for each city are illustrated in Fig. A1. Our method gives compact results, of similar sizes, and captures the core emissions of the cities we are studying.

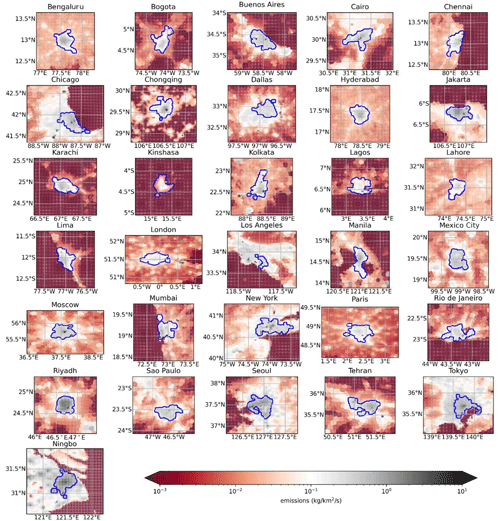
Figure A1 Illustration of the target areas selected for the inversions. The emission maps are taken from ODIAC. In blue are the boundaries of the areas we are targeting. The frame of the figures coincides with the area covered by the 150 km square synthetic images described in Sect. 2.3.

Appendix B: Extension of the study to other inversion methods

Section B1 describes the inversion methods and their differences with the method described in the main text. Section B2 and B3 are constructed according to the same model as that described in Sect. 5.1 and 5.2, with the preliminary analysis (independent of the decision tree) in Sect. (5.1) and the analysis of the decision tree method results in Sect. 5.2.

B1 Inversion methods

Three other inversion methods have been investigated by Danjou et al. (2024) and tested here: one based on the optimization of a rotating Gaussian plume model (denoted GP3), one based on flux estimates of plume cross sections (denoted CS) and one based on a CO₂ mass balance in the plume (integrated mass enhancement method, denoted IME). Details of these methods can be found in Danjou et al. (2024). Concerning the pre-processing steps (i to vi; cf. Sect. 3), those for the method based on a rotating-plume model are the same as those described in Sect. 3 for the straight-plume model. For the other two inversion methods (CS and IME), the steps of defining the analysis area and estimating the effective wind (steps v and vi) are different: the analysis area is the plume area within 1 times the radius of the city along the central axis of the plume, and the effective wind is estimated with the wind tangent to the central axis of the plume in the analysis area according to Danjou et al. (2024). The Gaussian plume method used in the main body of the article will now be referred to as GP2 for clarity.

B2 Preliminary analysis

When we apply the CS, IME and GP3 inversion methods to our 9920 images, we get a result in over 98 % of the cases for each of the three methods. At first sight, the error distribution of the emission estimate seems less biased for CS and IME (bias less than 10 %) than for GP2 and GP3 (bias between −13 % and −16 %). The IQRs of the error distributions are, however, larger for CS and IME (90 %–91 %) than for GP2 and GP3 (78 %–86 %). When we discard synthetic images for which the spatial variability in the wind direction is above 7° (as prescribed in Danjou et al., 2024), the underestimation of the emissions by the GP2 and GP3 methods disappears: the error distributions have bias of between −5 % and 7 % for the inversions based on GP2 and GP3, as well as for those based on CS and IME. The IQR of the distributions also decreases: it is 75 %–76 % for the inversions based on CS and IME and between 64 % and 67 % for those based on GP2 and GP3. After filtering, we are left with 53 % of the images. For CS, IME and GP3, like the results presented for GP2 in Sect. 5.1, the relative error in the emissions shows strong disparities between the cities, even after applying the Danjou et al. (2024) filtering based on the spatial variability in the wind direction. Here we will detail the sensitivities of the error in the emission estimate to the variables of interest. This qualitative study is much reduced in Sect. 5.1 to keep the message concise and clear in the main body of the article.

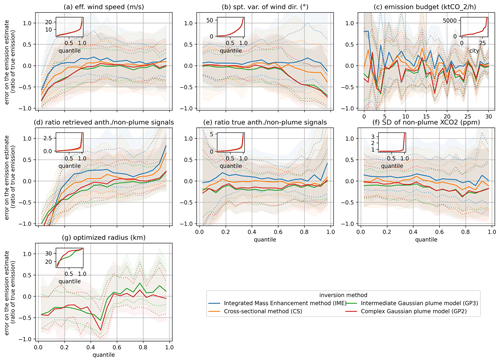
Figure B1 Sensitivity of the emission estimation error to different variables of interest. For each panel, the main plot shows the evolution of the error distribution as a function of the quantile of the variable of interest: the solid line indicates the median, the dotted lines the first and third quartiles, and the highlighted area the quantiles at 15.9 % and 84.1%. The small inset panel shows the values taken by the variables of interest for the different quantiles. Panel (c) is an exception: as we have only one value of emission budget per city, we plot the evolution of the error distribution as a function of the rank of the city regarding the variable of interest. The optimized radius shown in panel (g) is a parameter of the Gaussian plume models (see Sect. 4.3) and is therefore not calculated for the other methods.

The emissions are strongly underestimated when the wind is weak or when the spatial variability in the wind direction is strong (see Fig. B1a and b); the results are more accurate (lower bias and IQR) when the meteorological conditions favor the ventilation of the emitted CO₂ in a straight plume that is not very diffuse, i.e., with high wind speed and low variability in the wind direction, but when the emitted CO₂ accumulates over and in the vicinity of the city in a diffuse plume with high XCO₂ values or forms a plume with a complex structure, the results contain significant errors.

Figure B1c shows a sensitivity of the error in the emission estimate to the actual emission budget. Despite noise, we can see that the IQR of the error decreases when the emissions increase. Cities with important emissions have a plume that stands out more strongly from the background signal and allows a more accurate emission estimation.

The sensitivity of the error to the ratio of the average anthropogenic signal to the variability in the background signal is shown in Fig. B1d for the estimated anthropogenic signal and in Fig. B1e for the actual anthropogenic signal. This actual signal-to-background ratio is close to that used by Schuh et al. (2021). The error sensitivities to these two ratios are similar when this ratio is high, i.e., when the signal from the city differs most strongly from the variability in the background signal. In this case, the estimated anthropogenic signal is close to the real anthropogenic signal. The sensitivities of the error to these two ratios are, however, different when these ratios are low. This can be explained by different reasons for the low ratios. For the estimated background ratio, poorly defined plume boundaries lead to an overestimation of the background signal and thus to a low estimated anthropogenic signal and an underestimation of emissions. For the actual background ratio, low emissions result in a weak anthropogenic signal that is difficult to discern and thus to a higher uncertainty in the emission estimate.

Finally, the error in the emission estimate is very sensitive to the radius of the city optimized during the inversion for the inversions based on a Gaussian plume (GP2 and GP3; see Fig. B1g). However, when we discard synthetic images for which the spatial variability in the wind direction is above 7° as prescribed in Danjou et al. (2024), this sensitivity almost disappears. Indeed, when the spatial variability in the wind direction is large, a dome, or at least a very diffuse plume, forms over the city and disturbs the optimization of the city radius.

The error in the emission estimate thus shows sensitivities to several variables, some of which are correlated. These sensitivities can be complex, and it is difficult at this stage to determine, on the basis of these sensitivities, which of the variables are the most discriminating regarding the error in the emission estimation and thus to determine the optimal criteria for discriminating the synthetic images.

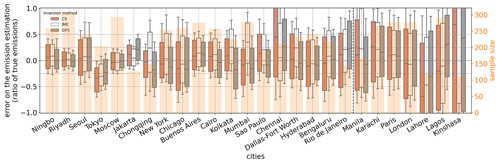
Figure B2 Distribution of the error in the emission estimates (boxplot) for the synthetic images passing the selection criterion based on the spatial variability in the wind direction (> 12°). The orange bars show the number of synthetic images used. The dashed line separates the cities according to the discrimination criterion based on the city's emission budget, with, on the left, the cities passing the criterion (emissions >2.1 kt CO₂ h⁻¹) and, on the right, the cities not passing it. The cities are ranked in descending order according to their emission budget.

B3 Application of the decision tree method

B3.1 Application for predictable variables

The application of our learning tree method to inversions with GP3 gives very similar results to those described for GP2 in Sect. 4.2. The pair of criteria that emerges is the same (spatial variability in wind direction and emission balance), with a slightly higher number of occurrences (95 for GP3, 82 for GP2). For the inversions with CS and IME, the same pair of criteria is also found but with a lower number of occurrences (53 and 63, respectively).

The distributions of threshold values for the criteria are similar for all methods. The medians of the thresholds found for the spatial variability in wind direction are 10° for the GP3 method, 10° for the CS method and 11° for the IME method. For the emission budget, they are 1.9 kt CO₂ h⁻¹ for the GP3 method, 2.0 kt CO₂ h⁻¹ for the CS method and 1.9 kt CO₂ h⁻¹ for the IME method.

The bias (< 10 %) and IQR (between 52 % and 70 %) of the emission estimate for the subsets of synthetic images passing the criteria, as well as the size of these subsets (between 36 % and 55 %), are similar for the different inversion configurations. The subsets that do not pass the discrimination criteria show differences depending on the inversion configuration. The results with GP3 are similar to those with GP2 in terms of bias and the IQR of the error in the emission estimate and plume size, but for CS and IME, the biases are smaller (between 6 % and 12 % in absolute value for CS and IME, between −25 % and −37 % for GP2 and GP3) and the IQRs are larger (higher than 120 % for CS and IME, lower than 107 % for GP2 and GP3).

B3.2 Application for diagnostic variables

In this section, the set of synthetic images used for the analysis is the one formed by the synthetic images passing the criteria on wind direction variability and on the emission balance. The inversion methods (GP3, IME, CS) are tested separately. For all these methods, no pair of criteria has more than 40 occurrences when the tree depth is set to 2. We therefore also reduce the tree depth to 1. Plume size appears as the main criterion for IME and CS, with 44 and 42 occurrences, respectively. As this criterion appears for less than half of the samples, we do not consider it as sufficiently relevant. For GP3, the error in the optimization appears as the main criterion, without standing out here either (42 occurrences). We therefore choose not to retain these criteria.

B4 Study of the results by city

As the threshold distributions are similar for all inversion methods, we choose to use the same threshold values as those found for the GP2 method (cf. Sect. 5.2.1). We have the same five cities (Bogota, Lima, Los Angeles, Mexico City and Tehran) for which more than 90 % of the synthetic images do not pass the selection criterion based on the spatial variability in the wind direction.

As with the GP2 method, we can see (see Fig. B2) that the spread of the error generally decreases when the emission budget increases. However, again, this parameter does not fully explain the disparity of the results between cities.