New quantitative measurements and spectroscopic line parameters of ammonia in the 685–1250 cm⁻¹ spectral region for atmospheric remote sensing

Ammonia (NH₃) is a toxic pollutant, generally linked to agricultural emissions, and plays a major role in the formation of fine aerosols which have a significant and detrimental effect on human health. NH₃ is one of the most significant gases that can be monitored by satellite instruments orbiting the Earth, including the Infrared Atmospheric Sounding Interferometer (IASI) and the Cross-track Infrared Sounder (CrIS). The interpretation of these measured atmospheric spectra requires accurate radiative transfer modelling, which relies on the quality of the input spectroscopic line parameters.

In this work we present new high quality high-resolution infrared spectra of self- and air-broadened NH₃ at 296 K using a Bruker IFS 125HR spectrometer and a 24.45 cm pathlength sample cell with silver chloride windows. Using a multispectrum fitting approach, we then determine new spectroscopic line parameters over the range 685 to 1250 cm⁻¹ for the NH₃ 0100 00 0 s ← 0000 00 0 a and 0100 00 0 a ← 0000 00 0 s transitions associated with the v₂ mode; the Q branches of these transitions are the strongest NH₃ features observed in atmospheric spectra. Our analysis utilises the Voigt lineshape, with speed-dependent Voigt and Rosenkranz line mixing for the strongest lines. To date this is the most complete experimental and multispectrum analysis of air-broadened NH₃ over this spectral region. Our derived spectroscopic line parameters reproduce the new measurements substantially better than line parameters from the HITRAN 2020 database, which were derived from a mixture of ab initio calculations and previous laboratory measurements. We have revised values for parameters such as line intensities and air-broadened Lorentz halfwidths, in some cases by almost 10 %. We have substantially lowered the uncertainties of key parameters, such as line intensities. In addition to the measured speed dependence and Rosenkranz line mixing parameters, which we believe are the first reported for the v₂ band of NH₃ in air, we also determine a range of parameters for the v₂ band that are not currently in HITRAN, for example self- and air-pressure-induced shifts. We expect these new parameters to provide a more accurate basis for incorporation into atmospheric radiative transfer models to measure NH₃ concentrations from satellite.

1 Introduction

Ammonia (NH₃) is found throughout the universe, from the interstellar medium (Ho and Townes, 1983) to the atmospheres of exoplanets, e.g. GJ 504 b (Mâlin et al., 2025). Closer to home, it can be found throughout the Solar System, e.g. in the atmospheres of the gas giants Jupiter and Saturn (Irwin et al., 2025), and also in the Earth's atmosphere where it is the most abundant alkaline gas. On Earth, it is emitted through a range of anthropogenic sources (Sutton et al., 2008; Behera et al., 2013; Wyer et al., 2022) of which agriculture, mostly accounted for by livestock and nitrogen-based fertilisers, is responsible for over 80 % of the global total emissions (Van Damme et al., 2021). Atmospheric NH₃ is responsible for a variety of negative environmental and health effects. It contributes to the eutrophication and acidification of aquatic ecosystems, causing adverse effects on a variety of different flora (Sutton et al., 2009; García-Gómez et al., 2014). Additionally, NH₃ serves as a significant precursor to fine particulate matter, PM_2.5 (Brunekreef et al., 2015; Megaritis et al., 2013; Thakrar et al., 2020). It is estimated that atmospheric NH₃ accounts for 30 % and 50 % of the total production of PM_2.5 in the US and Europe, respectively (Erisman and Schaap, 2004; Behera and Sharma, 2010; Bauer et al., 2016; Han et al., 2020). PM_2.5 contributes to visibility degradation (Ting et al., 2022; Yang et al., 2022) and, when inhaled, can cause a number of diseases, including chronic obstructive pulmonary disorder (COPD) and lung cancer (Apte et al., 2018; Lelieveld et al., 2015; Yu et al., 2000).

Atmospheric NH₃ can be monitored near the Earth's surface using a variety of in situ methods such as wet chemistry or spectroscopic techniques (Twigg et al., 2022). Increasingly over the last few decades, it has been possible to monitor NH₃ by infrared spectrometers onboard satellites, such as the Infrared Atmospheric Sounding Interferometer (IASI) (Clarisse et al., 2009; Van Damme et al., 2014, 2018; Clarisse et al., 2019), the Cross-track Infrared Sounder (CrIS) (Shephard and Cady-Pereira, 2015), the Atmospheric InfraRed Sounder (AIRS) (Warner et al., 2016, 2017), and the Tropospheric Emission Spectrometer (TES) (Shephard et al., 2011). Among the most prominent NH₃ features in the infrared used for remote sensing are the two Q branches of the ν₂ ammonia band at ∼ 10.4 and 10.7 µm. Accurate retrievals of NH₃ concentrations from the measurements recorded by the various instruments mentioned above depend upon our ability to model atmospheric radiative transfer, which in turn depends on the underlying NH₃ spectroscopic line parameters. It is therefore crucially important that the line parameters for the ν₂ NH₃ band are both accurately and precisely characterised.

In 2013, a full re-analysis of ¹⁴NH₃ spectroscopy was conducted (Down et al., 2013). In particular, line positions and intensities for the ν₂ band were revised. This work led to the most recent significant spectroscopic update for NH₃ in the HITRAN 2012 (Rothman et al., 2013) and GEISA 2015 (Jacquinet-Husson et al., 2016) databases. A study was also conducted to determine self- and air-broadened Lorentz halfwidths at half-maximum (HWHM) for the ν₂ ¹⁴NH₃ band for J ≤ 9 (Nemtchinov et al., 2004); these results were included in the HITRAN 2012 database. In the case of ¹⁴NH₃ lines where J > 9, the self-broadened halfwidths at each K level are set to 0.5, and the air-broadened halfwidths at each K level (K ≤ 9) are assigned the corresponding values for the J = 9 levels, except for K > 9 levels for which set values are assigned to fit the trend for other K values. High resolution spectra of ¹⁵NH₃ have been recorded (Canè et al., 2019, 2020), and line positions derived from these studies being included in the HITRAN 2020 database (Gordon et al., 2021) with line intensities derived through ab initio calculations (Yurchenko, 2015). Currently, no lines of other minor isotopologues of NH₃, such as NH₂D, are included in the HITRAN database.

In this work, we label vibrational states by v₁v₂v₃v₄l₃l₄li, where v_n represents the quantum number of the nth vibrational mode. Unlike the non-degenerate modes ν₁ and ν₂, ν₃ and ν₄ are doubly degenerate and give rise to the vibrational angular momentum labels l₃ and l₄, respectively, which can take the values −v, $-v+\mathrm{2}$, …, v−2, v. These two angular momenta couple to produce the total vibrational angular momentum, l. The v₂ mode is associated with the inversional umbrella motion between the two equivalent equilibrium structures, and is considered a classic textbook example of quantum mechanical tunnelling. As a result of this large amplitude vibration, each energy level of ammonia splits into a symmetric and antisymmetric level. For this reason, vibrational states additionally require an inversion label, i, denoted by s or a depending on whether the state is symmetric or antisymmetric on inversion through the planar configuration. The rotational levels are characterised by J, the total angular momentum quantum number, and K, its component along the molecular axis, which can take the values 0, 1, 2, …, J.

In this work, we derive a set of new line parameters for the ν₂ NH₃ band, including positions, intensities, self- and air-broadened halfwidths and, for the first time, a complete set of self- and air-pressure-induced shifts, and, where possible, speed dependence and Rosenkranz line mixing parameters. Although this work has focused primarily on deriving new line parameters for the 0100 00 0 s ← 0000 00 0 a and 0100 00 0 a ← 0000 00 0 s transitions (excitation from the ground state to v₂ = 1) of ¹⁴NH₃, which are of particular importance for remote sensing, we have also derived line parameters within the 685–1250 cm⁻¹ spectral window for the same transitions of ¹⁵NH₃, alongside a variety of other less intense ¹⁴NH₃ lines in the ν₄, 2ν₂ (first overtone), and ν₂+ν₄ (combination) bands. The line parameters for these weaker bands are more fully detailed in the Supplement. We note also that, due to the small range of pressures for the pure NH₃ spectra in our analysis, the self parameters tend to have larger uncertainties than the air parameters, in particular the self-pressure-induced line shifts. The measurements and analysis were optimised for atmospheric remote sensing applications, and the NH₃ amount fractions are small enough that the self contribution to the air-broadened spectra are smaller than the experimental uncertainty. The self-induced values were derived from the lower pressure pure NH₃ spectra in the multispectrum fit.

2 Experimental details

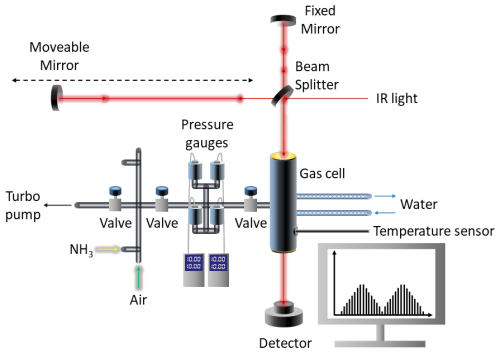
A new laboratory for the purposes of producing spectroscopic data for remote sensing of trace gases in the Earth's atmosphere has recently been set up at Space Park Leicester. Dubbed the SPectroscopy for ENvironmental SEnsing Research (SPENSER) facility, the principal instrument is a Bruker IFS 125HR spectrometer. In this work, we carried out measurements of pure and air-broadened NH₃ samples at 296 K with a focus on the spectral window 685–1250 cm⁻¹. A glass sample cell, situated inside the sample compartment of the spectrometer, was configured with high IR transmission AgCl windows. The cell pathlength was determined as 24.45 cm using high resolution measurements of the 0002 ← 0000 band of N₂O and high accuracy line intensities from a previous study at the Physikalisch-Technische Bundesanstalt (Werwein et al., 2017). The pressure inside the absorption cell and gas line was monitored by four calibrated Inficon SKY CDG-45D manometers, with different full-scale pressures ranging from 0.1 to 1000 Torr. The temperature of the sample was maintained at a constant value of 296 K using a F32-HE Julabo circulator that flowed water around the outer jacket of the cell; the temperature was measured by four calibrated PRTs connected to an Isotech milliK precision thermometer and millisKanner channel expander. A schematic of the experimental setup is shown in Fig. 1. The spectrometer settings and additional measurement information are listed in Table 1.

Figure 1 Schematic representation of the experimental setup.

Table 1 Spectrometer settings and measurement information for the pure and air-broadened NH₃ spectra.

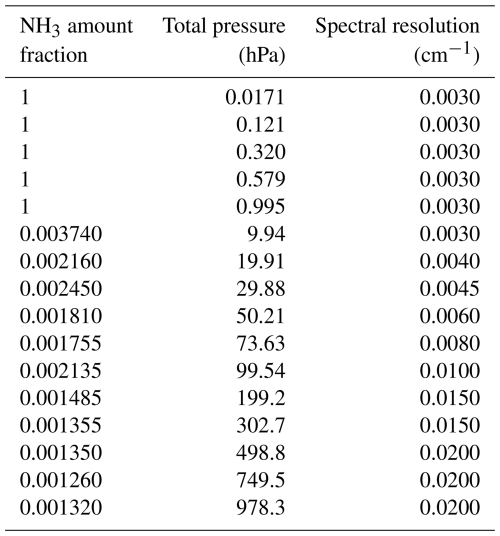
Sample gas mixtures were made from high purity gases, namely NH₃ (BOC; 99.98 % purity) and dry synthetic air (primary reference material (PRM) from the National Physical Laboratory (NPL); 0.95 % Ar, 20.95 % O₂ in N₂, relative uncertainties Ar 1.0 %, O₂ 0.2 %). For the pure NH₃ measurements, a spectral resolution of 0.003 cm⁻¹ was used, defined as the Bruker instrument resolution of 0.9 per MOPD; MOPD = maximum optical path difference. For the air-broadened measurements, the spectral resolution was reduced according to the linewidth, with a lowest resolution of 0.02 cm⁻¹ used where the total pressure approached 1000 hPa. Table 2 lists the pressures and resolutions selected for the measurements, which were optimised for the Earth's atmospheric conditions. These mixtures were found to be stable for many hours of scanning, with no signal degradation observed that might otherwise be attributed to reactions with the cell windows, for example. For the analysis, NH₃ spectra were ratioed against appropriate empty cell spectra (taken at 0.03 cm⁻¹ spectral resolution) to produce transmittance spectra. The generation of these transmittance spectra was handled by the Bruker OPUS program, which zero-fills the backgrounds to provide a point-by-point division on the grid of the single channel sample scans. These spectra were unapodised except for the highest resolution measurements (< 0.005 cm⁻¹, equivalent to MOPD > 180 cm) for which the following apodisation function (a_p) was applied (Devi et al., 2003):

$$\begin{array}{}\text{(1)}& {\left[\mathrm{1}-{\left({\displaystyle \frac{p}{\mathrm{MOPD}}}\right)}^{\mathrm{2}}\right]}^{\mathrm{2}},\end{array}$$

where p is the path difference, and a_p is defined as zero when p > MOPD. Finally, additional N₂O spectra were recorded for the purposes of calibrating the wavenumber scales of the NH₃ spectra. This is discussed in more detail in Sect. 3.

Table 2 Experimental conditions for the measured NH₃ spectra.

3 Analysis and data retrievals

The pure and air-broadened ammonia spectra taken in this study were analysed using a nonlinear least-squares multispectrum fitting software package known as Labfit (Benner et al., 1995), which has an extensive history in deriving non-Voigt line parameters for remote sensing (e.g. Benner et al., 2016). In this work, line parameters were determined for both Voigt and speed-dependent Voigt lineshapes with Rosenkranz first order line mixing (Rosenkranz, 1988). The normalised Voigt lineshape with Rosenkranz line mixing is defined in Labfit (Benner et al., 1995; Letchworth and Benner, 2007) as:

$$\begin{array}{}\text{(2)}& I=\sqrt{{\displaystyle \frac{\ln \left(\mathrm{2}\right)}{\mathit{\pi }}}}{\displaystyle \frac{\mathrm{1}}{{\mathrm{\Gamma }}_{\mathrm{D}}}}\left[K\left(x,y\right)+YL\left(x,y\right)\right],\end{array}$$

where Y is the Rosenkranz line mixing parameter,

$$\begin{array}{}\text{(3)}& K\left(x,y\right)={\displaystyle \frac{y}{\mathit{\pi }}}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\displaystyle \frac{\exp \left(-t^{\mathrm{2}}\right)}{{\left(x-t\right)}^{\mathrm{2}}+y^{\mathrm{2}}}}\mathrm{d}t,\end{array}$$

and

$$\begin{array}{}\text{(4)}& L\left(x,y\right)={\displaystyle \frac{\mathrm{1}}{\mathit{\pi }}}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\displaystyle \frac{\left(x-t\right)\exp \left(-t^{\mathrm{2}}\right)}{{\left(x-t\right)}^{\mathrm{2}}+y^{\mathrm{2}}}}\mathrm{d}t.\end{array}$$

These are simply related to the complex probability function, W, by

$$\begin{array}{}\text{(5)}& W\left(z\right)=K\left(x,y\right)+iL\left(x,y\right)={\displaystyle \frac{i}{\mathit{\pi }}}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}{\displaystyle \frac{\exp \left(-t^{\mathrm{2}}\right)}{x+iy-t}}\mathrm{d}t\end{array}$$

where x and y are given by

$$\begin{array}{}\text{(6)}& x=\sqrt{\ln \left(\mathrm{2}\right)}\left(\mathit{\nu }-{\mathit{\nu }}_{\mathrm{0}}-\mathrm{\Delta }\right)/{\mathrm{\Gamma }}_{\mathrm{D}}\end{array}$$

and

$$\begin{array}{}\text{(7)}& y=\sqrt{\ln \left(\mathrm{2}\right)}{\mathrm{\Gamma }}_{\mathrm{0}}/{\mathrm{\Gamma }}_{\mathrm{D}}\end{array}$$

In the above equations, ν−ν₀ is the wavenumber detuning relative to the unperturbed line centre ν₀, Γ₀ is the Lorentz (collisional) halfwidth at half maximum, Γ_D the Doppler halfwidth at half maximum, and Δ the pressure-induced shift of the line centre (so that $\mathit{\nu }-{\mathit{\nu }}_{\mathrm{0}}-\mathrm{\Delta }$ represents the wavenumber detuning relative to the pressure-shifted line centre, ν₀+Δ).

When the speed dependence of collisions is accounted for, the Voigt lineshape is modified into the speed-dependent Voigt profile. With the inclusion of Rosenkranz line mixing, the mathematical form of this profile is defined in Labfit (Benner et al., 1995; Ciurylo, 1998) by rewriting the Lorentz halfwidth as a function of v, defined as the ratio of the speed of an absorbing molecule to its most probable speed, and integrating over the full range of velocities. This leads to K and L being redefined as:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}& K\left(x,y,a_{\mathrm{w}}\right)=\\ & {\displaystyle \frac{\mathrm{2}}{\mathit{\pi }}}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}v{e}^{-v^{\mathrm{2}}}\arctan \left[{\displaystyle \frac{x+v}{y+a_{\mathrm{w}}y\left(v^{\mathrm{2}}-\mathrm{3}/\mathrm{2}\right)}}\right]\mathrm{d}v\end{array}\end{array}$$

and

$$\begin{array}{}\text{(9)}& \begin{array}{rl}& L\left(x,y,a_{\mathrm{w}}\right)=\\ & {\displaystyle \frac{\mathrm{1}}{\mathit{\pi }}}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}v{e}^{-v^{\mathrm{2}}}\ln \left\{\mathrm{1}+{\left[{\displaystyle \frac{x+v}{y+a_{\mathrm{w}}y\left(v^{\mathrm{2}}-\mathrm{3}/\mathrm{2}\right)}}\right]}^{\mathrm{2}}\right\}\mathrm{d}v\end{array}\end{array}$$

where

$$\begin{array}{}\text{(10)}& a_{\mathrm{w}}={\displaystyle \frac{{\mathrm{\Gamma }}_{\mathrm{2}}}{{\mathrm{\Gamma }}_{\mathrm{0}}}}\end{array}$$

and Γ₂ is the (quadratic) speed-dependence parameter for the Lorentz halfwidth. In this work, we do not consider the speed-dependence of the pressure-induced shifts. These shifts are expected to be small, and difficult to separate from the effects of line mixing.

Table 3 Line parameters derived in this study.

The parameters Γ₀, Δ, and Y, introduced in Eqs. (2)–(10), are pressure dependent and can be expanded as

$$\begin{array}{}\text{(11)}& {\displaystyle }{\mathrm{\Gamma }}_{\mathrm{0}}=p\left[{\mathit{\gamma }}_{\mathrm{air}}^{\mathrm{0}}\left(\mathrm{1}-x\right)+{\mathit{\gamma }}_{\mathrm{self}}^{\mathrm{0}}x\right]\text{(12)}& {\displaystyle }\mathrm{\Delta }=p\left[{\mathit{\delta }}_{\mathrm{air}}^{\mathrm{0}}\left(\mathrm{1}-x\right)+{\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}x\right]\text{(13)}& {\displaystyle }Y=p{Y}_{\mathrm{air}}^{\mathrm{0}}\end{array}$$

In the above expressions, γ⁰, δ⁰, and Y⁰ are defined at p_ref = 1 atm, p is the pressure in atmospheres, and x is the amount fraction of NH₃ in the sample. As all measurements in this work were taken at 296 K, we have not considered temperature dependence terms in Eqs. (2)–(13). Also note that for each line in the spectrum, the current version of Labfit can only fit one speed dependence parameter (a_w) and one Rosenkranz line-mixing parameter (Y⁰) in a solution, making no distinction between self and foreign contributions; however, the NH₃ amount fractions in the high-pressure measurements are very small (less than ∼ 0.004) so that the self contributions to the air-broadened spectra are smaller than the experimental uncertainty. The definitions of the retrieved line parameters are summarised in Table 3.

In addition to line parameters, Labfit is able to correct during the analysis for minor imperfections in the spectra associated with the field of view or residual phase errors. The software can also fit spectral baselines using Chebyshev polynomials, and the zero level of individual spectra, and all spectra can be weighted in accordance with their individual signal-to-noise ratios (SNRs).

Using Labfit (Benner et al., 1995) it is possible to relate line positions via the corresponding upper and lower state rovibrational energies, and parameterise them in terms of the band centre and the rotational constants B, D, H, etc. By constraining line positions to these quantum mechanical expressions, fewer parameters are floated and correlations between parameters are reduced. This method has the advantage that blended lines can easily be separated using appropriate constraints. In Labfit, however, these position constraints are optimised for linear molecules such as carbon dioxide. Fitting spectra of ammonia, a symmetric rotor whose energy levels require an additional quantum number, K, adds an additional level of complexity to the problem that is too cumbersome without substantial modifications to the programming code. Therefore, for this work all line parameters, including positions, were solved on a line-by-line basis. This does present challenges, for example, when fitting two lines of similar intensity that are blended even in the lowest pressure spectra. In such cases, some parameters of one or both of the lines need to be fixed, as outlined in Sect. 4. In all cases, preference is given to fitting lines from the ν₂ band.

The multispectrum fitting technique requires that all spectra are consistently calibrated prior to the spectral fitting. Lines present in the measured spectra originating from water absorption inside the evacuated portion of the spectrometer (not the cell) were used to provide a relative wavenumber calibration between spectra; in this case we utilised averages of single channel sample scans rather than the full transmittance spectra on account of the mismatch between sample and background spectral resolutions. The absolute calibration of the wavenumber scales of these water lines was determined by measuring a low-pressure spectrum of N₂O at room temperature and calibrating against NIST heterodyne calibration tables (Maki and Wells, 1991).

The NH₃ multispectrum fit was initialized using parameters from HITRAN 2020 (Gordon et al., 2021), and proceeded by fitting all pure sample spectra before adding the air-broadened spectra to the solution and floating selected parameters for all spectra simultaneously. Initial fits were carried out over the entire 685–1250 cm⁻¹ region, however there was evidence from the saturated lines in the pure sample spectra that the zero level was not constant across this wide fitted interval; the current version of Labfit can only apply a single zero level offset correction to each spectrum. To counter this situation as much as possible, the spectra were split into three regions (685–900, 885–1015 and 1000–1250 cm⁻¹), allowing three different offsets to be applied to each spectrum as required.

The approach taken here was to fit all absorption features within the fitted interval, and adjust positions, intensities, Lorentz halfwidths, pressure-induced shifts, Rosenkranz line mixing parameters, and quadratic speed dependence for each line separately. Line mixing and speed dependence parameters were included in the fit as judged by inspection of the fit residuals and the derived uncertainties determined by the fit.

4 Discussion of results and comparison with HITRAN 2020

The final multispectrum fit for all 16 NH₃ spectra (self- and air-broadened) over the entire 685–1250 cm⁻¹ range is plotted in Fig. 2. The top panel shows the superimposed weighted spectral fit residuals (observed minus calculated), with the bottom panel showing the observed spectra. The vast majority of the residuals, including the entire Q branch region, are within ±0.5 %. The only exceptions are a small number of saturated features in the R branch region of the pure NH₃ spectra, which are slightly greater. These small but persistent residuals are predominantly associated with the lowest pressure measurements, and are likely caused by small variations in the zero level for these spectra that are not adequately captured by Labfit (Benner et al., 1995).

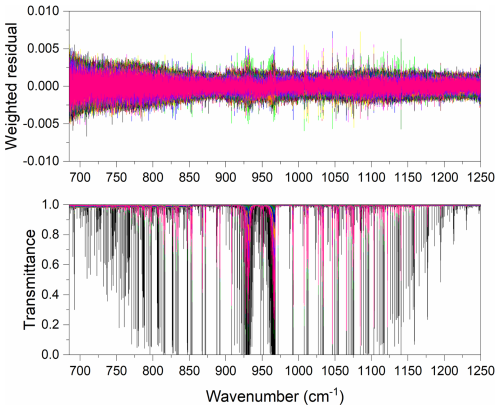
Figure 2 Overlay of all the transmittance spectra across the entire measured spectral region, 685–1250 cm⁻¹, alongside their weighted fit residuals, defined as the difference between the observed and calculated spectra.

Table 4 Main NH₃ bands analysed in this study within the 685–1250 cm⁻¹ spectral region. Some bands were only partially observed in the spectral window, for which only R branch lines were fit. The number ranges in columns 5 to 7 denote the range of analysed J^′′ values for the observed transitions. However, a number of lines associated with K sub-levels are not included in the fit if the relevant lines are either outside the measured spectral window or have an intensity below the fitting threshold of 1 × 10⁻²³ cm⁻¹ (molec. cm⁻²)⁻¹ at 296 K.

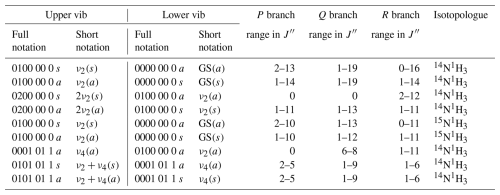
Table 5 The number of each type of fitted line parameter for the main NH₃ bands analysed in this study.

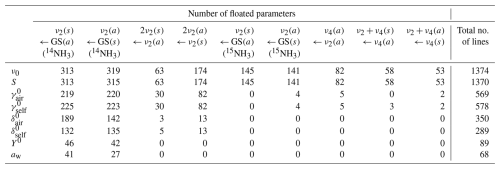
The principal focus of this work is the ν₂ band, however there are a number of other weaker bands present in the spectral region of interest. Table 4 lists the vibrational assignments of these bands along with the rotational lines and isotopologues that were included in the fit. In total, parameters were fit for 1374 lines with intensities above a threshold of 1 × 10⁻²³ cm⁻¹ (molec. cm⁻²)⁻¹. For the weakest of these lines, only positions and intensities were determined; for the strongest, the whole suite of parameters listed in Table 3 were determined. In general, self- and air-broadened Lorentz halfwidths were fit for lines with intensities above 4 × 10⁻²² cm⁻¹ (molec. cm⁻²)⁻¹ and self- and air-pressure-induced shifts for lines with intensities above 1.5 × 10⁻²¹ cm⁻¹ (molec. cm⁻²)⁻¹. Selected lines of intensity > 7.5 × 10⁻²¹ cm⁻¹ (molec. cm⁻²)⁻¹ were fit for one or both of speed dependence and Rosenkranz line mixing parameters. The total number of each type of line parameter determined for each of the bands listed in Table 4 is given in Table 5.

Table 6 Measured parameters at 296 K for lines (labelled ${}^{\mathrm{\Delta }}K\mathrm{\Delta }J(J^{\prime \prime },K^{\prime \prime }{)}_{i^{\prime \prime }}$) with spectral intensity > 1 × 10⁻²¹ cm⁻¹ (molec. cm⁻²)⁻¹ for the transition ν₂(s)←GS(a). The numbers in parentheses are 1σ uncertainties in the units of the last digit listed. Missing entries indicate a lack of convergence for a given parameter, which was set to zero in the final solution. An asterisk (^∗) indicates that the line parameter was fixed to its value in HITRAN 2020. A table of line parameters with spectral intensity < 1 × 10⁻²¹ cm⁻¹ (molec. cm⁻²)⁻¹ for this transition is provided in the Supplement.

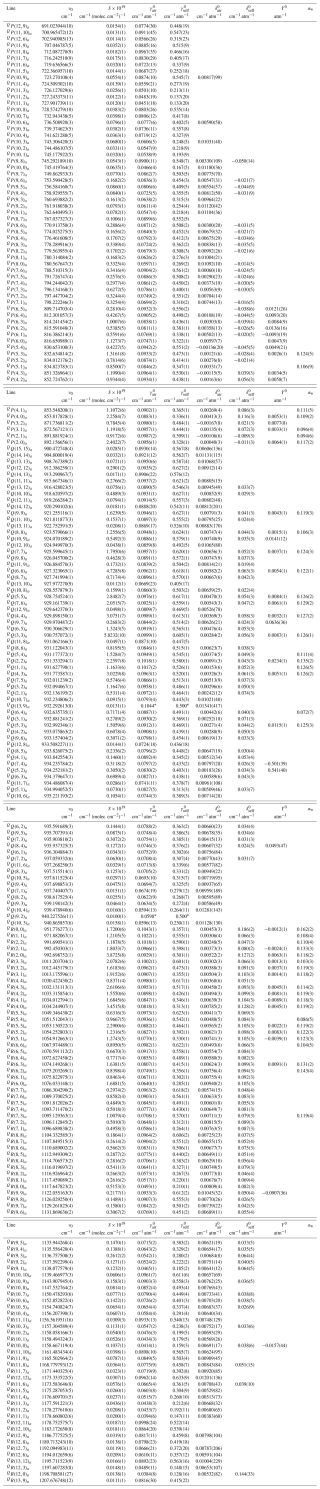
Table 7 Measured parameters at 296 K for lines (labelled ${}^{\mathrm{\Delta }K}\mathrm{\Delta }J(J^{\prime \prime },K^{\prime \prime }{)}_{i^{\prime \prime }}$) with spectral intensity > 1 × 10⁻²¹ cm⁻¹ (molec. cm⁻²)⁻¹ for the transition ν₂(a)←GS(s). The numbers in parentheses are 1σ uncertainties in the units of the last digit listed. Missing entries indicate a lack of convergence for a given parameter, which was set to zero in the final solution. An asterisk (^∗) indicates that the line parameter was fixed to its value in HITRAN 2020. A table of line parameters with spectral intensity < 1 × 10⁻²¹ cm⁻¹ (molec. cm⁻²)⁻¹ for this transition is provided in the Supplement.

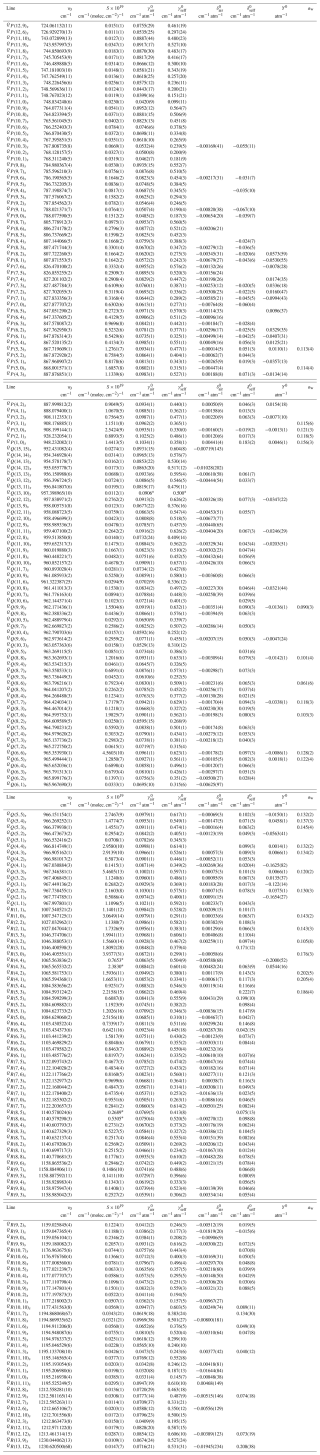
Tables 6 and 7 list the newly derived line parameters for lines with an intensity > 1 × 10⁻²¹ cm⁻¹ (molec. cm⁻²)⁻¹ at 296 K for the 0100 00 0 s ← 0000 00 0 a and the 0100 00 0 a ← 0000 00 0 s transitions. This intensity cut-off was selected because in all but two cases, it was the minimum required to enable floating of the pressure-induced line shift parameters. Throughout this work we will often refer to these transitions using the shorthand notation ν₂(s)←GS(a) and ν₂(a)←GS(s), respectively. Tables in the Supplement include line parameters for the lines with lower intensity, line parameters for the ¹⁵NH₃ isotopologue, and the other transitions listed in Table 4.

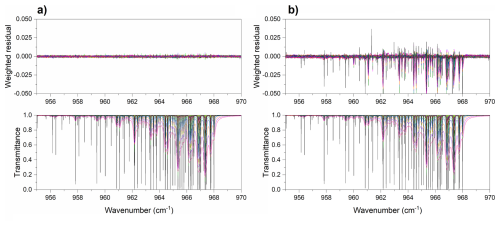
Figure 3 Overlay of all the transmittance spectra across the ν₂(a)←GS(s) Q branch, 955–970 cm⁻¹, alongside their weighted residuals using (a) the new line parameters determined in the present study, and (b) the line parameters from the HITRAN 2020 database.

Figure 3 shows the spectral region covering the ν₂(a)←GS(s) Q branch, with spectral residuals that result from our fit (Fig. 3a) compared to those obtained using the values from HITRAN 2020 (Fig. 3b). A significant improvement over the fit residuals in Fig. 3b are obtained in Fig. 3a as a result of using the line parameters determined from our multispectrum fit.

In order to analyse our measured dataset, we produced a number of plots of the individual line parameters, comparing our new line parameters for the NH₃ ν₂ band to those reported in the HITRAN 2020 database (Gordon et al., 2021). HITRAN is chosen here for the primary comparison because its NH₃ linelist forms the basis for the majority of remote sensing datasets of NH₃ in the Earth's atmosphere. Unless explicitly stated otherwise, the plots shown in the following sections display comparisons of data for the Q branch of the ν₂(a)←GS(s) transition. Analogous comparison plots for the P and R branch for this transition, along with the P, Q and R branches of the ν₂(s)←GS(a) transition, can be found in the Supplement. As long as sufficient parameters were available, similar comparison plots are shown in the Supplement for the other, less intense bands found in the measured spectral window. In every case, the uncertainties in the plots represent Labfit internal uncertainties at three standard deviations (3σ) for additional clarity. All uncertainties in tables are listed at 1σ.

4.1 Uncertainties of the retrieved parameters

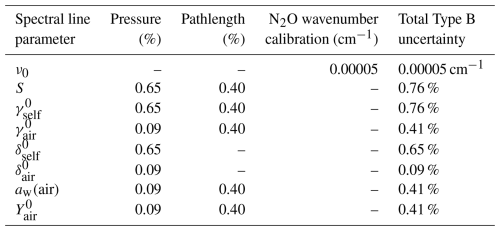
The line parameter uncertainties directly provided by Labfit (Benner et al. 1995) correspond to Type A uncertainties (Joint Committee for Guides in Metrology, 2008), and are determined from the noise level of the spectrum, the spectral residuals, and the derived parameters in the solution. Labfit does not report Type B uncertainties (Joint Committee for Guides in Metrology, 2008) of the line parameters arising from uncertainties in quantities such as the sample conditions (i.e., temperature, pressure, pathlength), the partition sums, issues with the instrumental lineshape of the spectrometer, and uncertainties arising from a poor choice of lineshape function, so we calculate these Type B contributions separately. The overall uncertainty can be found by adding the Type A and Type B contributions in quadrature and taking the square root.

Table 8 Type B uncertainties (k = 1) for the measured NH₃ line parameters.

Type B contributions are outlined in Table 8 and detailed below. The assumption we made in this study is that 1σ measurement uncertainties can be used to represent the maximum Type B uncertainty contributions to the derived line parameters; therefore all uncertainties presented here correspond to a 68 % confidence interval with a coverage factor k = 1. There are a number of contributions that are very small and so are not included in this table. For example, as the majority of parameters are temperature-dependent, there will be a very small uncertainty due to possible deviation of the true temperature from 296 K. An uncertainty of 0.05 K will contribute no more than 0.02 % to the Type B budget. Additionally, the stated NH₃ purity was 99.98 %, so we can assume that the uncertainty on the absorber amount is no more than 0.02 %.

The NIST N₂O lines (Maki and Wells, 1991) used for the wavenumber calibration in the present analysis have stated uncertainties of ∼ 0.00005 cm⁻¹, which we can equate to a Type B uncertainty in the retrieved line positions. The other line parameters have contributions to their Type B uncertainty from uncertainties in pathlength and absorber pressure. The pathlength contribution is determined from the calibration process, namely 0.1 % uncertainty in N₂O pressures, 0.24 % uncertainty in N₂O line intensities (Devi et al., 2003), and 0.3 % resulting from the spectral fit.

Uncertainties in the pressures depend on which of the manometer pressure gauges were used for the pressure measurements and their calibrations; all were factory calibrated using reference gauges traceable to the PTB standard. During the multispectrum fitting procedure, some of the pressures for the pure spectra needed small adjustments on account of small inconsistencies in the spectral residuals. We made the assumption that the highest pure pressure (0.995 hPa) was the most reliable because it was made near the full scale of the (1 Torr) manometer; we spent the most attention in the lab to ensure this measurement was as accurate as possible. Inconsistencies in the lower pressures were assumed to arise from problems with outgassing in the cell; there was no evidence of this for the 0.995 hPa pure spectrum. The line intensity, self-broadened halfwidth, and self-pressure-induced shift parameters are most sensitive to the pure NH₃ pressure measurements, which are estimated to have ∼ 0.65 % uncertainty (derived from the 0.995 hPa pure spectrum). The air-broadened halfwidths, air-pressure-induced shifts, speed dependence of the air-broadened halfwidth and line mixing parameters are most sensitive to the partial pressure of air. For the range 200–1000 mbar pressure of air used in our experiments we have assumed a representative estimation of 0.09 % uncertainty. Given the small amount fraction of NH₃ in air (less than ∼ 0.004), the contribution of NH₃ partial pressure uncertainties is minimal. Also note that the pressure-induced shifts do not depend on cell pathlength, and represent wavenumber differences so that the absolute wavenumber calibration has minimal contribution. Lastly, it should be noted that Rosenkranz line mixing used in the present analysis is only an approximation, and therefore the uncertainty contributions from its use cannot easily be quantified.

The total uncertainties in our line parameters compare favourably to those for the corresponding line parameters in HITRAN 2020. For the strongest lines, uncertainties in line positions are comparable, in the range 0.00001–0.0001 cm⁻¹. For the strongest lines in the Q branches of the v₂ band, the total uncertainties of our line intensities, and self- and air-broadened Lorentz halfwidths are of the order of 1 %, a significant improvement over those reported in HITRAN 2020: 10 %–20 %, 2 %–5 %, and 2 %–5 %, respectively.

4.2 Line positions

Newly determined line positions (ν₀) have been compared with those from the HITRAN 2020 database, whose positions are based upon the analysis of Down et al. (2013), by plotting the position differences in Fig. 4a. For the ν₂(a)←GS(s) Q branch lines up to J = 6, our line positions are higher by up to 0.00005 cm⁻¹, comparable to the uncertainty (∼ 0.00005 cm⁻¹) of the N₂O lines from the NIST heterodyne wavenumber calibration tables (Maki and Wells, 1991) used in the wavenumber calibration. For lines with J > 6, our line positions tend to be lower than those reported in HITRAN 2020, although these lines are weaker with lower SNR in our overall analysis, and therefore the differences show more scatter. Table 9 reports that the average position difference between the new values and those from HITRAN is positive for the P, Q and R branches of both the ν₂(a)←GS(s) and ν₂(s)←GS(a) transitions, with the P and R branches displaying a greater shift in position than the Q branches.

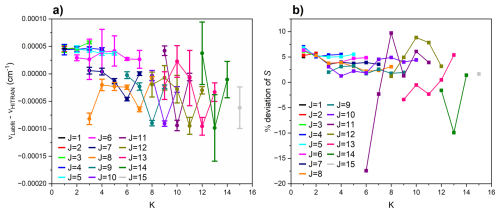
Figure 4 (a) Differences between the measured line positions and those from HITRAN 2020 (Gordon et al., 2021) for the NH₃ ν₂(a)←GS(s) Q branch lines, with 3σ error bars, and (b) percentage deviations in intensity between the measured line intensities and those from HITRAN 2020 for the NH₃ ν₂(a)←GS(s) Q branch lines. For both cases, only lines with intensity > 1 × 10⁻²¹ cm⁻¹ (molec. cm⁻²)⁻¹ are plotted.

Table 9 Average absolute position differences, and percentage deviations of intensity and Lorentz halfwidths between parameters derived in this work and those in HITRAN 2020 (Gordon et al., 2021); the percentage deviations are calculated as 100 (Labfit $/$ HITRAN − 1). The values were determined from lines with intensity S > 1 × 10⁻²¹ cm⁻¹ (molec. cm⁻²)⁻¹ at 296 K. Halfwidth deviations were only determined for those lines with distinct halfwidth parameters for the analogous lines in HITRAN 2020, as opposed to set values discussed in Sect. 4.4.

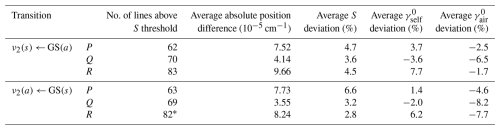
^∗ For the ν₂(a)←GS(s) R branch, four lines (two pairs) were blended together. In order to fit the other line parameters, their intensities were fixed to the values from HITRAN 2020.

4.3 Line intensities

The line intensity calculation is driven by the five pure NH₃ spectra in the multispectrum fit. Of these, the lowest pressure (0.0171 hPa) NH₃ spectrum has no saturated lines; the transmittance of the strongest line is ∼ 0.17. Each line has at least one, usually more, unsaturated pure measurements from which to derive intensities. Because the lowest pressure measurements are less accurate, pressure values are adjusted in the fit so that the residuals align with those for the spectrum with the most accurate pressure (0.995 hPa). This adjustment is largely driven by the unsaturated lines that are present throughout multiple spectra. While Fig. 4a shows differences between our measured line positions and those from HITRAN 2020 (Gordon et al., 2021) for the NH₃ ν₂(a)←GS(s) Q branch lines, Fig. 4b shows a plot of the percentage deviations of our measured spectral line intensities (S) against those from the HITRAN 2020 database (Gordon et al., 2021), again with intensities based on the work of Down et al. (2013). The scatter in percentage deviation as J increases is a consequence of the relative decrease in SNR for these high-J lines. Overall, our line intensities are slightly higher than those in HITRAN 2020. Considering only lines with S > 1 × 10⁻²¹ cm⁻¹ (molec. cm⁻²)⁻¹ at 296 K, we report an average increase in S of 3.4 % for lines in the two ν₂←GS Q branches. Similar increases of 3 %–7 % are observed for the P and R branches; see Table 9 for further information.

4.4 Self- and air-broadened Lorentz halfwidths

Figures 5a and 6a show the present measured self- (${\mathit{\gamma }}_{\mathrm{self}}^{\mathrm{0}}$) and air- (${\mathit{\gamma }}_{\mathrm{air}}^{\mathrm{0}}$) broadened halfwidths for all lines with intensity > 1 × 10⁻²¹ cm⁻¹ (molec. cm⁻²)⁻¹ at 296 K compared to the corresponding values from HITRAN 2020, which were derived by Nemtchinov et al. using a polynomial function of m and K, apparently only from measurements in the P and R branches of the ν₂ band (Nemtchinov et al., 2004). Our measured values are found to show the same general trend, with both ${\mathit{\gamma }}_{\mathrm{self}}^{\mathrm{0}}$ and ${\mathit{\gamma }}_{\mathrm{air}}^{\mathrm{0}}$ increasing with K for the same J value. However, there are notable differences between the magnitudes of our halfwidths and those from HITRAN. Average percentage deviations of our measured parameters from HITRAN for the ν₂(a)←GS(s) Q branch are plotted in Figs. 5b and 6b, with averages for other branches listed in Table 9 for both ${\mathit{\gamma }}_{\mathrm{self}}^{\mathrm{0}}$ and ${\mathit{\gamma }}_{\mathrm{air}}^{\mathrm{0}}$. We observe significant deviations from the Nemtchinov-derived values, 4 %–10 % for ${\mathit{\gamma }}_{\mathrm{self}}^{\mathrm{0}}$ and 2 %–8 % for ${\mathit{\gamma }}_{\mathrm{air}}^{\mathrm{0}}$. Analysis of the individual branches shows that the ${\mathit{\gamma }}_{\mathrm{self}}^{\mathrm{0}}$ are 2 %–4 % lower than the Nemtchinov values in the Q branches but 1 %–4 % and 6 %–8 % higher for the P and R branches, respectively. The ${\mathit{\gamma }}_{\mathrm{air}}^{\mathrm{0}}$ percentage deviations demonstrate a consistent pattern of overestimation by HITRAN 2020; our values are 2 %–5 %, 6 %–8 %, and 2 %–8 % lower for the P, Q, and R branches, respectively. In addition, we report values of the halfwidth parameters for J^′′ > 8 for the first time. Previously, in HITRAN 2020, ${\mathit{\gamma }}_{\mathrm{self}}^{\mathrm{0}}$ values for J^′′ > 8 were set to 0.5, while ${\mathit{\gamma }}_{\mathrm{air}}^{\mathrm{0}}$ values for J^′′ > 8 were based on the widths reported for lower J values, using an extrapolation of the width parameters determined by Nemtchinov et al. (2004).

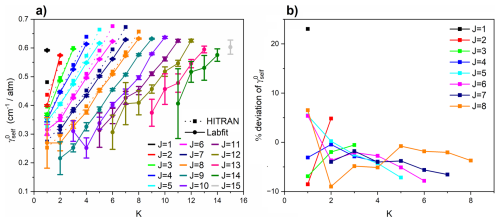
Figure 5 Plots of (a) self-broadened halfwidth, ${\mathit{\gamma }}_{\mathrm{self}}^{\mathrm{0}}$, and (b) percentage deviations from HITRAN of ${\mathit{\gamma }}_{\mathrm{self}}^{\mathrm{0}}$ plotted against K for each J value of the ν₂(a)←GS(s) Q branch. The Labfit values of ${\mathit{\gamma }}_{\mathrm{self}}^{\mathrm{0}}$ are included with uncertainties of 3σ. For J > 8, HITRAN values for the self-broadened halfwidth were all set to 0.5, so percentage deviations have not been calculated for these cases.

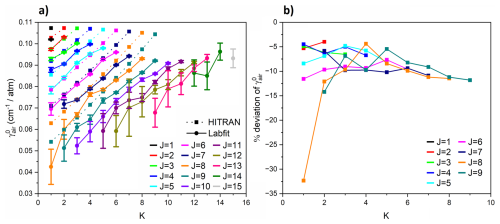
Figure 6 Plots of (a) air-broadened halfwidth, ${\mathit{\gamma }}_{\mathrm{air}}^{\mathrm{0}}$, and (b) percentage deviations from HITRAN of ${\mathit{\gamma }}_{\mathrm{air}}^{\mathrm{0}}$ plotted against K for each J value of the ν₂(a)←GS(s) Q branch. The Labfit values of ${\mathit{\gamma }}_{\mathrm{air}}^{\mathrm{0}}$ are included with uncertainties of 3σ. For J > 9, HITRAN values for the air-broadened halfwidth were set to the same value as their corresponding K value at J = 9 (with values of K > 9 set to the value for K = 9), so percentage deviations have not been calculated for these cases.

4.5 Self- and air-pressure-induced shifts

Figure 7 reports the self- (${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$) and air- (${\mathit{\delta }}_{\mathrm{air}}^{\mathrm{0}}$) pressure-induced shifts for lines with an intensity > 1 × 10⁻²¹ cm⁻¹ (molec. cm⁻²)⁻¹ at 296 K. Since the HITRAN 2020 database does not list any values for ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ or ${\mathit{\delta }}_{\mathrm{air}}^{\mathrm{0}}$ for NH₃, we report values for these parameters for the complete ν₂ band for the first time. Due to the optimisation of our experimental measurements for atmospheric conditions, i.e. the smaller range of NH₃ pressures than air pressures, we observe larger errors in our determination of ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ compared with ${\mathit{\delta }}_{\mathrm{air}}^{\mathrm{0}}$.

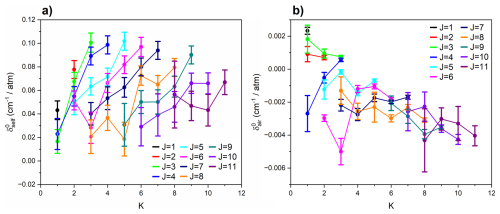
Figure 7 Plots of (a) self-pressure-induced shifts, ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$, and (b) air-pressure-induced shifts, ${\mathit{\delta }}_{\mathrm{air}}^{\mathrm{0}}$, against K for each J value of the ν₂(a)←GS(s) Q branch. Measured values are plotted with uncertainties of 3σ. The HITRAN 2020 database does not include values for these parameters.

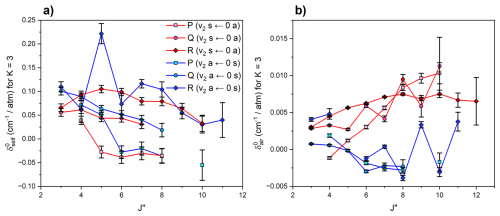
Figure 8 Plots of (a) self-pressure-induced shifts, ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$, and (b) air-pressure-induced shifts, ${\mathit{\delta }}_{\mathrm{air}}^{\mathrm{0}}$, against J^′′ for K = 3, for the P, Q and R branches of the ν₂(s)←0(a) and ν₂(a)←GS(s) transitions. The present measured values are given with uncertainties of 3σ. The HITRAN 2020 database does not include values for these parameters in this band.

According to Fig. 7a, the values of our measured ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ parameters for the ν₂(a)←GS(s) transition tend to decrease with increasing J, but increase with increasing K. A plot of ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ against J^′′ for only K = 3 levels is shown in Fig. 8a, and further indicates that the decrease in ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ with increasing J holds for all three branches of the two ν₂←GS transitions, with the exception of a single line in the R branch. Figure 8b indicates a tendency for ${\mathit{\delta }}_{\mathrm{air}}^{\mathrm{0}}$ values associated with the ν₂(a)←GS(s) Q branch to decrease with both increasing J and K (apart from two more R branch lines). However, the plot of ${\mathit{\delta }}_{\mathrm{air}}^{\mathrm{0}}$ against J^′′ for K = 3 in Fig. 8b suggests that the trend of ${\mathit{\delta }}_{\mathrm{air}}^{\mathrm{0}}$ with J is dependent on the symmetry of the transition, unlike for ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$. For P, Q, R branches of the ν₂(s)←GS(a) transition, ${\mathit{\delta }}_{\mathrm{air}}^{\mathrm{0}}$ increases with J^′′, but for P, Q, R branches of the ν₂(a)←GS(s) transition, ${\mathit{\delta }}_{\mathrm{air}}^{\mathrm{0}}$ decreases with J^′′. There are not enough fitted ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ and ${\mathit{\delta }}_{\mathrm{air}}^{\mathrm{0}}$ values for the other transitions to provide a more detailed analysis of these J-dependent observations.

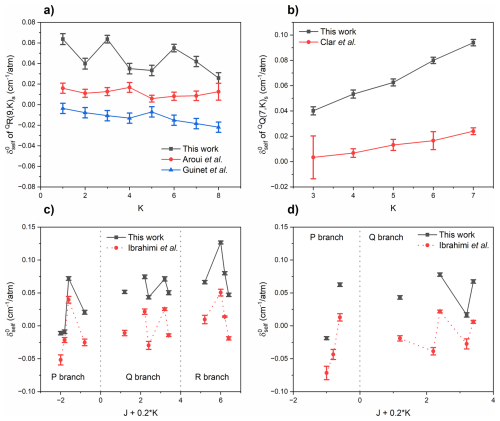
Figure 9 Comparison plots of self-pressure-induced shifts, ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$, from our work and other papers, against K, for (a) the R branch of the ν₂(s)←GS(a) transition, where J = 9; (b) the Q branch of the ν₂(a)←GS(s) transition, where J = 7; (c) the P, Q and R branches of the ν₂(s)←GS(a) transition; (d) the P and Q branches of the ν₂(a)←GS(s) transition. Unlike other plots, uncertainties are plotted here as 1σ to better compare with the previous studies. The HITRAN 2020 database does not include values for these parameters in this band.

Although values of ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ are not currently included in the HITRAN or GEISA databases, we were able to compare our values to previous data in the literature. Aroui et al. (2009) and Guinet et al. (2011) recorded measurements of several pure NH₃ spectra at wavenumbers > 1000 cm⁻¹ and at spectral resolutions of 0.0038 and 0.005 cm⁻¹ respectively. They determined ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ values for several lines in the ν₂(s)←GS(a) R branch. Figure 9a shows a comparison plot of ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ for our work against both studies, for values where J = 9. We predict higher ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ values, an average increase of 0.0333 cm⁻¹ atm⁻¹ from Aroui et al. (2009) and 0.0570 cm⁻¹ atm⁻¹ from Guinet et al. (2011). The data from Guinet et al. (2011) does however obey the same trend of ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ decreasing with K as found in our data.

With regards to the P and Q branches, Clar et al. (1988) and Ibrahimi et al. (1999) recorded measurements of several lines for both ν₂(s)←GS(a) and ν₂(a)←GS(s) transitions using tuneable diode laser spectrometers. Figure 9b shows a comparison plot of ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ values against the data from Clar et al. (1988) for ν₂(a)←GS(s), where J = 7. We observe an average increase of 0.0532 cm⁻¹ atm⁻¹ from the work of Clar et al. (1988), and the same general trend of increasing ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ with increasing K for the Q branch. Figure 9c and d show comparison plots of ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ against the values from Ibrahimi et al. (1999) for ν₂(s)←GS(a) and ν₂(a)←GS(s) respectively. We observe an average increase of 0.0545 cm⁻¹ atm⁻¹ from the work of Ibrahimi et al. (1999), and observe the same general trends of ${\mathit{\delta }}_{\mathrm{self}}^{\mathrm{0}}$ with J and K.

We found no studies reporting ${\mathit{\delta }}_{\mathrm{air}}^{\mathrm{0}}$ values, and thus cannot make any comparisons to our values.

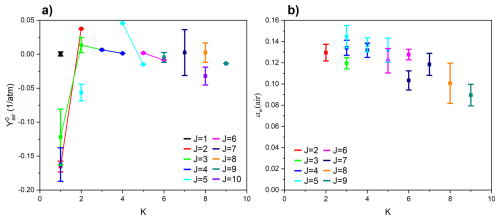
Figure 10 Plots of (a) Rosenkranz line mixing parameter, $Y_{\mathrm{air}}^{\mathrm{0}}$, and (b) speed dependence of the halfwidth parameter, a_w(air), against K for each J value of the ν₂(a)←GS(s) Q branch. The present measured values are shown with uncertainties of 3σ. The HITRAN 2020 database does not include values for these line parameters of NH₃.

4.6 Rosenkranz line mixing and speed dependence

Figure 10a shows the Rosenkranz line mixing parameters, $Y_{\mathrm{air}}^{\mathrm{0}}$, plotted against the quantum number K for lines of the ν₂(a)←GS(s) Q branch where values were determinable. The largest values of $Y_{\mathrm{air}}^{\mathrm{0}}$ for this transition occur for K =1 levels. The lines corresponding with the parameters in Fig. 10a span a wavenumber range of 1 cm⁻¹, and there is significant overlap between the lines when air-broadened at pressures approaching 1000 hPa. Line mixing parameters are almost exclusively fit for the Q branches, which are more congested than the P and R branches.

Figure 10b provides a plot of the speed dependence of the width parameter, a_w(air), where this parameter was determinable, against K for lines in the ν₂(a)←GS(s) Q branch. The results show a decrease in a_w as J and K increase, although this trend is not observed in the Q branch for the ν₂(s)←GS(a), where a_w remains constant across all values of J and K. We report an average value for a_w of 0.131 for ν₂(a)←GS(s) and 0.118 for ν₂(s)←GS(a).

As an illustration of the benefit in floating both $Y_{\mathrm{air}}^{\mathrm{0}}$ and a_w(air) parameters in the multispectrum fit, the plots in Fig. 11 show the final spectral fit residuals for both ν₂ Q branches, compared with residuals calculated from the same fit but with all $Y_{\mathrm{air}}^{\mathrm{0}}$ and a_w(air) values set to zero. It is clear that the inclusion of each parameter in the multispectrum fit improves the residuals, bringing them closer to zero.

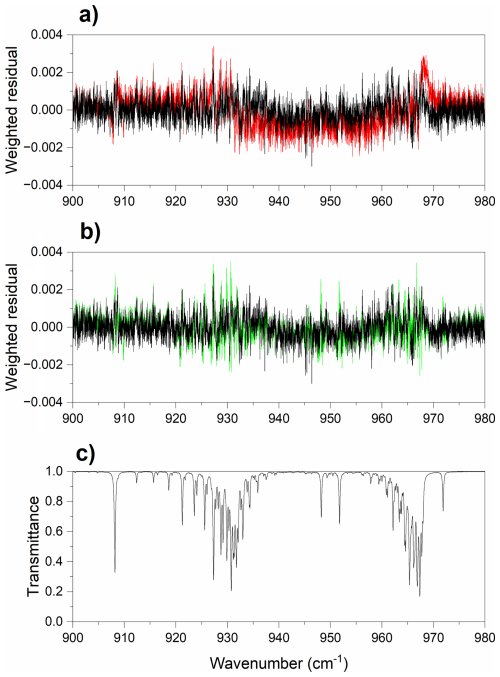
Figure 11 Comparison plots over the spectral region containing the ν₂ Q branches (900–980 cm⁻¹) of the weighted fit residuals for the measured highest-pressure spectrum (total pressure 978.3 hPa): (a) with (black) and without (red) the inclusion of Rosenkranz line mixing; (b) with (black) and without (green) the inclusion of speed dependence; panel (c) shows the measured laboratory transmittance spectrum.

5 Conclusions

We have carried out the most complete experimental and multispectrum analysis of air-broadened NH₃ over the 675 to 1250 cm⁻¹ spectral region to date. This spectral region covers the most intense NH₃ features observed in atmospheric spectra, the 0100 00 0 s ← 0000 00 0 a and 0100 00 0 a ← 0000 00 0 s transitions of the v₂ band. Our analysis utilises the Voigt and speed-dependent Voigt lineshapes (depending on the SNR of the lines), with Rosenkranz line mixing for congested Q-branches. In all, we derive line positions, line intensities, self- and air-broadened Lorentz halfwidths, self- and air-pressure-induced line shifts, the speed dependence of the air-broadened Lorentz halfwidths, and first-order (Rosenkranz) line mixing parameters. Our derived spectroscopic line parameters reproduce the new laboratory measurements substantially better than those from the HITRAN 2020 database. We have revised values for parameters such as line intensities and air-broadened Lorentz halfwidths, in some cases by almost 10 %. For the strongest lines, the total uncertainties of key parameters such as line intensities, and self- and air-broadened Lorentz halfwidths have been considerably improved to ∼ 1 %. In addition to the measured speed dependence and Rosenkranz line mixing parameters, which we believe are the first reported for the v₂ band of NH₃ in air, we also determine a range of parameters for the v₂ band that are not currently in HITRAN, for example self- and air-pressure-induced shifts. We expect these new parameters to provide a more accurate basis for incorporation into atmospheric radiative transfer models to measure NH₃ concentrations from satellite.