the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The ratio of transverse to longitudinal turbulent velocity statistics for aircraft measurements
Marie Lothon
Donald H. Lenschow
Szymon P. Malinowski
The classical theory of homogeneous isotropic turbulence predicts that the ratio of transverse to longitudinal structure functions or power spectra is equal to in the inertial subrange. For the typical turbulence cascade in the inertial subrange, it also predicts a power law scaling with an exponent of and for the structure functions and the power spectra, respectively. The goal of this study is to document the statistics of those ratios and exponents derived from aircraft observations, quantify their departures from theoretical predictions, and point out the differences among the aircraft.
We estimate the transverse-to-longitudinal ratios and the scaling exponents from in situ high-rate turbulence measurements collected by three research aircraft during four field experiments in two regimes of the marine atmospheric boundary layer: shallow trade-wind convection and subtropical stratocumulus. The bulk values representing the inertial subrange were derived by fitting power law formulae to the structure functions and to the power spectra computed separately for the three components of the turbulent wind velocity measured in horizontal flight segments. The composite scale-by-scale transverse-to-longitudinal ratios were derived by averaging over the segments at common non-dimensional scales.
The variability in the results can be attributed to how the wind velocity components are measured on each aircraft. The differences related to environmental conditions, e.g. between characteristic levels and regimes of the boundary layer, are of secondary importance. Experiment-averaged transverse-to-longitudinal ratios are 23 %–45 % smaller than predicted by the theory. The deviations of average scaling exponents with respect to the theoretical values range from −34 % to +47 % for structure functions and from −24 % to +22 % for power spectra, depending on experiment and velocity component. The composite scale-by-scale transverse-to-longitudinal ratios decrease and increasingly depart from with decreasing scale, in contrast to previous experimental studies on local isotropy. The reason for the disagreement in transverse-to-longitudinal ratios between the observations and the theory remains uncertain.
- Article
(8282 KB) - Full-text XML
- BibTeX
- EndNote
1.1 Theoretical background
According to the theory of homogeneous isotropic turbulence formulated by Kolmogorov (Kolmogorov, 1941), which is introduced in many classical textbooks (e.g. Pope, 2000, Chap. 6), the second-order longitudinal and transverse velocity structure functions in the inertial subrange can be approximated as
respectively, where r is the separation distance, ϵ is the turbulence kinetic energy dissipation rate, and BL and BT are constants. Due to isotropy and homogeneity, the ratio of those structure functions is
Analogous to structure functions, one-dimensional longitudinal and transverse velocity power spectra in the inertial subrange are
respectively, where k is the longitudinal wavenumber, CL and CT are constants, and
Only one of the four constants needs to be determined experimentally, as due to isotropy they are functionally related. The approximate values are BL ≈ 2.0, BT ≈ 2.6, CL ≈ 0.49 and CT ≈ 0.65 (e.g. Saddoughi and Veeravalli, 1994; Sreenivasan, 1995).
Kolmogorov did not specify precise limits for the applicability of his theory. Instead, his famous hypotheses state that sufficiently far from the boundaries of the domain for a turbulent fluid (e.g. the surface and top of the atmospheric boundary layer, ABL) and for a sufficiently large Reynolds number, a range of scales exists where the turbulent velocity statistics are isotropic and universal. Nevertheless, the simplicity of this theory is considered advantageous in experimental practice. On the other hand, we note that there have been some recent theoretical advancements examining non-stationary, non-homogeneous or non-isotropic conditions (e.g. Gomes-Fernandes et al., 2015; Wacławczyk et al., 2022).
Longitudinal direction is defined by the 2-point separation vector r. The directions perpendicular to it are transverse (see Pope, 2000, Chap. 6.2). In experimental studies, typically frozen turbulence approximation is invoked to compute multi-point statistics, such as structure functions or power spectra. Then, longitudinal direction is determined by the velocity vector of a probe with respect to a turbulent medium (see Pope, 2000, Chap. 6.5). In the case of a rapidly moving platform, e.g. aircraft, taking the limit of infinite probe velocity allows us to consider the measurement record as an instantaneous state of a turbulent medium, e.g. air, along a one-dimensional segment. In the case of a probe that is stationary with respect to the ground, e.g. at a meteorological mast, the velocity of the probe with respect to the air is simply opposite to the air velocity with respect to the ground, i.e. wind. The classical Taylor hypothesis (Taylor, 1938) allows us to use mean wind velocity to convert measured time series into an instantaneous state of turbulent air along a one-dimensional segment oriented in the same direction as the mean wind. Such approximations are justified as long as the probe velocity – true air speed for aircraft or mean wind for a mast – is much larger than the turbulence velocity scale. Often, the measurement method implies that the longitudinal direction is horizontal. Then, one of the transverse directions is vertical, and the remaining third dimension is called lateral. Following a typical convention, we denote the longitudinal, lateral and vertical velocity components as u, v and w, respectively. As both v and w are transverse, and as well as and are expected to equal in homogeneous isotropic turbulence.
1.2 Measurements in the surface layer
The local isotropy hypothesis has been extensively tested in wind tunnels (e.g. Saddoughi and Veeravalli, 1994) and with ground-based measurements in the atmospheric surface layer (e.g. Kaimal et al., 1972; Katul et al., 1995, 1997; Siebert and Muschinski, 2001; Chamecki and Dias, 2004). The ground-based experiments typically rely on three-component ultrasonic anemometers mounted at various heights z above the surface.
Kaimal et al. (1972) analysed measurements collected at three heights on a 32 m tower in a range of stable and unstable conditions during the 1968 Kansas experiment (Haugen et al., 1971). They examined the onset of local isotropy using scale-by-scale ratios of power spectra and found that the isotropic value of is gradually approached with decreasing scale. For , this is observed at wavelengths λ comparable to z in unstable conditions and 1/10 of the Obukhov length LO in stable conditions. In general, the critical wavelength decreases with the stability parameter . reaches the isotropic ratio at scales about 8 times larger than . The onset of local isotropy is directly related to the onset of the universal Kolmogorov scaling in Pw. The scaling in Pu starts at a larger scale, while in Pw it starts at a smaller scale than in Pv. Therefore, the adequate scaling observed in Pw implies local isotropy. Kaimal et al. (1972) explained their results by the combined effects of shear and buoyancy on small-scale eddies. They argued that only eddies with small timescales compared to the production scales can be isotropic.
Katul et al. (1995) and Katul et al. (1997) performed similar measurements up to z ≈ 5 m in the unstable surface layer. They found that and are approximately for the scales below . Katul et al. (1995) suggested that the two mechanisms responsible for anisotropy – buoyancy and wind shear – superimpose under stable conditions, where buoyancy damps the vertical and shear enhances the horizontal fluctuations, but counteract under unstable conditions, where buoyancy strengthens the vertical fluctuations instead. Therefore, local isotropy can be more easily achieved in unstable surface layers but is not observed down to the very small scales in stable surface layers, as was previously shown by Kaimal et al. (1972).
Siebert and Muschinski (2001) tested their ultrasonic anemometer at z = 2.8 and 5.5 m. They obtained the ratios and approaching at λ < in agreement with Kaimal et al. (1972). It was noted that decreases at small scales because the spectral transfer function representing the low-pass filtering at scales close to sonic path drops more rapidly with frequency for w than for u.
Chamecki and Dias (2004) measured wind velocity fluctuations at z ≈ 4 m in a range of stable and unstable conditions. They found that although and reach at small scales, and are systematically smaller than down to the scale of the instrument resolution (conservatively estimated as 36 cm for the horizontal and 63 cm for the vertical components). was even further from the isotropic value than was. It was attributed to a relatively shorter extension of inertial range in the structure functions in comparison to the power spectra.
1.3 Measurements above the surface layer
The measurements of turbulent wind velocity far from the surface require more advanced platforms. For example, Kaimal et al. (1976) probed the convective mixed layer up to ∼ 1200 m with a tethered kite balloon during the 1973 Minnesota experiment (Readings et al., 1974). Their system involved five lightweight cup anemometers mounted along the rope. Although they do not explicitly discuss the local isotropy, their results imply that the spectral ratios and are in the mixed layer at scales smaller than 1/10 of the ABL height zi. Kaimal et al. (1982) reached the lower mixed layer with the Boulder Atmospheric Observatory 300 m tower, which was instrumented with sonic anemometers analogous to those used in the surface layer (see Sect. 1.2). They observed the isotropic value for and at λ < . Siebert et al. (2006b) analysed two measurement series collected in shallow cumulus clouds at ∼ 760 and ∼ 1540 m with an instrumented platform, the Airborne Cloud Turbulence Observation System (ACTOS; Siebert et al., 2006a), that included a sonic anemometer, carried by a tethered balloon. In their first experiment, and were approximately in the range of scales about 0.4–8 m. In the second experiment, those ratios were also relatively close to the isotropic value, however with systematically higher and systematically lower than .
Nowak et al. (2021) analysed measurements from the same ACTOS platform, carried instead by a helicopter, in coupled and decoupled marine stratocumulus-topped ABLs during the Azores Stratocumulus Measurements of Radiation, Turbulence and Aerosols (ACORES) campaign (Siebert et al., 2021). They compared turbulence kinetic energy dissipation rates ϵ derived separately from u and w by fitting the Kolmogorov scaling Eqs. (1) and (3) to structure functions and power spectra in the range of 0.4–40 m, which was assumed to represent the inertial subrange. The ratios used in that work, one derived from structure functions and one from power spectra, within the selected range of scales are in fact equivalent to or , respectively. Those derived from power spectra were systematically lower than those derived from structure functions (the reason thereof was not clear). The results exhibit strong local fluctuations, which were attributed to the steep helicopter ascents or descents. The averaged values are nearly constant across the depth of the coupled ABL (equivalent to ≈ 1.16 and ≈ 0.88). In the decoupled ABL, they were smaller and differed between its sublayers (equivalent to ≈ 0.74 and ≈ 0.59 in the lower part and ≈ 0.53 and ≈ 0.47 in the cloud). Such a variation was explained by the separation of the ABL into two major circulations featuring contrasting turbulence properties.
In the same study, Nowak et al. (2021) presented the scale-by-scale spectral ratio computed from horizontal flight segments at a few heights. In the coupled ABL (at three levels therein), the isotropic value was approximately attained for the scales from 5 to 100 m. The ratio decreases for larger scales, presumably due to the finite distance from the surface or from the capping inversion (zi ∼ 850 m), and for smaller scales arguably due to instrumental issues. In the decoupled ABL, the maximum was larger than at intermediate scales. The range where ≳ was narrower and differed between the four levels considered. Interestingly, it was related to the fact that the depths of the two sections of the decoupled ABL are shallower than the coupled ABL, although the entire decoupled one is deeper in total (zi ∼ 1050 m). They also speculated that the scales where > might represent the typical sizes of surface layer plumes for the lowest segment and represent cloud-top downdraughts for the highest segment.
Despite several studies reviewed above that exploited very tall tower observatories, unique tethered balloon platforms or helicopter-borne platforms, turbulent wind velocity far from the surface is typically measured in situ from research aircraft in the course of intensive field experiments (e.g. Nicholls, 1984; Duynkerke et al., 1995; Lenschow et al., 2000; Malinowski et al., 2013; Brilouet et al., 2021). Research aircraft capable of turbulence measurements are often equipped with a five-hole radome probe with pressure transducers and a Pitot tube for air velocity measurements, as well as an inertial navigation system coupled to a GPS unit. The three components of the wind velocity are computed by adding the aircraft velocity with respect to the earth and the velocity of air with respect to the aircraft, which is inferred from the true air speed (TAS) and attack and sideslip angles (Brown et al., 1983; Lenschow, 1986; Lenschow and Spyers-Duran, 1989). TAS is obtained from the measurements of total and static pressure, whereas attack and sideslip angles are determined from the differential pressure between vertically and horizontally aligned ports of the five-hole probe, respectively. This technique requires careful calibration for each specific aircraft, which is carried out using a series of calibration manoeuvres (Lenschow and Spyers-Duran, 1989; Kalogiros and Wang, 2002). For a typical TAS of about 100 m s−1 and a sampling rate of a few tens of hertz, commonly used instruments provide a spatial resolution of a few metres. A few studies applied fast-response hot-wire or hot-film anemometers to reach better resolutions (Sheih et al., 1971; Merceret, 1976a, b; Lenschow et al., 1978), but ensuring the long-term maintenance of those instruments is more difficult.
Although the three components of the wind velocity are measured, many of the subsequent analyses utilize mostly the vertical component to calculate variance and turbulent fluxes (e.g. Nicholls and Leighton, 1986; Tjernström and Rogers, 1996; Faloona et al., 2005; Zheng et al., 2011), which are of primary interest for the structure of the ABL as well as for heat and moisture transport (Stull, 1988). Others estimate the turbulence kinetic energy dissipation rate ϵ, which is considered a practical measure of turbulence strength and an important parameter for cloud microphysics (Grabowski and Wang, 2013) and turbulence parameterization in mesoscale or global models (Mauritsen et al., 2007). Because the dissipative scales (of the order of millimetres) are hardly resolved in aircraft measurements, the microscopic definition of ϵ (e.g. Pope, 2000, Chap. 5) cannot be directly applied. Instead, the universal scaling of the turbulent velocity statistics in the resolved inertial subrange (Eqs. 1 or 3) is often exploited in practice to derive ϵ from moderate resolution airborne measurements (e.g. Lambert and Durand, 1999; Siebert et al., 2006b; Jen-La Plante et al., 2016; Wacławczyk et al., 2020). In such an approach, the assumptions of the theory, including local isotropy and homogeneity, are taken for granted even though in the atmosphere there are directions naturally distinguished on larger scales due to buoyancy and wind shear (e.g. Lenschow, 1974; Darbieu et al., 2015).
A few studies have attempted to consider the limitations of the theory, for example by comparing the estimates of ϵ derived from the three velocity components independently (e.g. Jen-La Plante et al., 2016). Lothon and Lenschow (2005a, 2007) reported transverse-to-longitudinal ratios of power spectra close to 1 instead of the theoretical in the DYCOMS-II experiment (Stevens et al., 2003) made with the NSF/NCAR C130 research aircraft (UCAR/NCAR - Earth Observing Laboratory, 1994) in marine stratocumulus. Lothon and Lenschow (2005b) extended this analysis for several other field experiments made with the same aircraft – GOTEX (Romero and Melville, 2010), IDEAS (Stith and Rogers, 2004), RICO (Rauber et al., 2007b) and EPIC (Raymond et al., 2004) – which covered marine and continental boundary layers, with stratocumulus, cumulus or clear-sky conditions. They found ratios equal to about 0.8 on average, but they suggested that the results might be influenced by the upstream flow distortion. This appears forward of the aircraft due to the air being deflected by the wings and the fuselage when approaching them. After applying a correction for upstream flow distortion due to the wings, became close to on average. However, this correction does not impact , which then remained approximately 0.8. Pedersen et al. (2018) considered the scale-by-scale ratio of horizontal-to-vertical velocity spectra below the stratocumulus top for the DYCOMS-II and POST (Carman et al., 2012; Malinowski et al., 2013; Gerber et al., 2013) experiments. They found strong scale dependence, with an average close to 1 at λ < zi and the values ranging from about 1 to 10 at higher λ (see Fig. 2 therein). Nevertheless, there are still rather few works investigating the proportion between transverse and longitudinal velocity statistics in airborne measurements in the ABL, likely because most estimates of the dissipation rate have been obtained from one wind velocity component only.
Likewise, the scaling exponents in the inertial subrange have not been extensively investigated experimentally in the ABL. Lothon and Lenschow (2005a, b, 2007) reported an average Pw exponent of about −2 instead of the theoretical in the five field experiments mentioned above. However, as a result of their upstream flow distortion correction, it became approximately −1.5. The exponents for Pv and Pu averaged about −1.8 and −1.5, respectively. Darbieu et al. (2015) studied the evolution of Pw in turbulence decay during the afternoon transition. They observed that the slopes of the spectra were steeper than the theoretical ones in the fully convective phase, which they potentially related to the role of coherent convective structures and associated anisotropy. On the other hand, they found that the slopes gradually flatten during the afternoon transition to become considerably flatter than the theoretical values around sunset. Nowak et al. (2021) found exponents for both structure functions and power spectra relatively close to those from the theory in coupled stratocumulus-topped ABL, but these exponents were significantly smaller in absolute values and highly variable with altitude in the decoupled case.
1.4 Overview of the current study
The inspiration for this study originates from the surprising results we encountered while analysing the dissipation rates derived independently from the three wind velocity components measured by an aircraft in a trade-wind ABL. This motivated us to generalize our analysis by focusing on the transverse-to-longitudinal ratio, by focusing on the scaling of second-order velocity statistics and by considering other aircraft participating in other field campaigns. Therefore, here we compare the observed ratio of transverse and longitudinal statistics (structure functions and power spectra) in the inertial subrange with the theoretical value of . Secondly, we compare the observed scaling of structure functions and power spectra with the theoretical exponents of and , respectively. For this purpose, we use open datasets for four field experiments involving three different aircraft.
The paper is structured as follows. Section 2 introduces the measurements of turbulence collected during four field experiments, together with the available datasets, and explains the selection of data for our study. Section 3 describes the methods used to derive the relevant parameters. Section 4 presents the transverse-to-longitudinal ratio and inertial subrange scaling and compares them with the theoretical predictions. Section 5 discusses the possible reasons for and consequences of the observed departure from the theoretical values. Finally, our findings are summarized in the last section.
2.1 Field experiments
The measurements considered in this study were performed during four field experiments:
-
EUREC4A (Elucidating the role of cloud–circulation coupling in climate) in January–February 2020 in a trade-wind cumulus regime in the northwestern Atlantic (Stevens et al., 2021),
-
RICO (Rain in Cumulus Over Ocean) in November 2004–January 2005 in a trade-wind cumulus regime in the northwestern Atlantic (Rauber et al., 2007b),
-
VOCALS-REx (Variability of the American Monsoon Systems Ocean-Cloud-Atmosphere-Land Study Regional Experiment) in October–November 2008 in a subtropical stratocumulus regime in the southeastern Pacific (Wood et al., 2011),
-
POST (Physics of the Stratocumulus Top) in July–August 2008 in a subtropical stratocumulus regime in the northeastern Pacific (Carman et al., 2012; Malinowski et al., 2013; Gerber et al., 2013).
The objectives, strategy and execution of the experiments are described in the references given above. EUREC4A addressed many research questions comprising atmospheric circulation, clouds, rain formation, life cycle of particulate matter, upper-ocean processes and air–sea interaction. The meteorological conditions and the structure of the ABL observed during EUREC4A are analysed in detail by Albright et al. (2022). RICO investigated the mechanism of rain formation in shallow cumuli and its feedback on the structure and variability in those clouds. VOCALS-REx studied interactions between aerosols, microphysics, precipitation and radiation in marine stratocumulus, as well as physical and chemical couplings between the upper ocean and the lower atmosphere in the region of one of the strongest coastal upwellings. POST focused in particular on processes occurring at the interface between the stratocumulus-topped ABL and the free troposphere.
2.2 Aircraft
The turbulence measurements in the ABL analysed here were obtained with three research aircraft:
-
SAFIRE (the French facility for airborne research) ATR42 (SAFIRE, 2024) during EUREC4A,
-
NSF/NCAR (National Science Foundation – National Center for Atmospheric Research) C130 (UCAR/NCAR - Earth Observing Laboratory, 1994) during RICO and VOCALS-REx,
-
NPS CIRPAS (Naval Postgraduate School – Center for Interdisciplinary Remotely Piloted Aircraft Studies) Twin Otter (TO; NASA Airborne Science Program, 2024) during POST.
The three aircraft are equipped with five-hole radome probes, and the three components of turbulent wind velocity are computed similar to the methods described by Lenschow (1986). The aircraft differ in size and cruising speed. The C130, ATR and TO feature wingspans of about 40, 25 and 20 m, respectively. The typical TAS of the ATR is ∼ 100 m s−1, which with a sampling rate of fs = 25 Hz provides a spatial resolution of Δr = TAS ∼ 4 m. The TAS, sampling rate and resolution for the C130 are the same as for the ATR. The typical TAS of the TO is ∼ 55 m s−1, which with fs = 40 Hz gives a resolution of Δr ∼ 1.4 m. For the ATR during EUREC4A, the instrumentation and sampling strategy are described in Bony et al. (2022), while the turbulence measurements are described in Brilouet et al. (2021).
2.3 Datasets
The turbulence data for the four experiments were downloaded from public datasets (Lothon and Brilouet, 2020; UCAR/NCAR - Earth Observing Laboratory, 2011a, b; Khelif, 2009, for EUREC4A, RICO, VOCALS-REx and POST, respectively). For EUREC4A, RICO and VOCALS-REx, turbulent wind velocity is given in the longitudinal–lateral–vertical coordinate system. The longitudinal direction is along the velocity of aircraft with respect to air as explained in Sect. 1.1. For POST, turbulent wind velocity is given in the eastward–northward–vertical coordinate system. We computed the longitudinal u and lateral v components by rotating eastward and northward components by the aircraft's true heading angle.
2.4 Flight segments
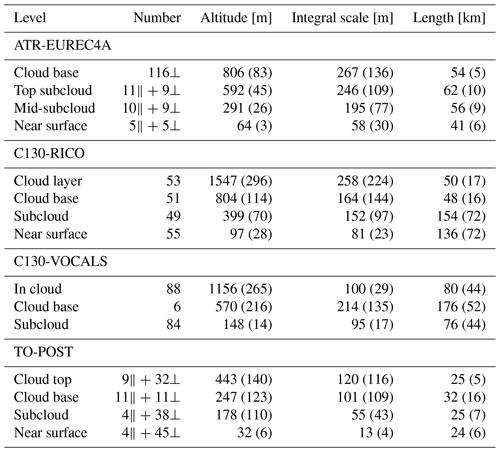
We analyse only horizontal flight segments in the ABL. The fixed flight pattern during EUREC4A included straight horizontal segments at four levels: close to the cloud base, near the top of the subcloud layer, in the middle of the subcloud layer and near the surface. The segments were flown either parallel or perpendicular to the mean wind direction. During RICO, the flights included horizontal circles (∼ 60 km diameter) above the surface and below the cloud base as well as straight horizontal segments at various heights in the subcloud and cloud layers. In VOCALS-REx, the flights included straight horizontal segments mostly at ∼ 100 m or inside the cloud. During POST, the flights included straight horizontal segments typically at three levels in the ABL: close to the cloud top, near the cloud base and near the surface.
For EUREC4A, we applied the definition of segments and their classification according to level (cloud base, top subcloud, mid-subcloud, near surface) from the same dataset as the turbulence records (Lothon and Brilouet, 2020). In the case of VOCALS-REx, we used segment timestamps and levels (in cloud, cloud base, subcloud) from the related dataset devoted to lidar measurements (Leon et al., 2011).
For RICO and POST, no a priori segment information is available, which is why we developed our own segmentation algorithm based on the conditions of small derivatives of altitude and true heading with respect to distance (see Appendix A). We also crudely classified the detected segments according to characteristic levels. The classification is only approximate, as the detailed characterization of ABL stratification in each of the flights is beyond the scope of this study. In the case of RICO, we marked the segments below 990 hPa as near surface, between 990 and 950 hPa as subcloud, between 950 and 900 hPa as cloud base, and between 900 and 800 hPa as cloud layer, following Fig. 5 of Rauber et al. (2007b). For POST, we exploited the information on average cloud base height and average cloud top height for each flight from Table 1 of Carman et al. (2012), together with the measurements of liquid water content (LWC) obtained from the Particle Volume Monitor (Gerber et al., 1994) available in a separate dataset (Gerber, 2009). The table given in Carman et al. (2012) misses one flight (RF09); hence, for this flight we inferred cloud top and cloud base heights from Table 1 of Gerber et al. (2013). We defined the cloud middle as the height halfway between the base and the top. Based on the LWC, we estimated cloud fraction in each segment as the fraction of data points where LWC > 0.02 g m−3. The segments below 60 m were marked as near surface. The segments above 60 m and below the cloud middle were considered subcloud if the cloud fraction was smaller than 0.5 and cloud base if the cloud fraction was at least 0.5. The segments above the cloud middle for which the cloud fraction was at least 0.5 were classified as cloud top. The others, which did not meet the above criteria, were not included in the analysis.
Brilouet et al. (2021) report several technical difficulties encountered during EUREC4A, e.g. concerning one of the radome transducers in flights RF02 to RF08 and the failure of inertial navigation in RF20, and conclude that flights RF09 to RF19 had much better quality data. For this reason, we considered those 11 flights only. From other experiments, we used all flights available in the datasets.
The segment number, average altitude and length for each experiment and level are summarized in Table 1. In EUREC4A and POST, most of the segments were flown either approximately parallel or perpendicular to the mean wind direction. Hence, we distinguish them in the following figures by filled and open symbols, respectively.
Table 1Statistics of the segments considered in the analysis: number of segments at each level, average altitude, length and integral length scale for vertical wind velocity (defined in Sect. 3). Standard deviations are given in parentheses. For EUREC4A and POST, the number of segments is written as the sum of the numbers of segments flown approximately parallel (∥) and perpendicular (⟂) to the mean wind direction.
The bulk lateral-to-longitudinal and vertical-to-longitudinal ratios of structure functions and the analogous ratios of power spectral densities and for each segment were calculated with the methods similar to those used in Sect. 4.3 of Nowak et al. (2021) to estimate dissipation rates. Structure functions Di computed for each velocity component i=u, v, w from linearly detrended records were averaged in five logarithmically equidistant bins covering the selected fitting range (defined further). The ratios were obtained by dividing parameters Bi resulting from the least-squares fit of the relationship (see Eq. 1):
Power spectral densities Pi were computed from linearly detrended velocity records using the Welch algorithm (Welch, 1967) with a window length of 1 km and a window overlap of 0.5 km. Similarly to Di, they were averaged in five logarithmically equidistant bins covering the fitting range, and the ratios were obtained by dividing parameters Ci resulting from the least-squares fit of the relationship (see Eq. 3):
where f is frequency. In addition, we evaluated the scaling exponents of structure functions si and power spectra pi with separate least-squares fits of the formulae,
performed on the same averaged points as for the fits of Eqs. (5) and (6). The parameters , are not used in further analyses. The estimation of the uncertainties in the computed transverse-to-longitudinal ratios and scaling exponents is discussed in Appendix B.
The choice of the fitting ranges was guided by the spatial resolution of the measurements (see Sect. 2.2), by the integral length scale for the vertical velocity (given in Table 1) and by the manual inspection of the observed extension of power-law scaling, in particular for the segments at the lowest levels. The integral length scale L was estimated as the distance at which the autocorrelation function of vertical velocity declines by a factor of e (see Nowak et al., 2021, Sect. 4.5). In the case of EUREC4A, RICO and VOCALS-REx, we applied the fitting ranges of [2Δr, L] for Di and [4Δr, 2L] for Pi. The lower ends correspond to twice the smallest r and twice the Nyquist frequency, respectively. For POST, we applied the ranges of [3Δr, L] and [6Δr, 2L] in order to avoid the influence of a spurious peak at ∼ 5.5 m corresponding to the frequency of ∼ 10 Hz, which is symptomatic in most of the segments. Figures 1 and 2 show structure functions and power spectra, respectively, together with the universal scaling reference and the corresponding fitting range for single segments from each of the four experiments. The sensitivity of the results to the choice of the fitting range is discussed in Appendix C.
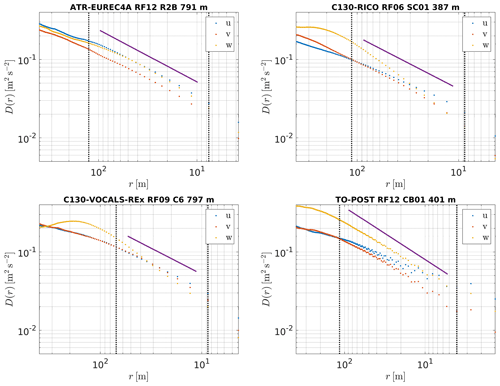
Figure 1Structure functions for single segments from each experiment. The aircraft, experiment, flight, segment name and segment altitude are given in the panel titles. The solid purple line denotes the universal scaling. The vertical dotted black lines mark the extents of the selected fitting ranges. Note that the orientation of the horizontal axis is from large to small scales.
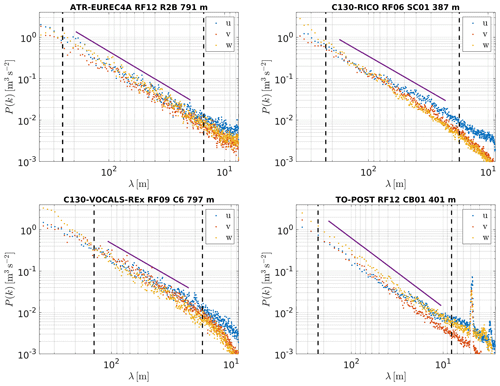
Figure 2Power spectral densities for single segments from each experiment. The aircraft, experiment, flight, segment name and segment altitude are given in the panel titles. The solid purple line denotes the universal scaling. The vertical dashed black lines mark the extents of the selected fitting ranges.
The different fitting ranges for Di and Pi are used here following the remarks given by Chamecki and Dias (2004) and Wacławczyk et al. (2020). The former found a shorter extension of the inertial subrange in the structure functions in comparison to the power spectra (which manifests in the diverging ratios and ). The latter derived ϵ with inertial scaling methods and found that the best agreement with reference ϵ is achieved for the structure function fitting range moved towards smaller scales in comparison to the fitting range for power spectra. We observed that the power law in power spectra typically extends to scales larger than our estimation of the integral length scale.
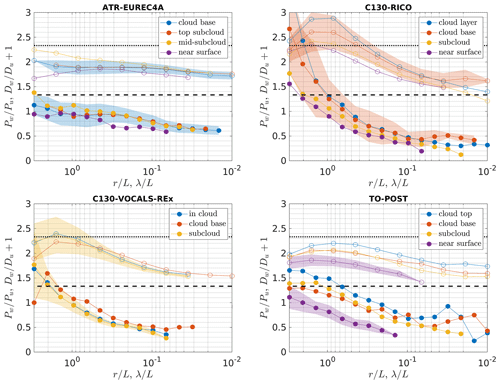
The scale-by-scale ratios of structure functions and power spectral densities were calculated similarly to Sect. 4b of Siebert et al. (2006b) and Sect. 4.4 of Nowak et al. (2021). The relevant statistics were first averaged in logarithmically equidistant bins covering the entire available range of scales (not only the fitting range as before), and the ratios were then computed point-by-point. This procedure is illustrated in Fig. 3 for an example segment. In order to obtain composite scale-by-scale ratios at the characteristic levels (see Table 1), the single-segment results, as those in the right panel of Fig. 3, were first interpolated to a fixed or grid, and the interpolated values were then averaged among the segments at each normalized scale.
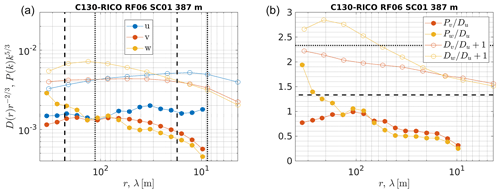
Figure 3Calculations of scale-by-scale transverse-to-longitudinal ratios of structure functions (open circles) and power spectra (filled circles) for a single segment. Panel (a) shows averaged and compensated statistics together with the corresponding fitting ranges from Figs. 1 (dotted black lines) and 2 (dashed black lines). Panel (b) shows their transverse-to-longitudinal ratios. Those for structure functions are shifted by 1 for clarity. The horizontal black lines mark the isotropic values.
The bulk lateral-to-longitudinal ratios and are presented in Fig. 4. In general, most of the points cluster in the vicinity of the value of for both ratios, in particular in the case of EUREC4A. This stands in striking contrast to the predicted for homogeneous isotropic turbulence. The largest variability is observed for POST, the smallest for EUREC4A. The former is likely connected to the segment lengths shorter than for other experiments, which increases random error (see Lenschow et al., 1994, Eq. 36); to relatively shallow ABL depth and to strong wind shear at the cloud top (Carman et al., 2012; Malinowski et al., 2013; Jen-La Plante et al., 2016). Nevertheless, and approximately agree with each other in all the experiments. There are only minor differences between the levels within the experiments; see the average values reported in Table 2. The level averages range from 0.67 to 0.97. The experiment averages range from 0.72 to 0.94, which is 30 %–46 % smaller than the theoretical value. The experiment-averaged lateral-to-longitudinal ratio is the largest for VOCALS-REx and the smallest for POST. The average values are roughly in agreement with Lothon and Lenschow (2005b) for all the experiments and levels.
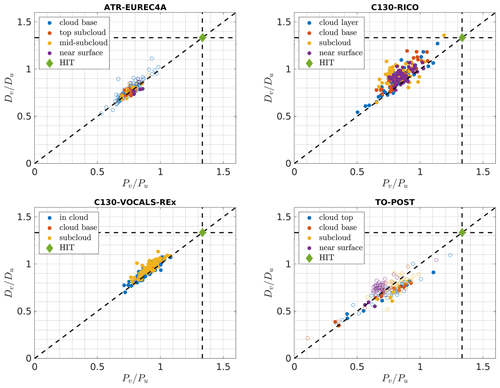
Figure 4The bulk lateral-to-longitudinal ratios of structure functions with respect to the analogous ratios of the power spectra. Each circle denotes one segment. For EUREC4A and POST, filled and open symbols correspond to the segments flown parallel and perpendicular to the mean wind direction, respectively. Colours denote characteristic levels of the boundary layer (see Sect. 2.4 and Table 1). Horizontal and vertical dashed black lines mark the value . The diagonal dashed black line denotes the 1:1 proportion. The green diamond shows the theoretical prediction for homogeneous isotropic turbulence (HIT).
Table 2Average values of the ratios of structure functions and power spectra. Standard deviations are given in parentheses.
The bulk vertical-to-longitudinal ratios and are shown in Fig. 5. Almost all of the points are far from the predicted value. The largest variability is observed for POST and RICO, the smallest for EUREC4A. In contrast to the lateral-to-longitudinal ratios, the differences between the aircraft are more significant. Apart from distinct variability, there is little difference between RICO and VOCALS-REx, both of which involved the C130. For EUREC4A and POST, approximately agrees with . For RICO and VOCALS-REx, is systematically higher than . There are also some variations between the levels (see the averages given in Table 2), possibly due to the impact of buoyancy or mean wind shear (see Darbieu et al., 2015; Pedersen et al., 2018; Akinlabi et al., 2019). For example, on average the mid-subcloud level exhibits higher ratios than other levels for EUREC4A, while there are lower ratios observed in the near surface than in the cloud layer and at the cloud base for POST and RICO. The level averages range from 0.80 to 1.11 for and from 0.64 to 1.10 for , which is 16 %–40 % and 17 %–52 % smaller than the theoretical value.
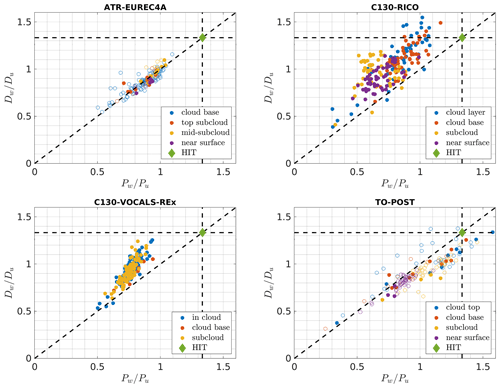
Figure 5As in Fig. 4 but for the vertical-to-longitudinal ratios. One point for RICO (in the cloud layer) and one point for POST (at the cloud top) lie outside the range presented here.
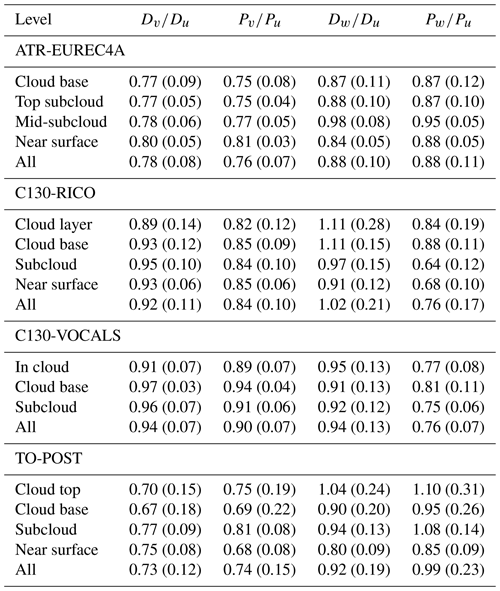
Figure 6 presents the exponents s and p. The points are dispersed in the neighbourhood of the predictions s = and p = . There are considerable differences between velocity components. The clusters of points representing the longitudinal component are almost separated from those for the transverse components in the case of RICO, VOCALS-REx and POST. The differences related to the aircraft are also visible. The variations among the levels within the experiments are rather minor. Hence, we report the average values for entire experiments in Table 3. The experiment-averaged structure function exponents can be from 0.44 for su to 0.98 for sw, i.e. 34 % lower and 47 % higher than the predicted . The experiment-averaged power spectra exponents take values from 1.26 for pu to 2.03 for pw, which are 24 % lower and 22 % higher than . Particularly close to the theoretical predictions are the average exponents for EUREC4A, su for RICO, and sv and pv for POST. For RICO and VOCALS, average pw is close to 2, in agreement with the results of Lothon and Lenschow (2005a, b, 2007) before applying their upstream flow distortion correction.
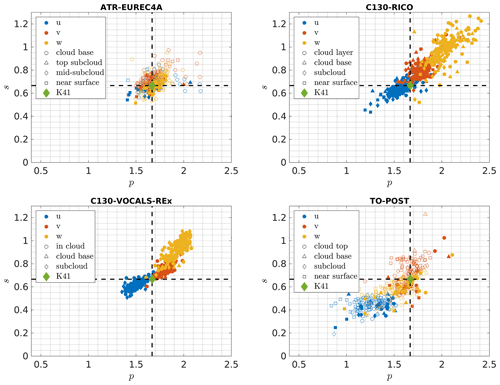
Figure 6The exponents of structure functions s with respect to the exponents of power spectra p. Each circle denotes one segment. For EUREC4A and POST, filled and open symbols correspond to the segments flown parallel and perpendicular to the mean wind direction, respectively. Colours denote velocity components, while different symbols denote characteristic levels of the boundary layer (see Sect. 2.4 and Table 1). Dashed black lines mark the theoretical values of and . The green diamond shows the prediction of the Kolmogorov theory (K41).
Table 3Average values of the scaling exponents of structure functions and power spectra. Standard deviations are given in parentheses.

The composite scale-by-scale lateral-to-longitudinal ratios are presented in Fig. 7 for the range of scales from about 0.01L to 3L. The ratios are significantly smaller than throughout these scales, except only for the largest 3L in the case of RICO, VOCALS-REx and POST. This is true for the composites as well as for the majority of the individual segments, which is illustrated by the shaded range defined by the standard deviation. For clarity, the shading is shown for only one level in each experiment, but the standard deviations for other levels are of the same order. Importantly, all the curves exhibit the same overall trend, decreasing and increasingly departing from with decreasing scale. This trend corresponds well to the scalings of Dv and Pv, which are steeper than for Du and Pu (see Fig. 6 and Table 3). It is apparently the weakest in the case of EUREC4A, where the difference in scaling exponents between v and u is the smallest. Moreover, the observed scale dependence is comparable for different levels of the ABL, except for the near surface, which might be influenced by wind shear and where the integral length scales are substantially smaller than at other levels (see Table 1).
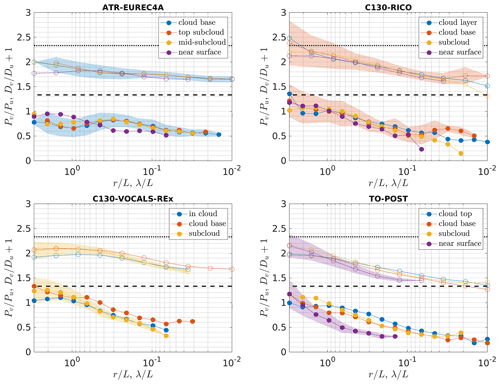
Figure 7The composite scale-by-scale lateral-to-longitudinal ratios for structure functions (open circles) and power spectra (filled circles). Colours denote characteristic levels of the boundary layers (see Sect. 2.4 and Table 1). The results for structure functions are shifted by 1 for clarity. The horizontal dotted and dashed black lines mark the isotropic values for the shifted structure functions and power spectra, respectively. The shading illustrates the range of ±1 standard deviation among the segments averaged to obtain the composite ratios. For clarity, it is drawn only for a selected level for each experiment: the cloud base for EUREC4A, the cloud base for RICO, the subcloud for VOCALS-REx and the near surface for POST.
The composite scale-by-scale vertical-to-longitudinal ratios in Fig. 8 show features similar to the lateral-to-longitudinal ratios. They are mostly smaller than , except for largest scales. With decreasing scale, they exhibit an overall decrease and an increasing departure from , in agreement with the derived scaling exponents. The curves at different levels are of similar shape but vary in magnitude more than the lateral-to-longitudinal ratios. Interestingly, particularly high values are reached at the largest scales in the case of RICO, which might be associated with cumulus convection containing strong vertical updraughts.
The increasing departure from isotropy with decreasing scale is in striking contrast to the investigations on the onset of local isotropy in the surface layer (Kaimal et al., 1972; Katul et al., 1997; Siebert and Muschinski, 2001; Chamecki and Dias, 2004), which found that the local isotropy is gradually approached with decreasing scale, and with the studies on scale-by-scale anisotropy above the surface layer (Kaimal et al., 1976, 1982; Siebert et al., 2006b; Pedersen et al., 2018; Nowak et al., 2021), which found transverse-to-longitudinal ratios relatively close to , at least in some range of scales unaffected by instrumental deficiencies.
The results of our analysis suggest that the variability in the transverse-to-longitudinal ratios and in the scaling exponents of velocity statistics can be attributed to how the velocity components are measured on the aircraft. The differences between field experiments and ABL levels seem to be of secondary importance. This motivates an examination of the details of measurement techniques and instrument properties. In general, airborne measurements suffer from errors that are often challenging to quantify because of flow distortion induced by the aircraft (Wendisch and Brenguier, 2013). Rauber et al. (2007a) reported that velocity measurements on the C130 during RICO showed attenuation at high frequencies for v and w. The measurements for VOCALS-REx probably suffered from the same issue. This can be spotted in the spectra in Fig. 2, which are representative of most of the segments. In contrast to Rauber et al. (2007a), we observe w to be more affected than v. A similar problem is evident for the TO during POST. In addition, the POST spectra exhibit a pronounced peak at ∼ 5.5 m corresponding to a frequency of ∼ 10 Hz, which is symptomatic for most of the segments. The peak may have resulted from an internal resonance of the measurement system (Djamal Khelif, personal communication, 2009). However, this effect influences the wavelengths outside our fitting range, so it does not explain the results, in particular the departure of the transverse-to-longitudinal ratios from the predicted .
The vertical-to-longitudinal ratios might be affected by the environmental conditions violating the isotropy assumption, mostly related to the impact of buoyancy. Our analysis involves measurements performed in the convective ABLs under the shallow trade-wind cumulus and subtropical stratocumulus regimes. The circulation inside both types of ABL is driven by buoyancy: primarily by negative buoyancy induced by longwave radiative cooling at the stratocumulus top (Wood, 2012) and by positive buoyancy due to surface heat fluxes in the trade-wind subcloud layer (Albright et al., 2022). Both situations lead to positive buoyancy flux across most of the mixed layer (parcels of negative buoyancy descend from the top while those with positive buoyancy rise from the surface). In general, the influence of buoyancy on turbulence anisotropy depends on the sign of the buoyancy flux, as documented, e.g. by the direct numerical simulation of stratocumulus by Akinlabi et al. (2019). Inside the cloud interior they found Pw of higher magnitude than predicted assuming local isotropy (CT ≈ 1, not 0.65). Such an excess of energy in w was attributed to buoyant forcing, which favours vertical motions, and pressure redistribution apparently insufficient to isotropise turbulence. At the very top of the cloud, Pw was strongly weakened with respect to isotropic prediction due to stable stratification and the corresponding negative buoyancy flux consuming kinetic energy. This implies > inside the cloud interior and < at its very top. Nowak et al. (2021) also observed ≳ in a stratocumulus-topped ABL within a limited range of scales. They speculated that those scales might represent typical horizontal sizes of surface layer plumes or cloud top downdraughts (see also Sect. 1.3).
In addition to buoyancy, wind shear can also modify anisotropy of turbulence by strengthening motions in a specific direction. For example, Akinlabi et al. (2019) found that large-scale flow instabilities induced by shear enhanced Pu; however this effect was limited to relatively large scales. Note that a similar idea of interplaying impacts of buoyancy and shear applies also to the surface layer. As mentioned in Sect. 1.2, Katul et al. (1995) suggested that under stable conditions buoyancy and shear superimpose in maintaining anisotropy, but under unstable conditions they counteract, resulting in more isotropic turbulence.
Nevertheless, although buoyancy and wind shear certainly affect the character of turbulence, it is unlikely that these factors explain our results. The computed and are smaller than at all levels of the ABL (see Table 2) and at almost all considered scales. Even if there was very strong wind shear, it should be concentrated near the surface and the top of the ABL. Also, the substantial deviations of and from are hardly possible to justify by either instrumental factors or boundary conditions, as they exist even in the interior (far from the surface and top) of the well-mixed ABL. Note that the uncertainties are also smaller than those deviations; see Appendix B.
Consequently, the reason for the disagreement between the observations and the theory remains uncertain. However, we presume that a potential explanation might be the uncertain influence of the flow around an aircraft, which has finite mass and complex geometry (e.g. upstream flow distortion). This issue deserves attention and further investigation, which would likely help us improve our measurements of turbulence.
In particular, the documented departure of the transverse-to-longitudinal ratio from the predicted isotropic value directly relates to the disparate estimates of the dissipation rate obtained separately for the three wind velocity components using the universal scaling as in Eqs. (1) and (3). We suggest that a way to solve this problem might be to carry out a study of the turbulence energy budget throughout the ABL with an aircraft equipped with the radome-based measuring system, using a flight and analysis strategy similar to that used by Lenschow (1974). This would be best carried out over a flat homogeneous surface in a situation of strong surface heating and light wind to maximize the ratio of buoyancy production of turbulence to shear production. By flying a series of horizontal flight legs at several levels throughout the ABL, the total production of turbulence within the ABL can be quantified from the integrated buoyancy flux, and possibly a small contribution from the shear production term near the surface, and compared to the total dissipation integrated throughout the ABL separately using all three wind component measurements to see which gives the best results. We also think that the longitudinal component is most likely to give the correct dissipation measurements since it is less affected by flow distortion and has a long history of use on many aircraft in many studies of atmospheric turbulence.
Another approach would be to compare aircraft measurements to measurements at the same height from a tall tower over a horizontally homogeneous surface. An example where this strategy was carried out is given by Kaimal et al. (1982), where turbulence measurements from a 300 m tower (the Boulder Atmospheric Observatory, which no longer exists) were compared with measurements at 150 and 300 m from a light twin-engine aircraft. They found good agreement among all the wind components in the inertial subrange, but in this case the transverse wind components on the aircraft were measured with vanes at the tip of a 3 m nose boom instead of a typical five-hole probe, which suggests that this may be an issue with the radome technique, and the comparison was carried out over gently rolling terrain.
Moreover, numerical modelling can be beneficial for quantifying the influence of flow distortion on the measurement of turbulent velocity with a five-hole probe located on the aircraft nose. For instance, large-eddy simulations of the flow around a popular model of an ultrasonic anemometer helped discern flow distortion errors depending on the azimuth angle and on the frequency of velocity variations (Huq et al., 2017). Numerical experiments are particularly important in situations where no laboratory or wind tunnel characterization is possible, such as with an accurately sized aircraft nose. However, an adequate model needs to be applied in order to account for compressibility, which may become important at inflow velocities relevant for typical aircraft.
The classical theory of homogeneous isotropic turbulence predicts that the ratios of transverse to longitudinal second-order velocity structure functions and power spectra are in the inertial subrange. In the inertial subrange, those statistics should exhibit power-law scaling with an exponent of and for the structure functions and power spectra, respectively.
We studied the transverse-to-longitudinal ratios and scaling exponents derived from high-rate pressure in situ measurements performed by three research aircraft (SAFIRE ATR42, NSF/NCAR C130, CIRPAS Twin Otter), all equipped with a high-rate five-hole radome probe, during four field experiments (EUREC4A, RICO, VOCALS-REx, POST) in two regimes of the marine atmospheric boundary layer (shallow trade-wind convection and subtropical stratocumulus).
The observed lateral-to-longitudinal ratios, and , significantly depart from the theoretical value. The experiment-averaged values are from 0.73 to 0.94, which are 30 %–46 % smaller than predicted. The differences between the levels of the ABL are hardly noticeable. There is good agreement of with .
The vertical-to-longitudinal ratios, and , exhibit higher variability. They also depart from . There are significant differences between the aircraft and some noticeable variations between the characteristic levels. Despite different ABL regimes, there is little difference between RICO and VOCALS-REx, both of which involved C130. The level averages are from 0.64 to 1.11, which are 16 %–52 % smaller than predicted.
On the other hand, the scaling exponents s and p are for the most part distributed around Kolmogorov's and power law exponents, respectively. The experiment averages differ from the predicted values by −34 % to +47 % for structure functions and by −24 % to +22 % for power spectra. There are significant differences between aircraft and between longitudinal and transverse wind velocity components. The variations among the levels are minor. The results for RICO and VOCALS-REx are similar in spite of a different ABL regime.
The composite scale-by-scale transverse-to-longitudinal ratios generally decrease and increasingly depart from with decreasing scale, in contrast to previous studies on local isotropy. The curves exhibit similar shapes but can vary in magnitude among the levels of the ABL considered.
In general, our results suggest that the variability in the transverse-to-longitudinal ratios and scaling exponents can be attributed to how the velocity components are measured on the aircraft. The differences between field experiments representing different ABL regimes and between ABL levels are of secondary importance. The explanation of the large departures of the transverse-to-longitudinal ratio from remains uncertain. This issue warrants further investigation as it is currently a major impediment to using aircraft measurements to study the structure of atmospheric turbulence.
In order to select horizontal segments in RICO and POST flights (see Sect. 2), we designed a simple algorithm that exploits the time series of altitude z, true heading ψ and TAS. The conditions are small derivatives of altitude and true heading with respect to distance x and large TAS. The continuous flight legs where all samples meet those conditions constitute segments. From such a set of segments, we take only those exceeding the minimum length (specified below) and with a small overall altitude trend.
The C130 and TO differ in size, cruising speed and other aircraft properties. Moreover, the RICO flight strategy utilized large circles at constant altitude, whereas POST utilized straight segments. Therefore, we adjusted the thresholds for those experiments separately. For C130 during RICO, we required a 4 km moving average of smaller than 10 m km−1, a 20 km moving average of smaller than 3 ° km−1 and a segment length larger than 30 km. For TO during POST, we required a 2 km moving average of smaller than 12 m km−1, a 2 km moving average of smaller than 5 ° km−1 and a segment length larger than 20 km. In both cases, the minimum acceptable TAS was 0.9 of its flight median, and the maximum acceptable altitude trend within the segment was 2 m km−1. An illustration of the segmentation algorithm applied to one of the RICO flights is given in Fig. A1.
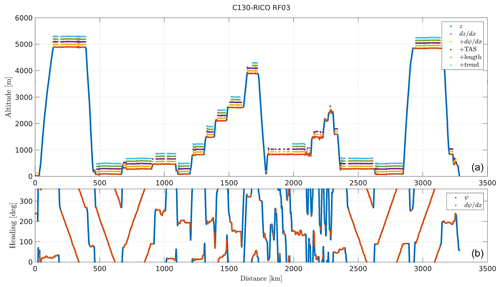
Figure A1The segmentation algorithm applied to C130 RICO flight RF03. (a) The altitude (blue) and the sample points meeting the progressively aggregated criteria of small (red), small (yellow), large TAS (purple), large segment length (green) and small overall altitude trend (cyan). (b) The true heading (blue). Sample points meeting the criterion of small are marked in red.
We did not consider the errors for the individual instruments on board research aircraft because the contributions to the final measurement error related to the characteristics of the flow around the fuselage and the environmental conditions are often significant but are hardly possible to quantify accurately. Instead, we evaluated the standard errors in the least-squares fits of the formulae in Eqs. (5), (6) and (7). Those errors are indirectly affected by the integral length scale estimates, which control the width of the fitting range.
The uncertainties in the results presented, i.e. the transverse-to-longitudinal ratios and scaling exponents, are obtained from appropriately propagated errors originating from the least-squares fits. We show their ranges in the form of box-and-whisker plots in Fig. B1. For the transverse-to-longitudinal ratios, the median values are below 0.2. In general, the lowest uncertainties are observed for EUREC4A, while the highest are for RICO and POST. The median uncertainties in s and p are below 0.05 and 0.1, respectively. Here, there is no clear tendency with respect to the experiment.

Figure B1Uncertainties in the transverse-to-longitudinal ratios and scaling exponents for structure functions and power spectra in the form of box-and-whisker plots illustrating the range of values among segments belonging to each level in each experiment. The dot inside the box denotes the median value, the box spans the interquartile range and the whiskers span the entire range.
We examined the sensitivity of the results with respect to the choice of the fitting range by repeating the computations of the transverse-to-longitudinal ratios and the scaling exponents for six different values for the upper end of this range: from 0.6L to 1.4L separation distance in the case of structure functions and from 1.2L and 2.8L wavelength in the case of power spectra. The upper end for power spectra was twice as large as for structure functions in each such test. The other parameters, including the lower end of the fitting range, were kept the same as in Sect. 3.
The results were not observed to change significantly with the fitting range. The plots in Figs. 4, 5 and 6 are to a large extent similar regardless of the fitting range considered (not shown). In Fig. C1 we present the experiment-averaged results for each test. The variations related to the changes in the fitting range are typically smaller than between the experiments and negligible in comparison to the variability among individual segments visible in Figs. 4–6.
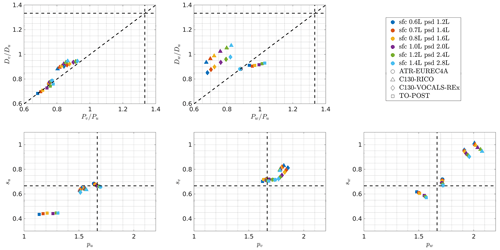
Figure C1Experiment-averaged results of transverse-to-longitudinal ratios and scaling exponents obtained for the different widths of the fitting range. Colours denote the choices for the upper end of the fitting range for structure functions (sfc) and power spectra (psd); the lower end is the same as given in Sect. 3. Different symbols denote the four experiments. The dashed black lines in the upper panels mark and the 1:1 proportion as in Figs. 4 and 5. In the lower panels, they mark the values of and as in Fig. 6. Note that the axes limits are different than in Figs. 4–6.
The data used in this study were downloaded from the public datasets at https://doi.org/10.25326/128 (Lothon and Brilouet, 2020), https://doi.org/10.5065/D64J0CDM (UCAR/NCAR - Earth Observing Laboratory, 2011a), https://doi.org/10.5065/D69K48JK (UCAR/NCAR - Earth Observing Laboratory, 2011b), https://doi.org/10.26023/KP56-KFJS-VC07 (Khelif, 2009), https://doi.org/10.26023/8KEJ-BQNG-W808 (Leon et al., 2011) and https://doi.org/10.26023/W2HT-F1E5-C50E (Gerber, 2009). The MATLAB code we developed for the purpose of this analysis is available in the repository at https://doi.org/10.5281/zenodo.11127722 (Nowak et al., 2024).
JLN designed and performed the analysis. JLN, ML, DHL and SPM wrote the paper.
At least one of the (co-)authors is a member of the editorial board of Atmospheric Measurement Techniques. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
We acknowledge the scientists and technical staff who contributed to the turbulence measurements in the four field experiments that are considered in this study.
This material is based upon work supported by the NSF National Center for Atmospheric Research, which is a major facility sponsored by the US National Science Foundation (grant no. 1852977). Jakub L. Nowak and Szymon P. Malinowski were funded by the European Union's Horizon 2020 research and innovation programme (grant no. 101003470). Jakub L. Nowak was also supported by the Foundation for Polish Science (FNP) (grant no. START050.2022).
This paper was edited by Cléo Quaresma Dias-Junior and reviewed by two anonymous referees.
Akinlabi, E. O., Wacławczyk, M., Mellado, J. P., and Malinowski, S. P.: Estimating turbulence kinetic energy dissipation rates in the numerically simulated stratocumulus cloud-top mixing layer: Evaluation of different methods, J. Atmos. Sci., 76, 1471–1488, https://doi.org/10.1175/JAS-D-18-0146.1, 2019. a, b, c
Albright, A. L., Bony, S., Stevens, B., and Vogel, R.: Observed Subcloud-Layer Moisture and Heat Budgets in the Trades, J. Atmos. Sci., 79, 2363–2385, https://doi.org/10.1175/JAS-D-21-0337.1, 2022. a, b
Bony, S., Lothon, M., Delanoë, J., Coutris, P., Etienne, J.-C., Aemisegger, F., Albright, A. L., André, T., Bellec, H., Baron, A., Bourdinot, J.-F., Brilouet, P.-E., Bourdon, A., Canonici, J.-C., Caudoux, C., Chazette, P., Cluzeau, M., Cornet, C., Desbios, J.-P., Duchanoy, D., Flamant, C., Fildier, B., Gourbeyre, C., Guiraud, L., Jiang, T., Lainard, C., Le Gac, C., Lendroit, C., Lernould, J., Perrin, T., Pouvesle, F., Richard, P., Rochetin, N., Salaün, K., Schwarzenboeck, A., Seurat, G., Stevens, B., Totems, J., Touzé-Peiffer, L., Vergez, G., Vial, J., Villiger, L., and Vogel, R.: EUREC4A observations from the SAFIRE ATR42 aircraft, Earth Syst. Sci. Data, 14, 2021–2064, https://doi.org/10.5194/essd-14-2021-2022, 2022. a
Brilouet, P.-E., Lothon, M., Etienne, J.-C., Richard, P., Bony, S., Lernoult, J., Bellec, H., Vergez, G., Perrin, T., Delanoë, J., Jiang, T., Pouvesle, F., Lainard, C., Cluzeau, M., Guiraud, L., Medina, P., and Charoy, T.: The EUREC4A turbulence dataset derived from the SAFIRE ATR 42 aircraft, Earth Syst. Sci. Data, 13, 3379–3398, https://doi.org/10.5194/essd-13-3379-2021, 2021. a, b, c
Brown, E. N., Friehe, C. A., and Lenschow, D. H.: The Use of Pressure Fluctuations on the Nose of an Aircraft for Measuring Air Motion, J. Appl. Meteorol. Clim., 22, 171–180, https://doi.org/10.1175/1520-0450(1983)022<0171:TUOPFO>2.0.CO;2, 1983. a
Carman, J. K., Rossiter, D. L., Khelif, D., Jonsson, H. H., Faloona, I. C., and Chuang, P. Y.: Observational constraints on entrainment and the entrainment interface layer in stratocumulus, Atmos. Chem. Phys., 12, 11135–11152, https://doi.org/10.5194/acp-12-11135-2012, 2012. a, b, c, d, e
Chamecki, M. and Dias, N. L.: The local isotropy hypothesis and the turbulent kinetic energy dissipation rate in the atmospheric surface layer, Q. J. Roy. Meteor. Soc., 130, 2733–2752, https://doi.org/10.1256/qj.03.155, 2004. a, b, c, d
Darbieu, C., Lohou, F., Lothon, M., Vilà-Guerau de Arellano, J., Couvreux, F., Durand, P., Pino, D., Patton, E. G., Nilsson, E., Blay-Carreras, E., and Gioli, B.: Turbulence vertical structure of the boundary layer during the afternoon transition, Atmos. Chem. Phys., 15, 10071–10086, https://doi.org/10.5194/acp-15-10071-2015, 2015. a, b, c
Duynkerke, P. G., Zhang, H. Q., and Jonker, P. J.: Microphysical and turbulent structure of nocturnal stratocumulus as observed during ASTEX, J. Atmos. Sci., 52, 2763–2777, https://doi.org/10.1175/1520-0469(1995)052<2763:MATSON>2.0.CO;2, 1995. a
Faloona, I., Lenschow, D. H., Campos, T., Stevens, B., van Zanten, M., Blomquist, B., Thornton, D., Bandy, A., and Gerber, H.: Observations of entrainment in eastern Pacific marine stratocumulus using three conserved scalars, J. Atmos. Sci., 62, 3268–3285, https://doi.org/10.1175/JAS3541.1, 2005. a
Gerber, H.: POST: Gerber scientific (GSI) 100-hz PVM - netCDF format, Version 1.0, UCAR/NCAR - Earth Observing Laboratory [data set], https://doi.org/10.26023/W2HT-F1E5-C50E, 2009. a, b
Gerber, H., Arends, B. G., and Ackerman, A. S.: New microphysics sensor for aircraft use, Atmos. Res., 31, 235–252, https://doi.org/10.1016/0169-8095(94)90001-9, 1994. a
Gerber, H., Frick, G., Malinowski, S. P., Jonsson, H., Khelif, D., and Krueger, S. K.: Entrainment rates and microphysics in POST stratocumulus, J. Geophys. Res.-Atmos., 118, 12094–12109, https://doi.org/10.1002/jgrd.50878, 2013. a, b, c
Gomes-Fernandes, R., Ganapathisubramani, B., and Vassilicos, J. C.: The energy cascade in near-field non-homogeneous non-isotropic turbulence, J. Fluid Mech., 771, 676–705, https://doi.org/10.1017/JFM.2015.201, 2015. a
Grabowski, W. W. and Wang, L.-P.: Growth of Cloud Droplets in a Turbulent Environment, Annu. Rev. Fluid Mech., 45, 293–324, https://doi.org/10.1146/annurev-fluid-011212-140750, 2013. a
Haugen, D. A., Kaimal, J. C., and Bradley, E. F.: An experimental study of Reynolds stress and heat flux in the atmospheric surface layer, Q. J. Roy. Meteor. Soc., 97, 168–180, https://doi.org/10.1002/qj.49709741204, 1971. a
Huq, S., De Roo, F., Foken, T., and Mauder, M.: Evaluation of Probe-Induced Flow Distortion of Campbell CSAT3 Sonic Anemometers by Numerical Simulation, Bound.-Lay. Meteorol., 165, 9–28, https://doi.org/10.1007/s10546-017-0264-z, 2017. a
Jen-La Plante, I., Ma, Y., Nurowska, K., Gerber, H., Khelif, D., Karpinska, K., Kopec, M. K., Kumala, W., and Malinowski, S. P.: Physics of Stratocumulus Top (POST): turbulence characteristics, Atmos. Chem. Phys., 16, 9711–9725, https://doi.org/10.5194/acp-16-9711-2016, 2016. a, b, c
Kaimal, J. C., Wyngaard, J. C., Izumi, Y., and Coté, O. R.: Spectral characteristics of surface-layer turbulence, Q. J. Roy. Meteor. Soc., 98, 563–589, https://doi.org/10.1002/QJ.49709841707, 1972. a, b, c, d, e, f
Kaimal, J. C., Wyngaard, J. C., Haugen, D. A., Coté, O. R., Izumi, Y., Caughey, S. J., and Readings, C. J.: Turbulence Structure in the Convective Boundary Layer, J. Atmos. Sci., 33, 2152–2169, https://doi.org/10.1175/1520-0469(1976)033<2152:TSITCB>2.0.CO;2, 1976. a, b
Kaimal, J. C., Eversole, R. A., Lenschow, D. H., Stankov, B. B., Kahn, P. H., and Businger, J. A.: Spectral Characteristics of the Convective Boundary Layer Over Uneven Terrain, J. Atmos. Sci., 39, 1098–1114, https://doi.org/10.1175/1520-0469(1982)039<1098:SCOTCB>2.0.CO;2, 1982. a, b, c
Kalogiros, J. A. and Wang, Q.: Calibration of a Radome-Differential GPS System on a Twin Otter Research Aircraft for Turbulence Measurements, J. Atmos. Ocean. Tech., 19, 159–171, https://doi.org/10.1175/1520-0426(2002)019<0159:COARDG>2.0.CO;2, 2002. a
Katul, G., Hsieh, C. I., and Sigmon, J.: Energy-inertial scale interactions for velocity and temperature in the unstable atmospheric surface layer, Bound.-Lay. Meteorol., 82, 49–80, https://doi.org/10.1023/A:1000178707511, 1997. a, b, c
Katul, G. G., Parlange, M. B., Albertson, J. D., and Chu, C. R.: Local isotropy and anisotropy in the sheared and heated atmospheric surface layer, Bound.-Lay. Meteorol., 72, 123–148, https://doi.org/10.1007/BF00712392, 1995. a, b, c, d
Khelif, D.: POST: UC Irvine 40-hz Probes - netCDF format, Version 1.0., UCAR/NCAR - Earth Observing Laboratory [data set], https://doi.org/10.26023/KP56-KFJS-VC07, 2009. a, b
Kolmogorov, A. N.: The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers, Dokl. Akad. Nauk SSSR, 30, 301–304, https://doi.org/10.1098/rspa.1991.0075, 1941. a
Lambert, D. and Durand, P.: The marine atmospheric boundary layer during semaphore. I: Mean vertical structure and non-axisymmetry of turbulence, Q. J. Roy. Meteorol. Soc., 125, 495–512, https://doi.org/10.1002/qj.49712555407, 1999. a
Lenschow, D. H.: Model of the Height Variation of the Turbulence Kinetic Energy Budget in the Unstable Planetary Boundary Layer, J. Atmos. Sci., 31, 465–474, https://doi.org/10.1175/1520-0469(1974)031<0465:MOTHVO>2.0.CO;2, 1974. a, b
Lenschow, D. H.: Aircraft Measurements in the Boundary Layer, in: Probing the Atmospheric Boundary Layer, American Meteorological Society, Boston, MA, 39–55, https://doi.org/10.1007/978-1-944970-14-7_5, ISBN 978-1-944970-14-7, 1986. a, b
Lenschow, D. H. and Spyers-Duran, P.: Air motion sensing, in: RAF Bulletin 23: Measurement techniques, University Corporation for Atmospheric Research, https://opensky.ucar.edu/islandora/object/:35505 (last access: 16 Decembe 2019), 1989. a, b
Lenschow, D. H., Friehe, C. A., and Larue, J. C.: The development of an airborne hot-wire anemometer system, in: Fourth Symp. on Meteorological Observations and Instrumentation, American Meteorological Society, Denver, 10–14 April 1978, 24, 463–466, 1978. a
Lenschow, D. H., Mann, J., and Kristensen, L.: How long is long enough when measuring fluxes and other turbulence statistics?, J. Atmos. Ocean. Tech., 11, 661–673, https://doi.org/10.1175/1520-0426(1994)011<0661:HLILEW>2.0.CO;2, 1994. a
Lenschow, D. H., Zhou, M., Zeng, X., Chen, L., and Xu, X.: Measurements of fine-scale structure at the top of marine stratocumulus, Bound.-Lay. Meteorol., 97, 331–357, https://doi.org/10.1023/A:1002780019748, 2000. a
Leon, D., Zuidema, P., and Leon, D.: VOCALS: NSF/NCAR C130 Radar, Lidar and Radiometer Integrated Dataset, Version 1.0, UCAR/NCAR - Earth Observing Laboratory [data set], https://doi.org/10.26023/8KEJ-BQNG-W808, 2011. a, b
Lothon, M. and Brilouet, P.: SAFIRE ATR42: Turbulence Data 25 Hz, Aeris [data set], https://doi.org/10.25326/128, 2020. a, b, c
Lothon, M. and Lenschow, D.: Status report on C-130 air-motion measurements, Tech. rep., University Corporation for Atmospheric Research, https://archive.eol.ucar.edu/raf/Projects/DYCOMS-II/DYCOMSII.issues.pdf (last access: 13 December 2023), 2005a. a, b, c
Lothon, M. and Lenschow, D.: Status-reminder report on C-130 air-motion measurements: Test of DYCOMS-II new datasets, Tech. rep., University Corporation for Atmospheric Research, https://archive.eol.ucar.edu/raf/Projects/DYCOMS-II/DYCOMS.report1_win07.pdf (last access: 13 December 2023), 2007. a, b, c
Lothon, M. and Lenschow, D. H.: Report on C-130 air-motion measurements: Spectra of the air velocity components, University Corporation for Atmospheric Research, 2005b. a, b, c, d
Malinowski, S. P., Gerber, H., Jen-La Plante, I., Kopec, M. K., Kumala, W., Nurowska, K., Chuang, P. Y., Khelif, D., and Haman, K. E.: Physics of Stratocumulus Top (POST): turbulent mixing across capping inversion, Atmos. Chem. Phys., 13, 12171–12186, https://doi.org/10.5194/acp-13-12171-2013, 2013. a, b, c, d
Mauritsen, T., Svensson, G., Zilitinkevich, S. S., Esau, I., Enger, L., and Grisogono, B.: A Total Turbulent Energy Closure Model for Neutrally and Stably Stratified Atmospheric Boundary Layers, J. Atmos. Sci., 64, 4113–4126, https://doi.org/10.1175/2007JAS2294.1, 2007. a
Merceret, F. J.: Airborne Hot-Film Measurements of the Small-Scale Structure of Atmospheric Turbulence During GATE, J. Atmos. Sci., 33, 1739–1746, https://doi.org/10.1175/1520-0469(1976)033<1739:AHFMOT>2.0.CO;2, 1976a. a
Merceret, F. J.: Measuring Atmospheric Turbulence with Airborne Hot-Film Anemometers, J. Appl. Meteorol. Clim., 15, 482–490, https://doi.org/10.1175/1520-0450(1976)015<0482:MATWAH>2.0.CO;2, 1976b. a
NASA Airborne Science Program: Twin Otter - CIRPAS - NPS, https://airbornescience.nasa.gov/aircraft/Twin_Otter_-_CIRPAS_-_NPS, last access: 25 April 2024. a
Nicholls, S.: The dynamics of stratocumulus: Aircraft observations and comparisons with a mixed layer model, Q. J. Roy. Meteor. Soc., 110, 783–820, https://doi.org/10.1002/qj.49711046603, 1984. a
Nicholls, S. and Leighton, J.: An observational study of the structure of stratiform cloud sheets: Part I. Structure, Q. J. Roy. Meteor. Soc., 112, 431–460, https://doi.org/10.1002/qj.49711247209, 1986. a
Nowak, J. L., Siebert, H., Szodry, K.-E., and Malinowski, S. P.: Coupled and decoupled stratocumulus-topped boundary layers: turbulence properties, Atmos. Chem. Phys., 21, 10965–10991, https://doi.org/10.5194/acp-21-10965-2021, 2021. a, b, c, d, e, f, g, h
Nowak, J. L., Lothon, M., Lenschow, D. H., and Malinowski, S. P.: The ratio of transverse to longitudinal turbulent velocity statistics for aircraft measurements: software, Zenodo [code], https://doi.org/10.5281/zenodo.11127722, 2024. a
Pedersen, J. G., Ma, Y. F., Grabowski, W. W., and Malinowski, S. P.: Anisotropy of observed and simulated turbulence in marine stratocumulus, J. Adv. Model. Earth Sy., 10, 500–515, https://doi.org/10.1002/2017ms001140, 2018. a, b, c
Pope, S. B.: Turbulent flows, Cambridge University Press, Cambridge, https://doi.org/10.1017/CBO9780511840531, ISBN 9780521598866, 2000. a, b, c, d
Rauber, R. M., Stevens, B., Ochs, H. T., Knight, C., Albrecht, B. A., Blyth, A. M., Fairall, C. W., Jensen, J. B., Lasher-Trapp, S. G., Mayol-Bracero, O. L., Vali, G., Anderson, J. R., Baker, B. A., Bandy, A. R., Burnet, E., Brenguier, J.-L., Brewer, W. A., Brown, P. R. A., Chuang, P., Cotton, W. R., Girolamo, L. D., Geerts, B., Gerber, H., Göke, S., Gomes, L., Heikes, B. G., Hudson, H. G., Kollias, P., Lawson, R. P., Krueger, S. K., Lenschow, D. H., Nuijens, L., O'sullivan, D. W., Rilling, R. A., Rogers, D. C., Siebesma, A. P., Snodgrass, E., Stith, J. L., Thornton, D. C., Tucker, S., Twohy, C. H., Zuidema, P., Rauber, R. M., Ochs Iii, H. T., and Di Girolamo, L.: A Supplement to Rain in Shallow Cumulus Over the Ocean: The RICO Campaign, B. Am. Meteorol. Soc., 88, S12–S18, https://doi.org/10.1175/BAMS-88-12-RAUBER, 2007a. a, b
Rauber, R. M., Stevens, B., Ochs, H. T., Knight, C., Albrecht, B. A., Blythe, A. M., Fairall, C. W., Jensen, J. B., Lasher-Trapp, S. G., Mayol-Bracero, O. L., Vali, G., Anderson, J. R., Baker, B. A., Bandy, A. R., Brunet, E., Brenguier, J. L., Brewer, W. A., Brown, P. R., Chuang, P., Cotton, W. R., Di Girolamo, L., Geerts, B., Gerber, H., Göke, S., Gomes, L., Heikes, B. G., Hudson, J. G., Kollias, P., Lawson, R. P., Krueger, S. K., Lenschow, D. H., Nuijens, L., O'Sullivan, D. W., Rilling, R. A., Rogers, D. C., Siebesma, A. P., Snodgrass, F., Stith, J. L., Thornton, D. C., Tucker, S., Twohy, C. H., and Zuidema, P.: Rain in Shallow Cumulus Over the Ocean: The RICO Campaign, B. Am. Meteorol. Soc., 88, 1912–1928, https://doi.org/10.1175/BAMS-88-12-1912, 2007b. a, b, c
Raymond, D. J., Esbensen, S. K., Paulson, C., Gregg, M., Bretherton, C. S., Petersen, W. A., Cifelli, R., Shay, L. K., Ohlmann, C., and Zuidema, P.: EPIC2001 and the Coupled Ocean–Atmosphere System of the Tropical East Pacific, B. Am. Meteorol. Soc., 85, 1341–1354, https://doi.org/10.1175/BAMS-85-9-1341, 2004. a
Readings, C. J., Haugen, D. A., and Kaimal, J. C.: The 1973 Minnesota Atmospheric Boundary Layer Experiment, Weather, 29, 309–312, https://doi.org/10.1002/J.1477-8696.1974.TB03314.X, 1974. a
Romero, L. and Melville, W. K.: Airborne Observations of Fetch-Limited Waves in the Gulf of Tehuantepec, J. Phys. Oceanogr., 40, 441–465, https://doi.org/10.1175/2009JPO4127.1, 2010. a
Saddoughi, S. G. and Veeravalli, S. V.: Local isotropy in turbulent boundary layers at high Reynolds number, J. Fluid Mech., 268, 333–372, https://doi.org/10.1017/S0022112094001370, 1994. a, b
SAFIRE: The SAFIRE ATR42 offers a big scientific payload, https://www.safire.fr/en/content_page/safire-utilisateurs/latr42-2.html, last access: 25 April 2024. a
Sheih, C. M., Tennekes, H., and Lumley, J. L.: Airborne Hot‐Wire Measurements of the Small‐Scale Structure of Atmospheric Turbulence, Phys. Fluids, 14, 201–215, https://doi.org/10.1063/1.1693416, 1971. a
Siebert, H. and Muschinski, A.: Relevance of a tuning-fork effect for temperature measurements with the Gill solent HS ultrasonic anemometer-thermometer, J. Atmos. Ocean. Tech., 18, 1367–1376, https://doi.org/10.1175/1520-0426(2001)018<1367:ROATFE>2.0.CO;2, 2001. a, b, c
Siebert, H., Franke, H., Lehmann, K., Maser, R., Saw, E. W., Schell, D., Shaw, R. A., and Wendisch, M.: Probing finescale dynamics and microphysics of clouds with helicopter-borne measurements, B. Am. Meteorol. Soc. 87, 1727–1738, https://doi.org/10.1175/BAMS-87-12-1727, 2006a. a
Siebert, H., Lehmann, K., and Wendisch, M.: Observations of small-scale turbulence and energy dissipation rates in the cloudy boundary layer, J. Atmos. Sci., 63, 1451–1466, https://doi.org/10.1175/JAS3687.1, 2006b. a, b, c, d
Siebert, H., Szodry, K.-E., Egerer, U., Wehner, B., Henning, S., Chevalier, K., Lückerath, J., Welz, O., Weinhold, K., Lauermann, F., Gottschalk, M., Ehrlich, A., Wendisch, M., Fialho, P., Roberts, G., Allwayin, N., Schum, S., Shaw, R. A., Mazzoleni, C., Mazzoleni, L., Nowak, J. L., Malinowski, S. P., Karpinska, K., Kumala, W., Czyzewska, D., Luke, E. P., Kollias, P., Wood, R., and Mellado, J. P.: Observations of Aerosol, Cloud, Turbulence, and Radiation Properties at the Top of the Marine Boundary Layer over the Eastern North Atlantic Ocean: The ACORES Campaign, B. Am. Meteorol. Soc., 102, E123–E147, https://doi.org/10.1175/bams-d-19-0191.1, 2021. a
Sreenivasan, K. R.: On the universality of the Kolmogorov constant, Phys. Fluids, 7, 2778–2784, https://doi.org/10.1063/1.868656, 1995. a
Stevens, B., Lenschow, D. H., Vali, G., Gerber, H., Bandy, A., Blomquist, B., Brenguier, J. L., Bretherton, C. S., Burnet, F., Campos, T., Chai, S., Faloona, I., Friesen, D., Haimov, S., Laursen, K., Lilly, D. K., Loehrer, S. M., Malinowski, S. P., Morley, B., Petters, M. D., Rogers, D. C., Russell, L., Savic-Jovcic, V., Snider, J. R., Straub, D., Szumowski, M. J., Takagi, H., Thornton, D. C., Tschudi, M., Twohy, C., Wetzel, M., and Van Zanten, M. C.: Dynamics and Chemistry of Marine Stratocumulus–DYCOMS-II, B. Am. Meteorol. Soc., 84, 579–594, https://doi.org/10.1175/BAMS-84-5-579, 2003. a
Stevens, B., Bony, S., Farrell, D., Ament, F., Blyth, A., Fairall, C., Karstensen, J., Quinn, P. K., Speich, S., Acquistapace, C., Aemisegger, F., Albright, A. L., Bellenger, H., Bodenschatz, E., Caesar, K.-A., Chewitt-Lucas, R., de Boer, G., Delanoë, J., Denby, L., Ewald, F., Fildier, B., Forde, M., George, G., Gross, S., Hagen, M., Hausold, A., Heywood, K. J., Hirsch, L., Jacob, M., Jansen, F., Kinne, S., Klocke, D., Kölling, T., Konow, H., Lothon, M., Mohr, W., Naumann, A. K., Nuijens, L., Olivier, L., Pincus, R., Pöhlker, M., Reverdin, G., Roberts, G., Schnitt, S., Schulz, H., Siebesma, A. P., Stephan, C. C., Sullivan, P., Touzé-Peiffer, L., Vial, J., Vogel, R., Zuidema, P., Alexander, N., Alves, L., Arixi, S., Asmath, H., Bagheri, G., Baier, K., Bailey, A., Baranowski, D., Baron, A., Barrau, S., Barrett, P. A., Batier, F., Behrendt, A., Bendinger, A., Beucher, F., Bigorre, S., Blades, E., Blossey, P., Bock, O., Böing, S., Bosser, P., Bourras, D., Bouruet-Aubertot, P., Bower, K., Branellec, P., Branger, H., Brennek, M., Brewer, A., Brilouet , P.-E., Brügmann, B., Buehler, S. A., Burke, E., Burton, R., Calmer, R., Canonici, J.-C., Carton, X., Cato Jr., G., Charles, J. A., Chazette, P., Chen, Y., Chilinski, M. T., Choularton, T., Chuang, P., Clarke, S., Coe, H., Cornet, C., Coutris, P., Couvreux, F., Crewell, S., Cronin, T., Cui, Z., Cuypers, Y., Daley, A., Damerell, G. M., Dauhut, T., Deneke, H., Desbios, J.-P., Dörner, S., Donner, S., Douet, V., Drushka, K., Dütsch, M., Ehrlich, A., Emanuel, K., Emmanouilidis, A., Etienne, J.-C., Etienne-Leblanc, S., Faure, G., Feingold, G., Ferrero, L., Fix, A., Flamant, C., Flatau, P. J., Foltz, G. R., Forster, L., Furtuna, I., Gadian, A., Galewsky, J., Gallagher, M., Gallimore, P., Gaston, C., Gentemann, C., Geyskens, N., Giez, A., Gollop, J., Gouirand, I., Gourbeyre, C., de Graaf, D., de Groot, G. E., Grosz, R., Güttler, J., Gutleben, M., Hall, K., Harris, G., Helfer, K. C., Henze, D., Herbert, C., Holanda, B., Ibanez-Landeta, A., Intrieri, J., Iyer, S., Julien, F., Kalesse, H., Kazil, J., Kellman, A., Kidane, A. T., Kirchner, U., Klingebiel, M., Körner, M., Kremper, L. A., Kretzschmar, J., Krüger, O., Kumala, W., Kurz, A., L'Hégaret, P., Labaste, M., Lachlan-Cope, T., Laing, A., Landschützer, P., Lang, T., Lange, D., Lange, I., Laplace, C., Lavik, G., Laxenaire, R., Le Bihan, C., Leandro, M., Lefevre, N., Lena, M., Lenschow, D., Li, Q., Lloyd, G., Los, S., Losi, N., Lovell, O., Luneau, C., Makuch, P., Malinowski, S., Manta, G., Marinou, E., Marsden, N., Masson, S., Maury, N., Mayer, B., Mayers-Als, M., Mazel, C., McGeary, W., McWilliams, J. C., Mech, M., Mehlmann, M., Meroni, A. N., Mieslinger, T., Minikin, A., Minnett, P., Möller, G., Morfa Avalos, Y., Muller, C., Musat, I., Napoli, A., Neuberger, A., Noisel, C., Noone, D., Nordsiek, F., Nowak, J. L., Oswald, L., Parker, D. J., Peck, C., Person, R., Philippi, M., Plueddemann, A., Pöhlker, C., Pörtge, V., Pöschl, U., Pologne, L., Posyniak, M., Prange, M., Quiñones Meléndez, E., Radtke, J., Ramage, K., Reimann, J., Renault, L., Reus, K., Reyes, A., Ribbe, J., Ringel, M., Ritschel, M., Rocha, C. B., Rochetin, N., Röttenbacher, J., Rollo, C., Royer, H., Sadoulet, P., Saffin, L., Sandiford, S., Sandu, I., Schäfer, M., Schemann, V., Schirmacher, I., Schlenczek, O., Schmidt, J., Schröder, M., Schwarzenboeck, A., Sealy, A., Senff, C. J., Serikov, I., Shohan, S., Siddle, E., Smirnov, A., Späth, F., Spooner, B., Stolla, M. K., Szkółka, W., de Szoeke, S. P., Tarot, S., Tetoni, E., Thompson, E., Thomson, J., Tomassini, L., Totems, J., Ubele, A. A., Villiger, L., von Arx, J., Wagner, T., Walther, A., Webber, B., Wendisch, M., Whitehall, S., Wiltshire, A., Wing, A. A., Wirth, M., Wiskandt, J., Wolf, K., Worbes, L., Wright, E., Wulfmeyer, V., Young, S., Zhang, C., Zhang, D., Ziemen, F., Zinner, T., and Zöger, M.: EUREC4A, Earth Syst. Sci. Data, 13, 4067–4119, https://doi.org/10.5194/essd-13-4067-2021, 2021. a
Stith, J. and Rogers, D. C.: Instrument development and education in airborne science, in: 13th Symposium on Education, 84th AMS Annual Meeting, Seattle, 10–13 January 2004, https://ams.confex.com/ams/84Annual/techprogram/paper_66280.htm (last access: 25 April 2024), 2004. a
Stull, R. B.: An Introduction to Boundary Layer Meteorology, Springer Netherlands, Dordrecht, https://doi.org/10.1007/978-94-009-3027-8, ISBN 978-90-277-2769-5, 1988. a
Taylor, G. I.: The Spectrum of Turbulence, P. Roy. Soc. A-Math. Phy., 1164, 476–490, 1938. a
Tjernström, M. and Rogers, D. P.: Turbulence structure in decoupled marine stratocumulus: A case study from the ASTEX field experiment, J. Atmos. Sci., 53, 598–619, https://doi.org/10.1175/1520-0469(1996)053<0598:TSIDMS>2.0.CO;2, 1996. a
UCAR/NCAR - Earth Observing Laboratory: NSF/NCAR Hercules C130 Aircraft, UCAR/NCAR - Earth Observing Laboratory, https://doi.org/10.5065/D6WM1BG0, 1994. a, b
UCAR/NCAR - Earth Observing Laboratory: NCAR/NSF C-130 Navigation, State Parameter, and Microphysics HRT Data - 25 Hz, Version 1.0, UCAR/NCAR - Earth Observing Laboratory [data set], https://doi.org/10.5065/D64J0CDM, 2011a. a, b
UCAR/NCAR - Earth Observing Laboratory: NCAR/NSF C-130 Navigation, State Parameter, and Microphysics HRT (25 sps) Data, Version 1.0, UCAR/NCAR - Earth Observing Laboratory [data set], https://doi.org/10.5065/D69K48JK, 2011b. a, b
Wacławczyk, M., Gozingan, A. S., Nzotungishaka, J., Mohammadi, M., and Malinowski, S. P.: Comparison of Different Techniques to Calculate Properties of Atmospheric Turbulence from Low-Resolution Data, Atmosphere, 11, 199, https://doi.org/10.3390/atmos11020199, 2020. a, b
Wacławczyk, M., Nowak, J. L., Siebert, H., and Malinowski, S. P.: Detecting Nonequilibrium States in Atmospheric Turbulence, J. Atmos. Sci., 79, 2757–2772, https://doi.org/10.1175/JAS-D-22-0028.1, 2022. a
Welch, P. D.: The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms, IEEE Transactions on Audio and Electroacoustics, 15, 70–73, https://doi.org/10.1109/TAU.1967.1161901, 1967. a
Wendisch, M. and Brenguier, J. L.: Airborne Measurements for Environmental Research, Wiley-VCH Verlag GmbH and Co. KGaA, Weinheim, Germany, https://doi.org/10.1002/9783527653218, ISBN 9783527653218, 2013. a
Wood, R.: Stratocumulus Clouds, Mon. Weather Rev., 140, 2373–2423, https://doi.org/10.1175/MWR-D-11-00121.1, 2012. a
Wood, R., Mechoso, C. R., Bretherton, C. S., Weller, R. A., Huebert, B., Straneo, F., Albrecht, B. A., Coe, H., Allen, G., Vaughan, G., Daum, P., Fairall, C., Chand, D., Gallardo Klenner, L., Garreaud, R., Grados, C., Covert, D. S., Bates, T. S., Krejci, R., Russell, L. M., de Szoeke, S., Brewer, A., Yuter, S. E., Springston, S. R., Chaigneau, A., Toniazzo, T., Minnis, P., Palikonda, R., Abel, S. J., Brown, W. O. J., Williams, S., Fochesatto, J., Brioude, J., and Bower, K. N.: The VAMOS Ocean-Cloud-Atmosphere-Land Study Regional Experiment (VOCALS-REx): goals, platforms, and field operations, Atmos. Chem. Phys., 11, 627–654, https://doi.org/10.5194/acp-11-627-2011, 2011. a
Zheng, X., Albrecht, B., Jonsson, H. H., Khelif, D., Feingold, G., Minnis, P., Ayers, K., Chuang, P., Donaher, S., Rossiter, D., Ghate, V., Ruiz-Plancarte, J., and Sun-Mack, S.: Observations of the boundary layer, cloud, and aerosol variability in the southeast Pacific near-coastal marine stratocumulus during VOCALS-REx, Atmos. Chem. Phys., 11, 9943–9959, https://doi.org/10.5194/acp-11-9943-2011, 2011. a
- Abstract
- Introduction
- Observations
- Analysis
- Results
- Discussion
- Summary
- Appendix A: Segmentation algorithm
- Appendix B: Uncertainties
- Appendix C: Sensitivity to fitting range
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Observations
- Analysis
- Results
- Discussion
- Summary
- Appendix A: Segmentation algorithm
- Appendix B: Uncertainties
- Appendix C: Sensitivity to fitting range
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References