Net CO₂ fossil fuel emissions of Tokyo estimated directly from measurements of the Tsukuba TCCON site and radiosondes

We present a simple statistical approach for estimating the greenhouse gas emissions of large cities using accurate long-term data of column-averaged greenhouse gas abundances collected by a nearby FTIR (Fourier transform infrared) spectrometer. This approach is then used to estimate carbon dioxide emissions from Tokyo.

FTIR measurements by the Total Carbon Column Observing Network (TCCON) derive gas abundances by quantitative spectral analysis of molecular absorption bands observed in near-infrared solar absorption spectra. Consequently these measurements only include daytime data.

The emissions of Tokyo are derived by binning measurements according to wind direction and subtracting measurements of wind fields from outside the Tokyo area from measurements of wind fields from inside the Tokyo area.

We estimate the average yearly carbon dioxide emissions from the area of Tokyo to be $\mathrm{70}\pm \mathrm{21}\pm \mathrm{6}\mathrm{MtC}{\mathrm{yr}}^{-\mathrm{1}}$ between 2011 and 2016, calculated using only measurements from the TCCON site in Tsukuba (north-east of Tokyo) and wind-speed data from nearby radiosondes at Tateno. The uncertainties are estimated from the distribution of values and uncertainties of parameters (±21) and from the differences between fitting residuals with polynomials or with sines and cosines (±6).

Our estimates are a factor of 1.7 higher than estimates using the Open-Data Inventory for Anthropogenic Carbon dioxide emission inventory (ODIAC), but when results are scaled by the expected daily cycle of emissions, measurements simulated from ODIAC data are within the uncertainty of our results.

The goal of this study is not to calculate the best possible estimate of CO₂ emissions but to describe a simple method which can be replicated easily and uses only observation data.

1 Introduction

Anthropogenic emissions of carbon dioxide are the strongest long-term control on global climate (Collins et al., 2013, Fig. 12.3, p. 1046), and the Paris agreement “recognizes the important role of providing incentives for emission reduction activities, including tools such as domestic policies and carbon pricing“ (UNFCCC secretariat, 2015). Implementing carbon pricing policies is widely regarded as an effective tool for reducing emissions. Such measures also motivate the development of new approaches for accurate measurements of carbon emissions (Kunreuther et al., 2014, chapters 2.6.4 and 2.6.5, pp. 181ff).

The carbon dioxide footprint of large-scale fossil-fuel-burning emitters like power plants or heating and personal transport in megacities has been retrieved from satellite (Hakkarainen et al., 2016; Hammerling et al., 2012; Ichii et al., 2017; Deng et al., 2014; Nassar et al., 2017; Hedelius et al., 2018) and from ground-based differential measurements using multiple mobile total column instruments (Hase et al., 2015; Chen et al., 2016; Butz et al., 2017; Viatte et al., 2017; Vogel et al., 2019; Luther et al., 2019). Inverse modelling allows the coupling of in situ measurements (which only capture enhancements in mixing ratio close to the ground) with atmospheric transport for similar investigations (e.g. Basu et al., 2011; Meesters et al., 2012; van der Velde et al., 2014; Babenhauserheide et al., 2015; van der Laan-Luijkx et al., 2017), but due to short mission times of satellites and differential measurement campaigns and high uncertainties when using in situ data, long-term changes in emissions are typically derived from economic fossil fuel and energy consumption data (e.g. Bureau of the Environment Tokyo, 2010; Andres et al., 2011; van der Velde et al., 2014; Le Quéré et al., 2015, 2016).

The Total Carbon Column Observing Network (TCCON; Toon et al., 2009; Wunch et al., 2011), described in Sect. 2, provides highly accurate and precise total column measurements of carbon dioxide mixing ratios with multi-year records of consistently derived data.

The aim of our study is to provide an estimate of the CO₂ emissions of Tokyo, Japan, by correlating measured XCO₂ with wind speed and direction, resulting in a measurement-driven approach to derive the annual carbon dioxide emissions of Tokyo city (Japan). The main emission sources of Tokyo are transport, residential, and industry, with about half the emissions coming from the large coal- and gas-fired power plants on the east side of Tokyo Bay, south-east of Tokyo city (Bureau of the Environment Tokyo, 2010). The quality of the data and long time series of available data enable us to infer fluxes from the measurements by statistical matching of measurements to wind directions without being dominated by measurement noise. We use 4 years of measurements at the TCCON site at Tsukuba, Japan, along with radiosonde measurements of daily local wind profiles.

This method provides an approach to estimate city emissions which is inexpensive when compared to satellite missions while being easy to reproduce and to establish, and it is suitable for long-term monitoring. Compared to still cheaper in situ measurements, the method has the advantage of directly measuring all emissions from a city in the air column, while ground-based in situ measurements only capture emissions in the lowermost part of the air profile.

This publication shows that emissions can be estimated from 4 years of data. Continued measurements will allow tracking of the change in emissions.

2 Observations

The column data from TCCON currently provides the most precise and accurate remote-sensing measurements of the column-averaged CO₂ abundances. The average station-to-station bias is less than 0.3 ppm (Messerschmidt et al., 2010).

The stations of the TCCON network measure the absorption of CO₂ and other molecular species using the sun as the background radiation source (Wunch et al., 2011). Dividing the retrieved column amount of the target species by the co-observed column amount of O₂ yields a pressure-independent measure for the concentration of carbon dioxide in the dry atmospheric column (XCO₂). The precision of these measurements is better than 0.1 %, as shown by Messerschmidt et al. (2011). Since our study restricts itself to a single station and the uncertainty budget is dominated by other factors, we can ignore any potential minor calibration bias of the selected station or the whole network.

Our study uses the current dataset of column-averaged carbon dioxide abundances generated with GGG2014 from solar absorption spectra recorded at the Tsukuba TCCON station, Japan (Ohyama et al., 2009; Morino et al., 2016). Publicly available data from Tsukuba at the TCCON data site used in our study (referenced from the “Code and data availability” section) extend from 4 August 2011 to 30 March 2016. The coordinates of the Tsukuba TCCON site are 36.05^∘ N, 140.12^∘ E, and the altitude is 31 m. Further information about the TCCON site in Tsukuba is available from the TCCON wiki.¹ In addition to concentration data of trace gases, the station provides wind direction and speed measured at the rooftop of the observatory.

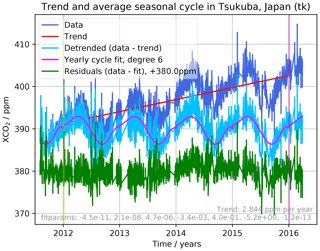
Figure 1 Detrending and deseasonalization of the XCO₂ total column measurements in Tsukuba, Japan. The data shown are individual measurements. The trend (shown as a red “trend” line) is removed with a linear least-squares fit to the data from background directions between 1 January 2012 and 1 January 2016 (denoted by the yellow and magenta vertical lines), the seasonal cycle from the signal due to photosynthesis, respiration, and decay (shown as “yearly cycle fit, degree 6”) is removed by fitting a polynomial of degree 6 to the combined yearly cycles of the detrended data. Degree 6 was chosen empirically to minimize structure in the residuum over all TCCON sites.

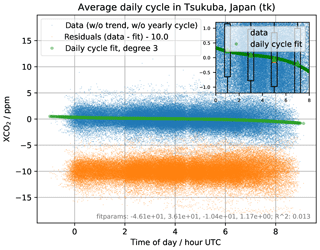
Figure 2 To remove a potential bias from correlation of wind direction with daytime, which would couple in the signal from photosynthesis and respiration, the daily cycle is removed by fitting and subtracting a polynomial of degree 3. Degree 3 was chosen empirically. The fit has low R² because the data are dominated by noise.

3 Removing trend and natural cycles

The approach chosen in this paper to estimate the CO₂ emissions of Tokyo is to separate CO₂ measurements by the wind direction for which they were measured. To make measurements from different wind directions comparable, they must be made accessible for simple statistical analysis; therefore the first step is to remove trends as well as yearly and daily cycles.

Column-averaged atmospheric CO₂ abundances are dominated by seasonal variations and a yearly rise of about 2.0 ppm per year (Hartman et al., 2013, p. 167 in Sect. 2.2.1.1.1). Additionally there is an average daily cycle of about 0.3 ppm in the densely measured daytime between 02:00 UTC and 07:00 UTC (local time between 11:00 and 16:00 GMT+9). To allow direct comparisons of values from different times of year and times of day, these cycles are removed by fitting and subtracting polynomials from the data: linear for the trend, degree 6 for the yearly cycle (roughly equivalent to granularity every 2 months), and degree 3 (roughly 3 h granularity) for the daily cycle.

Polynomials are used in this estimation to make the method as easy to implement as possible. Section S2 of the auxiliary material of our study (Babenhauserheide et al., 2020) provides results from an alternate implementation using harmonics instead, which gives comparable results.

The trend is fitted against measurements from background directions, but the yearly and daily cycle is fitted against measurements from all directions, so the fitting might remove a certain amount of the actual annual and daily cycle of emissions. However, the impact of this fitting in final estimates is limited to wind directions correlated with the cycle, since uncorrelated differences get reduced in statistical aggregation. Such a correlation between wind direction and the time of day exists, but mainly outside the densely measured daytime; a graph verifying this and the programmes applied for the data analysis are available in Sect. S1 of the Supplement (emissions-tokyo-auxiliary.pdf) of our study. Fitting the yearly cycle only against background directions creates artefacts; therefore this was avoided. Figures 1 and 2 show the fits and residuals resulting from the process. The calculations only use data provided directly from the TCCON network. The degrees of the fits were chosen empirically (by manual adjustment) to minimize the residuals over data from all TCCON sites available in 2016: polynomial fits with degrees between 3 and 9 were tested for the yearly cycle, and the residuals were checked for all TCCON sites. Degrees higher than 6 increased artefacts, and lower degrees increased the overall size of residuals.

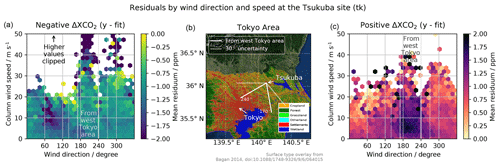
Figure 3 Panel (b) shows a map of Tokyo and its surroundings, retrieved from an ArcGIS REST service (retrieved as EPSG:4301 using a ESRI_Imagery_World_2D request to http://server.arcgisonline.com/ArcGIS, last access: 12 February 2020, via the basemap library in Matplotlib (Hunter, 2007) as described at http://basemaptutorial.readthedocs.io/en/latest/backgrounds.html#arcgisimage, last access: 17 May 2020. Used with permission (permission for publication of this graph under Creative Commons attribution license granted by Esri). © Authors for panels (a) and (c). Panel (b) is used by permission. © Esri, ArcGIS. (b) uses surface type overlays by Bagan 2014 (https://doi.org/10.1088/1748-9326/9/6/064015). All panels distributed under the Creative Commons Attribution 4.0 License.) with an overlay indicating the surface type. The colours in the overlay visualize land use and settlement density (taken from Bagan and Yamagata, 2014). It clearly shows decreasing population density with distance from Tokyo city, along with the long tail of Tokyo settlements towards the north-west. Close by Tokyo Bay in the lower centre of the map, at the south-east perimeter of Tokyo and on the opposite shore, there are multiple coal and gas power plants. The Tokyo city centre and the position of the TCCON site in Tsukuba are marked along with white lines which define an opening angle for incoming wind at Tsukuba which is interpreted as coming from the Tokyo area, along with additional widening by 30^∘ as an estimate of the actual origin of transported CO₂ arriving at Tsukuba from the given wind direction. These white lines denoting the incoming wind angle limits are reproduced in (c) and (a) as delimiting directions in which the wind blows from the west Tokyo area. Panel (c) shows the positive half of the residuals from Fig. 2, binned by wind direction and strength. The colour represents the mean value of the positive residuals within the bin. Panel (a) shows the negative half of the residuals from Fig. 2, binned by wind direction and strength. The colour represents the mean value of the negative residuals within the bin. The black arrow at the upper edge of (a) indicates that values for wind speeds above 50 m s⁻¹ have been left out to focus on the area between 5 and 15 m s⁻¹ used in the later evaluation. Displaying residuals which are lower than zero in a different graph than residuals which are higher than zero aids visual detection of emissions, because it separates the features of CO₂ sinks (lower than zero) from CO₂ sources (higher than zero). The strongly negative values in (a) at a wind direction around 60^∘ might be due to biospheric drawdown of CO₂ by woodland, but since the focus of this publication is the emissions from Tokyo, those values will not be evaluated further here. The split of the dataset applied here is purely for visualization: in the following calculations and graphs, negative and positive residuals are used together.

4 Directional dependence of remaining differences

To calculate the carbon source of Tokyo, the residuals generated by applying the procedures described in Sect. 3 are binned by wind direction and speed, as shown in Fig. 3. A major source of uncertainty in this endeavour is the actual extent of Tokyo in wind directions. This extent was chosen to be 170 to 240^∘ as seen from the TCCON site in Tsukuba, following the hexbin averages shown in the right panel in Fig. 3. The data in Fig. 3 are separated into positive and negative to ease identification of the limits for emissions from the Tokyo area. The quantitative evaluation uses both positive and negative residuals. Within these directional delimiters, all bins in the interval with wind speeds between 5 and 15 m s⁻¹ contain enhanced concentrations of CO₂. A perfect definition of these limits is not possible in the scheme presented here because the area can only be delimited orthogonally to the wind direction measured in Tsukuba. In the parallel direction the only limit is changes in wind direction over time: if wind speed is low enough that on average a direction change occurs before the air reaches Tsukuba, then concentration measurements from background locations and from Tokyo average out. This is indicated by the weaker enhancement seen for wind speeds below 5 m s⁻¹.

Using ΔXCO₂, a measure proportional to the carbon dioxide column enhancement, and the effective wind speed ascribed to these enhancements from the direction of Tokyo allows estimation of the emission source of Tokyo (described further in Sect. 5). However, the directly measured wind speed which is provided by the TCCON network only provides an approximate indication of the effective wind speed and direction in the altitude range carrying the enhanced carbon dioxide (similar to the effects discussed by Chen et al., 2016, for differential measurements of the emissions). For this study, the required effective wind speed is estimated from radiosonde data.

Effective wind speed

The wind speed at the station is measured close to the ground. The effective speed of the air column however depends on the wind speed higher up in the atmosphere. Estimating the wind speed of air with enhanced carbon dioxide concentrations due to emissions from Tokyo therefore requires taking the difference in height of the measured concentrations and the measured wind speed into account. To this end, the ground wind speed v can be replaced by the density-weighted average wind speed profile within the boundary layer. To calculate the required altitude extension of this profile, forward trajectories from Tokyo for 5 to 15 h were calculated with the HYbrid Single-Particle Lagrangian Integrated Trajectory model (HYSPLIT; Stein et al., 2015) using the Real-time Environmental Applications and Display sYstem (READY; Rolph et al., 2017), accessed via the HYSPLIT-WEB online service from NOAA² as described in the auxiliary material (Babenhauserheide et al., 2020). Since the calculations in this publication only use data from measurements with wind speeds of at least 5 m s⁻¹, 5 h suffices for all trajectories originating in Tokyo that reach Tsukuba. All the parameters used are contained in the graphs in Sect. 5 of the Supplement. The HYSPLIT profiles show that most air parcels from Tokyo arriving at Tsukuba are contained within the lowest 1000 m of the atmosphere. Therefore calculating the effective wind speed of the column with enhanced concentrations only requires wind speed measurements in this part of the atmosphere.

Direct measurements of the wind speed profile are available from radiosondes. Radiosonde data from Tateno, Japan, Ibaraki Prefecture, 36.06^∘ N, 140.13^∘ E, altitude 27 m, situated close to Tsukuba station, provide 7 years of measurements from 2009 to 2016. The data were retrieved from the Atmospheric Soundings site at the University of Wyoming (http://weather.uwyo.edu/upperair/sounding.html, last access: 21 May 2020). One example of these datasets is by Ijima (2016). Further details are available in the auxiliary material, provided in Babenhauserheide et al. (2020).

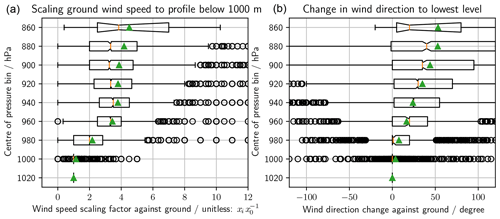
Figure 4 Wind speed profile statistics (a) and wind direction statistics (b) up to 1000 m at Tateno, Japan, using data from 2009 to 2016, from the Ijima (2016) dataset. Values are calculated by dividing the wind speed at a given pressure by the wind speed at the lowest level. The box plots show the median (red line) and the mean (green triangle). A total of 50 % of values are within the box, the whiskers include 95 % of the values, and the rest are shown as outliers (black circles). The notch in the box shows the uncertainty of the median calculated via resampling.

Figure 4 visualizes the variability of the wind speed profile weighted by atmospheric pressure from the radiosonde data measured at the Tateno site. The average wind speed in the profile with a lower limit of 31 m and an upper limit of 1000 m is used to derive daily scaling factors from the ground wind speed to the average profile wind speed. These scaling factors are applied to the ground wind speed measured at the TCCON site in Tsukuba to estimate the effective wind speed of the volume of air with enhanced carbon dioxide concentration in the total column.

These scaling factors are provided in the auxiliary material but provide a significant source of uncertainty, since their use rests on the assumption of uniform mixing of the carbon emissions across the boundary layer. The forward trajectory calculations with HYSPLIT provided in the Supplement suggest that a 50 km transport distance suffices for particles to reach the top of the boundary layer, but they do not prove that this suffices to generate a uniform CO₂ mixing ratio. Therefore, as also seen by Chen et al. (2016), the unknown actual transport pathway of emitted CO₂ to the measurement location is a significant source of uncertainty of the results.

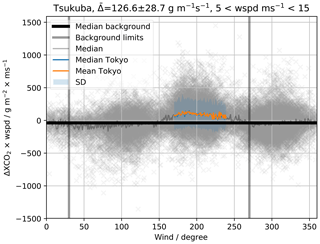
Figure 5 Residuals multiplied by wind speed plotted against the wind direction for scaled wind speeds between 5 and 15 m s⁻¹, measured by the TCCON site in Tsukuba, Japan. The mean enhancement $\stackrel{\mathrm{‾}}{\mathrm{\Delta }}$, the mean Tokyo and median Tokyo values and the standard deviation are calculated for the directions defined as from Tokyo in Fig. 3. The median background is calculated from the residuals outside the background limits (lower than 30^∘ or higher than 270^∘; limits drawn as vertical lines). The bin size is 1^∘.

5 Estimated carbon source of Tokyo

Figure 5 shows the data used to calculate $\stackrel{\mathrm{‾}}{\mathrm{\Delta }}$, the mean total column enhancement of XCO₂. $\stackrel{\mathrm{‾}}{\mathrm{\Delta }}$ is derived from the XCO₂ residuals, the result of subtracting the trend and fits from the yearly and daily cycle as described in Sect. 3: the median total column residual from background wind directions (chosen as 270 to 30^∘, using 0^∘ from north, clockwise, following meteorological conventions) is subtracted from the target direction residuals, and then the result is multiplied by the wind speed during the time of measurement. Finally it is converted from measured total column concentration $C_{{\mathrm{CO}}_{\mathrm{2}},t,\mathrm{col}}$ to total column mass $m_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{col}}$ using equations from Appendix A at time t and angle α.

To calculate the carbon source of Tokyo S_T, the measured total column enhancement E_m (in $\left[{\mathrm{g}}_{{\mathrm{CO}}_{\mathrm{2}}}\right]$) needs to be multiplied with the area affected per second by the emission source from within the Tokyo area, 𝒜 (m² s⁻¹):

$$\begin{array}{}\text{(1)}& S_{\mathrm{T}}=E_{\mathrm{m}}\cdot \mathcal{A}.\end{array}$$

By separating the affected area per second 𝒜 into the wind speed of the volume of air with enhanced concentrations at the measurement location v (approximately the average column wind speed within the boundary layer, 0–1000 m), v and the spread of the Tokyo area perpendicular to the wind speed s_⟂,

$$\begin{array}{}\text{(2)}& \mathcal{A}=v\cdot s_{⟂},\end{array}$$

this source can be derived from the mean total column enhancement of XCO₂ $\stackrel{\mathrm{‾}}{\mathrm{\Delta }}=\mathrm{127}\pm \mathrm{29}{\mathrm{g}}_{{\mathrm{CO}}_{\mathrm{2}}}{\mathrm{ms}}^{-\mathrm{1}}$ shown in Fig. 5 via

$$\begin{array}{}\text{(3)}& S_{\mathrm{T}}=E_{\mathrm{m}}\mathcal{A}\approx s_{⟂}\stackrel{\mathrm{‾}}{\mathrm{\Delta }}.\end{array}$$

The perpendicular spread s_⟂ is calculated by assuming that total columns of carbon dioxide from the Tokyo area are transported to the measurement location without effective divergence perpendicular to the wind direction and assuming roughly circular city structure. Therefore this spread can be approximated from the distance between the Tokyo city centre and the TCCON measurement site in Tsukuba:

$$\begin{array}{}\text{(4)}& s_{⟂}\approx \mathrm{2}\mathit{\pi }\cdot s_{\mathrm{Tsukuba}-\mathrm{Tokyo}}\cdot {\displaystyle \frac{\mathrm{\Delta }\mathit{\alpha }}{\mathrm{360}{}^{\circ }}},\end{array}$$

with Δα the opening angle of the limits of wind directions associated with Tokyo and $s_{\mathrm{Tsukuba}-\mathrm{Tokyo}}\approx \mathrm{52}$km. The city centre of Tokyo was chosen to be at the palace (35.6825^∘ N, 139.7521^∘ E), between the densely populated area and the power plants on the other side of Tokyo Bay. Treating 170 to 240^∘ as the wind direction coming from Tokyo, this yields a perpendicular spread of $\mathrm{2}\mathit{\pi }\cdot \mathrm{52}\mathrm{km}\cdot \frac{\mathrm{70}{}^{\circ }}{\mathrm{360}{}^{\circ }}=\mathrm{64}\mathrm{km}=\mathrm{64}\mathrm{000}\mathrm{m}$. The choice of the palace is arbitrary because the actual “centre of mass” of the emissions of Tokyo is unknown. Section 6 estimates the uncertainty due to this arbitrary choice.

For the approximation in Eq. (3), the angle-integrated E_m𝒜 is collected into contributions from different wind directions as shown in Eq. (5):

$$\begin{array}{}\text{(5)}& E_{\mathrm{m}}\mathcal{A}=\underset{{\mathit{\alpha }}_{\mathrm{0}}}{\overset{{\mathit{\alpha }}_{\mathrm{1}}}{\int }}{E}_{\mathrm{m},\mathit{\alpha }}{\mathcal{A}}_{\mathit{\alpha }}\mathrm{d}\mathit{\alpha }={\displaystyle \frac{s_{⟂}}{\mathrm{\Delta }\mathit{\alpha }}}\cdot \underset{{\mathit{\alpha }}_{\mathrm{0}}}{\overset{{\mathit{\alpha }}_{\mathrm{1}}}{\int }}{E}_{\mathrm{m},\mathit{\alpha }}{v}_{\mathit{\alpha }}\mathrm{d}\mathit{\alpha }=s_{⟂}\stackrel{\mathrm{‾}}{\mathrm{\Delta }}.\end{array}$$

Therefore the source of Tokyo can be derived from the mean enhancement $\stackrel{\mathrm{‾}}{\mathrm{\Delta }}$ as

$$\begin{array}{}\text{(6)}& \begin{array}{rl}{S}_{\mathrm{T}}& =\stackrel{\mathrm{‾}}{\mathrm{\Delta }}\cdot s_{⟂}=\mathrm{127}\pm \mathrm{29}{\mathrm{g}}_{{\mathrm{CO}}_{\mathrm{2}}}{\mathrm{ms}}^{-\mathrm{1}}\cdot \mathrm{64}\mathrm{000}\mathrm{m}\\ & =\mathrm{8.1}\pm \mathrm{1.9}{\mathrm{t}}_{{\mathrm{CO}}_{\mathrm{2}}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

The given uncertainty is taken from the standard deviation as shown in Fig. 5.

For comparison with city emission inventories, the CO₂ source is scaled to yearly carbon emissions.

$$\begin{array}{}\text{(7)}& {\displaystyle }{S}_{T,\mathrm{C},\mathrm{yearly}}& {\displaystyle }=\stackrel{\mathrm{‾}}{\mathrm{\Delta }}{\displaystyle \frac{M_{\mathrm{C}}}{M_{{\mathrm{CO}}_{\mathrm{2}}}}}{s}_{⟂}\cdot \mathrm{s}{\mathrm{yr}}^{-\mathrm{1}}\text{(8)}& {\displaystyle }& {\displaystyle }\begin{array}{rl}& =\mathrm{127}\pm \mathrm{29}\cdot {\displaystyle \frac{\mathrm{12}}{\mathrm{44}}}\left[\mathrm{g}{\mathrm{ms}}^{-\mathrm{1}}\right]\cdot \mathrm{64}\mathrm{000}\mathrm{m}\\ & \cdot \mathrm{31}\mathrm{557}\mathrm{600}\mathrm{s}{\mathrm{yr}}^{-\mathrm{1}}\end{array}\text{(9)}& {\displaystyle }& {\displaystyle }=\mathrm{70}\pm \mathrm{16}\mathrm{MtC}{\mathrm{yr}}^{-\mathrm{1}}\end{array}$$

For comparison with gridded emission inventories in Sect. 7, the CO₂ emissions are scaled to average monthly carbon emissions per wind direction (in 1^∘ steps).

$$\begin{array}{}\text{(10)}& {\displaystyle }{S}_{\mathit{\tau },{\mathrm{CO}}_{\mathrm{2}},\mathrm{average},\mathrm{deg},\mathrm{monthly}}& {\displaystyle }=\stackrel{\mathrm{‾}}{\mathrm{\Delta }}{\displaystyle \frac{M_{\mathrm{C}}}{M_{{\mathrm{CO}}_{\mathrm{2}}}}}{s}_{⟂}\cdot {\displaystyle \frac{\mathrm{s}}{\mathrm{month}\cdot \mathrm{degree}}}\text{(11)}& {\displaystyle }& {\displaystyle }\begin{array}{rl}& =\mathrm{127}\pm \mathrm{29}\left[{\displaystyle \frac{{\mathrm{g}}_{{\mathrm{CO}}_{\mathrm{2}}}}{\mathrm{ms}}}\right]\cdot {\displaystyle \frac{\mathrm{12}}{\mathrm{44}}}\left[{\displaystyle \frac{{\mathrm{g}}_{\mathrm{C}}}{{\mathrm{g}}_{{\mathrm{CO}}_{\mathrm{2}}}}}\right]\\ & \cdot \mathrm{914}\mathrm{m}\cdot \mathrm{2}\mathrm{592}\mathrm{000}{\displaystyle \frac{\mathrm{s}}{\mathrm{month}\cdot \mathrm{degree}}}\end{array}\text{(12)}& {\displaystyle }& {\displaystyle }=\mathrm{82}\pm \mathrm{19}{\displaystyle \frac{\mathrm{ktC}}{\mathrm{month}\cdot \mathrm{degree}}}\end{array}$$

6 Estimating uncertainties

In addition to the statistical uncertainty and the uncertainty of the wind profile discussed in Sect. 4.1, the estimated emission depends on the assumed extent of the Tokyo area and is limited by the unknown actual distribution of distances of emission sources from the measurement site at Tsukuba.

Choosing different opening angles for air from the Tokyo area yields a yearly emission range from 54.0±7.4 MtC year⁻¹ when choosing air from the Tokyo area between 180 and 220^∘ up to $\mathrm{93}\pm \mathrm{35}\mathrm{MtC}{\mathrm{year}}^{-\mathrm{1}}$ when choosing air from the Tokyo area between 150 and 260^∘. This uncertainty also plays a role in comparisons, if the actual wind direction higher up in the atmosphere is not distributed symmetrically around the wind direction at ground.

The distance of emission sources from the TCCON site in Tsukuba affects the estimated spread of the emission region perpendicular to the wind direction. This calculation assumes a distribution of emission strengths along the wind direction symmetrically around a centre given by the distance. This assumption is plausible since the most densely populated region of Tokyo extends to the north-west towards the prefecture of Saitama. However Bagan and Yamagata (2014) and Oda and Maksyutov (2011, 2016) show a similar extension towards the south, and the power plants are southward of the palace. Assuming an uncertainty of 10 km for the distance between the centre of mass and the measurement site increases the uncertainty.

$$\begin{array}{}\text{(13)}& {\displaystyle }{S}_{\mathrm{T}}& {\displaystyle }=\stackrel{\mathrm{‾}}{\mathrm{\Delta }}\cdot s_{⟂}=\stackrel{\mathrm{‾}}{\mathrm{\Delta }}\cdot \mathrm{2}\mathit{\pi }\cdot \mathrm{52}\pm \mathrm{10}\mathrm{km}\cdot {\displaystyle \frac{\mathrm{70}{}^{\circ }}{\mathrm{360}{}^{\circ }}}=\stackrel{\mathrm{‾}}{\mathrm{\Delta }}\cdot \mathrm{64}\pm \mathrm{12.3}\mathrm{km}\text{(14)}& {\displaystyle }& {\displaystyle }\begin{array}{rl}& =\mathrm{127}\pm \mathrm{29}{\mathrm{g}}_{{\mathrm{CO}}_{\mathrm{2}}}{\mathrm{ms}}^{-\mathrm{1}}\cdot \mathrm{64}\mathrm{000}\pm \mathrm{12}\mathrm{300}\mathrm{m}\\ & =\mathrm{8.1}\pm \mathrm{2.4}{\mathrm{t}}_{{\mathrm{CO}}_{\mathrm{2}}}{\mathrm{s}}^{-\mathrm{1}}\end{array}\text{(15)}& {\displaystyle }& {\displaystyle }\Rightarrow \mathrm{70}\pm \mathrm{21}\mathrm{MtC}{\mathrm{yr}}^{-\mathrm{1}}\text{(16)}& {\displaystyle }& {\displaystyle }\Rightarrow \mathrm{82}\pm \mathrm{24}{\displaystyle \frac{\mathrm{ktC}}{\mathrm{year},\mathrm{degree}}}.\end{array}$$

This uncertainty needs to be taken into account but can only be estimated. It gives a contribution of  MtC yr⁻¹.

The ground wind speed from TCCON data also varies by around 30 %, but this is part of the scatter in the data, so it is already averaged and reported. The scaling factors are calculated daily, so their uncertainty is part of the scatter in the data, too. Within the relevant pressure region here (860 hPa and more), the TCCON averaging kernels can vary, but this is also part of the scatter of the data. Systematic effects could be a slightly higher sensitivity in the morning and evening, but that is also the time with the least amount of data.

Another source of uncertainty is the accuracy of the background. A bias in the background translates into a bias of the result. For sites with a large forest in one direction but none close to the city, this would have to be taken into account.

The fitting procedure can affect the outcome. Repeating the same calculations with a different fitting procedure based on sines and cosines (e.g. Thoning et al., 1989), implemented using the ccgfilt library (referenced in the Code and data availability section) gives an idea of the impact of the fitting. As shown in Sect. 2 of the auxiliary material (Babenhauserheide et al., 2020), this calculation yields $\stackrel{\mathrm{‾}}{\mathrm{\Delta }}=\mathrm{138}\pm \mathrm{31}{\mathrm{g}}_{{\mathrm{CO}}_{\mathrm{2}}}{\mathrm{ms}}^{-\mathrm{1}}$ as a source instead of the $\mathrm{127}\pm \mathrm{29}{\mathrm{g}}_{{\mathrm{CO}}_{\mathrm{2}}}{\mathrm{ms}}^{-\mathrm{1}}$ found with polynomial fits. This corresponds to a relative difference of 8.3 % which is not captured by the internal variability of the residuals. For 70 MtC, the absolute difference is  MtC. The structure of this error is unknown, though; therefore it is shown separately.

Consequently the most robust estimate of the emissions of Tokyo is for yearly carbon emissions of Tokyo

$$\begin{array}{}\text{(17)}& S_{\mathrm{T},\mathrm{C},\mathrm{yearly}}=\mathrm{70}\pm \mathrm{16}\textcolor{red}{}\mathrm{MtC}{\mathrm{yr}}^{-\mathrm{1}}\end{array}$$

and for monthly carbon dioxide emissions of Tokyo

$$\begin{array}{}\text{(18)}& S_{\mathit{\tau },{\mathrm{CO}}_{\mathrm{2}},\mathrm{average},\mathrm{deg},\mathrm{monthly}}=\mathrm{82}\pm \mathrm{18}\textcolor{red}{}{\displaystyle }.\end{array}$$

These values provide an estimate of the source for Tokyo calculated directly from measurements. The measurements are only conducted between 00:00 and 08:00 UTC, though, and the fossil fuel sources of Tokyo might be different during nighttime due to reduced human activity. Nassar et al. (2013) provide hourly scaling factors for fluxes for global models. In the measurement interval these scaling factors are 1.09, 1.11, 1.13, 1.16, 1.16, 1.18, 1.20, 1.21, and 1.188, which gives an average factor of 1.16, with the standard deviation given as 0.15. Dividing the fluxes by 1.16 gives an estimate of the fluxes which would be derived from measurements through the day. This would result in a total emission estimate of $\mathrm{60}\pm \mathrm{18}\textcolor{red}{}\mathrm{MtC}{\mathrm{yr}}^{-\mathrm{1}}$.

Daily cycle corrected yearly emissions are

$$\begin{array}{}\text{(19)}& {\widehat{S}}_{\mathrm{T},\mathrm{C},\mathrm{yearly}}=\mathrm{60}\pm \mathrm{18}\textcolor{red}{}\mathrm{MtC}{\mathrm{yr}}^{-\mathrm{1}}.\end{array}$$

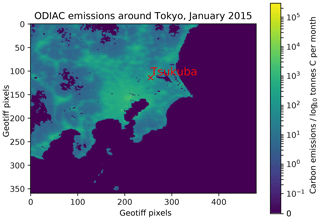
Figure 6 ODIAC carbon emissions per 1 km×1 km pixel for January 2015 in log₁₀ scale. This graph is created directly from the 1 km×1 km ODIAC dataset (Oda and Maksyutov, 2011, 2016) to visualize its structure. The model emissions are shown for the area visualized in the middle panel of Fig. 3. The unit is metric tonnes of carbon per cell and month as described in the README file at http://db.cger.nies.go.jp/dataset/ODIAC/readme/readme_2016_20170202.txt (last access: 21 May 2020).

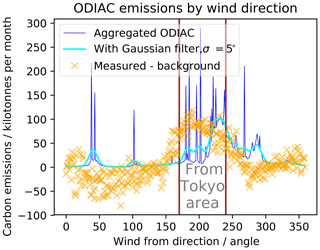
Figure 7 Sum of ODIAC carbon emissions by direction in angular degrees as seen from Tsukuba, Japan. The “aggregated ODIAC” emissions show emissions per direction from the beginning of 2011 to the end of 2016. The Gaussian filter data use a moving average to estimate signals measured at a distance. The measured dataset shows the median residuals from Fig. 5 for comparison.

7 Comparison with other datasets

To compare the results with the high-resolution Open-Data Inventory for Anthropogenic Carbon dioxide emission (ODIAC; Oda and Maksyutov, 2011) in version ODIAC2016 (Oda and Maksyutov, 2016), using the regional slice shown in Fig. 6, measurements are simulated from ODIAC by summing emissions by direction as seen from the position of Tsukuba station. For total emissions, all emissions within the arc spanned by the limits of Tokyo area from 2011 to 2016 are aggregated; then the sum of the emissions from background directions is subtracted. Emissions aggregated for each 1^∘ angle segment are shown in Fig. 7):

$$\begin{array}{}\text{(20)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{1}}{\mathrm{5}}}& \sum _{t=\mathrm{2011}-\mathrm{01}}^{\mathrm{2015}-\mathrm{12}}\left(\sum _{\mathit{\alpha }}^{\mathrm{Tokyo}}{E}_{\mathrm{ODIAC},t,\mathit{\alpha }}-\sum _{\mathit{\beta }}^{\mathrm{bg}}{E}_{\mathrm{ODIAC},t,\mathit{\beta }}\right)\\ & =\mathrm{40.4}\mathrm{MtC}{\mathrm{yr}}^{-\mathrm{1}},\end{array}\end{array}$$

which is around 60 % of the emissions estimated in this paper from TCCON measurement data and within 2 standard deviations (σ) of the estimated emissions. With the scaling for the time of day of the measurement, ODIAC results lie within 1 standard deviation of the estimate in this paper.

The peak of the distribution of emissions (from the Tokyo area) is shifted about 30^∘ anticlockwise from the model to measurements. This is within the expected changes due to the typical shift in wind direction between measurements conducted close to the ground and measurements higher up in the planetary boundary layer (Ekman, 1905). These discrepancies could be corrected by using more complex atmospheric transport, but that would require every person reproducing the estimates from our study to run such a transport, which would defeat the purpose of our study, namely to provide an easily reusable approach for estimating city emissions.

The economic data published by the Bureau of the Environment Tokyo (2010) report emissions of 57.7 MtCO₂ yr⁻¹ in the fiscal year 2006 for the Tokyo metropolitan area. This is equivalent to 15.7 MtC yr⁻¹ and shows a large discrepancy to our results. This discrepancy could stem from different definitions for the source area. Part of this discrepancy cannot be reconciled because the method shown in this study cannot limit the emission aggregation parallel to the wind direction and has around 30^∘ uncertainty of the direction, so it also includes some emissions from Kanagawa, Saitama, and Chiba, the prefectures around Tokyo which are part of the greater Tokyo area.

Pisso et al. (2019) estimate the emissions of Tokyo city as 22 MtC yr⁻¹ (80 MtCO₂ yr⁻¹) and of the Tokyo metropolitan area as 151 MtC yr⁻¹ (554 MtCO₂ yr⁻¹). With $\mathrm{70}\pm \mathrm{21}\textcolor{red}{}$ MtC yr⁻¹ ($\mathrm{256}\pm \mathrm{77}\textcolor{red}{}$ MtCO₂) this study lies between those values, which is to be expected because the definition of the metropolitan area used in Pisso et al. (2019) includes all the fluxes from the prefectures Kanagawa, Saitama, and Chiba, while this study only includes part of these fluxes. Pisso et al. (2019) also compare several other datasets with their source definition.

8 Conclusions and outlook

We find that a single multi-year dataset of precise column measurements provides valuable insights into the carbon emissions of city-scale emitters. The estimated emissions of $\mathrm{70}\pm \mathrm{21}\pm \mathrm{6}$ MtC yr⁻¹ found for Tokyo have less than 50 % uncertainty despite our intentional constraint to use only a basic evaluation scheme which can be repeated on any personal computer with publicly available data. While the operation of a TCCON station is a major effort, a decade of CO₂ column measurements of comparable quality can be conducted with affordable and easier-to-operate mobile spectrometers (see for example Frey et al., 2019), which opens an avenue for every country to measure and evaluate emissions of megacities. Placing a single total column measurement site in the vicinity of major cities can make it possible to estimate their emissions purely from these measurements. This can complement global source and sink estimates and improve acceptance of carbon trading programmes by enabling independent verification of findings.

Significant reduction of the uncertainties in these estimates without adding more measurement stations would require taking into account more detailed wind fields from meteorological models, correcting for the wind direction at different altitudes by using partial columns, more detailed correction for expected CO₂ take-up from the biosphere by wind direction, or correcting for the diurnal cycle of fossil fuel emissions. These corrections are already taken into account in source–sink estimates based on inverse modelling of atmospheric transport with biosphere models (e.g. van der Laan-Luijkx et al., 2017; Riddick et al., 2017; Massart et al., 2014; Basu et al., 2013); therefore this implementation keeps close to the simpler evaluation which allows us to use easily accessible data, which keeps our findings easy to replicate. A better classification of uncertainty due to the assumption of uniform vertical distribution of the emitted CO₂ could be given by measuring highly resolved vertical profiles from aircraft downwind of Tokyo.

Further uncertainty reductions can be achieved by establishing several observing sites within and around the source area (e.g. Hase et al., 2015; Turner et al., 2016). This approach also provides information about the spatial structure of emissions and can be used in focused measurement campaigns to obtain constraints for evaluation of measurements with coarser spatial resolution as well as long-term datasets. It would eliminate most of the uncertainty in the mean distance between measurement site and emitters.

Reduction of the bias due to measuring only during daytime, while keeping close to direct measurements, could be achieved by calculating the diurnal scaling of the emission source from CO₂ concentration measurements of an in situ instrument or by taking moonlight measurements (Buschmann et al., 2017).

To complete this outlook, we would like to suggest that the negative values seen in the left graph of Fig. 3 at a wind direction around 60^∘ indicate that it might also be possible to detect biospheric drawdown of CO₂ by woodland with just a single total column instrument and that this method can also be used to analyse other greenhouse gases measured by the TCCON network, including methane and carbon monoxide. Residuals for methane are shown in Fig. S6 of the Supplement.

We conclude that long-term ground-based measurements of column-averaged greenhouse gas abundances with sufficient precision for detecting the signals of local emission sources are an effective and cost-efficient approach to improve our knowledge about sources and sinks of greenhouse gases.

Appendix A: Units and definitions

Unit air column mass:	mair,col	$=\frac{p}{g}\times {\mathrm{10}}^{\mathrm{5}}\left[\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}\right]$
CO2 column mass	$m_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{col}}$	$=\frac{M_{{\mathrm{CO}}_{\mathrm{2}}}}{M_{\mathrm{air}}}\frac{m_{\mathrm{air},\mathrm{col}}}{f_{\mathrm{col}}}\cdot C_{{\mathrm{CO}}_{\mathrm{2}},t,\mathrm{col}}\left[\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}\right]$
Total column residuum:	R	$=m_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{col}}-m_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{col},\mathrm{seasonal}\mathrm{cycle}\mathrm{fit}}-m_{{\mathrm{CO}}_{\mathrm{2}},\mathrm{col},\mathrm{daily}\mathrm{cycle}\mathrm{fit}}\left[\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}\right]$ (described in Sect. 3)
Enhancement:	Em	$=R_{\mathrm{from}\mathrm{Tokyo}\mathrm{area}}-\mathrm{median}\left(R_{\mathrm{from}\mathrm{background}}\right)\left[\mathrm{g}{\mathrm{m}}^{-\mathrm{2}}\right]$
Molar mass of CO2	$M_{{\mathrm{CO}}_{\mathrm{2}}}$	$=\mathrm{44.0}\mathrm{g}{\mathrm{mol}}^{-\mathrm{1}}$
Molar mass of dry air	Mair	$=\mathrm{28.9}\mathrm{g}{\mathrm{mol}}^{-\mathrm{1}}$,
Column mass correction	fcol	=0.9975, following Bannon et al. (1997) to adjust for curved geometry
Tracer mass	mgas,col [g],
Total column dry-air mass	mair,col [g],
Column concentration	$C_{{\mathrm{CO}}_{\mathrm{2}},t,\mathrm{col}}\left[\mathrm{ppm}\right]$,
Acceleration due to gravity	g [m s−2]	(from TCCON a priori),
Pressure	p [g m s−2].	(with wet-air to dry-air correction)
Perpendicular spread	s⟂[m]