A review and framework for the evaluation of pixel-level uncertainty estimates in satellite aerosol remote sensing

Recent years have seen the increasing inclusion of per-retrieval prognostic (predictive) uncertainty estimates within satellite aerosol optical depth (AOD) data sets, providing users with quantitative tools to assist in the optimal use of these data. Prognostic estimates contrast with diagnostic (i.e. relative to some external truth) ones, which are typically obtained using sensitivity and/or validation analyses. Up to now, however, the quality of these uncertainty estimates has not been routinely assessed. This study presents a review of existing prognostic and diagnostic approaches for quantifying uncertainty in satellite AOD retrievals, and it presents a general framework to evaluate them based on the expected statistical properties of ensembles of estimated uncertainties and actual retrieval errors. It is hoped that this framework will be adopted as a complement to existing AOD validation exercises; it is not restricted to AOD and can in principle be applied to other quantities for which a reference validation data set is available. This framework is then applied to assess the uncertainties provided by several satellite data sets (seven over land, five over water), which draw on methods from the empirical to sensitivity analyses to formal error propagation, at 12 Aerosol Robotic Network (AERONET) sites. The AERONET sites are divided into those for which it is expected that the techniques will perform well and those for which some complexity about the site may provide a more severe test. Overall, all techniques show some skill in that larger estimated uncertainties are generally associated with larger observed errors, although they are sometimes poorly calibrated (i.e. too small or too large in magnitude). No technique uniformly performs best. For powerful formal uncertainty propagation approaches such as optimal estimation, the results illustrate some of the difficulties in appropriate population of the covariance matrices required by the technique. When the data sets are confronted by a situation strongly counter to the retrieval forward model (e.g. potentially mixed land–water surfaces or aerosol optical properties outside the family of assumptions), some algorithms fail to provide a retrieval, while others do but with a quantitatively unreliable uncertainty estimate. The discussion suggests paths forward for the refinement of these techniques.

1 Introduction

The capability to quantify atmospheric aerosols from spaceborne measurements arguably goes back to 1972 with the launch of the Multispectral Scanner System (MSS) aboard the first Landsat satellite (e.g. Griggs, 1975; Kaufman and Sendra, 1988), primarily designed for land surface characterization. Earlier satellite-based solar reflectance measurements were (with the exception of the three-colour camera on the Applications Technology Satellite 3, launched 1967) either panchromatic (and used for cloud mapping) or broadband (for radiation). While it was realized from experience with similar sensors on Mars (Hanel et al., 1972) that some aerosols could contribute to signals in the thermal infrared (tIR), they were largely treated as a contaminant in temperature and water vapour retrievals and not routinely quantified (Weaver et al., 2003). Landsat-1 MSS was followed in 1975 by a second Landsat launch and the Stratospheric Aerosol Measurement (SAM) instrument on the Apollo–Soyuz Test Project, a proof-of-concept for monitoring stratospheric aerosols (McCormick et al., 1979), and then by a gradually expanding variety of instruments from the late 1970s onwards.

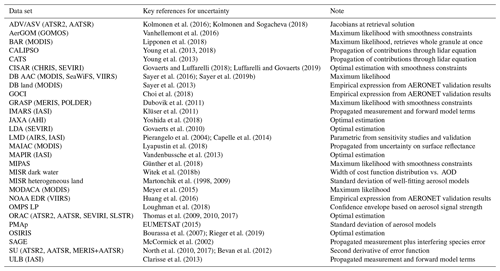
At present there are several dozen sensors of various types suitable for the quantification of aerosols in flight, and more that have begun and ended operations in between. In addition to the variety of instruments, a variety of algorithms have been developed to retrieve aerosol properties from these measurements (e.g. Kokhanovsky and de Leeuw, 2009; Lenoble et al., 2013; Dubovik et al., 2019, for some reviews of the principles behind various techniques). The majority of these sensors have been used to retrieve total-column aerosol optical depth (AOD) across some part(s) of the ultraviolet (UV), visible, near-infrared and shortwave infrared, and tIR spectral regions, where aerosol particles are optically active; the most commonly reported is the mid-visible AOD at a wavelength in the range 500–565 nm. Some sensors are able to retrieve profiles of aerosol extinction, which may be integrated vertically to give partial- or total-column AOD (dependent on whether or not profiling is possible down to the surface). This proliferation, combined with geophysical and mathematic terminology, makes aerosol remote sensing an incredibly acronym-heavy field; indeed, instruments and algorithms are often referred to by their acronyms rather than full names. Table 1 lists those sensors which have to date been used to process AOD data products, and Table 2 lists those which are able to provide extinction profiles; in many cases, two or more of each type of design, either identical or with small modifications, have been flown. Where multiples of a given sensor have flown the date ranges indicate period(s) of continuous coverage as opposed to launch or decommission dates for individual instruments.

Table 1 Satellite instruments which have been used for column AOD retrieval; arranged by sensor type.

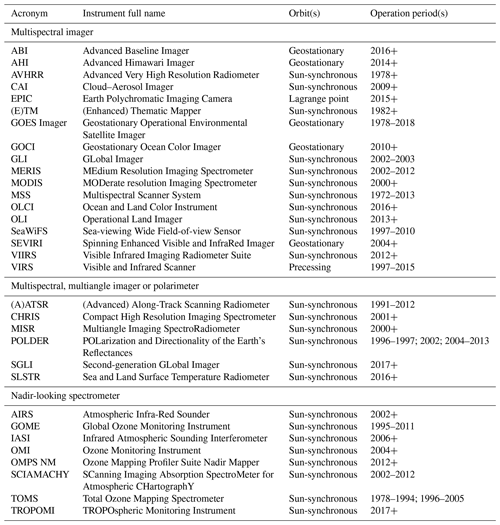
Table 2 As Table 1, except for satellite instruments which have been used for aerosol extinction profiling.

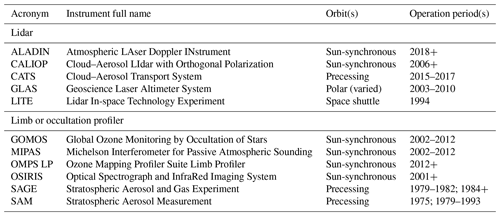
Retrieval algorithms are used to process the calibrated observations (referred to as level 1 or L1 data) to provide level 2 (L2) data products, consisting of geophysical quantities of interest. These L2 products are typically on the L1 satellite observation grid (or a multiple of it) and often further aggregated to level 3 (L3) products on regular space–time grids. For further background and a discussion of satellite data processing levels, see Mittaz et al. (2019). Table 3 provides acronyms and full names for some of the L2 processing algorithms which have been applied to L1 measurements from these instruments. Again, many of these algorithms have been applied (identically or with small modification) to multiple sensors. This table is provided as a convenience to the reader to decode acronyms and decrease clutter in later tables and discussions; specific relevant details and references are provided later. Acronyms often summarize either the principle of the technique or the institution(s) which developed the algorithm. Some algorithms are not listed in this table as they do not have acronyms and are typically referred to by data producers or users by the sensor or mission name. Further, this is not an exhaustive list as numerous other approaches have been proposed in the literature; the criteria for inclusion and broader discussion in this study are that data have been (1) processed and (2) also made generally available for scientific use. Likewise, algorithms which provide aerosol properties as a by-product but not a focus (e.g. land–ocean surface atmospheric correction approaches) are not discussed as often the aerosol components are less detailed and/or used as a sink for other error sources in the algorithm (e.g. Kahn et al., 2016).

Table 3 Acronyms for some aerosol retrieval algorithms, data records, and/or institution names applied to one or more satellite instruments from Tables 1 and 2.

L2 retrieval algorithm development is typically guided by information content studies, sensitivity analyses, and retrieval simulations to gauge which quantities a given sensor and algorithmic approach can retrieve and with what uncertainty (e.g. Tanré et al., 1996, 1997; Hasekamp and Landgraf, 2007; Veihelmann et al., 2007; Young and Vaughan, 2009). As aerosol remote sensing is an underdetermined problem and there is considerable heterogeneity in the underlying (surface and atmospheric) conditions giving rise to the L1 signals, sensitivities and uncertainties are typically highly context-dependent. For example, the retrieval of AOD from optical sensors over a dark ocean surface is typically much easier than over a bright snow-covered surface. After an algorithm has been developed, these analyses are typically complemented by validation against reference data sets, most commonly AOD from Sun photometers such as part of the Aerosol Robotic Network (AERONET; Holben et al., 1998) over land and from handheld instruments deployed on ocean cruises in the Maritime Aerosol Network (MAN; Smirnov et al., 2009, 2011). The resulting uncertainty estimates provided by these studies and validation analyses are diagnostic; i.e. for a known true state they diagnose the retrieval error (difference between retrieved and true states). This is useful to identify the general tendencies for bias or loss of sensitivity under different conditions and assess potential ways to improve on them.

Increases in the quality of instrumentation, retrieval algorithms, models, and computational power have prompted an increasing desire for the provision of pixel-level uncertainty estimates in L2 aerosol data products. This has been driven in part by data assimilation (DA) applications, which need a robust error model on data for ingestion into numerical models (Benedetti et al., 2018), often in near-real time. Diagnostic uncertainty estimates are less useful here since the true state is not known (only the retrieved state), so a prognostic (predictive) uncertainty model is needed instead. Early aerosol DA applications either treated diagnostic uncertainty estimates as prognostic ones (e.g. Collins et al., 2001; Matsui et al., 2004) or constructed their own prognostic error models as part of validation and bias-correction efforts (e.g. Zhang and Reid, 2006; Benedetti et al., 2009; Hyer et al., 2011; Shi et al., 2013). These uncertainty estimates are also valuable outside DA to identify when a retrieval is likely to be useful for a given purpose. As an example, air quality modelling also typically uses L2 retrievals and can benefit from these uncertainties. Climate applications often use L3 aerosol data for which uncertainty estimates have yet to be robustly developed; this is an important emerging area of research regarding both methods of aggregation and/or reporting (e.g. Levy et al., 2009; Kinne et al., 2017; Povey and Grainger, 2019; Sayer and Knobelspiesse, 2019) and the influence of sampling (e.g. Sayer et al., 2010b; Colarco et al., 2014; Geogdzhayev et al., 2014; Schutgens et al., 2016, 2017), and L2 uncertainty estimates will be an important input to this.

Driven by these needs, many AOD data sets now provide prognostic uncertainty estimates; in some cases these additions have been developed to satisfy these user needs, while in others they have always been available as they are inherent to the retrieval technique. Unlike AOD validation, however, which has had a fairly standard methodology (Ichoku et al., 2002), there is not yet a robust and well-used framework for evaluating these uncertainty estimates (sometimes called “validating the validation”). This study arose from discussions as part of the international AeroSat group of aerosol remote sensing researchers as a step toward remedying that gap. AeroSat is a grass-roots community who meet once a year, together with researchers involved in aerosol modelling (the AeroCom group) and measurement, to discuss and move toward solving common issues in the field of aerosol remote sensing. The purpose of this study is threefold:

1. to briefly review the ways in which uncertainty information has been conveyed in satellite aerosol data products (Sect. 2);

2. to provide a framework for the evaluation of pixel-level AOD uncertainty estimates in satellite remote sensing, which can be adopted as a complement to AOD validation exercises going forward, and use this framework to assess AOD uncertainty estimates in several AOD retrieval products (Sect. 3); and

3. to discuss the strengths and limitations of each these approaches, and suggest paths forward for improving the quality and use of L2 (pixel-level) uncertainty estimates in satellite aerosol remote sensing (Sects. 3, 4).

2 Uncertainty estimates in current satellite aerosol data sets

2.1 Terminology

The International Standards Organization document often known as the GUM (Guide to Uncertainty in Measurement) provides standardized terminology for discussing uncertainties (Working Group 1, 2008). In the interests of standardization and in line with other treatments of uncertainty and error in remote sensing (e.g. Rodgers, 2000; Povey and Grainger, 2015; Loew et al., 2017; Merchant et al., 2017; Mittaz et al., 2019; von Clarmann et al., 2019), the GUM terminology is also adopted here. Terms are often used inconsistently in writing or informal conversation (in particular “error” and “uncertainty”), so to assist the reader, definitions of relevant terms are as follows (and see previously cited references).

• A measurand is a quantity to be determined (measured), in the case of this study the AOD.

• A measurement is the application of a technique to quantify the measurand, in this case the application of L2 retrieval algorithms to L1 satellite observations.

• The measured value is the output of the measurement technique, i.e. here the result of the L2 retrieval algorithm, often referred to as the “retrieved AOD”.

• The uncertainty is in the general sense an expression of the dispersion of the measurand. For most of the data sets discussed in this study it is presented as a 1 standard deviation (1σ) confidence interval around the retrieved value (which is defined as the standard uncertainty by the GUM). The true value of the measurand (AOD) is expected to lie within this confidence interval ∼68.4 % of the time (corresponding to 1 standard deviation, colloquially 1σ), following Gaussian statistics.

• The error is the difference between the measured and true values of the measurand, i.e. here the difference between true and retrieved AOD. Following the GUM convention, a positive error means that the measured value minus the true value is positive (and vice versa).

The error can only be known when the true value of the measurand is also known, which is rare. This is the province of validation exercises: Loew et al. (2017) note that in the remote sensing community (and adopted here), validation refers to a quality assessment of a data set, which is a different definition from that of the metrology community. While Loew et al. (2017) omit mention of aerosols, the points discussed there are applicable to aerosol remote sensing as well. They also note that some authors (e.g. Rodgers, 2000) have adopted a stricter definition of validation to also explicitly include the question of whether the theoretical characterization and obtained properties of the data are consistent; the aforementioned “validating the validation” framework developed in the present study is one component of this.

For validation exercises AERONET AOD data are often taken as a reference truth because the uncertainty on AERONET AOD data (around 0.01 in the mid-visible; Eck et al., 1999) is generally much smaller than that of satellite retrievals. This enables the diagnosis of retrieval errors at the times and locations of matchups with AERONET (or similar reference data), which are often generalized to infer the likely error characteristics of retrievals under various aerosol, surface, and geometric conditions. The implicit assumption is that such a generalization is possible, but it is important to bear in mind that validation data are spatiotemporally sparse and may underrepresent or omit certain factors relative to the real world (Virtanen et al., 2018).

In contrast to error, the uncertainty can be estimated for each individual measured value (retrieval). The term “expected error” (EE) is often used in the aerosol remote sensing literature (e.g. Remer et al., 2005; Kahn et al., 2010; Sayer et al., 2013) to define these prognostic and diagnostic estimates of the magnitude of the uncertainty, highlighting (viz. “expected”) the fact that it is a statistical quantity; in hindsight the term “estimated uncertainty” might have been less confusing. The uncertainty is a statement about the level of confidence (expected magnitude of the error), while the actual error is a realization drawn from the uncertainty distribution. By analogy, rolling a single unbiased die has a mean value (expectation) of 3.5, although this result is impossible to achieve on a single roll (which can take only integer values from 1 to 6). The various techniques which have been applied to provide prognostic estimates for AOD are discussed in Sect. 2.2, while Sect. 2.3 discusses those data sets for which only diagnostic uncertainty estimates are available. A difficulty, which this study aims to tackle, is how to tell whether these uncertainty estimates are quantitatively useful and reliable. Six “conditions of adequacy” have been proposed by von Clarmann et al. (2019) for temperature and trace gas profile uncertainty estimates, namely that they are the following: (1) intercomparable between instruments and/or error estimation schemes; (2) independent of vertical retrieval grid (often less relevant for aerosols); (3) usable to the reader not familiar with instrument or retrieval technical details; (4) documented and traceable; (5) validatable (part of the focus of this study); and (6) can be summarized without excessive additional data volume overhead. These are desirable from the point of view of aerosols as well.

Kolmonen et al. (2016); Kolmonen and Sogacheva (2018)Vanhellemont et al. (2016)Lipponen et al. (2018)Young et al. (2013, 2018)Young et al. (2013)Govaerts and Luffarelli (2018); Luffarelli and Govaerts (2019)Sayer et al. (2016, 2019b)Sayer et al. (2013)Choi et al. (2018)Dubovik et al. (2011)Klüser et al. (2011)Yoshida et al. (2018)Govaerts et al. (2010)Pierangelo et al. (2004); Capelle et al. (2014)Lyapustin et al. (2018)Vandenbussche et al. (2013)Günther et al. (2018)Witek et al. (2018b)Martonchik et al. (1998, 2009)Meyer et al. (2015)Huang et al. (2016)Loughman et al. (2018)Thomas et al. (2009, 2010, 2017)EUMETSAT (2015)Bourassa et al. (2007); Rieger et al. (2019)McCormick et al. (2002)North et al. (2010, 2017); Bevan et al. (2012)Clarisse et al. (2013)

Table 4 AOD and extinction data sets providing prognostic uncertainty estimates as well as associated key references for uncertainty estimate calculation. Where applicable, algorithm names are given first with instrument names in parentheses. See Tables 1, 2, and 3 for acronyms.

2.2 Techniques for prognostic uncertainty estimates

Examples of existing prognostic uncertainty estimates for AOD or aerosol extinction data sets are given in Table 4. These fall into two broad camps: formal error propagation techniques accounting for individual terms thought to be relevant to the overall error budget and more empirical methods. The term “error budget” (not defined in the GUM, but in common colloquial use) here refers to, dependent on context, the overall collection of contributions to input or output uncertainty. Strictly, one might refer instead to “uncertainty budget” and “uncertainty propagation”, but for reader ease, the commonly used terms are adopted here.

2.2.1 Formal error propagation

The formal methods which have been applied to date are in general Bayesian approaches, which can be expressed in the formalism of Rodgers (2000), and are often referred to as optimal estimation (OE). OE approaches provide the maximum a posteriori (MAP) solution to the retrieval problem: maximization of the conditional probability $P\left(\mathit{x}\right|\mathit{y},{\mathit{x}}_{\mathrm{a}})$ of the retrieved state vector x, where y and x_a represent the satellite measurements and any a priori information on x, respectively. The MAP solution is achieved by minimization of a cost function J, and the formalism allows for the calculation of various contributions to the total uncertainty $\widehat{\mathbf{S}}$ on the retrieved state. OE accounts for uncertainty on the satellite measurements, retrieval forward model (e.g. atmospheric and surface structure assumptions, ancillary data), a priori information, and smoothness constraints (on e.g. spatial, temporal, or spectral variation of parameters). While notation differs between authors (see also Rodgers, 2000; Dubovik et al., 2011; Govaerts and Luffarelli, 2018), a general form of the cost function J can be written

$$\begin{array}{}\text{(1)}& \begin{array}{rl}J\left(\mathit{x}\right)=& {\left(\mathbf{F}\left(\mathit{x}\right)-\mathit{y}\right)}^T{\mathbf{S}}_y^{-\mathrm{1}}\left(\mathbf{F}\left(\mathit{x}\right)-\mathit{y}\right)\\ +& {\left({\mathit{x}}_{\mathrm{a}}-\mathit{x}\right)}^T{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}\left({\mathit{x}}_{\mathrm{a}}-\mathit{x}\right)\\ +& {\mathit{x}}^T{\mathbf{H}}_s^T{\mathbf{S}}_s^{-\mathrm{1}}{\mathbf{H}}_s\mathit{x}\\ +& \mathrm{\dots },\end{array}\end{array}$$

where S_y and S_a are covariance matrices; S_y describes the measurement and forward model uncertainty, S_a describes the a priori uncertainty, and F(x) is the forward-modelled measurements. The third term represents a generic smoothness constraint on the state vector (which might be spatial, temporal, spectral, or otherwise), where H_s is a block diagonal matrix and S_s its associated uncertainty; the ellipses in Eq. (1) indicate the potential for the expansion of J to include additional smoothness terms. These smoothness constraints were first introduced in the context of aerosol remote sensing by Dubovik and King (2000) for AERONET sky-scan inversions. In recent years they have become more widespread in satellite aerosol remote sensing as more capable sensors (e.g. POLDER) and/or algorithms with increased (spatiotemporal, spectral, or directional) dimensionality of measured or retrieved quantities (Dubovik et al., 2011; Govaerts and Luffarelli, 2018; Shi et al., 2019) have been developed. Candidate algorithms for aerosol retrieval from information-rich future sensors also tend to use smoothness constraints (e.g.  Xu et al., 2019). All these covariance matrices are assumed to be Gaussian, which may not always be true in practice.

Note that here S_y represents the total of measurement uncertainty, forward model uncertainty (due to approximations made in the radiative transfer), and the contribution of uncertainties in forward model parameters to the simulated signal at the top of the atmosphere (TOA). These model parameters are factors which affect the TOA signal but typically insignificantly enough to be retrieved. For example, many AOD retrieval algorithms ingest meteorological reanalysis to correct for the impact of absorbing trace gases (such as H₂O) on the satellite signal at TOA (Patadia et al., 2018) and to provide wind speed to calculate glint and whitecap contributions to sea surface reflectances (Sayer et al., 2010a). Sometimes these are represented in J instead by a “model parameter error” matrix denoted S_b and similar squared deviations, although mathematically since the terms in Eq. (1) are additive the two formalisms are equivalent if the model parameter uncertainty is transformed into measurement space and included in S_y (as is typically the case).

As S_y and S_a (etc.) are square matrices, correlations between wavelengths or parameters can (and, where practical, should) be accounted for. These terms often affect several satellite bands such that an error in e.g. reanalysis data ingested as part of an AOD retrieval would manifest in a correlated way between these bands. However, due to the difficulty in estimating these off-diagonal elements, in practice they are frequently neglected and the covariance matrices are often assumed to be diagonal (which does not, however, mean that $\widehat{\mathbf{S}}$ is diagonal). Dependent on the magnitude and sign of these correlations, their neglect can lead to overestimates or underestimates in the level of confidence in the solution. When the cost function has been minimized, the uncertainty $\widehat{\mathbf{S}}$ on the retrieved state is given by

$$\begin{array}{}\text{(2)}& \widehat{\mathbf{S}}={\left({\mathbf{K}}^T{\mathbf{S}}_y^{-\mathrm{1}}\mathbf{K}+{\mathbf{S}}_{\mathrm{a}}^{-\mathrm{1}}+{\mathbf{H}}_s^T{\mathbf{S}}_s^{-\mathrm{1}}{\mathbf{H}}_s\right)}^{-\mathrm{1}},\end{array}$$

where K, known as the weighting function or Jacobian matrix, is the sensitivity of the forward model to the state vector $\partial \mathbf{F}\left(\mathit{x}\right)/\partial \mathit{x}$, typically calculated numerically. The 1σ uncertainty on the retrieved AOD is then the square root of the relevant element on the diagonal of $\widehat{\mathbf{S}}$ (dependent on the contents of the state vector). Many current approaches in Table 4 omit a priori and/or smoothness constraints, in which case the corresponding terms in Eqs. (1) and (2) vanish. Only BAR and CISAR include both a priori and smoothness constraints. AerGOM, GRASP, and the MIPAS stratospheric aerosol data set use smoothness constraints without a priori on the aerosol state. Others (LDA, JAXA AHI, MAPIR, ORAC) use a priori but no smoothness constraints. Smoothness constraints are attractive for algorithms such as the GRASP application to POLDER, which includes the retrieval of binned aerosol size distribution and spectral refractive index (which are expected to be smooth for physical reasons), as well as those (e.g. BAR, CISAR, GRASP) moving beyond the independent pixel approximation to take advantage of the fact that certain atmospheric and/or surface parameters can be expected to be spatially and/or temporally smooth on relevant scales.

These smoothness and a priori constraints provide a regularization mechanism to suppress “noise-like” variations in the retrieved parameters when they are not well-constrained by the measurements alone, although there is a danger in that overly strong constraints can suppress real variability. As a result, a priori constraints on AOD itself are often intentionally weak compared to those on other retrieved parameters. Strictly, the MAP is a maximum likelihood estimate (MLE) only if the retrieval does not use a priori information, although it is often referred to as an MLE regardless (see Sect. 4.1 of Rodgers, 2000, for more discussion on this distinction). This distinction is made in the descriptions in Table 4.

The rest of the error propagation methods in Table 4, whether formulated as OE or not, are essentially propagating only measurement (and sometimes forward model) uncertainty through to the retrieval solution through Jacobians. MAIAC is a special case here because, rather than using the measurement uncertainty directly, it propagates the uncertainty of surface reflectance in the 470 nm band, which is thought to be the leading contribution to the total error budget (Lyapustin et al., 2018). It is important to note that the cost function and uncertainty estimate calculations in Eq. (2) are conditional on several factors.

1. The forward model must be appropriate to the problem at hand and capable of providing unbiased estimates of the observations. Typically if the forward model is fundamentally incorrect, and/or any a priori constraints strongly inappropriate, the retrieval will frequently not converge to a solution or have unexpectedly large J. For this reason, high cost values are often used in post-processing to remove problematic pixels (e.g. undetected cloud or snow) or candidate aerosol optical models from the provided data sets (Martonchik et al., 1998; Thomas et al., 2010).

2. The covariance matrices S_y,S_a, and S_s (on measurements, a priori, and smoothness) must be appropriate; if systematically too large or small, uncertainty estimates will likewise be too large or small. These can be tested, to an extent, by examining the distributions of residuals (on measurements and a priori) and the cost function and comparing to theoretical expectations (e.g. Sayer et al., 2010a, 2012c).

3. The forward model must be approximately linear with Gaussian errors near the solution. This assumption sometimes breaks down if the measurements are uninformative on a parameter and a priori constraints are weak or absent, and the resulting state uncertainty estimates will be invalid. This can be tested (Thomas et al., 2009; Sayer et al., 2016) by performing retrievals using simulated data, perturbing their inputs according to their assumed uncertainties, and assessing whether the dispersion in the results is consistent with the retrieval uncertainty estimates.

4. The retrieval must have converged to the neighbourhood of the correct solution (i.e. near the global, not a local, minimum of the cost function), which can be a problem if there are degenerate solutions. In practice algorithms try to use reasonable a priori constraints, first guesses, and make a careful selection of which quantities to retrieve vs. which to assume (e.g. Thomas et al., 2009; Dubovik et al., 2011). Note that the iterative method of convergence to the solution is not important in itself.

A detailed further discussion on these conditions from the perspective of temperature and trace gas retrievals, which share some similar conceptual challenges to aerosol remote sensing, is provided by von Clarmann et al. (2019).

2.2.2 Other approaches

A particular challenge for the formal error propagation techniques is the second point above: how to quantify the individual contributions to the error budget necessary to calculate the above covariance matrices? This difficulty has motivated some of the empirical approaches in Table 4.

Sayer et al. (2013) used the results of validation analyses against AERONET to construct an empirical relationship (discussed in more detail later) expressing the uncertainty in MODIS DB AOD retrievals as a function of various factors. This basic approach was later adopted for other data sets, including GOCI and NOAA VIIRS EDR aerosol retrievals (Huang et al., 2016; Choi et al., 2018). This has some similarity to diagnostic EE envelopes, although importantly these prognostic estimates are framed in terms of retrieved rather than reference AOD. An advantage of this method is that, if AERONET can be taken as a truth and collocation-related uncertainty is small (Virtanen et al., 2018), it empirically accounts for the important contributions to the overall error budget without having to know their individual magnitudes. However, there are some disadvantages: if validation data are sparse or do not cover a representative range of conditions, there is a danger of overfitting the expression, and for an ongoing data set there is no guarantee that past performance is indicative of future results as sensors age and the world changes. For a quantity without available representative validation data, the method cannot be performed. Further, programmatically, it requires processing data twice: once to perform the retrievals and do the validation analysis to derive the expression and a second time to add the resulting uncertainty estimates into the data files. The LMD IASI retrieval has a similar parametric approach (Capelle et al., 2014), although as validation data are sparse, the parametrization draws on the results from retrieval simulations as well.

The MISR algorithms use different approaches. Both the land and water AOD retrieval algorithms perform retrieval using each of 74 distinct aerosol optical models (known as “mixtures”) and calculate a cost function for each. In earlier algorithm versions (Martonchik et al., 1998) uncertainty was taken as the standard deviation of AOD retrieval from mixtures which fit with a cost below some threshold. This is equivalent to assuming that aerosol optical models are the dominant source of uncertainty in the retrieval and that the 74 mixtures provide a representative sampling of microphysical and optical properties.

This approach was refined (for retrievals over water pixels) by Witek et al. (2018b) by considering the variation of retrieval cost with AOD for each model and transforming this to give a probability distribution of AOD, with the uncertainty taken as the width of this distribution. A similar approach has been proposed for the OMAERO retrieval by Kauppi et al. (2017), although it has not yet been implemented on a large scale. It has conceptual similarities with the propagation of measurement error in Eq. (2), except calculating across the whole range of AOD state space rather than an envelope around the solution and summing the results from multiple distinct retrievals (corresponding to the aerosol mixtures). These methods are, however, reliant on the set of available optical models being sufficient.

Flamant et al. (2008); Flament et al. (2019)Sayer et al. (2012b, 2017, 2019a)Kaufman et al. (1997); Levy et al. (2013)Tanré et al. (1996, 1997); Levy et al. (2013)Mishchenko et al. (1999); Geogdzhayev and Mishchenko (2015)Fukuda et al. (2013)Nakajima et al. (2009)Laszlo and Liu (2017)Ignatov and Stowe (2000, 2002a, b); Zhao (2016)Torres et al. (2012); Jethva et al. (2018)Curier et al. (2008)Torres et al. (1998); Ahn et al. (2013)Mukai and Sano (2018)Sayer et al. (2012a, 2017, 2018)Holzer-Popp et al. (2002, 2008)Torres et al. (1998, 2002)Mei et al. (2017)

Table 5 AOD and extinction data sets providing sensitivity analyses and/or diagnostic uncertainty estimates, with associated key references for uncertainty. Where applicable, algorithm names are given first with instrument names in parentheses. See Tables 1, 2, and 3 for acronyms.

2.3 Examples of diagnostic uncertainty estimates

Available AOD data sets which do not currently provide prognostic uncertainty estimates are listed in Table 5. In these cases, algorithm papers typically summarize the results of sensitivity analyses to provide a rationale for choices made in algorithm development and to provide a summary of expected performance. Sensitivity analyses often include similar aspects to those employed in error propagation approaches: namely, characterization of the expected effects of uncertainties in sensor calibration and forward model limitations (e.g. assumed aerosol optical models, surface reflectance) on the retrieval solution, singly or jointly. In most cases these are provided for a subset of geometries and atmosphere–surface conditions. Compared to formal error propagation, this has the advantage of being easier to communicate to a reader concerned about a particular assumption (provided the results of the sensitivity analysis are representative), but on the other hand the summary results are specific to only the simulations performed, and real-world uncertainties may be more complicated, particularly when multiple retrieval assumptions are confounded.

Sensitivity analyses are often complemented by dedicated validation papers which summarize the results of comparisons against AERONET, MAN, or other networks (e.g. Remer et al., 2005; Kahn et al., 2010); aerosol remote sensing is fortunate compared to some other disciplines in that high-quality AOD validation data are fairly readily available. It is common for the results to be summarized in terms of EE envelopes or similar metrics; these envelopes are sometimes adjusted if pre-launch expectations prove too optimistic or pessimistic (e.g. Levy et al., 2013). Diagnostic and prognostic uncertainty estimates should not be regarded as exclusionary; diagnostic analysis is useful to guide algorithm refinement and assess assumptions, and many data products which provide prognostic uncertainties also show the results of diagnostic validation activities. However, extending the data sets in Table 5 to also provide prognostic estimates would improve their specificity and utility for applications like DA.

2.4 Systematic and random contributions to uncertainty

Both the diagnostic and prognostic techniques typically (implicitly or explicitly) make the assumption that the sensor and retrieval algorithm are unbiased and that the resulting uncertainty estimates are unbiased and symmetric. However, it is well-known that many of the key factors governing retrieval errors are globally (e.g. sensor calibration, Lyapustin et al., 2014) or seasonally–regionally (e.g. aerosol optical model, surface reflection, cloud contamination, Eck et al., 2013; Zhao et al., 2013; Gupta et al., 2016) systematic and that true random error (i.e. propagated noise) is often small. While these systematic factors may partially cancel each other out over large ensembles of data (drawn from e.g. different regions, seasons, or geometries), this is not a given.

Uncertainty propagation approaches such as OE can in principle account for systematic uncertainty sources, as they (and any spectral or parameter correlations) can be included in the required covariance matrices. This can produce estimates of total uncertainty which are reasonable for an individual retrieval, but the true (large-scale) error distributions would then not be symmetric, lessening their value. Likewise, systematically biased priors can lead to systematically biased retrievals. As a result, it would be desirable to remove systematic contributions to the retrieval system uncertainty as far as possible. In practice this is often done through validation exercises, whereby diagnostic comparisons can provide clues as to the source of biases, which are then (hopefully) lessened in the next version of the algorithm. Distributions of the residuals of predicted measurements at the retrieval solution can also be indicative of calibration and forward model biases at the wavelength in question.

A possible solution to this is to perform a vicarious calibration, calculating a correction factor to the sensor gain as a function of time and band by matching observed and modelled reflectances at sites where atmospheric and surface conditions are thought to be well-known (e.g. thick anvil clouds, Sun glint, and AERONET sites). The derived correction factor then accounts for the systematic uncertainty on calibration and the radiative transfer forward model, although if this latter term is non-negligible then the vicariously calibrated gains will still be systematically biased (albeit less so for the application at hand). This has the advantage of transforming the calibration uncertainty from a systematic to a more random error source at the expense of creating dependence on the calibration source and radiative transfer model. There is therefore a danger in creating a circular dependence between the vicarious calibration and validation sources as it can hinder understanding of the physics behind observed biases. Further, this has the side effect of potentially increasing the level of systematic error in other quantities or in conditions significantly different from those found at the vicarious calibration location if the forward model contribution to systematic uncertainty is significant (Kahn et al., 2016). Vicarious calibration is common within the ocean colour community (Franz et al., 2007), in which retrieval algorithms are in some cases more empirical and amenable to tuning than physically-driven aerosol retrieval algorithms. It has also been used for on-orbit calibration of instruments lacking on-board capabilities to track absolute calibration and degradation (e.g. Heidinger et al., 2010).

3 Statistical framework to evaluate pixel-level AOD uncertainty estimates

3.1 Background and methodology

The notation adopted herein is as follows. The AOD is denoted τ; unless specified otherwise, references to AOD indicate that at 550 nm. The reference (here AERONET) AOD is τ_A and satellite-retrieved AOD is τ_S. The 1σ estimated uncertainties on these are denoted ϵ_A and ϵ_S, respectively. If the reference AOD is assumed to be the truth, then the error Δ_S on the satellite AOD is given by ${\mathrm{\Delta }}_{\mathrm{S}}={\mathit{\tau }}_{\mathrm{S}}-{\mathit{\tau }}_{\mathrm{A}}$.

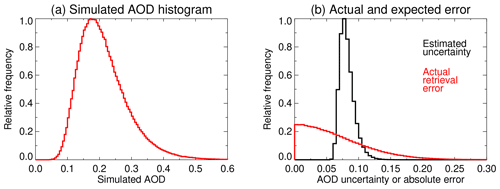
Figure 1 (a) Sample AOD histogram drawn from a lognormal AOD distribution with geometric mean 0.2 and geometric standard deviation 0.35. (b) Distribution of (black) estimated retrieval uncertainties and (red) actual absolute retrieval errors obtained if error characteristics followed the MODIS DT land model, ${\mathit{ϵ}}_{\mathrm{S}}=\pm (\mathrm{0.05}+\mathrm{0.15}\mathit{\tau })$.

Figure 1 provides a simulation experiment to illustrate the relationship between AOD, uncertainty, and error distributions. Panel (a) is a histogram of AOD generated (1 000 000 points) assuming a lognormal distribution with geometric mean 0.2 and geometric standard deviation 0.35, which is a typical shape for many locations in North America and Europe (O'Neill et al., 2000). Panel (b) shows two distributions: in black is the distribution of the expected AOD uncertainty magnitude (often, as discussed before, called expected error or EE), assuming error characteristics of the MODIS DT land retrieval, ${\mathit{ϵ}}_{\mathrm{S}}=\pm (\mathrm{0.05}+\mathrm{0.15}\mathit{\tau })$ (Levy et al., 2013). This is obtained simply by multiplying the histogram in Fig. 1a by the magnitude of uncertainty $\left|{\mathit{ϵ}}_{\mathrm{S}}\right|$. The red line, in contrast, is the distribution of actual absolute retrieval errors (i.e. $|{\mathit{\tau }}_{\mathrm{S}}-{\mathit{\tau }}_{\mathrm{A}}|$), which would be expected to be seen in a validation exercise against AERONET if the expression for ϵ_S holds true. This red line is obtained by taking draws from the AOD distribution and then, for each, generating a normally distributed random number with mean 0 and standard deviation ϵ_S to provide the retrieval error (note that the absolute value of this retrieval error is shown in Fig. 1b).

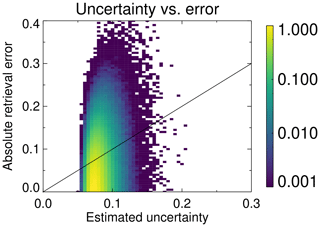
Figure 2 Scatter density joint histogram (on a logarithmic scale) of the simulated expected uncertainties and retrieval errors in Fig. 1b. The 1:1 line is shown in black. Bins containing no data are shown in white.

An important nuance which bears repeating is that the distributions of estimated uncertainty and actual error in Fig. 1 are quite different in shape. This is because the estimated uncertainty distribution is one of the expectations of ϵ_S (given the AOD distribution), while the distribution of errors is one of the realizations of (draws from) ϵ_S. Recall again the distinction between the expectation of rolling an unbiased die (i.e. a result of 3.5) and the actual realization (result) of rolling a die (1, 2, 3, 4, 5, or 6). The latter distribution is broader. This illustrates why comparing errors and uncertainties on a 1:1 basis, or comparing distribution magnitudes, is not expected to yield agreement, and an evaluation of consistency requires a statistical approach. Figure 2 shows this more directly: there is little correspondence between the two on an individual basis.

When comparing satellite and reference data, the total expected discrepancy (ED) between the two for a single matchup, denoted ϵ_T, should account for uncertainties on both the satellite and reference (here AERONET) data,

$$\begin{array}{}\text{(3)}& {\mathit{ϵ}}_{\mathrm{T}}=\sqrt{{\mathit{ϵ}}_{\mathrm{S}}^{\mathrm{2}}+{\mathit{ϵ}}_{\mathrm{A}}^{\mathrm{2}}},\end{array}$$

adding in quadrature under the assumption that the uncertainties on satellite and AERONET AOD are independent of one another. One can then define a normalized error Δ_N as the ratio of the actual error to the ED, i.e.

$$\begin{array}{}\text{(4)}& {\mathrm{\Delta }}_{\mathrm{N}}={\displaystyle \frac{{\mathrm{\Delta }}_{\mathrm{S}}}{{\mathit{ϵ}}_{\mathrm{T}}}}={\displaystyle \frac{{\mathit{\tau }}_{\mathrm{S}}-{\mathit{\tau }}_{\mathrm{A}}}{\sqrt{{\mathit{ϵ}}_{\mathrm{S}}^{\mathrm{2}}+{\mathit{ϵ}}_{\mathrm{A}}^{\mathrm{2}}}}}\end{array}$$

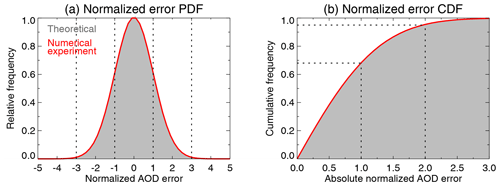
Figure 3 (a) PDF and (b) CDF of normalized error distributions drawn from the numerical simulations in Fig. 1; theoretical (grey shading) and simulation (red) results lie on top of one another. Note that the CDF is of absolute normalized error. Dashed lines indicate various well-known percentage points of Gaussian distributions.

In the ideal case ϵ_A≪ϵ_S, in which case the shape of Δ_N is dominated by the uncertainty and errors on the satellite-retrieved AOD. If the uncertainties on satellite and reference AOD have been calculated appropriately and the sample is sufficiently large, then the normalized error Δ_N should approximate a Gaussian distribution with mean 0 and variance 1. Thus, the distribution of Δ_N can be checked in several ways against expected shapes for Gaussian distributions, for example the probability distribution function (PDF) and cumulative distribution function (CDF) as shown in Fig. 3.

The above distribution analyses are informative on the overall magnitude of retrieval errors compared to expectations (as well as, in the case of the PDF analysis, whether there is an overall bias on the retrieved AOD). However, alone they say little about the skill in assessing variations in uncertainty across the population. Taking things a step further, the data can be stratified in terms of ED and a quantile analysis performed to assess consistency with expectations. This is equivalent to taking a single location along the x axis in Fig. 2 and assessing the distribution of retrieval errors found for the points from that histogram. These, too, should follow Gaussian statistics.

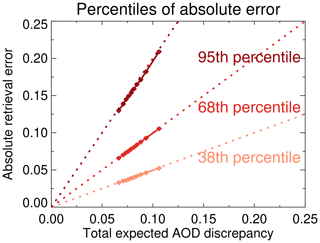
Figure 4 Expected AOD discrepancy against percentiles of absolute AOD retrieval error. Symbols indicate binned results from the numerical simulation; within each bin, paler to darker tones indicate the 38th, 68th, and 95th percentiles (approximate 0.5σ, 1σ, 2σ points) of absolute retrieval error. Dashed lines (0.5:1, 1:1, 2:1, respectively) show theoretical values for the percentiles of the same colour.

An example of this is shown in Fig. 4. The data are divided by expected discrepancy ϵ_T into 10 equally populated bins, and within each bin the 38th, 68th, and 95th percentiles (i.e. approximate 0.5σ, 1σ, 2σ points, following Gaussian statistics) of absolute retrieval error are plotted. If the uncertainties are appropriate, these should lie along the 0.5:1, 1:1, and 2:1 lines. This analysis provides a way of checking the validity of the uncertainty estimates across the spectrum from low to high estimated uncertainties as opposed to population-average behaviour (i.e. do the distributions of retrieval error change in the expected way as the estimated uncertainty varies?). The 68th percentile is of the most direct interest as it corresponds most directly to the expectation of the retrieval error, but examining other percentiles provides a way to assess whether the distribution is broader or narrower than expected (due to, perhaps, the presence of more or fewer outliers than expected).

The binned analysis is similar to the assessment of forecast calibration in meteorology (Dawid, 1982). Note in a forecast sense that the term calibration refers to a comparison of forecast vs. observed frequencies or magnitudes, distinct from the common meaning of calibration to refer to radiometric accuracy in remote sensing. By further analogy to the forecast community (compare to the expressions in Murphy, 1988), a calibration skill score s_cal can be defined,

$$\begin{array}{}\text{(5)}& s_{\mathrm{cal}}=\mathrm{1}-{\displaystyle \frac{\sum _{b=\mathrm{1}}^B{\left({\mathit{ϵ}}_{\mathrm{T},b}-\left|{\mathrm{\Delta }}_{\mathrm{S},b}^{\mathrm{1}\mathit{\sigma }}\right|\right)}^{\mathrm{2}}}{\sum _{b=\mathrm{1}}^B{\left(\stackrel{\mathrm{‾}}{\left|{\mathrm{\Delta }}_{\mathrm{S}}\right|}-\left|{\mathrm{\Delta }}_{\mathrm{S},b}^{\mathrm{1}\mathit{\sigma }}\right|\right)}^{\mathrm{2}}}},\end{array}$$

where $\left|{\mathrm{\Delta }}_{\mathrm{S},b}^{\mathrm{1}\mathit{\sigma }}\right|$ is the 1σ absolute retrieval error in bin b (Fig. 4) over B bins total. This compares the observed squared discrepancy from the 1:1 line in Fig. 4 with that which would be obtained if a data user assumed that the retrieval uncertainty was equal to the mean absolute retrieval error ($\stackrel{\mathrm{‾}}{\left|{\mathrm{\Delta }}_{\mathrm{S}}\right|}$) from a validation exercise at that location, which is what might be done in the absence of pixel-level uncertainty estimates. This skill score is computed using binned values rather than individual matchups due to the previously discussed nature of the relationship between uncertainty and error (Figs. 1, 2). The highest possible score is 1, and a score of 0 indicates that the uncertainty estimates do not have greater skill than simply assuming the average retrieval error. If the magnitudes of ϵ_T are in error then it is possible for s_cal to take unbounded negative values, in which case the uncertainties are said to be poorly calibrated (Dawid, 1982). This is quite a difficult test for a data set as a positive skill score requires that both the magnitudes of the uncertainty and the variations in both uncertainty and error must be accurate. This may be particularly difficult if the error does not vary much at a given location. As a result s_cal should not be used as a single metric in isolation but rather examined in a broader context.

Figures 3 and 4 provide the basis for the framework proposed in this study. An earlier version of this method was designed during the development and assessment of prognostic uncertainty estimates for MODIS DB retrievals by Sayer et al. (2013). It has been further advanced through discussions at annual AeroSat meetings. These ideas have been further practically applied to NOAA VIIRS AOD data by Huang et al. (2016), to GOCI data by Choi et al. (2018), to retrievals of absorbing aerosols above clouds against airborne measurements by Sayer et al. (2019b), and to the latest MISR product over ocean by Witek et al. (2019). The idea of looking at normalized retrieval error distributions was also explored for AOD by Popp et al. (2016) and Kinne et al. (2017) when evaluating ESA Climate Change Initiative (CCI) aerosol products and in a more general sense (with cloud-top height as an example) by Merchant et al. (2017). Indeed, the method is not restricted to AOD, although AOD has the advantage of comparatively readily available, high-quality reference data in AERONET and other networks.

3.2 Practical application to satellite data products

3.2.1 AERONET data used and matchup criteria

Here, the reference AOD τ_A is provided using level 2.0 (cloud-screened and quality assured) direct-Sun data from the latest AERONET version 3 (Giles et al., 2019). As AERONET Sun photometers do not measure at 550 nm, the AOD is interpolated using a second-order polynomial fit to determine the coefficients a₀,a₁, and a₂ for each measurement,

$$\begin{array}{}\text{(6)}& \log \left({\mathit{\tau }}_{\mathit{\lambda }}\right)=a_{\mathrm{0}}+a_{\mathrm{1}}\log \left(\mathit{\lambda }\right)+a_{\mathrm{2}}\log (\mathit{\lambda }{)}^{\mathrm{2}},\end{array}$$

where λ is the wavelength. All available (typically four) AOD measurements in the 440–870 nm wavelength range are used in the fit, which is more robust to calibration problems in individual channels than a bispectral approach and accounts for spectral curvature in log (τ_λ) (Eck et al., 1999; Schuster et al., 2006). The uncertainty on mid-visible AOD is dominated by sensor calibration and is ∼0.01 (Eck et al., 1999). The sampling cadence is typically once per 10 min in cloud-free, daytime conditions but is more frequent at some sites.

Table 6 AERONET sites used and their categorization.

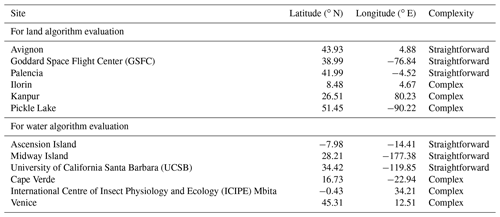
Data from a total of 12 AERONET sites, listed in Table 6, are used here to assess the AOD uncertainty estimates in various satellite data sets. This is evenly split to provide six sites to evaluate AOD retrievals from algorithms over land and six over water. Each category is further split; three sites are described as “straightforward”, for which the AOD retrieval problem is comparatively uncomplicated (i.e. likely no significant deviations from retrieval assumptions) and so the uncertainty estimates might be expected to be reasonable, and three sites are “complex”. These complex sites were chosen as they have complicating factors which are not well-captured by existing retrieval forward models and might be expected to lead to breakdowns in the techniques used by the retrieval algorithms to provide uncertainty estimates.

The reasons for identifying a particular site as complex are as follows. Over land, Ilorin (Nigeria) and Kanpur (India) can exhibit complicated mixtures of aerosols with distinct optical properties and vertical structure (Eck et al., 2010; Giles et al., 2012; Fawole et al., 2016). Many AOD retrieval algorithms, in contrast, assume a single aerosol layer of homogeneous optical properties. Pickle Lake (Canada) is in an area studded by lakes of sizes similar to or smaller than satellite pixel size. This might be expected to interfere with data set land masking (which often determines algorithm choice) and surface reflectance modelling in a non-linear way (Carroll et al., 2017). Over water, Cape Verde (on Sal Island, officially the Republic of Cabo Verde) is characterized by frequent episodes of Saharan dust outflow; these particles have complex shapes, which are often approximated in AOD retrieval algorithms by spheres or spheroids. This assumption leads to additional uncertainties in modelling the aerosol phase matrix and absorption cross section, which are larger than for many other aerosol types and may not be accounted for fully in the retrieval error budget (Mishchenko et al., 1997; Kalashnikova et al., 2005). ICIPE Mbita (hereafter Mbita, on the shore of Lake Victoria in Kenya) is similar to Pickle Lake but for water retrievals; i.e. it allows for the sampling of nominal water pixels which may be influenced by partial misflagging of coastlines, 3-D effects from the comparatively bright land, and outflow into the water affecting surface brightness. Finally, Venice (Italy) is in the northern Adriatic Sea, slightly beyond the outflow of the Venetian lagoon, and its water colour is strongly divergent from the Case 1 (brightness tied to chlorophyll a concentration; Morel, 1988) assumption employed by most AOD retrieval algorithms.

This breakdown is inherently subjective as all retrievals involve approximations; the dozen sites chosen are illustrative of different aerosol and surface regimes but not necessarily indicative of global performance. The purpose of this study is to define and demonstrate the framework for evaluating pixel-level uncertainties and provide some recommendations for their provision and improvement. It is hoped that, with growing acceptance of the need to evaluate pixel-level uncertainties, this approach can be applied on a larger scale. The sites were chosen as they are fairly well-understood and have multi-year data sets (data from all available years were considered from the analysis). Note that some of the satellite data sets considered here do not provide data at some sites for various reasons (discussed later).

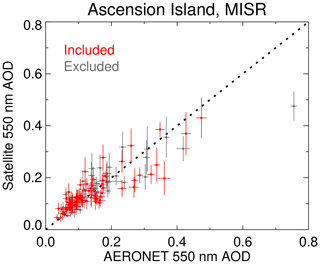
Figure 5 Example results of matchup and filtering criteria for MISR data at Ascension Island. Red points indicate matchups included for further analysis on the basis of filters described in the text, and grey indicates those excluded from analysis. Horizontal and vertical error bars indicate the 1σ uncertainty on AERONET and MISR data, respectively. The 1:1 line is dashed black.

The matchup protocol is as follows. AERONET data are averaged within ±15 min of each satellite overpass (providing τ_A) and compared with the closest successful satellite retrieval which has a pixel centre within 10 km of the AERONET site. This provides τ_S and ϵ_S. Each satellite data set's recommended quality assurance (QA) filtering criteria are applied as provided in the data products. The AERONET uncertainty, ϵ_A, is taken as the quadrature sum of the AERONET measurement uncertainty (±0.01; Eck et al., 1999) and standard deviation of the AERONET measurements (typically 2–3) during the ±15 min temporal window. Additionally, matchups are discarded if ϵ_A>0.02 or if only one AERONET measurement is obtained during the time window, as this indicates the potential for heterogeneous scenes. Dependent on the site and sensor, this additional filtering step removes around 10 %–60 % of potential matchups; Fig. 5 shows an example for MISR over-water retrievals at the Ascension Island site. As a reminder, the focus here is not on validating the AOD but rather validating the AOD uncertainty estimates (vertical lines in the figure).

These matchup criteria are stricter than what is commonly applied for AOD validation (e.g. Ichoku et al., 2002), which typically averages AERONET data within ±30–60 min and satellite retrievals within $\sim \pm \mathrm{25}$ km; the smaller spatiotemporal window and additional filtering criteria decrease the potential (unknown) contribution of collocation uncertainty to ϵ_A, which increases as the collocation criteria are loosened (Virtanen et al., 2018). The reasoning behind taking the nearest, rather than average, satellite retrieval is similar: averaging would have the potential to decrease the apparent retrieval error, which would make the comparison less useful for evaluating ϵ_S. Weakening these criteria could increase the data volume for analysis at the expense of increased collocation-related uncertainty, and there is no objective way to determine universal optimal thresholds. However, in the future, site-specific criteria could be guided by analysis of high-resolution (spatiotemporal) model simulations and surface observations.

This work considers satellite AOD products from seven algorithm teams; five of these contain both land and water retrievals (albeit sometimes with different algorithms), while two only cover land retrievals. Only pixels retrieved as land are used for comparison with AERONET data from land sites in Table 6, and vice versa for water sites. These data sets are briefly described below, and the reader is referred to the references cited here and in Tables 4 and 5 for additional information. Note in the discussion that the term “pixel” refers to individual L2 retrievals, sometimes referred to “superpixels” in the literature as they are often coarser than the source L1 data.

3.2.2 MODIS data sets

Four of the data sets (three land, one water) are derived from MODIS measurements; there are two MODIS sensors providing data since 2000 and 2002 on the Terra and Aqua satellites, respectively. The sensors have a 2330 km swath width, which is advantageous in providing a large data volume for analysis. Since launch, the MODIS aerosol data products have included AOD from the DT algorithm family, which has separate algorithms for water and vegetated land pixels (Levy et al., 2013). These data sets provide only diagnostic uncertainty estimates of the form ${\mathit{ϵ}}_{\mathrm{S}}=\pm (a+b{\mathit{\tau }}_{\mathrm{A}})$; in practice (and here) these are often treated as if they were framed instead in terms of τ_S with the same coefficients a and b when a prognostic estimate is needed. For retrievals over land, ${\mathit{ϵ}}_{\mathrm{S}}=\pm (\mathrm{0.05}+\mathrm{0.15}{\mathit{\tau }}_{\mathrm{A}})$, which is consistent with the expected performance of the algorithms at launch (Remer et al., 2005). Over water, the estimate has been revised since launch to ${\mathit{ϵ}}_{\mathrm{S}}=\pm (\mathrm{0.03}+\mathrm{0.1}{\mathit{\tau }}_{\mathrm{A}})$. Limited validation based on Collection 6 data by Levy et al. (2013) suggested that there might be an asymmetry to the envelope with the 1σ range over water being from $-\mathrm{0.02}-\mathrm{0.1}{\mathit{\tau }}_{\mathrm{A}}$ to $+\mathrm{0.04}+\mathrm{0.1}{\mathit{\tau }}_{\mathrm{A}}$. This has not yet been corroborated by a global validation of C6 or the latest Collection 6.1 (C6.1), and it is also plausible that calibration updates in C6.1 may have ameliorated some of this bias. As a result the symmetric envelope is used here.

The DB algorithm retrieves AOD only over land and was introduced to fill gaps in DT coverage due to bright surfaces such as deserts (although it has since been expanded to include vegetated land surfaces as well). The latest version is described by Hsu et al. (2019). Prognostic AOD retrieval uncertainties are estimated as described in Sayer et al. (2013),

$$\begin{array}{}\text{(7)}& {\mathit{ϵ}}_{\mathrm{S}}=\pm \left({\displaystyle \frac{a+b{\mathit{\tau }}_{\mathrm{S}}}{\frac{\mathrm{1}}{{\mathit{\mu }}_{\mathrm{0}}}+\frac{\mathrm{1}}{\mathit{\mu }}}}\right),\end{array}$$

where μ₀ and μ are the cosines of solar and view zenith angles, respectively, and a and b are coefficients depending on the QA flag value, sensor, and (since C6.1) surface type. The latest values of a and b are given by Hsu et al. (2019).

BAR also performs retrievals only over land; it uses the same radiative transfer forward model as DT but reformulates the problem to retrieve the MAP solution of aerosol properties and surface reflectance simultaneously for all vegetated pixels in a single granule (Lipponen et al., 2018). This includes both a priori information and spatial smoothing constraints. Uncertainty estimates are provided organically by the MAP technique (Eq. 2). Note that BAR data are only available at present for 2006–2017.

For all MODIS products, data from the latest C6.1 are used. All products are provided at nominal (at-nadir) 10 km horizontal pixel size. Identical algorithms (and approaches for estimating uncertainty) are applied to both Terra and Aqua measurements, and the results of the evaluation were not distinguishable for Terra and Aqua data. For conciseness and to increase data volume Terra and Aqua data are not separated in the discussion going forward.

3.2.3 MISR data sets

The MISR sensor also flies on the Terra platform and consists of nine cameras viewing the Earth at different angles, with a fully overlapped swath width around 380 km (Diner et al., 1998). The latest version 23, used here, provides AOD retrievals at 4.4 km horizontal pixel size. Both land and water retrievals (Garay et al., 2017; Witek et al., 2018b) attempt retrieval using each of 74 candidate aerosol mixtures, although they differ in their surface reflectance models and uncertainty estimates. The overland “heterogeneous surface” retrieval estimates uncertainty as the standard deviation of AOD retrieved using those aerosol mixtures which provide a sufficiently close match to TOA measurements (Martonchik et al., 1998, 2009). The “dark water” approach (Witek et al., 2018b) looks at the variation of a cost function across the range of potential AOD and aerosol mixtures,

$$\begin{array}{}\text{(8)}& f\left(\mathit{\tau }\right)={\displaystyle \frac{\mathrm{1}}{N}}\sum _{m=\mathrm{1}}^N{\displaystyle \frac{\mathrm{1}}{{\mathit{\chi }}_m^{\mathrm{2}}\left(\mathit{\tau }\right)}},\end{array}$$

where the sum is over N=74 aerosol mixtures and ${\mathit{\chi }}_m^{\mathrm{2}}$ is a cost function similar to the first term of Eq. (1). The uncertainty ϵ_S is then taken as the full-width at half maximum of f(τ), which is often found to be monomodal and close to Gaussian (Witek et al., 2018b). Note that MISR does not provide retrievals over Mbita or Venice as the dark water algorithm logic excludes pixels within the matchup radius used here as too bright and unsuitable; thus, the approach cannot be evaluated at those sites.

3.2.4 ATSR data sets

The ATSRs were dual-view instruments measuring near-simultaneously at nadir and near 55^∘ forward. ATSR2 (1995–2003) and AATSR (2002–2012) had four solar and three infrared bands, with approximately 1 km pixel sizes and a 550 km swath (although ATSR2 operated in a narrow-swath mode over oceans). Their predecessor ATSR1 lacked three of the solar bands and so has not been used widely for AOD retrieval. In 2016 the first of a new generation of successor instruments (the SLSTRs) was launched; SLSTR has several additional bands, a rear view instead of forward, the native spatial resolution of solar bands is finer, and the swath broader (Coppo et al., 2010). This study uses two data sets derived from this family of sensors.

ORAC is a generalized OE retrieval scheme which has been applied to multiple satellite instruments. Here, the version 4.01 ATSR2 and AATSR from the ESA CCI are used (Thomas et al., 2017), along with an initial version 1.00 of data from SLSTR. ORAC provides AOD retrievals over both land and ocean surfaces; the retrieval approaches are the same except for the surface reflectance models, which also inform the a priori and covariance matrices. Over water, surface reflectance is modelled according to Sayer et al. (2010a) with fairly strong a priori constraints. Over land, two approaches have been implemented in ORAC; the one used here is a model developed initially for the SU (A)ATSR retrieval algorithm (North et al., 1999), which assumes that the ratio between forward and nadir surface reflectance is spectrally invariant and has very weak a priori constraints. Note that AOD and aerosol effective radius have weak and strong a priori constraints, respectively. Retrievals are performed at native resolution, and cost functions and uncertainty estimates are as in Eqs. (1) and (2) without smoothness constraints. ORAC simultaneously retrieves aerosol and surface properties, performing an AOD retrieval for each of a number (here, 10) of candidate aerosol optical models (mixing four components defined by the aerosol CCI; Holzer-Popp et al., 2013) and choosing the one with the lowest cost as the most likely solution. Retrievals passing quality checks (Thomas et al., 2017) are then averaged to a 10 km Earth-referenced sinusoidal grid.

ADV uses the ATSR dual view over land to retrieve the contribution to total AOD from each of three aerosol CCI components (with the fraction of the fourth dust component prescribed from a climatology) by assuming that the ratio of surface reflectance between the sensor's two views is spectrally flat. This has some similarity with the North et al. (1999) approach, except for ADV the ratio is estimated from observations in the 1600 nm band at which the atmosphere is typically most transparent, rather than being a freely retrieved parameter (Kolmonen et al., 2016). Over the water, the algorithm only uses the instruments' forward view as this has a longer atmospheric path length and is less strongly affected by Sun glint. Because of this, the water implementation is often called ASV rather than ADV (Table 3), although for convenience here the term ADV is used throughout. Water surface reflectance is modelled as a combination of Fresnel reflectance and the chlorophyll-driven model of Morel (1988). The land and water algorithms treat other factors (e.g. aerosol optical models) in the same way. Unlike ORAC, ADV aggregates to a 10 km grid before performing the retrievals. ADV uncertainty estimates are calculated using Jacobians at the retrieval solution, i.e. the first component of Eq. (2), with S_y assumed diagonal. The uncertainty on the TOA measurements is taken as 5 %, which is somewhat larger than that assumed by ORAC, so ADV is implicitly adding some forward model uncertainty into this calculation. Version 3.11 of the data sets (Kolmonen and Sogacheva, 2018), also from the ESA aerosol CCI, is used here.

Aside from pixel and/or swath differences, for both ADV and ORAC the implementation of the algorithms is the same for the three sensors. Matchups from the two (for ADV) or all three (for ORAC) sensors are combined here in the analysis to increase data volume due to the similarity in sensor characteristics and algorithm implementation. Note, however, that the difference in viewing directions between (A)ATSR and SLSTR (i.e. forward vs. rear) means that different scattering angle ranges are probed over the two hemispheres, which influences the geographic distributions of retrieval uncertainties. For both of these data sets, a large majority of matchups (75 % or more) obtained are with AATSR, as the ATSR2 mission ended before the AERONET network became as extensive as it is at present, and the SLSTR record to date is short. The results do not significantly change if only AATSR data are considered.

3.2.5 CISAR SEVIRI

Unlike the other data sets considered here, the SEVIRI sensors fly on geostationary rather than polar-orbiting platforms. This analysis uses data from the first version of the CISAR algorithm (Govaerts and Luffarelli, 2018) applied to SEVIRI aboard Meteosat 9; due to computational constraints, only SEVIRI data for 2008–2009 have been processed and included here. This sensor has a sampling cadence of 15 min and observes a disc centred over North Africa, covering primarily Africa, Europe, and surrounding oceans. The horizontal sampling distance is 3 km at nadir, increasing to around 10 km near the limits of useful coverage. This sampling means that several of the AERONET sites (GSFC, Kanpur, Midway Island, Pickle Lake, UCSB) are not seen by the sensor and cannot be analysed.

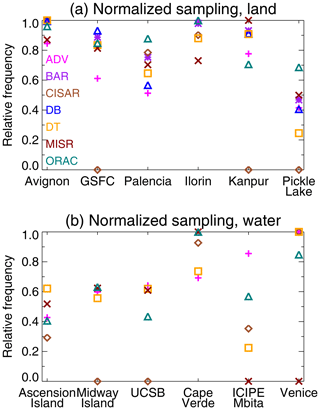
Figure 6 Site-to-site corrected sampling $\widehat{n}$ for each data set, shown on a relative scale. Symbols are used to aid in differentiating overlapping data points but carry no further information.

CISAR is also an OE retrieval scheme, which in its SEVIRI application accumulates cloud-free measurements from three solar bands over a period of 5 d and simultaneously retrieves aerosol and surface properties, reporting at each SEVIRI time step. Surface reflectance is modelled following Rahman et al. (1993) over land and Cox and Munk (1954a, b) over water, although the retrieval approach is otherwise the same between the two surface types. It employs a priori data and several smoothness constraints, so uncertainty estimates (Luffarelli and Govaerts, 2019) broadly follow Eq. (2).

Table 7 Number of matchups obtained for each AERONET site and data set, together with climatological cloud fraction.

3.3 Results

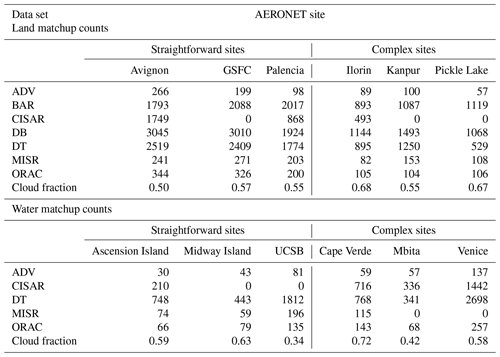
With the above criteria, the number of matchups n obtained for each AERONET site with each data set is shown in Table 7. This additionally includes the long-term climatological mean (March 2000–February 2019) daytime cloud fraction f_C from MODIS Terra, taken from the C6.1 level 3 monthly product (MOD08_M3) for the 1^∘ grid cell in which the AERONET site lies. The cloud-masking approach is described by Frey et al. (2008), with more recent updates listed in Sect. 3 of Baum et al. (2012). Data from Terra are used as the majority of the aerosol data sets, like Terra, have a late-morning overpass time.

To make the counts more comparable between sites a sampling-corrected count $\widehat{n}$ can be calculated,

$$\begin{array}{}\text{(9)}& \widehat{n}=n{\displaystyle \frac{\cos \left(\mathit{\varphi }\right)}{(\mathrm{1}-f_{\mathrm{C}})}}{\displaystyle \frac{m_{\mathrm{S}}}{m_{\mathrm{A}}}},\end{array}$$

where ϕ is the site's latitude (important as for polar-orbiting satellites a given latitude is overflown proportional to 1∕cos (ϕ)), m_S the number of months of the satellite record, and m_A the number of months during the satellite record for which the AERONET site was in operation. For example, CISAR data used here cover the period 2008–2009 (m_S=24); for these years, AERONET data at Ascension Island are available for 5 months in 2008 and 11 in 2009 (m_A=16). Equation (9) thus provides a first-order estimate of the number of matchups which would have been obtained in the absence of clouds (as the data sets consider cloud-free pixels only), an equal rate of being overflown, and with the AERONET site in constant operation through the satellite lifetime. Normalizing each satellite data set to the maximum of $\widehat{n}$ across sites (to account for swath width and mission length differences, which determine total counts) provides a relative measure of how often each data set provides a valid retrieval at each location; the resulting relative sampling frequencies are shown in Fig. 6. This measure will be used in the ongoing discussion. Note that as CISAR is applied to geostationary SEVIRI data, the factor of cos (ϕ) is omitted (since each point on the disc is sampled once per scan, and each point outside the disc is never seen).

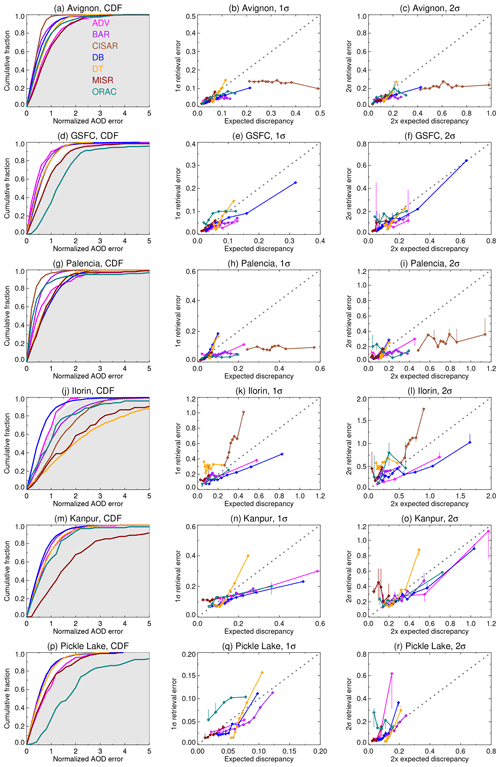
Figure 7 Evaluation of pixel-level uncertainty estimates for overland retrievals. Each row corresponds to a different AERONET site, and colours are used to distinguish data sets. The left-hand column shows a CDF of the absolute normalized retrieval error $\left|{\mathrm{\Delta }}_{\mathrm{N}}\right|$ (see Fig. 3b), and the middle and right columns show 1σ and 2σ expected discrepancy ED vs. absolute retrieval errors $\left|{\mathrm{\Delta }}_{\mathrm{S}}\right|$ (see Fig. 4), respectively. In the left column, theoretical expectations are shaded grey; in the others, the 1:1 line is indicated dashed in grey, and vertical bars indicate the uncertainty on the bin value, as described in the text.

Figure 8 As Fig. 7, except for AERONET sites used for over-water retrieval evaluation.

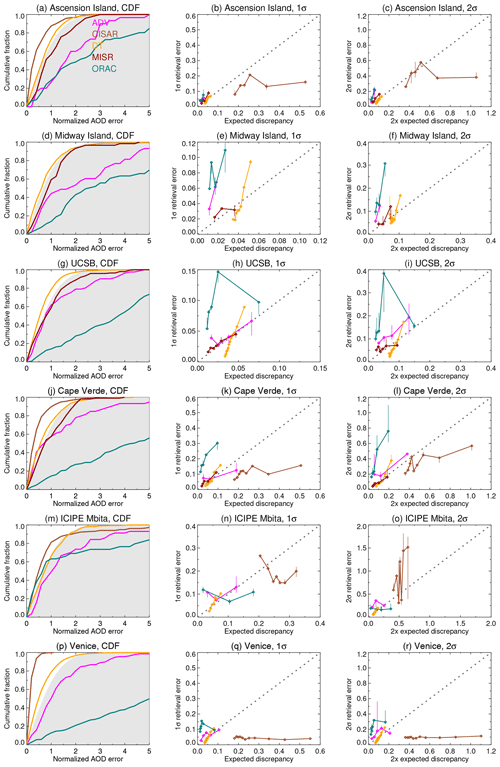
Graphical evaluations of the pixel-level uncertainties are shown in Figs. 7 and 8 for land and water retrievals, respectively. In both of these the left-hand column shows CDFs of absolute normalized error $\left|{\mathrm{\Delta }}_{\mathrm{N}}\right|$ against theoretical expectations (see Fig. 3b), and the middle and right columns show the ED ϵ_T and twice ED binned against the 1σ and 2σ points of absolute retrieval error $\left|{\mathrm{\Delta }}_{\mathrm{S}}\right|$, respectively (see Fig. 4). Due to the very different sampling between data sets and sites (Table 7), the number of bins is taken as the lesser of n∕20 or n^1∕3 (rounded to the nearest integer). This choice is a balance between well-populated bins to obtain robust statistics and the desire to examine behaviour across a broad range of ϵ_T. These figures also include an estimate of the digitization uncertainty on the binned values: for example, in a bin containing 100 matchups, the uncertainty on the 68th percentile (1σ point) binned value shown is taken as the range from the 67th to 69th matchup in the bin. For the MODIS-based records (which have the highest sampling) this digitization uncertainty is often negligible, but for others (ADV, MISR, ORAC) it is sometimes not.

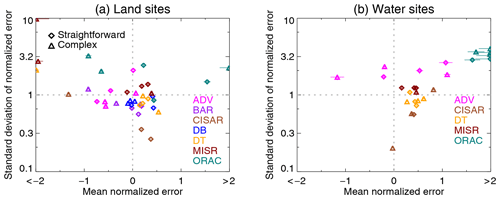
Figure 9 Mean and standard deviation of normalized error Δ_N obtained for each AERONET site and satellite data set for (a) land and (b) water sites. Horizontal and vertical bars indicate the standard errors on the estimates of the mean and standard deviation, respectively. Diamonds and triangles indicate straightforward and complex AERONET sites (Table 6). Note that the x axis is truncated and the y axis is logarithmic.

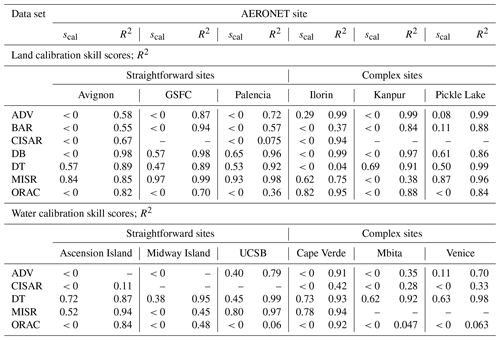
A further way to look at the data is provided by Fig. 9, which shows the mean and standard deviation of Δ_N for each data set and AERONET site; for unbiased retrievals with perfectly characterized errors (see Fig. 3a) the results should fall at coordinates (0, 1). This is a complement to the previously shown CDFs as it also provides measures of systematic bias in the AOD retrieval and systematic problems in estimating error magnitude: horizontal displacement from the origin indicates the relative magnitude and direction of systematic error, and vertical displacement indicates a general underestimation or overestimation of the typical level of error. Further, it shows how closely (or not) results from the different sites cluster together. For a larger-scale analysis of hundreds of AERONET sites, this type of plot could be expanded to a heat map. The CDFs in Figs. 7 and 8 assess the overall magnitude of normalized errors and the shape of the distribution, while the binned ED assesses the overall skill in the specificity of the estimates. In these figures, the top and bottom three rows show sites expected to be straightforward or complicated test cases for the uncertainty estimate techniques (Table 6). Table 8 provides the overall calibration skill scores for 1σ error at each site (Eq. 5), plus the coefficient of determination R² (where at least three bins were available) between binned uncertainty and 1σ error from the middle columns of Figs. 7 and 8. Together, these facilitate a visual and quantitative evaluation of the pixel-level uncertainty estimates.

Table 8 Calibration skill scores s_cal and coefficient of determination R² from binned 1σ uncertainties in Figs. 7 and 8.

3.3.1 Land sites

Turning to the land sites (Fig. 7), all the techniques show some skill in that the ED generally increases with retrieval error. There is, however, considerable variation between sites (which points to the utility of considering results site by site for this demonstration analysis) and data sets. For the straightforward sites, there is an overall tendency for the uncertainty estimates to be too large. This may indicate that the retrieval error budgets are a little too pessimistic; since overall errors and uncertainties also tend to be small at these sites, it is also possible that the uncertainty on the AERONET data (which can be a non-negligible contribution to ED here) is overestimated. A notable exception here is MISR, for which uncertainty estimates are very close to theoretical expectations. This implies that the overall assumptions made by this technique (that the principle contribution to error is in aerosol optical model assumptions, and the 74 mixtures provide a representative set such that the standard deviation of retrieved AOD between well-fitting mixtures is a good proxy for uncertainty) are valid. A second exception is CISAR, which more significantly overestimates the uncertainty, indicating that the retrieval is more robust than expected. For these sites the binned plots of 1σ and 2σ retrieval error vs. ED look similar, suggesting that, within each bin, the retrieval errors are roughly Gaussian (even if the magnitudes of uncertainty are not perfectly estimated). MODIS DT tends to overestimate uncertainty on the low end and underestimate on the high end, suggesting (at least for these sites) that the first and second coefficients in the expression ${\mathit{ϵ}}_{\mathrm{S}}=\pm (\mathrm{0.05}+\mathrm{0.15}\mathit{\tau })$ may need to be decreased and increased, respectively.

For the complex land sites, the picture is different. At Ilorin, MODIS DB and ADV tend to overestimate uncertainty, while the others underestimate it. This site was chosen as a test case because of the complexity of its aerosol optical properties, which are more absorbing than assumed by many retrieval algorithms and can show large spatiotemporal heterogeneity due to a complex mix of sources (Eck et al., 2010; Giles et al., 2012; Fawole et al., 2016). Using aircraft measurements, Johnson et al. (2008) found mid-visible single-scattering albedo (SSA) from smoke-dominated cases between 0.73 and 0.93, with a central estimate for the smoke component of 0.81. DB has a regional SSA map with more granularity (Hsu et al., 2019), while the other algorithms do not contain sufficiently absorbing particles, leading to a breakdown in their uncertainty estimates when strong absorption is present.

The most absorbing component in the MISR aerosol mixtures has an SSA of 0.80 at 558 nm; mixtures including this component have SSA from 0.81 to 0.96, and all other MISR mixtures have SSA >0.90 (Tables 2, 3 of Kahn et al., 2010). In smoke cases retrievals are biased low and the uncertainty estimates are too narrow because the set of candidate aerosol mixtures is not representative of optical properties at this location. MODIS DT and BAR (which uses the same optical models as DT) assume a fine-mode-dominated model with mid-visible SSA of 0.85 for December–May and 0.90 for June–November (Fig. 3 of Levy et al., 2007); this is mixed with a less absorbing coarse-dominated model, so they suffer from similar issues. CISAR retrieves AOD by a combination of aerosol vertices in SSA-asymmetry parameter space; the most absorbing (for SEVIRI's 640 nm band, which is the shortest wavelength) has SSA around 0.79 (Fig. 4 of Luffarelli and Govaerts, 2019). Due to the spectral curvature of smoke SSA, this would imply a weaker effective absorption in the mid-visible. ADV and ORAC share aerosol components prescribed by the aerosol CCI (Holzer-Popp et al., 2013); the most absorbing fine-mode component has mid-visible SSA around 0.80, although this is also always mixed with more weakly absorbing fine-mode (which have SSA of 0.98) and coarse-mode particles in varying proportions, so in practice the assumed SSA is always higher (Tables 1 and 2 of Thomas et al., 2017). It may be that ADV is providing reasonable estimates at this site despite this due to the somewhat larger assumed forward model uncertainty than ORAC. For Kanpur, except for MISR (which has similar issues as Ilorin) and CISAR (as SEVIRI does not observe the site), these issues are lessened. This may be because, while Kanpur has similar complex mixed aerosol conditions, the components are overall less strongly absorbing and so these issues are less acute, with a typical SSA (similar to that of Ilorin in mixed, as opposed to smoke-dominated, conditions) around 0.89 (Giles et al., 2012). The issues with MISR may imply that the wrong mixture(s) are being selected here.

The case at Pickle Lake is more diverse: similar to the straightforward sites, MODIS DT, DB, and BAR all overestimate uncertainty. ADV and MISR are fairly close to theoretical values; despite this, their skill scores are fairly low (Table 8) as the magnitudes of their uncertainties are not perfect and the range of 1σ retrieval errors is fairly small. All these algorithms provide retrievals significantly less often than would be expected by the site's cloud cover, latitude, and AERONET availability (Fig. 6). This implies that the algorithms may be coping with a potential violation of assumptions (i.e. land mask issues from numerous small lakes) by simply not providing a retrieval at all. ORAC underestimates uncertainties at this site but provides retrievals relatively more frequently than the other data sets. As the land–sea mask is determined at full (1 km) resolution and used to set the surface model, it is likely that some of the pixels within the 10 km grid will be affected by misflagging and/or mixed surface issues, contributing to additional errors which are not being caught by these quality checks. Which behaviour is more desirable (no data vs. more uncertain data than expected) is a philosophical and application-dependent matter. As it lies outside the SEVIRI disc, CISAR provides no retrievals at this site.

Aside from DB, DT, and MISR, skill scores (Table 8) are in most cases negative; for the former two the uncertainty estimates are somewhat empirical and not independent of the AERONET data, so the fact they are fairly well-calibrated is not surprising. Despite this R² is typically not negligible (although the small number of bins means the estimates of R² are somewhat uncertain). This implies that, while the absolute magnitudes of estimated uncertainty are often too small or large, the techniques do show some skill at predicting which retrievals are comparatively less or more uncertain at a variety of locations. Neither s_cal nor R² should be overinterpreted in terms of site-to-site variations, as these depend strongly on the number of bins, the range in estimated uncertainties, and the range in actual retrieval errors at a given site. The main points of note are whether s_cal>0 and whether there is a positive association between binned uncertainty and error.

3.3.2 Water sites

For the water sites (Fig. 8), only five satellite data sets are available – also recall that the MODIS DT uncertainty envelope is narrower than over land, and the MISR uncertainty is a PDF based on a cost function composited over AOD and aerosol mixtures rather than (as over land) a simple standard deviation. At the straightforward sites there is some commonality with the land sites. Specifically, the MISR approach works fairly well, CISAR overestimates uncertainty (although of the three, only Ascension Island is within the SEVIRI disc), and MODIS DT slightly overestimates uncertainty overall, with a tendency to overestimate on the low end and underestimate on the high end. In general a similar picture is also seen in terms of s_cal and R²: most data sets are not well-calibrated, although there is skill at assessing variations in uncertainty at individual sites.

ADV and ORAC are more systematic in their underestimation of uncertainty over water compared to over land, although as the over-water errors are often fairly small in absolute terms, they appear fairly large in relative terms. This difference in the ATSR-based records between land and ocean sites is intriguing. ADV assumes 5 % uncertainty in the TOA signal, while ORAC includes separate measurement and forward model terms for a slightly lower total uncertainty overall (typically 3 %–4 % dependent on band and view), which in part explains ORAC's larger normalized errors. The common behaviour either implies (1) that the calibration of the sensors may be biased or more uncertain than expected for these fairly dark ocean scenes or (2) that the over-water surface reflectance models or (for ORAC) their uncertainties (either in their contribution to forward model error in S_y or the strength of the a priori constraint in S_a) might be less reliable than assumed. Figure 9 implies that there is a significant systematic error source in ORAC contributing to a positive bias over water. A thorough comparison between the two data sets using the matchups collected here is difficult due to the fairly low data volumes involved, especially for ADV. ADV provides significantly fewer retrievals overall than ORAC (for both land and water), implying stricter pixel selection and/or retention criteria; this is consistent with ESA CCI validation analysis of earlier versions of these data sets by Popp et al. (2016) and Kinne et al. (2017).

Despite the expected complexities at Cape Verde from mixtures of low-level sea spray and higher-altitude nonspherical mineral dust (Mishchenko et al., 1997; Kalashnikova et al., 2005), the error characterization at this complex site does not appear different from that obtained at the more straightforward sites. Interestingly, these algorithms seem more selective about when to provide retrievals at the three straightforward sites than they are at Cape Verde (Fig. 6). The reasons for this are unclear unless the estimate provided by $\widehat{n}$ (Eq. 9) is not a good approximation for these sites; each is close to the coast and all should be roughly equally affected by Sun-glint sampling-related losses.

Mbita is in some sense the inverse of the land site Pickle Lake, and similar comments apply. MODIS DT uncertainties are reasonable, although the data volume is fairly low relative to expectations from Fig. 6. ADV and ORAC retrieve more frequently and perform well but with more high-error outliers than expected, likely due to mixed or misflagged land–water pixels. CISAR retrieves with a similar frequency at Mbita as Ascension Island (that is, less than expected but no less so than at the straightforward site). Looking at the binned ED vs. error, the errors for the 1σ points (Fig. 8n) are slightly overestimated and those for the 2σ points (Fig. 8o) underestimated, implying more extreme outliers than expected and indicating possible surface contamination issues. Note that MISR does not provide retrievals at this site as the algorithm does not consider Lake Victoria to be dark water.

Venice is sampled close to the expected rates by ADV, CISAR, MODIS DT, and ORAC (Fig. 6), and again it is excluded by MISR due to the bright, turbid water. Here, the CISAR 1σ retrieval error is ∼0.05 and the 2σ error is about double that, regardless of the ED; the uncertainty estimates do not show skill overall. As SEVIRI's wavelengths (640, 810, 1640 nm) are less strongly affected by water turbidity than the other sensors, the issues causing complexity here may not apply, and the overall tendency for CISAR to report too large an uncertainty may be dominating. ADV and DT results are reasonably in line with expectations, implying either that the turbid water is not a hindrance for the algorithm or that the additional uncertainty from this factor is compensated for by lower uncertainties in some other aspect of the algorithm. ORAC tends to more strongly underestimate the retrieval uncertainty. The water surface reflectance model (Sayer et al., 2010a) is based on low-turbidity Case I water (Morel, 1988), so it is likely providing a low-biased a priori for the retrieval with too strong a constraint, leading to a high bias in AOD retrievals with overly high confidence in the solution, which becomes large when expressed in normalized terms.

4 Conclusions and path forward

Pixel-level uncertainty estimates in AOD products are an important complement to the retrievals themselves to allow users to make informed decisions about data use for data assimilation and other applications. Ideal estimates are prognostic (predictive), and these are increasingly being provided within data sets; when they are absent, diagnostic estimates can be used as a stopgap. This study has reviewed existing diagnostic and prognostic approaches, provided a framework for their evaluation against AERONET data, and demonstrated this framework using a variety of satellite data products and AERONET sites. It is hoped that this methodology can be adopted by the broader community as an additional component of data product validation efforts. Several conclusions about the performance of these existing estimates follow.

1. All tested techniques show skill in some situations (in that the association between estimated uncertainty and observed error is positive, and on average magnitudes are reasonable), although none are perfect, and there is no clear single best technique. Small data volumes for some sensors and locations limit the extent to which performance in the high-uncertainty regime can be probed.

2. The points in Fig. 9 tend to cluster by data set more strongly than by site. This implies that some of the quantitative limitations in the uncertainty estimates provided within the current data sets are large-scale issues (e.g. persistent underestimate or overestimate of some aspect of the retrieval error budget). Further, as the performance at expected straightforward vs. complex AERONET sites was not always distinct, these limitations (or other unknown factors) may at present be more significant error sources than the issues associated with the ground sites.

3. While skilful, the uncertainties are not always well-calibrated; i.e. they are often systematically too large or too small. If characterization of the error budgets of the retrievals cannot be significantly improved, it is plausible that a simple scaling (using e.g. averages of the standard deviations on the y axis in Fig. 9) could be developed to bring the magnitudes more into line with the expected values.

4. The formal error propagation techniques (employed here by BAR, CISAR, and ORAC) are very powerful. Their differing behaviour and performance illustrate the difficulties in appropriately quantifying terms for the forward model, a priori covariance matrices, and appropriate smoothness constraints. For these sites, CISAR tends to overestimate the uncertainty most strongly, BAR to overestimate slightly, and ORAC to underestimate (more strongly over water than land). The simpler approach taken by ADV (Jacobians from a flat 5 % error on TOA reflectance) tends to be about right over land but also underestimates the true uncertainty over water.

5. The empirical validation-based MODIS DB approach works well but on average overestimates the total uncertainty and at these sites has little bias overall. That may indicate that the sites used here are coincidentally better-performing than the global results used to fit the expression. This points to the fact that the expression (which draws on AOD, geometry, quality flag, and surface types) captures many, but not all, of the factors relevant for quantifying total uncertainty.

6. The diagnostic MODIS DT approaches perform reasonably well if used instead as prognostic uncertainty estimates; they have a tendency to be insufficiently confident (overestimate uncertainty) on the low end and overconfident (underestimate uncertainty) on the high end. Despite the possibility for unphysical negative AOD retrievals in the DT land product, both land and ocean results indicate a systematic positive bias in the retrievals.

7. MISR's two approaches (applied for land and water surfaces) are both based on diversity between different candidate aerosol optical models. They both perform well at most sites, although they have a tendency to underestimate the total uncertainty slightly. The implication from this is that the diversity in AOD retrievals from different candidate optical models does capture the leading cause of uncertainty in the MISR retrievals. The fact that they are underestimates does imply at least one remaining important factor which is not captured by this diversity, which could perhaps be a systematic error source such as a calibration or retrieval forward model bias.

More broadly, these results suggest paths for the development and refinement of pixel-level AOD uncertainty estimates for existing and new data sets. For algorithms attempting AOD retrievals from multiple candidate aerosol optical models, the diversity in retrieved AOD between these different models could be a good proxy for part of the retrieval uncertainty. The MODIS DT ocean and ORAC algorithms both perform retrievals for multiple optical models. As ORAC is already an OE retrieval, this aerosol-model-related uncertainty is one of the few components not directly included in the existing error budget, so it could perhaps be added in quadrature to the existing uncertainty estimate. MODIS DT provides only a diagnostic AOD uncertainty estimate; diversity between possible solutions (which draw from 20 possible combinations of four fine modes and five coarse modes) could be explored as a first-order prognostic extension or replacement of that. One caveat is that this metric is only useful when the candidate set of optical models is representative; results at Ilorin, where aerosol absorption is often stronger than assumed in retrieval algorithms and the MISR approach does not perform well, illustrate that this is not always the case.

A general principle behind the error propagation techniques is the assumption of Gaussian departures from some underlying forward model. When this is not true, the techniques tend to fail. The Ilorin case is one such example of this. Another is the higher-level issue of coastal or lake areas, as most algorithms make binary retrieval decisions with non-linear implications (e.g. treat pixel as land or water for surface reflectance modelling), which cause problems if pixels are either misflagged or “contaminated” and contain mixed water or land. The algorithms tested here tend to deal with this in one of two ways. The first is simply to fail to provide a valid retrieval at all; in this case, the uncertainty estimates for available retrievals tend to be reasonable, although the data volume is significantly less than expected. The second option is to provide a retrieval but consequently provide a poor estimate (and typically an underestimate) of the associated uncertainty. Neither is entirely satisfactory. Performing retrievals at a higher spatial resolution with strict filtering might ameliorate these issues, as a smaller fraction might then be contaminated or misflagged; however, the resolutions of the sensor measurements and land mask (and its quality) place hard constraints on what could be achieved. Another option might be to attempt retrievals using both land and water algorithms for these pixels and either report both or an average (including the difference between them as an additional contribution to the uncertainty estimate). This would provide some measure of the potential effect of surface misclassification and at the least provide a larger uncertainty estimate to alert the data user about problematic retrieval conditions. A deeper understanding of the representativity of AERONET sites on satellite retrieval scales would be useful to better understand the distributions of retrieval success rates and errors. This is a topic of current research (e.g. Schutgens et al., 2016, 2017; Kinne et al., 2013; Li et al., 2016; Schutgens, 2019) although often on a temporal basis or on coarser spatial scales than relevant for L2 validation.

A further difficulty in the assumption of Gaussian random errors is that sensor calibration uncertainty tends to be dominated by systematic effects rather than random noise. While in practice it is often (as in the algorithms assessed here) treated as a random error source, when it is a dominant contribution to the retrieval error budget it will tend to skew the retrievals toward one end of the notional uncertainty envelopes. This may explain some of the systematic behaviour along the x axis in Fig. 9 within individual data sets (although the position along this axis is determined not only by the actual error, but also the estimated uncertainty). As discussed in Sect. 2.4, a pragmatic method for amelioration of this (if the forward model contribution to the systematic uncertainty cannot be significantly reduced by improvements to retrieval physics) would be to perform a vicarious calibration. Ship-borne AOD observations were also used as one part of the MISR calibration strategy for low-light scenes (Witek et al., 2018a); if this removes the bulk of the systematic calibration error, it may help explain why the uncertainty estimation technique (dispersion in possible solutions with different aerosol optical model assumptions) generally works so well.

The framework for evaluating uncertainties here is general and not restricted to AOD. In practice, however, it is difficult to extend it to other aerosol-related quantities at the present time. For profiling data sets (such as lidar), uncertainties in extinction profiles are often strongly vertically correlated as the effects of assumptions propagate down the profile (Young et al., 2013). An assessment would also have to account for the vertical resolution of the sensors and compute appropriate averaging kernels (Rodgers, 2000); this is by no means intractable and has been done using ground-based lidar systems for aerosol properties (e.g. Povey et al., 2014) as well as other geophysical quantities (e.g. atmospheric temperature by Sica and Haefele, 2015). Possibly a stronger limitation is that there are relatively few validation-quality data sets (i.e. with significantly smaller uncertainty than the spaceborne sensor) to compare them to, so the ground-based contribution to the total expected discrepancy would not be negligible.

For the total column, other key quantities of interest include the Ångström exponent (AE), fine-mode fraction (FMF) of AOD, and aerosol SSA. The AE can easily be assessed using this framework, although AERONET AE itself can be quite uncertain in the low-AOD conditions which predominate in many locations around the globe (Wagner and Silva, 2008). In that case the expected discrepancy would include significant contributions from AERONET uncertainty, so the comparison would be less informative about the quality of the satellite uncertainty estimate. These issues are somewhat lessened in high-AOD conditions, however. Similar comments apply to AERONET FMF, which has an uncertainty of the order of ±0.1 in moderate- to high-AOD conditions and larger when AOD is low (O'Neill et al., 2003, 2006). The framework presented here would not become invalid in these cases (although it becomes statistically problematic for locations where FMF is close to the bounds 0 or 1) but would become a measure of the joint consistency of both satellite and AERONET uncertainties, rather than a test primarily of the satellite uncertainty estimates. Some of these issues are lessened if, instead of FMF, fine-mode AOD (i.e. the product of FMF and AOD) and coarse-mode AOD are used. While AOD is also positive definite, numerical issues associated with AOD near 0 can be removed if retrievals are performed in log space, reflecting the closer-to-lognormal distributions of AOD found in nature (O'Neill et al., 2000; Sayer and Knobelspiesse, 2019); ORAC, for example, retrieves AOD in log space.

Issues with SSA are somewhat more difficult; AERONET almucantar inversions have an uncertainty in SSA around ±0.03 under favourable conditions (moderate to high AOD and large solar zenith angle) but uncertainties can be significantly larger otherwise (Dubovik et al., 2000). Given that SSA (like FMF) is inherently bounded in the range 0–1, and most aerosol types have SSA in the visible spectral region around 0.8–1 (e.g. Dubovik et al., 2002), in practical matters this uncertainty is a significant fraction of the variability in the parameter to be observed. Further, the hard boundary of SSA =1 means that the Gaussian statistics on which many uncertainty estimates and part of this framework rely will be less useful models of the real error characteristics. As such (similarly to FMF) it may be better to assess related optical properties, such as absorption AOD (AAOD), rather than SSA itself. This would address some of the statistical issues (plus AAOD is more directly connected to the radiative effect than SSA alone) but would not remove the underlying difficulty of accurate quantification of aerosol absorption, which remains both difficult to measure and difficult to retrieve from ground, airborne, or satellite remote sensing. Despite these difficulties with other aerosol properties (and the current limitations of techniques for quantifying AOD uncertainty), the routine provision, evaluation, and scientific use of prognostic AOD uncertainty estimates from satellite remote sensing will constitute an important step toward more optimal and robust applications of these data sets.