Three-dimensional radiative transfer effects on airborne and ground-based trace gas remote sensing

Air mass factors (AMFs) are used in passive trace gas remote sensing for converting slant column densities (SCDs) to vertical column densities (VCDs). AMFs are traditionally computed with 1D radiative transfer models assuming horizontally homogeneous conditions. However, when observations are made with high spatial resolution in a heterogeneous atmosphere or above a heterogeneous surface, 3D effects may not be negligible. To study the importance of 3D effects on AMFs for different types of trace gas remote sensing, we implemented 1D-layer and 3D-box AMFs into the Monte carlo code for the phYSically correct Tracing of photons In Cloudy atmospheres (MYSTIC), a solver of the libRadtran radiative transfer model (RTM). The 3D-box AMF implementation is fully consistent with 1D-layer AMFs under horizontally homogeneous conditions and agrees very well (<5 % relative error) with 1D-layer AMFs computed by other RTMs for a wide range of scenarios. The 3D-box AMFs make it possible to visualize the 3D spatial distribution of the sensitivity of a trace gas observation, which we demonstrate with two examples. First, we computed 3D-box AMFs for ground-based multi-axis spectrometer (MAX-DOAS) observations for different viewing geometry and aerosol scenarios. The results illustrate how the sensitivity reduces with distance from the instrument and that a non-negligible part of the signal originates from outside the line of sight. Such information is invaluable for interpreting MAX-DOAS observations in heterogeneous environments such as urban areas. Second, 3D-box AMFs were used to generate synthetic nitrogen dioxide (NO₂) SCDs for an airborne imaging spectrometer observing the NO₂ plume emitted from a tall stack. The plume was imaged under different solar zenith angles and solar azimuth angles. To demonstrate the limitations of classical 1D-layer AMFs, VCDs were then computed assuming horizontal homogeneity. As a result, the imaged NO₂ plume was shifted in space, which led to a strong underestimation of the total VCDs in the plume maximum and an underestimation of the integrated line densities that can be used for estimating emissions from NO₂ images. The two examples demonstrate the importance of 3D effects for several types of ground-based and airborne remote sensing when the atmosphere cannot be assumed to be horizontally homogeneous, which is typically the case in the vicinity of emission sources or in cities.

1 Introduction

Ground-based, space-based and airborne remote sensing of air pollutants and greenhouse gases from scattered sunlight are increasingly used for air pollutant monitoring (e.g., Frankenberg et al., 2005; Richter et al., 2004; McPeters et al., 2015; Burrows et al., 1999; Zhou et al., 2012; Nowlan et al., 2016) and for source detection and emission estimation (e.g., Mijling et al., 2013; Martin et al., 2003; Russell et al., 2012; Krueger et al., 1995). The most commonly applied trace gas retrieval method in the ultraviolet, visible and near-infrared spectral range is differential optical absorption spectroscopy (DOAS) (Platt and Stutz, 2008), which fits absorption cross sections of a trace gas to the measured spectra. The result of the DOAS analysis is a slant column density (SCD), which is the integrated trace gas concentration along the optical path of the sunlight scattered towards the spectrometer. The optical path depends on the illumination and viewing geometry, on absorption and scattering by air molecules, aerosols and clouds, and surface reflectance.

A physically more meaningful quantity that is independent of the measurement geometry is the vertical column density (VCD), which is the integrated trace gas concentration from the ground to the top of the atmosphere. The ratio between SCD and VCD is called air mass factor (AMF) (Solomon et al., 1987), which can be computed with a radiative transfer model (RTM). To account for the vertical variability in atmospheric properties, AMFs are computed for discrete vertical layers (layer AMFs) assuming horizontal homogeneity (Palmer et al., 2001; Wagner et al., 2007; Rozanov and Rozanov, 2010). In the past decades, numerous RTMs have been developed with the possibility to calculate one-dimensional layer AMFs (e.g., Berk et al., 1999; Postylyakov, 2004; Rozanov et al., 2005; Wagner et al., 2007; Spurr et al., 2001; Iwabuchi, 2006; Iwabuchi and Okamura, 2017). The computation of layer AMFs is implemented in most trace gas retrieval algorithms for satellite and ground-based observations applied today (Boersma et al., 2011; Irie et al., 2011; Wenig et al., 2008; Wu et al., 2013). An alternative method is direct fitting, which is used in few algorithms (e.g., Lerot et al., 2010).

Layer AMFs assume horizontal homogeneity, which is not valid when the parameters affecting scattering and absorption along the path of the photons vary also horizontally, for example, in limb geometry near the polar vortex (Puķīte et al., 2010) or in the presence of clouds (Mayer and Kylling, 2005). Horizontal homogeneity is usually a valid assumption in coarse-resolution trace gas remote sensing from satellites, where small-scale horizontal variability is averaged over a large pixel size. It is, however, often not valid for ground-based or airborne trace gas remote sensing at high resolution in polluted environments such as cities (e.g., Hendrick et al., 2014; Popp et al., 2012; Schönhardt et al., 2015; Tack et al., 2017). This is particularly true for nitrogen dioxide (NO₂), which has high spatial and temporal variability due to its short lifetime (Schaub et al., 2007). Other parameters affecting the path of the measured photons like surface reflectance and aerosol distributions may also have high spatial variability in cities.

To account for horizontal inhomogeneity, one-dimensional (1D) layer AMFs need to be extended to three-dimensional (3D) box AMFs. Notice that in previous studies (e.g., Rozanov and Rozanov, 2010) 1D-layer AMFs were sometimes referred to as box AMFs. In this study, we will use the terms 1D-layer and 3D-box AMFs to clearly distinguish between them. The 3D-box AMFs can be implemented most easily in radiative transfer models that compute the paths of many photons using a Monte Carlo approach to solve the radiative transfer equation (Deutschmann et al., 2011). In this study, we implemented both 1D-layer and 3D-box AMFs in the MYSTIC solver of the libRadtran RTM (Mayer and Kylling, 2005; Emde et al., 2016). The implementation was evaluated against the results of a RTM comparison study (Wagner et al., 2007). Finally, the advantage and necessity of using 3D-box AMFs is demonstrated for a range of realistic ground-based and airborne remote sensing scenarios.

2 Methods

2.1 Air mass factors

Atmospheric trace gases can be measured with ground-, aircraft- and space-based spectrometers that measure solar irradiance scattered into the line of sight of the instrument (see Fig. 1). In the case of aircraft- and space-based observations, a large fraction of the measured photons usually travels along a main path (thick dashed line) representing a single reflection at the surface. In the case of ground-based observations, the measured photons must follow a path with at least a single atmospheric scattering into the line of sight of the instrument (except for direct sun observations). Atmospheric scattering and absorption is determined by the distribution and properties of molecules, aerosols and clouds, and it depends on the wavelength of the radiation. Molecular scattering is particularly important in the UV range of the spectrum. Photons are absorbed by the trace gases along the optical path from the sun to the instrument. For a weak absorber such as NO₂, the abundance of the trace gas along the mean optical path can be obtained by fitting an absorption cross section to the measured spectrum. Thereby, the mean optical path is the total length of all individual photon paths divided by the number of photons collected by the instrument. The result of the fit is a SCD, which is defined as

$$\begin{array}{}\text{(1)}& \mathrm{SCD}=\underset{\mathrm{path}}{\int }c\left(l\right)\mathrm{d}l,\end{array}$$

with trace gas concentration c and optical path l. SCDs are not an intrinsic property of the atmosphere, since they depend on the illumination and viewing geometry. Therefore, for most applications, the main quantity of interest is the VCD. It is defined as

$$\begin{array}{}\text{(2)}& \mathrm{VCD}=\underset{z_{\mathrm{0}}}{\overset{\mathrm{TOA}}{\int }}c\left(z\right)\mathrm{d}z,\end{array}$$

with surface elevation z₀ and top of the atmosphere, TOA. AMFs, defined as

$$\begin{array}{}\text{(3)}& \mathrm{AMF}={\displaystyle \frac{\mathrm{SCD}}{\mathrm{VCD}}},\end{array}$$

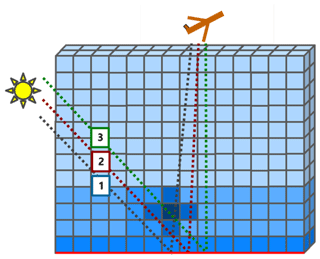
can be computed for a vertically varying atmosphere by dividing the atmosphere in layers with uniform properties (see Fig. 1a and b). The total AMF is then computed from the individual layer AMFs as

$$\begin{array}{}\text{(4)}& \mathrm{AMF}={\displaystyle \frac{{\sum }_{k=\mathrm{1}}^{n_z}{\mathrm{AMF}}_k{\mathrm{VCD}}_k}{{\sum }_{k=\mathrm{1}}^{n_z}{\mathrm{VCD}}_k}},\end{array}$$

with AMF_k and VCD_k being the AMF and VCD in the kth layer, respectively. The total AMF is thus a function not only of the atmospheric properties in each layer but also of the shape of the vertical profile of the trace gas (Palmer et al., 2001).

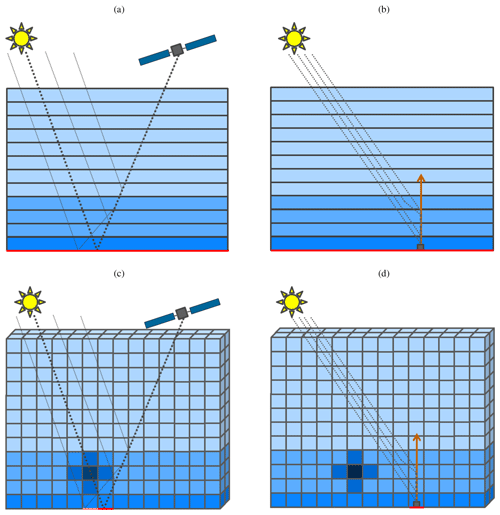
Figure 1 Illustration of the difference between (a, b) 1D-layer and (c, d) 3D-box AMFs for two scenarios with (a, c) downward-looking spaceborne and (b, d) upward-looking ground-based observations. Selected photon paths are shown as dashed lines. The 1D-layer AMFs implicitly assume horizontally uniform atmospheric and surface properties, whereas 3D-box AMFs fully account for both vertical and horizontal variability.

Similarly, the atmosphere can be divided into boxes in all three dimensions $(i,j,k)$ with homogeneous optical properties for each box (see Fig. 1c and d). The total AMF can be computed from the 3D-box AMFs $AM{F}_{i,j,k}$ as

$$\begin{array}{}\text{(5)}& \mathrm{AMF}={\displaystyle \frac{{\sum }_{i=\mathrm{1}}^{n_x}{\sum }_{j=\mathrm{1}}^{n_y}{\sum }_{k=\mathrm{1}}^{n_z}{\mathrm{AMF}}_{i,j,k}{\mathrm{VCD}}_{i,j,k}}{{\sum }_{k=\mathrm{1}}^{n_z}{\mathrm{VCD}}_k}},\end{array}$$

where the denominator is a sum over VCDs in k different vertical layers that could, for example, be taken at the location of an instrument or above the ground pixel of an aircraft- or space-based instrument. In this case, the AMF can be interpreted as the instrument sensitivity to the trace gas under investigation for measuring that specific VCD.

2.2 Implementation of AMFs in MYSTIC

The libRadtran RTM (available at http://www.libradtran.org, last access: 12 August 2020) can be used to calculate basic radiative quantities with different numerical solvers (Mayer and Kylling, 2005; Emde et al., 2016). One of its solvers is MYSTIC, which uses the Monte Carlo technique to trace individual photons on their way from the source (e.g., sun) to the target (e.g., measurement instrument). Scattering, absorption and reflection processes are treated as random decisions with respective probability distributions. MYSTIC calculates radiative quantities (irradiance, actinic flux at levels, radiance, absorption, emission, actinic flux, photon's path length and air mass factors) in 1D or 3D domains in spherical geometry or in plane-parallel geometry (Emde and Mayer, 2007; Emde et al., 2017). The 1D-layer and 3D-box AMFs were implemented following the same methodology as in McArtim, which to our knowledge is the only other existing RTM capable of computing 3D-box AMFs (Deutschmann et al., 2011; Richter et al., 2013). Note that McArtim is no longer actively developed.

AMFs depend on absorption and scattering processes affecting the light path in the atmosphere. AMFs can be readily calculated from the photon paths simulated by a Monte Carlo radiative transfer model. The Monte Carlo technique traces the paths of individual photons by describing the effects of absorption, scattering and reflection as random events with specific probabilities (Mayer, 2009). To obtain a robust measure of the mean optical path, a large number of photon paths need to be traced.

SCDs, VCDs and AMFs can be computed for the whole atmosphere, for individual vertical layers or for individual 3D boxes. For the general case of an atmospheric box i with constant concentration and optical properties, the AMF can be written as

$$\begin{array}{}\text{(6)}& {\mathrm{AMF}}_i={\displaystyle \frac{{\mathrm{SCD}}_i}{{\mathrm{VCD}}_i}}={\displaystyle \frac{{\int }_{\mathrm{path}}{c}_i\mathrm{d}l}{{\int }_{z_i}^{z_{i+\mathrm{1}}}{c}_i\mathrm{d}z}}={\displaystyle \frac{{\int }_{\mathrm{path}}\mathrm{d}l}{h_i}}={\displaystyle \frac{L_i}{h_i}},\end{array}$$

where $L_i={\int }_{\mathrm{path}}\mathrm{d}l$ is the mean optical path within the box of all photons that reach the instrument and h_i is the height of the box. Since the 3D-box/1D-layer AMFs are usually simulated for a sensor at a specific location in a three-dimensional model domain, the photons are traced backwards from the sensor towards the sun to increase computational efficiency as described in Marchuk et al. (1980) and Emde and Mayer (2007). In addition, the commonly used variance reduction method, known as “local estimate”, is applied at each scattering event (Marshak and Davis, 2005). The method computes the probability of an individual photon to be scattered into the direction of the sun that is assigned as a weight w_n to the photon. The weights of all photons can be summed up to obtain the radiance at the sensor. When a photon is scattered, a weighted photon path length (w_n⋅l_i) is also calculated, where l_i are the path lengths in each individual box i traversed by the photon before the scattering event. The mean optical path within a box i is then obtained by summing up the weighted photon path lengths of all photons as follows:

$$\begin{array}{}\text{(7)}& L_i={\displaystyle \frac{{\sum }_n^N{w}_n{l}_{i,n}}{{\sum }_n^N{w}_n}},\end{array}$$

where N is the total number of photons. L_i is then divided by the height of the box/layer to obtain the 3D-box/1D-layer AMF.

3 Validation of the AMF modules

3.1 Evaluation scenarios

The implementation of the 1D-layer and 3D-box AMF module in MYSTIC was evaluated against the results of different RTMs presented in an extensive RTM comparison study (Wagner et al., 2007). The simulated scenarios are representative for ground-based Multi-Axis-DOAS (MAX-DOAS) measurements of scattered sunlight spectra for different elevation angles (see Fig. 1b and d for the case of zenith-sky observations). The nine models included four models using full spherical geometry, four models using spherical geometry only for a subset of interactions and one model using plane-parallel geometry. The 1D-layer AMFs computed by these models agreed very well with differences mostly below 5 %, which could mainly be attributed to the different treatments and approximations of the Earth's sphericity and to model initialization parameters (Wagner et al., 2007).

For the comparison, we computed 1D-layer and 3D-box AMFs with MYSTIC in plane-parallel geometry as well as 1D-layer AMFs in spherical geometry for all scenarios presented in Wagner et al. (2007). The 3D-box AMFs have not yet been implemented with spherical geometry.

1D-layer and 3D-box AMFs were computed for five wavelengths (310, 360, 440, 477, 577 nm), seven elevation angles (1, 2, 3, 6, 10, 20, 90^∘) and three aerosol scenarios (aerosol extinction of 0.0, 0.1 and 0.5 km⁻¹). For the aerosol scenarios, an aerosol layer was prescribed between 0 and 2 km with an asymmetry parameter of 0.68 and a single-scattering albedo of 1.0. No aerosols were prescribed above 2 km. For the simulations, 17 vertical layers were used with a thickness of 100 m below 1000 m and a thickness of mostly 1000 m above (see Table 1 in Wagner et al., 2007). Profiles of temperature, pressure, density and ozone concentration were taken from the US Standard Atmosphere (United States Committee on Extension to the Standard Atmosphere, 1976). Ozone cross sections (in cm²) were $\mathrm{9.59}\times {\mathrm{10}}^{-\mathrm{20}}$, $\mathrm{6.19}\times {\mathrm{10}}^{-\mathrm{23}}$, $\mathrm{1.36}\times {\mathrm{10}}^{-\mathrm{22}}$, $\mathrm{5.60}\times {\mathrm{10}}^{-\mathrm{22}}$ and $\mathrm{4.87}\times {\mathrm{10}}^{-\mathrm{21}}$ at 310, 360, 440, 477 and 577 nm, respectively. Other atmospheric absorbers were ignored. Further details can be found in Wagner et al. (2007). For each scenario, we traced 1 million photons, which balances statistical noise expected from a Monte Carlo approach with computation time. The computed 3D-box AMFs were integrated horizontally to obtain 1D-layer AMFs that can be compared with the 1D-layer AMFs from other models. MYSTIC was mainly compared to SCIATRAN (Version 2.2; Rozanov et al., 2005). SCIATRAN was chosen because it agrees well with the mean of the models in Wagner et al. (2007), and because it is based on the discrete ordinate method to solve the radiative transfer equation, which is fundamentally different from a Monte Carlo solver, and finally because it offers both plane-parallel and spherical solutions. In addition, we compared MYSTIC to the mean of eight of nine RTMs in the comparison study. The PROMSAR/Italy model was not included because of its large deviation from the mean (see Wagner et al., 2007, for details).

3.2 Validation results

The comparison of 1D-layer AMF profiles calculated with the MYSTIC 1D modules with SCIATRAN for the 67 observation scenarios used in Wagner et al. (2007) is summarized in Fig. 2 in the form of a scatter plot. The horizontally integrated AMFs from MYSTIC's 3D module perfectly agree with its 1D module with plane-parallel geometry within the statistical noise of the Monte Carlo approach. When tracing 1 million photons, the difference between 1D and 3D module was smaller than 0.5 %. Therefore, only results from the 1D module were plotted against the SCIATRAN results. The agreement between MYSTIC and SCIATRAN is very good for almost all scenarios with relative differences mostly below 5 %. Overall, 97 % of the compared points are within a relative difference of 5 % for spherical geometry and 92 % for plane-parallel geometry. The mean of the relative differences for spherical geometry is 0.9 % and its standard deviation 2.0 %, and for the plane-parallel geometry the mean is 0.3 % with a standard deviation of 2.7 %.

Figure 2 Scatter plots of MYSTIC 1D-layer AMFs computed with (a) spherical and (b) plane-parallel geometries against 1D-layer AMFs computed with SCIATRAN (a) spherical and (b) plane parallel for 67 MAX-DOAS scenarios with 17 layers (1139 points). The solid black lines are the respective regression fits to the points.

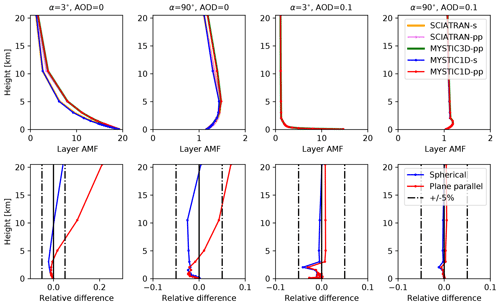
Figure 3 Upper row: MAX-DOAS AMF profiles for MYSTIC 1D spherical geometry (s), 1D plane-parallel geometry (pp) and 3D plane-parallel geometry (pp) for two selected elevation angles of 3 and 90^∘, a SZA of 20^∘, with and without aerosol for radiation at 577 nm. Corresponding profiles computed with the SCIATRAN RTM are shown for comparison. Lower row: profile of relative differences of MYSTIC and SCIATRAN results in spherical (s) and plane-parallel geometry (pp) (Wagner et al., 2007).

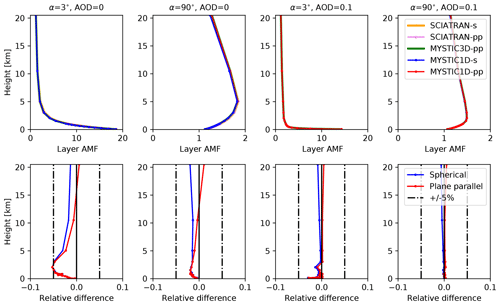
Figure 4 Upper row: MAX-DOAS AMF profiles for MYSTIC 1D spherical geometry (s), 1D plane-parallel geometry (pp) and 3D plane-parallel geometry (pp) for two selected elevation angles of 3 and 90^∘, a SZA of 20^∘, with and without aerosol for radiation at 360 nm. Corresponding profiles computed with the SCIATRAN RTM are shown for comparison. Lower row: profile of relative differences of MYSTIC and SCIATRAN results in spherical (s) and plane-parallel geometry (pp) (Wagner et al., 2007).

To illustrate the differences in AMF profiles between the two RTMs, we selected four scenarios with a wavelength of 577 nm, because at this wavelength we observe comparatively large differences between the two models. To illustrate a usual scenario with low difference, we also selected the same scenarios but with a 360 nm wavelength. The upper row of Fig. 3 (scenario at 577 nm) and Fig. 4 (scenario at 360 nm) shows MYSTIC 1D-layer AMF profiles for the selected scenarios with a low elevation angle of 3^∘ and a high elevation angle of 90^∘ (zenith) without and with aerosols, respectively. For comparison, the corresponding profiles computed with SCIATRAN are also shown. The lower row presents the relative differences between MYSTIC and SCIATRAN. Since plane-parallel and spherical modes have different geometrical assumptions, we compare plane-parallel models and spherical models separately.

In the upper atmosphere, the 1D-layer AMFs decrease with altitude in all scenarios (Figs. 3 and 4), because the atmospheric density is decreasing, which lowers the amount of scattering and, correspondingly, the mean photon path length. In the lowest layers, however, the profile shapes are different for the two elevation angles with a rapid decrease with altitude in the low elevation angle scenarios and a local maximum between 2 and 5 km in the high elevation angle scenarios. This local maximum is caused by multiple scattering, which contributes to the horizontal light paths in those layers. The reduction towards the surface in the latter scenarios is due to the low surface albedo. For an elevation angle of 3^∘, AMFs are high close to the ground because of the long light path in the layers due to the low elevation angle. Since aerosols increase scattering, photon path lengths and correspondingly 1D-layer AMFs are low in the lowest 2 km, when an aerosol layer is present.

1D-layer AMFs computed with spherical and plane-parallel geometry show noticeable differences for long wavelengths and low aerosol extinction, especially at altitudes above 5 km where extinction coefficients are small (see upper- and lower-left part in Fig. 3). In plane-parallel geometry, if one of these photons is traveling horizontally, it will strongly contribute to increase the mean photon path in that specific layer. In spherical mode, the same photon would change layer because of the curved atmospheric layers, and therefore its contribution to the mean photon path will be divided between the crossed layers. Furthermore, in a curved atmosphere, the zenith angle of the photon, which was initially traveling horizontally, will increase. At low altitude, these effects are smaller, and, conversely, 1D-layer AMFs computed with spherical and plane-parallel geometry agree better (mostly <5 %).

AMF profiles calculated with MYSTIC generally agree very well with those calculated with SCIATRAN with relative differences mostly smaller than 5 %. However, significant differences (up to 23 % relative difference) are seen between the plane-parallel solutions of the two models above 5 km for the scenarios without aerosols at 577 nm (Fig. 3). In contrast to the plane-parallel case, the spherical solution of MYSTIC is in good agreement with the spherical solution of SCIATRAN. The difference between SCIATRAN plane parallel and MYSTIC plane parallel is attributed to the different solution methods of the radiative transfer equation. A possible explanation is the following: in discrete ordinate methods, the directions of the radiation field are discretized and do not include the exact horizontal direction, for which in plane-parallel geometry the photon path length becomes extremely large in an optically thin medium like the higher atmosphere. In a Monte Carlo model, this horizontal direction is included; therefore the 1D-layer AMF might be larger. This hypothesis could be tested by including more streams (discrete directions) in SCIATRAN and verifying if the solution approaches the higher AMFs from the MYSTIC solution.

The simulations for the same scenarios but with 360 nm wavelength agree very well with SCIATRAN for both spherical and plane-parallel geometries (relative difference <5 %). The differences mentioned above are much smaller at this wavelength because atmospheric scattering events increase with lower wavelength and thus, prevent those very long photon paths. We also investigated a scenario with a wavelength of 440 nm, which is a typical wavelength of the window used for NO₂ fitting (see Fig. S4 in the Supplement), for which MYSTIC and SCIATRAN also agree very well (<5 % relative difference), but as for simulations at 577 nm discussed above, the simulations at 440 nm show significant differences between plane-parallel and spherical geometry for layers above 5 km. These differences are, however, smaller than at 577 nm because the optical thickness of Rayleigh scattering is higher at 440 nm.

Overall, MYSTIC agrees very well with SCIATRAN with differences mainly smaller than 5 %. An exception is the high elevation scenario without aerosols, where the plane-parallel solutions of MYSTIC and SCIATRAN differ by up to 23 % for a wavelength of 577 nm at altitudes above 5 km. It should be noted that for these cases the 1D-layer AMFs are very small, and therefore the absolute differences, which are relevant for most applications, are also small. The 1D-layer AMFs computed with MYSTIC also agree very well with the other models presented in Wagner et al. (2007). Differences larger than 5 % are mainly attributable to differences between plane-parallel and spherical solutions (see the Supplement). When comparing MYSTIC with the mean of the models, 88.3 % of the compared points are within a relative difference of 5 % for spherical geometry, 81.5 % for plane-parallel geometry, and 97.5 % for the mean of plane-parallel and spherical geometry. The mean of spherical and plane-parallel geometry agrees best because the models in Wagner et al. (2007) represents a mixture of spherical and plane-parallel solutions.

4 3D-box AMFs for MAX-DOAS observations

MAX-DOAS is a ground-based passive remote sensing technique allowing the retrieval of vertical concentration profiles of trace gases and aerosols (Wagner et al., 2004; Frieß et al., 2006; Irie et al., 2011; Hönninger and Platt, 2002). Information about the vertical distribution is obtained by measuring spectra at a prescribed sequence of elevation angles. Observations at different elevation angles have different sensitivity to the concentration in a given vertical layer. The 3D-box AMFs as computed by MYSTIC are particularly suitable to illustrate this, because 3D-box AMFs are a direct representation of the spatial distribution of the sensitivity of the measurements.

To illustrate the 3D distribution of 3D-box AMFs for a typical MAX-DOAS measurement, we simulated 3D-box AMFs at 450 nm for two scenarios with low and high aerosol optical depth, which correspond to a visibility of 50 and 10 km in the planetary boundary layer (PBL), respectively. A value of 450 nm is a typical wavelength for light absorption by NO₂. The instrument points northwards with an azimuth angle of 180^∘ and an elevation angle of 5^∘. The solar azimuth angle (SAA) is 344.7^∘ (164.7^∘ relative azimuth angle), and the solar zenith angle (SZA) is 24.6^∘. The MYSTIC input file is provided in the Supplement.

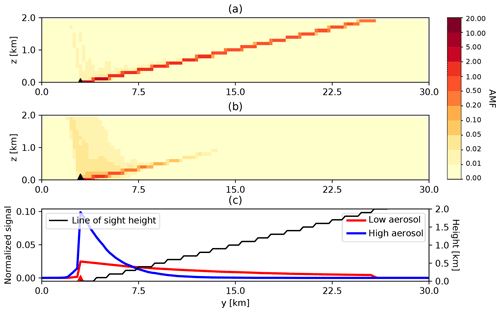
Figure 5 Cross section of 3D-box AMFs for a MAX-DOAS scenario with an instrument (black triangle) at the ground (z=0 km, x=20 km, y=3 km) pointing northwards and slightly upwards at a viewing angle of 5^∘. The sun is at an azimuth angle of 344.7^∘ and a zenith angle of 24.6^∘. The relative azimuth angle between sun and viewing direction is 164.7^∘. AMFs were simulated with two aerosol scenarios: a rural-type aerosol representative of spring–summer conditions in the aerosol layer (0–2 km), with a visibility of (a) 50 km and a visibility of (b) 10 km and a background aerosol above 2 km. Decay of vertically integrated AMFs with distance to the instrument is visualized (c) for the same scenarios with standard (red) and high aerosols (blue) as in panels (a) and (b). The altitude of the line of sight as a function of distance is shown in black.

Figure 5a and b show the 3D-box AMFs in the plane of the line of sight of the instrument for the two scenarios. In both cases, 3D-box AMFs are highest along the line of sight and reduce with distance from the instrument. Most of the photons collected by the instrument experienced a single scattering into the line of sight of the instrument. With increased aerosol amount (visibility of 10 km), photons scattered into the line of sight far away from the instrument have a high chance of being scattered out again. As a result, the sensitivity rapidly (within a few kilometers) decreases along the line of sight with increasing distance from the instrument. Multiple scattering becomes more important in this scenario, which explains the enhanced sensitivity to layers below and above the line of sight within a distance of up to 4 km of the instrument. The decrease in AMF with distance is further illustrated for the two scenarios in Fig. 5c, which shows the vertically integrated AMFs (in the aerosol layer) as a function of distance y to the instrument normalized with AMFs integrated horizontally in y direction. The figure also shows the height of the main optical path as a function of y.

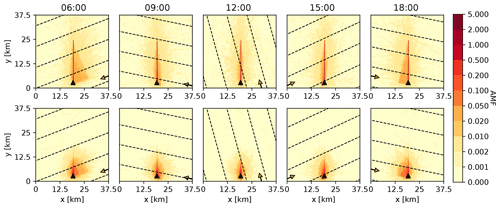
Figure 6 Top: vertically integrated 3D-box AMFs in the PBL (z<2.0 km) for an instrument at the ground pointing northwards with an instrument zenith angle of 5^∘ for different times of the day on the 21st of June in Zurich. Solar zenith angles are 77.4, 47.5, 24.6, 38.6 and 68.5^∘, and solar azimuth angles are 249.0, 281.5, 344.7, 65.2 and 101.7^∘. The arrows point away from the sun, and the dashed lines show the direction of photons coming from the sun. AMFs were simulated with a rural-type aerosol representative of spring–summer conditions in the aerosol layer (0–2 km) with a visibility of 50 km and a background aerosol above 2 km. Bottom: same as above but for a scenario with increased aerosol (visibility of 10 km).

To illustrate the horizontal spread of the sensitivity of the MAX-DOAS measurements in the PBL, Fig. 6 shows horizontal distributions of vertically integrated 3D-box AMFs (0–2 km) for the same scenarios with low (top row) and high (bottom row) aerosols and for five different sun positions corresponding to different times of the day on 21 July in the city of Zurich. The horizontal distribution of AMFs shows high values not only along the line of sight of the instrument but also in a surrounding region, which is up to a few kilometers wide. This region is wider for larger relative azimuth angles and is inclined towards the direction of the sun. The simulations show not only that the MAX-DOAS measurements are sensitive to NO₂ along the line of sight but also that they are also influenced by neighboring regions a few kilometers away.

For the different scenarios, we evaluated which part of the signal originated from a 0.25 km wide region centered on the northward pointing line of sight (referred to as main line in the following) and which part crossed boxes outside this range. For the low-aerosol scenario, between 63 % and 70 % originated from the main line. Thus, up to 37  % of the signal originated from photons crossing neighboring boxes. For the high-aerosol scenario with enhanced scattering, the part of the signal originating from the main line was correspondingly lower, between 30 % and 41 %. The lower values correspond to the scenarios with higher relative azimuth angles.

Depending on the viewing direction of the instrument relative to the position of nearby emission sources, this temporally varying spatial sensitivity could introduce a diurnal cycle in the measurement even when the trace gas concentration field was constant in time. Understanding the horizontal distribution of the sensitivity to NO₂ and its variation in time is thus particularly important for the interpretation of MAX-DOAS observations in polluted regions like cities with strong NO₂ gradients, for which 3D-box AMFs can be a valuable tool.

5 3D-box AMFs for airborne observations

In this section, we demonstrate the effect of the spatial variability in 3D-box AMFs on airborne NO₂ imaging spectroscopy. For this purpose, we simulated a NO₂ plume emitted from a stack to generate a scenario with a distinct three-dimensional trace gas structure. An airborne spectrometer was then assumed to fly parallel to the plume axis and to sample the plume in the across-track direction (see dashed lines in Fig. 8). We illustrate the distinct 3D-structure of the sensitivity of the measurements to NO₂ (as represented by the 3D-box AMFs) and demonstrate the limitations of using 1D-layer AMFs for such observations.

5.1 Synthetic observations of a NO₂ stack emission plume

The NO₂ plume was computed with the Graz Lagrangian dispersion Model (GRAL) (Oettl, 2015) for a 262.5 m tall stack located at x=1.9 km and y=1.3 km. NO₂ molecules were released at this altitude at a constant rate of 40 kg h⁻¹. NO_x chemistry was ignored for simplicity. The model domain had a size of 4 km × 4 km and extended from the surface to 21 km altitude. The simulated NO₂ was sampled on an output grid with a 100 m horizontal resolution and 20 vertical levels with 25 m resolution from 0 to 500 m. For the simulation we assumed neutral atmospheric stability and southerly wind with a speed of 5 m s⁻¹ at 12 m above ground. The full vertical wind profile is generated within the model based on similarity theory. The NO₂ background from the US Standard Atmosphere (United States Committee on Extension to the Standard Atmosphere, 1976) was added to the simulated NO₂ field, which was extended to 21 km altitude (see vertical resolution profile in the Supplement). The resulting NO₂ VCDs are shown in Fig. 8a. In the following, the simulated NO₂ concentration field and the corresponding NO₂ VCDs are referred to as the true NO₂ field and as the true total VCD, respectively. The true VCD will be used as a reference to demonstrate the limitations of 1D radiative transfer calculations.

Using MYSTIC, we computed the SCDs that would be observed from an airborne push-broom spectrometer flying parallel to the plume axis from south to north at an altitude of 6 km. The field of view in the across-track direction of the instrument covers the full x-direction of the model domain. The SCDs were obtained by computing 3D-box AMFs for each single observation (i.e., for each ground pixel) and multiplying these AMFs with the 3D NO₂ field from the simulation (which corresponds to the numerator in Eq. 5).

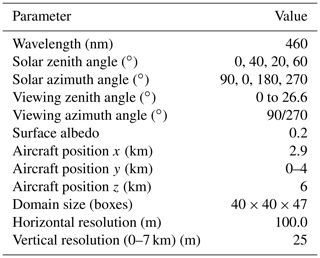
As an example, Fig. 7 illustrates the 3D-box AMFs for an instrument pointing downwards at a zenith angle of 4.8^∘ and an azimuth angle of 90^∘. The sun is placed in the west (SAA=90^∘) at a SZA of 20^∘ – i.e., the instrument is facing the sun. The figure shows the 2D cross section of 3D-box AMFs in the principal plane of the observations, which aligns with the x–z plane in this geometry. Figure 7b and c show the horizontally and vertically integrated 3D-box AMFs, i.e., layer and column AMFs, respectively. The layer AMFs are identical to 1D-layer AMFs. The 3D-box AMFs are high along the line of sight of the instrument and largest just below the aircraft. Most photons travel directly along the geometric path from the sun to the ground pixel and then to the instrument. Although 3D-box AMFs are highest along the geometric path due to the relatively bright surface, a non-negligible fraction of photons is scattered into the line of sight without reaching the surface, leading to an increase in 3D-box AMFs within a parallelogram bounded by the line of sight and the position of the sun.

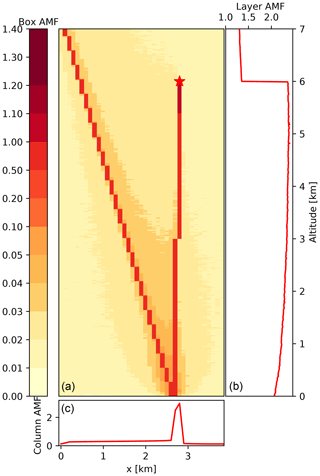
Figure 7 The 3D-box AMFs cross section at y=1.4 km for the aircraft scenario presented in this section. Aircraft (red star) placed at z=6 km, x=2.9 km and y=1.4 km pointing eastwards. The sun is at SAA=90^∘ (west) with a SZA of 20^∘. (b) Vertical profile of horizontally integrated AMFs (1D-layer AMFs). (c) Horizontal profile of vertically integrated AMFs (column AMFs). The default properties are a rural-type aerosol in the PBL, background aerosol above 2 km, spring–summer conditions and a visibility of 50 km.

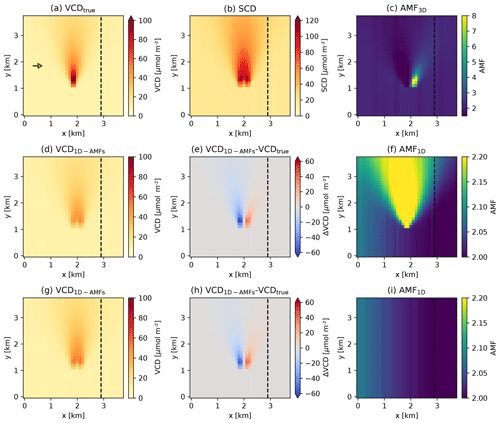
Figure 8 Airborne remote sensing of an NO₂ plume emitted from a 262.5 m tall stack located at x=1.9 km and y=1.3 km. The aircraft flies at an altitude of 6 km from south to north at x=2.9 km (dashed line) parallel to the plume axis and samples the plume in the across-track direction. The sun is located in the west (small arrow in panel a) at a zenith angle of 40^∘. The panels show (a) simulated (true) NO₂ VCDs, (b) synthetic SCDs computed from the simulated NO₂ distribution by applying 3D-box AMFs and (c) 3D-box AMFs computed with MYSTIC. The second row shows (d) VCDs calculated from the SCDs using 1D-layer AMFs and the “true” NO₂ profile above the ground pixel pointed by the instrument, (e) the difference between calculated and true VCDs, and (f) total AMFs from the MYSTIC 1D module. The third row (g–i) shows the same as panels (d)–(f) but using the background NO₂ profile to compute AMFs.

The column AMFs (Fig. 7c) are highest close to the instrument and decrease with distance to the instrument in the −x direction due to atmospheric scattering. After the “reflection point”, values continue to decrease with distance to the instrument but at a lower rate. Due to periodic boundaries this decrease continues on the right of the instrument (x≥3.9 km). Layer AMFs (i.e., 1D-layer AMFs) (Fig. 7b) are highest directly below the instrument. They change by a factor of 2 at the altitude of the aircraft because layers below are crossed (at least) twice by the photons, while layers above are only crossed once.

3D-box AMFs and corresponding SCDs were computed for four different solar zenith angles and four different relative azimuth angles between the sun and the plume axis (and flight direction). We used a default aerosol scenario with a rural-type aerosol representative of spring–summer conditions in the PBL (0–2 km) and a background aerosol above 2 km (visibility of 50 km in the PBL). The parameters used for the AMF calculation are summarized in Table 1. Note that with perfect knowledge of the relative NO₂ distribution, the true total VCD could be reproduced exactly from the SCDs using 3D radiative transfer calculations. The computational cost of calculating 3D-box AMFs is considerably larger than for 1D-layer AMFs. The computational time for calculating 3D-box AMFs for the scenarios here (see Table 1 with SZA=20^∘, SAA=90^∘, VAA=90^∘ and VZA=2^∘) is around 218 s with 1 million photons using a single core of our local machine (Intel Xeon W-2175 CPU @ 2.5 GHz). The computational time for the corresponding 1D-layer AMFs is only about 4 s with 1 million photons. Note, however, that even less photons would be sufficient to obtain a similar noise level as for the 3D-box AMFs.

Table 1 MYSTIC input parameters for the emission stack scenario.

The SCDs computed for the scenario with the sun illuminating the scene from the west at a solar zenith angle of 40^∘ are presented in Fig. 8b. The SCDs are larger than the VCDs (panel a) because the AMFs (panel c) are generally larger than 1. The SCD plume is wider and shifted towards the east compared to the VCD plume. The widening is due to both geometric effects and atmospheric scattering. Geometric effects are caused by the fact that photons following the main geometric path from the sun to the surface and to the instrument may traverse the plume either on the way from the sun to the surface or from the surface to the instrument (or both). These two pathways are separated horizontally. For high solar zenith angles (here SZA=40^∘) this leads to two SCD maxima close to the source as seen in Fig. 8b. The westerly maximum corresponds to the direct observation of the plume (photons reflected by the surface pass the plume on the direct way to the aircraft), whereas the easterly maximum corresponds to its mirror image (photons first travel through the plume before they get reflected at the surface and reflected to the aircraft). This is further illustrated in Fig. 9, where two of the three illustrated direct paths (i.e., three viewing zenith angles) cross the NO₂ maximum – main photon path (1) and (3) in Fig. 9. The main photon path for the observation angle (2) in Fig. 9 misses the plume maximum, which is why total SCD is lower for this observation. Atmospheric scattering leads to an additional horizontal smoothing of the plume, but in the case of a medium-high surface albedo of 0.2, the geometric effects dominate.

Figure 9 Schematic of the across-track measurement by the aircraft measuring a NO₂ plume (dark blue corresponding to high NO₂ concentrations) with three main photon paths for three measurement geometries (1, 2, 3).

5.2 Limitations of VCDs calculated from 1D-layer AMFs

For each scenario, total AMFs were also computed from 1D-layer AMFs, which requires a NO₂ profile (Eq. 4). The most obvious approach is to use the true NO₂ profile above the ground pixel the instrument is pointing towards, which is based on the idea that the AMF is used to convert an SCD to a VCD above a ground pixel (Fig. 8d, e, f). Alternatively, a NO₂ background profile from the US Standard Atmosphere (United States Committee on Extension to the Standard Atmosphere, 1976) was used for each ground pixel, which assumes that no information on the spatial variability in NO₂ is available (Fig. 8g, h, i).

Figure 8f and i show the total AMFs computed with the true and background NO₂ profile, respectively. In both cases, AMFs increase with distance from the aircraft due to the increasing viewing zenith angle. For the true NO₂ profiles, AMFs are higher inside the plume. This can be explained by the fact that the measurements are more sensitive to NO₂ inside the plume than to the background NO₂ outside because the plume is located at an altitude where the 1D-layer AMFs are higher.

Figure 8d and g show the VCDs obtained by dividing the true SCDs in Fig. 8b by the 1D-layer AMFs in Fig. 8f and i, respectively. Since geometric distortions and horizontal smoothing due to scattering cannot be corrected for when using a 1D radiative transfer model, all structures seen in the SCDs are essentially preserved in the VCDs, including the double peak structure, the widening of the plume and the horizontal displacement. Figure 8e and h show the differences in these VCDs from the true VCDs. In both cases, the location of the plume is shifted towards the aircraft relative to the true position. Within the maximum of the plume, this displacement leads to an underestimation of the true VCDs by −60.8 µmol m⁻² when using the NO₂ profile (Fig. 8e) above the ground pixel and by −54.6 µmol m⁻² when using the constant NO₂ profile (Fig. 8h).

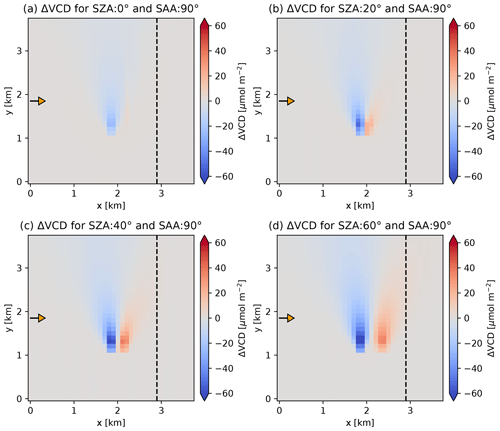
Figure 10 Absolute difference between total VCD from synthetic SCD and 1D box AMF with solar zenith angles (SZA) of (a) 0^∘, (b) 20^∘, (c) 40^∘ and (d) 60^∘ and the true total VCD.

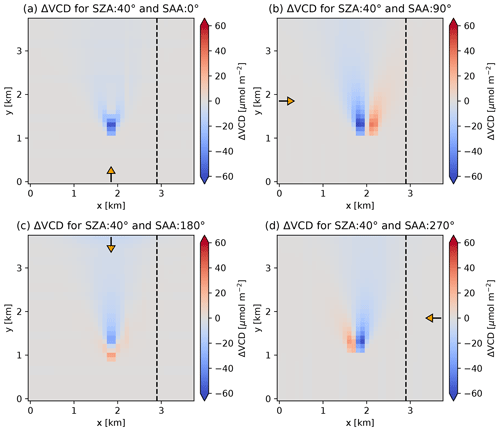
Figure 11 Absolute difference between total VCD from synthetic SCD and 1D box AMF with solar azimuth angle of (a) 0^∘, (b) 90^∘, (c) 180^∘ and (d) 270^∘ and the true total VCD.

The displacement of the calculated VCD plume and the magnitude of the bias depend on the position of the sun as demonstrated in Figs. 10 and 11. The shift increases with increasing SZA due to the geometric effects explained earlier. The relative azimuth angle between the viewing direction and the sun also plays a critical role. The displacement is smaller when the aircraft is flying directly away from the sun (SAA=0^∘) or towards the sun (SAA=180^∘) and the sun illuminates the scene along the plume axis, but even in these cases it is not negligible. Biases are typically larger when the spatial displacement is large.

5.3 Plume flux estimation

A possible application of airborne imaging spectroscopy is the estimation of NO₂ emissions from point sources. Measurements from airborne spectrometers have been used, for example, to estimate CO₂ emissions from power plants (Krings et al., 2011) or CH₄ emissions from coal mine ventilation shafts (Krings et al., 2013). The emissions can be estimated using a mass-balance approach by integrating the NO₂ VCD enhancement above the background across the plume and multiplying this integral (referred to as line density in the following) with a mean wind speed to obtain a flux. The flux is equivalent to the source strength under the assumption of steady-state conditions.

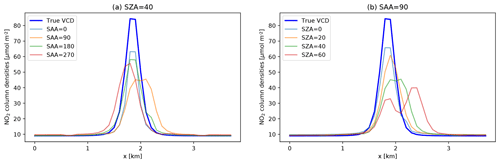
Figure 12 Plume VCD cross section at y=1.6 km (0.3 km downstream of the plume) for (a) the sun at SZA=40^∘ with different SAAs and (b) for the sun in the west with different SZAs.

We computed line densities 300 m downstream of the source for the true VCD field and for fields computed with 1D-layer AMFs for different solar zenith and azimuth angles. The VCD cross sections are shown in Fig. 12. The line densities were multiplied with a wind speed of 9.1 m s⁻¹, which is the wind speed at the stack height of 262.5 m in the GRAL simulation.

Table 2 Estimated NO₂ emissions from the retrieved VCD fields obtained from 1D-layer AMFs under different solar zenith angle (SZA) and solar azimuth angles (SAA).

Table 2 summarizes the computed line densities and fluxes for the different scenarios. In all scenarios, emissions were significantly underestimated by 9 %–37 % (relative to the true VCD) depending on the solar azimuth and zenith angle. Note that the emission estimation for the true VCD is slightly higher than the emission input for the dispersion model due to simplification of the mass-balance approach, which does not account for the vertical variability in wind speeds across the plume. The bias in the plume emission estimation using 1D-layer AMFs generally increases with solar zenith angle. This bias also depends on the solar azimuth angle. The largest bias occurs, when the SAA is 0 or 180^∘, i.e., the instrument is flying towards and away from the sun.

6 Conclusions

This study demonstrates the importance of 3D radiative transfer effects for a range of trace gas remote sensing applications such as ground-based MAX-DOAS and airborne imaging spectroscopy. To study these effects, 1D-layer and 3D-box AMFs were implemented in the Monte Carlo solver MYSTIC of the libRadtran RTM. The computation of AMFs is a central component in most trace gas retrieval algorithms to convert observed SCDs into VCDs, but so far these algorithms were limited to 1D RTMs. In the case of a horizontally homogeneous atmosphere and in plane-parallel geometry, the 3D-box and 1D-layer AMFs perfectly agree within the statistical noise of the Monte Carlo method. They also agree very well with 1D-layer AMFs calculated with other RTMs presented in a previous model intercomparison study by Wagner et al. (2007).

The importance of 3D effects was demonstrated for two examples. For a ground-based MAX-DOAS instrument, we showed that 3D-box AMFs are highest along the line of sight of the instrument (representing photons that have mostly scattered only once) but that the contribution from outside is not negligible and depends on sun position and aerosol optical depth. The spatial distribution of the vertically integrated 3D-box AMFs depends on the sun position, which can be important for interpreting MAX-DOAS observations, especially in urban areas or, more generally, in the vicinity of pollution sources. The spatial variability in the NO₂ distribution in the context of the MAX-DOAS instrument can affect the retrieval differently at different times of the day.

As second example, trace gas retrievals were studied for an airborne imaging spectrometer using simulations of a NO₂ plume emitted by a stack. We showed that when using 1D-layer AMFs, the NO₂ VCDs in the plume were significantly underestimated (up to 58 %) and that the position of the plume was artificially shifted towards the aircraft. Furthermore, integrals of the NO₂ enhancement in the across-plume direction (line densities) were also biased, which results in an underestimation of the NO₂ emissions from the stack when using a mass-balance approach. Using 1D-layer AMFs induces systematic errors even if the NO₂ profile above the ground pixels is known accurately, because a 1D RTM fails to properly represent the complex light path, which is required if the trace gas field is not horizontally homogeneous.

Our study showed that even for simple examples, 3D effects are not negligible if the trace gas field has a high spatial variability. This finding is particularly relevant for ground-based and airborne remote sensing in cities, where considering 3D effects is likely indispensable to reduce systematic errors. This will be addressed in a followup study where the potential impact of 3D radiative transfer effects on the horizontal smoothing of the retrieved trace gas fields will also be studied. The 3D effects are also important for tomographic inversion (e.g., Frins et al., 2006; Kazahaya et al., 2008; Casaballe et al., 2020) where the application of 3D-box AMFs will minimize errors caused by the use of pure geometric assumptions. The high spatial resolution of the next generation of satellite instruments might make it necessary to also consider 3D effects for space-based trace gas remote sensing. Especially when considering imaging spectrometers with very high spatial resolution to estimate emissions (e.g., Strandgren et al., 2020), 3D radiative transfer effects should be considered and studied. However, since 3D radiative transfer calculations are computationally expensive, efficient methods need to be developed for operational applications that provide an appropriate balance between accuracy and computational cost. To fully benefit from 3D-box AMFs, 3D radiative transfer calculations require high-resolution 3D distributions of trace gases and aerosols to calculate the total AMF. Such fields are generally difficult to obtain. In a followup study we plan to use 3D NO₂ fields from a building-resolving urban air quality model (Berchet et al., 2017) with a detailed representation of both near-surface and elevated (stack) emission sources to further analyze the added value of 3D-box AMFs. On the other hand, measuring different azimuth angles with a MAX-DOAS instrument could be used to constrain the 3D fields of trace gases (e.g., Dimitropoulou et al., 2019).