the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Revisiting wind speed measurements using actively heated fiber optics: a wind tunnel study
Justus G. V. van Ramshorst
Miriam Coenders-Gerrits
Bart Schilperoort
Bas J. H. van de Wiel
Jonathan G. Izett
John S. Selker
Chad W. Higgins
Hubert H. G. Savenije
Nick C. van de Giesen
Near-surface wind speed is typically only measured by point observations. The actively heated fiber-optic (AHFO) technique, however, has the potential to provide high-resolution distributed observations of wind speeds, allowing for better spatial characterization of fine-scale processes. Before AHFO can be widely used, its performance needs to be tested in a range of settings. In this work, experimental results on this novel observational wind-probing technique are presented. We utilized a controlled wind tunnel setup to assess both the accuracy and the precision of AHFO under a range of operational conditions (wind speed, angles of attack and temperature difference). The technique allows for wind speed characterization with a spatial resolution of 0.3 m on a 1 s timescale. The flow in the wind tunnel was varied in a controlled manner such that the mean wind ranged between 1 and 17 m s−1. The AHFO measurements are compared to sonic anemometer measurements and show a high coefficient of determination (0.92–0.96) for all individual angles, after correcting the AHFO measurements for the angle of attack. Both the precision and accuracy of the AHFO measurements were also greater than 95 % for all conditions. We conclude that AHFO has the potential to measure wind speed, and we present a method to help choose the heating settings of AHFO. AHFO allows for the characterization of spatially varying fields of mean wind. In the future, the technique could potentially be combined with conventional distributed temperature sensing (DTS) for sensible heat flux estimation in micrometeorological and hydrological applications.
- Article
(3716 KB) - Full-text XML
- BibTeX
- EndNote
This work presents the results of a wind tunnel study designed to test the novel actively heated fiber-optic (AHFO) (Sayde et al., 2015) wind speed measurement technique in controlled airflow conditions. The primary aim of the experiment was to assess the directional sensitivity and signal-to-noise ratio of AHFO.
Wind speed is most commonly observed using in situ point measurement techniques. As a result, the spatial distribution of field observations is limited. While it is possible to obtain distributed wind speed observations with remote sensing (e.g., Goodberlet et al., 1989; Bentamy et al., 2003), the spatial resolution is too low for many micrometeorological applications.
Many field experiments assume Taylor's frozen flow hypothesis (Taylor, 1938) in order to estimate fluxes with similarity theory (e.g., Higgins et al., 2009; Kelly et al., 2009; Bou-Zeid et al., 2010; Patton et al., 2011). However, similarity theory only holds for idealized homogeneous or stationary conditions, which are rarely met in practice, resulting in a model containing strong assumptions, which often leads to significant errors (Ha et al., 2007; Higgins et al., 2012; Thomas et al., 2012). In real, nonidealized situations, even slight surface heterogeneities can lead to dramatic impacts on the spatial structure of the flow in the surface boundary layer. Further, even if perfect surface homogeneity was possible, other atmospheric (surface) conditions are often nonstationary (Holtslag et al., 2013).
In the past decade, a new way to obtain spatially distributed measurements was introduced into environmental studies. High-spatial-resolution measurements could be used to directly check underlying spatial assumptions (e.g., full temperature and horizontal wind profiles) and would reduce the need for such assumptions in real-world cases. Distributed temperature sensing (DTS) technology measures temperature at high temporal and spatial resolution over distances of up to several kilometers by using fiber-optic (FO) cables as sensors (Selker et al., 2006a, b; Tyler et al., 2009). High-end DTS can measure the temperature at a 1 s and 0.3 m resolution (Sayde et al., 2014). The ability to report temperature at such high resolution has proven useful in many environmental studies (Selker et al., 2006a, b; Tyler et al., 2008, 2009; Steele-Dunne et al., 2010), including atmospheric experiments (Keller et al., 2011; Petrides et al., 2011; Schilperoort et al., 2018; Higgins et al., 2018; Izett et al., 2019). It has also been shown that it is possible to observe air temperature and the thermal structure of near-surface turbulence with DTS (Thomas et al., 2012; Euser et al., 2014; Zeeman et al., 2015; Jong et al., 2015).
In 2015, Sayde et al. (2015) introduced the AHFO technique whereby they aimed to use DTS to measure wind speed. The underlying concept of the proposed method is similar to that of a hot-wire anemometer; however, instead of single point measurements, AHFO enables distributed measurements to be made at high spatial resolution. Instead of only passively measuring the temperature in the fiber (as is done with DTS), one segment of the cable is actively heated. The heated segment is positioned parallel to the unheated reference segment with a small separation, in our case 0.1 m. The temperature difference between the heated and reference segment is measured, i.e., the heated fiber and the air temperature. The temperature difference between the cables depends on the energy input and on the wind speed of the ambient air, which determines the magnitude of the lateral heat exchange through convective heat loss. By setting up an energy balance for the heated cable, one can estimate the magnitude of this convective heat transport, which leads to an estimate of the wind speed.
Results from a field study by Sayde et al. (2015) demonstrated promising performance of the AHFO technique, but they recommended further tests on two aspects to be performed in controlled airflow conditions. First, the heat transfer model assumes a flow normal to the axis of the fiber. Hence, non-normal angles of attack need to be accounted for by using directional sensitivity equations. Following the recommendations of Sayde et al. (2015) we tested different directional sensitivity equations from hot-wire anemometry (Webster, 1962; Hinze, 1975; Perry, 1982; Adrian et al., 1984) in the controlled setting of our experiment. Second, Sayde et al. (2015) highlight the importance of a sufficient signal-to-noise ratio when conducting measurements. They show that the temperature difference between the heated and reference segments gives a good estimate of this ratio. The influence of directional sensitivity and the signal-to-noise ratio on the measurement accuracy and precision is investigated, and the results are used to propose a method to estimate precision for future experiments with AHFO; hence, our work will improve the possibilities for successful application of AHFO in future field experiments.
Finally, in the future it will be interesting to perform outdoor tests with AHFO for both micrometeorological and hydrological applications, as AHFO gives a lot of insights into spatially varying wind fields. AHFO can be especially interesting in nonhomogeneous field sites like forests, which are already studied with other DTS applications (Schilperoort et al., 2018, 2020). Moreover, the ability to measure spatially varying wind fields has the potential to be useful for estimating sensible heat fluxes in a variety of atmosphere–vegetation–soil continuums by applying Monin–Obukhov similarity theory (assuming no violation of its assumptions) to the measured vertical profile of the mean wind speed and temperature (Businger et al., 1971).
An overview of the experimental setup is presented in Sect. 2, with the accuracy and precision of the AHFO experiments presented in Sect. 3. In Sect. 3.4, a method for estimating the precision of AHFO experiments is introduced, followed by a short note on future studies.
2.1 DTS and signal-to-noise ratio analysis
Based on the backscattered signal of a laser pulse inside fiber-optic cables, a DTS machine measures temperature along a complete fiber-optic cable (Selker et al., 2006a, b). A main source of noise in DTS data is white noise induced by statistical variability in the photon count from backscatter (optical shot noise). The white noise can be reduced by averaging over multiple measurements in either space or time, assuming the observed temperature is or stays (relatively) constant (van de Giesen et al., 2012). Spatial resolution could be increased by making coils; however, (sharp) bends could be a potential source of signal loss (Hilgersom et al., 2016).
A sufficiently high signal-to-noise ratio is essential for measurement precision with DTS. In Sayde et al. (2015) it is shown that the signal-to-noise ratio can be described as , where Ts and Tf are the temperature (K) of the heated cable segment and (unheated) reference segment (i.e., air temperature). Hence, the signal-to-noise ratio is related to the ΔT () and the measurement error of the DTS, Terror. A large ΔT is obviously desirable; however, ΔT cannot be increased infinitely. The power controller can only deliver a limited amount of power to heat the FO cable, which is especially relevant for the heating of long lengths of FO cable (i.e., several hundred meters of FO cable). Additionally, larger temperature differences could cause other ways of transferring energy (e.g., free convection, radiative heat loss and diffusion) to become more dominant. The effect of ΔT is investigated by using three temperature differences during the experiment.
DTS temperature measurements contain a measurement error, which follows a normal distribution (Selker et al., 2006a). With long FO cables this measurement error changes over the length of the cable, and this error is also different for each DTS machine. In this experiment a short FO cable is used, which is close to the calibration bath. Therefore, the measurement error is calculated based on the calibration baths by taking the average of two baths, whereby the mean SD over the whole experiment is calculated. Given the fact that the signal used is ΔT containing the difference of two temperature measurements of Ts and Tf, Terror becomes . In this experiment , resulting in . In this experiment we used a single value; however, in experiments with longer FO cables, one could calculate a Terror changing along the cable (des Tombe et al., 2020).
The effect of the signal-to-noise ratio is quantified, and an equation to estimate the precision is presented. The measurement precision is an indication of the variability of wind speed measurements (e.g., root mean square deviation – RMSD) as opposed to accuracy, which describes a systematic measurement error that can be compensated for when using another device (in our case expressed by the bias).
2.2 Determination of wind speed
2.2.1 Original determination of wind speed, Sayde et al. (2015)
An energy balance is used to quantify the heat dissipation from the heated section and therefore estimate the wind speed with DTS. The convective cooling can be converted to wind speed because it is a function of wind speed and the temperature difference between the heated and unheated segments. The full energy balance (W) for a cable segment volume of length B is given by Sayde et al. (2015), and schematically shown in Fig. 1:
where r is the radius of the cable (6.7 × 10−4 m in our setup), V is the volume of the cable segment (πr2B, in m3), cs is the specific heat capacity of the FO cable (502 ) and ρv is the FO cable density (800 kg m−3). Ps is the heating rate per meter of cable (W m−1), and B is the length of a cable segment (in meters). and (W m−2) are the mean direct, diffuse and reflected shortwave radiation fluxes, respectively, with αs being the surface albedo of the ground, and αf is the FO cable optic surface albedo. and (W m−2) are the average downward and upward longwave radiation fluxes, respectively, and ϵ is the FO cable surface emissivity. Based on the kind of stainless steel, emissivity values can range from 0.3 to 0.7 (Baldwin and Lovell-Smith, 1992); however, we assume a value of 0.5 (Madhusudana, 2000). σ is the Stefan–Boltzmann constant, 5.67 × 10−8 (), and is the outgoing longwave radiation of the fiber, i.e., Lfiber; h is the convective heat transfer coefficient (W m−2K−1).
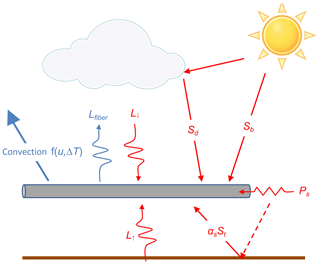
Figure 1Schematization of the energy balance from Sayde et al. (2015).
Simplification
The energy balance is simplified by dividing Eq. (1) by 2rπB, which is equal to the surface area of the FO cable. The energy balance now no longer depends on B, meaning the length of the FO cable segment does not need to be defined. The proposed final energy balance by Sayde et al. (2015) is as follows (W m−2):
where ρ is the FO cable density per meter of cable segment: 4.5 × 10−3 kg m−1.
Convective heat transfer coefficient
The convective heat transfer coefficient h () can by means of the dimensionless Nusselt (Nu), Prandtl (Pr) and Reynolds (Re) numbers be expressed as a function of the wind speed, h=f(uN). The Nusselt number is the ratio between the convective and conductive heat transfer, and the Nusselt number can be written as follows (Žukauskas, 1972):
with
where ds is the fiber characteristic length (2r), Ka is the thermal conductivity of air and υa is the kinematic viscosity of air (0.0255 and 1.5 × 10−5 m2 s−1) (Tsilingiris, 2008). Ka and υa are assumed to be constant due to the controlled conditions in the wind tunnel, but in field experiments this should be included as a variable, as Ka and υa are temperature and relative humidity dependent (Tsilingiris, 2008). C, m and n are empirical constants related to the forced advection of heat by air movement. In Sayde et al. (2015), C, m and n values of 0.51, 0.5 and 0.37 are set based on Žukauskas (1972). Pr is the Prandtl number and can be seen as the ratio between kinematic viscosity and thermal diffusivity, which we assume to be constant (0.72) for our range of temperatures (12–35 ∘C), as in Tsilingiris (2008), with Prs (the Prandtl number for the heated fiber segment) assumed to be the same as Pr due to the small temperature differences (max. 6 K). Lastly, Re is the Reynolds number, which is used to determine the flow regime of the air along the fiber segments; i.e., Re expresses if the flow regime is laminar or turbulent. Combining Eqs. (3) and (4) yields
The determination of the Nusselt number (Eq. 3) is only valid in certain ranges of Re (40–1000) and Pr (0.7–500). Re can be a limitation for higher wind speeds, especially when the diameter of the fiber is large; in our case wind speeds higher than approximately 11 m s−1 would be out of range.
In the derivation of the energy balance (Eq. 1), there is assumed to be no free convection induced by heating of the air close to the cable and no conduction of heat in the axial direction of the FO cable. It is also assumed there is no radiative exchange between objects close and parallel to the heated fiber; i.e., dispersion of heat from the heated cable to the reference cable is assumed to be negligible. Furthermore, a flow directed normal to the axis of the FO cable is assumed by the proposed energy balance; i.e., for flow directed in a different angle, compensation is necessary to accurately estimate the wind speed.
2.2.2 Revised simplified determination of wind speed
Due to the setup inside the wind tunnel, as opposed to outdoor conditions, some simplifications can be made. The shortwave radiation can be neglected because it is an indoor experiment (no sunlight). Furthermore, we assume that there is a uniform temperature inside the wind tunnel due to the enclosed conditions. This means the incoming radiation is dependent on the air temperature, Tf. Assuming incoming () to be black-body radiation (i.e., ), the net longwave radiation loss for the fiber can be simplified accordingly by merging the incoming longwave and outgoing longwave radiation as
One additional change is made based on our results obtained during testing of the performance of the AHFO technique. In processing the obtained wind tunnel data it was found that by using the calculation of the Nusselt number from Žukauskas (1972) in Eq. (3), an approximately 20 % additional bias in calculating the wind speed was created. By using a more recent version for calculating the empirical Nusselt number (Cengel and Ghajar, 2014), the bias in our study is reduced to ∼ 5 %. Therefore, Eq. (7) is proposed to calculate the Nusselt number, for which the constants C, m and n are still used but with the values from Table 7-1 ( and ) in Cengel and Ghajar (2014) rather than those in Žukauskas (1972). Next to the improved fit, the range of Re over which the equation is valid is much wider (40–4000 compared with 40–1000) and therefore more applicable in future AHFO experiments.
Consequently, the expression of h changes as well.
With the longwave and shortwave radiation simplifications, the energy balance becomes
By substituting the expression for h (Eq. 8), we can rearrange Eq. (9) to obtain an expression for wind speed. Equation (10) will be used to estimate the wind speed (uN) in our wind tunnel study.
2.3 Wind tunnel experiments
We conducted a series of experiments under tightly controlled airflow conditions to improve the applicability of AHFO in experimental (field) research and to study the directional sensitivity and influence of the signal-to-noise ratio. The experiments presented were performed in a wind tunnel at Oregon State University (Low Speed Wind Tunnel of the Experimental Fluid Mechanics Research Lab – College of Engineering). This wind tunnel has a closed circuit, which means the air inside is recycled. The test section of the wind tunnel has a cross section (height by width) of 1.23 by 1.52 m and an undisturbed horizontal section of roughly 5 to 6 m, which may be used for probing. During the experiment the heated and unheated reference cable segments were placed 8 cm apart. The FO cable has two FO cores; hence, each cable segment could be sampled twice. For validation, an independent sonic anemometer (IRGASON+EC100 and CR3000, Campbell Scientific, Logan, UT, USA) was placed approximately 0.2 m downwind of the fibers, which measures the wind speed in three directions at 10 Hz. As the FO cables are very thin, it is assumed that these do not significantly disturb the measurement of the sonic volume (particularly at larger averaging times). All equipment was mounted using custom-designed support material.
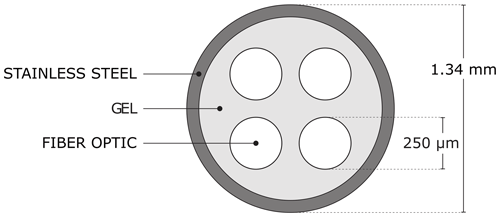
The cable (AFL, Spartanburg, SC, USA) mounted in the wind tunnel consisted of a 1.34 mm outer diameter stainless-steel casing that enclosed four multimode FO cores with a diameter of 250 µm (Fig. A1). The electrical resistance per meter of stainless-steel casing (Rs) is 1.67 (Ω m−1) and is constant along the length; for the length of a cable segment (B, (m)), R=RsB, and R (Ω) is the total resistance of a cable segment. Similarly, the heating rate is defined as Ps=I2Rs (W m−1) per meter of cable segment, where I (A) is the electrical current. Only two FO cores were used, and these were spliced at the end of the cable to create a duplexed FO core (using two FO cores in one cable), which results in double measurements for each measuring point along the FO cable using a single-ended configuration (Hausner et al., 2011). Both the FO cores were connected to a Silixa Ultima DTS machine (Ultima S, 2 km range, Silixa, London, UK) outside the wind tunnel; however, afterwards a single-ended configuration was used due to asymmetrical signal loss.
One cable segment was heated by connecting the stainless-steel casing to a power controller (MicroFUSION uF1HXTA0-32-P1000-F040) by 12 AWG (copper) cables (3.31 mm2) to heat the cable in a controlled way.
For calibration and validation of the DTS data, approximately 6 m of the FO cables was placed in a well-mixed ambient bath to calibrate the DTS temperature according to the single-ended method described by Hausner et al. (2011). The temperature was verified with one probe (RBRsolo2 T, RBR Ltd., Ottawa, Ontario, Canada). A circulating aquarium pump was placed inside the bath to prevent stratification.
In field experiments the wind speed and direction will vary; therefore, different angles of attack and wind speeds are tested. Additionally, different heating rates are used to quantify the importance of the signal-to-noise ratio. The following settings are used.
-
Angle of attack. The cable was mounted at four different angles in the wind tunnel, resulting in different angles of attack to mean flow direction, in order to gain more insights into directional sensitivity. In Fig. 2b the 90∘ setup is visible; however, the cable was also mounted at a 45, 30 and 15∘ angle with respect to the floor of the wind tunnel (see Fig. 2a, inset). During all setups, the lower part of the FO cable was fixed to the opening in the bottom of the wind tunnel, while the upper end was attached to an extruded aluminum bar that was moved over the fixed horizontal bars to achieve the desired cable angles.
-
Wind speed. To test the performance for a range of wind speeds, 10 different wind speeds were tested at every angle: 1, 3, 5, 7, 9, 11, 13, 15, 16 and 17 m s−1. The AHFO wind speed measurements can be adjusted by comparing the AHFO wind speed to a reference sonic anemometer. The wind speed in the wind tunnel was fixed at a constant value to create a stable, nonturbulent, steady-state flow (Appendix C).
-
Heating rate. The magnitude of the current needed to create a given temperature difference is dependent on the cable resistance and the wind speed; therefore, the current is adjusted for each individual experiment. The current was fixed to create a temperature difference (ΔT) of 2, 4 and 6 K between the heated and reference cable. Heating rates varied from 0.5 to 10 W m−1 during our setup.
In total, 120 (4 × 10 × 3) trials were conducted with the different parameters, each with a minimum duration of 10 min.
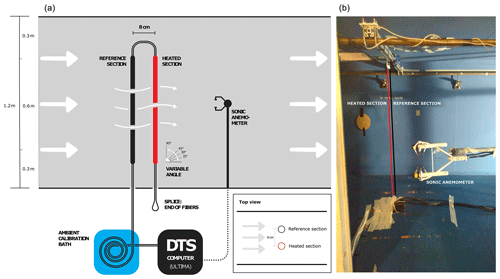
Figure 2(a) Schematic of the wind tunnel setup and (b) photograph of the experimental setup in the wind tunnel.
Temperatures along the FO cable were sampled at 0.125 m resolution with a sampling rate of 1 Hz. Splices connecting two fiber-optic cores are known to create an additional loss in signal, i.e., local higher attenuation (Tyler et al., 2009; van de Giesen et al., 2012); this loss is normally independent of the direction. However, in our setup the signal loss of the splice connecting the fiber-optic cores of our cable at the end of the array was not the same in both directions. Due to this asymmetrical structure of the splice loss, only the data from one channel were used to ensure the quality of the results, as this channel showed a regular splice loss.
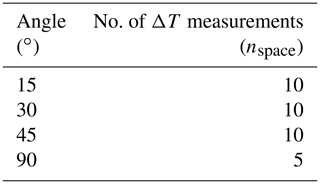
For each angle of attack only the five temperatures differences (×2 because of duplexed FO core) from the middle of the wind tunnel are used to prevent using AHFO wind speed measurements with side and/or boundary effects. We investigated the consequences of extending the spatial range and found there is limited difference between these measurements (see Table D1). During this extended spatial range analysis we found that some of the 90∘ data contained additional noise, which decreased the accuracy when everything was combined, and therefore we decided to take only five temperature differences for the 90∘ calculations. A potential reason for this additional noise could be the sharper bend for the 90∘ setup (Hilgersom et al., 2016); also, the FO cable is shorter for the 90∘ setup (due to the design of the setup), which means the fixations are closer to the middle of the cable, causing local disturbances in the temperature measurements. In Table D2 an overview of the number of measurements used for each setup is shown.
In our study we use the advantage of averaging over time and space to reduce (white) noise in the DTS measurements (van de Giesen et al., 2012; Selker et al., 2006b). For clarity we therefore introduce three parameters: ntime, nspace and n, where ntime is the number of measurements averaged over time, nspace is the number of measurements averaged over space, and n is the total number of measurements over time and space and can be expressed as . The machine specifications give the sample resolution as xsample=0.125 m. The highest actual spatial resolution is 0.3 m, indicating nspace≥2 according to the 10 %–90 % rule as described in Tyler et al. (2009). In this paper we will first work with nspace=10 (for 90∘ nspace=5) and finally we will propose an equation to predict the precision (see later Eq. 21), which is a function of nspace and ntime. We first use nspace=10 because to derive the precision prediction a unique constant (CDTS) is necessary. CDTS is derived from our measurements and can be used for predicting the precision in future experiments. CDTS is expected to be more accurate if the amount of (white) noise is reduced by averaging.
2.4 Directional sensitivity analysis
Equation (10) is derived for flows normal to the axis of the cable (as in Fig. 2b). Depending on the physical setup the wind will not always have a 90∘ angle compared to the axis of the cable, especially in outside atmospheric experiments. For angles smaller than 90∘ the wind speed will be underestimated, as the convective heat transfer is less efficient. While Sayde et al. (2015) adjusted the wind speed of the sonic anemometer using a geometric correction from hot-wire anemometry (e.g., Adrian et al., 1984), we adjusted the measured DTS wind speed uN (Eq. 10) to compare both wind speeds:
where kds is the directional sensitivity and φ is the angle of attack of the wind with respect to the axis of the cable, ranging from 0 to 90∘.
2.5 Accuracy and precision definition
The performance of our AHFO measurements will be assessed by looking at the accuracy and precision. The accuracy (σa) is defined by the normalized difference of the AHFO and sonic anemometer wind speed measurements as in Eq. (12):
where j is a specific wind speed setting, and 17 m s−1, and is the average of all individual measurements (i) for a given wind speed setting.
The precision (σp) is defined by the normalized RMSD between the AHFO and sonic anemometer wind speed measurements as in Eq. (13).
3.1 Proposed directional sensitivity equation
During analysis of the wind tunnel data it was found that Eq. (11) was not giving satisfying results (e.g., a 22 % bias between the 90 and 15∘ angle). In Adrian et al. (1984) it is shown that in hot-wire anemometry a variety of theoretical and empirical formulas have been proposed in the past in order to account for directional sensitivity. Alternatively, using the formula suggested by Bruun (1971) gives more satisfying results, diminishing the bias between the 90 and 15∘ angle to only a few percent. This is shown in the box plot in Fig. 3.
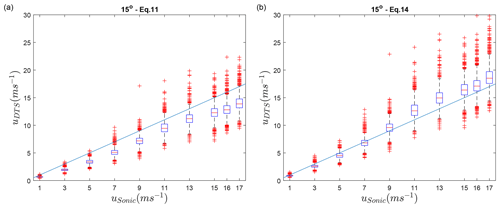
Therefore, Eq. (14) is used to account for directional sensitivity in our study, with the scaling exponent, m1, able to be optimized during calibration of the AHFO measurements. The value for m1 obtained during the calibration of our setup was 1.05.
3.2 Accuracy and precision
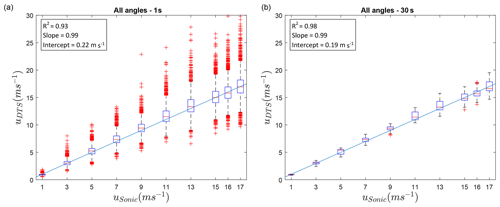
In Fig. 3b the AHFO wind speed measurements are compared to the velocity measured with the sonic anemometer. The comparison for all angles can be found in Figs. B1 and B2. The wind speeds measured with AHFO are calculated using 10 temperature differences (duplex setup with 2 × 5 heated and reference measurements); i.e., for the 90∘ setup this is equivalent to a height of ∼ 0.675 m in the wind tunnel.
Figure B1 shows the sample rate DTS data against the 1 s average sonic anemometer data for the four different angles of attack. For all four angles the results are satisfying. The 90, 45 and 30∘ angles slightly underestimate the wind speed. The 15∘ angle is overestimated, especially at higher wind speeds. Figure B2 shows the same dataset, but then combined for all angles, for a 1 s and temporally averaged 30 s resolution. A clear improvement of the precision is visible when temporal averaging is performed. Even though the directional sensitivity equation (Eq. 14) is not yet fully calibrated, the bias is negligible, with coefficients of determination ranging from 0.92 to 0.96, a slope ranging from 0.91 to 1.14, and an intercept ranging from −0.70 to 0.64 m s−1 (see Fig. B1 for each angle). The wind speed measurements are the least accurate for the 15∘ angle of attack.
To get more insight into the quality of the results, a dimensionless analysis is performed. In Fig. 4, the nondimensional wind speed accuracy for the whole wind tunnel experiment is shown. For all combinations (120 individual cases of varying wind speed (j), angle and ΔT), the accuracy is calculated according to Eq. (12). As can be seen in Fig. 4, σa depends on the spatial and temporal averaging of the FO data. The averaging time ntime is defined as , where tavg can only be an integer which is a multiple of tsample. Spatial averaging is defined as , where xavg can only be an integer which is a multiple of xsample. In Fig. 4 the accuracy is averaged over all wind speeds for each ΔT and angle combination, with nspace=10 and ntime varying from 1 to 30, resulting in 12 values for each time resolution.
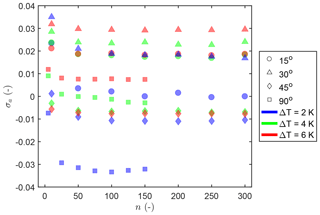
Figure 4Bias in AHFO wind speed as a function of averaging period for different angles of attack and different fiber heating, with n varying from 5 to 300.
For the dataset (n = 5–300), the maximum σa is ± 0.03, which is promising for future applications. The ΔT=6 K should be the best-performing heating setting; however, this is not always the case and there are fluctuations between the heating settings, which could be due to neglecting small energy losses, like free convection due to heating of air close to the heated cable (Sayde et al., 2015), which is temperature dependent. With such an energy loss included, the bias of each angle might change. Nevertheless, the bias is fairly constant after n=50 with increasing averaging time, which means further analysis can probably increase the accuracy. The change in bias from n=5 to n=50 is due to the precision of our AHFO measurements, which increases with averaging over a longer time (n increases) and is higher for a greater ΔT. This difference is bigger for the 90∘ cases, as nspace=5 instead of nspace=10 for the other angles, indicating that spatial averaging also has an effect on the bias.
While the accuracy (bias) remains fairly constant over the averaging period, the relative precision, σp, improves significantly (Fig. 5). The precision is calculated for all 120 ΔT, angle and wind speed combinations ( m s−1) using Eq. (13).
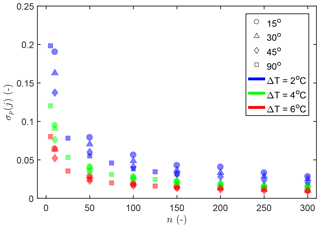
Figure 5Precision of the AHFO wind speed measurements as a function of averaging period, with n varying from 5 to 300.
For the calculation of the precision uDTS, we considered the variability of the wind speed, even though it is small in the wind tunnel. We assumed that this variability is measured by the sonic anemometer measurements, and we assume that this per definition is smaller than the variability of the DTS machine uDTS estimates. After applying Eq. (13) the variability of the DTS machine uDTS is obtained. For each of the 120 combinations, and are the average wind speeds for a j, where usonic(i,j) and uDTS(i,j) are single measurements for a j.
The precision was averaged over all wind speeds for each ΔT and angle combination in Fig. 5, which is justified because σp is normalized by the mean wind speed; hence, any linear dependency should be removed.
The precision improves to a σp less than 0.05 by averaging over time; hence, there is an increasing n. Improvement by averaging is expected due to the reduction of noise (van de Giesen et al., 2012). As mentioned, the main source of noise in DTS data is white noise; this explains the visible improvement of the precision by as signal averaging is applied, where n is the number of measurements (Selker et al., 2006b; Kaiser and Knight, 1979).
3.3 Normalized precision independent of sampling settings
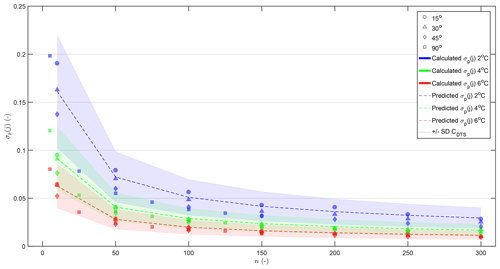
In order to remove the influence of different settings (such as the choice of ΔT) and determine a general prediction of precision in future experiments, we normalize the precision. First, the precision is normalized to ΔT (Fig. 6a) by multiplying Eq. (13) by , which can be written as Eq. (15).
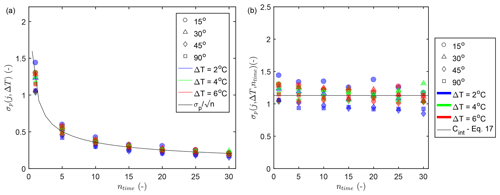
Figure 6(a) Precision of the AHFO wind speed measurements as a function of averaging period independent of ΔT. (b) Precision of the AHFO wind speed measurements as a function of averaging period independent of ΔT and averaging period, with nspace=10 and the nspace=5 of 90∘ calculated as nspace=10 using the rule.
As a result, dependence becomes even more clear, as shown by the black solid line showing , where is the average of Eq. (13), with nspace=10 (and the nspace=5 of 90∘ calculated as nspace=10 using the rule) and ntime=1. Second, the precision is also normalized to the behavior by multiplying Eq. (15) by , resulting in Eq. (16).
Terror and tsample are known and depend on the performance and setup of the DTS; in this case we use Terror=0.32 K and tsample=1 s, calculated as described earlier. It appears that the precision by taking the average can be condensed in one number, 1.13, which we denote by the symbol Cint (Fig. 6b). The intermediate constant Cint can be defined as in Eq. (17), with nspace=10.
Finally, a final constant for a 1 s and 0.125 m resolution is desired, so it can be used for different kinds of DTS machines, also when a DTS machine has different sampling resolutions. By using the shown dependency, we can convert Cint into CDTS by multiplying Cint by , as nspace is 10. This results in Eq. (18) with nspace=1 and ntime=1. CDTS is purposely not calculated at once in our paper but is derived using Cint. As the wind speed in the middle of the wind tunnel can be assumed constant, we expect CDTS to be better by using five measurements in the middle of the wind tunnel instead of picking one of these five.
3.4 Precision prediction
At the start of a new AHFO experiment it is unknown how to make sure the signal-to-noise ratio is sufficient such that σp is small. However, given the result that the increase in precision behaves similarly for each ΔT and the averaging time, it is possible to make a prediction for the precision of future work.
In outdoor experiments, the only setting that can be changed is the heating rate, Ps, which is assumed to be fixed at a single value. The idea behind the precision prediction is to guide the choice of a heating rate such that a preferred precision is achieved for a known dominant wind speed range. As the wind speed outside will vary naturally, ΔT will change accordingly. Therefore, to obtain an expression in which Ps is the only unknown, ΔT first needs to be expressed as a function of the wind speed uN and the heating rate (Ps). This can be done by using Eq. (10). To obtain a first estimate, some assumptions can be made. The numerator of Eq. (10) consists of three terms, the first of which with the heating rate (Ps) is dominant compared to the other ones, namely 10–100 times bigger. When these minor terms are neglected Eq. (10) can be simplified to
with , and , resulting in an expression for ΔT as a function of wind speed:
Knowing this expression of ΔT, Eq. (18) can again be rewritten into Eq. (21) (assuming the difference between and is negligible), which expresses the precision estimate, with Ps as the only parameter that can be changed during an experiment.
Here, nspace×ntime is the number of measurements over which the observed wind speed is averaged in either the space or time domain. By assuming that all constants are known from the literature and the setup, a first estimate of the error can be made for every velocity or heating rate given. If a dominant wind speed range for a new project is known, an associated heating rate can be found such that the error is sufficiently small.
As an example, Fig. 7 shows the estimated precision for our experiment at 1 s (ntime=1) and ∼ 0.675 m (nspace=10) resolution over a range of wind speeds and heating rates. If the diameter of the fiber is different, this is taken into account via term A from Eq. (21), which includes the radius (d=2r). Also, when a DTS machine with a different performance and setup is used, this can be implemented by calculating an appropriate Terror accordingly. Of course different applications will demand different space–time averaging windows, depending on the scientific research question to be answered with AHFO, which is included by .
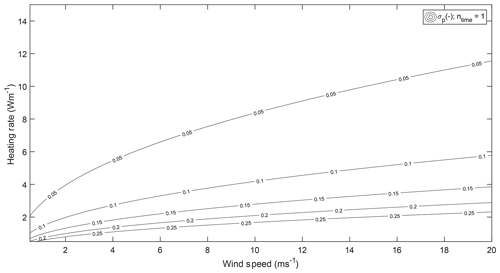
Figure 7Expected precision (contour lines) for a given heating rate and wind speed as calculated from Eq. (21), with nspace=10 and ntime=1; the angle of attack is 90∘.
In outdoor experiments, the influence of shortwave and longwave radiation will be present. However, as long as the radiation is the same for the heated and non-heated segment, this does not influence the error estimation, as for the signal-to-noise ratio, ΔT is the most important factor. When the heated and reference fibers are close to each other, which is also needed for properly estimating the wind speed, both fibers will experience a similar contribution of external radiation such that the overall ΔT will be relatively unaffected by this factor.
Verification of the precision prediction
For verification purposes the calculated precision (Eq. 13) is combined with the predicted precision (Eq. 21) in Fig. 8. As can be seen in Fig. 8, the precision of the AHFO system is estimated well and the one-time SD covers all calculated precisions. When using Eq. (21) one should consider the fact that uN is derived for a 90∘ angle of attack. If wind speeds with other angles of attack are expected, one should use Eq. (14) for prediction of the precision. uN is the measured wind speed normal to the FO cable, and the measured wind speed is lower in the case of an angle < 90∘. In this case one should use . Concluding, with our prediction equation we can predict all our settings within a 1 SD interval, showing general applicability.
3.5 Considerations using AHFO outdoors
The experiments described here were performed in a controlled wind tunnel environment. When performing outdoor AHFO experiments, several factors need to be considered. First of all, during field experiments the relative humidity and temperature might have such a big range that assuming certain parameters (e.g., Ka and υa) as constant is no longer applicable (Tsilingiris, 2008). Furthermore, for small wind speeds (e.g., < 1 m s−1), the neglection of energy losses like free convection seems not entirely applicable, as this term becomes more dominant in comparison to forced convection. This is confirmed in our study, wherein it was visible that the response is different between a well-ventilated and non-ventilated cable; hence, the accuracy is dependent on the wind speed. Although not shown in this paper, it seemed there was no time response difference between a vertical or horizontal mounted heated cable; however, by mounting the cable in a horizontal or vertical direction, free convection might influence the temperature measurements as the heated air is moving upward.
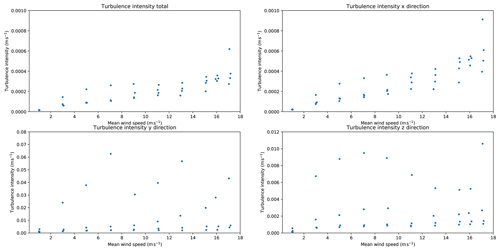
Also, the flow in the wind tunnel is laminar and has less turbulence than in outdoor conditions (Appendix C). This is a good setting for calibration of the AHFO method; however, in outdoor conditions (small-scale) turbulence around the cable is something to take into account. Especially with smaller wind speeds, the cooling by turbulence around the cable can be an additional heat loss component, which is not included in the energy balance and could therefore lead to overestimation of the wind speed. Furthermore, one should take into account that wet fibers, due to rain or dew fall, might have an altered heat loss.
It is shown that AHFO can give reliable wind speed measurements; however, the precision and accuracy are not as good as with a sonic anemometer. The major addition of AHFO is the possibility to sample the wind speed with a high spatial distribution. It should be taken into account that the time resolution is lower than that of a sonic anemometer, and therefore AHFO is less suitable for small-scale turbulence, but larger-scale turbulence (> 1 s; >0.3 m) can potentially be fully captured with a 2-D–3-D setup with distributed measurements. Despite the high potential resolutions (1 s and 0.3 m) the user should consider averaging in either the space or time domain to enhance the precision of the obtained data. The choice for averaging over space or time should be made based on the research topic.
Finally, when measuring in the field, the use of high-quality reference point measurements (e.g., sonic anemometer) is recommended, for example, to be able to compensate for possible biases. Using a vertical setup of the fibers would reduce the need to compensate for the angle of attack, as the mean wind speed is mostly parallel to the surface. However, in complex terrains such as inside canopies, one ancillary device could be insufficient due to the high variability of the wind field. In such a case, a more complex 3-D setup of DTS–AHFO (Zeeman et al., 2015) could be an indication of the angle of attack. A new method is also under development to measure the angle of attack with a single cable using microstructures attached to the fiber (Lapo et al., 2020).
Through a series of controlled wind tunnel experiments, new insights into the accuracy and precision of the newly introduced AHFO wind speed measuring technique were obtained. With high spatial (0.3 m) and temporal (1 s) resolution, the AHFO wind speed measurements agreed very well with the sonic anemometer measurements, with coefficients of determination of 0.92–0.96. It is also shown that the AHFO technique has the possibility to measure with a precision and accuracy of 95 %. Some additional work is needed, as there still is a small overestimation, which may be caused by neglecting some energy fluxes such as free convection due to heating of the air close the heated cable. Furthermore, it is possible to optimize the directional sensitivity compensation by extended calibration. Compensating for the directional sensitivity requires ancillary measurement devices in order to measure the angle of attack; however, in complex terrains such as inside canopies, one ancillary device could be insufficient due to the high variability of the wind field.
The error prediction equation (Eq. 21) is an important result of this work that will aid in the design of future experiments. This design tool helps with choosing a heating rate for the actively heated fiber in order to be able to create a sufficiently high precision. Based on the prevalent wind speeds of a potential field experiment site, a first estimate of an associated sufficient heating rate can be calculated. Due to the way this design tool is constructed, it can be a good first estimate for all kinds of fibers, DTS precisions, and user-preferred spatial and temporal resolutions.
The AHFO technique can reliably measure wind speeds under a range of conditions. The combination of high spatial and temporal resolution with the high precision of the technique opens possibilities for outdoor application, as the key feature of the AHFO is the ability to measure spatial structures in the flow over scales ranging from 1 m to several kilometers. In the future, the technique could be useful for micrometeorological and hydrological applications, allowing for the characterization of spatially varying fields of mean wind speed, such as in canopy flows or in sloping terrain.
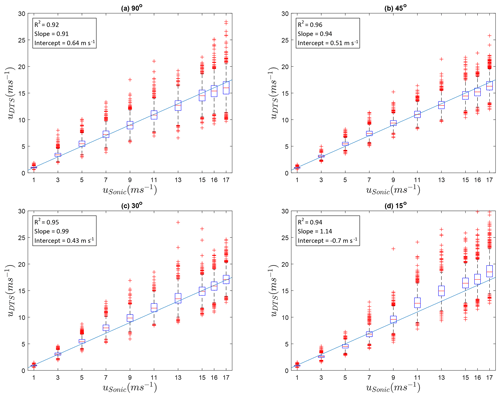
Figure B1Comparison of AHFO and sonic anemometer wind speed at a 1 s temporal resolution for the four different angles of attack: (a) 90∘, (b) 45∘, (c) 30∘ and (d) 15∘; nspace=10, ntime=1. The line represents the 1:1 line.
Table D1SD σspace of five pairs of AHFO measurements (duplex configuration) per wind speed and its normalized SD. It shows that the normalized SD is ≈ 3 % no matter if one takes the top, mid-top, center, mid-bottom or bottom pair.

For each angle and power rate, the uDTS was calculated with only the two temperature differences (duplex configuration) of the top of the wind tunnel or the mid-top, center, mid-bottom or bottom of the wind tunnel (thus nspace=2). From these five pairs we calculated the SD σspace per wind speed.
A dataset of wind speed measurements is made available via the 4TU data repository: https://doi.org/10.4121/12832118 (Van Ramshorst et al., 2020).
JGVvR prepared and performed the experiments and worked on analyzing the data and writing the paper. JSS and CWH assisted with the experiments and analyzing the data and contributed to the paper. MCG, BS, BJHvdW and JGI helped with analyzing the data and contributed to the paper. HHGS and NCvdG contributed to the paper.
The authors declare that they have no conflict of interest.
The authors are thankful for the practical assistance of Cara Walter and Jim Wagner with the AHFO–DTS setup; we express our appreciation to the people of the OPEnS LAB for assisting with the assembly of parts.
This research has been partly supported by the NWO-ALW, Veni project (grant no. 863.15.022), the Netherlands and the Holland Scholarship and CTEMPs.
This open-access publication was funded
by the University of Göttingen.
This paper was edited by Ad Stoffelen and reviewed by two anonymous referees.
Adrian, R. J., Johnson, R. E., Jones, B. G., Merati, P., and Tung, A. T.: Aerodynamic disturbances of hot-wire probes and directional sensitivity, J. Phys. E Sci. Instrum., 17, 62–71, https://doi.org/10.1088/0022-3735/17/1/012, 1984. a, b, c
Baldwin, A. J. and Lovell-Smith, J. E. R.: The emissivity of stainless steel in dairy plant thermal design, J. Food Eng., 17, 281–289, https://doi.org/10.1016/0260-8774(92)90045-8, 1992. a
Bentamy, A., Katsaros, K. B., Mestas-Nuñez, A. M., Drennan, W. M., Forde, E. B., and Roquet, H.: Satellite Estimates of Wind Speed and Latent Heat Flux over the Global Oceans, J. Climate, 16, 637–656, https://doi.org/10.1175/1520-0442(2003)016<0637:SEOWSA>2.0.CO;2, 2003. a
Bou-Zeid, E., Higgins, C., Huwald, H., Meneveau, C., and Parlange, M. B.: Field study of the dynamics and modelling of subgrid-scale turbulence in a stable atmospheric surface layer over a glacier, J. Fluid Mech., 665, 480–515, https://doi.org/10.1017/S0022112010004015, 2010. a
Bruun, H. H.: Interpretation of a Hot Wire Signal Using a Universal Calibration Law., J. Phys. E Sci. Instrum., 4, 225–231, https://doi.org/10.1088/0022-3735/4/3/016, 1971. a
Businger, J. A., Wyngaard, J. C., Izumi, Y., and Bradley, E. F.: Flux-Profile Relationships in the Atmospheric Surface Layer, J. Atmos. Sci., 28, 181–189, https://doi.org/10.1175/1520-0469(1971)028<0181:FPRITA>2.0.CO;2, 1971. a
Cengel, Y. and Ghajar, A.: Heat and mass transfer: fundamentals and applications, McGraw-Hill Higher Education, New York, USA, 2014. a, b
des Tombe, B., Schilperoort, B., and Bakker, M.: Estimation of Temperature and Associated Uncertainty from Fiber-Optic Raman-Spectrum Distributed Temperature Sensing, Sensors, 20, 2235, https://doi.org/10.3390/s20082235, 2020. a
Euser, T., Luxemburg, W. M. J., Everson, C. S., Mengistu, M. G., Clulow, A. D., and Bastiaanssen, W. G. M.: A new method to measure Bowen ratios using high-resolution vertical dry and wet bulb temperature profiles, Hydrol. Earth Syst. Sci., 18, 2021–2032, https://doi.org/10.5194/hess-18-2021-2014, 2014. a
Goodberlet, M. A., Swift, C. T., and Wilkerson, J. C.: Remote sensing of ocean surface winds with the special sensor microwave/imager, J. Geophys. Res., 94, 14547–14555, https://doi.org/10.1029/JC094iC10p14547, 1989. a
Ha, K.-J., Hyun, Y.-K., Oh, H.-M., Kim, K.-E., and Mahrt, L.: Evaluation of Boundary Layer Similarity Theory for Stable Conditions in CASES-99, Mon. Weather Rev., 135, 3474–3483, https://doi.org/10.1175/MWR3488.1, 2007. a
Hausner, M. B., Suárez, F., Glander, K. E., van de Giesen, N., Selker, J. S., and Tyler, S. W.: Calibrating single-ended fiber-optic raman spectra distributed temperature sensing data, Sensors, 11, 10859–10879, https://doi.org/10.3390/s111110859, 2011. a
Higgins, C. W., Meneveau, C., and Parlange, M. B.: Geometric Alignments of the Subgrid-Scale Force in the Atmospheric Boundary Layer, Bound.-Lay. Meteorol., 132, 1–9, https://doi.org/10.1007/s10546-009-9385-3, 2009. a
Higgins, C. W., Froidevaux, M., Simeonov, V., Vercauteren, N., Barry, C., and Parlange, M. B.: The Effect of Scale on the Applicability of Taylor's Frozen Turbulence Hypothesis in the Atmospheric Boundary Layer, Bound.-Lay. Meteorol., 143, 379–391, https://doi.org/10.1007/s10546-012-9701-1, 2012. a
Higgins, C. W., Wing, M. G., Kelley, J., Sayde, C., Burnett, J., and Holmes, H. A.: A high resolution measurement of the morning ABL transition using distributed temperature sensing and an unmanned aircraft system, Environ. Fluid Mech., 18, 683–693, https://doi.org/10.1007/s10652-017-9569-1, 2018. a
Hilgersom, K., van Emmerik, T., Solcerova, A., Berghuijs, W., Selker, J., and van de Giesen, N.: Practical considerations for enhanced-resolution coil-wrapped distributed temperature sensing, Geosci. Instrum. Method. Data Syst., 5, 151–162, https://doi.org/10.5194/gi-5-151-2016, 2016. a, b
Hinze, J.: Turbulence, McGraw-Hill Higher Education, New York, 1975. a
Holtslag, A. A., Svensson, G., Baas, P., Basu, S., Beare, B., Beljaars, A. C., Bosveld, F. C., Cuxart, J., Lindvall, J., Steeneveld, G. J., Tjernström, M., and Van De Wiel, B. J.: Stable atmospheric boundary layers and diurnal cycles: Challenges for weather and climate models, B. Am. Meteorol. Soc., 94, 1691–1706, https://doi.org/10.1175/BAMS-D-11-00187.1, 2013. a
Izett, J. G., Schilperoort, B., Coenders-Gerrits, M., Baas, P., Bosveld, F. C., and van de Wiel, B. J. H.: Missed Fog?, Bound.-Lay. Meteorol., 173, 289–309, https://doi.org/10.1007/s10546-019-00462-3, 2019. a
de Jong, S. A. P., Slingerland, J. D., and van de Giesen, N. C.: Fiber optic distributed temperature sensing for the determination of air temperature, Atmos. Meas. Tech., 8, 335–339, https://doi.org/10.5194/amt-8-335-2015, 2015. a
Kaiser, R. and Knight, W.: Digital signal averaging, J. Magn. Reson. (1969), 36, 215–220, https://doi.org/10.1016/0022-2364(79)90096-9, 1979. a
Keller, C. A., Huwald, H., Vollmer, M. K., Wenger, A., Hill, M., Parlange, M. B., and Reimann, S.: Fiber optic distributed temperature sensing for the determination of the nocturnal atmospheric boundary layer height, Atmos. Meas. Tech., 4, 143–149, https://doi.org/10.5194/amt-4-143-2011, 2011. a
Kelly, M., Wyngaard, J. C., and Sullivan, P. P.: Application of a Subfilter-Scale Flux Model over the Ocean Using OHATS Field Data, J. Atmos. Sci., 66, 3217–3225, https://doi.org/10.1175/2009JAS2903.1, 2009. a
Lapo, K., Freundorfer, A., Pfister, L., Schneider, J., Selker, J., and Thomas, C.: Distributed observations of wind direction using microstructures attached to actively heated fiber-optic cables, Atmos. Meas. Tech., 13, 1563–1573, https://doi.org/10.5194/amt-13-1563-2020, 2020. a
Madhusudana, C.: Accuracy in thermal contact conductance experiments - the effect of heat losses to the surroundings, Int. Commun. Heat Mass, 27, 877–891, https://doi.org/10.1016/S0735-1933(00)00168-8, 2000. a
Patton, E. G., Horst, T. W., Sullivan, P. P., Lenschow, D. H., Oncley, S. P., Brown, W. O. J., Burns, S. P., Guenther, A. B., Held, A., Karl, T., Mayor, S. D., Rizzo, L. V., Spuler, S. M., Sun, J., Turnipseed, A. A., Allwine, E. J., Edburg, S. L., Lamb, B. K., Avissar, R., Calhoun, R. J., Kleissl, J., Massman, W. J., Paw U, K. T., and Weil, J. C.: The Canopy Horizontal Array Turbulence Study, B. Am. Meteorol. Soc., 92, 593–611, https://doi.org/10.1175/2010BAMS2614.1, 2011. a
Perry, A.: Hot-wire anemometry, Clarendon Press, Oxford, UK, 1982. a
Petrides, A. C., Huff, J., Arik, A., van de Giesen, N., Kennedy, A. M., Thomas, C. K., and Selker, J. S.: Shade estimation over streams using distributed temperature sensing, Water Resour. Res., 47, W07601, https://doi.org/10.1029/2010WR009482, 2011. a
Sayde, C., Buelga, J. B., Rodriguez-Sinobas, L., El Khoury, L., English, M., van de Giesen, N., and Selker, J. S.: Mapping variability of soil water content and flux across 1-1000 m scales using the Actively Heated Fiber Optic method, Water Resour. Res., 50, 7302–7317, https://doi.org/10.1002/2013WR014983, 2014. a
Sayde, C., Thomas, C. K., Wagner, J., and Selker, J.: High-resolution wind speed measurements using actively heated fiber optics, Geophys. Res. Lett., 42, 10064–10073, https://doi.org/10.1002/2015GL066729, 2015. a, b, c, d, e, f, g, h, i, j, k, l
Schilperoort, B., Coenders-Gerrits, M., Luxemburg, W., Jiménez Rodríguez, C., Cisneros Vaca, C., and Savenije, H.: Technical note: Using distributed temperature sensing for Bowen ratio evaporation measurements, Hydrol. Earth Syst. Sci., 22, 819–830, https://doi.org/10.5194/hess-22-819-2018, 2018. a, b
Schilperoort, B., Coenders-Gerrits, M., Jiménez Rodríguez, C., van der Tol, C., van de Wiel, B., and Savenije, H.: Decoupling of a Douglas fir canopy: a look into the subcanopy with continuous vertical temperature profiles, Biogeosciences Discuss., https://doi.org/10.5194/bg-2020-216, in review, 2020. a
Selker, J., van de Giesen, N. C., Westhoff, M., Luxemburg, W., and Parlange, M. B.: Fiber optics opens window on stream dynamics, Geophys. Res. Lett., 33, 27–30, https://doi.org/10.1029/2006GL027979, 2006a. a, b, c, d
Selker, J. S., Thévenaz, L., Huwald, H., Mallet, A., Luxemburg, W., Van De Giesen, N., Stejskal, M., Zeman, J., Westhoff, M., and Parlange, M. B.: Distributed fiber-optic temperature sensing for hydrologic systems, Water Resour. Res., 42, 1–8, https://doi.org/10.1029/2006WR005326, 2006b. a, b, c, d, e
Steele-Dunne, S. C., Rutten, M. M., Krzeminska, D. M., Hausner, M., Tyler, S. W., Selker, J., Bogaard, T. A., and van de Giesen, N. C.: Feasibility of soil moisture estimation using passive distributed temperature sensing, Water Resour. Res., 46, W03534, https://doi.org/10.1029/2009WR008272, 2010. a
Taylor, G. I.: The Spectrum of Turbulence, P. Roy. Soc. A-Math. Phy., 164, 476–490, https://doi.org/10.1098/rspa.1938.0032, 1938. a
Thomas, C. K., Kennedy, A. M., Selker, J. S., Moretti, A., Schroth, M. H., Smoot, A. R., Tufillaro, N. B., and Zeeman, M. J.: High-Resolution Fibre-Optic Temperature Sensing: A New Tool to Study the Two-Dimensional Structure of Atmospheric Surface-Layer Flow, Bound.-Lay. Meteorol., 142, 177–192, https://doi.org/10.1007/s10546-011-9672-7, 2012. a, b
Tsilingiris, P.: Thermophysical and transport properties of humid air at temperature range between 0 and 100 ∘C, Energ. Convers. Manage., 49, 1098–1110, https://doi.org/10.1016/j.enconman.2007.09.015, 2008. a, b, c, d
Tyler, S. W., Burak, S. A., McNamara, J. P., Lamontagne, A., Selker, J. S., and Dozier, J.: Spatially distributed temperatures at the base of two mountain snowpacks measured with fiber-optic sensors, J. Glaciol., 54, 673–679, https://doi.org/10.3189/002214308786570827, 2008. a
Tyler, S. W., Selker, J. S., Hausner, M. B., Hatch, C. E., Torgersen, T., Thodal, C. E., and Schladow, S. G.: Environmental temperature sensing using Raman spectra DTS fiber-optic methods, Water Resour. Res., 45, W00D23, https://doi.org/10.1029/2008WR007052, 2009. a, b, c, d
van de Giesen, N., Steele-Dunne, S. C., Jansen, J., Hoes, O., Hausner, M. B., Tyler, S., and Selker, J.: Double-ended calibration of fiber-optic raman spectra distributed temperature sensing data, Sensors, 12, 5471–5485, https://doi.org/10.3390/s120505471, 2012. a, b, c, d
Van Ramshorst, J., Coenders, M., Schilperoort, B., van de Wiel, B. J. H., Izett, J., Selker, J. S., Higgins, C. W., Savenije, H. H. G., and van de Giesen, N. C.: Data from: Revisiting wind speed measurements using actively heated fiber optics: a wind tunnel study, 4TU.ResearchData, https://doi.org/10.4121/12832118, 2020. a
Webster, C. A. G.: A note on the sensitivity to yaw of a hot-wire anemometer, J. Fluid Mech., 13, 307–312, https://doi.org/10.1017/S0022112062000695, 1962. a
Zeeman, M. J., Selker, J. S., and Thomas, C. K.: Near-Surface Motion in the Nocturnal, Stable Boundary Layer Observed with Fibre-Optic Distributed Temperature Sensing, Bound.-Lay. Meteorol., 154, 189–205, https://doi.org/10.1007/s10546-014-9972-9, 2015. a, b
Žukauskas, A.: Heat Transfer from Tubes in Crossflow, Advances in Heat Transfer, 8, 93–160, https://doi.org/10.1016/S0065-2717(08)70038-8, 1972. a, b, c, d
- Abstract
- Introduction
- Experimental setup and methods
- Results and discussion
- Conclusions
- Appendix A: FO cable schematization
- Appendix B: Comparison of AHFO and sonic anemometer wind speed
- Appendix C: Wind tunnel flow characteristics
- Appendix D: Number of measurements
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Experimental setup and methods
- Results and discussion
- Conclusions
- Appendix A: FO cable schematization
- Appendix B: Comparison of AHFO and sonic anemometer wind speed
- Appendix C: Wind tunnel flow characteristics
- Appendix D: Number of measurements
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References