the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Evaluation of the reflectivity calibration of W-band radars based on observations in rain
Alexander Myagkov
Stefan Kneifel
Thomas Rose
This study presents two methods for evaluating the reflectivity calibration of W-band cloud radars. Both methods use natural rain as a reference target. The first approach is based on a self-consistency method of polarimetric radar variables, which is widely used in the precipitation radar community. As previous studies pointed out, the method cannot be directly applied to higher frequencies where non-Rayleigh scattering effects and attenuation have a nonnegligible influence on radar variables. The method presented here solves this problem by using polarimetric Doppler spectra to separate backscattering and propagational effects. New fits between the separated radar variables allow one to estimate the absolute radar calibration using a minimization technique. The main advantage of the self-consistency method is its lower dependence on the spatial variability in radar drop size distribution (DSD). The estimated uncertainty of the method is ±0.7 dB. The method was applied to three intense precipitation events, and the retrieved reflectivity offsets were within the estimated uncertainty range. The second method is an improvement on the conventional disdrometer-based approach, where reflectivity from the lowest range gate is compared to simulated reflectivity using surface disdrometer observations. The improved method corrects, first, for the time lag between surface DSD observations and the radar measurements at a certain range. In addition, the effect of evaporation of raindrops on their way towards the surface is mitigated. The disdrometer-based method was applied to 12 rain events observed by vertically pointed W-band radar and showed repeatable estimates of the reflectivity offsets at rain rates below 4 mm h−1 within ±0.9 dB. The proposed approaches can analogously be extended to Ka-band radars. Although very different in terms of complexity, both methods extend existing radar calibration evaluation approaches, which are inevitably needed for the growing cloud radar networks in order to provide high-quality radar observation to the atmospheric community.
- Article
(8818 KB) - Full-text XML
-
Supplement
(3901 KB) - BibTeX
- EndNote
During the last few decades, millimeter wavelength radars (also known as cloud radars) have become an invaluable source of information for cloud and precipitation research (Kollias et al., 2007). Due to the shorter wavelengths, cloud radars are not only sensitive to precipitating particles but also to cloud droplets, small ice particles, and fog. This makes these instruments extremely valuable tools for studying, for example, cloud formation, cloud microphysical processes, or the associated radiative effect of clouds. Consequently, cloud radars have been set up around the world. The US Department of Energy (DOE) Atmospheric Radiation Measurement (ARM) program maintains a number of fixed stations and mobile platforms equipped with 35 and 94 GHz radars (Mather and Voyles, 2013). In Europe, many universities and atmospheric research centers have deployed cloud radars (Haeffelin et al., 2005; Illingworth et al., 2007; Bouniol et al., 2010; Löhnert et al., 2015; Hirsikko et al., 2014). The majority of cloud radars sites provide their data to the CloudNet project (Illingworth et al., 2007), which is part of the European research infrastructure, i.e., Aerosols, Clouds, and Trace gases Research InfraStructure (ACTRIS; http://www.actris.eu, last access: January 2019). CloudNet provides algorithms for producing cloud and precipitation classification, and the data sets are converted into a unified format. This allows one to derive long-term cloud statistics, which, of course, rely strongly on proper radar calibration.
At CloudNet and ARM sites, cloud radars are often operated in co-location with a microwave radiometer and a lidar in order to derive the macrophysical (Wang and Sassen, 2001; Shupe et al., 2011), microphysical (Matrosov et al., 1998; Shupe et al., 2006; Shupe, 2011; Bühl et al., 2016; Kalesse et al., 2016; Acquistapace et al., 2017), and dynamical properties (Shupe et al., 2008; Bühl et al., 2015; Borque et al., 2016; Radenz et al., 2018) of clouds.
One of the most widely used radar observables is the equivalent radar reflectivity factor (henceforth called reflectivity). This parameter depends on the size, concentration, phase, shape, density, and orientation of particles. Many operational cloud property retrievals (Matrosov, 1997, 1999; Frisch et al., 2002; Hogan et al., 2006; Heymsfield et al., 2008) rely on accurate measurements of reflectivity. Some studies combine reflectivities at different frequencies in order to derive detailed microphysics of cloud particles (Matrosov, 2011; Leinonen et al., 2013; Kneifel et al., 2015) and, therefore, require precise calibration of all radar systems involved. For networks of cloud radars, which are supposed to provide long-term observations of cloud properties, methods for validating the quality of the reflectivity calibration are of key importance. This study focuses on the reflectivity calibration because it is one of the most commonly used parameters for retrievals and for model evaluation. This, nevertheless, does not imply that the calibration of Doppler and polarimetric observations is of less importance. Aspects of antenna pointing calibration, which is essential for accurate Doppler measurements, can be found in Huuskonen and Holleman (2007) and Muth et al. (2012). Moisseev et al. (2002) and Myagkov et al. (2015, 2016a) showed the calibration of polarimetric variables for cloud radars operating in different configurations.
Proper calibration and monitoring of reflectivity calibration are key, considering the growing number of meteorological radars worldwide. However, even radars operated within large observational networks have been shown to sometimes be prone to calibration errors (Protat et al., 2011; Ewald et al., 2019; Maahn et al., 2019; Kollias et al., 2019).
Chandrasekar et al. (2015) compiled a detailed review of the centimeter wavelength radar calibration techniques for an operational use. Many of the described aspects are also relevant for cloud radars. Maintaining accurate reflectivity measurements requires temperature stabilization of the radar housing, protecting antennas and radomes from water (Hogan et al., 2003; Delanoë et al., 2016), frequent automatic internal calibrations, and regular maintenance (Chandrasekar et al., 2015). Cloud radar manufacturers typically apply a budget calibration, i.e., characterizing individual radar components separately during manufacturing and taking the results into account in the reflectivity calculations (Görsdorf et al., 2015; Küchler et al., 2017; Ewald et al., 2019). The budget calibration has several shortcomings. First, it requires calibrated measurement equipment and experienced technical staff. Second, during the calibration, the analyzed radar is out of operation and has to be partly disassembled. Third, the calibration accuracy still depends on the component stability during operation. Finally, the calibration procedure may differ significantly for radars of different types, which is problematic for operational cloud radar networks.
A calibration using an external target with known properties (known as end-to-end calibration) allows for the mitigation of the abovementioned problems. One of the conventional external calibration methods of meteorological radars is based on point target observations (Chandrasekar et al., 2015). Unfortunately, its applicability to cloud radars is often limited. The target has to be mounted in the far field on a tower that is often not available. For precision pointing of the radar to the target, this method requires a scanning unit, which many of the currently deployed cloud radars are not equipped with. In principle, the target can be lifted up by a balloon or a drone, but it is challenging to achieve perfect pointing and spatial stability of the target. Both aspects are very critical due to the narrow antenna beams. In addition, as pointed out by Gorgucci et al. (1992) and Chandrasekar et al. (2015), the calibration with a point target does not directly take into account the volumetric scattering by clouds and precipitation.
Another approach is a comparison of observations of an inspected radar against a calibrated reference system. For instance, Protat et al. (2011) proposed a comparison of observations in ice clouds by ground-based cloud radars and the space-borne W-band radar CloudSat (Stephens et al., 2008). Based on the scattering from the sea surface, CloudSat reflectivity calibration is performed on a monthly basis and is accurate within ±0.5 dB (Tanelli et al., 2008). Due to the high velocity and 1.5 km footprint, direct comparison of the reflectivity value from CloudSat and a static ground-based radar leads to large uncertainties (standard deviation of 2–3 dB). In order to reduce the uncertainties, Protat et al. (2009) used time periods of the order of several months for the statistical comparisons. With the CloudSat flight cycle of 16 d and the requirement in pure ice nonprecipitating clouds during an overpass, this method is mainly applicable for long-term calibration monitoring (Kollias et al., 2019).
Using natural volume-distributed targets for the calibration verification is a well-established approach. The use of raindrops as reference targets allows one to directly account for the antenna properties in the calibration procedure. The first successful attempts to evaluate meteorological radars with rain date back to 1968 (Atlas, 2002). Since then, several different approaches have been developed. Among the most widely used methods is the one based on disdrometer observations. Drop size distributions (DSDs) observed in situ are converted to the radar reflectivity. Time series (Gage et al., 2004; Frech et al., 2017) or distributions (Kollias et al., 2019; Dias Neto et al., 2019) of calculated and observed reflectivities are then compared. Hogan et al. (2003) showed a calibration verification method suitable for W-band cloud radars only. They found that, for a range of DSDs, the reflectivity is about 19 dBZe for rain intensities from 5 to 20 mm h−1 at the range of 250 m from the radar. Clearly, one of the main sources of uncertainties for the methods using in situ rain observations is the vertical variability of rain properties. This variability might originate from a number of effects, among which are turbulence, wind shear, evaporation, drop breakup, and coalescence.
Goddard et al. (1994) proposed a self-consistency calibration method based on polarimetric radar observations at low elevation angles. Within this method, radar range bins are analyzed independently, and therefore, the methods is less sensitive to spatial variability of DSD. The method has been operationally used for the 3 GHz Chilbolton radar Hogan et al. (2003) and is well established in the weather radar community. Hogan et al. (2003) claim that the accuracy of this method is better than ±0.5 dB. Nevertheless, the authors pointed out that the method cannot be directly used for cloud radar calibration because of strong attenuation at millimeter wavelengths by liquid water and non-Rayleigh scattering effects.
This study presents two methods for evaluating the reflectivity calibration of W-band radars. The first approach is a new attempt at extending the polarimetric consistency method of Goddard et al. (1994) for cloud radars. Due to lower costs, polarimetric cloud radars have become increasingly available, and therefore, it is highly desirable to utilize their polarization capabilities for calibration monitoring. The second approach is an improvement of the conventional disdrometer-based method, using additional corrections for wind shear and evaporation. This method, which does not require scanning or polarimetric capabilities, is applicable to a large number of radar sites which are already equipped with disdrometers.
The paper is organized as follows. In Sect. 2 the instrumentation used is described. The calibration methods and their comparison are shown in Sects. 3 and 4. In Sect. 5 we summarize the estimated accuracy and discuss the applicability of the calibration evaluation methods.
For the comparison of different calibration methods, we combine observations from two sites. In this way, we are able to collect a data set with a wide range of rainfall rates observed with various radar and in situ instrumentation. During summer 2018, a number of convective rainfall events were recorded at the Radiometer Physics GmbH (RPG) site in Meckenheim, Germany (henceforth RPG site). The site is equipped with a demonstration W-band cloud radar and a weather station and disdrometer. The second data set was collected at the Jülich Observatory for Cloud Evolution Core Facility (JOYCE-CF; Löhnert et al., 2015) which is located ca. 50 km north of Meckenheim. JOYCE-CF is regularly equipped with cloud radars and a suite of remote sensing and in situ instruments including disdrometers. The permanently installed instrumentation has been extended by additional cloud radars and disdrometers during the measurement campaign of TRIple-frequency and Polarimetric radar Experiment for improving process observation of winter precipitation (TRIPEX-pol), which took place from October 2018 until February 2019. The larger range of rainfall rates observed at the RPG site allows us to test both calibration methods with the same data set. The continuous observations at JOYCE-CF are lacking more intense rainfall rates (larger than 7 mm h−1) required for the self-consistency method, but the longer time series allow for a more detailed evaluation of the calibration performance using disdrometers.
2.1 Radars
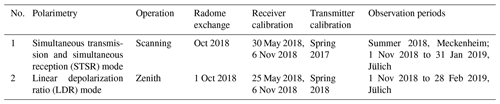
For this study, we use two 94 GHz cloud radars manufactured by Radiometer Physics GmbH (RPG), Meckenheim, Germany (Fig. 1). The radars are based on solid-state technology and use frequency-modulated continuous wave (FMCW) signals. Note that the methods described in this study are also applicable to any other W-band cloud radar (FMCW or pulsed) with a proper rain mitigation system. An overview of the used radar design, operation, and the budget calibration was described in Küchler et al. (2017). Typical radar specifications are summarized in Table 1. Configuration, maintenance, and observation periods for each radar are given in Table 2. Throughout the paper, the radars are denoted according to their numbers in Table 2 (see first column).

Figure 1Impressions of the two frequency-modulated continuous wave (FMCW) W-band radars used in this study, as indicated in Table 2. Images courtesy of the radar owners.
2.2 In situ instruments
The radars are equipped with Vaisala WXT520 weather stations (Basara et al., 2009) which provide atmospheric pressure, temperature, relative humidity, and a 1 min averaged rainfall rate derived from a piezoelectric sensor. The optical disdrometer PARSIVEL2 (hereafter Parsivel; Löffler-Mang and Joss, 2000; Tokay et al., 2014) and the rain-weighing gauge PLUVIO2 (denoted as Pluvio throughout the paper) are manufactured by OTT HydroMet GmbH, Kempten, Germany. They belong to the permanently installed instrumentation of JOYCE-CF (roof platform; 17 m above ground level). Due to a site maintenance, Parsivel and Pluvio were operated, until 27 November 2018, on a nearby roof at a ca. 50 m distance from the radars. From 27 November 2018 on, both instruments were reinstalled very close to the radars, with distances of less than 10 m. The Pluvio installed at JOYCE-CF has a 200 cm2 orifice and a single Alter-type wind shield (precipitation wind shield; OTT HydroMet GmbH; Kochendorfer et al., 2017). Data are recorded with a 1 min averaging period; the real-time output product is used for this study. Parsivel is an optical disdrometer which uses a laser band to detect the size and fall velocity of precipitating particles (Löffler-Mang and Joss, 2000; Löffler-Mang and Blahak, 2001; Tokay et al., 2014). The Parsivel software groups the measured drop sizes and velocities into a predefined 32×32 matrix. The size and velocity bins can be found in Angulo-Martínez et al. (2018). Rain rate and reflectivity are calculated using the raw data (32×32 matrix). A similar optical disdrometer, namely the laser precipitation monitor (LPM; Fig. 2a) from Adolf Thies GmbH & Co. KG (Angulo-Martínez et al., 2018), has continuously been operated at the RPG site since 14 June 2018. The LPM collected data during summer 2018 at RPG site; from 1 November 2018 to 6 December 2018 the LPM was installed at the JOYCE-CF site as part of TRIPEX-pol campaign. The LPM provides a particle event mode in which a message with the size and velocity of each individual particle is generated (Prata de Moraes Frasson et al., 2011). The particle event mode is normally used for calibration purposes. The particle’s size and velocity is provided separately, assuming either a spherical or a “hamburger” shape. The latter shape lacks a detailed description in the LPM manual; hence, we decided to only use the values for the spherical shape. Prata de Moraes Frasson et al. (2011) report that the data transfer rate may not be sufficient for a large number of particles. The manufacturer also notes in the LPM manual that not all particles may be registered at high precipitation rates. Unfortunately, a more detailed explanation of this issue and whether it is related to the data transfer rate or to other well-known issues of optical disdrometers, such as multiple particles in the field of view or partial beam filling, is missing. We developed a test device to estimate the underestimation of events due to limited data transfer rate. A chopper wheel with two closed and two open quadrants was mounted to either completely block or open the LPM laser beam (Fig. 2b). The event frequency was registered with a photo transducer and subsequently increased in steps from 3.7 to 83.2 s−1. The data from the LPM were transferred using a serial RS485 full duplex connection with 115 kBaud transfer rate. The LPM detected the event rate with an accuracy of 1 up to 77 s−1. Larger event rates were significantly underestimated by the LPM. If we assume a Marshall–Palmer distribution, the event rate due to a rainfall rate of 20 mm h−1 is 30 s−1. As most rainfall events analyzed in this study are well below this rainfall rate, the LPM data transfer problem is unlikely to introduce large uncertainties. A more serious issue for rainfall measurements with the LPM is splashing effects which have been found by Angulo-Martínez et al. (2018) to cause up to a 20 % overestimation of the particle number. In order to reduce the splashing effects, we covered all the LPM surfaces with spongy and cotton material (Fig. 2a). In order to further reduce the effects of splashing on the calculated rain rate and reflectivity, we followed the approach of Tokay et al. (2014) and rejected all particles with velocities outside the range of ±50 % relative to a theoretical size–velocity relation (Foote and Du Toit, 1969).
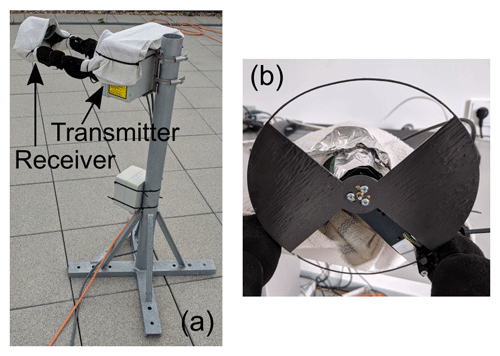
Figure 2The laser precipitation monitor (LPM) at the Radiometer Physics GmbH (RPG) site (a). Metal surfaces close to the laser beam are covered with spongy and/or cotton material to mitigate splashing. The chopper wheel (b) was mounted on side of the LPM detector to test the data transmission rate (see text for details).
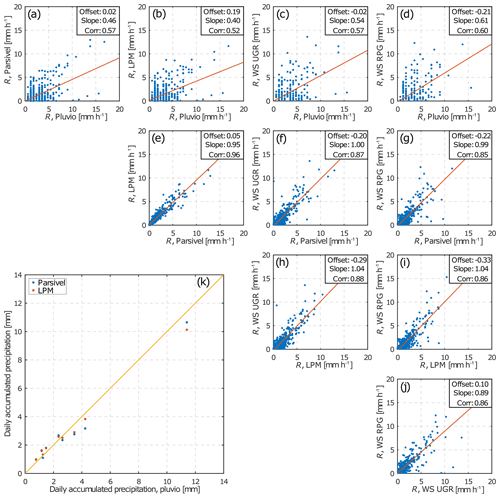
Figure 3A comparison of 1 min rain rates observed by Pluvio, Parsivel, LPM, and the two Vaisala WXT520 weather stations attached to the radars (a–j). The weather stations of radars 1 and 2 are denoted as WS UGR and WS RPG, respectively. The data set from the TRIPEX-pol campaign (1 November 2018 to 6 December 2018) contains 391 min of rainfall detected by all sensors simultaneously. Each subplot contains the estimated offset and the slope of a linear fit (red line) and the Pearson correlation coefficient. Panel (k) shows a comparison of the daily accumulated precipitation from Pluvio, Parsivel, and LPM from 10 precipitating days. The yellow line is the one-to-one relation.
Figure 3 shows a comparison of the measured 1 min rain rates from the four in situ sensors. The basis for the comparison is observations from 1 November 2018 to 6 December 2018. In total, we found 391 min of precipitation detected by all sensors. The observed rain rates were mainly below 7 mm h−1. The correlation between LPM and Parsivel rainfall rates is 0.96; LPM shows slightly smaller values than Parsivel. The two weather stations show a correlation with disdrometers varying from 0.84 to 0.88. These correlations are in an agreement with Prata de Moraes Frasson et al. (2011). The 1 min rainfall rates provided by Pluvio were found to be very noisy, with correlations to the other in situ sensors ranging from 0.5 to 0.6. Nevertheless, the 1 d accumulated precipitation from Pluvio correlates well with those from the Thies and Parsivel (0.997 and 0.99, respectively, calculated with 10 rainy days). As Pluvio is a weighting gauge, it measures the mass representing accumulation of droplets in the bucket. The rainfall rate is derived from the time derivative of accumulated mass, which can lead to more noisy rainfall rates. In contrast, optical disdrometers measure every single droplet crossing the laser beam and calculate the accumulated rainfall as an integral over time. The accumulated precipitation from Vaisala WXT520 weather stations has not been stored and, therefore, cannot be analyzed.
Goddard et al. (1994) developed a calibration approach for 3 GHz radars based on observations of reflectivity Z, differential reflectivity ZDR, and specific differential phase KDP in rain at low elevation angles. At the S band, ZDR defines the KDP∕Z ratio because Z and KDP depend on the number concentration of droplets, while ZDR is a proxy for drop median size (Ryzhkov et al., 2005; Kumjian, 2013). For ZDR exceeding 2 dB, which is often observed in strong rainfall, the relation between the three parameters is not affected by DSD variability. ZDR and Z profiles can thus be used in strong rainfall to reconstruct the expected differential phase ΦDP profile. The radar is considered to be well calibrated if the expected and the measured profiles of ΦDP agree. According to Chandrasekar et al. (2015), a standard accuracy, which can be achieved for ZDR, is about 0.1 dB. KDP is calculated as a range derivative and, therefore, is immune to the radar polarimetric calibration. As a small bias in ZDR affects the expected ΦDP profiles much less than a bias in Z, any difference between measured and expected profiles of ΦDP is assigned to a reflectivity offset. The reflectivity calibration factor is then simply determined by shifting the reflectivity profile until a minimum between the estimated and measured profiles of ΦDP is reached.
Hogan et al. (2003) noticed that the method of Goddard et al. (1994) is not directly applicable to W-band radars for the following reasons. First, attenuation due to rain is almost negligible at 3 GHz, while it strongly increases towards higher frequencies. Second, non-Rayleigh scattering causes reflectivity at the W band to increase much less with the rainfall rate as compared to lower frequencies. As a result, W-band reflectivities become less sensitive to the rain rate with increasing rain intensities (Hogan et al., 2003). Third, in contrast to lower frequencies, ZDR at the W band does not exceed 0.12 dB for rain rates up to 150 mm h−1 (Aydin and Lure, 1991). Fourth, an estimation of KDP from radar observations becomes more complicated. Otto and Russchenberg (2011) and Trömel et al. (2013) show that the total measured differential phase is the sum of a backscattering and a propagational component (see Eq. B6). At low frequencies, the backscattering differential phase δ is usually negligible, but it increases with larger frequencies. At millimeter wavelengths, even relatively small drops in the range of 2–3 mm diameter produce up to a 10∘ backscattering differential phase (Matrosov et al., 1999). For a polarimetric calibration method applicable to millimeter wavelengths, it is thus crucial to find a way to separate δ and KDP. In order to find a solution to the abovementioned problems, we identify a set of different propagation and backscattering variables to which an approach similar to Goddard et al. (1994) can be applied. To infer suitable relations between radar observables, we simulate them using the T-Matrix model (Mishchenko, 2000) and a range of particle size distributions (PSDs) similar to Hogan et al. (2003). We assume normalized gamma distributions with μ from 0 to 15 and NL from 5×102 to 2.5×104 mm−1 m−3. For the given μ and NL, the median volume diameter D0 was increased in 0.05 mm steps, starting at 0.1 mm until the rain rate reached 20 mm h−1. A detailed description of how the nonattenuated reflectivity Z0, one-way attenuation A, differential reflectivity ZDR, specific differential phase KDP, differential attenuation ADP, and backscattering differential phase δ are calculated can be found in Appendices A and B.
3.1 Replacement for ZDR
As discussed above, Mie scattering effects complicate the use of ZDR at the W band, and we need to find an alternative parameter which is closely related to D0. Trömel et al. (2013) found, at the X band, that δ is a suitable parameter which is independent of NL and sufficiently related to D0. As can be seen in Fig. 4, δ is nearly directly proportional to D0 at the W band for rain rates up to 7 mm h−1, and even at larger rain rates, δ seems to be a reasonable proxy for D0. Thus, we will use δ in the following as a replacement for ZDR used at lower frequencies in order to find relations between Z0 and propagation variables.
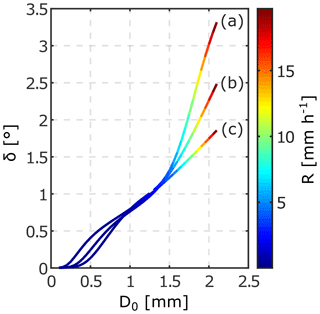
Figure 4Simulated relations between the backscattering differential phase δ and the median drop diameter D0 at 94 GHz. The curves show simulations for DSDs, with NL=2500 mm−1 m−3 and μ equal to 5 (a), 0 (b), and 15 (c). The corresponding rain rate R is color coded; the maximum rain rate for all simulations is limited to values smaller than 20 mm h−1. The calculations are made for a 20 ∘C and 30∘ elevation angle.
3.2 Relations between propagation and backscattering variables
In the original method of Goddard et al. (1994), a ratio of the propagation parameter KDP and the backscattering parameter Z0 is parameterized as a function of ZDR characterizing the median drop size. Using the large set of simulated rain PSDs introduced above and the corresponding forward-simulated radar parameters, we can parameterize the ratio KDP∕Z0 as a function of δ for the W band as follows:
At frequencies where rain attenuation is nonnegligible, we also need to parameterize specific attenuation A. The backscattering differential phase δ also defines the ratio ADP∕A as follows:
We also introduce an additional relation to constrain relations between Z0 and δ. This is done by coupling these two parameters via the absolute value of the specific attenuation A in dB km−1 as follows:
In Eqs. (1)–(3), f is the following function:
The approximations (Eqs. 1–3) were derived using the neural network approach. The used neural networks have one hidden layer with three neurons for Eqs. (1) and (2) and four neurons in Eq. (3). The neural networks were trained with the Levenberg–Marquardt backpropagation algorithm. This algorithm utilizes the advantages of the Gauss–Newton and the steepest descent methods. The Gauss–Newton algorithm converges fast if the current point is close enough to the optimum but is slow if it is far from the optimum. The deepest descent, in contrast, converges better if the current point is far from the optimum but has bad convergence in the area of the optimum. By combining these two approaches, the Levenberg–Marquardt algorithm, in general, converges faster. The problem of overfitting was avoided by using the low number of neurons in the hidden layer and applying the Bayesian regularization (MacKay, 1992), which restricts the magnitude of the weights. Further details and examples, with ready-to-use MATLAB codes of function approximations using neural networks, can be found in Demuth et al. (2014).
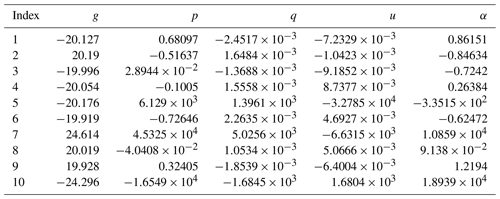
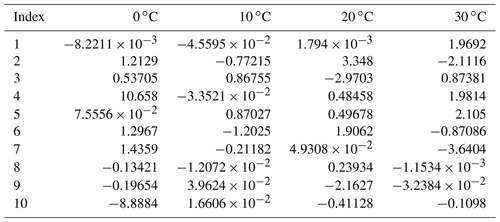
The fit coefficients a1−10, b1−10, and c1−17 are given in Tables A1, A2, and A3, respectively. In Eqs. (1)–(3) the units of Z0, A, KDP, ADP, and δ are mm6 m−3, dB km−1, ∘ km−1, dB km−1, and ∘ respectively. In the Supplement, we provide MATLAB and Octave functions for Eqs. (1)–(3). In order to take into account the possible variability in Eqs. (1)–(3) caused by environment temperature, the fit coefficients are provided for 0, 10, 20, and 30 ∘C.
Figure 5 shows the simulated polarimetric variables and the fitted approximations (Eqs. 1–3). The remaining root mean square error (RMSE) of the KDP∕Z0, ADP∕A, and A approximations is ∘ , dB km−1 dB−1 km, and 0.3 dB km−1, respectively. The correlations between the simulated variables and their approximations are 0.998. Figure 5a indicates that, at δ close to 0.5∘, KDP∕Z0 is close to 0, which represents a limit of the self-consistency method. The method becomes robust at δ values exceeding 1∘.
3.3 Separating propagational and backscattering components using Doppler spectra
Profiles of Z0, A, δ, ADP, and KDP are not directly measured by a dual polarized cloud radar. Instead, the radar measures variables (Z, ZDR, and ΦDP) which are combinations of propagational and backscattering effects, as can be seen in Eqs. (A1), (B5) and (B6). Several studies presented approaches to separate propagational and backscattering components for centimeter wavelength radars (Otto and Russchenberg, 2011; Schneebeli and Berne, 2012; Trömel et al., 2013). These approaches are based on relations between profiles of ZDR and δ (Otto and Russchenberg, 2011; Schneebeli and Berne, 2012) and A and KDP (Trömel et al., 2013). However, as already discussed above, those methods cannot be applied to the W band because of non-Rayleigh scattering and attenuation effects. As a result, ZDR becomes less informative, and relations between A and KDP vary for different DSDs when δ exceeds 1∘.
A common approach for separating backscattering from propagational effects is the use of Doppler spectra. In the absence of strong turbulence, smaller droplets populate in the slow-falling part of the spectrum, while the larger drops are found on the fast-falling side. Due to the relatively well-known relation of drop size and terminal velocity, the spectral power at each velocity bin can be associated to a certain drop size range (Kollias et al., 2002). The small droplets can be assumed to only be affected by propagational effects, while the larger drops are also affected by Mie scattering effects. Therefore, the spectral information can be used to separate the two components in low turbulence conditions. This approach has been applied to nonpolarimetric dual wavelength spectra in rainfall and snow to separate the attenuation and Mie scattering effects (Tridon and Battaglia, 2015; Tridon et al., 2017; Li and Moisseev, 2019). Here we follow the same idea but with polarimetric spectra.
Polarimetric Doppler spectra have only been sporadically used in the past, probably due to the demands regarding storage capacity and required high data quality. At centimeter wavelength, their potential has been shown for microphysical retrievals (Moisseev and Chandrasekar, 2007; Spek et al., 2008; Dufournet and Russchenberg, 2011; Pfitzenmaier et al., 2018) and efficient clutter suppression (Unal, 2009; Moisseev and Chandrasekar, 2009; Alku et al., 2015). The number of installed polarimetric Doppler cloud radars has only recently increased, with only a few studies, so far, exploring their potential for microphysical studies and retrievals (Oue et al., 2015, 2018; Myagkov et al., 2015, 2016b).
As shown by Aydin and Lure (1991), drops up to a size of 1.2 mm do not produce a strong backscattering differential reflectivity zDR at the W band. At sizes larger than 1.2 mm, the zDR spectrum reveals a series of minima and maxima. The authors also simulated a velocity zDR spectrum for 1 mm h−1. The values of zDR are nearly 0 dB below 3 m s−1 terminal velocity, and therefore, any changes in ZDR in this terminal velocity range can be addressed to differential attenuation.
We therefore derive differential reflectivity from the Doppler velocity range 0–2 m s−1, where we assume all particles to be Rayleigh scatterers (hereafter referred to as the small size part of a Doppler spectrum). Estimating this small particle ZDR individually for each range bin directly provides us with the profile of the cumulative differential attenuation DA as follows:
where CDA is an offset in differential reflectivity in dB due to the polarimetric calibration. Uncertainties of the DA profile can be characterized using the variances of ZDR over the small size part of the spectra. Unfortunately, Aydin and Lure (1991) do not show the size spectrum of δ. Nevertheless, as it is shown for lower frequencies (Matrosov et al., 1999; Ryzhkov, 2001; Trömel et al., 2013), and as we further show in Sect. 3.6, the spectrally resolved δ shows a similar oscillatory behavior to zDR. Applying the same approach as described above, we can estimate the cumulative differential phase DP from the ΦDP in the small size part of the spectrum as follows:
where CDP is an offset in differential phase in degrees due to the polarimetric calibration. The profile of δ can simply be estimated by subtracting DP from the ΦDP profile (see Eq. B6).
Spectral polarimetric observations are typically performed at low elevation angles (≤45∘; Unal and Moisseev, 2004; Spek et al., 2008) in order to maximize the polarimetric signatures of hydrometeors. Doppler velocities corresponding to each spectral bin represent projections of terminal velocities of drops, vertical air motions, and horizontal wind. In order to separate propagation and backscattering effects, the knowledge of the absolute terminal velocities is not required. The effect of air motions (both vertical and horizontal) can be roughly mitigated by shifting spectra in such a way that the rightmost detected spectral line, corresponding to drops with the slowest fall velocity, is set to 0 m s−1. As it is shown in Sect. 3.6, such a rough mitigation is good enough to separate small drops scattering in the Rayleigh regime from those producing resonance effects.
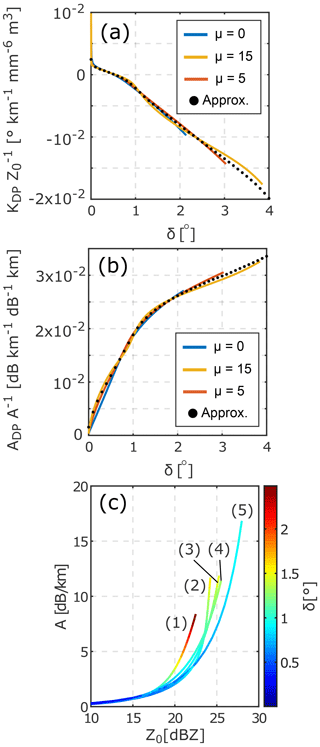
Figure 5Relations between KDP, Z0, and δ (a), ADP, A, and δ (b), and A, Z0, and δ (c) at 94 GHz. The solid lines show the calculations for different DSDs, and the black dots denote the fitted approximations (Eqs. 1a and 2b). In panel (c), the calculations are made for μ=5 and NL=2500 mm−1 m−3 (1), μ=15 and NL=8000 mm−1 m−3 (2), μ=5 and NL=8000 mm−1 m−3 (3), μ=0 and NL=8000 mm−1 m−3 (4), and μ=5 and NL=25000 mm−1 m−3 (5). The rain rates are all smaller than 20 mm h−1. All calculations are made for a 30∘ elevation angle and a temperature of 20 ∘C. The units of Z0, A, KDP, and ADP in panels (a) and (b) are mm6 m−3, dB km−1, ∘ km−1, and dB km−1, respectively.
3.4 Algorithm
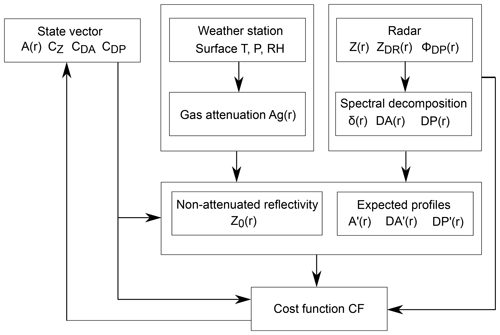
The different modules of the method are illustrated in Fig. 6. The method is based on finding a state vector corresponding to an optimal match of the expected and the observed radar variables. The matching is achieved by minimizing a cost function using a global stochastic optimization method called the differential evolution (DE) approach (Storn and Price, 1997). DE was recently used by Rusli et al. (2017) for a detailed characterization of drizzle and cloud liquid. In this study, we use the built-in Octave implementation of DE, which is based on Das et al. (2009). We use the default strategy DEGL/SAW/bin with a mutation factor of 0.8, a crossover probability of 0.9, a tolerance of 10−3, a maximum number of iterations of 200, and a population size of NP=20 Nv, where Nv is the number of elements in the state vector. DE stops when the maximum number of iterations is reached or the relative difference in the cost function between the best and the worst state vector in the population is below the specified tolerance. When DE reaches one of the stopping criteria, the state vector with the lowest cost function is taken as the output.
The state vector contains a range profile of A(r) (dB km−1) and the calibration factors of CZ (dB), CDA (dB), and CDP (∘). DE does not require an a priori state vector. Instead, it requires realistic limits for each element of the state vector (Table 3). Within each iteration, the DE algorithm stochastically creates NP state vectors.
From each generated state vector, a profile of Z0 is calculated as follows:
where Z(r) is the measured reflectivity profile in dBZ, and is the dielectric factor assumed in the radar software (0.74 for our radars). The two dielectric factors in Eq. (7) account for the differences in the actual dielectric properties of liquid water and those assumed in the radar software. Surface observations of temperature, relative humidity, and pressure are used to estimate the attenuation profile due to gases Ag(r) (see Sect. A2). The dielectric factor is calculated for liquid water at surface temperature. Using profiles of Z0 and δ, an expected profile DP′ is found using Eq. (1). The prime is used to discriminate the expected variable from the one estimated from measurements. Profiles of A and δ are used to estimate the expected DA′ profile from Eq. (2). Finally, the expected profile of A′ is calculated using the expected profiles of DA′ and DP′ and Eq. (3).
The profiles of A′, DA′, and DP′ are further used for the calculation of the cost function, CF, as follows:
where
In Eq. (9), i specifies a variable and wi contains the profile of the expected values for the ith variable (DA, DP, and A). The vector Wi contains the profile of the ith variable inferred from measurements. The attenuation profile in the current state vector is taken as WA. Si is the error covariance matrix of the ith variable. Nondiagonal elements of Si are assumed to be 0 since no correlation between errors in different range bins is expected. Based on uncertainty estimates of A (see Sect. 3.2) related to uncertainties in the approximation Eq. (3), diagonal elements of SA are set to (0.3 dB km−1)2. Estimation of DA and DP from radar observations and their diagonal elements in the error covariance matrix is done as described in Sect. 3.3.
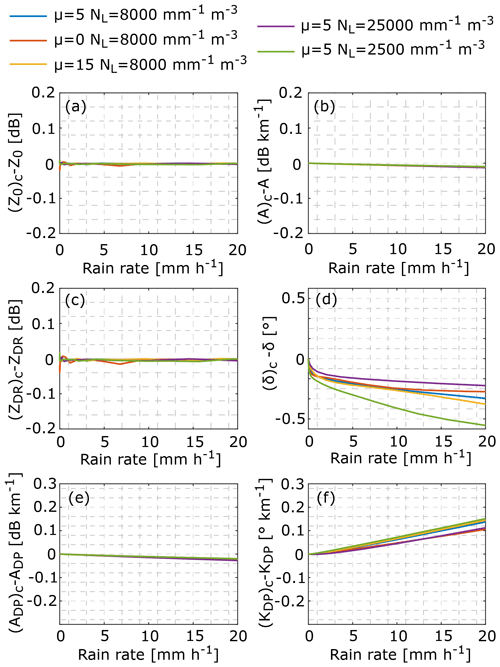
Figure 7Differences between reflectivity (a), specific attenuation (b), differential reflectivity (c), backscattering differential phase (d), differential attenuation (e), and specific differential phase (f) calculated with a 10 and 0∘ standard deviation of the canting angle distribution. Variables calculated with 10∘ are indicated by the index “c”. The differences are shown for different DSDs and are indicated by line colors.
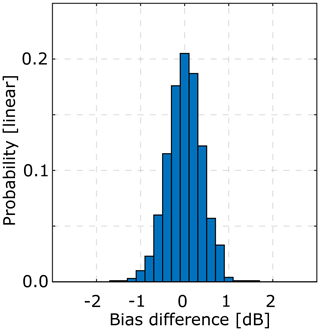
Figure 8Estimated uncertainty of the reflectivity calibration coefficient CZ using the self-consistency method (Sect. 3). Various rain DSDs were used to simulate ideal profiles of radar variables. Random noise was then added to these profiles and several calibration coefficients before applying the self-consistency method (also see details in the text). The distribution shows the difference between original CZ and the retrieved value. The 5th and 95th percentiles and the standard deviation of the distribution are −0.7, 0.7, and 0.4 dB, respectively.
3.5 Uncertainties of the method
In order to estimate the uncertainties of the method, we simulated 1000 samples of slanted 1 km profiles of Z0, A, ADP, KDP, and δ, as described in Appendices A and B. For the simulations, the normalized gamma DSD were used with μ and NL, randomly chosen for each sample and each range bin. The ranges of μ and NL were from 0 to 15 and from 5×102 to 2.5×104 mm−1 m−3, respectively. Size distributions with A less than 3 dB km−1 were excluded from the analysis because such attenuation values are close to the magnitude of the measurement variability. In order to take into account the measurement variability of radar reflectivity, a random Gaussian noise was added to Z0 with variance set to , where 20 is the typical number of spectra averaged by the used radars (Eq. 5.193 in Bringi and Chandrasekar, 2001). Taking into account that the signal-to-noise ratio in rain within the first kilometer typically exceeds 30 dB and the copolar correlation coefficient in rain approaches one, variability in the polarimetric variables is low (Sect. 6.5 in Bringi and Chandrasekar, 2001) and is thus neglected. With the simulated variables, the profiles of Z, DA, and DP were derived. Variability in the calibration constants of CZ, CDA, and CDP were randomly generated, assuming the uniform distributions given in Table 3, and added to Z, DA, and DP, respectively. The uncertainties in CZ, CDA, and CDP are assumed to be the same for all range bins for a single sample.
The forward model of the radar observables used in this study assumes that raindrops are oriented horizontally. A number of studies show that drops typically have a canting angle distribution with zero mean and a standard deviation up to 10∘ (Bringi and Chandrasekar, 2001; Huang et al., 2008). In order to check the level of uncertainty introduced by the drop orientation, we compared simulated radar variables with a 0 and 10∘ standard deviation of the canting angle distribution. The sensitivity experiment was made for a 0∘ elevation, when the strongest effect of the canting angle on polarimetric variables is expected. The canting angle is assumed to be in the polarization plane. The results shown in Fig. 7 indicate that the canting angle mainly affects the backscattering and specific differential phase. The uncertainties become larger with the rain rate due to the larger number of large oblate drops included. At 20 mm h−1 the uncertainties might reach ∼0.5∘ and 0.2∘ km−1 in the backscattering and specific differential phase, respectively. Uncertainties in the other variables are negligibly low. In order to take into account the uncertainties related to the canting angle distribution and also the separation of δ and DP, we added a random Gaussian noise with a standard deviation of 0.5∘ to DP and subtracted the corresponding values from δ. Similarly, a random Gaussian noise with a standard deviation of 0.3 dB was added to DA. All noise values were different for each range bin and each sample. As it will be shown in Sect. 3.6, standard deviations of DP and DA measured for a single spectral line corresponding to the Rayleigh scatterers are typically about 0.3∘ and 0.3 dB, respectively. An averaging over spectral lines, from 0 to 2 m s−1, would reduce the standard deviations by a factor of 3–4. Thus, the assumed uncertainties of 0.5∘ and 0.3 dB are conservative and exceed the actual measurement uncertainties.
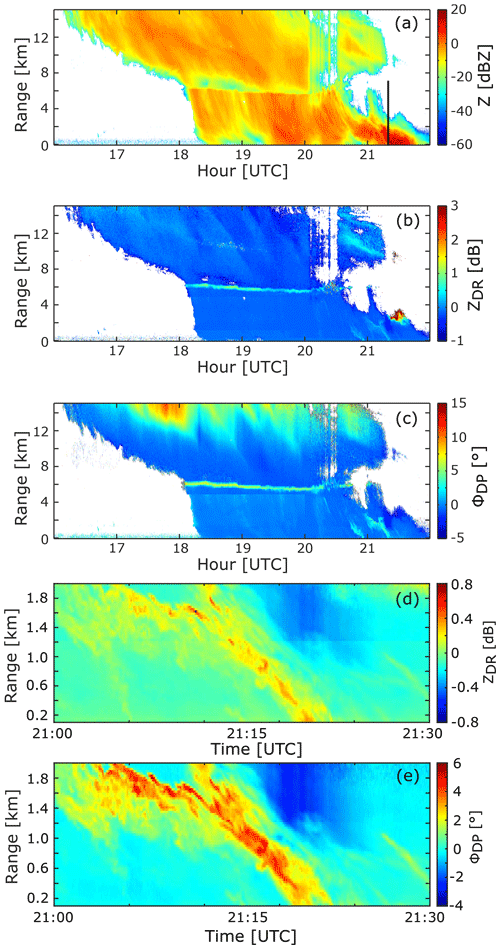
Figure 9Time range cross sections of radar reflectivity (a), differential reflectivity (b), and differential phase (c). Panels (d) and (e) are an enlarged view of the differential reflectivity and differential phase, respectively. The observations were taken by the radar 1 on 9 June 2018 in Meckenheim, Germany. The radar was pointed to a 30∘ elevation. The range corresponds to the slanted distance from the radar. The black vertical line in (a) indicates the time sample used for the spectral analysis shown in Fig. 10.
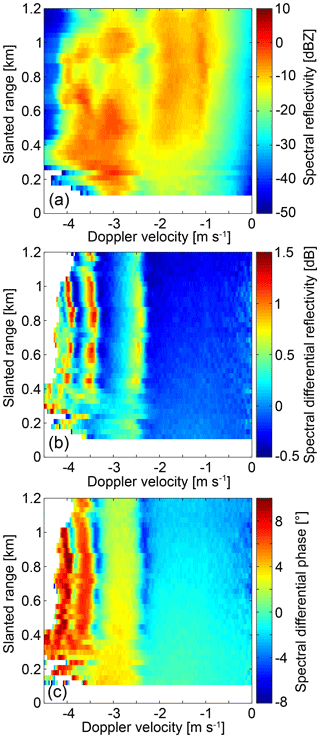
Figure 10Range profiles of Doppler spectra of reflectivity (a), differential reflectivity (b), and differential phase (c). The measurements were taken by radar 1 on 9 June 2018 at 21:19:23 Coordinated Universal Time (UTC) in Meckenheim, Germany. The radar was pointed to a 30∘ elevation. Negative velocities indicate movements towards the radar. Relatively slow (small) drops are on the right side of the spectrum profile, while the fast-falling (big) drops are on the left side. Note that, in order to make the figure easier to interpret, the horizontal wind contribution has been roughly mitigated by shifting the rightmost detected spectral line of a spectrum to 0 m s−1.
The method was tested using the simulated profiles of Z, DA, and DP as input. For each sample, the best estimate of CZ provided by the algorithm was then compared to CZ used for the simulation. The results shown in Fig. 8 show that 90 % of the differences are within ±0.7 dB.
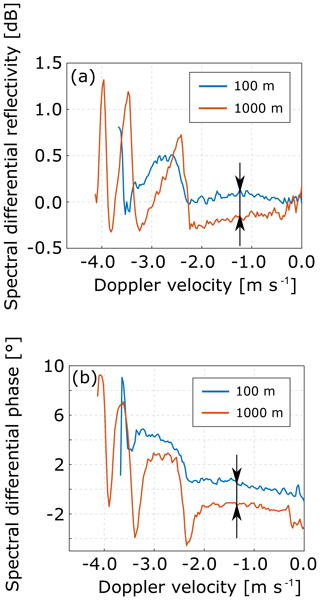
Figure 11Doppler spectra of differential reflectivity (a) and differential phase (b) taken at 0.1 (blue lines) and 1 km (red lines) for the case shown in Fig. 10. The differences between the observations in the area of relatively slow-moving particles, indicated by the arrows, are associated with the propagation effects, namely differential attenuation in (a) and propagation differential phase in (b).
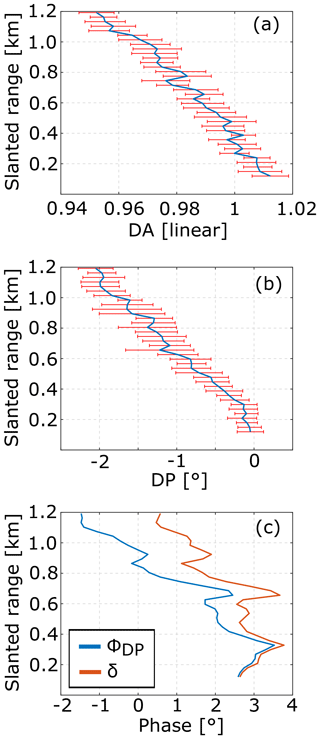
Figure 12Profiles of differential attenuation or DA (a) and differential phase or DP (b), which are solely due to propagational effects. The profiles have been derived using the spectral decomposition technique, illustrated in Fig. 11, applied to the profiles of spectra shown in Fig. 10. Blue lines and red bars indicate mean values and ±1 standard deviation, respectively. Panel (c) shows the profiles of the differential phase ΦDP (blue) and δ (red).
3.6 Application to measurements from radar 1
We now exemplarily demonstrate the different steps of the self-consistency method with a case study. A precipitation event, which includes drizzle and stronger rainfall, was observed at Meckenheim on 9 June 2018, operating the radar at a 30∘ elevation (Fig. 9). The melting layer can be depicted at the height of 2.5 km by enhanced values of ZDR and ΦDP. During the period between 18:00 and 21:00 UTC the rain sensor only registered drizzle on the ground, while later a short and more intense rainfall event with up to 15 mm h−1 rainfall took place. As expected, ZDR and ΦDP are close to zero in the drizzle part due to the near-spherical shape of the drops. Nonzero values are found during the stronger rainfall event due to the larger and, hence, more aspherical raindrops. Around 21:00 UTC positive and negative values in both ZDR and ΦDP are visible. These values indicate presence of backscattering and the propagational effects of raindrops.
Backscattering and propagational effects can be better separated when moving to the Doppler spectral space (Fig. 10). The spectra during the stronger rainfall event show the expected oscillatory behavior for larger Doppler velocities which are principally related to larger sizes. It should be noted that we only applied a very rough correction for horizontal wind as the method itself is not dependent on such a correction. The main goal in the spectral analysis is the separation of the Rayleigh scattering part (only affected by propagational effects) from the Mie scattering part (affected by both backscattering and propagational effects). The spectral part which is not affected by oscillations (approximately Doppler velocities slower than −2 m s−1) shows decreasing values for ZDR and ΦDP, with an increasing range caused by propagational effects (see also spectra plotted for constant ranges in Fig. 11). The reflectivity spectra themselves show a somewhat unexpected increase in range, and also, the oscillations are less pronounced than in the polarimetric variables. This can be explained by the fact that Z is also dependent on the particle concentration.
The spectral regions with oscillatory behavior represent drop sizes for which backscattering and propagational effects are convolved (Fig. 11). In the part where the smaller droplets scatter in the Rayleigh regime, we find a plateau-like region in the spectra of ZDR and ΦDP (Fig. 11). The deviation of the plateau from 0 dB indicates the propagational effects. It should be noted that calibration offsets would, of course, also result in a shifted plateau region; however, this is independent of range. ZDR and ΦDP of radar 1 have been calibrated using zenith observations in light rain, as described in Myagkov et al. (2016a). Vertical observations in light rain show ZDR and ΦDP values of 1.003±0.01 (linear units) and . After proper calibration, we can assign the shift of the plateau region solely to the propagation effects for which we derive mean and standard deviation for each range (Fig. 12). ADP and KDP are found, for this case, to be, on average, about 0.13 dB km−1 and −0.95∘ km−1, respectively.
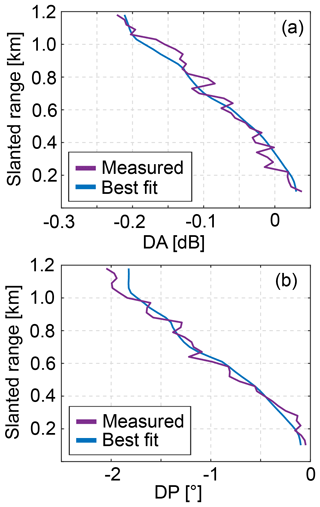
Figure 13Range profiles of DA (a) and DP (b). Blue solid lines correspond to the best fit found by the self-consistency method for radar 1, with dB. The magenta lines represent profiles estimated from the measurements (shown by blue lines in Fig. 12). The results are obtained for the cases shown in Figs. 10 and 12.
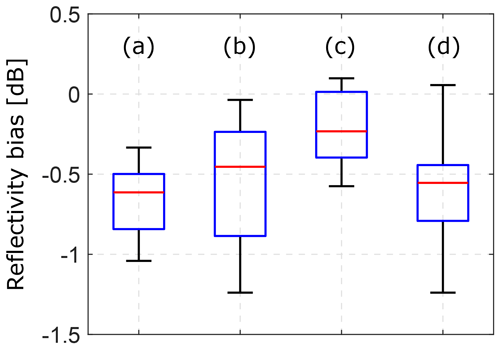
Figure 14Reflectivity biases, due to the calibration coefficient CZ, estimated using the self-consistency method applied to observations at a 30∘ elevation angle during rain events on 9 June 2018 at 21:00 UTC (a), 20 July 2018 at 17:00 UTC (b), and 28 July 2018 at 11:22 UTC (c). The box plot (d) shows the results for all 64 available samples. The measurements were taken with radar 1 at the RPG site. The total number of samples are 45 for (a), 11 for (b), and 8 for (c). The upper and lower edges of the boxes correspond to the 75th and 25th percentiles, respectively. The upper and lower whiskers indicate the 95th and 5th percentiles, respectively. The horizontal red bars correspond to the median values.
In order to estimate a profile of δ, which is used as an input for Eqs. (1) and (2), the profile of DP, shown in Fig. 12b, is subtracted from the profile of ΦDP. Profiles of ΦDP and δ are shown in Fig. 12c.
Figure 13a–b show the best fits for DA and DP profiles found by the optimization algorithm. The resulting best matching radar calibration coefficient for reflectivity CZ has been found for this time sample to be −0.7 dB, meaning that radar 1 slightly underestimates the reflectivity values.
The self-consistency method allows for an evaluation of the radar calibration even from a single sample. In order to test how repeatable the results of the self-consistency method are, we applied the method to 64 samples from three rain events. As shown in previous sections, the self-consistency method relies on propagation variables KDP and ADP, which are used to constrain profiles of Z. If the magnitudes of KDP and ADP are comparable with measurement noise, the method shows larger uncertainties. Using the approach described in Sect. 3.5, we identified the applicability range of the method. In order for the method to produce reasonable results, the rainfall events and associated profiles have to fulfill the following criteria: (1) rain rate observed at the surface by the weather station must be below 20 mm h−1, (2) δ has to be larger than 1∘ over at least a 900 m one-way range, (3) the median KDP must be lower than –0.3 ∘ km−1, and (4) the median ADP must be higher than −0.06 dB km−1. The results shown in Fig. 14 indicate that radar 1 has a small negative reflectivity bias. The mean CZ estimated from the 64 samples is −0.6 dB. The single sample estimate of CZ from the three rain events varies from −1 to 0 dB, which is within the uncertainty of the method estimated in Sect. 3.5. One might see an increasing trend in CZ, but taking into account the method uncertainty of ±0.7 dB and the few cases, the trend is not statistically significant. As will be shown further in the next section, a certain variability in CZ can be explained by imperfections in the removal of liquid water from the radome.
The 30∘ elevation used in this study was chosen, considering the following aspects: (1) the maximum Doppler resolution is obtained with zenith-pointing observations because the projection of the terminal velocity on the radar line of sight is the largest. However, at zenith the required polarimetric variables are close to zero. In the other extreme, (2) at a 0∘ elevation, polarimetric signatures are the strongest, but the projection of the terminal velocity on the radar beam is close to zero. Thus, a 30∘ elevation appears to be a good compromise for spectral polarimetry applications, but a detailed numerical study, which tries to identify the optimal elevation angle for this method, was not performed.
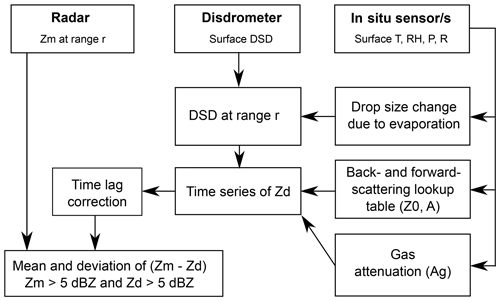
Figure 15Schematic illustration of the extended disdrometer-based method. Detailed descriptions can be found in the text.
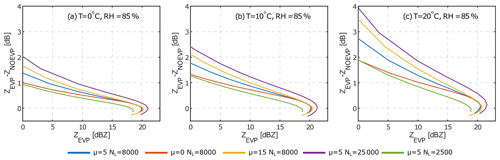
Figure 16Simulated impact of evaporation on the simulated reflectivity at a 250 m range for DSDs measured at the surface. ZNOEVP is the reflectivity at a 250 m range calculated with DSDs assumed at the surface, without taking evaporation into account. ZEVP is the reflectivity at a 250 m range assumed for the same surface rain DSDs but corrected for drop evaporation within the 250 m layer. For the shown evaporation scenario, surface temperature and humidity are assumed to be 10 ∘C and 85 %, respectively. The colors denote simulations with different rain DSD parameters. The effect of bending at ZEVP values around 20 dBZ results from a faster increase in attenuation, with a rain rate relative to nonattenuated reflectivity (Hogan et al., 2003).
The second method is based on a comparison of the measured reflectivities (denoted as Zm) at distances close to the surface with calculated reflectivities based on DSDs observed by colocated disdrometer (Zd hereafter). Values of Zd are calculated according to Appendix A. This well-known approach is generally applicable to radars operating at any frequency; however, the issue of variable rain properties between the lowest range gate and the disdrometer location remains a source of uncertainty. Using radar observations at the lowest range gates also requires that there are no antenna near the field or receiver saturation effects and that wet radome or wet antenna effects are minimized. For a two-antenna system, such as that used for the FMCW systems in this study, the incomplete beam overlap is corrected for using the method in Sekelsky and Clothiaux (2002). At ranges larger than 250 m from the radar, the beam overlap for all radars used is better than 90 %. For the following analysis, we use Zm at a 250 m range. It should be noted that the calculations in this section use altitude and not range; for the slanted path, a conversion of range to altitude has to be applied. In the following, we will describe our approach for mitigating the two main sources of uncertainty for this method in the rainfall cases analyzed. A schematic of the entire processing chain is illustrated in Fig. 15.
4.1 Mitigating the effect of rain evaporation
Evaporation of rain on its way towards the surface is often observed at our sites. Figure 16 shows a simulation of the impact of evaporation on the reflectivity at 250 m. It can be seen that in subsaturated conditions the difference in radar reflectivity caused by evaporation can be strong. The effect is particularly pronounced for light precipitation, where the difference can exceed 2 dB. In this case, the scattering is dominated by relatively small drops whose diameters decrease faster due to evaporation than for big drops. In order to mitigate the effect of evaporation, we use an evaporation model described in Appendix A3. Based on temperature, relative humidity, and drop size at surface level, the model predicts the corresponding drop size at 250 m altitude.
For the calculations of drop sizes at a 250 m altitude, all drops detected by the LPM within 1 min prior to a radar sample time are used. In the case of Parsivel, which typically has a time resolution of 1 min, the data closest to a radar sample time are taken. The LPM in the single event mode provides diameters of single particles, and the evaporation model (Eq. A6) is directly applied to all detected drops. For Parsivel data, the evaporation model is applied to mean bin sizes, and the number of particles per size bin is assumed to be constant with altitude. Note that, in this case, the width of the size bin changes with altitude. This is equivalent to keeping the 32×32 raw data matrix – which is the standard output of Parsivel – constant but changing the mean drop diameters assigned to each matrix cell.
The estimated DSD for 250 m are then used for the calculation of Z0 and A at 250 m, according to Table A5. Since the calculation of the whole attenuation profile with the evaporation effect accounted for is time consuming, A(r) is assumed to be constant and equal to the mean of A values at the surface and at 250 m taken in dB km−1.
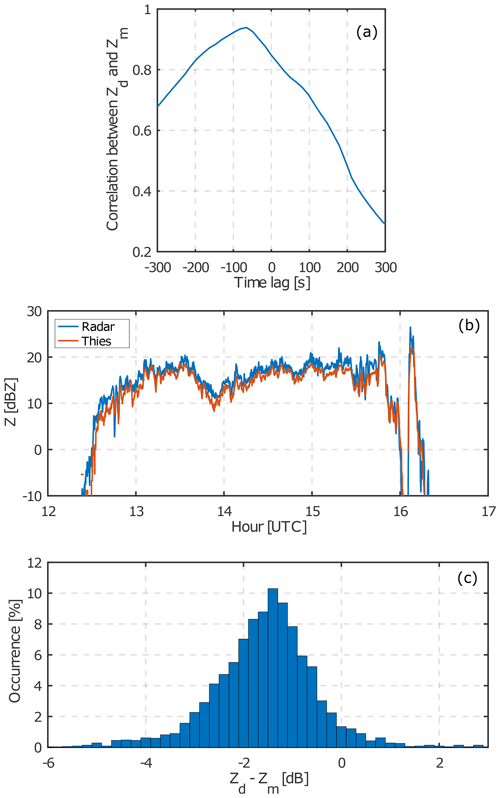
Figure 17Correlation (a) between Zd and Zm at a 250 m distance from the radar for the rain event on 1 November 2018, observed by radar 2. Various time lags are successively applied in order to detect the most likely time delay (maximum correlation) between a 250 m range and surface level. Time series (b) of the reflectivity Zm measured by radar 2 at 250 m altitude (blue line), and the reflectivity Zd modeled from the LPM observations (red line). Panel (c) shows the distribution of Zd−Zm. Only 3 s samples for which Zd and Zm exceed 5 dBZ are used. The mean reflectivity difference is dB. The standard deviation of the mean is calculated according to Appendix C.
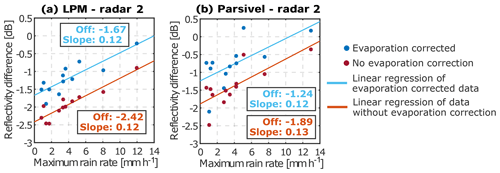
Figure 18The results of the disdrometer-based method from 12 rain events. The calibration evaluation is made for radar 2 using LPM (a) and Parsivel (b). Each dot represents a result for a single rain event. Solid lines show linear regressions. Offsets and slopes of the regressions are given in the corresponding boxes. The colors of the dots and lines indicate whether the evaporation correction has been applied (blue) or not (red).
4.2 Comparison of expected and measured reflectivity time series
In order to identify a potential time lag between Zm and Zd, we calculate their temporal correlation assuming a range of time shifts. The time lag for which the maximum correlation is found is used for correcting the time series, and the difference between Zm and Zd is analyzed. We recommend only using Zm and Zd larger than 5 dBZ because the number of drops sampled by the disdrometer might be too low and not representative for smaller reflectivities.
4.3 Case study
We apply the disdrometer-based method to observations of radar 2 from 1 November 2018. From 12:30 to 16:20 UTC there was light precipitation at the JOYCE-CF site. The mean precipitation rate was 0.5 mm h−1, with a maximum at 4.4 mm h−1. The LPM operated in the particle event mode (see Sect. 2.2). Zd are calculated according to Table A5. To calculate Zd, all drop sizes have been corrected for evaporation. Figure. 17a shows the correlations between Zd and Zm at different time lags. The time shift corresponding to the maximum correlation of 0.93 is −65 s, which is applied to Zd. After correcting for the time lag, Zm and Zd show a high correlation for values exceeding 5 dBZ (Fig. 17b). A direct comparison of Zm and Zd (Figs. 17c) shows that the mean difference in Zd−Zm is −1.2 dBZ, with a standard deviation of 0.3 dBZ (calculated according to Appendix. C).
4.4 Repeatability
In order to check how repeatable the results of the disdrometer-based method are, it was applied to LPM, Parsivel, and radar 2 observations in 12 rain events collected during the TRIPEX-pol campaign from 1 November 2018 to 6 December 2018. The same rain events are shown in Fig. 3. In the Supplement, we provide figures similar to Fig. 17 and statistical analysis for each rain event.
Figure 18 shows the reflectivity differences Zd−Zm for radar 2. The blue dots were calculated according to Sect. 4.1, while red dots were calculated without taking evaporation into account. Evaporation leads, on average, to about a 0.7 dB underestimation in Zd, which might be critical if a reflectivity accuracy within ±1 dB is desired.
In Fig. 18 the differences in Zd−Zm are shown as functions of maximum rain rate observed by the disdrometers. At rain rates lower than 4 mm h−1, values of Zd−Zm vary from −2 to −0.9 dB and from −2.1 to −0.5 dB, with mean values of −1.4 and −1.1 dB based on LPM and Parsivel (blue dots in Fig. 18a and c), respectively. On average, reflectivity values based on Parsivel observations are about 0.3 dB larger than those from LPM. The reason for this difference is likely related to the specific differences in the disdrometers; however, a detailed analysis of such differences is beyond the scope of this study. A comprehensive comparison of LPM and Parsivel disdrometers can be found, for example, in Angulo-Martínez et al. (2018) and Johannsen et al. (2020).
The results for both disdrometers indicate a dependence of the calibration offset on maximum rain rate observed during a precipitation event. Since the slope of the linear regressions is similar with and without the evaporation correction, we conclude that this effect may come from limitations in the rain mitigation system. However, the radome attenuation effects would certainly be much larger without a mitigation system. As shown by Hogan et al. (2003), those effects can easily exceed 10 dB for strong rainfall.
4.5 Comparison with the self-consistency method
As has been shown in the previous section, the comparison of radar 2 observations with LPM and Parsivel shows that the radar, on average, overestimates the reflectivity by 1.4 and 1.1 dB, respectively. The calibration of radar 1 was estimated using the self-consistency methods and indicates that the radar underestimates the reflectivity by 0.7 dB.
During the TRIPEX-pol campaign, radar 1 and radar 2 were operating at the JOYCE-CF site. Radar 1 was performing range–height indicator (RHI) and plan-position indicator (PPI) scans. As mentioned in Sect. 4.5, the disdrometer-based method does not often show consistent results when applied to scanning data. Nevertheless, radar 1 performed a PPI scan at a 85∘ elevation every 15 min. Therefore, we used vertical observations from radar 2 and the PPI scans from radar 1 to find a reflectivity difference between radars 1 and 2. The difference can be used to check the consistency of the two calibration evaluation methods. During the 12 rain events we identified more than 8000 samples for the comparison. For each sample of radar 1, a closest time sample of radar 2 was found. Within each sample, we identified the closest range bins with reflectivity values exceeding 5 dBZ. Radar 2 shows, on average, 2.1 dB higher reflectivity values in comparison to radar 1. This value is consistent with the difference of 2.0±1.3 dB between the biases found by the two methods separately for radars 1 and 2.
Monitoring and evaluation of radar reflectivity calibration is a key requirement in order to provide long-term observational radar data sets to the cloud and precipitation community. In this study, we describe and compare two methods requiring very different degrees of complexity in terms of instrumentation and retrieval technique. Both methods use natural stratiform rainfall as the reference target.
The first method is an extension of the widely used approach from Goddard et al. (1994) applied to precipitation radars. The original method uses the relation, but due to the more complex attenuation and scattering behavior, this method is not directly applicable to millimeter wavelengths. In this study, we provide a solution for this problem using spectral polarimetry obtained from a W-band radar. The use of the spectral information allows us to disentangle propagational and backscattering effects. The method requires observations of ZDR and ΦDP and is only applicable to slanted observations in rain with distinct backscattering and propagational polarimetric signatures. The backscattering differential phase should mostly exceed 1∘. The differential attenuation and specific differential phase should preferably be higher than 0.06 dB km−1 and lower than −0.3∘ km−1, respectively. The main advantage of this method is its low sensitivity to variabilities in rain DSD. We estimated the uncertainty of this method based on realistic assumptions of errors in the profiles of radar observables to be within ±0.7 dB.
We also tested and extended a much simpler and more commonly used method, which compares reflectivities based on disdrometer DSDs measured at the surface with radar reflectivity at a close range gate. We included corrections for the time lag between the surface and elevated observations and a correction for evaporation. The method allows for a repeatable evaluation of the radar reflectivity calibration within ±0.9 dB, even with only a few hours of observations in rain with intensity below 4 mm h−1. Averaging over a larger number of rain events allows us to further reduce the uncertainties of the method. The disdrometer-based method was tested with two common disdrometers of the LPM and Parsivel type. The results do not differ by more than 0.4 dB.
The two methods were used to evaluate the reflectivity calibration of two W-band radars. The self-consistency method showed that radar 1 underestimates the reflectivity by about 0.7±0.7 dB, while the disdrometer-based method indicated that radar 2 overestimates the reflectivity by 0.5–2.1 dB. Unfortunately, the rainfall rates during the parallel operation of the two radars at JOYCE-CF were not strong enough to compare the two methods directly. However, in case both methods provide reliable estimates for each radar, the reflectivity difference seen by both radars should be close to the sum of both offsets. Indeed, the observed reflectivity difference is, with 2.1 dB, quite consistent with the difference of 2.0±1.3 dB between the biases found separately by the two methods for radars 1 and 2. The derived calibration factors can be used to monitor the radar stability and to correct the observed reflectivity values, although we would also like to emphasize that a further evaluation of the two methods described here with other methods, e.g., using point target calibration or multi-frequency approach (Tridon et al., 2017) would be beneficial.
As wet radomes of W-band radar can cause attenuation exceeding 10 dB, the evaluation methods rely on efficient rain mitigation. We have found evidence that the reflectivity bias of the used radars is correlated to the maximum rain rate, and the slope of the linear regression is about 0.15 dB mm h−1. The uncertainty of the used rain mitigation method is much smaller than the uncertainties and wet antenna effects reported by (Hogan et al., 2003). Further investigations on this topic are required in order to understand the effects limiting the performance of the rain mitigation systems used.
Summarizing the results, we recommend the disdrometer-based method for continuous monitoring of cloud radar calibration. Many operational sites are already equipped with disdrometers, which allows for a straightforward application of the technique. The method can be applied to both vertical and slanted observations, though continuous scanning may limit the applicability of the method. The extended consistency method is less sensitive to DSD variability and also allows calibration evaluation if only a few rainfall cases are available. Both methods can analogously be derived for Ka-band systems.
The radar reflectivity factor Z along a path of rainfall with constant properties can be calculated as follows:
where Z0 (dBZ) is the nonattenuated reflectivity, A (dB km−1) is the one-way attenuation by rain, Ag (dB km−1) is one-way gas attenuation, and r is in kilometers. The factor of 2 is related to the two-way propagation.
Table A1Coefficients a1−10 for the ratio KDP∕Z0 in Eq. (1). The coefficients were calculated for a 30∘ elevation.
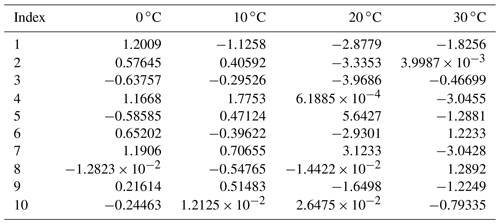
Table A2Coefficients b1−10 for the ratio ADP∕A in Eq. (2). The coefficients were calculated for a 30∘ elevation.
A1 Nonattenuated reflectivity and attenuation by rain
For the DSD of rain, we assume the widely used normalized gamma distribution (Illingworth and Blackman, 2002) as follows:
where , D is the equivalent sphere diameter in millimeters, D0 is the median volume diameter in mm, NL is the concentration parameter in mm−1 m−3, and μ is the distribution shape parameter. For numerical calculations, we discretized the DSD, with Di describing the mean diameter and Ni denoting the drop number of the ith size bin. Di are equidistant from 10−2 up to 8 mm, with a constant bin width of 10−2 mm.
We approximate raindrops with oblate spheroids. The shape–size relation was taken from Pruppacher and Pitter (1971). Based on video disdrometer observations, Huang et al. (2008) showed that raindrops are mostly aligned horizontally, with a canting angle standard deviation of 8∘. Aydin and Lure (1991) showed that this fluttering of drop orientation has a relatively small effect at 94 GHz. Even for the reflectivity difference between horizontal and vertical polarization for which one expects the effect of particle orientation to be maximum, the differences do not exceed 0.12 dB for rainfall rates up to 150 mm h−1. In the following calculations, we therefore assume the raindrops to be horizontally aligned.
We calculate backscattering Sjk(Di) and forward-scattering Fjk(Di) coefficients using the T-matrix method (Mishchenko, 2000). Here, indices j and k stand for the polarization of transmitted and received waves, respectively. The temperature dependence of the refractive index of liquid water is taken from Ray (1972). Using Shh(Di) and Fhh(Di), the nonattenuated reflectivity Zi in mm6 m−3 and specific one-way attenuation due to liquid water Ai in dB km−1 for one drop with the diameter Di per unit volume are calculated with the following:
where is the dielectric factor of liquid water, λ is the wavelength, and k is the wave number.
The final rainfall rate, reflectivity, and one-way attenuation are calculated as the sum over the DSD. The equations used for the different in situ instruments are summarized in Table A5.
A2 Gas attenuation
Unlike for longer wavelength radars (e.g., precipitation radars), gas attenuation cannot be neglected for the W band. The major contributions to gas attenuation at the W band are due to water vapor and oxygen, which we calculate with the model by Liebe (1989). As continuous profile information of temperature, water vapor, and pressure are unavailable at the RPG site and JOYCE-CF, we use the surface measurements of the weather station to approximate the vertical profiles. For the temperature profile, we use a constant empirical lapse rate Kt. Based on the radiosonde database from Essen (station no. 10410; 90 km from Meckenheim; 75 km from Jülich), the lapse rate Kt was estimated to be K m−1. The launches from 1 January 2010 to 23 October 2018 with surface relative humidity exceeding 65 % were used. For the Kt estimation, only the lowest 3 km of radiosonde ascends were taken. Relative humidity is assumed to be constant with height. The statistics of the calculated one-way gas attenuation profiles are shown in Fig. A1.
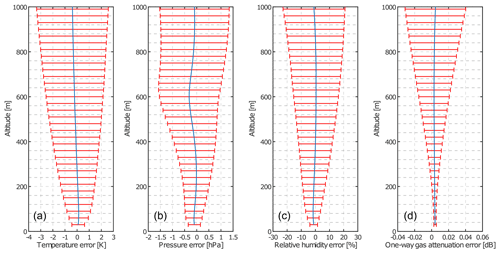
Figure A1Uncertainties in the derived profiles of temperature (a), pressure (b), relative humidity (c), and one-way gas attenuation (d) when using only surface values from a weather station. The uncertainties have been estimated with a large set of radiosonde profiles restricted to a minimum surface relative humidity of 65%. The blue lines and the red bars show mean and ± 1 standard deviation of the corresponding difference, respectively.
A3 Drop evaporation
Xie et al. (2016) showed that a change in the drop size due to evaporation can be derived from the following equation:
where D and v are the diameter and velocity of a drop, respectively, H is a vertical range traveled by the drop, S−1 is the supersaturation with respect to liquid water, and FK and FD are coefficients related to heat conduction and vapor diffusion, respectively. The calculation of FK and FD is based on Kumjian and Ryzhkov (2010).
Equation (A5) relates an initial drop size at a certain altitude to the drop size at the surface. The disdrometer-based method requires an opposite relation; i.e., what would the drop size be at a 250 m altitude if its size at the surface is known? The relation can also be found by solving Eq. (A5). The equation is solved numerically for surface diameters Ds from 0.06 to 3 mm, with a grid of 0.01 mm, using an iterative approach. Large drops are less influenced by evaporation (Xie et al., 2016); therefore, for drops larger than 3 mm, the size change is neglected. The surface drop size is taken as the first guess of the drop size at 250 m D250. Using Eq. (A5), the corresponding size at the surface Dsm is calculated and compared with Ds. In case the difference is smaller than 0.01 mm, D250 is taken as the solution for corresponding Ds. If the difference is larger, D250 is changed until the condition is satisfied. For a minimization of the difference, the differential evolution method (Das et al., 2009) is applied, although any other optimization algorithm can be also used. Even though the convergence for a single size is fast, the application of such evaporation correction to a number of sizes and different environment conditions is time consuming. Therefore, a set of precalculated Ds–D250 relations at surface temperatures from 0 to 20 ∘C, with the 5 ∘C step, and surface relative humidity from 60 % to 100 %, with the 5 % step at the 1000 hPa surface pressure, is used for the Ds–D250 function approximation as follows:
where D250 and Ds are in millimeters, T is in degrees Celsius and has to be in the range from 0 to 30 ∘C, and RH is in percent and should be in the range from 60 % to 100 %. The coefficients g, p, q, u, and α are given in Table A4, β=20.038. For the given ranges of the input parameters, the root mean square difference between the simulated and approximated values of D250 is 5.8 µm. In the Supplement, we provide a MATLAB and Octave function for Eq. (A6).
Table A3Coefficients c1−17 for A in Eq. (3). The coefficients were calculated for a 30∘ elevation.
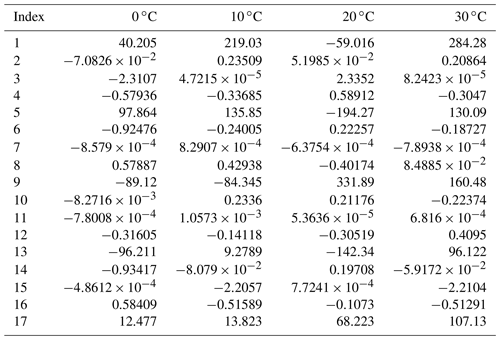
Table A5Summary of calculation formulas for rain rate, reflectivity, and attenuation for the normalized gamma DSD, DSD from Parsivel, and drops detected by LPM. For the normalized gamma DSD and Parsivel, the index i ranges over n diameter bins, while for LPM it varies over n drops detected by the instrument 1 min prior to a radar sample time. The index j moves over m velocity bins of Parsivel. Ci,j is the cell of the Parsivel raw data matrix. Ni is a number of particles in the diameter bin i. Vi and vi are volume in cubic meters and terminal velocity in meters per second of a drop with the diameter Di, respectively. Zi and Ai are reflectivity and attenuation for one drop, with the diameter Di in a unit volume, respectively. is the effective sampling area in square meters of a disdrometer, with Lb and Wb being the length and the width of the disdrometer laser beam (Tokay et al., 2014). is the dielectric factor of water at a certain temperature. is the constant dielectric factor of water at 8∘C set in the processing routine of the used radars.

The T-matrix calculations are also used to derive polarimetric variables such as backscattering differential reflectivity zDR (dB), backscattering differential phase δ (∘), one-way differential attenuation ADP (dB km−1), and specific differential phase KDP (∘ km−1) as follows:
where ∗ denotes the complex conjugation.
Differential reflectivity ZDR(r) (dB) and differential phase ΦDP(r) (∘) at a certain range r (km) from the radar are the sum of corresponding backscattering and propagational components as follows:
where DA and DP are propagation components in differential reflectivity and differential phase, respectively.
A variance (denoted as var) of an average of Ns samples can be found as follows:
where cov stands for covariance, s is a sample with a lag is indicated by the subscripts i and j. The covariance cov(si,sj) is calculated as a multiplication of the standard deviations of the corresponding variables and their correlation. Assuming that the analyzed process is stationary with the standard deviation σs, cov(si,sj) can be written as follows:
Here ρτ is the normalized autocovariance function at the lag . Substituting Eq. (C2) into Eq. (C1) as follows:
A similar relation for analytic functions was derived by Leith (1973). In the case of uncorrelated samples, the normalized autocovariance function is a delta function, the double sum in Eq. (C3) is equal to Ns, and the variance can be found using the well-known relation . This relation is widely used in the weather radar community to improve the signal detection (Eq. 5.193 in Bringi and Chandrasekar, 2001; Görsdorf et al., 2015). In contrast, when all the samples are highly correlated within the averaging period, the double sum is equal to , and as expected, the variance of the average does not change. In the general case, when the analyzed process has a certain coherency time, the variance is within the range between and .
The supplement related to this article is available online at: https://doi.org/10.5194/amt-13-5799-2020-supplement.
AM developed and tested the self-consistency method. AM and SK added the time lag and evaporation corrections to the disdrometer-based method. SK organized the TRIPEX-pol measurement campaign. AM applied the disdrometer-based method. AM and SK evaluated the results of the calibration evaluation. AM and SK prepared the paper. TR developed the scanning polarimetric W-band radar and reviewed the paper.
Stefan Kneifel has no competing interests. Alexander Myagkov and Thomas Rose are employees of Radiometer Physics GmbH.
We would like to acknowledge Juan-Antonio Bravo Aranda, University of Granada, for providing the vertically pointed LDR-mode W-band radar for the TRIPEx-pol campaign. We also acknowledge the staff at RPG and the University of Cologne research center in Jülich, especially Birger Bohn, Rainer Haseneder-Lind, and Avdulah Saljihi for their help with the installation of the W-band radars, and Kai Schmidt for the preparation of the scanning polarimetric W-band radar for the TRIPEx-pol campaign.
Radiometer Physics GmbH funded the contribution of Alexander Myagkov and Thomas Rose, provided the Radar 1 for the TRIPEX-pol campaign, and covered publication fees. The contributions by Stefan Kneifel have been funded by the Deutsche Forschungsgemeinschaft (DFG – German Research Foundation; grant no. KN 1112/2-1) as part of the Emmy Noether Research Group of OPTIMIce. The TRIPEX-pol campaign has also been supported by the DFG Priority Program (SPP 2115) under the Fusion of Radar Polarimetry and Numerical Atmospheric Modelling Towards an Improved Understanding of Cloud and Precipitation Processes (PROM) project (grant no. 408011764).
This paper was edited by Alexis Berne and reviewed by two anonymous referees.
Acquistapace, C., Kneifel, S., Löhnert, U., Kollias, P., Maahn, M., and Bauer-Pfundstein, M.: Optimizing observations of drizzle onset with millimeter-wavelength radars, Atmos. Meas. Tech., 10, 1783–1802, https://doi.org/10.5194/amt-10-1783-2017, 2017. a
Alku, L., Moisseev, D., Aittomäki, T., and Chandrasekar, V.: Identification and Suppression of Nonmeteorological Echoes Using Spectral Polarimetric Processing, IEEE Trans. Geosci. Remote Sens., 53, 3628–3638, https://doi.org/10.1109/TGRS.2014.2380476, 2015. a
Angulo-Martínez, M., Beguería, S., Latorre, B., and Fernández-Raga, M.: Comparison of precipitation measurements by OTT Parsivel2 and Thies LPM optical disdrometers, Hydrol. Earth Syst. Sci., 22, 2811–2837, https://doi.org/10.5194/hess-22-2811-2018, 2018. a, b, c, d
Atlas, D.: RADAR CALIBRATION, B. Am. Meteorol. Soc., 83, 1313–1316, https://doi.org/10.1175/1520-0477-83.9.1313, 2002. a
Aydin, K. and Lure, Y.-M.: Millimeter wave scattering and propagation in rain – A computational study at 94 and 140 GHz for oblate spheroidal and spherical raindrops, IEEE Trans. Geosci. Remote Sens., 29, 593–601, https://doi.org/10.1109/36.135821, 1991. a, b, c, d
Basara, J. B., Illston, B. G., Winning, Jr., T. E., and Fiebrich, C. A.: Evaluation of Rainfall Measurements from the WXT510 Sensor for Use in the Oklahoma City Micronet, The Open Atmos. Sci. J., 3, 39–47, https://doi.org/10.2174/1874282300903010039, 2009. a
Borque, P., Luke, E., and Kollias, P.: On the unified estimation of turbulence eddy dissipation rate using Doppler cloud radars and lidars, J. Geophys. Res.-Atmos., 121, 5972–5989, https://doi.org/10.1002/2015JD024543, 2016. a
Bouniol, D., Protat, A., Delanoë, J., Pelon, J., Piriou, J.-M., Bouyssel, F., Tompkins, A. M., Wilson, D. R., Morille, Y., Haeffelin, M., O'Connor, E. J., Hogan, R. J., Illingworth, A. J., Donovan, D. P., and Baltink, H.-K.: Using Continuous Ground-Based Radar and Lidar Measurements for Evaluating the Representation of Clouds in Four Operational Models, J. Appl. Meteorol. Climatol., 49, 1971–1991, https://doi.org/10.1175/2010JAMC2333.1, 2010. a
Bringi, V. N. and Chandrasekar, V.: Polarimetric Doppler Weather Radar, Cambridge University Press, Cambridge, 2001. a, b, c, d
Bühl, J., Leinweber, R., Görsdorf, U., Radenz, M., Ansmann, A., and Lehmann, V.: Combined vertical-velocity observations with Doppler lidar, cloud radar and wind profiler, Atmos. Meas. Tech., 8, 3527–3536, https://doi.org/10.5194/amt-8-3527-2015, 2015. a
Bühl, J., Seifert, P., Myagkov, A., and Ansmann, A.: Measuring ice- and liquid-water properties in mixed-phase cloud layers at the Leipzig Cloudnet station, Atmos. Chem. Phys., 16, 10609–10620, https://doi.org/10.5194/acp-16-10609-2016, 2016. a
Chandrasekar, V., Baldini, L., Bharadwaj, N., and Smith, P. L.: Calibration procedures for global precipitation-measurement ground-validation radars, URSI Radio Sci. Bull., 2015, 45–73, 2015. a, b, c, d, e
Das, S., Abraham, A., Chakraborty, U. K., and Konar, A.: Differential Evolution Using a Neighborhood-Based Mutation Operator, IEEE Trans. Evolut. Comput., 13, 526–553, https://doi.org/10.1109/TEVC.2008.2009457, 2009. a, b
Delanoë, J., Protat, A., Vinson, J.-P., Brett, W., Caudoux, C., Bertrand, F., Parent du Chatelet, J., Hallali, R., Barthes, L., Haeffelin, M., and Dupont, J.-C.: BASTA: A 95-GHz FMCW Doppler Radar for Cloud and Fog Studies, J. Atmos. Ocean. Technol., 33, 1023–1038, https://doi.org/10.1175/JTECH-D-15-0104.1, 2016. a
Demuth, H. B., Beale, M. H., De Jess, O., and Hagan, M. T.: Neural Network Design, Martin Hagan, Stillwater, OK, USA, 2nd Edn., 2014. a
Dias Neto, J., Kneifel, S., Ori, D., Trömel, S., Handwerker, J., Bohn, B., Hermes, N., Mühlbauer, K., Lenefer, M., and Simmer, C.: The TRIple-frequency and Polarimetric radar Experiment for improving process observations of winter precipitation, Earth Syst. Sci. Data, 11, 845–863, https://doi.org/10.5194/essd-11-845-2019, 2019. a
Dufournet, Y. and Russchenberg, H. W. J.: Towards the improvement of cloud microphysical retrievals using simultaneous Doppler and polarimetric radar measurements, Atmos. Meas. Tech., 4, 2163–2178, https://doi.org/10.5194/amt-4-2163-2011, 2011. a
Ewald, F., Groß, S., Hagen, M., Hirsch, L., Delanoë, J., and Bauer-Pfundstein, M.: Calibration of a 35 GHz airborne cloud radar: lessons learned and intercomparisons with 94 GHz cloud radars, Atmos. Meas. Tech., 12, 1815–1839, https://doi.org/10.5194/amt-12-1815-2019, 2019. a, b
Foote, G. B. and Du Toit, P. S.: Terminal Velocity of Raindrops Aloft, J. Appl. Meteorol., 8, 249–253, https://doi.org/10.1175/1520-0450(1969)008<0249:TVORA>2.0.CO;2, 1969. a
Frech, M., Hagen, M., and Mammen, T.: Monitoring the Absolute Calibration of a Polarimetric Weather Radar, J. Atmos. Ocean. Technol., 34, 599–615, https://doi.org/10.1175/JTECH-D-16-0076.1, 2017. a
Frisch, S., Shupe, M., Djalalova, I., Feingold, G., and Poellot, M.: The Retrieval of Stratus Cloud Droplet Effective Radius with Cloud Radars, J. Atmos. Ocean. Technol., 19, 835, https://doi.org/10.1175/1520-0426(2002)019<0835:TROSCD>2.0.CO;2, 2002. a
Gage, K. S., Clark, W. L., Williams, C. R., and Tokay, A.: Determining reflectivity measurement error from serial measurements using paired disdrometers and profilers, Geophys. Res. Lett., 31, L23107, https://doi.org/10.1029/2004GL020591, 2004. a
Goddard, J. W. F., Tan, J., and Thurai, M.: Technique for calibration of meteorological radars using differential phase, Electro. Lett., 30, 166–167, https://doi.org/10.1049/el:19940119, 1994. a, b, c, d, e, f, g
Görsdorf, U., Lehmann, V., Bauer-Pfundstein, M., Peters, G., Vavriv, D., Vinogradov, V., and Volkov, V.: A 35-GHz polarimetric Doppler radar for long term observations of cloud parameters – Description of system and data processing, J. Atmos. Ocean. Technol., 32, 675–690, https://doi.org/10.1175/JTECH-D-14-00066.1, 2015. a, b
Gorgucci, E., Scarchilli, G., and Chandrasekar, V.: Calibration of radars using polarimetric techniques, IEEE Trans. Geosci. Remote Sens., 30, 853–858, https://doi.org/10.1109/36.175319, 1992. a
Haeffelin, M., Barthès, L., Bock, O., Boitel, C., Bony, S., Bouniol, D., Chepfer, H., Chiriaco, M., Cuesta, J., Delanoë, J., Drobinski, P., Dufresne, J.-L., Flamant, C., Grall, M., Hodzic, A., Hourdin, F., Lapouge, F., Lemaître, Y., Mathieu, A., Morille, Y., Naud, C., Noël, V., O'Hirok, W., Pelon, J., Pietras, C., Protat, A., Romand, B., Scialom, G., and Vautard, R.: SIRTA, a ground-based atmospheric observatory for cloud and aerosol research, Ann. Geophys., 23, 253–275, https://doi.org/10.5194/angeo-23-253-2005, 2005. a
Heymsfield, A. J., Protat, A., Austin, R. T., Bouniol, D., Hogan, R. J., Delanoë, J., Okamoto, H., Sato, K., van Zadelhoff, G.-J., Donovan, D. P., and Wang, Z.: Testing IWC Retrieval Methods Using Radar and Ancillary Measurements with In Situ Data, J. Appl. Meteorol. Climatol., 47, 135, https://doi.org/10.1175/2007JAMC1606.1, 2008. a
Hirsikko, A., O'Connor, E. J., Komppula, M., Korhonen, K., Pfüller, A., Giannakaki, E., Wood, C. R., Bauer-Pfundstein, M., Poikonen, A., Karppinen, T., Lonka, H., Kurri, M., Heinonen, J., Moisseev, D., Asmi, E., Aaltonen, V., Nordbo, A., Rodriguez, E., Lihavainen, H., Laaksonen, A., Lehtinen, K. E. J., Laurila, T., Petäjä, T., Kulmala, M., and Viisanen, Y.: Observing wind, aerosol particles, cloud and precipitation: Finland's new ground-based remote-sensing network, Atmos. Meas. Tech., 7, 1351–1375, https://doi.org/10.5194/amt-7-1351-2014, 2014. a
Hogan, R. J., Bouniol, D., Ladd, D. N., O'Connor, E. J., and Illingworth, A. J.: Absolute Calibration of 94/95-GHz Radars Using Rain, J. Atmos. Ocean. Technol., 20, 572, https://doi.org/10.1175/1520-0426(2003)20<572:ACOGRU>2.0.CO;2, 2003. a, b, c, d, e, f, g, h, i, j
Hogan, R. J., Mittermaier, M. P., and Illingworth, A. J.: The Retrieval of Ice Water Content from Radar Reflectivity Factor and Temperature and Its Use in Evaluating a Mesoscale Model, J. Appl. Meteorol. Climatol., 45, 301–317, https://doi.org/10.1175/JAM2340.1, 2006. a
Huang, G.-J., Bringi, V. N., and Thurai, M.: Orientation Angle Distributions of Drops after an 80-m Fall Using a 2D Video Disdrometer, J. Atmos. Ocean. Technol., 25, 1717, https://doi.org/10.1175/2008JTECHA1075.1, 2008. a, b
Huuskonen, A. and Holleman, I.: Determining Weather Radar Antenna Pointing Using Signals Detected from the Sun at Low Antenna Elevations, J. Atmos. Ocean. Technol., 24, 476, https://doi.org/10.1175/JTECH1978.1, 2007. a
Illingworth, A. J. and Blackman, T. M.: The Need to Represent Raindrop Size Spectra as Normalized Gamma Distributions for the Interpretation of Polarization Radar Observations., J. Appl. Meteorol., 41, 286–297, https://doi.org/10.1175/1520-0450(2002)041<0286:TNTRRS>2.0.CO;2, 2002. a
Illingworth, A. J., Hogan, R. J., O'Connor, E. J., Bouniol, D., Delanoë, J., Pelon, J., Protat, A., Brooks, M. E., Gaussiat, N., Wilson, D. R., Donovan, D. P., Baltink, H. K., van Zadelhoff, G.-J., Eastment, J. D., Goddard, J. W. F., Wrench, C. L., Haeffelin, M., Krasnov, O. A., Russchenberg, H. W. J., Piriou, J.-M., Vinit, F., Seifert, A., Tompkins, A. M., and Willén, U.: Cloudnet, B. Am. Meteorol. Soc., 88, 883–898, https://doi.org/10.1175/BAMS-88-6-883, 2007. a, b
Johannsen, L. L., Zambon, N., Strauss, P., Dostal, T., Neumann, M., Zumr, D., Cochrane, T. A., Blöschl, G., and Klik, A.: Comparison of three types of laser optical disdrometers under natural rainfall conditions, Hydrol. Sci. J., 65, 524–535, https://doi.org/10.1080/02626667.2019.1709641, 2020. a
Kalesse, H., Szyrmer, W., Kneifel, S., Kollias, P., and Luke, E.: Fingerprints of a riming event on cloud radar Doppler spectra: observations and modeling, Atmos. Chem. Phys., 16, 2997–3012, https://doi.org/10.5194/acp-16-2997-2016, 2016. a
Kneifel, S., von Lerber, A., Tiira, J., Moisseev, D., Kollias, P., and Leinonen, J.: Observed relations between snowfall microphysics and triple-frequency radar measurements, J. Geophys. Res.-Atmos., 120, 6034–6055, https://doi.org/10.1002/2015JD023156, 2015. a
Kochendorfer, J., Nitu, R., Wolff, M., Mekis, E., Rasmussen, R., Baker, B., Earle, M. E., Reverdin, A., Wong, K., Smith, C. D., Yang, D., Roulet, Y.-A., Buisan, S., Laine, T., Lee, G., Aceituno, J. L. C., Alastrué, J., Isaksen, K., Meyers, T., Brækkan, R., Landolt, S., Jachcik, A., and Poikonen, A.: Analysis of single-Alter-shielded and unshielded measurements of mixed and solid precipitation from WMO-SPICE, Hydrol. Earth Syst. Sci., 21, 3525–3542, https://doi.org/10.5194/hess-21-3525-2017, 2017. a
Kollias, P., Albrecht, B. A., and Marks, F.: Why Mie?, B. Am. Meteorol. Soc., 83, 1471–1484, https://doi.org/10.1175/BAMS-83-10-1471, 2002. a
Kollias, P., Clothiaux, E. E., Miller, M. A., Albrecht, B. A., Stephens, G. L., and Ackerman, T. P.: Millimeter-Wavelength Radars: New Frontier in Atmospheric Cloud and Precipitation Research, B. Am. Meteorol. Soc., 88, 1608–1624, https://doi.org/10.1175/BAMS-88-10-1608, 2007. a
Kollias, P., Puigdomènech Treserras, B., and Protat, A.: Calibration of the 2007–2017 record of Atmospheric Radiation Measurements cloud radar observations using CloudSat, Atmos. Meas. Tech., 12, 4949–4964, https://doi.org/10.5194/amt-12-4949-2019, 2019. a, b, c
Küchler, N., Kneifel, S., Löhnert, U., Kollias, P., Czekala, H., and Rose, T.: A W-Band Radar-Radiometer System for Accurate and Continuous Monitoring of Clouds and Precipitation, J. Atmos. Ocean. Technol., 34, 2375–2392, https://doi.org/10.1175/JTECH-D-17-0019.1, 2017. a, b
Kumjian, M. R.: Principles and Applications of Dual-Polarization Weather Radar. Part I: Description of the Polarimetric Radar Variables, J. Operational Meteor., 1, 226–242, https://doi.org/10.15191/nwajom.2013.0119, 2013. a
Kumjian, M. R. and Ryzhkov, A. V.: The impact of evaporation on polarimetric characteristics of rain: Theoretical model and practical implications, J. Appl. Meteorol. Climatol., 49, 1247–1267, https://doi.org/10.1175/2010JAMC2243.1, 2010. a
Leinonen, J., Moisseev, D., and Nousiainen, T.: Linking snowflake microstructure to multi-frequency radar observations, J. Geophys. Res.-Atmos., 118, 3259–3270, https://doi.org/10.1002/jgrd.50163, 2013. a
Leith, C. E.: The Standard Error of Time-Average Estimates of Climatic Means, J. Appl. Meteorol., 12, 1066–1069, https://doi.org/10.1175/1520-0450(1973)012<1066:TSEOTA>2.0.CO;2, 1973. a
Li, H. and Moisseev, D.: Melting Layer Attenuation at Ka- and W-Bands as Derived From Multifrequency Radar Doppler Spectra Observations, J. Geophys. Res.-Atmos., 124, 9520–9533, https://doi.org/10.1029/2019JD030316, 2019. a
Liebe, H. J.: MPM – An atmospheric millimeter-wave propagation model, Int. J. Infra. Milli. Waves, 10, 631–650, https://doi.org/10.1007/BF01009565, 1989. a
Löffler-Mang, M. and Blahak, U.: Estimation of the Equivalent Radar Reflectivity Factor from Measured Snow Size Spectra, J. Appl. Meteorol., 40, 843–849, https://doi.org/10.1175/1520-0450(2001)040<0843:EOTERR>2.0.CO;2, 2001. a
Löffler-Mang, M. and Joss, J.: An Optical Disdrometer for Measuring Size and Velocity of Hydrometeors, J. Atmos. Ocean. Technol., 17, 130, https://doi.org/10.1175/1520-0426(2000)017<0130:AODFMS>2.0.CO;2, 2000. a, b
Löhnert, U., Schween, J. H., Acquistapace, C., Ebell, K., Maahn, M., Barreraverdejo, M., Hirsikko, A., Bohn, B., Knaps, A., O'connor, E., Simmer, C., Wahner, A., and Crewell, S.: JOYCE: Jülich observatory for cloud evolution, B. Am. Meteorol. Soc., 96, 1157–1174, https://doi.org/10.1175/BAMS-D-14-00105.1, 2015. a, b
Maahn, M., Hoffmann, F., Shupe, M. D., de Boer, G., Matrosov, S. Y., and Luke, E. P.: Can liquid cloud microphysical processes be used for vertically pointing cloud radar calibration?, Atmos. Meas. Tech., 12, 3151–3171, https://doi.org/10.5194/amt-12-3151-2019, 2019. a
MacKay, D. J. C.: Bayesian Interpolation, Neural Comput., 4, 415–447, https://doi.org/10.1162/neco.1992.4.3.415, 1992. a
Mather, J. H. and Voyles, J. W.: The Arm Climate Research Facility: A Review of Structure and Capabilities, B. Am. Meteorol. Soc., 94, 377–392, https://doi.org/10.1175/BAMS-D-11-00218.1, 2013. a
Matrosov, S. Y.: Variability of Microphysical Parameters in High-Altitude Ice Clouds: Results of the Remote Sensing Method, J. Appl. Meteorol., 36, 633–648, https://doi.org/10.1175/1520-0450-36.6.633, 1997. a
Matrosov, S. Y.: Retrievals of vertical profiles of ice cloud microphysics from radar and IR measurements using tuned regressions between reflectivity and cloud parameters, J. Geophys. Res.-Atmos., 104, 16741, https://doi.org/10.1029/1999JD900244, 1999. a
Matrosov, S. Y.: Feasibility of using radar differential Doppler velocity and dual-frequency ratio for sizing particles in thick ice clouds, J. Geophys. Res.-Atmos., 116, D17202, https://doi.org/10.1029/2011JD015857, 2011. a
Matrosov, S. Y., Heymsfield, A. J., Kropfli, R. A., Martner, B. E., Reinking, R. F., Snider, J. B., Piironen, P., and Eloranta, E. W.: Comparisons of Ice Cloud Parameters Obtained by Combined Remote Sensor Retrievals and Direct Methods, J. Atmos. Ocean. Technol., 15, 184, https://doi.org/10.1175/1520-0426(1998)015<0184:COICPO>2.0.CO;2, 1998. a
Matrosov, S. Y., Kropfli, R. A., Reinking, R. F., and Martner, B. E.: Prospects for measuring rainfall using propagation differential phase in X- and Ka-radar bands, J. Appl. Meteorol., 38, 766–776, https://doi.org/10.1175/1520-0450(1999)038<0766:PFMRUP>2.0.CO;2, 1999. a, b
Mishchenko, M. I.: Calculation of the Amplitude Matrix for a Nonspherical Particle in a Fixed Orientation, Appl. Opt.s, 39, 1026–1031, https://doi.org/10.1364/AO.39.001026, 2000. a, b
Moisseev, D. N. and Chandrasekar, V.: Nonparametric Estimation of Raindrop Size Distributions from Dual-Polarization Radar Spectral Observations, J. Atmos. Ocean. Technol., 24, 1008–1018, https://doi.org/10.1175/JTECH2024.1, 2007. a
Moisseev, D. N. and Chandrasekar, V.: Polarimetric Spectral Filter for Adaptive Clutter and Noise Suppression, J. Atmos. Ocean. Technol., 26, 215–228, https://doi.org/10.1175/2008JTECHA1119.1, 2009. a
Moisseev, D. N., Unal, C. M. H., Russchenberg, H. W. J., and Ligthart, L. P.: Improved Polarimetric Calibration for Atmospheric Radars, J. Atmos. Ocean. Technol., 19, 1968, https://doi.org/10.1175/1520-0426(2002)019<1968:IPCFAR>2.0.CO;2, 2002. a
Muth, X., Schneebeli, M., and Berne, A.: A sun-tracking method to improve the pointing accuracy of weather radar, Atmos. Meas. Tech., 5, 547–555, https://doi.org/10.5194/amt-5-547-2012, 2012. a
Myagkov, A., Seifert, P., Wandinger, U., Bauer-Pfundstein, M., and Matrosov, S. Y.: Effects of antenna patterns on cloud radar polarimetric measurements, J. Atmos. Ocean. Technol., 32, 1813–1828, https://doi.org/10.1175/JTECH-D-15-0045.1, 2015. a, b
Myagkov, A., Seifert, P., Bauer-Pfundstein, M., and Wandinger, U.: Cloud radar with hybrid mode towards estimation of shape and orientation of ice crystals, Atmos. Meas. Tech., 9, 469–489, https://doi.org/10.5194/amt-9-469-2016, 2016a. a, b
Myagkov, A., Seifert, P., Wandinger, U., Bühl, J., and Engelmann, R.: Relationship between temperature and apparent shape of pristine ice crystals derived from polarimetric cloud radar observations during the ACCEPT campaign, Atmos. Meas. Tech., 9, 3739–3754, https://doi.org/10.5194/amt-9-3739-2016, 2016b. a
Otto, T. and Russchenberg, H. W. J.: Estimation of specific differential phase and differential backscatter phase from polarimetric weather radar measurements of rain, IEEE Geosci. Remote Sens. Lett., 8, 988–992, https://doi.org/10.1109/LGRS.2011.2145354, 2011. a, b, c
Oue, M., Kumjian, M. R., Lu, Y., Verlinde, J., Aydin, K., and Clothiaux, E. E.: Linear depolarization ratios of columnar ice crystals in a deep precipitating system over the Arctic observed by zenith-pointing Ka-band Doppler radar, J. Appl. Meteorol. Climatol., 54, 1060–1068, https://doi.org/10.1175/JAMC-D-15-0012.1, 2015. a
Oue, M., Kollias, P., Ryzhkov, A., and Luke, E. P.: Toward Exploring the Synergy Between Cloud Radar Polarimetry and Doppler Spectral Analysis in Deep Cold Precipitating Systems in the Arctic, J. Geophys. Res.-Atmos., 123, 2797–2815, https://doi.org/10.1002/2017JD027717, 2018. a
Pfitzenmaier, L., Unal, C. M. H., Dufournet, Y., and Russchenberg, H. W. J.: Observing ice particle growth along fall streaks in mixed-phase clouds using spectral polarimetric radar data, Atmos. Chem. Phys., 18, 7843–7862, https://doi.org/10.5194/acp-18-7843-2018, 2018. a
Prata de Moraes Frasson, R., Kindl da Cunha, L., and Krajewski, W. F.: Assessment of the Thies optical disdrometer performance, Atmos. Res., 101, 237–255, 2011. a, b, c
Protat, A., Bouniol, D., Delanoë, J., May, P. T., Plana-Fattori, A., Hasson, A., O'Connor, E., Görsdorf, U., and Heymsfield, A. J.: Assessment of Cloudsat Reflectivity Measurements and Ice Cloud Properties Using Ground-Based and Airborne Cloud Radar Observations, J. Atmos. Ocean. Technol., 26, 1717, https://doi.org/10.1175/2009JTECHA1246.1, 2009. a
Protat, A., Bouniol, D., O'Connor, E. J., Klein Baltink, H., Verlinde, J., and Widener, K.: CloudSatas a Global Radar Calibrator, J. Atmos. Ocean. Technol., 28, 445–452, https://doi.org/10.1175/2010JTECHA1443.1, 2011. a, b
Pruppacher, H. R. and Pitter, R. L.: A Semi-Empirical Determination of the Shape of Cloud and Rain Drops, J. Atmos. Sci., 28, 86–94, https://doi.org/10.1175/1520-0469(1971)028<0086:ASEDOT>2.0.CO;2, 1971. a
Radenz, M., Bühl, J., Lehmann, V., Görsdorf, U., and Leinweber, R.: Combining cloud radar and radar wind profiler for a value added estimate of vertical air motion and particle terminal velocity within clouds, Atmos. Meas. Tech., 11, 5925–5940, https://doi.org/10.5194/amt-11-5925-2018, 2018. a
Ray, P. S.: Broadband complex refractive indices of ice and water, Appl. Opt., 11, 1836–1844, https://doi.org/10.1364/AO.11.001836, 1972. a
Rusli, S. P., Donovan, D. P., and Russchenberg, H. W. J.: Simultaneous and synergistic profiling of cloud and drizzle properties using ground-based observations, Atmos. Meas. Tech., 10, 4777–4803, https://doi.org/10.5194/amt-10-4777-2017, 2017. a
Ryzhkov, A. V.: Interpretation of polarimetric radar covariance matrix for meteorological scatterers: Theoretical analysis, J. Atmos. Ocean. Technol., 18, 315–328, https://doi.org/10.1175/1520-0426(2001)018<0315:IOPRCM>2.0.CO;2, 2001. a
Ryzhkov, A. V., Schuur, T. J., Burgess, D. W., Heinselman, P. L., Giangrande, S. E., and Zrnic, D. S.: The Joint Polarization Experiment: Polarimetric Rainfall Measurements and Hydrometeor Classification., B. Am. Meteorol. Soc., 86, 809–824, https://doi.org/10.1175/BAMS-86-6-809, 2005. a
Schneebeli, M. and Berne, A.: An Extended Kalman Filter Framework for Polarimetric X-Band Weather Radar Data Processing, J. Atmos. Ocean. Technol., 29, 711–730, https://doi.org/10.1175/JTECH-D-10-05053.1, 2012. a, b
Sekelsky, S. M. and Clothiaux, E. E.: Parallax Errors and Corrections for Dual-Antenna Millimeter-Wave Cloud Radars, J. Atmos. Ocean. Technol., 19, 478–485, https://doi.org/10.1175/1520-0426(2002)019<0478:PEACFD>2.0.CO;2, 2002. a
Shupe, M. D.: Clouds at Arctic atmospheric observatories. Part II: Thermodynamic phase characteristics, J. Appl. Meteorol. Climatol., 50, 645–661, https://doi.org/10.1175/2010JAMC2468.1, 2011. a
Shupe, M. D., Matrosov, S. Y., and Uttal, T.: Arctic Mixed-Phase Cloud Properties Derived from Surface-Based Sensors at SHEBA, J. Atmos. Sci., 63, 697–711, https://doi.org/10.1175/JAS3659.1, 2006. a
Shupe, M. D., Kollias, P., Persson, P. O. G., and McFarquhar, G. M.: Vertical Motions in Arctic Mixed-Phase Stratiform Clouds, J. Atmos. Sci., 65, 1304, https://doi.org/10.1175/2007JAS2479.1, 2008. a
Shupe, M. D., Walden, V. P., Eloranta, E., Uttal, T., Campbell, J. R., Starkweather, S. M., and Shiobara, M.: Clouds at Arctic Atmospheric Observatories. Part I: Occurrence and Macrophysical Properties, J. Appl. Meteorol. Climatol., 50, 626–644, https://doi.org/10.1175/2010JAMC2467.1, 2011. a
Spek, A. L. J., Unal, C. M. H., Moisseev, D. N., Russchenberg, H. W. J., Chandrasekar, V., and Dufournet, Y.: A new technique to categorize and retrieve the microphysical properties of ice particles above the melting layer using radar dual-polarization spectral analysis, J. Atmos. Ocean. Technol., 25, 482–497, https://doi.org/10.1175/2007JTECHA944.1, 2008. a, b
Stephens, G. L., Vane, D. G., Tanelli, S., Im, E., Durden, S., Rokey, M., Reinke, D., Partain, P., Mace, G. G., Austin, R., L'Ecuyer, T., Haynes, J., Lebsock, M., Suzuki, K., Waliser, D., Wu, D., Kay, J., Gettelman, A., Wang, Z., and Marchand, R.: CloudSat mission: Performance and early science after the first year of operation, J. Geophys. Res.-Atmos., 113, D00A18, https://doi.org/10.1029/2008JD009982, 2008. a
Storn, R. and Price, K.: Differential Evolution – A Simple and Efficient Heuristic for global Optimization over Continuous Spaces, J. Global Optim., 11, 341–359, https://doi.org/10.1023/A:1008202821328, 1997. a
Tanelli, S., Durden, S. L., Im, E., Pak, K. S., Reinke, D. G., Partain, P., Haynes, J. M., and Marchand, R. T.: CloudSat's Cloud Profiling Radar After Two Years in Orbit: Performance, Calibration, and Processing, IEEE Trans. Geosci. Remote Sens., 46, 3560–3573, https://doi.org/10.1109/TGRS.2008.2002030, 2008. a
Tokay, A., Wolff, D. B., and Petersen, W. A.: Evaluation of the New Version of the Laser-Optical Disdrometer, OTT Parsivel2, J. Atmos. Ocean. Technol., 31, 1276–1288, https://doi.org/10.1175/JTECH-D-13-00174.1, 2014. a, b, c, d
Tridon, F. and Battaglia, A.: Dual-frequency radar Doppler spectral retrieval of rain drop size distributions and entangled dynamics variables, J. Geophys. Res.-Atmos., 120, 5585–5601, https://doi.org/10.1002/2014JD023023, 2015. a
Tridon, F., Battaglia, A., Luke, E., and Kollias, P.: Rain retrieval from dual-frequency radar Doppler spectra: validation and potential for a midlatitude precipitating case-study, Q. J. Roy. Meteorol. Soc., 143, 1364–1380, https://doi.org/10.1002/qj.3010, 2017. a
Tridon, F., Battaglia, A., and Watters, D.: Evaporation in action sensed by multiwavelength Doppler radars, J. Geophys. Res.-Atmos., 122, 9379–9390, https://doi.org/10.1002/2016JD025998, 2017. a
Trömel, S., Kumjian, M. R., Ryzhkov, A. V., Simmer, C., and Diederich, M.: Backscatter Differential Phase–Estimation and Variability, J. Appl. Meteorol. Climatol., 52, 2529–2548, https://doi.org/10.1175/JAMC-D-13-0124.1, 2013. a, b, c, d, e
Unal, C.: Spectral Polarimetric Radar Clutter Suppression to Enhance Atmospheric Echoes, J. Atmos. Ocean. Technol., 26, 1781–1797, https://doi.org/10.1175/2009JTECHA1170.1, 2009. a
Unal, C. M. H. and Moisseev, D. N.: Combined Doppler and Polarimetric Radar Measurements: Correction for Spectrum Aliasing and Nonsimultaneous Polarimetric Measurements, J. Atmos. Ocean. Technol., 21, 443, https://doi.org/10.1175/1520-0426(2004)021<0443:CDAPRM>2.0.CO;2, 2004. a
Wang, Z. and Sassen, K.: Cloud Type and Macrophysical Property Retrieval Using Multiple Remote Sensors., J. Appl. Meteorol., 40, 1665–1683, https://doi.org/10.1175/1520-0450(2001)040<1665:CTAMPR>2.0.CO;2, 2001. a
Xie, X., Evaristo, R., Troemel, S., Saavedra, P., Simmer, C., and Ryzhkov, A.: Radar Observation of Evaporation and Implications for Quantitative Precipitation and Cooling Rate Estimation, J. Atmos. Ocean. Technol., 33, 1779–1792, https://doi.org/10.1175/JTECH-D-15-0244.1, 2016. a, b
- Abstract
- Introduction
- Data and instrumentation
- Method 1: the self-consistency method for W-band polarimetric cloud radars
- Method 2: disdrometer-based method
- Summary
- Appendix A: Reflectivity calculation
- Appendix B: Polarimetric variables
- Appendix C: Variance of a numerical average
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Data and instrumentation
- Method 1: the self-consistency method for W-band polarimetric cloud radars
- Method 2: disdrometer-based method
- Summary
- Appendix A: Reflectivity calculation
- Appendix B: Polarimetric variables
- Appendix C: Variance of a numerical average
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement