the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A new method for operating a continuous-flow diffusion chamber to investigate immersion freezing: assessment and performance study
Gourihar Kulkarni
Naruki Hiranuma
Ottmar Möhler
Kristina Höhler
Swarup China
Daniel J. Cziczo
Paul J. DeMott
Glaciation in mixed-phase clouds predominantly occurs through the immersion-freezing mode where ice-nucleating particles (INPs) immersed within supercooled droplets induce the nucleation of ice. Model representations of this process currently are a large source of uncertainty in simulating cloud radiative properties, so to constrain these estimates, continuous-flow diffusion chamber (CFDC)-style INP devices are commonly used to assess the immersion-freezing efficiencies of INPs. This study explored a new approach to operating such an ice chamber that provides maximum activation of particles without droplet breakthrough and correction factor ambiguity to obtain high-quality INP measurements in a manner that previously had not been demonstrated to be possible. The conditioning section of the chamber was maintained at −20 ∘C and water relative humidity (RHw) conditions of 113 % to maximize the droplet activation, and the droplets were supercooled with an independently temperature-controlled nucleation section at a steady cooling rate (0.5 ∘C min−1) to induce the freezing of droplets and evaporation of unfrozen droplets. The performance of the modified compact ice chamber (MCIC) was evaluated using four INP species: K-feldspar, illite-NX, Argentinian soil dust, and airborne soil dusts from an arable region that had shown ice nucleation over a wide span of supercooled temperatures. Dry-dispersed and size-selected K-feldspar particles were generated in the laboratory. Illite-NX and soil dust particles were sampled during the second phase of the Fifth International Ice Nucleation Workshop (FIN-02) campaign, and airborne soil dust particles were sampled from an ambient aerosol inlet. The measured ice nucleation efficiencies of model aerosols that had a surface active site density (ns) metric were higher but mostly agreed within 1 order of magnitude compared to results reported in the literature.
- Article
(4602 KB) - Full-text XML
-
Supplement
(1922 KB) - BibTeX
- EndNote
Atmospheric ice nucleation plays an important role in initiating precipitation in clouds that consist of a mixture of supercooled liquid water droplets and ice crystals and in catalyzing the formation of ice particles within high-altitude cirrus clouds (Lohmann and Feichter, 2005; Boucher et al., 2013). This important step toward ice formation also affects the lifetime and radiative properties of these clouds; however, ice nucleation mechanisms are poorly understood and parameterized in cloud models (e.g., Hoose and Möhler, 2012; Murray et al., 2012; Kulkarni et al., 2012; Kanji et al., 2017; Knopf et al., 2018). Homogeneous ice nucleation is responsible for the formation of ice particles in dilute water and supercooled solution droplets at temperatures lower than ≈ −38 ∘C (Pruppacher and Klett, 1997). Ice nucleation can also proceed through heterogeneous ice nucleation triggered by ice-nucleating particles (INPs) (Vali et al., 2015). Multiple heterogeneous ice nucleation mechanisms have been proposed, such as deposition nucleation (ice formation on INPs directly from the vapor phase), contact freezing (freezing initiated by INPs the moment they come into contact with a supercooled droplet), and condensation and immersion freezing (freezing initiated by immersed INPs within the supercooled water or solution droplets). Deposition nucleation has also been referred to as a pore condensation and freezing mechanism because it is similar to immersion freezing but occurs in pores (Marcolli 2014). Nevertheless, the immersion-freezing mode is thought to be the most important process for the formation of ice particles within mixed-phase clouds (e.g., Ansmann et al., 2009; Westbrook and Illingworth, 2013).
Immersion-freezing measurements are commonly made using continuous-flow diffusion chamber (CFDC) devices (e.g., Rogers, 1988; Chen et al., 1998; Stetzer et al., 2008; Kanji and Abbatt, 2009; DeMott et al., 2010; Friedman et al., 2011; Chou et al., 2011; Jones et al., 2011; Kanji et al., 2013; Boose et al., 2016; Garimella et al., 2016, Schiebel, 2017; Zenker et al., 2017). These chambers consist of two ice-coated parallel walls held at different temperatures, and different ice supersaturations are achieved by regulating the temperature gradient. Aerosols sampled into CFDCs are subjected to known discrete temperature and relative humidity conditions, and when the water relative humidity (RHw) is more than a few percent above 100 %, droplets will activate on the majority of particles within the growth section of the chambers. CFDCs also typically have an evaporation section at the bottom of the chamber where the wall temperatures are controlled in order to evaporate the droplets that do not freeze. Frozen droplets are counted using an optical particle counter (OPC) to determine the atmospheric INP concentrations (Garimella et al., 2017). However, the maximum RHw values achievable in this manner can limit the ability to determine the maximum immersion-freezing fraction (DeMott et al., 2015).
Here, we have expanded the capabilities of the CFDC-style device to achieve the maximum activation of particles to detect the immersion-freezing number concentrations of INPs at various supercooled temperatures. We present data to assess the performance from a newly developed CFDC in which all individual aerosol particles are activated to droplets, and these droplets are exposed to a sequence of supercooled temperatures. This is accomplished by modifying the existing design of the Pacific Northwest National Laboratory (PNNL) ice chamber (e.g., Friedman et al., 2011; Kulkarni at al., 2012). In the modified version, the growth section of the chamber was maintained at a higher RHw level under moderate supercooling conditions to activate all particles to supercooled droplets, whereas the evaporation section was always held at ice-saturated conditions and cooled over a range of temperatures at a known constant rate. The evaporation section serves two purposes in this case: it induces the freezing of droplets and evaporates the unfrozen droplets. Validation experiments using standard salt solutions are presented. Various INP proxies for mineral dust types that have previously shown ice nucleation ability over a wide span of supercooled temperatures were used to test the performance of the modified chamber.
2.1 Description of the existing and modified chamber
The PNNL CFDC-style ice chamber operated in the traditional mode, referred to as the Compact Ice Chamber (CIC)-PNNL, has been described previously (e.g., Friedman et al., 2011; Kulkarni at al., 2012). The chamber consists of two sections: a growth section and an evaporation section joined together but thermally isolated from each other. Each section consists of two parallel vertical surfaces that are coated with a thin layer of ice, and these plates are independently temperature-controlled using external cooling baths (Lauda Brinkmann Inc.). Application of an ice layer (≈ 0.5 mm thick) on these surfaces involved three consecutive steps: cooling the plates of the chamber to −25 ∘C, filling the gap between the two parallel surfaces with deionized water (≈ 18 MΩ cm), and expelling the water after 20 s. To produce the desired water or ice supersaturation conditions, a horizontal linear temperature gradient between the plates was applied, and the corresponding temperature and RHw or relative humidity with respect to ice (RHice) were calculated using the Murphy and Koop (2005) vapor pressure formulations. The single sheath and sample flow rates were 5 and 1 liters per minute (L min−1), respectively, resulting in a total particle residence time of ≈ 10 s in the chamber. The temperature gradient was applied such that supersaturation conditions RHw≈ 106 % were achieved in order to investigate the immersion-freezing efficiencies of both atmospheric and laboratory-generated INPs. An OPC (CLiMET, model CI-3100) was used to classify the particles as ice crystals if they were greater than a certain size threshold (≈ 3 µm in diameter). The ice fraction (Fice) was calculated by using the ratio of the ice crystal concentration classified by the OPC to the total condensation nuclei (CN) concentration that entered the chamber. The CN concentration was provided by a condensation particle counter (CPC; TSI 3775). Blank experiments using dry and filtered sample air were also performed at the beginning and end of each experiment for ≈ 10 min to calculate the background number of ice particles. Further, these ice particles were subtracted from the ice crystal concentration measured by the OPC, and the Fice was corrected.
Figure 1 shows the vertical cross-sectional geometry of the modified mode PNNL ice chamber, which is now referred to as the modified compact ice chamber (MCIC). This chamber design has a parallel-plate CFDC-style geometry, whose principle of generating a supersaturation between the two parallel surfaces and determining the Fice is similar to that of the existing CIC chamber but with modifications as described here. The growth and evaporation sections of the MCIC chamber are now referred to as the conditioning and nucleation sections, respectively. The lengths of the two sections are identical (0.45 m), which limits the total particle residence time to ≈ 10 s. The droplet residence and nucleation times within the chamber are a maximum of 6.5 and 2 s, respectively. The chamber wall temperature values as a function of time during one typical ice nucleation experiment are shown in Fig. 2. During our study, the temperature controller of the cooling thermostat was programmed such that the warm and cold wall temperatures of the conditioning section were set to −9 and −27 ∘C, respectively. The resulting water and ice saturation conditions are shown in Fig. 3. Here, the conditioning section temperature was chosen based on previous knowledge about the onset temperature of the INP test species being needed to induce the nucleation of ice at colder temperatures (< −20 ∘C) and the lower detection limit being needed to measure ice concentrations for temperatures warmer than −20 ∘C. The shaded region shows the period (≈ 30 min) of one ice nucleation measurement; i.e., the OPC data from this period only are analyzed. The Fice now indicates the cumulative fraction of droplets frozen as a function of the decreasing temperature in the nucleation section (see Text S1 in the Supplement). This metric of reporting ice nucleation results is commonly used to report frozen fraction vs. temperature (Fice vs. T) results (see e.g., DeMott et al., 2018; Kanji et al., 2017; Kohn et al., 2016). The isothermal conditions of the nucleation section are maintained at ice saturation and cooled at a steady rate (0.5 ∘C min−1) by a separate cooling bath in order to determine the immersion-freezing efficiency of INPs as a function of supercooled temperature. The choice of steady-state cooling rate is empirical at this moment, and the experiment is terminated when the nucleation section reaches ≈ −44 ∘C. This additional supercooling below the onset of homogeneous freezing temperature allowed for freezing data to be obtained for use in controlling the data quality and in accounting for the uncertainty within the temperature. The implications of higher cooling rates for INP measurements were also explored. The particle residence time (≈ 5 s) and ice-saturated conditions of the nucleation section allow a sufficiently sized differential between supercooled droplets and ice crystals and in fact prevent “droplet breakthrough” (Stetzer et al., 2008). While keeping the conditioning section conditions constant, the temperature of the nucleation section is raised to ≈ −20 ∘C to prepare for the next ice nucleation measurement. This operation allows us to probe the immersion-freezing efficiency of INPs at various temperatures (−20 to −44 ∘C) multiple times (∼ 5) before another layer of ice coating is applied. After more than five ice nucleation measurements or after approximately 3 h, we see the reduced Fice of standard solution droplets (discussed below). The particle pulse experiments (Garimella et al., 2017) using size-selected 300 nm mobility diameter ammonium sulfate particles and ≈ 10.5 s pulses were performed. The temperature of the conditioning and nucleation sections were held constant at 20 ∘C, and the particle concentration at the chamber outlet using the CPC was measured. These measurements show that ≈ 16 % of total particles that enter the chamber have moved outside of the lamina (Fig. S1). Therefore, higher RHw values are used in the chamber to activate these particles to droplets (see below). Simulations (see below) were performed to investigate the sensitivity of polydisperse particles. The particle residence times of three different monodisperse particles (0.3, 1.0, and 2.0 µm) traversing the chamber were calculated (Fig. S1). Results show that the residence times of these particles are similar, indicating that monodisperse size pulse experiments are also applicable to other size particles.
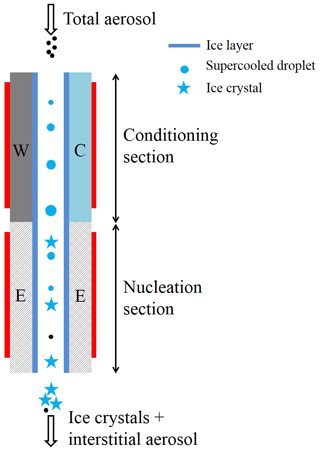
Figure 1Schematic showing the geometry of the MCIC (expanded for clarity). INP proxies are activated to droplets within the conditioning section, and these supercooled droplets are steadily cooled within the nucleation section, from ≈ −20 to ≈ −42 ∘C, to induce freezing of droplets and evaporate unfrozen supercooling droplets. The residence time in each section of the chamber is ≈ 5 s, and the ice layer spans both sections of the chamber. A cyclone impactor upstream of the ice chamber is used to remove the larger particles (> 1.5 µm in diameter) while sampling airborne arable dust particles. The heating tapes (red rectangular strip) are attached to the walls to precisely control the temperature of the walls. W: warm wall; C: cold wall; E: nucleation section wall. The length of both the conditioning and nucleation section is 0.45 m. The width of the chamber is 0.15 m. The gap between warm and cold walls is 0.01 m.
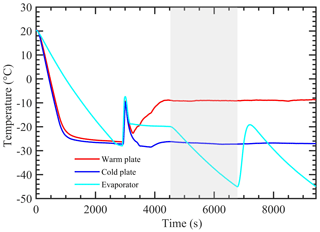
Figure 2Measured temperature of warm, cold, and nucleation section walls during a typical experiment. The shaded area indicates the experimental conditions during one ice nucleation measurement. During this INP measurement, the temperature of both warm and cold walls is kept constant, while the nucleation section is cooled at a steady rate (0.5 ∘C min−1).
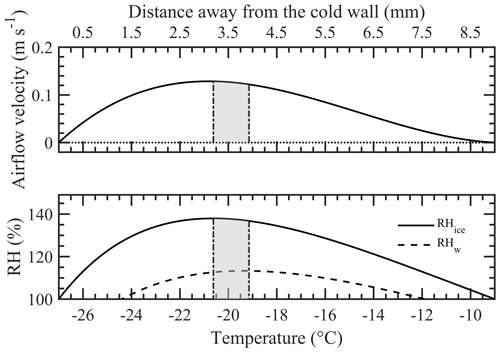
Figure 3Steady-state airflow velocity and relative humidity (RH) conditions calculated using the mathematical model developed by Rogers (1988) within the conditioning section of the ice chamber. The chamber warm wall (left) and the cold wall (right) are at −9 and −27 ∘C, respectively. The shaded area between the two vertical dash-dotted lines shows the boundaries of aerosol lamina under at these above temperatures and flow conditions (sheath flow: 5 L min−1; sample flow: 1 L min−1). The profiles are asymmetric because of the thermophoretic drift of the flow, caused by the thermal gradient between the walls, towards the colder wall. The conditioning section is always supersaturated with respect to ice (RHice > 100 %), and except the near-wall positions, the section is also supersaturated with respect to water (RHw > 100 %).
2.2 Numerical modeling
At the entrance of the nucleation section, the temperature and RHw profiles can be unsteady. To better understand the flow patterns of these profiles within the transition zone and the zone's impact on droplet behavior, numerical simulations using computational fluid dynamics (CFD) were performed. In this study, the warm and cold walls of the conditioning section were maintained at −9 and −27 ∘C, respectively, and the nucleation section was maintained at −20 ∘C. Analytical steady-state calculations based on Rogers (1988) were also used to understand the nature of the flow velocity profile and the position of the aerosol lamina between the warm and colder walls (Fig. 3). The results show that the operating conditions of the chamber produce a skewed velocity profile and that the aerosol lamina is displaced toward the colder wall. The aerosol lamina is surrounded by filtered sheath flow, and its width is determined by the ratio of sample to sheath airflow. Because sample flow ideally occupies this fraction of the total flow, the aerosol lamina experiences a range of temperature and saturation conditions. The center temperature and RHw conditions, including uncertainty across the aerosol lamina (assuming ideal confinement in the lamina), are −19.7 ± 0.7 ∘C and 113 ± 0.5 %, respectively. Additional simulations were performed to understand the center temperature and RHw conditions required to confine the particles that are moved out of the aerosol lamina. We found that the revised uncertainties for center temperature and RHw conditions were ±0.9 ∘C and ±0.7 %, respectively.
CFD simulations were performed to achieve a complete description of the velocity, ice saturation, and temperature conditions within the chamber (Fig. 4a). A three-dimensional mesh of the chamber geometry was generated and exported to the commercially available CFD software ANSYS Inc (2016). The CFD software solver was the pressure-based steady-state Navier–Stokes equation, which has implicit and absolute velocity formulations. The viscous model – the standard renormalization group theory (RNG) κ–ε turbulence model – was used. This model treats velocity fluctuations better than other turbulence models for such a geometry. This turbulence model was used in conjunction with species transport modeling capability such that the effects of smaller eddies of fluid motion were better captured. The pressure outlet boundary condition was used, as were the CFD solution method to couple the pressure–velocity and the default SIMPLE scheme. The Lagrangian discrete-phase model was used to simulate the potential INP trajectories released from the sample injection region to the outlet end of the chamber. The simulations were performed using an “uncoupled approach”, which means the motion of INP particles does not influence the fluid-flow pattern. The temperature and RHw fields of the INP trajectories were used to calculate the droplet growth and evaporation trajectories using a water vapor diffusion growth theory (Rogers and Yau, 1989) that neglects temperature corrections and kinetic and ventilation effects and assumes perfect mass and thermal accommodation coefficients (Text S2).
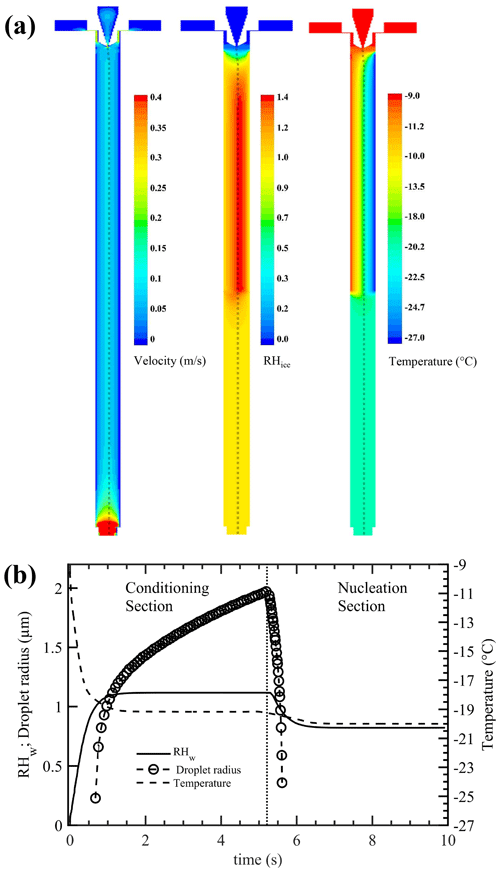
Figure 4(a) Contours of CFD-calculated airflow velocity, RHice, and temperature profiles within the ice chamber. Warm and cold walls of conditioning section are maintained at −9 and −27 ∘C, respectively. The nucleation section is maintained at −20 ∘C. The dashed line shows the trajectory of a single INP within the aerosol lamina transiting through the chamber. (b) CFD-calculated temperature and RHw profiles of a potential INP released from the sample injection region to the outlet end of the chamber. Analytical calculations of droplet growth and evaporation of such a potential INP (0.3 µm in diameter) are also shown. The left and right sides of the vertical dotted line represent the conditioning and nucleation sections, respectively. See the text for more details. Simulation results at other nucleation section temperatures are shown in Figs. S1–S4.
The CFD-simulated airflow velocity and RHice profiles from the central region of the conditioning section are nearly similar to the analytical solution (Fig. 4a). Both calculations show the presence of maximum humidity values near the middle of the chamber but slightly displaced values toward the cold wall. The fluid-flow temperature characteristics from the moment the aerosol lamina joins the sheath flow show that the aerosol sample quickly (< 0.5 s) cools at the entrance of the conditioning section. To gain a better understanding of RHw and temperature conditions within the conditioning and nucleation sections, the simulated data set of a potential INP trajectory transiting within the chamber is shown (Fig. 4b). The potential INPs experience nearly constant RHw and temperature conditions within a short time, ≈ 1 s, after entering the conditioning section. The potential INPs are assumed (i.e., sub-saturated particle growth is ignored) to activate to droplets because they are greater in size than cloud CN sizes (Seinfeld and Pandis, 2016) and grow as long as RHw is increasing or remains constant. As the INPs enter the nucleation section, their RHw and temperature values equilibrate with the nucleation section conditions. These calculations show that the droplets grow to ≈ 4 µm in diameter, and they shrink as the RHw and temperature decrease (within the nucleation section). Note that droplet freezing within the nucleation section is not simulated in these simulations.
Additional simulations with the nucleation section temperature set to −30 and −37.5 ∘C were also performed (Figs. S2–S5). These simulations show that the RHw field of a potential INP slightly decreases (≈ 0.5 %) and then increases within a very short period of time (< 0.5 s) at the entrance region of the nucleation section. However, calculations show that such a perturbation does not affect the droplet evaporation behavior within the nucleation section because they all evaporate within ≈ 1 s after they enter the nucleation section and within the uncertainty limits of the set temperature of the nucleation section but not before they reach the set temperature (see Figs. S2–S4). The simulations are extended to understand the RHw and temperature conditions of potential INPs released from different regions of the inlet section of the chamber. Simulations of five potential INPs are shown in Fig. S5. It is observed that INPs experience various temperature conditions (−17 to −19.5 ∘C) within the conditioning section, but after ≈ 0.5 s they all enter the nucleation section, and the temperature of each trajectory is identical.
Additional evaporative cooling calculations were performed to understand the suppression of droplet temperature while they enter the nucleation section. In the nucleation section the supercooled droplets experienced sub-saturation (RHw > 0.8) and colder temperature conditions (> −37.5 ∘C). The Kulmala evaporative model (Su et al., 2018) was used to determine the surface temperature of these droplets using steady-state aerosol lamina airflow velocity (Fig. 3) and theoretically predicted RHw fields (Figs. S2–S4). The calculations (Table S1) show the negligible effect of evaporative cooling on the droplet temperature such that additional supercooling is within the reported temperature uncertainty (= ± 0.7 ∘C) across the aerosol lamina, and therefore evaporating-droplet cooling effects within the nucleation section are ignored.
2.3 Homogeneous freezing of ammonium sulfate particles
The temperature conditions within the nucleation section were validated using size-selected ammonium sulfate (AS) particles. These particles were generated by atomization of an aqueous solution made by dissolving AS (1 g) and Milli-Q water (18.2 MΩ cm; 100 g), resulting in a 1 wt % solution concentration using a constant output atomizer (TSI 3076). The atomized droplets were transported through a diffusion drier to obtain the dry particles, which were further transported to the differential mobility analyzer (DMA; TSI 3081) to obtain size-selected particles that had mobility diameters of 200 nm. The choice of this size allowed for the generation of the maximum number concentration of monodisperse particles. The concentration of these size-selected particles was measured using a CPC, and the particles were further transported to the ice chamber. As stated previously, the temperature and RHw conditions within the conditioning section were −20 ∘C and ≈ 113 %, respectively, and these conditions were held constant, which led to droplet activation of size-selected AS particles. Next, the nucleation section was steadily cooled from −20 to −40 ∘C, and the ice particles exiting the chamber were classified as ice particles. The ice particle size distribution with supercooling is shown in Fig. 5a. The results show that the droplets began to freeze via a homogeneous freezing mode at ≈ −37.5 ∘C. The maximum number of ice particle concentrations was observed at ≈ −38.5 ∘C, when all the droplets froze. The nucleation section is always maintained at RHice= 100 % (see Fig. 4a), and such ice saturation conditions do not grow or sublimate the ice crystals. Therefore, ice particle size measured by the OPC can be representative of the size of the droplet while freezing. At slightly warmer temperatures (between −38.5 and −37.5 ∘C), we observe ice particles of ≈ 2.0 µm in diameter. The appearance of these smaller ice crystals could be because of the freezing of these smaller droplets (a consequence of evaporation within the entrance zone of the nucleation section) compared to ≈ 5.0 µm droplets at ≈ −38.5 ∘C. These homogeneous freezing threshold temperature values are in agreement with previous studies (e.g., Ignatius et al., 2016; Kohn et al., 2016). For example, Kohn et al. (2016) found 100 % freezing of supercooled dilute aqueous solution droplets at ≈ −38.2 ∘C. Theoretical calculations using a homogeneous nucleation rate (e.g., Earle et al., 2010; Atkinson et al., 2016) were performed to predict the homogeneous freezing curves of droplets that were 4 µm in diameter. Homogeneous freezing curves for various probable droplet residence times within the nucleation section are shown in Fig. S6. Note the good agreement between the experimental and predicted freezing temperatures. These results also show the complete evaporation of supercooled droplets within the nucleation section because no ice particles are observed above −37.5 ∘C, and therefore the freezing results (see Sect. 3) at warmer temperatures (> −37 ∘C) can be ascribed to the heterogeneous freezing of the droplets or immersion freezing.
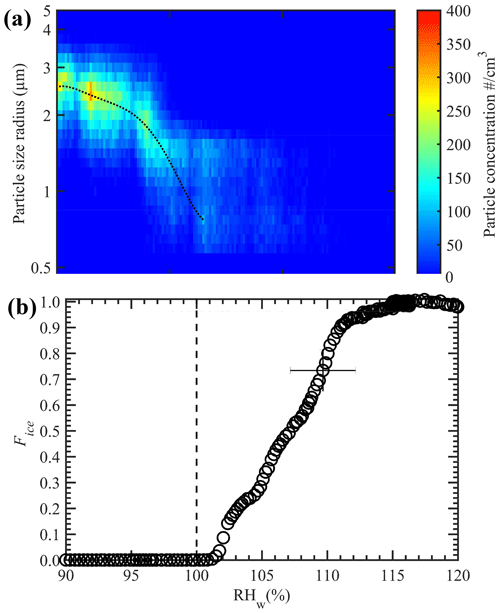
Figure 5Homogenous freezing of water droplets containing 1 wt % ammonium sulfate solution. (a) OPC-classified ice particle concentrations as a function of ice crystal diameter at different temperatures. Warm and cold walls of conditioning section are maintained at −9 and −27 ∘C, respectively. (b) The fraction of frozen solution droplets with RHw, where the temperature of the nucleation section is maintained constant at −42 ∘C to induce droplet freezing via the homogeneous freezing mode, and RHw within the conditioning section was steadily increased from 90 % to 120 %. Slightly colder temperature (−42 ∘C) than homogeneous freezing limit (≈ −38.5 ∘C; panel a) is used to account for the uncertainty within temperature and RHw conditions. The dashed line in panels (a) and (b) indicate the increase in freezing fraction of droplets trend (for illustration purposes) and the onset of saturation line, respectively. The uncertainty in RHw is shown as an error bar (see the text for more details). The uncertainty in Fice is 1 standard deviation (n = 3). For clarity, error bars are shown only for one data point.
This experimental setup was further applied to understand the relationship between the Fice of AS particles relative to the RHw conditions within the conditioning section. The aim was to investigate the RHw value at which all the size-selected AS particles activate to droplets. Here, the nucleation section was held at −42 ∘C to induce homogeneous freezing of solution droplets, while the RHw within the conditioning section was steadily increased. It can be seen that RHw values close to 113 % are required before all the AS particles are activated to droplets and measured as ice crystals (Fig. 5b). Higher RHw values enable the encapsulation of all particles that are within and may spread outside of the width of aerosol lamina into droplets (Garimella et al., 2017). In addition, high-saturation conditions help grow the droplets to the larger size, so they survive long enough to induce the freezing of droplets within the nucleation section.
2.4 Sample preparation
The immersion-freezing efficiency of K-feldspar, illite-NX, Argentinian soil dust, and airborne soil dusts from arable region particles was measured to test the performance of the MCIC. K-feldspar (BCS376) was purchased from the Bureau of Analysed Sampled Ltd, UK. Dry-dispersed (TSI 3433) K-feldspar particles that had a mobility diameter of 400 nm were size-selected by a DMA, and the nearly monodisperse particles were transported to the CPC and ice nucleation chamber. Based on theoretical calculations (Baron and Willeke, 2001), the distribution of these classified particles may also contain sub-populations of double- (≈ 700 nm) and triple-charged (≈ 985 nm) particles. Laboratory measurements showed that the contribution of double- and triple-charged particles was less than 7 % and 3 %, respectively, which also justified the choice of 400 nm size particles. Therefore, the multiply charged particle contribution is ignored, and the K-feldspar aerosol stream is assumed to consist only of particles whose mobility diameter equals 400 nm. However, the surface area of multiply charged particles could influence Fice because these large particles (> 400 nm) provide larger surface areas (Lüönd et al., 2010). Illite-NX and Argentinian soil dust were sampled at the AIDA (Aerosol Interaction and Dynamics in the Atmosphere) chamber facility during the Fifth International Ice Nucleation Workshop (FIN-02) campaign (DeMott et al., 2018). During the campaign, the two aerosol types were dry-dispersed in two different chambers: an 84 m3 AIDA chamber and a 4 m3 aerosol particle chamber (APC); but in this study, we sampled directly from the APC. The details of particle generation and aerosol properties are described by DeMott et al. (2018). The direct sampling of these two aerosol types corresponds to experiment numbers 8 and 10 conducted on 16 and 17 March 2015, respectively.
Airborne soil dust from an arable region or shortly airborne arable dust particles were sampled at the PNNL sampling site during a regional windblown dust event. The PNNL sampling site is located within the Columbia Plateau, WA, USA, which is confined by the Rocky Mountains to the east, the Blue Mountains to the south, and the Cascade Mountains to the west. The region was once covered with basalt lava but is now built up with loose topsoil–loess. This fine soil, which is erodible, and the agricultural dryland farming practices make this dry soil susceptible to wind erosion. The sampling was performed during one dust event on 11 May 2017, and the average temperature, humidity, and wind speed during that day were 18 ∘C, 60 %, and 6.26 m s−1, respectively. The sampling port was ≈ 9 m above the ground on the rooftop of the Atmospheric Measurements Laboratory located on the PNNL campus in Richland, WA. The airborne dust particles were drawn into the laboratory through a cyclone impactor (URG-200-30EH), which was operated at 30 L min−1 to obtain a cut point diameter equal to 1.5 µm. This size-selective sampling allowed for removal of the larger particles (> 1.5 µm) and therefore helped to classify unambiguously the ice crystals larger than 3 µm using an OPC. The CN concentration of airborne arable dust particles (> 0.1 µm) was measured using a laser aerosol spectrometer (LAS; TSI 3340). The Fice was calculated by determining the ratio of ice crystals provided by the OPC to the CN counts measured by the LAS. In parallel to INP measurements, the particles were collected on a carbon type-B film (Ted Pella Inc.; 01814-F) for scanning electron microscopy–energy dispersive X-ray spectroscopy (SEM–EDS) analysis to better understand the size distribution and composition of these airborne dust particles. The films were mounted on the C and D stages of an SKC Sioutas impactor that had 50 % cut points of 0.5 and 1.0 µm, respectively. The impactor was operated at 9 L min−1, and a total of 1183 particles were analyzed. Figure S7 shows the exemplary SEM images. The images reveal that the particles are mostly composed of minerals, and the size distribution shows the mean area equivalent diameter of ≈ 0.53 µm. The input aerosol concentration of all four INP species varied from 100 to 800 cm−3, and the sampling duration was ∼ 30 min.
The MCIC was operated to measure the maximum immersion-freezing fraction of INPs. The modified design allowed for the faster (≈ 30 min) accumulation of immersion-freezing data points to develop a continuous representation of the immersion-freezing behavior of INPs compared to the traditional CIC-PNNL design, in which immersion freezing was investigated at discrete temperatures. These expanded capabilities were demonstrated by measuring the immersion-freezing properties of four INP substances: K-feldspar, illite-NX, Argentinian soil dust, and airborne arable dust particles.
The measurements of the immersion-freezing properties of the four samples were investigated at temperatures between −20 and −38 ∘C. The averaged Fice data over ΔT= 0.25 ∘C temperature intervals were plotted against the midpoint temperature of each bin (Fig. 6). The vertical and horizontal error bars are equal to 1 standard deviation of the Fice measurements (n = 3) and temperature uncertainty (±0.4 ∘C) across the nucleation section, respectively. Freezing experiments with AS solution droplets show the homogeneous freezing threshold temperature conditions being below ≈ −38 ∘C, and therefore Fice data points above this temperature can be attributed to the immersion-freezing mode only. Figure 6 shows that four INP materials exhibit a distribution of immersion-freezing temperatures. The Fice of all INP species increased with decreasing temperature, consistent with many past studies (e.g., Kanji et al., 2017). The droplets containing immersed K-feldspar particles froze at the higher temperatures. The median freezing temperatures (i.e., the temperature at which 50 % of the droplets froze) of K-feldspar, illite-NX, Argentinian soil dust, and airborne arable dust particles were −25.4, −32.6, −31.4, and −31.8 ∘C, respectively, and the difference between freezing temperatures corresponding to Fice equal to 90 % and 10 % was approximately between ≈ 4.5 and 7.5 ∘C for all four INP materials.
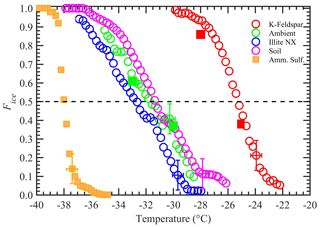
Figure 6The Fice of four INP test species as a function of temperature. The vertical error bar represents the 1 standard deviation of the three repeat experiments (n = 3). Temperature measurements had ±0.4 ∘C uncertainty. For clarity, error bars are shown for only one data point. Solid square orange markers represent the freezing temperatures of water droplets containing 1 wt % AS. Other solid square markers represent data collected when the chamber was operated in a steady-state temperature mode (instead of steady cooling). The dashed horizontal line represents 50 % Fice.
Additional experiments were performed to confirm that the dynamic temperature conditions (steady-state cooling) of the nucleation section do not affect the freezing behavior of particles. The measurements were conducted on K-feldspar and airborne arable dust particles that were prepared as described above in the sample preparation section. The temperatures of the warm and cold walls of the conditioning section were maintained at −9 and −27 ∘C, respectively, and the nucleation section temperature was held constant (instead of steady-state cooling). The immersion-freezing fraction data points of these two species are shown as solid symbols in Fig. 6. Good agreement with the results obtained from MCIC was observed, which suggests that the temperature-ramping operation of the nucleation section (0.5 ∘C min−1) does not affect the performance of INP activation experiments. The experiments with higher cooling rates (2.5 and 7.0 ∘C min−1) had negligible effects on Fice of airborne arable dust species (Fig. S8). Further, the time-dependent immersion-freezing framework (e.g., Vali and Snider, 2015; Herbert et al., 2014) suggests that the rapid cooling of the droplets could shift the cumulative ice fraction toward the colder temperature based on the cooling rate and particular INP material constant. However, these input parameters for the time-dependent model are not available currently to quantify the temperature shift for the present experimental conditions. Future studies that involve collocated direct and post-processing INP instruments would be needed.
These Fice measurements were further analyzed using the ice nucleation active site density (ns) approach that allows a comparison with other studies (see below). This approach also allowed us to compare results directly with literature data obtained using different experimental setups and various direct and post-processing INP instruments and particle generation methods. The ns indicates the cumulative number of ice active sites that are present per unit area of particle surface and that induce nucleation of ice upon cooling from 0 ∘C to experimental temperature T. In this calculation, time dependence is neglected, and it is assumed that the different active sites present within the droplets are responsible for the nucleation of ice. The ns calculation follows Hiranuma et al. (2015) and DeMott et al. (2018):
where A is the surface area per particle, and the approximation is valid for Fice ≪ 1.0 in Eq. (1). For K-feldspar and airborne arable dust particle analysis, the surface area is calculated assuming the particles are spherical, and this assumption may overestimate the ns; therefore, calculations should be viewed as the upper estimates of ns. The size distribution and CPC concentrations were used to calculate the A of individual airborne arable dust particles, as described by Niemand et al. (2012). For illite-NX and Argentinian soil dust particles, the A was obtained from the FIN-02 data archive (DeMott et al., 2018). The error in ns (Eq. 1) was calculated using the error propagation method based on the uncertainties in the Fice and A.
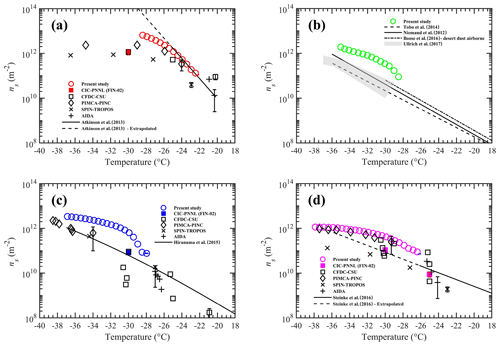
Figure 7Ice nucleation active site density (ns) as a function of temperature for four INP test species tested in this study. The panels (a) to (d) show ns densities for K-feldspar, airborne arable dust, illite-NX, and Argentinian soil dust, respectively. Solid and dash-dotted lines represent various parameterizations from the literature. See the text for details. Dashed lines in panels (a) and (d) indicate the extrapolated data calculated outside the temperature limits recommended in these ns parameterizations. The black color symbols represent ns values from various other instruments that participated in FIN-02 activity (DeMott et al., 2018). Filled color symbols show the data from the CIC-PNNL chamber but operated at steady-state temperature and RHw= 106 % conditions at FIN-02. For clarity, confidence intervals are shown only for one data point from each study.
Figure 7 shows ns for the four INP materials tested in this work in comparison to parameterizations reported in previous studies. The ns for K-feldspar is compared to the fit published by Atkinson et al. (2013). There is a good agreement with our measurements for temperatures warmer than −26 ∘C. Atkinson et al. (2013) used a droplet-freezing cold stage technique, in which a known amount of K-feldspar material was present in each droplet sized between 14 and 16 µm. These droplets were cooled at a rate of 1 ∘C min−1, and droplet-freezing temperature data were used to construct the ns parameterization. Note that the ns fit from Atkinson et al. (2013) is valid up to −25 ∘C. In our work, we extrapolated the fit outside this limit to colder temperatures for comparison. However, such linear extrapolation to colder temperatures may not be correct because, as both Niedermeier et al. (2015) and DeMott et al. (2018) (the latter from the FIN-02 campaign) have shown, the ns values level off at temperatures colder than −25 ∘C. The ns for airborne arable dust was compared with the previous studies. Niemand et al. (2012) derived the ns fit using combined immersion-freezing data from various natural dusts (Asian soil dust, Canary island dust, Saharan dust, and Israel dust). Recently, Ullrich et al. (2017) developed ns parameterization using immersion-freezing ns densities of various arable dusts (Saharan desert dust, Asian desert dust, Israel desert dust, Canary Island dust) for the temperature range from −14 to −30 ∘C. Tobo et al. (2014) investigated the INP abilities of agriculture soils dusts collected from Wyoming, USA. Boose et al. (2016) investigated the INP efficiencies of airborne dust samples from four locations (Crete, Egypt, Peloponnese, and Tenerife) and generated the minimum to maximum bounds of ns from −29 to −37 ∘C. The comparison of our results with these previous results shows good agreement within 1 order of magnitude at colder temperatures, but the data diverge at warmer temperatures. This could be the consequence of a particularly active soil dust present in the local region. The ns for illite-NX was compared to that of Hiranuma et al. (2015), who combined immersion-freezing data from several direct-processing INP methods to develop an ns parameterization. Here, we used the Gumbel cumulative distribution linear fit parameters derived from dry dispersion measurements to generate the ns fit. Our data agree within 1 order of magnitude at warmer (−28 to −30 ∘C) and colder temperatures (−34 to −38 ∘C), but at other temperatures (−30 to −34 ∘C) the data diverge. Finally, we compared our data with ns parameterization from Steinke et al. (2016). Steinke et al. (2016) used immersion-freezing data from four soil dust samples (Mongolian soil, Karlsruhe soil, German soil, and Argentinian soil) to produce an ns fit that is valid over a temperature range between −26 and −11 ∘C. We extrapolated the ns fit toward colder temperatures, and the comparison shows higher ns values but overlaps within the order of magnitude with others.
Figure 7a, c, and d also show the ns results reported by five different direct-processing INP instruments used in the FIN-02 campaign (DeMott et al., 2018). Our data for K-feldspar nearly align with the others at warmer temperatures (> −28 ∘C). For the illite-NX sample, agreement with the PIMCA–PINC (Portable Immersion Mode Cooling chAmber–Portable Ice Nucleation Chamber) method is within 1 order of magnitude, but the agreement is observed within 2 orders of magnitude with others. The present data for Argentinian soil dust align with the PIMCA–PINC method and agree with the others within 1 order of magnitude. The discrepancy between our results and others' could be attributed to the different capabilities employed by individual measurement methods to investigate the immersion-freezing properties. The experimental uncertainties (e.g., ice crystal detection limit, RH, and temperature error limits) from these methods could also influence the ns results. Previously, evaporative freezing by contact nucleation inside-out has been hypothesized to explain the higher freezing temperatures and rates of ice formation observed during droplet evaporation (Durant and Shaw, 2005). Durant and Shaw (2005) showed that water droplets containing individual insoluble INPs freeze at a higher temperature compared to the immersion-freezing mechanisms. We cannot rule out that the evaporative freezing mechanism may be occurring in our experiments, and it would be responsible for the higher ns values to be compared to those of other studies. The comparison with the CIC-PNNL chamber showed that our data agree within 1 order of magnitude. Note that CIC-PNNL (PNNL ice chamber but operated in a traditional mode; Friedman et al., 2011; Kulkarni et al., 2012) was operated at RHw= 106 %, and its operation limited investigating immersion freezing on the entire particle population. It can be observed that for illite-NX and Argentinian soil dust samples a correction factor of 4 to 5 is needed to apply to the CIC-PNNL data to match with the data from the MCIC.
Our results can guide design considerations for future CFDC-style ice chambers. The length of the conditioning section can be increased so that higher RHw values would not be necessary to activate all the particles to sufficiently large droplet sizes (≈ 2 µm in diameter). This design feature could help to increase the lifetime of the ice layer. Based on CFD results (Figs. S3–S5), the minimum evaporation or nucleation length required is 0.2 m. In addition, by implementing a separate refrigeration system to independently cool the nucleation section, the new operation mode presented here can be adapted.
An alternative method of operating a CFDC-style ice chamber – the MCIC – was explored to determine the immersion-freezing ability of INPs. This new mode of operation allowed us to obtain maximum immersion-freezing fractions of INPs without droplet breakthrough ambiguity. Here, instead of investigating immersion freezing at discrete temperatures, immersion freezing was investigated by activating particles to droplets at high RHw followed by steady cooling under imposed ice-saturated conditions. The chamber performance was evaluated by testing the ice nucleation ability of four INP materials: K-feldspar, illite-NX, Argentinian soil dust, and airborne arable dust particles. In addition, we performed CFD simulations to evaluate flow, humidity, and temperature performance. The results indicate that these three thermodynamic conditions are locally fully developed, which confirms constant mass and thermal flux and therefore steady operating conditions within the chamber. Tests using size-selected AS particles showed that homogeneous freezing of solution droplets occurs in agreement with theory and previous study results and that, to activate all the particles to droplets, high RHw values of ≈ 113 % are needed. Analytical and CFD calculations indicate that such high values are needed to grow the droplets to larger sizes so that they can survive long enough to induce freezing and to allow the particles that may have escaped the aerosol lamina to activate into droplets. Tests using the four INP materials demonstrated the activation of all individual particles to generate immersion-freezing spectra in terms of Fice and ns. Experimental results indicate that K-feldspar minerals induced detectable ice formation at ≈ −22 ∘C, and maximum Fice (= 90 %) was observed at −28 ∘C. The other three samples induced nucleation of ice at temperatures colder than −26 ∘C, and their maximum Fice (= 90 %) was observed to be ≈ −36 ∘C. The Fice was normalized using particle surface area to calculate the ns, and these ns calculations show that our results are comparable to the parameterizations and data reported in the literature. We find that the majority of our ns results are higher within 1 order of magnitude than others. Analysis of such high-temporal-resolution immersion-freezing measurements could offer better insights into the freezing properties of INPs, thereby moving us toward improved representations of the immersion-freezing ability of INPs for cloud models.
Data plotted in this paper are available upon request.
The supplement related to this article is available online at: https://doi.org/10.5194/amt-13-6631-2020-supplement.
GK analyzed the data and wrote the paper. NH, OM, KH, SC, DJC, and PJD contributed and commented on all results. SC provided airborne arable dust composition and morphology results.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Fifth International Workshop on Ice Nucleation (FIN)”. It is not associated with a conference.
We thank the microscopy capability group for performing SEM-EDX analysis at the Environmental Molecular Sciences Laboratory, which is a national scientific user facility located at PNNL in Richland, Washington. PNNL is operated for the US DOE by the Battelle Memorial Institute under contract DEAC05-76RL0 1830. We also acknowledge support from the AIDA team and organizers of the FIN-02 campaign.
This research has been supported by the Office of Science of the US Department of Energy (DOE) as part of the Atmospheric System Research Program and the US National Science Foundation (grant nos. 1358495 and 1660486). The FIN-02 campaign was partially supported by the US National Science Foundation (grant no. AGS-1339264) and by the US DOE's Atmospheric System Research, an Office of Science, Office of Biological and Environmental Research program (grant no. DE-SC0014487).
This paper was edited by Mingjin Tang and reviewed by Gabor Vali and two anonymous referees.
Ansmann, A., Tesche, M., Seifert, P., Althausen, D., Engelmann, R., Fruntke, J., Wandinger, U., Mattis, I., and Muller, D.: Evolution of the ice phase in tropical altocumulus: SAMUM lidar observations over Cape Verde, J. Geophys. Res. Atmos., 114, D17208, https://doi.org/10.1029/2008jd011659, 2009.
ANSYS Inc: ANSYS Fluent 14.0, Canonsburg, PA, USA, 2016.
Atkinson, J. D., Murray, B. J., Woodhouse, M. T., Whale, T. F., Baustian, K. J., Carslaw, K. S., Dobbie, S., O'Sullivan, D., and Malkin, T. L.: The importance of feldspar for ice nucleation by mineral dust in mixed-phase clouds (vol. 498, p. 355, 2013), Nature, 500, 491–491, https://doi.org/10.1038/nature12384, 2013.
Atkinson, J. D., Murray, B. J., and O'Sullivan, D.: Rate of Homogenous Nucleation of Ice in Supercooled Water, J. Phys. Chem. A, 120, 6513–6520, https://doi.org/10.1021/acs.jpca.6b03843, 2016.
Baron, P. A. and Willeke, K.: Aerosol Measurement: Principles, Techniques, and Applications, 2nd edn., Wiley-Interscience Publications, Hoboken, New Jersey, USA, 2001.
Boose, Y., Kanji, Z. A., Kohn, M., Sierau, B., Zipori, A., Crawford, I., Lloyd, G., Bukowiecki, N., Herrmann, E., Kupiszewski, P., Steinbacher, M., and Lohmann, U.: Ice Nucleating Particle Measurements at 241 K during Winter Months at 3580m MSL in the Swiss Alps, J. Atmos. Sci., 73, 2203–2228, https://doi.org/10.1175/Jas-D-15-0236.1, 2016.
Boucher, O., Randall, D., Artaxo, P., Bretherton, C., Feingold, G., Forster, P., Kerminen, V.-M., Kondo, Y., Liao, H., Lohmann, U.,Rasch, P., Satheesh, S. K., Sherwood, S., Stevens, B., and Zhang, X. Y.: Climate Change 2013 The Physical Science Basis; Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Stocker, T. F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S. K., Boschung, J., Nauels, A., Xia, Y., Bex, V., and Midgley, P. M., Cambridge, United Kingdom and New York, NY, USA, 571–657, 2013.
Chen, Y. L., Kreidenweis, S. M., McInnes, L. M., Rogers, D. C., and DeMott, P. J.: Single particle analyses of ice nucleating aerosols in the upper troposphere and lower stratosphere, Geophys. Res. Lett., 25, 1391–1394, https://doi.org/10.1029/97gl03261, 1998.
Chou, C., Stetzer, O., Weingartner, E., Jurányi, Z., Kanji, Z. A., and Lohmann, U.: Ice nuclei properties within a Saharan dust event at the Jungfraujoch in the Swiss Alps, Atmos. Chem. Phys., 11, 4725–4738, https://doi.org/10.5194/acp-11-4725-2011, 2011.
DeMott, P. J., Prenni, A. J., Liu, X., Kreidenweis, S. M., Petters, M. D., Twohy, C. H., Richardson, M. S., Eidhammer, T., and Rogers, D. C.: Predicting global atmospheric ice nuclei distributions and their impacts on climate, P. Natl. Acad. Sci. USA, 107, 11217–11222, https://doi.org/10.1073/pnas.0910818107, 2010.
DeMott, P. J., Prenni, A. J., McMeeking, G. R., Sullivan, R. C., Petters, M. D., Tobo, Y., Niemand, M., Möhler, O., Snider, J. R., Wang, Z., and Kreidenweis, S. M.: Integrating laboratory and field data to quantify the immersion freezing ice nucleation activity of mineral dust particles, Atmos. Chem. Phys., 15, 393–409, https://doi.org/10.5194/acp-15-393-2015, 2015.
DeMott, P. J., Möhler, O., Cziczo, D. J., Hiranuma, N., Petters, M. D., Petters, S. S., Belosi, F., Bingemer, H. G., Brooks, S. D., Budke, C., Burkert-Kohn, M., Collier, K. N., Danielczok, A., Eppers, O., Felgitsch, L., Garimella, S., Grothe, H., Herenz, P., Hill, T. C. J., Höhler, K., Kanji, Z. A., Kiselev, A., Koop, T., Kristensen, T. B., Krüger, K., Kulkarni, G., Levin, E. J. T., Murray, B. J., Nicosia, A., O'Sullivan, D., Peckhaus, A., Polen, M. J., Price, H. C., Reicher, N., Rothenberg, D. A., Rudich, Y., Santachiara, G., Schiebel, T., Schrod, J., Seifried, T. M., Stratmann, F., Sullivan, R. C., Suski, K. J., Szakáll, M., Taylor, H. P., Ullrich, R., Vergara-Temprado, J., Wagner, R., Whale, T. F., Weber, D., Welti, A., Wilson, T. W., Wolf, M. J., and Zenker, J.: The Fifth International Workshop on Ice Nucleation phase 2 (FIN-02): laboratory intercomparison of ice nucleation measurements, Atmos. Meas. Tech., 11, 6231–6257, https://doi.org/10.5194/amt-11-6231-2018, 2018.
Durant, A. J. and Shaw, R. A.: Evaporation freezing by contact nucleation inside-out, Geophys. Res. Lett., 32, L20814, https://doi.org/10.1029/2005gl024175, 2005.
Earle, M. E., Kuhn, T., Khalizov, A. F., and Sloan, J. J.: Volume nucleation rates for homogeneous freezing in supercooled water microdroplets: results from a combined experimental and modelling approach, Atmos. Chem. Phys., 10, 7945–7961, https://doi.org/10.5194/acp-10-7945-2010, 2010.
Friedman, B., Kulkarni, G., Beranek, J., Zelenyuk, A., Thornton, J. A., and Cziczo, D. J.: Ice nucleation and droplet formation by bare and coated soot particles, J. Geophys. Res.-Atmos., 116, D17203, https://doi.org/10.1029/2011jd015999, 2011.
Garimella, S., Kristensen, T. B., Ignatius, K., Welti, A., Voigtländer, J., Kulkarni, G. R., Sagan, F., Kok, G. L., Dorsey, J., Nichman, L., Rothenberg, D. A., Rösch, M., Kirchgäßner, A. C. R., Ladkin, R., Wex, H., Wilson, T. W., Ladino, L. A., Abbatt, J. P. D., Stetzer, O., Lohmann, U., Stratmann, F., and Cziczo, D. J.: The SPectrometer for Ice Nuclei (SPIN): an instrument to investigate ice nucleation, Atmos. Meas. Tech., 9, 2781–2795, https://doi.org/10.5194/amt-9-2781-2016, 2016.
Garimella, S., Rothenberg, D. A., Wolf, M. J., David, R. O., Kanji, Z. A., Wang, C., Rösch, M., and Cziczo, D. J.: Uncertainty in counting ice nucleating particles with continuous flow diffusion chambers, Atmos. Chem. Phys., 17, 10855–10864, https://doi.org/10.5194/acp-17-10855-2017, 2017.
Herbert, R. J., Murray, B. J., Whale, T. F., Dobbie, S. J., and Atkinson, J. D.: Representing time-dependent freezing behaviour in immersion mode ice nucleation, Atmos. Chem. Phys., 14, 8501–8520, https://doi.org/10.5194/acp-14-8501-2014, 2014.
Hiranuma, N., Augustin-Bauditz, S., Bingemer, H., Budke, C., Curtius, J., Danielczok, A., Diehl, K., Dreischmeier, K., Ebert, M., Frank, F., Hoffmann, N., Kandler, K., Kiselev, A., Koop, T., Leisner, T., Möhler, O., Nillius, B., Peckhaus, A., Rose, D., Weinbruch, S., Wex, H., Boose, Y., DeMott, P. J., Hader, J. D., Hill, T. C. J., Kanji, Z. A., Kulkarni, G., Levin, E. J. T., McCluskey, C. S., Murakami, M., Murray, B. J., Niedermeier, D., Petters, M. D., O'Sullivan, D., Saito, A., Schill, G. P., Tajiri, T., Tolbert, M. A., Welti, A., Whale, T. F., Wright, T. P., and Yamashita, K.: A comprehensive laboratory study on the immersion freezing behavior of illite NX particles: a comparison of 17 ice nucleation measurement techniques, Atmos. Chem. Phys., 15, 2489–2518, https://doi.org/10.5194/acp-15-2489-2015, 2015.
Hoose, C. and Möhler, O.: Heterogeneous ice nucleation on atmospheric aerosols: a review of results from laboratory experiments, Atmos. Chem. Phys., 12, 9817–9854, https://doi.org/10.5194/acp-12-9817-2012, 2012.
Ignatius, K., Kristensen, T. B., Järvinen, E., Nichman, L., Fuchs, C., Gordon, H., Herenz, P., Hoyle, C. R., Duplissy, J., Garimella, S., Dias, A., Frege, C., Höppel, N., Tröstl, J., Wagner, R., Yan, C., Amorim, A., Baltensperger, U., Curtius, J., Donahue, N. M., Gallagher, M. W., Kirkby, J., Kulmala, M., Möhler, O., Saathoff, H., Schnaiter, M., Tomé, A., Virtanen, A., Worsnop, D., and Stratmann, F.: Heterogeneous ice nucleation of viscous secondary organic aerosol produced from ozonolysis of α-pinene, Atmos. Chem. Phys., 16, 6495–6509, https://doi.org/10.5194/acp-16-6495-2016, 2016.
Jones, H. M., Flynn, M. J., DeMott, P. J., and Möhler, O.: Manchester Ice Nucleus Counter (MINC) measurements from the 2007 International workshop on Comparing Ice nucleation Measuring Systems (ICIS-2007), Atmos. Chem. Phys., 11, 53–65, https://doi.org/10.5194/acp-11-53-2011, 2011.
Kanji, Z. A. and Abbatt, J. P. D.: The University of Toronto Continuous Flow Diffusion Chamber (UT-CFDC): A Simple Design for Ice Nucleation Studies, Aerosol Sci. Tech., 43, 730–738, 910471828, https://doi.org/10.1080/02786820902889861, 2009.
Kanji, Z. A., Welti, A., Chou, C., Stetzer, O., and Lohmann, U.: Laboratory studies of immersion and deposition mode ice nucleation of ozone aged mineral dust particles, Atmos. Chem. Phys., 13, 9097–9118, https://doi.org/10.5194/acp-13-9097-2013, 2013.
Kanji, Z. A., Ladino, L. A., Wex, H., Boose, Y., Burkert-Kohn, M., Cziczo, D. J., and Krämer, M.: Overview of ice nucleating particles, Meteorol. Monogr., 58, 1.1–1.33, https://doi.org/10.1175/AMSMONOGRAPHS-D-16-0006.1, 2017.
Knopf, D. A., Alpert, P. A., and Wang, B. B.: The Role of Organic Aerosol in Atmospheric Ice Nucleation: A Review, Acs Earth Space Chem., 2, 168–202, https://doi.org/10.1021/acsearthspacechem.7b00120, 2018.
Kohn, M., Lohmann, U., Welti, A., and Kanji, Z. A.: Immersion mode ice nucleation measurements with the new Portable Immersion Mode Cooling chAmber (PIMCA), J. Geophys. Res.-Atmos., 121, 4713–4733, https://doi.org/10.1002/2016JD024761, 2016.
Kulkarni, G., Fan, J., Comstock, J. M., Liu, X., and Ovchinnikov, M.: Laboratory measurements and model sensitivity studies of dust deposition ice nucleation, Atmos. Chem. Phys., 12, 7295–7308, https://doi.org/10.5194/acp-12-7295-2012, 2012.
Lohmann, U. and Feichter, J.: Global indirect aerosol effects: a review, Atmos. Chem. Phys., 5, 715–737, https://doi.org/10.5194/acp-5-715-2005, 2005.
Lüönd, F., Stetzer, O., Welti, A., and Lohmann, U.: Experimental Study on the Ice Nucleation Ability of Size-Selected Kaolinite Particles in the Immersion Mode, J. Geophys. Res.-Atmos., 115, D14201, https://doi.org/10.1029/2009jd012959, 2010.
Marcolli, C.: Deposition nucleation viewed as homogeneous or immersion freezing in pores and cavities, Atmos. Chem. Phys., 14, 2071–2104, https://doi.org/10.5194/acp-14-2071-2014, 2014.
Murphy, D. M. and Koop, T.: Review of the vapour pressures of ice and supercooled water for atmospheric applications, Q. J. Roy. Meteor. Soc., 131, 1539–1565, https://doi.org/10.1256/qj.04.94, 2005.
Murray, B. J., O'Sullivan, D., Atkinson, J. D., and Webb, M. E.: Ice nucleation by particles immersed in supercooled cloud droplets, Chem. Soc. Rev., 41, 6519–6554, https://doi.org/10.1039/c2cs35200a, 2012.
Niedermeier, D., Augustin-Bauditz, S., Hartmann, S., Wex, H., Ignatius, K., and Stratmann, F.: Can we define an asymptotic value for the ice active surface site density for heterogeneous ice nucleation?, J. Geophys. Res.-Atmos., 120, 5036–5046, https://doi.org/10.1002/2014jd022814, 2015.
Niemand, M., Mohler, O., Vogel, B., Vogel, H., Hoose, C., Connolly, P., Klein, H., Bingemer, H., DeMott, P., Skrotzki, J., and Leisner, T.: A Particle-Surface-Area-Based Parameterization of Immersion Freezing on Desert Dust Particles, J. Atmos. Sci., 69, 3077–3092, https://doi.org/10.1175/Jas-D-11-0249.1, 2012.
Pruppacher, H. R. and Klett, J. D.: Microphysics of Clouds and Precipitation, Springer Publications, New York, USA, 954 pp., 1997.
Rogers, D. C.: Development of a continuous flow thermal gradient diffusion chamber for ice nucleation studies, Atmos. Res., 22, 149–181, https://doi.org/10.1016/0169-8095(88)90005-1, 1988.
Rogers, R. R. and Yau, M. K.: A Short Course in Cloud Physics, Pergamon Press, New York, USA, 99–120, 1989.
Schiebel, T.: Ice Nucleation Activity of Soil Dust Aerosols, PhD Dissertation, Institute for Meteorology and Climate Research – Atmospheric Aerosol Research (IMK-AAF), Karlsruhe, Germany, 131 pp., 2017.
Seinfeld, J. H. and Pandis, S. N.: Atmospheric Chemistry and Physics: From air pollution to climate change, 3rd edn., John Wiley & Sons, New York, USA, chap. 17, 2016.
Steinke, I., Funk, R., Busse, J., Iturri, A., Kirchen, S., Leue, M., Möhler, O., Schwartz, T., Schnaiter, M., Sierau, B., Toprak, E., Ullrich, R., Ulrich, A., Hoose, C., and Leisner, T.: Ice nucleation activity of agricultural soil dust aerosols from Mongolia, Argentina, and Germany, J. Geophys. Res.-Atmos., 121, 3559–13576, https://doi.org/10.1002/2016JD025160, 2016.
Stetzer, O., Baschek, B., Luond, F., and Lohmann, U.: The Zurich Ice Nucleation Chamber (ZINC) – A new instrument to investigate atmospheric ice formation, Aerosol Sci. Tech., 42, 64–74, https://doi.org/10.1080/02786820701787944, 2008.
Su, Y. Y., Miles, R. E. H., Li, Z. M., Reid, J. P., and Xu, J.: The evaporation kinetics of pure water droplets at varying drying rates and the use of evaporation rates to infer the gas phase relative humidity, Phys. Chem. Chem. Phys., 20, 23453–23466, https://doi.org/10.1039/c8cp05250f, 2018.
Tobo, Y., DeMott, P. J., Hill, T. C. J., Prenni, A. J., Swoboda-Colberg, N. G., Franc, G. D., and Kreidenweis, S. M.: Organic matter matters for ice nuclei of agricultural soil origin, Atmos. Chem. Phys., 14, 8521–8531, https://doi.org/10.5194/acp-14-8521-2014, 2014.
Ullrich, R., Hoose, C., Mohler, O., Niemand, M., Wagner, R., Hohler, K., Hiranuma, N., Saathoff, H., and Leisner, T.: A New Ice Nucleation Active Site Parameterization for Desert Dust and Soot, J. Atmos. Sci., 74, 699–717, https://doi.org/10.1175/Jas-D-16-0074.1, 2017.
Vali, G. and Snider, J. R.: Time-dependent freezing rate parcel model, Atmos. Chem. Phys., 15, 2071–2079, https://doi.org/10.5194/acp-15-2071-2015, 2015..
Vali, G., DeMott, P. J., Möhler, O., and Whale, T. F.: Technical Note: A proposal for ice nucleation terminology, Atmos. Chem. Phys., 15, 10263–10270, https://doi.org/10.5194/acp-15-10263-2015, 2015.
Westbrook, C. D. and Illingworth, A. J.: The formation of ice in a long-lived supercooled layer cloud, Q. J. Roy. Meteor. Soc., 139, 2209–2221, https://doi.org/10.1002/qj.2096, 2013.
Zenker, J., Collier, K. N., Xu, G., Yang, P., Levin, E. J. T., Suski, K. J., DeMott, P. J., and Brooks, S. D.: Using depolarization to quantify ice nucleating particle concentrations: a new method, Atmos. Meas. Tech., 10, 4639–4657, https://doi.org/10.5194/amt-10-4639-2017, 2017.





