A method for resolving changes in atmospheric He ∕ N₂ as an indicator of fossil fuel extraction and stratospheric circulation

The atmospheric $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ ratio is expected to increase due to the emission of He associated with fossil fuels and is expected to also vary in both space and time due to gravitational separation in the stratosphere. These signals may be useful indicators of fossil fuel exploitation and variability in stratospheric circulation, but direct measurements of $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ ratio are lacking on all timescales. Here we present a high-precision custom inlet system for mass spectrometers that continuously stabilizes the flow of gas during sample–standard comparison and removes all non-noble gases from the gas stream. This enables unprecedented accuracy in measurement of relative changes in the helium mole fraction, which can be directly related to the ⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ ratio using supplementary measurements of ${\mathrm{O}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}$, $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$ and CO₂. Repeat measurements of the same combination of high-pressure tanks using our inlet system achieves a $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ reproducibility of ∼ 10 per meg (i.e., 0.001 %) in 6–8 h analyses. This compares to interannual changes of gravitational enrichment at ∼ 35 km in the midlatitude stratosphere of order 300–400 per meg and an annual tropospheric increase from human fossil fuel activity of less than ∼ 30 per meg yr⁻¹ (bounded by previous work on helium isotopes). The gettering and flow-stabilizing inlet may also be used for the analysis of other noble-gas isotopes and could resolve previously unobserved seasonal cycles in $\mathrm{Kr}/{\mathrm{N}}_{\mathrm{2}}$ and $\mathrm{Xe}/{\mathrm{N}}_{\mathrm{2}}$.

1 Introduction

The atmospheric mole fraction of helium in dry air is typically ∼ 5.24 ppm (Glückauf, 1944), with an isotopic abundance of ⁴He about 10⁶ times greater than ³He. On geological timescales, the natural concentration of ⁴He in the atmosphere is set by a balance of ⁴He loss to space and ⁴He release from the Earth's crust, where it is produced by radioactive decay of uranium and thorium (Kockarts, 1973; Pierson-Wickmann et al., 2001; Sano et al., 2013; Torgersen, 1989; Zartman et al., 1961). Over the past century, human exploitation of fossil fuels likely has accelerated the release of crustal He (Boucher et al., 2018c; Lupton and Evans, 2013, 2004; Mabry et al., 2015; Oliver et al., 1984; Pierson-Wickmann et al., 2001; Sano et al., 1989), but direct observations of a secular increase in atmospheric ⁴He are lacking. Additionally, recent measurements and model simulations reveal a small depletion of the heavy gas argon in the stratosphere by gravitational separation (Belikov et al., 2019; Birner et al., 2020; Ishidoya et al., 2021, 2018, 2013, 2008; Sugawara et al., 2018), suggesting a corresponding enrichment of the light gas helium. Gravitational separation is only partially counteracted by the large-scale stratospheric circulation and mixing, which tends to homogenize the atmosphere. Variability in stratospheric circulation and stratosphere–troposphere exchange (STE) could therefore impact the degree of fractionation and cause additional interannual changes in the stratospheric and, to a much lesser extent, the tropospheric abundance of ⁴He.

Measurements of $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ may provide an alternative indicator of variations in stratospheric circulation and STE. An improved understanding of STE is critical because stratospheric circulation changes affect tropospheric trends of societally important greenhouse gases and geochemical tracers such as N₂O, CH₄, ¹⁴C, O₃ and chlorofluorocarbons (CFCs) (Arblaster et al., 2014; Graven et al., 2012; Hamilton and Fan, 2000; Hegglin and Shepherd, 2009; Montzka et al., 2018; Nevison et al., 2011; Simmonds et al., 2013). These gases all have significant sources or sinks in the stratosphere that cause strong stratosphere–troposphere concentration differences. Global circulation models consistently predict an acceleration of the stratospheric Brewer–Dobson circulation (BDC; Brewer, 1949; Dobson, 1956) under global warming (Butchart, 2014). Stratospheric circulation is also naturally modulated on a range of shorter timescales from synoptic-scale events to decadal variations (e.g., Holton et al., 1995; Li et al., 2012; Flury et al., 2013; Butchart, 2014; Ray et al., 2014). Circulation changes have typically been observed using measurements of numerous different trace gases in the stratosphere (e.g., CO₂, SF₆, H₂O, O₃, CO, or N₂O) (e.g., Bönisch et al., 2009; Engel et al., 2009, 2017; Ray et al., 2010; Haenel et al., 2015). However, interpretation of these tracers of stratospheric circulation is complicated by complex chemical sources, sinks and tropospheric histories, whereas gravitational fractionation of $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ is governed by comparatively simple physics and expected to increase smoothly in the troposphere.

Atmospheric $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ measurements may also provide an indication of the history of fossil fuel usage. Previous attempts to measure the fossil fuel signal in He have centered on measurements of changes in the atmospheric ${}^{\mathrm{3}}\mathrm{He}{/}^{\mathrm{4}}\mathrm{He}$ isotope ratio typically using multicollector, static vacuum mass spectrometers (Boucher et al., 2018c; Lupton and Evans, 2013, 2004; Mabry et al., 2015; Oliver et al., 1984; Sano et al., 1989). However, measurements of the ${}^{\mathrm{3}}\mathrm{He}{/}^{\mathrm{4}}\mathrm{He}$ ratio are fundamentally limited by the extremely low abundance of ³He (e.g., Mabry et al., 2015; Boucher et al., 2018c), with only about 1 in 730 000 He atoms being ³He. Therefore, the precision on individual ${}^{\mathrm{3}}\mathrm{He}{/}^{\mathrm{4}}\mathrm{He}$ analyses is currently limited to ∼ ±0.2 % (2σ). This is insufficient for the detection of the stratospheric and anthropogenic signals we are interested in, and which we estimate to cause variations in the atmospheric ⁴He abundance on the order of 0.0030 to 0.04 % yr⁻¹ (see Sect. 2.1 and 2.2.). Moreover, small changes in ³He from radioactive decay of tritium in nuclear warheads may complicate the interpretation of ${}^{\mathrm{3}}\mathrm{He}{/}^{\mathrm{4}}\mathrm{He}$ results (e.g., Boucher et al., 2018c; Lupton and Evans, 2004).

Thus far, the most promising direct measurements of the atmospheric ⁴He mixing ratio were produced by Holland and Emerson (1987). Holland and Emerson repeatedly introduced sample and standard air into a mass spectrometer through a charcoal trap to concentrate helium. However, their method also only achieved an instrument precision of 0.22 % (2σ) and is thus not suitable for the science discussed above.

Here we describe a method to measure relative differences in ⁴He mole fraction (${}^{\mathrm{4}}\mathrm{He}/\mathrm{M}$) between two large samples of air using a custom mass spectrometer inlet system. The helium mole fraction can later be mathematically translated to our target ratio, ⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$, given supplementary measurements of O₂, Ar, and CO₂ (see discussion). This is advantageous because N₂ is near-constant in the atmosphere, making ⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ more readily interpretable than ${}^{\mathrm{4}}\mathrm{He}/\mathrm{M}$. The ${}^{\mathrm{4}}\mathrm{He}/\mathrm{M}$ method depends on stabilization of the airflow to the ion source between a sample and standard gas to achieve high-precision differencing. Novel elements in our setup include continuous-flow removal of reactive gases via titanium gettering immediately upstream of the mass spectrometer inlet and the use of an actively controlled open split (Henneberg et al., 1975) for balancing pressures upstream of a shared capillary directed towards the mass spectrometer. Gas handling techniques, the inlet system and the continuous-flow getter oven are described in detail below.

1.1 Gravitational fractionation of $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ in the stratosphere

The notion that the stratospheric and tropospheric $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ ratio must vary in response to fluctuations in stratospheric circulation is based on studies of the atmospheric $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$ ratio (Birner et al., 2020; Ishidoya et al., 2021). Relative changes in the $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$ ratio (or $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) are commonly expressed in delta notation:

$$\begin{array}{}\text{(1)}& \mathit{\delta }\left(\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}\right)={\displaystyle \frac{{\left(\frac{\mathrm{Ar}}{{\mathrm{N}}_{\mathrm{2}}}\right)}_{\mathrm{SA}}}{{\left(\frac{\mathrm{Ar}}{{\mathrm{N}}_{\mathrm{2}}}\right)}_{\mathrm{ST}}}}-\mathrm{1},\end{array}$$

where subscripts SA and ST refer to the ratio in a sample and a standard gas mixture, respectively. δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$) is multiplied by 10⁶ and expressed in per meg units.

Sensitivity tests with the 2-D chemical–dynamical–radiative model of the atmosphere SOCRATES by Ishidoya et al. (2021) indicate that significant temporal changes in stratospheric $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$ should occur in response to an acceleration or deceleration of the BDC. The simulations also suggest a weak stratospheric influence on tropospheric $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$. Ishidoya et al. (2021) find that imposing a gradual acceleration of the BDC of 4 % per decade leads to a 40 per meg per decade increase in δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$) at ∼ 35 km altitude in northern midlatitudes and a corresponding 1.3 per meg per decade decrease in δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$) in the troposphere. Furthermore, they find that imposing 3-year periodic changes of 10 % in BDC yields anomalies of ±25 and ±0.4 per meg in stratospheric and tropospheric δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$), respectively. Tropospheric observations of δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$) by Ishidoya et al. (2021) would be consistent with larger STE-induced interannual changes of tropospheric $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$. Variability of the BDC on the order of 10 % or more on seasonal to decadal timescales is consistent with published estimates (Flury et al., 2013; Ray et al., 2014; Salby and Callaghan, 2006).

The atmospheric $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ ratio must be more strongly impacted by gravitational fractionation than $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$ due to the larger mass difference and higher diffusivity of He than Ar, which brings He closer to gravitational equilibrium. The gravitational fractionation effect on $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ can be scaled from $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$ (Birner et al., 2020) using the molar mass difference to air ΔM_i ($\mathrm{\Delta }{M}_i=M_i-\mathrm{0.02896}$ kg mol⁻¹) and the molecular diffusivity D_i of gas i in air as

$$\begin{array}{}\text{(2)}& \begin{array}{rl}\mathit{\delta }\left({\displaystyle \frac{\mathrm{He}}{{\mathrm{N}}_{\mathrm{2}}}}\right)& ={\displaystyle \frac{{\left(\frac{\mathrm{He}}{{\mathrm{N}}_{\mathrm{2}}}\right)}_{\mathrm{SA}}}{{\left(\frac{\mathrm{He}}{{\mathrm{N}}_{\mathrm{2}}}\right)}_{\mathrm{ST}}}}-\mathrm{1}\\ & \approx {\displaystyle \frac{D_{\mathrm{He}}^{\mathrm{air}}\mathrm{\Delta }{M}_{\mathrm{He}}-D_{{\mathrm{N}}_{\mathrm{2}}}^{\mathrm{air}}\mathrm{\Delta }{M}_{{\mathrm{N}}_{\mathrm{2}}}}{D_{\mathrm{Ar}}^{\mathrm{air}}\mathrm{\Delta }{M}_{\mathrm{Ar}}-D_{{\mathrm{N}}_{\mathrm{2}}}^{\mathrm{air}}\mathrm{\Delta }{M}_{{\mathrm{N}}_{\mathrm{2}}}}}\mathit{\delta }\left(\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}\right).\end{array}\end{array}$$

Using the Fuller method (Reid et al., 1987), $D_{\mathrm{He}}^{\mathrm{air}}$ is 3.6 (3.5) times greater than $D_{\mathrm{Ar}}^{\mathrm{air}}$ ($D_{{\mathrm{N}}_{\mathrm{2}}}^{\mathrm{air}}$), and ΔM_He is more than twice as large and opposite in sign than ΔM_Ar ($\mathrm{\Delta }{M}_{\mathrm{He}}=-\mathrm{0.02496},\mathrm{\Delta }{M}_{\mathrm{Ar}}=\mathrm{0.01102},\mathrm{\Delta }{M}_{{\mathrm{N}}_{\mathrm{2}}}=-\mathrm{0.0009466}$). This makes δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) $\sim -\mathrm{7.5}$ times more strongly fractionated by gravity than δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$) in the stratosphere but in opposite direction.

1.2 Other controls on tropospheric $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$

A variety of known natural processes influence tropospheric ⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ and are summarized in Fig. 1 and Table 1. Natural ⁴He release from the Earth's crust is mediated by volcanism, ground water discharge and diffusive leakage. At the same time, helium is lost to space by thermal and non-thermal escape (Kockarts, 1973; Oliver et al., 1984; Pierson-Wickmann et al., 2001; Sano et al., 2013; Torgersen, 1989). Based on these natural fluxes and the total atmospheric burden, the atmospheric residence time of ⁴He is estimated to be ∼ 1 million years.

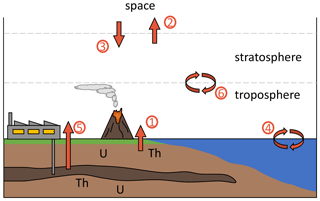
Figure 1 Schematic depiction of ⁴He fluxes to and from the troposphere. Different processes are numbered and listed in Table 1.

Table 1 Processes contributing to variations in the tropospheric and stratospheric ⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ ratio.

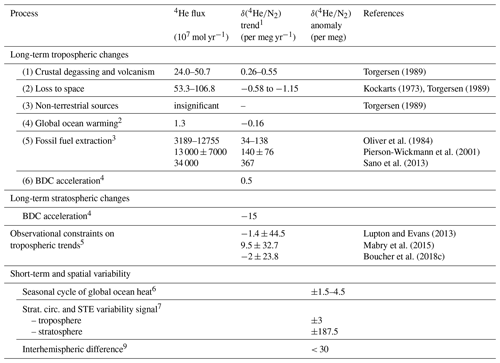
¹ δ(⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) trends are calculated using first column and assuming total atmospheric ⁴He = 9.268 × 10¹⁴ moles. N₂ changes are generally neglected except for ocean degassing. Tropospheric trends are globally uniform because the troposphere is well mixed. Stratospheric trend estimates are given for 35 km in the midlatitude Northern Hemisphere.
² Calculated from ⁴He and N₂ solubility changes (Hamme and Emerson, 2004; Weiss, 1971) for an ocean heat content trend of 10 ZJ yr⁻¹ at a mean water temperature of 10 ^∘C.
³ Oliver et al. (1984) includes natural gas, coal and uranium; Pierson-Wickmann et al. (2001) and Sano et al. (2013) include natural gas, petroleum and coal.
⁴ δ(⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) rescaled from δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$) assuming 7.5× greater gravitational separation. The secular δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$) trend was simulated in the SOCRATES model for an accelerating BDC scenario (+4 % per decade) by Ishidoya et al. (2021). The δ(⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) trend is adjusted to reflect a more plausible BDC acceleration of +2 % per decade.
⁵ Observed ${}^{\mathrm{3}}\mathrm{He}{/}^{\mathrm{4}}\mathrm{He}$ trends are translated to ⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ trends assuming ${}^{\mathrm{3}}\mathrm{He}{/}^{\mathrm{4}}\mathrm{He}$ = 3 × 10⁻⁸ for fossil fuel associated helium (Sano et al., 2013).
⁶ Scaled from seasonal δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$) changes of 5–15 per meg (Keeling et al., 2004) using the solubility–temperature dependency of He, N₂ and Ar in a 10 ^∘C warm surface ocean (Hamme and Emerson, 2004; Weiss, 1971).
⁷ Tropospheric and stratospheric δ(⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) rescaled from δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$). Ishidoya et al. (2021) report a ±0.4 and ±25 per meg δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$) change in the troposphere and stratosphere in the SOCRATES model for a sinusoidal ±5 % change in BDC strength over 3 years.
⁸ Assuming that industrial He release is confined to the Northern Hemisphere and assuming an annual δ(⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) increase of ∼ 30 per meg (consistent with the current observational error) yields an interhemispheric δ(⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) difference < 30 per meg. Differences in STE of He between the hemispheres are neglected here but could be important.

Over the few last centuries, He release from fossil fuel extraction has dwarfed the natural release rates of ⁴He by several orders of magnitude. Based on knowledge of fossil fuel usage and He content of the material (Table 1), the additional ⁴He release rate is estimated to be of order 3 to 30 × 10¹⁰ mol yr⁻¹ (e.g., Oliver et al., 1984; Sano et al., 1989, 2013; Pierson-Wickmann et al., 2001), implying that ${}^{\mathrm{3}}\mathrm{He}{/}^{\mathrm{4}}\mathrm{He}$ should be decreasing at rates between 35 and 350 per meg yr⁻¹. However, in contrast to these predictions and some earlier observations (Oliver et al., 1984; Pierson-Wickmann et al., 2001; Sano et al., 2010, 1989), no significant trend in atmospheric ${}^{\mathrm{3}}\mathrm{He}{/}^{\mathrm{4}}\mathrm{He}$ has been observed using archived air samples spanning from the beginning of the 20th century to today. These more recent observations bound any trend in ${}^{\mathrm{3}}\mathrm{He}{/}^{\mathrm{4}}\mathrm{He}$ to within roughly ±30 per meg yr⁻¹ (2σ), suggesting similarly small increase rates in δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) (Boucher et al., 2018c; Lupton and Evans, 2013, 2004; Mabry et al., 2015).

He release from fossil fuel extraction is also expected to impose an interhemispheric gradient in δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$). A rough upper bound can be estimated by assuming all fossil-fuel-derived He emissions occur in the Northern Hemisphere, and interhemispheric mixing of the atmosphere has a timescale of about one year. This would yield a north–south difference of 30 per meg, equal to the expected annual rise in δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$).

Seasonal and long-term ocean warming can cause small changes in $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$, mainly due to the impact on N₂. From observations of δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$) (Keeling et al., 2004) and solubility data of Ar, He and N₂ (Hamme and Emerson, 2004; Weiss, 1971), we estimate that the impact on $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ of air–sea exchanges is on the order of 0.16 per meg yr⁻¹ for the secular ocean warming trend and 3–9 per meg for seasonal heat exchanges. Therefore, the ratio of stratospheric signals to ocean warming is ∼ 12 times greater for $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ than $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$, and the effect of slow ocean warming is over 2 orders of magnitude smaller than the influence of fossil fuel exploitation.

The $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ ratio could also be impacted by processes changing atmospheric N₂. However, the annual removal of 7.5 × 10¹² mol N₂ yr⁻¹ by anthropogenic nitrogen fixation in agriculture, combustion and industry is clearly negligible compared to the ∼ 1.4 × 10²⁰ moles of N₂ in the whole atmosphere (Fowler et al., 2013). Volcanic emissions of N₂ are likewise negligible, on the order of 10⁹ mol yr⁻¹.

2 Methods

Our $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ analysis method relies on measuring the helium mole fraction relative difference between an air sample and a standard gas using a single collector for ⁴He⁺ on a magnetic sector mass spectrometer (MS). Crucially, whole dry air is pressure stabilized to a high level prior to gettering, so that the beam intensity ratio being measured is effectively the ⁴He-to-air ratio. Measurements of the He mole fraction difference can also be expressed similarly to Eq. (1) as δ(${}^{\mathrm{4}}\mathrm{He}/\mathrm{M}$), where M is total moles. By applying small corrections for variations in ${\mathrm{O}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}$, $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$ and CO₂, the quantity δ(${}^{\mathrm{4}}\mathrm{He}/\mathrm{M}$) is easily related to δ(⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$).

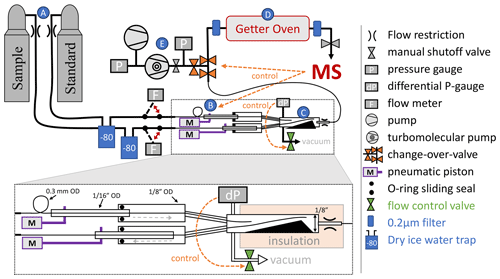
Figure 2 Schematic depiction of the flow-stabilizing MS inlet system. Dashed orange arrows highlight important control pathways, and letters A–E in blue circles label the main sections of the inlet system. Red double arrows indicate the manual switching option in the inlet system. Sample or standard gas is delivered from high-pressure cylinders (A). The flow can be measured by two Omron flow meters before entry into the pressure stabilization chamber (C). Pistons (B) alternately move fine metal tubing in the pressure stabilization chamber, pushing either the sample or standard gas stream deeper into the stabilization chamber where the gas will be picked up by a single capillary leading to the MS. A sliding seal is made using lubricated O-rings between $\mathrm{1}/\mathrm{8}$ (0.3175 cm) and $\mathrm{1}/\mathrm{16}$ in. (0.15875 cm) o.d. tubing at the entry to the pressure-stabilized chamber. This ensures sufficient rigidity and protects the fine metal tubing inside. The chamber is exhausted to a vacuum system and the pressure is monitored and controlled by a differential pressure gauge combined with an automatic MKS flow control valve. The stainless-steel getter oven (D) has an inner diameter of $\mathrm{1}/\mathrm{2}$ in. (1.27 cm) and is filled with 10–12 g of titanium sponge. 2 µm filters prevent particles from contaminating the MS and gas delivery system. In case of an anomalous pressure change in the MS or when venting the getter oven, the getter oven can be isolated from the pressure-stabilization chamber with a changeover valve controlled directly by the MS software. The entire inlet vacuum system is backed by a diaphragm vacuum pump and a turbomolecular pump (E). A manual shutoff valve can isolate the getter oven from the MS.

The MS is interfaced to a custom inlet system with online gettering and active flow stabilization using an actively pressure controlled open split (Henneberg et al., 1975), as shown in Fig. 2.

2.1 The inlet system

The design of the inlet system incorporates elements of an open split (Henneberg et al., 1975) but further stabilizes the pressure using active control elements and allows active switching between a sample (SA) and reference standard gas stream (ST). Pneumatically actuated pistons (B in Fig. 2) alternately slide 0.3 mm tubes exhausting sample or standard gas close to a shared intake capillary, which is placed at the end of the stabilization chamber (C in Fig. 2) and connects the chamber to the getter oven and MS. Air actuation of the pistons is controlled by the MS through an electronic valve assembly (Clippard, model EMS-08). The flexible 0.3 mm tubes are mounted leak tight inside sturdier $\mathrm{1}/\mathrm{16}$ in. (0.15875 cm) o.d. tubing, which is fixed to the piston and moved with a stroke length of 7 cm. A sliding seal is made between the $\mathrm{1}/\mathrm{8}$ in. (0.3175 cm) o.d. outer tubing and the $\mathrm{1}/\mathrm{16}$ in. (0.15875 cm) o.d. tubing using a compressed O-ring lubricated with TorrLube vacuum grease. This setup creates a movable feedthrough port for the 0.3 mm tubes containing sample and standard gas and the pressure stabilization chamber, thus allowing the chamber to be operated at a selected pressure above or below ambient. The default setting is 14 psia (96.5 kPa).The chamber is shaped as a funnel to guide the sliding tubing into a reproducible resting position. Variations in chamber pressure are measured with a 0.2 Torr MKS 223B differential pressure gauge and are limited to better than 1 part in 10⁶ by opening an MKS type 248 control valve, which allows most of the gas in the stabilization chamber to be pumped away by a vacuum pump. The valve is controlled via an MKS 250E control module. The shared outlet capillary from the pressure-stabilization chamber is crimped and thermally insulated to avoid changes in conductance and thus airflow caused by room temperature fluctuations. The pressure in the getter oven (D in Fig. 2) is about 2 mTorr (0.3 Pa) because the getter material effectively acts as a vacuum pump.

2.2 Continuous-flow gettering

In the getter chamber (D in Fig. 2), 99.9 % pure titanium sponge (Ti) irreversibly reacts with N₂, O₂, CO₂ and other non-noble gases in air to form titanium nitride (TiN), titanium dioxide (TiO₂), titanium carbide (TiC) and other compounds at ∼ 850 ^∘C. This increases the concentration of He in the gas mixture by a factor of about 100, boosting precision. The getter oven has an inner diameter of 0.94 cm and a length of 22.5 cm. It is manufactured from heat-resistant stainless steel (SS310) and equipped with VCR face seals for easy maintenance. The temperature of the getter oven is determined by manually adjusting the power provided to two OMEGA CRWS semi-cylindrical heaters surrounding the getter. The heaters are additionally equipped with an independent limit controller for safety.

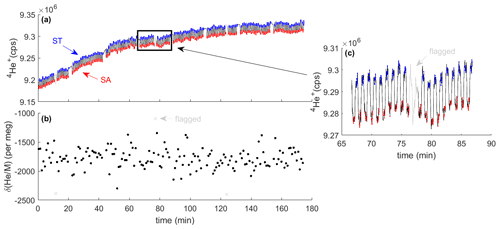
Figure 3 Typical analysis results from the measurement of two high-pressure cylinders. The MS monitors the ⁴He⁺ ion beam during switching between sample (SA) and standard (ST) gas (a). Red and blue shaded data points highlight the periods used for integration and calculation of the delta value (b). They are separated by idle times (black lines) to allow complete flush-out after switching. Data are quality controlled and flagged periods are shown in gray. Inset (c) shows one block of 20 sample–standard comparisons, including one pair of cycles that was flagged as an outlier.

The gettering efficiency depends on the heaters' temperature and must be balanced against material tolerance and increased evolution of H₂ gas from the metal in the getter. H₂ forms a solid solution in Ti and is continuously released to the gas stream when Ti is heated. The solution process is reversible and H₂ is absorbed if the Ti is cooled down. H₂ could interact with He⁺ in the source or combine with ionized gas to form hydride compounds such as ArH⁺ (Fig. 3). However, since the H₂ flux into the gas stream varies slowly compared to the 30 s timescale of switching between sample and standard gas, the impact of H⁺ cancels during sample–standard comparison. In its current size (∼ 10–12 g Ti), the getter can be used for 70–80 h before the Ti must be replaced to prevent N₂ breakthrough. This requires breaking vacuum in the inlet approximately once every 4 weeks depending on usage. After replacement, fresh titanium is gradually heated to 900 ^∘C over ∼ 12 h in isolation from the MS to allow degassing without contaminating the MS. A coarse mesh of metal wire and 2 µm SWAGELOK filters on both sides of the getter prevent getter-derived dust from entering the vacuum system and MS.

2.3 Inlet operation

We have developed customized scripts using the software Isodat provided with any MAT 253 mass spectrometer to control the inlet system and operate the pneumatic actuators for $\mathrm{He}/\mathrm{M}$ analysis (Fig. 3). In a typical run, the instrument performs sample–standard gas switching with a ∼ 30 s switching time (∼ 60 s full cycle), using a conservative 18 s idle time to allowing the MS signal to stabilize before integration. As is customary in dynamic MS noble-gas application, we group each analysis into blocks consisting of (i) adjusting the accelerating voltage to find the center of the ⁴He peak followed by (ii) 20 sample–standard comparisons. Background concentrations of ⁴He in the MS are determined by closing the inlet upstream of the getter oven and subtracted daily. Data are quality controlled, and anomalous cycles are rejected when delta values deviate by more than 3 standard deviations from the smoothed time series or when there are abrupt changes detected in the ion beam associated with instability in the MS source (not shown). Isodat also monitors the MS source pressure and closes the external changeover valve (Fig. 2) to protect the MS in case of a pressure control failure.

2.4 Gas handling and sample delivery systems

Air is delivered to the inlet system from a pair of high-pressure gas cylinders (A in Fig. 2). For $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ standard gas, we rely on compressed dry air stored in high-pressure cylinders, as is conventional for atmospheric measurements of ${\mathrm{O}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}$, CO₂ and $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$ (Keeling et al., 2007). All cylinders are stored horizontally for 2 d in a thermal enclosure at ambient temperature before analysis to minimize the risk of thermal fractionation. The pressure is dropped to slightly above ambient directly at the head valve of high-pressure cylinders using capillaries rather than regulators. The use of capillaries ensures that all wetted parts are exclusively metal, which is impermeable to He, and eliminates problems we encountered using regulators during initial tests. Due to the use of capillaries, the gas delivery system cannot be evacuated efficiently and instead must be purged for several hours ahead of analysis until the signal stabilizes. The flow rates in the lines are monitored using 0.1 L min⁻¹ Omron DF6-P flow meters and are manually balanced at around 27–28 cm³ min⁻¹ before every analysis by adjusting the crimping of both 316 stainless-steel capillaries. Sample and standard gas streams are both dried before entering the pressure stabilization chamber (C in Fig. 2) by flowing through U-shaped cold traps made from about 25 cm of $\mathrm{1}/\mathrm{4}$ in. (0.635 cm) stainless-steel tubing. The traps are held at about −80 ^∘C by submerging the metal tubing in a dry ice and ethanol mixture for the duration of the analysis.

2.5 Converting δ($\mathrm{He}/\mathrm{M}$) to δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$)

δ($\mathrm{He}/\mathrm{M}$) can be related to δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) using

$$\begin{array}{}\text{(3)}& \begin{array}{rl}\mathit{\delta }\left(\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}\right)& \simeq \mathit{\delta }\left(\mathrm{He}/\mathrm{M}\right)+\mathit{\delta }\left({\mathrm{O}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}\right)X_{{\mathrm{O}}_{\mathrm{2}}}+\mathit{\delta }\left(\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}\right)X_{\mathrm{Ar}}\\ & +\mathrm{d}{X}_{{\mathrm{CO}}_{\mathrm{2}}}\end{array}\end{array}$$

as derived in Box 1, using independent measurements of δ(${\mathrm{O}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}$), δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$) and d$X_{{\mathrm{CO}}_{\mathrm{2}}}$ (Keeling et al., 2004, 1998). These corrections are relatively small and therefore do not significantly contribute to the overall uncertainty of δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$). Analytical uncertainty for measurements of δ(${\mathrm{O}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}$), δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$) and d$X_{{\mathrm{CO}}_{\mathrm{2}}}$ is typically better than 1.5 per meg, 11 per meg and 0.2 ppm (Keeling et al., 1998, 2004), yielding uncertainties of 0.3, 0.11 and 0.2 per meg in the terms $\mathit{\delta }\left({\mathrm{O}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}\right)X_{{\mathrm{O}}_{\mathrm{2}}}$, $\mathit{\delta }\left(\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}\right)X_{\mathrm{Ar}}$ and d$X_{{\mathrm{CO}}_{\mathrm{2}}}$. The long-term atmospheric changes in δ(${\mathrm{O}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}$) ∼ −19 per meg yr⁻¹ and d$X_{{\mathrm{CO}}_{\mathrm{2}}}$ ∼ 2.5 ppm yr⁻¹ yield corrections of approximately −4 and +2.5 per meg yr⁻¹, respectively. The seasonal variations in δ(${\mathrm{O}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}$)X${}_{{\mathrm{O}}_{\mathrm{2}}}$ and d$X_{{\mathrm{CO}}_{\mathrm{2}}}$ partly cancel, yielding net seasonal corrections of ∼ 10 per meg in both hemispheres. The term δ($\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$)X_Ar contributes variations less than 1 per meg on all timescales.

Box 1 Deriving the helium-to-nitrogen ratio from δ($\mathrm{He}/\mathrm{M}$).

3 Results

3.1 Gettering performance

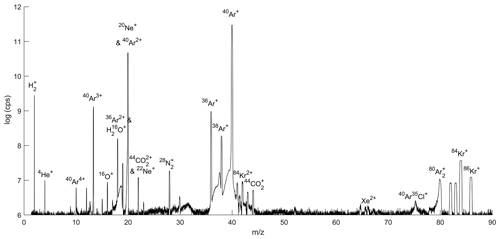
A mass scan of air introduced through the gettering and flow-stabilizing inlet system revealed that N₂ and O₂ are almost completely removed from the air by the online getter (Fig. 4). He is effectively preconcentrated in the gas mixture. ⁴⁰Ar ions with one or more charges yield the largest beams in the scan followed by ³⁶Ar, with H₂ evolving from the hot metal in the getter oven.

Figure 4 Mass scan of ambient air. Ion beam intensity is shown as the logarithm of the ions counted per second, and select ion species are labeled.

3.2 Response time

Our setup demonstrates the ability to transition between sample and standard gas with an e-folding timescale of ∼ 4 s (Fig. 5). The e-folding time is primarily controlled by the volume of the getter and the total flow of gas through the getter. Regions of the inlet system upstream of the getter experience $\sim \mathrm{100}\times$ faster flushing than downstream of the getter because the gas upstream still contains N₂ and O₂ and hence flows much faster. An associated large drop in pressure however ensures that all parts of the inlet system are flushed out similarly quickly. The e-folding time does not change substantially over the life span of the getter.

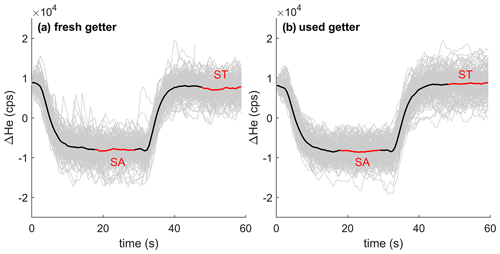
Figure 5 Stack of ⁴He ion count difference (10⁴ counts per second, cps) when switching between the same standard (ST) and sample (SA) gas stream using fresh titanium sponge (a) and nearly depleted getter material (b). Gray lines show individual records forced to align at time equals zero, and the thick black line shows the average of all stacked switching events. The analysis cycle consists of (i) switching to SA with an idle time of ∼ 18 s, (ii) a ∼ 12 s integration of ions from SA, (iii) switching back to ST, again with a ∼ 18 s idle time, and finally (iiii) a ∼ 12 s integration of ST.

3.3 Analytical precision

Using the default 60 s sample–standard cycle, the gettering and flow-stabilizing inlet system achieves an internal precision in δ($\mathrm{He}/\mathrm{M}$) of approximately ±15 per meg over 1.5 h and ±8 per meg for samples run 6 h or longer (1σ, standard error of ∼ 90 and ∼ 360 cycles respectively). The (external) reproducibility of repeated 6–8 h measurements of the same sample and standard gas cylinder combination is comparable and essentially as expected from the shot noise on the ⁴He ion current (Figs. 6 and 7).

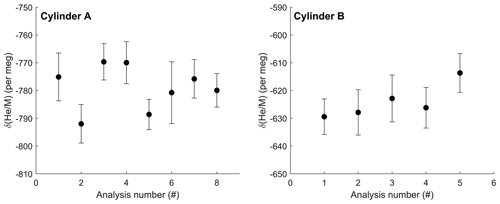
Figure 6 Repeat δ($\mathrm{He}/\mathrm{M}$) analysis of two high-pressure cylinders against ambient La Jolla air collected in 2019. Each data point shown is the average of at least 300 individual 12 s measurements with 1σ error bars representing the standard error of each measurement. Repeat analyses show a standard deviation of 8.1 and 6.3 per meg (1σ) for cylinder A and cylinder B respectively. Analysis 6 for cylinder A was shorter, resulting in a larger uncertainty for that measurement. Data are not corrected for zero enrichment effects discussed in the text.

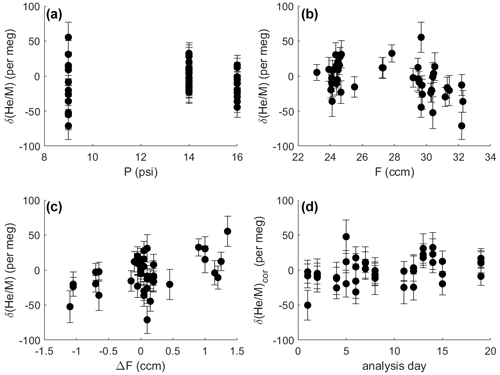
Figure 7 Difference in δ($\mathrm{He}/\mathrm{M}$) between two identical gas streams (i.e., the zero enrichment) measured repeatedly under different conditions over 1.5–3 h. Error bars show 1σ uncertainty (internal precision). Measurements were made at different pressure levels (a), with slightly varying gas flows to the stabilization chamber (b) and imbalances in flow between the SA and ST side (c). The same shared capillary was used for all analysis. Therefore, the pressure in the stabilization chamber controls the intensity of the ion beam and the internal precision of the analysis, illustrated by the greater scatter of observations at 9 psi (62.1 kPa). Delta values shown in panel (d) were corrected for the influence of pressure, mean flow and flow imbalance according to coefficients found by multiple linear regression (see text). For a pressure of 14 psi (96.5 kPa), corrected delta values generally show scatter as expected from shot-noise behavior, and corrected delta values are stable over time.

The zero enrichment, i.e., the delta value observed when introducing the same gas through sample and standard side of the inlet, is generally small and stable over time. It is tested by mounting the crimped delivery capillaries (A in Fig. 2) to a tee fitting, which splits the gas stream at high pressure from a single tank of air. This tee minimizes thermal fractionation by dividing the flow at a junction machined into the center of a large brass block (Keeling, 1988). Identical delta values (within error) obtained after reversing the outlet from the tee demonstrate that no measurable fractionation occurs within the tee and therefore that the zero enrichment reflects a persistent asymmetry somewhere downstream, most likely within the pressure stabilization chamber. The typical zero enrichment varies slightly with the mean flow of gas into the stabilization chamber (F), the pressure in the chamber (P), and the flow offset between the SA and ST side (ΔF) before entering the stabilization chamber (Fig. 7). Weighted multiple linear regression analysis using three different pressure levels (9, 14 and 16 psi – i.e, 62.1, 96.5 and 110.3 kPa) and predictors F, P and ΔF reveals that the zero enrichment value decreases by 2.8 ± 0.9 per meg for each cubic centimeter per minute change in mean flow away from 27.5 cm³ min⁻¹ and increases by 17.2 ± 4.8 per meg for each cubic centimeter per minute flow imbalance between SA and ST (1σ). The dependence of δ($\mathrm{He}/\mathrm{M}$) on F and ΔF is significant at the 5 % level. For a balanced flow of 27.5 cm³ min⁻¹ and a pressure of 62.1, 96.5 and 110.3 kPa in the stabilization chamber, the mean zero enrichment is −9.61 ± 7.2, 1 ± 3.7 and −15.7 ± 4.7 per meg, respectively. For actual measurements, P is held constant at 96.5 kPa with very high precision. F and ΔF are stable over 8 h to within ±0.2 cm³ min⁻¹. This typically yields a correction for mean gas flow and flow imbalance of less than 10 per meg with an uncertainty smaller than 6 per meg, which increases the overall analytical uncertainty in repeat tank analysis from 8 to 10 per meg.

4 Discussion

The gettering and flow-stabilizing inlet system has demonstrated the ability to determine the helium mole fraction difference between a sample and standard gas, δ($\mathrm{He}/\mathrm{M}$), to about 10 per meg in a single 6–8 h analysis and has a range of possible applications. Our primary targets are (i) to use stratospheric δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) as a tracer of the large-scale stratospheric circulation and (ii) to evaluate tropospheric δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) trends as a possible indicator of anthropogenic fossil fuel exploitation.

We expect an excellent signal-to-noise ratio for the detection of stratospheric changes in δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$). Interannual variability in stratospheric δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) is likely on the order 300–400 per meg (Table 1). Repeat 6–8 h measurements of a high-pressure cylinder currently achieve a precision of ∼ 10 per meg, or about 40 times less than the stratospheric signal. Associated changes in tropospheric δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$), in contrast, are likely much smaller at around 6 per meg and therefore at or below the current limit of detection even after averaging of multiple samples.

Tropospheric $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ measurements can help quantify the anthropogenic ⁴He release over time due to fossil fuel extraction (Boucher et al., 2018c; Lupton and Evans, 2013, 2004; Mabry et al., 2015; Oliver et al., 1984; Sano et al., 2010, 1989). Although theoretical predictions clearly support an anthropogenic ⁴He increase, past observational studies produced conflicting evidence. Recent improvements in analytical methods and sampling have narrowed the uncertainty in ${}^{\mathrm{3}}\mathrm{He}{/}^{\mathrm{4}}\mathrm{He}$ trend estimates to < 30 per meg yr⁻¹ with a mean statistically indistinguishable from zero (Table 1). However, with a precision of ∼ 10 per meg on single samples, measurements of δ(⁴$\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) on decades-old archived air may allow trend detection to ∼ 1 per meg yr⁻¹ or better, while also avoiding possible complications from ³He emissions that could bias estimates of the ⁴He source from ${}^{\mathrm{3}}\mathrm{He}{/}^{\mathrm{4}}\mathrm{He}$.

Another possible application is the investigation of spatial gradients in atmospheric δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) caused by the distribution of local volcanic or anthropogenic sources (e.g., Sano et al., 2010; Boucher et al., 2018a, b). High-precision δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) may allow the detection of diffuse helium release in regions of volcanic activity (Boucher et al., 2018b). Furthermore, global north–south δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) gradients from anthropogenic emission sources concentrated in the Northern Hemisphere are likely on the order of 10s of per meg and thus may also be detectable directly. Alternatively, studies could target more local gradients around oil or natural gas facilities that are likely even greater.

The method developed here is potentially applicable to measure the abundance of any noble gas in air. The intensity of the ion beam and thus the precision for different noble gases depends on their natural abundance and ionization efficiency in the MS source. ²⁰Ne and ²²Ne have isobaric interferences from doubly charged Ar and CO₂, but Kr and Xe yield usable ion beams (Table 2). We estimate a precision of ∼ 5 and ∼ 19 per meg for repeat 6–8 h analyses of δ(${}^{\mathrm{84}}\mathrm{Kr}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}}$) and δ(${}^{\mathrm{129}}\mathrm{Xe}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}}$) respectively, by assuming that precision scales with the square root of the total ions counted as expected from shot-noise behavior. This estimate compares favorably to the precision currently reported in conventional dual-inlet mass spectrometry studies (Baggenstos et al., 2019; Bereiter et al., 2018). For example, Baggenstos et al. (2019) achieved a precision of 88 per meg and 203 per meg for repeat ∼ 2h analyses of δ(${}^{\mathrm{84}}\mathrm{Kr}{/}^{\mathrm{40}}\mathrm{Ar}$) and δ(${}^{\mathrm{132}}\mathrm{Xe}{/}^{\mathrm{40}}\mathrm{Ar}$) in ambient air, respectively.

Table 2 Summary of observed ion beams in Fig. 4. Relative ion beam intensities on MAT 253 are calculated from the scan with identical source tuning. Xe isotope beams were not observed but scaled from previous observations in the lab.

^∗ Xe isotopes were not measured directly here because of the limited dynamic range
of the MAT 253 when set to measure He. Instead we report expected Xe ion beam intensities that were calculated using Kr ion beam intensities from this experiment
and relative ion beam yields of Kr and Xe determined on a separate MAT 253 in the
lab.

The improved precision enabled by our inlet system should be sufficient to resolve the previously unobserved annual cycle of Kr and Xe caused by the seasonal release and uptake of both gases by the ocean as it warms and cools. The seasonal cycle of δ(${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}}$) has an amplitude of 5–15 per meg in the extratropics (Keeling et al., 2004). δ(${}^{\mathrm{84}}\mathrm{Kr}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}}$) and δ(${}^{\mathrm{132}}\mathrm{Xe}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}}$), however, are ∼ 3.4 and ∼ 8.9 times more sensitive than δ(${}^{\mathrm{40}}\mathrm{Ar}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}}$) to changes in ocean temperature owing to the different temperature dependences of Ar, Kr and Xe solubility in seawater (Hamme and Emerson, 2004; Jenkins et al., 2019). This implies that seasonal variations in δ(${}^{\mathrm{84}}\mathrm{Kr}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}}$) and δ(${}^{\mathrm{132}}\mathrm{Xe}{/}^{\mathrm{28}}{\mathrm{N}}_{\mathrm{2}}$) have a magnitude of 17–51 and 45–134 per meg, respectively, which would be readily resolved if the precision of our system scales as expected with signal strength.

The gettering inlet and MS system was applied here only for single ion (He⁺) detection but alternately could be applied for multi-ion collection. The acquisition of Kr and Xe isotope ratios for example would provide valuable additional information for detecting artifactual fractionation during sampling and allow further improvements in precision by increasing the total number of ions collected.

The need for only a single ion detector also allows the gettering and flow-stabilizing inlet to be interfaced with simpler and more affordable mass spectrometers, such as quadrupole systems. The performance of the system will depend on the stability of the ⁴He⁺ ion beam over the timescale of switching and will need to be evaluated critically, but any variability on timescales longer than the switching time is canceled by sample–standard differencing.

Additional work is needed to further improve calibration methods and to establish standard procedures for collecting air samples while avoiding artifacts in $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ at the 10 per meg level. We currently need samples of ∼ 16–20 L for a full 8 h analysis because long purging and analysis times are necessary to achieve a precision of 10 per meg. If reduced precision is acceptable, analyses time can be shortened, but purging of the inlet system for at least 1 h is needed before each analysis even for lower-precision work. Furthermore, air samples must currently be provided at pressure greater than 3 atm to allow sufficient flow through the narrow tubing into the pressure-stabilization chamber. The reproducibility of measurements also depends on adequate calibration strategies. The short-term reproducibility of high-pressure cylinders shown in Fig. 6 and the long-term stability established for ${\mathrm{O}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}$, CO₂ and $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$ standard gases in previous work (Keeling et al., 2007) suggest that long-term stability in δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) is achievable but needs further evaluation.

5 Conclusions

Here, we present a new method for high-precision measurements of changes in the ⁴He mole fraction of atmospheric air, which can be directly related to changes in $\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$ ratio. The method relies on monitoring of the ⁴He⁺ ion beam in a mass spectrometer during sample–standard switching. The ion beam is stabilized by flowing sample and standard air through a single capillary into the MS from an actively pressure controlled open split (Henneberg et al., 1975), such that variability of the ⁴He⁺ ion beam directly reflects differences in the helium mole fraction of the gas mixtures. Measurements of the helium mole fraction can easily be converted to δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) if ${\mathrm{O}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}$, $\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$ and CO₂ concentrations of the sample are determined as well. An online getter preconcentrates He and other noble gases before entry into the MS by chemically removing > 99.99 % of all N₂ and O₂ in a reaction with titanium sponge. Our method thereby avoids the need for peak jumping and a multi-collector mass spectrometer, while achieving a precision of ∼ 10 per meg (1σ) on repeat analysis of δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) in high-pressure tanks of air.

In future work, the gettering and flow-stabilizing inlet system could be used to investigate possible interannual to decadal changes in stratospheric δ($\mathrm{He}/{\mathrm{N}}_{\mathrm{2}}$) linked to variability in stratospheric circulation and stratosphere–troposphere exchange processes. Additional applications could include the search for a signal of anthropogenic helium release during fossil fuel extraction and burning, or measurements of spatial gradients resulting from localized human or natural sources of helium. The setup is also suitable for the analysis of other noble gases and could therefore be used to study seasonal ocean warming associated with degassing or uptake of Kr and Xe from the ocean (Baggenstos et al., 2019; Bereiter et al., 2018).