Smartphone pressure data: quality control and impact on atmospheric analysis

Smartphones are increasingly being equipped with atmospheric measurement sensors providing huge auxiliary resources for global observations. Although China has the highest number of cell phone users, there is little research on whether these measurements provide useful information for atmospheric research. Here, for the first time, we present the global spatial and temporal variation in smartphone pressure measurements collected in 2016 from the Moji Weather app. The data have an irregular spatiotemporal distribution with a high density in urban areas, a maximum in summer and two daily peaks corresponding to rush hours. With the dense dataset, we have developed a new bias-correction method based on a machine-learning approach without requiring users' personal information, which is shown to reduce the bias of pressure observation substantially. The potential application of the high-density smartphone data in cities is illustrated by a case study of a hailstorm that occurred in Beijing in which high-resolution gridded pressure analysis is produced. It is shown that the dense smartphone pressure analysis during the storm can provide detailed information about fine-scale convective structure and decrease errors from an analysis based on surface meteorological-station measurements. This study demonstrates the potential value of smartphone data and suggests some future research needs for their use in atmospheric science.

1 Introduction

A lack of high-resolution observational data is one of the obstacles that limits the advance of numerical weather prediction (Bauer et al., 2015). This limitation can be extended to all areas in atmospheric research. In recent years, many new observational technologies have emerged, including built-in smartphone sensors, such as those for pressure, temperature, humidity and aerosols (Overeem et al., 2013; Snik et al., 2014; Muller et al., 2015; Droste et al., 2017; Meier et al., 2017; Zheng et al., 2018). With over 2.7 billion people in possession of smartphones (Bankmycell, 2019) and an increasing trend in equipping smartphones with atmospheric measurement sensors, smartphone data can potentially be an auxiliary resource for global, high-density observations capable of resolving convective-scale features with a resolution lower than 2 km (Mass and Madaus, 2014).

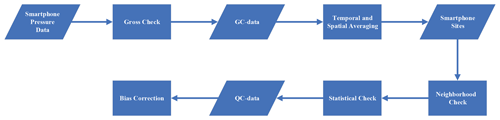
Figure 1 The workflow for smartphone pressure data quality control and preprocessing. See text for details.

Table 1 Parameters used for machine learning.

The smartphone sensors monitor atmospheric parameters and convert them into electrical signals which can then be collected by different platforms, such as mobile weather applications. Low-cost smartphone sensor data have been used in several atmospheric research studies. Overeem et al. (2013) and Droste et al. (2017) used smartphone battery data to study air temperature and their application to urban heat islands. Snik et al. (2014) mapped atmospheric aerosols using smartphone spectropolarimeters. Surface pressure is one of the most useful variables because it can reflect information about the whole atmospheric column and is less sensitive to the observational background (e.g., indoors/outdoors or the influence of the underlying surface versus other variables like temperature and wind; Mass and Madaus, 2014; Hanson, 2016); therefore, smartphone pressure data have received considerable attention from researchers. In addition to applications in weather forecasting (Mass and Madaus, 2014; Madaus and Mass, 2017; McNicholas and Mass, 2018b; Hintz et al., 2019), smartphone pressure data can be used to monitor atmospheric tides (Price et al., 2018).

While smartphone pressure data may have potential value, they require validation and quality control before use. Price et al. (2018) and Hintz et al. (2019) showed that, although the variability between smartphone pressure data and meteorological-station observations is highly correlated, there exists noticeable bias. Price et al. (2018) calibrated the long-term stable bias using a one-point calibration method, while Hintz et al. (2019) developed screening methods to reduce observational noise. Machine learning has also been applied to correct atmospheric pressure data (Kim et al., 2015, 2016; McNicholas and Mass, 2018a). Most previous publications on smartphone data calibration adopted a user-based approach which required the identification of each unique user and personal information. However, this raises privacy and ethical issues that pose a concern to the public. As highlighted by Muller et al. (2015) and Mooney et al. (2017), collecting as little personal information as possible and keeping raw data private are guiding principles of privacy preservation. Moreover, without a stable data collocation platform, performing user-based calibration can be time and resource consuming, especially for densely populated regions. It is therefore imperative to develop a new method that can efficiently calibrate smartphone pressure bias while protecting user privacy. It is worth noting that the need for such an effort has been recognized by other researchers, and similar efforts are being undertaken (McNicholas, 2020).

Figure 2 Locations of global pressure observations in 2016 from the Moji Weather application.

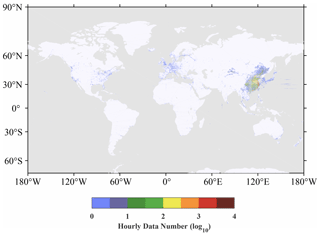
Figure 3 Hourly pressure observation counts (log10 transformed) averaged over the year 2016. Data are binned into a 0.1^∘ × 0.1^∘ grid.

China has one of the world's most densely distributed smartphone user bases (Bankmycell, 2019) which can potentially produce highly dense observations. In this paper, we present, for the first time, a year-long dense and extensive smartphone dataset collected by the Moji Weather app, which is developed and operated by the internet environmental meteorological corporation Moji. The Moji Weather app is a popular smartphone weather app used in many countries with a 53.90 % market share and more than 500 million users, as well as over 100 million weather queries made every day (Moji, 2019a, b). In the present study, we use the Moji smartphone pressure data for all of 2016 to show the spatial and temporal distribution of the dataset. With this highly dense network, we demonstrate the feasibility of a new machine-learning bias-correction method that does not require users' private information, thereby ameliorating ethical issues. The dense network also makes it possible to study the detailed structure of atmospheric convection, which is demonstrated in this study by applying the bias-corrected data to the fine-scale analysis of a hailstorm that occurred in Beijing.

This paper is organized as follows. Sect. 2 describes the data and methods used in our research. The statistical characteristics of this dataset, bias-correction results and its application to a hailstorm case are presented in Sects. 3, 4 and 5, respectively. Conclusions and discussion are given in the final section.

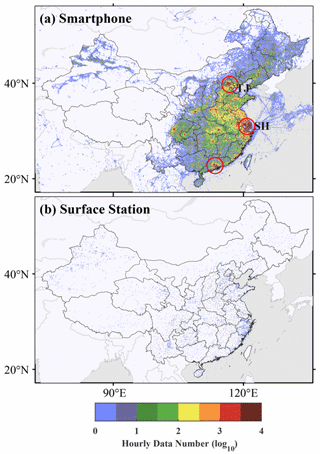
Figure 4 (a) Hourly pressure observation counts (log10 transformed) averaged over the year 2016. (b) Same as (a) but for the Chinese Meteorological Administration (CMA) surface stations. Data are binned into a 0.1^∘ × 0.1^∘ grid in (a) and (b). The location of the port of Shanghai and the port of Tianjin are labeled as “SH” and “TJ” in (a). The red circles indicate the urban agglomerations of (from north to south) Beijing–Tianjin–Hebei region, Shanghai and nearby cities, and Guangzhou and nearby cities.

Figure 5 (a) Seasonal variation in global hourly counts of smartphone data for each month. (b) Diurnal variation in global smartphone data counts. (c) Annual mean hourly data count at different local standard times (LSTs) and months.

2 Data and methods

2.1 Data description

Three types of datasets were used to perform this research. (1) Pressure data were collected by a smartphone mobile weather application every second in 2016. The application collects longitude, latitude, time and pressure data for each user without an unencrypted or encrypted ID. (2) Pressure data were collected every 5 min by CMA (Chinese Meteorological Administration) in 2016. There are 68 909 stations (including automatic weather stations, AWSs, and conventional stations) collecting meteorological data across the country, but only 13.32 % of the stations make pressure observations. These weather station surface data are used as the authentication for the bias correction of smartphone pressure data and for the verification of the surface analysis. (3) Land-use and land-cover data for China in 2015 at a resolution of 1 km were accessed via the Data Center for Resources and Environmental Sciences, Chinese Academy of Sciences (RESDC; Xu et al., 2018). These geographical data provide additional information necessary for our machine-learning-based bias-correction method.

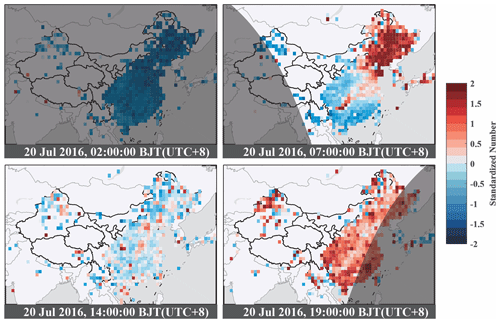
Figure 6 Spatial distribution of the standardized value of the data number at each site for each hour on 20 July 2016. The time is shown in Beijing standard time (BJT). The standardized number is defined as the difference between the data number in this grid at a specific hour and daily mean of the number divided by the standard deviation of the number. The dark gray color fill stands for the region in nighttime. Warm colors indicate a rise in data volume, while cool colors indicate a decrease.

2.2 Quality control and preprocessing

The quality-control and preprocessing procedure of the smartphone pressure data is described as follows. A workflow diagram is shown in Fig. 1 summarizing the main processes of the procedure. First, a gross check is conducted; pressure values lower than 890 hPa or higher than 1080 hPa are considered outliers and discarded (Kim et al., 2015; Madaus and Mass, 2017). The gross-checked data are referred to as GC-data hereafter. Next, we perform temporal and spatial averaging. As described by McNicholas and Mass (2018a) and Hintz et al. (2019), there is a spin-up time for each measurement, and location retrieval for smartphones has an estimation error. To reduce such temporal and spatial errors, the GC-data are averaged within a specified window of time and space. The time window size is 5 min to match the temporal interval of the weather station data or 6 min to match the radar update interval whenever necessary. The spatial window size is 0.0001^∘ latitude and longitude, i.e., the individual smartphone observation points are binned into specific sites with fixed locations to eliminate the need for user IDs. The bias correction is then conducted on the aggregated data in a 0.0001^∘ × 0.0001^∘ grid box (∼10 m × 10 m). In the rest of this paper, the aggregated data points will be referred to as “smartphone sites” for convenience. The next step in the quality-control procedure is a neighborhood check within each area of 0.01^∘ × 0.01^∘ latitude and longitude. Data with values greater than 3 times the standard deviation of the mean pressure in the area are removed. Finally, we perform a statistical check. The boxplot approach is used to detect and handle climatological outliers (Iglewicz and Hoaglin, 1993). For each boxplot, the upper quartile (Q3) is 75 % for the smartphone air-pressure data, and the lower quartile (Q1) is 25 %. Data that are 1.5 times the interquartile range (Q3–Q1) above Q3 and below Q1 are removed. The quality-controlled data after all the above steps are referred to as QC-data hereafter.

It should be noted that the quality-control procedure above does not include elevation correction of the pressure data not only because the Moji smartphone data do not include the elevation information but also because the elevation-based pressure correction may contain notable errors due to the uncertainties in GPS elevation positioning (Kaplan and Hegarty, 2006; Ye et al., 2018) and in assumed pressure–height relations. As an alternative, we use a neighborhood-based bias-correction approach, as described below, to correlate local pressure bias with the land-cover condition using the machine-learning technique.

2.3 Bias correction

Previous studies have demonstrated the importance of implementing appropriate validation and bias-correction procedures before using smartphone pressure data in meteorological analysis (Muller et al., 2015; Hanson, 2016; McNicholas and Mass, 2018a). In our study, three machine-learning techniques from the Waikato Environment for Knowledge Analysis (WEKA) suite (Witten et al., 2011) are used to correct the smartphone pressure data, and their effectiveness are compared. Unlike previous studies in which an individual model was trained for each smartphone, in this study, we developed a method, named the neighborhood-based bias-correction method, that trains a single model in a specified area rather than for a single phone. Properly choosing the area size is crucial for the method to work effectively. It should be small enough to ensure some degree of homogeneity in terms of geographical conditions, and on the other hand, it cannot be too small because the machine learning requires a large enough data amount to work properly. Since both users' behavior and synoptic weather background differ among seasons, we conducted the training for each season. The data were randomly separated into training and test sets (Overeem et al., 2013). The parameters used as input in the machine learning are listed in Table 1, including pressure from QC-data, longitude, latitude, time, land cover, number and standard deviation of raw data aggregated in a grid box, and distance of each smartphone site from the domain center. The land cover is used to provide geographic information, which is an important input parameter for the neighborhood-based bias-correction approach. The number and standard deviation of raw data aggregated in a grid box are used to provide data uncertainty. The true pressure value used for the machine leaning is provided by the 5 min pressure observations from AWS that are interpolated to each smartphone site. To ensure some consistency in the two types of pressure data, training data with a pressure bias (the difference of pressure values between smartphone and AWS) greater than 15 hPa are removed.

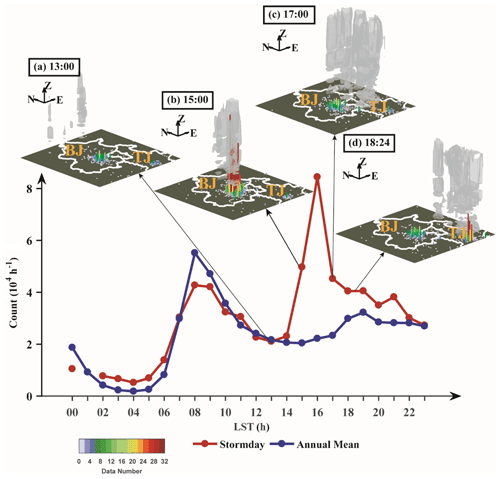
Figure 7 Diurnal variation in the data volume for smartphone data on the day of the hailstorm (red line) and the annual mean value (blue line) for 39–41^∘ N, 115–118^∘ E. Panels (a)–(d) show a 3D view of data counts in a 0.05^∘ × 0.05^∘ grid over 6 min (colored columns) before each radar volume and radar echo (gray columns). The color and height of each column represent the value of the data count. BJ, Beijing; TJ, Tianjin.

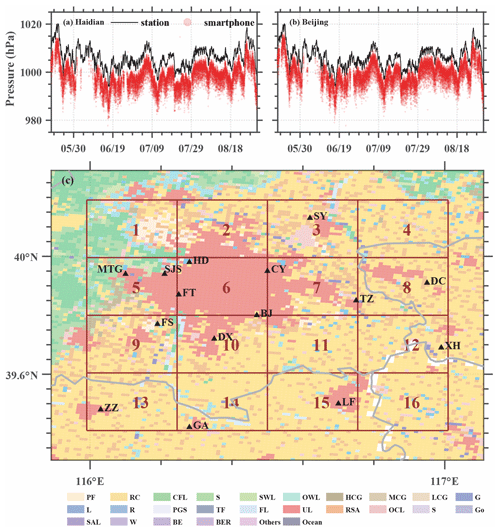
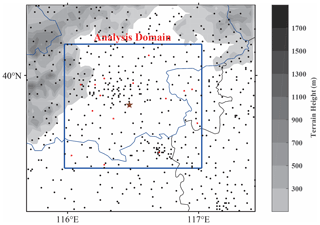
Figure 8 (a, b) Pressure time series during the training period for the AWS (black line) and smartphones (red dots); smartphone pressure was interpolated into station location using the inverse distance weighting method. (c) The domains of the machine-learning area. Shaded areas are regional land use (PF, paddy field; RC, rainfed cropland; CFL, closed forest land; S, shrubbery; SWL, sparse woodland; OWL, open woodlot; HCG, high-coverage grassland; MCG, moderate coverage grassland; LCG, low-coverage grassland; G, graff; L, lake; R, reservoir pond; PGS, permanent glacier snow; TF, tidal flat; FL, flood land; UL, urban land; RSA, rural settlement area; OCL, other construction land; S, sand; Go, Gobi; SAL, saline-alkali land; W, wetland; BE, barren earth; BER, bare exposed rock). Automatic weather stations (AWSs) with pressure observations are shown by black triangles (HD: Haidian; MTG: Mentougou; SJS: Shijingshan; FT: Fengtai; CY: Chaoyang; SY: Shunyi; FS: Fangshan; BJ: Beijing; TZ: Tongzhou; DX: Daxing; DC: Dachang; XH: Xianghe; LF: Langfang; GA: Guan; ZZ: Zhuozhou).

In order to evaluate the performance of the neighborhood-based bias-correction method, three experiments with the following machine-learning methods, multilayer perceptron (MP) (Pal and Mitra, 1992), support vector machine (SVM) (Shevade et al., 2000; Smola and Schölkopf, 2004), and random forest (RF) (Breiman, 2001), were conducted, and their results will be compared later.

2.4 Objective analysis

It is well known that an accurate 2D surface analysis is extremely useful for nowcasting severe weather and studying convective processes. Traditionally, this type of analysis is mainly obtained from surface weather station observations. However, since most of the weather stations do not have pressure measurements, the surface pressure analysis from them can only depict gross features of large-scale flow. The dense pressure observations from smartphones create an opportunity to improve the surface pressure analysis. In this study, we use an objective analysis method modified from Barnes (1964) to conduct the analysis. The modified Barnes analysis method, described below, interpolates randomly distributed data into a uniformly spaced coordinate system using a two-pass successive correction method.

If a variable f_k is observed at a location (x_obs,y_obs), then the first pass analysis at a grid point g₀(x_g,y_g) is obtained by Eq. (1):

$$\begin{array}{}\text{(1)}& g_{\mathrm{0}}\left(x_g,y_g\right)={\displaystyle \frac{{\sum }_k{w}_k{f}_k\left(x_{\mathrm{obs}},y_{\mathrm{obs}}\right)}{\sum _k{w}_k}},\end{array}$$

where the weight w_k for the observation point is given by Eq. (2):

$$\begin{array}{}\text{(2)}& w_k=\left\{\begin{array}{ll}\exp \left(-\frac{r_k^{\mathrm{2}}}{\mathit{\gamma }{L}^{\mathrm{2}}}\right),& r\le r_e\\ \mathrm{0},& r>r_e\end{array},\right.\end{array}$$

where r_k is the distance from the grid point (x_g,y_g) to the kth observation point; γ is the convergence factor which controls the refinement between the two passes (Barnes, 1974) and lies between 0 and 1 $(\mathrm{0}<\mathit{\gamma }\le \mathrm{1})$; L is the length scale that controls the rate of falloff of the weighting function; and r_e is the radius of influence within which the observations have an impact on the grid point. Different from the standard Barnes interpolation technique using a uniform length scale over the analysis domain, an adaptive Barnes scheme is applied in this paper in which the length scale automatically adapts to data density, i.e., a spatially variable length scale is computed according to the data density.

The analysis in subsequent refinement pass is described by Eq. (3):

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{g}_{\mathrm{1}}\left(x_g,y_g\right)& =g_{\mathrm{0}}\left(x_g,y_g\right)\\ & +{\displaystyle \frac{{\sum }_k{w}_k(f_k\left(x_{\mathrm{obs}},y_{\mathrm{obs}}\right)-g_{\mathrm{0}}(x_{\mathrm{obs}},y_{\mathrm{obs}}\left)\right)}{{\sum }_k{w}_k}},\end{array}\end{array}$$

where g₀(x_obs,y_obs) is the estimate value of g₀ at an observation point which is given by bilinear interpolation.

The objective analysis method described above was applied to generate analysis fields with a 1 km grid spacing for a hailstorm case. In Sect. 5, we will show that the high-resolution analysis fields can be used to analyze fine-scale pressure patterns for the hailstorm.

3 Statistical characteristics

3.1 Spatial distribution

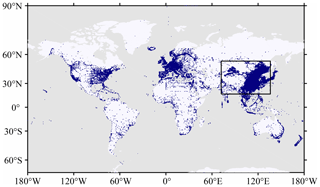
We used the GC-data to analyze the spatial and temporal distribution of the smartphone data counts in 2016. The data location map in Fig. 2 shows that smartphone data are distributed over nearly all continents, although most of the data counts occur in China with much higher data density (Fig. 3). The global mean density of the data is 40 per bin per hour, whereas in China, the density is 176 per bin per hour. The hourly pressure observation counts for the entire year of 2016 for China and its surroundings (black box in Fig. 2) are binned using a 0.1^∘ × 0.1^∘ grid and shown in Fig. 4a, which indicates that the data density is higher in megacities, such as the densely populated urban agglomerations of the Yangtze River Delta (Shanghai and nearby cities), Pearl River Delta (Guangzhou and nearby cities), and Beijing–Tianjin–Hebei region (marked by red circles in Fig. 4a). Because people carry mobile phones while traveling internationally, ship trajectories can be seen from two ports, the port of Shanghai (SH) and the port of Tianjin (TJ) (Fig. 4a), but the amount of data at sea is much lower than on land. However, in comparison with the surface observations of the Chinese Meteorological Administration (CMA) (Fig. 4b), the amount and spatial coverage of the smartphone data are remarkable in nearly all regions.

3.2 Temporal distribution

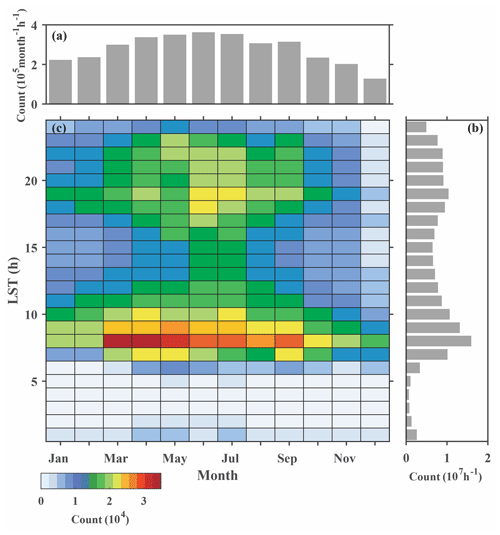
The seasonal and diurnal distributions of the GC-data are displayed in Fig. 5 The data volume peaks during the Northern Hemisphere summer and reaches a minimum in winter (Fig. 5a, c). The annual mean data volume is 279 377 per hour, which far exceeds the value of 47 000 per day in Korean shown in Kim et al. (2015), suggesting a large user base of the Moji Weather app. The data seasonality indicates that people check the weather more frequently in summer than in winter, owing to the fact that the app can only get the pressure information when the network is available and when the users open the app either on the front end or back end. The diurnal variation in global data volume (Fig. 5b, c) shows two peaks at 07:00 and 18:00 local standard time (LST), corresponding to the rush hour in the morning and evening, respectively. Additionally, there is a steep decrease in data volume at night, which is consistent with a previous report that smartphone data are inhomogeneously distributed throughout the day (Hintz et al., 2019). The diurnal distribution characteristic indicates that users tend to check the weather before going to work in the morning and getting off work in the evening. To demonstrate this more clearly, the spatial distribution of the standardized value of the hourly data number at each site is computed for 2 d and displayed in Fig. 6. Interestingly, the data volume peak occurs earlier in northeast China, which corresponds well with an earlier sunrise (Fig. 6b).

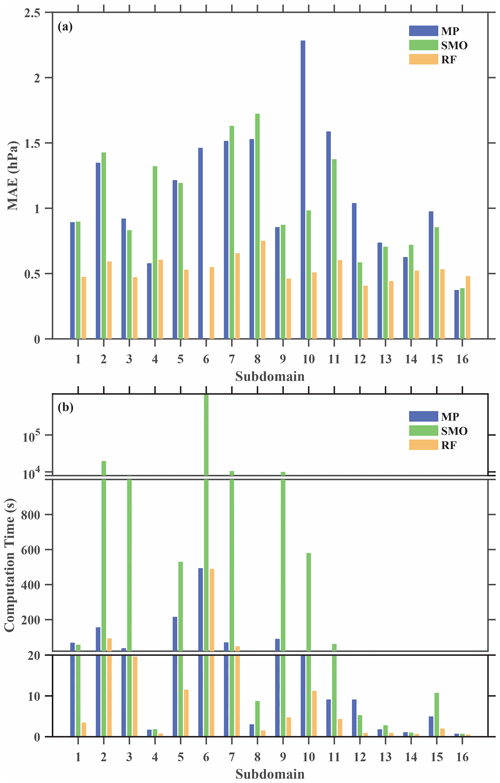
Figure 9 (a) Mean absolute error (MAE) distribution at different training subdomains for different machine-learning methods (MP refers to multilayer perception method; SMO refers to support vector machine method; RF refers to random forest method). Panel (b) is the same as (a) but for computation time.

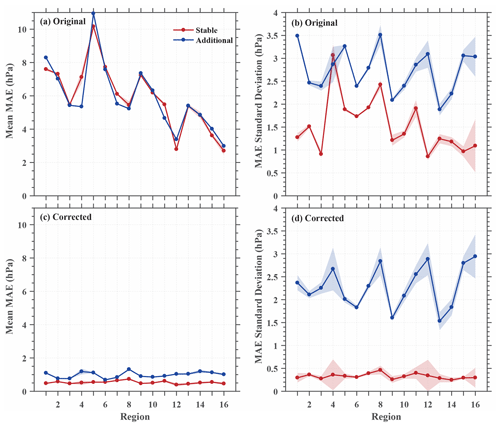
Figure 10 Distribution of domain-average mean absolute error (MAE; a, c) of ensemble mean and standard deviation (b, d) for different subdomains for the original dataset (a, b) and the bias-corrected dataset (c, d). The line marked by dots is the ensemble mean value, and shading is the double standard deviation ensemble spread. The red line is the result for stable sites, and the blue line is the result for additional sites. See text for the definitions of stable sites and additional sites.

Analysis during a hailstorm that occurred in Beijing further reveals that people respond promptly to severe weather events. The hailstorm occurred on 10 June 2016 as a squall line passed through Beijing city from 14:00 to 17:00 LST. The hourly data volume on the day of the hailstorm and annual mean hourly data within 39–41^∘ N, 115–118^∘ E are plotted in Fig. 7. The diurnal cycle on the day of the hailstorm shows that, in addition to the two peaks in the morning and evening, another peak appeared at 16:00 LST with a data volume 3 times that of the annual mean. A 3D view of the data volume and radar echo accumulated within 6 min (Fig. 7b–d) clearly shows a rise in data volume (Fig. 7b, d) as the storm approaches Beijing and Tianjin and a drop after the storm passes (Fig. 7c), which demonstrates the influence of severe weather on human behavior.

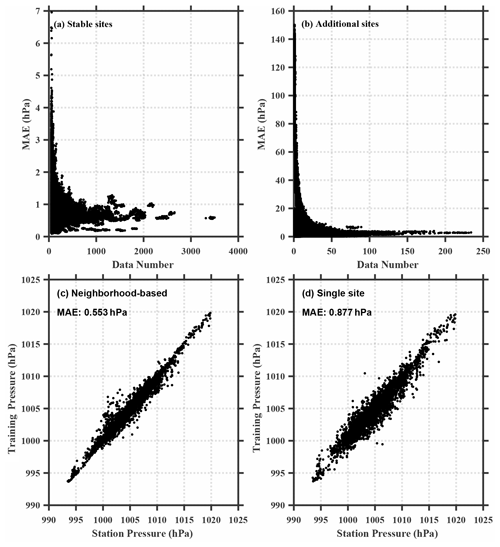
Figure 11 (a, b) Scatter plot of mean absolute error (MAE) versus the data number of observation sites for (a) stable sites and (b) additional sites. (c, d)  Scatter plot of station pressure versus bias-corrected pressure for (c) the neighborhood-based method and (b) single-site method of one ensemble member. Averaged mean absolute errors (MAEs) of the two methods are shown in the plot.

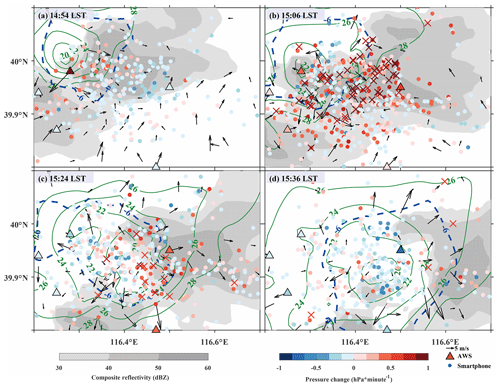
Figure 12 The 5 min pressure change from surface stations (triangles) and the 6 min pressure change from smartphones (points), temperature observations from surface station (green contour), wind field (black arrow), and composite radar reflectivity (shaded) during a hailstorm that occurred on 10 June 2016 in Beijing, China. The station pressure change is shown at the time closest to that of the radar volume. The “×” symbol marks the locations where the 6 min pressure change perturbation is greater than 0.52 hPa. The dashed blue line is the $\mathrm{\Delta }{\mathit{\theta }}_{\mathrm{e}}=-\mathrm{6}$ K isoline from the analysis of surface observations (Δθ_e is defined as the difference between the equivalent potential temperature at a point and the domain-averaged value).

Figure 13 Objective analysis domain (blue box), terrain height (shaded), the distribution of surface stations (black and red dots with the red dots representing the surface stations with pressure measurements) and Beijing radar station (star). The boundary of Beijing is shown with the blue line.

4 Evaluation of the bias-correction method

Three neighborhood-based bias-correction experiments, each using one of the aforementioned machine-learning methods, were conducted on a domain covering Beijing and its surrounding area from May to August 2016. The machine-learning bias correction was performed in each of the subdomains in Fig. 8c using surface observations as the truth and the smartphone input parameters listed in Table 1. The region was affected by the 10 June 2016 hailstorm and had a high density of smartphone pressure observations (Fig. 7a–d).

Constrained by the requirements of adequate data samples and reasonable computation cost, we chose 16 subdomains of 0.25^∘ (longitude) × 0.20^∘ (latitude) in size. The pressure time series from two representative stations in Fig. 8a and b show that, although the trend in the weather station and smartphone is consistent, bias is clearly present, which is consistent with the results of Price et al. (2018) and Hintz et al. (2019).

Figure 9 shows the mean absolute error (MAE) and computation time at different training regions for the three methods; it is evident that the RF method is more accurate and time saving. The computation times for subdomain 2 and subdomain 6 using the SMO method are more than 9 h. From this comparison, we have found that the RF algorithm is more suitable for the neighborhood-based bias correction of smartphone observations without requiring users' personal information. Furthermore, we discovered that the random data separation into training set and test set can cause random errors in the bias-corrected data; hence, in order to eliminate these errors, the correction procedure was repeated for 50 times to generate an ensemble result.

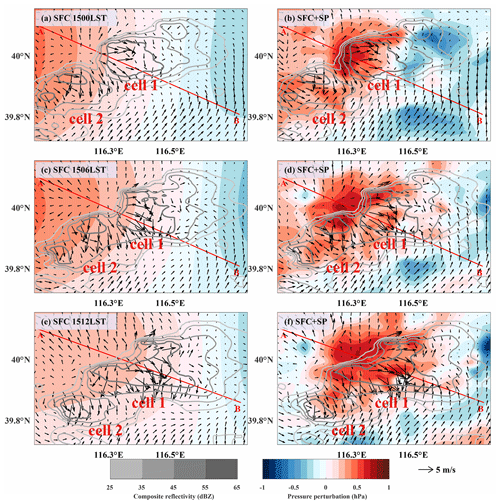
Figure 14 Surface pressure perturbation analyses (shaded) from the experiment SFC (a, c, e) and SFC + SP (b, d, f) overlaid by VDRAS wind field at 150 m (thick black arrows) and column maximum radar reflectivity (contours). The valid time is 15:00 LST for the top row, 15:06 LST for the middle row and 15:12 LST for the bottom row.

Collecting smartphone data through a weather app is convenient and common; however, the approach relies on the loyalty of users. Calibrating smartphone pressure individually can be only applied to data from long-term users, but it cannot be used for recently added users. In contrast, performing data correction for the aggregated data in a 0.0001^∘ × 0.0001^∘ grid box in a subdomain makes it possible to collect data from both user groups. In order to evaluate the applicability of our method on data from both types of users, we define the data sites appearing in both the training set and test set as stable sites and those only appearing in the test set as additional sites. To quantify the performance of bias correction, the domain-average MAE and standard deviation of ensemble mean for the 16 subdomains are displayed in Fig. 10 for the raw and bias-corrected data from both the stable sites and the additional sites. The MAE was calculated using data from the smartphone sites for each subdomain. Comparing the MAEs between the raw (Fig. 10a) and bias-corrected data (Fig. 10c), it is evident that the neighborhood-based bias-correction method is capable of substantially reducing the MAE not only for the stable sites but also for the additional sites with slightly more reduction for the stable sites (from 5.95 to 0.53 hPa) than for the additional sites (from 5.90 to 0.99 hPa). It is also shown that the method reduces the MAE spread by 78 % for the stable sites and by 16 % for the additional sites (Fig. 10b, d). A lower MAE and spread reduction for the additional sites is not surprising because they are newly added data with shorter data history and hence have fewer data samples (Fig. 11a, b). Encouragingly, our results suggest that the neighborhood-based method can partially mitigate the difficulty related to recently added data with shorter data history. In comparison with the bias-correction method based on a single site, the neighborhood-based method resulted in a substantially smaller MAE (see Fig. 11c, d).

5 Impact of smartphone data on hailstorm analysis

High-density pressure observations can potentially help identify small-scale surface pressure patterns beneath a thunderstorm (Johnson and Hamilton, 1988). Although the quality-controlled gridded smartphone pressure data reduce the number of data points, they are still adequate to represent the fine-scale pressure patterns. In this section, we first show what small-scale information the quality-controlled high-density pressure data at the smartphone sites (with a spatial resolution of 0.0001^∘ or approximately 10 m) can provide and then demonstrate the impact of the smartphone data on the gridded 1 km pressure analysis that is obtained using the objective analysis method described in Sect. 2.4.

Figure 12 shows a composite plot of radar reflectivity, pressure changes calculated from surface weather station observations and from smartphone data, and wind and equivalent potential temperature from the station observations. To be consistent with the time interval of the radar volume scan, the smartphone QC-data averaged every 6 min were used to generate the 6 min pressure tendency. Further, because the weather station data are at a 5 min interval, the pressure change and temperature from these data are shown at times closest to those of the radar volume scan. Since there are only 15 weather stations providing pressure observations in this region, they are unable to locate the leading edge of the cold pool. In contrast, the smartphone pressure observations are much denser and hence are able to capture the fine-scale pressure change associated with the cold pool, as depicted in Fig. 12 by the “×” symbol representing the 6 min change in perturbation pressure (i.e., domain mean subtracted) greater than 0.52 mb. Compared with the cold pool leading edge identified by θ_e, following Schlemmer and Hohenegger (2014), from the analysis of surface observations, the leading edge of the cold pool based on the smartphone pressure change is about 10 km ahead at 15:06 LST (Fig. 12b) and quite close at 15:24 LST (Fig. 12c). At 14:54 LST (Fig. 12a), the pressure change is largely negative ahead of the cold pool, whereas Fig. 12d mainly shows negative pressure changes after the leading edge has passed the area; both are consistent with the surface station observations but are more detailed.

We conducted three objective analysis experiments using the method described in Sect. 2.4 to demonstrate the potential benefit of using smartphone observations along with surface weather station observations to improve surface pressure analyses, i.e., the station observation experiment (SFC) using only weather station pressure observations, smartphone experiment (SP) using only smartphone data, and SFC + SP using both the station and smartphone data. The analysis grid spacing is 1 km. Figure 13 shows the domain for surface analysis and the locations of the Beijing radar and surface stations.

The analyses of perturbation pressure (i.e., relative to domain mean) from the experiments SFC (Fig. 14a, c, e) and SFC + SP (Fig. 14b, d, f) are compared at 15:00, 15:06 and 15:12 LST in Fig. 14. To illustrate the coupling between pressure and wind in the storm region, the wind field at 150 m from VDRAS (Variational Doppler Radar Analysis System) and the composite reflectivity observation are overlaid. VDRAS is a rapid update analysis system based on the variational technique that blends radar radial velocity and surface wind observations to produce 3D wind analyses (Sun and Crook, 1997, 1998). We first note that the perturbation pressure analysis from SFC + SP (right column) displays small-scale features in and around the storm that are absent in SFC (left column). The high center of pressure perturbation is nearly collocated with the center of the outflow near the northwest flank of the main body of the storm system (Fig. 14b, d, f). The vertical cross sections shown in Fig. 15 through the line A–B (see Fig. 14) indicate that the high-pressure perturbation corresponds to the rear-flank downdraft aloft behind the intense radar echoes of the southeastward moving convective system. Although the relatively low-pressure regions are seen in front of the convective system in both experiments, only the SFC + SP experiment captures the relatively low-pressure region northwest of the system. The overall distribution pattern of pressure perturbation in SFC + SP is consistent with the conceptual model of Markowski and Richardson (2010), but the current analysis reveals that the surface high-pressure region and low-level divergence center slightly lag behind the center of the intense reflectivity echoes rather than right beneath it, as in their conceptual model. We believe the difference results from the higher resolution of the smartphone data applied in this study, but further studies are needed to draw a definite conclusion. Furthermore, the pressure analysis from SFC + SP provides more detailed information about storm evolution than what is shown in SFC. As the storm moves southeastward, the cell in the southwest, denoted as cell 2 in Fig. 14, separates into two (Fig. 14b), and the northern one merges into cell 1 (Fig. 14d, f). During the merging process, the high-pressure region behind cell 1 becomes stronger and wider, which may indicate the enhancement of cell 1 in correspondence with the increased downdraft and updraft, as shown in Fig. 15c.

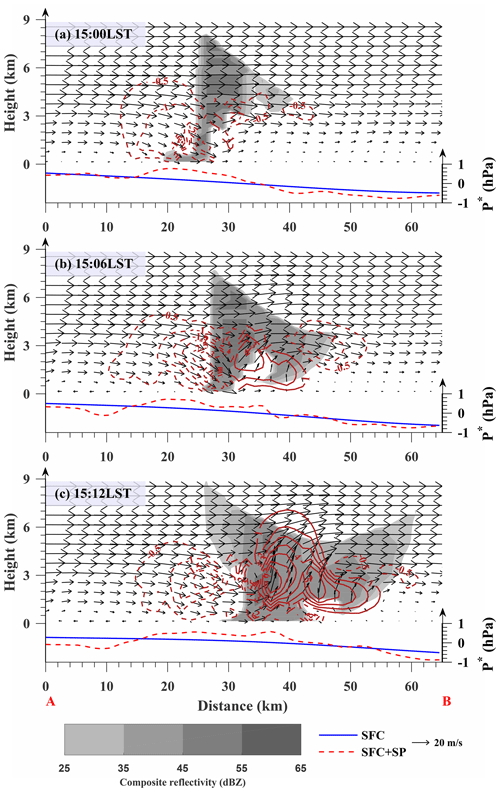
Figure 15 Vertical cross section of the radar reflectivity (shaded), VDRAS wind field (thin black arrows) and vertical velocity field (brown contours with dash lines for downward motion and solid lines for upward motion) along the line A–B in Fig. 10. The solid blue line and dashed red line are the surface pressure perturbation along the A–B line from SFC and SFC + SP, respectively.

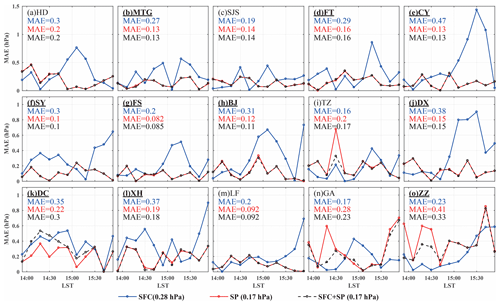
Figure 16 (a)–(o) Temporal distribution of mean absolute error (MAE) between model analyses and observations at different surface stations for the smartphone experiment (SP; red line), the station observation experiment (SFC; blue line) and the station observation plus smartphone experiment (SFC + SP; black dash line), respectively. The temporally averaged MAE is also shown within each plot, and the average MAEs over all stations for the three experiments are shown below the plots. The underlined and bold station names indicate that the MAE difference between SFC and SP at those stations is significant with the confidence level of 90 %. The stations are as follows: HD: Haidian; MTG: Mentougou; SJS: Shijingshan; FT: Fengtai; CY: Chaoyang; SY: Shunyi; FS: Fangshan; BJ: Beijing; TZ: Tongzhou; DX: Daxing; DC: Dachang; XH: Xianghe; LF: Langfang; GA: Guan; ZZ: Zhuozhou.

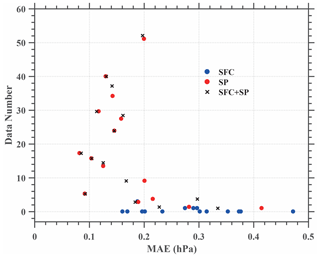
Figure 17 Scatter plot of mean absolute error (MAE) versus observation number within 10 km and 5 min of the verifying weather station. The blue dots stand for the station observation experiment (SFC), red dots represent the smartphone experiment (SP), and the station observation plus smartphone experiment (SFC + SP) is shown as black crosses.

Analysis accuracy for the two experiments was verified against the 15 weather station pressure measurements in the domain. In order to avoid dependence between the analysis and verification, both experiments were repeated 15 times; each alternately excludes the measurement from the specific station to be verified against. The temporal distributions of MAE between model analysis and observation at different surface stations are shown in Fig. 16. The results confirm that the experiment SFC + SP reduces the analysis error at most stations, even at those around which there are relatively fewer smartphone observations, such as the stations Xianghe (XH) and Langfang (LF). Although at the stations where there are much fewer smartphone observations, such as Guan (GA) and Zhuozhou (ZZ), the analysis with smartphone pressure data alone in the experiment SP results in a larger error than in the experiment SFC; adding the station observations in SFC + SP results in reduced analysis error (Fig. 16n, o). The correlation between the smartphone data density and the analysis accuracy is more clearly illustrated by Fig. 17, which shows that the MAE is less than 0.20 hPa as long as there are more than three smartphone sites around the verifying weather station measurement.

In summary, our quantitative verification results demonstrate that the high-resolution smartphone data generally improve surface pressure analysis in comparison with the weather station data; combining these two datasets results in a further improvement, especially at the locations where the smartphone data are sparse.

6 Conclusions and discussion

This study focused on smartphone pressure data acquired from the Moji Weather app in 2016 and showed their characteristics for the first time. A neighborhood-based bias-correction method applying machine-learning techniques was developed without any privacy information needed. The bias-corrected data were employed to explore the potential value of these data for improving atmospheric analysis through the case of a hailstorm in Beijing, China.

Since these data are produced by citizens at large, their spatial and temporal distributions are affected by human behavior. It was shown that the data are mostly distributed around urban areas, and data volume peaks during summer. There is also a diurnal cycle in which the data volume is higher during the day than at night, with two peaks appearing at 07:00 and 18:00 LST. Our case study showed an anomalous increase in data volume when the hailstorm occurred, suggesting that public concern increases in anticipation of high-impact weather situations, which means the data can be useful for disaster prevention.

We proposed and demonstrated a neighborhood-based bias-correction method that can address user privacy issues. Despite growing concern from the public regarding personal privacy, few studies have addressed how to circumvent the problem. Since Moji protects data privacy during the collection and processing stages, no private information was included in the raw data that we received, and the bias-correction method proposed in this study does not require such information. Our results showed that the MAE and MAE spread can be successfully reduced not only for long-term stable sites but also for recently added sites that present a challenge using the traditional user-based bias-correction method.

With this feasible and effective bias-correction method, the potential utility of the high-resolution smartphone data (approximately 10 m horizontal resolution) is shown using a hailstorm case. We have found that the 6 min pressure change can provide convective-scale information such as cold pool leading edge, especially in megacities where the data are most dense. Using a modified Barnes objective analysis method on a 1 km grid, we also showed that the data can be used in conjunction with weather station data to improve surface pressure analysis. The analysis is capable of depicting the high pressure associated with the rear-flank downdraft of the hailstorm and temporal variation in pressure perturbation related to the splitting and merging process within the convective system.

Through the current study, we have gained an understanding of the smartphone pressure data characteristics, developed a practical and effective quality-control and bias-correction method, and demonstrated the value of the data in surface objective analysis; our next step is to explore whether the data can be useful in improving convective weather forecasting through data assimilation. Previous data assimilation research with smartphone pressure data mainly focused on assessing whether the data have a positive impact on regions where weather stations are not available (McNicholas and Mass, 2018b; Hintz et al., 2019). However, it may present a greater challenge to demonstrate that the smartphone data can yield additional benefits to the existing weather station network mainly because of the uneven distribution of the smartphone data across the globe. Efforts are needed to develop data assimilation approaches that can make best use of the smartphone data in numerical weather prediction models by taking into account the characteristics of these data. The current study also points to the need of an improved smartphone data collection mechanism. The data volume collected by a weather app relies heavily on the popularity of the application that serves as the data-collection platform (Kim et al., 2015; Hintz et al., 2019). As such, the data distribution relies heavily on the severity of local weather. Thus, a more stable and widely used platform is needed to provide useful high-resolution global observations without a correlation to local weather. Additionally, the smartphone information included in our research is limited; additional auxiliary information, such as smartphone models, sensor types and the altitude at which smartphone data were measured, would be conducive to the bias-correction procedure and subsequent analysis.