Towards the use of conservative thermodynamic variables in data assimilation: a case study using ground-based microwave radiometer measurements

This study aims at introducing two conservative thermodynamic variables (moist-air entropy potential temperature and total water content) into a one-dimensional variational data assimilation system (1D-Var) to demonstrate their benefits for use in future operational assimilation schemes. This system is assessed using microwave brightness temperatures (TBs) from a ground-based radiometer installed during the SOFOG3D field campaign, dedicated to fog forecast improvement.

An underlying objective is to ease the specification of background error covariance matrices that are highly dependent on weather conditions when using classical variables, making difficult the optimal retrievals of cloud and thermodynamic properties during fog conditions. Background error covariance matrices for these new conservative variables have thus been computed by an ensemble approach based on the French convective scale model AROME, for both all-weather and fog conditions. A first result shows that the use of these matrices for the new variables reduces some dependencies on the meteorological conditions (diurnal cycle, presence or not of clouds) compared to typical variables (temperature, specific humidity).

Then, two 1D-Var experiments (classical vs. conservative variables) are evaluated over a full diurnal cycle characterized by a stratus-evolving radiative fog situation, using hourly TB.

Results show, as expected, that TBs analysed by the 1D-Var are much closer to the observed ones than the background values for both variable choices. This is especially the case for channels sensitive to water vapour and liquid water. On the other hand, analysis increments in model space (water vapour, liquid water) show significant differences between the two sets of variables.

1 Introduction

Numerical weather prediction (NWP) models at convective scale need accurate initial conditions for skilful forecasts of high impact meteorological events taking place at a small scale such as convective storms, wind gusts or fog. Observing systems sampling atmospheric phenomena at a small scale and high temporal frequency are thus necessary for that purpose (Gustafsson et al., 2018). Ground-based remote-sensing instruments (e.g. rain and cloud radars, radiometers, wind profilers) meet such requirements and provide information on wind, temperature and atmospheric water (vapour and hydrometeors). Moreover, data assimilation systems are evolving towards ensemble approaches where hydrometeors can be initialized together with typical control variables. This is the case for the Météo-France NWP limited area model AROME (Seity et al., 2011; Brousseau et al., 2016), where, on top of wind (U,V), temperature (T) and specific humidity q_v, the mass content of several hydrometeors can be initialized (cloud liquid water q_l, cloud ice water q_i, rain q_r, snow q_s and graupel q_g; Destouches et al., 2021). However, these variables are not conserved during adiabatic and reversible vertical motion.

The accuracy of the analysed state in variational schemes highly depends on the specification of the so-called background error covariance matrix. Background error variances and cross-correlations between variables are known to be dependent on weather conditions (Montmerle and Berre, 2010; Michel et al., 2011). This is particularly the case during fog conditions with much shorter vertical correlation length scales at the lowest levels and large positive cross-correlations between temperature and specific humidity (Ménétrier and Montmerle, 2011). In this context, Martinet et al. (2020) have demonstrated that humidity retrievals could be significantly degraded if sub-optimal background error covariances are used during the minimization. New ensemble approaches allow for better approximation of background error covariance matrices but rely on the capability of the ensemble data assimilation (EDA) to correctly represent model errors, which might not always be the case during fog conditions. This is why it would be of interest to examine, in a data assimilation context, the use of variables that are more suitable to times when water phase changes take place.

It is well known that most data assimilation systems were based on the assumptions of homogeneity and isotropy of background error correlations. To test these hypotheses, Desroziers and Lafore (1993) and Desroziers (1997) implemented a coordinate change inspired by the semi-geostrophic theory to test flow-dependent analyses with case studies from the Front-87 field campaign (Clough and Testud, 1988), where the local horizontal coordinates were transformed into the semi-geostrophic space during the assimilation process. Another kind of flow-dependent analyses were made by Cullen (2003) and Wlasak et al. (2006), who proposed a low-order potential vorticity (PV) inversion scheme to define a new set of control variables. Similarly, analyses on potential temperature θ were made by Shapiro and Hastings (1973) and Benjamin et al. (1991), and more recently by Benjamin et al. (2004) with moist virtual θ_v and moist equivalent θ_e potential temperatures.

The aim of the paper is to test a one-dimensional data assimilation method that would be less sensitive to the average vertical gradients of the ($T,q_{\mathrm{v}},q_{\mathrm{l}},q_{\mathrm{i}}$) variables. To this end, two conservative variables will be proposed, generalizing previous uses of θ (as a proxy for the entropy of dry air) to moist-air variables suitable for data assimilation. The new conservative variables are the total water content $q_{\mathrm{t}}=q_{\mathrm{v}}+q_{\mathrm{l}}+q_{\mathrm{i}}$ and the moist-air entropy potential temperature θ_s defined in Marquet (2011), which generalize the two well-known conservative variables (q_t,θ_l) of Betts (1973).

The focus of the study will be on a fog situation from the SOFOG3D field campaign using a one-dimensional variational data assimilation system (1D-Var) for the assimilation of observed microwave brightness temperatures (TBs) sensitive to T, q_v and q_l from a ground-based radiometer. Short-range forecasts from the convective scale model AROME (Seity et al., 2011) will be used as background profiles, the ground-based version of the fast Radiative Transfer for the TIROS Operational Vertical Sounder (RTTOV-gb) model (De Angelis et al., 2016; Cimini et al., 2019) will allow for the accurate simulation of the TBs and suitable background error covariance matrices will be derived from an ensemble technique.

Section 2 presents the methodology (conservative variables, 1D-Var, change of variables). Section 3 describes the experimental setting, the meteorological context, the observations and the different components of the 1D-Var system. The results are commented in Sect. 4. Finally, conclusions and perspectives are given in Sect. 5.

2 Methods

This section presents the methodology chosen for this study. The definition of the moist-air entropy potential temperature θ_s is introduced, as well as the formalism of the 1D-Var assimilation system, before describing the “conservative variable” conversion operator.

2.1 Moist-air entropy potential temperature

The motivation for using the absolute moist-air entropy in atmospheric science was first described by Richardson (1919, 1922), and then fully formalized by Hauf and Höller (1987). The method comprises taking into account the absolute value for dry air and water vapour and to define a moist-air entropy potential temperature variable called θ_s.

However, the version of θ_s published in Hauf and Höller (1987) was not really synonymous with the moist-air entropy. This problem has been solved with the version of Marquet (2011) by imposing the same link with the specific entropy of moist air (s) as in the dry-air formalism of Bauer (1908), leading to

$$\begin{array}{}\text{(1)}& {\displaystyle }s=c_{p\mathrm{d}}\ln \left({\displaystyle \frac{{\mathit{\theta }}_{\mathrm{s}}}{T_{\mathrm{0}}}}\right)+s_{\mathrm{d}\mathrm{0}}(T_{\mathrm{0}},p_{\mathrm{0}}),\end{array}$$

where c_pd≈1004.7 $\mathrm{J}{\mathrm{K}}^{-\mathrm{1}}{\mathrm{kg}}^{-\mathrm{1}}$ is the dry-air specific heat at constant pressure, T₀=273.15 K is a standard temperature and $s_{\mathrm{d}\mathrm{0}}(T_{\mathrm{0}},p_{\mathrm{0}})\approx \mathrm{6775}$ $\mathrm{J}{\mathrm{K}}^{-\mathrm{1}}{\mathrm{kg}}^{-\mathrm{1}}$ is the reference dry-air entropy at T₀ and at the standard pressure p₀=1000 hPa. Because c_pd, T₀ and s_d0(T₀,p₀) are constant terms, θ_s defined by Eq. (1) is synonymous with, and has the same physical properties as, the moist-air entropy s.

The conservative aspects of this potential temperature θ_s and its meteorological properties (in e.g. fronts, convection, cyclones) have been studied in Marquet (2011), Blot (2013) and Marquet and Geleyn (2015). The links with the definition of the Brunt–Väisälä frequency and the PV are described in Marquet and Geleyn (2013) and Marquet (2014), while the significance of the absolute entropy to describe the thermodynamics of cyclones is shown in Marquet (2017) and Marquet and Dauhut (2018).

Only the first-order approximation of θ_s, denoted (θ_s)₁ in Marquet (2011), will be considered in the following, written as

$$\begin{array}{}\text{(2)}& {\displaystyle }{\mathit{\theta }}_{\mathrm{s}}\approx ({\mathit{\theta }}_{\mathrm{s}}{)}_{\mathrm{1}}=\mathit{\theta }\exp \left(-{\displaystyle \frac{L_{\mathrm{vap}}{q}_{\mathrm{l}}+L_{\mathrm{sub}}{q}_{\mathrm{i}}}{c_{p\mathrm{d}}T}}\right)\exp \left({\mathrm{\Lambda }}_{\mathrm{r}}{q}_{\mathrm{t}}\right),\end{array}$$

where $\mathit{\theta }=T{\left(p/p_{\mathrm{0}}\right)}^{\mathit{\kappa }}$ is the dry-air potential temperature, p the pressure, κ≈0.2857 and L_vap(T) and L_sub(T) the latent heat of vaporization and sublimation respectively. The explanation for Λ_r follows later in the section.

The first term θ on the right-hand side of Eq. (2) leads to a first conservation law (invariance) during adiabatic compression and expansion, with joint and opposite variations of T and p keeping θ constant. Here lies the motivation for using θ to describe dry-air convective processes, also used in data assimilation systems by Shapiro and Hastings (1973) and Benjamin et al. (1991).

The first exponential on the right-hand side of Eq. (2) explains a second form of conservation law. Indeed, this exponential is constant for reversible and adiabatic phase changes, for which $d\left(c_{p\mathrm{d}}T\right)\approx d(L_{\mathrm{vap}}{q}_{\mathrm{l}}+L_{\mathrm{sub}}{q}_{\mathrm{i}})$ due to the approximate conservation of the moist static energy $c_{p\mathrm{d}}T-L_{\mathrm{vap}}{q}_{\mathrm{l}}-L_{\mathrm{sub}}{q}_{\mathrm{i}}$, and therefore has joint variations of the numerator and denominator and a constant fraction into the first exponential. It should be mentioned that the product of θ by this first exponential forms the Betts (1973) conservative variable θ_l, which is presently used together with q_t to describe the moist-air turbulence in general circulation models (GCMs) and NWP models.

While the variable θ_l was established with the assumption of a constant total water content q_t in Betts (1973), the second exponential in Eq. (2) sheds new light on a third and new conservation law, where the entropy of moist air can remain constant despite changes in the total water q_t. This occurs in regions where water-vapour turbulence transport takes place, or via the evaporation process over oceans, or at the edges of clouds via entrainment and detrainment processes.

We consider here “open-system” thermodynamic processes, for which the second exponential takes into account the impact on moist-air entropy when the changes in specific content of water vapour are balanced, numerically, by opposite changes of dry air, namely with $d{q}_{\mathrm{d}}=-d{q}_{\mathrm{t}}\ne \mathrm{0}$. In this case, as stated in Marquet (2011), the changes in moist-air entropy depend on reference values (with subscript “r”) according to d[q_d (s_d)_r+q_t (s_v)_r], and thus with (s_d)_r and (s_v)_r being constant and with the relation $q_{\mathrm{d}}=\mathrm{1}-q_{\mathrm{t}}$, leading to [(s_v)_r−(s_d)_r] dq_t.

This explains the new term ${\mathrm{\Lambda }}_{\mathrm{r}}=\left[\right(s_{\mathrm{v}}{)}_{\mathrm{r}}-\left(s_{\mathrm{d}}{)}_{\mathrm{r}}\right]/c_{p\mathrm{d}}\approx \mathrm{5.869}\pm \mathrm{0.003}$, which depends on the absolute reference entropies for water vapour (s_v)_r≈12671 $\mathrm{J}{\mathrm{K}}^{-\mathrm{1}}{\mathrm{kg}}^{-\mathrm{1}}$ and dry air (s_d)_r≈6777 $\mathrm{J}{\mathrm{K}}^{-\mathrm{1}}{\mathrm{kg}}^{-\mathrm{1}}$. This also explains that these open-system thermodynamic effects can be taken into account to highlight regimes where the specific moist-air entropy (s), θ_s and (θ_s)₁ can be constant despite changes in q_t, which may decrease or increase on the vertical (see Marquet, 2011, for such examples).

Although it should be possible to use (θ_s)₁ as a control variable for assimilation, it appeared desirable to define an additional approximation of this variable for a more “regular” and more “linear” formulation, insofar as tangent-linear and adjoint versions are needed for the 1D-Var system. Considering the approximation $\exp \left(x\right)\approx \mathrm{1}+x$ for the two exponentials in Eq. (2), neglecting the second-order terms in x², also neglecting the variations of L_v(T) with temperature and assuming a no-ice hypothesis (q_i=0), the new variable is written as

$$\begin{array}{}\text{(3)}& {\displaystyle }({\mathit{\theta }}_{\mathrm{s}}{)}_a=\mathit{\theta }\left[\mathrm{1}+{\mathrm{\Lambda }}_{\mathrm{r}}{q}_{\mathrm{t}}-{\displaystyle \frac{L_{\mathrm{vap}}\left(T_{\mathrm{0}}\right)q_{\mathrm{l}}}{c_{p\mathrm{d}}T}}\right],\text{(4)}& {\displaystyle }({\mathit{\theta }}_{\mathrm{s}}{)}_a={\displaystyle \frac{\mathrm{1}}{c_{p\mathrm{d}}}}{\left({\displaystyle \frac{p_{\mathrm{0}}}{p}}\right)}^{\mathit{\kappa }}\left[c_{p\mathrm{d}}(\mathrm{1}+{\mathrm{\Lambda }}_{\mathrm{r}}{q}_{\mathrm{t}})T-L_{\mathrm{vap}}\left(T_{\mathrm{0}}\right)q_{\mathrm{l}}\right],\end{array}$$

where L_vap(T₀)≈2501 kJ kg⁻¹. This formulation corresponds to $S_{\mathrm{m}}/c_{p\mathrm{d}}$, where S_m is the moist static energy defined in Marquet (2011, Eq. 73) and used in the European Centre for Medium-Range Weather Forecasts (ECMWF) NWP global model by Marquet and Bechtold (2020).

The new potential temperature (θ_s)_a remains close to (θ_s)₁ (not shown) and keeps almost the same three conservative properties described for (θ_s)₁. This new conservative variable (θ_s)_a will be used along with the total water content $q_{\mathrm{t}}=q_{\mathrm{v}}+q_{\mathrm{l}}$ in the data assimilation experimental context described in the following sections.

2.2 1D-Var formalism

The general framework describing the retrieval of atmospheric profiles from remote-sensing instruments by statistical methods can be found in Rodgers (1976). In the following we present the main equations of the one-dimensional variational formalism. Additional details are given in Thépaut and Moll (1990), who developed the first 1D-Var inversion applied to satellite radiances using the adjoint technique.

The 1D-Var data assimilation system searches for an optimal state (the analysis) as an approximate solution of the problem minimizing a cost function 𝒥 defined by

$$\begin{array}{}\text{(5)}& \begin{array}{rl}\mathcal{J}\left(\mathit{x}\right)& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathit{x}-{\mathit{x}}_b{)}^T{{\mathbf{B}}_x}^{-\mathrm{1}}(\mathit{x}-{\mathit{x}}_{\mathrm{b}})\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}[\mathit{y}-\mathcal{H}(\mathit{x}\left){]}^T{\mathbf{R}}^{-\mathrm{1}}\right[\mathit{y}-\mathcal{H}\left(\mathit{x}\right)].\end{array}\end{array}$$

The symbol ^T represents the transpose of a matrix.

The first (background) term measures the distance in model space between a control vector x (in our study, T, q_v and q_l profiles) and a background vector x_b, weighted by the inverse of the background error covariance matrix (B_x) associated with the vector x. The second (observation) term measures the distance in the observation space between the value simulated from the model variables ℋ(x) (in our study, the RTTOV-gb model) and the observation vector y (in our study, a set of microwave TBs from a ground-based radiometer), weighted by the inverse of the observation error covariance matrix (R). The solution is searched iteratively by performing several evaluations of 𝒥 and its gradient:

$$\begin{array}{}\text{(6)}& {\displaystyle }{\mathrm{\nabla }}_x\mathcal{J}\left(x\right)={{\mathbf{B}}_{\mathbf{x}}}^{-\mathrm{1}}(\mathit{x}-{\mathbf{x}}_{\mathrm{b}})-{\mathbf{H}}^T{\mathbf{R}}^{-\mathrm{1}}[\mathit{y}-\mathcal{H}(\mathit{x}\left)\right],\end{array}$$

where H is the Jacobian matrix of the observation operator representing the sensitivity of the observation operator to changes in the control vector x (H^T is also called the adjoint of the observation operator).

2.3 Conversion operator

The 1D-Var assimilation defined previously with the variables $x=(T,q_{\mathrm{v}},q_{\mathrm{l}})$ can be modified to use the conservative variables $z=\left(\right({\mathit{\theta }}_{\mathrm{s}}{)}_a,q_{\mathrm{t}})$. A conversion operator that projects the state vector from one space to the other can be written as x=ℒ(z). In the presence of liquid water q_l, an adjustment to saturation is made to separate its contribution to the total water content q_t from the water-vapour content q_v. This is equivalent to distinguishing the “unsaturated” case from the “saturated” one. Therefore, starting from initial conditions $(T_I,q_I)=(T,q_{\mathrm{v}})$ and using the conservation of (θ_s)_a given by Eq. (4), we look for the variable T^∗ such that

$$\begin{array}{}\text{(7)}& T^{\ast }+\mathit{\alpha }{q}_{\mathrm{sat}}\left(T^{\ast }\right)=T_I+\mathit{\alpha }{q}_I,\end{array}$$

where

$$\begin{array}{}\text{(8)}& \mathit{\alpha }={\displaystyle \frac{L_{\mathrm{vap}}\left(T_{\mathrm{0}}\right)}{c_{p\mathrm{d}}(\mathrm{1}+{\mathrm{\Lambda }}_{\mathrm{r}}{q}_{\mathrm{t}})}},\end{array}$$

and q_sat(T^∗) is the specific humidity at saturation.

For the unsaturated case $(q_{\mathrm{v}}<q_{\mathrm{sat}}(T^{\ast }\left)\right)$, we obtain the variables $(T,q_{\mathrm{v}},q_{\mathrm{l}})$ directly from Eq. (4):

$$q_{\mathrm{l}}=\mathrm{0},q_{\mathrm{v}}=q_{\mathrm{t}},$$

and

$$\begin{array}{}\text{(9)}& T=({\mathit{\theta }}_{\mathrm{s}}{)}_a{\left({\displaystyle \frac{p}{p_{\mathrm{0}}}}\right)}^{\mathit{\kappa }}{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+{\mathrm{\Lambda }}_{\mathrm{r}}{q}_{\mathrm{t}}}}.\end{array}$$

For the saturated case ($q_{\mathrm{v}}\ge q_{\mathrm{sat}}\left(T^{\ast }\right)$), we write

$$q_{\mathrm{l}}=q_{\mathrm{t}}-q_{\mathrm{sat}}\left(T^{\ast }\right),$$

and

$$\begin{array}{}\text{(10)}& q_{\mathrm{v}}=q_{\mathrm{sat}}\left(T^{\ast }\right).\end{array}$$

In this situation, it is necessary to implicitly calculate the temperature T^∗, given by Eq. (7). We numerically compute an approximation of T^∗ by using Newton's iterative algorithm.

Taking into account this change of variables, the cost function can be written as

$$\begin{array}{}\text{(11)}& \begin{array}{rl}\mathcal{J}\left(\mathit{z}\right)& ={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathit{z}-{\mathit{z}}_b{)}^T{\mathbf{B}}_z^{-\mathrm{1}}(\mathit{z}-{\mathit{z}}_b)\\ & +{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}[\mathit{y}-\mathcal{H}(\mathcal{L}\left(\mathit{z}\right)\left){]}^T{\mathbf{R}}^{-\mathrm{1}}\right[\mathit{y}-\mathcal{H}\left(\mathcal{L}\right(\mathit{z}\left)\right)].\end{array}\end{array}$$

Then, its gradient given by Eq. (6) becomes

$$\begin{array}{}\text{(12)}& {\mathrm{\nabla }}_z\mathcal{J}\left(\mathit{z}\right)={\mathbf{B}}_z^{-\mathrm{1}}(\mathit{z}-{\mathit{z}}_b)-{\mathbf{L}}^T{\mathbf{H}}^T{\mathbf{R}}^{-\mathrm{1}}[\mathit{y}-\mathcal{H}(\mathcal{L}\left(\mathit{z}\right)\left)\right],\end{array}$$

where L^T is the adjoint of the conversion operator ℒ.

The second term on the right-hand side of Eqs. (11) and (12) indicates that the conversion operator ℒ is needed to compute the TBs from the observation operator ℋ. Indeed RTTOV-gb requires profiles of temperature, specific humidity and liquid water content as input quantities. This space change is required at each step of the minimization process. For the computation of the gradient of the cost function ∇_z𝒥, the linearized version (adjoint) of ℒ is also necessary. In practice, the operator L^T provides the gradient of the TBs with respect to the conservative variables, knowing the gradient with respect to the classical variables.

3 Experimental set-up

The numerical experiments to be presented afterwards will use measurements made during the SOFOG3D field experiment (https://www.umr-cnrm.fr/spip.php?article1086, last access: 31 March 2022; SOuth west FOGs 3D experiment for processes study) that took place from 1 October 2019 to 31 March 2020 in south-western France to advance understanding of small-scale processes and surface heterogeneities leading to fog formation and dissipation.

Many instruments were located at the Saint-Symphorien super-site (Les Landes region), such as a HATPRO (Humidity and Temperature PROfiler, Rose et al., 2005), a 95 GHz BASTA Doppler cloud radar (Delanoë et al., 2016), a Doppler lidar, an aerosol lidar, a surface weather station and a radiosonde station. One objective of this campaign was to test the contribution of the assimilation of such instrumentation on the forecast of fog events by NWP models.

3.1 Conditions on 9 February 2020

This section presents the experimental context of 9 February 2020 at the Saint-Symphorien site characterized by (i) a radiative fog event observed in the morning and (ii) the development of low-level clouds in the afternoon and evening.

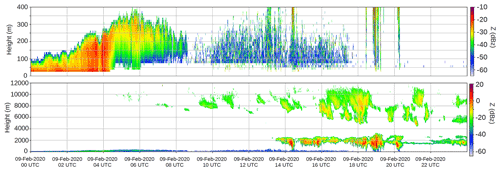
Figure 1 Reflectivity profiles at 95 GHz (dBZ) measured by the BASTA cloud radar in the first 500 m (top) and up to 12 000 m altitude (bottom), with UTC times given on the x axis, for the day of 9 February 2020 at Saint-Symphorien (Les Landes region). From http://basta.projet.latmos.ipsl.fr/?bi=bif (last access: 31 March 2022).

Figure 1 shows a time series of cloud radar reflectivity profiles (W-band at 95 GHz) measured by the BASTA instrument (Delanoë et al., 2016) in the lowest hundred metres (top panel) between 9 February 2020 at 00:00 UTC and 10 February 2020 at 00:00 UTC. The instrument reveals a thickening of the fog between 00:00 UTC and 04:00 UTC (9 February 2020). The fog layer thickness is located between 90 and 250 m. After 04:00 UTC, the fog layer near the ground rises, lifting into a “stratus” type cloud (between 100 and 300 m). After 08:00 UTC, the stratus cloud dissipates. In the bottom panel, BASTA observations up to 12 000 m (≈ 200 hPa) indicate low-level clouds after 14:00 UTC, generally between 1000 m (≈ 900 hPa) and 2000 m (≈ 780 hPa), with a fairly good agreement with AROME short-range (1 h) forecasts (see Fig. 2f). Optically thin (reflectivity below 0 dBZ) high-altitude ice clouds are also captured by the radar.

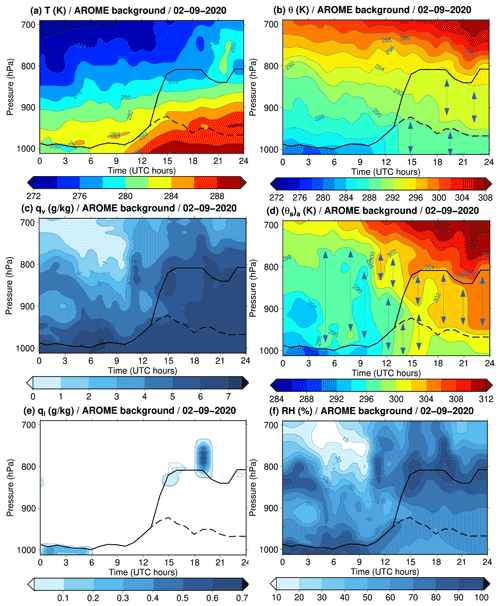
Figure 2 Vertical profiles derived from 1 h forecasts of AROME background for all hours of the day 9 February 2020 at Saint-Symphorien (Les Landes region in France) for (a) absolute temperature T every 2 K, (b) dry-air potential temperature θ every 0.2 K, (c) water-vapour specific content q_v every 1 g kg⁻¹, (d) entropy potential temperature (θ_s)_a every 0.2 K, (e) cloud liquid-water specific content q_l (contoured for 0.00001 and 0.002 g kg⁻¹, then every 0.1 g kg⁻¹ above 0.1 g kg⁻¹) and (f) relative humidity (RH) every 10 %. The black curves (solid and dashed lines) represent the planetary boundary layer (PBL) heights determined from the maximum of the vertical gradients of θ. The vertical arrows in (b) and (d) indicate areas where potential temperatures are almost homogeneous or constant along the vertical.

Figure 2 depicts the diurnal cycle evolution in terms of the vertical profiles of (a) absolute temperature T, (b) dry-air potential temperature θ, (c) water-vapour specific content q_v, (d) entropy potential temperature (θ_s)_a, (e) cloud liquid water specific content q_l and (f) relative humidity (RH), from 1 h AROME forecasts (background) of 9 February 2020 at Saint-Symphorien. At this stage, it is important to note that the AROME model has a 90-level vertical discretization from the surface up to 10 hPa, with high resolution in the planetary boundary layer (PBL) since 20 levels are below 2 km.

Figure 2e and f, for q_l and RH, show two main saturated layers: a fog layer close to the surface between 00:00 and 09:00 UTC with the presence of a thin liquid cloud layer aloft at 850 hPa at 00:00 UTC, and the presence of a stratocumulus cloud between 14:00 UTC and midnight (24:00 UTC) at 850 hPa. During the night, the near-surface layers cool down, with a thermal inversion that sets at around 01:00 UTC and persists until 07:00 UTC. After the transition period between 06:00 and 09:00 UTC, when the dissipation of the fog and stratus takes place, the air warms up and the PBL develops vertically (see the black curves plotted where vertical gradients of θ in Fig. 2b are large). Towards the end of the day, the thickness of the PBL remains important until 24:00 UTC, probably due to the presence of clouds between 800 and 750 hPa, which reduces the radiative cooling (see Fig. 2c and f for q_v and RH).

Figure 2d reveals weaker vertical gradients for the (θ_s)_a profiles, notably with contour lines often vertical and less numerous than those of the T, θ and q_v profiles in panels (a), (b) and (c), as also shown by more extensive and more numerous vertical arrows in panel (d) than in panel (b). Here we see the impact of the coefficient Λ_r≈5.869 in Eqs. (3)–(4), which allows the vertical gradients of θ in Fig. 2b and q_v in Fig. 2c to often compensate each other in the formula for (θ_s)_a. This is especially true between 980 and 750 hPa in the morning between 04:00 and 10:00 UTC, and also within the dry and moist boundary layers during the day.

Note that the dissipation of the fog is associated with a homogenization of (θ_s)_a in Fig. 2d from 04:00 to 05:00 UTC in the whole layer above, in the same way as the transition from stratocumulus toward cumulus was associated with a cancellation of the vertical gradient of (θ_s)₁ in Fig. 6 of Marquet and Geleyn (2015). This phenomenon cannot be easily deduced from the separate analysis of the gradients of θ and q_v in Fig. 2b and c. Therefore, three air mass changes can be clearly distinguished during the day. The vertical gradients of (θ_s)_a are stronger during cloudy situations, first (i) at night and early morning before 04:00 UTC and just above the fog, then (ii) at the end of the day above the top-cloud level at 800 hPa and (iii) turbulence-related phenomena in between that mix the air mass and (θ_s)_a, up to the cloudy layer tops that evolve between 950 and 800 hPa from 13:00 to 17:00 UTC.

Table 1 Channel numbers, band frequencies (GHz) and observation uncertainties (K) prescribed in the observation error covariance matrix (from Martinet et al., 2020).

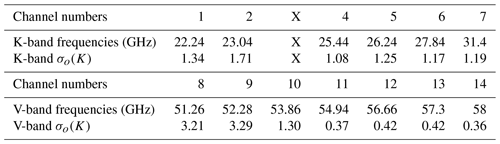
The observations to be assimilated are presented in the following. The HATPRO MicroWave Radiometer (MWR) measures TBs at 14 frequencies (Rose et al., 2005) between 22.24 and 58 GHz: 7 are located in the water-vapour absorption K-band and 7 are located in the oxygen absorption V-band (see the Table 1). For our study, the third channel (at 23.84 GHz) was eliminated because of a receiver failure identified during the campaign. In this preliminary study, we have only considered the zenith observation geometry of the radiometer for the sake of simplicity.

The ℋ RTTOV-gb model needed to simulate the model equivalent of the observations, which, together with the choice of the control vector and the specification of the background and observation error matrices, are presented in the next section.

3.2 Components of the 1D-Var

In 1D-Var systems, the integrated liquid water content, liquid water path (LWP), can be included in the control vector x as initially proposed by Deblonde and English (2003) and more recently used by Martinet et al. (2020). A first experimental set-up has been defined where the minimization is performed with the control vector being $(T,q_{\mathrm{v}},\mathrm{LWP})$. It will be considered as the reference, named REF. The 1D-Var system chosen for the present study is the one developed by the EUMETSAT NWP SAF (Numerical Weather Prediction Satellite Application Facility), where the minimization of the cost function is solved using an iterative procedure proposed by Rodgers (1976) with a Gauss–Newton descent algorithm. During the minimization process, only the amount of integrated liquid water is changed. In this approach, the two “moist” variables q_v and LWP are considered to be independent (no cross-covariances for background errors between these variables). The second experimental framework, where the control vector is $\mathit{z}=\left(\right({\mathit{\theta }}_{\mathrm{s}}{)}_a,q_{\mathrm{t}})$, corresponding to the conservative variables, is named EXP. The numerical aspects of the 1D-Var minimization are kept the same as in REF.

Then, a set of reference matrices B_x(T,q_v) was estimated every hour using the EDA system of the AROME model on 9 February 2020. These matrices were obtained by computing statistics from a set of 25 members providing 3 h forecasts for a subset of 5000 points randomly selected in the AROME domain to obtain a sufficiently large statistical sample. Then, matrices associated with fog areas, denoted B_x(T,q_v)_fog, were computed every hour by applying a fog mask (defined by areas where q_l is above 10⁻⁶ kg kg⁻¹ for the three lowest model levels), in order to select only model grid points for which fog is forecast in the majority of the 25 AROME members. The background error covariance matrices B_z((θ_s)_a,q_t) and B_z((θ_s)_a,q_t)_fog were obtained in a similar way.

The observation errors are those proposed by Martinet et al. (2020) with values between 1 and 1.7 K for humidity channels (frequencies between 22 and 31 GHz), values between 1 and 3 K for transparent channels affected by larger uncertainties in the modelling of the oxygen absorption band (frequencies between 51 and 54 GHz) and values below 0.5 K for the most opaque channels (frequencies between 55 and 58 GHz).

The RTTOV model is used to calculate TBs in different frequency bands from atmospheric temperature, water vapour and hydrometeor profiles together with surface properties (provided by outputs from the AROME model). This radiative transfer model has been adapted to simulate ground-based microwave radiometer observations (RTTOV-gb) by De Angelis et al. (2016).

4 Numerical results

The 1D-Var algorithm was tested on the day of 9 February 2020 with observations from the HATPRO microwave radiometer installed at Saint-Symphorien. This section presents and discusses three aspects of the results obtained: (1) the study of background error cross-correlations; (2) the performance of the 1D-Var assimilation system in observation space by examining the fit of the simulated TB with respect to the observed ones; and (3) the performance of the 1D-Var assimilation system in model space in terms of analysis increments for temperature, specific humidity and liquid water content.

4.1 Background error cross correlations

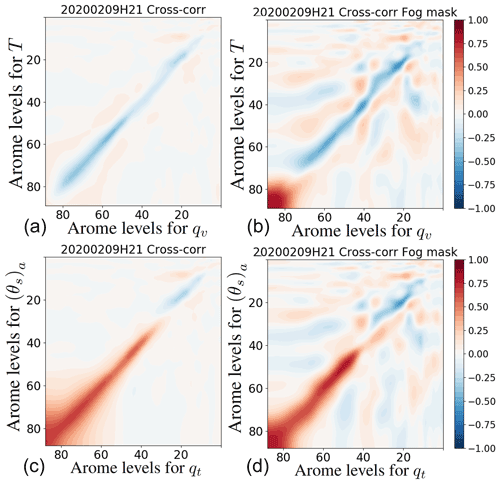
Figure 3 displays for the selected day at 06:00 UTC the cross-correlations between T and q_v (top) and between (θ_s)_a and q_t (bottom), with (right) and without (left) a fog mask. For the classical variables the correlations are strongly positive in the saturated boundary layer with the fog mask from levels 75 to 90 (between 1015 and 950 hPa), while with profiles in all-weather conditions the correlations between T and q_v are very weak in the lowest layers. On the other hand, the atmospheric layers above the fog layer exhibit negative correlations between temperature and specific humidity along the first diagonal.

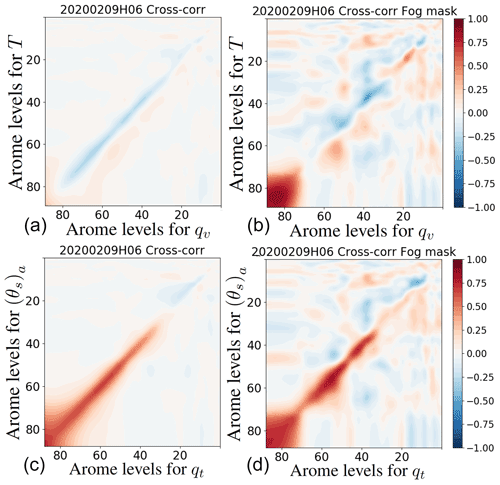
Figure 3 Background error cross-correlation matrices at 06:00 UTC 9 February 2020 without (a, c) and with (b, d) a fog mask. (a, b) Between the classical variables (T,q_v). (c, d) Between the new conservative variables ((θ_s)_a,q_t). The axes correspond to the levels of the AROME vertical grid (1 at the top and 90 for the first level above the surface). Correlations are between −1 (blue) and 1 (red) as shown in the colour bars (the same for the four plots).

When considering conservative variables, the correlations along the diagonal show a consistently positive signal in the troposphere (below level 20 located around 280 hPa). Contrary to the classical variables, which are rather independent in clear-sky atmospheres as previously shown by Ménétrier and Montmerle (2011), the B_z matrix reflects the physical link between the two new variables (shown by Eq. 4) as diagnosed from the AROME model. The correlations are positive with and without a fog mask. This result shows that the matrix B_z((θ_s)_a,q_t) is less sensitive to fog conditions than the B_x matrix. It could therefore be possible to compute a B_z((θ_s)_a,q_t) matrix without any profile selection criteria that would be nevertheless suitable for fog situations, resulting in a more robust estimate. This result is key for 1D-Var retrievals which are commonly used in the community of ground-based remote-sensing instruments to provide databases of vertical profiles for the scientific community. In fact, the accuracy of 1D-Var retrievals is expected to be more robust with less flow-dependent B matrices.

We also note that these background error statistics are less dependent on the diurnal cycle and on the meteorological situation (e.g. in the presence of fog at 06:00 UTC and low clouds at 21:00 UTC), contrary to the B_x(T,q_v) matrix, where there is a reduction in the area of positive correlation in the lowest layers between 06:00 and 21:00 UTC (Fig. 4).

Figure 4 Same as Fig. 3, but at 21:00 UTC.

The 1D-Var results are now assessed in observation space by examining innovations (differences between observed and simulated TBs) from AROME background profiles and residuals. In the following, we have only used background error covariance matrices estimated at 06:00 UTC with a fog mask, for a simplified comparison framework of the two 1D-Var systems.

4.2 1D-Var analysis fit to observations

Figure 5 presents both (a) innovations and (b, c) residuals obtained with the two 1D-Var systems (Fig. 5b: REF and Fig. 5c: EXP) for the 13 channels (1, 2, 4–14) and for each hour of the day. The innovations are generally positive for water-vapour-sensitive channels during the day, and negative for temperature channels, especially in the morning. The differences are mostly between −2.5 and 5 K. For channels 8, 9 and 10, which are sensitive to liquid water content, the innovations can reach higher values exceeding 10 K (in the afternoon) or around −5 K (in the morning).

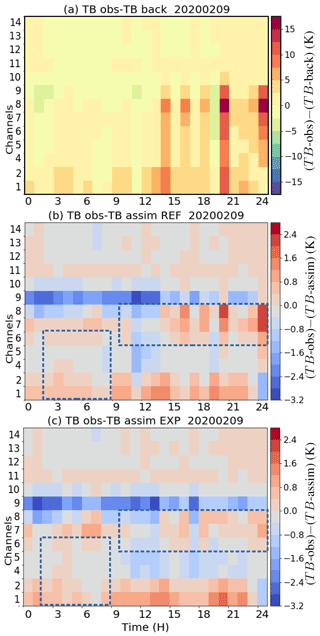
Figure 5 Differences in observed (channels 1, 2 and 4 to 7 located between 22 and 31 GHz and channels 8 to 14 located between 51 and 58 GHz, HATPRO radiometer) and simulated (with RTTOV-gb) TBs (in Kelvin): (a) from AROME background profiles, (b) from 1D-Var analyses from the REF configuration and (c) from 1D-Var analyses from the EXP configuration for all hours of the day on 9 February 2020 at Saint-Symphorien (Les Landes region). The dashed blue boxes indicate the channels and times where EXP is improved with respect to REF. Colour bars are in unit of K.

In terms of residuals, as expected from 1D-Var systems, both experiments significantly reduce the deviations of the observed TB from those calculated using the background profiles, especially for the first eight channels sensitive to water vapour and liquid water. We can note that the residuals are not as reduced for channel 9 (52.28 GHz) compared to other channels. Indeed, channels 8 and 9 (51.26 and 52.28 GHz) suffer from larger calibration uncertainties (Maschwitz et al., 2013) and larger forward model uncertainties dominated by oxygen line mixing parameters (Cimini et al., 2018) than other temperature-sensitive channels. However, by comparing simulated TB with different absorption models (Hewison, 2007), or through monitoring with simulated TB from clear-sky background profiles (De Angelis et al., 2017; Martinet et al., 2020), larger biases are generally observed only at 52.28 GHz. Consequently, the higher deviations observed in Fig. 5 for channel 9 mostly originate from larger modelling and calibration uncertainties, which are taken into account in the assumed instrumental errors (prescribed observation errors of about 3 K for these two channels compared to <1 K for other temperature-sensitive channels) and also possibly from larger instrumental biases.

The temperature channels used in the zenith mode are only slightly modified as the deviations from the background values are much smaller than for the other channels. During the second half of the day, characterized by the presence of clouds around 800 hPa (see Fig. 2e and f), the residual values are largely reduced in the frequency bands sensitive to liquid water for channels 6, 7 and 8, especially for EXP as shown by the comparison of the pixels in the dashed rectangular boxes in Fig. 5b and c. Residuals are also slightly reduced for EXP in the morning and during the fog and low temperature period for the first five channels (1, 2, 4–6) between 02:00 and 08:00 UTC.

Table 2 Bias/RMSE (K) of the background and analyses produced by EXP and REF against MWR TB observations. Statistics are computed either using all data or restricted to channels 1 to 5 between 02:00 and 08:00 UTC or channels 7 to 9 between 10:00 and 24:00 UTC (these two sub-samplings are represented by the dashed rectangular boxes in Fig. 5b and c).

In order to quantify these results for the 9 February 2020 dataset (all hours and all channels), the bias and root mean square error (RMSE) values are computed for the background and the analyses produced by REF and EXP. The innovations are characterized by a RMSE of 3.20 K and a bias of 1.32 K. Both assimilation experiments reduce these two quantities by modifying model profiles. The RMSEs are 0.71 K for EXP and 0.72 K for REF and the biases are −0.17 K for EXP and −0.11 K for REF. These statistics have also been calculated by restricting the dataset to the two dashed rectangular boxes presented in Fig. 5b and c. A significant improvement is observed for the most sensitive channels to liquid water in the afternoon with the RMSE decreasing from 4.3 K in the background to 0.57 K in REF and 0.37 K in EXP. For all computed statistics, EXP always provides the best performance in terms of RMSE. Table 2 summarizes the bias and RMSE values obtained for the different samples.

4.3 Vertical profiles of analysis increments

After examining the fit of the two experiments to the observed TBs, we assess the corrections made in model space. Figure 6 shows the increments of (a, b) temperature, (c, d) specific humidity and (e, f) liquid water for the two experiments REF (left panels) and EXP (right panels). In addition, the increments of (θ_s)_a are shown in panels (g)–(h).

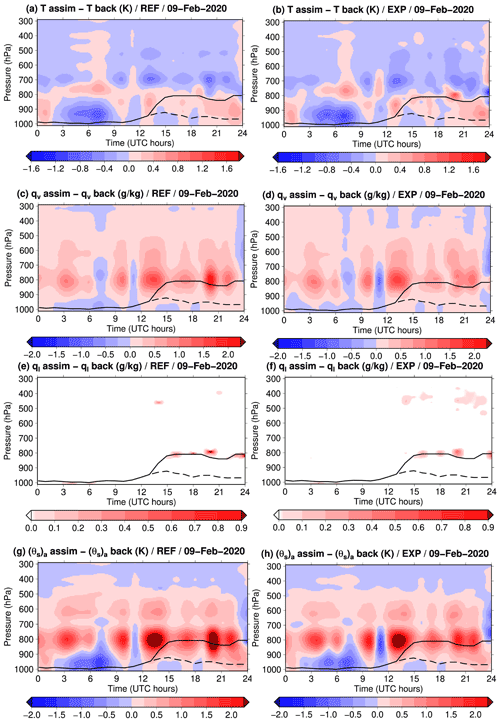
Figure 6 Profiles of analysis increments resulting from two 1D-Var experiments: REF (left) and EXP (right) for (a–b) T in K, (c–d) q_v in g kg⁻¹, (e–f) q_l in g kg⁻¹ and (g–h) (θ_s)_a in K. Colour bars have the same units (K or g kg⁻¹) as the variables.

The temperature increments are mostly located in the lower troposphere (below 650 hPa) with a dominance of negative values of small amplitude (around 0.5 K). This is consistent with the negative innovations observed in the temperature channels, highlighting a warm bias in the background profiles. The areas of maximum cooling take place in cloud layers (inside the thick fog layer below 900 hPa until 09:00 UTC and around 700 hPa after 12:00 UTC). The increments are rather similar between REF and EXP, but the positive increments appear to be larger with EXP (e.g. at 08:00 and 20:00 UTC around 800 hPa).

Concerning the profiles associated with moist variables, the structures show similarities between the two experiments but with differences in intensity. During the night and in the morning, the q_v increments near the surface are negative. These negative increments are projected into increments having the same sign as T by the strong positive cross-correlations of the B_fog matrix up to 900 hPa (Fig. 3). Thus, the largest negative temperature and specific humidity increments remain confined in the lowest layers.

Liquid water is added in both experiments between 03:00 and 07:00 UTC, close to the surface, where the Jacobians of the most sensitive channels to q_l (6 to 8) have significant values in the fog layer present in the background (see Fig. 2e). After 14:00 UTC, values of q_v between 850 and 700 hPa and q_l around 800 hPa are enhanced in both cases, with larger increments for the REF case, in particular at 20:00 UTC and around 24:00 UTC (midnight). Most of the liquid water is created in low clouds. Additionally, increments of q_l above 600 hPa are larger and more extended vertically and in time in EXP, where condensation occurs over a thicker atmospheric layer between 500 and 300 hPa after 12:00 UTC. In the REF experiment, the creation of liquid water above 500 hPa only reaches values of 0.3 g kg⁻¹ sporadically, for example at 21:00 UTC. In this experimental set-up, condensed water can be created or removed over the whole column by means of the supersaturation diagnosed at each iteration of the minimization process (since RTTOV-gb needs $(T,q_{\mathrm{v}},q_{\mathrm{l}})$ profiles for the TB computation). This is a clear advantage of EXP over REF, which keeps the vertical structure of the q_l profile unchanged from the background. In REF, liquid water is only added where it already exists in the background because once the LWP variable is updated, the analysed q_l profile is just modified proportionally to the ratio between the LWP of the analysis and of the background, as explained in more details by Deblonde and English (2003).

The profiles of increments for (θ_s)_a show structures similar to the increments of q_v around 800 hPa and to the increments of T below, where temperature Jacobians are the largest (see Fig. 7 in De Angelis et al., 2016). The conversion of T, q_v and q_t changes obtained with REF into (θ_s)_a increments (Fig. 6g) highlights the main differences between the two systems. They take place around 800 hPa with larger increments produced by the new 1D-Var particularly between 11:00 and 14:00 UTC.

Some radiosoundings (RSs) have been launched during the SOFOG3D IOPs. As only one RS profile was launched at 05:21 UTC in the case study presented in the article, no statistical evaluation of the profile increments can be carried out. However, we have conducted an evaluation of the analysis increments obtained at 05:00 and 06:00 UTC (the 1D-Var retrievals were performed at a 1 h temporal resolution in line with the operational AROME assimilation cycles) around the RS launch time. As the AROME temperature background profile extracted at 06:00 UTC was found to have a vertical structure closer to the RS launched at 05:21 UTC, Fig. 7 compare the AROME background profile and 1D-Var analyses performed with the REF and EXP experiments valid at 06:00 UTC against the RS profile.

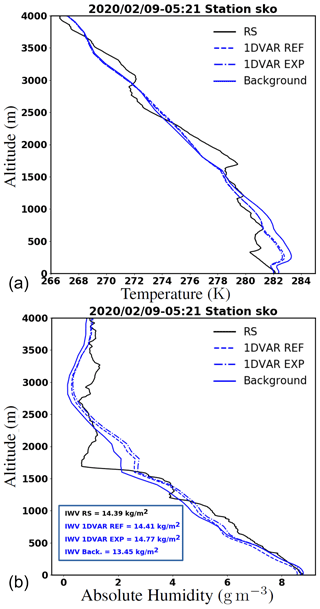
Figure 7 Vertical profiles of absolute temperature T (a, in K) and absolute humidity ρ_v (b, in g m⁻³) for 9 February 2020 and showing the RS launched at 05:21 UTC (solid black), the AROME background valid at 06:00 UTC (solid blue) and the 1D-Var retrievals at 06:00 UTC obtained with REF (dashed blue) and EXP (dot–dashed blue). Integrated water vapour (IWV) retrievals are also compared to the RS IWV (in the blue box in the bottom panel).

The temperature increments are a step in the right direction by cooling the AROME background profile in line with the observed RS profile. The two 1D-Var analyses are close to each other, but the EXP analysis produces a temperature profile slightly cooler compared to the REF analysis. In terms of absolute humidity (${\mathit{\rho }}_{\mathrm{v}}=p_{\mathrm{v}}/\left(R_{\mathrm{v}}T\right)$, with p_v the partial pressure and R_v the gas constant for water vapour), the background profile already exhibits a similar structure compared to the RS profile. The 1D-Var increments are thus small and close between the two experiments. However, we can note that the EXP profile is slightly moister than the REF profile from the surface up to 3500 m, which leads to a somewhat better agreement with the RS profile below 1500 m. In terms of integrated water vapour (IWV), a significant improvement of the background IWV with respect to the RS IWV is observed with the difference reduced from almost 1 kg m⁻² in the background to less than 0.4 kg m⁻² in the analyses. These analyses confirm the improvement brought to the model profiles by both the REF and EXP analysis increments, with some enhanced improvement for EXP.

5 Conclusions

The aim of this study was to examine the value of using moist-air entropy potential temperature (θ_s)_a and total water content q_t as new control variables for variational assimilation schemes. In fact, the use of control variables less dependent on vertical gradients of ($T,q_{\mathrm{v}},q_{\mathrm{l}},q_{\mathrm{i}}$) variables should ease the specification of background error covariance matrices, which play a key role in the quality of the analysis state in operational assimilation schemes.

To that end, a 1D-Var system has been used to assimilate TB observations from the ground-based HATPRO microwave radiometer installed at Saint-Symphorien (Les Landes region in south-western France) during the SOFOG3D measurement campaign (winter 2019–2020).

The 1D-Var system has been adapted to consider these new quantities as control variables. Since the radiative transfer model needs profiles of temperature, water vapour and cloud liquid water for the simulation of TB, an adjustment process has been defined to obtain these quantities from (θ_s)_a and q_t. The adjoint version of this conversion has been developed for an efficient estimation of the gradient of the cost function. Dedicated background error covariance matrices have been estimated from the EDA system of AROME. We first demonstrated that the matrices for the new variables are less dependent on the meteorological situation (all-weather conditions vs. fog conditions) and on the time of the day (stable conditions at night vs. unstable conditions during the day) leading to potentially more robust estimates. This is an important result as the optimal estimation of the analysis depends on the accurate specification of the background error covariance matrix, which is known to highly vary with weather conditions when using classical control variables.

The new 1D-Var has produced rather similar results in terms of the fit of the analysis to observed TB values when compared to the classical one using temperature, water vapour and LWP. Nevertheless, quantitative results reveal smaller biases and RMSE values with the new system in low cloud and fog areas. We also note that atmospheric increments are somewhat different in cloudy conditions between the two systems. For example, in the stratocumulus layer that formed during the afternoon, the new 1D-Var induces larger temperature increments and reduced liquid water corrections. Moreover, its capacity to generate cloud condensates in clear-sky regions of the background has been demonstrated. As a preliminary validation, the retrieved profiles from the 1D-Var have been compared favourably against an independent observation data set (one radiosounding launched during the SOFOG3D field campaign). The new 1D-Var leads to profiles of temperature and absolute humidity slightly closer to observations in the PBL.

The encouraging results obtained from this feasibility study need to be consolidated by complementary studies. Observed TBs at lower elevation angles should be included in the 1D-Var for a better constraint on temperature profiles within the atmospheric boundary layer. Indeed, larger differences in the temperature increments might be obtained between the classical 1D-Var system and the 1D-Var system using the new conservative variables when additional elevation angles are included in the observation vector. Other case studies from the field campaign could also be examined to confirm our first conclusions.

Finally, the conversion operator could be improved by accounting not only for liquid water content q_l but also for ice water content q_i (e.g. using a temperature threshold criteria). Indeed, inclusion of q_i in the conversion operator should lead to more realistic retrieved profiles of cloud condensates, and a 1D-Var system with only q_l can create water clouds at locations where ice clouds should be present, as done in our experiment around 400 hPa between 15:00 and 24:00 UTC. However, since the frequencies of HATPRO are not sensitive to ice water content, the fit of simulated TBs to observations could be reduced. As a consequence, the synergy with an instrument sensitive to ice water clouds, such as a W-band cloud radar, would be necessary for improved retrievals of both q_i and q_l. It is worth noting that the variable (θ_s)_a can easily be generalized to the case of the ice phase and mixed phases by taking advantage of the general definition of θ_s and (θ_s)₁, where L_vap q_l is simply replaced by L_vap q_l+L_sub q_i.