Retrieval of microphysical parameters of monsoonal rain using X-band dual-polarization radar: their seasonal dependence and evaluation

Multiyear measurements from a Joss–Waldvogel disdrometer (5 years) and X-band dual-polarization radar (2 years) made at Gadanki (13.5^∘ N, 79.18^∘ E), a low-latitude station, are used to (i) retrieve appropriate raindrop size distribution (DSD) relations for monsoonal rain, (ii) understand their dependency on temperature, the raindrop size shape model and season and (iii) assess polarimetric radar DSD retrievals by various popular techniques (the exponential (Exp), constrained Gamma (CG), normalized Gamma (N-Gamma) and β methods). The coefficients obtained for different DSD relations for monsoonal rain are found to be different from those of existing relations elsewhere. The seasonal variation in DSD is quite large and significant, and as a result, the coefficients also vary considerably between the seasons. The slope of the drop size–shape relation, assumed to be constant in several studies, varies considerably between the seasons, with warmer seasons showing a smaller slope value than the cold season. It is found that the constant (0.062) used in linear drop shape models is valid only for the cold season. The derived coefficients for the CG method for different seasons coupled with those available in the literature reveal that the warm seasons/regions typically have larger curvature and slope values than in the cold seasons/regions. The coefficients of the mass-weighted mean diameter (D_m) and differential reflectivity (Z_DR) exhibit a strong dependency on the drop shape model, while those for the derivation intercept parameter exhibit a strong seasonal dependency. Using the retrieved relations and X-band polarimetric radar at Gadanki, four popular DSD methods are evaluated against disdrometer measurements collected over 12 events. All the methods estimated D_m reasonably well with the small root mean square error but failed to estimate the intercept parameter accurately. Only the N-gamma method estimated the normalized intercept parameter reasonably. Problems associated with specific differential-phase (K_DP)-based estimates close to the radar location, particularly during overhead convection, are also discussed.

1 Introduction

Raindrop size distribution (DSD) is the fundamental property of precipitation, and its space–time variability depends on a variety of microphysical and dynamical processes inside and below clouds (Radhakrishna and Rao, 2009; Rao et al., 2009; Rosenfeld and Ulbrich, 2003). Such information is crucial even for numerical weather prediction models as these microphysical processes are fundamental blocks in microphysical schemes (Gao et al., 2011). Knowledge of DSD is not only required for fundamental understanding of microphysical processes, but also for a variety of operational applications in the fields of the hydrology, meteorology, agriculture, and road transportation sectors (Rosenfeld and Ulbrich, 2003; Serio et al., 2019; Uijlenhoet, 2001, and references therein). Disdrometers provide this crucial information continuously but only at the Earth's surface. Radars, on the other hand, provide DSD in both space and time and therefore play a major role in improving our understanding of microphysical processes in a variety of precipitating systems (Ryzhkov and Zrnic, 2019).

Remarkable progress has been made in polarimetric (dual-polarization) radar technology and its utilization for research and operational applications in the recent past (Bringi and Chandrasekar, 2001; Rauber and Nesbitt, 2018; Ryzhkov et al., 2022; Ryzhkov and Zrnic, 2019). Besides improving the rain rate estimation, the polarimetric radars offer unique information on microphysical properties of precipitation, like the DSD (Anagnostou et al., 2008a; Cao and Zhang, 2009; Gorgucci et al., 2001; Koffi et al., 2014; Maki et al., 2005; Moisseev and Chandrasekar, 2007; Penide et al., 2013; Seliga and Bringi, 1976; Zhang et al., 2001). They also provide information on the shape, orientation and phase state of hydrometeors by employing sophisticated hydrometeor classification algorithms like fuzzy logic and Bayesian classification (Liu and Chandrasekar, 2000; Marzano et al., 2007; Vivekanandan et al., 1999; Zrnic et al., 2001). Several earlier studies demonstrated that the DSD parameters can be used not only to understand the microphysics of precipitation and clouds, but also to improve rain rate estimation (Zhang et al., 2001; Gorgucci et al., 2001; Vivekanandan et al., 2003; Vulpiani et al., 2006; Brandes et al., 2004a; Cao et al., 2010, 2008; Gosset et al., 2010; Anagnostou et al., 2013; Koffi et al., 2014; Ryzhkov and Zrnic, 2019). They have shown that DSD-based rain rate estimation outperforms the fixed power law rainfall estimation from reflectivity fields and is equivalent to those derived with multi-parameter retrievals of rainfall with polarimetric radars (Anagnostou et al., 2010; Brandes et al., 2003; Vivekanandan et al., 2003).

Earlier studies followed various approaches to retrieve the DSD from polarimetric radars: statistical techniques and physics-based empirical relations between DSD model parameters and polarimetric products. Statistical methods, including neural networks (Vulpiani et al., 2006), Bayesian (Cao et al., 2010) and different variants of Bayesian, like variational methods (Cao et al., 2013; Yoshikawa et al., 2016), find the nonlinear relationships between DSD and polarimetric parameters by making use of mathematical techniques. These methods either train the chosen model or build an a priori database using existing information, which will then be used to retrieve DSD parameters. Physics-based methods assume that the DSD follows some functional form (exponential, gamma or normalized gamma) and derive a relation between DSD model parameters and polarimetric radar parameters empirically. Different methods have evolved over the years since: the Seliga and Bringi (1976) exponential method (Exp.), including constrained gamma (CG) (Zhang et al., 2001), Beta (β) (Gorgucci et al., 2000), normalized gamma (N-Gamma) (Bringi et al., 2002; Anagnostou et al., 2008a; Tokay et al., 2020a), the generalized gamma model (Thurai and Bringi, 2018), the double-moment model (Raupach and Berne, 2017), self-consistent with optical parameterization attenuation correction and microphysics estimation (SCOPE-ME) (Anagnostou et al., 2009), and the inverse model (Alcoba et al., 2022; Wen et al., 2018).

Among the above methods, the Exp., CG, N-Gamma and β methods are extensively used by researchers. The two-parameter exponential model assumes that the distribution of raindrops follows an exponential form, and its parameters can be retrieved from two polarimetric measurements, namely, the horizontal reflectivity factor (Z_H) and differential reflectivity (Z_DR) (Seliga and Bringi, 1976). The CG method assumes that the DSD follows a gamma distribution (Ulbrich, 1983), and the retrieval of the three gamma parameters is achieved using two independent polarimetric measurements and an empirically derived constrained relation between shape (μ) and slope (Λ) parameters of the gamma distribution (Brandes et al., 2004a; Zhang et al., 2001). The β method follows the normalized DSD concept, described in Willis (1984), Illingworth and Blackman (2002) and Testud et al. (2001). Here, the DSD is normalized with respect to liquid water content, which allows the study of variations in DSD shape by accounting for variations of water content. In addition, this method considers the raindrop shape–diameter relation to be a variable (Gorgucci et al., 2001) instead of a fixed relation for the equilibrium shape of a raindrop (Pruppacher and Beard, 1970). The Z_H, Z_DR and specific differential phase (K_DP) are used to obtain the slope (β) of the above relation, which intrinsically considers changes in drop oblateness that increase with the size of a raindrop.

Earlier studies derived/generated several empirical relations relating to polarimetric variables at different frequencies to obtain the DSD parameters. Some of these relations are obtained from simulations or parameterizations, and the others from observations (Adirosi et al., 2020; Anagnostou et al., 2008a, b; Brandes et al., 2004a, b; Gorgucci et al., 2001; Maki et al., 2005; Rao et al., 2006; Seliga and Bringi, 1976; Tang et al., 2014; Tokay et al., 2020b; Zhang et al., 2001, and references therein). Unfortunately, the above relations are found to be quite different at different locations due to large DSD variations (Brandes et al., 2004b; Chen et al., 2017; Chu and Su, 2008; Kim et al., 2020; Kumar et al., 2011; Rao et al., 2006; Seela et al., 2018; Tang et al., 2014; Zhang et al., 2001; Zheng et al., 2020). Not only between regions, the DSD and μ-Λ relations are also found to vary between different regimes (i.e., eye wall and rain bands) of a cyclone (Bao et al., 2020). These variations are caused primarily by different prevailing atmospheric conditions (in different geographical regions), in which the drop forms and the DSD evolves (Lee and Zawadzki, 2005). The above-reported relations are based on the data from America, Japan, Taiwan, Singapore, Italy and China and therefore are more appropriate for the above regions, while such relations do not exist for India (barring one study by Rao et al. (2006) using a limited dataset). The first objective of this paper is to derive suitable DSD retrieval relations at the X-band for monsoonal rainfall over the Indian region, where several X-band polarimetric radars are either installed or being installed. An X-band dual-polarization radar (DROP-X – Dual polarization Radar for Observing Precipitation at X-band), developed indigenously, recently became operational at Gadanki (13.5^∘ N, 79.18^∘ E) (Rao et al., 2023).

It is also known from earlier studies that the DSD varies not only with the climatic regime, but also with the season at the same location. For example, the DSD at a single station can be influenced by both the oceanic and continental systems, depending on the wind and circulation patterns (Kozu et al., 2006; Radhakrishna and Rao, 2009; Rao et al., 2009, 2001; Tokay et al., 2002; Lavanya et al., 2019). Recently, Rao et al. (2018) noted large differences in the coefficients of attenuation correction relations in different seasons. Given such large variability in DSD from one season to the other in southeastern peninsular India, one should also examine the impact of the observed seasonal variation on the DSD retrieval methods. This forms the second objective of this paper.

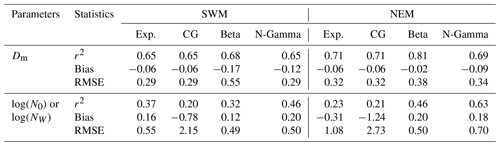
There have been differences of opinion about the validity of the retrieval of the above relations (μ–Λ relation and β method), the usage of the DSD models (exponential vs. gamma vs. normalized gamma) and the drop shape–size relations (linear and constant vs. linear but variable vs. polynomial). Earlier, a few studies compared different DSD retrieval techniques (Anagnostou et al., 2008b, a; Brandes et al., 2006, 2004a; Tokay et al., 2020b; Zhang et al., 2006). Such efforts were not made for monsoonal rain. Given the large seasonal variability in DSD, it is important to evaluate such schemes using observations from polarimetric radars. The present study, therefore, evaluates the retrieved mass-weighted mean diameter (D_m) and intercept parameter (N₀) or normalized intercept parameter (N_W) of DSD from DROP-X measurements and the derived relations.

The remainder of this paper is organized as follows. Section 2 describes the instruments, data and methodology (scattering simulations, deriving polarimetric products and DSD models) used in the present study. Relations between polarimetric products and exponential/gamma model parameters are empirically derived in Sect. 3. Seasonal dependence of the coefficients of the above relations and their variation with temperature are also discussed in Sect. 3. The retrieved DSD parameters from radar measurements are evaluated against the independent reference dataset in Sect. 4. Section 5 summarizes important findings from the present study.

2 Data and methodology

2.1 Data and instrumentation

Measurements from DROP-X and the collocated Joss–Waldvogel disdrometer (JWD) at the National Atmospheric Research Laboratory (NARL), Gadanki, are used in the present study. Gadanki is located in a complex hilly terrain of varying heights in the range of 200–500 m above ground level. It is located in southeastern India and experiences rain in three seasons. The southwestern monsoon (SWM – June through September) is the main monsoon season, in which it receives ∼ 53 % of its annual rainfall. This region also receives considerable rainfall (35 % of annual rainfall) during the northeastern monsoon (NEM – October through December), and the remaining annual rainfall occurs during the pre-monsoon season (PRE – March through May) (Rao et al., 2009; Radhakrishna and Rao, 2021). The rainfall is predominantly convective in nature (53.3 % of the total rainfall), while stratiform rain (30.2 %) and shallow rain (16.6 %) contribute considerably (Rao et al., 2008; Saikranthi et al., 2014).

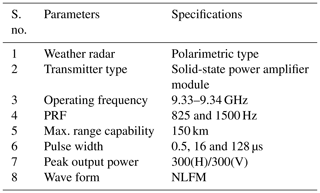
DROP-X was developed in-house by the Radar Development Area (RDA) of the ISRO Telemetry, Tracking and Command Network (ISTRAC) and NARL. The radar is placed on top of a building of 13 m height constructed on a small hillock to minimize blockages due to the local canopy. DROP-X operates in the frequency range of 9.33–9.34 GHz and has two independent channels for transmission and reception for horizontal and vertical polarized signals. It is equipped with two solid-state transmitters with a peak power of 300 W, one each for each polarization. Other important specifications of the radar are given in Table 1. For the present study, measurements made during 2019 and 2020 are utilized. During the above period, DROP-X was operated in regular plan position indicator (PPI) mode with a revolution speed of two revolutions per minute (rpm) and at 10 elevations (1–10^∘ with an interval of 1^∘). Each volume scan takes ∼ 6 min.

Table 1 Important specifications of DROP-X.

The JWD (RD-80) at Gadanki, used in the present study, is an impact-type disdrometer that records the number of raindrops hitting the 50 cm² surface of the sensor. It can identify 128 sizes of raindrops with diameters ranging from 0.3 to 5.4 mm and later arranges the data collected in 1 min into 20 drop-sized channels. All rain integral parameters like reflectivity (Z), rainfall rate (R) and D_m are estimated directly from the measured DSD using standard formulae (Rao et al., 2001). The measurements were corrected for the dead time of the instrument (Sheppard and Joe, 1994). Five years (2016–2020) of JWD measurements were used in the present study. First, 3 years of data are used to obtain coefficients of the relations between polarimetric radar measurements and geophysical parameters. Few quality checks have been performed to retain good-quality data. The data are considered to be valid only when R is greater than 0.5 mm h⁻¹ and available in at least four continuous drop-sized channels of the disdrometer. A total of 26 449 min of DSD data satisfied the above quality checks and are used in the present study. The latter 2 years of data are also subjected to the above quality checks and then are used to evaluate the performance of DSD retrievals with DROP-X. The disdrometer is located ∼ 200 m away from the radar location and at an azimuth angle of 77.5^∘. To match the radar temporal resolution (i.e., ∼ 6 min for the completion of one volume scan), disdrometer data are averaged over 6 min. The radar measurements around the disdrometer are also averaged to obtain the statistically robust estimate. For averaging, data of three range bins each in three azimuthal directions centered around the disdrometer location and at three elevation angles (4, 5 and 6^∘) are utilized (i.e., a volume averaging of 450 m × 10.5 m × 10.5 m at a height of 17 m above the disdrometer). The elevation angles are chosen in such a way that the targeted volume is as close as possible to the reference disdrometer but not contaminated by the ground clutter.

2.2 Methodology to retrieve polarimetric parameters

The scattering and extinction amplitudes are calculated using T-matrix scattering simulations (Mishchenko et al., 1996), following raindrop size shape models and parameters used for these simulations. Scattering amplitudes are computed at 9.34 GHz frequency with four standard raindrop size–shape models (Pruppacher and Beard, 1970; Beard and Chuang, 1987; Andsager et al., 1999; Brandes et al., 2002). Though simulations with the Andsager et al. (1999) model are finally used in our analysis, simulations with the other raindrop size shape models mentioned above are also performed to check the dependency of scattering amplitudes and retrieved polarimetric radar parameters on the drop shape model. The axis ratio is assumed to be the same as that given by the above drop shape models. Since the Brandes et al. (2002) model has accounted for the effect of raindrop oscillations in their axis ratio, no additional canting angle distribution is considered when it is used in simulations. For simulations with other drop shape models, the Gaussian canting angle distribution with a mean of 0^∘ and a standard deviation of 10^∘ is considered. Simulations are performed at different environmental temperatures, from 0 to 30 ^∘C with an interval of 5 ^∘C, to understand the dependency of scattering amplitudes on temperature, as performed by Rao et al. (2018).

The polarimetric radar parameters Z_HH, Z_DR and K_DP can be written as follows.

$$\begin{array}{}\text{(1)}& {\displaystyle }\begin{array}{rl}{Z}_{\mathrm{HH}}& =\mathrm{10}{\log }_{\mathrm{10}}\left[{\displaystyle \frac{\mathrm{4}\times {\mathrm{10}}^{\mathrm{10}}{\mathit{\lambda }}^{\mathrm{4}}}{{\mathit{\pi }}^{\mathrm{4}}\times {\left|K_w\right|}^{\mathrm{2}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\left[{\left|s_{\mathrm{VV}}^{\left(\mathit{\pi }\right)}\right|}^{\mathrm{2}}\right.\right.\\ & -\mathrm{2}\times \mathrm{Re}\left(s_{\mathrm{VV}}^{\ast \left(\mathit{\pi }\right)}\left(s_{\mathrm{VV}}^{\left(\mathit{\pi }\right)}-s_{\mathrm{HH}}^{\left(\mathit{\pi }\right)}\right)\right)\times A_{\mathrm{2}}\\ & \left.\left.+{\left|s_{\mathrm{VV}}^{\left(\mathit{\pi }\right)}-s_{\mathrm{HH}}^{\left(\mathit{\pi }\right)}\right|}^{\mathrm{2}}\times A_{\mathrm{4}}\right]N\left(D\right)\mathrm{d}D\right]\end{array}\text{(2)}& {\displaystyle }\begin{array}{rl}{Z}_{\mathrm{VV}}& =\mathrm{10}{\log }_{\mathrm{10}}\left[{\displaystyle \frac{\mathrm{4}\times {\mathrm{10}}^{\mathrm{10}}{\mathit{\lambda }}^{\mathrm{4}}}{{\mathit{\pi }}^{\mathrm{4}}\times {\left|K_w\right|}^{\mathrm{2}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\left[{\left|s_{\mathrm{VV}}^{\left(\mathit{\pi }\right)}\right|}^{\mathrm{2}}\right.\right.\\ & -\mathrm{2}\times \mathrm{Re}\left(s_{\mathrm{VV}}^{\ast \left(\mathit{\pi }\right)}\left(s_{\mathrm{VV}}^{\left(\mathit{\pi }\right)}-s_{\mathrm{HH}}^{\left(\mathit{\pi }\right)}\right)\right)\times A_{\mathrm{1}}\\ & \left.\left.+{\left|s_{\mathrm{VV}}^{\left(\mathit{\pi }\right)}-s_{\mathrm{HH}}^{\left(\mathit{\pi }\right)}\right|}^{\mathrm{2}}\times A_{\mathrm{3}}\right]N\left(D\right)\mathrm{d}D\right]\end{array}\text{(3)}& {\displaystyle }{K}_{\mathrm{DP}}={\displaystyle \frac{\mathrm{180}\times \mathit{\lambda }\times F_{\mathrm{orient}}}{\mathit{\pi }}}\underset{\mathrm{0}}{\overset{D_{max}}{\int }}\mathrm{Re}\left[s_{\mathrm{VV}}^{\left(\mathrm{0}\right)}-s_{\mathrm{HH}}^{\left(\mathrm{0}\right)}\right]N\left(D\right)\mathrm{d}D\text{(4)}& {\displaystyle }{Z}_{\mathrm{DR}}={\displaystyle \frac{Z_{\mathrm{HH}}}{Z_{\mathrm{VV}}}}\end{array}$$

D (mm) is the equivalent diameter of raindrops, λ (mm) is the radar wavelength and $s_{\mathrm{HH},\mathrm{VV}}^{(\ast ,\mathit{\alpha })}$ is the complex scattering amplitude at horizontal or vertical polarization for raindrops of diameter D, with the parameter α being the angle between the incident and scattering direction (in radian, 0 for forward scattering and π for back scattering). Re means the real part of a complex number (Bringi and Chandrasekar, 2001; Doviak and Zrnić, 1993; Ryzhkov and Zrnic, 2019). A₁, A₂, A₃ and A₄, are angular moments for the orientation of the raindrop, and F_orient is the orientation factor which depends on the width of the canting angle distribution (Ryzhkov and Zrnic, 2019). Z_HH and Z_VV (dBZ) are the reflectivity factors in the horizontal (both transmission and reception) and vertical (both transmission and reception) polarizations, respectively.

3 Retrieval of DSD relations: their dependency on seasons and temperature

3.1 Seasonal variation in DSD

Earlier studies have shown large seasonal variations in DSD in southeastern India and studied their impact on Z–R relations and attenuation correction algorithms (Kozu et al., 2006; Radhakrishna et al., 2009; Rao et al., 2018, 2009, 2001; Sulochana et al., 2016). Since the present dataset is different from that used in earlier studies (Radhakrishna et al., 2009; Rao et al., 2009, 2001), the seasonal means of N(D) at different R and variation of Z and D_m with R are examined to check whether the present dataset is able to reproduce earlier results on the seasonal behavior of DSD. Figure 1a and b show the variation of the seasonal mean N(D) with D for different seasons in two rain rate class intervals (5–10 and 15–20 mm h⁻¹), respectively. The DSD exhibits clear seasonal variation at both rain rates, with smaller drops predominantly occurring during the NEM and a considerable number of bigger drops during the warm seasons (PRE and SWM). The observed seasonal variation corroborates earlier studies and also reaffirms that these variations are robust and characteristic features of this region. The reduction of smaller drops during the warm seasons is attributed to the dominance of some microphysical processes, like evaporation and drop sorting, during those seasons (Radhakrishna et al., 2009).

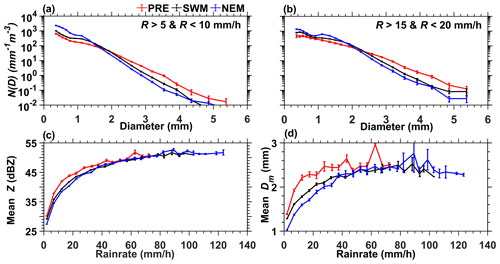
Figure 1 Seasonal mean DSD variation between the three seasons for two rain rate intervals, i.e., (a) 5–10 and (b) 15–20 mm h⁻¹. Variation of (c) mean Z and (d) mean D_m with R during different seasons. The data within each rain rate interval are averaged to obtain mean values. The error bar represents the standard deviation of the mean in each rain rate interval.

Due to the observed large seasonal variations in DSD, the bulk rainfall parameters like Z, R and D_m may also vary. Figure 1c and d, respectively, show the variation of mean values of D_m and Z (along with standard errors) with R in different seasons. The means are taken over the entire data in the respective R class intervals (5 mm h⁻¹). As expected, clear seasonal differences are apparent in bulk rain parameters also. Both D_m and Z are larger during the PRE, the hottest and convection-dominant season (Saikranthi et al., 2014), than in the other seasons, when R is less than 60 mm h⁻¹. These values are small during the NEM among all the seasons, mainly due to the presence of more (fewer) smaller (bigger) drops than in the other seasons, as can be evidenced from Fig. 1. The seasonal differences in bulk parameters are somewhat ambiguous at very high R (> 70 mm h⁻¹).

3.2 Retrieval of DSD relations for different seasons with various DSD models

3.2.1 Exponential method

The two-parameter exponential distribution with an intercept parameter (N₀) and slope parameter (Λ) is the most widely used model to represent DSD in microphysical parameterization schemes and is mathematically represented as follows:

$$\begin{array}{}\text{(5)}& N\left(D\right)=N_{\mathrm{0}}\exp \left(-\mathrm{\Lambda }D\right).\end{array}$$

To obtain the intercept and slope parameters of the exponential distribution, first, the D_m is derived from the polarimetric measurement of Z_DR using an empirically derived relation. As D_m and Λ of the exponential distribution are related by a simple equation, $\mathrm{\Lambda }=\frac{\mathrm{4}}{D_{\mathrm{m}}}$, the Λ can be estimated from D_m. The other parameter N₀ is derived from Z_H and the retrieved D_m using another empirical relation between them (Seliga and Bringi, 1976). The most important step in this process is to derive appropriate empirical relations between D_m and Z_DR and $Z_{\mathrm{H}}/N_{\mathrm{0}}$ and D_m: both vary with DSD and therefore are region-dependent.

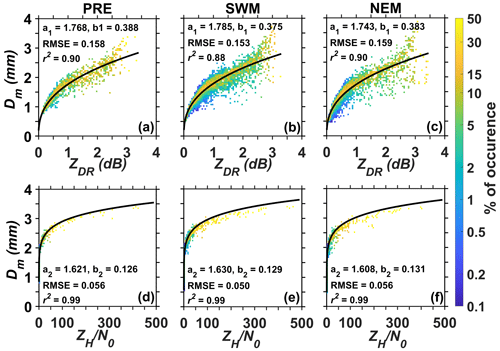
Figure 2 Scatter plots between Z_DR and D_m for the (a) PRE, (b) SWM and (c) NEM seasons. (d–f) Same as (a)–(c) but for $Z_{\mathrm{H}}/N_{\mathrm{0}}$ and D_m. The color indicates the percentage occurrence of data in each cell. The power law regression fit is overlain (solid line) on the data.

These empirical relations are retrieved from the scatter plots between Z_DR, D_m, $\log (Z_{\mathrm{H}}/N_{\mathrm{0}})$ and D_m (Fig. 2). Some of these parameters required for the scatter plots are computed directly from disdrometer measurements (R, Z and D_m), while other polarimetric products are estimated from T-matrix scattering simulations (Eqs. 1–4). The exponential parameters are estimated using the method of moments following Smith (2003). A power law fit, of the form given below, is applied to the data in Fig. 2 to obtain the coefficients in different seasons.

$$\begin{array}{}\text{(6)}& {\displaystyle }{D}_{\mathrm{m}}=a_{\mathrm{1}}{Z}_{\mathrm{DR}}^{b_{\mathrm{1}}}\text{(7)}& {\displaystyle }{D}_{\mathrm{m}}=a_{\mathrm{2}}{\left({\displaystyle \frac{Z_{\mathrm{H}}}{N_{\mathrm{0}}}}\right)}^{b_{\mathrm{2}}}\end{array}$$

Z_DR is represented in normal units.

Power law regression fits of the form shown in Eq. (6) are fitted to the data, and the coefficients (prefactor and exponent) are also shown in the figure. Good correlation is found between Z_DR and D_m in all the seasons, with correlation coefficients (r²) of 0.9, 0.88 and 0.9 for PRE, SWM and NEM, respectively. The correlation and root mean square error (RMSE) values during SWM indicate that the correlation is relatively weak during that season. Although some scatter exists around the regression fits, the majority of the points (as can be seen from the color bar) are close to the fit. The variance due to the scatter provides the theoretical limit on the retrieval of DSD parameters. The coefficients of the relation change with season in accordance with the seasonal variations in DSD. From the retrieved coefficients it is clear that the D_m values will be larger for the same Z_DR during PRE and NEM than in SWM. Also, the errors due to the usage of a single relation compared to seasonal relations are estimated in different seasons (not shown here). It is found that the usage of a single relation will produce considerable error during SWM (mean error of 6 % ± 4.2 %), the main rainy season for the study region. The correlation between $Z_{\mathrm{H}}/N_{\mathrm{0}}$ and D_m (Fig. 2d–f) is excellent in all seasons, with an r² of 0.99. The data also closely follow the regression fits, indicating the goodness of the fit. Though the prefactor is nearly equal in all the seasons, the variation in the exponent makes a difference of ∼ 20 %–30 % in the N₀ value between the seasons for the same $Z_{\mathrm{H}}/N_{\mathrm{0}}$ and D_m. In other words, separate relations are required for different seasons to reduce the uncertainty in DSD retrievals.

Only a few studies exist (Gosset et al., 2010; Matrosov et al., 2005) on the exponential method for the retrieval of microphysical information with X-band radars. Most of the existing studies were done at longer wavelengths, at the S and C bands. Gosset et al. (2010) obtained these power law coefficients using 11 600 DSD samples collected during the AMMA field campaign in Africa. They also noted large differences in coefficients, when they retrieved different raindrop size shape models. The coefficients with the Pruppacher and Beard (1970) model, in particular, are quite different from those obtained with other models in Africa, as seen at Gadanki. The coefficients derived at Gadanki are nearly equal to those obtained in Africa, when they are retrieved with the Andsagar et al. (1999) and Goddard et al. (1995) models. On the other hand, Matrosov et al. (2005) noted a weak dependency of coefficients on drop shape models (< 6 %) based on disdrometric measurements made along the western coast of the United States of America, which is considered to be negligible compared to the scatter in the data used to derive the above relation.

3.2.2 Constrained gamma method

Ulbrich (1983) noted that the exponential model may not adequately represent all variations in DSD, particularly in the lower drop regime in tropical precipitation. A three-parameter gamma model is then proposed to represent all types of raindrop spectra (Ulbrich, 1983), which are expressed in the form of

$$\begin{array}{}\text{(8)}& N\left(D\right)=N_{\mathrm{0}}{D}_{\mathit{\mu }}\exp \left(-\mathrm{\Lambda }D\right),\end{array}$$

where μ is the shape factor of the DSD.

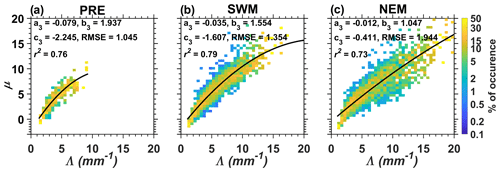
Figure 3 Scatter plots between μ and Λ during the (a) PRE, (b) SWM and (c) NEM seasons. The color indicates the percentage occurrence of data in each cell. The power law regression fit is overlain (solid line) on the data. The statistics of regression fits are also depicted in each panel of the figure.

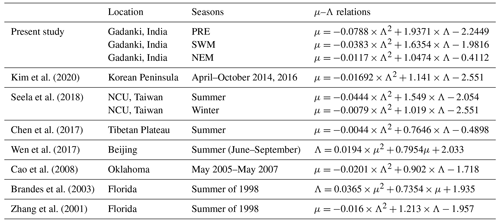
To estimate three parameters of the gamma distribution, three independent polarimetric variables are required. Earlier studies have shown that the three parameters of the gamma DSD model are not completely independent (Chandrasekar and Bringi, 1987; Haddad et al., 1997; Kozu and Nakamura, 1991; Ulbrich, 1983). This can be of great significance because it reduces the three parameters of the gamma DSD to two parameters by constraining any two parameters, which provides us with the retrieval of DSD parameters from a pair of independent radar measurements. Zhang et al. (2001) found a high correlation between μ and Λ and proposed an empirical μ–Λ relation. To improve the retrieval of smaller values of μ and Λ associated with higher rain rates, the relation was re-derived based on the truncated moment method in Brandes et al. (2003). Subsequently, several μ–Λ relations were retrieved in different regions with varying coefficients, indicating that the μ–Λ relation indeed varies with the climatic regime. A new μ–Λ relation has been derived for monsoonal rain at Gadanki by using 3 years (2016–2018) of disdrometer data. The data are considered for further processing only when the drop count exceeds 1500 m⁻³ and the rain rate is > 5 mm h⁻¹ to better retrieve values of μ and Λ associated with higher rain rates and a larger number of drop counts. The functional form of the relationship is

$$\begin{array}{}\text{(9)}& \mathit{\mu }=a_{\mathrm{3}}{\mathrm{\Lambda }}^{\mathrm{2}}+b_{\mathrm{3}}\mathrm{\Lambda }+c_{\mathrm{3}}.\end{array}$$

Figure 3 shows retrieved μ–Λ relations for the PRE, SWM and NEM seasons for monsoonal rain. The r² is nearly equal among all seasons; however, the coefficients for the μ–Λ relation are found to be different for different seasons. The correlation is somewhat weaker during NEM, with a smaller r² and larger RMSE than in the other seasons. Some scatter is also seen at higher μ and Λ values, but their occurrence is very low. It indicates that the μ–Λ relation is not only region-dependent but also varies with season at the same location. The coefficients of the μ–Λ relation appear to be temperature-dependent, as we see a gradual change in coefficients from the warmest PRE to the coldest NEM. Also, the warmest seasons of PRE and SWM have higher slope and curvature values compared to those in NEM. This means μ will be higher during PRE and SWM than in NEM for the same Λ for the majority of the data (i.e., when Λ and μ values are less than 8). The NEM with an abundance of smaller drops with fewer bigger drops (compared to PRE and SWM) typically has a smaller μ, even for a larger Λ.

Table 2 Comparison of μ–Λ relations obtained at Gadanki with those reported elsewhere.

As such relations are available at different locations, a comparison with them will be intuitive, which may also allow us to draw some generalized conclusions. The range of the curvature parameter from the published literature (Table 2) varies from 0.004 to 0.078, while the slopes and intercepts are in the ranges of 0.7–1.9 and 0.4–2.5, respectively. One can see that the curvature values vary by an order of magnitude between the regions. The differences in curvature and slope values are strikingly apparent between the warm/cold seasons/regions. The warm seasons/regions typically have larger curvature and slope values than in cold seasons/regions. In fact, the smallest value of the curvature (and also slope) is reported from the Tibetan Plateau. Smaller values of curvature and slope are also noted during the winter monsoon season at Gadanki and in Taiwan (Seela et al., 2018). It is very clear from these comparisons that the μ–Λ relation is region-dependent, corroborating earlier studies, but it can be broadly categorized into warm and cold seasons/regions.

Using the μ–Λ relations retrieved above, the gamma parameters are computed as follows. Similarly to the exponential method, the D_m is obtained from the Z_DR measurement. D_m is related to μ and Λ according to the following relationship:

$$\begin{array}{}\text{(10)}& \mathit{\mu }=\mathrm{\Lambda }{D}_{\mathrm{m}}-\mathrm{4}.\end{array}$$

From Eqs. (9) and (10), the following quadratic equation for Λ is obtained:

$$\begin{array}{}\text{(11)}& a_{\mathrm{3}}{\mathrm{\Lambda }}^{\mathrm{2}}+\left(b_{\mathrm{3}}-D_{\mathrm{m}}\right)\mathrm{\Lambda }+\left(c_{\mathrm{3}}+\mathrm{4}\right)=\mathrm{0}.\end{array}$$

Solving the above quadratic equation yields two solutions for Λ: one is positive, and the other is negative, from which the only physically possible positive Λ value is considered. The shape parameter can be computed from the retrieved Λ using Eq. (9). The intercept parameter N₀ is retrieved from radar reflectivity using the following equation (Zhang, 2017):

$$\begin{array}{}\text{(12)}& N_{\mathrm{0}}={\displaystyle \frac{Z_{\mathrm{H}}}{{\left(\frac{D_{\mathrm{m}}}{\mathrm{4}+\mathit{\mu }}\right)}^{(\mathrm{7}+\mathit{\mu })}\times \mathrm{\Gamma }(\mathit{\mu }+\mathrm{7})}}.\end{array}$$

3.2.3 Normalized gamma method

Testud et al. (2001) proposed the normalized gamma distribution model of the form shown below to represent the DSD, which was used later in several studies (Anagnostou et al., 2008a; Tokay et al., 2020a):

$$\begin{array}{}\text{(13)}& \begin{array}{rl}N\left(D\right)=& N_W{\displaystyle \frac{\mathrm{\Gamma }\left(\mathrm{4}\right)}{{\mathrm{3.67}}^{\mathrm{4}}}}{\displaystyle \frac{(\mathrm{3.67}+\mathit{\mu }{)}^{\mathrm{4}+\mathit{\mu }}}{\mathrm{\Gamma }(\mathrm{4}+\mathit{\mu })}}{\left({\displaystyle \frac{D}{D_{\mathrm{0}}}}\right)}^{\mathit{\mu }}\\ & \exp \left[-(\mathrm{3.67}+\mathit{\mu }){\displaystyle \frac{D}{D_{\mathrm{0}}}}\right],\end{array}\end{array}$$

where D₀ is the median volume diameter and N_W is the normalized form of the intercept parameter, which is related to D_m and liquid water content (LWC) as

$$\begin{array}{}\text{(14)}& N_W={\displaystyle \frac{{\mathrm{4}}^{\mathrm{4}}\mathrm{LWC}}{\mathit{\pi }{\mathit{\rho }}_W{D}_{\mathrm{m}}^{\mathrm{4}}}}.\end{array}$$

D_m and N_W can also be estimated empirically from radar parameters of Z_H and Z_DR and as follows (Tokay et al., 2020a).

$$\begin{array}{}\text{(15)}& {\displaystyle }{D}_{\mathrm{m}}=a_{\mathrm{4}}{Z}_{\mathrm{DR}}^{\mathrm{3}}+b_{\mathrm{4}}{Z}_{\mathrm{DR}}^{\mathrm{2}}+c_{\mathrm{4}}{Z}_{\mathrm{DR}}+d_{\mathrm{4}},\text{(16)}& {\displaystyle }{N}_W=a_{\mathrm{5}}{Z}_{\mathrm{H}}{D}_{\mathrm{m}}^{b_{\mathrm{5}}}\end{array}$$

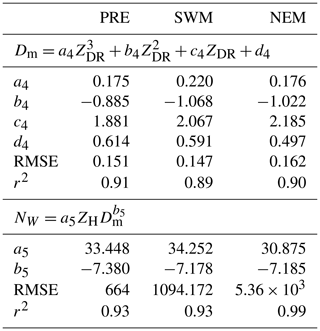
Figure 4a–c show the variation of D_m with Z_DR in the PRE, SWM and NEM seasons, respectively. A third-order polynomial fit of the form given in Eq. (15) has been adopted to obtain the coefficients separately for each season. Table 3 provides coefficients and fitting statistics (r² and RMSE) for each season. The variation in coefficients between the seasons is as large as 25 %, indicating the strong seasonal dependency exhibited by these relations. The coefficients obtained for monsoonal rain are also different from that reported by Tokay et al. (2020b) from different field campaigns (IFloodS, IPHEx and OLYMPEx). Figure 4d–f show variation of log (N_W) with D_m for the PRE, SWM and NEM seasons, respectively. Coefficients for the retrieval of N_W are obtained from the regression fit using Eq. (16). The color in the figure represents Z_H, and the solid curves are obtained with retrieved coefficients for different Z_H values. One can clearly see the differences in data distribution, here also with a considerable population at smaller D_m (and larger N_W) during the NEM, mainly due to the preponderance of smaller drops. One can also see the near absence of smaller D_m values (< 1 mm) during the premonsoon, mainly due to strong evaporation and drop sorting. These differences cause considerable seasonal variation in the retrieved coefficients (Table 3). The prefactor is found to be larger during the warmer seasons (PRE and SWM) than in the colder seasons. The prefactor values are comparable to those reported by Tokay et al. (2020a) from six field campaigns.

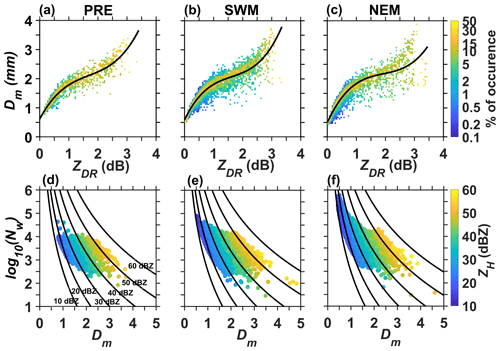
Figure 4 Scatter plots between Z_DR and D_m for the (a) PRE, (b) SWM and (c) NEM seasons. The solid line is the third-order polynomial fit (Eq. 15). (d–f) Scatter plots between log (N_W) and D_m as a function of Z_H for PRE, SWM and NEM, respectively. The solid lines indicate the variation of log (N_W) with D_m for different Z_H values, estimated using appropriate coefficients obtained with Eq. (16).

Table 3 Empirically derived coefficients of the D_m–Z_DR and N_W–(Z_H,D_m) relations for the PRE, SWM and NEM seasons and statistics of curve fittings.

3.2.4 Beta (β) method

Most of the studies that retrieve relations between polarimetric radar products and geophysical parameters (like DSD or rain rate) assume an equilibrium drop shape model, proposed by Pruppacher and Beard (1970), which predicts an almost linear decrease in the spheroidal raindrop aspect ratio r as a function of D,

$$\begin{array}{}\text{(17)}& r=\mathrm{1.03}-\mathrm{0.062}D,\end{array}$$

where $r=b/a$ is the axis ratio and b and a are the semi-minor and major axes of the raindrop, respectively (Pruppacher and Beard, 1970). The above equation gives aspect ratios close to those reported by Pruppacher and Pitter (1971). Drops less than about 0.5 mm were usually assumed to be spherical in shape. A number of later studies (e.g., Andsager et al., 1999; Gorgucci et al., 2001, 2000; Keenan et al., 2001) indicate that the equilibrium drop shape is not unique, and the variability in drop aspect ratio–diameter relations can be significant. The generalized form of the relation is, therefore, given as (Matrosov et al., 2002)

$$\begin{array}{}\text{(18)}& r=\mathrm{1.03}-\mathit{\beta }D,\end{array}$$

where β is the shape factor (mm), which is considered to be a variable rather than a fixed value by Pruppacher and Bread (1970). It is clear that the mean shape-sized relation of raindrops plays an important role in the interpretation of polarimetric radar measurements. In order to obtain the estimator β, the Z_H, Z_DR and K_DP are used as follows.

$$\begin{array}{}\text{(19)}& \mathit{\beta }=a_{\mathrm{6}}{\left({\displaystyle \frac{K_{\mathrm{DP}}}{Z_{\mathrm{H}}}}\right)}^{a_{\mathrm{7}}}{\mathit{\xi }}_{\mathrm{DR}}^{a_{\mathrm{8}}}\end{array}$$

Here, the Z_H is in mm⁻⁶ m⁻³, ξ_DR is Z_DR is on a linear scale and K_DP is in ^∘ km⁻¹.

Table 4 Coefficients of D_m and N_W retrieval equations.

The D_m and N_W are estimated from polarimetric variables using the following equations.

$$\begin{array}{}\text{(20)}& {\displaystyle }{D}_{\mathrm{m}}=b_{\mathrm{6}}{\left({\displaystyle \frac{{\mathit{\xi }}_{\mathrm{DR}}-\mathrm{0.8}}{\mathit{\beta }}}\right)}^{b_{\mathrm{7}}}\text{(21)}& {\displaystyle }{N}_W=c_{\mathrm{6}}{\left({\displaystyle \frac{{\mathit{\xi }}_{\mathrm{DR}}-\mathrm{0.8}}{\mathit{\beta }}}\right)}^{c_{\mathrm{7}}}{Z}_{\mathrm{H}}^{c_{\mathrm{8}}}\end{array}$$

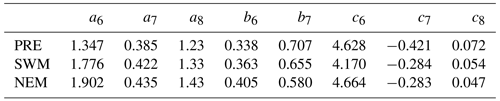
The coefficients a_6–8, b_6,7, and c_6–8 of Eqs. (19)–(21) are derived by computing the nonlinear regression analysis between each beta and the corresponding polarimetric measurements. Here, the computation has been carried out by considering the raindrop distribution to follow a normalized gamma DSD. The intrinsic shape of the DSD is obtained by normalizing the number density by N₀ (Testud et al., 2001). The retrieved coefficients in equations for β,D_m and N_W are given in Table 4. The mean value of β estimated using the retrieved coefficients and Eq. (19) is between 0.054 and 0.056 for warm seasons and ∼ 0.065 for NEM. The value obtained during NEM is closer to the default value (0.062) given by Pruppacher and Beard (1970), whereas the values obtained for PRE and SWM are much smaller, indicating that the slope of the drop-shape-sized relation is seasonally dependent. Like other DSD relations, the coefficients in the beta method also exhibit a large seasonal dependency, with some of the coefficients varying by as large as a factor of ∼ 2.

3.3 Dependence of DSD relations on temperature and drop shape models

A temperature of 20 ^∘C is used in the above T-matrix scattering simulations for computing radar parameters. To understand the dependency of retrieved coefficients on temperature, the exercise is repeated by varying temperatures from 0 to 30 ^∘C in increments of 5 ^∘C, and each time, coefficients of the above relations (Eqs. 6 and 7) are retrieved. Figure 5 shows the variation of prefactors and exponents in Eqs. (6) and (7) with temperature for different seasons. Except for a₂ (the prefactor in Eq. 7), all coefficients decrease monotonically with increasing temperature, albeit with different slopes. Clearly, the variation of the exponent in all relations with temperature is considerable in all seasons and is up to 6.7 %, while the prefactor does not vary much with temperature, and its variation is less than 2 %. Among seasons, the variation in coefficients of DSD relations with temperature is larger in hot seasons than in cold seasons (i.e., NEM) by a factor of 2 to 6. Therefore, the variation in D_m or N₀, for a given Z_DR and Z_H, due to temperature variation is within 5 % in any season and is much less in NEM (< 2 %). However, the impact of the seasonal variation of coefficients on derived DSD parameters is relatively larger and is up to 20 %, as discussed above.

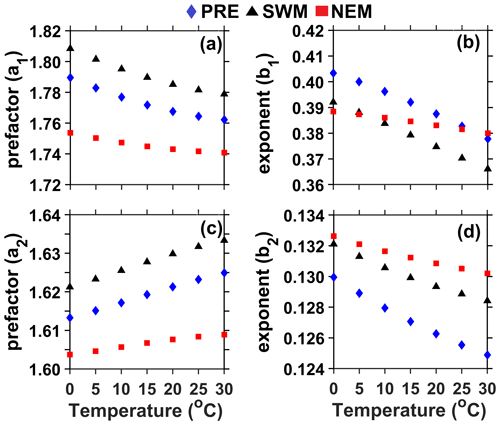
Figure 5 Temperature dependency of coefficients of DSD parameter relations in different seasons. (a, b) Variation of a₁ and b₁ in Eq. (6) with temperature in different seasons. (c, d) Same as (a) and (b) but for Eq. (7).

To examine the dependency of these coefficients on drop shape models, they are retrieved by using different drop shape models (Andsager et al., 1999; Beard and Chuang, 1987; Brandes et al., 2002; Pruppacher and Beard, 1970). The difference in coefficients in Eq. (6) derived with different drop shape models is quite large (7 %–15 % in the prefactor and up to 28 % in the exponent) and in fact larger than the seasonal difference. The prefactor (exponent) is found to be smaller (larger) with the Pruppacher and Beard drop shape model than with other models. On the other hand, the dependency of coefficients in Eq. (7) on the drop shape model is weak, and all the models yield nearly equal coefficients. The seasonal dependency of coefficients in Eq. (7) is quite high compared to their dependency on drop shape models.

4 Assessment of DROP-X-retrieved DSD

The degree of agreement of radar-derived DSD parameters with disdrometer-derived parameters depends on several factors: (1) the differences in sampling volumes of the radar and disdrometer, (2) the vertical variability of DSD from the radar-measured volume to the surface (or disdrometer measurement height) and (3) the accuracy of the empirical relations between polarimetric parameters (Z_DR, Z_H and K_DP) and DSD model parameters (D_m, N₀, μ and Λ). The radar sampling volume depends on the range, beam width and pulse length. For the given radar beam width of 1^∘, range resolution of 150 m and range of 450 m, the estimated sampling volume of the radar is 7264 m³. To match the radar temporal resolution, the disdrometer data are averaged over 6 min (360 s). The sampling volume of the disdrometer for a given surface area of 50 cm² (for the JW disdrometer) and a characteristic drop size, represented by a D_m (or terminal velocity) of 2 mm (6.5 m s⁻¹), is less than 12 m³. Thus, the sampling volumes differ by a factor greater than 600, which is much less than the similar comparisons made elsewhere, wherein the sampling volumes differ by a factor of 10⁵ to 10⁷ (Cao et al., 2008; Tokay et al., 2020a). This is mainly due to the fact that the comparisons were made at a longer range in earlier studies. Another advantage of using a shorter range for comparison studies, as is done in the present study, is the proximity of the radar-measuring volume to the surface. In the present study, the sampling volume is at a height of ∼ 20 m above the disdrometer location. This reduces the bias caused by the time–height ambiguity due to the vertical variability of DSD. The retrieval accuracy also depends on empirical relations between the radar and DSD parameters, as these relations vary with season (as shown in Sect. 3). However, appropriate relations have been used for comparison in the present study to reduce such ambiguity.

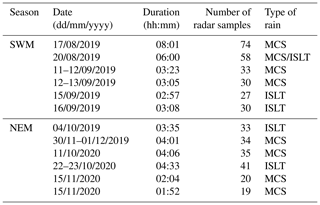
Evaluation of DROP-X derived DSD parameters, using retrieved coefficients in the different DSD formulations discussed above, is carried out by comparing them with those derived with disdrometer observations. For this purpose, the disdrometric dataset during 2019–2020, which has not been used for the retrieval of coefficients, is used for comparison. Long-duration events (longer than 2 h) are selected for the evaluation of DSD retrieval techniques. A total of six events each from SWM and NEM are selected for this purpose (Table 5). These events include a variety of precipitating systems, including thunderstorms and mesoscale convective systems.

Table 5 Details of rain events (date, duration, number of radar samples within the event and type of event) used for the assessment of four DSD retrievals.

4.1 Case studies

Figure 6 shows variation of rainfall bulk parameters and spatial maps of DROP-X-derived Z_H during two precipitation events, one each from SWM (on 12 September 2019) and NEM (on 15 November 2020) chosen as case studies. On 12 September 2019, a convective cell originated southwest of the study region at 16:00 IST and has grown quickly into a mesoscale storm with a leading convective and trailing stratiform region. It propagated eastward and passed the radar location around 22:00 IST as an intense storm stretched in the north–south direction. DROP-X has tracked this storm when it passed over the radar site. The DROP-X-measured Z_H is in the range of 50–52 dBZ during the storm's passage across the radar site at 22:00 IST. The collocated disdrometer also shows Z as large as 52 dBZ and a rain rate of 38 mm h⁻¹ at the time of passage of the core of the storm. The disdrometer-estimated D_m is also found to be large (2.7 mm) at that time (Fig. 6). Light to moderate rain with Z, R and D_m in the range of 23–38 dBZ, 0.5–5 mm h⁻¹ and 1–2 mm, respectively, continued for about 3 h after the passage of this intense convective cell over the radar site.

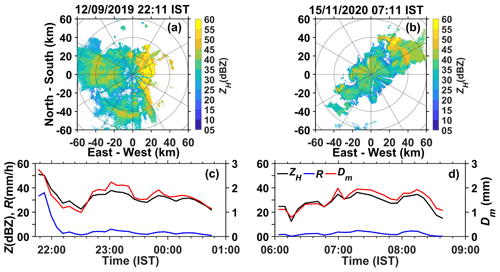
Figure 6 Spatial variation of Z_H measured by DROP-X on (a) 12 September 2019 and (b) 15 November 2020. (c, d) Temporal variation of rainfall bulk parameters (Z_H, R and D_m) measured by the disdrometer on the above dates, respectively.

The second case study is from the NEM that occurred on 15 November 2020. The NEM was active on the day with a wide spread clouds over southeastern peninsular India. A rain band of width ∼ 40 km stretching in the southwest–northeast direction moved northwestward and produced widespread rainfall over the study region for about 2.5 h. Rain intensity is light to moderate during the above period, with R always less than 5 mm h⁻¹ and Z_H varying in the range of 10–40 dBZ. The disdrometer-derived D_m is also found to be small (1–2 mm) during the above period.

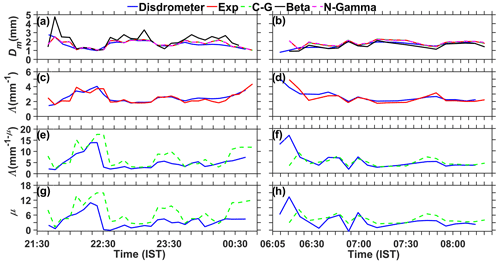
Figure 7 Comparison of (a, b) D_m, (c, d) Λ by assuming an exponential distribution, (e, f) Λ by assuming a gamma distribution, and (g, h) μ by assuming a gamma distribution on 12 September 2019 and 15 November 2020, respectively, with disdrometer-derived values.

The D_m, shape and slope parameters of different DSD models estimated from DROP-X measurements using retrieved coefficients (Sect. 3) are compared with those obtained with the disdrometer in Fig. 7. In general, D_m values obtained by all methods show good correspondence to those derived by the disdrometer. However, the temporal variation of D_m by β method shows more and larger spikes relative to the reference, in particular on 12 September 2019 (Fig. 7a). It is expected that the noisy K_DP and Z_DR at lower rain rates will lead to large errors in the estimation of β (Gorgucci et al., 2002). However, Figs. 6 and 7 show that the disagreement between the β method and disdrometer- and other radar-derived D_m is significant even at a moderate to high rain rate (R > 5 mm h⁻¹). Anagnostou et al. (2008a) also noted such large differences by the β method during convective regimes and attributed them to inadequate attenuation correction. The disdrometer location in the present study is very near to the radar (∼ 200 m), and, therefore, attenuation (and correction) is negligible. On the other hand, the observed differential phase, supposed to represent the differential propagation phase, is contaminated with the differential backscattered phase in the presence of strong convection (Trömel et al., 2013). Adaptive Kalman filtering is used in the present study to smooth out the fluctuations and differential backscattered phase, which is found to be very effective in removing the above affects. However, some uncertainty remained in the removal of the differential backscattered phase when strong convection occurs close to the radar location. It could be the reason for the small bias in D_m by techniques based on K_DP.

As expected (given that there is a good agreement in D_m by radar and disdrometer and the relation $\mathrm{\Lambda }=\frac{\mathrm{4}}{D_{\mathrm{m}}}$), the temporal variation of radar-derived Λ by the exponential method matches well with that of the disdrometer in both cases (Fig. 7c and d). Though the temporal variation of Λ and μ by the CG method matches reasonably well with those obtained with the disdrometer, their magnitudes differ from the reference data, and in particular, overestimation of both parameters is noted in the 12 September 2019 case.

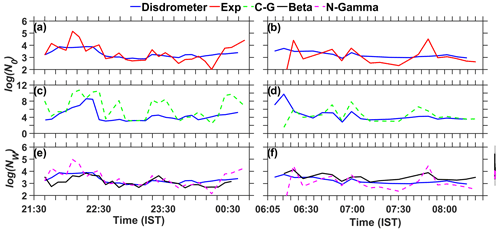
Figure 8 Comparison of log N₀ (a, b) by assuming an exponential distribution and (c, d) by assuming gamma distributions on 12 September 2019 and 15 November 2020, respectively, with a disdrometer-derived log N₀. (e, f) Comparison of the log N_W by N-Gamma and β methods with the disdrometer-derived log N_W on the above days.

The temporal variations of log N₀ with the Exp. and CG methods and log N_W with the N-Gamma and β methods along with those of the disdrometer are shown in Fig. 8. The agreement with the reference is generally good for the log N_W by the β and N-Gamma methods. The N₀ values obtained with the Exp. method also agree reasonably well with those obtained by the disdrometer. However, the agreement is poor with the CG method, and it generally overestimates log N₀ values relative to disdrometer values, mainly due to the overestimation of μ. Except for the CG method, all RMSEs between the retrieved and reference $N_{\mathrm{0}}/N_W$ are ≤ 1.

4.2 Statistical assessment

As shown in Table 4, data from six long events, each from the SWM and the NEM, are used to assess the radar-derived D_m and $N_{\mathrm{0}}/N_W$ against those obtained with the disdrometer. These events include a variety of precipitation systems from isolated thunderstorms to mesoscale-scale convective systems. Figure 9 shows the statistical comparison of D_m and $N_{\mathrm{0}}/N_W$ derived by the radar (four methods) and the disdrometer for all the events given in Table 6. The colored symbols in each scatter diagram represent the data from the different seasons (green solid triangle – SWM – and red open square – NEM). Table 2 summarizes different comparison statistics of the four retrieval methods under testing for the SWM and NEM seasons. Clearly, the statistical comparison also shows that the comparison is better for the retrieval of D_m than $N_{\mathrm{0}}/N_W$ by all the methods. All the methods show a correlation of better than 0.65 (r²) and an RMSE of less than 0.55. Among D_m retrievals by the different methods, the β method shows a better correlation than the others in both seasons but suffers with large RMSE values. The distribution of data is also wider in the case of the β method. The agreement between radar retrievals and the disdrometer-derived D_m is relatively better during the NEM than in the SWM. On the other hand, the retrieval of N_W by the N-Gamma method is much better in both seasons compared to the other methods. The CG method shows weaker correlations and larger RMSE values than the other methods, mainly because of the problems related to K_DP and μ.

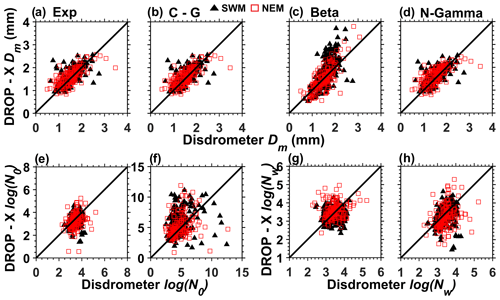
Figure 9 Scatter plots of D_m obtained by the disdrometer and DROP-X with the (a) exponential, (b) constrained gamma, (c) β and (d) normalized gamma methods for the SWM (solid green triangle) and NEM (open red square) seasons. (e–h) Same as (a)–(d) but for $\log N_{\mathrm{0}}/N_W$.

Table 6 Evaluation statistics of D_m and log $N_{\mathrm{0}}/N_W$ by the Exp., CG and N-Gamma β methods for SWM and NEM.

5 Summary and conclusion

Five years of disdrometric measurements and 2 years of DROP-X measurements have been used, for the first time, to (i) obtain relations for the retrieval of DSD parameters appropriate for monsoonal rain and to study their dependency on temperature and drop size–shape relations, (ii) understand the seasonal variation of coefficients and (iii) assess the DROP-X-derived DSD by various DSD retrieval methods. Using 3 years of disdrometer-measured DSD, various polarimetric parameters have been computed using T-matrix simulations. Coefficients of four commonly used DSD relations are retrieved empirically from simulated data. Important results coming from the study are summarized as follows.

The coefficients for obtaining DSD parameters by the exponential, CG, N-Gamma and β methods for monsoonal rain are found to be different from other regions, indicating that they are region-dependent. The mean value of β estimated at Gadanki is closer to the default value (0.062) given by Pruppacher and Beard (1970) during the NEM, whereas the values obtained for PRE and SWM are much smaller, indicating that the slope of the drop-shape-sized relation is season-dependent and 0.062 is more applicable for the colder season. To understand the dependency of the coefficients of these relations on temperature and drop shape models, the coefficients of the Exp. method are retrieved for different temperatures and drop shape models. It is found that the variation in D_m or N₀, for a given Z_DR and Z_H, due to temperature variation is within 5 % in any season and is much less in NEM (< 2 %). However, the dependency of coefficients in the D_m–Z_DR equation on the drop shape model is high (7 %–15 % in the prefactor and 28 %–28 % in the exponent) and in fact is higher than on seasons. The dependency of coefficients on drop shape models is found to be different in different geographical regions. While the dependency is found to be high at Gadanki and in Africa, it is found to be weak along the western coast of the United States of America.

The present study corroborates some of the earlier studies that showed that the μ–Λ relation is region-dependent. It clearly shows that this relation is also season- and temperature-dependent, as we see a gradual change in coefficients from the warmest PRE to the coldest NEM. Also, the warmest seasons of PRE and SWM have higher slope and curvature values compared to those in NEM. This means that μ will be higher during PRE and SWM than in NEM for the same Λ for the majority of data (i.e., when Λ and μ values are less than 8). A comparison of μ–Λ relations obtained in different seasons at Gadanki with those available in the literature elsewhere clearly reveals that warm seasons/regions typically have larger curvature and slope values than cold seasons/regions.

The disdrometer data clearly show large seasonal variation with a preponderance of smaller drops during NEM compared to the warm seasons, corroborating earlier findings (Rao et al., 2001, 2009; Radhakrishna et al., 2009). As a result, the obtained coefficients also show large seasonal variation. From the retrieved coefficients it is clear that the D_m values will be larger for the same Z_DR during PRE and SEM than in NEM. Though the prefactor is nearly equal in all seasons, the variation in the exponent makes a difference of ∼ 20 %–30 % in the N₀ value between the seasons for the same $Z_{\mathrm{H}}/N_{\mathrm{0}}$ and D_m. Among seasons, the variation in coefficients of DSD relations with temperature is larger in hot seasons than in the cold season (i.e., NEM) by a factor of 2 to 6. However, the impact of seasonal variations of coefficients on derived DSD parameters is relatively larger and is up to 20 %. Therefore, appropriate coefficients need to be used while retrieving DSD from polarimetric measurements.

The four commonly used radar retrieval methods of DSD are evaluated with the help of two case studies (one each from SWM and NEM) and data from 12 events. All the methods retrieve D_m reasonably well and produce a high correlation and small RMSE against the reference. The β method alone produced a wide range of D_m values similar to that of the disdrometer. However, the scatter is large, particularly in convection, mainly due to the fact that the comparison is made close to the radar site, where the differential phase is often contaminated by a differential backscattering phase. As a result, the RMSE exhibited by the β method is also found to be large. Comparison of retrievals of $N_{\mathrm{0}}/N_W$ with those of the disdrometer shows the superiority of the N-Gamma method over other methods. All other methods compare poorly with disdrometer-derived $N_{\mathrm{0}}/N_W$, with small r² and large RMSE values. Considering all the factors (Table 4), the N-Gamma method is found to be better in retrieving the DSD parameters. However, such assessment studies are also planned at longer ranges (10 and 35 km) with DROP-X to understand the strengths and limitations of the above methods in retrieving DSD accurately.