Field assessments on the impact of CO₂ concentration fluctuations along with complex-terrain flows on the estimation of the net ecosystem exchange of temperate forests

CO₂ storage (F_s) is the cumulation or depletion in CO₂ amount over a period in an ecosystem. Along with the eddy covariance flux and wind-stream advection of CO₂, it is a major term in the net ecosystem CO₂ exchange (NEE) equation. The CO₂ storage dominates the NEE equation under a stable atmospheric stratification when the equation is used for forest ecosystems over complex terrains. However, estimating F_s remains challenging due to the frequent gusts and random fluctuations in boundary-layer flows that lead to tremendous difficulties in capturing the true trend of CO₂ changes for use in storage estimation from eddy covariance along with atmospheric profile techniques. Using measurements from Qingyuan Ker Towers equipped with NEE instrument systems separately covering mixed broad-leaved, oak, and larch forest towers in a mountain watershed, this study investigates gust periods and CO₂ fluctuation magnitudes and examines their impact on F_s estimation in relation to the terrain complexity index (TCI). The gusts induce CO₂ fluctuations for numerous periods of 1 to 10 min over 2 h. Diurnal, seasonal, and spatial differences (P < 0.01) in the maximum amplitude of CO₂ fluctuations (A_m) range from 1.6 to 136.7 ppm, and these differences range from 140 to 170 s in a period (P_m) at the same significance level. A_m and P_m are significantly correlated to the magnitude of and random error in F_s with diurnal and seasonal differences. These correlations decrease as CO₂ averaging time windows become longer. To minimize the uncertainties in F_s, a constant [CO₂] averaging time window for the F_s estimates is not ideal. Dynamic averaging time windows and a decision-level fusion model can reduce the potential underestimation of F_s by 29 %–33 % for temperate forests in complex terrain. In our study, the relative contribution of F_s to the 30 min NEE observations ranged from 17 % to 82 % depending on turbulent mixing and the TCI. The study's approach is notable as it incorporates the TCI and utilizes three flux towers for replication, making the findings relevant to similar regions with a single tower.

1 Introduction

The accurate estimation of the net ecosystem exchange (NEE) of carbon dioxide (CO₂) in forest ecosystems is crucial for a comprehensive understanding of the global carbon cycle. The eddy covariance (EC) technique has been widely used in forest ecosystems due to its capacity to directly measure the NEE with measurement conditions satisfying the underlying theory. The EC technique is based on a simplified mass conservation equation (after Reynolds averaging), given by

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\text{NEE}& =\underset{\text{I}}{{\displaystyle \frac{\mathrm{1}}{V_{\mathrm{m}}}}\underset{\mathrm{0}}{\overset{h}{\int }}\left({\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{c}}{\partial t}}\right)\mathrm{d}z}+\underset{\text{II}}{{\displaystyle \frac{\mathrm{1}}{V_{\mathrm{m}}}}{\left(\stackrel{\mathrm{‾}}{w^{\prime }{c}^{\prime }}\right)}_h}\\ & +{\displaystyle \frac{\mathrm{1}}{V_{\mathrm{m}}}}\underset{\mathrm{0}}{\overset{h}{\int }}\left(\underset{\text{IIIa}}{\stackrel{\mathrm{‾}}{w}\left(z\right){\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{c}}{\partial z}}}+\underset{\text{IIIb}}{\stackrel{\mathrm{‾}}{c}\left(z\right){\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{w}}{\partial z}}}\right)\mathrm{d}z\\ & +\underset{\text{IV}}{{\displaystyle \frac{\mathrm{1}}{V_{\mathrm{m}}}}\underset{\mathrm{0}}{\overset{h}{\int }}\left(\stackrel{\mathrm{‾}}{u}\left(z\right){\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{c}}{\partial x}}+\stackrel{\mathrm{‾}}{v}\left(z\right){\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{c}}{\partial y}}\right)\mathrm{d}z},\end{array}\end{array}$$

​​​​​​​where V_m is the volume of dry air in the control volume; c is the CO₂ mixing ratio; t is the time; h is the measurement height; u, v, and w denote the velocity components in the x, y, and z directions, respectively; and an overbar denotes Reynolds averaging. This equation conceptualizes the NEE within a control volume from the ground to the measurement height (h) while ignoring the horizontal turbulence term divergence (Feigenwinter et al., 2004). In this equation, term I is the CO₂ storage (F_s) representing the change in the average CO₂ concentration (hereafter [CO₂]). Terms II, IIIa, IIIb, and IV represent the vertical turbulent flux (F_c); the vertical advection; the interface vertical mass advection, such as the evaporation process (Webb et al., 1980); and the horizontal advection, respectively.

Most flux measurements typically lack solutions for terms III and IV and can only estimate the NEE by summing F_c and F_s, and a significant number of sites even ignore F_s. F_s in the vertical gas column within a canopy can be substantial, requiring attention in NEE estimates (Aubinet et al., 2000). F_s contributes ∼ 60 % to nocturnal turbulent flux underestimation in forest ecosystems with “ideal” topography (McHugh et al., 2017). During atmospherically stable periods such as the early morning, sunset, and nighttime transitions, F_s has an especially significant impact on the NEE. For 30 min ecosystem carbon flux measurements, ignoring F_s would cause the NEE to be underestimated (Zhang et al., 2010). The F_s value typically ranges from −2 to −5 µmol m⁻² s⁻¹ in the early morning, and it is about 1–3 µmol m⁻² s⁻¹ after sunset for temperate forests. The effect of F_s on the NEE of forest ecosystems decreases with an increase in the timescale (Li et al., 2020). However, neglecting the F_s value can lead to misunderstanding the CO₂ exchange processes, such as ecosystem respiration and photosynthesis, and their relationship with key control factors such as solar radiation, temperature, and moisture (McHugh et al., 2017). Therefore, it is imperative not to overlook F_s to ensure more precise NEE estimates of forest ecosystems, particularly in complex terrain.

Despite the challenges inherent in monitoring forest conditions, understanding the carbon flux of forest ecosystems in complex terrain or with heterogeneous underlying surfaces remains an area of great interest. Topography complexity plays a complex role in the transportation of momentum, energy, and mass in the atmospheric boundary layer, with direct impacts on airflow patterns, spatiotemporal characteristics, and gas concentration fluctuations (Sha et al., 2021; Finnigan et al., 2020). Differences in airflow along a slope, lateral CO₂ discharge downhill, and spatiotemporal variations in soil respiration result in the CO₂ outflow from slopes and valleys lagging behind the flat tops of mountains (de Araújo et al., 2010). At night, under stable atmospheric stratification, cold air moves from the valley forest canopy to the ground and then flows to low-lying areas, causing a “carbon pooling” effect. The gradient of [CO₂] below the EC sensors fluctuates significantly, and the cold-air discharge above the canopy reduces CO₂ storage, leading to an underestimation of forest ecosystem respiration (Yao et al., 2011; de Araújo et al., 2008, 2010).

According to the theoretical definition, F_s estimates are derived by averaging the [CO₂] of the control volume at the beginning and the end of the EC averaging period (30 min or 1 h) and dividing this by the EC averaging period (Finnigan, 2006). The estimation of F_s at numerous sites frequently employs a vertical profile system. This approach operates under the assumption that F_s represents the integration of the time derivative of the vertically determined column-averaged [CO₂]. It is noteworthy that the column-averaged [CO₂] may not accurately represent the average [CO₂] of the control volume in cases of inadequate air mixing, leading to insufficient sampling. A previous study showed that relying solely on tower-top measurements can lead to the underestimation of F_s by up to 34 % compared to using an eight-level profile approach (Gu et al., 2012). The NEE magnitude with F_s based on a 2 min [CO₂] averaging time window (instantaneous-concentration approach) was found to be 5 % higher than that with F_s based on a 30 min window (averaging-concentration approach), particularly during the nighttime in the growing season (Wang et al., 2016). A proper measuring system that improves horizontal representativeness can reduce the bias in F_s to 2 %–10 % (Nicolini et al., 2018). Most research has examined how the vertical and horizontal gas concentration sampling point distribution affects the uncertainty in F_s estimation (Bjorkegren et al., 2015; Wang et al., 2016; Yang et al., 2007, 1999), with a small number of studies examining the effect of [CO₂] sampling frequency on F_s (Finnigan, 2006; Heinesch et al., 2007). Certain studies have experimentally validated new concepts, such as correlating the gas sampling point concentration with the horizontal distribution (Nicolini et al., 2018). Some studies have approached the true value theoretically, such as through defining the control volume represented by flux measurements (Metzger, 2018; Xu et al., 2019). However, the number of complete column samples required to describe the column-averaged [CO₂] of each 30 min or 1 h F_s estimate is still undetermined.

Previous studies have emphasized the significance of F_s to the NEE and the influence of [CO₂] dynamics on F_s estimates in complex terrain. To overcome any disparities between sensors and obtain precise changes in the [CO₂] gradient above and below the forest canopy, individual gas analyzers are extensively utilized to measure [CO₂] levels vertically (Siebicke et al., 2011). However, a single gas analyzer introduces time delays when monitoring multi-point [CO₂] curves. Accurately determining the F_s estimates can be challenging due to the spatial and temporal resolution of [CO₂] measurements (Wang et al., 2016). The random error in the F_s estimates using one complete column sample is considerably high due to short-term [CO₂] fluctuations (Nicolini et al., 2018). The calculation of F_s using time-averaged [CO₂] profiling leads to significant information loss at a high frequency, resulting in a substantial underestimation bias. Furthermore, time-averaged [CO₂] profiling is employed to represent the [CO₂] average within the control volume due to resource constraints. This leads to the systematic bias and random error in F_s estimates being irreconcilable. This issue necessitates further efforts to characterize [CO₂] fluctuations across different sites and to demonstrate the mechanisms influencing F_s magnitudes, F_s uncertainties, and their contributions to NEE observations in complex terrain. Thus, this study aims to bridge this gap by introducing a statistical method to estimate F_s values and their uncertainties.

This paper employs an innovative EC experimental setup with three flux towers (Qingyuan Ker Towers) to monitor three typical types of temperate forest stands located in complex terrain in northeastern China. This study introduces a decision-level fusion model based on weighting the underestimation bias and random error in F_s to obtain more accurate results. The objectives of this study were to (1) compare diurnal, seasonal, and spatial differences in [CO₂] fluctuations, F_s, and its uncertainty; (2) examine the variation in F_s uncertainty with different [CO₂] averaging time windows; and (3) investigate the response of F_s and its uncertainty to [CO₂] fluctuations, wind above the canopy, and terrain complexity, quantifying the impact of F_s on the NEE estimates under these conditions.

2 Materials and methods

2.1 Study site and instrumental setup

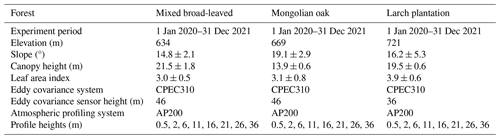
This study was conducted in temperate forests in a watershed based on Qingyuan Ker Towers (Zhu et al., 2021; Gao et al., 2020), situated in northeast China (41°50^′ N, 124°56^′ E). The region experiences a temperate continental monsoon climate, with an average annual temperature of 4.3 °C and annual rainfall of 758 mm from 2010 to 2021 (Li et al., 2023). Qingyuan Ker Towers consist of three 50 m high EC towers (Fig. 1) that observe a mixed broad-leaved forest (MBF), a Mongolian oak forest (MOF), and a larch plantation forest (LPF).

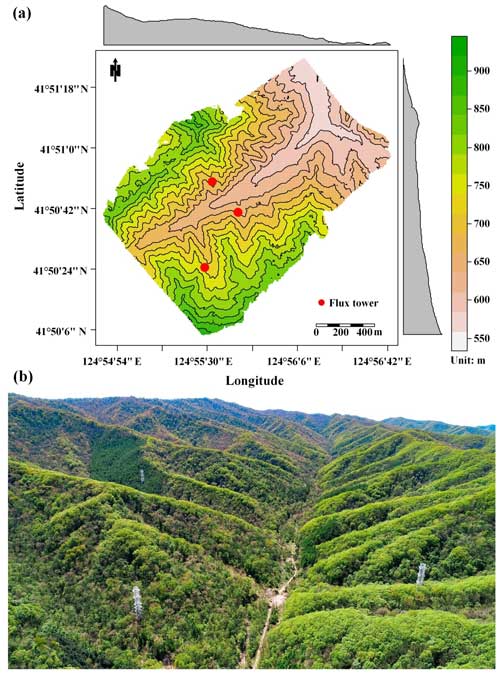
Figure 1 Overview of the study area. Panel (a) depicts the topography of the study site, with black curves indicating elevation contours and marginal distributions represented as a gray graph, averaged over rows and columns. Panel (b) features an aerial photograph of Qingyuan Ker Towers captured in the growing season (Gao et al., 2020).

Table 1 Basic information about Qingyuan Ker Towers.

Basic information regarding Qingyuan Ker Towers in this study is presented in Table 1. The CPEC310 integrated system from Campbell Scientific, comprising an EC155 closed-path infrared gas analyzer (IRGA) and a CSAT3A sonic anemometer, was employed to monitor the three-dimensional wind speed and CO₂ and H₂O concentrations (10 Hz). An atmospheric profiling system (AP200, Campbell Scientific, Inc., Logan, UT, USA) was utilized to measure the CO₂ and H₂O concentrations with eight height levels. Each level was measured for 15 s (with 10 s for the flushing of the manifold and 5 s for logging the average), leading to a measurement cycle of 2 min. Due to calibration, filter changes, and rugged weather, 10 % of CPEC310 data and 3 % of AP200 data were missed in our study period.

2.2 Calculation of storage flux

Averaging [CO₂] in a time window was utilized to calculate the F_s values, in addition to data on the air pressure, CO₂ and H₂O molar fractions, and air temperature at different heights above the ground surface (Finnigan, 2006; Montagnani et al., 2018; Xu et al., 2019). The molar mixing ratio and mass mixing ratio are quantities conserved with the variation in air temperature, air pressure, and water vapor concentration, whereas the molar fraction is not. This study determined F_s using the molar mixing ratio obtained from CO₂ and H₂O molar fraction observations, applying the ideal gas law and Dalton's partial pressure law (Montagnani et al., 2009). The water vapor molar mixing ratio (χ_v) in mmol mol⁻¹ is given by

$$\begin{array}{}\text{(2)}& {\mathit{\chi }}_{\mathrm{v}}={\displaystyle \frac{c_{\mathrm{v}}}{\mathrm{1}-c_{\mathrm{v}}\times {\mathrm{10}}^{-\mathrm{3}}}},\end{array}$$

where c_v is the water vapor molar fraction in mmol mol⁻¹. The CO₂ molar mixing ratio (χ_c) in µmol mol⁻¹ is given by

$$\begin{array}{}\text{(3)}& {\mathit{\chi }}_{\mathrm{c}}={\displaystyle \frac{c_{\mathrm{c}}}{\mathrm{1}-c_{\mathrm{v}}\times {\mathrm{10}}^{-\mathrm{3}}}},\end{array}$$

where c_c is the CO₂ molar fraction in µmol mol⁻¹.

The dry air density (${\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{d}}$) in mol m⁻³ is calculated as follows:

$$\begin{array}{}\text{(4)}& {\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{d}}={\displaystyle \frac{\stackrel{\mathrm{‾}}{P}}{\left(\stackrel{\mathrm{‾}}{T}+\mathrm{273.15}\right)\times \left(R^{\ast }+{\mathit{\chi }}_{\mathrm{v}}\times {\mathrm{10}}^{-\mathrm{3}}\cdot R^{\ast }\cdot \frac{M_{\mathrm{d}}}{M_{\mathrm{v}}}\right)}},\end{array}$$

where R^∗ is the air gas constant (8.31441 Pa m³ K⁻¹ mol⁻¹), $\stackrel{\mathrm{‾}}{P}$ is the air pressure in pascals, and $\stackrel{\mathrm{‾}}{T}$ is the average air temperature in degrees Celsius. M_d and M_v are the dry air and water vapor molar mass (18.015 g mol⁻¹), respectively. M_d is calculated from the CO₂ molar mixing ratio (Khélifa et al., 2007):

$$\begin{array}{}\text{(5)}& M_{\mathrm{d}}=\mathrm{28.9635}+M_{\mathrm{c}}\cdot \left({\mathit{\chi }}_{\mathrm{c}}\times {\mathrm{10}}^{-\mathrm{6}}-\mathrm{0.0004}\right),\end{array}$$

where M_c is the carbon molar mass (12.011 g mol⁻¹).

The F_s values estimated from eight-level profiles are calculated as follows:

$$\begin{array}{}\text{(6)}& F_{\mathrm{s}}={\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{d}}\underset{\mathrm{0}}{\overset{h}{\int }}{\displaystyle \frac{\mathrm{d}{\stackrel{\mathrm{‾}}{\mathit{\chi }}}_{\mathrm{c}}}{\mathrm{d}t}}\mathrm{d}z\dot{=}{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{d}}\sum _{i=\mathrm{1}}^{\mathrm{8}}{\displaystyle \frac{\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\chi }}}_{{\mathrm{c}}_i}\mathrm{\Delta }{h}_i}{\mathrm{\Delta }t}},\end{array}$$

where ${\stackrel{\mathrm{‾}}{\mathit{\chi }}}_{\mathrm{c}}$ is the average CO₂ molar mixing ratio and Δh_i is the height represented by each level.

When measuring F_s by sampling CO₂ at several levels using a single analyzer, synchronous observations of the CO₂ profile are impractical. Consequently, discrete temporal sampling and time averaging become necessary. To ensure the temporal alignment of F_s with F_c, the average [CO₂] measurements within the control volume at the beginning and end (t) of an averaging period (30 min) are calculated by averaging over a time window (τ min) as follows:

$$\begin{array}{}\text{(7)}& {\stackrel{\mathrm{‾}}{\mathit{\chi }}}_{{\mathrm{c}}_i}={\displaystyle \frac{\mathrm{2}}{\mathit{\tau }}}\sum _{t-\frac{\mathit{\tau }}{\mathrm{2}}<t\le t+\frac{\mathit{\tau }}{\mathrm{2}}}{\mathit{\chi }}_{{\mathrm{c}}_i}\left(t\right),\end{array}$$

where τ = 4, 8, …, 28 min. Theoretically, the time window should be kept as short as possible in comparison to the turbulence flux averaging period to comply with the principle of Reynolds decomposition. We use large windows here for CO₂ averaging in an attempt to demonstrate the effects of different window sizes on the accuracy of storage flux estimates.

2.3 Data analysis

To evaluate the impact of [CO₂] fluctuations on F_s measurements and corresponding uncertainty, empirical modal decomposition (EMD) and Fourier spectrum analysis (FSA) were used to extract the period and amplitude of fluctuations in the high-frequency [CO₂] time series (10 Hz). EMD was used to decompose the [CO₂] time series into intrinsic mode functions based on local signal properties (Huang and Wu, 2008), which yielded instantaneous frequencies as functions of time and allowed for the identification of embedded structures of eddies. EMD is applicable to nonlinear and nonstationary processes (Huang et al., 1998). The period and amplitude of [CO₂] fluctuations above the forest canopies reflected the eddy size. Subsequently, the maximum period and amplitude of [CO₂] fluctuations in the short term (2 h) were indicative of large eddies under the influence of gusts.

Due to the diurnal and seasonal variability in flux measurements, this study defined the transition period and growing season. The solar elevation angle was used to define the transition period as 1 h before sunrise (sunset) to 2 h after sunrise (sunset). The growing degree days (GDDs) were calculated using the base temperature (T_base) to determine the beginning and end of the growing season, and the formula for this was as follows (McMaster and Wilhelm, 1997):

$$\begin{array}{}\text{(8)}& \text{GDD}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(T_{max}+T_{min}\right)-T_{\mathrm{base}},\end{array}$$

where T_base is 6 °C. Considering the persistent need for temperature levels to support vegetation growth, the fourth day of the first GDD greater than zero (less than zero) over a span of 5 consecutive days was defined as the starting (ending) time of the growing season.

The main data processing and analysis steps are outlined below:

1. EMD and Fourier spectrum analysis of [CO₂] high-frequency time series were used to extract the maximum amplitude (A_m) and corresponding period (P_m) of [CO₂] fluctuations every 2 h. The data were divided into two subsets based on P_m, with a cutoff of 150 s.

2. CO₂ storage fluxes were calculated for different [CO₂] averaging time windows (τ), ranging from 4 to 28 min in increments of 4 min.

3. The standardized major axis (SMA) regression model (Warton et al., 2012) was used to compare the slope differences (bias) between F_{s_τ} and F_{s_28} ​​​​​​​ for different P_m values and the forest stands. The SMA model offers routines for comparing parameters a and b among groups for symmetric problems.

4. The normalized root mean square error (NRMSE) and slope were used to evaluate the relative error and bias between F_{s_τ} and F_{s_28}. The NRMSE is calculated as

   $$\begin{array}{}\text{(9)}& \text{NRMSE}=\mathrm{100}\times \sqrt{{\displaystyle \frac{{\sum }_{i=\mathrm{1}}^N{\left(F_{\mathrm{s}\mathit{\_}\mathit{\tau }}^{\left(i\right)}-F_{\mathrm{s}\mathrm{\_}\mathrm{28}}^{\left(i\right)}\right)}^{\mathrm{2}}}{{\sum }_{i=\mathrm{1}}^N{\left(F_{\mathrm{s}\mathrm{\_}\mathrm{28}}^{\left(i\right)}-\stackrel{\mathrm{‾}}{F_{\mathrm{s}\mathrm{\_}\mathrm{28}}}\right)}^{\mathrm{2}}}}},\end{array}$$

   where i indicates the ith observation.

5. The normalized weighting coefficient (w) of F_{s_τ} was estimated based on the NRMSE and slope (Wang et al., 2020). Details are shown in Appendix A1. Then, using the decision-level fusion model, F_{s_comb} was calculated as

   $$\begin{array}{}\text{(10)}& F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}=w_{\mathrm{1}}^{\ast }\cdot F_{\mathrm{s}\mathrm{\_}\mathrm{4}}+w_{\mathrm{2}}^{\ast }\cdot F_{\mathrm{s}\mathrm{\_}\mathrm{8}}+\mathrm{\dots }+w_{\mathrm{7}}^{\ast }\cdot F_{\mathrm{s}\mathrm{\_}\mathrm{28}}.\end{array}$$

The decision-level fusion model automatically assigned weights to F_s based on different [CO₂] averaging time windows. Its purpose in this study was to balance the relative error and bias in F_s estimates caused by [CO₂] sampling. The analysis was performed using the EMD and smatr R packages (Warton et al., 2012; Huang et al., 1998).

2.4 Uncertainty analysis

To improve the accuracy of estimating the uncertainty in F_s using an individual tower, this work has made modifications to the 24 h difference method by extending the sampling time windows and applying meteorological-condition constraints (Hollinger and Richardson, 2005). This method trades time for space to estimate the uncertainty in F_s. To determine the uncertainty in F_s, expressed as σ(ε_s), in this case, we compared the observations at moment i within a day to the average of several observations during a similar period and with similar meteorological conditions. The specific computations were as follows:

$$\begin{array}{}\text{(11)}& {\displaystyle }{\stackrel{\mathrm{‾}}{F_{\mathrm{s}}}}^{\left(i\right)}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{t\in \mathrm{\Omega },{\mathit{\lambda }}_t\in \mathrm{\Lambda }}I\left({\mathit{\lambda }}_t\right)\cdot F_{\mathrm{s}}^{\left(t\right)},\text{(12)}& {\displaystyle }\mathrm{\Lambda }=\left\{{\mathit{\lambda }}_t|\sqrt{\begin{array}{c}{\displaystyle \frac{{\left(u_{\ast }^{\left({\mathit{\lambda }}_t\right)}-u_{\ast }^{\left(i\right)}\right)}^{\mathrm{2}}}{{\mathit{\sigma }}_{u_{\ast }}}}+{\displaystyle \frac{{\left({T_{\mathrm{a}}}^{\left({\mathit{\lambda }}_t\right)}-{T_{\mathrm{a}}}^{\left(i\right)}\right)}^{\mathrm{2}}}{{\mathit{\sigma }}_{T_{\mathrm{a}}}}}\\ +{\displaystyle \frac{{\left(H^{\left({\mathit{\lambda }}_t\right)}-H^{\left(i\right)}\right)}^{\mathrm{2}}}{{\mathit{\sigma }}_H}}\end{array}}<\mathit{\delta }\right\},\text{(13)}& {\displaystyle }{\mathit{\epsilon }}_{\mathrm{s}}^{\left(i\right)}=F_{\mathrm{s}}^{\left(i\right)}-{\stackrel{\mathrm{‾}}{F_{\mathrm{s}}}}^{\left(i\right)},\text{(14)}& {\displaystyle }{\stackrel{\mathrm{‾}}{{\mathit{\epsilon }}_{\mathrm{s}}}}^{\left(i\right)}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{t\in \mathrm{\Omega },{\mathit{\lambda }}_t\in \mathrm{\Lambda }}I\left({\mathit{\lambda }}_t\right)\cdot {\mathit{\epsilon }}_{\mathrm{s}}^{\left(t\right)},\text{(15)}& {\displaystyle }\mathit{\sigma }{\left({\mathit{\epsilon }}_{\mathrm{s}}\right)}^{\left(i\right)}=\sqrt{{\displaystyle \frac{\mathrm{1}}{N}}\sum _{t\in \mathrm{\Omega },{\mathit{\lambda }}_t\in \mathrm{\Lambda }}I\left({\mathit{\lambda }}_t\right)\cdot {\left({\mathit{\epsilon }}_{\mathrm{s}}^{\left(t\right)}-{\stackrel{\mathrm{‾}}{{\mathit{\epsilon }}_{\mathrm{s}}}}^{\left(i\right)}\right)}^{\mathrm{2}}},\end{array}$$

where Ω is the moment interval (i−0.5 h, i+0.5 h) within a certain time window (15 d); I is the indicator function; the set represented by Λ consisted of elements that meet similar meteorological conditions, including u_∗, air temperature (T_a), and sensible heat flux (H); ${\mathit{\sigma }}_{u_{\ast }}$, ${\mathit{\sigma }}_{T_{\mathrm{a}}}$, and σ_H are the standard deviation of u_∗, T_a, and H, respectively; δ is the threshold of Euclidean distance; and ε_s is the random error in F_s.

After estimating the uncertainty in F_s, this study extended the work conducted by Richardson et al. (2008) to analyze its relationship with the magnitude of flux measurements ($\left|F_{\mathrm{s}}\right|$), [CO₂] fluctuations (A_m and P_m), u_∗, and the terrain complexity index (TCI). A comprehensive description of the TCI can be found in Appendix A2. This relationship can be approximated using the following equation:

$$\begin{array}{}\text{(16)}& \mathit{\sigma }\left({\mathit{\epsilon }}_{\mathrm{s}}\right)={\mathit{\beta }}_{\mathrm{0}}+\sum _{i=\mathrm{1}}{\mathit{\beta }}_i\cdot x_i,\end{array}$$

where the nonzero intercept term β₀ indicates the size of the random uncertainty as x_i approaches 0, which varies with the observation site, with larger values of β₀ indicating greater uncertainty. The slope term β_i indicates the sensitivity of the size of the random uncertainty in x_i, with smaller β_i values indicating a probability distribution of uncertainty closer to white noise.

3 Results

3.1 Characterization of [CO₂] fluctuation and F_s variations

The high-frequency [CO₂] time series above the forest canopies were decomposed using EMD, and this was followed by spectral analysis to extract the fluctuation period and amplitude of [CO₂] on different timescales. As depicted in Fig. 2, it became evident that the [CO₂] above the canopies displayed short-term fluctuations with periods ranging from 1 to 10 min, and the amplitude of these fluctuations showed an increasing trend with longer periods. This observation strongly suggests the presence of large eddies influenced by gusts above the canopies, and these eddies were responsible for the increasing amplitude of [CO₂] fluctuations as their size increased.

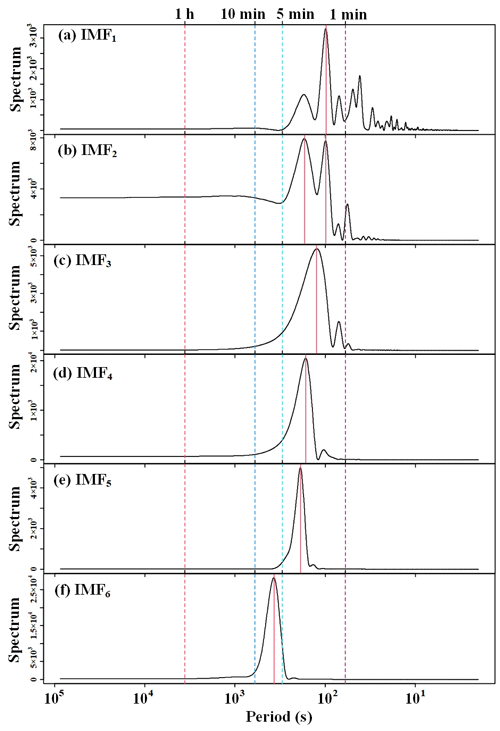
Figure 2 Power spectral density of the intrinsic mode function (IMF) of above-canopy CO₂ concentrations in the Mongolian oak forest on 2 July 2020 (24 h).

Table 2 The means of A_m in parts per million (ppm) and P_m in seconds (s) for three forest stands in different periods.

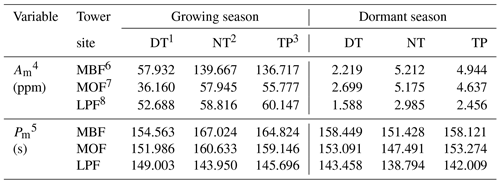
¹ DT represents daytime. ² NT represents nighttime. ³ TP represents the transition period. ⁴ A_m represents the maximum amplitude of short-term CO₂ concentration fluctuations. ⁵ P_m represents the corresponding period of maximum amplitude. ⁶ MBF represents mixed broad-leaved forest. ⁷ MOF represents Mongolian oak forest. ⁸ LPF represents larch plantation forest.

To examine the spatiotemporal variations in large eddies, this study compared the A_m and P_m values above canopies across different forest stands. The analysis utilized data from daytime, nighttime, and transition periods in both the growing and the dormant seasons. The averages of A_m and P_m for the above-canopy [CO₂] in the three forest stands ranged from 1.588 to 136.667 ppm and from 2.313 to 2.784 min, respectively (Table 2). Figure 3 demonstrates significant seasonal and diurnal differences (P < 0.01) in P_m, with higher values during the daytime in the growing season and lower values during the daytime in the dormant season. Moreover, P_m was significantly different (P < 0.01) among different forest stands during the same time period, with the MBF stand having the highest values, followed by MOF and then LPF with the lowest values. During the growing season, the A_m values were significantly higher than those during the dormant season, with both daytime and nighttime values also exhibiting significant differences (P < 0.01) among different forest stands. This observation provides evidence of significant spatiotemporal variability in the large eddies influenced by gusts.

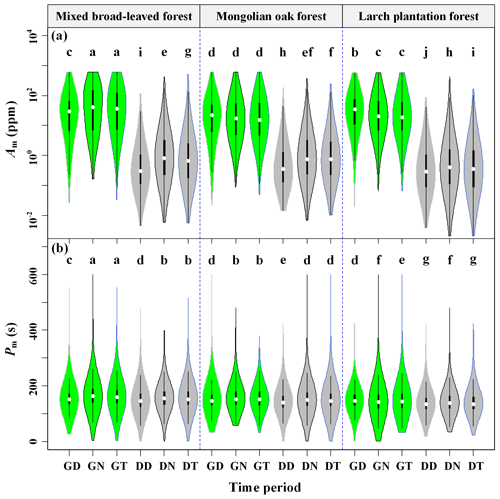
Figure 3 The maximum amplitude (A_m) (a) and corresponding period (P_m) (b) of short-term CO₂ concentration fluctuations in different forest stands for seasonal and diurnal variations, where GD, GN, GT, DD, DN, and DT denote the growing-season daytime, growing-season nighttime, growing-season transition period, dormant-season daytime, dormant-season nighttime, and dormant-season transition period, respectively. Columns with different lowercase letters are significantly different (P < 0.05) according to Fisher's least significant difference test.

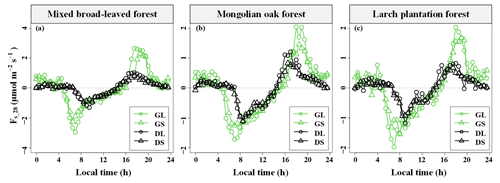
Figure 4 Median diurnal variation in CO₂ storage flux (F_s) based on 28 min CO₂ concentration averaging time windows in the three forest stands during different seasons. GS indicates the growing season and a short period of maximum amplitude (P_m), GL indicates the growing season and a high P_m, DS indicates the dormant season and a low P_m, and DL indicates the dormant season and a high P_m (the L in the abbreviations is derived from long and the S from short).

To estimate the uncertainty in F_s using an individual tower, a comprehensive analysis of the diurnal and seasonal dynamics, as well as the functional relationship between F_s and u_∗, was necessary. Significant diurnal variations and seasonal differences in F_s were observed across the three forest stands, as shown in Fig. 4. During the growing season, the median diurnal variation in F_s for the three forest stands ranged from −2.960 to 2.647 µmol m⁻² s⁻¹, whereas during the dormant season, it ranged from −1.306 to 1.012 µmol m⁻² s⁻¹. Comparing the extent of F_s diurnal variation among the three forest stands, MBF exhibited the largest extent during the growing season, while the extents of the three forest stands were similar during the dormant season. Notably, it was observed that the amplitudes for higher P_m values were greater than those for lower P_m values. This observation indicates that the larger the eddies, the greater the magnitude of F_s.

Furthermore, a u_∗ threshold value was identified for the variation in F_s with u_∗ during the daytime in both the dormant and the growing seasons (Fig. 5). When u_∗ fell below the u_∗ threshold, the magnitude of F_s ($\left|F_{\mathrm{s}}\right|$) decreased with increasing u_∗. Conversely, when u_∗ exceeded the u_∗ threshold, $\left|F_{\mathrm{s}}\right|$ tended to remain relatively constant. Notably, a maximum point for $\left|F_{\mathrm{s}}\right|$ was observed when u_∗ was less than 0.5 m s⁻¹ during the growing season, whereas this was not the case during the dormant season. This phenomenon was particularly evident during the nighttime and transition periods of the growing season, when $\left|F_{\mathrm{s}}\right|$ exhibited an initial increase followed by a subsequent decrease with u_∗. These observations strongly indicate that the effect of the turbulent mixing strength on $\left|F_{\mathrm{s}}\right|$ over complex terrain is nonlinear and exhibits diurnal and seasonal differences.

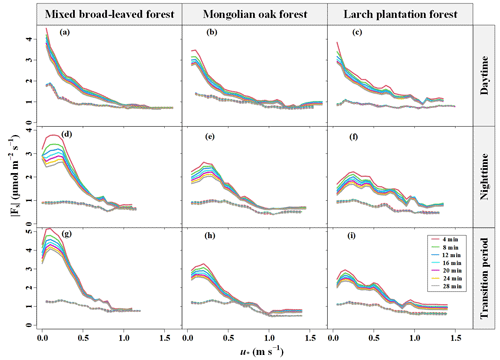
Figure 5 Magnitudes of CO₂ storage flux ($\left|F_{\mathrm{s}}\right|$) determined with different CO₂ concentration averaging time windows as a function of the friction velocity (u_∗) and moving-block averages from all 30 min data for the years 2020–2021. Dashed and solid lines indicate the dormant and growing seasons, respectively.

3.2 Effect of [CO₂] fluctuations on F_s and its uncertainty

To investigate the influence of the [CO₂] fluctuation periods on the error in F_s measurement, this study computed the diurnal average of the standard deviation σ(ε_s) of the 30 min F_s uncertainty (ε_s) separately for different P_m values and the seasons. The overall distribution of ε_s showed a non-normal distribution with a high peak (kurtosis > 2 and P < 0.05; results presented in Tables S1–S4 in the Supplement). The daily variation curves of σ(ε_s) in various [CO₂] averaging time windows are presented in Fig. 6. It was observed that the diurnal-variation range of σ(ε_s) was higher during the growing season compared to the dormant season, regardless of the P_m lengths, indicating a seasonal difference independent of P_m. Additionally, during the growing season, both MBF and MOF demonstrated evident diurnal variation in σ(ε_s), with the peak occurring at night and the trough during the daytime. The diurnal-variation range of σ(ε_s) varied across the three forest stands, with MBF exhibiting the largest amplitude.

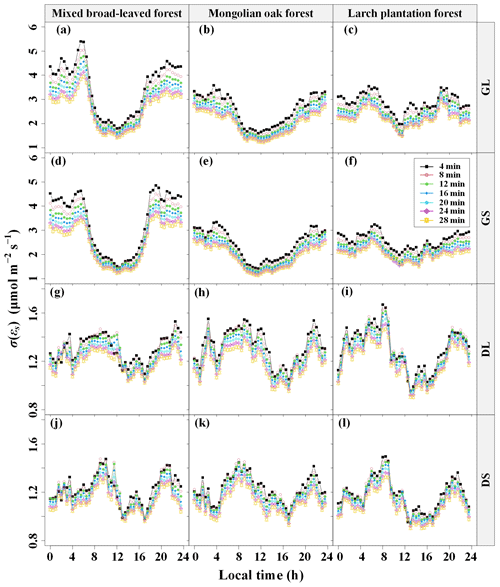
Figure 6 Diurnal variations in the random uncertainty (σ(ε_s)) of CO₂ storage flux (F_s) errors (ε_s) in different CO₂ concentration ([CO₂]) averaging time windows and their seasonal differences, where GS indicates the growing season and a short period of maximum amplitude (P_m) of [CO₂] fluctuations, GL indicates the growing season and a high P_m, DS indicates the dormant season and a low P_m, and DL indicates the dormant season and a high P_m (the L in the abbreviations is derived from long and the S from short).

Furthermore, a significantly positive correlation was observed between σ(ε_s) and $\left|F_{\mathrm{s}}\right|$ (P < 0.01), with site, seasonal, and diurnal differences (Fig. 7). The relationship between σ(ε_s) and $\left|F_{\mathrm{s}}\right|$ was characterized by intercepts and slopes ranging from 1.99 to 2.82 µmol m⁻² s⁻¹ and from 0.24 to 0.28, respectively (results presented in Tables S5–S6). Both decreased as the [CO₂] averaging time window increased, with the growing season exhibiting larger values compared to the dormant season (results shown in Tables S5 and S6). These findings suggest that increasing the [CO₂] averaging time window results in a reduction in the random error in F_s and the correlation coefficient between σ(ε_s) and $\left|F_{\mathrm{s}}\right|$. This indicates a decrease in variability in σ(ε_s) and behavior similar to white noise.

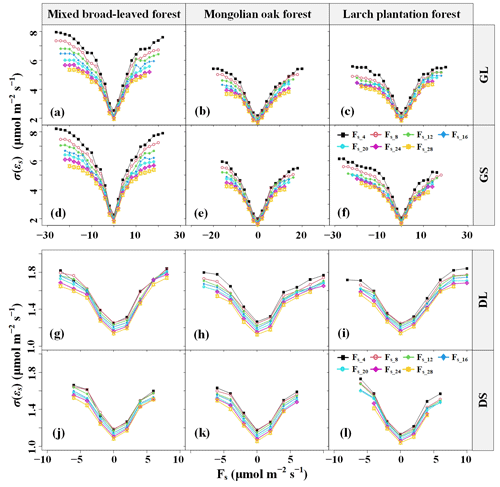
Figure 7 Random uncertainty σ(ε_s) in CO₂ storage flux (F_s) errors (ε_s) in different CO₂ concentration ([CO₂]) averaging time windows as a function of the F_s magnitude for mixed broad-leaved forest, Mongolian oak forest, and larch plantation forest during the growing and dormant seasons. GS indicates the growing season and a short period of maximum amplitude (P_m) of [CO₂] fluctuations, GL indicates the growing season and a high P_m, DS indicates the dormant season and a low P_m, and DL indicates the dormant season and a low P_m (the L in the abbreviations is derived from long and the S from short).

To assess the impact of [CO₂] fluctuations on the error and bias in F_s measurement, this study compared the NRMSE and slopes of F_s based on different [CO₂] averaging time windows, with reference to the baseline F_{s_28}, across various P_m values, time periods, and sites. As shown in Fig. 8, the NRMSE decreased and approached convergence as the [CO₂] averaging time windows increased. During both the daytime and the nighttime in the growing season, the NRMSE corresponding to higher P_m was greater than that corresponding to lower P_m, while the opposite trend was observed during the dormant season. Additionally, the longer the [CO₂] averaging time window, the greater the relative underestimation of F_s.

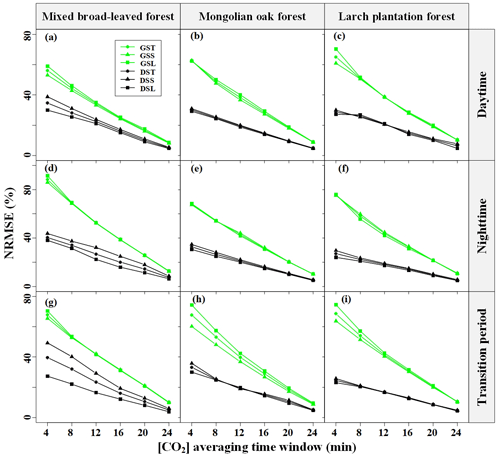
Figure 8 Seasonal and diurnal differences in the normalized root mean square error (NRMSE) of CO₂ storage flux (F_s) versus the respective F_{s_28} values for different CO₂ concentration ([CO₂]) averaging time windows. GST indicates the growing season and does not distinguish the period of maximum amplitude (P_m) of [CO₂] fluctuations, GSS indicates the growing season and a low P_m, GSL indicates the growing season and a high P_m, DST indicates the dormant season and does not distinguish P_m, DSS indicates the dormant season and a low P_m, and DSL indicates the dormant season and a high P_m (the L in the abbreviations is derived from long and the S from short).

A comparison of slopes between F_{s_4} and F_{s_28} in the three forest stands revealed interesting patterns, as depicted in Fig. 9. During the growing season, the slopes corresponding to the lower P_m of [CO₂] fluctuations were consistently lower than those for the higher P_m, indicating that the effect of P_m on F_s uncertainty decreased with increasing [CO₂] averaging time windows. However, for the MBF stand (Fig. 9d and g), the slopes corresponding to the lower P_m of [CO₂] fluctuations during the dormant-season nighttime were actually greater than those for the higher P_m, primarily due to diurnal variations in the daily dynamics of F_s. Overall, the influence of P_m on F_s uncertainty decreased with increasing [CO₂] averaging time windows. This suggests that averaging [CO₂] reduced the effect of gusts on the random uncertainty in estimating F_s but led to a systematic underestimation of F_s.

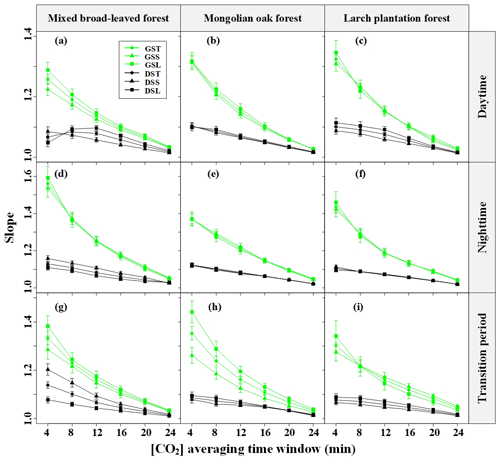
Figure 9 Seasonal and diurnal differences in the slope of CO₂ storage flux (F_s) versus F_{s_28} for the different CO₂ concentration ([CO₂]) averaging time windows. GST indicates the growing season and does not distinguish the period of maximum amplitude (P_m) cases, GSS indicates the growing season and a low P_m, GSL indicates the growing season and a high P_m, DST indicates the dormant season and does not distinguish P_m, DSS indicates the dormant season and a low P_m, and DSL indicates the dormant season and a high P_m (the L in the abbreviations is derived from long and the S from short).

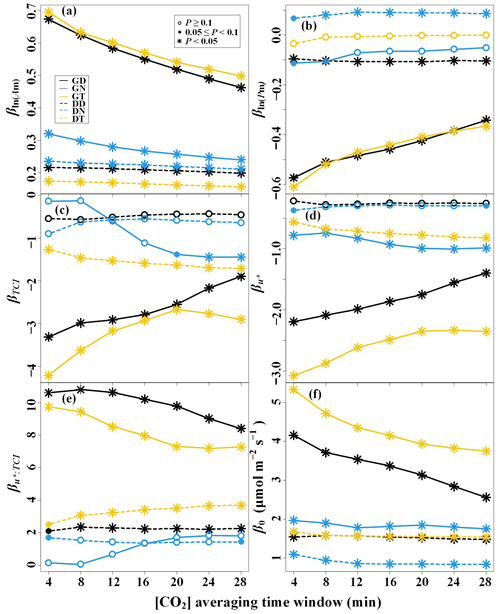
Figure 10 Linear regression coefficients of the CO₂ storage flux (F_s) magnitude – driving-factor relationships for the seven CO₂ concentration ([CO₂]) averaging time windows. The predictors of the multiple linear models are (a) the logarithm of maximum amplitude of [CO₂] fluctuations (ln (A_m)), (b) the logarithm of the corresponding period of maximum amplitude (ln (P_m)), (c) the terrain complexity index (TCI), (d) the friction velocity (u_∗), and (e) the interaction term of the TCI and u_∗. (f) β₀ represents the intercept term.

To analyze the effect of [CO₂] fluctuations on $\left|F_{\mathrm{s}}\right|$ in complex terrain, this study developed a multiple linear regression model, considering the interaction effects of turbulent mixing and terrain complexity on $\left|F_{\mathrm{s}}\right|$, as shown in Fig. 10. A_m exhibited a significant positive correlation with $\left|F_{\mathrm{s}}\right|$ in all time periods (P < 0.05). Conversely, P_m showed a significant negative correlation with $\left|F_{\mathrm{s}}\right|$ during the dormant-season daytime, the growing-season daytime, and the transition periods (P < 0.05). Additionally, their correlation coefficient decreased with increasing τ. In Fig. 10d and e, a u_∗ threshold is observed during the growing-season nighttime. When u_∗ was below the threshold, higher TCI values resulted in smaller $\left|F_{\mathrm{s}}\right|$ values, whereas when u_∗ was above the threshold, higher TCI values led to larger $\left|F_{\mathrm{s}}\right|$ values. During the growing-season nighttime and transition periods, u_∗ showed a significant negative correlation (P < 0.05) with $\left|F_{\mathrm{s}}\right|$, and the correlation coefficient decreased with increasing TCI values. These observations suggest that the effect of turbulent mixing on the $\left|F_{\mathrm{s}}\right|$ uncertainty is regulated by terrain complexity.

A multiple linear regression model was used to analyze the effect of [CO₂] fluctuations on the random uncertainty in F_s, σ(ε_s), in complex terrain. This model considered the interaction effects of [CO₂] fluctuations and terrain complexity on σ(ε_s), as shown in Fig. 11. As evident from Fig. 11a and e, A_m exhibited a significant positive correlation (P < 0.05) with σ(ε_s) during both the dormant season's nighttime and the growing season. Throughout the transition period of the growing season, P_m displayed a significant negative correlation with σ(ε_s) (P < 0.05). The magnitude of these correlation coefficients decreased with the increasing [CO₂] averaging time windows. During the transition period of the dormant season, a TCI threshold was observed, with P_m showing a significant positive correlation (P < 0.05) with σ(ε_s) when the TCI was below the threshold and a significantly negative correlation (P < 0.05) with σ(ε_s) when the TCI exceeded the threshold (Fig. 11b and f). The u_∗ value showed a significantly negative correlation with σ(ε_s) during the daytime and transition periods of the growing season (P < 0.05), while in other time periods, u_∗ was significantly positively correlated with σ(ε_s) (P < 0.05). $\left|F_{\mathrm{s}}\right|$ demonstrated a significant positive correlation with σ(ε_s) (P < 0.05) in all time periods, with its correlation coefficient being greater during the growing season than during the dormant season. These observations suggest that the relationship between the random uncertainty in F_s and [CO₂] fluctuations is moderated by topographic complexity. Increasing the [CO₂] averaging time window reduces the effect of [CO₂] fluctuations on the random uncertainty in F_s.

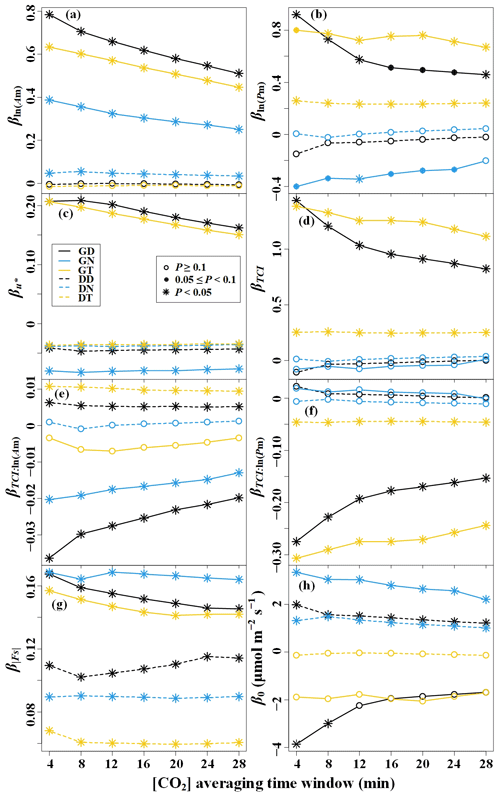
Figure 11 Linear regression coefficients of the random uncertainty in CO₂ storage flux (σ(ε_s)) – driving-factor relationships determined with Eq. (11) for the seven CO₂ concentration ([CO₂]) averaging time windows. The predictors of the multiple linear models are (a) the logarithm of maximum amplitude of [CO₂] fluctuations (ln (A_m)), (b) the logarithm of the corresponding period of maximum amplitude (ln (P_m)), (c) the friction velocity (u_∗), (d) the terrain complexity index (TCI), (e) the interaction term of the TCI and ln (A_m), (f) the interaction term of the TCI and ln (P_m), and (g) the magnitude of storage flux ($\left|F_{\mathrm{s}}\right|$). (h) The intercept term is represented by β₀.​​​​​​​

3.3 Effect of CO₂ storage flux uncertainty in NEE observations

The 30 min F_{s_comb} was obtained by weighting the bias and random error in F_s using different [CO₂] averaging time windows and P_m values. This study then focused on the magnitude of F_{s_comb} in relation to the F_c magnitude and its diurnal, seasonal, and site variations. To assess the significance of F_s in NEE observations, the relative contribution ratio of F_{s_comb} magnitude ($\left|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\right|/\left(\right|F_{\mathrm{c}}|+|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\left|\right)$) was employed. $\left|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\right|/\left(\right|F_{\mathrm{c}}|+|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\left|\right)$ showed a decreasing trend towards convergence with increasing u_∗ (Fig. 12). On average, $\left|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\right|/\left(\right|F_{\mathrm{c}}|+|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\left|\right)$ ranged from 17.2 % to 82.0 %, with a higher value during the dormant season compared to the growing season. This indicated that as turbulence intensity increased, the contribution of F_s to the NEE in forests decreased to a constant value. Nevertheless, even under strong turbulence intensity, F_s still played a significant role in the NEE observations of forests in complex terrain.

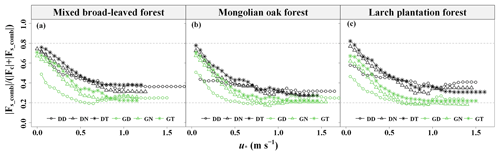
Figure 12 Relative contribution ratio of the CO₂ storage flux magnitude ($\left|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\right|/\left(\right|F_{\mathrm{c}}|+|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\left|\right)$) determined by the decision-level fusion model as a function of the friction velocity (u_∗) moving-block averages from all 30 min data for the years 2020–2021. GD represents the growing season's daytime, GN represents the growing season's nighttime, GT represents the growing season's transition period, DD represents the dormant season's daytime, DN represents the dormant season's nighttime, and DT represents the dormant season's transition period.

Table 3 Linear regression coefficients of the relative contribution ratio of F_{s_comb} magnitudes to NEE observations ($\left|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\right|/\left(\right|F_{\mathrm{c}}|+|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\left|\right)$) – driving-factor relationships for the six time periods.

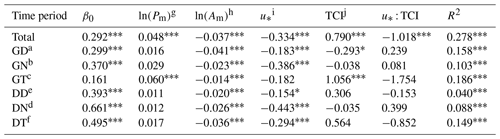
^a GD represents the growing season's daytime. ^b GN represents the growing season's nighttime. ^c GT represents the growing season's transition period. ^d DD represents the dormant season's daytime. ^e DN represents the dormant season's nighttime. ^f DT represents the dormant season's transition period. ^g P_m represents the corresponding period of maximum amplitude. ^h A_m represents maximum amplitude. ⁱ u_∗ represents friction velocity. ^j TCI denotes the terrain complexity index.
${}^{\ast \ast \ast }$ P < 0.001. ${}^{\ast \ast }$ P < 0.01. ^∗ P < 0.05.

As indicated in Table 3, both P_m and the TCI exhibited a significant positive correlation with $\left|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\right|/\left(\right|F_{\mathrm{c}}|+|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\left|\right)$ (P < 0.05), while both A_m and u_∗ showed a significant negative correlation with $\left|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\right|/\left(\right|F_{\mathrm{c}}|+|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\left|\right)$ (P < 0.05). Notably, seasonal variations in correlation coefficients were observed. The correlation between u_∗ and $\left|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\right|/\left(\right|F_{\mathrm{c}}|+|F_{\mathrm{s}\mathrm{\_}\mathrm{comb}}\left|\right)$ was more pronounced during both the dormant season's transition period and the growing season, and it decreased with increasing TCI values during the dormant season's daytime and nighttime.

To evaluate the impact of F_{s_comb} on NEE_obs (F_c+F_s), we further evaluated the slope (with intercept terms forced to zero) and NRMSE of F_c+F_{s_comb} compared to F_c+F_{s_28}, as presented in Tables S7 and S8. F_{s_28} in the three forest stands was underestimated by 28.6 %–33.3 % compared to F_{s_comb}, and the NRMSE of F_{s_comb} versus F_{s_28} ranged from 59.2 % to 67.2 %. NEE_obs with F_{s_28} was underestimated by 1.9 %–4.3 % compared to NEE_obs with F_{s_comb}. The NRMSE of NEE_obs with F_{s_comb} versus F_{s_28} in the three forest stands ranged from 16.0 % to 25.4 %. The analysis suggested that combining the F_s values based on different averaging [CO₂] time windows in the decision-level fusion model could successfully weight potential underestimation bias and random uncertainties.

The influences of F_s on the relationship between NEE observations and meteorological drivers indicated the effect of uncertainty in F_s estimates on NEE observations. Our analysis showed that the correlations between NEE observations derived from F_c+F_s and both photosynthetic photon flux density (PPFD) and air temperature are lower compared to those obtained from F_c alone (Figs. S1 and S2 in the Supplement). Additionally, the estimated light-saturated net CO₂ assimilation (A_max) is greater when NEE observations are estimated by F_s+F_c, as opposed to when the NEE is estimated solely by F_c. This suggests that F_s significantly affects the daytime NEE and can correct the estimation of A_max and related parameters. The relationship between NEE observations and PPFD is influenced by the size of the averaging time window the F_s measurement. A larger averaging window results in less random uncertainty in the F_s estimation, thereby increasing the correlation between NEE observations and meteorological drivers, including PPFD and T_a.

4 Discussion

4.1 Short-term [CO₂] fluctuations above the forest canopy and F_s estimates in complex terrain

Compared to flat and uniform underlying surfaces, complex terrain and heterogeneous canopies modify the trajectory, speed distribution, and direction of the airflow. Increased wind speeds and shifting wind directions also increase turbulent activity above the canopy, facilitating the mixing and dispersion of CO₂. This study found that short-term fluctuations in [CO₂] above the canopy exhibited a range of 1 to 10 min (Fig. 2). These fluctuations were characterized by an average P_m ranging from 2.313 to 2.784 min (Table 2). Our results are in line with previous research using wavelet analysis, which reported fluctuation periods of [CO₂] within and above the forest canopy to be between 14 and 116 s (Cava et al., 2004). These previous observations of the canopy waves during periods of extreme atmospheric stability (when $z/L\gg \mathrm{1}$) exhibited a dominant period of 1–2 min, which is consistent with our findings. The period of [CO₂] fluctuations was found to be predominantly influenced by turbulent fluxes and the residence time of CO₂ within the canopy. This indicated a potential correlation between P_m and the residence time of CO₂ within the canopy. Fuentes et al. (2006) employed a Lagrangian model and calculated the residence time of air parcels released near the ground and in the canopy, finding values ranging from 3 to 10 min and from 1 to 10 min, respectively. Similarly, Edburg et al. (2011) used the standard deviation of [CO₂] averages to determine the CO₂ residence time at different locations, including at the ground, within the canopy, and in their gas mixtures, yielding values of 8.6, 3.6, and 5.6 min, respectively. The results of these simulation experiments are consistent with our study, further supporting the association between [CO₂] fluctuations above the forest canopy and CO₂ residence time.

Tree density and canopy structure also play a role in influencing the air parcel residence time; on flat terrain, the air parcel residence time correlates with u_∗ (Gerken et al., 2017), and an increase in the vegetation leaf area leads to longer residence times when turbulence is not fully penetrative. During the growing season, forests in our study site exhibit a higher leaf area index and greater canopy densities than during the dormant season (Li et al., 2023), resulting in higher P_m values of short-term [CO₂] fluctuations above the canopy (Fig. 3). Additionally, at night, stable atmospheric conditions lead to longer residence times due to suppressed turbulent mixing, resulting in relatively high nighttime P_m values compared to daytime and transition periods (Fig. 3).

Complex terrain introduces complex changes into airflow structures, including gravity-induced waves, drainage, and nonlinear waves induced by single gusts, leading to dramatic [CO₂] fluctuations. These dynamics contribute to uncertainties in estimating F_s. At night, the difference between incoming and outgoing longwave radiation over the valley soil surface and vegetation canopy gives rise to radiative cooling. Subsequently, the air near the soil surface experiences a gravity-induced downslope acceleration, potentially causing katabatic flow. As inertia-driven upslope winds are halted by katabatic acceleration, a local shallow drainage flow is established, reaching a quasi-equilibrium state approximately 1.5 h after sunset (Nadeau et al., 2013). Under stable atmospheric conditions, even gentle slopes (around 1°) can generate strong gravity-driven waves (Belušić and Mahrt, 2012). Consequently, advection may complicate the interpretation of nighttime EC measurements at certain relatively gentle sites, but this complexity is not evident during daytime measurements (Leuning et al., 2008). Advection plays a role in depleting the CO₂ accumulated within the canopy, resulting in lower F_s fluxes and establishing an inverse relationship between storage and advection (van Gorsel et al., 2011). The occurrence of larger F_s values for high P_m values suggests weaker advection compared to low P_m values (Fig. 4). In our study, we observed that the F_s magnitude was relatively large during nighttime and transition periods, while it was smaller during the daytime (Fig. 4), which is consistent with the findings reported by Wang et al. (2016).

The terrain unevenness and the complexity of canopy structure significantly affect the airflow divergence in the atmospheric boundary layer. This results in weakened air circulation within the canopy and spatial variation in the patterns and extent of airflow separation (Grant et al., 2015). During nighttime and transition periods in a closed canopy, the turbulent coupling state above and below the canopy gradually decouples, eventually reaching complete decoupling as u_∗ decreases (Fig. 5). However, this decoupling does not lead to stable stratification within the canopy. Despite the occurrence of decoupling and advection in the closed canopy, waves are unlikely to exist within the canopy itself (van Gorsel et al., 2011). As a result, a consistent trend in the variation in F_s with τ is observed across the three forest stands during the growing season, independent of P_m (Fig. 9). Conversely, in an open canopy where waves are present, the observations of F_s become more complex. This complexity could be the primary reason for the variation in F_s with [CO₂] averaging time windows differing between the three forest stands for low P_m values during the dormant-season daytime (Fig. 9). The presence of waves introduces additional variability into the measurements, leading to differences in F_s estimates based on different [CO₂] averaging time windows in these particular conditions.

4.2 Uncertainty in forest ecosystem F_s measurement in complex terrain

The random uncertainty in F_s shares similarities with NEE estimation. For example, the magnitude of F_s measurements is positively correlated with the standard deviation of random uncertainty in F_s. Additionally, the overall distribution of F_s measurements exhibits a non-Gaussian distribution with a high peak, aligning with the statistical properties of NEE uncertainty (Richardson et al., 2006, 2008). The uncertainty in the storage term depends a great deal on the setup used, together with the biological activity of the ecosystem and the height of the control volume. In addition, various factors contribute to the uncertainty in F_s estimates, including the flux measurement footprint variations, sampling frequency, the spatial sampling resolution of CO₂ and H₂O concentrations, and instrumental measurement accuracy. The accuracy and precision requested for the CO₂ and H₂O concentration measurements are ±1 µmol mol⁻¹ and ±1 mmol mol⁻¹, respectively (Montagnani et al., 2018). The uncertainty arising from variations in the flux measurement footprint is considerable, typically on the order of tens of percent, which is an order of magnitude higher than typical sensor errors (Metzger, 2018). AP200 adopts buffer volumes to mix the gas. The LI-850 analyzer integrated within AP200 exhibits a sensitivity to water vapor of less than 0.1 µmol CO₂ per mmol mol⁻¹ H₂O and a sensitivity to CO₂ of less than 0.0001 mmol mol⁻¹ H₂O per µmol CO₂. Efforts to reduce random errors in [CO₂] originating from pressure fluctuations include adding buffer volumes before IRGA pumping tests (Marcolla et al., 2014). The buffer volumes are fully mixed during gas extraction, and a weighted average of [CO₂] instantaneous measurements is obtained to minimize the sampling error for each level's [CO₂] measurement (Cescatti et al., 2016).

The F_s estimates can be influenced by singular eddies that penetrate the canopy (Finnigan, 2006). Accurate calculation of F_s requires considering the period of [CO₂] fluctuations with the eddy coherence structure. The spectral energy of the F_s time series is primarily concentrated between 0.001 and 0.2 Hz (500 and 5 s, respectively). However, even with sampling frequencies of 2 Hz and below, significantly lower F_s values are obtained (Bjorkegren et al., 2015). The Nyquist–Shannon sampling theorem dictates that accurate measurements of [CO₂] require a sampling period that is no longer than half the period of [CO₂] fluctuations. Consequently, to monitor short-term changes in [CO₂], measurements must be taken over a period that is no longer than half of the period corresponding to the maximum amplitude (or major energy) of [CO₂] fluctuations. In this study, the average P_m for [CO₂] fluctuations fell within the range of 2.313–2.784 min (Table 2). Therefore, it is crucial to ensure that the sampling period for [CO₂] does not exceed 1.256 to 1.392 min, which corresponds to half the average P_m range. Monitoring fluctuations in P_m for less than 4 min during a 2 min monitoring period of [CO₂] presents a significant challenge. This is a primary reason for the systematic bias and random error in the F_s estimate with a single-profile system being irreconcilable (Wang et al., 2016). Short-term [CO₂] fluctuations are mainly influenced by boundary-layer turbulence, and sampling errors in incomplete fluctuation cycles are superimposed with the real advection flux (anisotropy) dispersion in complex terrain (van Gorsel et al., 2011). This substantially increases the random uncertainty in F_s based on shorter [CO₂] averaging time windows (Figs. 6 and 8). As a result, the deviation of NEE estimates from the actual value expands.

Fluxes in heterogeneous regions are significantly higher than in uniform regions. The energy transfer from the ground surface to large eddies occurs primarily in areas with pronounced heterogeneity, and this energy distribution is uneven across the region (Aubinet et al., 2012). Once large-scale eddies acquire energy, their cascading of energy to smaller-scale eddies is influenced by topographic features, leading to variations in these smaller-scale eddies along different flow streams (Chen et al., 2023). In complex terrain, the bidirectional airflow within forests along slopes can cause the decoupling of soil CO₂ fluxes from EC measurements above the forest canopy (Feigenwinter et al., 2008; Aubinet et al., 2003), leading to significant errors in CO₂ flux measurements. Forest soil serves as the primary source of CO₂ gas, and regions of high flux over complex terrain act like chimneys, transporting air parcels from the soil surface within forests (Chen et al., 2019). By increasing the number of gas concentration sampling points near the ground, the horizontal representativeness can be enhanced, thereby reducing the bias in the estimation of F_s (Nicolini et al., 2018). In situations where turbulence is not well developed and CO₂ mixing is inadequate, the trend of F_s with turbulence intensity aligns with that of advective fluxes, which is the opposite to that of turbulent fluxes (McHugh et al., 2017). The temporal dynamics and amplitudes of F_s changes are influenced by topography complexity and wind conditions above the forest canopy (Fig. 10). Locations with more complex and sloping topography at the flux tower are more likely to generate advective fluxes that may not be easily observed at a single point.

Estimating landscape CO₂ fluxes in complex terrain solely based on measurements from a single flux tower can introduce significant errors and biases that are not acceptable. The magnitude of these errors in F_s estimates is dependent on the height of the forest canopy and the endogenous source/sink (Chen et al., 2020). To mitigate errors and biases associated with estimating F_s in complex terrain, we employed a regression modeling approach using the decision-level fusion model. This method involves computing a weighted average of F_s based on different [CO₂] averaging time windows, effectively reducing errors and biases in the estimation of F_s (see Table 5). In fact, from the definition of storage flux, it can be seen that weighting the storage flux essentially means weighting the [CO₂] in the averaging time window, which in turn means replacing spatial sequences with temporal sequences for weighting. The weighting coefficients used to construct the model were based on the relative errors and biases in F_s estimation, with the weighting coefficient decreasing as the represented moment's length increased. To obtain more accurate estimates of forest ecosystem F_s in complex terrain, further research should focus on understanding the spatiotemporal patterns and dynamics of [CO₂].

5 Conclusions

This study investigated the impact of short-term [CO₂] fluctuations on the estimation of F_s in temperate forest ecosystems within complex terrain. Additionally, it examined the F_s uncertainty and the contribution of F_s to the NEE using data from three flux towers. To enhance F_s uncertainty estimation, statistical sampling techniques were applied based on an individual-tower approach.

The results highlighted the significance of considering multiple time windows for averaging [CO₂] when estimating F_s, as [CO₂] above the forest canopies exhibited fluctuations with periods ranging from 1 to 10 min. Diurnal, seasonal, and spatial variations were observed in the amplitude and periodicity of [CO₂] fluctuations, highlighting the need for thoughtful sampling strategies. The use of individual gas analyzers to sample the CO₂ in the control volume was inadequate, leading to systematic biases and random errors in the F_s estimates. Increasing [CO₂] averaging time windows mitigated the effect of [CO₂] fluctuations on F_s estimates, reducing both their magnitude and their uncertainty.

The study also revealed that the uncertainty in F_s followed a non-normal distribution, with its standard deviation positively correlated with F_s magnitude, which has important implications for quality control. To improve F_s estimation, a decision-level fusion model was introduced, integrating F_s estimates from multiple [CO₂] averaging time windows, effectively reducing the impact of short-term [CO₂] fluctuations while considering underestimation bias and random errors. The contribution of F_s to the NEE exhibited diurnal, seasonal, and spatial variations associated with u_∗, contributing to the NEE observations at rates ranging from 17.2 % to 82.0 % depending on the turbulent mixing and terrain complexity. The influence of terrain complexity on the relationship between [CO₂] fluctuations, turbulent mixing, and the contribution of F_s to the NEE was also evident. The findings from the three flux towers allowed for the generalization of these results beyond the study site. These insights provide crucial scientific support for the practical application of the eddy covariance technique and advance our understanding of accurately estimating the NEE in forest ecosystems in complex terrain.

Appendix A

A1 The weight parameters of the decision-level fusion model

For each 30 min CO₂ storage flux (F_s) estimate based on the CO₂ concentration ([CO₂]) averaging time window (τ), the weight in the decision-level fusion model can be obtained by weighting the random uncertainty and bias in F_{s_τ}.

The weight of the random uncertainty for F_{s_τ} is expressed as follows:

$$\begin{array}{}\text{(A1)}& w_{\mathit{\tau }}={\displaystyle \frac{\frac{\mathrm{1}}{\mathit{\sigma }\left({\mathit{\epsilon }}_{\mathit{\tau }}\right)}}{{\sum }_j\frac{\mathrm{1}}{\mathit{\sigma }\left({\mathit{\epsilon }}_j\right)}}},\end{array}$$

where σ(ε_τ) is the random uncertainty in F_{s_τ}, qualified as the standard deviation.

The weight of the bias for F_{s_τ} is expressed as follows:

$$\begin{array}{}\text{(A2)}& W_{\mathit{\tau }}={\displaystyle \frac{K_{\mathit{\tau }}}{{\sum }_j{K}_j}},\end{array}$$

where K_τ is the slope between F_{s_τ} and F_{s_28}.

Ultimately, the weight of F_{s_τ} in the decision-level fusion model can be calculated using the following equation:

$$\begin{array}{}\text{(A3)}& w_{\mathit{\tau }}^{\ast }=r{w}_{\mathit{\tau }}+\left(\mathrm{1}-r\right)W_{\mathit{\tau }},\end{array}$$

where r represents the proportion of the weight of random uncertainty.

A2 Complex-terrain index

This study employed a novel descriptor called the terrain complexity index (TCI) to quantify the complexity of the three-dimensional terrain. For a given unit area, the TCI equation can be expressed as follows:

$$\begin{array}{}\text{(A4)}& \mathrm{TCI}=\left(\mathrm{1}-P_{\mathrm{d}}\cos {\mathit{\alpha }}_{\mathrm{d}}\right)\left(\mathrm{1}-Z_{\mathrm{d}}^{-\mathrm{1}}\right){\left(D_{\mathrm{f}}-\mathrm{2}\right)}^{-\frac{H}{\ln \left(\mathrm{12}\right)}},\end{array}$$

where P_d represents the volume of terrain above the lowest elevation of an area unit (V_u) divided by the product of its largest vertically projected area (S_v) and the edge length of the side of the area unit (d), expressed as $P_{\mathrm{d}}=\frac{V_{\mathrm{u}}}{S_{\mathrm{v}}d}$; P_d is defined as 1 when S_v is 0. Given V_u, an increase in S_v correlates with a higher degree of terrain complexity. Notably, P_d is defined as 1 when the terrain volume is 0 or when the terrain surface of the area unit is parallel to the horizontal plane and is smooth and homogeneous. α_d indicates the slope of the area unit. Z_d denotes the terrain roughness, which is defined as the ratio of the terrain surface area to the projected horizontal plane (Loke and Chisholm, 2022). The value of Z_d was in the range of [1, +∞). The larger the Z_d, the more complex the terrain. D_f is the fractal dimension of the terrain surface area, which ranged from 2 to 3 and describes the complexity in the spatially self-similar structure of the local surface within the area unit and the area unit surface (Mandelbrot, 1967; Taud and Parrot, 2005). Employing the terrain surface area, the box-counting method was used to estimate the fractal dimension of the unit area. H represents the Shannon–Wiener index and is expressed as $H=-\sum _{i=\mathrm{1}}^n{P}_i\ln \left(P_i\right)$, capturing the uniformity of the spatial distribution of the pixel aspects within the area unit (Brown, 1997). When the aspect of each pixel is divided into 30° segments, P_i denotes the proportion of the ith type of pixel aspects within the area unit and n is the total number of pixel aspect types within the area unit. A larger H indicates a more complex terrain. When the number of pixel aspect types in the area unit is kept constant, it is essential to recognize that greater uniformity in the distribution of all pixel aspects in the area unit results in a larger H. Similarly, when the uniformity of the distribution of pixel aspects in the area unit is kept constant, a larger H is achieved with an increase in the observation of the number of pixel aspect types.

To quantify the terrain complexity of the underlying surface around the flux towers, we computed the quartiles of the TCI for all area units within a sector (divided by 30°) with a radius of 380 m. A weighted geometric mean was employed to construct TCI_s, which describes the statistical distribution of the TCI of the sector. TCI_s represents the topographic complexity of the sector and is calculated using the following equation:

$$\begin{array}{}\text{(A5)}& {\mathrm{TCI}}_{\mathrm{s}}={\left({\mathrm{TCI}}_{\mathrm{5}}{\mathrm{TCI}}_{\mathrm{25}}{\mathrm{TCI}}_{\mathrm{50}}{\mathrm{TCI}}_{\mathrm{75}}{\mathrm{TCI}}_{\mathrm{95}}\right)}^{\frac{\mathrm{1}}{\mathrm{5}}},\end{array}$$

where TCI₅, TCI₂₅, TCI₅₀, TCI₇₅, and TCI₉₅ are the quartiles of 5 %, 25 %, 50 %, 75 %, and 95 %, respectively. The TCI_s values range from 0 to 1, with higher values indicating greater terrain complexity.