Direct high-precision radon quantification for interpreting high-frequency greenhouse gas measurements

We present a protocol to improve confidence in reported radon activity concentrations, facilitating direct site-to-site comparisons and integration with co-located greenhouse gas (GHG) measurements within a network of three independently managed observatories in the UK. Translating spot measurements of atmospheric GHG amount fractions into regional flux estimates (“top-down” analysis) is usually performed with atmospheric transport models (ATMs), which calculate the sensitivity of regional emissions to changes in observed GHGs at a finite number of locations. However, the uncertainty of regional emissions is closely linked to ATM uncertainties. Radon, emitted naturally from the land surface, can be used as a tracer of atmospheric transport and mixing to independently evaluate the performance of such models. To accomplish this, the radon measurements need to have a comparable precision to the GHGs at the modelled temporal resolution. Australian Nuclear Science and Technology Organisation (ANSTO) dual-flow-loop two-filter radon detectors provide output every 30 min. The measurement accuracy at this temporal resolution depends on the characterization and removal of instrumental background, the calibration procedure, and response time correction. Consequently, unless these steps are standardized, measurement precision may differ between sites. Here we describe standardized approaches regarding (1) instrument maintenance, (2) quality control of the raw data stream, (3) determination and removal of the instrumental background, (4) calibration methods, and (5) response time correction (by deconvolution). Furthermore, we assign uncertainties for each reported 30 min radon estimate (assuming these steps have been followed) and validate the final result through comparison of diurnal and sub-diurnal radon characteristics with co-located GHG measurements. While derived for a network of UK observatories, the proposed standardized protocol could be equally applied to two-filter dual-flow-loop radon observations across larger networks, such as the Integrated Carbon Observation System (ICOS) or the Global Atmosphere Watch (GAW) baseline network.

1 Introduction

The Paris Agreement aims to keep this century's mean global temperature rise well below 2 °C and pursue efforts to limit it to 1.5 °C above pre-industrial levels. Meeting this goal requires better understanding of greenhouse gas (GHG) emissions to enable the most efficient mitigation policies to be implemented. Current GHG emission information is dominated by “bottom-up” (prior) estimates derived from aggregated activity data, emission factors, and facility-level measurements (from local to country scale) that rely on reported data and knowledge of natural systems (e.g. Ciais et al., 2014; Gurney et al., 2016; Nisbet and Weiss, 2010). Since there can be large uncertainties associated with the spatial and temporal variability of these emission factors across sectors, as well as potential biases from sources that are unaccounted for, especially for non-CO₂ GHGs, it is prudent to seek independent verification of the resulting emission estimates. To this end, a distributed network of precise, high-frequency, in situ GHG observations can provide opportunities for independent “top-down” verification of GHG emissions estimate.

In recent decades many GHG monitoring stations have been developed throughout Europe. The Integrated Carbon Observation System (ICOS) (https://www.icos-cp.eu/, last access: 24 March 2024) constitutes Europe's primary research infrastructure for standardized, traceable, high-precision observations of atmospheric GHG amount fractions. This atmospheric monitoring network includes 46 stations across 16 European countries (Yver Kwok et al., 2015; Yver-Kwok et al., 2021) (https://www.icos-cp.eu/observations/atmosphere/stations, last access: 25 March 2024). The corresponding UK GHG network is UK DECC (UK Deriving Emissions related to Climate Change), consisting of five stations (Fig. 1): Mace Head (MHD), a World Meteorological Organization (WMO) Global Atmosphere Watch (GAW) baseline station, Tacolneston (TAC), Ridge Hill (RGL), Bilsdale (BSD), and Heathfield (HFD), each of which having at least one inlet 90 m or more above ground level (a.g.l.) (Stanley et al., 2018; Stavert et al., 2019).

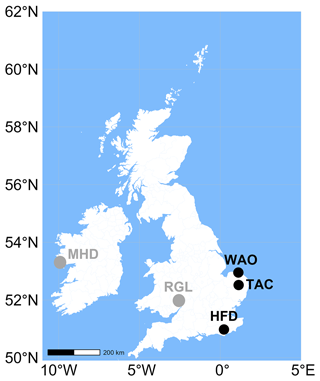
Figure 1 Geographical position of UK DECC stations measuring radon activity concentration (TAC, HFD, RGL, and MHD), along with affiliated WAO – an ICOS site. Note that measurements from MHD and RGL, highlighted in grey, are not considered in this study.

The most commonly used top-down method for making GHG emission estimates is through the use of inverse modelling, where high-quality GHG measurements are combined with atmospheric transport models (ATMs) and prior information to make optimal emission estimates (Arnold et al., 2018; Bergamaschi et al., 2015, 2018; Brown et al., 2023; Ganesan et al., 2015; Lunt et al., 2021; Manning et al., 2011, 2021). Another method is the radon tracer method (RTM), which utilizes simultaneous, co-located observations of ²²²Rn (hereafter radon) and a GHG, in combination with an estimated radon source function. Different implementations of this approach allow either local- or regional-scale GHG emission estimates to be made from the same fetch region influencing the radon observations (e.g. Biraud et al., 2000; Grossi et al., 2018; Hirsch, 2007; Levin, 1987; Levin et al., 2021; van der Laan et al., 2014; Vogel et al., 2012; Wada et al., 2013).

Despite recent improvements in the spatio-temporal density of observations and the excellent quality of GHG measurements (relative uncertainties often < 0.1 %), as well as the mathematical elegance of ATMs (e.g. Baker et al., 2006; Dentener et al., 1999; Tolk et al., 2008; Zhang et al., 2021), large uncertainties remain in total annual top-down GHG emission estimates (e.g. ∼ 10 % for the UK N₂O emission estimate; UK's National Inventory Report to the United Nations Framework Convection on Climate Change 2022). A key contributor to the overall uncertainty in top-down inverse model estimates of GHG emissions is the ATMs themselves. The challenge of quantifying ATM uncertainty is evident in tasks such as boundary layer height estimation and parameterization of meteorological variables, where errors are related to the resolution of the model (e.g. Geels et al., 2007; Gerbig et al., 2008; Liu et al., 2011; Munassar et al., 2023; Tolk et al., 2008). As yet, no optimal method exists to evaluate the discrepancies between a priori and a posteriori emission estimates (bias). Until it is possible to accurately quantify an ATM's uncertainty, full realization of the potential offered by high-quality atmospheric measurements from a comprehensive tower network cannot be achieved. This is a crucial step for improving national inventories and developing policy that the international community should have while strengthening the 2015 Paris Agreement.

To this end, measurements of the naturally occurring, passive tracer radon could provide a means of evaluating ATM performance. Moreover, subject to the measurement location and sampling height, among other things, radon observations can be a valuable tool for atmospheric baseline monitoring (e.g. Chambers et al., 2016), evaluating the performance of regional or global chemical transport models (e.g. Chambers et al., 2019a; Zhang et al., 2021), or characterizing the atmospheric mixing state (Chambers et al., 2019b; Kikaj et al., 2023; Perrino et al., 2001; Williams et al., 2016). Consequently, efforts to broaden the international radon monitoring network and harmonize the resulting measurements not only stand to improve GHG emissions estimate via atmospheric inversion studies, but also provide a second independent top-down method to estimate local- to regional-scale GHG emissions via the RTM, as well as other research opportunities.

Radon is the gaseous decay product of ²²⁶Ra (radium), a member of the ²³⁸U (uranium) decay chain, which is ubiquitous all over the Earth's crust. When emitted into the atmosphere, radon experiences the same atmospheric transport and mixing as all other gases released near the surface. Being an inert gas, radon (²²²Rn) does not chemically react with any atmospheric constituents, and its low solubility makes it resistant to dry and wet deposition, leaving radioactive decay (half-life of 3.82 d) as its sole atmospheric sink. Its half-life, conveniently between the timescales of diurnal and synoptic atmospheric processes, is ideal for characterizing a wide range of meteorological phenomena (Galmarini, 2006; Kikaj et al., 2019; Williams et al., 2013; Zahorowski et al., 2004). It is therefore considered a powerful and convenient tracer at mesoscale, synoptic scales, and global scales for improving, testing, and validating atmospheric models (Chambers et al., 2015, 2019b; Israël et al., 1966; Jacob et al., 1997; Taguchi et al., 2002; Zhang et al., 2021).

Since its discovery in 1900, radon's unique physical characteristics have led to its use in studies of vertical mixing and air mass history (Eve, 1908; Wigand and Wenk, 1928; Wright and Smith, 1915). Early studies employed a variety of discrete measurement techniques but were often lacking in sensitivity or temporal resolution. The most significant progress in utilizing radon as a relative tracer for vertical mixing and transport near the Earth's surface has been achieved since the 1960s, mainly driven by advancements in continuous measurement techniques. Initially, public health (indoor) applications dominated instrument development, but the large indoor-to-outdoor gradient in radon activity concentrations (henceforth radon concentrations) limited the utility of these instruments in the outdoor environmental atmosphere. The first semi-continuous radon detector was developed in the mid-1960s (Taylor and Lucas, 1967). While suitable for near-surface inland measurements, this type of detector was not sufficiently sensitive for measurements at coastal or island sites. The capability to measure radon concentrations typical of the remote marine atmosphere began to emerge post-1970 (Lambert et al., 1970; Polian et al., 1986; Pereira and Da Silva, 1989; Levin, 1987). More recently still, refinement of the original two-filter radon detector (Thomas and Leclare, 1970) by Whittlestone and Zahorowski (1998) greatly improved both the sensitivity and temporal resolution of radon measurements, better aligning them with advances in GHG measurements and modelling resolution. This growing collection of one- and two-filter radon monitors constituted the first of the “research-grade” instruments. Following these developments, the popularity of radon increased as a quantitative tracer in atmospheric modelling (Chevillard et al., 2002; Dentener et al., 1999; Jacob et al., 1997; Hirao et al., 2008; Mahowald et al., 1995; Zahorowski et al., 2004; Zhang et al., 2021) and estimation of GHG fluxes on the local to regional scale by the RTM (Biraud et al., 2000; Grossi et al., 2018; Levin, 1987; Levin et al., 2021; van der Laan et al., 2009, 2014).

Contemporary research-grade radon monitors are based on three fundamentally different measurement techniques: (i) indirect one-filter α- or β- activity detectors, which directly filter ambient aerosol-bound radon progeny from the atmosphere and count them, assuming equilibrium between atmospheric radon and its progeny (Biraud et al., 2000; Levin et al., 2002; Levin, 1987; Polian et al., 1986); (ii) direct two-filter detectors that first remove ambient radon progeny, before filtering out and counting new unattached radon progeny formed inside a large measurement volume under controlled conditions (Chambers et al., 2022; Griffiths et al., 2016; Whittlestone and Zahorowski, 1998); and (iii) direct electrostatic deposition monitors, which also remove ambient progeny and allow new progeny to form inside a small measurement volume but deposit these progeny electrostatically on a detector (Grossi et al., 2012; Pereira and Da Silva, 1989; Wada et al., 2013).

Continuous, long-term atmospheric radon measurements are currently performed worldwide using the three principles of measurement mentioned above. Maximizing the value and utility of such large datasets across a range of applications requires a traceability chain for calibrations and standardized data processing techniques appropriate to each type of detector. Although there have already been some efforts to compare and harmonize radon measurements across the existing eclectic global network (Grossi et al., 2020; Xia et al., 2010; Schmithüsen et al., 2017), more attention needs to be given to preparation of a standardized protocol for retrieving the highest-quality, most directly comparable atmospheric radon datasets from each kind of contributing instrument. Due to the distinct measurement principles of each instrument, tailored approaches are necessary to maximize consistency and comparability of datasets. For instance, indirect one-filter detectors require corrections for tube loss, equilibrium (for inlets below 80–100 m a.g.l.), and exclusion of foggy/rainy conditions. While two-filter detectors are highly sensitive and independent of tube length, measurement height, or weather conditions, the larger models (700 and 1500 L) can have a 4 %–8 % uncertainty in individual field calibrations (unless a transfer standard is used) and require response time correction. Meanwhile, electrostatic deposition monitors need to dry their sample air (and/or correct for water vapour) and remove or correct for thoron (²²⁰Rn). Therefore, to maximize consistency and comparability across various instruments, it is essential to establish a standardized processing procedure for each instrument type. This instrument-specific standardized procedure should be applicable to any atmospheric station measuring radon concentration with that type of instrument and would enable optimal utilization of radon measurements by the atmospheric composition research community, particularly in studies verifying GHG emission estimates.

To this end, here we present a new protocol for processing measurements made by the fastest (30 min temporal resolution), most sensitive (detection limit ∼ 0.025 Bq m⁻³), and most widely used radon detectors within global and European atmospheric monitoring networks – the 1500 L “two-filter dual flow-loop” detector, developed by the Australian Nuclear Science and Technology Organisation (ANSTO). In the last 28 years, 50 two-filter radon detectors have been part of campaigns or have been integrated within global and European atmospheric monitoring networks (39 of which are still operational), 11 (4) of which are part of the ICOS (UK DECC) network. Compared to indirect detectors, two-filter detectors provide a measure of radon concentration that is independent of height above ground, distance from land, meteorological conditions (e.g. fog/rain), fetch conditions, ambient aerosol loading, and length or type of sampling tube. Consequently, their calibration traceability is more readily achievable under a wide range of measurement conditions (Chambers et al., 2022).

This study utilizes 1 year (September 2020–August 2021) of radon measurements by 1500 L two-filter detectors at the three UK sites with contrasting sample inlet heights: TAC, HFD (UK DECC sites), and Weybourne Atmospheric Observatory (WAO, a UK ICOS and affiliated DECC site). The specific objectives are to (i) outline the expected maintenance protocol for these detectors, (ii) outline a proposed standard processing protocol for near-real-time data use, including calibration, response time correction (Griffiths et al., 2016), standard temperature and pressure (STP) correction, and, optionally, correcting output to dry-air amount fractions; (iii) validate the timing of response-time-corrected radon concentrations using well-defined calibration events; and (iv) assess the precision of the resulting radon signal by comparing it with high-resolution GHG (CO₂, CH₄, and N₂O) amount fraction measurements aggregated to 60 min values.

2 Measurement sites and instrumentation

2.1 Measurement sites

This study focuses on atmospheric radon concentration and GHG (CO₂, CH₄, and N₂O) amount fraction measurements made at three sites of the UK DECC network with contrasting inlet heights (TAC, HFD, and WAO; Fig. 1). Measurements at RGL (51.998° N, 2.540° W) were excluded due to the limited calibration and background measurement history within this study's time frame. Measurements at MHD were also excluded since radon concentrations at this station are conducted with a one-filter detector (Biraud et al., 2000). Each station in the UK DECC network measures at least CO₂, CH₄, N₂O, and sulfur hexafluoride (SF₆). However, some also measure carbon monoxide (CO), stable isotopic ratios (δ¹³C(CH₄), δ²H(CH₄)), radiocarbon in atmospheric CO₂ (Δ¹⁴CO₂), and the oxygen $/$ nitrogen (O₂ $/$ N₂) ratio.

For the results here, measurements of radon concentration, CO₂, CH₄, and N₂O amount fractions have been aggregated to hourly temporal resolution and reported in local solar time (LST; equivalent to Universal Time Coordinated (UTC) in these locations). The Northern Hemisphere seasonal convention has been adopted (i.e. autumn: September–November; winter: December–February; spring: March–May; summer: June–August).

2.1.1 Tacolneston (TAC)

The TAC tall tower (52.518° N, 1.139° E; 56 m above sea level – a.s.l.) is situated southwest of Norwich, 28 km east of Thetford, Norfolk. Sampling inlets are arranged at three heights: 54, 100, and 185 m a.g.l. Since 2012, measurements of CO₂, CH₄, N₂O, CO, and SF₆ amount fractions have been taken at all heights. In 2020, radon concentration started being sampled from 175 m a.g.l. Additional technical details regarding the tower setup can be accessed in Stanley et al. (2018). As well as being part of the UK DECC network, TAC is part of the Advanced Global Atmospheric Gases and Experiment (AGAGE) network and is a WMO GAW regional site.

2.1.2 Heathfield (HFD)

The HFD tall tower (50.977° N, 0.231° E; 157 m a.s.l.) is situated in southeast England, 20 km from the coast, surrounded by woodland and agricultural green space. Measurements at this site are being conducted from an existing telecommunication tower. Sampling began in January 2014, and measurements of key GHGs (CO₂, CH₄, N₂O, and SF₆) are being made from two sampling inlet heights (50 and 100 m a.g.l). Atmospheric radon measurements were introduced in 2020, with an independent inlet at 100 m a.g.l. Further information on technical details of the tower setup can be found in Stavert et al. (2019).

HFD is a part of the UK DECC network and is also a WMO GAW regional site. HFD is considered to be a background site of the UK DECC network as the predominant southwesterlies experience little land fetch prior to reaching HFD from the Atlantic Ocean (see Fig. 1). However, it can also experience high-pollution events since it is relatively close to the conurbation Royal Tunbridge Wells (17 km north-northeast), greater London (40 km north-northeast), and continental Europe (southwest).

2.1.3 Weybourne Atmospheric Observatory (WAO)

The WAO (52.951° N, 1.122° E; 17 m a.s.l.) is situated on the northern Norfolk coast, approximately 35 km north-northwest of Norwich, 170 km northeast of London, and 200 km east of Birmingham. WAO is an ICOS site, a regional WMO GAW site, and also an affiliated UK DECC site. WAO was established in 1992 (Penkett et al., 1999), and a wide array of atmospheric gas species (GHG amount fractions, stable isotopic ratio, reactive gases, as well as radon since March 2018) are measured there from a sampling inlet at 10 m a.g.l. Due to its location, WAO receives a variety of air masses from a range of sources including well-mixed background air (Atlantic, Arctic, North Sea) and polluted air (European, UK) (Adcock et al., 2023; Fleming et al., 2012; Forster et al., 2012).

2.2 Radon instrument: 1500 L dual-flow-loop two-filter

2.2.1 Operating principle

Atmospheric radon concentration is measured at all three sites (HFD, TAC, and WAO) using 1500 L dual-flow-loop two-filter radon detectors, designed and built by ANSTO, which provide half-hourly, high accurately and precision measurements. The principle of operation is described in detail elsewhere (Chambers et al., 2022; Griffiths et al., 2016; Thomas and Leclare, 1970; Whittlestone and Zahorowski, 1998) and is only summarized here. The detector relies on gross α counting, making the signal sensitive to other radon isotopes (e.g. ²²⁰Rn, half-life of 55.6 s; actinon: ²¹⁹Rn, half-life of 4 s) as well. To eliminate contributions from unwanted radon isotopes (of which the longest-lived is ²²⁰Rn), this system includes a “thoron delay volume” prior to the first filter, which acts to delay the sampled air for ∼ 5 min, allowing time for all unwanted radon isotopes to decay to their aerosol progeny. Following this, the sampled air is filtered (by the “primary filter”) to remove the progeny of all radon isotopes and any ambient aerosols before it passes through to the main delay chamber, where a portion of the sampled ambient ²²²Rn decays under controlled conditions to produce unattached aerosol progeny. These new unattached progeny (particularly the short-lived α emitters ²¹⁸Po and ²¹⁴Po) are then efficiently collected on a 20 µm stainless-steel mesh (the second filter). The instrument then reports the number of α decays counted each 30 min using silver-activated zinc-sulfide (ZnS(Ag)) scintillation material coupled to a photomultiplier (referred to as the “measurement head”). Output from the photomultiplier is amplified and fed into a discriminator. Total counts above a threshold of 0.5 V are recorded as LLD (lower level of discrimination), and total counts above a threshold of 1.0 V are recorded as ULD (upper level of discrimination). It has been empirically determined that ULD counts essentially represent different forms of noise, so it is the number of counts that lie within the 0.5–1.0 V pulse-height window that are used to calculate the activity concentration of radon (in Bq m⁻³). The time stamp associated with a count represents the end of the measurement period.

2.2.2 Instrument maintenance

Although ANSTO two-filter radon monitors are designed to require minimal maintenance, a degree of periodic maintenance is required to minimize ongoing operational costs and ensure consistent optimal performance, a prerequisite for effectively harmonizing measurements across a network. Most crucial to ongoing performance is the detector's measurement head, which contains the second filter and a plastic sheet impregnated with ZnS(Ag) powder. These materials should be replenished every 5 years. The second filter will slowly accumulate lead (²¹⁰Pb, half-life of 22.3 years) and cannot be cleaned. If the background becomes too high (e.g. > 8–10 counts min⁻¹), then the detection limit will deteriorate. The integrity of the ZnS(Ag) powder will also deteriorate over time (faster in very humid environments) and progressively reduce the detector's sensitivity to radon (typically a change of 0.5 %–1.5 % yr⁻¹). If the detector is in a high-vibration environment, there should be an annual check that the measurement head is still properly seated in the central pipe (following instructions in the detector's commissioning document). Likewise, if the detector is moved vigorously with the measurement head still inside, the seating of the head in the central pipe should be checked.

The next most important maintenance consideration is the detector's calibration system. If a pump is used to flush the radon source (rather than compressed gas), the stability of the delivery flow rate (0.10–0.15 L min⁻¹) should be checked every 3–6 months or radon delivery during calibrations may become inconsistent. The desiccant tube attached to the calibration system inlet should be checked and refilled every 3 months to maintain consistent humidity levels. Fluctuations in humidity within the source capsule could potentially affect the radon emanation rate. Conversely, compressed-gas calibration systems only require a replacement of the gas bottle for maintenance very 2 years.

To protect the radon detector's sampling pump and extend the life of the primary filter, it is essential to prevent dust from passing too far through the sampling line. Typically, an easily accessible and cost-effective coarse aerosol filter is installed upstream of the pump. Depending on the expected aerosol loading at each site, this pre-filter should be inspected and/or replaced every 6–12 months.

The detector should be checked for leaks annually, with the leak rate not exceeding 2 L min⁻¹. To prevent near-surface radon-rich air from entering the detection volume due to potential small leaks, it is crucial to maintain an operating overpressure of the detector's main (1500 L) delay volume between 1–2 hPa. Note that if a long exhaust line is fitted to the detector the associated flow impedance may increase the overpressure to between 2–3 hPa. The inlet line (from the base of the sampling tower to the inlet of the detector) should also be checked for leaks annually.

The internal clock of the detector's data logger should be synchronized to the networked operating computer quarterly and the logger's internal battery replaced every 5 years. All moving parts of the detector should be replaced every 10 years to avoid mechanical failure, and all electrical components (particularly power supplies) should be replaced every 10 years to prevent electrical noise from developing.

2.2.3 Instrument calibration

ANSTO two-filter detectors are too large to be moved periodically and traceably calibrated in a controlled climate chamber, and their high sampling rate (90 L min⁻¹) makes it financially and logistically impractical to attempt regular, traceable calibrations directly in situ (which would require a 90 L min⁻¹ flow of radon-free air for around 8 h, either through a filtration system or a large bank of gas cylinders). The ideal calibration approach would be to transfer a traceable calibration to the operating detector using a mobile calibration transfer device (Chambers et al., 2022; Röttger et al., 2023). While few such devices are currently available, inquiries about obtaining one can be sent to radon@ansto.gov.au. The compromise usually adopted is to conduct approximate in situ calibrations using a portable radon source while the instrument continues to sample ambient air. The procedure for a single calibration event is described below.

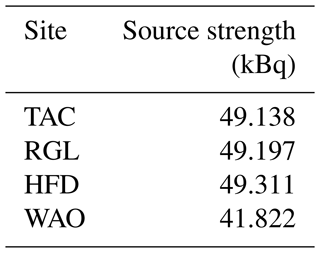
All ANSTO two-filter radon detectors in this study are calibrated using passive Pylon 2000A ²²⁶Ra sources ∼ 49 kBq (Pylon Electronics, https://pylonelectronics-radon.com/radioactive-sources/, last access: 24 March 2024; the source strength at each site is reported in Table A1). The timing of calibrations, duration of calibrations, and source flushing times are all user-defined and can slightly change from site to site.

Prior to initiating a calibration, the ²²⁶Ra source should be well-flushed, with the exhaust directed to the outside ambient air at a point well removed from the detector sampling location. The optimal flushing time for each calibration setup is assessed by the shape of the calibration curve. The curve should rise monotonically to a near-constant concentration after ∼ 5 h. If the curve rises steeply, overshoots, and then begins to decrease again, the source was not sufficiently flushed. The flushing time should be determined empirically for each installation and will depend on factors such as the source strength, the flushing flow rate, and the time since the source was last flushed. The flushing flow rate is usually lower (0.08–0.15 L min⁻¹) if the source is being flushed with ambient air (to minimize the amount of ambient ²²²Rn and ²²⁰Rn introduced to the system) but can be higher (0.15–0.25 L min⁻¹) if being flushed with dry, radon-free air (to improve the consistency of radon delivery). A flushing period between 5–10 h is usually sufficient. Once the initial flushing is complete, a calibration is then performed by continuing to pass air through the source, but this time directed into the detector's sampling airstream, for a period of 5 h while the detector continues to operate normally (see Fig. 2). After injection finishes, it can take up to 6 h for the radon concentration inside the detector to return to ambient values.

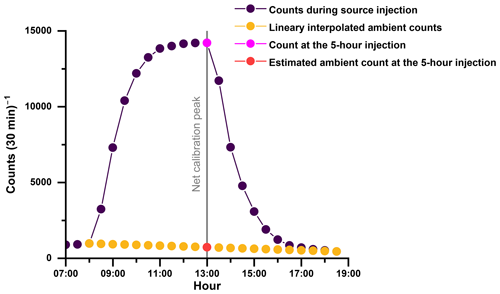
Figure 2 Example calibration peak resulting from a 5 h injection and net calibration peak magnitude derived from linearly estimated ambient radon concentration at the time of peak counts.

Once the calibration injection has been performed the calibration coefficient, c_cal (counts s⁻¹ (Bq m⁻³)⁻¹), is calculated through the following equation:

$$\begin{array}{}\text{(1)}& c_{\mathrm{cal}}={\displaystyle \frac{\left({\mathrm{LLD}}_{\mathrm{peak}}-{\mathrm{LLD}}_{\mathrm{peak},\mathrm{a}}\right)}{\mathrm{1800}}}\times {\displaystyle \frac{F_{\mathrm{ex}}}{d_{\mathrm{source}}}}\times s,\end{array}$$

where LLD_peak is the count recorded at the 5 h injection, LLD_peak,a is the estimated ambient count (at the 5 h peak counts), F_ex (m³ s⁻¹) is the sampling flow rate, d_source (Bq s⁻¹) is the radon delivery rate of the ²²⁶Ra calibration source, and s is a dimensionless scaling factor.

The scaling factor is required to account for the fact that after only 5 h of injection from the source, the radon concentration within the detector will not have completely come to equilibrium due to its logarithmic growth curve. Based on a model of the detector response (Griffiths et al., 2016) after 5 h of injection into a 1500 L radon detector sampling at 90 L min⁻¹ the concentration of radon inside the detector will have reached ∼ 99.3 % of the equilibrium value. This leads to scaling factor of 1.007 (reciprocal of ∼ 99.3) for a 1500 L detector. A Python notebook has been written which provides an analytical solution to the model equations and can be used to calculate the scaling factor (Griffiths, 2024a)​​​​​​​.

Assuming that the calibration unit is functioning reliably, the largest source of uncertainty in the field calibration process is in the estimation of LLD_peak,a. Typically, an assumption is made that ambient radon concentrations change little, and linearly, over the duration of the calibration event (10–11 h; yellow line, Fig. 2). However, the accuracy of this assumption is influenced by many factors, including timing of the calibration injection within a diurnal cycle, ambient wind speed during the calibration event, air mass fetch conditions, and day length (see Fig. 7a in Chambers et al., 2022). Consequently, at flat inland sites calibrations are best performed during windy conditions and the source injection should be timed to finish around 13:00–14:00 LST, when the boundary layer is deepest and most well-mixed. For coastal or island sites calibrations are best performed under windy conditions with oceanic fetch. Under oceanic fetch conditions the calibration injection duration can be increased to 6 h to reduce the magnitude of the required scaling factor, s. At high mountain sites calibrations are best conducted at night under katabatic flow conditions. Calibrations can be initiated remotely during suitable conditions, or they can be set on a regular schedule, and events occurring during non-ideal conditions can be excluded.

To minimize relative uncertainty introduced by the LLD_peak,a estimation process, the detectors are usually calibrated at a radon concentration that is at least an order of magnitude greater than the expected annual maximum ambient radon concentration at the site. Despite being calibrated at relatively high radon concentrations, the resulting calibrations have been proven to be quite linear down to very low radon concentrations (Röttger et al., 2023).

To this end, consistent, application-specific calibration approaches need to be agreed upon and formalized (a key goal of this study) rather than users at different sites simply applying each monthly calibration coefficient. As previously mentioned, if a calibration transfer device is available (Chambers et al., 2022; Röttger et al., 2023) then a traceable calibration can be transferred to an operating 1500 L detector in situ, over a period of around 2 weeks, without the need for approximate monthly calibrations. In this case, it would only be necessary to calibrate the detector once per year to characterize the slow change in sensitivity over the 5-year period until the measurement head is refreshed. If one portable calibration transfer device was allocated to a network of five 1500 L two-filter radon detectors, the cost would be less than buying individual calibration devices for the five large detectors.

In the absence of a calibration transfer device, the next most accurate calibration approach (as described in Chambers et al., 2022) is to develop a linear calibration model for the 5-year period between detector head replacements, since the gradual degradation of the ZnS(Ag) scintillation material is the primary cause of changing detector sensitivity. However, this calibration method can only be applied retrospectively. While the level of calibration accuracy provided by this approach is necessary for deriving consistent vertical radon gradient measurements from tall towers, an alternative calibration approach (with a slightly increased uncertainty) is necessary if the observed radon concentrations need to be used in near-real time (described in Sect. 3.2 and 3.3). Regarding gradient measurements, during the day, when mixing in the atmospheric boundary layer is strongest, radon gradients over the lowest 50 to 100 m of the atmosphere can be as low as 0.1–0.2 Bq m⁻³ (e.g. Chambers et al., 2011). The response time of two-filter radon detectors is too slow for a single detector to be multiplexed for multi-height (gradient or profile) measurements. This means that separate (independently calibrated) detectors are required to measure concentrations at each height. Since daytime radon concentrations over land in the surface layer are typically 1–3 Bq m⁻³ and the measurement uncertainty of ANSTO 1500 L detectors is $<\sim$ 10 % for radon concentration (see Grossi et al., 2020), it is usually possible to reliably determine such gradients when detectors are appropriated calibrated.

2.2.4 Instrumental background

The instrumental background, LLD_bg (counts per 30 min), of ANSTO two-filter detectors arises from various contributing factors, such as (i) cosmic radiation; (ii) natural radioactivity of surrounding rocks, soils, or building materials; (iii) accumulation of ²¹⁰Pb as well as the intrinsic background count rate of the photomultiplier caused by other effects (e.g. photons; Wright, 2017) on the detector's second filter; and (iv) self-generation of radon (by trace amounts of ²²⁶Ra in the detector building materials). The first two factors are small, site-specific, and relatively constant. ²¹⁰Pb accumulation gives rise to an increasing α count (due to subsequent ²¹⁰Po decay). Self-generation of radon inside a detector is also constant (due to the 1600-year half-life of ²²⁶Ra) and typically small, and it varies from build to build of each detector. Considered over multiple years, the detector's background count increases approximately linearly.

Ideally, the background should be determined while the detector is operating normally, sampling radon-free air at 90 L min⁻¹ for a period of at least 10–12 h. However, the necessary supply of radon-free air for regular tests of this kind is logistically and financially impractical. The compromise for field LLD_bg is to simply shut the sampling system down for a 24 h period. It is advised to conduct these checks every 2 to 3 months. Background measurements are conducted by deactivating blowers in both the external and internal flow loops, as well as closing the detector's inlet solenoid valve for 24 h. This process is divided into three stages.

1. Decay (5.5 h). This 5.5 h period marks the decay of the short-lived radon progeny on the detector's second filter below detection limits within 5–6 h of the detector shutdown.

2. Background (18.5 h). The count reading stabilizes (with a degree of uncertainty) to a constant background level.

3. Recovery (1–2 h). Upon reactivating the blowers and opening the detector's inlet solenoid valve, the instrument undergoes several 30 min measurement cycles (1–2 h) to readjust itself and return to the ambient levels.

During a background check the detector's inlet is blocked to prevent flow through the detector arising from Venturi effects across the inlet line (near the top of the sampling tower). However, the detector's exhaust valve is left open, making it possible for back diffusion of radon to occur into the detector. This is usually only a concern at sites where nocturnal radon concentrations at the detector's location are high. Closing both the inlet and exhaust valves of the detector during a background measurement is not advisable unless the detector is in a temperature-controlled environment or equipped with a pressure relief mechanism. Diurnal temperature variations could lead to pressure fluctuations within the detector, potentially causing leaks. The inlet valve is closed in preference to the exhaust valve during a background check to prevent overpressuring the detector if the powerful external flow loop blower is accidentally restarted before the exhaust valve is opened.

If the 18 h background data in step 2 above are observed to gradually decrease, rather than being approximately constant, ²²⁰Rn contamination of the second filter (in the measurement head) is likely. This is indicative of a leak (e.g. in the sampling line or the detector) or an accumulation of ²²⁴Ra-containing dust in the detector's thoron delay volume.

2.3 Greenhouse gas (GHG) instruments

At HFD, continuous, high-frequency (0.2 Hz) CO₂ and CH₄ measurements are made using a G2401 cavity ring-down spectrometer (CRDS; Picarro Inc., USA), while (0.4 Hz) N₂O measurements are made using G5310 CRDS. At TAC, (0.3 Hz) CO₂ and CH₄ measurements are made using a G2301 CRDS, while (1 Hz) N₂O measurements are made using an off-axis integrated cavity output spectrometer (OA-ICOS; Los Gatos Research Inc., USA). Sampling occurs alternately at different inlet heights along the tower, resulting in measurements from various heights not being simultaneous. For instance, at HFD air is sampled for about 20 min at 50 m a.g.l., followed by another 40 min of sampling at 100 m a.g.l. with a minute of flushing in between to avoid contributions from the previous level. To address this height switching during sampling, measurements are linearly interpolated to create a continuous hourly time series instead of straightforwardly averaging over an hour. Data are corrected for daily linear instrumental drift using standard gases (natural composition) and for instrumental non-linearity using calibration gases (natural composition). Further information on instrumentation, including flow diagrams, measurement protocol, calibration of standards, and uncertainty estimation, can be found in Stanley et al. (2018) and Stavert et al. (2019).

At WAO, 1 min measurements of CH₄ and N₂O are made using a commercial Fourier transform infrared spectrometer (FTIR) instrument (ACOEM Spectronus™): a detailed description of the FTIR can be found in Hammer et al. (2013). The instrument is routinely calibrated with gases provided by the ICOS Flask and Calibration Laboratory (FCL) and amount fractions are traceable to the WMO calibration scales (Crotwell et al., 2017; Yver-Kwok et al., 2021). The CO₂ amount fraction is measured every second and averaged to 2 min by a non-dispersive infrared (NDIR) analyser from Siemens Corp. Full details on instrumentation, measurement protocol, and calibration strategy can be found in Adcock et al. (2023).

3 Processing of atmospheric radon data: towards a standard protocol

3.1 Detector control and data collection

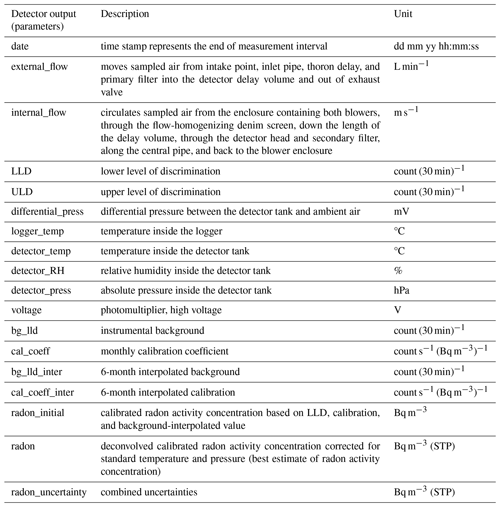
Operation of the ANSTO detectors, their data logger, and calibration units are controlled by Radon Detector Monitor (RDM) software installed on local site computers. For PC operating systems prior to Windows 10, a Visual Basic GUI version of RDM was distributed. For Windows 10 or later, as well as for Linux systems, a Python-based GUI version of RDM has been available since August 2022 (https://github.com/anstoradonlab/radon-monitor/releases/, last access: 24 March 2024). RDM is responsible for the collection, display, and storage of all raw detector output (see Fig. 3 and elaborated further in Table A2), and based on user-defined parameters, it maintains full control of scheduled calibration and background events. However, calibrations and backgrounds can also be remotely reconfigured and initiated if the computer has network connectivity.

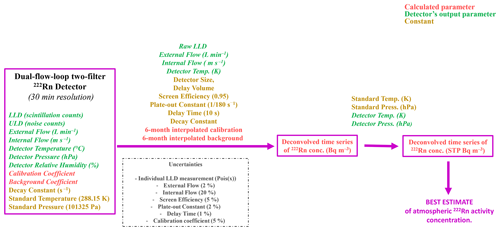
Figure 3 Workflow to calculate the best estimate of radon activity concentration: this flow illustrates the processing steps from measured “raw” detector output through calculated parameters and constants to derive the best estimate of radon activity concentration, as described in detail in Sect. 3. The parameters which influence the uncertainty derived from the deconvolution process are also highlighted (described in Sect. 3.7).

All measurement and diagnostic quantities associated with the radon detector operation are polled by the internal Campbell Scientific CR800 data logger every 10 s, then totalled or averaged every 30 min. Totalized counts include LLD, ULD, and sample flow rate (measured using a domestic gas meter that has a 2.0 L cyclic volume with individual cycles counted optically), while all other parameters are averaged (see Fig. 3).

RDM retrieves data from the logger every 30 min and saves monthly files in two formats: CSV and SQL database files. The CSV files only contain 30 min records of raw measurement and diagnostic quantities, kept small (< 140 kB per month) for ease of remote file transfer. The database files contain all 10 s and 30 min raw and diagnostic quantities, full status and operational information from the calibration system, and a complete log of system and error messages (< 2 MB per month).

3.2 Data quality control, background determination, and calibration

The first step of quality control is to check and correct any data time-stamping errors. Issues such as power supply disruptions, logger malfunctions, or communication errors can lead to missed, duplicated, or incomplete data records.

LLD counts. The internal and external flow rate, ULD, high voltage, and tank pressure are the critical factors that give an indication of whether the LLD count is going to be flagged as valid or invalid. For a given time point, if these parameters vary beyond designated site-specific limits determined to reduce their accuracy, LLD is rejected. LLD values below instrumental background were set to a radon concentration of zero.

The ratio of detector volume (e.g. 1500 L) to sampling flow rate (external flow loop; L min⁻¹) determines the time that sampled air is delayed inside the detector (during which some of the sampled ²²²Rn will decay). The delay time should be between 15–20 min, necessitating a flow rate between 75–100 L min⁻¹.

The flow rate of the internal flow loop should be sufficient to exchange all the air within the detector through the measurement head in less than 3 min (the half-life of ²¹⁸Po). Flow within central pipe of the detector is measured as a velocity (V) with an insertion probe at the centre of the 50 mm inner diameter pipe. Based on the typical velocity profile in a pipe, the actual flow rate is estimated as 80 % of the maximum flow rate (Q_max). While a flow rate of around 5.5 m s⁻¹ is technically sufficient for this purpose, a faster rate is desirable, and values of 6–12 m s⁻¹ are typically achievable (based on individual blower performance and flow impedance of the measurement head).

The main detector volume is kept at a slight positive pressure with respect to ambient (described in more detail in Sect. 2.2.2) to prevent near-surface air from entering the detector should any leaks develop. A large leak would reduce this pressure and a system blockage downstream would increase it. The micro mass flow controller used to estimate this overpressure has a millivolt (mV) output (prone to some calibration drift). An option exists to enter user-defined calibration coefficients for this sensor (ideally updated annually) to retrieve output in Pa, but raw output in the range 2200–2400 mV approximately corresponds to an overpressure of 1.0–1.2 hPa.

The sensitivity of the photomultiplier tube in the measurement head changes with the supply voltage. The operating high voltage is unique to each detector counting system and is determined when the detector is commissioned (and rechecked if any of the detector electronics are changed). Once set, this value should not be allowed to change by more than ±10 V without being manually readjusted back to the nominated value.

The counting system of two-filter detectors is sensitive to electrical, electromagnetic, and some radio frequency noise. Ideally the detectors should be operated on their own power circuit or through an uninterruptible power supply (UPS), and large electrical motors (e.g. pumps, compressors) should not be operated nearby. These forms of noise typically result in raw counts of a higher voltage than counts due to α decay. A voltage discrimination threshold of 1.0 V is set within the counting electronics to distinguish between raw α counts from radon progeny (LLD) and noise counts (ULD). Ideally, the ULD counts represent the number of LLD counts that are due to noise. When few noise counts are present (e.g. ≤ 1 counts min⁻¹; site-specific), net counts (LLD–ULD) can still be representative of the raw radon count. Notably, at TAC, ULD counts consistently ranged between 3–7 counts min⁻¹ throughout the entire measurement period. It is important to note that this noise originated from the pump of another instrument. Discarding all measurements made it impractical to implement flagging in this context. Nevertheless, ongoing efforts are being made to develop solutions aimed to mitigate the noise, alongside the ongoing evaluation of uncertainties associated with these noise counts.

As an example, Table 1 summarizes the designated acceptable limits of diagnostic quantities for the HFD 1500 L radon monitor.

Table 1 Quality check parameters for LLD flagging: critical factors (internal and external flow rate, ULD, high voltage, differential pressure) with minimum and maximum values – highlighted through HFD site-specific thresholds.

The final considerations for flagging the LLD data are background, calibration, and maintenance events or power failures. The detector is out of operation for the entire 24 h background check, as well as up to 2 h after the detector restarts. The detector is also out of operation for the 5 h source injection period of a calibration, as well as the 6 h period required to flush the enhanced radon out of the detector. During maintenance periods there are higher risks of ²²⁰Rn contamination (if the detector has been opened) or diagnostic parameters being out of range. After power failures it can take the detector 1–2 h to return to normal monitoring conditions. All such periods should be flagged out of the final raw dataset prior to further processing.

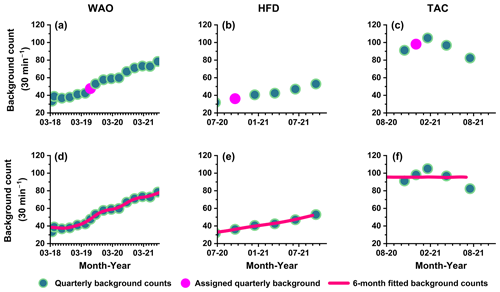
Figure 4 Instrumental background events for three sites: (a) WAO, (b) HFD, and (c) TAC, covering the period from the initiation of measurements until August 2021. Assigned background events are highlighted (see Sect. 3.3 for details of assigned values). Corresponding 6-month fitted instrumental background rates are shown for (d) WAO, (e) HFD, and (f) TAC (see Sect. 3.3 for details of fitting).

Instrumental background event. Once background checks had been initiated as outlined in Sect. 2.2.4 and other diagnostic parameters (high voltage and noise; Table 1) were verified to be within acceptable ranges, each background (Fig. 4a–c) was processed as follows: the initial 6 h of the 24 h period were removed, the last 30 min sample was excluded if the blowers restarted early (due to the small time differences that can happen between the PC clock and the logger clock if they are not regularly synchronized), and a check was made that the remaining data were approximately constant and free of noise counts. The median of these values was then taken to be the background reading.

During the measurement period presented here, an important observation is that each of the three sites depicted in Fig. 4a–c experienced an instance where a background event was not recorded. In each case this missing background event was labelled “assigned background”, for which the method of determination is explained in Sect. 3.3. Typically, instrumental background checks are automated and scheduled quarterly. However, a deviation from this established routine sometimes occurred due to a software crash, leading to a significant gap in the background check process.

Calibration event. The calibration plan for all radon detectors in this study was for monthly calibrations (scheduled in RDM to occur on the same day of each month) such that the calibration peak (LLD_peak) occurred between 13:00–14:00 LST to coincide with a deep, well-mixed boundary layer. Consequently, any calibration events for which LLD_peak did not occur within this time window were rejected. All sites in this study also had regular exposure to “baseline” atmospheric conditions (medium- to long-term oceanic fetch conditions, with low variability in radon concentrations). Consequently, a site-specific threshold value was set for the ambient radon count representing the upper limit of baseline variability (50 counts min⁻¹), and any calibration event for which the estimated LLD_peak,a exceeded this value was flagged.

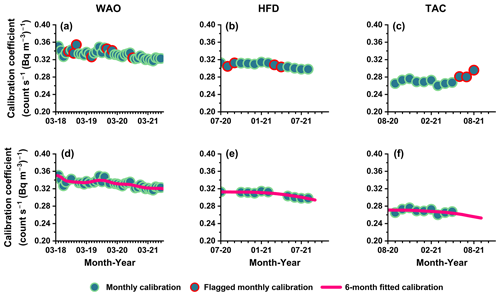
Figure 5 Monthly calibration coefficients for three sites: (a) WAO, (b) HFD, and (c) TAC, covering the period from the initiation of measurements until August 2021. Flagged calibration events are highlighted (see Sect. 3.2 for exclusion criteria). Corresponding 6-month fitted calibration coefficients are shown for (d) WAO, (e) HFD, and (f) TAC (see Sect. 3.3 for details of fitting).

Derived monthly calibration factors for all three sites (WAO, HFD, TAC) are presented in Fig. 5a–c, covering the period from the initiation of measurements until August 2021. At HFD (Fig. 5b), the first 6 months were flagged due to sampling flow problems caused by a partial blockage of the inlet line. Other causes of flagged calibration events in Fig. 5a–c were attributed to the threshold exceedance of LLD_peak,a, calibrations occurring at night due to software crashes, and insufficient flushing of the source. For example, the last three calibration events at TAC (Fig. 5c, June, July and August 2021) were all too high due to a poorly flushed source. The source flushing time at all sites was originally set to 5 h (typical for 20 kBq ²²⁶Ra sources). However, all sources in this study had activities > 30 kBq ²²⁶Ra (see Table A1) and it was determined that effective flushing of the source capsules required flushing periods lasting 8–12 h at 0.15 L min⁻¹. Older-style calibration systems were used in this study (using pumps and needle-valve flow control, not compressed gas and a mass flow controller), so it was important to regularly check and correct the source's flushing.

3.3 Data continuity: fitting instrument calibration and background

Under normal detector operation, there is no physical basis for short-term deviations from a slow, long-term linear decrease in detector sensitivity (this is controlled by gradual deterioration of consumable materials inside the measurement head). Therefore, such events evident in Fig. 5d–f are more likely a result of uncertainty in the calibration process than real changes in detector performance. This is why the linear model for calibrations described in Chambers et al. (2022), applied retrospectively, is more accurate. When applying fitting algorithms, as described in the following section, to enable continuous near-real-time access to calibrated radon concentrations, it should be understood that additional uncertainty is introduced. To ensure a continuous time series and to avoid unnecessary step changes, the Savitzky–Golay fitting method is used on successive subsets of calibration coefficients and instrumental background counts. This method involves the following steps.

1. Fitting window size. Calibration and background values are selected within a specific range. This range as a 184 d moving window centred on each of the time stamps.

2. Fitting. Within the defined window, a curve is fitted through the selected values using a first-order polynomial linear fit based on the data points available in the defined window.

3. Smoothing window size. The result of the moving fit requires further smoothing. The centre moving average is used as the 184 d moving window centred on each of the time stamps.

4. Smoothing. The centre moving average is performed on the results of Step 2. This is to smooth out the effect of multiple adjacent data points sharing the same measurements for the fitting, which may result in step changes.

5. Handling edge data. To ensure a smooth transition at the beginning of the dataset, the data points prior to the first calibration and/or background measurement will be assigned the fitted value from that measurement. Similarly, for the end of the dataset, the fitted value from the last calibration and/or background measurement will be used to fill in the remaining data points.

For the purpose of reproducibility, the implemented code is provided in the Supplement.

In the rolling fit process, it is crucial to compare the current fitting with the preceding one, particularly in periods of overlap. In this regard, two types of data ranges are recommended: (i) the data range for selecting raw data and performing the fit and (ii) the data range where the fitted data will actually be utilized. Additionally, the effectiveness of the Savitzky–Golay fitting method can be affected by gaps within the defined window. This issue is evident across the three sites, with distinct gaps in background counts observed (see Fig. 4). To address this, the concept of “assigned” values is introduced. First, data gaps larger than either the defined half-window size for fitting or a predetermined maximum gap are identified. The number of points to be inserted into these gaps is then determined using the ceiling function:

$$\begin{array}{}\text{(2)}& n=⌈{\displaystyle \frac{t_{\mathrm{1}}-t_{\mathrm{0}}}{{\mathrm{gap}}_{max}}}⌉,\end{array}$$

where t₁ and t₀ are the time coordinates at either end of the gap. The resulting data points to be input are inserted evenly within the gap, with spacing adjusted to the nearest 30 min. The gap is then linearly interpolated between the closest available data points to construct this number of new data points, evenly spaced across the gap to the nearest 30 min. For HFD, gap_max is set to 93 d.

Figures 4d–f and 5d–f display fitted instrumental background (f_bg) and the fitted calibration coefficient (f_cal) for three sites: WAO, HFD, and TAC. The fitted coefficients reveal a site-dependent annual reduction in detector sensitivity, varying from 3.2 % to 4.7 %. These reduction percentages are calculated based on the fitted calibration coefficients and represent the decline relative to the preceding year. At WAO, situated along the coast with the lowest source strength (see Table A1) and a sampling inlet, the calibration coefficient experienced a 3.2 % yr⁻¹ decrease. Similarly, TAC, with the highest sampling inlet, also witnessed sensitivity reductions of 3.3 % yr⁻¹, although it recorded the highest background rates among the three sites. The main reason for increased background is the ULD noise, but other factors may also contribute such as ²²⁰Rn contamination at this site and ingrowth of radon from ²²⁶Ra inside the detector. In contrast, the HFD detector exhibited a notably faster sensitivity decrease of 4.7 %, accompanied by the lowest background counts. The acceleration of reduction in sensitivity and increase in background rate will vary for each instrument, as every batch of materials used for making components has distinct levels of trace contamination of ²²⁶Ra and different consumable materials within the detector head, specifically the ZnS(Ag) scintillation material. However, it is also worth noting that the fitting procedure can make the annual rate of decline appear larger compared to a linear model of calibration sensitivity change. This effect is sometimes more pronounced in certain cases, such as in Fig. 5d, where edge effects come into play.

3.4 Instrument response time correction

The operational principle of the two-filter detector, briefly discussed in Sect. 2.2.1, inherently causes a delay in reporting the true LLD signal. Approximately 40 % of the signal is observed 1 h after the radon pulse is delivered (Griffiths et al., 2016). This delay necessitates time response correction, particularly when employing sub-diurnal radon measurements for quantitative analysis or comparison with fast-response instruments like GHG detectors. Griffiths et al. (2016) explored methods to correct for the detector's slow response, highlighting the effectiveness of a Bayesian approach using a Markov chain Monte Carlo sampler – a methodology employed here for deconvoluting the radon time series. The aim of deconvolution is to estimate the true signal within the temporal context while preserving the radon concentration levels. The deconvolution is performed on the LLD counts, where all flagged LLD counts are removed prior to this step. Along with LLD counts, the fitted calibration coefficient, and instrumental background, the deconvolution routine also requires several output parameters: both external and internal flow rates, the detector's temperature, and the physical detector's parameters, including its size and the thoron delay volume. The fitted instrumental background values are subtracted from the deconvolved LLD counts (LLD_dec). Following this subtraction, the LLD_dec values are then processed to calculate the activity concentration (Bq m⁻³) of ²²²Rn, and the equation is as follows.

$$\begin{array}{}\text{(3)}& {}^{\mathrm{222}}\mathrm{Rn}={\displaystyle \frac{\left({\mathrm{LLD}}_{\mathrm{dec}}-f_{\mathrm{bg}}\right)}{\mathrm{1800}\times f_{\mathrm{cal}}}}\end{array}$$

For a given time stamp in the time series, the mean of the deconvolution result at that time stamp is reported as the radon concentration of that particular time stamp.

3.5 Standard reference temperature and pressure correction

The last step of data processing involves normalizing the deconvolved concentration of radon to standard reference temperature (T_stp) and pressure (p_stp) conditions (Bq m⁻³ STP). For our case, we adapted the International Standard Atmosphere (288.15 K and 101 325 Pa). This standard was selected mainly due to its representative average, as 15 °C approximates the average annual ambient temperature of the Earth's surface in temperate regions and makes it easier to compare across different regions and times of the year. This normalization is achieved through a correction term as follows:

$$\begin{array}{}\text{(4)}& {}^{\mathrm{222}}\mathrm{Rn}={\displaystyle \frac{\left({\mathrm{LLD}}_{\mathrm{dec}}-f_{\mathrm{bg}}\right)}{\mathrm{1800}\times f_{\mathrm{cal}}}}\times \left({\displaystyle \frac{T_{\mathrm{inst}}}{p_{\mathrm{inst}}}}\times {\displaystyle \frac{p_{\mathrm{stp}}}{T_{\mathrm{stp}}}}\right),\end{array}$$

where (T_inst) and (p_inst) are temperature and pressure inside the detector's main delay volume.

This correction removes sensitivity to measurement height, facilitating comparison with modelled activity concentrations, and ensures that observed trends in radon concentration are solely due to environmental variations in mixing ratio brought about by changing air mass fetch and transport times.

Regarding the harmonization of radon observations across European and global networks, it should be noted that some atmospheric radon monitors operating within ICOS and other networks (e.g. the HRM; Levin et al., 2002) automatically implement an STP correction that assumes different pressure and temperature reference values (T_stp=273.15 K, p_stp=100 000 Pa). Other monitors (e.g. the ARMON; Grossi et al., 2012) do not measure pressure and temperature directly within the instrument delay volume and can therefore only make approximate STP corrections.

3.6 Atmospheric water vapour corrections

Water is a volatile component of the atmosphere. As such, water vapour can vary rapidly in space and time. Through the dilution effect, these changes can influence observed concentrations of other atmospheric constituents. Some radon monitors in European networks (e.g. the ARMON) dry sampled air prior to analysis. Furthermore, modelled radon values are usually reported as dry-air mole fractions. For harmonization and intercomparison purposes, radon monitors should provide the ability to correct for water vapour effects.

ANSTO radon detectors measure the pressure, temperature, and relative humidity (RH) of air in the main delay volume, directly adjacent to the detector measurement head, providing a pathway for water vapour correction if required. However, the process of accurately converting RH into water vapour pressure involves navigating several challenges, including temperature dependencies, measurement accuracy, environmental variability, and assumptions in calculation equations. One commonly used method for this conversion is the Clausius–Clapeyron equations, refined with the Magnus approximation, with constants from Alduchov and Eskridge (1996). The equations are based on certain assumptions and empirical data, which might not reflect all environmental conditions, therefore introducing systematic errors. Another critical aspect to consider is that calibration of the radon detector is not based on dry air (the ambient air is used to flush the source), complicating the direct comparisons.

Table 2 Comparison of dry and wet air across UK extreme climate conditions: evaluating the need for water vapour correction.

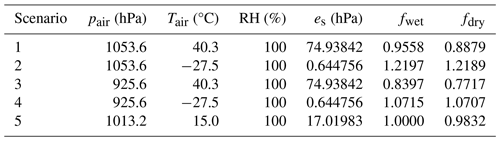
Note that the wet-air correction factor (f_wet) is calculated with the formula $f_{\mathrm{wet}}=\frac{T_{\mathrm{stp}}}{p_{\mathrm{stp}}}\times \frac{p_{\mathrm{air}}}{T_{\mathrm{air}}+\mathrm{273.15}}$. Similarly, the dry-air correction factor (f_dry) employs the formula $f_{\mathrm{dry}}=\frac{T_{\mathrm{stp}}}{p_{\mathrm{stp}}}\times \frac{p_{\mathrm{air}}-e_{\mathrm{s},\mathrm{RH}=\mathrm{100}}}{T_{\mathrm{air}}+\mathrm{273.15}}$.

To assess the necessity of correcting water vapour, a simple calculation was carried out to compare the difference between dry (f_dry) and wet (f_wet) air across a spectrum of UK extreme climate conditions, as indicated in Table 2. The maximum observed discrepancy of 7.1 % indicated the difference in water vapour concentration between dry and wet air in scenarios of the highest temperature and pressure. The discrepancy was minimal (0 %–2 %) for air temperature spanning 0 to 30 °C. Considering the minimal impact of correcting the water vapour and potential for such correction to introduce noise or errors through another layer of data analysis, especially after the deconvolution process, this correction was omitted. However, detector temperature and RH are reported along with radon concentration so that data users can make this correction themselves if necessary.

3.7 Combined measurement uncertainty

The uncertainty associated with the reported radon concentration is derived from the posterior distribution resulting from the deconvolution process. This uncertainty is influenced by the following.

• Gross α counting. Governed by a Poisson distribution, this uncertainty reflects the statistical variability inherent in counting process.

• Flow rate variability. The external flow rate introduces an uncertainty of 2 %. Variations in the external flow rate, especially rapid changes, can significantly affect the response time of the detector. Griffiths et al. (2016) demonstrated that the deconvolution tends to over-correct the time series if the external flow rate is halved. The internal flow rate contributes a substantial uncertainty of 20 %. Optimizing the internal flow rate is critical for a few reasons: (i) to account for the rapid decay of radon's first α-emitting progeny (²¹⁸Po, half-life of 3.1 min) and (ii) to minimize the time for plate-out of unattached radon progeny on the internal surfaces of the detector. To further reduce opportunities for the plate-out of radon progeny inside the detector, a flow homogenization screen is implemented to reduce strong turbulent mixing inside the detector's main delay volume. This screen ensures a more laminar (plug-like) flow towards the measurement head.

• Plate-out effect. An absolute uncertainty of 2 % is given to the plate-out effect.

• Screening efficiency. A 5 % absolute uncertainty is associated with the screening efficiency in homogenizing airflow and reducing turbulence.

• Delay time. The delay time represents the lag in the system, with an absolute uncertainty of 1 %, and can arise from various sources such as extended inlet lines and synchronization of the data logger. While this delay time does not significantly impact the deconvolution routine, it will become critical when aligning the detector's response time with a large, brief spike of counts.

• Field calibration coefficient. The calibration coefficient, with an overall uncertainty of 5 %, incorporates several aspects: the ²²⁶Ra source accuracy with an absolute uncertainty of 4 % and an additional 1 % uncertainty arising from variation in the radon production rate, scaling factor, and decay constant.

In addition to the abovementioned uncertainties, there are other significant uncertainties that, although not currently addressed, should be considered in future analyses. These include uncertainties related to STP corrections, which typically stem from the accuracy, calibration, and response time of temperature and pressure sensors. A critical area to address is the uncertainty associated with field calibration of 1500 L detectors, which involves interpolating ambient counts (see Sect. 2.2.3), although this problem can be eliminated by employing a portable calibration transfer standard detector (Chambers et al., 2022; Röttger et al., 2023). Another improvement in the uncertainty quantification includes instrumental background and calibration events themselves, alongside the “assigned” values (see Sect. 3.3), with the latter having higher uncertainties.

For reporting, half of the difference between the 16th and 84th percentile of the deconvolution result for a particular time stamp is taken as the uncertainty of the radon concentration.

4 Assessing the accuracy of the best radon activity concentration estimate

Two approaches are used to evaluate the accuracy of the deconvolved radon concentration. The first approach, under “controlled conditions”, employs calibration events to validate both the absolute achieved concentration and the temporal alignment between estimated and measured radon values. The second approach, based on “real-world conditions”, directly compares estimated radon concentrations with the GHG amount fractions obtained from fast-response detectors.

4.1 Validating radon activity concentration estimates under controlled conditions

Figure 6a–b depict calibration events in July 2021 from two locations: HFD and WAO. In each case, radon concentrations (²²²Rn_ini) were measured following a direct 5 h injection from a ²²⁶Ra source, and then the deconvolution algorithm was applied (²²²Rn).

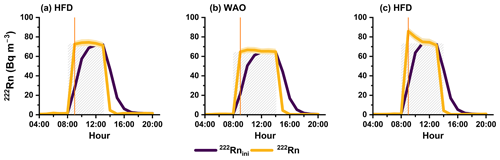
Figure 6 Comparison of initial and best radon concentration estimates (with the 16th–84th percentile range shaded) during a calibration event with a constant-delivery radon concentration in July 2021 at (a) HFD and (b) WAO, alongside a calibration event with non-constant radon delivery in August 2021 at (c) HFD. The orange line shows that the signal reached only 85 % of its target by 09:00 LST. The shaded area represents the ideal square wave.

Specifically in the case of these events, when the deconvolution algorithm was applied some adjustments were necessary to enhance the algorithm's efficiency. Firstly, because the calibration stream of radon was injected directly into the detector (not at the sampling inlet point), the thoron delay volume value was set to zero. Secondly, since environmental atmospheric radon concentrations do not usually exhibit abrupt changes of the magnitude seen during calibration events, the smoothness constraints of the deconvolution routine were adjusted to accurately track the sudden change in radon concentration as the calibration source is turned on and off.

The purpose of the deconvolution algorithm is to correct the delay between the sampled radon concentration and the detected signal, and here we demonstrate that the implementation of the deconvolution algorithm is successful at the HFD and WAO sites. In the case of a defined calibration injection period from a well-flushed source, the target result is essentially a square wave (bearing in mind that the detector reports concentrations at the end of each measurement period and continues to sample ambient air throughout the injection period). As shown in Fig. 6a–b, despite the source injection being initiated at 08:00 LST at both sites, the signal from both detectors (purple line) had only reached around 85 % of its target value by 09:00 LST. Similarly, after injection stops (13:00 LST at HFD, 14:00 LST at WAO), the signal from each detector takes around 3 h to return to near ambient. By comparison, the deconvolved signal (yellow line) exhibits a full increase in concentration within the first hour (the temporal resolution of these measurements) and shows an almost complete return to ambient concentrations in the hour after injection stops. The observed behaviour of the response-time-corrected data demonstrates the effectiveness of the deconvolution process in recreating sudden, unrealistically large changes in radon concentration, lending credence to the claimed accuracy, precision, and reliability under real-world scenarios.

As evident in Fig. 6a–b, when the deconvolved radon signal from a calibration injection depicts a near-ideal square wave, it usually takes the uncorrected detector output 3 to 5 h to reach a similar activity concentration (based on overlapping uncertainty bounds). Often, something that is more clearly evident in the deconvolved output for calibration injection events are times when the source capsule has not been adequately flushed prior to the start of an injection (see Fig. 6c). In these cases, a clear “overshoot” of radon concentration is observed, followed by a gradual return to the target concentration over the 5 h injection period as the excess radon is flushed from the detector's main delay volume. These tests of the deconvolution routine on extreme changes under controlled conditions provide confidence in the fidelity of the technique under real-world conditions.

4.2 Validation of the best estimated radon activity concentration under real-world conditions

Changes in air mass fetch, transitioning from terrestrial to oceanic or vice versa, lead to significant variations in atmospheric trace gas constituents. When associated with strong frontal systems, such changes can occur over short timescales – comparable to the 3–5 h it takes a two-filter radon detector to fully respond to a sustained calibration injection.

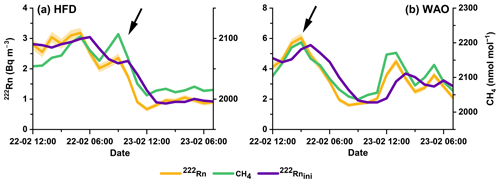
Figure 7 Response of CH₄ and radon (initial and best estimate) to rapid air mass changes in winter: (a) HFD and (b) WAO.

In Fig. 7, we illustrate the response of CH₄ as measured by a fast-response analyser (0.4 Hz) to a rapid change in air mass fetch during the winter period (22–23 February 2021) at HFD and WAO. Additionally, Fig. 7 presents the corresponding radon measurements, both with and without response time correction via deconvolution.

Initially, on 22 February, a period of pollution is evident, characterized by elevated radon concentrations and CH₄ amount fractions, attributed to continental influences. However, a rapid transition to baseline conditions for both gases occurs as air masses shift towards cleaner oceanic origins on 23 February. This transition is corroborated by air history maps generated using the Met Office NAME Lagrangian atmospheric dispersion model for each site (not shown here).

Analysing the reference CH₄ time series reveals the elimination of the time lag between CH₄ amount fraction and deconvolved radon compared to the initial measurements. Moreover, at both sites, the duration of CH₄ transition from polluted peak to baseline conditions aligns with deconvolved radon measurements.

Accurately representing radon concentrations holds significant importance, particularly when radon is used as a quantitative tracer for improving and validating ATMs as well as estimating local to regional GHG fluxes via RTM (Biraud et al., 2000; Levin et al., 2021).

Trace gases can mix through the depth of the planetary boundary layer (PBL) on timescales of around 1 h (Stull, 1988). Consequently, before attempting to employ radon to improve understanding of the dilution of atmospheric constituents with surface sources it is crucial that instrument response time is accounted for (see Fig. 10 in Griffiths et al., 2016). Here we further demonstrate the effectiveness of the deconvolution technique under real-world conditions by analysing diurnal composites of radon, CH₄, CO₂, and N₂O. The diurnal cycle of trace gases with surface sources is characterized by a morning maximum, when the mixing depth is shallowest, and an afternoon minimum, when convective mixing is deepest. After sunrise, when the nocturnal inversion breaks down and the daytime inversion begins to grow, concentrations are rapidly reduced from their morning maximum to their afternoon minimum values. In the absence of short-term sinks (e.g. photosynthesis) or temporal changes in source function, all gases should be impacted equally by this dilution.

Focusing primarily on the warmer season – summer – is crucial for our analysis because of gases' pronounced diurnal variation in PBL height. This variation offers an ideal testing ground to evaluate the effectiveness of the radon deconvolution tool.

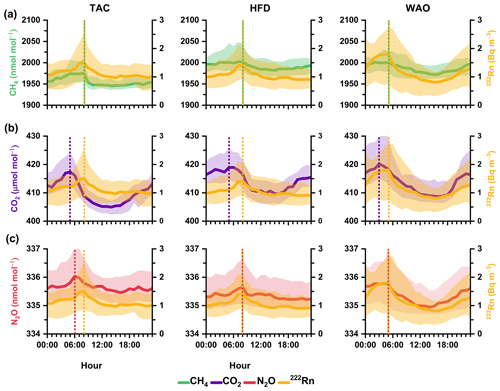
Figure 8 Summer diurnal composites of the best estimates of radon activity concentration and GHG amount fractions at TAC, HFD, and WAO for (a) radon and CH₄, (b) radon and CO₂, and (c) radon and N₂O. Composites are based on hourly median values spanning June to August. Shaded areas indicate the 25th to 75th percentile to visualize variability of gases.

Hourly median summer diurnal composites of the best estimates of radon (deconvolved and STP corrected) and GHGs at TAC, HFD, and WAO are presented in Fig. 8. At each of these sites, radon and the GHGs were sampled from the same (uppermost) inlet height. However, there was an exception at TAC, where radon was sampled at 175 m a.g.l., while GHGs were sampled slightly higher at 185 m a.g.l.

During summer nights, the sampling inlets at TAC (175 and 185 m a.g.l.) and HFD (100 m a.g.l.) are typically positioned above the inversion layer. However, the results presented here are based on seasonal median values, which exclude the most extreme and strongly stable nighttime conditions. As a result, for the plots shown (see Fig. 8a–b), the inlet heights are effectively situated just at the top of the inversion layer.

The rate of increase in nocturnal median levels of trace gases at these sites is small, and a noticeable increase begins around 05:00 LST (coinciding with sunrise) and peaks at 08:00 LST. Figure 8a (TAC and HFD) indicates synchronous 08:00 LST peaks in radon and CH₄ at both towers. This behaviour is consistent with the destruction of the inversion layer at some time after 05:00 LST, allowing these gases that had accumulated near the surface to mix upwards slowly, past the sampling inlets (typically at or before 08:00 LST). By contrast, WAO measurements are consistently made well within the nocturnal inversion (10 m a.g.l.), and a distinct pattern of decreasing CH₄ and radon levels is observed after sunrise (WAO: Fig. 8a).

The observation of simultaneous peaks in CH₄ and deconvolved radon across all three sites with contrasting sampling heights is a clear validation of the deconvolution technique, highlighting its ability to accurately represent the significant impact of diurnal atmospheric processes on radon concentrations.

The difference in radon concentration peaks compared to CO₂ amount fractions at all sites, however, highlights the unique response of these gases to both physical and biological processes (Fig. 8b–c). The morning peak of CO₂ is observed to occur 3 h earlier than the radon peak at both TAC and HFD sites. This difference can be attributed to the onset of photosynthetic activity. CO₂, being continuously released by soil respiration, is more quickly affected by surface air movements and sunlight-triggered processes like photosynthesis. As a result, CO₂ is rapidly absorbed by vegetation, resulting in a notable reduction in atmospheric CO₂ levels. In contrast, radon, CH₄, and N₂O are less affected by these immediate factors and thus take longer to mix upward from accumulation near the surface at a slower rate.

It is commonly assumed that mixing within the nocturnal boundary layer is uniform; however, this is not the case. A concentration gradient exists from just below the inversion layer to the surface. This gradient is illustrated in Fig. 9, which shows CO₂ measurements at both the lowest sampling point at HFD (50 m a.g.l.) and the highest sampling point (100 m a.g.l.). The breakdown of the inversion layer around 05:00 LST facilitates vertical mixing of accumulated CO₂ at 50 m a.g.l., a process clearly depicted in Fig. 9, which also affects the readings from the 100 m inlet.

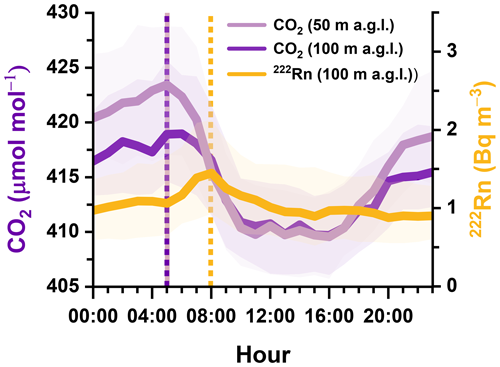
Figure 9 Diurnal composites of the best estimates of radon activity concentration and CO₂ amount fractions measured at 50 and 100 m a.g.l. at HFD during summer. Composites are based on hourly median values. Shaded areas indicate the 25th to 75th percentile to visualize variability of gases.

At TAC, the morning peak of N₂O is observed at 06:00 LST, 2 h earlier than the radon peak at 08:00 LST (see Fig. 8c). This earlier peak can be attributed to soil microbial activity, particularly during nitrification and denitrification processes that are triggered by rising temperatures and increasing sunlight. In contrast, at the HFD and WAO sites, where the inlet is positioned 85 and 175 m lower than at TAC, N₂O and radon peaks occur simultaneously. This difference in inlet height significantly affects the mixing dynamics at these locations.

At the WAO coastal site, the difference in median peak times between radon and CO₂ is likely driven by their distinct source and sink functions (Fig. 8b), as well as land–sea breezes. Radon exhibits a relatively constant source and sink function compared to CO₂. Consequently, the radon concentration observed at 10 m a.g.l. is primarily influenced by atmospheric dynamics, particularly the formation and breakdown of the nocturnal inversion, with the peak typically occurring just before the inversion breaks down. Conversely, CO₂ experiences influences from both dynamics and a temporally variable source and sink function. At WAO, CO₂ peaks earlier than radon because photosynthesis begins immediately when the sun rises, drawing CO₂ out of the nocturnal inversion before convective mixing begins, which typically takes an hour or two to initiate due to the warming up process. However, the shaded areas representing the 25th to 75th percentile range for CO₂ variability suggest that this peak frequently coincides with the radon peak.

5 Recommendations

5.1 Instrument maintenance

As detailed in Sect. 2.2.2 some periodic maintenance of the ANSTO two-filter radon detectors is required. Note that some of this information is also included in the commissioning report for the ANSTO instrument.

Weekly.

• Visually check that data are updating half-hourly to ensure continuous logging. This can be done remotely.

Monthly.

• Synchronize the data logger and PC clocks.

• Verify that scheduled events such as calibrations and backgrounds have occurred. This can also be done remotely.

Quarterly.

• If not using a compressed-air calibration system, inspect and shake the calibration unit's desiccant tube. Confirm that the injection flow rate is within the range of 0.10–0.15 L min⁻¹.

Yearly.

• Check the detector and inlet system for leaks, with half-yearly checks recommended for detectors located outside.

• Inspect the plumbing of the calibration system.

• Check or replace the coarse aerosol filter on the inlet line.

2-yearly.

• If using a compressed-air calibration system, replace the gas bottle.

5-yearly.

• Refresh the materials inside the detector head (stainless-steel mesh filter and ZnS(Ag) sheet). If components of the aluminium frame of the head have started to corrode, the head casing should also be replaced. ANSTO can provide this service or instructions for replacement (contact: radon@ansto.gov.au).

10-yearly.

• Replace all moving and electrical parts, including power supplies. ANSTO can assist with this service or provide instructions.

5.2 Instrument calibration and background

By default, the user specifies a schedule for instrument calibration and background checks. From a meteorological perspective, the calibration events will occur randomly. Each year, some calibrations will occur under conditions that closely satisfy the assumptions of the calibration process. Only these events should be retained.

Alternatively, background events can still be scheduled on an automatic regular basis, but the calibrations can be remotely triggered every 1–2 months, according to forecast meteorological conditions better meeting the assumptions of the calibration process. Automatic background checks will not account for any self-generation of radon inside the detector by trace amounts of ²²⁶Ra. To ensure continuity in the case of software crashes or other issues, it is recommended to schedule background events to run automatically on a 2-monthly basis.

To achieve the lowest possible calibration uncertainty, a mobile calibration transfer standard device can be moved to the site once per year to run in parallel with the 1500 L radon detector for around 2 weeks to transfer a traceable calibration and instrumental background. The transferred background will account for self-generation of radon inside the detector by trace amounts of ²²⁶Ra. Information about the availability of these transfer standard instruments can be obtained by contacting radon@ansto.gov.au.

5.3 Software

For Windows 10 operating systems and higher the Visual Basic version of the RDM control software has been increasingly unstable. For these systems, or to operate the software from a Unix/Linux platform, we recommend moving to the Python-based version of RDM (Griffiths, 2024b). Additional features of the Python-based control software include access to raw 10 s output of all detector parameters (as well as the 30 min averages), access to a log of all system messages and error messages, and access to a comprehensive log of all operational parameters of the calibration unit (if using a compressed-air Bürkert calibration system).

Graphical radon data processing software to perform all procedures described in Sect. 3.2 on the 30 min instrument output apart from the deconvolution process was developed (available upon request). The software was currently developed and tested under Windows 10 or higher platforms.

5.4 Quality health workflow

A three-stage data quality control regime is recommended.

• Monthly. New data files should be checked for time-stamping errors (missing, partial, or duplicate records) and data flagged if key diagnostic parameters are out of range (Table 1).

• Quarterly. Monthly calibrations and quarterly background checks should be processed and reviewed, and if feasible fitting should be conducted.

• 6-month (final data product). The 6-month fitted calibration coefficient and instrumental background are reviewed, along with the executing of deconvolution code and STP correction, to derive the best estimate of radon concentration together with associated uncertainties. At this stage, it is recommended that a simultaneous review of data from multiple sites be conducted. This approach enables comprehensive analysis and comparison, facilitating the identification of any anomalies or inconsistencies that may require further investigation.

5.5 Data levels for dissemination

Data obtained from ANSTO two-filter radon detectors can be disseminated across various temporal scales, including near-real-time (level 1) and 6-month (level 1) or long-term intervals. Each temporal scale is associated with different relative uncertainties, which should be clearly documented in the metadata. To process raw counts into radon concentrations, aside from response time correction, it is necessary to remove background counts and apply calibration. Both the background count and the calibration coefficient can be modelled, with the accuracy and complexity of these models varying based on the available data.

When a detector is first commissioned, initial estimates of the calibration coefficient and instrumental background count are determined. These values serve as constants for deriving near-real-time radon concentrations during the first 6 months of operation. Subsequently, the calibration and background history is reviewed, and fitted values for the next 6 months are derived. To update the calibration coefficient and instrumental background for the subsequent month (e.g. month 7), the last value from the fitting is utilized. It is noteworthy that the commissioning background check may involve thoron contamination and may need to be disregarded. For near-real-time measurements, deconvolution can be run routinely, with the code taking about 1 min to process 1 d of data. Deconvolution is then re-run in post-processing after the finalization of the calibration coefficients and background count rate time series.

The availability of level 1 data on a 6-monthly basis is highly desirable for modellers, particularly for evaluating operational data model integration, in this case employing radon to assess the accuracy of ATMs. Implementing a routine and operational radon approach facilitates the ongoing assessment of the accuracy of these transport models, thereby enhancing the accuracy of GHG emission estimates.

After 1 full year of measurements are available, the consistency and seasonality of calibration factors can be assessed and a representative average value calculated for the year. The available background checks can be assessed for consistency and a linear model applied. This year of data should be processed with this information and archived, and this calibration factor and background model should then be used to generate the “near-real-time” data for the subsequent year of measurements. This process is complete after 5 years when the detector's measurement head is replaced, and the process starts again.

Data from the UK radon network are stored at the Centre for Environmental Data Analysis (CEDA), while data from the ICOS network may be made accessible through the ICOS portal; additionally, GAW/WMO radon data can be archived and made available at the World Data Centre for Greenhouse Gases (WDCGG).

6 Conclusions

In this study, we have developed a comprehensive protocol to enhance the reliability of reported radon activity concentrations for near-real-time applications, enabling their direct comparison to GHG measurements within a monitoring network of three independently managed observatories in the UK.

Our protocol emphasizes the importance of achieving radon measurements with accuracy and resolution comparable to GHGs, necessitating specific procedures for quality control, calibration, deconvolution, and uncertainty assignment. Validation of this protocol through meticulous analysis of calibration events and comparison with GHG measurements establishes a foundation for standardizing protocols across networks (ICOS and GAW) using two-filter instruments to measure radon.

The critical role of deconvolution in preserving the true signal of radon, particularly for quantitative tracer applications in atmospheric studies, is underscored. Our analysis demonstrates the adaptability of the deconvolution technique across seasonal variations and distinct atmospheric dynamics, ensuring accuracy in tracking GHG trends across all sites and validating ATM outputs. Synchronization of radon peaks with GHGs, especially during summer diurnal variations, further validates the effectiveness of our deconvolution method in real-world conditions, highlighting radon's importance as a tracer in understanding atmospheric mixing.

This study offers a robust protocol for radon measurement within GHG monitoring networks and underscores the invaluable role of radon as an independent metric in ATMs. By ensuring the accuracy and comparability of radon measurements, it may contribute to refining GHG emissions estimates and improving understanding of atmospheric processes, and it could be a significant contribution to climate change mitigation and the achievement of the Paris Agreement.

Appendix A

Table A1 Site-specific radon source strength (Pylon 2000A ²²⁶Ra).

Table A2 Summary of dual-flow-loop two-filter radon detector outputs, description, and units.