the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Benchmarking data-driven inversion methods for the estimation of local CO2 emissions from synthetic satellite images of XCO2 and NO2
Diego Santaren
Janne Hakkarainen
Gerrit Kuhlmann
Erik Koene
Frédéric Chevallier
Iolanda Ialongo
Hannakaisa Lindqvist
Janne Nurmela
Johanna Tamminen
Laia Amorós
Dominik Brunner
Grégoire Broquet
The largest anthropogenic emissions of carbon dioxide (CO2) come from local sources, such as cities and power plants. The upcoming Copernicus CO2 Monitoring (CO2M) mission will provide satellite images of the CO2 and NO2 plumes associated with these sources at a resolution of 2 km × 2 km and with a swath of 250 km. These images could be exploited using atmospheric-plume inversion methods to estimate local CO2 emissions at the time of the satellite overpass and their corresponding uncertainties. To support the development of the operational processing of satellite imagery of the column-averaged CO2 dry-air mole fraction (XCO2) and tropospheric-column NO2, this study evaluates data-driven inversion methods, i.e., computationally light inversion methods that directly process information from satellite images, local winds, and meteorological data, without resorting to computationally expensive dynamical atmospheric transport models. We designed an objective benchmarking exercise to analyze and compare the performance of five different data-driven inversion methods: two implementations with different complexities for the cross-sectional flux approach (CSF and LCSF), as well as one implementation each for the integrated mass enhancement (IME), divergence (Div), and Gaussian plume (GP) model inversion approaches. This exercise is based on pseudo-data experiments with simulations of synthetic true emissions, meteorological and concentration fields, and CO2M observations across a domain of 750 km × 650 km, centered on eastern Germany, over 1 year. The performance of the methods is quantified in terms of the accuracy of single-image emission estimates (from individual images) or annual-average emission estimates (from the full series of images), as well as in terms of the number of instant estimates for the city of Berlin and 15 power plants within this domain. Several ensembles of estimations are conducted using different scenarios for the available synthetic datasets. These ensembles are used to analyze the sensitivity of performance to (1) data loss due to cloud cover, (2) uncertainty in the wind, or (3) the added value of simultaneous NO2 images. The GP and LCSF methods generate the most accurate estimates from individual images. The deviations between the emission estimates and the true emissions from these two methods have similar interquartile ranges (IQRs), ranging from ∼ 20 % to ∼ 60 % depending on the scenario. When taking cloud cover into account, these methods produce 274 and 318 instant estimates, respectively, from the ∼ 500 daily images, which cover significant portions of the plumes from the sources. Filtering the results based on the associated uncertainty estimates can improve the statistics of the IME and CSF methods but does so at the cost of a large decrease in the number of estimates. Due to a reliable estimation of uncertainty and, thus, a suitable selection of estimates, the CSF method achieves similar, if not better, accuracy statistics for instant estimates compared to the GP and LCSF methods after filtering. In general, the performance of retrieving single-image estimates improves when, in addition to XCO2 data, collocated NO2 data are used to characterize the structure of plumes. With respect to the estimates of annual emissions, the root mean square errors (RMSEs) for the most realistic benchmarking scenario are 20 % (GP), 27 % (CSF), 31 % (LCSF), 55 % (IME), and 79 % (Div). This study suggests that the Gaussian plume and/or cross-sectional approaches are currently the most efficient tools for providing estimates of CO2 emissions from satellite images, and their relatively light computational cost will enable the analysis of the massive amount of data to be provided by future satellite XCO2 imagery missions.
- Article
(14638 KB) - Full-text XML
- BibTeX
- EndNote
Satellite imagery of the column-averaged dry-air mole fraction of CO2 (XCO2) has been identified as an essential component of a future atmospheric observing system for monitoring anthropogenic CO2 emissions and, in particular, for detecting and monitoring hotspot atmospheric plumes and, thus, emissions in order to verify emission reductions or assess national budgets (Ciais et al., 2015; Pinty et al., 2017). The Copernicus CO2 Monitoring (CO2M) mission has been designed to meet these objectives with a constellation of two to three low-Earth-orbit (LEO) satellites flying in a sun-synchronous low-Earth orbit, crossing the Equator at around 11:30 local time. Each satellite will carry an imaging spectrometer providing images of XCO2 and of NO2 tropospheric-column densities (referred to as NO2 hereinafter) along a 250 km wide swath with a resolution of 2 km × 2 km (Sierk et al., 2019). Current satellite missions – such as the Sentinel-5 Precursor (Sentinel-5P) and the third Orbiting Carbon Observatory (OCO-3), when targeting specific sources in its snapshot area mapping (SAM) mode – already deliver NO2 column density and XCO2 images; however, the former does so at a resolution coarser than that of the CO2M mission, and the latter does so over smaller areas and at a lower frequency compared to the CO2M mission. Upcoming missions, such as the Global Observing SATellite for Greenhouse gases and Water cycle (GOSAT-GW; Kasahara et al., 2020), MicroCarb (in its “city-mode” function; Pascal et al., 2017), and the Twin ANthropogenic Greenhouse gas Observers (TANGO) mission (Landgraf et al., 2020), are expected to increase the number of CO2 and NO2 images of plumes from emission hotspots.
Operational services, such as the Copernicus CO2 Monitoring and Verification Support (CO2MVS) capacity (Pinty et al., 2017; Janssens-Maenhout et al., 2020), are being developed both to process these XCO2 and NO2 images for the monitoring of emissions in a systematic and global way at spatial and temporal scales relevant for policymakers and to support emission mitigation actions. Plume inversion systems are used to derive estimates of CO2 emissions from local sources using satellite images of the corresponding atmospheric plumes. One of the key elements of operational services will thus be standard plume inversion methods providing precise and reliable data in an automated and fast manner. Various plume inversion approaches and implementations are now regularly used to process existing spaceborne atmospheric-plume images (Varon et al., 2018; Zheng et al., 2020; Kuhlmann et al., 2021; Nassar et al., 2021; Jacob et al., 2022; Hakkarainen et al., 2023a). Therefore, there is a need to benchmark, in a quantitative way, plume inversion methods for the estimation of local emissions of CO2 and, more generally, greenhouse gases and pollutants.
Monitoring anthropogenic CO2 emissions from point sources or cities using satellite XCO2 images is challenging as corresponding column-averaged enhancements are often small compared to local fluctuations in the background CO2 field due to biogenic CO2 fluxes and neighboring anthropogenic sources, as well as the typical level of errors in XCO2 retrievals (Buchwitz et al., 2013). Despite this challenge, the potential of CO2 imagers to estimate anthropogenic emissions has been demonstrated, using Observing System Simulation Experiments (OSSEs) with synthetic data, for power plants (Bovensmann et al., 2010); for cities (Pillai et al., 2016; Broquet et al., 2018; Wang et al., 2020); and, in a more general way, at local to national scales (Santaren et al., 2021). Furthermore, several studies have shown that the joint analysis of co-located NO2 satellite observations strongly enhances the ability to detect XCO2 enhancement plumes from sources in XCO2 images and, consequently, to estimate the corresponding CO2 emissions (Reuter et al., 2019; Kuhlmann et al., 2021). NO2 observations are indeed characterized by a better signal-to-noise ratio and a generally small, low-amplitude background field, due to the relatively short lifetime of nitrogen oxides (NOx).
CO2 emissions of large point sources and cities can be estimated from satellite images by plume inversion systems that integrate observations with dynamical transport model simulations of atmospheric CO2 concentrations (e.g., Broquet et al., 2018; Ye et al., 2020; Santaren et al., 2021). In principle, the use of such dynamical models could support the analysis of 3-D dynamical patterns of the observed plume and, thus, the accuracy of the inversion. They could also support the derivation of the spatial distribution of emissions within cities and that of the temporal variation in emissions corresponding to a plume in the hours preceding each satellite overpass. However, they can be strongly impacted by modeling errors, which become critical at local scales when trying to model plumes from emission hotspots over distances of a few tens to a few hundreds of kilometers (Brunner et al., 2023). Furthermore, their computational burden hinders their use for global and routine coverage of sources in an operational context. Data-driven plume inversion methods appear to be currently more suitable for such broad-scale applications (Ehret et al., 2022). These are computationally light inversion methods that directly process information from satellite images, along with local wind and meteorological data (typically from operational weather analyses), without resorting to dynamical atmospheric transport models.
The main data-driven approaches for estimating local emissions based on satellite images of plumes, which have been tested and analyzed in a significant number of studies, are as follows:
-
First, we have the integrated mass enhancement (IME) approach, which relates the total mass of plumes to the corresponding emissions. It has been used for retrieving CH4 emissions from airborne observations (Frankenberg et al., 2016) or from fine-scale satellite data (Varon et al., 2018).
-
Second, we have the Gaussian plume approach, which extracts emissions from the fit of plume shapes using Gaussian functions and was applied, for instance, to estimate power plant CO2 emissions from Orbiting Carbon Observatory-2 (OCO-2) satellite data (Nassar et al., 2017, 2021).
-
Third, we have the cross-sectional flux approach, which infers emissions from the fluxes passing through cross sections of the plumes and whose potential to estimate CO2 emissions from power plants using CO2 and NO2 satellite imagery data was assessed, for instance, by Kuhlmann et al. (2021).
-
Finally, the divergence (Div) approach is used, which derives emissions from the application of the divergence operator to fields of fluxes. This approach was originally designed to estimate nitrogen oxide (NOx) emissions from NO2 data provided by TROPOMI satellite imagery (e.g., Beirle et al., 2019, 2021, 2023) and was more recently adapted for the quantification of CO2 emissions (Hakkarainen et al., 2022). Contrary to the other methods in this study, the Div method is generally used to generate annual estimates from average fields extracted from multiple images.
Against this background, the aim of this study is to benchmark these four data-driven plume inversion approaches for the monitoring of CO2 emission hotspots with CO2M images. We present a benchmarking framework to objectively evaluate and compare the performance of different implementations of the four data-driven approaches (Sect. 2.1) to estimate local CO2 emissions from such satellite data. For this purpose, we use synthetic satellite observations collected over 1 year that closely mimic those expected from the upcoming CO2M mission (Sect. 2.2). These observations were generated in the SMARTCARB project, funded by the European Space Agency (ESA), via high-resolution atmospheric transport simulations (e.g., Brunner et al., 2019; Kuhlmann et al., 2020). Emissions from the city of Berlin and 15 large power plants are estimated using these synthetic satellite data, and the ability of the different inversion methods is assessed by comparing their estimates to the corresponding true values used by the atmospheric transport model. The performances of the different inversion approaches are evaluated for (1) single-image estimates that are retrieved from daily images (Sect. 3) and (2) annual estimates that are computed from the inversion of 1 year of data (Sect. 4). Furthermore, performances are analyzed for different scenarios regarding the data used by the inversions, where the impacts of considering cloud cover in the data, the uncertainties in the wind, and the use of collocated NO2 data are assessed. Finally, the results are discussed by analyzing (1) the potential of ensemble approaches that combine different inversion methods and (2) the trade-off between overall accuracy and the number of estimates when the cases are filtered based on the uncertainties in the estimates computed by the plume inversion methods (Sect. 5).
2.1 Data-driven inversion methods
Five different emission quantification methods are evaluated in this study: (1) the integrated mass enhancement (IME) method, (2) the cross-sectional flux (CSF) method, (3) the light cross-sectional flux (LCSF) method, (4) the Gaussian plume (GP) method, and (5) the divergence (Div) method. More precisely, what is studied here are specific configurations of certain methods, as is the case for the CSF and LCSF methods, which are derived from the same general approach. However, hereinafter, we will refer to these configurations as methods to avoid weighing down the text. The general approaches have been widely used and described in previous papers, such as Varon et al. (2018) and Beirle et al. (2019, 2021). The specific implementations of the CSF and Div methods tested here have been used extensively by authors of previous studies (Kuhlmann et al., 2019, 2020a, b, 2021; Hakkarainen et al., 2022). They have been slightly upgraded in the course of this benchmarking exercise to improve their stability, accuracy, and ability to run in a fully automated way. Details of the methods are presented in an accompanying study by Kuhlmann et al. (2023). Further details about the theory of the Div method and its application are given in Koene et al. (2024) and Hakkarainen et al. (2022, 2023b). All algorithms and tools used in this work have been integrated into a Python library for data-driven emission quantification (“ddeq”), which has been made publicly available and is described in Kuhlmann et al. (2024). We provide a short description of these methods below, with an emphasis on their relative advantages and limitations, as well as on the way they estimate uncertainty. The main features of the methods are summarized in Table 1 and illustrated in Figs. 1 and A1. Table 1 also lists the computation times of the methods calculated for the same inversion example using the same hardware. As the methods have all been implemented in the same Python package, the timings are directly comparable.
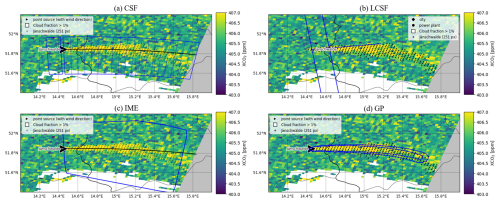
Figure 1Illustrations of different inversion methods for a plume produced by the Jänschwalde power plant on 23 April 2015. In all panels, pixels with dots indicate the selected enhancements representing the plume. Panel (a) shows the CSF method: blue boxes depict the areas where Gaussian fits of the plume cross sections are performed, and the black line represents the centerline of the plume. Panel (b) shows the LCSF method: blue lines represent the domain where Gaussian fits of the plume cross sections are performed, and the black line represents the along-wind direction at the source. Panel (c) shows the IME method: the blue box outlines the domain over which mass enhancements are integrated. Panel (d) shows the GP method: blue contour lines correspond to the 2-D Gaussian curve that fits the plume.
Table 1Summary of the characteristics of the benchmarked methods.
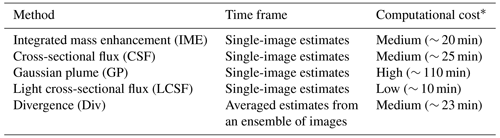
* The computation time was estimated by inverting 1 month of cloud-free CO2 and NO2 SMARTCARB data on the same server using the “ddeq” package (Kuhlmann et al., 2023).
All methods except the Div method can provide estimates derived from individual satellite images. The Div approach, as implemented here, is based on the averaging of information contained within multiple images and, hence, typically delivers annual estimates. We will hereinafter refer to the IME, CSF, LCSF, and GP methods as single-image methods. These methods share a common algorithmic sequence that starts with identifying clusters of enhancements above a background in satellite images. Subsequently, these clusters are assigned to plumes from specific known sources, and finally, the emissions of the corresponding sources are estimated. The plume detection combines the first two stages and can be used to discern plumes from unreported sources; however, the ability of the different approaches to detect unknown point sources has not been studied here as the primary focus is to analyze their potential to detect and process plumes from known sources using CO2M-like satellite images (see Sect. 2.2). It is worth mentioning that the divergence, cross-sectional flux, and machine-learning approaches are particularly well suited for the automatic detection of plumes from unknown sources (Zheng et al., 2020; Beirle et al., 2021; Schuit et al., 2023). Moreover, as previously mentioned, a benefit of the CO2M mission is the availability of co-registered XCO2 and NO2 columns, which can further benefit the plume detection and emission quantification steps.
Obtaining column enhancements over the background can be achieved with different thresholding techniques, as detailed below. When it comes to NO2, the global background field is insignificant, but in the case of CO2, its amplitude is important and can vary significantly in space and time due to biogenic and other anthropogenic fluxes surrounding the sources of interest and due to gradients in the background. Another common feature is the need for defining an effective wind speed, which describes the average mass transport of CO2 within the plumes. This a major challenge as wind speed varies with altitude, whereas satellite images contain integrated column measurements with no vertical resolution. Additionally, the horizontal resolutions of wind products are generally different from those of satellite images. To address these limitations, the methods determine effective winds in a more or less sophisticated manner.
Finally, all methods have implemented some quality control on their estimates. These checks are more or less restrictive depending on the methods and may, for example, filter out cases with overlapping plumes originating from neighboring sources. Further details are provided in Kuhlmann et al. (2023). It is worth emphasizing the fact that our implementation of the GP method discards values that are below 0.25 or beyond 4 times the true values averaged 1 h before the satellite overpass (10:00 to 11:00 UTC); this filtering stabilizes the otherwise underdetermined inversion. Unlike the other methods, the GP method thus uses a priori information about the source strength, which artificially improves its performance.
2.1.1 Cross-sectional flux (CSF) inversion method
The cross-sectional flux inversion method has been used in many studies, such as in the determination of CH4 emissions from point sources using high-resolution satellite data, where its superiority over other methods was demonstrated within the framework of the study by Varon et al. (2018). In brief, this method calculates fluxes through single or multiple cross sections of plumes as the product of effective winds and integrals of column mass enhancements along plume transects (line densities). Under the assumption of steady-state conditions, these fluxes are equivalent to the emissions. The CSF method used in this study was used by Kuhlmann et al. (2020a, b, 2021) for the estimation of CO2 emissions from CO2 and NO2 images. These studies have demonstrated that the inclusion of NO2 observations significantly increases the number and precision of the estimates.
The plume detection module of the CSF approach determines, in the first stage, the CO2 or NO2 pixels that are significantly enhanced above the background using a statistical z test (Kuhlmann et al., 2021). To perform this, a Gaussian kernel is applied to average local observation values, and the background field is computed at this stage by applying a median filter. The parameters defining the z test were carefully assessed in order to obtain enough valid pixels to describe a plume while avoiding false detections (Kuhlmann et al., 2019). The detected pixels are then grouped by a labeling algorithm and assigned to a source. Finally, a curve representing the centerline of the plume is fitted to the detected pixels.
For the quantification of CO2 emissions, the CSF method groups the detected plume pixels into sub-polygons along the curved plume, whose width is ∼ 5 km (2–3 pixels of CO2M data). All detected pixels within a sub-polygon are used to construct a single estimate of the line density. Following Reuter et al. (2019), the CSF method assumes that the plume transect exhibits a Gaussian behavior after removing the background signal with a normalized convolution. To obtain the line densities, the integration of the fitted Gaussian functions does not require any additional computation as the line integrals are simply equal to the amplitude parameters of the fitted Gaussian functions. Then, in order to be converted into fluxes, the line densities are multiplied by the effective winds, which are the horizontal winds at the corresponding source locations and times of the satellite overpasses, vertically weighted by the SNAP-11 emission profiles (Brunner et al., 2019).
Finally, the CO2 emission of a given source retrieved from a given satellite image is computed by averaging the estimated CO2 fluxes of all the sub-polygons describing the plume downstream of the source. The uncertainty in the emission estimate is then computed by propagating the uncertainties in the line density computation and in the wind; the uncertainties in the line densities are extracted from the standard deviation of the sub-polygon estimates and capture mostly satellite data noise through uncertainty in the Gaussian fitting.
When NO2 data are used in conjunction with CO2, detections of plumes are first performed for NO2, while the CO2 and NO2 enhancements are fitted simultaneously by Gaussian functions that share the same mean (or central location) and the same standard deviation. Thus, the fit of CO2 enhancements takes advantage of the better signal-to-noise ratio of NO2 data by better constraining the parameters of the Gaussian functions, which provides more accurate estimates of CO2 line densities and, hence, CO2 emissions.
2.1.2 Light cross-sectional flux (LCSF) inversion method
The light cross-sectional flux method shares the same theoretical foundations as the CSF method, but its implementation is largely different. It is derived from a method originally developed by Zheng et al. (2020) to estimate CO2 emissions from cities and industrial areas in China that produce atmospheric plumes clearly detectable in transects of OCO-2 data. These data are characterized by a resolution of a few square kilometers and a swath about 10 km wide, which is almost 25 times narrower than the ∼ 250 km wide swath of the CO2M instruments. This method has been applied to routine and automatic estimations of isolated clusters of CO2 emissions worldwide (Chevallier et al., 2020) and to studies of temporal variability in emissions based on several years of OCO-2 and OCO-3 data (Chevallier et al., 2022). This method has undergone significant modifications in this comparative study, in which the locations of the emission sources are known, in order to fully harness the potential of high-resolution satellite imagery.
For a given source and satellite overpass, the LCSF method performs a simple detection of the plume by extracting from the satellite image an area that is 100 km wide in the across-wind (perpendicular) direction and extends downwind of the source over a distance equal to the distance traveled by the wind in 1 h. The method then selects the pixels from the extracted area where XCO2 or NO2 enhancements – simply defined as differences between data values and the average data of the area – are greater than the spatial variability, i.e., the standard deviation of the data contained within the area.
The quantification of the source emission is then performed on each selected enhancement by again extracting a 100 km wide across-wind area centered on the enhancements and extending 10 km (∼ 5 pixels of CO2M data) downwind of the enhancements. The sums of linear terms accounting for large-scale variations in the background fields and Gaussian functions describing the plume cross section perpendicular to the wind direction are then fitted to the data contained within these areas. The plume detection and fitting of the enhancements can be carried out in the same way when NO2 data are available. Moreover, the standard deviations and means of the Gaussian functions fitted with NO2 data are then used to fit CO2 enhancements; CO2 data, in this case, only constrain the amplitudes of the CO2 Gaussian functions. This allows for the transfer of information derived from NO2 data when estimating CO2 emissions from CO2 data.
CO2 line densities are, as with the CSF method, derived from the Gaussian functions fitted with CO2 data and converted into emission estimates through multiplication with the effective wind. For the LCSF method, this effective wind is extracted at the location of the enhancements and at an altitude of 100 m above ground as preliminary tests have shown that extracting winds at this altitude yields better inversion results for the LCSF approach compared to when using other altitudes or alternative methods of computing the effective winds. This result may reflect a trade-off between the need to account for emission injection heights higher than 100 m when considering isolated power plants and the need to account for those lower than 100 m when considering the mix of sources within cities, whose emissions are not dominated by large power plants (Brunner et al., 2023). The automatic process of selecting sources limits the ability to derive a case-by-case selection of the height for wind extraction, but a finer option for future analysis might involve discriminating this selection as a function of the type of target (considering at least isolated power plants vs. urban areas).
Finally, under steady-state atmospheric conditions, the cross-sectional CO2 flux derived at each selected enhancement is equivalent to the upwind source emissions. Therefore, as several enhancements belonging to the same atmospheric signature of a source are generally processed, the algorithm produces multiple individual estimates of the source emissions. The estimate computed by the method for a given source and from a given image is then calculated as the median value of these individual estimates, with the use of the median helping to reduce the impact of outliers. Moreover, uncertainties in the individual estimates provided by the LCSF method are computed by propagating the errors derived by the fitting algorithm when generating the line densities. Uncertainties in the final estimates are finally calculated as the median of these uncertainties.
2.1.3 Gaussian plume (GP) inversion method
The Gaussian plume inversion approach assumes that observed plumes can be described with Gaussian plume models. This approach has been widely used, for example, in the determination of CH4 point source emissions (Varon et al., 2018), when employing OCO-2 data to quantify CO2 emissions from power plants (Nassar et al., 2017), and in frameworks for estimating CO2 emissions from large cities and point sources at a global scale (Wang et al., 2020). Compared to previous Gaussian plume inversion methods, the GP inversion method used in this work enables the Gaussian plume model (similar to the CSF method) to handle curved plumes (see Sect. 3.2.1 in Hakkarainen et al., 2023b).
The detection of plumes, i.e., CO2 or NO2 enhancements from the background, is carried out using the same algorithm as that used for the CSF method. Then, the inversion uses a Levenberg–Marquardt least-squares optimization to find the optimal parameters of the Gaussian functions fitting the enhancements, as well as those of the Bézier curves describing the centerlines of the plumes (Hakkarainen et al., 2023b). If NO2 data and CO2 data are simultaneously available, then the Gaussian plume model is first fitted to the NO2 observations, and the optimized parameters regarding the plume shape are subsequently used as first guesses for fitting the CO2 observations. These derived parameters are constrained to remain close to the optimized parameters obtained from the fitting of NO2 data. Finally, uncertainties in the Gaussian plume estimates are obtained by propagating the uncertainties in the fitted parameters for wind speed and source strength.
To ensure the convergence of the minimization algorithm, first-guess values of the fitted parameters need to be carefully prescribed. Parameters of the centerline curves, for example, are initialized from the curves retrieved by the plume detection algorithm, and the initial wind speed is calculated as in the CSF method (see Sect. 2.1.1). Most importantly, the prior values of the emission parameters are set to the true summertime source emission strength. Thus, unlike any of the other methods studied in this work, the GP method integrates an important constraint on the emissions, which implies that the estimated values, i.e., the method's performance, are not entirely determined by the information contained within the synthetic satellite observations. This limitation should be taken into account when applying this method to invert emissions from real satellite data derived from sources whose amplitudes are barely known.
2.1.4 Integrated mass enhancement (IME) method
The IME method integrates the total mass enhancements of CO2 or NO2 above the background that can be associated with detectable plumes. Then, following Frankenberg et al. (2016), the relationship between IMEs and emissions (Q) can be approximated by a linear relationship defined by the residence time (τ) of the species within the plumes (Eq. 1).
The residence time can, in turn, be expressed as a characteristic plume length (L) divided by the effective wind speed (Ueff) (Eq. 2). For example, Varon et al. (2018), who applied the IME method using CH4 observations, derived Ueff from 10 m wind speeds using large-eddy simulations (LESs). Here, the plume detection algorithm, which identifies either CO2 or NO2 enhancements from the background, is the same as the one used in the CSF and GP methods, but the detected area of the plume over which the integration is performed is dilated using a circular kernel in order to increase the number of integrated pixels (Hakkarainen et al., 2023b). Missing values are filled using a normalized convolution, and estimates are rejected when fewer than 75 % of the valid pixels are available for the detected plume. The characteristic length (L) is computed as the arc length from the centerline of the plume to the most distant detected pixel minus 10 km (measuring at least 10 km). Moreover, the effective wind speed (Ueff) is extracted using the same vertically weighted average as that used for the CSF method. If NO2 observations are used in conjunction with CO2 observations, the integration area is established by applying the plume detection algorithm to NO2 data. Then, to estimate CO2 emissions, the IME is calculated over this area using CO2 observations. Finally, the uncertainty in the IME estimates is computed by propagating the uncertainty from the single-sounding precision of satellite data and an estimate of the uncertainty in the wind speed.
2.1.5 Divergence method
The divergence method, initially introduced by Beirle et al. (2019, 2021), was used to estimate NOx emissions based on TROPOMI NO2 observations. For this study, this method has been modified in order to estimate CO2 emissions, as outlined in Hakkarainen et al. (2022), where a detailed theoretical analysis of this approach can be found in the supplementary material. The divergence method is based on the continuity equation in a steady state (Jacob, 1999), where the divergence of a vector field, flux (F), is defined as the difference between the emissions (E) and sink (S) (Eq. 3).
Since the CO2 lifetime is extremely long, the sink term can be neglected. However, before applying the divergence operator to XCO2 images, the atmospheric background needs to be removed in order to extract only the XCO2 enhancements. For this purpose, a median filter is applied to the data, and the resulting field is subtracted from the original data. Moreover, in order to improve the accuracy of the estimates when CO2 noise levels are high, the data first undergo a denoising process using a 5×5 pixel mean filter. The flux field (F) is then defined at each pixel using Eq. (4), where ΔI is the vertical-column-density enhancement above the background and Ueff and Veff are the eastward and northward winds, respectively. These winds, interpolated at the location of the pixel and at the time of the satellite observations, and are vertically averaged using the SNAP-1 emission profiles (Brunner et al., 2019).
Divergence maps are computed from the mass flux field using a finite-difference approximation. The divergence map is then averaged over a long period to enhance the emission signal while reducing the impact of noise and the spatiotemporal variations in the CO2 background. Here, divergence maps are averaged over 1 year. In theory, the divergence method can also be used to estimate emissions from single-overpass images, much like the cross-sectional flux method (as the two methods are theoretically similar; see Koene et al., 2024). However, we choose, in this study, to focus on the standard application of this method (e.g., Beirle et al., 2019, 2021, 2023; Hakkarainen et al., 2022; Sun et al., 2022), which provides temporally averaged estimates. Appendix A provides a brief overview of the performance demonstrated in estimating emissions from individual images with different versions of the divergence approach.
For a specific source, the annual estimate of the emissions is then computed from the enhancement in the averaged divergence field using a peak-fitting approach, which fits the divergence map with a function that includes both a Gaussian term and a linear term centered on the source (Beirle et al., 2021). The emissions – and, more generally, the parameters – of the peak function are determined by an adaptive Markov chain Monte Carlo (MCMC), which also provides the uncertainties in the estimates based on the standard deviations of the sampled posterior distributions of the parameters.
2.2 Synthetic satellite observations of CO2 and NO2
In this study, synthetic satellite observations of CO2 and NO2 were generated from atmospheric simulations in order to evaluate and compare the ability of the methods described in Sect. 2.1 to retrieve CO2 or NO2 emissions from point sources or urban areas using satellite imagery akin to that provided by the upcoming CO2M mission. These simulated satellite data are readable by the “ddeq” Python library, were produced as part of the SMARTCARB project, and have been extensively described and used in previous works (e.g., Brunner et al., 2019; Kuhlmann et al., 2019, 2020, 2021). They are openly accessible from https://doi.org/10.5281/zenodo.4048227 (Kuhlmann et al., 2020b).
Atmospheric concentrations of CO2 and NO2 were simulated by the COSMO-GHG atmospheric transport model (Jähn et al., 2020), with a vertical resolution of 60 levels up to an altitude of 24 km and a horizontal resolution of about 1 km × 1 km for a domain centered over the city of Berlin. The domain extends about 750 km from east to west and 650 km from north to south. Simulations provided hourly outputs for nearly the entire year of 2015. In order to generate realistic simulations, initial and lateral boundary conditions for meteorological variables and tracers were extracted from products provided by the European Centre for Medium-Range Weather Forecasts (ECMWF) and MeteoSwiss (Kuhlmann et al., 2019). Furthermore, CO2 emissions included both anthropogenic and biospheric components, which were interpolated onto the COSMO-GHG grid at a temporal resolution of 1 h. Anthropogenic emissions were largely derived from the TNO_MACC-III inventory (Kuenen et al., 2014), and biospheric fluxes were simulated with the Vegetation Photosynthesis and Respiration Model (VPRM; Mahadevan et al., 2008). NOx emissions were also derived from the TNO_MACC-III inventory, and atmospheric simulations used a simplified NOx chemistry with a fixed NOx decay time of 4 h. NOx concentrations were converted to NO2 concentrations using an empirical equation for the evolution of NO2 : NOx ratios downwind of emission sources (Düring et al., 2011).
To generate synthetic satellite observations similar to CO2M observations, the XCO2 and NO2 column densities derived from the COSMO-GHG simulations were sampled at a resolution of 2 km × 2 km along 250 km wide satellite tracks (Kuhlmann et al., 2019); these tracks were computed using an orbit simulator and correspond to a hypothetical constellation of six CO2M satellites. In addition to XCO2 and NO2 column-averaged data, a cloud mask was generated from the total cloud fraction computed by the COSMO-GHG model. For CO2 data, all pixels with a cloud fraction larger than 1 % were removed as CO2 retrievals are strongly impacted by clouds (Taylor et al., 2016). For NO2 data, which are less sensitive to clouds, a threshold of 30 % on the cloud fraction was used to select valid pixels (e.g., Boersma et al., 2011). Figure 2 illustrates a COSMO-GHG simulation of XCO2 over the SMARTCARB domain, where synthetic XCO2 data corresponding to a CO2M satellite overpass are represented.
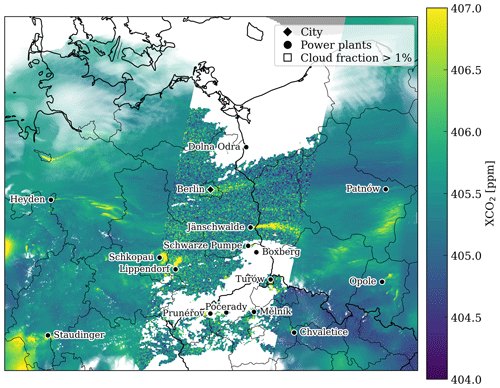
Figure 2Simulations of XCO2 over the SMARTCARB domain on 23 April 2015. Synthetic XCO2 observations over a 250 km wide swath are shown in the center of the figure for a low-noise scenario. Missing XCO2 observations due to a cloud fraction larger than 1 % are shown in white. The 16 emission sources considered in this study are highlighted, along with their names.
For the purposes of this benchmarking study, we use the configuration of the SMARTCARB dataset in which the CO2M constellation consists of three satellites. By choosing this configuration, we follow the recommendation of Kuhlmann et al. (2021), who proposed that a constellation of at least three CO2M satellites is necessary for a proper estimation of annual emissions from weak sources, particularly in regions such as central Europe, where cloud cover dramatically reduces the number of estimates. When ignoring clouds, this constellation of three satellites allows for the observation of each local source within the SMARTCARB domain once every other day. If we consider that a satellite image is usable only if there are at least 50 data pixels next to and downwind of the source, then we can use about 3000 images to determine the emissions of the 16 local sources considered in this study. However, if we consider cloud cover, only 500 images remain usable.
The characteristics of the uncertainties in the synthetic CO2M observations were computed using three different uncertainty scenarios (low, medium, and high). Simulated XCO2 column densities were thus assigned random errors by employing various levels of instrumental noise in the error parameterization formula. This formula, used for generating the errors, takes into account the solar zenith angle (SZA) and surface albedos (Buchwitz et al., 2013). The NO2 column densities were assumed to be characterized by random uncertainties with different constant values depending on the chosen uncertainty scenario. These values were defined for clear-sky conditions and increased in the presence of clouds, nearly doubling for a cloud fraction of 30 %. No systematic errors were prescribed for either XCO2 or NO2 column-averaged data. In this study, the characteristics of the random uncertainties prescribed to the synthetic data are chosen according to the requirements of the CO2M mission (Meijer et al., 2019). For XCO2 retrievals, random errors are generated with the error parameterization formula, using a single-sounding precision of 0.7 ppm for vegetation albedos and an SZA of 50°. For NO2 retrievals, a single-sounding precision under cloud-free conditions of 2×1015 molec. cm−2 is prescribed.
2.3 Benchmarking scenarios
The relative performance of the different inversion methods for estimating CO2 emissions is evaluated for the 15 strongest point sources in the SMARTCARB domain and for the city of Berlin (Fig. 2 and Table 1 in Kuhlmann et al., 2021). These 16 sources cover a large emission range, extending from 3.7 Mt CO2 yr−1 for the power plant located in Chvaletice (Czechia) to 40.3 Mt CO2 yr−1 for the power plant located in Jänschwalde (Germany), with these values corresponding to the annual mean emissions at the time of the satellite overpass (10:30 UTC) used in the COSMO-GHG simulations. It is worth mentioning that the distribution of the source emissions is skewed toward the lowest value as the median emission rate in the collection is around 9.6 Mt CO2 yr−1, with 75 % of the sources emitting less than 14 Mt CO2 yr−1.
In order to thoroughly evaluate the relative performances of the different methods and the sensitivity of these performances to different factors, the benchmarking study is carried out according to several scenarios that share the same features for the simulated data and the source collection described above. The most optimistic or ideal scenario corresponds to the application of inversions to CO2 and NO2 images without the removal of pixels associated with cloud cover, ignoring the clouds modeled with the COSMO-GHG model (we label such inversions as cloud-free hereafter), and with perfect knowledge of the wind field, i.e., using the winds directly from the COSMO-GHG model (denoted SMARTCARB winds). It is the ideal case because (1) the joint analysis of NO2 and CO2 images strengthens the estimates compared to the analysis of CO2 images only and (2) ignoring the potential loss of data due to cloud cover in the CO2 and NO2 images yields full images, whose analysis is more robust than that of partial images, thus providing a higher number and precision of estimates. The results derived from this benchmarking scenario should be seen as an upper limit of what the inversion methods could achieve in terms of accuracy and the number of estimates. The most realistic scenarios take cloud cover into account and use winds extracted from the ERA5 wind product (Hersbach et al., 2020), which is independent of the inverted data and whose resolution (∼ 0.25°) is much coarser than that of the SMARTCARB winds (∼ 0.01°). The results derived from this benchmarking scenario should be seen as the lower limit for the method's performance.
The differences between the ERA5 and SMARTCARB wind products are significant at the 16 sources considered in this study: the annual mean biases between these two wind products for 2015 range from 0.1 to 1.5 m s−1 depending on the source, with an average value across the sources of 0.6 m s−1, while RMSEs range from 1.1 to 2.1 m s−1 depending on the source, with an average value across the sources of 1.5 m s−1 (Fig. A2). The biases per source are systematically positive since SMARTCARB tends to provide larger winds than ERA5. With such differences, comparing scenarios with the same characteristics but different wind products allows us to gain insight into each method's sensitivity to wind uncertainties. Additional benchmarking scenarios were designed to test the sensitivity of the methods with respect to other factors, including the consideration of cloud cover in satellite data and the use of NO2 for plume detection and characterization. All benchmarking scenarios are listed in Table 2.
Table 2List of the different benchmarking scenarios – from the most optimistic (scenario 1), which considers inversions with cloud-free data and SMARTCARB winds, to the most realistic (scenario 8), which uses cloud-filtered data and ERA5 winds. Note that a cloud fraction threshold of x % corresponds to the rejection of data pixels if the pixels' cloud cover exceeds x %, meaning that a cloud fraction of 100 % yields full images without any loss of data pixels.

2.4 Benchmarking metrics
For a given benchmarking scenario, the performance of the different inversion methods can be evaluated through the number of single-image estimates that can be retrieved based on the number of available satellite images – ∼ 500 or ∼ 3000, depending on whether cloud cover in the data is considered or ignored, respectively. Performance can also be assessed through the quality of the estimates. The accuracies of the methods are then assessed by comparing the estimates retrieved from single satellite overpasses to the corresponding true values that were used to generate the synthetic satellite data. More precisely, inversion results are analyzed in terms of the distributions of the differences between the estimated and true emissions of all the sources considered in this study. We will refer to these differences in the following as deviations. More precisely, our analysis will mostly focus on examining the distributions of relative deviations, calculated by dividing the differences between estimated and true emissions by the true emissions, in order to fairly compare results across sources with significantly different magnitudes (Sect. 2.3). Furthermore, to properly describe distributions that may be very different from Gaussian distributions, box plots are used, in which the median values, the interquartile ranges (IQRs), and the 10th and 90th percentiles of the distributions are represented.
The ability of the different inversion methods to estimate source emissions can also be analyzed by studying the annual or monthly averages of the single-image estimates. Benchmarking results are then evaluated for each source in terms of the relative deviations of the annual (monthly) estimates from the true annual (monthly) emissions and in terms of root mean square errors (RMSEs) in order to provide a global indicator of the accuracy of the annual (monthly) estimates across all sources.
In this study, the annual (monthly) averages of the single-image estimates for a given source are computed using three different methods: (1) using the arithmetic means of all single-image estimates of the source emissions generated from inverting 1 year (month) of data; (2) using the means of these estimates, where the means are weighted by the inverse of their computed variances (Sect. 2.1); and (3) using the medians of these estimates. The annual (monthly) inverse-variance-weighted means incorporate the information provided by the methods on the quality of the estimates when averaging, whereas the annual (monthly) medians are statistical indicators that are more robust to outliers than the means. Moreover, since the Div method is applied by temporally averaging satellite observations over the year, it produces only a single annual estimate for each source; we will thus consider that the three types of annual (monthly) estimates are all equal to this single estimate.
It is important to note that the annual and monthly estimates are affected by temporal sampling biases when inversion methods use data filtered by cloud cover. Specifically, the presence of denser cloud cover during winter generally results in the overrepresentation of emission estimates during summer and, hence, could lead to an underestimation of annual estimates as emissions are higher during winter due to increased fossil fuel consumption, associated with electricity and heat production. Although more advanced methods – such as fitting periodic curves to capture seasonal cycles, as demonstrated by Kuhlmann et al. (2021) – could potentially enhance the accuracy of estimates, they are not included in this study. However, these temporal sampling biases are integrated into the results as the annual (monthly) estimates are compared to the true annual (monthly) emissions, which are computed by considering all the days of the year (month).
The following subsections present a comparative study of the CSF, GP, IME, and LCSF methods for estimating emissions from single images. In the following, we will refer to these kinds of estimates as single-image estimates. It is worth mentioning that, as these methods use different algorithms for plume detection and emission quantification, including different rejection criteria (Sect. 2.1), they produce different sets of estimates.
3.1 Sensitivity to the emission strengths of the sources
In the optimal scenario (cloud-free CO2 and NO2 data with SMARTCARB winds), all methods tend to provide more accurate estimates for strong sources than for weak sources, and this trend is particularly noticeable for the IME and CSF methods (Fig. 3). The median values of the absolute relative deviations for weak sources (with emissions ranging from 0 to 6.9 Mt CO2 yr−1, as shown in the first row of Fig. 3) are 207 % (IME method) and 54 % (CSF method). In contrast, for strong sources (with emissions ranging from 15.6 to 53.2 Mt CO2 yr−1, as shown in the fourth row of Fig. 3), these values are approximately 47 % (IME) and 28 % (CSF). The inversion methods are also more prone to producing unrealistic values for weak sources as the distributions are strongly skewed for this type of source. Indeed, the 95th-percentile accuracy indicator is 1128 %, 584 %, 172 %, and 178 % for the IME, CSF, GP, and LCSF inversion models, respectively (first row of Fig. 3). For strong sources, this indicator is significantly lower, decreasing to 200 %, 108 %, 90 %, and 76 %, respectively (fourth row of Fig. 3). Atmospheric signals generated by strong sources are more distinct from the background than those generated by weak sources, and, as a result, the signal-to-noise ratio in the XCO2 and NO2 images is better, which helps to reduce uncertainties in the determination of the emissions of XCO2 and NO2. For low-emitting sources, the performance of the inversion methods can be degraded by the limited number of enhanced pixels that are detected in images with noise; this limitation makes the identification of plume centerlines by the CSF, IME, and GP methods challenging (Sect. 2.1). This problem could have impacted the GP method, but its current implementation incorporates prior knowledge, filtering out estimates that fall outside the 25 % to 400 % range of the prior. This filtering process is expected to improve the accuracy of the GP method, especially for weak sources.
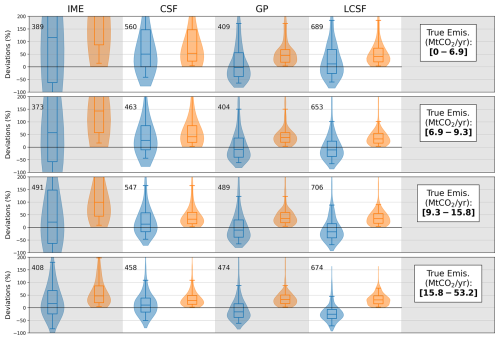
Figure 3Performance when estimating CO2 emissions from individual images obtained using the different single-image inversion methods (columns) across different ranges of true emissions (rows), with SMARTCARB winds and cloud-free CO2 and NO2 data applied. The distributions of relative deviations (in blue) and relative absolute deviations (in orange) are illustrated using violin plots. The interquartile ranges are represented by the boxes, while the whiskers indicate the 5th and 95th percentiles, and the medians are indicated by the lines inside the boxes. The numbers alongside the boxes show the number of estimates corresponding to the ranges of true emissions (True Emis.) and inversion methods.
Biases in the emission estimates may also depend on the strength of the source, as observed in the IME and CSF methods, which strongly overestimate the emissions of weak sources compared to those of strong sources. For weak sources, the median of the deviation distributions for the IME and CSF models (blue plots in the first row of Fig. 3) is +116 % and +50 %, respectively, compared to +16 % and +11 % for strong sources (blue plots in the fourth row of Fig. 3). This discrepancy is probably due to the plume detection algorithm, which, for weak sources, may wrongly attribute enhancements from other sources in the vicinity to the source of interest and thus artificially increase the amplitude of the detected emissions. Conversely, the LCSF approach tends to underestimate the emissions of strong sources while slightly overestimating those of weak sources, with the median of the deviation distribution being −26 % (blue plot in the fourth row of Fig. 3) and +12 % (blue plot in the first row of Fig. 3), respectively. The underestimation of source emissions could be attributed to the tendency of the method to overestimate the amplitudes of the background for non-isolated sources: contrary to the other methods, the LCSF method does not remove the influence of neighboring plumes when computing the background around a given source. Another explanation could lie in the fact that this method uses 100 m winds as effective winds, while, especially for high-emitting sources, these winds are lower than the SNAP-1-averaged winds used by the other methods.
3.2 Impact of the use of NO2 images for the detection of plumes
The use of NO2 data to identify and characterize plumes increases the number of estimates for all inversion methods compared to when CO2-only inversions are used, as shown in Fig. 4 (blue vs. orange plots). The increase is significant for the IME and GP methods (∼ 93 % and ∼ 70 %, respectively), moderate for the CSF method (∼ 34 %), and slight for the LCSF method (∼ 4 %). The IME, GP, and CSF methods rely on a plume detection algorithm that is less reliable when using only CO2 observations (Kuhlmann et al., 2019). Of these three methods, the CSF method requires fewer pixels to detect and quantify plumes, resulting in a larger proportion of still-quantified plume cases compared to the IME and GP methods when using CO2 data alone. Detection of plumes by the LCSF method is performed on data slices whose pixels are relatively close to sources, where XCO2 enhancement signals due to emissions are thus relatively strong. This may explain the small benefit of this method in using joint CO2 and NO2 images to better determine the shape of the plumes.
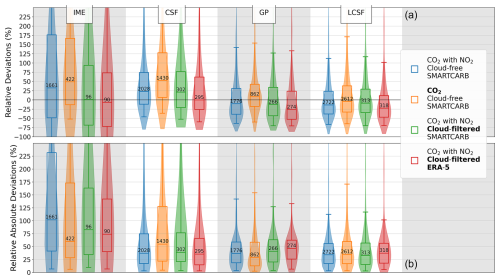
Figure 4Performances of the inversion methods when estimating emissions from single images for different benchmarking scenarios: cloud-free CO2 and NO2 data with SMARTCARB winds (in blue), cloud-free CO2 data only with SMARTCARB winds (in orange), cloud-filtered CO2 and NO2 data with SMARTCARB winds (in green), and cloud-filtered CO2 and NO2 data with ERA5 winds (in red). Bold text in the legend indicates the elements of the benchmarking scenarios that differ from those of the ideal benchmarking scenario. Distributions of the relative deviations (a) and relative absolute deviations (b) are illustrated using violin plots. The boxes represent the interquartile ranges of the distributions, the whiskers indicate the 5th and 95th percentiles, and the lines within the boxes represent the medians. The numbers in the interquartile-range boxes indicate the number of estimates for each benchmarking scenario and inversion method.
When using CO2 and NO2 data, the maximum number of estimates obtained from each inversion method varies significantly: the IME method produces the smallest number of estimates, with 1661, while the LCSF method produces the largest, with 2722. The GP and CSF methods, based on the same plume detection algorithm as the IME method, produce up to 1776 and 2012 estimates, respectively. These differences can be attributed to the differences in the number of detected pixels below which the algorithm rejects plumes and to differences in the emission quantification algorithms used by the different methods. In addition, the overall complexity of the IME, CSF, and GP methods, which use a relatively large number of rejection criteria, likely explains why these three methods deliver far fewer estimates than the LCSF method. The relative efficiency and robustness of the plume detection algorithm of the LCSF method are evidenced when using CO2 data only to determine emissions: the number and accuracy of estimates are hardly changed compared to when the inversions are performed with CO2 and NO2 data. This is in contrast to the other methods, whose algorithms are more sensitive to uncertainties in XCO2 data and which need NO2 data to accurately fit a plume coordinate system to the data.
The inclusion of NO2 data does not appear to significantly improve the overall performance of the GP and LCSF methods in terms of the accuracy of the CO2 emission estimates (Fig. 4b). However, for the LCSF method, there is a notable reduction in the 95th percentile of the relative absolute deviations – from 175 % without NO2 to 115 % with NO2. For the CSF method, the use of NO2 data strongly improves its overall performance as, for example, the third quartile and the median of the absolute residuals are significantly decreased, from ∼ 127 % to ∼ 74 % and from ∼ 54 % to ∼ 36 %, respectively. As the CSF method rejects fewer estimates when using CO2 data only compared to the GP method, its accuracy decreases because, with more permissive filtering, it may include complex cases for which emissions are difficult to estimate. This may also explain why the CSF estimates are less biased, with a significantly lower median relative deviation, in cases where inversions also use NO2 data (Fig. 4a).
In contrast, the precision of the IME method decreases when using NO2 data, but this fact could be related to a numerical artifact: the IME method performs much better with high-emitting sources than with low-emitting sources (see Sect. 3.1), and the use of NO2 data likely allows us to constrain small sources more efficiently than when using CO2 data only. Therefore, when adding NO2 data, the number of low-emitting sources that are estimated increases more than the number of high-emitting sources, meaning the overall performance degrades. This bias, associated with the relatively poor estimation of low-emitting sources, is confirmed when deviations are used to assess performance instead of relative deviations: the absolute deviations associated with the IME estimates globally decrease with the use of NO2 data, with the median error, for example, decreasing from ∼ 15 to ∼ 11.5 Mt CO2 yr−1.
3.3 Impact of cloud cover
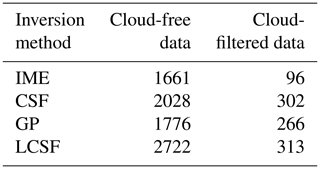
The impact of clouds is studied by comparing inversions with cloud-free images to inversions with cloud-filtered images (Sect. 2.3). When cloudy pixels in the XCO2 and column-averaged NO2 data are disregarded, the number of estimates from all the methods is considerably reduced, with decreases of 94 %, 85 %, 85 %, and 88 % for the IME, CSF, GP, and LCSF methods, respectively (Table 3). The number of estimates that can be provided for the cloud-filtered configuration with SMARTCARB winds reaches a maximum of 313 (LCSF) and decreases to 96 for the IME method, which can only provide robust estimates for cloud-free images as it requires integrating enhancements over the full extent of the plumes. As sources are characterized by different levels of cloud cover, the number of estimates per year and per source ranges from 1 to 12 (IME), 6 to 28 (CSF), 8 to 23 (GP), and 15 to 26 (LCSF).
Table 3Number of estimates for each inversion method when data with or without clouds are used. Inversions are performed with CO2 and NO2 data and with SMARTCARB winds.
Furthermore, filtering data pixels to remove those with significant cloud cover not only affects the number of estimates, but also impacts the performance of the methods, albeit to a much lesser extent. When comparing results obtained from the same images, cloud-free inversions produce slightly better results than cloud-filtered inversions (Fig. A3). This is because, in images partially masked by cloud cover, some pixels containing useful information are likely removed, which can lead to a less accurate determination of emissions. Similarly, if the threshold of cloud cover above which XCO2 images are discarded from the analysis is increased from 1 % to 2 % or 5 %, the performance of the methods does not significantly increase, unlike the number of estimates, which can increase, for example, by 12 % and 29 %, respectively, when using the LCSF method (Fig. A4).
3.4 Impact of uncertainty in the wind
As mentioned above, in order to assess the impact of potential uncertainties in the wind, a series of inversions is carried out using a different wind product than the one used to generate the synthetic XCO2 and NO2 data. For this purpose, the SMARTCARB winds are replaced by ERA5 winds, and the differences between these two wind products are characterized at the sites of this study by random and systematic components (Sect. 2.3 and Fig. A3). Notably, ERA5 winds show systematically lower values.
For all inversion methods, the global accuracies of the estimates, evaluated in terms of relative absolute deviations, are only slightly reduced when using ERA5 winds instead of SMARTCARB winds (green vs. red plots in Fig. 4b). There are a few possible explanations for this: the temporal or spatial uncertainties in wind components are only a minor source of uncertainty compared to other factors impacting the determination of estimates by the different inversion methods, such as uncertainties in the XCO2 and NO2 column densities (Sect. 2.2) or oversimplified assumptions in plume detection or quantification algorithms. Kuhlmann et al. (2020, 2021) showed, for instance, that the determination of the CO2 background field could introduce significant uncertainties into the estimates. Furthermore, as indicated by Reuter et al. (2019), one of the important benefits of satellite imagery is that uncertainties related to meteorological variables likely average out when emission estimates are sampled along significant areas of plumes.
However, the fact that ERA5 wind values are systematically lower than values of SMARTCARB winds has an impact on the median values of the relative deviations, i.e., the biases in the estimates. While the accuracies in terms of relative absolute deviations are slightly affected when using either of the wind products (green vs. red plots in Fig. 4b), biases may be significantly increased, as in the cases of the GP and LCSF methods, whose estimates are, on average, underestimated if inversions use ERA5 winds instead of SMARTCARB winds. The lower amplitudes of the ERA5 winds also explain why the results for the IME and CSF methods improve, especially regarding the 95th percentiles of the absolute deviation distributions, which decrease from around 504 % and 411 % to 370 % and 286 %, respectively. The systematic overestimation of the estimates evidenced above for the CSF and IME methods is therefore mitigated when using ERA5 winds (Fig. 4a).
As mentioned previously (Sect. 2.3), the benchmarking scenario in which inversions are performed with ERA5 winds and data filtered for cloud cover is the closest approximation to real conditions for monitoring emissions from data images delivered by satellites. In this scenario with CO2 and NO2 data, the GP and LCSF methods show the best performances in terms of global accuracy, with IQRs of 25 %–62 % and 17 %–55 %, respectively, for the distributions of the absolute relative deviations (red boxes in Fig. 4). It is interesting to note that the overall accuracies of these methods are similar for this realistic scenario and the ideal scenario, where inversions are performed with cloud-free data and SMARTCARB winds. Conversely, the number of estimates strongly decreases when inversions are performed with cloud-filtered data – for example, from 2722 to 318 estimates for the LCSF method (see Table 3).
4.1 Annual estimates
To evaluate how well an inversion method performs on an annual basis, we include all image estimates generated by the method, regardless of their uncertainty. We calculate annual estimates for a given source using the following three methods, as described in Sect. 2.4: (1) taking the average of all available image estimates for the source over the entire year, (2) taking the weighted average of these image estimates based on their uncertainty, and (3) taking the median value of these image estimates. Because the Div method only provides one estimate per year, its annual estimates are the same, irrespective of the calculation method used. In order to compare, for a given source, the three estimated annual values to the true emissions, we define the latter as the arithmetic mean of the true emission values for the source over all 365 days of the year.
As noted earlier (Sect. 2.1.5), the Div method computes an annual emission estimate for a given source by averaging the divergence map from all available overpasses corresponding to 2015. However, the other methods select overpasses that succeed in detecting plumes, likely increasing the reliability of their estimates. These selections generally correspond to conditions – in terms of wind, background variability, or emission strength – that should be favorable to all methods, including the Div method. The lack of selection, and thus the use of unfavorable overpasses when applying the Div method, may therefore hamper the comparison between the annual estimates from the Div method and those from the other methods.
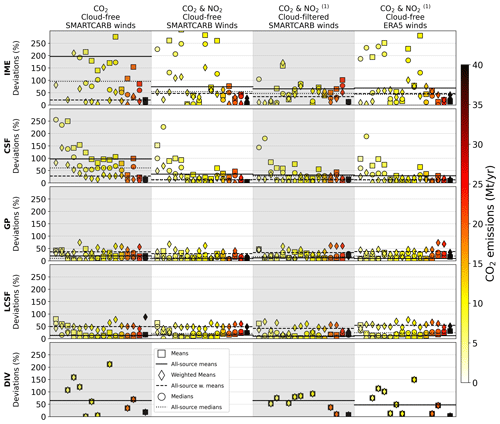
Figure 5Performance of the inversion methods for annual estimates of CO2 emissions. The markers represent, for a given source, the relative absolute deviations from the true annual emissions of the arithmetic means (squares), the weighted (w.) means (diamonds), and the medians (circles) of the estimates over a year. The lines represent the median values of the annual estimates over the entire set of sources. The inversions are performed using cloud-free CO2 data and SMARTCARB winds (first column), cloud-free CO2 and NO2 data and SMARTCARB winds (second column), cloud-filtered CO2 and NO2 data and SMARTCARB winds (third column), and cloud-free CO2 and NO2 data and ERA5 winds (fourth column). Note that “(1)” indicates that for the divergence method, the inversions in the third and fourth columns are performed using CO2 data only. The marker color indicates the true annual CO2 emissions of the corresponding source.
When annual estimates are calculated as arithmetic means or medians of individual image estimates, the GP and LCSF methods generally outperform the other methods. Indeed, for cloud-free inversions with CO2 and NO2 data, the median deviations for the annual arithmetic means (solid lines in the second column of Fig. 5) are 8 % (GP), 14 % (LCSF), 73 % (IME), 35 % (CSF), and 64 % (Div), and the median deviations for the annual medians (dotted lines in the second column of Fig. 5) are 14 % (GP), 21 % (LCSF), 54 % (IME), 13 % (CSF), and 64 % (Div). However, if annual estimates are calculated as the means of image estimates weighted by their uncertainty, the relative performance of the methods changes. In this case, the median deviations for the annual weighted means (dashed lines in the second column of Fig. 5) are 28 % (GP), 48 % (LCSF), 46 % (IME), and 12 % (CSF). Thus, using weighted means to calculate annual estimates significantly improves the performance of the IME and CSF methods, especially for low-emitting sources, while having a negative impact on the GP and LCSF methods. This finding indicates the reliability of the uncertainties in the estimates produced by the IME and CSF methods compared to those of the other methods, and if we use weighted means to compute the annual estimates, the accuracies of the IME and CSF methods increase significantly.
Figure 6 displays the inversion results for the annual estimates in a different but complementary way compared to Fig. 5: the estimated annual emissions are represented with respect to the true ones, which, in particular, highlights whether annual estimates are over- or underestimated for a certain type of source and by a given inversion method. In order to consider the best performance for each method according to what has been shown above, the annual estimates represented in Fig. 6 and used in the analysis of the results below are the arithmetic means of single-image estimates for the LCSF and GP methods, while they are the weighted means for the IME and CSF methods. Furthermore, Fig. 6 illustrates more clearly than Fig. 5 that, when weighted averages are used as annual estimates, the latter methods produce annual estimates whose precision is comparable for both weak and strong sources, whereas the global precision of estimates derived from single images by these methods is significantly lower for weak sources (Fig. 3). Averaging single-image estimates weighted by their uncertainty thus strongly increases the performance of the IME and CSF methods at the annual scale for low-emitting sources. However, even though the amplitudes of the relative deviations are similar between strong and weak sources, they have opposite signs: annual estimates for strong sources are generally underestimated, while annual estimates for weak sources are generally overestimated.
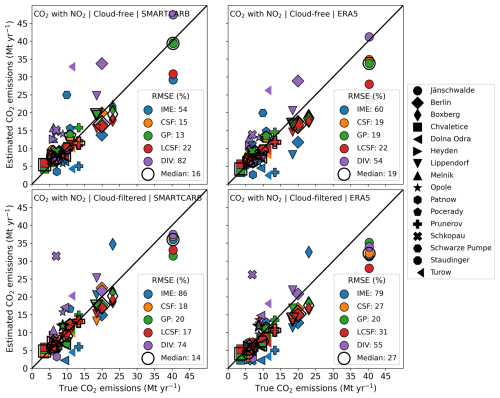
Figure 6Estimated vs. true annual emissions for four inversion scenarios (titles of the panels). For the IME and CSF methods, annual estimates are calculated as weighted means of the single-image estimates, while they are calculated as arithmetic means for the GP, LCSF, and Div methods. Each marker represents a given emission source, and each color indicates a given inversion method. The unfilled markers represent the median values of all the estimates for each source. The divergence inversion method uses CO2 data for all the inversion scenarios. The plain line represents the 1:1 line. In each panel, the legend in the bottom-right corner displays, for each inversion method, the relative RMSE, which is calculated by dividing the RMSE between the estimated and true annual emissions by the median of the true annual CO2 emissions from all sources (∼ 9.6 Mt yr−1).
Contrary to the results for the estimates retrieved from single images (Fig. 4), the CSF, GP, and LCSF approaches show similar performance, with a slight advantage for the GP method when estimating annual emissions and considering the ensemble of the benchmarking scenarios. For example, in the case of inversions from cloud-filtered CO2 and NO2 data with SMARTCARB (ERA5) winds, the relative RMSEs are 18 % (27 %) (CSF), 20 % (20 %) (GP), and 17 % (31 %) (LCSF). The analysis in Fig. 3 shows that the LCSF method produces single-image estimates that are slightly more accurate but more biased than those of the GP method. Thus, compensating for errors when averaging single-image estimates over a year may be less effective for the LCSF method than for the GP method, leading to similar global accuracies for both methods. For instance, the LCSF method has a greater tendency to underestimate high emissions (fourth row of Fig. 3), which likely explains why, contrary to the GP method, it systematically underestimates the emissions from the high-emitting power plant located in Jänschwalde, regardless of the inversion scenario used (Fig. 6). With respect to its results for single-image estimates, the CSF method shows significantly better results at the annual scale when annual estimates are computed as weighted averages of the single-image estimates.
Even when annual estimates are computed for the IME method as weighted averages of the single-image estimates, this method still shows lower accuracy compared to the CSF, GP, and LCSF methods. For example, the median values of the deviations for the annual estimates are 39 % (IME), 20 % (CSF), 11 % (GP), and 21 % (LCSF) when considering the best scores for the inversions performed with ERA5 winds and cloud-filtered data (fourth column of Fig. 5). The relative performance of the IME method is even worse when analyzing performance in terms of RMSE because, despite weighting estimates according to their quality or uncertainty in the annual averages, this method produces annual estimates that, for some sources, strongly deviate from the actual values, as seen in the cases of the Boxberg and Schwarze Pumpe power plants (Fig. 6). Moreover, the deviations of the Div method compared to those of the CSF, GP, and LCSF methods are higher for most of sources, except for strong sources (with true annual emissions exceeding 15 Mt CO2 yr−1), when inversions are performed using cloud-filtered data and ERA5 winds (fourth column of Fig. 5).
It is noteworthy that annual estimates for most inversion methods are comparable between inversions using data with clouds and those using data without clouds (cf. the second and third columns in Fig. 5), and, surprisingly, the deviations of the IME and Div approaches are even smaller for inversions with cloud-filtered data. Despite significant differences in the number of image estimates between the two inversion configurations (i.e., cloud-filtered and cloud-free), annual estimates are, on average, only slightly affected when cloud cover is considered in the data, at least with respect to the year and sources examined in this study. However, even though the relatively small number of image estimates in the inversion configuration with clouds does not hinder most methods from determining annual emissions for most sources, discrepancies can be high for some sources when estimates do not correctly sample the entire year, thus introducing a significant temporal bias. For example, the GP method mostly estimates emissions during summer for the Jänschwalde power plant when it uses the cloud-filtered inversion setup, explaining the strong underestimation of the annual emissions of this source compared to the cloud-free case (top-left vs. bottom-left panels of Fig. 6). This also explains why the RMSE increases significantly for the GP method (from 13 % to 20 % when inversions use SMARTCARB winds) when cloud cover limits the number of single-image estimates. The IME method is also impacted by this temporal bias when the number of estimates is too small to properly capture the seasonal cycle of the emissions, as in the case of the Boxberg power plant. Moreover, regardless of the benchmarking scenario, most inversion methods produce annual estimates for all the sources studied in this work, with the notable exception of the Div approach, which estimates annual emissions for only 10 out of 16 sources. This limitation, also present for cloud-free data configurations, is related to the fact that some sources do not produce strong enough divergence peaks from which annual estimates can be made using this method.
As for the results concerning single-image estimates, the use of ERA5 winds instead of SMARTCARB winds has, on average, a very low impact on the annual estimates delivered by the IME, CSF, GP, and LCSF methods. For emissions estimated from cloud-free CO2 and NO2 data, the median deviations obtained when inversions use SMARTCARB winds are 46 % (IME), 12 % (CSF), 8 % (GP), and 14 % (LCSF), and when inversions use ERA5 winds, they are 46 % (IME), 12 % (CSF), 9 % (GP), and 12 % (LCSF), as shown in the comparison between the second and fourth columns of Fig. 5. On the other hand, the overall accuracy of the Div method improves when inversions use ERA5 winds rather than SMARTCARB winds to estimate emissions. In this case, annual estimates are less prone to overestimation due to the generally lower amplitude of ERA5 winds compared to that of SMARTCARB winds (Fig. A2). This also explains the stronger underestimation of the emissions of strong sources by the LCSF method, resulting in a decrease in the accuracy of the annual estimates for these types of sources when this method uses ERA5 instead of SMARTCARB winds (bottom-left vs. bottom-right panels of Fig. 6).
The overall precision of the annual estimates computed by the IME, CSF, GP, and LCSF methods is, for all the benchmarking scenarios, significantly higher than the overall precision of their single-image estimates. For example, when inversions are performed with ERA5 winds and cloud-filtered data, which is the benchmarking scenario with the poorest results, the median deviations of the annual estimates are 39 %, 20 %, 11 %, and 21 % for the IME, CSF, GP, and LCSF methods, respectively, whereas the median deviations of the single-image estimates are 73 %, 35 %, 46 %, and 37 %, respectively. Despite the biases that can hamper the image estimates, compensating for errors when averaging across a year allows us to generate annual estimates that are more precise, and this positive effect is amplified when error-weighted averages are used, as in the cases of the IME and CSF methods.
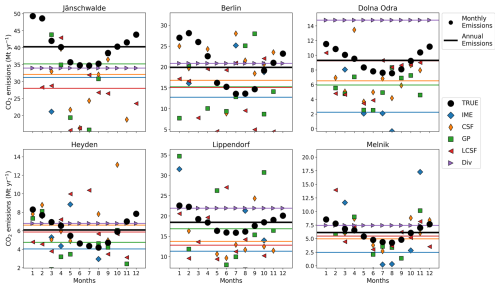
Figure 7Annual and monthly estimates of true and estimated emissions for different sources and different inversion methods. Each panel is associated with a given source. Plain lines and markers represent annual averages and monthly averages, respectively. Colors and markers are associated with different inversion methods (true emissions are represented by black circles). Annual and monthly estimates for the IME and CSF methods are the weighted means of image estimates. Annual and monthly estimates for the GP and LCSF methods are the means of image estimates, while for the divergence method, we also use the annual estimates for monthly estimates. All inversion methods use cloud-filtered CO2 and NO2 data (with only CO2 data used for the Div method) and ERA5 winds.
4.2 Monthly estimates and seasonal cycles
Monthly estimates can be computed using the same three methods as those used for the annual estimates, but, according to the results analyzed in the previous section, we choose to estimate monthly emissions using the method that leads to the best performance at the annual scale. Monthly estimates are thus calculated as arithmetic means for the GP and LCSF methods and as weighted means for the CSF and IME methods. Accordingly, considering the distributions of image estimates month by month allows us to study how well inversion approaches capture the seasonal cycle of the true emissions. The analysis in Fig. 7, however, shows that none of these approaches are able to do this when the cloudy pixels are masked: the seasonal cycle of the actual monthly emissions, i.e., the maximal/minimal emissions for winter/summer months, is not reproduced by the inversion methods, whose estimates are characterized by an erratic monthly evolution, leading to inconsistent seasonal cycles. Even when a method correctly estimates annual emissions, some of its monthly estimates may be in significant disagreement with the true monthly emissions, as is the case for the CSF method using the Heyden source and the LCSF method using the Dolna Odra source (Fig. 7). Moreover, the methods generally fail to produce estimates for the winter months of the year due to the temporal sparsity of data when the impact of cloud cover is taken into account.
If the number of estimates is higher, i.e., when clouds are not considered in the data, seasonal cycles derived from monthly estimates are in better agreement with those of the observations for most of the inversion methods, and the amplitude of the seasonal cycle of the data can be well reproduced, as is the case for the Jänschwalde and Dolna Odra sources, for example (Fig. A5). However, the averaged values of the seasonal cycles of the monthly estimates, i.e., the annual estimates, can still be in strong disagreement with those of the data, even when the number of estimates is higher. This fact supports the presence of systematic biases in the estimates, which were evidenced for most of the methods in the analysis of the results for single-image estimates (Sect. 3.1).
5.1 Accuracy vs. number of estimates
For a given benchmarking scenario, the analysis conducted in Sect. 3 evaluated the performance of the different methods in inferring estimates from individual images by considering all the estimates provided by each method for this scenario. In other words, the analysis did not integrate any diagnostics regarding the quality of the estimates from these methods. However, we demonstrated in Sect. 4.1 that computing annual means of estimates weighted by their uncertainties can significantly improve the accuracy of the annual estimates when uncertainties are effectively characterized, as in the cases of the IME and CSF methods. Therefore, a study of the performance of the inversion methods in generating single-image estimates from synthetic XCO2 images should also integrate a characterization of the quality of these estimates. More precisely, different performance indicators or error estimates can be derived from the application of the inversion methods, and such indicators can be used to identify and select the most reliable estimates. Nevertheless, there are no objective criteria for imposing a threshold on the quality of the estimates; higher-quality thresholds come with smaller sets of estimates, and optimal values depend on the inversion method. Indeed, not only do the different inversion methods calculate uncertainties in the estimates in different ways, but these computed uncertainties also reflect only part of the total/actual uncertainties, focusing on subsets of sources of uncertainties that differ across the different methods.
For a given inversion method, we attempt to create an effective quality indicator (QI) that would allow us to select estimates in such a way that the global accuracy of the method increases as the QI increases and that would provide indications of the actual/total errors. We assume that the uncertainties in the estimates derived from the methods provide the best basis we can obtain from the algorithms described in Sect. 2.1 for the derivation of such an indicator. In principle, since we are dealing with sources of quantitatively different amplitudes (see Sect. 2.3), we should derive the QI in terms of relative uncertainty. Moreover, if we define the QI as a threshold, selecting the estimates whose relative uncertainties are below it, we should select the most reliable estimates, regardless of the strength of the source they are associated with. However, this would be true if the methods operated independently with respect to the amplitudes of the emissions, and this is not the case for most methods, as illustrated in Sect. 3.1. The CSF and IME methods, for example, strongly overestimate low-emitting sources compared to high-emitting sources, which implies that the relative uncertainties in weak sources are underestimated by these methods (Fig. 3). Therefore, if the threshold value of relative uncertainty were decreased, we would tend to select more bad estimates than good ones, and the overall performance would decrease. Therefore, for these methods, we prefer to select estimates based on their uncertainties rather than their relative uncertainties, which mitigates the impact of bias on the estimation of low-emitting sources.
In any case, determining whether a QI should be based on absolute or relative uncertainties depends on whether the overall performance of the method improves when estimates with decreasing absolute or relative uncertainties are chosen. Preliminary tests (not shown here) have established that the overall accuracy of the IME and CSF methods increases when the absolute uncertainty below which estimates are selected decreases. For the GP and LCSF methods, this behavior is observed when relative uncertainties are used to discriminate estimates. Consistently, for all methods, an increase in performance is associated with a reduction in the number of estimates, and, in order to obtain a significant number of high-quality estimates, the value of uncertainty corresponding to the maximal accuracy of the method is arbitrarily set to the 10th percentile of the distribution of the absolute or relative uncertainties. Then, by varying the QI between this value and the maximal uncertainty in its estimates, each method can be associated with a range of accuracies and the respective number of estimates for a specific benchmarking scenario (e.g., the cloud-filtered or cloud-free configuration). In other words, inversion results can be represented by curves illustrating accuracy vs. the number of estimates, which provides, for each inversion method, a complete overview of its performance in terms of accuracy and the number of estimates.
To assess the inherent performance of the methods without considering the impact of cloud cover or uncertainty in the winds, inversion results are analyzed with respect to the inversion configuration using cloud-free XCO2 and NO2 data and SMARTCARB winds, i.e., the same winds used to generate the synthetic XCO2 and NO2 observations. Figure 8 illustrates that the overall accuracies of the CSF and IME methods are highly dependent on their selection of estimates and are therefore strongly correlated with the number of estimates they provide. For instance, the IME and CSF methods exhibit large increases in the third quartiles of their deviation distributions when the QIs of their estimates decrease, rising from 81 % to 231 % (IME) and from 43 % to 75 % (CSF). For these methods, selecting estimates based on their quality indicators appears to be effective as the third quartiles and 95th percentiles, which indicate the proportion of poor estimates, significantly decrease with an increasing quality index, i.e., with a decreasing number of estimates. Therefore, the IME and CSF methods are very likely to produce reliable uncertainty estimates in the individual emission estimates, and the definition and derivation of their QIs reflect the level of accuracy of their estimates.
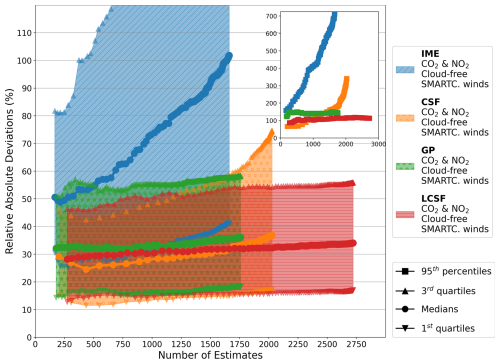
Figure 8Accuracy of inversions vs. the number of single-image estimates. The inversion methods shown here use cloud-free CO2 and NO2 data and SMARTCARB (SMARTC.) winds. The filled areas represent the interquartile ranges of the distributions of the relative absolute deviations, based on the number of estimates. The 95th percentiles of the distributions are represented in the inset. Points belonging to the same curve are associated with different QIs, and from left to right along the curves, points are associated with a decreasing QI. The points at the left and right ends of the curves are associated with the maximal and minimal QIs, respectively.
The LCSF and GP methods display a slight correlation between most of their accuracy indicators and the number of estimates. For instance, the third quartiles of the distributions of relative absolute deviations remain relatively stable, varying only from 46 % to 56 % and from 51 % to 59 % for the LCSF and GP methods, respectively, over the entire range of the number of estimates. For these methods, the trade-off between precision and the number of estimates is not a critical issue, and retrieving a significant number of estimates does not imply a significant deterioration in accuracy. On the other hand, this also indicates that the current quality indicators for the GP and LCSF methods do not reflect the total/actual uncertainties in their estimates.
As the methods present different sensitivities of accuracy to the number of estimates, the relative performances of the methods in terms of accuracy change according to the number of estimates. In other words, as is the case for the LCSF and CSF methods (Fig. 8), one method may outperform another method depending on the number of estimates we consider. Indeed, when considering fewer than 1000 estimates, the CSF method is characterized by better precision than the LCSF method for all statistical indicators and, in particular, for the 95th percentile of the deviation distribution. The best performance of the CSF method in terms of precision is then reached when using ∼ 400 estimates, where the median of the deviations is ∼ 25 % compared to ∼ 29 % for the LCSF method. However, if the number of estimates increases beyond 1000, the LCSF method starts outperforming the CSF method with respect to the 95th percentile, and when estimates are not filtered by their QI (right ends of the curves in Fig. 8), it totally outperforms the CSF method, not only in terms of precision, but also in terms of the number of estimates. If all estimates are considered, the LCSF (CSF) method generates 2722 (2028) estimates, whose deviations from the truth are characterized by an IQR of 17 %–56 % (17 %–75 %). Furthermore, the LCSF method discards outliers much more efficiently than the CSF method, insofar as the 95th percentile of the deviation distribution is much lower for the former method (118 %) than for the latter method (341 %).
Selecting one method over another involves making a trade-off between precision and the number of estimates obtained. Taking the example from Fig. 8, if the primary objective of an application is to obtain as many estimates as possible, the LCSF method is the preferred choice as it can provide 2722 estimates, with the IQR of the deviations ranging from 17 % to 56 %. On the contrary, if the main priority is to obtain estimates with the highest precision, the CSF method is more suitable, providing approximately 400 estimates, with the IQR of the deviations ranging from 11 % to 45 %. The trade-off between accuracy and the number of estimates in the choice of method is even more accentuated in the case where inversions are made with ERA5 as the use of this wind product increases the accuracy of the CSF method by compensating for biases (Sect. 3.4). In this case, using the CSF method, maximum precision can be obtained, with an IQR ranging from 11 %–42 % for 650 estimates. If, on the other hand, the LCSF method is used, a maximum number of estimates (2670) can be obtained with an IQR of 18 %–55 % (Fig. A6).
The difficulty in achieving the best possible precision for a given method lies in determining an appropriate QI for its estimates. Here, we adopted a relatively simple approach by defining high-quality estimates as those with relative or absolute errors below the 10th percentile of the distribution relative to all the uncertainties in the estimates. However, as seen in the curves in Fig. 8, the highest precision may not be achieved at this value but at a higher one, as seen in the examples of the IME and CSF methods. This is because misleading estimates, such as those resulting from the overlap of plumes from two sources, can be characterized simultaneously by both very small uncertainties and significant deviations from the truth, and their impact on the results becomes significant when the number of estimates is relatively small. More generally, the QIs defined in this study reflect the actual uncertainties in the estimates to varying degrees, and the definition of a more reliable QI that ensures increased accuracy with higher index values and delivers the maximum achievable precision for all of the methods is beyond the scope of this study as it likely requires extensive research in order to provide a common and accurate characterization of the total uncertainties in the estimates for all the inversion methods. Finally, we note that all the qualitative insights stated above about the relationships between accuracy and the number of estimates are also valid when considering inversions using cloud-filtered data and ERA5 winds (Fig. A7).
5.2 Single methods vs. ensemble approaches
In this study, we create ensemble approaches by averaging the single-image estimates – for the same source and from the same individual image – produced by different inversion methods. The aim is to obtain more robust and reliable predictions when individual biases and errors associated with each approach compensate for one another. We thus want to analyze whether an ensemble method, although more expensive from a computational point of view, would perform quantitatively better than any single method among the CSF, GP, and LCSF approaches, with these methods clearly outperforming the IME method in terms of accuracy and the number of estimates.
Four sets of ensemble approaches are considered: the first one integrates the CSF, GP, and LCSF inversion methods, and the remaining three integrate pairs of methods (CSF and GP, CSF and LCSF, and GP and LCSF). Moreover, in order to assess the impact of the QIs of the different inversion methods on the performance of the ensemble methods, results are analyzed by considering (1) all estimates and (2) only the best estimates produced by each method. As results are assessed for inversions using ERA5 winds and cloud-filtered data, which provide a relatively small number of estimates, we consider the best estimates to be those whose relative/absolute errors are below the 25th percentile of their respective error distributions.
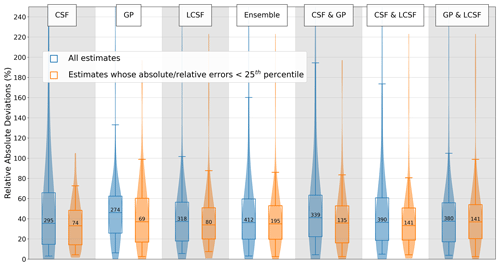
Figure 9Performance of the inversion methods and ensemble approaches when estimating emissions with cloud-filtered CO2 and NO2 data and ERA5 winds. The distributions of the relative absolute deviations for all inversion results (in blue) and for the best estimates (in orange), provided by each method (see the text), are illustrated using violin plots. The boxes represent the interquartile ranges of the distributions, the whiskers indicate the 5th and 95th percentiles, and the lines within the boxes represent the medians. Numbers in the interquartile-range boxes represent the number of estimates for each benchmarking scenario and inversion method.
The ensemble approaches do not provide clear improvements in terms of estimate accuracy over the individual methods from which they are derived (Fig. 9), except with regard to the significant number of outliers produced by the CSF method when estimates are not filtered: the 95th percentile of the deviation distribution corresponds to 286 % for the CSF method only, while it decreases to 160 % for the ensemble approach combining the CSF, GP, and LCSF methods. On the other hand, the skewness of the CSF distribution of deviations leads to an increase in the 95th percentile of the deviations of the ensemble approaches compared to the 95th percentiles of the deviations of the LCSF and GP methods. Otherwise, the IQR of the deviations is similar for all the ensemble and individual approaches, roughly ranging from 15 % to 65 % when estimates are not selected based on their uncertainty and from 15 % to 60 % when the best estimates are selected. Therefore, errors and biases in the estimates produced by a given method are generally not compensated for by the estimates of other inversion methods, which suggests that, in general, for the same images and sources, the estimates produced by other inversion methods may also present larger errors or similar biases.
The great benefit of using ensemble approaches lies in the significant increase in the number of estimates, which is a crucial issue in the real world when the amount of satellite data is strongly limited by cloud cover. The ensemble approach combining the CSF, GP, and LCSF methods can supply a maximum of 412 estimates over the year analyzed in this study, representing a 30 % increase compared to the LCSF method, which is the individual method that supplies the most estimates (318). This result indicates that the CSF, GP, and LCSF methods can provide estimates from different images; i.e., if one method does not provide an estimate from a given image, another method in the ensemble may, conversely, provide one (Fig. A8). This allows the ensemble method to produce a maximum number of estimates (412) that is close to the number of usable satellite images (∼ 500). When only the best estimates are considered, the ensemble approach generates more than twice as many values compared to the LCSF method (195 vs. 80), whereas the other ensemble approaches (CSF and GP, CSF and LCSF, and GP and LCSF) only provide about 140 estimates.
While combining the estimates generated by the CSF, GP, and LCSF methods seems to be the optimal choice for an ensemble approach, providing the largest number of predictions, the computational cost of using these methods together may not outweigh the benefits in terms of the number of estimates produced compared to when using a single method. For example, in the most realistic scenario of inversions conducted with cloud-filtered data and ERA5 winds, the computational time required for the CSF–GP–LCSF ensemble method is more than 3 times that of the LCSF method alone (see Sect. 2.1), whereas the overall precision of the LCSF method is better, and the increase in the number of estimates is only 30 % when using the ensemble approach. Therefore, if the performance of computer systems remains an important factor to take into account, one would prefer to use the LCSF method, which is the fastest method in this study, instead of an ensemble approach.
In order to investigate the benefit of using ensemble approaches for the estimation of annual emissions, we use the same three individual methods (i.e., the LCSF, GP, and CSF approaches), which produce much better results than the IME and Div methods (see Sect. 4.1). However, we consider different definitions of the annual estimates depending on the inversion method: annual estimates are calculated as arithmetic means of image estimates for the LCSF and GP methods, whereas they are computed as weighted means for the CSF method. This choice corresponds to the best performance at the annual scale found in this study for each method (Sect. 4.1.) Besides, no selection of the estimates was performed to compute the annual estimates, although the quality of the estimates is integrated within the annual estimates of the CSF method, which are averages weighted by the errors in the estimates. Among the ensemble methods considered here, for most of the benchmarking scenarios, only the approach combining the CSF and GP methods yields better results than the best individual method included in it (Fig. A9). For example, when inversions are performed with cloud-filtered data and SMARTCARB winds, the CSF method, the GP method, and their ensemble approach are characterized by relative RMSEs equal to 18 %, 20 %, and 16 %, respectively. The benefit of using ensemble methods for estimating annual estimates is thus questionable, especially considering that the gain in accuracy, if any, is very small compared to the accuracy of the individual methods, which, depending on the inversion scenario, produce more accurate annual estimates. This is due to the fact that the inversion methods generate annual estimates that are generally biased in the same way: emissions from strong sources are generally underestimated, while emissions from weak sources are generally overestimated (see the median values in Fig. 6).
In this paper, we tested and benchmarked several lightweight data-driven inversion methods for estimating local (city and power plant) emissions from XCO2 and NO2 satellite images. The five methods studied were the integrated mass enhancement (IME), cross-sectional flux (CSF), Gaussian plume (GP), light cross-sectional flux (LCSF), and divergence (Div) methods, with the latter generating only annual estimates. Using a domain centered over the city of Berlin, extending about 750 km from east to west and 650 km from south to north, inversions were performed with almost 1 year of synthetic SMARTCARB XCO2 and tropospheric-column NO2 satellite observations, featuring characteristics similar to those of the upcoming CO2M mission. The ability of the inversion methods to estimate emissions was assessed by comparing the deviations of the estimates from the corresponding true values used in the simulations across 16 sources, including the city of Berlin and 15 power plants. To obtain a complete overview of the performance, several benchmarking scenarios were considered in order to analyze the benefits of using auxiliary NO2 data, as well as the impacts of cloud cover on the data and uncertainties in wind data.
In terms of quantifying emissions from single satellite images, the implementations of the CSF, GP, and LCSF methods used in this study outperform that of the IME method. Furthermore, we have demonstrated that the performance, in terms of accuracy and the number of estimates, varies to a greater or lesser extent depending on the method, with the selection of the estimates based on their relative or absolute uncertainty. The overall accuracy of the IME and CSF methods is significantly enhanced when a strict screening for high-quality estimates is applied, but this is at the cost of a notable decrease in the number of estimates. The GP and LCSF methods, on the other hand, perform more robustly, showing only a variation in their global precision with increasing quality screening. This behavior highlights the need for these methods to better characterize the uncertainties in the estimates. When estimates are filtered, the CSF method yields the best results in terms of accuracy, whereas when estimates are not filtered, the LCSF method provides the highest number of estimates, with a slight decrease in accuracy. Overall, the CSF, GP, and LCSF methods show similar accuracies for all the benchmarking scenarios, and when the less reliable estimates of the CSF method are removed, most of IQRs of the absolute deviations range from 15 % to 60 %, with the average of the median values being around 35 %. Moreover, for the most realistic benchmarking scenario, i.e., for the inversions using cloud-filtered NO2 and CO2 data and ERA5 winds, the IME, CSF, GP, and LCSF methods generate, on average, 6 (IME), 18 (CSF), 17 (GP), and 20 (LCSF) estimates per source per year, with great differences observed between sources (see Sect. 3.3). This is equivalent to a maximum number of estimates of 96 (IME), 295 (CSF), 274 (GP), and 318 (LCSF) for all 16 sources. These figures are significantly lower than the number of usable images (∼ 500) that a hypothetical constellation of three satellites can provide, as analyzed here. This suggests that methodological improvements could increase the number of estimates.
The accuracy of the CSF and IME methods was found to depend on the strength of the sources, with significant errors occurring when determining low emissions; the GP and LCSF methods, in contrast, showed similar performances across different ranges of emissions. Moreover, the advantage of using co-located NO2 signals for plume detection and quantification appeared to be clear for the CSF, IME, and GP methods, for which the number of single-image estimates significantly increased, whereas this advantage was rather weak for the LCSF method. When a cloud cover mask was applied to the data, the number of estimates significantly decreased for all the inversion methods, with an average reduction of 85 %. The global precision, however, hardly decreased and even improved for the IME method. For all the inversion methods, the sensitivities of the results to wind uncertainties were surprisingly found to be insignificant when replacing the SMARTCARB winds (used in the simulation) with ERA5 reanalysis winds. Finally, if we do not take computational cost into account, the interest in using ensemble approaches instead of a single method lies mainly in the increased number of single-image estimates as the available estimates from the different methods complement each other.
Part of the effectiveness of the implementations of the cross-sectional flux method may come from the generation of multiple estimates of cross-sectional fluxes along plumes and subsequent averaging in order to obtain a unique emission estimate for a given source and satellite overpass. It is probable that errors in the satellite data or in the simplifying assumptions of the cross-sectional approaches partly cancel each other out when averaging. The CSF implementation uses a complex algorithm for plume detection, which makes it possible to use the total detectable plume, probably leading to estimates more accurate than those of the LCSF implementation, which only uses observations near the source. However, plume detection and the computation of the curved centerline can fail for weak sources (i.e., short plumes), resulting in a large number of outliers. In contrast, the LCSF implementation uses a simpler but more robust algorithm that employs the wind vector to estimate the location of the plume, which likely explains why this method generates more estimates and does so without the need for NO2 data, unlike the CSF implementation. However, efforts should be made to correct the systematic underestimation of strong emissions by the LCSF implementation. A way forward could involve merging the CSF and LCSF methods into a single algorithm that leverages the advantages of both approaches.
When compared to other methods, the relative ability of the GP method in estimating emissions probably relies on the use of a Gaussian function, whose optimization determines the emissions while taking into account the entire structure of the plumes, and on calculating effective winds that are consistent with those of the plumes. However, this optimization – and thus the performance of the GP method – highly depends on the first-guess values assigned to its parameters (not shown). Moreover, in this study, the first-guess values of the emissions correspond to the summer average emissions for each source; this could serve as a strong constraint on the estimated values and may lead to an overestimation of the GP method's performance in this benchmarking study. Finally, the GP method is computationally expensive due to its “heavy” plume detection algorithm and the multi-parameter optimization required for the Gaussian fitting of the plumes (Table 1).
The IME method also integrates information retrieved from the entire structure of the plumes, but, unlike the GP method, it does not use this information when computing effective winds. Therefore, these winds may be inconsistent with the characteristic lengths of the plumes used in the IME method to estimate CO2 emissions (Sect. 2.1.4), which could explain the relatively poor performance of the IME method in this study. Varon et al. (2018) probably found that the IME method was adapted to estimate CH4 emissions from high-resolution plumes because they inferred a relationship between the effective winds and characteristic lengths through LESs. Another drawback of the IME method is that it is very sensitive to missing data as it requires complete coverage of the plume area by data to efficiently integrate the total mass enhancement. Other single-image methods (GP, CSF, and LCSF) are less sensitive to missing data as they fit functions to the data and can handle data gaps; this explains why these methods provide a much larger number of estimates when the impact of cloud cover on data is considered (see Sect. 3.3).
In this study, we chose not to analyze the potential of the divergence method for estimating instant emissions from single satellite overpasses due to the lack of studies on such an application of this method. As highlighted in the Introduction, our aim is to compare proven approaches for the local-scale estimation of strong sources (such as the application of the divergence method to time averages of satellite images). Moreover, the strong spatial variability in the divergence fields derived from single images suggests that only averaged fields could be processed properly with the version of the divergence approach used here for annual estimates, which relies on the peak fitting of temporally averaged divergence fields. However, we conducted some preliminary analysis on a version of the divergence method that integrates the divergence signal spatially (over disks centered on the sources). The results, documented in Appendix A, demonstrate that with a range of integration radii close to that of the spatial resolution of the image, this approach could yield estimates that would be comparable in terms of accuracy and quantity to those of the best inversion methods in our benchmark evaluation for single-image-based estimates. A better understanding of the behavior of this approach as a function of the integration radius, as well as an assessment of the estimation errors, is needed to conduct a proper comparison with the other methods. This deserves further investigation. However, these preliminary results raise optimistic perspectives regarding the potential of using the divergence method for estimating instant emissions from single-overpass images.
When estimating annual emissions, the CSF, GP, and LCSF methods outperform the Div and IME methods when annual estimates are computed as error-weighted means of single-image estimates for the CSF method and as arithmetic means of these estimates for the GP and LCSF methods. Across the different benchmarking scenarios, the GP method shows better precision in its annual estimates because its single-image estimates exhibit similar absolute deviations from the truth but are less affected by biases compared to the CSF and LCSF methods (see Fig. 3). However, despite biases, errors in the single-image estimates provided by the CSF, GP, and LCSF methods are likely compensated for when averaging, and these methods also generate annual estimates with better precision compared to that used to generate single-image estimates. In the most realistic benchmarking scenario – where inversions use cloud-filtered XCO2 and NO2 data and ERA5 winds (and where performance is the lowest compared to other scenarios) – the relative RMSEs for the annual emissions of the 16 sources are 20 % (GP), 27 % (CSF), 31 % (LCSF), 55 % (IME), and 79 % (Div). The relatively weak performance of the Div method could be explained by the fact that this method was originally developed for the estimation of NOx emissions and by how the fields of this chemical species are generally characterized by stronger divergence peaks compared to those of CO2 fields. Its performance may also be hindered by the fact that our implementation of this method does not select the overpasses from which the annual divergence maps are derived (see Sect. 4.1). Further investigation is needed to determine whether filtering the overpasses, which could be favorable to the method, would strongly increase the accuracy of the method's annual estimates. The performance of ensemble approaches, which combine several inversion methods with respect to annual estimates, is not better – and in some cases, even worse – than the individual methods. Finally, none of the methods were able to correctly reproduce the monthly seasonal cycle of the emissions when the data underwent cloud filtering, i.e., when data were not available for some months, which highlights the need for extensive temporal coverage of the observations when aiming to capture the monthly variability in emissions.
In addition to the technical improvements that could be made to the algorithms of the methods, further developments could extend this study, such as the integration of new data streams for estimating CO2 emissions. These include satellite data of co-emitted gases other than NO2, e.g., CO data provided by TROPOMI. A companion paper (Hakkarainen et al., 2024) analyzes the ability of the inversion methods to determine NOx emissions from synthetic and TROPOMI NO2 satellite data derived from the Matimba and Medupi power plants in South Africa. The synthetic NO2 data are extracted from the high-resolution MicroHH large-eddy simulations (LESs) (van Heerwaarden et al., 2017) and are used, in particular, to study the NO2-to-NOx scaling factors that are required for satellite-based estimations of NOx emissions. Moreover, the capacity of the inversion methods to estimate city emissions has been analyzed in this study using the single example of the city of Berlin, and, as most of the methods provided correct estimates for its emissions, it would be interesting to expand this study to other cities and other local sources. Finally, this benchmarking study has not integrated the new and promising inversion methods derived from deep learning techniques (e.g., Lary et al., 2016). After a potentially complex training phase, deep learning methods could quickly process large amounts of data and provide estimates with similar or better accuracy than those generated by the methods studied here (Dumont le Brazidec et al., 2024). They could also complement these methods by enabling finer differentiation of the plumes from the background using advanced image segmentation techniques.
The aim of this study is to contribute to the development of the CO2 Monitoring and Verification Support system, which will use satellite data from the upcoming CO2M mission. Moreover, although this benchmarking study was performed using synthetic observations, the methods studied here can be easily adapted for the analysis of real satellite observations and to deal with sources of unknown locations, as demonstrated in Hakkarainen et al. (2024).
In this study, the performance of the divergence approach in estimating local CO2 emissions from synthetic satellite images of XCO2 and NO2 is assessed using a standard version of this approach (e.g., Beirle et al., 2021; Hakkarainen et al., 2022), which provides temporally averaged estimates. Thus, in the main part of this paper, results concerning the divergence approach are analyzed in terms of annual means. However, following the suggestions of a reviewer (Steffen Beirle), we also tested the potential of this method for estimating instant emissions using single-overpass images. For this purpose, we used two versions of the divergence approach that were modified for single-image geometry, as described in Beirle et al. (2023).
Figure A1Illustration of the divergence method used for the Jänschwalde power station in 2015, based on the synthetic SMARTCARB dataset (see the text). The panels represent the annual fields of the computed CO2 divergence (a) and the modeled CO2 divergence (b), as well as the difference between both quantities (c). The sink terms are considered negligible for CO2, while the divergence fields are considered equal to the emission fields for CO2.
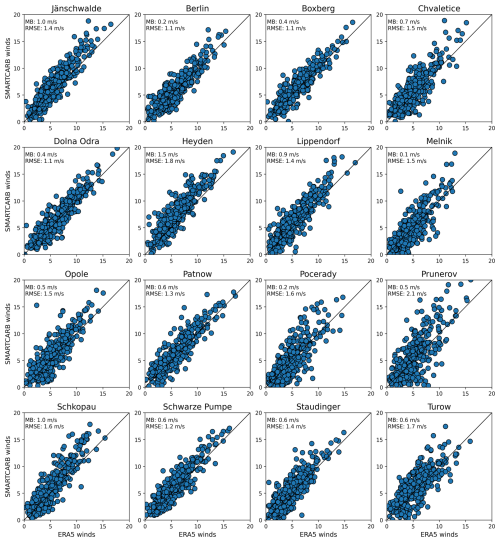
Figure A2Norms of the ERA5 winds vs. norms of the SMARTCARB winds at the sources considered in this study for all the days of 2015. Black lines each represent the 1:1 agreement line. Mean biases of the SMARTCARB norms minus the ERA5 norms, as well as the RMSEs, are noted in the top-left corners of the panels. MB: mean bias.
For both versions, the computation of the divergence fields is performed by only considering the advective term () of the full expression of the horizontal flux divergence (), where Mair is the dry-air mass, U is the wind vector, and VCD is the vertical column density (expressed in parts per million). Such reformulation of the divergence method, which does not compute the divergence of the wind term, was also used by Beirle et al. (2023) for NO2. The advantage of this reformulation for CO2 is that the background (e.g., a constant offset of 400 ppm) is implicitly removed.
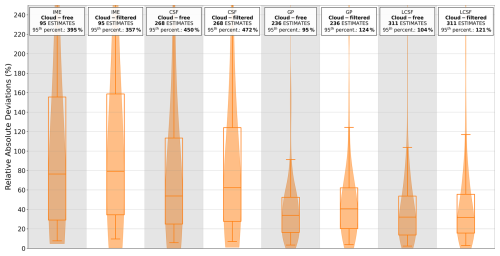
Figure A3Performance of the inversion methods when using data with or without clouds for emissions estimated from the same images. The inversion methods use CO2 and NO2 data and SMARTCARB winds. The boxes represent the interquartile ranges of the distributions of the absolute relative deviations, the whiskers indicate the 5th and 95th percentiles, and the lines within the boxes represent the medians. Note that “percent.” stands for percentile.
Figure A4Performance of the LCSF method when estimating emissions from single images of CO2 and NO2 without considering clouds (in red) and for different cloudiness thresholds (1 % (in blue), 2 % (in orange), and 5 % (in green)). Distributions of the relative deviations (a) and relative absolute deviations (b) are illustrated using violin plots. The boxes represent the interquartile ranges of the distributions, the whiskers indicate the 5th and 95th percentiles, and the lines within the boxes represent the medians. Numbers in the interquartile-range boxes represent the number of estimates for each benchmarking scenario.
These versions of the divergence approach differ from each other in how they compute emissions from the divergence maps associated with single-overpass images. The first version integrates the divergence fields over disks centered on the sources (Fig. A10). Moreover, to mitigate the impact of the uncertainties in the observations, the emission estimate for a given satellite overpass and source can be computed as the average of the estimates when integrating the divergence signal over disks of different radii. This version of the divergence approach will be referred to hereinafter as the integral divergence method. The second version proceeds in a similar way to the one used in the main part of the article and fits a 2-D Gaussian function to the divergence maps in order to retrieve source emissions (e.g., Beirle et al., 2020). The modified peak-fitting model is similar to the original model but has a reduced number of estimated parameters. Namely, the parameters related to the background and those related to the location correction are removed from the model. This version of the divergence approach will be referred to hereinafter as the peak-fitting divergence method.
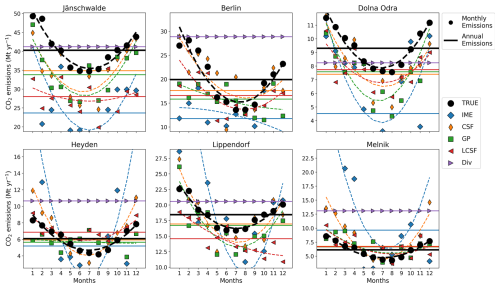
Figure A5Annual and monthly estimates of true and estimated emissions for different sources and different inversion methods. Each panel is associated with a given source. Plain lines and markers represent annual averages and monthly averages, respectively. Dashed lines represent the fits of the monthly estimates by a second-order polynomial. Colors are associated with different inversion methods (true emissions are shown in black). Annual and monthly estimates for the IME and CSF methods are the weighted means of image estimates. Annual and monthly estimates for the GP and LCSF methods are the means of image estimates, while for the divergence method, we also use the annual estimates for monthly estimates. All inversion methods use cloud-free CO2 and NO2 data (with only CO2 data used for the Div method) and ERA5 winds.
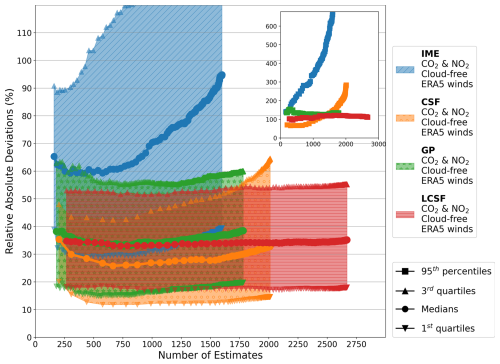
Figure A6Accuracy of inversions vs. the number of instant estimates. The inversion methods shown here use cloud-free CO2 and NO2 data and ERA5 winds. The filled areas represent the interquartile ranges of the distributions of the relative absolute deviations, based on the number of estimates. The 95th percentiles of the distributions are represented in the inset. Points belonging to the same curve are associated with different QIs, and from left to right along the curves, points are associated with a decreasing QI. The points at the left and right ends of the curves are associated with the maximal and minimal QIs, respectively.
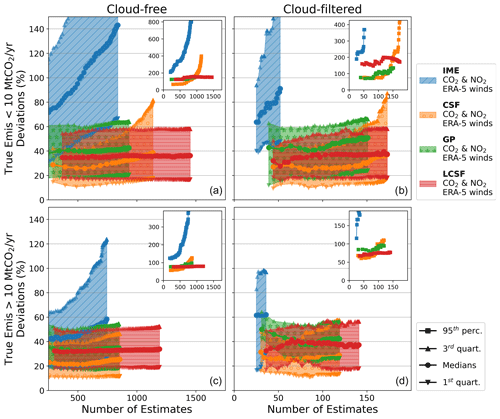
Figure A7Accuracy of inversions vs. the number of instant estimates. The inversion methods shown here use CO2 and NO2 data, ERA5 winds, and either cloud-free (a, c) or cloud-filtered data (b, d). Results are shown for cases where true CO2 emissions from sources are below (a, b) or above (c, d) 10 Mt yr−1. The filled areas represent the interquartile ranges of the distributions of the relative absolute deviations, based on the number of estimates. The 95th percentiles of the distributions are represented in the insets. Each point belonging to the same curve is associated with a different QI, and from left to right along the same curve, points are associated with a decreasing QI. “True Emis” stands for true emissions, “perc.” for percentile, and “quart.” for quartile.
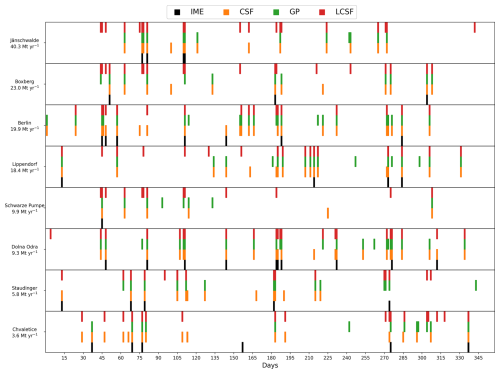
Figure A8Estimates produced by the IME, CSF, GP, and LCSF methods across the days of 2015 (x axis) for CO2 emissions from eight sources (y axis). For a given day, the availability of an estimate from a given inversion method is illustrated by a color bar (for an explanation of the colors, see the figure legend). Inversions use cloud-filtered CO2 and NO2 data and ERA5 winds.
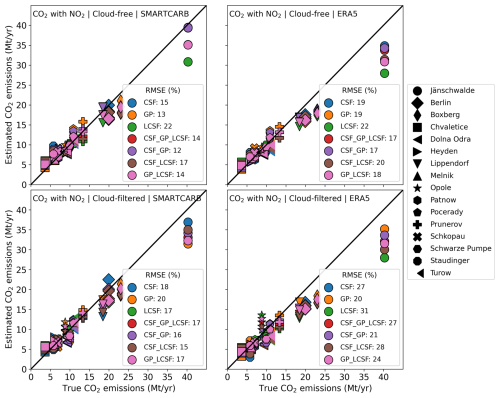
Figure A9Estimated vs. true annual emissions for four inversion scenarios (titles of the panels). Results are displayed for the CSF, GP, and LCSF methods, as well as for the ensemble methods, which combine two or three of these individual methods (e.g., CSF_GP). For the CSF method, annual estimates are calculated as weighted means of the instant estimates, while they are calculated as arithmetic means for the GP and LCSF methods. Each marker represents a given emission source, and each color indicates a given inversion method. The divergence inversion method uses CO2 data only for all the inversion scenarios. The plain line represents the 1:1 line. In each panel, the legend in the bottom-right corner displays, for each inversion method, the relative RMSE, which is calculated by dividing the RMSE between estimated and true annual emissions by the median of the true annual emissions from all sources (∼ 9.6 Mt CO2 yr−1).
For both versions, potential peaks are detected using NO2 fields, which are integrated over disks with a 6 km radius centered on the sources. If the integral of the divergence map on the disk is larger than the integral of the area outside the disk, then the enhancement, related to a given source and satellite overpass, is considered strong enough, and the emission estimation can be carried out. Many sources in the SMARTCARB dataset are weak, and enhancements may be barely visible, which causes challenges for both versions.
To evaluate the potential of these two versions of the divergence approach, we use the SMARTCARB dataset described in Sect. 2.2, which provides about 3000 images, to determine the emissions of the 16 local sources that are considered in this study (if we take cloud cover into account, only 500 images remain usable). Furthermore, we consider two benchmarking scenarios where inversions are performed using CO2 and NO2 data with SMARTCARB winds (see Table 2 and Sect. 2.3). In one case, we use cloud-free data, while in the other, we use cloud-filtered data.
An analysis of the deviations from the truth of the instant estimates shows that the integral divergence approach is strongly sensitive to the radius of the integration disks (Fig. A11). No clear trend appears; however, errors increase sharply for radii greater than 10 km, with a significant presence of outliers. Below this value, the absolute relative deviations (Fig. A11b) may increase or decrease, depending on the value of the radius. Furthermore, the integral divergence approach may underestimate or overestimate emissions, depending on whether the radius is smaller or greater than ∼ 4 km. A possible explanation for this behavior could be that the impacts of the two main sources of errors in the divergence method – namely, the uncertainties in the observations and the influence of additional, but unwanted, sources on the background of the divergence fields – evolve in opposite directions as the integration radius increases. The impact of the uncertainties is mitigated when the area of the integration disk increases because errors are more likely to cancel each other out. Conversely, the impact of neighboring sources on the background of the divergence field intensifies as the integration radius increases because the likelihood of capturing features in the divergence maps that are not directly related to the emissions of the targeted sources grows. This impact consistently introduces a positive bias into the estimates (as we capture more sources) and is likely more important than the one related to the uncertainties as the overall performance degrades when the integration radius increases.
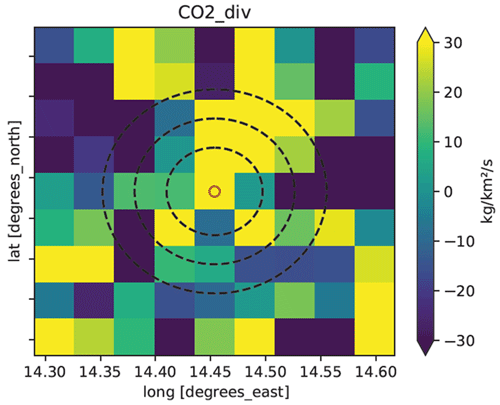
Figure A10Divergence map estimated around the Jänschwalde power station on 12 January 2015. Dashed circles indicate different radii (3, 5, and 7 km) that define integration disks that can be used by the integral divergence method.
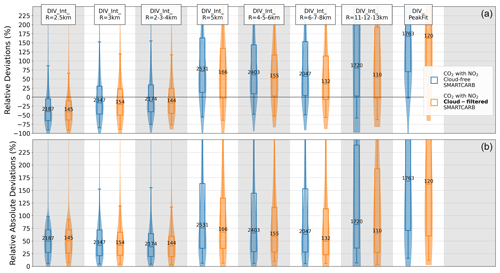
Figure A11Performances of the different versions of the divergence inversion method when estimating emissions from 1 year of single images for different benchmarking scenarios: cloud-free CO2 and NO2 data with SMARTCARB winds (in blue) and cloud-filtered CO2 and NO2 data with SMARTCARB winds (in orange). Distributions of the relative deviations (a) and relative absolute deviations (b) are illustrated using violin plots. The boxes represent the interquartile ranges of the distributions, the whiskers indicate the 5th and 95th percentiles, and the lines within the boxes represent the medians. Numbers in the interquartile-range boxes represent the number of estimates for each benchmarking scenario and inversion method. The methods “DIV_Int_R = x km” and “DIV_PeakFit” are the integral version (for an integration radius of x km) and peak-fitting version of the divergence approach, respectively. For a given overpass and source, the emission estimate of the method “DIV_Int_R = x–y–z km” is the average of the estimates when integrating over circles with radii of x, y, and z km around the source.

Figure A12Performances of the inversion methods when estimating emissions from 1 year of single images for different benchmarking scenarios: cloud-free CO2 and NO2 data with SMARTCARB winds (in blue) and cloud-filtered CO2 and NO2 data with SMARTCARB winds (in orange). Distributions of the relative deviations (a) and relative absolute deviations (b) are illustrated using violin plots. The boxes represent the interquartile ranges of the distributions, the whiskers indicate the 5th and 95th percentiles, and the lines within the boxes represent the medians. Numbers in the interquartile-range boxes represent the number of estimates for each benchmarking scenario and inversion method. The methods “DIV_Int_R = 2–3–4 km” and “DIV_PeakFit” are the integral and peak-fitting versions of the divergence approach, respectively. For a given overpass and source, the emission estimate of the method “DIV_Int_R =2–3–4 km” is the average of the estimates when integrating over circles with radii of 2, 3, and 4 km around the source.
The peak-fitting divergence method is characterized by poor performance compared to the integral divergence method across the ensemble of integration radii considered here (Fig. A11). Estimating low-emitting sources may be more difficult for the peak-fitting version as the fit of the 2-D Gaussian function to the data associated with these sources often fails and does not provide optimal and reliable parameter combinations, yielding poor and often overestimated emission estimates. Therefore, even though the peak-fitting divergence method is generally more efficient at the annual scale, these results suggest that this is not the case when estimating instant emissions from single-overpass images.
The configuration of the integral divergence method, which averages estimates across the integration radii of 2, 3, and 4 km, shows the best performance amongst the configurations that we have tested. This is probably due to how the impacts of the data uncertainties and the background are well balanced for this range of radii and the fact that averaging estimates across three different radii further reduces the influence of the data uncertainties on the results. When compared to other inversion methods analyzed in this study, the performance of this configuration of the integral divergence method is similar to that of the best inversion methods (Fig. A12). For the benchmarking scenario considering cloud-free data, the relative absolute deviations are characterized by a median value of ∼ 38 % and an interquartile range (IQR) of ∼ 19 % to ∼ 64 %; these values are comparable to deviations associated with the light cross-sectional flux (LCSF) method, which has a median value of ∼ 32 % and an IQR of ∼ 15 % to ∼ 56 %. Notably, the integral divergence method generates fewer estimates (2174) than the LCSF method (2722) but more than the Gaussian plume (GP) method (1776).
These preliminary results regarding the potential of the integral divergence method for estimating local CO2 emissions from single-overpass images of XCO2 and NO2 appear promising, especially since this method allows for the detection of plumes from unknown sources (Beirle et al., 2021). However, further investigation is required to properly assess factors such as the integration radius based on data resolution and to generalize this method with respect to various types of satellite data. Additionally, a thorough quantitative error assessment would be essential for evaluating the accuracy of the estimates, enabling their classification and selection, which would enhance the method's overall performance.
The code for the “ddeq” Python library (version 1.0) is available in the supplement of Kuhlmann et al. (2024) via https://doi.org/10.5194/gmd-17-4773-2024. The code repository is available on GitLab (https://gitlab.com/empa503/remote-sensing/ddeq, last access: 8 January 2025).
DS performed the diagnostics and led the analysis for the intercomparison of the results from the different inversion methods. All co-authors contributed to decisions regarding the configuration, diagnostics, and analysis of the intercomparison. DS wrote the paper with input from all co-authors. DS, GB, and FC carried out the analysis specific to the LCSF method. JH, II, HL, JN, and LA carried out the analysis specific to the Div method. GK developed the original “ddeq” library, which served as the basis for the application of the different methods, and provided the SMARTCARB dataset used to test the different methods. GK also carried out the analysis specific to the IME method. EK carried out the analysis specific to the CSF and GP inversion methods. The project was coordinated by JT, DB, and GB.
At least one of the (co-)authors is a member of the editorial board of Atmospheric Measurement Techniques. The peer-review process was guided by an independent editor, and the authors also have no other competing interests to declare.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
Most of the work presented in this paper was carried out within the framework of the EU H2020 CoCO2 project (grant no. 958927). The Finnish Meteorological Institute team would like to thank the Research Council of Finland (decision no. 353082). All authors would like to thank the ICOS Carbon Portal for providing access to JupyterLab servers, which were used for code development and data sharing. Finally, the authors would like to thank the two reviewers for their insightful comments, especially Steffen Beirle, who provided suggestions on the application of the divergence approach for estimating instant emissions.
This study has been funded by the European Union's Horizon 2020 research and innovation program (grant no. 958927) (“Prototype system for a Copernicus CO2 service”).
This paper was edited by Peer Nowack and reviewed by Steffen Beirle and one anonymous referee.
Beirle, S., Borger, C., Dörner, S., Li, A., Hu, Z., Liu, F., Wang, Y., and Wagner, T.: Pinpointing nitrogen oxide emissions from space, Sci. Adv., 5, 11, https://doi.org/10.1126/sciadv.aax9800, 2019.
Beirle, S., Borger, C., Dörner, S., Eskes, H., Kumar, V., de Laat, A., and Wagner, T.: Catalog of NOx emissions from point sources as derived from the divergence of the NO2 flux for TROPOMI, Earth Syst. Sci. Data, 13, 2995–3012, https://doi.org/10.5194/essd-13-2995-2021, 2021.
Beirle, S., Borger, C., Jost, A., and Wagner, T.: Improved catalog of NOx point source emissions (version 2), Earth Syst. Sci. Data, 15, 3051–3073, https://doi.org/10.5194/essd-15-3051-2023, 2023.
Boersma, K. F., Eskes, H. J., Dirksen, R. J., van der A, R. J., Veefkind, J. P., Stammes, P., Huijnen, V., Kleipool, Q. L., Sneep, M., Claas, J., Leitão, J., Richter, A., Zhou, Y., and Brunner, D.: An improved tropospheric NO2 column retrieval algorithm for the Ozone Monitoring Instrument, Atmos. Meas. Tech., 4, 1905–1928, https://doi.org/10.5194/amt-4-1905-2011, 2011.
Bovensmann, H., Buchwitz, M., Burrows, J. P., Reuter, M., Krings, T., Gerilowski, K., Schneising, O., Heymann, J., Tretner, A., and Erzinger, J.: A remote sensing technique for global monitoring of power plant CO2 emissions from space and related applications, Atmos. Meas. Tech., 3, 781–811, https://doi.org/10.5194/amt-3-781-2010, 2010.
Broquet, G., Bréon, F.-M., Renault, E., Buchwitz, M., Reuter, M., Bovensmann, H., Chevallier, F., Wu, L., and Ciais, P.: The potential of satellite spectro-imagery for monitoring CO2 emissions from large cities, Atmos. Meas. Tech., 11, 681–708, https://doi.org/10.5194/amt-11-681-2018, 2018.
Brunner, D., Kuhlmann, G., Marshall, J., Clément, V., Fuhrer, O., Broquet, G., Löscher, A., and Meijer, Y.: Accounting for the vertical distribution of emissions in atmospheric CO2 simulations, Atmos. Chem. Phys., 19, 4541–4559, https://doi.org/10.5194/acp-19-4541-2019, 2019.
Brunner, D., Kuhlmann, G., Henne, S., Koene, E., Kern, B., Wolff, S., Voigt, C., Jöckel, P., Kiemle, C., Roiger, A., Fiehn, A., Krautwurst, S., Gerilowski, K., Bovensmann, H., Borchardt, J., Galkowski, M., Gerbig, C., Marshall, J., Klonecki, A., Prunet, P., Hanfland, R., Pattantyús-Ábrahám, M., Wyszogrodzki, A., and Fix, A.: Evaluation of simulated CO2 power plant plumes from six high-resolution atmospheric transport models, Atmos. Chem. Phys., 23, 2699–2728, https://doi.org/10.5194/acp-23-2699-2023, 2023.
Buchwitz, M., Reuter, M., Bovensmann, H., Pillai, D., Heymann, J., Schneising, O., Rozanov, V., Krings, T., Burrows, J. P., Boesch, H., Gerbig, C., Meijer, Y., and Löscher, A.: Carbon Monitoring Satellite (CarbonSat): assessment of atmospheric CO2 and CH4 retrieval errors by error parameterization, Atmos. Meas. Tech., 6, 3477–3500, https://doi.org/10.5194/amt-6-3477-2013, 2013.
Chevallier, F., Zheng, B., Broquet, G., Ciais, P., Liu, Z., Davis, S. J., Deng, Z., Wang, Y., Bréon, F.-M., and O'Dell, C. W.: Local anomalies in the column-averaged dry air mole fractions of carbon dioxide across the globe during the first months of the coronavirus recession, Geophys. Res. Lett., 47, e2020GL090244, https://doi.org/10.1029/2020gl090244, 2020.
Chevallier, F., Broquet, G., Zheng, B., Ciais, P., and Eldering, A.: Large CO2 emitters as seen from satellite: Comparison to a gridded global emission inventory, Geophys. Res. Lett., 49, e2021GL097540, https://doi.org/10.1029/2021GL097540, 2022.
Ciais, P., Crisp, D., v. d. Gon, H., Engelen, R., Heimann, M., Janssens-Maenhout, G., Rayner, P., and Scholze, M.: Towards a European Operational Observing System to Monitor Fossil CO2 emissions – Final Report from the expert group, Copernicus climate Change Service, Report, European Commission, Brussels, 68 pp., https://www.copernicus.eu/sites/default/files/2019-09/CO2_Blue_report_2015.pdf (last access: 9 January 2025), 2015.
Dumont Le Brazidec, J., Vanderbecken, P., Farchi, A., Broquet, G., Kuhlmann, G., and Bocquet, M.: Deep learning applied to CO2 power plant emissions quantification using simulated satellite images, Geosci. Model Dev., 17, 1995–2014, https://doi.org/10.5194/gmd-17-1995-2024, 2024.
Düring, I., Bächlin, W., Ketzel, M., Baum, A., Friedrich, U., and Wurzler, S.: A New Simplified NO NO2 Conversion Model under Consideration of Direct NO2-Emissions, Meteorologische Z., 20, 67–73, https://doi.org/10.1127/0941-2948/2011/0491, 2011.
Ehret, T., De Truchis, A., Mazzolini, M., Morel, J. M., D'aspremont, A., Lauvaux, T., Duren, R., Cusworth, D., and Facciolo, G.: Global tracking and quantification of oil and gas methane emissions from recurrent sentinel-2 imagery, Environ. Sci. Technol., 56, 10517–10529, 2022.
Frankenberg, C., Thorpe, A. K., Thompson, D. R., Hulley, G., Kort, E. A., Vance, N., Borchardt, J., Krings, T., Gerilowski, K., Sweeney, C., and Conley, S.: Airborne methane remote measurements reveal heavy-tail flux distribution in Four Corners region, P. Natl. Acad. Sci. USA, 113, 9734–9739, https://doi.org/10.1073/pnas.1605617113, 2016.
Hakkarainen, J., Ialongo, I., Koene, E., Szeląg, M., Tamminen, J., Kuhlmann, G., and Brunner, D.: Analyzing local carbon dioxide and nitrogen oxide emissions from space using the divergence method: An application to the synthetic SMARTCARB dataset, Front. Remote Sens., 3, 878731, https://doi.org/10.3389/frsen.2022.878731, 2022.
Hakkarainen, J., Ialongo, I., Oda, T., Szeląg, M. E., O'Dell, C. W., Eldering, A., and Crisp, D.: Building a bridge: Characterizing major anthropogenic point sources in the South African Highveld region using OCO-3 carbon dioxide Snapshot Area Maps and Sentinel-5P/TROPOMI nitrogen dioxide columns, Environ. Res. Lett., 18, 035003, https://doi.org/10.1088/1748-9326/acb837, 2023a.
Hakkarainen, J., Tamminen, J., Nurmela, J., Lindqvist, H., Santaren, D., Broquet, G., Chevallier, F., Koene, E., Kuhlmann, G. and Brunner, D.: Benchmarking of plume detection and quantification methods. Technical Report, FMI, https://www.coco2-project.eu/node/366 (last access: 9 January 2025), CoCO2: Prototype system for a Copernicus CO2 service, 2023b.
Hakkarainen, J., Kuhlmann, G., Koene, E., Santaren, D., Meier, S., Krol, M. C., van Stratum, B. J. H, Ialongo, I., Chevallier, F., Tamminen, J., Brunner, D., and Broquet, G.: Analyzing nitrogen dioxide to nitrogen oxide scaling factors for data-driven satellite-based emission estimation methods: a case study of Matimba/Medupi power stations in South Africa, Atmospheric Pollution Research, Vol. 15, 102171, ISSN 1309-1042, https://doi.org/10.1016/j.apr.2024.102171, 2024.
Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., Nicolas, J., Peubey, C., Radu, R., Schepers, D., Simmons, A., Soci, C., Abdalla, S., Abellan, X., Balsamo, G., Bechtold, P., Biavati, G., Bidlot, J., Bonavita, M., De Chiara, G., Dahlgren, P., Dee, D., Diamantakis, M., Dragani, R., Flemming, J., Forbes, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hogan, R.J., Hólm, E., Janisková, M., Keeley, S., Laloyaux, P., Lopez, P., Lupu, C., Radnoti, G., de Rosnay, P., Rozum, I, Vamborg, F., Villaume, S. and Thépaut, J-N: The ERA5 global reanalysis, Q. J. Roy. Meteorol. Soc., 1, 51, https://doi.org/10.1002/qj.3803, 2020.
Jacob, D. J.: Introduction to Atmospheric Chemistry, Princeton University Press), 280 pp., 1999.
Jacob, D. J., Varon, D. J., Cusworth, D. H., Dennison, P. E., Frankenberg, C., Gautam, R., Guanter, L., Kelley, J., McKeever, J., Ott, L. E., Poulter, B., Qu, Z., Thorpe, A. K., Worden, J. R., and Duren, R. M.: Quantifying methane emissions from the global scale down to point sources using satellite observations of atmospheric methane, Atmos. Chem. Phys., 22, 9617–9646, https://doi.org/10.5194/acp-22-9617-2022, 2022.
Jähn, M., Kuhlmann, G., Mu, Q., Haussaire, J.-M., Ochsner, D., Osterried, K., Clément, V., and Brunner, D.: An online emission module for atmospheric chemistry transport models: implementation in COSMO-GHG v5.6a and COSMO-ART v5.1-3.1, Geosci. Model Dev., 13, 2379–2392, https://doi.org/10.5194/gmd-13-2379-2020, 2020.
Janssens-Maenhout, G., Pinty, B., Dowell, M., Zunker, H., Andersson, E., Balsamo, G., Bézy, J.-L., Brunhes, T., Bösch, H., Bojkov, B., Brunner, D., Buchwitz, M., Crisp, D., Ciais, P., Counet, P., Dee, D., Denier van der Gon, H., Dolman, H., Drinkwater, M., Dubovik, O., Engelen, R., Fehr, T., Fernandez, V., Heimann, M., Holmlund, K., Houweling, S., Husband, R., Juvyns, O., Kentarchos, A., Landgraf, J., Lang, R., Löscher, A., Marshall, J., Meijer, Y., Nakajima, M., Palmer, P., Peylin, P., Rayner, P., Scholze, M., Sierk, B., Tamminen, J., and Veefkind, P.: Towards an operational anthropogenic CO2 emissions monitoring and verification support capacity, B. Am. Meteorol. Soc., 101, E1439–E1451, https://doi.org/10.1175/BAMS-D-19-0017.1, 2020.
Kasahara, M., Kachi, M., Inaoka, K., Fujii, H., Kubota, T., Shimada, R., and Kojima, Y.: Overview and current status of GOSAT-GW mission and AMSR3 instrument, in: Sensors, Systems, and Next-Generation Satellites XXIV, Vol. 11530, p. 1153007, SPIE, https://doi.org/10.1117/12.2573914, 2020.
Koene, E. and Brunner, D.: Assessment of plume model performance. Technical Report. Empa, https://www.coco2-project.eu/node/357 (last access: 9 January 2025), CoCO2: Prototype system for a Copernicus CO2 service, 2023.
Koene, E. F. M., Brunner, D., and Kuhlmann, G.: On the theory of the divergence method for quantifying source emissions from satellite observations, J. Geophys. Res.-Atmos., 129, e2023JD039904. https://doi.org/10.1029/2023JD039904, 2024.
Kuenen, J. J. P., Visschedijk, A. J. H., Jozwicka, M., and Denier van der Gon, H. A. C.: TNO-MACC_II emission inventory; a multi-year (2003–2009) consistent high-resolution European emission inventory for air quality modelling, Atmos. Chem. Phys., 14, 10963–10976, https://doi.org/10.5194/acp-14-10963-2014, 2014.
Kuhlmann, G., Broquet, G., Marshall, J., Clément, V., Löscher, A., Meijer, Y., and Brunner, D.: Detectability of CO2 emission plumes of cities and power plants with the Copernicus Anthropogenic CO2 Monitoring (CO2M) mission, Atmos. Meas. Tech., 12, 6695–6719, https://doi.org/10.5194/amt-12-6695-2019, 2019.
Kuhlmann, G., Brunner, D., Broquet, G., and Meijer, Y.: Quantifying CO2 emissions of a city with the Copernicus Anthropogenic CO2 Monitoring satellite mission, Atmos. Meas. Tech., 13, 6733–6754, https://doi.org/10.5194/amt-13-6733-2020, 2020.
Kuhlmann, G., Clément, V., Marshall, J., Fuhrer, O., Broquet, G., Schnadt-Poberaj, C., Löscher, A., Meijer, Y., and Brunner, D.: Synthetic XCO2, CO and NO2 Observations for the CO2M and Sentinel-5 Satellites, Zenodo [data set], https://doi.org/10.5281/zenodo.4048227, 2020b.
Kuhlmann, G., Henne, S., Meijer, Y., and Brunner, D.: Quantifying CO2 Emissions of Power Plants With CO2 and NO2 Imaging Satellites, Front. Remote Sens., 2, 14, https://doi.org/10.3389/frsen.2021.689838, 2021.
Kuhlmann, G., Koene, E., Meier, S., Santaren, D., Broquet, G., Chevallier, F., Hakkarainen, J., Nurmela, J., Amorós, L., Tamminen, J., and Brunner, D.: The ddeq Python library for point source quantification from remote sensing images (version 1.0), Geosci. Model Dev., 17, 4773–4789, https://doi.org/10.5194/gmd-17-4773-2024, 2024.
Landgraf, J., Rusli, S., Cooney, R., Veefkind, P., Vemmix, T., de Groot, Z., Bell, A., Day, J., Leemhuis, A., and Sierk, B.: The TANGO mission: A satellite tandem to measure major sources of anthropogenic greenhouse gas emissions, EGU General Assembly 2020, Online, 4–8 May 2020, EGU2020-19643, https://doi.org/10.5194/egusphere-egu2020-19643, 2020.
Lary, D. J., Alavi, A. H., Gandomi, A. H., and Walker, A. L.: Machine learning in geosciences and remote sensing, Geosci. Front., 7, 3–10, 2016.
Mahadevan, P., Wofsy, S. C., Matross, D. M., Xiao, X., Dunn, A. L., Lin, J. C., Gerbig, C., Munger, J. W., Chow, V. Y., and Gottlieb, E. W.: A satellite-based biosphere parameterization for net ecosystem CO2 exchange: Vegetation Photosynthesis and Respiration Model (VPRM), Global Biogeochem. Cy., 22, 2, https://doi.org/10.1029/2006GB002735, 2008.
Meijer, Y., Boesch, H., Bombelli, A., Brunner, D., Buchwitz, M., Ciais, P., Crisp, D., Engelen, R., Holmlund, H., Houweling, S., Janssens-Maenhout, G., Marshall, J., Nakajima, M., Pinty, B., and Scholze, M.: Copernicus CO2 monitoring mission Requirements document (MRD). Netherlands, Europe: European Space Agency, Earth Mission Sci. Division, 2019.
Nassar, R., Hill, T. G., McLinden, C. A., Wunch, D., Jones, D. B. A., and Crisp, D.: Quantifying CO2 emissions from individual power plants from space, Geophys. Res. Lett., 44, 10045–10053, https://doi.org/10.1002/2017GL074702, 2017.
Nassar, R., Mastrogiacomo, J. P., Bateman-Hemphill, W., McCracken, C., MacDonald, C. G., Hill, T., O'Dell, C.W., Kiel, M. and Crisp, D.: Advances in quantifying power plant CO2 emissions with OCO-2, Remote Sens. Environ., 264, 112579, https://doi.org/10.1016/j.rse.2021.112579, 2021.
Nassar, R., Moeini, O., Mastrogiacomo, J.-P., O'Dell, C. W., Nelson, R. R., Kiel, M., Chatterjee, A., Eldering, A., and Crisp, D.: Tracking CO2 emission reductions from space: A case study at Europe's largest fossil fuel power plant, Front. Remote Sens., 3, 1028240, https://doi.org/10.3389/frsen.2022.1028240, 2022.
Pascal, V., Buil, C., Loesel, J., Tauziede, L., Jouglet, D., and Buisson, F.: An improved microcarb dispersive instrumental concept for the measurement of greenhouse gases concentration in the atmosphere, in: International Conference on Space Optics – ICSO 2014, Vol. 10563, 1028-1036, SPIE, 2017.
Pillai, D., Buchwitz, M., Gerbig, C., Koch, T., Reuter, M., Bovensmann, H., Marshall, J., and Burrows, J. P.: Tracking city CO2 emissions from space using a high-resolution inverse modelling approach: a case study for Berlin, Germany, Atmos. Chem. Phys., 16, 9591–9610, https://doi.org/10.5194/acp-16-9591-2016, 2016.
Pinty, B., Janssens-Maenhout, G., Dowell, M., Zunker, H., Brunhes, T., Ciais, P., Dee, D., Denier van der Gon, H. A. C., Dolman, H., Drinkwater, M., Engelen, R., Heimann, M., Holmlund, K., Husband, R., Kentarchos, A., Meyer, A., Palmer, P., and Scholze, M.: An operational anthropogenic CO2 emissions monitoring and verification support capacity. Baseline requirements, model components and functional architecture, EUR28736 EN, European Commission Joint Research Centre, Ispara, Italy, https://doi.org/10.2760/08644, 2017.
Reuter, M., Buchwitz, M., Schneising, O., Krautwurst, S., O'Dell, C. W., Richter, A., Bovensmann, H., and Burrows, J. P.: Towards monitoring localized CO2 emissions from space: co-located regional CO2 and NO2 enhancements observed by the OCO-2 and S5P satellites, Atmos. Chem. Phys., 19, 9371–9383, https://doi.org/10.5194/acp-19-9371-2019, 2019.
Santaren, D., Broquet, G., Bréon, F.-M., Chevallier, F., Siméoni, D., Zheng, B., and Ciais, P.: A local- to national-scale inverse modeling system to assess the potential of spaceborne CO2 measurements for the monitoring of anthropogenic emissions, Atmos. Meas. Tech., 14, 403–433, https://doi.org/10.5194/amt-14-403-2021, 2021.
Schuit, B. J., Maasakkers, J. D., Bijl, P., Mahapatra, G., van den Berg, A.-W., Pandey, S., Lorente, A., Borsdorff, T., Houweling, S., Varon, D. J., McKeever, J., Jervis, D., Girard, M., Irakulis-Loitxate, I., Gorroño, J., Guanter, L., Cusworth, D. H., and Aben, I.: Automated detection and monitoring of methane super-emitters using satellite data, Atmos. Chem. Phys., 23, 9071–9098, https://doi.org/10.5194/acp-23-9071-2023, 2023.
Sierk, B., Bézy, J.-L., Löscher, A., and Meijer, Y.: The European CO2 Monitoring Mission: Observing Anthropogenic Greenhouse Gas Emissions from Space 11180, Proceedings, International Conference on Space Optics – ICSO 2018. 12 July 2019, Chania, Greece, 111800M, https://doi.org/10.1117/12.2535941, 2019.
Sun, K.: Derivation of emissions from satellite-observed column amounts and its application to TROPOMI NO2 and CO observations, Geophys. Res. Lett., 49, e2022GL101102, https://doi.org/10.1029/2022gl101102, 2022.
Taylor, T. E., O'Dell, C. W., Frankenberg, C., Partain, P. T., Cronk, H. Q., Savtchenko, A., Nelson, R. R., Rosenthal, E. J., Chang, A. Y., Fisher, B., Osterman, G. B., Pollock, R. H., Crisp, D., Eldering, A., and Gunson, M. R.: Orbiting Carbon Observatory-2 (OCO-2) cloud screening algorithms: validation against collocated MODIS and CALIOP data, Atmos. Meas. Tech., 9, 973–989, https://doi.org/10.5194/amt-9-973-2016, 2016.
van Heerwaarden, C. C., van Stratum, B. J. H., Heus, T., Gibbs, J. A., Fedorovich, E., and Mellado, J. P.: MicroHH 1.0: a computational fluid dynamics code for direct numerical simulation and large-eddy simulation of atmospheric boundary layer flows, Geosci. Model Dev., 10, 3145–3165, https://doi.org/10.5194/gmd-10-3145-2017, 2017.
Varon, D. J., Jacob, D. J., McKeever, J., Jervis, D., Durak, B. O. A., Xia, Y., and Huang, Y.: Quantifying methane point sources from fine-scale satellite observations of atmospheric methane plumes, Atmos. Meas. Tech., 11, 5673–5686, https://doi.org/10.5194/amt-11-5673-2018, 2018.
Wang, Y., Broquet, G., Bréon, F.-M., Lespinas, F., Buchwitz, M., Reuter, M., Meijer, Y., Loescher, A., Janssens-Maenhout, G., Zheng, B., and Ciais, P.: PMIF v1.0: assessing the potential of satellite observations to constrain CO2 emissions from large cities and point sources over the globe using synthetic data, Geosci. Model Dev., 13, 5813–5831, https://doi.org/10.5194/gmd-13-5813-2020, 2020.
Ye, X., Lauvaux, T., Kort, E., Oda, T., Feng, S., Lin, J., Yang, E., and Wu, D.: Constraining Fossil Fuel CO2 Emissions From Urban Area Using OCO-2 Observations of Total Column CO2, J. Geophys. Res.-Atmos., 1–29, 125, https://doi.org/10.1029/2019JD030528, 2020.
Zheng, B., Chevallier, F., Ciais, P., Broquet, G., Wang, Y., Lian, J., and Zhao, Y.: Observing carbon dioxide emissions over China's cities and industrial areas with the Orbiting Carbon Observatory-2, Atmos. Chem. Phys., 20, 8501–8510, https://doi.org/10.5194/acp-20-8501-2020, 2020.
“SNAP” stands for Selected Nomenclature for Air Pollutants.
- Abstract
- Introduction
- Data and methods
- Results of emission estimates based on individual images
- Results of the annual and monthly emission averages
- Discussion
- Conclusions
- Appendix A: Potential of the divergence approach for estimating local CO2 emissions from single-overpass satellite images of XCO2 and NO2
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Data and methods
- Results of emission estimates based on individual images
- Results of the annual and monthly emission averages
- Discussion
- Conclusions
- Appendix A: Potential of the divergence approach for estimating local CO2 emissions from single-overpass satellite images of XCO2 and NO2
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References





