An instrument for quantifying heterogeneous ice nucleation in multiwell plates using infrared emissions to detect freezing

Low concentrations of ice-nucleating particles (INPs) are thought to be important for the properties of mixed-phase clouds, but their detection is challenging. Hence, there is a need for instruments where INP concentrations of less than 0.01 L⁻¹ can be routinely and efficiently determined. The use of larger volumes of suspension in drop assays increases the sensitivity of an experiment to rarer INPs or rarer active sites due to the increase in aerosol or surface area of particulates per droplet. Here we describe and characterise the InfraRed-Nucleation by Immersed Particles Instrument (IR-NIPI), a new immersion freezing assay that makes use of IR emissions to determine the freezing temperature of individual 50 µL droplets each contained in a well of a 96-well plate. Using an IR camera allows the temperature of individual aliquots to be monitored. Freezing temperatures are determined by detecting the sharp rise in well temperature associated with the release of heat caused by freezing. In this paper we first present the calibration of the IR temperature measurement, which makes use of the fact that following ice nucleation aliquots of water warm to the ice–liquid equilibrium temperature (i.e. 0 ^∘C when water activity is ∼1), which provides a point of calibration for each individual well in each experiment. We then tested the temperature calibration using ∼100 µm chips of K-feldspar, by immersing these chips in 1 µL droplets on an established cold stage (µL-NIPI) as well as in 50 µL droplets on IR-NIPI; the results were consistent with one another, indicating no bias in the reported freezing temperature. In addition we present measurements of the efficiency of the mineral dust NX-illite and a sample of atmospheric aerosol collected on a filter in the city of Leeds. NX-illite results are consistent with literature data, and the atmospheric INP concentrations were in good agreement with the results from the µL-NIPI instrument. This demonstrates the utility of this approach, which offers a relatively high throughput of sample analysis and access to low INP concentrations.

1 Introduction

Cloud droplets can freeze homogeneously below about −33 ^∘C (Herbert et al., 2015), but the presence of ice-nucleating particles (INPs) can induce freezing at much warmer temperatures (Kanji et al., 2017). The glaciation of clouds at these warmer temperatures has a substantial impact on a cloud's reflective properties and lifetime, and therefore the overall climate of the planet, but is poorly represented in many models (Hoose and Möhler, 2012; Vergara-Temprado et al., 2018). INPs can cause nucleation through a number of pathways (Vali et al., 2015), but in mixed-phase clouds it is thought that the pathways where particles become immersed in droplets are most important (Hande and Hoose, 2017; Hoose et al., 2010; Murray et al., 2012). Even small concentrations of INPs can influence cloud properties; for example, in a modelling study of Southern Ocean shallow mixed-phase clouds, Vergara-Temprado et al. (2018) showed that, while concentrations of INPs greater than ∼1 L⁻¹ cause profound changes in cloud properties, clouds are sensitive to concentrations many orders of magnitude smaller.

The ability to quantify INP spectra (INP concentrations as a function of temperature) and test the efficiency of proxy materials for ice-nucleating efficiency is invaluable for improving our understanding of cloud glaciation and developing computationally inexpensive parameterisations for atmospheric models. However it is not a trivial task, in part because INP concentrations relevant for clouds are low (< 0.1 L⁻¹) (DeMott et al., 2010) and the sites on the surfaces which cause nucleation at warm temperatures (Vali, 2014; Whale et al., 2017) are rare. There are several different methods of conducting ice nucleation experiments, including continuous-flow diffusion chambers (CFDC's) (e.g. Garimella et al., 2016; Kanji and Abbatt, 2009; Kohn et al., 2016; Rogers et al., 2001; Salam et al., 2006; Stetzer et al., 2008), cloud expansion chambers (e.g. Cotton et al., 2007; Niemand et al., 2012), wind tunnels (e.g. Diehl and Mitra, 1998; Pitter and Pruppacher, 1973) and droplet freezing assays (e.g. Beall et al., 2017; Budke and Koop, 2015; Häusler et al., 2018; Knopf and Alpert, 2013; Murray et al., 2011; Vali, 2008; Whale et al., 2015). Each of these methods has its limitations and advantages which must be understood and accounted for when conducting an experiment and interpreting the results. For example CFDCs cannot be used for measurements at temperatures warmer than about −11 ^∘C, but they do allow for specific saturation conditions to be controlled, something which other instruments cannot achieve. For more information on the capabilities and limitations of the various techniques see the comprehensive reviews and intercomparisons conducted by Hiranuma et al. (2015) and DeMott et al. (2018). Haüsler et al. (2018) also present a summary of the features of various techniques.

A significant challenge in sampling INPs in the atmosphere is their low concentration. At present there is a dearth of published, atmospherically relevant INP measurements globally (Kanji et al., 2017; Vergara-Temprado et al., 2017). Not only is the global spatial and temporal coverage of INPs inadequate, but the range of activation temperatures and INP concentrations covered in any one set of measurements is typically limited. No single instrument has the capability of measuring INP concentrations over the full range of conditions relevant to mixed-phase clouds. Online instruments, such as CFDCs, can measure over a wide range of relevant conditions, but their detection limit is limited to $\sim {\mathrm{10}}^{-\mathrm{1}}$ L⁻¹ (Al-Naimi and Saunders, 1985; DeMott et al., 2010; Eidhammer et al., 2010; Prenni et al., 2009). This can be improved with aerosol concentrators (Prenni et al., 2013; Tobo et al., 2013), but is still above the INP concentrations that models suggest influence the properties of certain cloud types, such as high-latitude cold-sector clouds (Vergara-Temprado et al., 2018). The alternative approach is therefore to increase the number of particles within each aliquot of water. In principle, increasing the number of particles per droplet, and therefore the surface area of nucleator, per droplet will increase the sensitivity of the experiment to rarer INPs. This enables quantification of lower INP concentrations. To increase the number of aerosol particles per volume of liquid, the time period over which an atmospheric sample is collected could be extended, but in doing so temporal resolution would be lost. A method of increasing the sensitivity of an immersion mode technique is to increase the volume of the collected suspension used in each aliquot, while maintaining the concentration of particles per unit volume. This increases the number of particles per aliquot of liquid and therefore makes it more likely that rarer INPs will be detected. The use of larger-volume droplet suspensions has been exploited in the past (e.g. Bigg, 1953; Vali, 1971) and has been the strategy employed in the development of some recent instruments (e.g. Beall et al., 2017; Conen et al., 2012; Du et al., 2017; Stopelli et al., 2014). These large-volume assays capture the rarer, more active INPs but often miss the more abundant but less active INPs. Hence they should ideally be used alongside a smaller droplet instrument to generate complimentary datasets.

While many instruments use optical cameras to detect freezing events (Beall et al., 2017; Budke and Koop, 2015; Häusler et al., 2018; Whale et al., 2015), some researchers have used techniques to detect the release of latent heat associated with freezing. For example differential scanning calorimetry (Marcolli et al., 2007; Pinti et al., 2012) and infrared emissions (Zaragotas et al., 2016; Kunert et al., 2018) have been used. Zaragotas et al. (2016) used a thermal camera to measure the temperature of individual aliquots within a 96-well plate partially submerged within an alcohol bath. This study investigated plant samples but suggested that the technique may be adapted for atmospheric purposes. Very recently, Kunert et al. (2018) presented a similar setup to investigate biological samples and collected aerosol. Unlike Zaragotas et al. (2016), Kunert et al. (2018) do not measure individual droplet temperatures via infrared emissions but instead use multiple thermistors embedded in the sample holders to infer temperature for the droplet array.

Here we present a new technique, the InfraRed-Nucleation by Immersed Particle Instrument (IR-NIPI), for the detection of INPs using large volumes of sample in the immersion mode. This instrument is part of the NIPI suite of instruments that includes the µL-NIPI. When used together, these devices allow measurements to be taken over a very wide range of INP concentrations. The use of an infrared camera allows temperature measurements to be made for individual droplets, which helps reduce errors from horizontal gradients across the array of droplets and the effect of heat release on the temperature of neighbouring wells. The unique design, in combination with a Stirling cryocooler-based chiller, is also compact, making it ideal for field-based measurements, and the use of multiwell plates lends itself to future automation.

2 Instrument design

2.1 Operating principle

Drop assays have been used extensively for ice nucleation experiments (e.g. Budke and Koop, 2015; Conen et al., 2011; Garcia et al., 2012; Knopf and Forrester, 2011; Stopelli et al., 2014; Vali, 1995, 1971; Whale et al., 2015). This is due partly to their simplicity compared to other techniques but also to the ability to scale the amount of nucleator with droplet size. In brief, aqueous suspensions are prepared and droplets of a well-quantified size are placed onto a substrate or immersed in oil. These droplets tend to be monodispersed, but polydispersed experiments are also possible (Murray et al., 2011; Vali, 1971). The system is then cooled and the fraction of droplets frozen is recorded. The cooling can be conducted at a constant rate or with a stepped rate to hold the droplets at a specified temperature for a period of time (i.e. isothermally) to explore the time dependence aspect of ice nucleation (Herbert et al., 2014; Sear, 2014; Vali, 1994). The droplets are monitored and the freezing temperature of each droplet is recorded. The fraction of the droplet population frozen throughout the explored temperature range can then be determined, from which the ice-nucleating active site density or INP concentration can be derived (Vali et al., 2015).

If the surface area of nucleant per droplet is known, then it is common to express the nucleating ability of a material as the density of active sites per unit surface area of nucleator, n_s(T) (Connolly et al., 2009; DeMott, 1995). This approach is based on the assumption that specific sites on a nucleator's surface are responsible for ice formation. n_s is a cumulative term; i.e. as you move to cooler temperatures, there are more features which may behave as an active site as the energy barrier for ice formation decreases. n_s(T) is calculated via Eq. (1):

$$\begin{array}{}\text{(1)}& n_{\mathrm{s}}\left(T\right)={\displaystyle \frac{\left(-\ln (\mathrm{1}-\frac{n\left(T\right)}{N})\right)}{A}},\end{array}$$

where n(T) is the number of droplets frozen at a given temperature and N is the total number of droplets. A is the surface area of nucleator within each droplet. Nucleation is a time-dependent stochastic process, but in determining n_s(T) the time dependence is neglected. This assumption is justified for many materials because the diversity in activity of active sites leads to a much greater spread in freezing temperatures than the shift in freezing temperatures associated with changes in cooling rate (Herbert et al., 2014; Vali, 2008).

2.2 IR-NIPI design

In brief an aqueous suspension is prepared and aliquots pipetted into the wells of a 96-well plate which is then placed on a temperature-controlled stage. The cold stage and multiwell plate are enclosed by a Perspex cover with an infrared camera mounted in its lid (Fig. 1). The system is cooled at $\sim -\mathrm{1}$ ^∘C min⁻¹ until all droplets are frozen (typically in a temperature range of 0 to −30 ^∘C). The temperature of the individual aliquots is monitored using the IR camera, which records a temperature map every 20 s. The temperature map is then analysed with a semi-automated process using custom Python code to yield the freezing temperatures of individual wells.

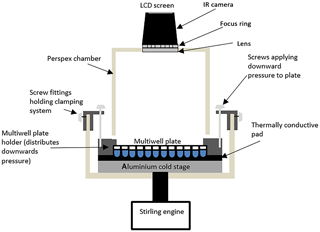
Figure 1 Schematic diagram of the IR-NIPI system (not to scale). The IR camera is positioned above the multiwell plate and monitors the freezing events as the cold stage cools.

The IR-NIPI has been designed around an Asymptote Ltd. VIA Freeze^™ Stirling cryocooler (Fig. 1). The VIA Freeze uses a Stirling engine to provide a convenient means of cooling without refrigerants or circulating liquids and was primarily designed for use in cryopreservation applications. This chiller can achieve temperatures of −90 ^∘C; hence it has more than enough cooling capacity for our application and has sufficiently low power requirements that allow it to be run from an automotive 12 V inverter. It also features an onboard data logger and internal computer with touch screen control. The VIA Freeze has been developed to accommodate multiwell plates onto its aluminium cooling stage, which are ideal for large-volume drop assays as they hold up to 200 µL per aliquot (for the 96 well plates), allow the separation of droplets to reduce interference across cells and can be supplied medically sterile. These multiwell plates have anywhere from 12 to 1536 wells (with maximum working volumes of 6.9 mL to 2 µL, respectively). The most useful for this freezing assay are the 96×200 or 384×50 µL aliquot arrays, and in the tests reported here 50 µL droplets (∼2300 µm volume equivalent diameter) are used in 96-well plates. We have used both polystyrene (Corning, CLS3788) and polypropylene plates (Greiner, M8060) and observed no difference in freezing results between the two. To aid thermal contact between the multiwell plate and the VIA Freeze a thermally conductive gap pad (RS components, 7073452) is located between the cold plate and the multiwell plate, while a clamping system with screw threads applies mechanical pressure to the multiwell plate to push the wells into the pad (Fig. 1). A specially designed Perspex hood then encloses the system to reduce contamination from the surroundings. The IR camera slots into the hood and captures an image of the multiwell plate every 20 s (Fig. 2a), storing the corresponding temperature data (Fig. 2b) on a removable memory card. The IR camera used here is a Fluke Ti9 Thermal Imager with 160×120 pixels. The Stirling engine chiller is then set to cool down at 1.3 ^∘C min⁻¹, which corresponds to 1 ^∘C min${}^{-\mathrm{1}}\pm \mathrm{0.06}$ ^∘C in the wells due to a measured offset between the plate and aliquot temperatures. This ramp rate was selected based on preliminary runs, and justification for this cooling rate being equivalent to 1 ^∘C min⁻¹ can be seen in the well temperatures over time (Fig. 2b). Once the system has initially cooled to 5 ^∘C, the temperature is held for 5 min to allow time for the system to equilibrate. Following this the system continues to ramp down in temperature while recording IR heat maps of the multiwell plate.

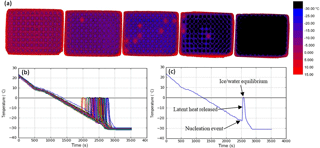
Figure 2 Illustration of the use of the IR camera to measure temperature and freezing events. (a) A sequence of colour maps taken during the course of an experiment. The leftmost image shows the start of an experiment with all droplets unfrozen, moving to all droplets frozen in the rightmost image. Warmer temperatures are represented in red, transitioning to blue for colder temperatures and finally black at −30 ^∘C and below. Freezing events in individual wells are evident when they warm up to 0 ^∘C. (b) An example of the output of an experiment with the temperature of each of the 96 wells plotted against time. The sharp increases in temperature are related to ice formation. The cooling rate was 1 ^∘C min⁻¹. The calibration described in Sect. 2.2 was applied here. Note that one well had a higher temperature than the others, likely due to poor thermal contact with the aluminium substrate. By using IR thermometry to measure the temperature of each well individually, such variability is accounted for. (c) Plot of temperature vs. time for a single well within a multiwell plate containing a 50 µL aliquot of water.

In order to determine the temperature of individual wells, the analysis code locates a pixel centred in the middle of each well, reporting this temperature as the well temperature. Profiles of temperature vs. time are shown in Fig. 2b and c. The freezing temperature of each individual well is determined by comparing each temperature reading, for a certain well, with the temperature recorded 20 s prior. If the temperature reading increases by more than 2 ^∘C, this is recorded as a freezing event (Fig. 2c). The 2 ^∘C threshold occasionally needs to be optimised to capture freezing events while eliminating the detection of false freezing events. For example, samples that freeze above −3 ^∘C are more difficult to detect because there is less heat released on initial freezing and crystallisation happens over a longer period of time (see Sect. 2.4). Manual inspection is required in this temperature regime, and the 2 ^∘C threshold is adjusted accordingly. The code then prints out the number of events recorded, along with a time–temperature plot (Fig. 2b) and the corresponding event temperatures for the user to quality-control check, and then exports the data as a “.csv” file.

The whole process from sample preparation to final analysis takes approximately 1 h. In order to achieve higher throughput of samples, albeit with a reduced number of replicates, multiple samples and internal blanks can be placed within one multiwell plate. For example, when performing dilutions, we might run 12 wells as a handling blank and three lots of 28 wells that contain three different sample dilutions. This not only speeds up analysis; it also reduces the effect of any time-dependent ageing processes such as the rapid deactivation of an albite sample suspended in water observed by Harrison et al. (2016).

2.3 Temperature measurements with an infrared camera

By using an IR camera to view the thermal emission of each individual well of suspension, we are able to obtain temperatures associated with individual wells. This contrasts with the approaches adopted in other experiments where the temperature is recorded and assumed to be representative for all droplets, for example when employing a cold stage housing an embedded thermocouple whose reading is used to represent the temperature of the droplet array. We note that in our system there was a lateral gradient across the entire multiwell plate in the IR-NIPI of up to 6 ^∘C (in extreme cases). This is likely due to there not being an even thermal contact of the multiwell plate with the underlying cold plate. The typical gradient was 4 ^∘C; hence temperature measurements of the individual wells were necessary.

2.4 Temperature calibration

The IR camera we use was quoted for use between −20 and +250 ^∘C with an uncertainty of ±5 ^∘C and is intended for use in a wide range of applications with a range of materials of different emissivity. In our application, we only need to measure the temperature of one material, water, over a relatively narrow range of temperatures; hence we perform a calibration for our specific experimental setup. Our calibration is based on the fact that, when an aliquot of water in a multiwell plate freezes, the released latent heat raises the temperature of the aliquot to the ice–water equilibrium temperature (0 ^∘C when the water activity of the sample is ∼1, as it is in these experiments). This is illustrated in Fig. 2c, which shows the phases of crystallisation that the aliquots go through. Initially, the crystal growth is rapid with a rapid release of latent heat and a corresponding rise in temperature of the aliquot within the 20 s time between frames. Visual inspection of the live screen display of the IR camera revealed that the temperature reached a maximum within 1 s. The temperature of an ice–water mixture will necessarily be 0 ^∘C; hence the aliquot cannot warm above 0 ^∘C, and the temperature will remain at 0 ^∘C until all of the water has frozen and no more heat is evolved. The rate of crystallisation in this regime is determined by the loss of heat to the surroundings, in this case the cold stage, as well as to the surrounding droplets and the multiwell plate. This stage of crystallisation takes longer at higher freezing temperatures where the temperature differential between the cold stage and the aliquot is smaller. Hence, freezing when nucleation takes place at −12 ^∘C takes around 100 s, whereas when nucleation takes place at −20 ^∘C freezing takes around 20–40 s. Once all of the water has frozen, the temperature of the aliquot decreases rapidly back to that of the multiwell plate within 20–40 s. The fact that the aliquots spend tens of seconds at 0 ^∘C provides a very useful calibration point for each individual well. In the following we describe a novel method for calibrating the IR temperature measurements that takes advantage of this process and proceed to justify this approach.

Using the analysis code, an event is identified and recorded. The code then reads the temperature of the frame directly after this freezing event and calculates the difference of this value compared to 0 ^∘C to give an offset correction value; i.e. if the frame after freezing read 2 ^∘C, then the correction factor for this well would be −2 ^∘C. This offset value is then subtracted from all of the temperature recordings for that specific well. The average correction value calculated for the IR camera via this method is −1.9 ^∘C with a standard deviation ±0.5 ^∘C. It should be noted that one of the limitations of the setup used by Zaragotas et al. (2016) was that the IR camera was calibrated only once by the factory; however our calibration method mitigates this limitation.

A standard freezing experiment was then performed, and the thermocouple data were contrasted to those of the IR camera which was calibrated using the above method (Fig. 3). The comparison in Fig. 3a shows that the IR and thermocouple temperature were in excellent agreement, and this is also readily seen in residuals plotted in Fig. 3b. The scatter around the zero line in the residual plot is ±0.9 ^∘C (2 standard deviations) in the regime after the equilibrium step at +5 ^∘C and before the first freezing event. We used this value as an estimate of the temperature uncertainty associated with the IR technique generally. We did not use data in the red and blue shaded areas of Fig. 3b to calculate this uncertainty. The temperature readings in the red shaded area were discarded as they had not been held at +5 ^∘C for 5 min to equilibrate. Temperature readings after the initial freezing event were also discarded as thermal conductivity of ice is different to that of water and neighbouring wells release heat on freezing which influence the temperature of surrounding wells.

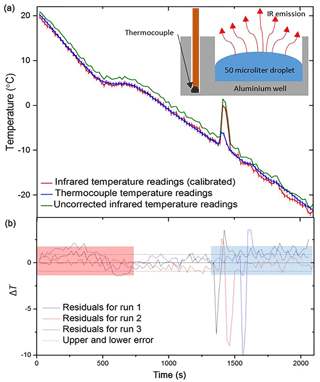
Figure 3 Tests of the IR temperature measurement using aluminium wells with embedded thermocouples (i.e. not using the standard multiwell plates). (a) The temperature measurement from a thermocouple (shown in blue) placed within an aluminium well vs. infrared measurements taken using the IR camera. Uncorrected IR data are shown in green, whilst corrected IR data following the calibration described in Sect. 2.2 are shown in red. Inset is a schematic of the experimental setup. (b) The difference in temperature (residual; ΔT) between the thermocouple readings for three aluminium wells and the corresponding IR data ($\mathrm{\Delta }T=T_{\mathrm{IR}}-T_{\mathrm{Thermocouple}}$.). The negative spikes are a result of the IR camera directly reading the water temperature as it is heated by ice formation, whereas the thermocouple measurement is reading the temperature of the aluminium well, which is less affected by the latent heat release. The estimated error in temperature for the IR camera of ±0.9 ^∘C is indicated with dashed lines. The range over which freezing occurs is highlighted with a blue rectangle as this is where the thermal properties of ice and the initiation of heat release affect the temperature readings. Highlighted in red is the section of data before the well has equilibrated, and so the IR camera is likely reading a warmer surface temperature than the thermocouple. See text for discussion.

We also tested the IR temperature measurement using T type thermocouples distributed in specific wells of a polypropylene multiwell plate. The IR camera could not take an accurate reading of wells that had a thermocouple placed inside them; therefore neighbouring unfrozen wells were assumed to be representative of each other (see inset in Fig. 4). As mentioned above, there is a gradient across the entire plate (Fig. 2a), and so a series of preliminary experiments were undertaken to find suitable placement locations for the thermocouples in which the surrounding wells displayed similar temperature readings compared to one another. The thermocouples were placed in the base of the well along with 50 µL of Milli-Q grade water, and four surrounding well temperatures were measured using the IR system. The thermocouple wire crossed one of the four IR-measured wells, and so only three wells adjacent to the thermocouple monitored well were used for comparison.

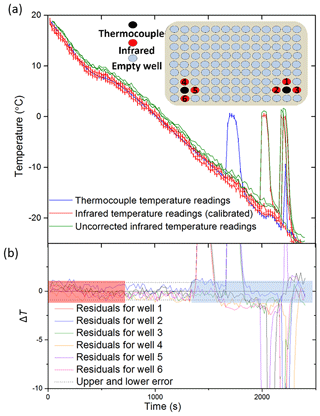
Figure 4 Tests of the IR temperature measurements using thermocouples positioned in a polyethylene multiwall plate. (a) The temperature measurement from a thermocouple placed within a well vs. three IR measurements of surrounding wells corrected using the calibration described in Sect. 2.2. The uncorrected IR data can be seen in green, with the corrected IR data in red and the thermocouple readings in blue. A diagram of the wells within a 96-well plate chosen for the comparison of IR and thermocouple measurements is displayed as an inset. The numbers of the wells correspond to the residuals in (b). Red wells represent the wells measured with the infrared camera, and black wells represent those measured with thermocouples. It should be noted that one of the four surrounding IR well temperature readings was discarded from each experiment as the thermocouple wire impeded the temperature measurement. Note that the freezing events at ∼2000 s appear to cause some heating in the adjacent well. (b) Plot of the difference in temperature between the thermocouple readings for two wells and six corresponding wells measured with the IR camera as in Fig. 3. The estimated error in temperature for the IR camera is indicated with dashed lines (±0.9 ^∘C). The range of freezing is highlighted in blue as this is where the thermal properties of ice and the initiation of heat release will affect the temperature readings. Highlighted in red is the section of data before the well had equilibrated, and so the IR camera was likely reading a warmer surface temperature than the thermocouple.

A total of six IR measurements were recorded with the corresponding thermocouple readings over a series of experiments spanning a temperature range of 20 to −25 ^∘C. An example of a thermocouple measurement contrasted to three IR measurements can be seen in Fig. 4a. The residual temperatures for all six thermocouple temperatures are also shown (Fig. 4b). The IR temperature uncertainty derived from the aluminium well experiment is also plotted and shows that the multiwell temperature data are consistent with an uncertainty of ±0.9 ^∘C.

3 Test experiments and analysis

3.1 Control experiments

In larger-volume freezing assays (tens of microliters) it is extremely challenging to remove all background INPs from the water and substrates; hence freezing is typically observed at temperatures well above what one would expect for homogenous freezing (Koop and Murray, 2016). Homogeneous nucleation is expected to result in 50 % of 50 µL droplets freezing at around −33 ^∘C, whereas 50 % of the Milli-Q water droplets froze around −22 ^∘C in our control experiments (Fig. 5). Filtering of the Milli-Q water to 0.2 µm reduced the temperature at which pure water droplets froze by 2–3 ^∘C. Sartorius Minisart, non-pyrogenic, single-use filters were used for this (product code 17597-K). Blanks were run initially with entire 96-well plates, and then 12 wells of each experiment thereafter were allocated for an internal blank when testing samples of INPs (i.e. 12 aliquots of Milli-Q water and 84 aliquots of sample suspension). Comparison of fraction frozen curves for typical IR-NIPI blanks with curves obtained for droplets containing various ice-nucleating materials (discussed below) shows that there is a clear heterogeneous freezing signal (Fig. 5). We hope to improve the baseline in the future, through further improvements in the cleanliness of the system (Polen et al., 2018), but for the purpose of these experiments the nucleants tested were active at sufficiently warm temperatures to be well above the baseline.

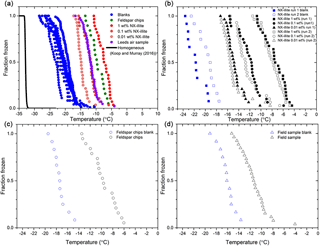
Figure 5 The fraction of droplets frozen as a function of temperature on cooling for a range of samples. (a) The fraction frozen curves for the IR-NIPI experiment showing standard blank runs and the sample runs from this study. The homogeneous freezing of water as predicted with the Koop and Murray (2016) parameterisation is also shown in black. (b) Fraction frozen plot for the internal blanks vs. the corresponding NX-illite runs. (c) Fraction frozen plot for the internal blank vs. the corresponding feldspar chip run. (d) Fraction frozen plot for the internal blank vs. the corresponding field sample run.

3.2 Feldspar chips

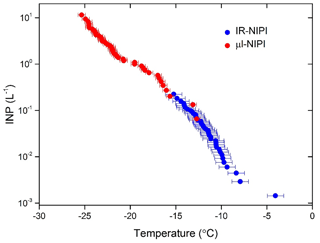
To further test the temperature readings from the IR-NIPI instrument, a set of experiments was performed where each droplet contained a single ∼100 µm sized grain of K-feldspar in both the IR-NIPI and contrasted to the standard µL-NIPI employing 1 µL droplets. The µL-NIPI is a well-established technique (Whale et al., 2015) which compares well with other similar instruments (DeMott et al., 2018; Hiranuma et al., 2015). The purpose of this experiment was to have the same amount of material per droplet in each experiment and to have the material at the base of the droplet so that the results from the two instruments could be directly compared. In doing so, we could investigate the extent to which the gradient within the 50 µL wells might be a problem. This experiment was adapted from the procedure described by Whale et al. (2018) and involved taking K-feldspar-rich chips from a bulk rock of pegmatite and selecting individual grains (pegmatite is an igneous intrusive rock rich in K-feldspar with large grain sizes often being larger than 2.5 cm and hence easy to separate). This material was chosen because K-feldspar is known to exhibit excellent ice-nucleating properties (Atkinson et al., 2013; Harrison et al., 2016; Peckhaus et al., 2016). A total of 19 grains that were ∼100 µm in diameter were separated by eye and assigned a number, and their position tracked through the course of each experiment. The same feldspar chips were tested in both the µL-NIPI and the IR-NIPI. For the IR-NIPI experiments single grains of feldspar were placed into the bottom of a multiwell plate, and 50 µL of Milli-Q water was then pipetted into each well. The experiment was then carried out as normal, and the freezing temperatures of the wells were recorded. The grains were then used in the µL-NIPI experiment by placing the grains onto a glass cover slip atop a cold plate and pipetting a single 1 µL droplet onto each grain, before carrying out a standard µL-NIPI experiment. Briefly, the temperature of the cold plate was reduced at 1 ^∘C min⁻¹, and the temperature of the droplet freezing events recorded via a camera. The resulting fraction frozen plot for this experiment can be seen in Fig. 6a, and the corresponding correlation plot is shown in Fig. 6b. The two instruments yielded similar fraction frozen curves, and the individual feldspar grains nucleated ice at a similar temperature in both experiments. The correlation plot in Fig. 6b shows that the freezing temperatures of a single grain were not identical in the two experiments, which is consistent with the stochastic nature of nucleation at active sites that have a characteristic freezing temperature (Vali, 2014, 2008). The agreement between the two instruments suggests that the temperature measurement and calibration of the IR-NIPI were robust and that there is no major temperature gradient within the aliquots in the multiwell plates.

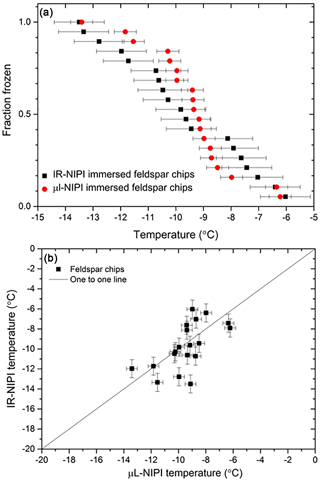
Figure 6 Comparison of nucleation induced by feldspar chips in the IR-NIPI and µL-NIPI instruments. (a) The fraction frozen curves for single feldspar particles per droplet in both the µL-NIPI (using 1 µL droplets) and IR-NIPI (using 50 µL droplets) experiments. The error bars indicate the error in temperature measurement on both instruments. (b) The freezing temperature for the individual feldspar chips as measured by the IR-NIPI and µL-NIPI instruments.

3.3 NX-illite

The mineral dust NX-illite was chosen as a test sample as it has been used in an extensive intercomparison study (Hiranuma et al., 2015) and contains some common components which are found in atmospheric mineral dusts (Broadley et al., 2012). NX-illite was taken from the same batch as that used by the Leeds group in the Hiranuma et al. (2015) intercomparison and no further processing of the material was carried out. Aqueous suspensions of the sample were prepared by weighing a known amount of material and suspending it in a corresponding volume of water to make up a weight percent suspension (i.e. 0.1 g of mineral in 9.9 g of water to yield a 1 wt % suspension). NX-illite concentrations of 0.01, 0.1 and 1 wt % were prepared in this manner, and in each case a Teflon-coated magnetic stirrer bar was used to keep the particles suspended whilst the sample was pipetted into the wells of the multiwell plate. Each concentration of NX-illite was tested using the IR-NIPI, and the resultant fraction frozen curves are shown in Fig. 5.

By employing a suspension of known concentration composed of a material with a known specific surface area, the surface area of nucleator per droplet can be calculated and used alongside the fraction frozen curves to determine n_s(T), as described in Eq. (1). The n_s(T) derived from IR-NIPI with 0.01, 0.1 and 1 wt % NX-illite are shown in Fig. 7a. They are in good agreement, with one another with lower-weight-percent suspensions yielding data at lower temperatures and higher n_s(T) values, as expected. The few data points from the 0.01 wt % NX-illite run 2 which appear as outliers may indicate that the particles were not evenly distributed throughout the droplets. Further to this, a freeze–thaw experiment of 0.1 wt % suspension was conducted where the sample was frozen once, thawed and then frozen again (see Fig. 8). The agreement between the two runs show that the material did not alter on freezing.

The values of n_s(T) for NX-illite derived from 0.01–1 wt % suspensions are shown in Fig. 7a together with the literature data for this material in Fig. 7b. This material has also been investigated by Beall et al. (2017) using an instrument that also uses 50 µL droplets: the Automated Ice Spectrometer (AIS). The results of Beall et al. (2017) are therefore directly comparable to the results from the IR-NIPI. All of the wet suspension techniques have been grouped together in black in Fig. 7b, apart from the AIS data shown in green and the IR-NIPI data in red. Both the IR-NIPI and AIS data are in good agreement with one another. It can be seen that the larger-volume assays (IR-NIPI and AIS) give results towards the upper spread of literature data but are still consistent with other results (Fig. 7b). Dry-dispersed techniques have also been plotted as unfilled blue squares in Fig. 7b, but none of these techniques are sensitive in the range of n_s(T) seen by the large-droplet instruments. The new data from the IR-NIPI have extended the dataset for NX-illite to warmer temperatures than in previous measurements, illustrating the utility of the technique.

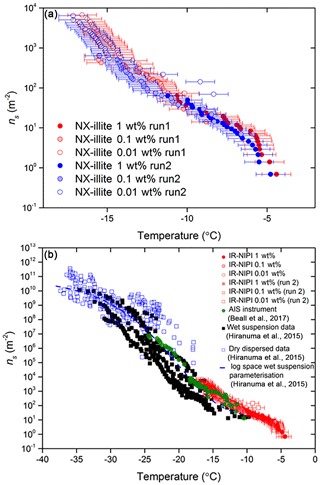
Figure 7 Active site densities, n_s(T), for NX-illite. (a) The active site density for a dilution series of NX-illite run on the IR-NIPI instrument for a range of concentrations. The data for a repeat experiment are also shown. The error bars represent the temperature error of ±0.9 ^∘C. (b) The active site density for NX-illite from this study compared to literature data. Data from wet-dispersed techniques are displayed in black, with the IR-NIPI highlighted in red and Automated Ice Spectrometer (AIS) in green. Data from dry-dispersed techniques are also plotted as hollow blue squares.

It should be noted that in preliminary experiments some discrepancies between dilutions of NX-illite were observed which highlighted the importance of accurately making up suspensions. In the following we note some issues that had to be solved. In some initial experiments the dilutions of a suspension would yield a higher-than-expected n_s(T). On further investigation this issue was resolved via gravimetrically weighing suspensions (i.e. preparing a known mass of a sample in a known mass of water) rather than diluting a bulk stock suspension. Further to this, great care was taken when sampling from the bulk NX-illite sample so as to make sure no bias was introduced when selecting material since a powder can separate on the basis of grain size. This was avoided by shaking the container horizontally and selecting material from the centre of the bulk sample. Magnetic stirrer bars were used to keep particles suspended, but when it came to collecting the suspension using a pipette the suspension was taken from the magnetic stirrer plate to stop the vortex within the vial. As the suspension was not stirring for a short period of time, particles did not have time to fall out of suspension and there was no longer a vortex created by the stirrer bar which could bias particle distribution when sampling. The above emphasises the importance of selecting samples in a reproducible way and may explain some of the variability between the literature data seen in Fig. 7b.

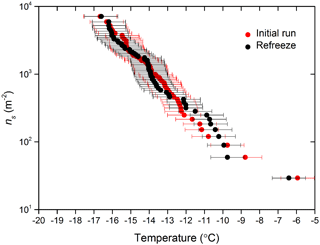
Figure 8 The active site density, n_s(T), for a 0.01 wt % NX-illite suspension and n_s(T) from a corresponding second freezing run with the same droplets after they had been thawed out and refrozen.

Figure 9 INP concentrations per litre of air sampled on 5 November 2017 in Leeds. Aerosol were collected onto filters for later extraction into water and analysis of the resulting suspensions with the IR-NIPI and µL-NIPI instruments.

3.4 Atmospheric aerosol sample

In order to demonstrate the utility of this approach for atmospheric aerosol samples, a filter sample was collected in Leeds as part of a field campaign held on the evening of 5 November. A sample of atmospheric aerosol was collected using a Mesa PQ100 air sampler for 100 min. An inlet head with an upper cut-off of 10 µm was utilised, and air was sampled at 16.7 L min⁻¹ onto a 0.4 µm polycarbonate track-etched Whatman filter, with a total of 1670 L of air sampled. The filter was then placed into 6 mL of Milli-Q water and vortexed for 5 min to wash the particles from the filter and into suspension. This analysis is similar to that described by O'Sullivan et al. (2018).

The aqueous sample was then analysed on the IR-NIPI and µL-NIPI (Whale et al., 2015). The concentration of INPs per litre of air, [INP]_T, was subsequently calculated using Eq. (2) (DeMott et al., 2016):

$$\begin{array}{}\text{(2)}& [\mathrm{INP}{]}_T=-\ln \left({\displaystyle \frac{N_{\mathrm{u}}\left(T\right)}{N}}\right)\left({\displaystyle \frac{V_{\mathrm{w}}}{V_{\mathrm{a}}{V}_{\mathrm{s}}}}\right),\end{array}$$

where N_u(T) is the number of unfrozen droplets at a given temperature, N is the total number of droplets, V_w is the volume of wash water, V_a is the volume of an aliquot and V_s is the volume of air sampled.

The resulting INP concentrations from the combination of these two instruments spanned 4 orders of magnitude and covered a temperature range of 20 ^∘C (see Fig. 9). The data from both instruments were in good agreement and yielded complementary information. This illustrates how the IR-NIPI can be used to extend the measurements of INP concentrations to higher temperatures and lower INP concentrations. Since high-resolution regional modelling of the effect of INP on shallow clouds suggests that 0.1 to 1 INP L⁻¹ is a critical concentration and much lower concentrations still impact clouds (Vergara-Temprado et al., 2018), measurements with IR-NIPI will be extremely useful, particularly in environments with low INP concentrations.

4 Summary and conclusions

The IR-NIPI technique is a novel approach to measuring freezing events in immersion mode nucleation studies. We demonstrate that IR thermometry is a sound method for determining the freezing temperature of 50 µL water droplets in multiwell plates. This method overcomes potential distorting influences such as thermal gradients across the plate, the effect of freezing wells warming surrounding wells and poor thermal contact to the underlying cold plate. A freezing event is detected as a sharp rise in freezing temperature to the equilibrium melting point, and a novel calibration method has been proposed which relies on the return of water droplets to the equilibrium melting temperature of water, 0 ^∘C, after initial freezing. This gives an individual calibration for every run and every well. When this calibration technique is compared to thermocouple readings, the data are consistent to within ±0.9 ^∘C. The use of this calibration method is further supported when looking at experiments using single grains of feldspar, with the results being consistent with those of the established µL-NIPI instrument that employs 1 µL droplets on a cold stage. Results for the ice-nucleating ability of NX-illite with the IR-NIPI, a mineral dust which has been the subject of an extensive intercomparison, are consistent with literature measurements. In particular, the IR-NIPI is in good agreement with another well-characterised large-droplet instrument (AIS) (Beall et al., 2017). However, it is unclear why both of these large-volume instruments produce n_s results at the high end of the range of n_s values reported previously. The utility of IR-NIPI for the analysis of atmospheric samples was also demonstrated by collecting and analysing an aerosol sample from the city of Leeds, England. The sample was analysed simultaneously with the µL-NIPI instrument. Results from the two instruments were in good agreement with one another. The IR-NIPI instrument extended the range of INP concentrations shown by the µL-NIPI by 2 orders of magnitude, covering a regime critical for cloud formation with a modest sampling time of just 100 min at 16.67 L min⁻¹.