Free-fall experiments of volcanic ash particles using a 2-D video disdrometer

Information of aerodynamic parameters of volcanic ash particles, such as terminal velocity, axis ratio, and canting angle, are necessary for quantitative ash-fall estimations with weather radar. In this study, free-fall experiments of volcanic ash particles were accomplished using a two-dimensional video disdrometer under controlled conditions.

Samples containing a rotating symmetric axis were selected and divided into five types according to shape and orientation: oblate spheroid with horizontal rotating axis (OH), oblate spheroid with vertical axis (OV), prolate spheroid with horizontal rotating axis (PH), prolate spheroid with vertical rotating axis (PV), and sphere (Sp). The horizontally (OH and PH) and vertically (OV and PV) oriented particles were present in proportions of 76 % and 22 %, and oblate and prolate spheroids were in proportions of 76 % and 24 %, respectively. The most common shape type was OH (57 %).

The terminal velocities of OH, OV, PH, PV, and Sp were obtained analyzing 2-D video disdrometer data. The terminal velocities of PV were highest compared to those of other particle types. The lowest terminal velocities were found in OH particles. It is interesting that the terminal velocities for OH decreased rapidly in the range $\mathrm{0.5}<D<\mathrm{1}$ mm, corresponding to the decrease in axis ratio (i.e., smaller the particle, the flatter the shape). The axis ratios of all particle types except Sp were found to be converged to 0.94 at D>2 mm.

The histogram of canting angles followed unimodal and bimodal distributions with respect to horizontally and vertically oriented particles, respectively. The mean values and the standard deviation of entire particle shape types were close to 0 and 10^∘, respectively, under calm atmospheric conditions.

1 Introduction

Volcanic eruptions are considered one of the most severe types of natural phenomena and can lead to human casualties and property damage. Ash consists of very fine-grained fragments, their volume-equivalent spherical particle diameter (D in mm) is generally smaller than 2 mm, and they are generally dominated by broken glass shards rather than crystal and lithic fragments. Wilson et al. (2012) give an overview of the ash's effects on critical infrastructure, including from ash fall and acid rain. Hilman et al. (2012) investigate the effect ash particles have on human health in the case of Sakurajima's volcanic eruptions. More comprehensive descriptions of volcanic ash's impacts on society are found in Sigurdsson et al. (2015) and Wilson et al. (2015). Following an eruption, fine airborne volcanic ash flows for several tens of kilometers, which can cause major problems by increasing aviation traffic (e.g., Bonadonna et al., 2012; Langmann et al., 2012); this was seen after the eruption of Eyjafjallajökull volcano in Iceland during the period 14–21 April 2010; see, e.g., Bonadonna et al. (2011). From the viewpoint of volcanological hazard reduction, accurate description of transport and deposition in a numerical forecasting model of volcanic ash clouds is vitally important (Poulidis et al., 2017).

Terminal fall velocity (V_T) of a particle is affected by its shape, density, size, and atmospheric properties. Wilson and Huang (1979), Dellino (2005), and Coltelli et al. (2008) introduced the influence of ash particle shapes on its V_T. Haider and Levenspile (1989) and Ganser (1993) analyzed V_T of volcanic ash particles on the drag coefficient (C_D), which is dependent on particle shape and atmospheric condition. Transport and sedimentation of volcanic ash are complex processes, and the residence time and fall velocity of ash is critically dependent on particle size (Bonadonna et al., 1998), where, with respect to the latter, smaller particles could be flowing in the atmosphere further from the vent.

Aerodynamic properties are important for safe aviation and for studying the effects of volcanic ash on climate change, since these parameters determine the residence time of ash particles in the atmosphere (e.g., Folch et al., 2009). The V_T of particles varies widely due to their irregular shapes and material components (e.g., Wilson, 1972; Harris and Rose, 1983; Bonadonna et al., 2011; Maki et al., 2016). Bonadonna et al. (2011) analyzed V_T of volcanic ash particles with various particle densities (ρ_s) from 990 to 2738 kg m⁻³, and Maki et al. (2016) summarized the list of various V_T relationships suggested by previous studies. Volcanic ash particles have a range of shapes, and this presents a major challenge when analyzing their characteristics. Recently, the irregularity of volcanic ash particles was analyzed in detail based on the features of various regular particles, such as cubes, cylinders, and disks (Bagheri and Bonadonna, 2016), using a computed tomography (CT) scanner (Dioguardi et al., 2017; Garboczi and Bullard, 2017).

There are two approaches to studying these aerodynamic properties. The first approach is theoretical, where a numerical simulation model is used to calculate terminal velocities, drag force, and Reynolds number (Re); examples of this approach can be found in Happel and Brenner (2012). The second approach is related to experimental research, in which the aforementioned relationships are determined experimentally. For instance, Bagheri et al. (2013) and Bagheri and Bonadonna (2016) analyzed the aerodynamic features of irregularly shaped ash particles from the free-fall experiments. Dioguardi et al. (2018) suggested a new model of fluid drag for irregularly shaped particles using previous research. Since the aerodynamic feature depends on atmospheric condition and it can affect the retrieval of V_T, it could be suggested that it can be analyzed through the free-fall laboratory experiments for the following main reasons: (1) there is little chance to measure natural falling ash particles, (2) it could be possible to control the size of ash particle in the free-fall experiments, (3) and it could reduce the wind effect in the experiments.

The present study applies the second approach (experimental research) to clarify the physical characteristics of volcanic ash particles analyzing the experimental data. The rest of this paper is organized as follows. Section 2 describes the free-fall experiments of ash particles and methods of analysis, Sect. 3 presents the results of the free-fall experiments, Sect. 4 is discussion, and Sect. 5 summarizes the results.

2 Data and methods

2.1 Two-dimensional (2-D) video disdrometer

The 2-D video disdrometer (2DVD) was developed by Joanneum Research (Graz, Austria) to detect single raindrop particles, and the instrument has been modified to cover the errors caused by turbulence effects (Nešpor et al., 2000). The device is able to observe the shape, V_T, and β of a single particle using optical light. The ability to analyze a single particle is a significant advantage compared to other disdrometers, such as the Joss–Waldvogel disdrometer (Joss and Waldvogel, 1967), the Precipitation Occurrence Sensor System (Sheppard, 1990), and Parsivel (Löffler-Mang and Joss, 2000). For instance, Parsivel considers a fixed measurement area without any consideration of particle shape (e.g., Tokay et al., 2014), while 2DVD observes particles by passing them through a 100 cm² observation area consisting of two light sources, i.e., reflecting mirrors and two cameras, with one camera set 6.2 mm above the other and collecting data with a resolution of 630 pixels; this results in a pixel size of 0.2 mm at 55 kHz (Kruger and Krajewski, 2002). Particles passing through the observation area yield shape information according to the radiation intensity of the light sources, which is helpful for calculation of γ and β. The V_T of particles is calculated using the height difference between the two cameras. Based on these advantages, the oscillation and particle shape of raindrops can be analyzed by 2DVD (Thurai and Bringi, 2005). Böhm (1989) analyzed the aerodynamic properties of an irregular hydrometeor and Huang et al. (2010, 2015) used 2DVD to analyze the features of irregularly shaped snow. There have been few previous aerodynamic analyses of volcanic ash particles performed using 2DVD, which is able to detect and analyze volcanic ash particles with a range of irregular shapes. Thus, 2DVD offers a unique approach as a new observation strategy.

Figure 1 Accumulated contoured images of volcanic ash particles, with D measured by a two-dimensional video disdrometer (2DVD).

2.2 Definition of particle shape type

Volcanic ash particles have various shapes that can be detected by 2DVD (Fig. 1). In the case of raindrops, the drop size distribution (DSD) is dependent upon the break-up and coalescence processes occurring via up and downdrafts, since the forces of gravity and buoyancy can easily affect raindrop shapes (Rosenfeld and Ulbrich, 2003). However, solid particles do not readily change shape when falling without the influence of forces such as collision. It is thus inferred that many particle shapes would be found in the atmosphere, and that it would be possible to define and classify each particle shape type if we were able to accurately detect a single particle. Thus, the range of γ for solid particles would be expected to be wide compared to that of raindrops, and various values of V_T and β would likely be observed. The γ_x of a particle is defined as the ratio of height to width for the observation direction x, and its representative value is calculated using the geometric means of the two γ (γ₁, γ₂) detected by cameras 1 and 2, respectively (Eq. 1):

$$\begin{array}{}\text{(1)}& {\mathit{\gamma }}_{\mathrm{1}\left(\mathrm{2}\right)}={\displaystyle \frac{{\text{Height}}_{\mathrm{1}\left(\mathrm{2}\right)}}{{\text{Width}}_{\mathrm{1}\left(\mathrm{2}\right)}}},\mathit{\gamma }=\sqrt{{\mathit{\gamma }}_{\mathrm{1}}{\mathit{\gamma }}_{\mathrm{2}}}.\end{array}$$

The difference in angle between the rotating symmetric axis and vertical axis is defined as β. The counter-clockwise (clockwise) movement of the rotating symmetric axis has a positive (negative) value and the entire range is 180^∘ (from −90 to 90^∘) with 0^∘ as the center.

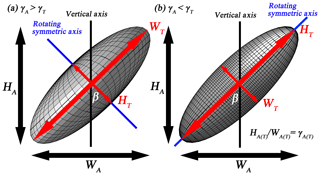
Figure 2 Conceptual model of an (a) oblate and (b) prolate spheroid with the same canting angle (β). W_A(T) and H_A(T) are the apparent (true) width and height of the particle, respectively. γ_A(T) is the apparent (true) axis ratio.

It is necessary to consider the true axis ratio (γ_T) to correctly define the particle shape (Fig. 2). The apparent axis ratio (γ_A) considers the effect of β but the γ_T does not. The 2-D coordinates (x,z) of the particle shape with β are defined as follows:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{x}_{\mathrm{A}}=r\cos (\mathit{\theta }+\mathit{\beta }),z_{\mathrm{A}}=r\sin (\mathit{\theta }+\mathit{\beta }),\\ {\displaystyle }& {\displaystyle }{x}_{\mathrm{T}}=r\cos \mathit{\theta },z_{\mathrm{T}}=r\sin \mathit{\theta },\end{array}$$

where subscript A is the coordinate of the original data coordinate considering the β and subscript T is the modified data coordinate. The symbol r refers to the length from the data point to the center and the symbol θ represents the degrees of data coordinates from the positive x axis, which range between 0 and 180^∘. In this paper, γ stands for γ_A for convenience.

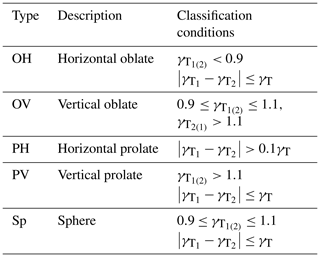
An objective criterion for particle shape type was considered since particle shapes can be highly diverse and irregular (e.g., Bagheri and Bonadonna, 2016; Dioguardi et al., 2017, 2018; Garboczi and Bullard, 2017). In the case of irregular particles, the γ can change according to the observation direction; however, any criterion should be able to define the particle shape types strictly and reliably. To solve this problem, particles with a rotating symmetric axis were the main target of the present study. Therefore, we considered oblate spheroid (O), prolate spheroid (P), and sphere (Sp), which all have a rotating symmetric axes. Among these particle types, the major axes of the oblate and prolate spheroids could be horizontally (H) and vertically (V) oriented with respect to the ground, respectively. Thus, the various particle shapes were divided into five types as follows; oblate spheroid with horizontal rotating axis (OH), oblate spheroid with vertical axis (OV), prolate spheroid with horizontal rotating axis (PH), prolate spheroid with vertical rotating axis (PV), and Sp.

To define these particle shape types, a strict definition of the γ_T is required, which can be calculated from the β. As with the γ, the two β values are automatically calculated by 2DVD. In the case where the β is assumed to be 0^∘, the rotating symmetric axis for OH and PV can be defined, since it is observed for any observation direction parallel to the ground. However, in the case of OV and PH particles, the rotating symmetric axis cannot be defined when the observation direction is parallel. In the case where the β is not 0^∘, γ_T for all particle shape types would not change when oscillation occurs in a direction orthogonal to the observation direction, but it is difficult to estimate both γ_T and β when particle oscillation appears in a direction parallel to the observation direction. The ability to restore the γ_T and β relative to this observation direction is limited, which is one of the main disadvantages of the 2-D observation strategy.

Based on these facts, a major β was selected based on the following reasoning: (i) a β for the observation direction with lower (higher) γ_T for OH (PV) is selected. (ii) In the case of OV (PH), for which the rotating symmetric axis was observed for only one observation direction, β was considered where the value of β had a higher (lower) γ_T than that of the other observation direction. Therefore, β with a lower (higher) γ_T in two observation directions for the case of an oblate (prolate) particle was considered a meaningful value. The perfect sphere could not have their value of β determined theoretically because there is the possibility of a rotating symmetric axis in any direction.

Based on the definition of β (Fig. 2), the perfect condition with respect to ellipsoids is satisfied when $\left|\mathit{\beta }\right|=\mathrm{0}{}^{\circ }$ (90^∘) for OH and PV (OV and PH); these values are defined as the center values. However, 2DVD calculated that the β for each particle shape type was concentrated around $\left|\mathit{\beta }\right|=\mathrm{0}{}^{\circ }$ (90^∘) with respect to horizontally (vertically) oriented particles, which correspond to OH and PH (OV and PV). Furthermore, analysis of particles with an orthogonal center angle from 0^∘ is difficult, since they have two center angles (±90^∘). To address observation errors and enhance the convenience of analysis, all center angles were set to $\left|\mathit{\beta }\right|=\mathrm{0}{}^{\circ }$ and modified to give the representative canting angle, β_R, using the following equation:

$${\mathit{\beta }}_{\mathrm{R}}=\mathit{\beta }-{\mathit{\beta }}_{\mathrm{0}},$$

where β₀ is the orienting angle, defined by the central angle of oscillation. In the case of vertically oriented particles (OV and PV), β₀ could be defined as ±90^∘. The sign of β₀ follows that of β.

Table 1 Ash particle classification criteria.

After removing β, each particle shape was defined using γ_T (Table 1). Note that a 10 % bias range was allowed, to take observational error into account. For example, a particle was considered a sphere when $\mathrm{0.9}<{\mathit{\gamma }}_{\mathrm{T}}<\mathrm{1.1}$, which is an applied 10 % bias range from γ_T=1. In addition, the particle types OH and PV (OV and PH) were classified when the value of |γ₁–γ₂| was smaller (larger) than 0.1γ_T, to consider particles with only a rotating symmetric axis.

2.3 Calculate the terminal velocity for the various particle shape types

The V_T of volcanic ash is required to estimate the R_A (kg m⁻² s⁻¹) on the ground where this depends on atmospheric density (ρ_g in g cm⁻³), T, Re, C_D, D, ρ_s, and its shape. Kunii and Levenspiel (1969) developed a theoretical V_T equation:

$$\begin{array}{}\text{(2)}& V_{\mathrm{T}}={\left({\displaystyle \frac{\mathrm{4}\left({\mathit{\rho }}_{\mathrm{s}}-{\mathit{\rho }}_g\right)gD}{\mathrm{3}{\mathit{\rho }}_g{C}_{\mathrm{D}}}}\right)}^{\mathrm{0.5}}({\mathrm{10}}^{\mathrm{0}}<Re<{\mathrm{10}}^{\mathrm{4}}).\end{array}$$

Later, Suzuki (1983) developed a theoretical V_T equation for tephra. Bonadonna et al. (2011) then modified the theoretical V_T equation suggested by Kunii and Levenspiel (1969) with observed ash data, which implied that the result of the theoretical V_T equation could be unsuitable for nonspherical particles. Based on these equations, various C_D equations considering nonspherical particles were subsequently developed. Tran-Cong et al. (2004) developed a new equation for C_D using the function of circularity, and Hölzer and Sommerfeld (2008) introduced a progressed C_D equation considering two types of sphericity: lengthwise (${\mathrm{\Phi }}_{\left|\right|}$) and crosswise (Φ_⊥). This equation is as follows:

$$\begin{array}{}\text{(3)}& \begin{array}{rl}& C_{\mathrm{D}}={\displaystyle \frac{\mathrm{8}}{Re}}{\displaystyle \frac{\mathrm{1}}{{\sqrt{\mathrm{\Phi }}}_{\left|\right|}}}+{\displaystyle \frac{\mathrm{16}}{Re}}{\displaystyle \frac{\mathrm{1}}{\sqrt{\mathrm{\Phi }}}}+{\displaystyle \frac{\mathrm{3}}{\sqrt{Re}}}{\displaystyle \frac{\mathrm{1}}{{\mathrm{\Phi }}^{\mathrm{3}/\mathrm{4}}}}\\ & +\mathrm{0.42}\times {\mathrm{10}}^{\mathrm{0.41}(-\log (\mathrm{\Phi }){)}^{\mathrm{0.2}}}{\displaystyle \frac{\mathrm{1}}{{\mathrm{\Phi }}_{\perp }}}.\end{array}\end{array}$$

The Re is defined as follows:

$$\begin{array}{}\text{(4)}& Re={\displaystyle \frac{{\mathit{\rho }}_g{V}_{\mathrm{T}}\mathrm{D}}{\mathit{\mu }}},\end{array}$$

where μ is the dynamic viscosity (kg m⁻¹ s⁻¹), which we assumed to be $\mathrm{1.983}\times {\mathrm{10}}^{-\mathrm{5}}$ based on atmospheric conditions at a T of 25 ^∘C. Three types of sphericity were defined as follows:

$$\begin{array}{}\text{(5)}& \mathrm{\Phi }={\displaystyle \frac{\mathit{\pi }{D}^{\mathrm{2}}}{\mathrm{SA}}},\end{array}$$

where SA is the surface area of the particle (mm²). The lengthwise sphericity is defined as the ratio between the cross-sectional area of the volume-equivalent sphere and the difference between half the surface area and the mean of the projected vertical cross-sectional area (A_V) of the particle (Eq. 6):

$$\begin{array}{}\text{(6)}& {\mathrm{\Phi }}_{\left|\right|}={\displaystyle \frac{\mathit{\pi }{D}^{\mathrm{2}}}{\mathrm{4}(\mathrm{0.5}\times \mathrm{SA}-A_{\mathrm{V}})}}.\end{array}$$

The crosswise sphericity is the same as the lengthwise sphericity, except for the denominator, which includes the projected horizontal cross-sectional area of the particle (A_H), defined as follows:

$$\begin{array}{}\text{(7)}& {\mathrm{\Phi }}_{\perp }={\displaystyle \frac{\mathit{\pi }{D}^{\mathrm{2}}}{\mathrm{4}{A}_{\mathrm{H}}}}.\end{array}$$

It is noteworthy that the V_T is required to calculate the Re and V_T, which refers to the final product. To solve this problem, the theoretical V_T (Eq. 2) was used as the input value of Eq. (4) until Eq. (2) converged.

Figure 3 The locations of tephrometers and Showa crater on Sakurajima, Japan. Black symbols indicate the locations of tephrometers, and the star, square, and circle symbols correspond to data sets A, B and C–E, respectively. The white circle symbol represents the location of Showa crater.

2.4 Sakurajima

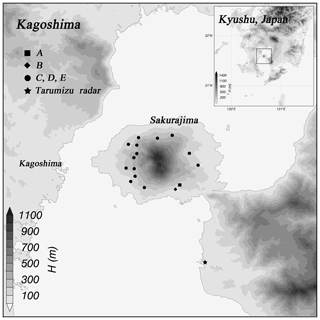
Japan has around 10 % (110) of all of the active volcanos in the world. Sakurajima (1117 m.a.s.l, 31.58^∘ N, 130.65^∘ E, Kyushu, Japan) is an active volcanic island formed around 13 000 yr ago, and its tephra is approximately 60 %–66 % S_iO₂ Peléan type (Oguchi et al., 2009; Takahashi et al., 2013). The major eruptive events in the historic age of Sakurajima were 1471–1476 (Bunmei era), 1779–1782 (An'ei era), and 1914 (Taishō era). Sakurajima is an andesitic volcano with two peaks (Kita-dake and Minami-dake). Volcanic activity at Kita-dake ended around 4900 yr ago when it changed to Minami-dake. Activity has centered on Showa crater from 2006 (Iguchi, 2013). Showa crater is located on the eastern flank, approximately 500 m east of Minami-dake (southern peak) on Sakurajima. It was appeared in 1939 after 1 month of eruptions (Yokoo and Ishihara, 2007). The Minami-dake summit crater was the only active center of Sakurajima until the recommencement of Showa crater from 1948 to 2006. The eruptive activity of Showa crater resumed in June 2006, and vulcanian eruptions gradually increased in the autumn of 2009 (Hotta et al., 2016). The Japan Meteorological Agency (JMA) reported that the eruption frequency of Sakurajima would increase significantly from 2009, and the accumulated ash fall exceeded 3.5 kg m⁻² in Kagoshima in 2012. The Ministry of Land, Infrastructure, Transport, and Tourism (MLITT) installed an operational X-band radar 10.7 km from the vent, as well as 16 automatic volcanic ash weight measurements, to observe volcanic eruptions in 2011 (Fig. 3).

Figure 4 Real images of volcanic ash particles used in the present study. The particles were classified as (a) 0.125 mm D≤0.25 mm, (b) 0.25 mm D≤1 mm, (c) 1 mm D<2 mm, and (d) $\mathrm{2}<D\le \mathrm{4}$ mm.

Table 2 Information on the collected volcanic ash particles.

2.5 Free-fall experiments

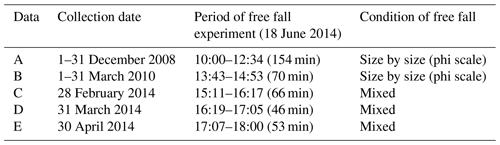
The data were collected by automatic volcanic ash weight measurements performed on Sakurajima (Tajima et al., 2015; Maki et al., 2014, 2016). The free-fall experiments were divided into two types: one was performed for each phi scale ($\mathrm{\Phi }=-{\log }_{\mathrm{2}}D$) from Φ=3 to −4 ($\mathrm{0.125}<D<\mathrm{16}$ mm) and the other was not considered on a particle-size scale. The former data, expressed by A and B (Type 1), were collected at two sites and screened by size (Fig. 4); the latter data, expressed as C–E (Type 2), were collected at 18 sites (Table 2). Free-fall experiments on collected volcanic ash particles were carried out in the large-scale rainfall simulator of the National Research Institute for Earth Science and Disaster Prevention (NIED) in Tsukuba, Japan. The collected particles were dropped manually around 17 m from the ground and re-collected by a third-generation 2DVD (Maki et al., 2016). Each sample was dropped for 30 s to stimulate dispersion, and the measurement period was 1 min. To avoid wind effects including turbulence, the 2DVD was surrounded by a 3 m³ wind-breaking wall (Fig. 5).

Figure 5 Free-fall experiment conditions of volcanic ash particles on the (a) outside and (b) inside of the wind-breaking wall covering the disdrometers in the large-scale rainfall simulator of the National Research Institute for Earth Science and Disaster Prevention (NIED).

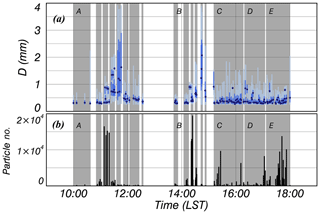
The free-fall experiments were conducted at intervals of 1 min over 6.5 h, as shown in Fig. 6. The number of particles detected by 2DVD was less than 10 000 for 1 min, and the particle size range of the Type 1 data set was proportional to its phi scale, since small particles may be contained by screening.

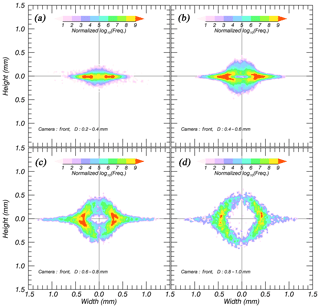
Figure 7 shows the distribution of raw data (the number of data: 274 215) for V_T and γ with D. There were various γ from 0 to 2 when D<2 mm, and most of the data were concentrated near γ=0. The γ values converged around 1 and their distributional range decreased with D. The median value with a 0.25 mm D interval corresponded well to the center of the data contour. The median line converged around γ=0.935 based on the correlation coefficient value (CC). When this was higher than 0.95 for each D interval, the data converged. According to this condition, the range of $\mathrm{2}<D<\mathrm{5}$ mm was satisfied and the mean value was calculated using these data. The V_T had a wider range when D<2 mm but the median line corresponded well to the center of the data (Fig. 7b). The line representing the largest number of data is lower than the volcanic ash discussed by Bonadonna et al. (2011). To select a available range of D, a theoretical terminal velocity equation (V_T,Ref) for a non-sphere corresponding to Eqs. (2)–(7) was used as the reference. The particle density associated with the eruption of Sakurajima is between 2.43 and 2.59 g cm⁻³ (Oguchi et al., 2009), but the actual particles contain air vacuoles (Van Eaton et al., 2012). This means that ρ_s including vacuoles is smaller than ρ_s alone. Therefore, the minimum ρ_s was considered to be 2.43 g cm⁻³, and this was used as an input parameter. The atmospheric conditions of T and P were considered from an automatic weather station (AWS), supported by the JMA. The falling height of a particle, which followed the aforementioned conditions (γ=0.935, ρ_s=2.43 g cm⁻³) when D=4 was lower than that under the condition of the free-fall experiment (17 m) and it reached 90 % of V_T (13.9 m); therefore, the available data range is considered to be D≤4 mm, and this would satisfy the terminal fall velocity. The detailed equations used in the present study are shown in Appendix A.

Figure 6 The 1 min interval time series of D and the number of particles in the free-fall experiment conducted at the NIED.

2.6 Quality control procedures

The 2DVD was originally developed to detect raindrop hydrometeors. For this reason, additional quality control (QC) checks were deemed necessary to ensure applicability to non-hydrometeors, such as volcanic ash particles. Specifically, we performed the following three QC procedures for accurate analysis of the data.

• i.

  Particle D>0.25 mm was selected in consideration of the minimum spatial resolution of 2DVD.

• ii.

  If the major axis observed by 2DVD was 10 % longer than that of the value calculated directly based on data coordinates, the data were considered erroneous and thus removed. A 10 % bias range was considered due to mathematical error, the irregular particle shape, and the limitation of the spatiotemporal resolution of 2DVD.

• iii.

  To consider volcanic ash particles, the sample that satisfied the criteria in the chosen range of the terminal velocity relationship was selected. If we consider a single V_T QC measurements for the entire particle shape type, a number of available data will be removed, since V_T critically depends on particle shape. Therefore, we applied a 60 % V_T QC threshold (Jaffrain et al., 2011) for each particle shape type. It could be applied once the V_T relationship of volcanic ash particles is obtained. After selecting the particle shape types and applying these two QC procedures (i and ii), 19.31 % of the data (62 953) remained (Table 1).

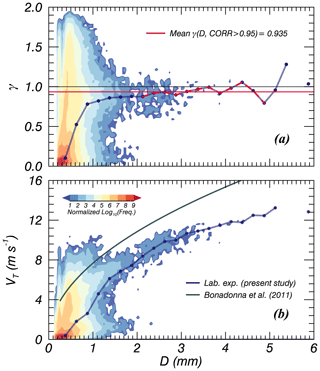
Figure 7 Contour image of volcanic ash particles for (a) the axis ratio (γ) and (b) terminal velocity (V_T). The solid red line is the averaged γ satisfying the condition that the correlation coefficient exceeds 0.95. The solid grey line is the relationship of volcanic ash particles suggested by Bonadonna et al. (2011).

3 Results

3.1 Ash particle shape

The ash particle size over the entire volcanic ash sample was skewed leftward, and the dominant particle shape type changed with particle size (Fig. 8). The particles were predominantly horizontally oriented (75.51 %) and vertically oriented (21.60 %). Oblate and prolate spheroids made up 76.26 % and 23.85 % of the particles, respectively. Hence, the particles were mainly OH (57.38 %) or PH (15.88 %) (Table 2). The particles were predominantly $\mathrm{0.25}<D<\mathrm{0.5}$ mm (63.00 %) or $\mathrm{0.5}<D<\mathrm{1}$ mm (32.80 %). Relatively few particles had D>1 mm (4.20 %).

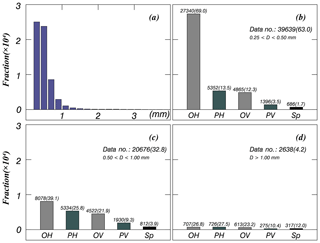
Figure 8 Histograms of volcanic ash particles for (a) all particle types and (b–d) each particle shape type of the phi scale. The grey-shaded and dark-grey-shaded (patterned) bars indicate horizontal oblate (OH) (vertical oblate, OV) and horizontal prolate (PH) (vertical prolate, PV), respectively. The black bar corresponds to spherical (Sp) particles. The number on the top of each bar plot is the number of data points, and the number in parentheses is the percentage for each phi scale.

There was large variation in shape among particles $\mathrm{0.25}<D<\mathrm{0.5}$ mm, but the variation decreased with increasing D. All of the particle shape types had the largest number of particle at D>1.0 mm and the next largest were shown at $\mathrm{0.5}<D<\mathrm{1.0}$ mm, except for OH. In total, 95.80 % of OH particles had D<1 mm, at D<0.5 mm the value was 75.68 %, and at D=0.5–1 mm it was 22.36 %. In the cases of PH and OV, 93.63 % and 93.87 % of these particles, respectively, had D<1 mm. Beyond D>1 mm, the differences in the number of particles for each particle shape type were considerably decreased.

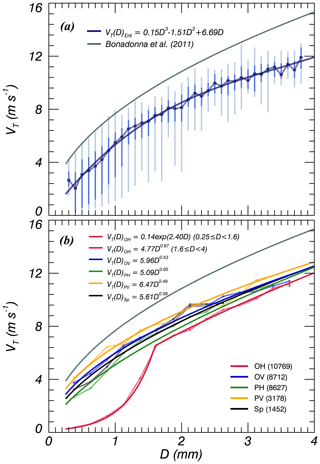
Figure 9 Distribution of (a) quartile and (b) median terminal velocity (V_T) values after applying the 60 % V_T QC threshold for all shape types and each individual particle shape type, respectively. The solid grey line shows the relationships of the volcanic ash particles suggested by Bonadonna et al. (2011).

3.2 Terminal velocity

The V_T for the entire particle shape types follows a polynomial regression analysis that was applied to define the nonlinear relationship between V_T and D (Fig. 9a). It corresponds to that obtained by Miwa et al. (2015), who analyzed Parsivel data using the same laboratory experiments. The inflection point of V_T was at D<1.3 mm and it came from an increase in the number of OH and a decrease in their V_T when D<1 mm. As a result, the V_T relationship for each particle shape type can be seen clearly.

The observed values of V_T were well classified by particle shapes (Fig. 9b). The highest values of V_T were recorded in the following order: prolate, sphere, and oblate. Vertically oriented particles had higher V_T values than horizontal ones. The V_T for every particle type can be expressed in a power law form, except for OH. OH particles followed the regression line relatively closely and showed the highest CC and root-mean-square error (RMSE) values of 0.94 and 0.46 m s⁻¹, respectively. Horizontally oriented particles had relatively high correlations (OH: 0.94; PH: 0.87) compared to those with a vertical orientation (OV: 0.75; PV: 0.71). The V_T relationships and those of statistical parameters are summarized in Table 3.

Table 3 Relationships of terminal velocity, with the number of data points, the value of the correlation coefficient (CC), and the root-mean-square error (RMSE), after applying the 60 % V_T QC threshold for each particle shape type.

To verify the reliability of the particle data obtained by 2DVD, which was originally developed to detect liquid raindrops, ρ_s, C_D, and Re, as well as theoretical V_T values according to these parameters, were analyzed. To calculate the parameters of interest, including the surface area and cross-sectional area of irregular particles, we applied the irregular particle volume estimation equations of Huang et al. (2010).

Figure 10 Same as Fig. 9 but for particle density (ρ_s).

3.3 Aerodynamic properties

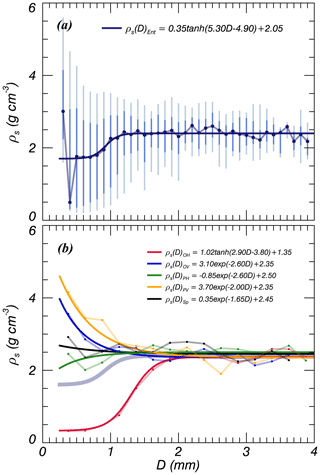
Particle densities were estimated using the V_T,Ref, converged to 2.37 g cm⁻³ when D<1.5 mm (Fig. 10a). This value corresponds well to that of the minimum ρ_s (2.43 g cm⁻³) reported by Oguchi et al. (2009). The slight difference is likely due to observation errors and the presence of vesicles (e.g., Seligman et al., 2016). The median value of ρ_s is changed to $\mathrm{0.5}<D<\mathrm{1.5}$ mm, and this range corresponds to that of V_T. Horizontally oriented particles (OH and PH) have relatively smaller ρ_s and vertically oriented particles (OV and PV) have higher density (Fig. 10b); spheres have particle densities that accord best with D. The median ρ_s values for all particle shapes converged when D<2 mm, and the converged ρ_s values ranged from 2.35 to 2.50 g cm⁻³.

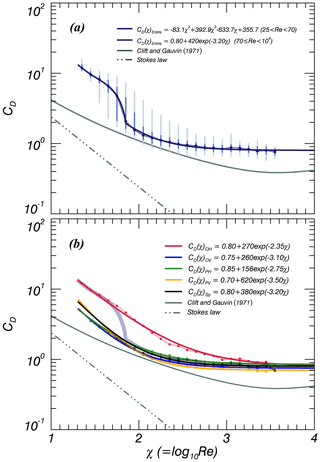
Figure 11 Same as Fig. 9 but for Reynolds number (Re) and drag coefficient (C_D). The solid grey and broken grey lines in (a) are the relationships of spheres suggested by Clift and Gauvin (1971) and Stokes (1851), respectively.

The Re and C_D for the all particle shapes ranged from 10 to 4000 and 0.6 to 20, respectively (Fig. 11a). Higher values of C_D were observed when log(Re)<1.845 (Re<70); above this threshold, C_D dramatically decreased. These results were derived according to the number of OH particles, which mainly had D<0.5 mm and had higher C_D and lower Re. Particle shape was divided into two types: OH and others (Fig. 11b). OH particles had higher C_D compared to the other particle shapes, which in turn showed few differences among themselves. The OH particles experience strong drag forces under the same flow conditions, leading to lower V_T. The differences between OH and other particles diminished with Re<1000. The other particle shapes had relatively higher C_D in the range $\mathrm{10}<Re<\mathrm{3000}$. Rong et al. (2015) analyzed the relationship between Re and C_D for oblate and prolate particles and showed that OH particles had higher C_D compared to the reference line (Clift and Gauven, 1971) in the range $\mathrm{0}<Re<\mathrm{400}$. Each relationship is summarized in Fig. 11.

3.4 Axis ratio

The γ of a particle affects the backscattering power of electromagnetic waves and is necessary to calculate the horizontal reflectivity (Z in dBZ), differential reflectivity (Z_DR in dB), and specific differential phase shift (K_DP in ^∘ km⁻¹). Note that previous studies have analyzed the γ distribution for raindrops and snow, including hail; however, few studies have been reported on γ of ash particles compared to those for hydrometeors.

Figure 12 Same as Fig. 9 but for γ.

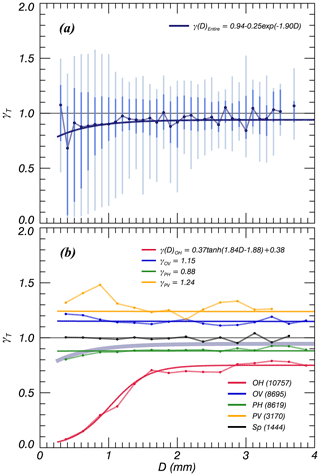
Figure 12 shows the quartiles and median values of γ for all particle shapes and for each individual particle shape type. The γ had a higher standard deviation (σ_γ) of >0.25 when D<0.75 mm, which decreased and converged to σ_γ=0.15 when D>1 mm (Fig. 12a). The γ in the lower σ_γ range converged to γ=0.94 and could be expressed as follows:

$$\begin{array}{}\text{(8)}& \mathit{\gamma }\left(D\right)=\mathrm{0.94}-\mathrm{0.25}\exp (-\mathrm{1.90}D).\end{array}$$

The particles are more easily classified by shape than by V_T (Fig. 12b). Every particle shape type was independent of D, except for OH. The γ of each particle type is expressed via the following relationships (Eqs. 9–12).

$$\begin{array}{}\text{(9)}& {\displaystyle }\mathit{\gamma }{\left(D\right)}_{\mathrm{OH}}=\mathrm{0.37}\text{tanh}\left(\mathrm{1.84}D-\mathrm{1.88}\right)+\mathrm{0.38}\text{(10)}& {\displaystyle }{\mathit{\gamma }}_{\mathrm{OV}}=\mathrm{1.15}\text{(11)}& {\displaystyle }{\mathit{\gamma }}_{\mathrm{PH}}=\mathrm{0.88}\text{(12)}& {\displaystyle }{\mathit{\gamma }}_{\mathrm{PV}}=\mathrm{1.24}\end{array}$$

The parameter γ(D)_OH was calculated using the hyperbolic tangent (tanh) for the following reasons: (i) its range of values was wider than those of other particle types, (ii) its data distribution changed continuously with D, and (iii) it was present in a higher proportion (30.44 %) compared to the other parameters. We found that variations in γ decreased with D and the proportion of Sp shapes increased when D>2 mm. The particle types OV and PH showed a wide distribution over $\mathrm{1}<\mathit{\gamma }<\mathrm{1.5}$ and $\mathrm{0.4}<\mathit{\gamma }<\mathrm{1.0}$, respectively, when D<2 mm, but the variability in median values was relatively low. The relationships of γ for each particle shape type could be expressed by constant values at γ=0.75 (OH), 0.88 (PH), 1.15 (OV), and 1.24 (PV), respectively, and these differences are around γ=0.12.

Figure 13 Histograms of representative canting angle (β_R) for each particle shape type, including the data for all particles.

3.5 Canting angle

Statistical analysis of β is required to understand the aerodynamic properties of volcanic ash particles and the input parameters of T-matrix scattering simulations to verify the observed radar variables. The histogram of β_R is shown in Fig. 13.

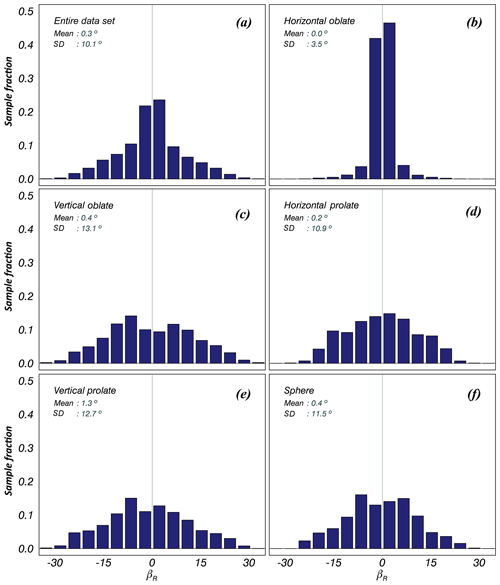
More than 95 % of β values for each particle shape type were concentrated in the range $\left|{\mathit{\beta }}_{\mathrm{R}}\right|\le \mathrm{30}{}^{\circ }$, with 0^∘ as the center (Fig. 13). The particles were symmetrically distributed around 0^∘ and more than 50 % were concentrated in the range $\left|{\mathit{\beta }}_{\mathrm{R}}\right|<\mathrm{4}{}^{\circ }$. The horizontally oriented β distribution was relatively narrow $\left(\right|{\mathit{\beta }}_{\mathrm{R}}|<\mathrm{20}{}^{\circ })$ and exhibited a unimodal distribution. It is noteworthy that 90 % of OH particles were concentrated in the range $\left|{\mathit{\beta }}_{\mathrm{R}}\right|<\mathrm{4}{}^{\circ }$. The vertically oriented β distribution was relatively broad $\left(\right|{\mathit{\beta }}_{\mathrm{R}}|<\mathrm{30}{}^{\circ })$ and followed a bimodal distribution. PV exhibited a bimodal form, but this was not symmetrical around 0^∘. For spheres, the β distribution was narrower, similar to horizontally oriented particles, and it had a bimodal distribution, similar to vertically oriented particles, indicating that the independent features of both orientations were combined.

The values of $\left|\stackrel{\mathrm{‾}}{{\mathit{\beta }}_{\mathrm{R}}}\right|$ and $\left|{\mathit{\sigma }}_{\mathit{\beta }}\right|$ for OH and PV (OV, PH) were 0 and 3.5^∘ (0.4, 13.1^∘) and 1.3 and 12.7^∘ (0.2, 10.9^∘), respectively. OV (OH) had the highest (lowest) value of $\left|{\mathit{\sigma }}_{\mathit{\beta }}\right|$. This validates the assumption of Marzano et al. (2012) under stable conditions $\left(\right|{\mathit{\sigma }}_{\mathit{\beta }}|=\mathrm{10}{}^{\circ })$. Therefore, we believe that the tumbling phenomenon $\left(\right|{\mathit{\sigma }}_{\mathit{\beta }}|>\mathrm{30}{}^{\circ })$ of the particles under calm atmospheric conditions was likely to be minor.

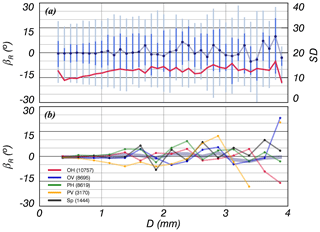
Figure 14 Distribution of β_R with D for each particle shape type including the data for all particles. The solid red line indicates the standard deviation.

To analyze the correlation between particle D and β, quartiles for each particle D interval were calculated (Fig. 14). The particles were concentrated at $\left|{\mathit{\beta }}_{\mathrm{R}}\right|<\mathrm{30}{}^{\circ }$ regardless of D, and median values were stable when D<1 mm for the entire particle shape types; however, fluctuation increased with D (Fig. 14a). The $\left|{\mathit{\sigma }}_{\mathit{\beta }}\right|$ values gradually increased from 10 to 13^∘ when $\mathrm{0.3}<D<\mathrm{1.3}$ mm, and variability was greatest around the center (13^∘). This increase in $\left|{\mathit{\sigma }}_{\mathit{\beta }}\right|$ would not be expected in the case of a relatively small number of particles (Fig. 8a), since their standard deviation is largely maintained at about 13^∘ regardless of data set size.

Variability in the median values for individual particles was more apparent. The values converged around 0^∘ but fluctuation increased with greater D from the zero line. The median $\left|{\mathit{\beta }}_{\mathrm{R}}\right|$ values exceeded 3, 5, 10, and 15^∘ when D>1 mm, $\mathrm{1}<D<\mathrm{2}$ mm, $\mathrm{2}<D<\mathrm{3}$ mm, and D>3 mm, respectively (Fig. 14b).

4 Discussions

The results of present study can be extended in viewpoint of the radar meteorology: (i) the radar observation and (ii) ash-fall rate (R_A) estimations. Weather radar operates for a similar purpose to that of meteorological satellites, and provides information for determining the volume, mass, and echo top height of weather systems. Short-duration eruptions, i.e., less than 1 h, can be detected at high spatiotemporal resolution, especially in the early period of an eruption. The temporal resolution of weather radar is a few minutes for a single volume scan and depends on the observation strategy and radar band. The spatial resolution of weather radar is a few hundred meters and is proportional to the radar frequency. A number of ash cloud detections were reported in several observational cases in the US and Japan (Maki and Doviak, 2001; Maki et al., 2012). Marzano et al. (2013) summarized 28 major explosive volcanic eruptions detected by weather radars from 1970 to 2011. Harris and Rose (1983) attempted to analyze volcanic ash particle size and total mass using a C-band weather radar. Maki and Doviak (2001) proposed the method to retrieve particle size distribution (PSD) from radar measurements of volcanic ash, and Donnadieu et al. (2012) detected volcanic eruptions using an L-band fixed radar. Marzano et al. (2006, 2012) and Maki et al. (2012, 2014) detected and analyzed volcanic eruptions using weather radars from theoretical (physical) and experimental (engineering) perspectives, respectively. Thus, observability of volcanic ash clouds using weather radar can be confirmed from previous researches. To verify radar-based volcanic ash cloud observations, a scattering simulation can be considered. The basic parameters, axis ratio and canting angle, are the results presented in this study and the input information of scattering simulations used to simulate the theoretical radar variables. In particular, the T-matrix scattering simulation developed by Waterman (1971) is useful for calculation of the theoretical backscattering power of nonspherical particles.

Second, V_T is one of the main parameters for R_A (kg m⁻² h⁻¹) and is defined in terms of PSD and V_T as follows:

$$\begin{array}{}\text{(13)}& R_{\mathrm{A}}=V_r{\displaystyle \frac{\mathrm{3.6}}{{\mathrm{10}}^{\mathrm{3}}}}\underset{D_{\mathrm{1}}}{\overset{D_{\mathrm{2}}}{\int }}{V}_{\mathrm{T}}\left(D\right)N\left(D\right)D^{\mathrm{3}}\mathrm{d}D,\end{array}$$

where V_r is the particle volume ratio. In case of sphere, it is considered π∕6.

Marzano et al. (2012b) proposed Z–C_A relationships using the ash-fall concentration (C_A in g m⁻³) and z. Maki et al. (2016) introduced R_A–z relationship for Sakurajima eruption case (18 August 2013) using the time integration of R_A (S_A in kg m⁻²) obtained by automatic volcanic ash weight measurements. However, once we use a disdrometer, such as 2DVD, it will be possible to estimate R_A directly since 2DVD can measure PSD, V_T, and γ. Therefore, basic parameters could help to simulate radar variables and estimate R_A, which are necessary to develop the quantitative ash-fall estimation (QAE) method.

5 Summary and conclusions

The basic parameters (V_T, γ, and β) of volcanic ash particles were analyzed from the free-fall experiments with 2DVD. Data were collected with 18 automatic volcanic ash weight measurements performed on Sakurajima, Japan (31.58^∘ N, 130.65^∘ E). To identify the aerodynamic properties of the volcanic ash particles in the samples, a free-fall experiment was conducted in the large-scale rainfall simulator of the NIED, and 274 215 samples were analyzed.

Radar variables are highly dependent on the $|K{|}^{\mathrm{2}}$, size, and shape of particles. Particle types with rotating symmetric axes were assumed to represent volcanic ash particles that have a wide variety of irregular shapes. Their orientation was also considered with respect to horizontally (OH, PH) and vertically (OV, PV) oriented oblate and prolate spheroids.

The dominant particle shapes were comprised of horizontally and vertical oriented particles and present in proportions of 75.51 % and 21.60 %, respectively. Regarding particle shape, oblate (prolate) spheroids comprised 76.26 % (23.85 %) of all particles in the samples. The most common particle shape type was OH, accounting for 59 % of all particles when D<1 mm and 69 % when D<0.5 mm. Overall, 95.80 %, 93.87 %, and 93.63 % of the OH, OV, and PH particles had D<1 mm, respectively.

The V_T of the particles were classified in the following order: PV, OV, Sp, PH, and OH. These results are consistent with the V_T,Ref, which suggests that 2DVD is reliable for observing volcanic ash particles under stable weather conditions. A noticeable increase in V_T for OH in the range $\mathrm{0.5}<D<\mathrm{1}$ mm occurred through an increase in γ; this was not observed for other particle types.

The estimated ρ_s converged to 2.37 g cm⁻³ when D>1.5 mm, and the median value changed over the range $\mathrm{0.5}<D<\mathrm{1.5}$ mm. The converged value of ρ_s is consistent with the value for Sakurajima reported by Oguchi et al. (2009). The relationship of C_D and Re were divided into two particle type categories (OH and the others) and C_D(OH) was dramatically increased in the range of Re<70. These results were derived from the particle concentration of OH, which was highest when D<0.5 mm; at this threshold, C_D was higher and Re was lower. The range of V_T over $\mathrm{0.7}<D<\mathrm{1.3}$ mm was informed by both γ and ρ_s.

The σ_γ decreased in the range of D>0.75 mm to 0.15 and converged to γ=0.94. Maki et al. (2014) introduced the radar variables and found that Z_DR gradually increased with time; the dominant values at 10 and 18 min after the eruption were close to 1 and 2 dB, respectively. The results presented in this study corresponded to volcanic eruption clouds with positive Z_DR since it is a function of $|K{|}^{\mathrm{2}}$ and γ (Herzegh and Jameson, 1992). In addition, it can be explained by using the results of present study, that the size sorting of ash particle (e.g., Beckett et al., 2015; Stevenson et al., 2015) will affect the increase in Z_DR.

The $\left|{\mathit{\sigma }}_{\mathit{\beta }}\right|$ of OV particles with $\left|{\mathit{\beta }}_{\mathrm{0}}\right|=\mathrm{90}{}^{\circ }$ was largest (13.1^∘) among all particle types and OH particles had the lowest $\left|{\mathit{\sigma }}_{\mathit{\beta }}\right|$ at 3.5^∘. Based on the $\left|{\mathit{\sigma }}_{\mathit{\beta }}\right|$ results, the tumbling phenomenon would not be dominant under calm atmospheric conditions. The quartiles were stable when D<1 mm for the entire particle shape types but increased with D. The value of σ_β was higher when D<1.3 mm and started to converge around 13^∘ due to a decrease in the number of OH particles.

These results could be the essential information to develop the new approaches for detecting non-hydrometeors and numerical model. The axis ratio and canting angle of ash particles obtained from the present study are necessary for scattering simulations. V_T obtained by the present study suggests that smaller particles can be transported over longer distances. Therefore, it will be useful for scattering simulation of ash particles to develop QAE and help to improve the numerical model using V_T obtained by the present study.

Appendix A

The theoretical fall velocity and falling distance with time are calculated as follows:

$$\begin{array}{}\text{(A1)}& {\displaystyle }F=ma=F_g-F_{\mathrm{D}},\text{(A2)}& {\displaystyle }{F}_g=mg,\text{(A3)}& {\displaystyle }{F}_{\mathrm{D}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\rho }}_g{V}^{\mathrm{2}}{C}_{\mathrm{DA}},\end{array}$$

where F_g is universal gravitation, F_D is drag force, m is mass, and a is the free-fall acceleration. In Eq. (A2), g is the acceleration due to gravity, considered to be 9.81 m s⁻², and V and C_D in Eq. (A3) correspond to the values in Eqs. (2)–(7). The symbols μ and ρ_g are the dynamic viscosity and density of the atmosphere and were assumed to be $\mathrm{1.837}\times {\mathrm{10}}^{-\mathrm{5}}$ kg m⁻¹ s⁻¹ and $\mathrm{1.194}\times {\mathrm{10}}^{-\mathrm{5}}$ g cm⁻³, respectively. The results were based on conditions at an atmospheric T as 25 ^∘C.

To ensure accuracy, we considered the surface roughness effect of a volcanic ash particle (1.07⁻¹) on the fall velocity, as suggested by Bagheri and Bonadonna (2016), and the results for D=4 mm are shown in Fig. A1.

Figure A1 Theoretical (a) fall velocity and (b) falling height for a spheroid with D=4 mm, considering the surface roughness coefficient of the volcanic ash particle (1.07⁻¹) relative to its fall velocity (Bagheri and Bonadonna, 2016).