Retrieval of intrinsic mesospheric gravity wave parameters using lidar and airglow temperature and meteor radar wind data

We analyse gravity waves in the upper-mesosphere, lower-thermosphere region from high-resolution temperature variations measured by the Rayleigh lidar and OH temperature mapper. From this combination of instruments, aided by meteor radar wind data, the full set of ground-relative and intrinsic gravity wave parameters are derived by means of the novel WAPITI (Wavelet Analysis and Phase line IdenTIfication) method. This WAPITI tool decomposes the gravity wave field into its spectral component while preserving the temporal resolution, allowing us to identify and study the evolution of gravity wave packets in the varying backgrounds. We describe WAPITI and demonstrate its capabilities for the large-amplitude gravity wave event on 16–17 December 2015 observed at Sodankylä, Finland, during the GW-LCYCLE-II (Gravity Wave Life Cycle Experiment) field campaign. We present horizontal and vertical wavelengths, phase velocities, propagation directions and intrinsic periods including uncertainties. The results are discussed for three main spectral regions, representing small-, medium- and large-period gravity waves. We observe a complex superposition of gravity waves at different scales, partly generated by gravity wave breaking, evolving in accordance with a vertically and presumably also horizontally sheared wind.

1 Introduction

The impact of atmospheric gravity waves (GWs) on the energy and momentum budget, especially in the upper-mesosphere, lower-thermosphere (MLT) region has long been recognized (Lindzen, 1981; Holton, 1982, 1983; Vincent and Reid, 1983). However, many mechanisms are not fully understood today, for example regarding generation, intermittency, and interactions or breaking of GWs (see Fritts and Alexander, 2003, for a review). Understanding of these processes requires detailed case studies with a complete description of intrinsic gravity wave parameters and the atmospheric background. A well-established and capable technique to observe mesospheric GWs is the imaging of OH layer emissions, which provides compelling detail of the spatial and temporal characteristics of GWs (Swenson and Mende, 1994; Taylor et al., 1995; Nakamura et al., 2003; Suzuki et al., 2007; Vargas et al., 2016). Analysis methods applied to images of the OH layer in order to infer horizontal wavelengths, ground-relative wave periods and phase speeds, and propagation directions include filtering with selected bandwidths, e.g. to enhance GW signatures, fitting routines to specific (e.g. cyclic) wave structures (e.g. Hapgood and Taylor, 1982), time-difference and correlation techniques (Swenson et al., 1999; Tang et al., 2003), cross-spectral and wavelet analysis (Frey et al., 2000), three-dimensional fast Fourier transform (Matsuda et al., 2014), and maximum entropy methods (Sedlak et al., 2016). In order to retrieve horizontal wavelengths larger than the field of view (FOV) of the imager, Takahashi et al. (2009) and Fritts et al. (2014) analysed keogram representations of airglow imager data. In addition to process studies, also large-period observations of OH layer emissions with imaging instruments are employed to derive statistics and seasonal variations in GW parameters at different locations (Walterscheid et al., 1999; Nakamura et al., 1999; Suzuki et al., 2004; Li et al., 2016, 2018; Shiokawa et al., 2009).

The detection of GWs by means of OH layer intensity observations depends on the (usually unknown) width and height of the OH layer as well as the GW period and vertical wavelength (Gardner and Taylor, 1998; Dunker, 2018). To obtain intrinsic periods, OH imaging data are often combined with meteor radar observations of the ambient wind (e.g. Nyassor et al., 2018). Mangognia et al. (2016) proposed a multi-channel instrument to deduce vertical wavelengths which must otherwise be determined from the dispersion relation or in combination with other observation techniques. Especially sodium lidar instruments, providing vertical soundings of vertical wind and temperature in the sodium layer located above the OH layer, were essential in order to derive vertical wavelengths, phase speeds and momentum fluxes in the MLT region (Swenson et al., 1999; Jia et al., 2016). This technique allowed for the study of GW dispersion, refraction or breaking in the MLT region (Smith et al., 2005; Yuan et al., 2016). Isler et al. (1997) and Hecht et al. (1997) also incorporated wind measurements by MF radar to investigate ducting, evanescence and breaking of GWs.

Lidar soundings of the middle atmosphere are ideally suited for studying gravity waves at high vertical and temporal resolution (e.g. Hostetler and Gardner, 1994; Lu et al., 2009; Baumgarten et al., 2015; Zhao et al., 2017; Fritts et al., 2018). In the stratosphere and lower mesosphere, climatologies of gravity wave potential energy densities were derived from lidar backscatter (Wilson et al., 1991; Sivakumar et al., 2006; Sica and Argall, 2007; Thurairajah et al., 2010; Alexander et al., 2011; Mzé et al., 2014; Kaifler et al., 2015; Kogure et al., 2018). Due to limitations in power and/or efficiency of Rayleigh lidars, often a gap remains in the upper mesosphere between the top altitude of Rayleigh-lidar temperature profiles and coincident sodium lidar measurements. Recent developments in Rayleigh-lidar technology allow for high-resolution temperature and GW measurements at altitudes above ∼85 km within the OH layer (Kaifler et al., 2017, 2018). Also, modern OH imaging instruments utilize different OH emission lines to perform spectroscopy in order to derive the spatial temperature field, thus facilitating synergy of OH layer imaging and vertical lidar soundings that has not been possible before.

In recognition of the prospects of multi-instrument approaches for middle atmosphere GW studies, several field campaigns combining a large number of ground-based and airborne instruments have been undertaken in recent years, e.g. the GW-LCYCLE-1 (Gravity Wave Life Cycle Experiment) campaign in northern Scandinavia in 2013 (Wagner et al., 2017; Witschas et al., 2017) and the DEEPWAVE campaign in New Zealand in 2014 (Fritts et al., 2016). During the winter of 2015–2016, the season when GWs of high amplitude were able to propagate from the troposphere to the mesosphere, the GW-LCYCLE-II aircraft campaign took place in northern Scandinavia. During and beyond the campaign period, the high-powered Compact Rayleigh Autonomous Lidar (CORAL), the Advanced Mesospheric Temperature Mapper (AMTM) and an All-Sky Interferometric Meteor Radar (SKiYMET) were co-located at Sodankylä, Finland. For the first time, common-volume observations at resolutions below 1 h can thus be exploited for detailed studies of gravity waves in the MLT region. We develop a consistent analysis method to derive the full set of GW parameters by means of wavelet analysis and a phase line identification (WAPITI – Wavelet Analysis and Phase line IdenTIfication) algorithm and apply it to the combined data set. Wavelet analysis is a well-established method in atmospheric science in general but also with respect to the study of atmospheric GWs. It is applied to in situ, remote-sensing and satellite observations, and reanalysis data, with the goal of characterizing GW parameters, deriving global maps, or studying generation processes in the troposphere or stratosphere and turbulence generation by breaking GWs (Stockwell et al., 1996; Alexander and Barnet, 2007; Zhang et al., 2001; Dörnbrack et al., 2018; Koch et al., 2005). The key advantage is the preserved temporal resolution, allowing for the detection of spatially and temporally localized wave packets. We present a systematic spectral decomposition of AMTM keograms (a two-dimensional representation of pixel columns and rows evolving with time; see, e.g. Taylor et al., 2009) and lidar data in order to detect and characterize GW packets observed by the three instruments. Using this technique, co-existing, interacting and evolving GW packets can be studied.

We demonstrate our analysis for the GW event on 16–17 December 2015, when large-amplitude propagating GWs were observed in the mesosphere. The instruments are described in Sect. 2 together with their respective data sets. The WAPITI algorithm developed to derive GW parameters like horizontal and vertical wavelengths, propagation directions, and phase velocities for waves of different scales is described in Sect. 3. It is applied to the data sets of 16–17 December 2015 in Sect. 4, followed by a discussion of the spectral characteristics of the identified waves in Sect. 5. Conclusions are given in Sect. 6.

2 Instruments and data sets

During the GW-LCYCLE-II campaign in winter 2015–2016, three instruments were co-located at Sodankylä, Finland (67.4^∘ N, 26.6^∘ E), collecting complementary data sets. CORAL provided vertical profiles of middle-atmospheric temperature and GW perturbations (27–98 km). The AMTM imager detected GWs in the horizontal plane at the altitude of the OH layer (∼86 km). The Sodankylä-Leicester Ionospheric Coupling Experiment (SLICE) meteor radar provided horizontal wind measurements in the upper mesosphere (82–98 km). Simultaneous observations of all three instruments were obtained during 78 nights between September 2015 and April 2016. Here we selected the night of 16–17 December 2015, when large-amplitude GWs occurred in order to demonstrate our retrieval of the full set of GW parameters.

2.1 CORAL

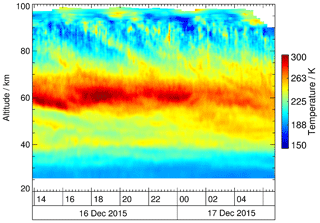
CORAL was built by the German Aerospace Center (DLR) and installed at the Finnish Meteorological Institute Sodankylä site in September 2015. CORAL is a Rayleigh backscatter lidar for the middle atmosphere. It incorporates a 12 W laser operated at 532 nm wavelength as a transmitter, a 63 cm diameter receiving telescope and two height-cascaded receiving channels equipped with avalanche photodiodes run in the photon-counting mode (Kaifler et al., 2017, 2018). CORAL was designed with the capability for remote control and automatic operation in order to maximize operation hours. During 6 months of operation, 492 h of high-quality data were collected during nighttime. In the absence of aerosols, the received photon counts are directly proportional to the density of the atmosphere. Following Hauchecorne and Chanin (1980) we infer atmospheric temperatures by top-down integration of atmospheric density profiles assuming hydrostatic equilibrium. This is first performed for the nightly average profile smoothed with a filter of ∼2 km width using SABER measurements as a seed value at the 100–110 km altitude. Then, in an iterative manner, temperature profiles of subsequently higher resolutions of 120, 60, 30, 20 and 10 min are obtained by seeding at their top altitudes with the respective lower-resolution profiles. For this study, we use temperature data at the 2070 m vertical and 10 min time resolution computed on a grid of 90 m × 1 min, which is intrinsic to the temperature retrieval. Above ∼92 km the temporal resolution gradually decreases from 10 min to 2 h due to longer integration times. The uncertainties in absolute temperatures caused by photon noise and in part by the temperature seeding process amount to 0.3 K between 25 and 50 km, 1.6 K between 50 and 75 km, and 9.9 K between 75 and 100 km. Figure 1 shows the temperature measurement of 16–17 December 2015. We see the stratopause at 60 km, with strong wave activity above in the mesosphere and periods of about 4 h. A more detailed description is given in Sect. 3.

Figure 1 Time–altitude section of temperature obtained by CORAL on 16–17 December 2015. Above ∼92 km, the temporal resolution decreases gradually, from 10 min to 2 h.

2.2 AMTM

The AMTM was built by Utah State University and yields temperature maps based on detected IR radiation originating from the OH layer (Pautet et al., 2014; Fritts et al., 2014). This layer is commonly described as Gaussian-shaped, with an average peak altitude of 86.8 ± 2.6 km and a full width at half maximum (FWHM) of 8.6 ± 3.1 km, although the local height and thickness can vary (Baker and Stair Jr, 1988). The temperature is a function of the brightness ratio of two spectral lines in the Meinel (3,1) rotation–vibration hydroxyl bands, namely B[P₁(2)]∕B[P₁(4)]. The spatial and temporal resolution of the AMTM is 625 m at zenith and ∼30 s, and the field of view is about 200 km × 160 km. Temperature uncertainties are of the order of 1–2 K for clear sky conditions. Due to strong contamination by sunlight, the AMTM operates only during darkness. To gain better insight into the temporal evolution of the temperature maps, we analyse AMTM data in the keogram representation. The AMTM's FOV is oriented in the cardinal directions, as shown in Fig. 2a. Concatenating pixel rows (columns) of successive temperature maps at ∼30 s resolution results in a south–north (west–east) keogram projecting GWs onto this particular direction. AMTM data for 16–17 December 2015 in this representation are shown in Fig. 2b. The position of the lidar laser beam is in the zenith of the AMTM's FOV, as indicated by the dashed lines in Fig. 2b. For the analysis, we interpolated the AMTM data sets on a 1 min grid to be able to compare them with lidar data and to reduce noise.

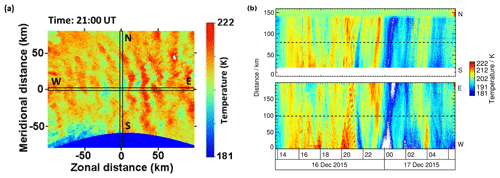
Figure 2 (a) AMTM temperature map at 21:00 UT on 16 December 2015 with indicated pixel rows and columns used for keogram representation. (b) South–north keogram of AMTM temperature measurements (top) and west–east keogram (bottom) on 16–17 December 2015. The central dashed lines indicate the position of the lidar laser beam.

2.3 Meteor radar

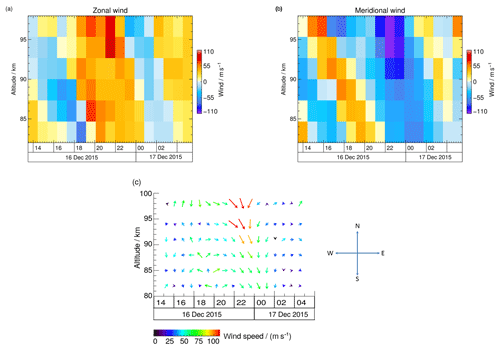
SLICE is a SKiYMET meteor radar (MR) and provides measurements of horizontal wind speeds in the altitude range of 82–98 km at a vertical and temporal resolution of 2.7 km × 1 h (Lukianova et al., 2018). The MR is operated by the Sodankylä Geophysical Observatory. Wind data are retrieved from the line-of-sight velocity of the ionized meteor trails detected in a FOV of about 300 km in diameter (Hocking et al., 2001). Figure 3a–c show zonal and meridional wind speeds as well as the wind direction during the night of 16–17 December 2015. The wind field is complex, with both vertical and horizontal reversals and shears on small scales. We therefore expect time-varying parameters of GWs observed by CORAL and the AMTM.

Figure 3 (a) Zonal wind, (b) meridional wind and (c) wind direction observed by the SLICE meteor radar on 16–17 December 2015.

3 Analysis

In the following, we present our newly developed WAPITI algorithm used to retrieve observed and intrinsic GW parameters based on three complementary data sets at mesospheric altitudes. From AMTM temperature data, we obtain horizontal wavelengths as well as propagation directions at the altitude of the OH layer. Vertical wavelengths and directionality of the vertical propagation are derived from CORAL vertical temperature profiles. In combination with meteor radar wind speeds, we estimate intrinsic periods. As a cross check, we use the dispersion relation to retrieve vertical wavelengths based on horizontal wavelengths and intrinsic periods and compare the result with vertical wavelengths retrieved from lidar data.

3.1 Spectral filtering of temperature data

The AMTM provides data in a temporally resolved keogram representation in horizontal dimensions x and y, while CORAL observations yield time series of temperature at different altitudes z. Following Torrence and Compo (1998) we apply a wavelet transformation with 6th-order Morlet wavelets to all the time series within the common FOV of both instruments, i.e. for the lidar position at OH layer altitudes.

The discrete periods used for the wavelet transformations are given by

$$\begin{array}{}\text{(1)}& {\mathit{\tau }}_j={\displaystyle \frac{\mathrm{4}\mathit{\pi }\cdot \mathrm{d}t\cdot {\mathrm{2}}^{j/\mathrm{8}+\mathrm{1}}}{{\mathit{\omega }}_{\mathrm{0}}+\sqrt{\mathrm{2}+{\mathit{\omega }}_{\mathrm{0}}^{\mathrm{2}}}}}.\end{array}$$

Here, the non-dimensional frequency, ω₀=6, is the order of the wavelet. The time resolution is represented by dt=1 min, and j is the index of the wavelet, ranging from 0 to 71, selecting periods between 2 min and 16.2 h. The resulting wavelet spectra show spectral power based on squared amplitudes of temperature perturbations as a function of the time and observed period (Fig. 4). The cone of influence (COI), inside of which edge effects due to the finite time series may result in an underestimation of spectral power, is indicated by a hatched region. Significance levels of 95 %, 50 % and 20 % calculated relative to red-noise spectra are shown as contour lines to highlight potential GW structures within each spectrum. To assess the effect of temperature uncertainties in the wavelet spectrum, we perform Monte Carlo simulations. We add 100 Gaussian-distributed samples of white noise with a standard deviation of the temperature measurement uncertainty to the actual temperature time series and apply a wavelet transformation. One standard deviation range is shown with dashed lines together with the global wavelet spectra (Fig. 4b, c, e).

Alexander (1998) applies instrumental filter functions to model data in order to make GW spectra from model output and measurements comparable. In order to compare wavelet spectra of CORAL and the AMTM, we weighted lidar temperatures between 78 and 95 km with a Gaussian distribution with a FWHM of 8.6 km centred at 86.8 km. Figure 4a shows the natural logarithm of the squared absolute value of the spectral amplitude of the CORAL temperature time series averaged over the OH layer. An impression of the spectral variability with height is given in Fig. 4c, where we present global wavelet spectra at different altitudes. The Monte Carlo simulation revealed increasing noise levels in global wavelet spectra with smaller periods, especially below 0.5 h. Hence, we decided to focus on the spectral range between the 0.5 and 8 h observed period. Figure 4d displays the wavelet spectrum for the zenith time series of AMTM temperature (dashed lines in Fig. 2b). A detailed description of the spectra is given in Sect. 4.

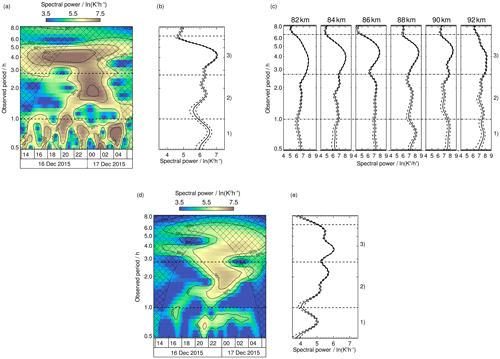
Figure 4 (a) Wavelet power spectrum of Gaussian-weighted lidar time series and (b) global wavelet spectrum including standard deviation. (c) CORAL global wavelet spectra including standard deviations for six altitudes between 82 and 92 km. (d) Wavelet power spectrum of the zenith time series of the AMTM and (e) global wavelet spectrum including standard deviation. The hatched areas mark the COI. Solid lines indicate the 20 %, 50 % and 95 % significance levels. Three period ranges with dominant waves are indicated by numbers on the right axis.

We analyse wavelet power at 32 discrete periods in which τ_j>30 min and reconstruct the respective temperature perturbations for each spatial dimension x, y (AMTM) and z (CORAL). If GWs with periods τ_j are present in the data set, they are observed as a pattern of phase lines of significant amplitude in the wavelet reconstruction. Two examples are shown in Fig. 5b and c. Periods not supported by the data exhibit very small reconstructed temperature perturbations. From the progression of phase lines, we derive phase velocities in each direction.

3.2 Phase line identification

In order to detect phase lines in the reconstructed data, we need to identify points belonging to the same phase, e.g. points along wave crests or troughs. They are detected by looking for a change of sign in the derivative of the temperature time series with respect to time. In order to allow for a robust phase line detection, the wavelet reconstructions are smoothed with a boxcar window with a width of 5 km in the spatial domain for keograms and 2 km for vertical profiles and τ_j∕4 in the time domain. The identified extrema are connected in space in order to determine the phase angle in the zenith position by a linear fit to phase lines.

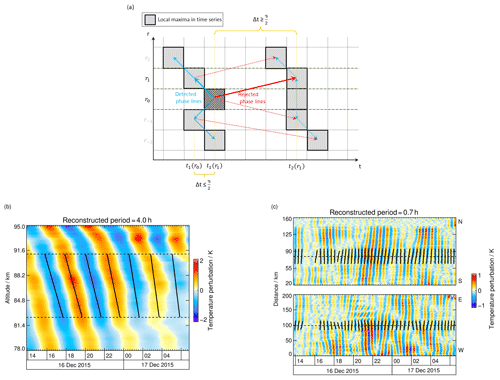
Figure 5 (a) Sketch illustrating the phase line detection of the WAPITI algorithm. The grid represents data resolved in space and time. Grey boxes represent local temperature maxima in each time series r_i. Blue arrows point to adjacent maxima that are affiliated with a phase line. Red arrows point to adjacent maxima that are too far away and therefore do not belong to the considered phase line. Solid arrows describe the first step in the algorithm, and sketched time intervals refer to these solid arrows. Dotted arrows describe further steps of the algorithm. (b) Phase line identification applied to reconstructed temperature perturbations in lidar data with a period of 4.0 h and (c) in airglow data with a period of 0.7 h. Solid black lines are fitted linear functions.

Figure 5a illustrates the phase line detection of our WAPITI algorithm. To isolate a number of i phase lines, we find points of time t_i(r) which follow the position of wave crests and troughs in each data set. For example, the first maximum in the zenith time series occurs at t₁(r₀). In the time series adjacent to r₀ we find the maximum which is closest to t₁ and at most $\mathrm{\Delta }t<{\mathit{\tau }}_j/\mathrm{2}$ apart. This maximum is identified as belonging to the phase line i=1. This step is repeated for all r values within the window $\mathrm{\Delta }r=\mathrm{12}\mathrm{km}{\mathrm{h}}^{-\mathrm{1}}{\mathit{\tau }}_j+\mathrm{20}$ km for keograms and Δr=8.6 km for the lidar data set. The window width for lidar data contains the average thickness of the OH layer. We choose a dynamic range for keograms; i.e. the range increases with the selected period τ_j because larger structures tend to be more coherent. In a second step we fit a linear function $t_i\left(r\right)=a_{i}r+b_i$ to the detected phase lines and calculate the 1σ uncertainty estimates Δa_i and Δb_i. The coefficient a_i has the dimension of an inverse velocity, while b_i is a constant time parameter.

Examples of reconstructed time series and detected phase lines are shown in Fig. 5b and c. Increased amplitudes indicate the presence of GWs with the selected τ_j. The matching of temperature reconstructions and estimated phase lines is very good for short as well as for large periods.

3.3 Horizontal wavelength and direction of propagation

The observed horizontal wavelength λ_h can be retrieved directly from the OH airglow images. However, in this case, the maximum wavelength is of the order of the dimension of the FOV (∼200 km). Larger horizontal wavelengths can be retrieved from the detected phase lines from above. Then, λ_h is given by the product of the phase velocity c and the period of the GW τ. Hence, in order to retrieve the phase velocities c_i in each direction at time t_i(r₀), we calculate the inverse of the derivative of the linear fit t_i(r) with respect to space,

$$\begin{array}{}\text{(2)}& c_i\left(t_i\right(r_{\mathrm{0}}\left)\right)={\left({\displaystyle \frac{\mathrm{d}{t}_i\left(r\right)}{\mathrm{d}r}}\right)}^{-\mathrm{1}}={\displaystyle \frac{\mathrm{1}}{a_i}}.\end{array}$$

To estimate the uncertainty of the phase velocity Δc_i, we calculate the propagated error of Δa_i given by

$$\begin{array}{}\text{(3)}& \mathrm{\Delta }{c}_i\left(t_i\right(r_{\mathrm{0}}\left)\right)=c_i\left(t_i\right(r_{\mathrm{0}}){)}^{\mathrm{2}}\mathrm{\Delta }{a}_i.\end{array}$$

We now have an estimate for phase velocity and its uncertainty at discrete points in time. As an approximation, we assume that the fitted parameters vary linearly between these discrete points. Consequently, a_i, b_i, Δa_i and Δb_i are linearly interpolated. To simplify the equations, we drop the explicit time dependence from now on in the notation. We obtain wavelengths λ_x and λ_y by

$$\begin{array}{}\text{(4)}& {\displaystyle }{\mathit{\lambda }}_x& {\displaystyle }=\mathit{\tau }{c}_x,\text{(5)}& {\displaystyle }{\mathit{\lambda }}_y& {\displaystyle }=\mathit{\tau }{c}_y.\end{array}$$

Uncertainties for these and following quantities are given in Appendix A. We consider no uncertainty for the period of the wavelet transformation defined in Eq. (1). We also note that uncertainties in the spectral amplitude of the wavelet spectrum do not lead to uncertainties in the reconstructed period but to uncertainties in the amplitude of the reconstructed signal. Thus, structures are conserved.

The horizontal wavelength is determined by λ_x and λ_y (Eq. 5), as illustrated in Fig. 6a:

$$\begin{array}{}\text{(6)}& {\mathit{\lambda }}_{\mathrm{h}}={\displaystyle \frac{{\mathit{\lambda }}_y{\mathit{\lambda }}_x}{\sqrt{{\mathit{\lambda }}_y^{\mathrm{2}}+{\mathit{\lambda }}_x^{\mathrm{2}}}}}.\end{array}$$

As the phase velocities can have positive and negative signs, λ_h can be positive or negative depending on the propagation direction. However, the direction of propagation is usually expressed as an angle relative to north, thus making the information encoded in the sign of the horizontal wavelength redundant. Following this convention, we drop the sign and consider absolute values only.

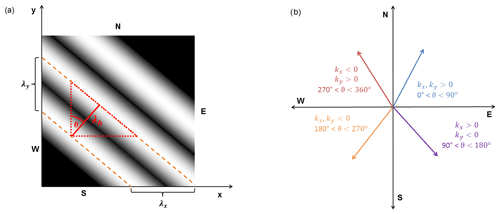
Figure 6 (a) Sketch to illustrate the relation between wavelengths. λ_h is defined as the height of a right triangle (red) with sides λ_x and λ_y. (b) Definition of the propagation angle. The horizontal direction of propagation is given by the relation of wavelengths in the x and y direction. Coloured arrows describe different propagation directions.

The propagation angle θ is defined clockwise starting at 0^∘, with θ=0^∘ being north. Figure 6b illustrates propagation directions in the horizontal plane. For λ_x>0 the wave propagates eastward and $\mathit{\theta }=\frac{\mathit{\pi }}{\mathrm{2}}+{\tan }^{-\mathrm{1}}\left(-\frac{{\mathit{\lambda }}_x}{{\mathit{\lambda }}_y}\right)$. For λ_x<0 the wave propagates westward and $\mathit{\theta }=\frac{\mathrm{3}}{\mathrm{2}}\mathit{\pi }+{\tan }^{-\mathrm{1}}\left(-\frac{{\mathit{\lambda }}_x}{{\mathit{\lambda }}_y}\right)$. With knowledge of wave propagation and wind direction, we calculate the background wind u₀ in the direction of propagation, which is needed for the estimation of intrinsic parameters.

3.4 Intrinsic period

The observed phase velocity of a GW is given by $c=c_{\mathrm{I}}+u_{\mathrm{0}}$ (Nappo, 2002), with c_I being the intrinsic phase velocity and u₀ being the background wind. Furthermore, $c_{\mathrm{I}}=\frac{{\mathit{\lambda }}_{\mathrm{h}}}{{\mathit{\tau }}_{\mathrm{I}}}$, with τ_I being the intrinsic period and λ_h being the horizontal wavelength. If we rearrange this definition and solve for the intrinsic period τ_I, we obtain

$$\begin{array}{}\text{(7)}& {\mathit{\tau }}_{\mathrm{I}}={\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{h}}}{c-u_{\mathrm{0}}}}.\end{array}$$

The background wind projected onto the GW propagation direction is calculated as

$$\begin{array}{}\text{(8)}& u_{\mathrm{0}}\left(\mathit{\theta }\right)=U\sin \left(\mathit{\theta }\right)+V\cos \left(\mathit{\theta }\right),\end{array}$$

with U and V being the zonal and meridional wind components. Both components are weighted with a Gaussian distribution over an altitude range of 82–95 km, with a FWHM of 8.6 km centred at 86.8 km and averaged over this range. For u₀=0, the intrinsic period equals the observed period. Assuming a constant horizontal wavelength, i.e. no horizontal gradients in the horizontal wind (Marks and Eckermann, 1995), the intrinsic period becomes larger than the observed period if the background wind is oriented in the same direction as the observed phase velocity and $\mathrm{0}<u_{\mathrm{0}}<c$. The intrinsic period becomes smaller than the observed period if the background wind is oriented against the observed phase velocity and u₀<0. The intrinsic frequency Ω of vertically propagating GWs is limited to $f<\mathrm{\Omega }<N$ (Nappo, 2002), with N being the Brunt–Väisälä frequency and f being the Coriolis parameter. We estimate the range for τ_I at 5 min $<{\mathit{\tau }}_{\mathrm{I}}<\mathrm{13}$ h for typical values of N and f at 67.4^∘ N. For u₀=c the intrinsic period becomes infinite, and the wave reaches a critical level and breaks. The uncertainty for the intrinsic period is given in Appendix A.

3.5 Vertical wavelength

The vertical wavelength λ_z is derived using two independent methods. From the phase line detection applied to lidar data, we derive the vertical phase velocity c_z. Multiplying it by the period τ yields the vertical wavelength λ_z. The uncertainty Δλ_z=τΔc_z is given by the 1σ uncertainty estimate from the linear fit applied during the phase line detection. Like the observed horizontal phase velocity, the observed vertical phase velocity can have both signs as well. For upward-propagating waves, c_z<0, and for downward-propagating waves, c_z>0. According to Dörnbrack et al. (2017) this condition holds for $u_{\mathrm{0}}>-c_{\mathrm{I}}$. Otherwise waves appear to be propagating upward in lidar data, while they are in reality propagating downward and vice versa.

The second approach uses the dispersion relation and the parameters retrieved from AMTM data to derive a vertical wavelength. In Sect. 4 we show both results for λ_z, which we discuss in Sect. 5. The dispersion relation reads

$$\begin{array}{}\text{(9)}& m^{\mathrm{2}}={\displaystyle \frac{N^{\mathrm{2}}}{(c-u_{\mathrm{0}}{)}^{\mathrm{2}}}}+{\displaystyle \frac{u_{\mathrm{0}}^{\prime \prime }}{(c-u_{\mathrm{0}})}}-{\displaystyle \frac{\mathrm{1}}{H_{\mathrm{s}}}}{\displaystyle \frac{u_{\mathrm{0}}^{\prime }}{(c-u_{\mathrm{0}})}}-{\displaystyle \frac{\mathrm{1}}{\mathrm{4}{H}_{\mathrm{s}}^{\mathrm{2}}}}-k^{\mathrm{2}},\end{array}$$

where m is the vertical wave number and H_s is the scale height (Nappo, 2002). Primes indicate the derivative with respect to z. We substitute $c_{\mathrm{I}}=\frac{{\mathit{\lambda }}_{\mathrm{h}}}{{\mathit{\tau }}_{\mathrm{I}}}=c-u_{\mathrm{0}}$, and when we solve the dispersion relation for λ_z, we get

$$\begin{array}{}\text{(10)}& {\mathit{\lambda }}_z={\displaystyle \frac{\mathrm{2}\mathit{\pi }}{\sqrt{{\left(\frac{N{\mathit{\tau }}_{\mathrm{I}}}{{\mathit{\lambda }}_{\mathrm{h}}}\right)}^{\mathrm{2}}+\frac{u_{\mathrm{0}}^{\prime \prime }{\mathit{\tau }}_{\mathrm{I}}}{{\mathit{\lambda }}_{\mathrm{h}}}-\frac{u_{\mathrm{0}}^{\prime }{\mathit{\tau }}_{\mathrm{I}}}{H_{\mathrm{s}}{\mathit{\lambda }}_{\mathrm{h}}}-{\left(\frac{\mathrm{1}}{\mathrm{2}{H}_{\mathrm{s}}}\right)}^{\mathrm{2}}-{\left(\frac{\mathrm{2}\mathit{\pi }}{{\mathit{\lambda }}_{\mathrm{h}}}\right)}^{\mathrm{2}}}}}.\end{array}$$

We derived expressions for λ_h and τ_I in previous sections. H_s is defined as $H_{\mathrm{s}}=RT/g$, with $R=\mathrm{287}\mathrm{J}{\mathrm{kg}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}$ being the universal gas constant for dry air and $g=\mathrm{9.81}\mathrm{m}{\mathrm{s}}^{-\mathrm{2}}$ being the acceleration due to gravity. The Brunt–Väisälä frequency N is defined as

$$\begin{array}{}\text{(11)}& N=\sqrt{{\displaystyle \frac{g}{T}}\left({\displaystyle \frac{\partial T}{\partial z}}+{\displaystyle \frac{g}{c_{\mathrm{p}}}}\right)},\end{array}$$

with $c_{\mathrm{p}}=\mathrm{1.005}\mathrm{kJ}{\mathrm{kg}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}$ being the specific heat capacity for air at constant pressure. We calculate the nightly mean of N in the altitude range of 82–91 km based on background temperature profiles which are obtained by low-pass filtering of lidar temperature profiles following Ehard et al. (2015). We derive $N=\mathrm{0.0202}\pm \mathrm{0.0016}{\mathrm{s}}^{-\mathrm{1}}$ and $H_{\mathrm{s}}=\mathrm{5.60}\pm \mathrm{0.08}$ km at OH layer altitudes. We assume N and H_s to be constant and also assume a uniform wind in the horizontal plane, i.e. a constant λ_h. The derivatives of horizontal wind with respect to altitude $u_{\mathrm{0}}^{\prime }$ and $u_{\mathrm{0}}^{\prime \prime }$ are determined between 82 and 95 km and averaged over this altitude range in the same way as for the Gaussian-weighted average of the background wind (see Sect. 3.4). In the next section, we apply our WAPITI algorithm to GWs observed on the 16–17 December 2015.

4 Results

During the night of 16–17 December 2015, strong GW signals were detected by the AMTM and CORAL above Sodankylä, Finland. The wavelet spectra (Fig. 4) reveal a broad distribution of observed periods with high spectral power throughout the night. In the lidar data, we find three regions with significance levels >95 %. The most prominent region lies at the ∼4 h observed period between 17:00 and 02:00 UT. Another region lies close to the 2 h observed period at 00:00 UT, while the third region consists of three peaks between the 0.5 and 1.0 h observed period and 23:00–05:00 UT (Fig. 4a). In AMTM data we see GW amplitudes with significance levels >95 % from 19:00 UT until the end of the night. Dominant GWs exhibit observed periods in the range of 1.5–6.5 h (Fig. 4d). We calculate global wavelet spectra (Fig. 4b, c, e) and divide them into three regions based on local maxima in spectral power. Region (I) is defined from the 30–60 min observed period and contains small-period GWs. The second region ranges from 1.0 to 2.8 h. Region (III) comprises periods of 2.8–6.5 h. We restrict our analysis to periods below 6.5 h due to the finite data sets and the respective COI. Amplitudes in AMTM data at longer wavelengths are too small for reliable detection of phase lines by our algorithm. The insensitivity of our method to changes at scales above 6.5 h at the same time ensures our focus on GWs and attributes the action of tides and planetary waves to the GW background. We keep in mind that both may interact and alter the GW parameters. In general, the spectra of AMTM and CORAL are in good agreement. However, amplitudes in the lidar spectrum are larger.

As stated in Sect. 3 we retrieved wavelengths and propagation angles for 32 reconstructed periods such that the GW parameters can be displayed as a function of the time and observed period. To give an overview, the retrieved parameters in the three spectral regions defined above are organized in probability density distributions next to the full spectra. We do a kernel density estimation (KDE) for this purpose. Each value is represented as a normalized Gaussian distribution, with a standard deviation given by its uncertainty. Finally all Gaussian distributions are added and divided by the number of values taken into account in order to normalize the probability density distribution. Values with small uncertainties are represented as peaks with a small FWHM, while values with large uncertainties are represented as flat and broad peaks in the distribution. In comparison to a standard histogram the KDE takes the uncertainty of each value into account. Hence, the distribution is independent of a chosen bin size, and each peak is reliable. In the background we show the total density distribution of each parameter comprising all values within the 20 % significance contour line in light grey. This enables us to investigate how each spectral region contributes to the total distribution. Additionally we hatched the parts of each distribution which show parameters within the COI to be aware of their contribution. Figure 7a and b show horizontal wavelengths retrieved from AMTM data. We see a large variation in λ_h, ranging from 75 to 2000 km. The uncertainties lie of the order of a few percent in significant regions. Figure 7c shows horizontal propagation directions of the waves identified by the WAPITI algorithm. The density distributions in Fig. 7d show waves predominantly propagating in northward directions. Figure 8a and b display the wind every wave is exposed to, i.e. wind speed in the direction of propagation. Most waves propagate against the mean flow, resulting in negative wind speeds of up to −80 m s⁻¹. Figure 8c and d show estimated intrinsic periods based on wind speeds. Due to the motion in opposite directions, the majority of intrinsic periods are Doppler-shifted to larger observed periods. Vertical wavelengths retrieved from lidar data are shown in Fig. 9a and b, where we find values of 6–50 km. A background wind field varying in space and time has an impact on the observed period of GWs and hence affects the temperature reconstructions. Therefore phase lines in our data sets are bent, and we find locally large wavelengths. Vertical wavelengths between 1 and 50 km are retrieved using the dispersion relation (Fig. 9c and d).

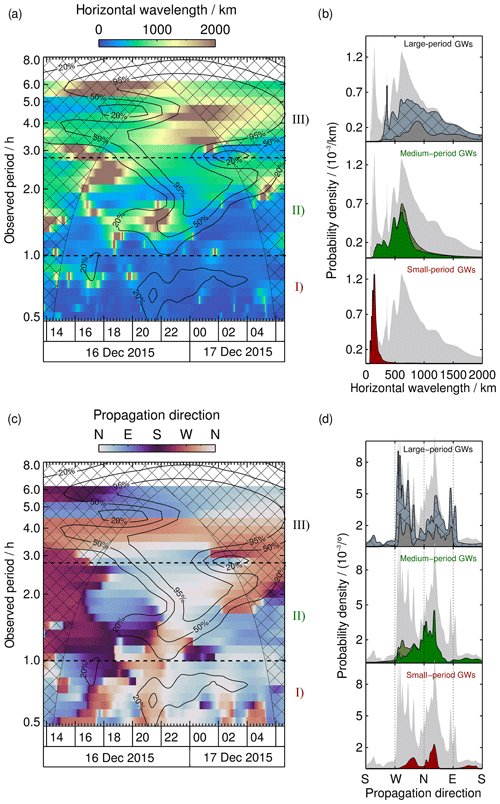
Figure 7 (a) Horizontal wavelengths observed by the AMTM as function of time and observed period. The hatched area represents the COI. Contour lines mark the 20 %, 50 % and 95 % significance levels. (b) Density distributions for significance levels >20 % for region I (red), region II (green) and region III (grey). The grey distribution in the background shows the total probability density distribution of all values with significance level >20 %. Hatched areas indicate values within the COI. (c) Same as (a) for propagation directions based on horizontal wavelengths. (d) Density distributions for each region as in (b). Dotted lines mark the cardinal directions.

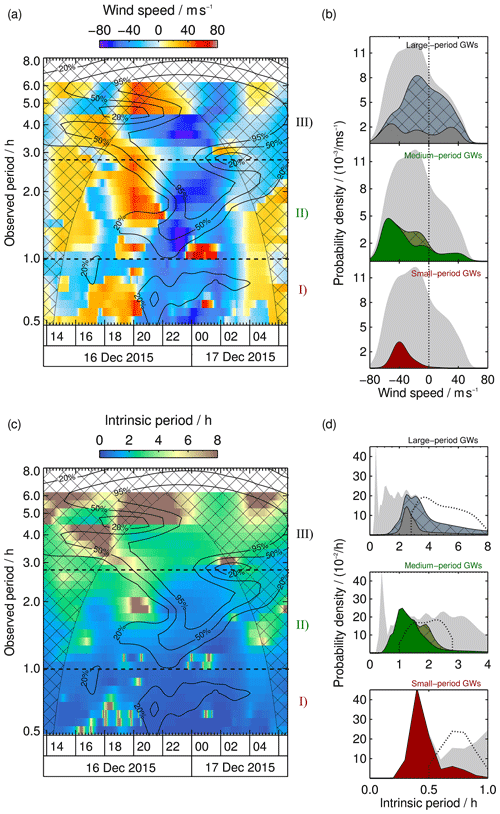
Figure 8 (a) Same as Fig. 7a but for horizontal wind speeds in the direction of horizontal propagation. (b) Density distributions for each region as in Fig. 7b. The dotted line represents zero wind speed. (c) Same as Fig. 7a but for intrinsic periods based on horizontal wavelengths and the background wind. (d) Density distributions for each region as in Fig. 7b. Additionally, the distributions of observed periods are given (dashed lines).

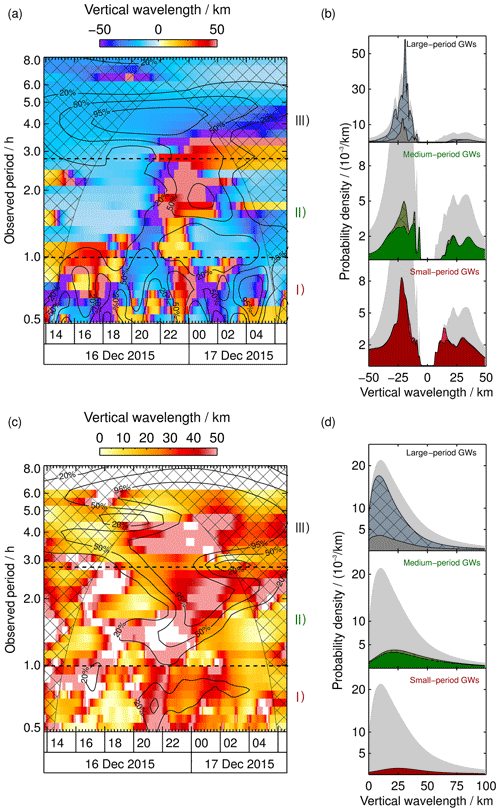
Figure 9 (a) Same as Fig. 7a but for vertical wavelengths derived from lidar data. Positive vertical wavelengths indicate downward-propagating waves (upward-slanted phase lines), and negative vertical wavelengths indicate upward-propagating waves (downward-slanted phase lines). (b) Density distributions for each region as in Fig. 7b. (c) Same as Fig. 7a but for vertical wavelengths retrieved from the dispersion relation. White gaps indicate a complex wavelength. (d) Density distributions for each region as in Fig. 7b.

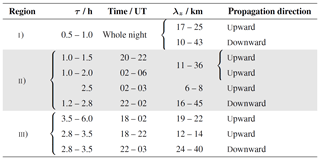
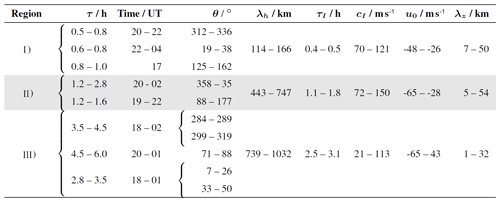
Tables 1 and 2 summarize the range of GW parameters of a number of likely GW packets across the three spectral ranges for the discussion.

Table 1 GW parameters derived from AMTM and SLICE data for selected dominant GW packets. The ranges describe the FWHM of peaks in each density distribution. Values for τ and time refer to identified peaks in the propagation direction.

Table 2 Vertical wavelengths derived from CORAL data. The ranges describe the FWHM of peaks in the density distribution.

5 Discussion

Before we discuss the presented results of our analysis, we want to point out the assumptions and limitations in this case study. As we mentioned in Sect. 2, the OH layer peak altitude is on average located at 86.6 km and has a thickness of 8.6 km. Because no satellite soundings of OH are available for the period of the case study, we use these climatological values. However, we note that the actual peak altitude and thickness of the OH layer may deviate from the climatological mean, leading to uncertainties in the wavelet spectra, as we average Gaussian-weighted lidar temperatures over the altitude range of the OH layer. The same holds true for averaged wind data. Wind speeds are systematically averaged over an area of ∼300 km in diameter. We take this into account by asserting large uncertainties to the retrieved wind speeds (see Appendix A). Another limitation is that lidar measurements are restricted to the centre of the OH imager's FOV, with decreasing resolution towards higher altitudes. We highlighted the congruent altitude range of the three instruments' data. However, resolutions and observational volumes differ. We chose a 20 % significance level to maximize the overlapping areas in lidar and AMTM wavelet spectra, especially for short periods, as Fig. 5c has proven that also at this significance level, detectable and coherent structures can be retrieved.

Dörnbrack et al. (2017) showed that upward-propagating waves appear to be propagating downward in lidar data for $u_{\mathrm{0}}<-c_{\mathrm{I}}$. In the majority of cases this condition is not fulfilled, and the intrinsic vertical propagation direction matches the observed vertical propagation direction (upward–downward).

5.1 Small-period gravity waves

Spectral region (I) comprises GWs with observed periods between 0.5 and 1.0 h. Comparison of the global wavelet spectra of CORAL (Fig. 4b) and the AMTM (Fig. 4e) yields coinciding peaks at the ∼0.7 h observed period. The difference in spectral amplitudes mentioned above is reflected in the levels of significance. The spectra in Fig. 4c show an increase in spectral amplitude with altitude. As long as no wave breaking occurs, we expect increasing amplitudes with altitude due to decreasing density. From comparing both spectra, we are confident to see the same GWs with both instruments but with different sensitivities at different times.

We find that the majority of horizontal wavelengths lie between 114 and 166 km (Fig. 7b). When we compare the distribution of region (I) with the total density distribution (grey background), we discover that almost all GWs with smaller horizontal wavelengths (<300 km) are located within region (I). The density distributions reveal three preferred propagation directions (Fig. 7d). The FWHMs of the three peaks are given in Table 1. We treat each peak as a GW packet. A first packet propagates southeastward at about 17:00 UT, and a second packet travels northwestward at 20:00 UT. The latter either turns northeastward after 22:00 UT or a third packet appears. The background wind in the propagation direction is negative at all times for all waves (Fig. 8b), indicating wave propagation against the mean flow. In accordance with the propagation against the background wind, intrinsic periods are smaller than observed periods (Fig. 8b). Again, almost all small-period GWs with intrinsic periods below 0.6 h are found in region (I). Our WAPITI algorithm identifies mainly upward-propagating waves in lidar data, with the majority of vertical wavelengths between 17 and 25 km (Fig. 9b). The probability density distribution shows another broader peak between 10 and 43 km, affiliated with downward-propagating waves. Figure 9a and b also show vertical wavelengths larger than 50 km. We emphasize that these large values are retrieved only in the altitude range of the OH layer (82.5–91.1 km). Phase lines that are locally very steep (e.g. due to vertical wind shear) seem to exhibit very large vertical wavelengths. Upward- and downward-propagating waves alternate throughout the night. The reason for this may be refraction levels or vertical wind shear. The calculated vertical wavelengths in Fig. 9d peak between 7 and 50 km. The peaks identified in lidar data overlap largely with this range (Fig. 9b).

In summary, region (I) contains small-period waves travelling predominantly northwestward against the background wind, resulting in a Doppler shift of intrinsic periods to larger observed periods. These small-period waves dominate the density distributions for horizontal wavelengths <300 km and intrinsic periods <0.6 h. In AMTM time-lapse videos, we observe GW breaking at 21:00 UT. This coincides with the appearance of large amplitudes in spectral region (I) in the AMTM wavelet spectrum. One explanation could be that small-period GWs are generated by longer-period GWs breaking at 21:00 UT. Amplitudes in the CORAL spectrum confirm the presence of large-period waves. Another possibility is a change of background conditions (e.g. induced by tides) at 21:00 UT in such a way that afterwards, small-period GWs can be detected by the AMTM. The rapid change of sign of the vertical wavelength shows that this region is dominated by vertical wind shear, i.e. $\frac{\partial u}{\partial z}\ne \mathrm{0}$. Alternating λ_z may also be a sign for reflection of waves (ducted waves). The comparison of absolute values of vertical wavelengths from the two retrievals shows that both methods are in good agreement. However, vertical wavelengths retrieved by the WAPITI algorithm have a narrower distribution than the values we derived from the dispersion relation. Discrete peaks in the density distribution of the propagation direction help to distinguish between GW packets.

5.2 Medium-period gravity waves

Region (II) comprises observed periods between 1.0 and 2.8 h. The peaks in the global wavelet spectra of CORAL (Fig. 4b) and the AMTM (Fig. 4e) are slightly shifted. For CORAL, the peak lies at 1.8 h, while it is at 2.2 h for the AMTM. This difference may result from the different sensitivities of the instruments or the variability in the OH layer thickness and altitude. In comparison to region (I) we find a large overlapping area of statistical significance in both spectra. Figure 4c shows a slight increase in spectral amplitude with altitude compared to region (I), suggesting growing wave amplitudes.

Most of the horizontal wavelengths lie between 443 and 747 km (Fig. 7b). Taking the values within the COI into account does not alter, in general, the shape of the peak. When we compare the distribution of region (II) with the total density distribution (grey background), we see that region (II) contributes to all wavelengths. However, its contribution to larger wavelengths is weaker. Sometimes phase lines are locally very steep in both keograms, and therefore λ_h attains large values. One example is evident at 22:00 UT for the 1.5 h observed period. After 23:00 UT, λ_h decreases rapidly within 1 h, from 2000 to 200 km. This is a clear sign for a gradient in the horizontal wind field, as $\frac{\partial {\mathit{\lambda }}_{\mathrm{h}}}{\partial t}\sim \frac{\partial u}{\partial x}$ (Marks and Eckermann, 1995; Stober et al., 2018). As evident from Fig. 7c the propagation direction is first westward and becomes northeastward later. Our explanation is that the waves appear to rotate in AMTM data due to a horizontal wind gradient. This leads to bent phase lines in the temperature reconstructions which are identified as very large horizontal wavelengths. The dominant propagation direction is northward to northeastward. Later, waves turn westward. The northward propagation results in negative wind speeds (Fig. 8b). Only small spectral areas comprising waves with an eastward component experience positive wind speeds. Wind speeds from region (II) dominate the total density distribution (grey background) between −80 and −50 m s⁻¹. As we have seen in region (I), a propagation against the background wind leads to a Doppler shift of intrinsic periods towards larger observed periods. This is in general also the case in region (II), where the majority of waves with intrinsic periods between 1.1 and 1.8 h are Doppler-shifted towards observed periods between 1.0 and 2.8 h (Fig. 8c). Values within the COI slightly broaden the distribution. Intrinsic periods from region (II) dominate the total density distribution (grey background) between 0.6 and 2.1 h. Most of the vertical wavelengths derived from lidar data lie between 11 and 36 km (Fig. 9b) and are affiliated with upward-propagating waves. We identify two additional peaks between 6 and 8 km (upward) and 16 and 45 km (downward). On the left-hand side of Fig. 9a, we find that waves first propagate upward and then turn downward at 22:00 UT and back upward at ∼ 02:00 UT. As mentioned in region (I) the change of propagation direction indicates vertical wind shear or levels of reflection (ducted waves). The distribution of vertical wavelengths estimated using the dispersion relation shows an even broader peak, as in region (I), with values between 5 and 54 km (Fig. 9b). Vertical wavelengths within the COI increase slightly the probability density at the position of the peak. Absolute values of the density distribution of λ_z and the FWHM of the respective peaks are in general agreement (Fig. 9b and d and Tables 1 and 2). To note is the white gap between 21:00 and 23:00 UT in Fig. 9c. In this area the condition for a real λ_z is not fulfilled. Waves in this area either do not propagate or the vertical wind shear is underestimated.

We state that the appearance of GWs in region (II) coincides with a wave breaking event at 21:00 UT and a strengthening of the mean flow. The retrieved parameters show a large variability which may follow from a non-uniform wind speed distribution within the FOV of the AMTM and altitude range of the OH layer. Interestingly not all parts of the GW spectrum react in the same way to the changing background wind.

5.3 Large-period gravity waves

A wide range of observed periods from 2.8 to 6.5 h is detected in spectral region (III). When we compare the global wavelet spectra of CORAL (Fig. 4b) and the AMTM (Fig. 4e) we find the most prominent peak at the 4.2 h observed period in the CORAL spectrum and a slightly shifted peak at 3.8 h in the AMTM spectrum. We assert that both instruments are sensitive to waves in this spectral domain, although there are some striking exceptions. The contour line of the 20 % significance level in the AMTM spectrum covers the whole night and comprises observed periods between 2.8 and 8.0 h. The statistically significant area in the CORAL spectrum is more focused and comprises observed periods between 2.8 and 6.0 h. Right at the position of maximum amplitude in the CORAL spectrum, we find a gap in the spectrum of the AMTM. This gap results most probably from waves with small vertical wavelengths which cannot be detected by the AMTM. Another explanation is an OH layer altitude that is higher or lower than assumed. Looking at Fig. 4c we find a peak shifting from the 3.5 h observed period at an 82 km altitude to 4.5 h at 90 km. This behaviour might be indicative of separate waves at different altitudes, or the same wave being Doppler-shifted to multiple observed periods at different altitudes, which then implies a vertical gradient in horizontal wind speed. Such a vertical gradient is supported by SLICE meteor wind measurements (Fig. 3). From $\frac{\partial {\mathit{\lambda }}_z}{\partial t}\sim \frac{\partial u}{\partial z}$, we expect a changing vertical wavelength with time, as we find a vertical gradient in horizontal wind speed. Figures 9a and c show a changing λ_z.

We find a rather broad distribution of horizontal wavelengths, with a peak between 739 and 1032 km (Fig. 7b). To note are two areas reaching at least a 2000 km horizontal wavelength. A major peak is located at 01:00 UT and the 4.4 h observed period, and a smaller peak is located at 01:30 UT and the 3.3 h observed period. As mentioned above, phase lines appear to be locally steep in the temperature reconstructions likely due to a gradient in horizontal wind. At the same time, waves appear to be rotating in propagation direction. Both peaks in Fig. 7a show a rapid turning of waves, with an angular change of >90^∘ within 2 h. Overall, considering the distribution of propagation directions we identify three different GW packets (Fig. 7d). The first comprises observed periods between 2.8 and 3.5 h and propagates in a northward–northeastward direction between 18:00 and 01:00 UT. The second packet exhibits observed periods between 3.5 and 4.5 h, propagates westward, and turns northward during the night. Between the 4.5 and 6.0 h observed period, we find a third wave packet propagating eastward and turning northward during the duration of the measurement. Interesting to observe is the bidirectionality of the GW packets, which is also reflected in the distribution of wind speeds. Most of the waves propagate against the wind, i.e. wind speeds are negative, but there is also a large part of waves travelling with the wind (Fig. 8b). The first GW packet experiences tailwind at 18:00 UT, but at 19:00 UT the wind turns and strengthens negative values. Negative winds are present for the second GW packet between 20:00 and 04:00 UT as well. The third packet experiences positive and decreasing wind speeds between 18:00 and 01:00 UT. Values inside the COI modify the distribution such that it changes from a plateau to a peak shape. Wind speeds from region (III) dominate the total density distribution (grey background) between −50 and 80 m s⁻¹. Figure 8b shows that most of the waves outside the COI are Doppler-shifted from small intrinsic periods between 2.5 and 3.1 h to larger observed periods between 2.8 and 6.5 h. Intrinsic periods from region (III) dominate the total density distribution (grey background) between 2.1 and 8.0 h. Based on lidar data the WAPITI algorithm identifies a majority of vertical wavelengths between 19 and 22 km (Fig. 9a). Vertical wavelengths from region (III) dominate the total density distribution (grey background) for negative values. We find two smaller peaks between 12 and 14 km (upward) and 24–40 km (downward). This is in good agreement with values retrieved using the dispersion relation (Fig. 9b). Due to large uncertainties in the calculation of vertical wavelengths, the density distribution is very broad. Hence, values for λ_z smaller than the OH layer thickness are also retrieved. In Fig. 9c we find another white gap, indicating a complex vertical wave number. This area coincides with a domain of extremely large horizontal wavelengths (Fig. 7a) and fast wave rotation (Fig. 7c). As mentioned above, this is an indication for a gradient in the horizontal wind field. Vertical wavelengths are relatively small and slowly increasing, which is in agreement with the non-detection by the AMTM in the beginning of the measurement due to the lack of sensitivity to small vertical wavelengths. At the same time the variation in λ_z provides evidence for a vertical wind shear. We rearrange the ray-tracing equations stated by Marks and Eckermann (1995), yielding

$$\begin{array}{}\text{(12)}& {\displaystyle \frac{\partial u}{\partial z}}={\displaystyle \frac{{\mathit{\lambda }}_{\mathrm{h}}}{{\mathit{\lambda }}_z^{\mathrm{2}}}}{\displaystyle \frac{\mathrm{d}{\mathit{\lambda }}_z}{\mathrm{d}t}},\end{array}$$

with u being the horizontal wind speed in an arbitrary direction. λ_h and λ_z are averaged at an observed period of 4 h between 20:00 and 03:00 UT, i.e. a time span in which both wavelet spectra exhibit large significance levels. The vertical wavelength changes from −15 to −30 km within this time span. Hence, $\frac{\partial u}{\partial z}=\frac{\mathrm{900}\mathrm{km}}{{\mathrm{20}}^{\mathrm{2}}{\mathrm{km}}^{\mathrm{2}}}\frac{\mathrm{15}\mathrm{km}}{\mathrm{7}\mathrm{h}}=\mathrm{1.3}\frac{\mathrm{m}{\mathrm{s}}^{-\mathrm{1}}}{\mathrm{km}}$. When we multiply this value by the thickness of the OH layer, we get a total difference in wind speed of Δu=11.5 m s⁻¹. The mean absolute wind speed retrieved from SLICE between 20:00 and 03:00 UT increases from 41 m s⁻¹ at 82 km to 51 m s⁻¹ at 90 km (Fig. 3). This value is in very good agreement with our estimate. We conclude that with the help of our method, we are able to derive vertical wind gradients and possibly even horizontal gradients.

In region (III) we identify two GW packets moving in opposite directions (westward and eastward) turning slowly northward. Both propagate upward. These changes of propagation direction are most probably due to wind gradients. The existence of large-period waves is one condition for the supposed gravity wave breaking at 21:00 UT. Another cause for gravity wave breaking at mesospheric altitudes could be interaction with tides.

In summary, we demonstrated that our analysis is capable of determining the full set of GW parameters covering a wide range of values that are known to be typical for gravity waves. Typical values for λ_h in airglow data are in the range of 10–200 km (Nakamura et al., 2003; Diettrich et al., 2005; Matsuda et al., 2014; Lu et al., 2015; Nyassor et al., 2018). By analysing keograms, Fritts et al. (2014) retrieve even larger λ_h values reaching 4000 km. They decompose temperature perturbations into a few dominant modes and find a wide range of values for the horizontal wavelength (24–∼4000 km), vertical wavelength (17.6–∼30 km), intrinsic period (∼10 min–12 h), intrinsic phase velocity (33 to >200 m s⁻¹) and background wind (∼14–51 m s⁻¹). Vertical wavelengths retrieved from lidar data are typically between 2 and 20 km (Kaifler et al., 2017). Values for λ_z>50 km are an indication for ducted waves (Snively and Pasko, 2003).

6 Conclusions

In this study we combined three complementary data sets obtained from co-located instruments. Vertical temperature profiles by CORAL and the AMTM's horizontal temperature maps provide three-dimensional insight into the behaviour of GWs in the MLT region. Additional wind information provided by the SLICE meteor radar made it possible to investigate the intrinsic propagation of these GWs. Our newly developed WAPITI algorithm combines spectral filtering using wavelet analysis with a phase line identification algorithm. Based on this method, we were able to retrieve observed as well as intrinsic GW parameters with estimations of their uncertainties as a function of time and ground-relative period. This facilitates separation and characterization of GW packets without using the dispersion relation.

Although the sensitivities of the instruments differ, by comparing wavelet spectra, we confirm that AMTM and CORAL observed, in general, the same GWs. For the case study on 16–17 December 2015, the night started with large-scale waves between the 3 and 5 h ground-relative period. At 21:00 UT wave breaking occurred, resulting in spectral broadening and creation of small-period waves. The mean flow turns in the southeastward direction and strengthens. The detected GWs propagate predominantly against this background wind in a northward direction, resulting in a Doppler shift of about 1 h. The vertical wind shear caused a steepening of phase lines, i.e. an increase in vertical wavelengths. Additionally we find very large horizontal wavelengths and wave rotation, indicating a horizontal wind shear as well. We were not looking for isolated wave events but investigated all data sets, interpreting the observations as a superposition of several GWs. All retrieved parameters are highly variable in time and observed period. This provides evidence for a non-uniform wind field in space and time and points out the complex interaction between waves and the background flow. As only parts of the spectra are sensitive to wind gradients, we conclude that small-period waves see large-period ones as disturbances in the background. Only the distribution of propagation directions exhibited multiple discrete peaks which help to distinguish clearly between GW packets. The GW parameters can be used to calculate momentum fluxes, to perform forward and backward ray tracing, and to derive a horizontally resolved wind field. The largest uncertainty of intrinsic parameters derived with our method arises due to the unknown precise altitude and shape of the OH layer. A reliable method to determine the precise OH profile is needed in order to improve GW results and to allow for better differentiation between GW packets. We plan to automate our method and apply it to more case studies and eventually to the whole data set, with the goal of studying propagation and interaction of GWs with the mean flow from a statistical point of view. In order to assess spatial properties of GWs, we want to extend our analysis to the whole FOV of the imager.

Appendix A: Uncertainties

In this section, we present uncertainty calculations for the retrieved parameters' horizontal wavelength, direction of propagation, intrinsic period, wind in propagation direction, wind shear, wind curvature and vertical wavelength derived from the dispersion relation. The uncertainty of the intrinsic period contains wind speed uncertainties Δu₀, which comprises three sources. First we average the Gaussian-weighted wind speed over an altitude range of 82–95 km, with a FWHM of 8.6 km centred at 86.8 km. This is the average altitude and thickness of the OH layer. As mentioned in Sect. 2.2, these parameters are variable; therefore it is possible that the OH layer is partly below 82 km or above 91 km, and we do not average over the correct altitude range. Second, we calculate the wind speed in the direction of propagation, which is based on the estimated θ. As θ may be inaccurate, there is some uncertainty in the projected wind speed as well. Finally, for the wind measurements itself, we assume uncertainties of 10 m s⁻¹. As we average over at least three independent values, the uncertainty is reduced to 5.6 m s⁻¹:

$$\begin{array}{}\text{(A1)}& {\displaystyle }\mathrm{\Delta }{\mathit{\lambda }}_x& {\displaystyle }=\mathit{\tau }\mathrm{\Delta }{c}_x,\text{(A2)}& {\displaystyle }\mathrm{\Delta }{\mathit{\lambda }}_y& {\displaystyle }=\mathit{\tau }\mathrm{\Delta }{c}_y,\text{(A3)}& {\displaystyle }\mathrm{\Delta }{\mathit{\lambda }}_{\mathrm{h}}& {\displaystyle }=\left|{\displaystyle \frac{\partial {\mathit{\lambda }}_{\mathrm{h}}}{\partial {\mathit{\lambda }}_x}}\right|\mathrm{\Delta }{\mathit{\lambda }}_x+\left|{\displaystyle \frac{\partial {\mathit{\lambda }}_{\mathrm{h}}}{\partial {\mathit{\lambda }}_y}}\right|\mathrm{\Delta }{\mathit{\lambda }}_y\text{(A4)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\left|{\mathit{\lambda }}_y\right|\mathrm{\Delta }{\mathit{\lambda }}_x+\left|{\mathit{\lambda }}_x\right|\mathrm{\Delta }{\mathit{\lambda }}_y}{({\mathit{\lambda }}_x^{\mathrm{2}}+{\mathit{\lambda }}_y^{\mathrm{2}}{)}^{\mathrm{3}/\mathrm{2}}}}.\text{(A5)}& {\displaystyle }\mathrm{\Delta }\mathit{\theta }& {\displaystyle }={\displaystyle \frac{\left|{\mathit{\lambda }}_y\right|\mathrm{\Delta }{\mathit{\lambda }}_x+\left|{\mathit{\lambda }}_x\right|\mathrm{\Delta }{\mathit{\lambda }}_y}{{\mathit{\lambda }}_y^{\mathrm{2}}+{\mathit{\lambda }}_x^{\mathrm{2}}}}.\text{(A6)}& {\displaystyle }\mathrm{\Delta }{\mathit{\tau }}_{\mathrm{I}}& {\displaystyle }=\left|{\displaystyle \frac{\partial {\mathit{\tau }}_{\mathrm{I}}}{\partial {\mathit{\lambda }}_{\mathrm{h}}}}\right|\mathrm{\Delta }{\mathit{\lambda }}_{\mathrm{h}}+\left|{\displaystyle \frac{\partial {\mathit{\tau }}_{\mathrm{I}}}{\partial u_{\mathrm{0}}}}\right|\mathrm{\Delta }{u}_{\mathrm{0}}\text{(A7)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{\left|u_{\mathrm{0}}\right|\mathrm{\Delta }{\mathit{\lambda }}_{\mathrm{h}}+\left|{\mathit{\lambda }}_{\mathrm{h}}\right|\mathrm{\Delta }{u}_{\mathrm{0}}}{(c-u_{\mathrm{0}}{)}^{\mathrm{2}}}}.\text{(A8)}& {\displaystyle }\mathrm{\Delta }{u}_{\mathrm{0}}\left(\mathit{\theta }\right)& {\displaystyle }=\left|{\displaystyle \frac{\partial u_{\mathrm{0}}}{\partial \mathit{\theta }}}\right|\mathrm{\Delta }\mathit{\theta }+\left|{\displaystyle \frac{\partial u_{\mathrm{0}}}{\partial U}}\right|\mathrm{\Delta }U+\left|{\displaystyle \frac{\partial u_{\mathrm{0}}}{\partial V}}\right|\mathrm{\Delta }V\text{(A9)}& {\displaystyle }& {\displaystyle }\begin{array}{rl}=\left|U\cos \right(\mathit{\theta })-V\sin (\mathit{\theta }\left)\right|\mathrm{\Delta }\mathit{\theta }& +\left|\sin \right(\mathit{\theta }\left)\right|\mathrm{\Delta }U\\ & +\left|\cos \right(\mathit{\theta }\left)\right|\mathrm{\Delta }V.\end{array}\text{(A10)}& {\displaystyle }\mathrm{\Delta }{u}_{\mathrm{0}}^{\prime }& {\displaystyle }={\displaystyle \frac{\sqrt{\mathrm{2}}\mathrm{\Delta }{u}_{\mathrm{0}}}{\mathrm{d}z}},\text{(A11)}& {\displaystyle }\mathrm{\Delta }{u}_{\mathrm{0}}^{\prime \prime }& {\displaystyle }={\displaystyle \frac{\mathrm{2}\mathrm{\Delta }{u}_{\mathrm{0}}}{\mathrm{d}{z}^{\mathrm{2}}}}.\end{array}$$

$$\begin{array}{}\text{(A12)}& \begin{array}{rl}\mathrm{\Delta }{\mathit{\lambda }}_z& =\left|{\displaystyle \frac{\partial {\mathit{\lambda }}_z}{\partial {\mathit{\lambda }}_{\mathrm{h}}}}\right|\mathrm{\Delta }{\mathit{\lambda }}_{\mathrm{h}}+\left|{\displaystyle \frac{\partial {\mathit{\lambda }}_z}{\partial {\mathit{\tau }}_{\mathrm{I}}}}\right|\mathrm{\Delta }{\mathit{\tau }}_{\mathrm{I}}+\left|{\displaystyle \frac{\partial {\mathit{\lambda }}_z}{\partial N}}\right|\mathrm{\Delta }N\\ & +\left|{\displaystyle \frac{\partial {\mathit{\lambda }}_z}{\partial H_{\mathrm{s}}}}\right|\mathrm{\Delta }{H}_{\mathrm{s}}+\left|{\displaystyle \frac{\partial {\mathit{\lambda }}_z}{\partial u_{\mathrm{0}}^{\prime }}}\right|\mathrm{\Delta }{u}_{\mathrm{0}}^{\prime }+\left|{\displaystyle \frac{\partial {\mathit{\lambda }}_z}{\partial u_{\mathrm{0}}^{\prime \prime }}}\right|\mathrm{\Delta }{u}_{\mathrm{0}}^{\prime \prime }\end{array}\end{array}$$

$$\begin{array}{}\text{(A13)}& {\displaystyle }& {\displaystyle }=\mathit{\pi }{\left({\displaystyle \frac{{\mathit{\lambda }}_z}{\mathrm{2}\mathit{\pi }}}\right)}^{\mathrm{3}}\left|{\displaystyle \frac{\mathrm{8}{\mathit{\pi }}^{\mathrm{2}}-\mathrm{2}{N}^{\mathrm{2}}{\mathit{\tau }}_{\mathrm{I}}^{\mathrm{2}}}{{\mathit{\lambda }}_{\mathrm{h}}}}+{\displaystyle \frac{u_{\mathrm{0}}^{\prime }{\mathit{\tau }}_{\mathrm{I}}}{H_{\mathrm{s}}}}-u_{\mathrm{0}}^{\prime \prime }{\mathit{\tau }}_{\mathrm{I}}\right|{\displaystyle \frac{\mathrm{\Delta }{\mathit{\lambda }}_{\mathrm{h}}}{{\mathit{\lambda }}_{\mathrm{h}}^{\mathrm{2}}}}\text{(A14)}& {\displaystyle }& {\displaystyle }+\mathit{\pi }{\left({\displaystyle \frac{{\mathit{\lambda }}_z}{\mathrm{2}\mathit{\pi }}}\right)}^{\mathrm{3}}\left|{\displaystyle \frac{\mathrm{2}{N}^{\mathrm{2}}{\mathit{\tau }}_{\mathrm{I}}}{{\mathit{\lambda }}_{\mathrm{h}}}}-{\displaystyle \frac{u_{\mathrm{0}}^{\prime }}{H_{\mathrm{s}}}}+u_{\mathrm{0}}^{\prime \prime }\right|{\displaystyle \frac{\mathrm{\Delta }{\mathit{\tau }}_{\mathrm{I}}}{\left|{\mathit{\lambda }}_{\mathrm{h}}\right|}}\text{(A15)}& {\displaystyle }& {\displaystyle }+\mathit{\pi }{\left({\displaystyle \frac{{\mathit{\lambda }}_z}{\mathrm{2}\mathit{\pi }}}\right)}^{\mathrm{3}}\left|{\displaystyle \frac{\mathrm{2}N{\mathit{\tau }}_{\mathrm{I}}^{\mathrm{2}}}{{\mathit{\lambda }}_{\mathrm{h}}^{\mathrm{2}}}}\right|\mathrm{\Delta }N\text{(A16)}& {\displaystyle }& {\displaystyle }+\mathit{\pi }{\left({\displaystyle \frac{{\mathit{\lambda }}_z}{\mathrm{2}\mathit{\pi }}}\right)}^{\mathrm{3}}\left|{\displaystyle \frac{\mathrm{1}}{H_{\mathrm{s}}}}+{\displaystyle \frac{u_{\mathrm{0}}^{\prime }{\mathit{\tau }}_{\mathrm{I}}}{{\mathit{\lambda }}_{\mathrm{h}}}}\right|{\displaystyle \frac{\mathrm{\Delta }{H}_{\mathrm{s}}}{H_{\mathrm{s}}^{\mathrm{2}}}}\text{(A17)}& {\displaystyle }& {\displaystyle }+\mathit{\pi }{\left({\displaystyle \frac{{\mathit{\lambda }}_z}{\mathrm{2}\mathit{\pi }}}\right)}^{\mathrm{3}}\left|{\displaystyle \frac{{\mathit{\tau }}_{\mathrm{I}}}{H_{\mathrm{s}}{\mathit{\lambda }}_{\mathrm{h}}}}\right|\mathrm{\Delta }{u}_{\mathrm{0}}^{\prime }\text{(A18)}& {\displaystyle }& {\displaystyle }+\mathit{\pi }{\left({\displaystyle \frac{{\mathit{\lambda }}_z}{\mathrm{2}\mathit{\pi }}}\right)}^{\mathrm{3}}\left|{\displaystyle \frac{{\mathit{\tau }}_{\mathrm{I}}}{{\mathit{\lambda }}_{\mathrm{h}}}}\right|\mathrm{\Delta }{u}_{\mathrm{0}}^{\prime \prime }.\end{array}$$