Caution with spectroscopic NO₂ reference cells (cuvettes)

Spectroscopic measurements of atmospheric trace gases, for example, by differential optical absorption spectroscopy (DOAS), are frequently supported by recording the trace-gas column density (CD) in absorption cells (cuvettes), which are temporarily inserted into the light path. The idea is to verify the proper functioning of the instruments, to check the spectral registration (wavelength calibration and spectral resolution), and to perform some kind of calibration (absolute determination of trace-gas CDs). In addition, trace-gas absorption cells are a central component in gas correlation spectroscopy instruments. In principle DOAS applications do not require absorption-cell calibration; however, in practice, measurements with absorption cells in the spectrometer's light path are frequently performed.

Since NO₂ is a particularly popular molecule to be studied by DOAS, and at the same time it can be unstable in cells, we chose it as an example to demonstrate that the effective CD seen by the instrument can deviate greatly (by orders of magnitude) from expected values. Analytical calculations and kinetic model studies show the dominating influence of photolysis and dimerization of NO₂. In particular, this means that the partial pressure of NO₂ in the cell matters. However, problems can be particularly severe at high NO₂ pressures (around 10⁵ Pa) as well as low NO₂ partial pressures (of the order of a few 100 Pa). Also, it can be of importance whether the cell contains pure NO₂ or is topped up with air or oxygen (O₂). Some suggestions to improve the situation are discussed.

1 Introduction

There are a number of reasons for using absorption cells in conjunction with instruments measuring trace-gas column densities (CDs) by absorption spectroscopy, e.g. by differential optical absorption spectroscopy (DOAS). These include the verification of the overall functioning of the instrument, stray-light determination, or a check of the instrument's absolute wavelength calibration.

Field calibration of a spectrometer is not necessary for UV-visible absorption spectroscopy (see e.g. Platt and Stutz, 2008), since the instrument can be calibrated by using high-resolution absorption cross-section spectra of the particular gases. This is accomplished by (1) determining the instrument function (IF) and (2) convoluting a high-resolution trace-gas cross-section spectrum with this IF and then (3) fitting the resulting trace-gas cross section to measured spectra in order to obtain the trace-gas CD. The details of this process are explained in studies, e.g. by Platt and Stutz (2008). However, it may be tempting to perform the calibration process simply by recording the CD of an absorption cell filled with a known amount of trace gas brought into the light path of the instrument. This approach complicates the measurements and may introduce additional errors due to uncertainties in the trace-gas CD in the cell. Nevertheless such procedures may work for a series of gases, like O₂, CO, CO₂, and CH₄, which do not (at ambient temperature) undergo self-reaction and which are neither photolysed by ambient solar radiation near the Earth's surface nor by the radiation typically used for their absorption spectroscopic measurement. On the other hand, if a trace-gas cell is used to determine absolute wavelength calibration of a spectrometer, the absolute trace-gas CD in the cell is usually not critical.

In addition, gas correlation spectroscopy measurements (e.g. Ward and Zwick, 1975; Sandsten et al., 1996, 2004; Kebabian et al., 2000) require absorption cells containing the gas to be measured at CDs leading to optical densities around unity.

In general, there are a number of issues with using gas cells for these purposes, including the following:

• optical problems with the cell

• stability of the gas in the cell due to photolysis and/or other chemical reactions

• temperature dependence of chemical equilibria within the cell

• temperature dependence of the optical density.

In the following we discuss the above problems for the case of NO₂-absorption cells; however some of the discussed issues will also apply to cells with other gases.

2 Optics of cells

In principle the introduction of an absorption cell into the optical path of a remote-sensing instrument (e.g. a spectrometer) is straightforward. The cell is mounted in front of the entrance optics, and in the first approximation the absorption due to the trace gas in the cell (i.e. due to the trace-gas CD) is added to the trace-gas absorption seen without the cell. While this view is correct in some approximation, in detail there are a number of problems that need investigation.

2.1 Path length in an isolated cell

In a realistic cell, partial reflection (reflectance R) occurs at the cell windows. For simplicity we assume an index of refraction of n=1.5 for the cell window material and accordingly (Fresnel formula)

$$\begin{array}{}\text{(1)}& R={\left({\displaystyle \frac{n-\mathrm{1}}{n+\mathrm{1}}}\right)}^{\mathrm{2}}\approx \mathrm{0.04},\end{array}$$

i.e. about 4 % reflection per surface for near-normal incidence (see Fig. 1). The reduction of the incoming intensity by (1−R)⁴, or about 15 %, is probably of minor importance; however (if we neglect the absorption by the trace gas in the cell) a fraction of about $(\mathrm{1}-R{)}^{\mathrm{2}}\cdot (R+R{)}^{\mathrm{2}}\approx \mathrm{0.59}$ % of the incoming radiation and 0.69 % of the transmitted radiation passes the cell three times (this effect will be lower at high trace-gas optical densities and also could be reduced by adding anti-reflective coatings to the cell windows). Due to this multiply reflected light the total absorption of the cell (and thus the trace-gas slant column density – SCD – S_C) will be enhanced by about 2 % over the CD S₀ for a single traverse. We note that the case of nearly normal incidence is quite realistic in many cases; for instance multi-axis DOAS (MAX-DOAS) instruments (e.g. Hönninger and Platt, 2002; Platt and Stutz, 2008) have total aperture angles of the order of 1^∘, i.e. incidence angles of −0.5 to +0.5^∘. A typical use of a cell would be to mount it just in front of the instrument's telescope. In this arrangement the enhancement of the light path inside the cell (and thus the trace-gas column density S_C) due to the finite aperture angle of the radiation passing the cell will vary according to $S_{\mathrm{C}}=S_{\mathrm{0}}/\cos \left(\mathit{\vartheta }\right)$, with S₀ denoting the trace-gas CD for rays parallel to the cell axis. An angle of ϑ=0.5^∘ would lead to an enhancement in S_C∕S₀ of ≈1.000038 or 0.004 %.

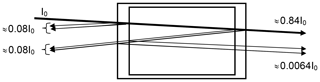
Figure 1 Sketch of the optics of a gas absorption cell; parallel rays are assumed, and the (small) tilt of the incoming ray with respect to the cell axis is introduced to distinguish the rays. The described effect will also be there at strictly normal incidence. We assume an index of refraction of n=1.5 for the cell window material and accordingly 4 % reflection per surface (for near-normal incidence). Note that a fraction of about 0.69 % of the transmitted radiation passes the cell three times, thus adding ≈2 % to the total absorption (if the trace-gas absorption in the cell is small).

Thus a slight (few degrees) tilt of the cell will not lead to noticeable light path extension in the cell, but already a 1^∘ tilt, leading to 0.015 % light path extension, would be sufficient to direct the multiple reflected light outside the field of view of the telescope. Thus, the additional 2 % cell absorption would disappear. On the other hand, larger tilts of the cell, for example of 10^∘, would increase the cell absorption again by 1.5 % and should therefore be avoided. This could be accomplished by a rigid mount which fixes the (removable) cell at a defined angle with respect to the cell optical axis (normal of the windows), e.g. at 2^∘.

As will be discussed below, the acceptance angle of the cell to ambient direct or scattered sunlight can play a significant role. Therefore, this small aperture angle allows for shielding the cell from sunlight, since solar radiation only needs to enter from a small solid angle (of the order of 10⁻³ sr), for instance, by mounting the cell inside a relatively long tube made of nontransparent material.

2.2 Path length in a cell as part of an optical system

In Sect. 2.1 we discussed the behaviour of an isolated cell; however the idea is to incorporate an absorption cell into an optical system, i.e. to just hold it in front of a MAX-DOAS instrument. In this case there can be interaction between the cell and the entrance optics of the instrument (for instance due to reflection of light at the surface of the telescope lens). As described by Lübcke et al. (2013) this can further enhance the trace-gas CD in the cell as seen by the instrument looking through it.

In the case of using gas cells in imaging instruments, for instance imaging spectrometers (e.g. Lohberger et al., 2004) or gas correlation instruments (e.g. Ward and Zwick, 1975), a larger aperture angle is required. This causes two potential problems. First, the aperture angle of the cell has to be much larger than in the case of a one-pixel (narrow field of view) instrument, for instance, typically a 30^∘ total angle. Thus the acceptance angle for solar radiation becomes considerably larger (e.g. 0.22 sr instead of 10⁻³ sr), and consequently the photolysis frequencies for the gases inside the cell will be enhanced (see below). Second, the trace-gas CD of the cell becomes dependent on the observation angle ϑ (angle between the optical axis and the actual viewing direction within the field of view) as described above. For a total aperture angle of 30^∘ this would amount to an enhancement of the S_C(15^∘) over $S_{\mathrm{0}}=S_{\mathrm{C}}\left(\mathrm{0}{}^{\circ }\right)$ of about 3.5 %.

3 Chemistry in NO₂-absorption cells

Nitrogen dioxide (NO₂) is a quite reactive gas (see rest of the section); therefore a series of chemical processes in an absorption cell can occur. Since they can alter the NO₂ concentration – and thus the NO₂ CD in the cell – considerably, they have to be watched. In the following subsections we discuss the relevant chemical processes, starting with important reactions and then proceeding to further reactions which are only relevant under certain conditions or if high accuracy is required.

We first discuss simplified chemistry, just encompassing the pertinent reactions, and then we proceed to a more comprehensive discussion of the chemistry in the following subsections.

3.1 The (initial) NO₂-only chemistry – simple case

In a cell (initially) filled only with NO₂ we can expect a series of reactions to occur, which are described in the following (bi-molecular rate constants are given in cm³ molec.⁻¹ s⁻¹, termolecular rate constants are given in cm⁶ molec.⁻² s⁻¹ for 25 ^∘C and 1000 hPa, and details on temperature and pressure dependence as well as literature references can be found in Table 1). In fact, when buying NO₂ from a manufacturer, some of the described reactions can already proceed in the initial gas, which therefore might already contain impurities (e.g. of NO, HONO, and HNO₃).

Usually cells are exposed to sunlight or radiation needed for the measurement; thus NO₂ in the cell can be photolysed:

$$\begin{array}{}\text{(R1)}& {\mathrm{NO}}_{\mathrm{2}}+h\mathit{\nu }\to \mathrm{NO}+\mathrm{O}{(}^{\mathrm{3}}\mathrm{P}),J_{\mathrm{1}}\approx \mathrm{8}\times {\mathrm{10}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}$$

The above value for J₁ is reached in full sunshine around noontime (see e.g. Jones and Bayes, 1973 or Kraus and Hofzumahaus, 1998). Of course this figure (and in fact all photolysis frequencies in the cell; see Table 1) is highly variable, depending on solar zenith angle (i.e. latitude, season, and time of day), cloudiness, atmospheric turbidity, and the shading situation at the measurement site. In the case of active DOAS systems the photolysis frequencies will depend on the intensity of the light source and on the fraction of the cell cross-section area covered by the light beam. Nevertheless, it is frequently seen that calibration cells are used in full sunshine without any shielding; moreover, as is shown below (see Sect. 4), the effects on the NO₂ chemistry are similar over a wide range of photolysis frequencies.

In the following, ground-state oxygen atoms O(³P) will be denoted by O. The threshold wavelength for Reaction (R1) is about 398 nm (e.g. Johnston and Graham, 1974; Burkholder et al., 2015); however, due to vibrational excitation of the ground-state molecule there is noticeable photolysis up to about 430 nm. If the cell is only illuminated with radiation of a wavelength longer than 430 nm, NO₂ will not photolyse and J₁ will be essentially zero.

Although it is only a small effect it is worth noting that the photolysis frequency inside a cell is not different from the value in the air surrounding the cell despite reflectance of the cell walls, as described by, for example, Bahe et al. (1979).

The oxygen atoms produced in Reaction (R1) can (1) recombine

$$\begin{array}{}\text{(R2)}& \begin{array}{rl}& \mathrm{O}+\mathrm{O}+M\to {\mathrm{O}}_{\mathrm{2}}+M,\\ & k_{\mathrm{2}}(\mathrm{298}\mathrm{K},{\mathrm{10}}^{\mathrm{5}}\mathrm{Pa})\approx \mathrm{2.5}\times {\mathrm{10}}^{-\mathrm{14}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

However, this is a slow process, because the O-atom concentration will be very low (see Figs. 4 to 8). Alternatively, (2) O atoms may react with the wall where they predominantly recombine (see e.g. Cartry et al., 2000):

$$\begin{array}{}\text{(R3)}& \mathrm{O}+\mathrm{O}\to \text{Wall}\to {\mathrm{O}}_{\mathrm{2}}.\end{array}$$

Also, (3) O atoms can react with NO₂ to form NO:

$$\begin{array}{}\text{(R4)}& \begin{array}{rl}& \mathrm{O}+{\mathrm{NO}}_{\mathrm{2}}\to \mathrm{NO}+{\mathrm{O}}_{\mathrm{2}},\\ & k_{\mathrm{4}}\left(\mathrm{298}\mathrm{K}\right)\approx \mathrm{2.52}\times {\mathrm{10}}^{-\mathrm{12}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

Further, (4) oxygen atoms also may react with NO to form NO₂:

$$\begin{array}{}\text{(R5)}& \begin{array}{rl}& \mathrm{O}+\mathrm{NO}+M\to {\mathrm{NO}}_{\mathrm{2}}+M,\\ & k_{\mathrm{5}}(\mathrm{298}\mathrm{K},{\mathrm{10}}^{\mathrm{5}}\mathrm{Pa})\approx \mathrm{2.2}\times {\mathrm{10}}^{-\mathrm{12}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

The final possibility, (5) formation of NO₃ – as well as further reactions, will be addressed in Sect. 3.4 below.

In addition there is the termolecular reaction of the O₂ formed in Reactions (R4) or (R2) (or added to the cell filling) that oxidizes NO to NO₂:

$$\begin{array}{}\text{(R6)}& \begin{array}{rl}& \mathrm{2}\mathrm{NO}+{\mathrm{O}}_{\mathrm{2}}\to \mathrm{2}{\mathrm{NO}}_{\mathrm{2}},\\ & k_{\mathrm{6}}\approx \mathrm{1.95}\times {\mathrm{10}}^{-\mathrm{38}}{\mathrm{cm}}^{-\mathrm{6}}{\mathrm{molec}.}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

In an attempt to obtain a first-order quantitative understanding of the processes in the cell, we just consider a pure NO₂ initial filling and Reactions (R1) (NO₂ photolysis), (R4) (O+NO₂), and (R6) (2NO+O₂).

From the combination of Reactions (R1) and (R4) we derive the rates of NO and O₂ formation under illumination,

$$\begin{array}{}\text{(2)}& P\left(\mathrm{NO}\right)={\displaystyle \frac{d}{\mathrm{d}t}}\left[\mathrm{NO}\right]\approx \mathrm{2}\cdot P\left({\mathrm{O}}_{\mathrm{2}}\right)\approx \mathrm{2}\cdot \left[{\mathrm{NO}}_{\mathrm{2}}\right]\cdot J_{\mathrm{1}},\end{array}$$

which ultimately (i.e. in the stationary state) must equal the rate of NO destruction, D(NO) and NO₂ formation, and P(NO₂) due to Reaction (R6):

$$\begin{array}{}\text{(3)}& D\left(\mathrm{NO}\right)=-{\displaystyle \frac{d}{\mathrm{d}t}}\left[\mathrm{NO}\right]\approx P\left({\mathrm{NO}}_{\mathrm{2}}\right)\approx \mathrm{2}\cdot {\left[\mathrm{NO}\right]}_S^{\mathrm{2}}\cdot \left[{\mathrm{O}}_{\mathrm{2}}\right]\cdot k_{\mathrm{6}}.\end{array}$$

Since $P\left({\mathrm{O}}_{\mathrm{2}}\right)\approx \mathrm{0.5}\cdot P\left(\mathrm{NO}\right)$ and the concentration of both species are zero initially, we have $\left[\mathrm{NO}\right]\approx \mathrm{2}\cdot \left[{\mathrm{O}}_{\mathrm{2}}\right]$. Substituting this relationship,

$$\begin{array}{}\text{(4)}& D\left(\mathrm{NO}\right)=-{\displaystyle \frac{d}{\mathrm{d}t}}\left[\mathrm{NO}\right]\approx {\left[\mathrm{NO}\right]}^{\mathrm{3}}\cdot k_{\mathrm{6}},\end{array}$$

and equating P(NO) with D(NO), we obtain

$$\begin{array}{}\text{(5)}& \mathrm{2}\left[{\mathrm{NO}}_{\mathrm{2}}\right]\cdot J_{\mathrm{1}}\approx {\left[\mathrm{NO}\right]}_S^{\mathrm{3}}\cdot k_{\mathrm{6}}.\end{array}$$

Further substituting $\left[{\mathrm{NO}}_{\mathrm{2}}\right]\approx [{\mathrm{NO}}_{\mathrm{2}}{]}_{\mathrm{0}}-[\mathrm{NO}{]}_S$,

$$\begin{array}{}\text{(6)}& {\left[{\mathrm{NO}}_{\mathrm{2}}\right]}_{\mathrm{0}}-{\left[\mathrm{NO}\right]}_S\approx {\left[\mathrm{NO}\right]}_S^{\mathrm{3}}\cdot {\displaystyle \frac{k_{\mathrm{6}}}{\mathrm{2}{J}_{\mathrm{1}}}},\end{array}$$

or

$$\begin{array}{}\text{(7)}& {\left[{\mathrm{NO}}_{\mathrm{2}}\right]}_{\mathrm{0}}\approx {\left[\mathrm{NO}\right]}_S^{\mathrm{3}}\cdot {\displaystyle \frac{k_{\mathrm{6}}}{\mathrm{2}{J}_{\mathrm{1}}}}+{\left[\mathrm{NO}\right]}_S.\end{array}$$

This cubic equation can be solved for the stationary-state NO concentration [NO]_S as a function of the initial [NO₂]₀ as given in Appendix A.

Examples. (1) As an example, and to obtain a first idea of what might be happening in the cell, we assume about 1 atm (1000 hPa) of pure NO₂ (initially); i.e. the initial NO₂ concentrations in the cell will be $[{\mathrm{NO}}_{\mathrm{2}}{]}_{\mathrm{0}}\approx \mathrm{2.4}\times {\mathrm{10}}^{\mathrm{19}}$ cm⁻³ and the very simple chemical system just comprising Reactions (R1), (R4), and (R6). As we show below, the simplified reaction system – with the exception of the NO₂ dimer (N₂O₄) formation (see Sect. 3.2) – is quite adequate. Also, such a cell would have a peak optical density (at around 440 nm) of about 14 at 1 cm length but much lower at other wavelengths.

In the dark (J₁=0) nothing will happen, while in sunlight ($J_{\mathrm{1}}=\mathrm{8}\times {\mathrm{10}}^{-\mathrm{3}}$): NO+O formation will take place followed by Reaction (R4) of NO₂ with O. Thus the (initial) rate of NO formation P(NO) will be

$$\begin{array}{}\text{(8)}& P\left(\mathrm{NO}\right)\approx \mathrm{2}{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}_{\mathrm{0}}\cdot J_{\mathrm{1}}\approx \mathrm{3.8}\times {\mathrm{10}}^{\mathrm{17}}{\mathrm{cm}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}$$

This will lead to an initial decay time ${\mathit{\tau }}_{{\mathrm{NO}}_{\mathrm{2}}}=[{\mathrm{NO}}_{\mathrm{2}}{]}_{\mathrm{0}}/P(\mathrm{NO})=\mathrm{1}/(\mathrm{2}{J}_{\mathrm{1}})\approx \mathrm{63}$ s. The stationary-state NO concentration can be calculated according to Eq. (7) and the solution given in Appendix A to be $[\mathrm{NO}{]}_S\approx \mathrm{2.57}\times {\mathrm{10}}^{\mathrm{18}}$ molec. cm⁻³, or about 10.7 % of the initial NO₂ level. In other words, the NO₂ concentration will be reduced to 89.3 % of its initial value [NO₂]₀. The corresponding NO rate of destruction will be

$$D\left(\mathrm{NO}\right)\approx {\left[\mathrm{NO}\right]}^{\mathrm{3}}\cdot k_{\mathrm{6}}\approx \mathrm{3.32}\times {\mathrm{10}}^{\mathrm{17}}\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}},$$

matching

$$P\left(\mathrm{NO}\right)\approx \mathrm{2}[{\mathrm{NO}}_{\mathrm{2}}{]}_S\cdot J_{\mathrm{1}},$$

from NO₂ photolysis .

(2) We give a further example using about 1 hPa of pure NO₂ (initially) corresponding to $[{\mathrm{NO}}_{\mathrm{2}}{]}_{\mathrm{0}}\approx \mathrm{2.4}\times {\mathrm{10}}^{\mathrm{16}}$ cm⁻³, and the same simple chemical system, just comprising Reactions (R1), (R4), and (R6), as above. Such a cell would have an initial differential optical density in the vicinity of 450 nm of about $\mathrm{2.4}\times {\mathrm{10}}^{-\mathrm{3}}$ and would thus appear ideal to test the sensitivity of an NO₂ spectrometer.

In sunlight we have $D\left({\mathrm{NO}}_{\mathrm{2}}\right)\approx \mathrm{1.92}\times {\mathrm{10}}^{\mathrm{14}}$ cm⁻³ s⁻¹. In this case, the resulting stationary-state NO level becomes $[\mathrm{NO}{]}_S\approx \mathrm{2.4}\times {\mathrm{10}}^{\mathrm{16}}$, or about 100 % of the initial NO₂. In other words after illumination the remaining NO₂ concentration and thus the NO₂ CD of the cell will only be a very small fraction of the expected value $\left(\right[{\mathrm{NO}}_{\mathrm{2}}{]}_S\cdot J_{\mathrm{1}}=D\left(\mathrm{NO}\right)$ or $[{\mathrm{NO}}_{\mathrm{2}}{]}_S=D(\mathrm{NO})/J_{\mathrm{1}}\approx \mathrm{1.7}\times {\mathrm{10}}^{\mathrm{13}}$ cm⁻³, i.e. < 0.1 % of the initial [NO₂]). After a short (of the order of 1 min) exposure to sunlight the NO₂ in the cell will practically vanish.

On the other hand, in this simplified calculation, the NO reconversion, D(NO), to NO₂ will be much slower than the initial photolysis:

$$D\left(\mathrm{NO}\right)\approx \mathrm{0.5}\cdot {\left[\mathrm{NO}\right]}^{\mathrm{3}}\cdot k_{\mathrm{6}}\approx \mathrm{1.35}\times {\mathrm{10}}^{\mathrm{11}}\mathrm{molec}.{\mathrm{cm}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}.$$

Recovery from illumination. A further interesting question concerns the time for the chemical system to recover from a period of photolysis. Equation (4) gives the rate of NO destruction as a function of [NO]. In the case of example (1), above NO would decay with an initial rate of $D\left(\mathrm{NO}\right)/\left[\mathrm{NO}\right]\approx \mathrm{0.11}$ s⁻¹ (ca. 11 % per second, suggesting a 9 s time constant for recovery). However, D(NO) varies with the third power of [NO]. When, for example, 90 % the NO is consumed (i.e. 1.4 % of [NO] is still left) the time constant would increase by a factor of 1000 to around 3 h.

In the case of example (2), the initial reconversion rate would only be $\mathrm{5.6}\times {\mathrm{10}}^{-\mathrm{6}}$ s⁻¹ (or ≈49 % per day), which would seem to imply a recovery time of somewhat more than 2 d. But again the dependence on the cube of the NO concentration means that the recovery time becomes much longer later on. For some model results, see Fig. 9.

3.2 The NO₂↔N₂O₄ equilibrium

An additional problem in NO₂ cells – in particular if high NO₂ concentrations approaching 1000 hPa are used – is the formation of the dimer N₂O₄ (see also Roscoe et al., 1993):

$$\begin{array}{}\text{(R7)}& \begin{array}{rl}& \mathrm{2}{\mathrm{NO}}_{\mathrm{2}}+M\to {\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{4}}+M,\\ & k_{\mathrm{7}}(\mathrm{298}\mathrm{K},{\mathrm{10}}^{\mathrm{5}}\mathrm{Pa})\approx \mathrm{3.3}\times {\mathrm{10}}^{-\mathrm{14}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

There is a thermal decay of the dimer,

$$\begin{array}{}\text{(R8)}& \begin{array}{rl}& {\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{4}}+M\to \mathrm{2}{\mathrm{NO}}_{\mathrm{2}}+M,\\ & k_{\mathrm{8}}(\mathrm{298}\mathrm{K},{\mathrm{10}}^{\mathrm{5}}\mathrm{Pa})\approx \mathrm{1.47}\times {\mathrm{10}}^{\mathrm{5}}{\mathrm{s}}^{-\mathrm{1}},\end{array}\end{array}$$

leading to an equilibrium with the equilibrium constant (298K; from Atkinson et al., 2004),

$$\begin{array}{}\text{(9)}& K_{\mathrm{Eq}}={\displaystyle \frac{k_{\to }}{k_{\leftarrow }}}={\displaystyle \frac{\left[{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{4}}\right]}{{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}^{\mathrm{2}}}}\approx \mathrm{2.29}\times {\mathrm{10}}^{-\mathrm{19}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}.\end{array}$$

Note that the time to attain the equilibrium is shorter than $\mathrm{1}/k_{\mathrm{8}}\approx \mathrm{7}$ µs (at 298 K and 1000 hPa). Thus, one can assume that there is always equilibrium between NO₂ and N₂O₄. From this follows, for the [NO₂]∕[N₂O₄] ratio,

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{\mathrm{1}}{K_{\mathrm{Eq}}\left[{\mathrm{NO}}_{\mathrm{2}}\right]}}={\displaystyle \frac{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}{\left[{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{4}}\right]}}\text{or}\left[{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{4}}\right]=K_{\mathrm{Eq}}\cdot {\left[{\mathrm{NO}}_{\mathrm{2}}\right]}^{\mathrm{2}}.\end{array}$$

What is usually most interesting is the fraction of NO₂ of the total amount of NO₂+N₂O₄ (i.e. pressure during filling) in the cell. The fraction is given by $\left[{\mathrm{NO}}_Z\right]=\left[{\mathrm{NO}}_{\mathrm{2}}\right]+\left[{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{4}}\right]$ and thus

$$\begin{array}{}\text{(11)}& \begin{array}{rl}{\displaystyle \frac{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}{\left[{\mathrm{NO}}_Z\right]}}& ={\displaystyle \frac{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}{\left[{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{4}}\right]+\left[{\mathrm{NO}}_{\mathrm{2}}\right]}}={\displaystyle \frac{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}{K_{\mathrm{Eq}}\cdot {\left[{\mathrm{NO}}_{\mathrm{2}}\right]}^{\mathrm{2}}+\left[{\mathrm{NO}}_{\mathrm{2}}\right]}}\\ & ={\displaystyle \frac{\mathrm{1}}{K_{\mathrm{Eq}}\cdot \left[{\mathrm{NO}}_{\mathrm{2}}\right]+\mathrm{1}}},\end{array}\end{array}$$

which can be transformed into

$$\begin{array}{}\text{(12)}& \begin{array}{rl}{K}_{\mathrm{Eq}}\cdot \left[{\mathrm{NO}}_{\mathrm{2}}\right]+\mathrm{1}& ={\displaystyle \frac{\left[{\mathrm{NO}}_Z\right]}{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}}\\ & \Rightarrow \left[{\mathrm{NO}}_Z\right]=K_{\mathrm{Eq}}\cdot {\left[{\mathrm{NO}}_{\mathrm{2}}\right]}^{\mathrm{2}}+\left[{\mathrm{NO}}_{\mathrm{2}}\right],\end{array}\end{array}$$

and solved for [NO₂],

$$\begin{array}{}\text{(13)}& {\left[{\mathrm{NO}}_{\mathrm{2}}\right]}^{\mathrm{2}}+{\displaystyle \frac{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}{K_{\mathrm{Eq}}}}-{\displaystyle \frac{\left[{\mathrm{NO}}_Z\right]}{K_{\mathrm{Eq}}}}=\mathrm{0},\end{array}$$

with the only positive solution:

$$\begin{array}{}\text{(14)}& {\left[{\mathrm{NO}}_{\mathrm{2}}\right]}_{\mathrm{1}}=-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}{K}_{\mathrm{Eq}}}}+\sqrt{{\displaystyle \frac{\mathrm{1}}{\mathrm{4}{K}_{\mathrm{Eq}}^{\mathrm{2}}}}+{\displaystyle \frac{\left[{\mathrm{NO}}_Z\right]}{K_{\mathrm{Eq}}}}},\end{array}$$

or

$$\begin{array}{}\text{(15)}& {\left[{\mathrm{NO}}_{\mathrm{2}}\right]}_{\mathrm{1}}={\displaystyle \frac{\mathrm{1}}{K_{\mathrm{Eq}}}}\left(-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}+\sqrt{{\displaystyle \frac{\mathrm{1}}{\mathrm{4}}}+\left[{\mathrm{NO}}_Z\right]\cdot K_{\mathrm{Eq}}}\right).\end{array}$$

The relationship between NO₂ and [NO₂]∕[NO_Z] in the cell as a function of total $\left[{\mathrm{NO}}_Z\right]=\left[{\mathrm{NO}}_{\mathrm{2}}\right]+\left[{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{4}}\right]$ is shown in Fig. 2.

For example, $\left[M\right]=\mathrm{2.4}\times {\mathrm{10}}^{\mathrm{19}}$ (1000 hPa or ca. 1 atm of total pressure, at 298 K), resulting in $[{\mathrm{NO}}_{\mathrm{2}}{]}_{\mathrm{1}}\approx \mathrm{8.29}\times {\mathrm{10}}^{\mathrm{18}}$ molec. cm⁻³ and $[{\mathrm{NO}}_{\mathrm{2}}{]}_{\mathrm{1}}/[{\mathrm{NO}}_Z]\approx \mathrm{0.344}$. Thus, filling a cell from an NO₂ reservoir (e.g. an NO₂ tank) to 1 atm of total pressure will lead to only 34 % of this pressure being present as NO₂ (see also Fig. 2).

At 100, 10, and 1 hPa (ca. 0.1, 0.01, and 0.001 atm) of NO₂+N₂O₄, the corresponding figures for [NO₂]₁∕[NO_Z] would be 0.717, 0.95, and 0.995, respectively. These figures are independent of an additional topping with air or oxygen to a full atmosphere of total pressure, as is described below. In other words, unless the NO₂ partial pressure is below around 10 Pa, the actual NO₂ partial pressure (and thus the concentration of NO₂) will be below expected levels by two-digit percentages.

A further problem associated with the NO₂–N₂O₄ equilibrium is the marked temperature dependence of the equilibrium constant. In the usual Arrhenius expression, it is given as

$$\begin{array}{}\text{(16)}& K_{\mathrm{Eq}}\left(T\right)=A\cdot e^{\frac{B}{T}},\end{array}$$

with $A=\mathrm{1.07}\times {\mathrm{10}}^{-\mathrm{28}}$ cm⁻³ molec.⁻¹ and B=6400 K (see Table 1). The (relative) temperature dependence of K_Eq is given by

$$\begin{array}{}\text{(17)}& \begin{array}{rl}{\displaystyle \frac{\mathrm{1}}{K_{\mathrm{Eq}}\left(T\right)}}& {\displaystyle \frac{d}{\mathrm{d}T}}\left(K_{\mathrm{Eq}}\left(T\right)\right)={\displaystyle \frac{\mathrm{1}}{K_{\mathrm{Eq}}\left(T\right)}}A\cdot e^{\frac{B}{T}}{\displaystyle \frac{d}{\mathrm{d}T}}\left({\displaystyle \frac{B}{T}}\right)\\ & ={\displaystyle \frac{\mathrm{1}}{K_{\mathrm{Eq}}\left(T\right)}}\cdot -{\displaystyle \frac{AB}{T^{\mathrm{2}}}}\cdot e^{\frac{B}{T}}=-{\displaystyle \frac{B}{T^{\mathrm{2}}}},\end{array}\end{array}$$

and with the above values for A and B, we obtain, for the relative change in the equilibrium constant,

$$\begin{array}{}\text{(18)}& {\displaystyle \frac{\mathrm{1}}{K_{\mathrm{Eq}}\left(T\right)}}{\displaystyle \frac{d}{\mathrm{d}T}}\left(K_{\mathrm{Eq}}\left(T\right)\right)=-{\displaystyle \frac{B}{T^{\mathrm{2}}}}\approx -\mathrm{0.072}{\displaystyle \frac{\mathrm{1}}{K}}.\end{array}$$

In other words the equilibrium constant is reduced by more than 7 % K⁻¹ of heating. Fortunately the effect on NO₂ is somewhat smaller, ranging from nearly zero change at very small NO₂ levels to about a 3 % increase per degree of heating at 1000 hPa (see Appendix B).

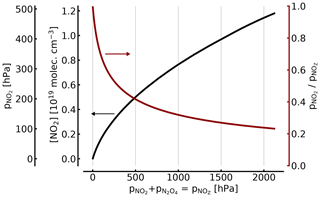
Figure 2 NO₂ concentration (black line in units of 10¹⁹ molec. cm⁻³ and hPa; left axes) and fraction of NO₂ (red line; right axis) of the total $\left[{\mathrm{NO}}_Z\right]=\left[{\mathrm{NO}}_{\mathrm{2}}\right]+\left[{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{4}}\right]$ as a function of [NO_Z] (given in pressure units for 25 ^∘C). At atmospheric pressure (1000 hPa) in the cell, only about 34 % of the total NO_Z (or ≈344 hPa partial pressure) exists as NO₂.

3.3 NO₂+O₂ chemistry

The addition of O₂ (or air) to the NO₂ filling can greatly help with stabilizing the NO₂ concentration in a cell under certain conditions.

In the presence of molecular oxygen, following the photolysis of NO₂, ozone is formed in the cell:

$$\begin{array}{}\text{(R9)}& \begin{array}{rl}& \mathrm{O}+{\mathrm{O}}_{\mathrm{2}}+M\to {\mathrm{O}}_{\mathrm{3}}+M,\\ & k_{\mathrm{9}}(\mathrm{298}\mathrm{K},{\mathrm{10}}^{\mathrm{5}}\mathrm{Pa})\approx \mathrm{1.46}\times {\mathrm{10}}^{-\mathrm{14}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

This in turn can react with NO to form NO₂:

$$\begin{array}{}\text{(R10)}& \begin{array}{rl}& {\mathrm{O}}_{\mathrm{3}}+\mathrm{NO}\to {\mathrm{NO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}},\\ & k_{\mathrm{10}}\left(\mathrm{298}\mathrm{K}\right)\approx \mathrm{1.9}\times {\mathrm{10}}^{-\mathrm{14}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

The reaction scheme encompassing the reaction pathways discussed above is sketched in Fig. 3.

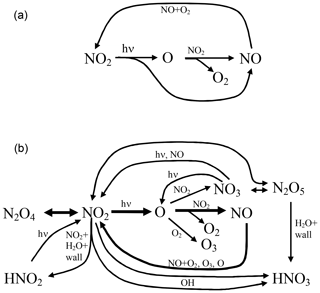
Figure 3 Scheme of the chemical reactions in an illuminated NO₂ cell; (a) only basic reactions and (b) complete system excluding the formation of OH.

Here we can distinguish two regimes. The first regime assumes comparable concentrations of O₂ and NO₂, i.e. [O₂]∕[NO₂] around unity. In this case the termolecular oxidation of NO by O₂ dominates. This is similar to the situation discussed in Sect. 3.1; however we can take the O₂ concentration [O₂] to be essentially constant. This reduces the third-order kinetics of Eq. (7) to pseudo-second-order or second-order kinetics, and we obtain

$$\begin{array}{}\text{(19)}& \begin{array}{rl}& \left[\mathrm{NO}\right]=\sqrt{{\displaystyle \frac{P_{\mathrm{NO}}}{\mathrm{2}\left[{\mathrm{O}}_{\mathrm{2}}\right]k_{\mathrm{NO}}}}}\underset{P_{\mathrm{NO}}\text{substituted}}{\underbrace{\approx }}\sqrt{{\displaystyle \frac{\left[{\mathrm{NO}}_{\mathrm{2}}\right]\cdot J}{\left[{\mathrm{O}}_{\mathrm{2}}\right]k_{\mathrm{NO}}}}}\\ & {\displaystyle \frac{\left[\mathrm{NO}\right]}{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}}\approx \sqrt{{\displaystyle \frac{J}{\left[{\mathrm{O}}_{\mathrm{2}}\right]\left[{\mathrm{NO}}_{\mathrm{2}}\right]k_{\mathrm{NO}}}}}.\end{array}\end{array}$$

For example we may assume 0.5 atm (500 hPa) each of pure NO₂ and O₂ (initially); i.e. the initial concentrations of either species in the cell will be $[{\mathrm{O}}_{\mathrm{2}}{]}_{\mathrm{0}}=[{\mathrm{NO}}_{\mathrm{2}}{]}_{\mathrm{0}}\approx \mathrm{1.2}\times {\mathrm{10}}^{\mathrm{19}}{\mathrm{cm}}^{-\mathrm{3}}$. In sunlight we have NO₂ photolysis (Reaction R1) followed by O+NO₂ (Reaction R4) plus oxidation of NO by O₂;

$$D\left(\mathrm{NO}\right)\approx \mathrm{2}{\left[\mathrm{NO}\right]}^{\mathrm{2}}\cdot \left[{\mathrm{O}}_{\mathrm{2}}\right]k_{\mathrm{NO}}=P\left(\mathrm{NO}\right).$$

From this stationary-state assumption we can calculate [NO]_s:

$${\left[\mathrm{NO}\right]}_S\approx \sqrt{{\displaystyle \frac{P_{\mathrm{NO}}}{\mathrm{2}\left[{\mathrm{O}}_{\mathrm{2}}\right]k_{NO}}}}\approx \mathrm{0.054}\cdot \left[{\mathrm{NO}}_{\mathrm{2}}\right].$$

Thus, the NO₂ concentration would be reduced by only 5.4 % from its initial value once the cell is exposed to sunlight.

The second regime assumes a high [O₂]∕[NO₂] ratio (for instance larger than 10⁴) so that the reaction of O atoms formed in NO₂ photolysis is much more likely to react with O₂ than with NO₂. In this case for each molecule of NO₂ photolysed nearly one molecule of O₃ is formed, which will react with the NO molecule produced in the NO₂ photolysis. The O₃ concentration will rise until its reaction with NO balances the rate of NO₂ photolysis:

$$\begin{array}{}\text{(20)}& \left[\mathrm{NO}\right]\left[{\mathrm{O}}_{\mathrm{3}}\right]k_{\mathrm{10}}=\left[{\mathrm{NO}}_{\mathrm{2}}\right]\cdot J_{\mathrm{1}}.\end{array}$$

Since [NO]≈[O₃] we obtain

$$\begin{array}{}\text{(21)}& {\left[\mathrm{NO}\right]}^{\mathrm{2}}{k}_{\mathrm{10}}\approx \left[{\mathrm{NO}}_{\mathrm{2}}\right]\cdot J\Rightarrow \left[\mathrm{NO}\right]\approx \sqrt{{\displaystyle \frac{\left[{\mathrm{NO}}_{\mathrm{2}}\right]\cdot J}{k_{\mathrm{10}}}}}.\end{array}$$

For instance at $\left[{\mathrm{NO}}_{\mathrm{2}}\right]=\mathrm{2.4}\times {\mathrm{10}}^{\mathrm{15}}$ cm⁻³ and about 1 atm (1000 hPa) of O₂, the stationary-state NO level would be $\left[\mathrm{NO}\right]\approx \mathrm{4.4}\times {\mathrm{10}}^{\mathrm{13}}$ cm⁻³, or about 1.8 % of the initial NO₂ concentration. Note that a small fraction (about 10⁻⁴ in this example) of the O atoms produced in the NO₂ photolysis would still react with NO₂ and form NO without a corresponding O₃ production (rate about 2×10⁹ cm⁻³ s⁻¹); thus the NO fraction in the cell would slowly grow until Reaction (R6) balances this process. At the above NO level the rate of NO₂ formation would be around 10⁹ cm⁻³ s⁻¹; thus the NO level would slightly grow (by about 50 %) during several days of continuous illumination of the cell.

3.4 The (initial) NO₂-only chemistry – some complications

In addition to the three reactions described above, O atoms can recombine with NO₂ to form nitrate radicals, NO₃:

$$\begin{array}{}\text{(R11)}& \begin{array}{rl}& \mathrm{O}+{\mathrm{NO}}_{\mathrm{2}}+M\to {\mathrm{NO}}_{\mathrm{3}}+M,\\ & k_{\mathrm{11}}(\mathrm{298}\mathrm{K},{\mathrm{10}}^{\mathrm{5}}\mathrm{Pa})\approx \mathrm{2.5}\times {\mathrm{10}}^{-\mathrm{11}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

The NO₃ radicals formed in Reaction (R11) can be photolysed:

$$\begin{array}{}\text{(R12a)}& {\displaystyle }& {\displaystyle }{\mathrm{NO}}_{\mathrm{3}}+h\mathit{\nu }\to {\mathrm{NO}}_{\mathrm{2}}+\mathrm{O},J_{\mathrm{12}\mathrm{a}}\approx \mathrm{0.19}{\mathrm{s}}^{-\mathrm{1}},\text{(R12b)}& {\displaystyle }& {\displaystyle }{\mathrm{NO}}_{\mathrm{3}}+h\mathit{\nu }\to \mathrm{NO}+{\mathrm{O}}_{\mathrm{2}},J_{\mathrm{12}\mathrm{b}}\approx \mathrm{0.016}{\mathrm{s}}^{-\mathrm{1}}.\end{array}$$

The threshold wavelength is much longer than in the case of NO₂ (J₁), and the photolysis is much faster. Alternatively, NO₃ may react with NO (from Reaction R1) to re-form NO₂,

$$\begin{array}{}\text{(R13)}& \begin{array}{rl}& {\mathrm{NO}}_{\mathrm{3}}+\mathrm{NO}\to \mathrm{2}{\mathrm{NO}}_{\mathrm{2}},\\ & k_{\mathrm{13}}\left(\mathrm{298}\mathrm{K}\right)\approx \mathrm{2.6}\times {\mathrm{10}}^{-\mathrm{11}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}},\end{array}\end{array}$$

or undergo self-reaction,

$$\begin{array}{}\text{(R14)}& \begin{array}{rl}& {\mathrm{NO}}_{\mathrm{3}}+{\mathrm{NO}}_{\mathrm{3}}\to \mathrm{2}{\mathrm{NO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}},\\ & k_{\mathrm{14}}\left(\mathrm{298}\mathrm{K}\right)\approx \mathrm{2.3}\times {\mathrm{10}}^{-\mathrm{16}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

Finally, and typically most likely, NO₃ will react with NO₂ to form dinitrogen pentoxide, N₂O₅:

$$\begin{array}{}\text{(R15)}& \begin{array}{rl}& {\mathrm{NO}}_{\mathrm{3}}+{\mathrm{NO}}_{\mathrm{2}}+M\to {\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{5}}+M,\\ & k_{\mathrm{15}}(\mathrm{298}\mathrm{K},{\mathrm{10}}^{\mathrm{5}}\mathrm{Pa})\approx \mathrm{1.34}\times {\mathrm{10}}^{-\mathrm{12}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

Dinitrogen pentoxide is thermally unstable and decays:

$$\begin{array}{}\text{(R16)}& \begin{array}{rl}{\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{5}}& +M\to {\mathrm{NO}}_{\mathrm{3}}+{\mathrm{NO}}_{\mathrm{2}}+M,\\ & k_{\mathrm{16}}(\mathrm{298}\mathrm{K},{\mathrm{10}}^{\mathrm{5}}\mathrm{Pa})\approx \mathrm{0.07}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

In the absence of water (dry system) N₂O₅ will just be another reservoir potentially sequestering some of the NO₂. On the other hand, N₂O₅ is the anhydride of nitric acid and may react with water to form HNO₃. While the reaction of N₂O₅ plus water vapour appears to be exceedingly slow in the gas phase, it may react with a layer at the cell surface; details are given in Sect. 3.5.

Analysing the above system of reactions, one notices that loss of O atoms other than by Reactions (R4) or (R11) are of minor importance. This is underlined by the results of the model calculations using the full chemical system (see Table 1) presented in Sect. 4.

Therefore, we can summarize that each photolysis Reaction (R1) is followed by a conversion of NO₂ to NO (Reaction R4) or to NO₃ (Reaction R11). However, NO₃ is largely converted back to NO₂ by Reactions (R12a), (R13), and (to a minor extent) (R14); thus, in effect each photolysis act of NO₂ leads to the loss of approximately two NO₂ molecules. Essentially NO₂ would be converted to NO+O₂. In bright sunshine with $J_{\mathrm{1}}\approx \mathrm{8}\times {\mathrm{10}}^{-\mathrm{3}}$ s⁻¹, this would lead to an NO₂ lifetime in the cell of $\mathit{\tau }\left({\mathrm{NO}}_{\mathrm{2}}\right)\approx \mathrm{1}/(\mathrm{2}\cdot J_{\mathrm{1}})\approx \mathrm{63}$ s, or roughly 1 min. Even if the cell is kept in the shade or is only exposed to indoor illumination where J₁ could be estimated to be 10 times (shade) to 100 times (indoor) smaller than in bright sunshine the conversion could be expected to proceed within around 10 min (shade) to 100 min (indoor) or even faster.

3.5 ${\mathrm{NO}}_{\mathrm{2}}+{\mathrm{O}}_{\mathrm{2}}+$ (trace) H₂O chemistry

Since water is by far the most abundant (typical mixing ratios around 1 %) reactive trace gas in the ambient atmosphere (not counting nobel gases, CO₂, H₂, or N₂O), it may be possible that if traces of water enter the cell when it is filled, then a series of additional reactions may play a role (see e.g. Bahe et al., 1979):

$$\begin{array}{}\text{(R17)}& {\mathrm{O}}_{\mathrm{3}}+h\mathit{\nu }\to \mathrm{O}{(}^{\mathrm{1}}\mathrm{D})+{\mathrm{O}}_{\mathrm{2}},J_{\mathrm{17}}\approx \mathrm{3}\times {\mathrm{10}}^{-\mathrm{5}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}$$

Followed by quenching of O(¹D) to O(³P) or the formation of hydroxyl (OH) radicals,

$$\begin{array}{}\text{(R18)}& \begin{array}{rl}& \mathrm{O}{(}^{\mathrm{1}}\mathrm{D})+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\to \mathrm{2}\mathrm{OH},\\ & k_{\mathrm{18}}\left(\mathrm{298}\mathrm{K}\right)\approx \mathrm{2.0}\times {\mathrm{10}}^{-\mathrm{10}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

In an NO₂ cell, OH radicals are most likely to react with NO₂ (or NO) to form nitric acid (or nitrous acid; see below):

$$\begin{array}{}\text{(R19)}& \begin{array}{rl}& \mathrm{OH}+{\mathrm{NO}}_{\mathrm{2}}+M\to {\mathrm{HNO}}_{\mathrm{3}}+M,\\ & k_{\mathrm{19}}(\mathrm{298}\mathrm{K},{\mathrm{10}}^{\mathrm{5}}\mathrm{Pa})\approx \mathrm{1.05}\times {\mathrm{10}}^{-\mathrm{11}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

Nitric acid is photolysed very slowly, and also its reaction with OH (to form NO₃) is slow; thus it will constitute a final sink of NO₂ (and water) in the cell. Alternatively, OH may react with NO to form nitrous acid:

$$\begin{array}{}\text{(R20)}& \begin{array}{rl}& \mathrm{OH}+\mathrm{NO}+M\to {\mathrm{HNO}}_{\mathrm{2}}+M,\\ & k_{\mathrm{20}}(\mathrm{298}\mathrm{K},{\mathrm{10}}^{\mathrm{5}}\mathrm{Pa})\approx \mathrm{9.7}\times {\mathrm{10}}^{-\mathrm{12}}{\mathrm{cm}}^{\mathrm{3}}{\mathrm{molec}.}^{-\mathrm{1}}{\mathrm{s}}^{-\mathrm{1}},\end{array}\end{array}$$

which – in turn – is lost by photolysis,

$$\begin{array}{}\text{(R21)}& \begin{array}{rl}& {\mathrm{HNO}}_{\mathrm{2}}+h\mathit{\nu }\to \mathrm{OH}+\mathrm{NO},\\ & J_{\mathrm{21}}\left(\mathrm{298}\mathrm{K}\right)\approx \mathrm{1.34}\times {\mathrm{10}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}.\end{array}\end{array}$$

In addition, N₂O₅, formed in Reaction (R15), can react with (liquid) water adsorbed at the wall of the cell, also forming HNO₃:

$$\begin{array}{}\text{(R22)}& {\mathrm{N}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{5}}+{\left({\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}_{\mathrm{liq}}\to \mathrm{2}{\left({\mathrm{HNO}}_{\mathrm{3}}\right)}_{\mathrm{liq}}.\end{array}$$

Finally NO₂ is also known to heterogeneously react with water:

$$\begin{array}{}\text{(R23)}& {\mathrm{NO}}_{\mathrm{2}}+{\mathrm{NO}}_{\mathrm{2}}+{\left({\mathrm{H}}_{\mathrm{2}}\mathrm{O}\right)}_{\mathrm{liq}}\to {\mathrm{HNO}}_{\mathrm{2}}+{\left({\mathrm{HNO}}_{\mathrm{3}}\right)}_{\mathrm{liq}}.\end{array}$$

Although this reaction appears to be second order in NO₂, several studies (e.g. by Kleffmann et al., 1998) found a first-order dependence of HONO formation on the NO₂ concentration probably because the NO₂ reaction with NO₂ adsorbed at the wall is rate limiting. Therefore, heterogeneous reactions of N₂O₄ with water are probably not important. HNO₂ will photolyse relatively quickly to form OH + NO (with OH in most cases reacting according to Reaction R19); and HNO₃ from the above two reactions will remain. Our model calculations actually show that all H₂O is ultimately (typically after a few hours in full sunshine) converted to HNO₃, sequestering equivalent amounts of NO₂ and water; thus no HONO will remain after this time.

For example a cell having been filled with a very small amount of NO₂ (e.g. 10 hPa or 2.4×10¹⁷ molec. cm⁻³) is topped with ambient (e.g. laboratory) air (which is of course not recommended; see Sect. 5.2) at 25 ^∘C and 70 % relative humidity. Thus the approximate amount of water admitted is 70 % of the saturation vapour pressure of H₂O at that temperature (70 % of 31.6 hPa = 22.1 hPa or 5.3×10¹⁷ molec cm⁻³). Some of this water will form a film at the inside of the cell and allow heterogeneous Reactions (R22) and (R23), converting NO₂ into HNO₃, although it is hard to judge how fast this process will proceed. In addition, upon illumination with UV-radiation Reactions (R9), (R17), (R18), and (R19) will provide (relatively slow) gas-phase conversion of NO₂ to HNO₃. Since the amount of H₂O in this example exceeds the amount of NO₂ it is likely that ultimately all NO₂ is converted to HNO₃, as can be seen in Figs. 4 to 8.

Table 1 Summary of reaction rate constants.

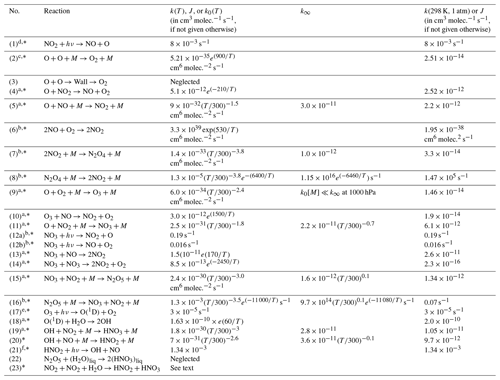
^a Data from Burkholder et al. (2015) JPL Publication No. 15–10. ^b Data from Atkinson et al. (2004). ^c Data from Tsang and Hampson (1986). ^d Data from Trebs et al. (2009). ^e Data from Bahe and Schurath (1978). ^f Data from Alicke et al. (2002). The reactions marked with ^* are included in the kinetic model; see Sect. 4.

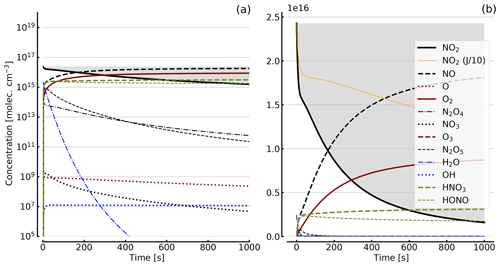
Figure 4 Results of calculations with the full model (reactions marked with ^* in Table 1). Shown are the temporal evolutions of [NO₂], [NO₂] with J values scaled to 1∕10, [NO], [O], [O₂], [O₃], [N₂O₄], [NO₃], [N₂O₅], [H₂O], [OH], [HNO₃], and [HONO] in an illuminated NO₂ cell. Initial [NO₂]₀=1 hPa (2.4×10¹⁶ molec. cm⁻³). Zero initial O₂ concentration was assumed; (a) logarithmic scale and (b) linear scale.

4 Gas kinetic simulations

We performed a series of gas-kinetic-simulation calculations in order to illustrate the behaviour of the reaction system described above under various conditions of initial NO₂ and amounts of added O₂. In a one-box model, the system of coupled ordinary differential equations resulting from the above reactions was solved numerically. This allows following the temporal evolution of the concentration of the individual gases in the cell under given conditions. Our full model includes Reactions (R1) to (R23), except (R3) and (R22) of Table 1 (marked with an asterisk in column 1). The heterogeneous Reaction (R23) was included in the simulation, with the parameterization proposed by Kleffmann et al. (1998) $k_{\mathrm{23}}=\mathrm{0.25}\cdot S/V\cdot v\cdot \mathit{\gamma }$, with uptake coefficient $\mathit{\gamma }={\mathrm{10}}^{-\mathrm{6}}$, the molecular velocity of NO₂ v, and the surface-to-volume ratio S∕V). We assumed a typical cell (cylindrical, radius of 1 cm, and length of 5 cm, $S/V=\mathrm{240}$ m⁻¹) as well as estimates of the amount of H₂O in this cell from assuming a monolayer of water at the inner surface of the cuvette. Of course – given the uncertainties in heterogeneous reactions – this approach can only provide a rough estimate of the HONO concentration in the cell.

Also some runs with a subset of the reactions were performed as described in Appendix B in order to check on the simplified analytical calculations in the previous section. Table 2 shows a comparison of the NO₂ reduction after 1000 s given by the analytical calculations and the simplified model.

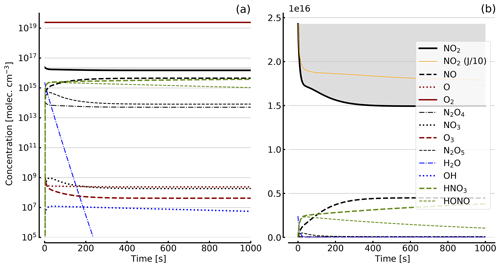
Figure 5 Results of calculations with the full model (reactions marked with ^* in Table 1). Same as Fig. 4, but with initial O₂ assumed; (a) logarithmic scale and (b) linear scale.

Table 2 Comparison of the analytical calculations and the simplified model encompassing Reactions (R1), (R4), and (R6).

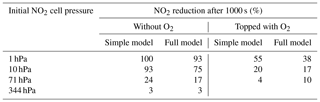
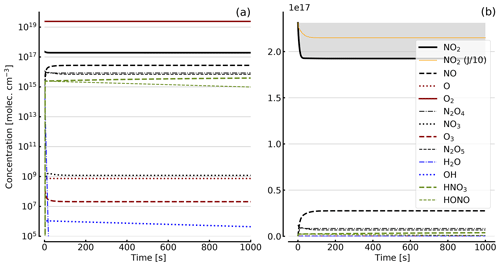
Figure 6 Results of calculations with the full model (reactions marked with ^* in Table 1). Same as Fig. 5, but initial [NO₂]₀=10 hPa (2.4×10¹⁷ molec. cm⁻³) with initial O₂ assumed; (a) logarithmic scale and (b) linear scale.

Further calculations encompass the full range of Reactions (R1) to (R23), except (R3) and (R22) as given in Table 1 (marked with an asterisk), where an analytical solution is not practical or is probably even impossible. Figures 4 to 8 show the results of these model runs for NO₂, NO, O atoms, O₂, N₂O₄, NO₃, O₃, N₂O₅, H₂O, OH, HNO₃, and HONO in an illuminated NO₂ cell for initial, N₂O₄-equilibrated [NO₂]₀ of 1, 10, 71, and 344 hPa (2.4×10¹⁶, 2.4×10¹⁷, 1.7×10¹⁸, and 0.84×10¹⁹ molec. cm⁻³). In Fig. 4 no initial O₂ was assumed, and the remaining figures (Figs. 5 to 8) show time series with initial O₂. The left and right panels have logarithmic and linear concentration scales, respectively. Comparison of the result with the data in Figs. 5 to 8 shows that there are no fundamental differences in the NO₂ time series between the simple model and the full model (see also Table 2).

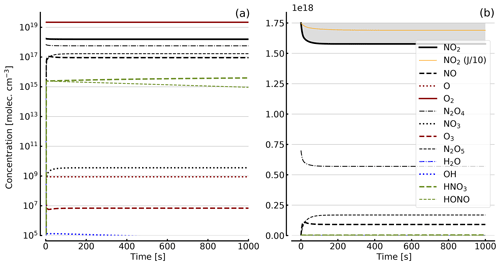
Figure 7 Results of calculations with the full model (reactions marked with ^* in Table 1). Same as Fig. 5, but initial [NO₂]₀=71 hPa (1.7×10¹⁸ molec. cm⁻³) with initial O₂ assumed; (a) logarithmic scale and (b) linear scale.

In order to study the effect of different photolysis frequencies, we also performed model runs with all J values scaled to 1∕10 of the figures given in Table 1. The resulting temporal evolutions of NO₂ are also included in Figs. 4 to 8 (note that the time series of all other species are for the J values as given in Table 1). As can be seen from these figures there is still a rather large loss of NO₂, even with J being only 1∕10 of its value in full sunshine. This is due to the fact that the NO₂ loss scales only with the second or third root of the photolysis frequency (see analytical solutions in Sect. 3 and Appendix A).

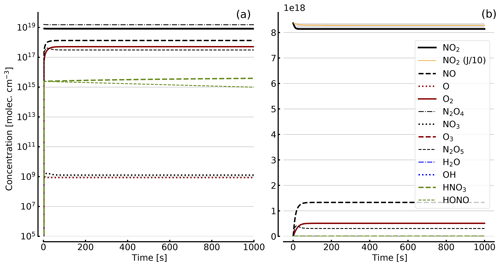
Figure 8 Results of calculations with the full model (reactions marked with ^* in Table 1). Same as Fig. 5, but initial [NO₂]₀=344 hPa (0.84×10¹⁹ molec. cm⁻³) with initial O₂ assumed; (a) logarithmic scale and (b) linear scale.

As discussed in Sect. 3.1 the recovery of NO₂ in the dark after initial illumination (e.g. due to a use of the cell in a measurement) is an important question. Figure 9 shows model calculations of the temporal evolution of NO₂, NO, and O₂ according to the full model (Reactions R1 to R23, except Reactions R3 and R22 – see Table 1; at 298 K). The NO₂ cell is initially illuminated for 1500 s and then left in the dark afterwards for initial, N₂O₄-equilibrated [NO₂]₀ of 1, 10, 71, and 344 hPa (2.4×10¹⁶, 2.4×10¹⁷, 1.7×10¹⁸, and 0.84×10¹⁹ molec. cm⁻³, respectively). At the two highest [NO₂]₀ levels the initial NO₂ was chosen such that total pressures of 100 and 1000 hPa were reached. It can be seen that the NO₂ recovery at low NO₂ levels can take days to hours. Adding O₂ to the cell again has a strong impact on the [NO₂] evolution (see thin blue lines in Fig. 7), reducing the recovery time to a fraction of the NO₂-only case. For larger initial NO₂ concentrations (e.g. 71 hPa) and added O₂, a hysteresis between initial [NO₂] and equilibrium [NO₂] in the dark can be observed; i.e. the NO₂ level does not return to its initial value after illumination. This is due to the formation of N₂O₅ in the illuminated period.

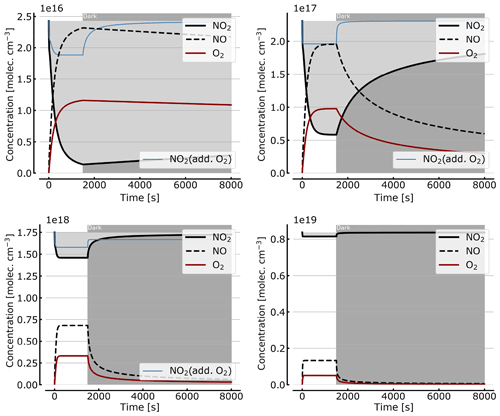
Figure 9 Recovery of NO₂ in the dark after initial illumination. Model calculations of the temporal evolution of [NO₂] (thick solid black line), [NO] (dashed black line), and [O₂] (solid brown line) calculated with the full model (reactions marked with ^* in Table 1). The NO₂ cell is initially illuminated for 1500 s and then left in the dark afterwards. Initial [NO₂]₀ of 1, 10, 71, and 344 hPa (2.4×10¹⁶, 2.4×10¹⁷, 1.7×10¹⁸, and 0.84×10¹⁹ molec. cm⁻³). The blue thin line in the plots for 1, 10, and 71 hPa show [NO₂] for O₂-topped-up cell.

5 Summary and conclusions

We conclude that the use of NO₂ cells requires careful consideration, in particular when quantitative measurements of the NO₂ CD in the cell are desired. If unfortunate parameters are chosen (e.g. rather low NO₂ pressures or no O₂ or air added), practically no NO₂ might be found in the cell at all. Also, one cannot conclude that particularly high or low NO₂ concentrations in the cell are the superior choice. At high NO₂ concentrations (approaching atmospheric pressure) a large fraction of the NO₂ is converted to the dimer N₂O₄, which not only reduces the NO₂ CD way below expected values but also introduces a large temperature dependence (up to 3 % per degree) of the NO₂ CD in the cell (also, there might be some additional uncertainty due to uncertainty of the equilibrium constant, as pointed out by Roscoe and Hind, 1993). On the other hand, at low NO₂ levels (e.g. 1 hPa) photolysis may convert much (if not virtually all) of the NO₂ to NO. Although NO₂ eventually recovers, this process may take long (days) to complete. Thus, the actual NO₂ CD of the cell may become dependent on the illumination and recovery history of the cell and may be rather unpredictable for a particular cell.

Unfortunately, the two described effects are not even the full story; therefore the potential problems are listed below. Fortunately, there are ways to minimize the problems, like oxygen addition to the cell and choosing the right NO₂ concentration, which may help in reducing the uncertainty of the NO₂ CD of a given cell to the single-digit percentage range.

5.1 Summary of problems

As discussed above, the NO₂ concentration in a cell – and thus the NO₂ CD of the cell – can deviate from expectations due to a number of reasons:

1. Optical effects, namely multiple reflection in the cell and tilt of the cell with respect to the optical axis, can enhance the light path and thus the apparent NO₂ CD.

2. Photolysis of NO₂ can reduce the NO₂ CD in the cell.

3. Sequestration of NO₂ as N₂O₄ due to the thermodynamic equilibrium between the two species can reduce NO₂ in the cell and cause temperature dependence of the NO₂ CD.

4. Formation or re-formation of NO₂ from NO in the cell leads to slow recovery of NO₂.

5. Irreversible conversion or conversion of NO₂ to HNO₃ can lead to long-term loss of NO₂.

6. Wall loss of NO_X species like N₂O₄ or N₂O₅ can lead to long-term loss of NO₂

5.2 Some ideas to remedy the situation

One approach for minimizing loss of NO₂ in the cell is certainly to reduce the photolysis of NO₂ (Reaction R1); this can be achieved by a series of measures.

1. Only expose the cell to measurement radiation by, for example, putting it in a nontransparent tube.

2. Minimize exposure time by, for example, putting the cell in a light-tight box when not in use.

3. Use a filter in front of the cell which only admits radiation at wavelengths > 450 nm; this, however, may interfere with the measurements.

Also, it may be good to avoid ozone photolysis in the cell to minimize OH formation by using a UV-nontransparent cell material, e.g. glass instead of quartz. In addition, it is a good idea to keep the gas in the cell as dry as possible to avoid formation of HNO₃ or HNO₂ and to further minimize OH formation. Furthermore, it may be a good idea to illuminate a freshly filled cell initially (for a few hours) to allow all remaining water to be converted to HNO₃, thus (1) minimizing later changes in the NO₂ concentration due to HNO₃ formation and (2) avoiding HONO formation.

A further important measure is to add O₂ to the cell in order to enhance reconversion of any NO formed to NO₂.

The problems associated with excessive N₂O₄ formation in the cell (reduction of the NO₂ CD, temperature dependence of the NO₂ CD, and HNO₃ formation) can be reduced by using lower NO₂ concentrations in the cell. The length of the cell may need to be extended to still achieve a desired NO₂ CD. In principle the cell may also be heated to lower the amount of steady-state N₂O₄.

Problems with the optics of the cell are also difficult to avoid; fortunately they usually lead to changes in the NO₂ CD of < 10 %. In principle wedged cell windows or anti-reflective coatings could be used on the cell windows to minimize the problems described in Sect. 2. Another approach would be to tilt the entire cell with respect to the optical axis; thus reflected radiation would not reach the entrance optics of the spectrometer.

Appendix A: Solution of the cubic equation for the stationary-state NO concentration

The above Eq. (7) is a cubic equation, which we recognize as Cardano's formula after substituting z=[NO]:

$$\begin{array}{}\text{(A1)}& z^{\mathrm{3}}+pz+q=\mathrm{0},\end{array}$$

for which the solution is well known as (Bronstein et al., 2013)

$$\begin{array}{}\text{(A2)}& z=u+v,\end{array}$$

with

$$\begin{array}{}\text{(A3)}& u=\sqrt[\mathrm{3}]{-{\displaystyle \frac{q}{\mathrm{2}}}+\sqrt{\mathrm{\Delta }}},v=\sqrt[\mathrm{3}]{-{\displaystyle \frac{q}{\mathrm{2}}}-\sqrt{\mathrm{\Delta }}},\end{array}$$

and

$$\begin{array}{}\text{(A4)}& \mathrm{\Delta }={\left({\displaystyle \frac{q}{\mathrm{2}}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{p}{\mathrm{3}}}\right)}^{\mathrm{3}}.\end{array}$$

Equation (7) for z=[NO] thus becomes

$$\begin{array}{}\text{(A5)}& {\left[\mathrm{NO}\right]}^{\mathrm{3}}\cdot {\displaystyle \frac{k_{\mathrm{6}}}{\mathrm{2}{J}_{\mathrm{1}}}}+\left[\mathrm{NO}\right]-{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}_{\mathrm{0}}=\mathrm{0}.\end{array}$$

It is transformed with $a=\mathrm{2}{J}_{\mathrm{1}}/k_{\mathrm{6}}\approx \mathrm{4}\times \mathrm{8}\times$ ${\mathrm{10}}^{-\mathrm{3}}/\mathrm{1.95}\times {\mathrm{10}}^{-\mathrm{38}}\approx \mathrm{8.205}\times {\mathrm{10}}^{\mathrm{35}}$ molec.² cm⁻⁶ to

$$\begin{array}{}\text{(A6)}& {\left[\mathrm{NO}\right]}^{\mathrm{3}}+a\left[\mathrm{NO}\right]-a{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}_{\mathrm{0}}=\mathrm{0}.\end{array}$$

Sample solutions include the following.

1. 1000 hPa of initial NO₂, i.e. $[{\mathrm{NO}}_{\mathrm{2}}{]}_{\mathrm{0}}=\mathrm{2.4}\times {\mathrm{10}}^{\mathrm{19}}$, with p=a and $q=-a{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}_{\mathrm{0}}\approx -\mathrm{2.4}\times {\mathrm{10}}^{\mathrm{19}}\cdot \mathrm{8.205}\times {\mathrm{10}}^{\mathrm{35}}\approx -\mathrm{1.969}\times {\mathrm{10}}^{\mathrm{55}}$, and

   $$\begin{array}{}\text{(A7)}& \begin{array}{rl}\mathrm{\Delta }& ={\left({\displaystyle \frac{q}{\mathrm{2}}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{p}{\mathrm{3}}}\right)}^{\mathrm{3}}={\displaystyle \frac{a^{\mathrm{2}}{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}_{\mathrm{0}}^{\mathrm{2}}}{\mathrm{4}}}+{\displaystyle \frac{a^{\mathrm{3}}}{\mathrm{27}}}\\ & \approx \mathrm{9.694}\times {\mathrm{10}}^{\mathrm{109}}+\mathrm{2.046}\times {\mathrm{10}}^{\mathrm{106}}\\ & \approx \mathrm{9.696}\times {\mathrm{10}}^{\mathrm{109}},\end{array}\end{array}$$

   we obtain the only positive and real solution:

   $$\begin{array}{}\text{(A8)}& \begin{array}{rl}\left[\mathrm{NO}\right]& =u+v=\sqrt[\mathrm{3}]{-{\displaystyle \frac{a{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}_{\mathrm{0}}}{\mathrm{2}}}+\sqrt{\mathrm{\Delta }}}\\ & +\sqrt[\mathrm{3}]{-{\displaystyle \frac{a{\left[{\mathrm{NO}}_{\mathrm{2}}\right]}_{\mathrm{0}}}{\mathrm{2}}}-\sqrt{\mathrm{\Delta }}}\\ & \approx \sqrt[\mathrm{3}]{\mathrm{1.969}\times {\mathrm{10}}^{\mathrm{55}}}+\sqrt[\mathrm{3}]{-\mathrm{2}\times {\mathrm{10}}^{\mathrm{51}}}\\ & \approx \mathrm{2.700}\times {\mathrm{10}}^{\mathrm{18}}-\mathrm{1.26}\times {\mathrm{10}}^{\mathrm{17}}\\ & \approx \mathrm{2.574}\times {\mathrm{10}}^{\mathrm{18}}.\end{array}\end{array}$$

   This means that [NO]∕[NO₂]₀ is about $\mathrm{2.574}\times {\mathrm{10}}^{\mathrm{18}}/\mathrm{2.4}\times {\mathrm{10}}^{\mathrm{19}}\approx \mathrm{10.7}$ % of the initial NO₂.

2. At 100 hPa of initial NO₂ ([NO₂]₀= 2.4×10¹⁸), we obtain $\left[\mathrm{NO}\right]/[{\mathrm{NO}}_{\mathrm{2}}{]}_{\mathrm{0}}\approx \mathrm{2.4}\times {\mathrm{10}}^{\mathrm{18}}\approx \mathrm{42.9}$ % of the initial NO₂.

3. At 10 hPa of initial NO₂ ([NO₂]₀= 2.4×10¹⁷), we obtain $\left[\mathrm{NO}\right]/[{\mathrm{NO}}_{\mathrm{2}}{]}_{\mathrm{0}}\approx \mathrm{2.4}\times {\mathrm{10}}^{\mathrm{17}}\approx \mathrm{94.0}$ % of the initial NO₂.

4. At 1 hPa of initial NO₂, ([NO₂]₀= 2.4×10¹⁶), we obtain $\left[\mathrm{NO}\right]/[{\mathrm{NO}}_{\mathrm{2}}{]}_{\mathrm{0}}\approx \mathrm{100}$ % of the initial NO₂.

Appendix B: The simplified model

Reaction kinetic box-model calculations show the temporal evolution of [NO₂], [NO], and [O₂], according to the simple reaction system (Reactions R1, R4, and R6) in an illuminated NO₂ cell. In addition we initially neglect the NO₂ dimer formation. These calculations merely serve to demonstrate that the analytical solution as derived in Sect. 3.1 matches the model calculations.

Figure B1 shows some results of this oversimplified model, assuming (as above) initial NO₂ levels [NO₂]₀ of 1, 10, 100, and 1000 hPa (2.4×10¹⁶, 2.4×10¹⁷, 2.4×10¹⁸, and 2.4×10¹⁹ molec. cm⁻³, respectively). As expected the initial NO₂ concentration drops within the first few seconds (at high initial NO₂) to minutes (at low NO₂) until the back reaction kicks in and leads to stationary-state levels of all species after this initial period. At 1 hPa of initial NO₂ its concentration drops to very small levels (< 0.1 %), as shown in Sect. 3.1, while at 1000 hPa we still see about a 10.7 % loss of initial NO₂. These figures are exactly the same as those found from the steady-state calculations (see Appendix A).

Figure B2 shows some results of the simplified model (Reactions R1, R4, and R6), but including the NO₂–N₂O₄ equilibrium (Reactions R7 and R8) for initial NO₂ levels, [NO₂]₀ of 1, 10, 71, 344 hPa (2.4×10¹⁶, 2.4×10¹⁷, 1.7×10¹⁸, 0.84×10¹⁹ molec. cm⁻³, due to filling the cell with NO₂ levels of 1, 10, 100, and 1000 hPa, respectively, which then immediately undergo N₂O₄ equilibration). For the lower initial NO₂ levels (1 and 10 hPa), there is little difference to Fig. B1. The initial NO₂ concentration drops within the first few seconds to minutes to small fractions of the initial [NO₂]₀. As discussed above (Sect. 3.3), the situation can be improved by adding initial O₂ (topped up to 1000 hPa). The thin blue line in the plots for [NO₂]₀ of 1, 10, and 71 hPa indicates the results for the corresponding NO₂ profiles. In particular at higher initial NO₂ levels (e.g. 71 hPa) the ultimate NO₂ levels are considerably enhanced by O₂ addition. However at higher initial NO₂ levels (see plots for 71 and 344 hPa initial NO₂) there is a large reduction in NO₂ due to the NO₂-dimer formation, inducing stronger temperature dependence.

In order to get a feeling for the influence of temperature changes in the model run for [NO₂]₀=344 hPa the temperature was raised by 5 K (298 to 303 K) after 100 s; the corresponding plot (bottom right in Fig. B2) shows an increase in NO₂ (thin blue line) of about 16 % due to this temperature rise.

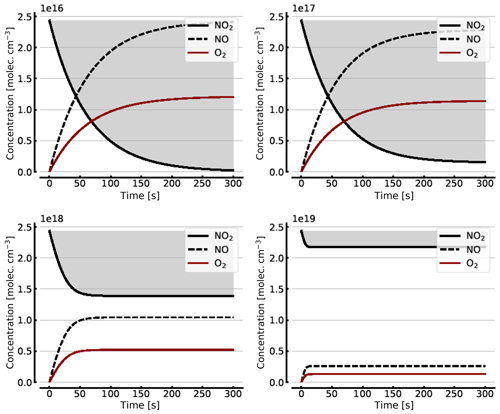
Figure B1 Model calculations of the temporal evolution of [NO₂] (thick solid black line), [NO] (dashed black line), and [O₂] (solid brown line) according to the simple reaction system (Reactions R1, R4, and R6 only, at 298 K) in an illuminated NO₂ cell. Here the NO₂–N₂O₄ chemical equilibrium is neglected, which makes in particular the plots for initial [NO₂]₀=1000 hPa unrealistic. All time series are for calculation with no added initial O₂. Initial [NO₂]₀ of 1, 10, 100, and 1000 hPa (2.4×10¹⁶, 2.4×10¹⁷, 2.4×10¹⁸, and 2.4×10¹⁹ molec. cm⁻³, respectively).

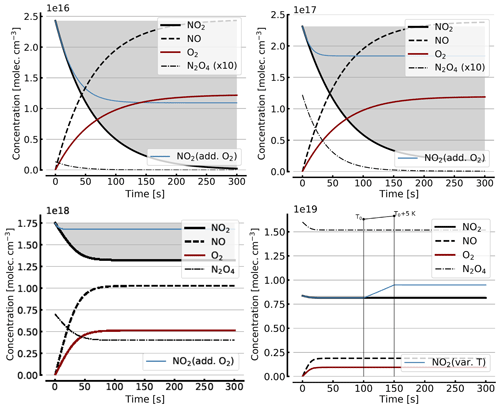
Figure B2 Same model calculations as shown in Fig. B1, but including N₂O₄. Initial [NO₂]₀ of 1, 10, 71, and 344 hPa (2.4×10¹⁶, 2.4×10¹⁷, 1.7×10¹⁸, and 0.8×10¹⁹ molec. cm⁻³, respectively; see text). Temporal evolution of [NO₂] (thick solid black line), [NO] (dashed black line), [O₂] (solid brown line), and [N₂O₄] (thin dashed–dotted line; ×10 in the upper two panels) according to the simple reaction system (Reactions R1, R4, R6, R7, and R8 only, at 298 K) in an illuminated NO₂ cell. All time series with the exception of the thin blue line (in the plots for [NO₂]₀=1, 10, and 71 hPa) are for calculation with no added initial O₂. The thin blue line (in the plots for [NO₂]₀ of 1, 10, and 71 hPa) indicates the evolution of NO₂ for a calculation with initial O₂ topped up to 1000 hPa. The plot for [NO₂]₀=344 hPa additionally shows the increase in NO₂ (thin blue line) at a temperature rise of 5 K (298 to 303 K).