Determining the daytime Earth radiative flux from National Institute of Standards and Technology Advanced Radiometer (NISTAR) measurements

The National Institute of Standards and Technology Advanced Radiometer (NISTAR) onboard the Deep Space Climate Observatory (DSCOVR) provides continuous full-disk global broadband irradiance measurements over most of the sunlit side of the Earth. The three active cavity radiometers measure the total radiant energy from the sunlit side of the Earth in shortwave (SW; 0.2–4 µm), total (0.4–100 µm), and near-infrared (NIR; 0.7–4 µm) channels. The Level 1 NISTAR dataset provides the filtered radiances (the ratio between irradiance and solid angle). To determine the daytime top-of-atmosphere (TOA) shortwave and longwave radiative fluxes, the NISTAR-measured shortwave radiances must be unfiltered first. An unfiltering algorithm was developed for the NISTAR SW and NIR channels using a spectral radiance database calculated for typical Earth scenes. The resulting unfiltered NISTAR radiances are then converted to full-disk daytime SW and LW flux by accounting for the anisotropic characteristics of the Earth-reflected and emitted radiances. The anisotropy factors are determined using scene identifications determined from multiple low-Earth orbit and geostationary satellites as well as the angular distribution models (ADMs) developed using data collected by the Clouds and the Earth's Radiant Energy System (CERES). Global annual daytime mean SW fluxes from NISTAR are about 6 % greater than those from CERES, and both show strong diurnal variations with daily maximum–minimum differences as great as 20 Wm⁻² depending on the conditions of the sunlit portion of the Earth. They are also highly correlated, having correlation coefficients of 0.89, indicating that they both capture the diurnal variation. Global annual daytime mean LW fluxes from NISTAR are 3 % greater than those from CERES, but the correlation between them is only about 0.38.

1 Introduction

The Earth's climate is determined by the amount and distribution of the incoming solar radiation absorbed and the outgoing longwave radiation (OLR) emitted by the Earth. Satellite observations of the Earth radiation budget (ERB) provide critical information needed to better understand the driving mechanisms of climate change; the ERB has been monitored from space since the early satellite missions of the late 1950s and the 1960s (House et al., 1986). Currently, the Clouds and the Earth's Radiant Energy System (CERES) instruments (Wielicki et al., 1996; Loeb et al., 2016) have been providing continuous global top-of-atmosphere (TOA) reflected shortwave radiation and OLR since 2000. CERES data have been crucial to advancing our understanding of the Earth's energy balance (e.g., Trenberth et al., 2009; Kato et al., 2011; Loeb et al., 2012; Stephens et al., 2012), aerosol direct radiative effects (e.g., Satheesh and Ramanathan, 2000; Zhang et al., 2005; Loeb and Manalo-Smith, 2005; Su et al., 2013), and aerosol–cloud interactions (e.g., Loeb and Schuster, 2008; Quaas et al., 2008; Su et al., 2010b), as well as evaluating global general circulation models (e.g., Pincus et al., 2008; Su et al., 2010a; Wang and Su, 2013; Wild et al., 2013).

The Earth's radiative flux data record is augmented by the Deep Space Climate Observatory (DSCOVR) launched on 11 February 2015. DSCOVR is designed to continuously monitor the sunlit side of the Earth, being the first Earth-observing satellite at the Lagrange-1 (L1) point, ∼1.5 million km from Earth, where it orbits the Sun at the same rate as the Earth (see Fig. 1a). DSCOVR is in an elliptical Lissajous orbit around the L1 point and is not positioned exactly on the Earth–Sun line; therefore, only about 92 %–97 % of the sunlit Earth is visible to DSCOVR. As illustrated in Fig. 1b, the daytime portion (A_h) is not visible to DSCOVR. Strictly speaking, the measurements from DSCOVR are not truly “global” daytime measurements. However, for simplicity we refer to them as global daytime measurements. Onboard DSCOVR, the National Institute of Standards and Technology Advanced Radiometer (NISTAR) provides continuous full-disk global broadband irradiance measurements over most of the sunlit side of the Earth (viewing the sunlit side of the Earth as one pixel). Besides NISTAR, DSCOVR also carries the Earth Polychromatic Imaging Camera (EPIC), which provides 2048 by 2048 pixel imagery 10 to 22 times per day in 10 spectral bands from 317 to 780 nm. On 8 June 2015, more than 100 d after launch, DSCOVR started orbiting around the L1 point.

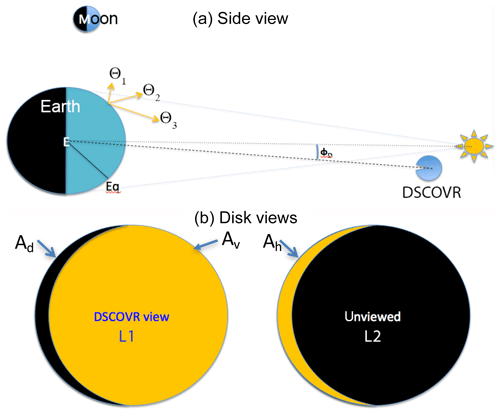
Figure 1 Schematic of the (a) Earth–Sun–DSCOVR geometry and (b) Earth disk visible to the L1 DSCOVR view (left with an area fraction of A_t) and to the L2 view (right). The golden area on the left shows the daytime area fraction (A_v) visible to DSCOVR, the black area on the left shows the night portion (A_d) within the DSCOVR view, and the golden area on the right is the daytime portion (A_h) missed by DSCOVR. Not to scale.

The NISTAR instrument was designed to measure the global daytime shortwave (SW) and longwave (LW) radiative fluxes. The original objective of NISTAR was to monitor the energy from the sunlit side of the Earth continuously and to understand the effects of weather systems and clouds on the daytime energy. However, one limitation of NISTAR is its relatively low signal-to-noise ratios, which necessitates averaging significant time periods to adequately reduce the instrument noise levels. This constrains the temporal resolution of meaningful results to about 4 h, thus preventing us from “continuously” monitoring the sunlit side of the Earth. Nevertheless, NISTAR measurements can still be useful for assessing the hourly fluxes produced by combining the observations from multiple low-Earth orbit and geostationary satellites (Doelling et al., 2013) and for model evaluation using the spectral ratio information (Carlson et al., 2019). NISTAR measures an irradiance at the L1 point at a small relative azimuth angle, ϕ_o, which varies from 4 to 15^∘, as shown in Fig. 1a. As such, the radiation it measures comes from the near-backscatter position, which is different from that seen at other satellite positions, as indicated in Fig. 1a by the varying arrow lengths corresponding to scattering angles, Θ₁−Θ₃. Other types of Earth-orbiting satellites view a given spot on the Earth from various scattering angles that vary as a function of local time (e.g., geostationary) or overpass time (e.g., Sun-synchronous). When averaged over the globe, the uncertainties in the anisotropy corrections are mitigated by compensation. That is, any small biases at particular angles are balanced by observations taken at other angles. In contrast, instruments on DSCOVR view every spot on the Earth from a single scattering angle that varies slowly within a small range over the course of the Lissajous orbit. Thus, the correction for anisotropy is critical. The biases in the anisotropy correction for the DSCOVR scattering angle are mitigated and potentially minimized by the wide range of different scene types viewed in a given NISTAR measurement (Su et al., 2018).

Su et al. (2018) described the methodology to derive the global mean daytime shortwave (SW) anisotropic factors by using the CERES angular distribution models (ADMs) and a cloud property composite based on lower-Earth orbit satellite imager retrievals. These SW anisotropic factors were applied to EPIC broadband SW radiances, which were estimated from EPIC narrowband observations based upon narrowband-to-broadband regressions, to derive the global daytime SW fluxes. Daily mean EPIC and CERES SW fluxes calculated using concurrent hours agree with each other to within 2 %. They concluded that the SW flux agreement is within the calibration and algorithm uncertainties, which indicates that the method developed to calculate the global anisotropic factors from the CERES ADMs is robust and that the CERES ADMs accurately account for the Earth's anisotropy in the near-backscatter direction.

In this paper, the same global daytime mean anisotropic factors developed by Su et al. (2018) are applied to the NISTAR measurements to derive the global daytime mean SW and longwave (LW) fluxes. The NISTAR data and the unfiltering algorithms developed for the NISTAR shortwave and near-infrared channels are detailed in Sect. 2. The data and methodology used to derive the global daytime mean anisotropic factors are presented in Sect. 3. Hourly daytime SW and LW fluxes calculated from NISTAR measurements and comparisons with the CERES synoptic flux products (SYN1deg; Doelling et al., 2013) are detailed in Sect. 4, followed by conclusions and a discussion in Sect. 5.

2 NISTAR observation

The NISTAR instrument measures Earth irradiance data for an entire hemisphere using cavity electrical substitution radiometers (ESRs) and filters covering three channels: shortwave (SW, 0.2–4.0 µm), near-infrared (NIR, 0.7–4.0 µm), and total (0.2–100 µm). Each channel has a dedicated ESR that by itself is sensitive to radiation from 0.2 to 100 µm. For the NIR and SW channels, filters are positioned in front of each ESR to limit the incident radiation to spectral bands. The filters reside in a filter wheel that, during normal operation, configures each ESR to measure contemporaneously in a different band. Additionally, each ESR has a shutter that modulates the Earth signal by cycling between open and closed states continually with a 50 % duty cycle and a period of 4 min. The modulation is necessary as the ESRs only measure changes in the incident optical power and, being thermal detectors, they have large offsets (background signals) that drift over relatively short time frames (hours) but not significantly over a shutter cycle. Demodulating the resulting signal removes those offsets and the associated drifts and/or noise. What remains is a much more stable shutter-modulated background that is measured during periodic views of dark space and subsequently subtracted from the signal. The shutter-modulated background is largest for the total channel and much smaller for the SW and NIR channels.

The NISTAR-calibrated Level 1B data products are derived from prelaunch system-level optical calibration and on-orbit offset measurements. The former involved optical response measurements of each active cavity radiometer without a filter in place using a narrowband calibration source whose irradiance was measured with a NIST-calibrated (National Institute of Standards and Technology) reference detector. Those measurements establish the irradiance responsivity of each spectrally flat broadband radiometer. Additionally, measurements of the transmittance of the SW and NIR filters were made. This was done at NIST prior to installation into the NISTAR filter wheel at wavelengths ranging from 200 nm to approximately 18 µm. Further, system-level filter transmittance measurements at discrete visible and near-infrared wavelengths were made using the external light source and the NISTAR photodiode channel as a detector. The two transmittance measurements agreed to within a few tenths of a percent. Radiometric offsets are measured on-orbit monthly when NISTAR briefly views dark space. The offset measurement uncertainty is determined by the instrument noise level and the relatively short time allotted to the space views.

NISTAR Level 1B radiometric products are derived by first subtracting the offsets from Earth-view measurements and then dividing by the laboratory-measured responsivity. The result is irradiance measured at the instrument aperture. Radiance (I) is then calculated from the irradiance data and the solid angle (Θ) determined from the DSCOVR-to-Earth distance and the Earth dimensions. When averaging over a 4 h period, the NISTAR total and SW channel uncertainties (k=1) are 1.5 % and 2.1 %, respectively. As the LW is derived from the difference between the total and unfiltered SW channels, it contains noise contributions from both. The LW uncertainty is about 3.3 % (8 Wm⁻²) given that the daytime mean LW and SW fluxes are approximately 210 and 240 Wm⁻², respectively, and that the uncertainties between the total and SW channels are largely uncorrelated.

As mentioned before, filters are placed in front of the radiometers to measure the energies from the SW and NIR portions of the spectrum. Since no corrections for the impact of filter transmission were applied to the NISTAR L1B data, the SW and NIR radiances from NISTAR must first be unfiltered before they can be used to derive the daytime Earth radiative flux. Here we follow the algorithm developed by Loeb et al. (2001) to convert measured NISTAR-filtered radiances to unfiltered radiances.

Unfiltered SW and NIR radiances are defined as follows:

$$\begin{array}{}\text{(1)}& I_{\mathrm{u}}^{\mathrm{band}}={\int }_{{\mathit{\lambda }}_{\mathrm{1}}}^{{\mathit{\lambda }}_{\mathrm{2}}}{I}_{\mathit{\lambda }}\mathrm{d}\mathit{\lambda },\end{array}$$

where “band” represents either SW or NIR, λ(µm) is the wavelength, and I_λ (Wm⁻² sr⁻¹ µm⁻¹) is the spectral SW radiance. The filtered radiance is the radiation that passes through the spectral filter and is measured by the detector:

$$\begin{array}{}\text{(2)}& I_f^{\mathrm{band}}={\int }_{{\mathit{\lambda }}_{\mathrm{1}}}^{{\mathit{\lambda }}_{\mathrm{2}}}{S}_{\mathit{\lambda }}^{\mathrm{band}}{I}_{\mathit{\lambda }}\mathrm{d}\mathit{\lambda },\end{array}$$

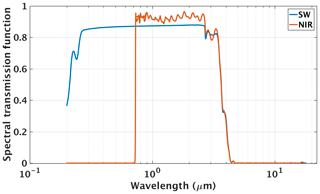
where $S_{\mathit{\lambda }}^{\mathrm{band}}$ is the spectral transmission function. Figure 2 shows the NISTAR SW and NIR spectral transmission functions. These functions are determined from ground testing done in 1999 and 2010 at the National Institute of Standards and Technology (NIST). The spectral radiance database is calculated using a high-spectral-resolution radiative transfer model (Kato et al., 2002). Unfiltered radiances are determined by integrating spectral radiances over the appropriate wavelength intervals using Gaussian quadrature. Similarly, filtered radiances are computed by integrating over the product of spectral radiance and spectral transmission function. The calculations are done for 480 angles: 6 solar zenith angles (0.0, 29.0, 41.4, 60.0, 75.5, 85.0^∘), 8 viewing zenith angles (0, 12, 24, 36, 48, 60, 72, 84^∘), and 10 relative azimuth angles (0 to 180, at every 20^∘).

Table 1 Summary of the cases included in the spectral radiance database. AOD is for aerosol optical depth, and COD is for cloud optical depth.

Figure 2 NISTAR SW and NIR spectral transmission function.

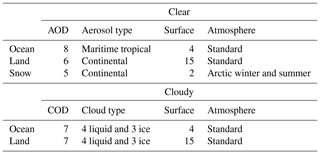
The database includes spectral radiances calculated over ocean, land–desert, and snow–ice surfaces for clear and cloudy conditions. Table 1 summarizes the numbers of each variable that are included in the database; there are a total of 142 clear-sky cases and a total of 931 cloudy-sky cases for each Sun-viewing geometry. This is a much larger database compared with that used by Loeb et al. (2001).

Table 2 Mean ratio and standard deviation (in parenthesis) of filtered radiance to unfiltered radiance for SW and NIR bands over different scene types.

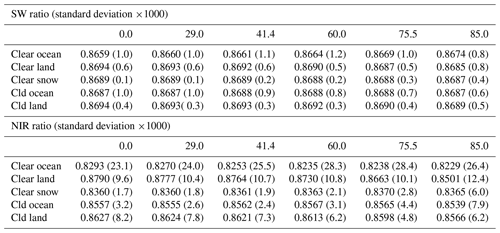
For CERES unfiltering, regression coefficients between filtered and unfiltered radiances were derived as functions of scene type and Sun-viewing geometry (Loeb et al., 2001). Given that NISTAR views the Earth as a single pixel, a mix of scenes and many Sun-viewing geometries are observed at the same time. The method used for CERES is not feasible for unfiltering NISTAR observations. We instead investigated the feasibility of using the ratio, κ, between filtered and unfiltered radiances for unfiltering the NISTAR observations. Table 2 lists the mean and the standard deviations of the ratios at different solar zenith angles. The ratios for the SW band are extremely stable, varying less than 0.3 % among the scenes and Sun-viewing geometries considered (the smallest ratio, 0.8659, occurs for clear ocean under overhead Sun and the largest ratio, 0.8694, occurs for clear or cloudy land under overhead Sun). Furthermore, the ratios are not sensitive to the atmospheric profile and the aerosol type used. For example, using a tropical profile instead of the standard atmosphere, and using the maritime clean instead of maritime tropical aerosol type for clear ocean, only changes the ratios to the fourth decimal point. As the ratio is not sensitive to the scene type and the Sun-viewing geometry, the SW unfiltering for NISTAR can be accomplished by

$$\begin{array}{}\text{(3)}& I_{\mathrm{u}}^{\mathrm{sw}}={\displaystyle \frac{I_f^{\mathrm{sw}}}{{\mathit{\kappa }}^{\mathrm{sw}}}},\end{array}$$

where $I_f^{\mathrm{sw}}$ represents the filtered radiances directly from the NISTAR L1B data. As the NISTAR view always contains clouds, we choose to use the mean ratios of the cloudy ocean and land cases in Table 2, which is 0.8690 for the SW band. The estimated uncertainty of using this single ratio for unfiltering the SW band is less than 0.3 %.

On the other hand, the variability in the ratios of the NIR band can be as large as 6 %. Fortunately, the large variability only occurs between clear ocean and clear land. As mentioned earlier, the NISTAR view always contains clouds, and the mean ratios of the cloudy ocean and land cases, which is 0.8583, is used to unfilter the NISTAR NIR observations. This mean ratio can differ with the individual ratios for different solar zenith angles under cloudy conditions by about 1 %–2 %. The mean ratio of the NIR bands is used to convert the filtered radiances to unfiltered radiances:

$$\begin{array}{}\text{(4)}& I_{\mathrm{u}}^{\mathrm{nir}}={\displaystyle \frac{I_f^{\mathrm{nir}}}{{\mathit{\kappa }}^{\mathrm{nir}}}}.\end{array}$$

In this paper, the measurements from the NISTAR NIR channel are not used. The unfiltering of the NIR channel is reported here for readers who intend to use this channel.

As there is no filter placed in front of the total channel, the radiance from the total channel does not need to be unfiltered. The LW (4–100 µm) radiance can be derived by subtracting the unfiltered SW radiance from the total:

$$\begin{array}{}\text{(5)}& I_{\mathrm{u}}^{\mathrm{lw}}=I^{\mathrm{tot}}-I_{\mathrm{u}}^{\mathrm{sw}}.\end{array}$$

The unfiltered radiances ($I_{\mathrm{u}}^{\mathrm{sw}}$ and $I_{\mathrm{u}}^{\mathrm{lw}}$) will be used hereafter to derive the daytime mean radiative flux. Although NISTAR L1B data provide observations every second, hourly data (smoothed with 4 h running mean) are used to derive fluxes because of the level of noise presented in the measurements (DSCOVR NISTAR data quality report v02).

3 Global daytime shortwave and longwave anisotropic factors

To derive the global daytime mean SW and LW fluxes from the NISTAR unfiltered radiances, the anisotropy of the TOA radiance field must be considered. The CERES Edition 4 empirical ADMs and a cloud property composite based upon lower-Earth orbit satellite retrievals are used here to estimate the global mean shortwave and longwave anisotropic factors.

3.1 CERES ADMs

The Edition 4 CERES ADMs (Su et al., 2015) are constructed using the CERES observations taken during the rotating azimuth plane (RAP) scan mode. In this mode, the instrument scans in elevation as it rotates in azimuth, thus acquiring radiance measurements from a wide range of viewing combinations. The CERES ADMs are derived for various scene types, which are defined using a combination of variables (e.g., surface type, cloud fraction, cloud optical depth, cloud phase, aerosol optical depth, precipitable water, lapse rate, etc). To provide accurate scene-type information within CERES footprints, imager (Moderate Resolution Imaging Spectroradiometer – MODIS – on Terra and Aqua), cloud, and aerosol retrievals (Minnis et al., 2010, 2011) are averaged over CERES footprints by accounting for the CERES point spread function (PSF, Smith, 1994) and are used for scene-type classification. Over a given scene type (χ), the CERES-measured radiances are sorted into discrete angular bins. Averaged radiances ($\widehat{I}$) in all angular bins are calculated, and all radiances in the upwelling directions are integrated to provide the ADM flux ($\widehat{F}$). The ADM anisotropic factors (R) for scene type χ are then calculated as

$$\begin{array}{}\text{(6)}& \begin{array}{rl}R({\mathit{\theta }}_{\mathrm{0}},\mathit{\theta },\mathit{\varphi },\mathit{\chi })& ={\displaystyle \frac{\mathit{\pi }\widehat{I}({\mathit{\theta }}_{\mathrm{0}},\mathit{\theta },\mathit{\varphi },\mathit{\chi })}{{\int }_{\mathrm{0}}^{\mathrm{2}\mathit{\pi }}{\int }_{\mathrm{0}}^{\frac{\mathit{\pi }}{\mathrm{2}}}\widehat{I}({\mathit{\theta }}_{\mathrm{0}},\mathit{\theta },\mathit{\varphi },\mathit{\chi })\cos \mathit{\theta }\sin \mathit{\theta }\mathrm{d}\mathit{\theta }\mathrm{d}\mathit{\varphi }}}\\ & ={\displaystyle \frac{\mathit{\pi }\widehat{I}({\mathit{\theta }}_{\mathrm{0}},\mathit{\theta },\mathit{\varphi },\mathit{\chi })}{\widehat{F}({\mathit{\theta }}_{\mathrm{0}},\mathit{\chi })}},\end{array}\end{array}$$

where θ₀ is the solar zenith angle, θ is the CERES viewing zenith angle, and ϕ is the relative azimuth angle between CERES and the solar plane.

3.2 EPIC composite data

As stated in the section above, the anisotropy of the radiation field at the TOA was constructed for different scene types, which were defined using many variables including cloud properties such as cloud fraction, cloud optical depth, and cloud phase (Loeb et al., 2005; Su et al., 2015). Although the EPIC L2 cloud product includes a threshold-based cloud mask, which identifies the EPIC pixels as high confident clear, low confident clear, high confident cloudy, and low confident cloudy (Yang et al., 2019), the low resolution of EPIC imagery (24×24 km²) and its lack of infrared channels diminish its capability to identify clouds and to accurately retrieve cloud properties. As EPIC lacks the channels that are suitable for cloud size and phase retrievals (Meyer et al., 2016), two cloud optical depths are determined assuming the cloud phase is liquid or ice using a constant cloud effective radius (14 µm for liquid and 30 µm for ice) for cloudy EPIC pixels. These cloud properties are not sufficient to provide the scene-type information necessary for ADM selections. Therefore, more accurate cloud property retrievals are needed to provide anisotropy characterizations to convert radiances to fluxes.

To accomplish this, we take advantage of the cloud property retrievals from multiple imagers on low-Earth orbit (LEO) satellites and geostationary (GEO) satellites. The LEO satellite imagers include MODIS on the Terra and Aqua satellites, the Visible Infrared Imaging Suite (VIIRS) on the Suomi-National Polar-orbiting Partnership satellite, and the Advanced Very High Resolution Radiometer (AVHRR) on the NOAA and MetOps platforms. The GEO imagers are on the Geostationary Operational Environmental Satellites (GOES), the Meteosat series, and Himawari-8 to provide semi-global coverage. All cloud properties were determined using a common set of algorithms, the Satellite ClOud and Radiation Property retrieval System (SatCORPS; Minnis et al., 2008a, 2016), based on the CERES cloud detection and retrieval system (Minnis et al., 2008b, 2010, 2011). Cloud properties from these LEO–GEO imagers are optimally merged together to provide a seamless global composite product at 5 km resolution by using an aggregated rating that considers five parameters (nominal satellite resolution, pixel time relative to the EPIC observation time, viewing zenith angle, distance from day–night terminator, and Sun glint factor to minimize the usage of data taken in the glint region) and selects the best observation at the time nearest the EPIC measurements. About 80 % of the LEO–GEO satellite overpass times are within 40 min of the EPIC measurements, while 96 % are within 2 h of the EPIC measurements. Most of the regions covered by GEO satellites (between around 50^∘ S and 50^∘ N) have a very small time difference, in the range of ±30 min, because of the availability of hourly GEO observations. The polar regions are also covered very well by polar orbiters. Thus, larger time differences generally occur over the 50 to 70^∘ latitude regions. Given the temporal resolution of the currently available GEO–LEO satellites, this is the best collocation possible for those latitudes.

The global composite data are then remapped into the EPIC field of view (FOV) by convolving the high-resolution cloud properties with the EPIC point spread function (PSF) defined with a half-pixel accuracy to produce the EPIC composite. As the PSF is sampled with half-pixel accuracy, the nominal spacing of the PSF grid is about the same size as in the global composite data. Thus, the accuracy of the cloud fraction in the EPIC composite is not degraded compared to the global composite (Khlopenkov et al., 2017). PSF-weighted averages of radiances and cloud properties are computed separately for each cloud phase because the LEO–GEO cloud products are retrieved separately for liquid and ice clouds (Minnis et al., 2008a). Ancillary data (i.e., surface type, snow and ice map, skin temperature, precipitable water, etc.) needed for anisotropic factor selections are also included in the EPIC composite. These composite images are produced for each observation time of the EPIC instrument (typically 300 to 600 composites per month). Detailed descriptions of the method and the input used to generate the global and EPIC composites are provided in Khlopenkov et al. (2017).

Figure 3a shows an image from EPIC taken on 15 May 2017 at 12:17 UTC; the corresponding total cloud fraction (the sum of liquid and ice cloud fractions) from the EPIC composite is shown in Fig. 3b. The liquid and ice cloud fraction, optical depth, and effective height are shown in Fig. 3c–h. For this case, most of the clouds are in the liquid phase. Optically thick liquid clouds with effective heights of 2 to 4 km are observed in the northern Atlantic Ocean and in the Arctic. Ice clouds with effective heights of 8 to 10 km are observed off the west coast of Africa and Europe.

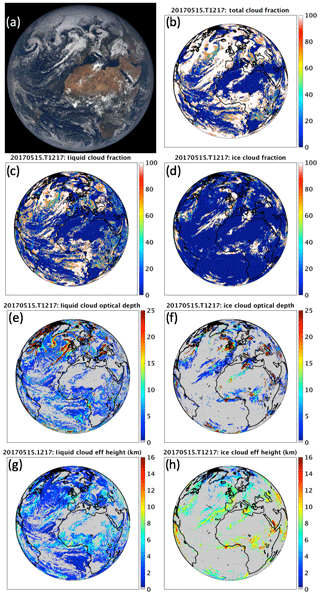
Figure 3 EPIC RGB image for 15 May 2017 at 12:17 UTC (a) and the corresponding total cloud fraction (b; %). Liquid and ice cloud fractions are shown in (c) and (d), liquid and ice cloud optical depths are shown in (e) and (f), and liquid and ice cloud effective height (km) are shown in (g) and (h). Panels (b) to (h) are all derived from the EPIC composite. Figure 3a is taken from: https://epic.gsfc.nasa.gov (last access: 29 January 2020).

3.3 Calculating global daytime anisotropic factors

To determine the global daytime mean anisotropic factors, we use the anisotropies characterized in the CERES ADMs, and they are selected based upon the scene-type information provided by the EPIC composite for every EPIC FOV. For a given EPIC FOV (j), its anisotropic factor is determined based upon the Sun–EPIC viewing geometry and the scene identification information provided by the EPIC composite:

$$\begin{array}{}\text{(7)}& R_j({\mathit{\theta }}_{\mathrm{0}},{\mathit{\theta }}^{\mathrm{e}},{\mathit{\varphi }}^{\mathrm{e}},{\mathit{\chi }}^{\mathrm{e}})={\displaystyle \frac{\mathit{\pi }{\widehat{I}}_j({\mathit{\theta }}_{\mathrm{0}},{\mathit{\theta }}^{\mathrm{e}},{\mathit{\varphi }}^{\mathrm{e}},{\mathit{\chi }}^{\mathrm{e}})}{\widehat{F_j}({\mathit{\theta }}_{\mathrm{0}},{\mathit{\chi }}^{\mathrm{e}})}},\end{array}$$

where θ^e is the EPIC viewing zenith angle, ϕ^e is the relative azimuth angle between EPIC and the solar plane, and χ^e is the scene identification from the EPIC composite. Here ${\widehat{I}}_j$ is the radiance from CERES ADMs and ${\widehat{F}}_j$ is the flux from CERES ADMs (see Eq. 6). To derive the global mean anisotropic factor, we follow the method developed by Su et al. (2018) and calculate the global daytime mean ADM radiance as

$$\begin{array}{}\text{(8)}& \stackrel{\mathrm{‾}}{\widehat{I}}={\displaystyle \frac{{\sum }_{j=\mathrm{1}}^N{\widehat{I}}_j({\mathit{\theta }}_{\mathrm{0}},{\mathit{\theta }}^{\mathrm{e}},{\mathit{\varphi }}^{\mathrm{e}},{\mathit{\chi }}^{\mathrm{e}})}{N}}.\end{array}$$

To calculate the global mean ADM flux, we first grid the ADM flux ($\widehat{F}$) for each EPIC pixel into 1^∘ latitude by 1^∘ longitude bins ($\widehat{F}(\mathrm{lat},\mathrm{lon})$). These gridded ADM fluxes are then weighted by the cosine of latitude to provide the global daytime mean ADM flux:

$$\begin{array}{}\text{(9)}& \stackrel{\mathrm{‾}}{\widehat{F}}={\displaystyle \frac{{\sum }_{j=\mathrm{1}}^M{\widehat{F}}_j(\mathrm{lat},\mathrm{lon})\cos \left({\mathrm{lat}}_j\right)}{\sum \cos \left({\mathrm{lat}}_j\right)}}.\end{array}$$

The global mean anisotropic factor is calculated as

$$\begin{array}{}\text{(10)}& \stackrel{\mathrm{‾}}{R}={\displaystyle \frac{\mathit{\pi }\stackrel{\mathrm{‾}}{\widehat{I}}}{\stackrel{\mathrm{‾}}{\widehat{F}}}}.\end{array}$$

We use $\stackrel{\mathrm{‾}}{R_{\mathrm{sw}}}$ and $\stackrel{\mathrm{‾}}{R_{\mathrm{lw}}}$ to denote the mean SW and LW anisotropic factors. The mean SW anisotropic factor is then used to convert the NISTAR SW unfiltered radiance to flux:

$$\begin{array}{}\text{(11)}& F_{\mathrm{n}}^{\mathrm{sw}}={\displaystyle \frac{\mathit{\pi }{I}_{\mathrm{u}}^{\mathrm{sw}}}{\stackrel{\mathrm{‾}}{R_{\mathrm{sw}}}}}.\end{array}$$

The LW flux is similarly derived from the following:

$$\begin{array}{}\text{(12)}& F_{\mathrm{n}}^{\mathrm{lw}}={\displaystyle \frac{\mathit{\pi }{I}_{\mathrm{u}}^{\mathrm{lw}}}{\stackrel{\mathrm{‾}}{R_{\mathrm{lw}}}}}.\end{array}$$

Figure 4 shows an example of SW and LW anisotropic factors for every EPIC FOV. The SW anisotropic factors are generally smaller over clear than over cloudy oceanic regions. Over land, however, the SW anisotropic factors are larger over clear regions than over cloudy regions because of the hot spot effect, which leads to anisotropic factors greater than 1.6 over clear land regions at large viewing zenith angles. The LW anisotropic factors show much less variability compared to the SW anisotropic factors, with limb darkening being the dominant feature. The mean SW and LW anisotropic factors for this case are 1.275 and 1.041, respectively.

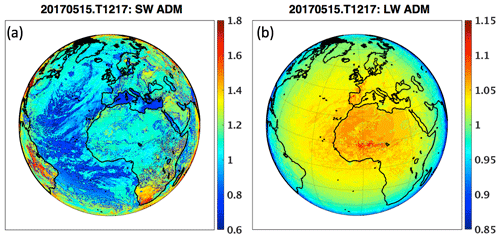
Figure 4 SW anisotropic factors (a) and LW anisotropic factors (b) derived from the CERES ADMs using the EPIC composite for scene identification for 15 May 2017 at 12:17 UTC.

Figure 5 SW flux (blue) and LW flux (red) derived from NISTAR measurements for April (a) and July (b) 2017.

4 NISTAR shortwave and longwave flux

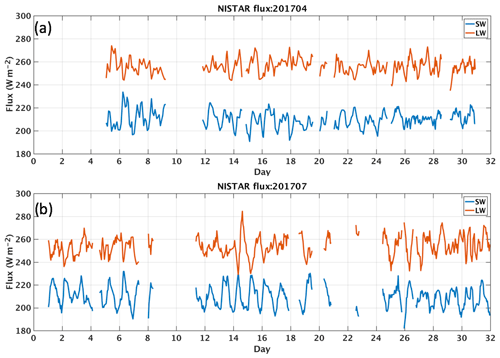
The temporal resolution of the NISTAR Level 1B data is 1 s; however, meaningful changes in the data only occur over many shutter cycles (each shutter cycle is 4 min) due to the demodulation algorithm, which includes a boxcar filter having the width of a shutter period. The filter reduces noise and rejects higher harmonics of the shutter frequency. Following demodulation, significant instrument noise remains. Therefore, further averaging in time over a minimum of 2 h is recommended to further reduce the noise levels (https://eosweb.larc.nasa.gov/project/dscovr/DSCOVR_NISTAR_Data_Quality_Report_V02.pdf, last access: 24 January 2020). In this study, we use hourly radiances averaged from 4 h running means as suggested by the NISTAR instrument team. The hours that are coincident with the EPIC image times are converted to fluxes using the global anisotropic factors calculated using the EPIC composites for scene identification. Figure 5 shows the hourly SW and LW fluxes derived from NISTAR for April (a) and July (b) 2017. For both months, the SW fluxes fluctuate around 210 Wm⁻², with the difference between the daily maximum and minimum as large as 30 Wm⁻². The LW fluxes fluctuate around 260 Wm⁻² and exhibit surprisingly large diurnal variations.

These NISTAR fluxes are compared to the CERES synoptic radiative fluxes and clouds product (SYN1deg; Doelling et al., 2013), which provides hourly cloud properties and fluxes for each 1^∘ latitude by 1^∘ longitude. Within the SYN1deg data product, fluxes between CERES observations are inferred from hourly GEO visible and infrared imager measurements between 60^∘ S and 60^∘ N using observation-based narrowband-to-broadband radiance and radiance-to-flux conversion algorithms. However, the GEO narrowband channels have a greater calibration uncertainty than MODIS and CERES. Several procedures are implemented to ensure consistency between the MODIS-derived and GEO-derived cloud properties and between the CERES fluxes and the GEO-based fluxes. These include calibrating GEO visible radiances against the well-calibrated MODIS 0.65 µm radiances by ray-matching MODIS and GEO radiances; applying similar cloud retrieval algorithms to derive cloud properties from MODIS and GEO observations; and normalizing GEO-based broadband fluxes to CERES fluxes using coincident measurements. Comparisons with broadband fluxes from the Geostationary Earth Radiation Budget (GERB; Harries et al., 2005) indicate that SYN1deg hourly fluxes are able to capture the subtle diurnal flux variations. Comparing with the GERB fluxes, the bias of the SYN SW fluxes is 1.3 Wm⁻², the monthly regional all-sky SW flux root mean square (RMS) error is 3.5 W m⁻², and the daily regional all-sky SW flux RMS error is 7.8 W m⁻² (Doelling et al., 2013). These uncertainties could be overestimated, as the GERB domain has a disproportionate number of strong diurnal cycle regions compared with the globe.

To account for the missing energy from the daytime portion that is not observed by NISTAR (A_h in Fig. 1b) and the energy from the nighttime sliver within the DSCOVR view (A_d in Fig. 1b; only applicable to LW flux), the hourly gridded SYN fluxes are integrated by considering only the grid boxes that are visible to NISTAR to produce the global mean daytime fluxes that are comparable to those from the NISTAR measurements:

$$\begin{array}{}\text{(13)}& \stackrel{\mathrm{‾}}{F_{\mathrm{syn}}}={\displaystyle \frac{\sum F_j\cos \left({\mathrm{lat}}_j\right){\mathit{\omega }}_j}{\sum \cos \left({\mathrm{lat}}_j\right){\mathit{\omega }}_j}}.\end{array}$$

Here, F_j is the gridded hourly CERES SYN fluxes, “lat” is the latitude, and ω indicates whether a grid box is visible to NISTAR (1 when visible, 0 when not visible). Figure 6a shows an example of the gridded SYN SW fluxes at 13:00 UTC on 1 February 2017. SW fluxes for the daytime grid boxes are shown in color, while all nighttime grid boxes are shown in white. Figure 6b shows the daytime areas (in red) and the nighttime areas (in grey) visible to the NISTAR view. Daytime areas of northern high latitudes and North America are not within the NISTAR view and are therefore not included in the comparison with the NISTAR fluxes, and the nighttime slivers in the southern high latitudes of the Indian Ocean and Pacific Ocean are included in the LW flux comparison with NISTAR.

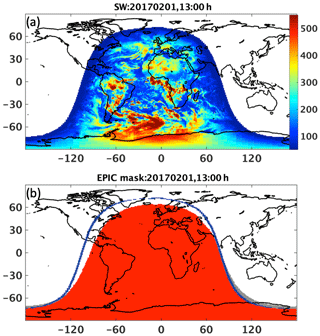
Figure 6 An example of the daytime SW flux distributions from the CERES SYN1deg product at 13:00 UTC on 1 February 2017 (a) and the corresponding daytime areas (in red) and nighttime areas (in grey) that are visible to NISTAR and the terminator boundary (in blue) (b).

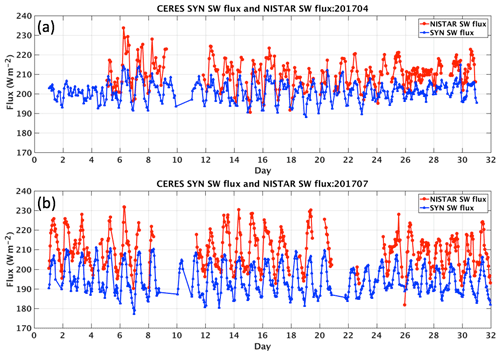
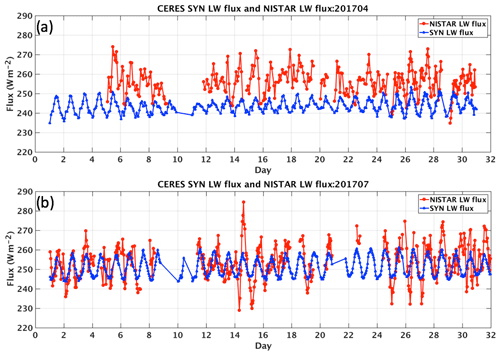
Figure 7 compares the SW fluxes from NISTAR with those from the CERES SYN1deg product integrated for the NISTAR view (Eq. 19) for April (a) and July (b) 2017. The CERES SW fluxes oscillate around 200 and 195 Wm⁻² for April and July, whereas the NISTAR counterparts are about 10 to 20 Wm⁻² greater. The maxima and minima of SW fluxes from NISTAR align well with those from CERES, though the differences between the daily maximum and minimum from NISTAR appear to be larger than those from CERES. The diurnal variations of SW flux derived from EPIC showed a much better agreement with those from CERES (Su et al., 2018). The exact cause for these larger diurnal variations from the NISTAR SW flux is not known. LW flux comparisons are shown in Fig. 8. The daily maximum–minimum LW differences from CERES are typically less than 15 Wm⁻² and exhibit small day-to-day and month-to-month variation. However, the daily maximum–minimum LW differences from NISTAR can vary from 10 to 50 Wm⁻². This larger than expected variability of NISTAR LW fluxes is due to the fact that noise and offset variabilities from both the NISTAR total and SW channel are present in the NISTAR LW radiances. The NISTAR LW fluxes are consistently greater than CERES LW fluxes by about 10 to 20 Wm⁻² in April. The LW fluxes agree better for July, but the NISTAR LW fluxes show larger diurnal variations than the CERES fluxes.

Table 3 SW flux comparisons between NISTAR and CERES SYN1deg for all coincident observations of 2017. F_n is the NISTAR flux (Wm⁻²), F_s is the SYN flux (Wm⁻²), and RMS is the root mean square error between them (Wm⁻²).

Table 4 LW flux comparisons between NISTAR and CERES SYN1deg for all coincident observations of 2017. F_n is the NISTAR flux (Wm⁻²), F_s is the SYN flux (Wm⁻²), and RMS is the root mean square error between them (Wm⁻²).

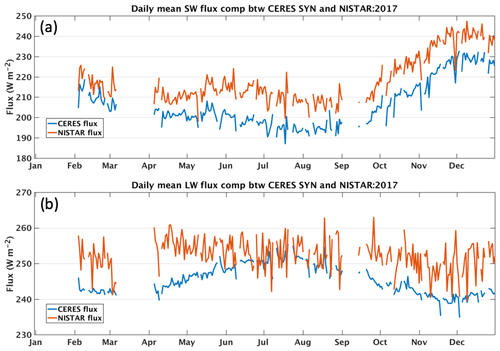
Figure 9 compares the SW and LW fluxes from the CERES SYN1deg product with those from NISTAR at all coincident hours of 2017. The mean SW fluxes are 203.7 and 217.0 Wm⁻², respectively, for CERES and NISTAR, and the RMS error is 14.6 Wm⁻² (Fig. 9a). The mean LW fluxes are 246.0 and 252.8 Wm⁻² for CERES and NISTAR, and the RMS error is 10.5 Wm⁻² (Fig. 9b). Tables 3 and 4 summarize the flux comparisons between NISTAR and CERES for all months of 2017. The NISTAR SW fluxes are consistently greater than those from CERES SYN1deg by about 3.4 % to 7.8 %, and the NISTAR LW fluxes are also greater than those from CERES SYN1deg by 1.0 % to 5.0 %. Furthermore, the SW fluxes from NISTAR are highly correlated (correlation coefficient of about 0.89) with those from CERES SYN1deg, but the correlation for the LW fluxes is rather low (correlation coefficient is about 0.38). Note that when inverting fluxes from hourly mean NISTAR radiances (instead of 4 h running mean radiances), it changed the monthly mean SW and LW fluxes by less than 1.0 and 0.5 Wm⁻², respectively. However, the RMS errors increased for both SW and LW fluxes due to the noise presented in the NISTAR observation.

Figure 7 SW flux (Wm⁻²) comparisons between NISTAR and CERES SYN for April (a) and July (b) 2017.

Figure 8 LW flux (Wm⁻²) comparisons between NISTAR and CERES SYN for April (a) and July (b) 2017.

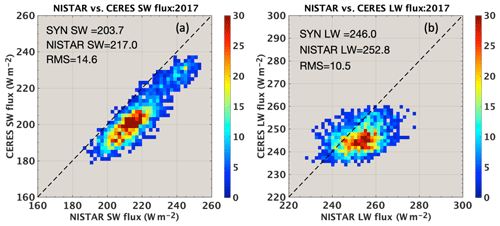
Figure 9 Comparison of coincident hourly SW and LW fluxes from NISTAR and CERES SYN1deg for 2017. The color bar indicates the number of occurrences.

NISTAR fluxes derived at the EPIC image times are averaged into daily means and compared with the daily means from CERES SYN1deg using concurrent hours (Fig. 10). The NISTAR SW fluxes are consistently higher than those from CERES by about 10 to 15 Wm⁻². CERES SW fluxes show a strong annual cycle, which is driven by the incident solar radiation that is affected by the Earth–Sun distance. This annual cycle is also evident in the NISTAR SW fluxes, although the fluxes during the period from April to August are flatter than those from CERES. The NISTAR LW fluxes are greater than those from CERES except during the boreal summer months, with the largest difference of 10 Wm⁻² in February and the smallest difference of a few Watts per meter during the boreal summer months. The CERES LW fluxes show an annual cycle of about 10 Wm⁻², with the largest LW fluxes occurring during the boreal summer when the vast landmasses of the Northern Hemisphere are warmer than during the other seasons. The annual cycle of the NISTAR LW fluxes shows less seasonal variation. From April to October, the NISTAR LW fluxes oscillate around 255 Wm⁻², and they oscillate around 250 Wm⁻² for other months. Additionally, the CERES LW fluxes exhibit much smaller day-to-day variations than their NISTAR counterparts. Note that some of the variations of daily mean fluxes shown in Fig. 10 are due to temporal sampling changes when data transmissions encountered difficulties and/or during spacecraft maneuvers.

Figure 10 Daily mean SW flux (a) and LW flux (b) comparisons between CERES SYN1deg (blue) and NISTAR (red) for 2017.

5 Conclusions and discussion

The SW radiances included in the NISTAR L1B data are filtered radiances, and the effect of the filter transmission must be addressed before these measurements can be used to derive any meaningful fluxes. A comprehensive spectral radiance database has been developed to investigate the relationship between filtered and unfiltered radiances using theoretically derived values simulated for typical Earth scenes and the NISTAR spectral transmission functions. The ratio between filtered and unfiltered SW radiances is very stable, varying less than 0.3 % for the scenes and the Sun-viewing geometries included in the database. The mean ratio of 0.8690 is used to derive the unfiltered SW radiance from the NISTAR L1B filtered SW radiance measurements.

To convert these unfiltered radiances into fluxes, the anisotropy of the radiance field must be taken into account. We use the scene-type-dependent CERES angular distribution models to characterize the global SW and LW anisotropy. These global anisotropies are calculated based upon the anisotropies for each EPIC pixel. To accurately account for the anisotropy for each EPIC pixel, an EPIC composite was developed that includes all information needed for angular distribution model selections. The EPIC composite includes cloud property retrievals from multiple imagers on the LEO and GEO satellites. Cloud properties from these LEO and GEO imagers are optimally merged together to provide a global composite product at 5 km resolution by using an aggregated rating that considers several factors and selects the best observation at the time nearest the EPIC measurements. The global composite data are then remapped into the EPIC FOV by convolving the high-resolution cloud properties with the EPIC PSF to produce the EPIC composite. PSF-weighted averages of radiances and cloud properties are computed separately for each cloud phase, and ancillary data needed for anisotropic factor selections are also included in the EPIC composite.

These global anisotropies are applied to the NISTAR radiances to produce the global daytime SW and LW fluxes, and they are validated against the CERES synoptic 1^∘ latitude by 1^∘ longitude flux product. Only the grid boxes that are visible to the NISTAR view are integrated to produce global mean daytime fluxes that are comparable to the fluxes from the NISTAR measurements. The NISTAR SW fluxes are consistently greater than those from CERES SYN1deg by 10 to 15 Wm⁻² (3.3 % to 7.8 %), but these two SW flux datasets are highly correlated, indicating that the diurnal and seasonal variations of the SW fluxes are fairly similar for both of them. The NISTAR LW fluxes are also greater than those from CERES SYN1deg, but the magnitude of the difference has larger month-to-month variations than that for the SW fluxes. The largest difference of about 14 Wm⁻² (∼5.5 %) occurred in April 2017, and the smallest difference of about ∼4 Wm⁻² (∼1.6 %) occurred during July. Furthermore, the NISTAR LW fluxes have very low correlations with the CERES LW fluxes. NISTAR LW fluxes exhibit a nearly flat annual variation, whereas the CERES LW fluxes exhibit a distinct annual cycle, with the highest LW flux occurring in July when the vast Northern Hemisphere landmasses are warmest. The NISTAR LW fluxes also exhibit unrealistically large day-to-day variations.

The SW flux discrepancy between NISTAR and CERES is caused by (1) CERES instrument calibration uncertainty, (2) CERES flux algorithm uncertainty, (3) NISTAR instrument measurement uncertainty, and (4) NISTAR flux algorithm uncertainty. The CERES SW channel calibration uncertainty is 1 % (1σ; McCarthy et al., 2011; Priestley et al., 2011; Loeb et al., 2018), which corresponds to about 2.1 Wm⁻² for daytime mean SW fluxes. The CERES algorithm uncertainty includes radiance-to-flux conversion error, which is 1.0 Wm⁻² according to Su et al. (2015), and diurnal correction uncertainty, which is estimated to be 1.9 Wm⁻² when Terra and Aqua are combined (Loeb et al., 2018). The NISTAR SW channel measurement uncertainty is 2.1 %, which corresponds to 4.4 Wm⁻². The NISTAR algorithm uncertainty is essentially the radiance-to-flux conversion error. The estimation of this error source is not readily available given the unique NISTAR viewing perspective. However, if we assume that the discrepancy between the EPIC-derived SW flux and CERES SW flux (Su et al., 2018) is also from uncertainty sources (1) and (2) listed above, plus the EPIC calibration, narrowband-to-broadband conversion, and radiance-to-flux conversion for EPIC, then we can deduce that the radiance-to-flux conversion uncertainty for the NISTAR viewing geometry should be less than 2 Wm⁻². Thus, the total difference expected from these uncertainty sources should be $({\mathrm{2.1}}^{\mathrm{2}}+{\mathrm{1.9}}^{\mathrm{2}}+{\mathrm{1.0}}^{\mathrm{2}}+{\mathrm{4.4}}^{\mathrm{2}}+{\mathrm{2.0}}^{\mathrm{2}}{)}^{\mathrm{1}/\mathrm{2}}=\mathrm{5.7}$ Wm⁻².

Similarly, the LW flux discrepancy between NISTAR and CERES is due to the same sources of error. The daytime CERES LW flux uncertainty from calibration is 2.5 Wm⁻² (1σ; Loeb et al., 2009). The CERES LW radiance-to-flux conversion error is about 0.75 Wm⁻² (Su et al., 2015), and diurnal correction uncertainty is estimated to be 2.2 Wm⁻² (Loeb et al., 2018). However, the CERES LW ADMs were developed without taking the relative azimuth angle into consideration, which has little impact on the CERES LW flux accuracy because of its Sun-synchronous orbit. Given that NISTAR only views the Earth from the backscattering angles, the LW flux uncertainty due to radiance-to-flux conversion could be larger for the clear-sky footprints (Minnis et al., 2004). As the clear-sky occurrences are small at the EPIC footprint size level, our best estimate of this uncertainty is no more than 0.4 Wm⁻². The calibration uncertainty for NISTAR LW is deduced from the calibration uncertainties of total and SW channels. The total channel calibration uncertainty is 1.5 %, which is about 6.8 Wm⁻² assuming the total radiative energy of 450 Wm⁻². The SW channel measurement uncertainty is 4.4 Wm⁻². The resulting LW channel measurement uncertainty is thus equal to $({\mathrm{6.8}}^{\mathrm{2}}+{\mathrm{4.4}}^{\mathrm{2}}{)}^{\mathrm{1}/\mathrm{2}}=\mathrm{8.1}$ Wm⁻². Although no direct estimation of the radiance-to-flux conversion uncertainty for LW is available, we do not expect that it exceeds its SW counterpart of 2.0 Wm⁻². Thus, the total difference expected from these uncertainty sources should be $({\mathrm{2.5}}^{\mathrm{2}}+{\mathrm{0.75}}^{\mathrm{2}}+{\mathrm{0.4}}^{\mathrm{2}}+{\mathrm{2.2}}^{\mathrm{2}}+{\mathrm{8.1}}^{\mathrm{2}}+{\mathrm{2.0}}^{\mathrm{2}}{)}^{\mathrm{1}/\mathrm{2}}=\mathrm{9.1}$ Wm⁻².

The uncertainty sources listed above can explain part of the SW flux differences and all of the LW flux differences between CERES and NISTAR. The error sources related to NISTAR are preliminary and are under careful evaluation. Although the LW flux differences between CERES and NISTAR are within the uncertainty estimation, the correlation between NISTAR and CERES is rather low, about 0.38. This is because the NISTAR LW radiance is derived as the difference between total channel radiance and SW channel radiance; thus, the noise and offset variability of both the NISTAR total and SW channels is present in the NISTAR LW fluxes. As a result, more variability is expected in the LW data, which leads to the low correlation. Although the noise level present in the NISTAR measurements prevents the production of a high-frequency SW flux, the current 4 h running mean fluxes are highly correlated with the CERES product. The NISTAR SW flux can be used to test the diurnal variations of SW flux in the high-temporal-resolution model outputs from the Coupled Model Intercomparison Project. Furthermore, the spectral ratio information from NISTAR presents a new way to evaluate the models and opens a new perspective on exoplanet observations (Carlson et al., 2019).