Linking rain into ice microphysics across the melting layer in stratiform rain: a closure study

This study investigates the link between rain and ice microphysics across the melting layer in stratiform rain systems using measurements from vertically pointing multi-frequency Doppler radars. A novel methodology to examine the variability of the precipitation rate and the mass-weighted melted diameter (D_m) across the melting region is proposed and applied to a 6 h long case study, observed during the TRIPEx-pol field campaign at the Jülich Observatory for Cloud Evolution Core Facility and covering a gamut of ice microphysical processes. The methodology is based on an optimal estimation (OE) retrieval of particle size distributions (PSDs) and dynamics (turbulence and vertical motions) from observed multi-frequency radar Doppler spectra applied both above and below the melting layer. First, the retrieval is applied in the rain region; based on a one-to-one conversion of raindrops into snowflakes, the retrieved drop size distributions (DSDs) are propagated upward to provide the mass-flux-preserving PSDs of snow. These ice PSDs are used to simulate radar reflectivities above the melting layer for different snow models and they are evaluated for a consistency with the actual radar measurements. Second, the OE snow retrieval where Doppler spectra are simulated based on different snow models, which consistently compute fall speeds and electromagnetic properties, is performed. The results corresponding to the best-matching models are then used to estimate snow fluxes and D_m, which are directly compared to the corresponding rain quantities. For the case study, the total accumulation of rain (2.30 mm) and the melted equivalent accumulation of snow (1.93 mm) show a 19 % difference. The analysis suggests that the mass flux through the melting zone is well preserved except the periods of intense riming where the precipitation rates were higher in rain than in the ice above. This is potentially due to additional condensation within the melting zone in correspondence to high relative humidity and collision and coalescence with the cloud droplets whose occurrence is ubiquitous with riming. It is shown that the mean mass-weighted diameter of ice is strongly related to the characteristic size of the underlying rain except the period of extreme aggregation where breakup of melting snowflakes significantly reduces D_m. The proposed methodology can be applied to long-term observations to advance our knowledge of the processes occurring across the melting region; this can then be used to improve assumptions underpinning spaceborne radar precipitation retrievals.

1 Introduction

The accurate quantification of ice cloud macro-physical (height, thickness) and micro-physical properties (characteristic particle size and shape, mass content, and number concentration) is paramount for understanding the current state of Earth's hydrological cycle and energy budget and to improve the representation of clouds for climate model predictions (Stephens, 2005; Tao et al., 2010). Macro-physical properties can be well captured by active remote sensing instruments (Stephens et al., 2018); on the other hand, the characterization of ice microphysics remains one of the most challenging problems (Heymsfield et al., 2018) because of the substantial number of assumptions about the particle size distribution (PSD) and the particle “habit” type (such as dendrites, columns, rosettes, aggregates or rimed particles) required in remote sensing techniques. While the characterization of small ice crystals is particularly relevant for detailing the radiative effects of high ice clouds, understanding processes like aggregation, riming and deposition is essential for accurately modeling precipitation.

The study of stratiform precipitation encompasses the investigation of such processes “within the context of relatively gentle upward air motion” (Houze, 1997). Stratiform precipitation accounts for (> 85 %) 73 % of the area covered by rain and (> 77 %) 40 % of the total rain amount across the (mid-latitudes) tropics (Daniel Watters, personal communication, 2020; Schumacher and Houze, 2003). Stratiform rain can be identified well in radar data displays by a bright band, i.e., a pronounced layer of enhanced reflectivity corresponding to the melting layer (Fabry and Zawadzki, 1995).

In the past decade, several remote-sensing studies characterized micro-physical processes occurring in the ice (e.g. Kneifel et al., 2011, 2015; Kalesse et al., 2016; Leinonen and Moisseev, 2015; Oue et al., 2015b; Stein et al., 2015; Mason et al., 2018; Tridon et al., 2019) and rain part of clouds (e.g. Williams, 2016; Tridon et al., 2017b). The commonality of all these studies resides in exploiting ground-based active (radar and lidar) and passive (microwave radiometer) instruments in a synergistic manner, with multi-frequency and/or Doppler and/or polarimetric radars constituting the backbone of the observing system. Multi-frequency methods (Battaglia et al., 2020a) rely on the fact that, when the wavelength of the radars becomes comparable to the size of the particles being probed (“non-Rayleigh” regime), the measured reflectivity changes (typically decreases) relative to the Rayleigh regime, because the backscattered waves from different parts of the scatterer interfere (in a typically destructive way) with one another. Previous studies have demonstrated that dual- and triple-frequency radar observations can provide additional information on bulk density and the characteristic size of the ice PSD (Kneifel et al., 2015; Battaglia et al., 2020b). Doppler (full spectral) information allows separation of particles with different terminal velocities. While this information is more valuable in rain than in ice, since the velocity of raindrops is unambiguously related to their mass and size (which is not true of snow), Doppler spectra allow the detection of the presence of riming, which leads to an acceleration of the particle fall velocities above the typical 1 m s⁻¹ observed for snow aggregate (Kneifel and Moisseev, 2020). The increasing terminal velocity of rimed particles causes the spectra to be first skewed, and, at larger riming, to become bi-modal (Zawadzki et al., 2001; Kalesse et al., 2016; Vogel and Fabry, 2018). Polarimetric radar observations are particularly sensitive to depositional growth in temperature regions which favor growth of non-spherical particle shapes (e.g. needles, plates, dendrites). Observations obtained at the North Slope of Alaska (NSA) Atmospheric Radiation Measurement (ARM) site have shown large signatures of differential reflectivity Z_DR from plate-like crystals (Oue et al., 2015a) whilst analysis of linear depolarization ratio (LDR) in the spectral domain enabled the identification of columnar ice crystal growth originating in liquid-cloud layers through secondary ice production (Oue et al., 2015b).

Whilst several studies have looked at the microphysical processes occurring within the melting layer (Drummond et al., 1996) and at the link between microphysical processes in snow above the freezing level and within the melting layer (Zawadzki et al., 2005; Li et al., 2020, and references therein), less attention has been paid to the analysis of quantitative relationships between ice microphysics just above the freezing level and rain microphysics just below the melting layer. This investigation can contribute to a holistic understanding of the chain of processes occurring in the cloud that lead to precipitation at the ground, which is key for model development but which may also help in better constraining full-column remote sensing retrievals, e.g. those applicable to spaceborne radars like GPM, CloudSat and EarthCARE (Battaglia et al., 2020a) but also for improving quantitative precipitation estimation (QPE) from ground-based radar observations (Gatlin et al., 2018).

A common assumption used across the melting layer is the conservation of water mass flux (e.g. Drummond et al., 1996) which follows from assuming a stationary process and neglecting evaporation and condensation effects. The mass flux continuity assumption underpins several spaceborne radar stratiform precipitation retrieval algorithms (e.g. Haynes et al., 2009; Mason et al., 2017); in other retrievals where this constraint is not adopted, large discontinuities between mass fluxes above and just below the melting layer (Fig. 10 in Heymsfield et al., 2018) are reported. This inconsistency between rain and snow mass fluxes pinpoints at the presence of some underlying issues in the snow retrievals, which are more uncertain (Heymsfield et al., 2018; Tridon et al., 2019).

In addition to water mass flux continuity, several studies (Szyrmer and Zawadzki, 1999; Matrosov, 2008) further assume a one-to-one correspondence between the snowflake falling across the zero isotherm and the raindrop into which it melts (i.e., aggregation and breakup are neglected). We will refer to this as to the “melting-only steady-state” (“MOSS”) assumption. Under this condition, there is a unique correspondence between the drop size distribution (DSD) of raindrops and the PSD of snowflakes. If true this property could indeed be used to constrain the retrieval of hydrometeor vertical profiles in stratiform precipitation like done in Haynes et al. (2009) for the CloudSat spaceborne radar.

The goal of this study is to propose a methodology applicable to multi-frequency Doppler polarimetric vertically pointing radar measurements which enables the investigation of the relationship between the microphysics of snow and of the rain produced via melting. Some of the science questions (SQ) that will be addressed in this paper are as follows.

• SQ1.

  What is the relationship between mass fluxes above and below the melting layer? How much does it deviate from the commonly used constant mass flux assumption?

• SQ2.

  Can information about rain microphysics and DSD (e.g. about the mean characteristic size) be used to better constrain the microphysical properties and PSD of the snow above?

• SQ3.

  Are there specific ice cloud regimes (e.g. dominated by aggregation or riming) where the MOSS or the flux-continuity assumptions are more likely violated?

The paper is organized as follows: the dataset and the proposed methodology are presented in Sects. 2 and 3, respectively; Sect. 4 discusses the results for a case study in relation to the science questions; conclusions are drawn in Sect. 5.

2 Dataset

2.1 TRIPEx-pol field campaign

This study exploits the data collected during the “TRIple-frequency and Polarimetric radar Experiment for improving process observation of winter precipitation” (TRIPEx-pol). The campaign was conducted at the Jülich Observatory for Cloud Evolution Core Facility, Germany (JOYCE-CF 50^∘54^′31^′′ N, 6^∘24^′49^′′ E, 111 m above mean sea level; see Löhnert et al., 2015) from November 2018 until February 2019. JOYCE-CF is a triple-frequency radar site (Dias Neto et al., 2019) including permanent installations of X-, Ka- and W-band vertically pointing Doppler radars. The quality of the remote measurements is continuously monitored with a number of auxiliary sensors, including a Pluvio rain gauge, Parsivel optical disdrometer (Löffler-Mang and Joss, 2000), microwave radiometers and a Doppler wind lidar installed close to the radars. In order to maximize radar volume matching, all three radars are installed on the same roof platform within 10 m (see Table 1 for the technical specifications of the radars). Due to differences in the integration time of the radars and differences in the antenna beam widths, the data were averaged over 6 s in order to at least partially compensate for these factors. Because differences in the range resolution do not exceed 20 % and are difficult to correct for, the data at the W- and X-bands are simply interpolated at the Ka-band range bin resolution.

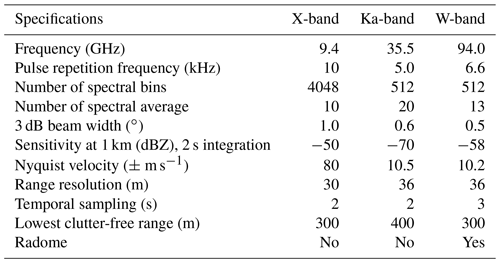
Table 1 Technical specifications and settings of the three vertically pointing radars operated during TRIPEx-pol at JOYCE-CF. Note that the W-band radar is a FMCW system for which chirp repetition frequency, number of spectral average, Nyquist velocity and range resolution change for different range intervals (see details in Dias Neto et al., 2019); values are provided here are for the lowest range gate region from 220 to 1480 m. Additionally, the radome of the W-band is equipped with a strong blower system which presents rain from accumulating.

The absolute pointing accuracy of the scanning Ka-band radar has been estimated to be better than ±0.1^∘ in elevation and azimuth using a sun-tracking method. Following the methodology of Kneifel et al. (2016), the mean Doppler velocity of the X- and W-band radars has been compared to the Ka-band system for several cases with different horizontal wind velocities and directions. This analysis showed that the relative misalignment of the three radars is in the range of 0.1^∘, which is expected to ensure a very high quality of the multi-frequency measurements.

2.2 The 24 November 2018 case study

The focus of our analysis is on a short time period (06:00–12:00 UTC) during a rain event on 24 November 2018. Selected radar measurements for this event are depicted in Fig. 1. The top and bottom of the melting layer have been derived with the linear depolarization ratio (LDR) from the Ka-band radar following the method described in Devisetty et al. (2019). This approach is based on a very strong bright band signature in the LDR data in correspondence to the melting regardless of the rainfall intensity. In this study, the inflection points around the LDR peak are used as the top and the bottom of the melting zone. Over the presented time period, the altitude of the 0 ^∘C isotherm was very stable and decreased by only 300 m from 1.1 km at 06:00 UTC to 0.8 km at 12:00 UTC. Radar reflectivity data below the bright band indicate two intervals of intensified rainfall: the first period is from 06:45 to 07:45 UTC with the peak at 07:30 UTC and a shorter interval that occurs around 09:00 UTC. Although for both periods similar X-band reflectivities are measured close to the ground (approximately 27 dBZ), the reflectivity and the dual-frequency ratio (DFR) data suggest completely different ice microphysics aloft. The first period is characterized by larger X-band echoes in the ice part coinciding with extremely large DFR^X-Ka values reaching 16 dB, which is a signature of strong aggregation and presence of very large snowflakes (Kneifel et al., 2015). Almost no DFR is measured after 07:45 UTC, which indicates relatively small ice particles. Note that the DFR data in ice were corrected for attenuation prior to the analysis. The attenuation due to the rain was derived from the Rayleigh part of the dual-frequency spectral ratio (see e.g., Tridon et al., 2013) assuming negligible attenuation at the X-band. The extinction due to melting particles was estimated from the rainfall rates retrieved below the melting layer with the methodology of Matrosov (2008). This technique has been shown to be in agreement with multi-frequency Doppler spectra estimates (Li and Moisseev, 2019). These two components were added together and were used as a path-integrated attenuation correction factor that is applied to the column. This methodology does not account for any attenuation within snow but this should be minimal at the X- and Ka-bands, which seems to be confirmed by the fact that the DFR at the cloud top (Fig. 1), where Rayleigh targets are expected, is close to 0 dB.

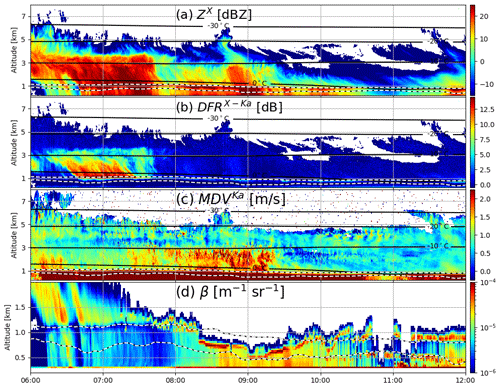
Figure 1 Time–height plots of radar variables measured at JOYCE on 24 November 2018: (a) X-band radar reflectivity factor (dBZ); (b) dual-frequency ratio (DFR) of X- and Ka-bands (Z^X−Z^Ka); (c) mean Doppler velocity (MDV, Ka-band); (d) lidar backscattering cross section (note the difference in the range of the presented altitudes). The dashed lines indicate the top and the bottom of the melting level derived from the Ka-band linear depolarization ratio (LDR). Black contour lines show isotherms derived from ECMWF analysis.

The mean Doppler velocity (MDV) is depicted in Fig. 1c. Despite high temporal variability of the Doppler data (the result of vertical air motion and turbulence), a difference in dynamical properties of ice for the two periods is evident. MDVs of approximately 1–1.5 m s⁻¹ in the first period are in agreement with simulations of large aggregates. Much larger velocities, especially after 08:00 UTC, suggest the presence of rimed ice crystals (Kneifel and Moisseev, 2020).

Figure 1d shows the measured lidar backscattering cross section from the ceilometer that is located less than 5 m away from the radars. Thanks to these measurements, periods where the environmental conditions are favorable for riming can by identified. Liquid clouds, which are essential for riming, appear as optically thick layers that strongly attenuate the light signal (Delanoë and Hogan, 2010; Van Tricht et al., 2014). The presented measurements exclude their presence before 08:00 UTC for altitudes below 2 km. Afterwards, liquid clouds are detected in the vicinity or within the melting region. Unfortunately, due to strong attenuation no information about the presence of mixed-phase clouds aloft is available.

3 Methodology

This study aims at relating rain and ice microphysics immediately below and above the melting layer in stratiform precipitation. The overall logic of our approach is summarized in the schematic of Fig. 2. In a first approximation, retrieved rain properties can be exploited to infer information about the ice particles aloft via the MOSS assumption (follow black arrows). Rainfall properties can be derived with less uncertainty than for ice because terminal velocities and backscattering cross sections of raindrops are much more constrained than those of ice and snow particles. The predicted ice PSDs can then be used to simulate radar snow spectra but only once a “snow model” is selected; the comparison between simulated and measured snow spectra allows the establishment of which snow models are more compatible with measurements and how realistic the MOSS assumption is. This bottom-up approach is not novel and has already been applied in the past (e.g. Drummond et al., 1996; Battaglia et al., 2003).

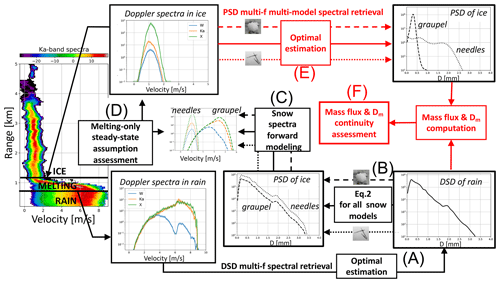
Figure 2 Schematic illustrating the rationale of the spectra closure study: by linking microphysical properties of rain just below the melting layer and of ice just above, the MOSS (black arrows) and the mass flux continuity (red arrows) assumptions can be evaluated.

Here, thanks to the multi-frequency Doppler spectra approach, we can attempt a more elaborate “closure study” where more accurate ice microphysical properties (and vertical wind) can be retrieved by matching spectra in ice at all frequencies via an optimal-estimation (OE) technique. For the a priori ice PSD, we use the exponential PSD that best fits the spectral measurements. From ice PSDs and vertical wind, fluxes and PSD moments can be derived that can be directly compared to their counterparts in rain in a top-down approach, thus addressing the science questions (Sect. 1). Such a procedure is featured in Fig. 2 with red-colored boxes and arrows. We now describe in detail the key steps of the whole approach.

3.1 Rain DSD retrieval from multi-frequency radar Doppler spectra

Vertically pointing Doppler radars usually provide the full Doppler spectrum, i.e., the spectral distribution of the return power over the range of the line-of-sight velocities. Because the raindrop terminal velocity is an increasing and well-constrained function of the raindrop size (Atlas et al., 1973), these measurements can be used to resolve the drop size distribution (DSD), once the vertical wind and turbulence are known (e.g., Williams et al., 2016; Tridon et al., 2017a; Giangrande et al., 2012).

Our DSD retrieval in the range bins below the melting zone closely follows the steps described in Tridon and Battaglia (2015). The only modification introduced here is the extension of the observation vector from two to three frequency bands in order to fully exploit the measurement capabilities of the radar site. The retrieval is based on Bayes' theorem (Rodgers, 2000): it minimizes the cost function that is composed of two equally weighted components. The first component computes the weighted distance to the triple-frequency spectra measurements, with the inverse variance of the measurement error used as a weight. The other term calculates the deviation from the prior knowledge of the DSD. For this retrieval, a widely adopted gamma-shaped DSD that fits the spectral measurements the best is used as the a priori estimate (for more detail see Tridon and Battaglia, 2015). The backscattering cross sections of raindrops are computed with a T‐matrix method using the Python code of Leinonen (2014). The refractive index of water is computed at 10 ^∘C using a model of Turner et al. (2016). Terminal velocities of raindrops are interpolated from a dataset of Gunn and Kinzer (1949) whereas the aspect ratio is calculated with a formula of Brandes et al. (2005). The orientation of raindrops is assumed to follow a normal distribution of about 0^∘ with a standard deviation of 8^∘ (Huang et al., 2008). Doppler spectra are simulated according to the methodology described in Tridon and Battaglia (2015) accounting for turbulence, vertical wind and radar noise level.

The algorithm retrieves binned DSD along with two dynamical parameters: turbulence and vertical wind.

An example of the measurements and the corresponding retrieval is presented in Fig. 3. As expected, the spectral power for velocities below 4 m s⁻¹ is nearly identical for the different frequencies, which is a result of Rayleigh (∝D⁶) scattering at all bands for drops smaller than approximately 1 mm. This Rayleigh part of the spectrum can be used to determine differential path-integrated attenuation for different radar bands (Tridon et al., 2013). The spectrally derived differential attenuation has been accounted for, prior to the retrieval. A significant reduction in the measured power at the W-band compared to the other frequency measurements can be found for velocities exceeding 4 m s⁻¹. This fall velocity regime corresponds to particle sizes for which non-Rayleigh scattering effects increase and culminate at the first resonant minimum, expected at 5.95 m s⁻¹ according to Gunn and Kinzer (1949) data. The difference between the measured and the anticipated position of the peak in the spectrum corresponds to the vertical air velocity (Kollias et al., 2002).

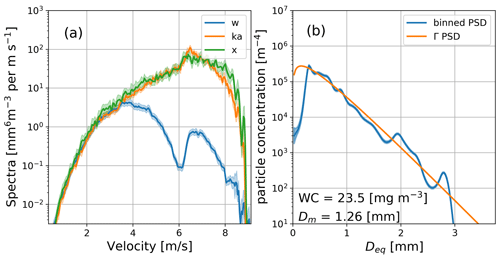
Figure 3 (a) Doppler spectra measured in rain just below the melting zone at 07:01:34 UTC. The green, orange and blue lines correspond to X-, Ka- and W-band data, respectively. The shaded areas represent the measurement uncertainties. (b) The corresponding binned DSD retrieval (blue) and the best fit gamma DSD (orange). The x axis is the melted-equivalent diameter. The water content (WC) and mass-weighted mean diameter (D_m) corresponding to the binned DSD are shown as text in the corner.

The blue line in Fig. 3b shows the retrieved DSD that minimizes the cost function. This solution fits the measured radar reflectivity with an accuracy of 0.25 dB at all frequency bands (not shown). As it can be seen, the widely used gamma model (orange line) represents the bulk shape of the binned DSD for drops up to 3 mm in size well. Nevertheless, some subtle features of the Doppler spectra, such as an increase in the X- and Ka-band spectra around 6 m s⁻¹ that corresponds to a local DSD maximum around 2 mm, cannot be modeled with the gamma function. It should be noted that although we assume a gamma-shaped PSD as a prior, no explicit functional shape is assumed for the retrieved DSD. This is an important advantage of the spectral retrieval as it allows the retrieval of complex DSDs, such as multi-modal distributions.

3.2 Deriving snow PSD from rain DSD via the melting-only steady-state assumption

In order to connect properties of ice with the properties of rain, several assumptions are made. Firstly, processes across the melting layer are assumed to be in steady state. Secondly, effects of condensation or evaporation are neglected. The radiosonde launched at 09:00 UTC showed RH values exceeding 90 % in the proximity to the freezing level, which effectively excludes the possibility of evaporation. However, the possibility of condensation on melting ice particles and collision–coalescence with cloud droplets cannot be ruled out. Due to the saturation problem of the GRAW humidity sensor the RH measurements are likely to be underestimated, which is confirmed by lidar measurements where signatures of liquid clouds are present within the melting zone after 08:15 UTC (Fig. 1d), which indicates water vapor supersaturation conditions. Despite the potential inconsistencies of our assumptions with the actual state of the atmosphere, neglecting condensation and evaporation is used as a simplifying hypothesis that implies the flux of mass through the melting zone is conserved. Furthermore, following Szyrmer and Zawadzki (1999), Zawadzki et al. (2005), and Matrosov (2008), no breakup and no interaction between melting particles are assumed. Consequently, we might assume that one ice particle is converted into one raindrop and the mass of each particle is preserved through the melting layer (m_s(D_s)=m_r(D_r)); thus the particle number flux is conserved at any size. Mathematically,

$$\begin{array}{}\text{(1)}& N_{\mathrm{s}}\left(D_{\mathrm{s}}\right)\left[V_{\mathrm{s}}\left(D_{\mathrm{s}}\right)+w_{\mathrm{s}}\right]\mathrm{d}{D}_{\mathrm{s}}=N_{\mathrm{r}}\left(D_{\mathrm{r}}\right)\left[V_{\mathrm{r}}\left(D_{\mathrm{r}}\right)+w_{\mathrm{r}}\right]\mathrm{d}{D}_{\mathrm{r}},\end{array}$$

where N_s and N_r denote the concentrations, and V_s and V_r are the still-air terminal velocities of snowflakes above the freezing level (subscript s) and raindrops below the melting zone (subscript r), respectively. Vertical air motions w_s and w_r in snow and rain are assumed to be negative when upwards. Vertical air motions in stratiform precipitation can be assumed to be small compared to sedimentation velocities and hence they are neglected in the following. We will refer to this set of assumptions as the “melting-only steady-state” hypothesis. It is convenient to formulate Eq. (1) in terms of the equivalent melted diameter D_eq, which is a quantity preserved through the melting process:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}& N_{\mathrm{s}}\left(D_{\mathrm{eq}}\right)V_{\mathrm{s}}\left(D_{\mathrm{eq}}\right)\mathrm{d}{D}_{\mathrm{eq}}=N_{\mathrm{r}}\left(D_{\mathrm{eq}}\right)V_{\mathrm{r}}\left(D_{\mathrm{eq}}\right)\mathrm{d}{D}_{\mathrm{eq}}\\ & \Rightarrow N_{\mathrm{s}}\left(D_{\mathrm{eq}}\right)=N_{\mathrm{r}}\left(D_{\mathrm{eq}}\right){\displaystyle \frac{V_{\mathrm{r}}\left(D_{\mathrm{eq}}\right)}{V_{\mathrm{s}}\left(D_{\mathrm{eq}}\right)}}.\end{array}\end{array}$$

Equation (2) expresses a link between the PSD of ice and the DSD of rain resulting from melting of snow. It shows how the V−D relationship for ice particles influences the shape of the underlying distribution of rain. This relation should be understood as a first-order approximation that can be applied only when (1) the process is steady state, (2) collision, coalescence and breakup are negligible, and (3) the relative humidity is close to the saturation level.

To verify whether or where the MOSS assumption holds, the procedure shown in Fig. 2 as the black arrows is applied. First, the triple-frequency measurements are extracted from the ranges just below the melting zone. Then, the full Doppler spectra are used to retrieve a binned rain PSD (step A). By applying the MOSS assumption through the melting zone, the rain DSD is mapped into the PSD of ice (step B, Eq. (2)). The procedure is applied to 18 different snow models, described in detail hereafter in Sect. 3.3. For ease of display, only two models (needles and graupel) representative of two extremes are illustrated in the insets of Fig. 2. The number concentration predicted for the ice particles just above the melting layer depends on the snow model due to differences between their aerodynamical properties; e.g. the aggregate models are characterized by higher particle concentration than rimed particles (compare the dashed–dotted with the dashed line in Fig. 2, panel “PSD of ice”). Doppler spectra corresponding to each snow model are derived with scattering and aerodynamical models (step C). The resulting simulated spectra at the three bands are compared with the actual measurements (step D). As a first closure attempt, simulated radar reflectivities for ice (corrected for attenuation using the methodology described in Sect. 2.1) and Doppler velocities are compared with the measurements.

3.3 Snow models and Doppler spectrum simulator

The Doppler spectrum measured by a vertically pointing radar transmitting at the wavelength λ is given by

$$\begin{array}{}\text{(3)}& S_{\mathit{\lambda }}\left(V\right)=A_{\mathit{\lambda }}\times \left(S_{\mathit{\lambda },w,\mathrm{target}}\ast T_{\mathrm{air}}\right)\left(V\right),\end{array}$$

where A_λ is the two-way attenuation, $S_{\mathit{\lambda },w,\mathrm{target}}$ is the reflectivity spectrum due to scattering from radar targets affected by the vertical wind w, T_air is the air broadening kernel and ∗ denotes the convolution operator (for more detail see Doviak and Zrnic, 1993). Note that the vertical wind only shifts the spectrum, i.e.,

$$\begin{array}{}\text{(4)}& S_{\mathit{\lambda },w,\mathrm{target}}\left(V\right)=S_{\mathit{\lambda },\mathrm{target}}(V-w).\end{array}$$

The reflectivity spectrum, S_λ,target, can be expressed in terms of the particle size distribution and the backscattering cross section as

$$\begin{array}{}\text{(5)}& S_{\mathit{\lambda },\mathrm{target}}\left(V\right)={\displaystyle \frac{{\mathit{\lambda }}^{\mathrm{4}}}{{\mathit{\pi }}^{\mathrm{5}}|K{|}^{\mathrm{2}}}}N\left(D_{\mathrm{eq}}\right){\mathit{\sigma }}_{\mathit{\lambda }}\left(D_{\mathrm{eq}}\right){\displaystyle \frac{\mathrm{d}{D}_{\mathrm{eq}}}{\mathrm{d}V}},\end{array}$$

where σ_λ gives the backscattering cross section of a target of a given size and $|K{|}^{\mathrm{2}}$ denotes its radar dielectric factor, and V is its terminal velocity that is assumed to be dependent on the particle size. In this study a wide gamut of “snow models” are considered to account for the large variability of scattering and aerodynamical properties of ice crystals. Each snow model entails a mass–size and an area–size relationship and provides size-dependent backscattering and extinction cross sections and fall speeds.

Broadly speaking two snow classes are analyzed in this study. The first class consists of unrimed aggregates of different ice habits, i.e., needles, plates, columns and dendrites. These aggregates were created using the aggregation code described in detail in Leinonen and Moisseev (2015). In total, approximately 30 500 aggregates were generated. The total number of monomers, as well as their size distribution have been varied, in order to produce a large variety of shapes and densities. The monomers are distributed according to an inverse exponential size distribution, with the characteristic size ranging from 0.2 to 1 mm with a minimum and maximum monomer size of 0.1 and 3 mm, respectively. The final aggregates consist of up to 1000 monomers and reach sizes of 2 cm. The scattering properties were obtained with the self-similar Rayleigh–Gans approximation (SSRGA; Hogan and Westbrook, 2014; Hogan et al., 2017). The SSRGA allows the approximation of the scattering properties of an ensemble of self-similar, low-density particles (such as aggregates) with an analytical expression and a set of corresponding fitting parameters which characterize the structural properties of the simulated snowflakes. For more detail on the SSRGA model used in this study see Ori et al. (2020a).

The second considered class contains snow particles generated by Leinonen and Szyrmer (2015) and Leinonen et al. (2017) comprised of aggregates of dendrites with different degrees of riming. Three riming scenarios are included in this dataset: particles, which grew by riming only (model C, LS15C), aggregation and riming occurring simultaneously (model A, LS15A), or aggregation and riming occurring subsequently (model B, LS15B). The degree of riming is expressed in terms of the equivalent liquid water path ranging from 0 kg m⁻² for dry aggregates to 2 kg m⁻² for graupel-like particles. For instance, “LS15A1.0” denotes the model of aggregates grown by simultaneous riming and aggregation, where particles passed through a layer of 1 kg m⁻² of cloud droplets.

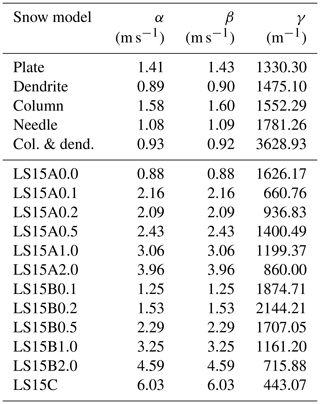
The terminal velocities of individual particles in the two snow classes are simulated for a standard atmosphere using the methodology of Böhm (1992). Then the expected velocity–size formula for each snow model is generated by a least-square difference fit of the generated data to the Atlas-like formula (Atlas et al., 1973) (suggested by Seifert et al., 2014, as also applicable):

$$\begin{array}{}\text{(6)}& V\left(D_{\mathrm{eq}}\right)=\mathit{\alpha }-\mathit{\beta }\exp \left(-\mathit{\gamma }{D}_{\mathrm{eq}}\right),\end{array}$$

where α, β and γ are the optimal fitting parameters. The shape of this fitting function is more realistic than the frequently used power-law fits since it can reproduce velocity saturation at larger sizes. Moreover, this parametrization is characterized by considerably smaller root-mean-square error of the fit than the traditional power-law approach. A complete list of the fitting parameters corresponding to the different snow models is given in Table 2.

Table 2 Coefficients of the Atlas-like velocity–size relation (Eq. 6) for different snow models.

3.4 Optimal estimation retrieval of ice PSD based on multi-frequency Doppler spectra

While the bottom-up approach (comparing measured and simulated ice Doppler spectra based on rain DSD) only provides a qualitative evaluation of the MOSS assumption, we aim to directly derive the ice PSD from the measured multi-frequency Doppler spectra just above the freezing level. The principal of this OE retrieval is very similar to the OE retrieval used for rain. Of course, the more complex scattering and terminal velocity behavior of snow must be accounted for and will also likely increase the retrieval uncertainties.

In rain, we used the gamma model DSD that best fits the spectra (Tridon and Battaglia, 2015); in ice, the exponential PSD that best fits the spectral ratios and the radar reflectivity at the X-band is used as a prior estimate. An uncertainty of a factor of 2 is assumed for the prior binned PSD concentration. A prior for turbulence is derived using the method proposed by Borque et al. (2016). The velocity of the slowest detectable radar targets in ice is used as the prior for the vertical velocity (step E). The uncertainties of these estimates are set to 175 % for the turbulence and 0.16 m s⁻¹ for the vertical wind. These uncertainty values are derived from the corresponding root-mean-square differences between the first guesses and the final estimates in rain over the analysis period. The retrieval is performed for all the selected models independently; the distance between the simulated and the measured spectra, δ_model, is used as a measure of quality of the retrievals at each time step. The final estimate of the posterior PSD is derived as a weighted mean of all the solutions. The weights of each model, W_model, are computed as the softmax function of the distances to the spectral measurements, i.e.,

$$\begin{array}{}\text{(7)}& W_{\mathrm{model}}=e^{-{\mathit{\delta }}_{\mathrm{model}}^{\mathrm{2}}}{\left(\sum _{\mathrm{models}}{e}^{-{\mathit{\delta }}_{\mathrm{model}}^{\mathrm{2}}}\right)}^{-\mathrm{1}}.\end{array}$$

The snow retrievals that do not fit the measurements well do not contribute much to the final estimate due to the exponential decay, and the models that resemble the spectral measurements well contribute the most. The uncertainty estimate of the final retrieval is derived from the weighted standard deviation of the solutions. Uncertainties of individual retrievals are neglected in the final estimate because they are much smaller than the variability corresponding to different snow models. For the final solution, parameters like mass flux and equivalent mass-weighted size can be computed and directly compared with the same parameters in the rain (step F). This allows us to achieve the “closure” and, for instance, to assess the validity of the flux continuity assumption.

4 Results

4.1 DSD retrieval

The goal of this study is to link the properties of rain with the characteristics of the overlying ice in stratiform precipitation. As the rain DSD is the basis for this closure analysis, we first compare the spectra-retrieved DSD with the Parsivel2 measurements at the ground (Fig. 4). Despite the vertical distance of approximately 700–800 m between the disdrometer and the radar-retrieved DSD just below the melting zone, the two methodologies provide comparable results. The comparison reveals several advantages of the radar-derived DSDs. First, it is able to retrieve smaller drop sizes (D_eq<0.5 mm) that are not detected by the disdrometer (Thurai et al., 2019; Thurai and Bringi, 2018; Raupach and Berne, 2015). Second, it has much higher temporal resolution (6 versus 60 s). Third, it provides more reliable estimate of the number of large drops that are very infrequent and may not be captured by the limited sampling volume of the disdrometer. Note that the spectral method also has its limitations; e.g. the retrieval for D_eq<0.2 mm must be interpreted with caution due to increasing uncertainties (see Tridon et al., 2017a).

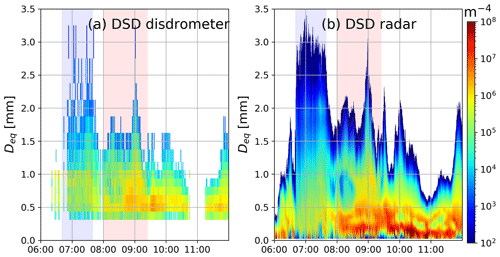
Figure 4 (a) DSD measurements at the ground with a Parsivel disdrometer. (b) DSD retrieved with multi-frequency Doppler spectra below the melting zone at ca. 700–800 m. The period shaded in blue corresponds to the region of large DFR^X-Ka values above the melting layer that indicates aggregation. The period of enhanced Doppler velocities indicating riming is marked in red.

Throughout the rest of the paper, the period of large DFR_X-Ka values (aggregation) is marked by the light blue color, whereas the domain of enhanced Doppler velocity (riming) is shaded in red. The DSDs during the two periods are quite distinct: the aggregation-dominated period (almost 1 h) is associated with a larger number of big drops and almost exponential DSDs. During the following riming period, a much larger concentration of small droplets and multi-modalities of the DSD are found. There are two potential sources of this high concentration of small droplets: super-cooled drizzle that forms aloft by coalescence of supercooled cloud droplets or secondary ice crystals, e.g. generated by the Hallett–Mossop process (Mossop, 1976). In the first scenario, the slowly falling mode does not significantly change its intensity and position in the Doppler spectrum while passing through the melting zone (Zawadzki et al., 2001) because there is no phase change of the particles. In the second scenario, the melting process changes the velocities and backscattering properties of the hydrometeors, thus resulting in a shift and a change in amplitude of the spectral power of the mode. The following analysis of the evolution of the Doppler spectra from the ice to the rain part is therefore expected to better explain the source of the small droplet mode.

4.2 Doppler spectral features during the investigated time periods

Differences between riming and aggregation regimes are reflected in the Doppler spectra that are shown in Fig. 5. During aggregation, the spectra in the ice phase are unimodal and the position of the peak is relatively constant at different heights, which indicates weak vertical air motion (Fig. 5a). The transition from ice to rain, corresponding to a strong broadening of the spectra, happens very rapidly within less than 200 m. The “aggregates” have a consistent spectral peak to 4 km, while the “rimed” particles also show a vertically coherent peak, but only up to 1.75 km in altitude. The spectra from the riming period (Fig. 5b) are characterized by a much thicker melting layer (approximately 400 m) and by bimodal distributions both in rain and in ice. The secondary ice mode appears approximately 1–1.5 km above the melting level, which corresponds to temperatures ranging between −4 and −6.5 ^∘C according to the radiosonde launched at 09:00 UTC. There is high vertical variability in the position of the main peak, which indicates more dynamical conditions. The secondary mode increases its intensity while approaching the melting level but remains clearly separated from the main peak (see Fig. 5b). In the melting zone this separation disappears, and the fall speed of the secondary mode increases so that the secondary peak stretches out in the velocity domain and merges with the primary mode. This behavior excludes the scenario of super-cooled drizzle above the freezing level as it was discussed before. The LDR measurements at the Ka-band (Fig. 5d) are in agreement with this theory. The slowly falling mode corresponds to LDR reaching −15 dB; such values are much larger than those expected for nearly spherical drizzle droplets. This spectral feature is similar to the enhanced LDR signatures found in Oue et al. (2015b) and Giangrande et al. (2016). They related the high-LDR region to columnar ice crystals grown in liquid-cloud layers through secondary ice production. Interestingly, the high-LDR signature of the small ice mode can also be detected during the melting of these particles, which might imply that the columnar crystals are of considerable size as they seem to maintain their asymmetric shape for quite some time until they are completely melted into drops (Fig. 5d). During aggregation, the opposite is true, i.e., the Ka-band LDR of large snowflakes is clearly larger than that of small ice crystals. This increase in LDR for large aggregates is principally consistent with scattering simulations of realistic snowflakes in Tyynelä et al. (2011, their Fig. 7) where LDR values are predicted to increase for maximum sizes exceeding 5 mm.

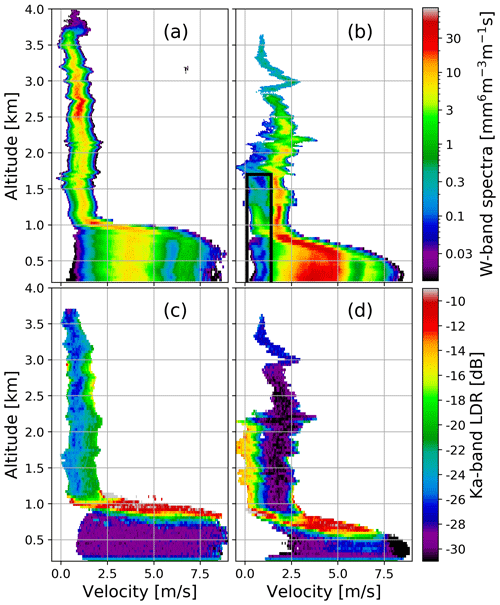
Figure 5 W-band Doppler spectra (a, b) and Ka-band spectral LDR (c, d). Panels (a) and (c) correspond to the measurements at 07:01 UTC dominated by aggregation; panels (b) and (d) were sampled at 08:58 UTC, when mean Doppler velocities indicate the presence of rimed particles. Only the data where SNR>3 dB are shown. The black box in panel (b) marks the secondary modes in ice and rain. Positive Doppler velocities indicate motions towards the radar.

Note that the secondary mode in rain (Fig. 5b) appears to be disconnected from the secondary mode in ice during riming. At an altitude of approximately 800 m there is a clear gap between them, which is shown by the black box in Fig. 5b. This separation is present over several minutes, which suggests that the small rain droplets do not originate from the melting of ice crystals; thus the assumption of one-to-one correspondence between ice particles and raindrops may not hold for this profile. Lidar measurements (Fig. 1d) indicate the presence of a small droplets within the melting zone; therefore the secondary mode in rain is likely to be drizzle generated by this liquid layer or melting ice crystals (too little to be detected by the radar) that underwent rapid growth through collision–coalescence processes while passing through the cloud.

4.3 Inferring ice PSD based on rain DSD via the melting-only steady-state assumption

In a first step, we derive the DSD of ice from the PSD of rain via the MOSS assumption (Eq. 2). Figure 6a shows the DSD mass-weighted mean diameter (D_m) and the water content (WC), as it is retrieved from the Doppler spectra in the rain below the melting region. The aggregation period is characterized by smaller water content but larger characteristic size of raindrops compared to the riming period. With the MOSS assumption, the ice WC and the melted D_m of snow depend on the V−D relationship of ice and on the rain DSD. Because the velocities of raindrops are larger than those of the same-mass snowflakes of any density, it follows that N_s(D_eq)>N_r(D_eq). Consequently, the assumptions made in Sect. 3.2 imply that the ice WCs at the freezing level are always larger than the rain WCs just below the melting zone (Fig. 6b). In the most extreme scenario, i.e., in the case of slow dendrite aggregates, ice WC can be 7 times larger than rain WC. For rimed snowflakes, this difference is much smaller, but still a factor of 2 is expected for graupel-like particles. Because the ratio V_r(D_eq)∕V_s(D_eq) is not constant but rather monotonically increases with size, the ice PSD is not simply a scaled version of the underlying DSD of rain; i.e., the number concentration of large particles is increased compared to the small ones. This causes a reduction of the mean mass-weighted diameter (D_m) during melting; i.e., the expected characteristic size of the DSD below the melting zone is up to 30 % smaller than the corresponding size in the ice aloft (Fig. 6c), and this change is purely ascribed to aerodynamic effects combined with the mass flux conservation constraint. Note that for the majority of the particle models, the associated difference in D_m usually does not exceed 10 %; for rimed particles this change is even less pronounced and the characteristic melted-equivalent size is practically preserved.

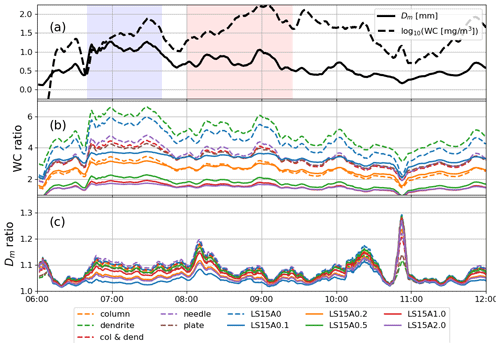
Figure 6 (a) Derived D_m and WC (in log units) for the rain DSD just below the melting zone. (b) Relative change of the WC when passing from rain to ice, i.e., WC_ice ∕ WC_rain. (c) The same as panel (b) but for D_m, i.e., $D_{\mathrm{m}}^{\text{ice}}/D_{\mathrm{m}}^{\text{rain}}$. Different colors correspond to different ice models as indicated in the legend. Dashed lines correspond to unrimed aggregates, and solid lines denote rimed particles. Blue and red shading indicates aggregation- and riming-dominated periods, respectively.

4.3.1 Discussion of the validity of the melting-only steady-state assumption

According to the “reflectivity flux” method proposed by Drummond et al. (1996) and Zawadzki et al. (2005), the ratio of the reflectivity fluxes in snow and rain,

$$\begin{array}{}\text{(8)}& \mathit{\gamma }\equiv {\displaystyle \frac{Z_{\mathrm{s}}{V}_{\mathrm{D},\mathrm{s}}}{Z_{\mathrm{r}}{V}_{\mathrm{D},\mathrm{r}}}},\end{array}$$

is equal to $\mathit{\mu }\equiv ({\mathit{\rho }}_{\mathrm{w}}/{\mathit{\rho }}_{\mathrm{i}}{)}^{\mathrm{2}}\left(|K_{\mathrm{i}}{|}^{\mathrm{2}}/|K_{\mathrm{w}}{|}^{\mathrm{2}}\right)=\mathrm{0.23}$, where the mean Doppler velocity is denoted by V_D, and the subscripts s and r indicate sampling in snow and rain, respectively, whereas the subscript i indicates ice. The relation is only valid for Rayleigh targets (which should hold for our X-band data) and under the MOSS assumption. Although the factor μ was computed assuming constant ice density, the derivation is based on the formula of Debye ($\left|K_{\mathrm{s}}\right|/{\mathit{\rho }}_{\mathrm{s}}=\mathrm{const}$), which implies the reflectivity of ice particles depends only on their mass not density. Therefore, the value of μ is independent of the snow morphology. Values between 0.15 and 0.30 are still compatible with the MOSS assumption when plausible vertical air motions (i.e., $w_{\mathrm{r}}=\pm \mathrm{1}$ m s⁻¹ and $w_{\mathrm{s}}=\pm \mathrm{0.5}$ m s⁻¹) are allowed (Drummond et al., 1996). If we introduce a normalized parameter in logarithmic units,

$$\begin{array}{}\text{(9)}& {\mathit{\gamma }}_{\mathrm{n}}\left[\mathrm{dB}\right]=\mathrm{10}{\log }_{\mathrm{10}}\left({\displaystyle \frac{\mathit{\gamma }}{\mathrm{0.23}}}\right),\end{array}$$

values of γ_n higher (lower) than 0 dB are indicative of breakup (collision–coalescence) or of a nonstationary process. Note that this method is based purely on the radar measurements. Thus it is not dependent on any snow or rain model. The methodology has been recently applied to X-band profiler data by Gatlin et al. (2018), where it was found that thicker melting layers generally correspond to negative γ_n, i.e., are indicative of dominant coalescence and/or aggregation while transitioning from ice to liquid. Moreover, by combining Eq. (8) for γ≡0.23 with Eq. (9), the ice reflectivity that would correspond to the MOSS assumption can be derived:

$$\begin{array}{}\text{(10)}& Z_{{\mathit{\gamma }}_{\mathrm{n}}\equiv \mathrm{0}}=Z_{\mathrm{m}}-{\mathit{\gamma }}_{\mathrm{n}},\end{array}$$

where Z_m is the reflectivity measured above the freezing level.

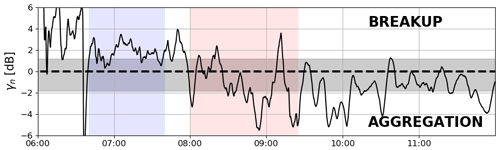
Figure 7 The normalized ratio between the reflectivity fluxes in ice and rain in the vicinity of the melting level as defined by Eq. (9).The grey shading highlights the uncertainty introduced by the variability in the vertical wind.

In order to match the data below and above the melting layer more precisely, for each 15 min time window the optimal time lag that maximizes the correlation between the X-band reflectivity in ice and rain is derived. All the results that follow use this optimal matching in time. Most of the time, γ_n is within the uncertainty limits introduced by vertical air motion (see Fig. 7). The root-mean-square difference over the case study between the ice reflectivity predicted with the MOSS hypothesis and the measurements is equal to 2.7 dB. The most consistent deviation from the uncertainty limits is reported during the period when large snow aggregates are expected above the 0 ^∘C level. Large positive γ_n values consistently suggest breakup as the main process occurring within the melting zone (Fig. 7). The behavior of γ_n is more variable during the period of riming, where it oscillates between −6 and 4 dB. This non-uniform behavior can be, at least partially, caused by a more turbulent environment, which might favor more non-stationary conditions. Also, the presence of fall streaks (e.g., around 09:00 UTC) can be seen as an indication for more heterogeneous conditions. Moreover, riming particles have a broader range of terminal fall velocities (compared to aggregates of the same mass), which favors collision–coalescence processes and thus violates the underlying MOSS assumption. Within the uncertainty introduced by the assumed vertical wind variability, our analysis confirms that the period before 08:00 UTC is mainly characterized by breakup whereas the period after 08:00 UTC is dominated by collision–coalescence within the bright band. This corroborates the previous hypothesis of preponderance of aggregation before 08:00 UTC and of riming after 08:00 UTC within the snow layer.

One of the difficulties of interpreting profile-type measurements is that they do not provide a full 3D picture of the atmosphere, but just a 2D slice. Therefore, the presented conclusions are based on the assumption that the observed system is locally homogeneous, i.e., despite horizontal winds the measurements taken below the melting layer correspond to the evolution of the ice PSD measured aloft. Considering the horizontal wind speed within the bright band (approx. 1.8 m s⁻¹ during the “aggregation” period according to the ECMWF model) and the time needed for the particles to melt (approx. 3 min based on the MDV data), the precipitating system must be uniform over 325 m to meet this criterion. Because the beam width of the X-band radar at the altitude of the melting zone is only 15 m, it is possible that the higher ice-phase reflectivity flux relative to rain can be a result of a horizontal gradient of the reflectivity that, for example, corresponds to the storm intensification along the wind direction. Note that, for most of the aggregation period the precipitation rate increases over time (see Fig. 9a), which supports this alternative interpretation.

4.3.2 Towards reconciling radar moments at the top of the melting layer by selecting an adequate snow model

Encouraged by the results on the matching of the reflectivity fluxes in rain and ice, in the following section we test whether the MOSS assumption combined with the information on the DSD in rain can help in constraining microphysical properties of ice in the vicinity of the melting level. For this purpose, the reflectivities at the three different frequencies are simulated for all the different snow models for the PSDs predicted with the MOSS assumption (Eq. 2). Regardless of the ice morphology the X-band reflectivity simulations cluster close together with a standard deviation between them ranging from 1 to 1.5 dB only (Fig. 8a). The envelope of simulations follows the X-band reflectivity predicted by assuming γ_n=0 dB (denoted later as $Z_{{\mathit{\gamma }}_{\mathrm{n}}\equiv \mathrm{0}}^{\mathrm{X}}$), which is plotted as a dashed black line in Fig. 8. The largest difference in the simulated reflectivities occurs between the models of graupel (LS15C) and aggregates of dendrites; this discrepancy reflects differences in the ice water content for different snow models (see Fig. 6b) but is always smaller than 5 dB. The inter-model variability of the reflectivity simulations is comparable to the variability of the γ_n, which suggests that X-band radar data alone can provide very limited guidance on the density of snow above the melting zone, even when detailed information of the rain, which originated from it, is available. The X-band simulations mirror the finding of Sect. 4.3.1, i.e., during the entire period of strong aggregation, the simulations underestimate the measurements by approximately 5 dB, which is a signature of the MOSS assumption being invalid at that time period.

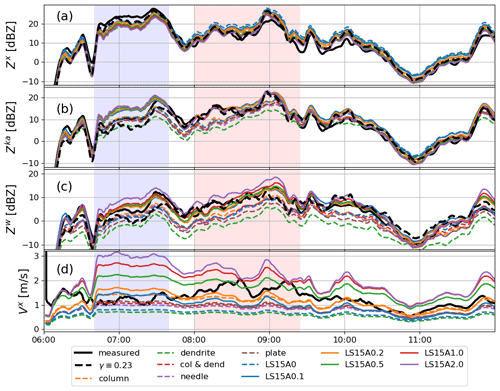
Figure 8 Measured (black lines) and simulated (colored lines) radar reflectivities at the X-, Ka-, W- and X-band MDV just above the melting level. The simulated values are predicted from the rain below the bright band by adopting the different snow models as listed in the legend. The black dashed lines show the reflectivity of snow derived with formula (8) for γ≡0.23, i.e., the reflectivity corresponding to the MOSS hypothesis based on the radar reflectivity measured in rain and on MDV values in rain and ice (only X-band). Note that the difference between the continuous and the dashed black line is equal to γ_n (Eq. 9).

The ranges of simulated Ka- and W-band reflectivities is much wider than that at the X-band, with differences between heavily rimed particles and unrimed aggregates reaching 10 and 14 dB at the Ka- and W-band, respectively. This is related to the fact that backscattering cross sections in non-Rayleigh scattering conditions become increasingly sensitive to the snow particle type and density rather than simply being proportional to the square of the mass. Because the variability of simulated Ka- and W-band reflectivities for different models is much larger than the range of γ_n values, the triple-frequency reflectivity data are more informative about the particle models that are more suitable during specific time periods. For a qualitative comparison, γ_n is used as a correction factor to the number concentration that makes triple-frequency measurements consistent with the MOSS simulations. This is done by reducing the measured reflectivities by γ_n derived for the X-band ($Z_{{\mathit{\gamma }}_{\mathrm{n}}\equiv \mathrm{0}}^{\mathrm{X}}=Z^{\mathrm{X}}-{\mathit{\gamma }}_{\mathrm{n}}$; $Z_{{\mathit{\gamma }}_{\mathrm{n}}\equiv \mathrm{0}}^{\mathrm{Ka}}=Z^{\mathrm{Ka}}-{\mathit{\gamma }}_{\mathrm{n}}$; $Z_{{\mathit{\gamma }}_{\mathrm{n}}\equiv \mathrm{0}}^{\mathrm{W}}=Z^{\mathrm{W}}-{\mathit{\gamma }}_{\mathrm{n}}$). The result of this correction is shown as the dashed black line in Fig. 8a–c. With this correction applied to the triple-frequency reflectivity data, it becomes clear that for the period before (after) 07:45 UTC, only models of unrimed aggregates (rimed particles) plotted with dashed (continuous) colored lines are consistent with the multi-frequency observations. Similar conclusions are drawn when considering the simulated and observed Doppler velocities (Fig. 8d).

The γ_n adjustment applied to all frequencies is a very crude approximation but it provides a significant improvement in terms of compatibility between triple-frequency-measured Doppler spectra moments. However it implies an “extensive” adjustment of the snow PSD; for instance a ±3 dB correction corresponds to doubling or halving the mass flux through the melting layer. Changes in the shape of the PSD could in principle lead to better fitting of the measurements and more continuous change in the mass flux. This is what is investigated next with the more exhaustive closure study.

4.4 Closure study: connecting PSD and mass flux retrieved above and below the melting layer

Instead of only a qualitative comparison of the MOSS assumption (step D in the schematic Fig. 2), we are now able to directly analyze the differences in mass flux and PSD above and below the melting layer by using the associated retrieval results for rain and ice. In this way, we can quantify the differences according to the dominating processes, which is expected to also be relevant for future modeling studies.

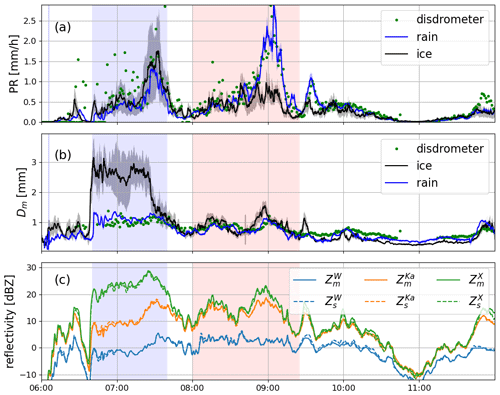
Figure 9 Results of the full Doppler spectra retrievals applied both below (Sect. 3.1) and above (Sect. 3.4) the melting zone. (a) Precipitation rate; (b) mean mass-weighted diameter; (c) measured (subscript m) and simulated (subscript s) radar reflectivity values in the ice region just above the freezing level. The green dots in panels (a) and (b) correspond to the disdrometer measurements at the ground. Shading around the retrievals shows the uncertainty (1 standard deviation) of the posterior estimate.

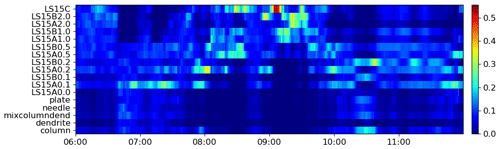
Figure 10 The contribution of each snow retrieval to the final PSD estimate. The weights depend on the distance between the simulated and the measured Doppler spectra above the freezing level.

The PSD multi-spectral retrieval described in Sect. 3.4 (step E in Fig. 2) is applied to the whole period, and the results are presented in Fig. 9. The mass flux and D_m above the melting level (continuous lines in Figs. 9a–b) are derived as an ensemble mean of the multi-frequency spectral OE ice retrievals where each solution is weighted by its distance to the observed spectra as is shown in Fig. 10. The most probable snow model for the “aggregate” period is aggregates of dendrites (LS15A0.1 represents aggregates of dendrites with very light riming). During the period of enhanced Doppler velocities, the retrieval suggests snow models of rimed particles. Rimed snow models also fit the measurements the best at later times, but because the characteristic size of particles is relatively low (Fig. 6), the mean Doppler velocity cannot be used to unequivocally confirm the presence of rimed particles. The agreement between the snow model selection discussed in Sect. 4.3.2 and the models suggested by the OE technique is quite remarkable, which confirms a potential of using the MOSS hypothesis to at least reduce the number of plausible snow models in the analysis of the spectra just above the melting layer.

As a consistency check, the reflectivities for the derived PSD and snow model are compared in Fig. 9c, illustrating a very good match with the observations. The comparison of the derived mass fluxes in rain and ice (Fig. 9a) suggests that for most of the time the mass flux across the melting zone is well preserved. The rain rate below the melting zone is within the uncertainty estimates of the precipitation rate above for the whole case study except a 30 min period around 09:00 UTC where strong riming occurs. The estimated total accumulations of rain (2.30 mm) and the melted equivalent accumulation of snow (1.93 mm) during the 6 h time period show only a 19 % difference. Interestingly, the mass flux during the aggregation period tends to be higher than the precipitation rate below while the opposite is true during the riming period. As expected, there is a strong correlation of 0.67 between the mass fluxes above and below the melting layer (CC = 0.82 if the 30 min period around 09:00 UTC is removed).

During the aggregation period, the snowfall rate is on average 34 % larger than the precipitation rate below the melting zone, which corresponds to a mean decrease from 0.43 to 0.32 mm h⁻¹. The characteristic size is found to be 84 % larger in ice than in rain and 67 % larger than one would expect, based on the MOSS assumption. Because aggregates are often composed of loosely connected crystals (Garrett et al., 2012), this change in size could be caused by the breakup of the melting snowflakes as already conjectured in Sect. 4.3.1. The breakup hypothesis is also supported by a recent simulation study (Leinonen and von Lerber, 2018), where it was shown that the melting of the fragile ice connections within unrimed aggregates causes the particles to break into multiple droplets. Laboratory measurements of melting of snow aggregates, recorded under controlled temperature, relative humidity and air velocity (Oraltay and Hallett, 2005), are also in agreement with this interpretation. However, the decrease in precipitation rate during the aggregation period cannot be explained by breakup that does not affect the mass flux. Other processes, such as evaporation and sublimation during melting would be needed to explain this reduction in the precipitation rate. If present, those processes would also contribute to a reduction of the characteristic size.

During the riming period the rain rate is approximately 44 % larger than the snowfall rate, with the largest difference reported between 08:45 and 09:15 UTC (approximately 58 % difference). This increase in precipitation rate could be explained by continuous riming within the melting layer. The ceilometer data (see Fig. 1d) seem to indicate a layer of small liquid drops within the melting layer which might contribute to the enhanced rain rate by either riming or later also collision–coalescence of the small cloud droplets with raindrops from already melted snowflakes. However, the characteristic size appears not to change during this period, which is inconsistent with this hypothesis. Therefore, we speculate that additional processes, such as shattering of large drops, might compensate for the raindrop size growth.

Considering the case study except the extreme aggregation period, we find the characteristic size of snow to be only 2 % larger than that of the rain underneath. The root-mean-square difference between them is equal to 0.18 mm only, whereas the correlation coefficient is 0.81. Recently published DWR statistics (Dias Neto et al., 2019) reveal that the very large DWR signals found in this case study due to aggregation are relatively infrequent, which suggests that the relationship between snow and underlying rain is quite robust. If this can be confirmed for different locations and a larger dataset, it would provide a very strong constraint for micro-physical retrievals (Tridon et al., 2019; Leinonen et al., 2018b).

5 Conclusions

This study investigates the link between rain and ice microphysics across the melting layer in stratiform rain. An OE technique applied to multi-frequency radar Doppler spectra is proposed in order to retrieve particle size distributions and dynamics both above and below the melting layer. This enables examining the variability of the precipitation rate and the mass-weighted melted diameter (D_m) across the melting region. The proposed technique is demonstrated for a 6h-long case study, observed during the TRIPEx-pol field campaign at the Jülich Observatory for Cloud Evolution Core Facility and covering a gamut of ice microphysical processes.

An initial assessment of the relationship between mass fluxes below and above the melting layer (scientific question 1) is based on the approach of Drummond et al. (1996) where the reflectivity fluxes (reflectivity × mean Doppler velocity) below and above the melting layer are compared. If the ratio of the two deviates from a value of 0.23 then the commonly adopted melting-only steady-state (MOSS) assumption is violated. During most of our case study, the reflectivity fluxes ratio is within the uncertainty limits introduced by the vertical air motion (see Fig. 7) and the reflectivity fluxes are highly correlated (CC = 0.94). However, during the period of enhanced dual wavelength ratios (DFR^X-Ka>10 dB), the reflectivity flux above the freezing level is systematically larger than in the underlying rain, indicating prevalent breakup during melting; therefore, the MOSS assumption seems to be breached, when large aggregates are present above the freezing level. More sophisticated analysis based on a comparison of binned PSDs retrieved in ice and rain from the triple frequency spectra measurements is consistent with the findings based on the approach of Drummond et al. (1996); the mass flux across the melting layer is relatively well preserved. Over the analyzed case study, the total accumulation of rain and snow differs by 19 % (i.e., it is within the uncertainty limits of the retrieval). The largest difference between the fluxes above and below the melting level occurs during the most intense riming periods. This analysis indicates that, not only the MOSS assumption but also the much weaker hypothesis of the mass-flux continuity across the melting zone is violated during the period of extreme riming.

In order to address the second science question related to linking characteristics of rain to the microphysical properties of ice aloft, the raindrop size distributions are retrieved below the melting level using the methodology of Tridon et al. (2017a). Then, the PSDs that would conserve the precipitation rate during melting are generated for all the analyzed snow models by imposing MOSS assumption. Triple frequency Doppler spectra and their corresponding moments (Z and MDV) in ice are simulated with the Self-Similar-Rayleigh-Gans approximation (Leinonen et al., 2018a). It is found that, at X-band, where snowflakes behave mainly as Rayleigh scatterers, radar reflectivity of MOSS-generated PSDs of snow is only weakly dependent on the ice morphology. The standard deviation between the snow models is smaller than 1.5 dB and the difference between the most distinct models does not exceed 5 dB. This range of simulated radar reflectivity values mainly reflects differences in the terminal velocities for different models and is comparable to the uncertainty of the MOSS hypothesis (see range of values of γ_n in Fig. 7) which suggests that the X-band data alone provides a very limited guidance on the snow density. The range of Ka- and W-band reflectivity simulations for different snow models is much wider and reaches up to 10 and 14 dB respectively, which is related to the increasing dependence of backscattering cross sections on ice density and inner mass distribution at the higher frequency bands. It is found that the region where high MDVs are measured above the melting layer is clearly more compatible with the reflectivity simulations of rimed aggregates. The region of low MDVs and large DFR^X-Ka can be better simulated with dry aggregate models. This indicates that when the high frequency radar data are available, the MOSS assumption combined with the information on the drop size distribution (DSD) can guide selection of the snow models that represent bulk microphysics above the freezing level.

The analysis of the spectral retrievals in rain and ice reveals a strong dependence between the mean mass-weighted hydrometeor sizes for different phases. On average, the characteristic size of snow is only 2 % larger than the size of rain below and they are highly correlated (CC = 0.8) if the period of extreme aggregation is neglected. The mean mass-weighted size of snow can be forecasted with an accuracy (RMSE) of 0.18 mm if the size of rain below is used; nevertheless such estimate leads to large underestimation during periods dominated by aggregation.

With respect to the third scientific question, whether there are specific ice cloud regimes where the MOSS assumption is more likely to be violated, we can only provide an answer for the relative short time period analyzed in this study. Regions dominated by aggregation above the melting layer tend to produce a reduction by approximately 34 % in the flux and a decrease by 84 % in the mean mass-weighted diameter when transitioning from ice to rain. In contrast, regions dominated by riming show an increase by approximately 44 % in the flux and a relatively constant mean mass-weighted diameter. We hypothesize that the flux changes are associated to the variability of the relative humidity within the melting layer, with the regions dominated by riming more likely to be supersaturated as confirmed by the presence of a cloud layer. Ideally, measurements with differential absorption radar systems capable of characterizing in-cloud water vapor like those proposed in Battaglia and Kollias (2019) and Roy et al. (2020) could assist in the interpretation of this kind of ground-based observations. On the other hand, the change of D_m could be related to an increased likelihood for large aggregates to preponderantly undergo breakup in the melting zone. This is in agreement with theoretical (Leinonen and von Lerber, 2018) and laboratory (Oraltay and Hallett, 2005) studies which report breakup due to melting of the fragile ice connections within aggregates.

Our methodology should be applied to long-term observations in order to produce statistically significant results. Relationships between fluxes and characteristic sizes in ice and rain in stratiform precipitation are of great relevance since they can be directly used to constrain retrieval algorithms like those currently implemented in the framework of the Global Precipitation Measurement mission or envisaged for the EarthCARE mission. Uncertainties related to snow scattering models remain an obstacle in the accurate quantification of the ice phase microphysics. The integration of the findings of this study in a full-column rain–snow micro-physical retrieval of stratiform precipitation can pave the way towards a more refined selection of the snow model in line with the predominant ice microphysical process, thus advancing the current approach based on a single snow model assumption (e.g. Liao et al., 2016; Seto et al., 2013 for GPM). The proposed approach should help to better characterize the ice and rain microphysics just above and just below the melting layer, which will also highly benefit modeling studies of the processes occurring in the melting zone, which remain highly uncertain. Moreover, statistics on riming frequency would advance our knowledge of stratiform precipitation processes and lead to improvements in numerical weather models.