Sensitivity analysis of DSD retrievals from polarimetric radar in stratiform rain based on the μ–Λ relationship

Raindrop size distributions (DSDs) play a crucial role in quantitative rainfall estimation using weather radar. Thanks to dual polarization capabilities, crucial information about the DSD in a given volume of air can be retrieved. One popular retrieval method assumes that the DSD can be modeled by a constrained gamma distribution in which the shape (μ) and rate (Λ) parameters are linked together by a deterministic relationship. In the literature, μ–Λ relationships are often taken for granted and applied without much critical discussion. In this study, we take another look at this important issue by conducting a detailed analysis of μ–Λ relations in stratiform rain and quantifying the accuracy of the associated DSD retrievals. Crucial aspects of our research include the sensitivity of μ–Λ relations to the temporal aggregation scale, drop concentration, inter-event variability, and adequacy of the gamma distribution model. Our results show that μ–Λ relationships in stratiform rain are surprisingly robust to the choice of the sampling resolution, sample size, and adequacy of the gamma model. Overall, the retrieved DSDs are in a rather decent agreement with ground observations (correlation coefficient of 0.57 and 0.74 for μ and D_m). The main sources of errors and uncertainty during the retrievals are calibration offsets in reflectivity (Z_hh) and differential reflectivity (Z_dr). Measurement noise and differences in scale between radars and disdrometers also play a minor role. The raindrop concentration (N_T) remains the most difficult parameter to retrieve, which can be off by several orders of magnitude. After careful data filtering and removal of problematic $Z_{\mathrm{hh}}/Z_{\mathrm{dr}}$ pairs, the correlation coefficient for the retrieved N_T values remained low, only slightly increasing from 0.12 into 0.24.

1 Introduction

Understanding the natural variability of raindrop size distributions (DSDs) is crucial for radar remote sensing applications and microphysical parameterizations in numerical weather prediction models (e.g., Thompson et al., 2004). Most precipitation-related quantities (e.g., rain rate, mean drop diameter, number concentration, fall velocity, or liquid water content) directly depend on the DSD. Similarly, most radar observables (e.g., Z_hh, Z_dr) are weighted moments of the DSD. For these reasons, DSD retrieval methods play a central role in numerous weather radar studies.

Efforts to improve quantitative rainfall estimates by retrieving information about DSDs from radar and satellite observations have captured a great deal of interest in the meteorological community, especially after the introduction of polarimetric weather radar (Seliga and Bringi, 1976). Retrievals based on the reflectivity factor at horizontal polarization (Z_hh), differential reflectivity (Z_dr), and specific differential phase (K_dp) are the most common choices because of their natural link to raindrop concentrations, sizes, and shapes.

According to the literature, DSDs can be parameterized in the form of relatively simple models such as a gamma distribution with the three parameters μ, Λ, and N₀ representing the shape, scale, and concentration, respectively. Algorithms for DSD retrievals take advantage of different relationships between radar observables and the three parameters of the gamma. Three main categories of retrieval methods can be distinguished: the first one consists of methods that use two radar observations Z_hh and Z_dr, as well as a constrained relationship between μ and Λ (Zhang et al., 2001, 2003) or N₀ and μ (Ulbrich, 1983). The second category proposed by Bringi et al. (2002) and Gorgucci et al. (2002) uses the three radar observables Z_hh, Z_dr, and K_dp. However, this method is known to be very sensitive to noise in K_dp estimates. To reduce the uncertainty, the differential phase needs to be filtered and down-sampled, which limits the accuracy and spatial resolution of the retrievals. The last category consists of various retrieval techniques that require special types of radars or measurements, such as double frequency (Rose and Chandrasekar, 2006), triple frequency (Mróz et al., 2020), and/or Doppler power spectra (Unal, 2015). In this paper, only the first category will be discussed.

The main challenges when retrieving DSDs from Z_hh and Z_dr are the choice of the N₀–μ or μ–Λ relationship and its validity across different rain types as well as spatial and temporal aggregation scales. In the literature, μ–Λ relationships are often taken for granted or transferred from one location or scale to another without much critical discussion. And while some studies have documented large differences in relationships across rain types (e.g.,, stratiform vs. convective), little is known about the sensitivity of μ–Λ relationships to the temporal sampling resolution of the disdrometer data used to infer them or the validity of the gamma assumption. Another important issue concerns the fact that the disdrometer data used to define μ–Λ relationships correspond to much smaller sampling volumes than the radar measurements to which they are applied. Therefore, it might be necessary to first apply a statistical transformation to the radar data before retrieving DSDs based on μ–Λ relationships or, equivalently, modify the μ–Λ relation to account for the difference in scale.

Finally, one last issue that tends to be overlooked is that radar measurements are likely to contain systematic errors in the form of calibration offsets in Z_hh and Z_dr. A possible error in the latter could induce large biases in the retrieved DSDs, especially in light rain with low Z_dr and a small signal-to-noise ratio. Several operational polarimetric weather radar networks such as the US Nexrad (Hubbert and Pratte, 2006) and the German DWD network (Frech and Hubbert, 2020) have already devoted extensive efforts toward mitigating these calibration issues. However, achieving and maintaining good calibration over time for research radars remain challenging.

In this paper, we perform a detailed analysis of the sensitivity of DSD retrievals from polarimetric radar to various error sources such as the validity of the μ–Λ relationship and its sensitivity to the temporal sampling resolution, inter-event variability, changes in number concentrations, and adequacy of the gamma distribution model. We also examine the sensitivity of the retrievals to measurement biases in Z_hh and potential biases in Z_dr due to differences in measurement scale. We illustrate the importance of all these issues by retrieving DSDs during several episodes of light to moderate stratiform rain in Cabauw, the Netherlands, and indirectly validating our retrievals by comparing them to disdrometer observations on the ground. The main focus is not on optimizing the DSD retrieval algorithm but on understanding its sensitivity to potential sources of errors, either directly linked to the radar measurements or indirectly through the critical modeling assumptions behind the method.

This paper is organized as follows. In Sect. 2, the data used are introduced. In Sect. 3, the methodology is presented. In Sect. 4, the main results for the μ–Λ relationship analysis are shown, followed by the sensitivity analysis of the DSD retrievals in Sect. 5. Finally, the conclusions are provided in Sect. 6.

2 Data

The data used in this study were collected in the Netherlands during the ACCEPT (Analysis of the Composition of Clouds with Extended Polarization Techniques) campaign between October and November 2014. During this campaign, a variety of different in situ and remote sensing measurements were collected at the CESAR (Cabauw Experimental Site for Atmospheric Research) observatory.

2.1 The disdrometer data

The ground DSD spectra used for calibration and validation were collected by a Parsivel² (Particle Size and Velocity) optical disdrometer. The working principle, strengths, and limitations of the Parsivel² have already been discussed in great depth in previous studies and will not be part of this study (Löffler-Mang and Joss, 2000; Tokay et al., 2014; Battaglia et al., 2010; Thurai et al., 2011; Raupach and Berne, 2015). For example, the Parsivel is susceptible to errors in the lower drop diameter range, which can affect the DSD shape and number concentrations. However, no efforts have been made to try to correct for these issues within the context of this study. The raw DSD data consist of particle counts across 32 nonuniformly spaced diameter classes ranging from 0 to 25 mm with a sampling resolution of 30 s. From the raw DSD, integrated quantities such as rainfall rate (R) and radar equivalent reflectivity factor (Z) can be derived (Bringi and Chandrasekar, 2001; Thurai and Bringi, 2008). The disdrometer measurements were used to fit gamma DSD models and derive constrained relations between μ and Λ parameters at different temporal resolutions, which is necessary for retrieving DSDs from polarimetric radar measurements. At the same time, the disdrometer measurements were also used to (indirectly) validate the radar retrievals and study their consistency over time and across different events.

Similarly to Gatidis et al. (2020), preprocessing is applied to the disdrometer data.

1. Only the liquid type of precipitation was considered for further analysis. All DSDs with observations above the 22nd diameter class (drop diameters greater than 7 mm) were discarded, since they correspond to mixed or solid precipitation.

2. Each DSD should be comprised of at least three different diameter size classes in order to exclude spurious observations not related to rain.

2.2 Radar data

The radar data used to perform the DSD retrievals were collected by TU Delft's polarimetric S-band (λ=9.1 cm) FMCW radar TARA (Transportable Atmospheric RAdar; Heijnen et al., 2000) in Cabauw, the Netherlands. TARA was collocated with additional sensors. This included a Parsivel disdrometer (see Pfitzenmaier et al., 2018, Fig. 1) provided by the Leibniz Institute for Tropospheric Research (TROPOS). For this experiment, the radar antenna elevation angle of TARA was fixed at 45^∘ with constant azimuth. The collected polarimetric radar observables included the reflectivity factor at horizontal polarization (Z_hh) and differential reflectivity (Z_dr) at 200 m of height (corresponding to the minimum range of TARA). The full specifications of TARA during the ACCEPT campaign are given in Table 1 of Pfitzenmaier et al. (2018).

Table 1 Overview of the selected events. Date, duration, number of samples, average rain intensity ($\stackrel{\mathrm{‾}}{\mathrm{RR}}$), average mass-weighted mean diameter ($\stackrel{\mathrm{‾}}{D_{\mathrm{m}}}$), average number concentration ($\stackrel{\mathrm{‾}}{N_{\mathrm{T}}}$), parameters of the μ–Λ relationship (α, β), their corresponding percentage relative errors, correlation coefficient between μ and Λ for each event, and root mean square deviation (RMSD) between μ and Λ points of each event as well as the overall relationship. Note that only the DSDs conforming to the gamma model (see Sect. 3.1, DSD model) were considered when computing these statistics.

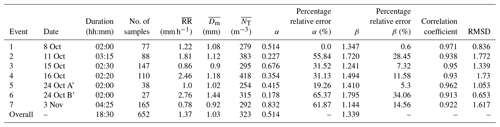
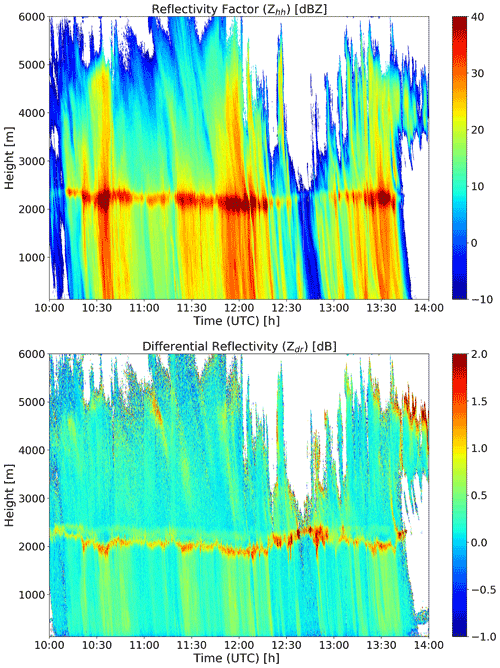
Figure 1 Height–time plots (top to bottom) of reflectivity factor (dBZ) and differential reflectivity (dB) on 11 October 2014.

In order to make the radar data comparable with the disdrometer data, all Z_hh and Z_dr measurements were down-sampled over successive 30 s sampling intervals. The radar and disdrometer data were then synchronized by determining the time shift that maximized the correlation coefficient between Z_hh Parsivel and Z_hh TARA.

Concerning the calibration of Z_hh and Z_dr, noise measurements were performed every day to account for possible variations in range, especially at the beginning and end of the IF filter. Before the start of the campaign, the calibration of Z_dr was verified using vertical profiling of drizzle and very light rain. The resulting histograms showed a mean offset of −0.11 dB with a standard deviation of 0.05 dB. Consequently, an offset of +0.11 dB was added to the measured Z_dr for the whole ACCEPT campaign. For the calibration of Z_hh, the transmit power was stored in the dataset, and there was a near-field correction for the non-full-overlap of the transmit and receive antenna beams using the method described in Sekelsky and Clothiaux (2002). However, an end-to-end calibration for Z_hh was missing.

2.3 List of events

A total of seven rain events over the whole measurement campaign were selected for further analysis. The criteria used to select events were as follows.

1. Each event must consist of predominantly stratiform rain and exhibit a well-defined melting layer signal in the radar data.

2. Each rain event must be at least 2 h in duration. This was deemed necessary to have enough data to fit a reliable μ–Λ relation and compute relevant performance metrics.

3. There should be no clear sign of changes in dynamics or microphysics (Jameson and Kostinski, 2001; Gorgucci et al., 2001; Uijlenhoet et al., 2003) with no long dry periods within each event.

4. Each event must contain several Z_dr and Z_hh values larger than 0.1 dB and 5 dBZ, respectively.

Table 1 presents a summary of the duration, rain intensity, and mass-weighted mean diameter (based on the disdrometer data) for each of the seven selected events. As can be seen, most of the events last between 120 and 150 min. The longest on 3 November is slightly longer than 4 h. The low rain intensity and mass-weighted mean drop diameter values confirm that the selected events are mostly comprised of light to moderate stratiform rain. This makes sense given the criteria used to select the events and the fact that the ACCEPT campaign took place in October–November in the Netherlands at a time when heavy convective events are rare.

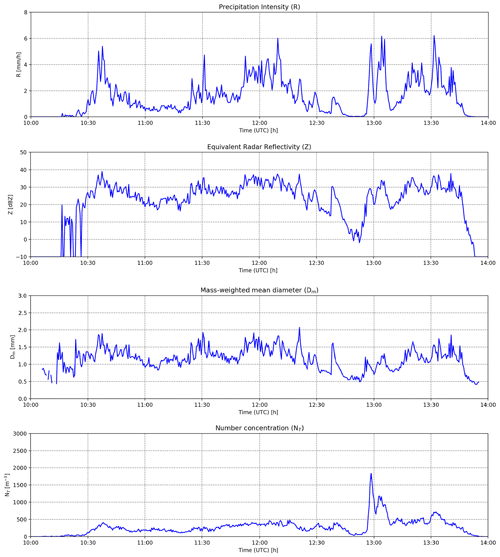
For illustration purposes, one of the seven events (E2, 11 October 2014) is plotted in Fig. 1. As can be seen, this event mostly consists of stratiform rain with a moderate intensity of approximately 1.8 mm h⁻¹ and a total duration of approximately 3 h between 10:30 and 13:45 UTC, including a short break between 12:45 and 12:55 UTC according to disdrometer observations on the ground (Fig. 2). The mass-weighted mean diameter is 1.1 mm, which is typical for light stratiform rain and small raindrop sizes. Event 2 was chosen because it has a relatively stable, well-defined melting layer around 2 km height as shown by the enhanced values of Z_hh and Z_dr in Fig. 1 at the top and bottom, respectively. The event also has a relatively low horizontal wind speed, which makes it easier to compare the radar retrievals aloft with the disdrometer measurements on the ground.

Figure 2 Time series (top to bottom) of precipitation intensity (mmh⁻¹), reflectivity factor (dBZ), mass-weighted mean diameter (mm), and number concentration (m⁻³) from Parsivel disdrometer data on 11 October 2014.

3 Methods

3.1 DSD model

The model used to approximate raindrop size distributions (DSDs) in this paper is the gamma distribution proposed by Ulbrich (1983):

$$\begin{array}{}\text{(1)}& N\left(D\right)=N_{\mathrm{0}}{D}^{\mathit{\mu }}{e}^{-\mathrm{\Lambda }D}=N_{\mathrm{T}}{\displaystyle \frac{{\mathrm{\Lambda }}^{\mathit{\mu }+\mathrm{1}}{D}^{\mathit{\mu }}}{\mathrm{\Gamma }(\mathit{\mu }+\mathrm{1})}}{e}^{-\mathrm{\Lambda }D},\end{array}$$

where N(D) is the raindrop size distribution in mm⁻¹ mm⁻³, μ is the shape parameter (unitless), Λ is the slope parameter (mm⁻¹), N₀ is the intercept parameter (mm^−1 μ m⁻³), and N_T is the total number concentration (m⁻³). The advantage of N_T over N₀ is that its unit does not depend on μ (Bringi and Chandrasekar, 2001). For convenience, the gamma model is reformulated in terms of the mass-weighted mean diameter D_m (mm) and the generalized intercept parameter N_w (mm⁻¹ m⁻³) (Testud et al., 2001; Bringi et al., 2003) to

$$\begin{array}{}\text{(2)}& {\displaystyle }N\left(D\right)=N_{\mathrm{w}}f\left(\mathit{\mu }\right){\left({\displaystyle \frac{D}{D_{\mathrm{m}}}}\right)}^{\mathit{\mu }}{e}^{-(\mathrm{4}+\mathit{\mu })\frac{D}{D_{\mathrm{m}}}},\end{array}$$

where f(μ), N_w, and D_m are given by

$$\begin{array}{}\text{(3)}& {\displaystyle }f\left(\mathit{\mu }\right)={\displaystyle \frac{\mathrm{6}}{{\mathrm{4}}^{\mathrm{4}}}}{\displaystyle \frac{(\mathit{\mu }+\mathrm{4}{)}^{(\mathit{\mu }+\mathrm{4})}}{\mathrm{\Gamma }(\mathit{\mu }+\mathrm{4})}},\text{(4)}& {\displaystyle }{N}_{\mathrm{w}}={\displaystyle \frac{{\mathrm{4}}^{\mathrm{4}}}{\mathit{\pi }{\mathit{\rho }}_{\mathrm{w}}}}\left({\displaystyle \frac{\mathrm{LWC}}{{D_{\mathrm{m}}}^{\mathrm{4}}}}\right),\text{(5)}& {\displaystyle }{D}_{\mathrm{m}}={\displaystyle \frac{\mathrm{4}+\mathit{\mu }}{\mathrm{\Lambda }}}.\end{array}$$

In the equations above, LWC denotes the liquid water content (in g m⁻³), and ρ_w is the density of liquid water (10⁻³ g mm⁻³).

It should be mentioned that even though the gamma distribution is the most popular and widely accepted model for representing DSDs in the literature, several studies have questioned its adequacy (Gatidis et al., 2020; Thurai et al., 2019; Cugerone and De Michele, 2015; Adirosi et al., 2016), setting criteria and proposing different tools to check the gamma hypothesis on a case-by-case basis.

3.2 Parameter fitting

The best parameters (μ, D_m, and N_w) for describing the DSDs measured by the disdrometer are obtained by using normalized parameterization of the gamma DSD model based on D_m (ratio of fourth- to third-order moment). To estimate μ, we first calculate D_m and N_w (directly from the measured DSD spectra). The value of μ is determined by testing all possible values of μ between −3 and 15 and choosing the one that minimizes the cost function (CF, Eq. 6). Finally, we derive Λ through its relationship with D_m and μ (Eq. 5):

$$\begin{array}{}\text{(6)}& \mathrm{CF}=\sum _{i=\mathrm{3}}^{\mathrm{22}}\mid {\log }_{\mathrm{10}}\left(N_{\mathrm{obs}}\right(D_i\left)\right)-{\log }_{\mathrm{10}}\left(N\right(D_i\mid \mathit{\mu }\left)\right)\mid ,\end{array}$$

where D_i is the center of the ith diameter class in the Parsivel disdrometer and N_obs (D_i) represents the volumetric size distribution measurements for each diameter class. Note that the index i ranges from 3 to 22 because the first two diameter classes in the Parsivel are always zero and the diameter classes above 22 correspond to particles that are too large to be associated with rain.

3.3 μ–Λ relation

When an empirical relation between shape and scale parameters is used the gamma model is often called constrained gamma. Note that the term “constrained gamma” denotes a gamma DSD model in which the shape and rate parameters are linked by a deterministic function. Mathematically, this is equivalent to reducing the number of free parameters from three to two, which is convenient in radar-based DSD retrievals. However, the uncertainty related to estimating μ and Λ based on observed DSD spectra remains. Hence, the constrained gamma DSD model and all its associated moments still remain stochastic in nature.

Numerous studies have used and proposed constrained relationships between these two DSD parameters. The most common models are based on second-order polynomial fits, firstly introduced by Zhang et al. (2001, 2003). Since then, several other studies have proposed updated polynomial μ–Λ relationships based on either seasonal (Seela et al., 2018) or regional criteria (Chen et al., 2016). Polynomial models between μ and Λ were also proposed for DSD retrievals using microwave link measurements (Berne and Schleiss, 2009; van Leth et al., 2020). In this study, μ–Λ relationships are modeled using a slightly different power-law model:

$$\begin{array}{}\text{(7)}& \mathrm{\Lambda }=\mathit{\alpha }(\mathit{\mu }+\mathrm{3}{)}^{\mathit{\beta }},\end{array}$$

with two coefficients α and β as given in Eq. (8).

The power-law model above was chosen mainly for mathematical reasons since it ensures that Λ remains positive across all scales and avoids the problem of having to choose between a first-, second-, or third-order polynomial. The power-law model is also easier to justify than a parabola from a physical and mathematical point in light of the scale invariance of DSDs under proper normalization, as pointed out by previous researchers (Torres et al., 1994; Testud et al., 2001). However, for the sake of completeness, we also examined the polynomial model during our study and concluded that it did not make a big difference from a practical point of view (i.e., it has similar goodness of fit over the considered range of μ values). Nevertheless, we decided to use the power-law model in this study since it is more appropriate than a polynomial from a theoretical point of view.

Note that the goal of this study is not to question the validity of previous μ–Λ relationships nor optimize the parameters behind them (which depend on the dataset used) but to take a closer look at the sensitivity of the obtained fits to various underlying assumptions. Critical aspects that were investigated include whether the μ–Λ relation remains stable with respect to different sampling resolutions, drop number concentrations, types of stratiform rain events, or the validity of the gamma DSD hypothesis itself. At the same time, one has to keep in mind that the limitation of the Parsivel in terms of the detection of small droplets might lead to overestimated D_m and μ values, since the width of the distribution will be underestimated.

3.4 DSD retrieval method

Because the gamma DSD model involves three parameters, three different radar measurements representative of three weighted moments of the DSD are required to retrieve the DSD in a given radar resolution volume. The retrieval method used in this paper is described in Zhang et al. (2001). It involves a combination of reflectivity factor at horizontal polarization (Z_hh), differential reflectivity (Z_dr), and a empirical relationship between the DSD shape parameter (μ) and slope parameter (Λ), commonly referred to as a μ–Λ relationship. The main steps of the retrieval method can be summarized as follows.

1. Impose a μ–Λ relationship Λ=g(μ) based on nearby disdrometer observations or literature values. In our case, a power-law relationship is used:

   $$\begin{array}{}\text{(8)}& \mathrm{\Lambda }=\mathrm{0.514}(\mathit{\mu }+\mathrm{3}{)}^{\mathrm{1.339}},\end{array}$$

   where the prefactor and exponent were determined by combining all the data from all seven events in Table 1.

2. Consider all possible values of μ between −3 and 15 in steps of 0.01. For each μ value, calculate Z_dr through Eq. (9):

   $$\begin{array}{}\text{(9)}& \begin{array}{rl}{Z}_{\mathrm{dr}}& ={\displaystyle \frac{Z_{\mathrm{hh}}}{Z_{\mathrm{vv}}}}={\displaystyle \frac{{\int }_{\mathrm{0}}^{D_{\max }}N\left(D\right){\mathit{\sigma }}_{\mathrm{hh}}\left(D\right)\mathrm{d}D}{{\int }_{\mathrm{0}}^{D_{\max }}N\left(D\right){\mathit{\sigma }}_{\mathrm{vv}}\left(D\right)\mathrm{d}D}}\\ & ={\displaystyle \frac{{\int }_{\mathrm{0}}^{D_{\max }}{D}^{\mathit{\mu }}{e}^{-g\left(\mathit{\mu }\right)D}{\mathit{\sigma }}_{\mathrm{hh}}\left(D\right)\mathrm{d}D}{{\int }_{\mathrm{0}}^{D_{\max }}{D}^{\mathit{\mu }}{e}^{-g\left(\mathit{\mu }\right)D}{\mathit{\sigma }}_{\mathrm{vv}}\left(D\right)\mathrm{d}D}}={\displaystyle \frac{h_{\mathrm{1}}\left(\mathit{\mu }\right)}{h_{\mathrm{2}}\left(\mathit{\mu }\right)}},\end{array}\end{array}$$

   where σ_hh (mm²) and σ_vv (mm²) are the copolar radar cross-sections of raindrops with equivolume spherical diameter D at horizontal and vertical polarizations, respectively, and D_max (mm) is a reasonable maximum drop diameter (e.g., 7 mm in our case). In the literature several studies tried to link D_max with D₀ such as Ulbrich and Atlas (1984), who concluded that $D_{\max }/D_{\mathrm{0}}>\mathrm{2.5}$ is what is typically observed in natural rainfall, and Carey and Petersen (2015), who recommended using $D_{\max }=\mathrm{3}\cdot D_{\mathrm{0}}$. The detailed expression of the radar cross-sections can be found in Eq. (3) in Unal (2015).

3. Keep the μ value for which the Z_dr value in Eq. (9) is closest to the measured Z_dr value by the radar.

4. Infer N_w from Z_hh in Eq. (10), where $\widehat{\mathit{\mu }}$ is the retrieved μ value from the previous step:

   $$\begin{array}{}\text{(10)}& \begin{array}{rl}{Z}_{\mathrm{hh}}& =N_{\mathrm{w}}{\displaystyle \frac{{\mathit{\lambda }}^{\mathrm{4}}f\left(\widehat{\mathit{\mu }}\right)}{{\mathit{\pi }}^{\mathrm{5}}|K_{\mathrm{w}}{|}^{\mathrm{2}}}}\underset{\mathrm{0}}{\overset{D_{\max }}{\int }}{\left({\displaystyle \frac{D}{{\widehat{D}}_{\mathrm{m}}}}\right)}^{\widehat{\mathit{\mu }}}{e}^{-(\mathrm{4}+\widehat{\mathit{\mu }})\frac{D}{{\widehat{D}}_{\mathrm{m}}}}\\ & {\mathit{\sigma }}_{\mathrm{hh}}\left(D\right)\mathrm{d}D,\end{array}\end{array}$$

   where λ is the radar wavelength in millimeters (i.e., 90.96 mm for TARA), $|K_{\mathrm{w}}{|}^{\mathrm{2}}$ is the dielectric factor of water, and ${\widehat{D}}_{\mathrm{m}}=\frac{\mathrm{4}+\widehat{\mathit{\mu }}}{g\left(\widehat{\mathit{\mu }}\right)}$.

5. Retrieve ${\widehat{N}}_{\mathrm{T}}$ by integrating the retrieved DSD:

   $$\begin{array}{}\text{(11)}& \begin{array}{rl}{\widehat{N}}_{\mathrm{T}}& =\underset{\mathrm{0}}{\overset{D_{\max }}{\int }}\widehat{N}\left(D\right)\mathrm{d}D=\underset{\mathrm{0}}{\overset{D_{\max }}{\int }}{\widehat{N}}_{\mathrm{w}}f\left(\widehat{\mathit{\mu }}\right){\left({\displaystyle \frac{D}{{\widehat{D}}_{\mathrm{m}}}}\right)}^{\widehat{\mathit{\mu }}}\\ & e^{-(\mathrm{4}+\widehat{\mathit{\mu }})\frac{D}{{\widehat{D}}_{\mathrm{m}}}}\mathrm{d}D.\end{array}\end{array}$$

4 Analysis of μ–Λ relationship

4.1 Variations in μ–Λ relationship from one event to another

In the following, we analyze the variations of the μ–Λ relationships from one event to another. For this, a filter was applied identical to Gatidis et al. (2020), and only the cases which satisfied the gamma model hypothesis were considered. The adequacy of the gamma model was assessed based on a combination of a Kolmogorov–Smirnov goodness-of-fit test and Kullback–Leibler divergence. In total, approximately 40 % of the DSDs passed the tests and were accepted. On an event-to-event basis, that number varies between 36 % and 45 %.

In order to investigate and visualize possible differences between events, all seven events were plotted using different colors in Fig. 3. The overall relationships by Zhang et al. (2001, 2003) were added for comparison. As can be seen in Fig. 3, most of the event-specific μ–Λ relations stay relatively close to the overall relation, except for events 2 and 6 for which larger deviations for higher values of μ (i.e., μ>8) are visible. For event 6, the differences can be explained by the limited range of μ, with most values remaining between 3 and 5 and only a single observation falling between 5 and 15. This limited range of variability significantly affects the reliability of the estimated μ–Λ relationship, especially for values smaller than 3 and larger than 5. For event 2, the differences can be explained by the presence of a few outliers in the upper-right part of the scatter plot, corresponding to DSDs with low number concentrations and high sampling uncertainties.

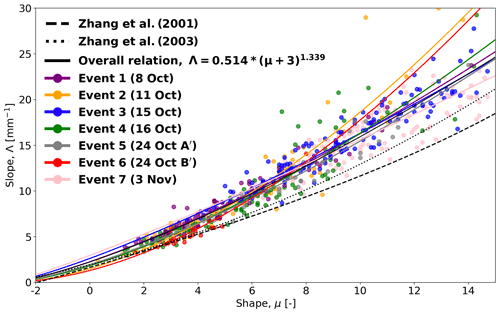
Figure 3 Scatter plot between μ and Λ of the selected events colored by event (only gamma DSDs were considered). The μ–Λ relationship of each event was fitted and plotted against the overall relationship. The proposed relations by Zhang et al. (2001, 2003) were plotted as a reference from the literature.

For each selected event, the sample sizes, the fitted power-law parameters α and β, and their percentage relative differences against the overall relation are presented in Table 1. The relative errors of the parameters depend on the characteristics of each event, with event 1 being the closest to the overall relation and event 6 exhibiting the largest differences. In order to have a more complete picture of each event, the correlation coefficient between μ and Λ as well as the root mean square deviation (RMSD) between μ and Λ points of each event and the overall relationship were calculated and are presented in Table 1. Even though event 6 has the weakest correlation coefficient, it has the lowest RMSD mainly due to its small sample size (the smallest in the event list) and the way the data are concentrated close to the fitted line. Event 1 shows the strongest relation between μ and Λ, while at the same time event 2 has the highest RMSD because of its outliers in the upper-right part of the scatter plot.

The event-specific and overall μ–Λ relations are clearly different from previously proposed relations by Zhang et al. (2001, 2003). For a fixed μ value, the overall μ–Λ relation for the seven selected events predicts higher Λ values compared with the ones by Zhang et al. (2001, 2003). This can be explained by the fact that Λ is inversely proportional to the mass-weighted mean diameter and that the Zhang et al. (2001, 2003) relations were derived under different climatological conditions in Oklahoma in the US, where convective rain events with larger raindrops are more common than in the Netherlands.

Although the overall relationship might not necessarily be optimal for each individual event, our results show that it still provides a fairly good approximation of the average μ–Λ relationship across all seven considered events. Also, one has to keep in mind that the low sample sizes and limited ranges for μ make it practically impossible to derive reliable and representative μ–Λ relations for each individual event. To avoid sampling issues such as those encountered in event 6 and increase the robustness of our results, all remaining sensitivity analyses and retrievals were therefore conducted using the overall μ–Λ relation.

4.2 Sensitivity of μ–Λ relationship to gamma hypothesis

One crucial factor that could affect the μ–Λ relationship is the gamma DSD assumption. To investigate this issue, we temporarily added back all DSDs that were excluded from the previous analysis because they did not conform to the gamma model according to the criteria set by Gatidis et al. (2020). For each event, we recalculated the individual μ–Λ relationship and compared the new results to the ones obtained using only the DSDs that satisfied the gamma assumption. In six out of seven cases, the inclusion of the non-gamma cases resulted in larger α and smaller β values. However, these changes were not reflected visually in the μ–Λ scatter plot as the two opposite changes compensate for each other. Therefore, apart from slightly changing the parameter values, the gamma hypothesis does not appear to have a strong effect on the overall μ–Λ relation. Also, the changes to α (0.518 from 0.514) and β (1.328 from 1.339) were rather small and not statistically significant. The fact that the overall μ–Λ relation is rather stable with respect to the gamma DSD hypothesis is an interesting result, especially given the fact that there are large differences in sample sizes between non-gamma (1829) and gamma DSDs (652).

4.3 Sensitivity of μ–Λ relationship to N_T

Using the overall relationship from Sect. 4.1 as a reference, the influence of the number concentration on the μ–Λ relationship was investigated. It would be interesting to investigate whether the events for which the DSD is predominantly number-controlled lead to more or less stable μ–Λ relationships than events with size-controlled DSDs. Three different N_T thresholds corresponding to different percentiles of N_T (25 %, 50 % and 75 %) were applied, and only the DSDs with number concentrations above these thresholds were considered. In Fig. 4, the three derived μ–Λ relations obtained after applying the N_T filters are shown against the overall relation (no filter). As the N_T threshold is increased from 225 to 300 and 390 m⁻³ (Figs. 4b–d), the μ–Λ relation remains relatively stable for lower μ values, gradually getting closer to the one proposed by Zhang et al. (2003), especially for higher values of the shape parameter (μ>7). This can be partly explained by the fact that, on average, higher N_T values correspond to higher rainfall intensities and larger drop diameters. Also, the average mass-weighted mean diameter increases by approximately 10 % as we increase the threshold on N_T. This may not represent a big change, but it can be enough to slightly affect the μ–Λ relation. However, we believe the main reason the μ–Λ relation changes with increasing N_T is sampling uncertainty. Indeed, our dataset predominantly features stratiform rain events with low rainfall intensities, low number concentrations, and relatively low and constant mass-weighted mean diameters (see Table 1). As we apply higher thresholds on N_T, the DSD samples that only contain a small number of drops and are associated with a higher sampling uncertainty get removed. Consequently, the remaining DSDs with higher number concentrations tend to be associated with lower sampling uncertainties, which leads to more reliable μ–Λ estimates. Moreover, it is worth pointing out that because of the way μ is estimated through the cost function in Eq. (6), the error distribution of μ tends to be positively skewed. On average, we are therefore more likely to overestimate μ and underestimate the spread of the DSD rather than the opposite. Since μ and Λ values are positively correlated through their relation with D_m in Eq. (5), any overestimated μ value automatically results in an overestimated Λ value (to compensate and get the correct D_m). Consequently, as we increase the N_T threshold, sampling errors get reduced and the positively skewed outliers with high μ and Λ values progressively disappear. This removes more and more points on the upper side of the μ–Λ curve, pushing the new relation down towards the one proposed by Zhang et al. (2003). Regarding the sensitivity of the α and β parameters describing the μ–Λ relationship, our analyses show that they exhibit an opposite behavior, increasing and decreasing, respectively, as we increase the threshold on N_T. The latter can be attributed to a gradual flattening of the relationship and increase of the intercept parameter. Note that another similar approach to reduce the uncertainty in the estimated μ–Λ relationship without applying a threshold on N_T could be to consider temporal aggregation intervals longer than 30 s. However, this would significantly reduce the amount of data available for analysis.

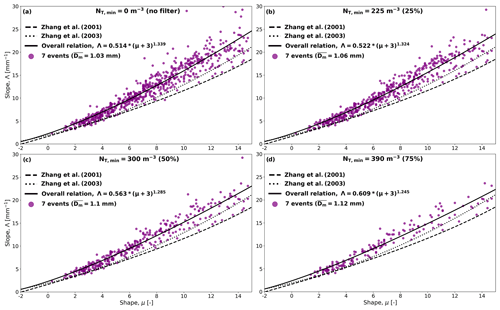
Figure 4 Four scatter plots between μ and Λ of the selected events using four different minimum N_T thresholds corresponding to different percentiles of N_T. The μ–Λ relationship of each N_T threshold was fitted and plotted against the proposed relations by Zhang et al. (2001, 2003). (a) $N_{\mathrm{T},\min }=\mathrm{0}$ m⁻³ (no filter), (b) $N_{\mathrm{T},\min }=\mathrm{225}$ m⁻³, (c) $N_{\mathrm{T},\min }=\mathrm{300}$ m⁻³, and (d) $N_{\mathrm{T},\min }=\mathrm{390}$ m⁻³.

4.4 Influence of sampling resolution on the overall μ–Λ relation

In the following, the DSD data corresponding to the seven selected events were resampled at four different temporal resolutions of 30, 60, 240, and 480 s to investigate the sensitivity of the μ–Λ relationship to the choice of the temporal resolution. Similarly to before, only the resampled DSDs which satisfied the gamma hypothesis were kept for analysis. Figure 5 shows that the overall μ–Λ relationship remains very stable, regardless of the considered sampling resolution. Table 2 shows more details about the fitted power-law parameters α and β at each resolution, including their percentage relative differences against the overall relation at 30 s. We can see that the relative error affecting the parameters slightly increases as the temporal resolution is reduced. The latter can be attributed to the lower number of samples available for fitting the parameters. Apart from these obvious sampling effects, the choice of the temporal aggregation scale seems to have very little effect on the overall μ–Λ relationship, which remains rather stable across multiple aggregation timescales.

Table 2 The parameters of the μ–Λ relationship (α, β) for different sampling resolutions and their percentage relative error against the corresponding values at 30 s.

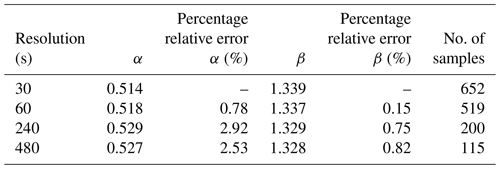
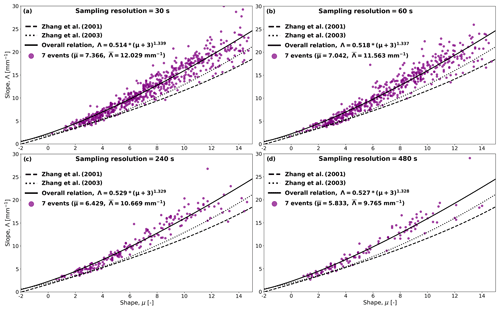
Figure 5 Four scatter plots between μ and Λ of the selected events using different resolutions. The μ–Λ relationship of each resolution was fitted and plotted against the proposed relations by Zhang et al. (2001, 2003). (a) 30 s, (b) 60 s, (c) 240 s, and (d) 480 s.

Note that as we decrease the temporal resolution, the mean values of μ and Λ (Fig. 5) also decrease. This means that there is a progressive transition from peaked DSDs at higher sampling resolutions to broader, more widespread DSDs at lower resolutions. Decreasing the sampling resolution therefore causes the μ and Λ values to shift toward the bottom-left part of the scatter plot. However, while the points shift, they remain remarkably close to the initial μ–Λ curve derived at the highest temporal resolution of 30 s. The fact that the μ and Λ values change with resolution but that the overall relation between them is preserved across scales suggests that there is a fundamental physical link between certain moments of the DSD, such as the spread and the mean. Also, this relation seems to be quite robust regardless of whether the gamma assumption is valid or not and is only slightly affected by N_T. In steady rainfall conditions, it should therefore be possible to use the same μ–Λ relationship for DSD retrievals across multiple temporal scales. This is of high importance given the fact that μ–Λ relations are often used to retrieve DSDs from radar observations, which have different sampling volumes and levels of aggregation than disdrometer data. Moreover, the use of a μ–Λ relationship may still be justified from a physical point of view, even if the underlying DSDs do not strictly comply with the gamma distribution hypothesis. Obviously, the fact that we have selected relatively similar stratiform events with low rainfall intensities and low temporal variability is a crucial factor here since it means that by resampling, we do not significantly change the properties of the DSDs or mix together different rainfall regimes. By contrast, larger differences in μ–Λ relationships can be expected for mixed-type rainfall events with multiple and rapid alternations between stratiform and convective rain.

On the other hand, there is still substantial controversy in the literature around the reason why μ–Λ relations exist in the first place and why certain DSD parameters are linked to each other. One justification could be that the effective number of parameters needed to describe most DSDs is probably fewer than three. In other words, under proper normalization, all DSDs look rather similar to each other. For example, Torres et al. (1994) introduced a single DSD normalization technique based on one reference moment (usually the rain rate). Later, Testud et al. (2001) and Lee et al. (2004) proposed a more general normalization technique based on two reference moments (usually the third and sixth moments). The existence of a μ–Λ relationship may just be the consequence of such scaling laws. In their study, Moisseev and Chandrasekar (2007) have also argued that data filtering can have a strong influence on the relation itself, leading to spurious links between μ and Λ. However, this is not the case in our study. On the contrary, our results show that when events with similar characteristics are chosen, the overall μ–Λ relationship can be rather stable, barely depending on the different filters applied to the data (e.g., inclusion or exclusion of non-gamma DSDs or minimum threshold for Z_hh and Z_dr). Other studies have pointed out that the constraints linking μ and Λ during parameter fitting can lead to correlated errors between estimated gamma DSD parameters and biased relationships (Williams et al., 2014; Moisseev and Chandrasekar, 2007). Indeed, because of the way we fit μ and Λ through D_m (see Sect. 3.1, DSD model), the parameters end up being positively correlated with each other. In other words, if μ is overestimated, Λ will also be overestimated because it has to compensate for the bias in μ. To address this, Williams et al. (2014) proposed a σ'–D_m relationship, wherein D_m is the mass-weighted mean diameter and σ' a new mass spectrum standard deviation, defined and constructed to be statistically independent of D_m. Even though their approach seems to lead to smaller biases, our results show that it is also possible to derive reliable μ–Λ relationships without defining a new σ, simply by excluding the non-gamma DSDs cases and carefully filtering out DSDs with very low N_T values.

5 Sensitivity of DSD retrievals

In this section, the sensitivity of the DSD retrieval method as a whole is evaluated. First, the TARA and Parsivel observations are compared with each other to highlight their differences and understand how possible biases in reflectivity or differential reflectivity affect the accuracy of the retrievals. Then, the sensitivity of the retrieved DSD parameters to different bias corrections, scale corrections, and data filters is quantified, and possible ways to mitigate errors during retrievals are proposed.

5.1 Overall agreement between radar and disdrometer

5.1.1 Agreement of Z_hh and Z_dr observations between TARA and Parsivel

In this section the agreement between the Parsivel and TARA measurements is investigated. For the sake of the comparison between TARA and Parsivel observables, the radar equivalent reflectivity factor derived from disdrometer data was used as the measured reflectivity factor at horizontal polarization (Z_hh,Pars). As for the differential reflectivity, using Rayleigh scattering, the calculated radar cross-sections of raindrops with equivolume spherical diameter D at horizontal and vertical polarization were used (Eq. 9) for estimating reflectivity at horizontal and vertical polarization, respectively. From those, the differential reflectivity value from the Parsivel (Z_dr,Pars) can be obtained.

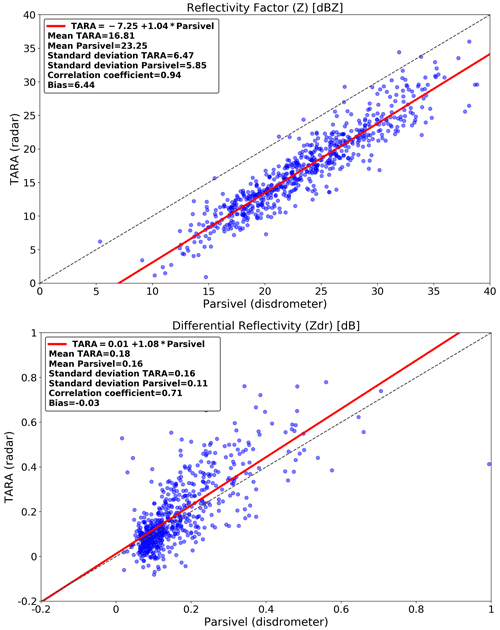
The goal is to quantify how well the measurements of the two sensors agree with each other before the DSD retrievals. Fig. 6 shows the scatter plots of the reflectivity factor (Z_hh, top) and differential reflectivity (Z_dr, bottom) from the disdrometer versus TARA at 200 m of height. For this first comparison, the Z_hh and Z_vv measurements of TARA were aggregated (in linear scale) to 30 s in order to be comparable with the disdrometer data. No other additional filter was applied. Figure 6a shows that Z_hh measurements are highly correlated (correlation coefficient = 0.94). However, the radar significantly underestimates Z_hh compared with the disdrometer. The offset in Z_hh slightly varies with time but is of the order of 6 to 7 dBZ (overall bias 6.44 dBZ). Additional bias analyses at a different height of 400 m show that the offset does not change substantially with height, which suggests that the FMCW incomplete beam overlap correction at near ranges (see Sect. 2.2, radar data) works well and that the offset in reflectivity is likely due to calibration issues of TARA rather than range-related issues. Unlike Z_hh, the differential reflectivity measurements appear to be in much better agreement with the disdrometer (overall bias −0.03 dB), as can be seen in the bottom panel of Fig. 6. However, the correlation for Z_dr is lower (correlation coefficient = 0.71) and there is significant scatter, especially for higher values of Z_dr. Note that the vast majority of Z_dr values are small (less than 0.2 dB), which makes sense given that we are mostly dealing with light stratiform rain and that the elevation angle of 45^∘ in TARA further reduces the magnitude of Z_dr.

Figure 6 Scatter plot between the observations of Z_hh (dBZ) and Z_dr (dB) from the disdrometer and the radar.

5.1.2 Z_hh–Z_dr relationships for TARA and Parsivel

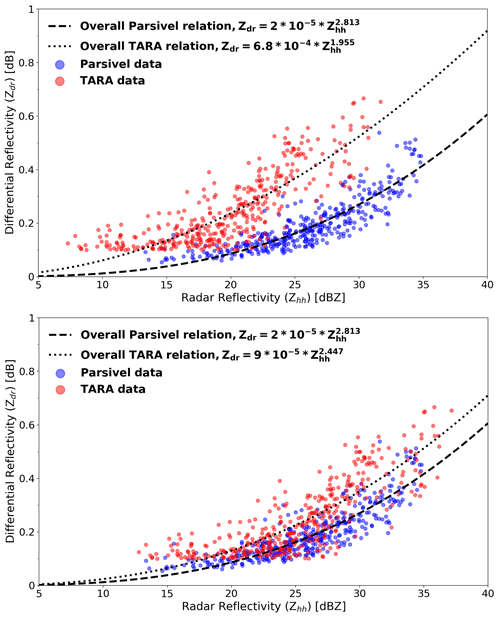
In the top panel of Fig. 7, the Z_hh–Z_dr relation of each sensor is presented. It shows that most of the time, TARA measures higher Z_dr values for a given Z_hh than the disdrometer. Once the calibration bias in Z_hh is removed (Fig. 7, bottom), the agreement improves and the radar and disdrometer-derived relationships nicely overlap with each other. Nevertheless, and despite the bias correction, TARA still tends to measure slightly higher Z_dr values than the Parsivel for a given Z_hh. This can be due to a difference in height or scale between the two measurements. The absence of a clear relation between Z_hh and Z_dr is not really a problem for the DSD retrieval method itself. In fact, a relation between Z_hh and Z_dr is not always expected since Z_hh depends on N_T, while Z_dr does not. However, the fact that TARA and the Parsivel disdrometer exhibit different Z_hh–Z_dr relationships might negatively impact the accuracy and consistency of the retrieved DSDs.

Figure 7 Z_hh–Z_dr relations between the disdrometer and the radar (top to bottom) before and after the calibration bias in Z_hh is removed.

5.1.3 First retrievals

In the following, we apply the DSD retrieval method described in Sect. 3.4 using Z_hh and Z_dr measurements from TARA and compare the results to the disdrometer data at 30 s resolution. For the retrievals, we used the overall μ–Λ relationship inferred in Sect. 3.4 (DSD retrieval method) from the disdrometer observations at 30 s sampling resolution.

For illustration purposes, the event on 11 October 2014 was chosen. The time series of retrieved μ, D_m, and N_T as well as observed Z_hh and Z_dr values for this event are presented in Figs. 8 and 9 (top). Overall, we see that there is rather good agreement in terms of the retrieved μ and D_m values as long as the Z_dr values are not too low (i.e., > 0.1 dB). When Z_dr is low (e.g., between 12:20 and 13:15 UTC), we see that the retrievals become very uncertain, exhibiting much larger fluctuations over time.

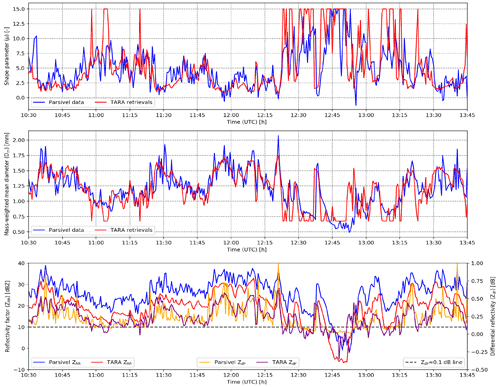
Figure 8 Time series of the DSD retrievals (μ and D_m) as well as Z_hh and Z_dr observations from the disdrometer and the radar.

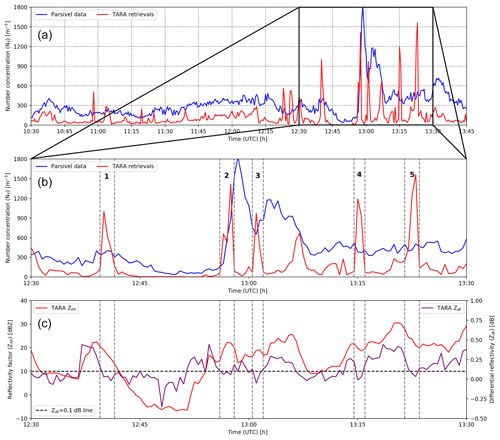
Figure 9 Time series of the N_T retrievals: (a) zoomed version for the period between 12:30 and 13:30 UTC (b) and the corresponding Z_hh and Z_dr observations from the disdrometer and the radar (c).

Compared with μ, the retrieved N_T values are substantially more uncertain. There are some outliers, and, on average, the retrieved N_T values from TARA are about 100 m⁻³ lower than those from the Parsivel disdrometer. This bias is attributed to the 6–7 dB offset in Z_hh in TARA, which propagates nonlinearly to N_T through the link between Z_hh and N_T in Eqs. (10)–(11). On the other hand, we also see some isolated cases in which N_T is overestimated, such as at the beginning (10:57 UTC) and end (13:15 and 13:23 UTC) of the event. These periods are characterized by underestimated Z_dr and D_m values by TARA, which, in combination with the relatively high Z_hh values, leads to an overestimation of N_T.

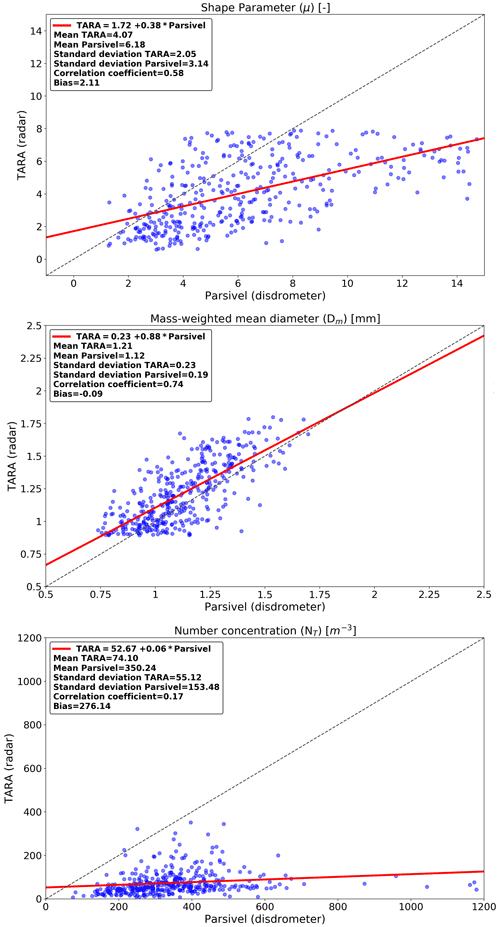
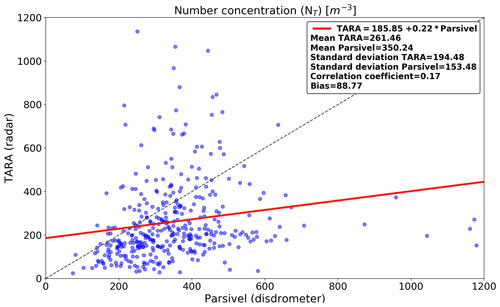
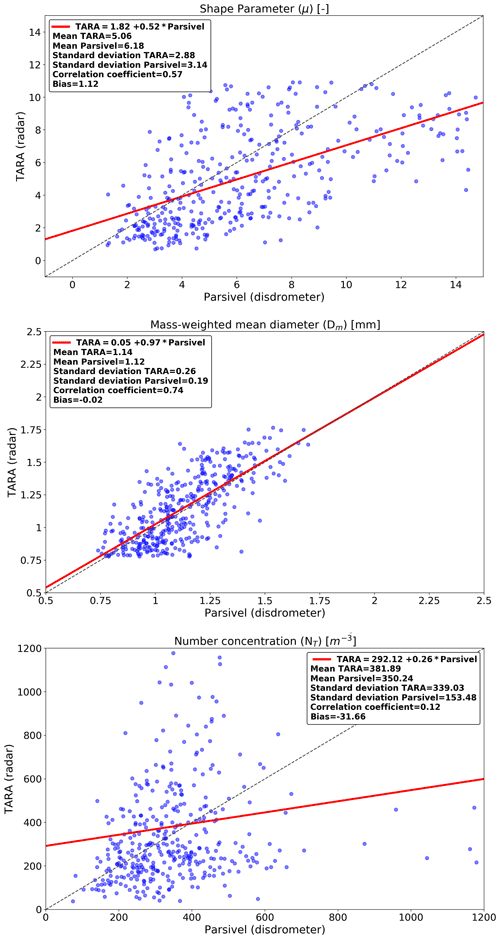
For a better overview, the retrieved DSD parameters (μ, D_m, and N_T) for all selected events are plotted against the ones from the disdrometer in Fig. 10. We can see that the retrieved μ values from the radar tend to be lower compared with the disdrometer. The overall bias in the retrieved μ values is 2.11, which is rather large and not immediately apparent from the case study on 11 October (Fig. 8). Note that the retrieved μ values from TARA can never exceed 8 due to the 0.1 dB cutoff applied to Z_dr observations (very light rain, peaked DSDs). Because of this, there is a slight conditional bias in the retrieved μ values for low Z_dr values. Since μ values are unaffected by the bias in reflectivity and Z_dr measurements appear to be well-calibrated, the bias we see in μ values must either be due to the μ–Λ relationship or to differences in scale, height, and measurement principles between the two sensors. Unlike μ, there is better agreement for D_m retrievals with −0.09 overall bias. This is the case for the case study on 11 October as well, for which D_m retrievals from Parsivel and TARA are almost similar throughout the event (Fig. 8, middle) except for the period between 12:45 and 13:00 when Z_dr is low. Looking at the number concentration (Fig. 10, bottom), we see a significant underestimation in N_T from TARA (overall bias = 276 m⁻³, multiplicative bias = 4.52), which can be explained by the large 6.44 dBZ bias in Z_hh in TARA and is consistent with the previously reported underestimation for the event on 11 October 2014.

Figure 10 Scatter plot of DSD retrievals (μ, D_m, and N_T) between the radar and disdrometer.

Despite the fact that N_T values tend to be underestimated on average, we can also see several large spikes in retrieved N_T values, such as during the second half of the case study event (Fig. 9, top). If we perform a more in-depth analysis of this period (i.e., between 12:30 and 13:30 UTC) in Fig. 9 (middle) and compare it with the Z_hh and Z_dr observations of the corresponding period (Fig. 9, bottom), we see that all five spikes in N_T correspond to low values of Z_dr and relatively high Z_hh values. The low Z_dr leads to large μ values and underestimated raindrop sizes during the retrieval. To compensate for this and achieve the correct reflectivity, N_T needs to be increased by a lot. Note that spikes in N_T can still occur even if Z_hh is modest or decreasing locally, as long as Z_dr is very small; for example, for spikes 2 and 3 there is a local maximum for Z_hh, while for the other spikes the Z_hh decreases.

The differences documented above are important because they show that DSD retrievals can be very sensitive to combined biases in Z_dr and Z_hh relative to each other. The latter can be linked to calibration issues. However, inconsistencies can also arise due to differences in height, sampling volumes, and temporal aggregation scales between radar and disdrometer measurements, also known as the nonuniform beam-filling problem (Ryzhkov, 2007; Durden and Tanelli, 2008).

5.2 Sensitivity to calibration bias correction

Given the systematic underestimation of the reflectivity factor in TARA, a bias correction was applied before proceeding with the DSD retrievals. Indeed, the bias correction was considered essential to get more reliable results, especially for N_T. Since the N_T retrievals require the reflectivity to be converted from logarithmic (dB) to linear scale (mm⁶ m⁻³), a multiplicative adjustment factor known as the $G/R$ ratio (i.e., the ratio of the sum of Parsivel to TARA reflectivity values) was used to bias-correct the TARA measurements, treating the disdrometer observations as the reference truth. The value of the $G/R$ ratio was 4.52, which confirmed the large calibration bias of TARA. To address the bias, all TARA reflectivity values (in linear scale) were multiplied by 4.52 and the new DSD parameters were retrieved. As expected, the first two DSD parameters μ and D_m were completely unaffected by the bias adjustment, as they only depend on Z_dr (see Sect. 3.4, DSD retrieval method). Figure 11, on the other hand, shows that N_T retrievals were substantially improved, and the bias decreased from 276 to 89 m⁻³. Despite the lower bias, we can see that large uncertainties remain in the retrieved N_T values, as highlighted by the large scatter and frequent outliers.

Figure 11 Scatter plot of N_T retrievals between the radar and disdrometer after applying the calibration bias correction to Z_hh.

5.3 Sensitivity to scale bias correction

In the following, a small additional bias adjustment was applied to Z_dr to try to account for the large difference in sampling volumes between the TARA radar and the Parsivel disdrometer. This second adjustment is conceptually different from the one applied to Z_hh, which was primarily due to calibration issues. Contrarily to Z_hh, the differential reflectivity Z_dr of TARA is assumed to be well-calibrated. Therefore, the differences in mean and standard deviation are primarily attributed to differences in scale, height, and measurement principles. Note that this scale bias also applies to Z_hh. However, for Z_hh, the effect is masked by the large calibration bias and the two cannot be separated.

According to Fig. 6 (bottom), the average Z_dr values measured by TARA are 0.03 dB larger than the ones from the Parsivel disdrometer; this makes sense given that the radar sees a larger measurement volume, which makes it more likely to contain at least a few larger drops. Even though a 0.03 dB difference seems small, such a bias can have a significant effect on the DSD retrievals given that the majority of Z_dr values are rather small (e.g., between 0.1 and 0.2 dB). A 0.03 dB bias in Z_dr therefore represents a relative error of 15 %–30 %.

Figure 12 shows the retrieved DSD parameters after correcting for the scale bias. We see a reduction of the bias affecting μ and D_m, which are directly linked to Z_dr. The bias affecting μ is halved from 2.11 to 1.12, and the bias affecting D_m is reduced from −0.09 to −0.02 mm. The correlation coefficient remains relatively stable, regardless of the scale correction. Despite the improvements for μ and D_m, the N_T retrievals remain problematic, with a low correlation coefficient of 0.12 (compared to 0.17 without scale bias correction) and moderate bias of −32 m⁻³ (compared to 89 m⁻³ without correction). Also, the average N_T value increased significantly from 261 to 382 m⁻³ (+46 %), which highlights the large sensitivity of N_T to changes in the differential reflectivity.

Figure 12 Scatter plot of DSD retrievals between the radar and disdrometer after applying the scale bias correction to Z_dr.

5.4 Sensitivity of N_T to outliers

The results presented in the previous sections have shown that, unlike μ and D_m, the uncertainty surrounding the N_T retrievals tends to be much larger. This can be explained by the fact that N_T is the last parameter to be retrieved in Eq. (11), which makes it more susceptible to error propagation and accumulation during the first steps of the retrieval procedure. Errors in retrieved N_T values can be due to the retrieval method itself (e.g., the assumed μ–Λ relation and gamma DSD model), biased radar observations (e.g., calibration errors in Z_hh or/and Z_dr), or additional biases due to differences in measurement scale, height, and measurement principle between radars and disdrometers. Considering the fact that the events used in this study mainly consist of weak or light stratiform rain, the errors and uncertainty affecting the measured Z_dr values are very likely to play an important role.

The scatter plot of retrieved N_T values versus disdrometer data in Fig. 10 (bottom) shows a low correlation coefficient and a significant underestimation from TARA, mainly due to the huge bias in Z_hh (6.44 dBZ). However, it is worth noticing that even after applying a calibration bias correction to Z_hh, there was no substantial improvement in terms of the N_T retrievals (Fig. 11). Even though the bias in N_T was reduced (89 m⁻³ compared to 276 m⁻³), the scatter increased and the correlation coefficient remained low (0.17). The scale correction for Z_dr results in even worse agreement (correlation coefficient 0.12; Fig. 12, bottom). In general, two distinct groups of data points with drastically different error properties can be seen. For the first, the retrieved N_T values are severely overestimated compared to the Parsivel disdrometer by up to 1 order of magnitude. For the second group, the retrieved N_T values are up to 10 times lower than the disdrometer values.

The conclusion is that there are two different types of combinations of Z_hh–Z_dr that result in unreliable N_T retrievals. The first group is comprised of low Z_dr values compared to Z_hh, which results in overestimated N_T values. These are all the pairs of Z_hh–Z_dr in the lower-right part of Fig. 14. Since Z_dr is low, the only way to get a high reflectivity is by increasing N_T. The second group consists of relatively high Z_dr values compared to Z_hh, which leads to underestimated N_T values. These points correspond to the top-left part of Fig. 14. Since Z_dr is large, the only way to get a low Z_hh is to decrease N_T. Together, these two different types of outliers are responsible for the large scatter observed in retrieved N_T values.

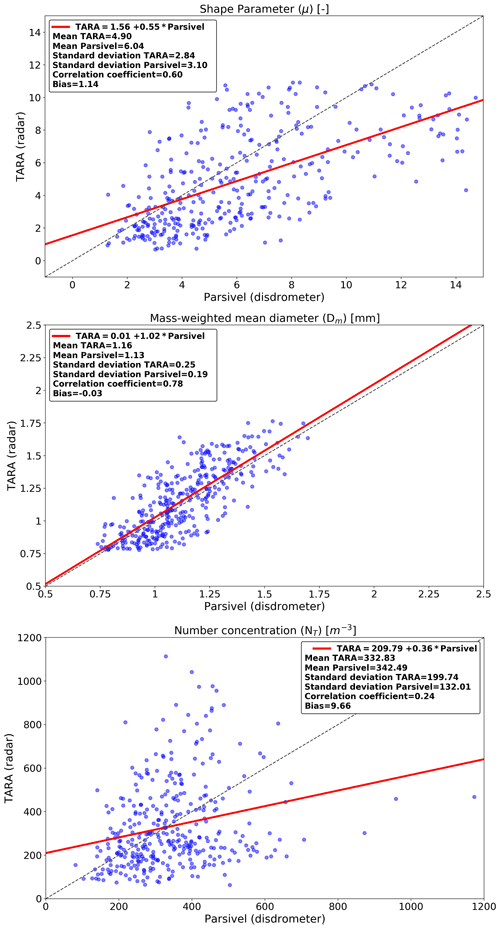
Figure 13 Scatter plot of DSD retrievals between the radar and disdrometer after applying the Z_hh–Z_dr relation outlier removal.

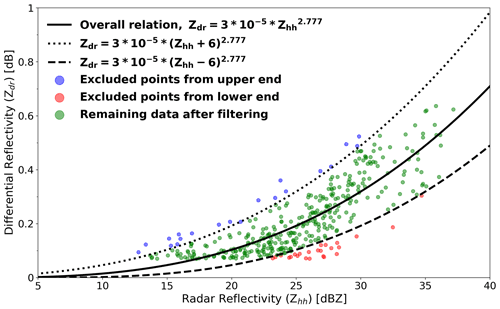
Figure 14 Example of the filtering based on the Z_hh–Z_dr relationship with the overall power-law fit and the corresponding ones for the upper and lower end using ±6 dBZ.

Each retrieval has its own uncertainty and error characteristic, depending on the pair of Z_hh–Z_dr. For example, the scale correction has different impacts on the different subgroups. Even though there is a general increase in N_T to compensate for the new reduced value of Z_dr, the aforementioned correction had a significant impact on the subgroup, which corresponds to the points that are overestimated by TARA and negligible for the ones that are underestimated.

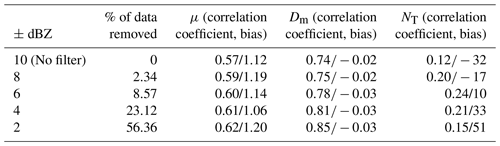
A possible way to reduce the uncertainty affecting the N_T retrievals and thereby avoid large errors is to filter out all potentially problematic combinations of Z_hh–Z_dr. In the following, a filter which aims to control the uncertainty in N_T by removing certain Z_hh–Z_dr combinations that are difficult to handle is applied. Note that these “outliers” in the Z_hh–Z_dr space are not necessarily wrong. They are just problematic in the sense that they can potentially result in very large errors in terms of retrieved N_T. The applied filter is two-dimensional depending on both Z_hh and Z_dr values since the uncertainty derives from their combination. A power-law model was used to fit the radar observables Z_hh and Z_dr after calibration and scale bias correction, respectively. Based on that model, an upper and lower curve defining the limits of acceptable Z_hh and Z_dr pairs is obtained by adding or subtracting a given tolerance from Z_hh as in Fig. 14. For illustration purposes ±6 dB was selected, but several other options (i.e., 2, 4, and 8 dB) were examined as well. Table 3 lists all options together with their corresponding performances for μ, D_m, and N_T. We see that by removing certain points beyond the lower and upper limits in the Z_hh–Z_dr space, it is possible to improve the correlation between the observed and retrieved μ, D_m, and N_T values while keeping a similar bias. For μ and D_m, the best tolerance (in terms of correlation) seems to be ±2 and ±4 dB. However, these are rather strict, which means that a large fraction of the data points would have to be discarded (i.e., 56 % and 23 %, respectively) for a modest gain in performance. For the N_T retrievals, the optimal tolerance appears to be ±6 dB, which discards less than 9 % of the data but still manages to increase the correlation (0.12 to 0.24) and decrease the absolute value of the bias (−32 to 10 m⁻³). Note that, contrarily to μ and D_m, filtering out more data points does not necessarily increase the performance in terms of the N_T retrievals. Figure 13 shows the final radar DSD retrieval results after applying a filter with a tolerance of ±6 dB.

Table 3 Filter performance (correlation coefficient, bias) of DSD retrievals (μ, D_m, and N_T) for different levels of tolerance (±2, 4, 6, 8, and 10 dBZ).

6 Conclusions

A previously proposed method for retrieving DSDs based on radar reflectivity measurements (Z_hh), differential reflectivity (Z_dr), and an empirical relation between the shape (μ) and slope (Λ) parameters of a gamma DSD model was investigated. Observations from a nearby optical disdrometer were used to derive the μ–Λ relationship as well as for performing an indirect validation of the retrieved DSDs. While the retrieval method itself is well-known, this study primarily focused on the critical assumptions behind it in order to outline potential sources of errors and uncertainties. First, a thorough sensitivity analysis of the μ–Λ relation to various factors such as the temporal sampling resolution, the adequacy of the gamma model hypothesis, sensitivity to the concentration number (N_T), and event-by-event variations was conducted. Then, the influence of calibration errors in radar observations and scale differences between radar and disdrometer observations were highlighted and investigated. Finally, a filter designed to mitigate uncertainty during N_T retrievals was proposed. According to the results the following conclusions can be drawn.

1. The μ–Λ relationship derived from a nearby disdrometer proved quite robust to the choice of the temporal sampling resolution, validity of the gamma model hypothesis, sample size, and event-by-event variability. However, only seven rather similar stratiform rain events were considered. More research is necessary to fully understand and quantify the inter-event variability of μ–Λ relationships in convective rain.

2. Radar calibration biases significantly affect the accuracy and reliability of the retrieved DSDs. Both Z_hh and Z_dr must be bias-corrected before retrieving the DSD.

3. Even for well-calibrated radars, a small additional bias correction to account for the scale difference between radar and disdrometer observations can be useful to reduce conditional biases in retrieved μ and N_T values.

4. Finding the right bias and scale corrections for Z_hh and Z_dr is not straightforward. Often the bias due to scale differences cannot be separated from the bias due to calibration errors and measurement noise. In our case, Z_dr was very well-calibrated, which allowed us to investigate the scale correction in more detail. However, due to the large calibration offset, the scale correction for Z_hh could not be determined.

5. Despite our best efforts, the retrieved N_T values remained highly uncertain. Two different types of outliers were identified, resulting in severely underestimated or overestimated N_T values. A simple filter for removing outliers in the Z_hh–Z_dr space was proposed. The filter gets rid of some problematic cases, which slightly improves the reliability of the N_T retrievals. But improvements remained modest and removing more data did not systematically result in better performances.

Finally, it should be mentioned that we do not expect the exact same adjustments to hold for other DSD retrieval algorithms or radar systems. The adjustments mentioned in this study are specific to the TARA radar and Parsivel optical disdrometer. For example, the radar elevation angle was 45^∘, which is not ideal for such retrievals. Uncertainties for lower elevation angles would probably be smaller due to higher Z_dr values. Depending on the radar system, corrections more elaborate than a simple shift in Z_dr might be necessary to achieve optimal performance across a larger number of rain events. Similarly, more convective rain events should be included to study the performance and reliability of DSD retrievals based on μ–Λ relationships during heavy convective rain with larger drop sizes. Finally, future work could look at the importance of μ–Λ relations in DSD retrievals from other relevant rainfall sensors, such as satellite observations, which have much larger sampling volumes and errors than ground-based radar and for which the scale corrections might therefore play a more important role.