the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Impact of varying lidar measurement and data processing techniques in evaluating cirrus cloud and aerosol direct radiative effects
Fabio Madonna
Marco Rosoldi
James R. Campbell
Ellsworth J. Welton
Jasper R. Lewis
Gelsomina Pappalardo
In the past 2 decades, ground-based lidar networks have drastically increased in scope and relevance, thanks primarily to the advent of lidar observations from space and their need for validation. Lidar observations of aerosol and cloud geometrical, optical and microphysical atmospheric properties are subsequently used to evaluate their direct radiative effects on climate. However, the retrievals are strongly dependent on the lidar instrument measurement technique and subsequent data processing methodologies. In this paper, we evaluate the discrepancies between the use of Raman and elastic lidar measurement techniques and corresponding data processing methods for two aerosol layers in the free troposphere and for two cirrus clouds with different optical depths. Results show that the different lidar techniques are responsible for discrepancies in the model-derived direct radiative effects for biomass burning (0.05 W m−2 at surface and 0.007 W m−2 at top of the atmosphere) and dust aerosol layers (0.7 W m−2 at surface and 0.85 W m−2 at top of the atmosphere).
Data processing is further responsible for discrepancies in both thin (0.55 W m−2 at surface and 2.7 W m−2 at top of the atmosphere) and opaque (7.7 W m−2 at surface and 11.8 W m−2 at top of the atmosphere) cirrus clouds. Direct radiative effect discrepancies can be attributed to the larger variability of the lidar ratio for aerosols (20–150 sr) than for clouds (20–35 sr). For this reason, the influence of the applied lidar technique plays a more fundamental role in aerosol monitoring because the lidar ratio must be retrieved with relatively high accuracy. In contrast, for cirrus clouds, with the lidar ratio being much less variable, the data processing is critical because smoothing it modifies the aerosol and cloud vertically resolved extinction profile that is used as input to compute direct radiative effect calculations.
- Article
(3710 KB) - Full-text XML
- BibTeX
- EndNote
According to the International Panel for Climate Change (IPCC, 2014), the major sources of uncertainty relating to current climate studies include direct and indirect radiative effects caused by anthropogenic and natural aerosols. Further, current estimates of the global aerosol direct radiative effect remain subject to large relative uncertainties affecting even the actual sign (indicating either net cooling or heating of the earth–atmosphere system), which may change from positive to negative diurnally (e.g., Campbell et al., 2016; Lolli et al., 2017a; Tosca et al., 2017). This depends on the so-called albedo effect (or the capability of aerosols to reflect incoming solar light) and whether or not it outweighs the greenhouse effect (or the capability of trapping/absorbing outgoing longwave radiation; Campbell et al., 2016)
Studies on cloud and aerosol optical, geometrical and microphysical properties greatly increased in the last 2 decades through the abundance of passive ground-based measurements (i.e., AErosol RObotic NETwork Network, AERONET; Holben et al., 1998; Dubovik et al., 2000; Smirnov et al., 2002; Eck et al., 2014; the Atmospheric Radiation Measurement program, ARM; Campbell et al., 2002; Ferrare et al., 2006; Perez-Ramirez et al., 2012; McComiskey and Ferrare, 2016; Aerosols, Clouds and Trace gases Research Infrastructure, ACTRIS; Asmi et al., 2013; Pappalardo et al., 2014) and the use of satellite sensors (i.e., MODerate resolution Infrared Spectroradiometer, MODIS; Tanré et al., 1997; King et al., 2003; Remer et al., 2005; Multi-angle Imaging Spectro-Radiometer, MISR; Diner et al., 1998; Di Girolamo et al., 2004; Kahn et al., 2009; Polarization and Anisotropy of Reflectances for Atmospheric science coupled with Observations from a Lidar, PARASOL; Tanré et al., 2011; NASA Aerosol-Cloud Ecosystem, ACE; Whiteman et al., 2018). Nevertheless, these measurements provide only an estimate of the columnar aerosol (or cirrus cloud) properties.
On the other hand, the Cloud-Aerosol Lidar with Orthogonal Polarization (CALIOP; Winker et al., 2007), on board the Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observations (CALIPSO) satellite launched by the National Aeronautics and Space Administration (NASA) in 2006, is capable of estimating range-resolved aerosol and cloud physical properties. However, the sun-synchronous orbit limits spatial and temporal coverage (orbital revisit time period of 16 days), making the datasets difficult to apply and interpret for specific forms of process study. The vertical structure of cloud and aerosol properties can also be retrieved through combined lidar and radar ground-based measurements as proposed in the frame of the CloudNet European Project (Illingworth et al., 2007). Still, the radar technique proves capable of characterizing only the relatively extreme fraction of the aerosol size distribution (Madonna et al., 2010, 2013).
Based on the progress in optical technologies in the late 1990s and the beginning of 2000s, federated ground networks of lidars were established (NASA Micro Pulse Lidar NETwork, MPLNET; Campbell et al., 2002; Welton et al., 2002; Lolli et al., 2013; European Aerosol Research LIdar NETwork, EARLINET; Pappalardo et al., 2014; Asian Dust NETwork, ADNET; Sugimoto et al., 2010; Latin American Lidar NETwork, LALINET; Antuña-Marrero et al., 2015; Lolli et al., 2015), the bulk of which are based on single- or dual-channel elastic and Raman lidar instruments. The Eulerian viewpoint of ground-based lidars is providing important contextual measurements relative to satellite profiling, like from CALIOP (Winker et al., 2007).
The emerging prominence of ground-based lidar, however, strengthens the necessity for further studies of optical, geometrical and microphysical aerosols and clouds properties resolved from multi-spectral lidar techniques, as claimed by several papers (Pappalardo et al., 2004a; Mona et al., 2006; Wang et al., 2012; Khor et al., 2015; Pani et al., 2016; Dionisi et al., 2013; Lolli et al., 2013, 2014, 2017a; Campbell et al., 2016). Multi-spectral and Raman lidars can retrieve aerosol and cloud properties with much better accuracy than elastic lidars, without many fundamental assumptions (e.g., Ansmann et al., 1992; Goldsmith et al., 1998; Mona et al., 2012; Pappalardo et al., 2014), though at greater operational expense. The High Spectral Resolution Lidar (HSRL; Shipley et al., 1983; Grund and Eloranta, 1991) technique allows for the separation of molecular and aerosol signals, and thus affords an independent retrieval of aerosols extinction and backscattering coefficients. However, the technology remains relatively complex and expensive, making it an unattractive choice for operational networks (e.g., Hair et al., 2008).
The Raman technique (Sect. 2.2) permits retrieval of aerosol and cloud vertically resolved extinction coefficients without any binding assumptions, which are the cornerstone of elastically based retrieval techniques (Sect. 2.1). Certain instabilities exist, however (Ansmann et al., 1992; Wandinger et al., 1995). In order to reduce the random uncertainty affecting the retrieval, a smoothing of the range-resolved profile is required at the expense of the effective vertical resolution (Pappalardo et al., 2004b; Iarlori et al., 2015) of the extinction coefficient profile.
Ultimately, different lidar techniques and/or processing algorithms lead to differences of the retrieved vertically resolved particulate optical properties, affecting the apparent significance, position and geometry of observed aerosol and cloud layers. The impact of these differences has never been extensively evaluated. Since lidar-derived optical properties obtained from different instrument techniques are more and more frequently being used to assess the direct radiative effects of clouds and aerosols (e.g., Campbell et al., 2016; Lolli et al., 2017a; Tosca et al., 2017), corresponding uncertainties in determining direct radiative effects, which may help reconcile inconsistencies in studies carried out at the global scale based on different lidar techniques, are compulsory, especially now that several new space missions with lidar on board have been launched (Cloud-Aerosol Transport System, CATS; McGill et al., 2015) or are scheduled (European Space Agency Earth Care mission; Illingworth et al., 2007).
The primary goal of this paper is to evaluate the relative differences between the aerosol and cloud direct radiative effects both at the surface (SFC) and at the top of the atmosphere (TOA) computed using the aerosol and cloud optical properties estimated from more sophisticated versus basic lidar techniques (i.e., Raman vs. elastic lidar). To reach this goal, we use the Fu–Liou–Gu (FLG; Fu and Liou, 1992, 1993; Gu et al., 2003, 2011; Lolli et al., 2017b) radiative transfer model to calculate the difference in net direct radiative effect for aerosols and clouds at TOA and SFC for profiles derived from both elastic and combined Raman–elastic lidar techniques.
2.1 Elastic and Raman lidar techniques
Elastic-scattering lidar instruments require assumptions and careful consideration of measurement strategies to constrain the single-scattering lidar equation (Eq. 1), defined as
where Pr(r) is the received power at a range r and O(r) is the overlap function, which depends on intersection between the respective telescope and laser field of view. O(r) equals unity for a distance r0 depending on the specific lidar system, spanning from few hundred meters to 4–5 km for Micro Pulse Lidar systems (MPL; Campbell et al., 2002). K is the so-called lidar constant (instrument dependent, function of detector quantum and optical efficiencies, telescope diameter, etc.), followed by the two unknown variables: β(r), the total backscattering coefficient, and α(r), the total extinction coefficient.
A classical method to solving Eq. (1) for single-channel elastic-backscatter lidars (Fernald, 1984) is based on the assumption of the columnar-averaged value of the ratio between the two unknown coefficients, typically indicated by S and called “lidar ratio”. The method, due to the large variability of S (i.e., 200–150 sr for aerosols; Ackermann, 1998; Ferrare et al., 2001; Sakai et al., 2003; Müller et al., 2007; Groß et al., 2011, 2013, 2015; Veselovskii et al., 2015) translates into large uncertainties associated with the retrieval of α and β (Lolli et al., 2013).
Through greater spectral complexity, it is possible to retrieve αand β with multi-spectral lidars without relying too heavily on fundamental assumptions. For instance, the combined detection of the elastically backscattered and inelastically backscattered radiation due to the Raman effect by nitrogen (or oxygen) molecules excited to a different vibrational or rotational energy level is possible. Using the Raman lidar technique, we can constrain and rewrite Eq. (1) as
where λL is the elastic wavelength, while λR is the wavelength of the Raman scattering; represents the particle (aerosols or clouds) extinction coefficient at elastic wavelength at range r, while and are the molecular extinction coefficients at wavelengths λL and λR, respectively; and Pr(r)r2 is the detected range-corrected Raman signal from range r, while nR(r) represents the number density of range-resolved scatter. The wavelength dependence of the particle extinction coefficient is described by the Ångström coefficient, å, defined from the relation
Equation (2) allows for independently retrieving vertically resolved optical coefficients with only very limited a priori assumptions (the Ångström coefficient should be estimated or assumed, but this estimate or assumption, involving a ratio, typically amounts to less than 5 % of total error; Ansmann and Müller, 2005). The particle backscattering coefficient, and , can be derived directly from the ratio of the Raman signal at λR and the elastic signal at λL.
2.2 Fu–Liou–Gu radiative transfer model
To calculate aerosol and cloud direct radiative effects, we use the one-dimensional FLG radiative transfer model, developed in the early 1990s. The original code has been adapted to retrieve cloud and aerosol direct radiative effects using the aerosol and cloud vertical profile of lidar extinction as input. There exist several parameterizations that provide the vertical profile of cloud microphysics using lidar-retrieved cloud extinction profile, each one with pros and cons, as shown in Comstock et al. (2007). For the purpose of this study and also considering authors' past experience (Campbell et al., 2016; Lolli et al., 2017a), we parameterize cirrus clouds through the Heymsfield et al. (2014) empirical relationship conceived expressly for lidar measurements. Here, the cirrus cloud ice crystal average diameter is directly proportional to the absolute atmospheric temperature (obtained through a radiosonde, regularly launched at measurement site, or numerical reanalysis dataset). Cirrus cloud optical depth and crystal size profiles are used to calculate the single-scattering albedo (SSA), phase function and asymmetry factor (AF) at each level.
Similarly, FLG calculates the direct radiative effect of aerosols as a function of the partial contribution of each aerosol species to the total optical depth at each altitude level. FLG uses a lookup table (LUT) with single-scattering properties for 18 different types of aerosols coming from the OPAC (Optical Properties of Aerosol and Clouds) database (d'Almeida et al., 1991; Tegen and Lacis, 1996; Hess et al., 1998). Among all aerosol species, for the initial cases introduced in Sect. 2.2 we assume that the dust layer is constituted by pure dust advected from the Saharan region (aerosol type 17 in FLG), while in the second case we assume pure biomass burning aerosol (aerosol type 11 in FLG). Nevertheless, if the measured aerosol atmospheric profiles do not match exactly the two-selected aerosol types, this does not affect the results because we are interested in evaluating the relative discrepancies among the different lidar techniques/data processing. Therefore, what is most relevant in the approach is the application of the same parameterization to each of the different techniques/data processing.
The aerosol–cloud direct radiative effect is calculated subtracting from the FLG total-sky run (where aerosols or clouds are present) the FLG run with a pristine atmosphere (control), expressed as
where DRE is the direct radiative effect (from aerosols or clouds), while the superscript TotalSky means that FLG is computed taking into account the aerosol–cloud profile and Pristine represents a hypothetical “clear-sky” atmosphere with no aerosols or clouds.
Direct measurements of aerosol microphysical properties require multi-wavelength lidar (e.g., Veselovskii et al., 2002, 2013), which are not common in many networks and also are sensitive to systematic and random errors in the optical data (Perez-Ramirez et al., 2013). We focus here on lidar systems that can operate continuously in different networks, and our direct radiative effect calculations do not vary much when changing effective radius and single-scattering albedo.
2.3 Direct radiative effect computation
For the analysis in this study, we analyzed lidar data collected with the MUlti-wavelength System for Aerosols (MUSA) lidar (Madonna et al., 2011), deployed at Consiglio Nazionale delle Ricerche (CNR), Istituto di Metodologie per l'Analisi Ambientale (IMAA) Atmospheric Observatory (CIAO) in Potenza, Italy (40.60∘ N, 15.72∘ E; 760 m above sea level, a.s.l). MUSA is a mobile multi-wavelength lidar system based on a Nd:YAG laser source equipped with second and third harmonic generators and on a Cassegrain telescope with a primary mirror of 300 mm diameter.
MUSA full-angle field of view (FOV) and laser beam divergence are large enough (1.0 mrad and 0.6 mrad, respectively) to add important multiple-scattering (MS) contributions to the retrieved cirrus extinction coefficient profiles. The Raman extinction coefficient profiles have been corrected for MS as described in Wandinger (1998), taking into account MS contributions by introducing in the respective lidar equation the multiple-scattering parameters. These parameters have been calculated by applying Eloranta's model (Eloranta, 1998) to estimate the contributions of individual orders of multiple scattering. In the model simulations, MUSA specifications (FOV and laser beam divergence) have been used, and a mono-disperse size distribution profile of cirrus cloud ice crystals has been assumed with effective diameters derived from the same parameterization used in the FLG model (Heymsfield et al., 2014). The first five scattering orders have been summed.
The MUSA lidar system is not tilted due to technical constraints. However, the averaged cirrus cloud retrieved lidar ratios from the combination of Raman and elastic lidar techniques (corrected for MS effects) are 24 and 26 sr, for cirrus cloud cases highlighted here from 10 June 2010 and 17 February 2014, respectively. Those values are consistent with a very low probability of significant specular reflection. The previous statement is supported by the fact that crystal size diameter computed with Heymsfield et al. (2014) parameterization is below 100 µm, a threshold value above which specular reflection can arise. Moreover, in Hogan and Illingworth (2003), it is found that specular reflection tends to be much stronger and more common for temperatures between 250 and 264 K (which corresponds to much lower altitudes with respect to the examined cirrus cloud cases), where plate crystals, which induce the greatest specular signal, are most common.
The three laser beams at 1064, 532 and 355 nm are simultaneously and coaxially transmitted into the atmosphere in a biaxial configuration. The receiving system has three channels for the detection of the radiation elastically backscattered from the atmosphere and two channels for the detection of the Raman radiation backscattered by the atmospheric N2 molecules at 607 and 387 nm. The elastic channel at 532 nm is split into parallel and perpendicular polarization components by means of a polarizer beamsplitter cube. The backscattered radiation at all the wavelengths is acquired both in analog and photon-counting mode. The typical vertical resolution of the raw profiles is 3.75 m with a temporal resolution of 1 min. The system is compact and transportable. It has operated since 2009, and it is one of the reference systems used for the intercomparison of lidar systems within the EARLINET (Pappalardo et al., 2014; Wandinger et al., 2016) quality assurance program. In this paper, the data analysis has been carried out considering four observation scenarios at night, as the Raman channel signal shows a much higher signal-to-noise ratio during nighttime:
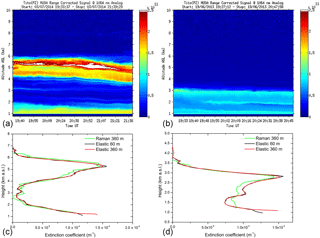
Figure 1(a) Composite plot of the range-corrected signal at 1064 nm showing a well-defined dust layer centered at about 5 km a.s.l. (b) and a biomass burning aerosol layer centered at about 2.5 km. (c) Aerosol lidar extinction profiles at 355 nm retrieved with the Raman (spatial resolution: 360 m) and the elastic lidar techniques with different spatial resolutions (60 and 360 m) for a dust (signal temporally integrated from 19:34 to 21:40 UT) outbreak on 3 July 2014 and for biomass burning (signal temporally integrated from 19:27 to 20:48 UT) on 19 June 2013 (d). The iterative method used a fixed lidar ratio value of S = 57 sr, determined by climatological measurements (Mona et al., 2006) for the dust aerosol layer. For the biomass burning we used the averaged value of S = 63 sr obtained from the MUSA Raman lidar.
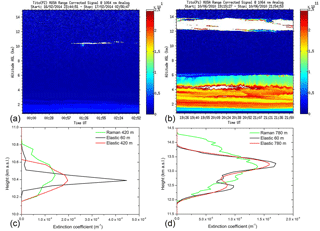
Figure 2(a) Composite plot of the range-corrected signal at 1064 nm showing a thin cirrus cloud at about 10 km (b) and an opaque cirrus cloud centered at about 13 km. (b) Lidar extinction profiles at 355 nm from the Raman and elastic channel of the cirrus cloud on 17 February 2014 (signal temporally integrated from 01:29 to 02:13 UT). The iterative method at the two different resolutions (60 and 420 m) used a fixed S value (26 sr), determined by climatological measurement. (d) Same as (c) but for a cirrus cloud detected on 10 June 2016 (signal temporally integrated from 19:42 to 20:44 UT). The Raman lidar channel is smoothed over a 420 and 780 m spatial window. On 10 June 2016, the elastic channel was retrieved using the MPLNET algorithm (Lewis et al., 2016) with S = 24 sr at 60 and 780 m respectively.
-
Dense dust aerosol and biomass burning events: the aerosol extinction profiles are retrieved using the UV (355 nm) channel. For each case, the extinction profile is both retrieved with the Raman technique (Ansmann et al., 1990; Whiteman et al., 1992; Veselovskii et al., 2015) and estimated using the sole elastic channel, applying an iterative algorithm (Di Girolamo et al., 1999) with an assigned lidar ratio (S = 57 sr for the dust case (Mona et al., 2006) and S = 63 sr for biomass burning, retrieved averaging the lidar ratio from the MUSA Raman channel). Both the Raman and elastic lidar signals have been smoothed by performing a binning of 16 range gates, resulting in a vertical resolution of 60 m. For the Raman channel retrieval, the extinction profile has been calculated using the sliding linear fit technique, with a bin number resulting in an effective vertical resolution of 360 m (Pappalardo et al., 2004b). For the elastic channel retrieval, the estimated extinction profile has been first calculated with the signal full vertical resolution of 60 m and then smoothed to the same effective vertical resolution as the Raman extinction profile (360 m), using a 2nd-order Savitzky–Golay smoothing filter (Press et al., 1992; Iarlori et al., 2015).
-
Thin and opaque cirrus clouds: like aerosols, cirrus cloud extinction profiles are retrieved using the UV (355 nm) channel with the Raman technique. The elastic channel retrieval for thin cirrus cloud is obtained applying the same iterative algorithm followed for dust and biomass burning. However, for the opaque cirrus cloud, due to convergence problems of the iterative method for higher cloud optical depths, we used the MPLNET Level 1.5 cloud product algorithm (Lewis et al., 2016) based on a Klett inversion (Klett, 1985). For both cases (iterative and MPLNET), we assumed a fixed lidar ratio value obtained from Raman and elastic measurements corrected by MS effects of 24 sr for thick and 26 sr for thin cirrus cloud.
The Raman extinction profile has been calculated with an effective vertical resolution of 420 m (thin cirrus cloud) and 780 m (opaque cirrus cloud). The iterative (thin cirrus) and MPLNET Level 1.5 cloud algorithm (opaque cirrus; Lewis et al., 2016) extinction profiles are calculated with the original signal vertical resolution of 60 m and smoothed at a resolution of 420 m (thin cirrus) and 780 m (opaque cirrus), using the Savitzky–Golay filter to match Raman channel spatial resolution.
-
The thermodynamic profile of the atmosphere, needed to calculate the direct radiative effect, is estimated using a standard thermodynamic profile (USS976) mid-latitude model. Emissivity and albedo values are taken from the MODIS Bidirectional Reflectance Distribution Function (BRDF)/Albedo algorithm product (Strahler et al., 1999), with a spatial resolution of 0.1∘ averaged over a 16-day temporal window (Campbell et al., 2016). As each measured cloud and aerosol extinction profile comes with a relative uncertainty per range bin, the sensitivity of FLG to the input parameters is evaluated applying a Monte Carlo technique. Each extinction profile is replicated 30 times (i.e., a statistically meaningful number), running the Monte Carlo code on the original profile random uncertainty. Likewise, for each replicated extinction profile, the Monte Carlo technique gives a value of surface albedo and profile temperature, based on their respective uncertainties. The direct radiative effect parameters derived for each profile are then represented with a box plot. It is possible then to quantify the effect of the smoothing calculating the uncertainty from the mean and the standard deviation of the values of net forcing.
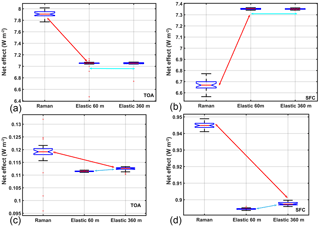
Figure 3The direct radiative effect for the dust aerosol case study (a, b) on 3 July 2014 and biomass burning case on 19 June 2013 (c, d) computed for retrievals obtained with Raman lidar channel smoothed over a window of 360 m, elastic channel at full resolution (60 m) and elastic channel smoothed over a 360 m window to be compared with the Raman channel . The results, represented as a distribution of values obtained with the Monte Carlo simulations by the box plots, are calculated at TOA (a, c) and SFC (b, d). As is clearly visible, the larger discrepancy in radiative effects is related mostly to the lidar measurements technique (red arrows), not the data processing constraints/assumptions (blue arrows).
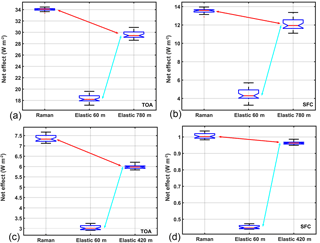
Figure 4Same as Fig. 3 but for two cirrus cloud cases (a, b: 17 February 2014; c, d: 10 June 2016). The Raman lidar channel is smoothed over a 420 m window for cirrus on 17 February 2014 and 780 m window for cirrus on 10 June 2010. The net radiative effect is calculated at TOA (a, c) and SFC (b, d). As is clearly visible, in both cases the larger discrepancy in radiative effect is related mostly to the data processing (blue arrows), not the lidar technique (red arrows).
3.1 Dust and biomass burning event
The analyzed dust event is retrieved from measurements taken on 3 July 2014 at CIAO. Figure 1 shows both the range-corrected composite signal at 1064 nm (Fig. 1a) and the lidar aerosol extinction profiles at 355 nm (Fig. 1c) obtained using the Raman technique with an effective resolution of 360 m and estimated using the elastic lidar technique at two different resolutions (60 and 360 m) and a fixed S value obtained analyzing climatological data (S = 57 sr; Mona et al., 2006). The Raman extinction profile is noisier than those obtained with the iterative method. All profiles, calculated with an integration time of 121 min, in the time window from 19:34 to 21:40 UT show no significant aerosol loading above 5.5 km.
Figure 3a shows the difference between the estimation of the direct radiative effect using the two considered lidar techniques and data processing at the top-of-the-atmosphere (TOA; Fig. 3a) and surface (SFC; Fig. 3b). The most important contribution to this difference in FLG calculations for this case is related to the adopted lidar technique (red arrows in Fig. 3a and b) and not to the effective vertical resolution determined by the smoothing (blue arrows in Fig. 3a and b). This characteristic is invariant, switching from TOA (Fig. 3b) to SFC (Fig. 3a), and is mainly the result of the assumption of a fixed lidar ratio to estimate the aerosol extinction profile using the elastic technique.
For the dust case, the net direct radiative effect determined with the two different lidar techniques differs by 0.7 W m−2 (5 %) at SFC and 0.85 W m−2 (6 %) at TOA. In absolute magnitudes, these net total forcing values are on average larger than the uncertainty of the direct effect estimated by IPCC (mean: −0.5 W m−2; range: −0.9 to −0.1). The contribution due to smoothing is negligible in comparison.
The analyzed biomass burning case study is retrieved from measurements taken on 19 June 2013 at CIAO integrating the signal temporally from 19:27 to 20:48 UT. The extinction profiles used as input into the FLG radiative transfer model were retrieved in the same way as for the dust case. Instead of a climatological lidar ratio value at 355 nm, however, we used S = 63 sr, obtained by averaging the lidar ratio profile retrieved with combined Raman–elastic techniques in the biomass burning layer. In Fig. 1d are the extinction profiles obtained from both the Raman and iterative methods (full resolution and smoothed over 360 m window). Figure 3b shows the difference in biomass burning direct radiative effects with respect to the different lidar and data processing techniques. Similar to the dust case event, the bigger differences are found to be related to the different lidar techniques both at SFC (0.05 W m−2 or 5 %; red arrows, Fig. 3d) and at TOA (0.007 W m−2 or 5 %; Fig. 3c).
The analysis shows how the mixing of different lidar techniques in a specific study or in the routine operations of an aerosol network at regional or global scale must take into account the uncertainties related to the assumptions that are behind the retrieval of the optical properties. This is important not only to provide a complete assessment of the total uncertainty budget for each lidar product but also to enable a physically consistent use of the lidar data in the estimation of the direct radiative effect and, likely, for many other user-oriented applications based on lidar data.
3.2 Cirrus cloud
Similar to Fig. 1, Fig. 2 shows the composite range-corrected signal and three extinction profiles retrieved from Raman lidar measurements of cirrus clouds with a vertical resolution of 420 m (thin cirrus, Fig. 2a, c) and 780 m (opaque cirrus, Fig. 2b, d), and with the elastic channel at two vertical resolutions (60 and 420 m, iterative method for thin cirrus cloud; 60 and 780 m, MPLNET Level 1.5 cloud product algorithm for opaque cirrus cloud) using a MS corrected lidar ratio of 24 sr (opaque cirrus) and 26 sr (thin cirrus). The obtained cloud extinction profiles from the different lidar and data processing techniques are averaged over 42 min, in the time window from 01:29 to 02:13 UT on 17 February 2014 (thin cirrus) and from 19:40 to 20:44 UT on 10 June 2010 (opaque cirrus).
Figure 4a and b depict the results obtained for cirrus cloud measurements taken on 17 February 2014. Here we have a completely different situation with respect to the aerosol cases. That is, the discrepancies between the Raman and elastic lidar techniques (red arrows in Fig. 4a, b) are much smaller than the discrepancies due to the effective vertical resolution of the extinction coefficient profile both at TOA and SFC (blue arrows in Fig. 4a, left and right panels). This is related to what is typically a much stronger extinction coefficient for clouds than for aerosols. In this cirrus cloud case, the direct radiative effect determined with the two different lidar techniques differs by about 1.2 W m−2 (16 %) at TOA and 0.04 W m−2 (4 %) at SFC, while the effect of smoothing within a window of 420 m provides an additional difference of 2.7 W m−2 (47 %) at TOA and about 0.55 W m−2 (53 %) at SFC.
Results from the opaque cirrus cloud (Fig. 4c, d) exhibit a similar behavior to the thin cirrus cloud, with signal smoothing outweighing the impact of the lidar technique (blue arrow). The order of magnitude is similar to the thin cirrus cloud, with a difference at TOA between techniques of 4.6 W m−2 (14 %) and 1.6 W m−2 (11 %) at SFC. In contrast, the difference in data processing is of 11.8 W m−2 (39 %) at TOA and 7.7 W m−2 (64 %) at SFC. The results are evidence of the critical need to study cirrus clouds using high-resolution profiles of the optical properties to provide an accurate estimation of the cloud direct radiative effect.
We applied the adapted Fu–Liou–Gu (FLG) radiative transfer model to quantitatively evaluate how much the lidar and/or data processing technique influence the net direct radiative effect exerted by two different upper atmospheric aerosol layers (dust and biomass burning) and a thin versus opaque cirrus cloud layer, both at the top of the atmosphere (TOA) and the surface (SFC). The evaluation has been made using aerosol–cloud extinction atmospheric profiles as inputs into the FLG radiative transfer model retrieved using the Raman–elastic technique and as estimated by lidar elastic measurements only (iterative method for aerosol layers and thin cirrus cloud; NASA Micro Pulse Lidar Network Level 1.5 cloud algorithm for opaque cirrus cloud). Because the Raman measurement retrieval is unstable due to the derivative of the signal at the numerator (see Eq. 2), a smoothing of the range-corrected signal is necessary to reduce the associated random uncertainty. The same processing treatment has also been applied to the elastic measurement signals.
The results show that the difference in direct radiative effect between the lidar and data processing/smoothing techniques applied is mostly unvaried at TOA and SFC. For the dust and biomass burning episodes, the data processing/smoothing does not play a major role, but instead the lidar measurement technique is more important with respect to the final result. This can be explained by the large variability of the lidar ratio (i.e., the unknown extinction-to-backscatter ratio used to constrain the single-solution lidar equation) compared to the assumed value. The opposite is true for cirrus clouds, where the applied data processing/smoothing plays a fundamental role in determining sensitivities in the final results. This is due to the smoothing effect on the observed sharp structures that strongly alters the vertical structure and the extinction of the cloud.
In summary, we found that for the aerosol cases the main difference both at TOA and SFC is driven by the respective lidar technique and not the data processing, with a difference the the dust direct radiative effect of 0.7 W m−2 (5 %) at SFC and 0.85 W m−2 (6 %) at TOA. Similarly, for biomass burning we found a discrepancy of 0.05 W m−2 (5 %) at SFC and 0.007 W m−2 (5 %) at TOA. For the cirrus clouds, the data smoothing is producing larger differences with respect to the lidar technique. However, using a different data processing/smoothing implies a larger difference in cirrus cloud direct radiative effect. A discrepancy of 0.55 W m−2 (53 %) is found at SFC, while a discrepancy of about 2.7 W m−2 (47 %) is found at TOA, for the thin cirrus cloud. Similarly for the opaque cirrus, the discrepancies produced by data processing/smoothing are larger with respect to the different lidar technique. At SFC we find a difference of 7.7 W m−2 (64 %) and 11.8 W m−2 at TOA (39 %).
A possible explanation of this different behavior is that the FLG radiative transfer model calculations are strongly dependent on the optical depth of the examined atmospheric layer. At coarse resolution (cloud) the smoothing is producing changes in the extinction profile that translate into creation/suppression of ice crystals that have a strong influence on direct radiative effect. At finer resolution, as in the case of aerosol case studies, the smoothing is just producing fluctuations that do not influence the total radiative effect. In this case, the lidar technique is making a big difference, as an assumed wrong value for lidar ratio (S) that has a much larger variability with respect to the clouds will amplify or suppress the aerosol peak, which will translate into a higher/lower radiative effect.
With this study, we wish to draw attention in speculating how dependent the derived aerosol and cloud radiative effect is on the lidar measurement and retrieval techniques, as well as on the data processing constraints/assumptions. This dependence looks increasingly relevant for existing and future space missions involving lidar instruments, as well as for the GAW Atmospheric LIdar Observation Network (GALION; Hoff et al., 2008; Bösenberg et al., 2008) project, which features the main objective of federating all existing ground-based lidar networks to provide atmospheric measurement profiles of the aerosol and cloud optical and microphysical properties with sufficient coverage, accuracy and resolution. For future work, it is imperative for the community to continue understanding and refining what the limits are of the each lidar technique along with the related retrieval algorithms adopted in each ground-based network. FLG or any other well-established radiative transfer model then can be used as a diagnostic tool to assure data quality through continued intercomparisons with real observation at ground level (using flux measurements), in situ (aircraft measurements) and at TOA (using satellite-based measurements).
Data are publicly available from the EARLINET Potenza observational site after registration at http://data.earlinet.org. Data are available upon request at: https://doi.org/10.5281/zenodo.1204353.
The authors declare that they have no conflict of interest.
This project has received funding from the
European Union's Horizon 2020 research and innovation programme under grant
agreement no. 654109.
Edited by: Andrew Sayer
Reviewed by: four
anonymous referees
Ackermann, J.: The Extinction-to-Backscatter Ratio of Tropospheric Aerosol: A Numerical Study, J. Atmos. Ocean. Tech., 15, 1043–1050, 1998.
Ansmann, A. and Müller, D.: Lidar and atmospheric aerosol particles, in: LIDAR – Range–resolved optical remote sensing of the atmosphere, edited by: Weitkamp, C., Springer, New York, USA, 105–141, 2005.
Ansmann, A., Riebesell, M., and Weitkamp, C.: Measurement of atmospheric aerosol extinction profiles with a Raman lidar, Opt. Lett., 15, 746–748, 1990.
Ansmann, A., Wandinger, U., Riebesell, M., Weitkamp, C., and Michaelis, W.: Independent measurement of extinction and backscatter profiles in cirrus clouds by using a combined raman elastic-backscatter lidar, Appl. Optics, 31, 7113–7131, 1992.
Antuña-Marrero, J. C., Landulfo, E., Estevan, R., Barja, B., Robock, A., Wolfram, E., Ristori, P., Clemesha, B., Zaratti, F., Forno, R., Armandillo, E., Bastidas, Á. E., de Frutos Baraja, Á. M., Whiteman, D. N., Quel, E., Barbosa, H. M., Lopes, F., Montilla-Rosero, E., and Guerrero-Rascado, J. L.: LALINET: The first Latin American-born regional atmospheric observational network, B. Am. Meteor. Soc., https://doi.org/10.1175/BAMS-D-15-00228.1, 2015.
Asmi, A., Collaud Coen, M., Ogren, J. A., Andrews, E., Sheridan, P., Jefferson, A., Weingartner, E., Baltensperger, U., Bukowiecki, N., Lihavainen, H., Kivekäs, N., Asmi, E., Aalto, P. P., Kulmala, M., Wiedensohler, A., Birmili, W., Hamed, A., O'Dowd, C., G Jennings, S., Weller, R., Flentje, H., Fjaeraa, A. M., Fiebig, M., Myhre, C. L., Hallar, A. G., Swietlicki, E., Kristensson, A., and Laj, P.: Aerosol decadal trends – Part 2: In-situ aerosol particle number concentrations at GAW and ACTRIS stations, Atmos. Chem. Phys., 13, 895–916, https://doi.org/10.5194/acp-13-895-2013, 2013.
Bösenberg, J. and Hoff, R.: GAW Aerosol Lidar Observation Network (GALION), WMO GAW Report WMO, Geneva, Switzerland, 2008.
Campbell, J. R., Hlavka, D. L., Welton, E. J., Flynn, C. J., Turner, D. D., Spinhirne, J. D., Scott III, V. S., and Hwang, I. H.: Full-time, eye-safe cloud and aerosol lidar observation at atmospheric radiation measurement program sites: Instruments and data processing, J. Atmos. Ocean. Tech., 19, 431–442, 2002.
Campbell, J. R., Lolli, S., Lewis, J. R., Gu, Y., and Welton, E. J.: Daytime Cirrus Cloud Top-of-the-Atmosphere Radiative Forcing Properties at a Midlatitude Site and Their Global Consequences, J. Appl. Meteorol. Climatol., 55, 1667–1679, 2016.
Comstock, J. M., McFarlane, S. A., d'Entremont, R., DeSlover, D., Turner,D. D., Mace, G. G., Matrosov, S. Y., Shupe, M. D., Minnis, P., Mitchell, D., Sassen, K., and Wang, Z.: An Intercomparison of Microphysical Retrieval Algorithms for Upper-Tropospheric Ice Clouds, B. Am. Meteor. Soc., 88, 191–204, https://doi.org/10.1175/BAMS-88-2-191, 2007.
d'Almeida, G. A., Koepke, P., and Shettle, E. P.: Atmospheric aerosols – global climatology and radiative characteristics, A. Deepak Publishing, Hampton, Virginia, 561 pp., 1991.
Di Girolamo, P., Ambrico, P. F., Amodeo, A., Boselli, A., Pappalardo, G., and Spinelli, N.: Aerosol observations by lidar in the nocturnal boundary layer, Appl. Optics, 38, 4585–4595, 1999.
Di Girolamo, L., Bond, T. C., Bramer, D., Diner, D. J., Fettinger, F., Kahn, R. A., Martonchik, J. V., Ramana, M. V., Ramanathan, V., and Rasch, P. J.: Analysis of Multi-angle Imaging SpectroRadiometer (MISR) aerosol optical depths over greater India during winter 2001–2004, Geophys. Res. Lett., 31, L23115, https://doi.org/10.1029/2004GL021273, 2004.
Diner, D. J., Beckert, J. C., Reilly, T. H., Bruegge, C. J., Conel, J. E., Kahn, R. A., Martonchik, J. V., Ackerman, T. P., Davies, R., Gerstl, S. A. W., Gordon, H. R., Muller, J.-P., Myneni, R. B., Sellers, P. J., Pinty, B., and Verstraete, M. M.: Multi-angle imaging spectroradiometer (MISR) instrument description and experiment overview, IEEE T. Geosci. Remote Sens., 36, 1072–1087, 1998.
Dionisi, D., Keckhut, P., Liberti, G. L., Cardillo, F., and Congeduti, F.: Midlatitude cirrus classification at Rome Tor Vergata through a multichannel Raman–Mie–Rayleigh lidar, Atmos. Chem. Phys., 13, 11853–11868, https://doi.org/10.5194/acp-13-11853-2013, 2013.
Dubovik, O., Smirnov, A., Holben, B. N., King, M. D., Kaufman, Y. J., Eck, T. F., and Slutsker, I.: Accuracy assessments of aerosol optical properties retrieved from Aerosol Robotic Network (AERONET) Sun and sky radiance measurements, J. Geophys. Res.-Atmos., 105, 9791–9806, 2000.
Eck, T. F., Holben, B. N., Reid, J. S., Arola, A., Ferrare, R. A., Hostetler, C. A., Crumeyrolle, S. N., Berkoff, T. A., Welton, E. J., Lolli, S., Lyapustin, A., Wang, Y., Schafer, J. S., Giles, D. M., Anderson, B. E., Thornhill, K. L., Minnis, P., Pickering, K. E., Loughner, C. P., Smirnov, A., and Sinyuk, A.: Observations of rapid aerosol optical depth enhancements in the vicinity of polluted cumulus clouds, Atmos. Chem. Phys., 14, 11633–11656, https://doi.org/10.5194/acp-14-11633-2014, 2014.
Eloranta, E. E.: Practical model for the calculation of multiply scattered lidar returns, Appl. Optics, 37, 2464–2472, 1998.
Ferrare, R., Feingold, G., Ghan, S., Ogren, J., Schmid, B., Schwartz, S. E., and Sheridan, P.: Preface to special section: Atmospheric Radiation Measurement Program May 2003 Intensive Operations Period examining aerosol properties and radiative influences. J. Geophys. Res.-Atmos., 111, D05S01, https://doi.org/10.1029/2005JD006908, 2006.
Ferrare, R. A., Turner, D. D., Brasseur, L. H., Feltz, W. F., Dubovik, O., and Tooman, T. P.: Raman lidar measurements of the aerosol extinction-to-backscatter ratio over the Southern Great Plains, J. Geophys. Res., 106, 20333–20347, 2001.
Fu, Q. and Liou, K. N.: On the correlated k-distribution method for radiative transferin nonhomogeneous atmospheres, J. Atmos. Sci., 49, 2139–2156, 1992.
Fu, Q. and Liou, K. N.: Parametrization of the radiative properties of cirrus clouds, J. Atmos. Sci., 50, 2008–2025, 1993.
Goldsmith, J. E. M., Blair, F. H., Bisson, S. E., and Turner, D. D.: Turn-Key Raman lidar for profiling atmospheric water vapor, clouds, and aerosols, Appl. Optics, 37, 4979–4990, 1998.
Groß, S., Tesche, M., Freudenthaler, V., Toledano, Ca., Wiegner, M., Ansmann, A., Althausen, D., and Seefeldner, M.: Characterization of Saharan dust, marine aerosols and mixtures of biomass-burning aerosols and dust by means of multi-wavelength depolarization and Raman lidar measurements during SAMUM 2, Tellus B, 63, 706–724, 2011.
Groß, S., Esselborn, M., Weinzierl, B., Wirth, M., Fix, A., and Petzold, A.: Aerosol classification by airborne high spectral resolution lidar observations, Atmos. Chem. Phys., 13, 2487–2505, https://doi.org/10.5194/acp-13-2487-2013, 2013.
Groß, S., Freudenthaler, V., Schepanski, K., Toledano, C., Schäfler, A., Ansmann, A., and Weinzierl, B.: Optical properties of long-range transported Saharan dust over Barbados as measured by dual-wavelength depolarization Raman lidar measurements, Atmos. Chem. Phys., 15, 11067–11080, https://doi.org/10.5194/acp-15-11067-2015, 2015.
Grund, C. J. and Eloranta, E. W.: University of Wisconsin High Spectral Resolution Lidar, Opt. Eng., 30, 6–12, 1991.
Gu, Y., Farrara, J., Liou, K. N., and Mechoso, C. R.: Parametrization of cloud-radiativeprocesses in the UCLA general circulation model, J. Climate, 16, 3357–3370, 2003.
Gu, Y., Liou, K. N., Ou, S. C., and Fovell, R.: Cirrus cloud simulations using WRF withimproved radiation parametrization and increased vertical resolution, J. Geophys. Res., 116, D06119, https://doi.org/10.1029/2010JD014574, 2011.
Hair, J. W., Hostetler, C. A., Cook, A. L., Harper, D. B., Ferrare, R. A., Mack, T. L., Welch, W., Izquierdo, L. R., and Hovis, F. E.: Airborne High Spectral Resolution Lidar for profiling aerosol optical properties, Appl. Optics, 47, 6734–6752, 2008.
Hess, M., Koepke, P., and Schult, I.: Optical properties of aerosols and clouds: The software package OPAC, B. Am. Meteor. Soc., 79, 831–844, 1998.
Heymsfield, A., Winker, D., Avery, M., Vaughan, M., Diskin, G., Deng, M., Mitev, V., and Matthey, R.: Relationships between ice water content and volume extinction coefficient from in situ observations for temperatures from 0∘ to −86 ∘C: Implications for spacebornelidar retrievals, J. Appl. Meteor. Climatol., 53, 479–505, 2014.
Hoff, R. M., Bösenberg, J., and Pappalardo, G.: The GAW Aerosol Lidar Observation Network (GALION). In Reviewed and Revised Papers Presented at the 24th International Laser Radar Conference, 23–27, 2008.
Iarlori, M., Madonna, F., Rizi, V., Trickl, T., and Amodeo, A.: Effective resolution concepts for lidar observations, Atmos. Meas. Tech., 8, 5157–5176, https://doi.org/10.5194/amt-8-5157-2015, 2015.
Illingworth, A. J., Hogan, R. J., O'connor, E. J., Bouniol, D., Delanoë, J., Pelon, J., and Donovan, D. P.: Cloudnet: Continuous evaluation of cloud profiles in seven operational models using ground-based observations, B. Am. Meteor. Soc., 88, 883–898, 2007.
Illingworth, A. J., Barker, H. W., Beljaars, A., Ceccaldi, M., Chepfer, H., Clerbaux, N., Cole, J., Delanoë, J., Domenech, C., Donovan, D. P., Fukuda, S., Hirakata, M., Hogan, R. J., Huenerbein, A., Kollias, P., Kubota, T., Nakajima, T., Nakajima, T. Y., Nishizawa, T., Ohno, Y., Okamoto, H., Oki, R., Sato, K., Satoh, M., Shephard, M. W., Velázquez-Blázquez, A., Wandinger, U., Wehr, T., and Van Zadelhoff, G.-J.: The earthcare satellite: The next step forward in global measurements of clouds, aerosols, precipitation, and radiation, B. Am. Meteor. Soc., 96, 1311–1332, 2015.
IPCC: Climate Change: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change edited by: Field, C. B., Barros, V. R., Dokken, D. J., Mach, K. J., Mastrandrea, M. D., Bilir, T. E., Chatterjee, M., Ebi, K. L., Estrada, Y. O., Genova, R. C., Girma, B., Kissel, E. S., Levy, A. N., MacCracken, S., Mastrandrea, P. R., and White, L. L., Cambridge University Press, Cambridge, UK and New York, NY, USA, 1132 pp., 2014.
Kahn, R. A., Nelson, D. L., Garay, M. J., Levy, R. C., Bull, M. A., Diner, D. J., Martonchik, J. V., Paradise, S. R., Hansen, E. G., and Remer, L. A.: MISR aerosol product attributes and statistical comparisons with MODIS, IEEE T. Geosci. Remote Sens., 47, 4095–4114, 2009.
Khor, W. Y., Matjafri, M. Z., Lim, H., Hee, W. S., and Lolli S.: One-year monitoring of the atmosphere over Penang Island using a ground-based lidar, Proc. SPIE, 9645, Lidar Technologies, Techniques, and Measurements for Atmospheric Remote Sensing, XI, 96450M, https://doi.org/10.1117/12.2195440, 2015.
King, M. D., Menzel, W. P., Kaufman, Y. J., Tanré, D., Gao, B.-C., Platnick, S., Ackerman, S. A., Remer, L. A., Pincus, R., and Hubanks, P. A.: Cloud and aerosol properties, precipitable water, and profiles of temperature and water vapor from MODIS, IEEE T. Geosci. Remote Sens., 41, 442–458, 2003.
Klett, J.: Lidar inversion with variable backscatter/extinction ratios, Appl. Optics 24, 1638–1643, 1985.
Lewis, J. R., Campbell, J. R., Welton, E. J., Stewart, S. A., and Haftings, P. C.: Overview of MPLNET, version 3, cloud detection, J. Atmos. Ocean. Tech., 33, 2113–2134, https://doi.org/10.1175/JTECH-D-15-0190.1, 2016.
Lolli, S. and Di Girolamo, P.: Principal component analysis approach to evaluate instrument performances in developing a cost-effective reliable instrument network for atmospheric measurements, J. Atmos. Ocean. Tech., 32, 1642–1649, 2015.
Lolli, S., Welton, E. J., and Campbell, J. R.: Evaluating light rain drop size estimates from multiwavelength micropulse lidar network profiling, J. Atmos. Ocean. Tech., 30, 2798–2807, 2013.
Lolli, S., Welton, E. J., Benedetti, A., Jones, L., Suttie, M., and Wang, S.-H.: MPLNET lidar data assimilation in the ECMWF MACC-II Aerosol system: evaluation of model performances at NCU lidar station, Proc. SPIE, 9246, Lidar Technologies, Techniques, and Measurements for Atmospheric Remote Sensing, X, 92460I, https://doi.org/10.1117/12.2068201, 2014.
Lolli, S., Campbell, J. R., Lewis, J. R., Gu, Y., Marquis, J. W., Chew, B. N., Liew, S., Salinas, S. V., and Welton, E. J.: Daytime Top-of-the-Atmosphere Cirrus Cloud Radiative Forcing Properties at Singapore, J. Appl. Meteor. Climatol., 56, 1249–1257, https://doi.org/10.1175/JAMC-D-16-0262.1, 2017a.
Lolli, S., Campbell, J. R., Lewis, J. R., Gu, Y., and Welton, E. J.: Technical note: Fu–Liou–Gu and Corti–Peter model performance evaluation for radiative retrievals from cirrus clouds, Atmos. Chem. Phys., 17, 7025–7034, https://doi.org/10.5194/acp-17-7025-2017, 2017b.
Madonna F., Amodeo, A., D'Amico, G., Mona, L., and Pappalardo, G.: Observation of non-spherical ultragiant aerosol using a microwave radar, Geophys. Res. Lett., 37, L21814, https://doi.org/10.1029/2010GL044999, 2010.
Madonna, F., Amodeo, A., Boselli, A., Cornacchia, C., Cuomo, V., D'Amico, G., Giunta, A., Mona, L., and Pappalardo, G.: CIAO: the CNR-IMAA advanced observatory for atmospheric research, Atmos. Meas. Tech., 4, 1191–1208, https://doi.org/10.5194/amt-4-1191-2011, 2011.
Madonna, F., Amodeo, A., D'Amico, G., and Pappalardo, G.: A study on the use of radar and lidar for characterizing ultragiant aerosol, J. Geophys. Res., 118, 10056–10071, https://doi.org/10.1002/jgrd.50789, 2013.
McComiskey, A. and Ferrare, R. A.: Aerosol Physical and Optical Properties and Processes in the ARM Program, Meteorol. Monogr., 57, 21.1–21.17, 2016.
McGill, M. J., Yorks, J. E., Scott, V. S., Kupchock, A. W., and Selmer, P. A.: The Cloud-Aerosol Transport System (CATS): A technology demonstration on the International Space Station, in: Lidar Remote Sensing for Environmental Monitoring XV (vol. 9612, p. 96120A). International Society for Optics and Photonics, Proc. SPIE, 9612, 96120A, https://doi.org/10.1117/12.2190841, 2015.
Mona, L., Amodeo, A., Pandolfi, M., and Pappalardo, G.: Saharan dust intrusions in the Mediterranean area: Three years of Raman lidar measurements, J. Geophys. Res.-Atmos., 111, D16203, https://doi.org/10.1029/2005JD006569, 2006.
Mona, L., Amodeo, A., D'Amico, G., Giunta, A., Madonna, F., and Pappalardo, G.: Multi-wavelength Raman lidar observations of the Eyjafjallajökull volcanic cloud over Potenza, southern Italy, Atmos. Chem. Phys., 12, 2229–2244, https://doi.org/10.5194/acp-12-2229-2012, 2012.
Müller, D., Ansmann, A., Mattis, I., Tesche, M., Wandinger, U., Althausen, D., and Pisani, G.: Aerosol-type-dependent lidar ratios observed with Raman lidar, J. Geophys. Res., 112, D16202, https://doi.org/10.1029/2006JD008292, 2007.
Pappalardo, G., Amodeo, A., Mona, L., Pandolfi, M., Pergola, N., and Cuomo, V.: Raman lidar observations of aerosol emitted during the 2002 Etna eruption, Geophys. Res. Lett., 31, L05120, https://doi.org/10.1029/2003GL019073, 2004a.
Pappalardo, G., Amodeo, A., Pandol, M., Wandinger, U., Ansmann, A., Bosenberg, J., Matthias, V., Amiridis, V., De Tomasi, F., Frioud, M., Iarlori, M., Komguem, L., Papayannis, A., Rocadenbosch, F., and Wang, X.: Aerosol lidar intercomparison in the framework of the EARLINET, project. 3. Raman lidar algorithm for aerosol extinction, backscatter and lidar ratio, Appl. Optics, 43, 5370–5385, 2004b.
Pappalardo, G., Amodeo, A., Apituley, A., Comeron, A., Freudenthaler, V., Linné, H., Ansmann, A., Bösenberg, J., D'Amico, G., Mattis, I., Mona, L., Wandinger, U., Amiridis, V., Alados-Arboledas, L., Nicolae, D., and Wiegner, M.: EARLINET: towards an advanced sustainable European aerosol lidar network, Atmos. Meas. Tech., 7, 2389–2409, https://doi.org/10.5194/amt-7-2389-2014, 2014.
Pérez-Ramírez, D., Lyamani, H., Olmo, F. J., Whiteman, D. N., and Alados-Arboledas, L.: Columnar aerosol properties from sun-and-star photometry: statistical comparisons and day-to-night dynamic, Atmos. Chem. Phys., 12, 9719–9738, https://doi.org/10.5194/acp-12-9719-2012, 2012.
Pérez-Ramírez, D., Whiteman, D. N., Veselovskii, I., Kolgotin, A., Korenskiy, M., and Alados-Arboledas, L.: Effects of systematic and random errors on the retrieval of particle microphysical properties from multiwavelength lidar measurements using inversion with regularization. Atmos. Meas. Tech., 6, 3039–3054, https://doi.org/10.5194/amt-6-3039-2013, 2013.
Press, W. H., Flannery, B. P., Teukolsky, S. A., and Vetterling, W. T.: Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed., Cambridge, University Press, Cambridge, 127–128, 644–647, 1992.
Remer, L. A., Kaufman, Y. J., Tanré, D., Mattoo, S., Chu, D. A., Martins, J. V., Li, R.-R., Ichoku, C., Levy, R. C., Kleidman, R. G., Eck, T. F., Vermote, E., and Holben, B. N.: The MODIS aerosol algorithm, products, and validation, J. Atmos. Sci., 62, 947–973, 2005.
Sakai, T., Shibata, T., Hara, K., Kido, M., Osada, K., Hayashi, M., Matsunaga, K., and Iwasaka, Y.: Raman lidar and aircraft measurements of tropospheric aerosol particles during the Asian dust event over central Japan: Case study on 23 April 1996, J. Geophys. Res., 108, 4349, https://doi.org/10.1029/2002JD003150, 2003.
Shipley, S. T., Tracy, D. H., Eloranta, E. W., Trauger, J. T., Sroga, J. T., Roesler, F. L., and Weinman, J. A.: High Spectral Resolution Lidar to Measure Optical-Scattering Properties of Atmospheric Aerosols, 1. Theory and Instrumentation, Appl. Optics, 22, 3716–3724, 1983.
Smirnov, A., Holben, B. N., Eck, T. F., Slutsker, I., Chatenet, B., and Pinker, R. T.: Diurnal variability of aerosol optical depth observed at AERONET (Aerosol Robotic Network) sites, Geophys. Res. Lett., 29, 2115, https://doi.org/10.1029/2002GL016305, 2002.
Strahler, A. H., Schaaf, C. B., Muller, J.-P., Warmer, W., Barnsley, M. J., d'Entremont, R., Hu, B., Lewis, P., Li, X., and Ruiz de Lope, E. V.: MODIS BRDF/albedo product: Algorithm theoretical basis document, NASA EOS-MODIS Doc, ATBD-MOD-09, version 5.0, 1999.
Sugimoto, N., Matsui, I., Shimizu, A., Nishizawa, T., Hara, Y., and Uno, I.: Lidar network observation of tropospheric aerosols, in: Lidar Remote Sensing for Environmental Monitoring XI, edited by: Mizutani, K., Singh, U. N., Jayaraman, A., Liu, D., Proceedings of SPIE Vol. 7860, SPIE, Bellingham, WA, USA, 78600J, 2010.
Tanré, D., Kaufman, Y. J., Herman, M., and Mattoo, S.: Remote sensing of aerosol properties over oceans using the MODIS/EOS spectral radiances, J. Geophys. Res.-Atmos., 102, 16971–16988, 1997.
Tanré, D., Bréon, F. M., Deuzé, J. L., Dubovik, O., Ducos, F., François, P., Goloub, P., Herman, M., Lifermann, A., and Waquet, F.: Remote sensing of aerosols by using polarized, directional and spectral measurements within the A-Train: the PARASOL mission, Atmos. Meas. Tech., 4, 1383–1395, https://doi.org/10.5194/amt-4-1383-2011, 2011.
Tegen, I. and Lacis, A. A.: Modeling of particle size distribution and its influence on the radiative properties of mineral dust aerosol, J. Geophys. Res., 101, 19237–19244, 1996.
Tosca, M. G., Campbell, J., Garay, M., Lolli, S., Seidel, F. C., Marquis, J., and Kalashnikova, O.: Attributing accelerated summertime warming in the southeast united states to recent reductions in aerosol burden: Indications from vertically-resolved observations, Remote Sens., 9, 674, https://doi.org/10.3390/rs9070674, 2017.
Veselovskii, I., Kolgotin, A., Griaznov, V., Muller, D., Wandinger, U., and Whiteman, D.: Inversion with regularization for the retrieval of tropospheric aerosol parameters from multiwavelength lidar sounding, Appl. Optics, 41, 3685–3699, 2002.
Veselovskii, I., Whiteman, D. N., Korenskiy, M., Kolgotin, A., Dubovik, O., Perez-Ramirez, D., and Suvorina, A.: Retrieval of spatio-temporal distributions of particle parameters from multiwavelength lidar measurements using the linear estimation technique and comparison with AERONET, Atmos. Meas. Tech., 6, 2671–2682, https://doi.org/10.5194/amt-6-2671-2013, 2013.
Veselovskii, I., Whiteman, D. N., Korenskiy, M., Suvorina, A., and Pérez-Ramírez, D.: Use of rotational Raman measurements in multiwavelength aerosol lidar for evaluation of particle backscattering and extinction, Atmos. Meas. Tech., 8, 4111–4122, https://doi.org/10.5194/amt-8-4111-2015, 2015.
Wandinger, U.: Multiple-scattering influence on extinction and backscatter coefficient measurements with Raman and high-spectral resolution lidars, Appl. Optics, 37, 417–427, 1998.
Wandinger, U., Ansmann, A., Reichardt, J., and Deshler, T.: Determination of stratospheric aerosol microphysical properties from independent extinction and backscattering measurements with a Raman lidar, Appl. Optics, 34, 8315–8329, 1995.
Wandinger, U., Freudenthaler, V., Baars, H., Amodeo, A., Engelmann, R., Mattis, I., Groß, S., Pappalardo, G., Giunta, A., D'Amico, G., Chaikovsky, A., Osipenko, F., Slesar, A., Nicolae, D., Belegante, L., Talianu, C., Serikov, I., Linné, H., Jansen, F., Apituley, A., Wilson, K. M., de Graaf, M., Trickl, T., Giehl, H., Adam, M., Comerón, A., Muñoz-Porcar, C., Rocadenbosch, F., Sicard, M., Tomás, S., Lange, D., Kumar, D., Pujadas, M., Molero, F., Fernández, A. J., Alados-Arboledas, L., Bravo-Aranda, J. A., Navas-Guzmán, F., Guerrero-Rascado, J. L., Granados-Muñoz, M. J., Preißler, J., Wagner, F., Gausa, M., Grigorov, I., Stoyanov, D., Iarlori, M., Rizi, V., Spinelli, N., Boselli, A., Wang, X., Lo Feudo, T., Perrone, M. R., De Tomasi, F., and Burlizzi, P.: EARLINET instrument intercomparison campaigns: overview on strategy and results, Atmos. Meas. Tech., 9, 1001–1023, https://doi.org/10.5194/amt-9-1001-2016, 2016.
Welton, E. J., Voss, K. J., Quinn, P. K., Flatau, P. J., Markowicz, K., Campbell, J. R., and Johnson, J. E.: Measurements of aerosol vertical profiles and optical properties during INDOEX 1999 using micropulse lidars, J. Geophys. Res., 107, 8019, https://doi.org/10.1029/2000JD000038, 2002.
Whiteman, D. N., Melfi, S. H., and Ferrare, R. A.: Raman lidar system for the measurement of water vapor and aerosols in the Earth's atmosphere, Appl. Optics, 31, 3068–3082, 1992.
Whiteman, D. N., Pérez-Ramírez, D., Veselovskii, I., Colarco, P., and Buchard, V.: Simulations of spaceborne multiwavelength lidar measurements and retrievals of aerosol microphysics. J.Quant. Spectrosc. Ra., 205, 27–39, 2018.
Winker, D. M., Hunt, W. H., and McGill, M. J.: Initial performance assessment of CALIOP, Geophys. Res. Lett., 34, L19803, https://doi.org/10.1029/2007GL030135, 2007.




