the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Using reference radiosondes to characterise NWP model uncertainty for improved satellite calibration and validation
Fabien Carminati
Stefano Migliorini
Bruce Ingleby
William Bell
Heather Lawrence
Stuart Newman
James Hocking
Andrew Smith
The characterisation of errors and uncertainties in numerical weather prediction (NWP) model fields is a major challenge that is addressed as part of the Horizon 2020 Gap Analysis for Integrated Atmospheric ECV CLImate Monitoring (GAIA-CLIM) project. In that regard, observations from the GCOS (Global Climate Observing System) Reference Upper-Air Network (GRUAN) radiosondes are being used at the Met Office and European Centre for Medium-Range Weather Forecasts (ECMWF) to assess errors and uncertainties associated with model data.
The software introduced in this study and referred to as the GRUAN processor has been developed to collocate GRUAN radiosonde profiles and NWP model fields, simulate top-of-atmosphere brightness temperature at frequencies used by space-borne instruments, and propagate GRUAN uncertainties in that simulation. A mathematical framework used to estimate and assess the uncertainty budget of the comparison of simulated brightness temperature is also proposed.
A total of 1 year of GRUAN radiosondes and matching NWP fields from the Met Office and ECMWF have been processed and analysed for the purposes of demonstration of capability. We present preliminary results confirming the presence of known biases in the temperature and humidity profiles of both NWP centres. The night-time difference between GRUAN and Met Office (ECMWF) simulated brightness temperature at microwave frequencies predominantly sensitive to temperature is on average smaller than 0.1 K (0.4 K). Similarly, this difference is on average smaller than 0.5 K (0.4 K) at microwave frequencies predominantly sensitive to humidity.
The uncertainty estimated for the Met Office–GRUAN difference ranges from 0.08 to 0.13 K for temperature-sensitive frequencies and from 1.6 to 2.5 K for humidity-sensitive frequencies. From the analysed sampling, 90 % of the comparisons are found to be in statistical agreement.
This initial study has the potential to be extended to a larger collection of GRUAN profiles, covering multiple sites and years, with the aim of providing a robust estimation of both errors and uncertainties of NWP model fields in radiance space for a selection of key microwave and infrared frequencies.
- Article
(1713 KB) - Full-text XML
- BibTeX
- EndNote
The works published in this journal are distributed under
the Creative Commons Attribution 4.0 License. This license does not affect
the Crown copyright work, which is re-usable under the Open Government Licence
(OGL). The Creative Commons Attribution 4.0 License and the OGL are interoperable
and do not conflict with, reduce or limit each other.
© Crown copyright 2018
Space-borne observational datasets are EOS key components that have led to significant advances in climate and weather applications (Joo et al., 2013; Bauer et al., 2015; Hollmann et al., 2013; Bojinski et al., 2014) and therefore must be subject to high standards of calibration and validation to meet user requirements. As part of an overall strategy for a harmonised and improved instrument calibration, the World Meteorological Organization (WMO), Coordination Group for Meteorological Satellites (CGMS), and Global Space-based Inter-Calibration System (GSICS) have advocated the need to tie the measurements to absolute references and primary standards (WMO, 2011, https://library.wmo.int/doc_num.php?explnum_id=3710, last access: 2 January 2019; GSICS, 2015, http://www.wmo.int/pages/prog/sat/documents/GSICS-RD002_Vision.pdf, last access: 2 January 2019). In most cases, however, commonly used validation techniques, as discussed by Zeng et al. (2015) and Loew et al. (2017), do not yet provide a full metrological traceability.
For a full metrological traceability and uncertainty quantification, Green et al. (2018) suggested mirroring the measurement protocols as described by Immler et al. (2010). Accordingly, consistency between two independent measurements, m1 and m2, is achieved when
where u1 and u2 are the total uncertainties associated with m1 and m2, respectively. σ represents the intrinsic uncertainties of the comparison. In the case of a comparison between radiosonde and satellite observations for example, this term can represent the collocation uncertainty (Calbet et al., 2017). k is a coverage factor expanding the confidence interval for normally distributed error probability.
In this paper, we use the terms error and uncertainty as described in the International Vocabulary of Metrology (VIM) (JCGM, 2012, https://www.bipm.org/en/publications/guides/vim.html, last access: 2 January 2019). The uncertainty is described in the VIM as a non-negative parameter characterising the dispersion of the quantity values being attributed to the quantity intended to be measured, based on the information used. It is emphasised that all components of the uncertainty contribute to this dispersion. This includes systematic effects arising from, for example, corrections or reference standards. If a systematic effect is unknown it is unaccounted for in the uncertainty budget but contributes to the error.
The error is defined as the measured quantity value minus the unknown true value and may be composed of a random and a systematic component.
For satellite data, pre-launch calibration characteristics are often provided by the instrument manufacturer or space agency. However at launch, an uncertainty chain that may have been metrologically traceable during the laboratory calibration phase can become compromised due to changes in the spacecraft during the launch process itself as well as changes in the satellite environment in orbit compared to the laboratory testing. Furthermore, the instruments also degrade over time, sometimes in quite a complex manner. These issues coupled with the current lack of true on-board traceable references make creating a metrologically traceable uncertainty chain difficult for the satellite data record.
This aspect is being addressed by the “Fidelity and uncertainty in climate data records from Earth Observations” (FIDUCEO) project (http://www.fiduceo.eu/, last access: 2 January 2019). The project aims to develop Fundamental Climate Data Record (FCDR) by reprocessing existing observations from raw satellite data to geolocated and calibrated radiances with traceable uncertainties from a set of different references at the pixel level. The uncertainty characterisation will account for the physical basis of the sensing process, the on-board calibration system, and an estimate for the uncertainties arising from the processing.
The (re)assessment of historical, well-established, and new space-borne instruments using data assimilation systems has become, over the past decade, common practice in numerical weather prediction (NWP) centres (Bell et al., 2008; Zou et al., 2011; Bormann et al., 2013; Lu and Bell, 2014). NWP models offer an interesting framework for the assessment of observational datasets due to a physically constrained, continuous, global, and homogeneous representation of the atmosphere. An optimal estimation of the state of the atmosphere is routinely performed in data assimilation systems by blending information from a large volume of observations (space-borne, air-borne, and ground based) with a short-range forecast. Diagnostics are calculated in satellite observation space, typically in brightness temperature, thanks to the radiative transfer models used by data assimilation systems (Saunders et al., 2018). This forward approach is better posed than the inverse problem, that is to say comparing model geophysical fields to retrieved satellite profiles, since multiple atmospheric states can provide solutions to the retrieval, introducing further uncertainty. NWP representation of atmospheric temperature and humidity fields is of sufficient quality to enable the characterisation of subtle biases in satellite observations as demonstrated in the work referenced herein. Loew et al. (2017) reported model field uncertainties in the satellite observation space ranging from 0.05 to 0.2 K at frequencies principally sensitive to mid-tropospheric and lower-stratospheric temperature and from 1 to 2 K at frequencies sensitive to mid- and upper-tropospheric humidity. However, those estimations arise from sensitivity studies and not from robust uncertainty analyses. Stochastic approaches, based on ensemble forecasting techniques, have been used to estimate forecast uncertainties, but with the caveat that they do not represent the systematic model biases (Leutbecher et al., 2017).
This lack of metrologically traceable characterisation has often hampered the recognition and consideration of model-based assessment outside of the NWP context, especially at space agency and instrument team levels. Key climate users can also benefit from this approach, which has begun to find resonance in the climate community (e.g. Massonnet et al., 2016).
It is also worth noting that bias correction schemes are generally applied to observations, especially satellite radiances, used in data assimilation systems. Corrections are performed with respect to the model background or analysis depending on the chosen scheme. Although this works for theoretical unbiased NWP models, real-world data assimilation systems also use reliable observations whose role is to anchor the analysis. These anchoring observations, although they may be slightly biased with respect to the truth, are not corrected in the data assimilation system. As a result, background and analysis are weighted by the average of the non-zero biases in the model and in the anchor observations. Eyre (2016), however, demonstrated that a risk inherent to bias correction schemes is a decrease in the weight given to anchor observations when the number of assimilated bias-corrected observations increases, which results in model background and analysis to be increasingly weighted toward the bias in the model. To avoid this situation, Eyre (2016) suggests that correction should be derived from areas where NWP model bias is expected to be small, along with the use of numerous anchor observations.
The Gap Analysis for Integrated Atmospheric ECV CLImate Monitoring (GAIA-CLIM) project (Thorne et al., 2017) aims to address those challenges by improving the use of in situ observations to rigorously characterise a set of atmospheric essential climate variables (ECVs) derived from satellite observations as well as the geolocated and calibrated spectral radiances (level 1b) from which these quantities are derived (http://www.gaia-clim.eu/, last access: 2 January 2019). The work presented here is embedded in that framework and focuses on developing NWP as a comprehensive reference by establishing traceability for the model fields through comparison with traceable comparator data.
The NWP model error and uncertainty budget can be expressed as a function of four main contributions:
- a.
the error and uncertainty in NWP temperature and humidity fields mapped to observation space (brightness temperature).
- b.
the error and uncertainty in the underlying radiative transfer modelling, including biases between fast radiative transfer models commonly used in NWP and reference line-by-line models; fundamental spectroscopic uncertainty; and surface emissivity uncertainty.
- c.
the error and uncertainty due to scale mismatch, which encompasses the different scales at which observation and model are resolved, and the scale of natural variability that is, especially for humidity, much smaller than both observation and model scales.
- d.
the error and uncertainty due to residual cloud; clear-sky scenes are generally preferred because simulated cloudy radiances are affected by uncertainties in model representation of cloud amounts and the absorption and scattering properties of hydrometeors.
This study aims to address the first contribution. To that end, the Met Office and European Centre for Medium-Range Weather Forecasts (ECMWF) models are compared to radiosondes from the Global Climate Observing System (GCOS) Reference Upper-Air Network (GRUAN) in a stand-alone module based on the core radiative transfer modelling capability of the fast radiative transfer model RTTOV and the Radiance Simulator (both available at http://www.nwpsaf.eu/, last access: 2 January 2019). This software, referred to as the GRUAN processor, enables the collocation of geophysical fields and simulation of top-of-atmosphere (TOA) brightness temperatures (Tb) from radiosondes and NWP models, with GRUAN uncertainties propagated into the radiative transfer calculation.
Section 2 introduces the datasets used for this study, namely GRUAN radiosondes and the NWP models from the Met Office and ECMWF. Sections 3 and 4 describe the GRUAN processor functionality and present an illustrative case study. A methodology statistically assessing the uncertainties is presented in Sect. 5. Section 6 concludes the study.
2.1 GRUAN
With 17 sites across the world (including two inactive sites in the Pacific), GCOS is building on existing infrastructures to develop a reference network for upper-air observations (http://www.gruan.org/, last access: 2 January 2019). GRUAN aims to provide long-term high-quality measurements of ECVs with vertically resolved uncertainty estimates. To meet the strict criteria for reference measurements, GRUAN data also include a comprehensive collection of metadata and documentation of correction algorithms.
To date, only the Vaisala RS92 radiosonde is used to produce the GRUAN-certified products (Sommer et al., 2016), referred to as RS92 GRUAN data product version 2 (RS92-GDP), but a new product based on the Vaisala RS41 is in preparation. The RS92 GRUAN processing is documented by Dirksen et al. (2014). This includes the correction of the radiosonde systematic errors, due to mainly solar radiation, and the derivation of the uncertainties for temperature, humidity, wind, pressure, and geopotential height. The total uncertainty budget accounts for correlated and uncorrelated contributions of both random sources of uncertainty and uncertainties from systematic error corrections, and it is expressed as the root sum square of all contributions. The uncertainty related to the short-wave radiation correction (used in the temperature uncertainty budget), the correlated uncertainty related to systematic error corrections, and uncorrelated uncertainty (standard deviation) derived from the GRUAN processing are available in the RS92-GDP files, in addition to the total uncertainty of each variable. However, not all correlated and uncorrelated components are independently available (albeit used in the calculation of the total uncertainty) and some sources of partially correlated uncertainty are not yet modelled in GRUAN algorithms (e.g. the pendulum motion of the radiosonde under the balloon). Therefore, only the total uncertainties of temperature, humidity, and pressure are considered in this study.
The results presented in this preliminary study focus on the profiles from Lindenberg (LIN), GRUAN lead centre, Germany (52.21∘ N, 14.12∘ E), for the year 2016.
2.2 Met Office NWP
Met Office model data files are extracted from the Managed Archive Storage System (MASS) and only ±5∘ latitude and longitude around the GRUAN launch site is kept to limit the data volume. For LIN, the model fields cover the area latitude 47.109–57.109 and longitude 9.0234–19.102. Each model data file contains four time steps starting at T+0, the analysis, and three successive 3 h forecasts referred to as T+3, T+6, and T+9. The Met Office data assimilation system is a hybrid four-dimensional variational analysis (4D-var) with a 6 h time window (Lorenc et al., 2000; Rawlins et al., 2007). Four analyses (and their successive forecasts) are available every day at 00:00, 06:00, 12:00, and 18:00 coordinated universal time (UTC). Assimilated satellite radiances are corrected with a variational bias correction similar to the scheme described by Auligné et al. (2007). The operational forecast model in 2016 had a resolution of approximately 17 km at mid-latitudes for 70 levels from the surface to 80 km (N768L70). The radiative transfer calculation was performed in 2016 by the fast radiative transfer model RTTOV version 9 (Saunders et al., 1999, 2007).
In the Met Office NWP system, the interpolation of background fields is performed twice, once for all observations and later just for those observations to be assimilated. The radiosonde profiles are averaged over the vertical model layers. Latitude, longitude, and time at each level are used in the first interpolation of background values, but fixed coordinates are used in the latter interpolation. A bias correction of radiosonde profiles is in place on a per station basis but is generally not applied where RS92 is used. As noted by Ingleby and Edwards (2015), radiation corrections are now often directly applied by the radiosonde manufacturer such as Vaisala, which reduces the need for correction in the NWP system. Bias correction and quality controls operationally applied to radiosonde at the Met Office are detailed in Appendix 1 of Ingleby and Edwards (2015).
2.3 ECMWF NWP
ECMWF data are extracted from the Meteorological Archival and Retrieval System (MARS, https://software.ecmwf.int/wiki/display/UDOC/MARS+user+documentation, last access: 2 January 2019). Data come from the operational data class atmospheric model long window 4D-var stream (see MARS documentation for details). The covered area is the same as for the Met Office. Each model data file contains six time steps of 3 h starting from T+0 to T+15. The ECMWF analysis/forecast system is documented by ECMWF (https://www.ecmwf.int/en/forecasts/documentation-and-support, last access: 2 January 2019). A cubic octahedral reduced Gaussian grid is currently used with a resolution of TCo1279 (horizontal grid spacing of about 9 km) and with 137 levels in the vertical. Note that from February 2006 until June 2013, there were 91 vertical levels, and from January 2010 until March 2016 a linear reduced Gaussian grid was used with a horizontal spacing of around 16 km. Data assimilation uses incremental 4D-var (Courtier at al., 1994) with a 12 h window, the nominal 00:00 UTC analysis uses data from 21:00 to 09:00 UTC. Forecasts and ensembles are run twice daily from early delivery 6 h window 4D-var analyses (Haseler, 2004). Flow-dependent ensemble information from the ECMWF ensemble of data assimilations is incorporated into the modelling of background-error covariances (Bonavita et al., 2016). Satellite radiative transfer calculations use the fast radiative transfer model RTTOV version 11.2 (Hocking et al., 2015), which has been used operationally since May 2015 (Lupu and Geer, 2015). Variational bias correction of satellite radiances (and, unlike the Met Office scheme, aircraft temperatures) is based on Dee (2004) and Auligné et al. (2007).
The treatment of radiosondes in the ECMWF system differs from that of the Met Office in that there is no average on model levels and each level is treated as a point value. In addition, the balloon drift in space and time was not accounted for in 2016 (i.e. the ascension was assumed instantaneous and vertical). The treatment of the radiosonde drift (from Binary Universal Form for the Representation of Meteorological data (BUFR) reports) has been introduced in the operational system in 2018 (Ingleby et al., 2018). Also in contrast to the Met Office, radiosondes at ECMWF are bias corrected for temperature and humidity. The correction, described by Agusti-Panareda et al. (2009), uses monthly statistics of background departure based on night-time RS92 and is applied as a function of radiosonde type, pressure, and solar elevation angle.
The GRUAN processor, a software based on the NWP Satellite Application Facility (SAF) Radiance Simulator (Smith, 2017), is designed to collocate NWP model fields from the Met Office or ECMWF with radiosondes from the GRUAN network and simulate TOA Tb from those collocated profiles. The simulations are performed at frequencies used by meteorological space-borne instruments and supported by RTTOV. Figure 1 illustrates the processor top-level design with its main processing steps.
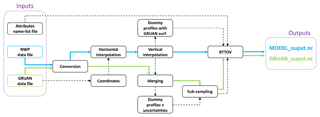
Figure 1GRUAN processor top-level design. Solid arrows show the main processing steps from input (blue for NWP model data and green for GRUAN data) to output. Dashed arrows represent the internal processing.
3.1 Inputs
The processor requires as input a GRUAN and a model data file. Supported products are GRUAN RS92-GDP, Met Office Unified Model (UM) field files (or PP files; see Smith, 2017), and ECMWF GRIB files. Both model file types must contain the minimum set of required variables as described by Smith (2017) for the Radiance Simulator. Processing options and RTTOV attributes are provided via a text file read by the processor. This file includes the instrument characteristics (e.g. channels) to be simulated and output options (output in unit of radiances or Tb for example). Optionally, RTTOV bias and root-mean-square error (RMSE) estimated from comparisons between RTTOV and line-by-line model calculations, as provided by NWP SAF (https://www.nwpsaf.eu/site/software/rttov/download/coefficients/comparison-with-lbl-simulations/, last access: 2 January 2019), can be written to the output files. Finally, an option allows one to opt for a model–radiosonde collocation following the balloon drift (in space and time; see Sect. 3.3) or assuming no drift. Note that all collocations presented in this paper account for the radiosonde drift.
3.2 Conversion
The conversion step ensures that both model and GRUAN variables (e.g. temperature or humidity) are expressed in the same units and that those units are compatible with RTTOV (see Sect. 3.5). Two main types of conversion are supported: temperature from potential temperature and specific humidity from relative humidity.
Model data files may sometimes contain potential temperature instead of temperature profiles, as is the case for the Met Office. Temperature (T) is therefore calculated as a function of potential temperature (θ) and pressure (P) as follows:
where P0 is the standard reference pressure equal to 1000 hPa and κ the ratio of the gas constant of air to the specific heat capacity at constant pressure.
Similarly, it is worth noting that model data files may not directly contain pressure profiles (e.g. in ECMWF files) or the pressure may be expressed on a different set of levels with respect to other variables (e.g. Met Office files). In both cases however, the pressure on model levels can be calculated from coefficients provided in the model data files.
The expression of humidity also needs to be harmonised. GRUAN provides profiles of relative humidity (RH), whereas the humidity from both NWP models is expressed in specific humidity (q), in units of kilogram per kilogram. GRUAN relative humidity is converted to q as follows:
where ε is the ratio of the molecular weight of water vapour to the molecular weight of dry air and es the saturation vapour pressure over liquid. For consistency with GRUAN and Vaisala processing, es is expressed as defined by Hyland and Wexler (1983), such that
with:
for es in pascals and T in kelvin.
3.3 Interpolations
The GRUAN processor generates a set of model profiles (i.e. one profile per variable), on model levels, interpolated in space and time along the radiosonde path, which are then vertically interpolated on a fixed set of 278 levels as follows.
First, model fields are linearly interpolated at the radiosonde coordinates (latitude–longitude–time), weighted by the distance to the eight closest grid points. Therefore, for an observation at the coordinate , as illustrated in Fig. 2, in a cube of vertices [(), (), (), (), (), (), (), and ()], where dx and dy represent the grid point interval in latitude and longitude, respectively, and dz the interval between the time T+n and , with associated field values Fp and , respectively, Fp is calculated as follows:
where wx, wy, and wz are the weights defined as
This operation is repeated along the radiosonde path with a time step of 15 s based on the radiosonde time profile. A unique model profile (one for each variable) is reconstructed by combining the model fields from the pressure levels crossed by the radiosonde between two consecutive interpolated model profiles.
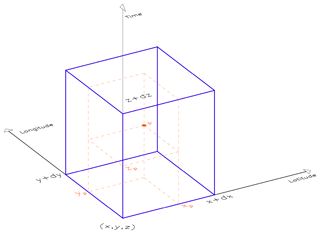
Figure 2Illustration of an observation of coordinate (xp, yp, zp) in a cube for which vertices represent the model latitude (x axis), longitude (y axis), and forecast time (z axis).
The reconstructed set of profiles is then interpolated on a fixed vertical grid of 278 pressure levels. The fixed grid, referred to as processor grid (Pg), has been designed to have at least one Pg level between any two levels of the coarser model (Met Office or ECMWF) grid, referred to as coarse grid (Cg). Therefore, for Pg of dimension n equal to 278 and Cg of dimension m (equal to 70 for the Met Office, 91 or 137 for ECMWF), the interpolation is calculated by weighting the fields with respect to the pressure via the interpolation matrix W of dimension n x m, such as
where for the jth pressure (P) level of Pg located between the ith and i+1th levels of Cg
The vertical interpolation of model profiles as well as the subsampling of the radiosonde profiles (see Sect. 3.4) to the processor grid aims to provide a homogenised number of vertical levels on which the radiative transfer equation is calculated. Although the coarse model grid and the fine radiosonde grid could be directly used as input in RTTOV, it was observed that the lack of homogenisation between model and radiosonde profiles causes a bias in radiance space. It was therefore decided to interpolate the model profiles and provide a way to estimate the uncertainty associated with this interpolation (see Sect. 5).
Figure 3 illustrates the change from a collocated Met Office temperature profile (LIN 31 December 2016, 16:00 UTC) on model levels (70 levels) (Fig. 3a) to a collocated Met Office profile interpolated on the processor grid (278 levels) (Fig. 3b).
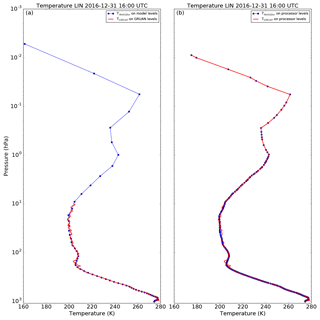
Figure 3(a) GRUAN temperature profile (red line) from Lindenberg on 31 December 2016 at 16:00 UTC as provided in the RS92-GDP data file with full GRUAN vertical resolution and a collocated Met Office temperature profile (blue dotted line) on the model vertical levels. (b) GRUAN temperature profile subsampled at the processor 278 pressure levels and merged with the Met Office profile above 9.8 hPa (red line) and collocated Met Office temperature profile interpolated on the processor vertical levels (blue dotted line).
3.4 Merging and subsampling
A caveat of processing radiosonde profiles in RTTOV is the lack of information between the top of a profile (bursting point of the balloon) and the TOA. This is addressed by merging the radiosonde profiles with the model profiles above the last available point of the radiosonde. Note that this step occurs after the interpolation of the model profiles so that the upper merged parts of the radiosonde and model profiles are strictly identical.
Similarly, RTTOV requires surface information: 2 m temperature and humidity, surface pressure and altitude, 10 m wind (u and v components, used for microwave simulations over ocean), and skin temperature. While GRUAN provides the surface pressure, temperature, relative humidity, and altitude at launch site in all the data files, the skin temperature () has to be derived from the difference between the model skin () and the 2 m temperature () applied to the GRUAN surface temperature () such as
Although the 10 m wind could be provided by the Vaisala wind profiles (available in GRUAN data files) or calculated from GRUAN profiles of wind speed and direction, the chaotic rotation of the radiosonde just after launch results in unreliable wind information near the surface. Therefore, the model 10 m wind (u and v components) is also merged with the GRUAN data. Note that 10 m wind is used to calculate the sea surface emissivity (for microwave simulations) and therefore only concerns GRUAN sites on small island sites (i.e. La Réunion, Nauru, Manau, Ny-Ålesund, Graciosa, and Tenerife).
In the raw RS92 data and GRUAN data, the samplings are provided every second but filtering reduces the effective resolution of temperature to approximately 10 s at low levels; the effective resolution of humidity is similar but it is reduced to 40–50 s at upper levels (Dirksen et al., 2014). As a result, GRUAN profiles count several thousand levels in the vertical that need to be reduced to the number of levels on the processor grid. This is achieved with a subsampling of the radiosonde profiles to the nearest levels for each of the 278 processor pressure levels, at levels at which data are available, with the imposed constraint that the ratio radiosonde pressure by processor pressure must be less than 0.1 %.
The subsampling of GRUAN profiles has been preferred over layer-averaging or convolution techniques for several reasons. First, we aimed to avoid all unnecessary modification of the GRUAN profiles, used as reference in this study. Second, GRUAN uncertainties are vertically resolved and their processing would have resulted in an information loss. Third, the aim of the processor is to evaluate uncertainties in radiance space. During the testing phase, we observed that neither the choice of averaged layers nor subsampled levels significantly affects the calculation of radiative transfer and the resulting brightness temperatures.
Figure 3 shows the changes from a GRUAN temperature profile (LIN 31 December 2016, 16:00 UTC) as provided in the RS92-GDP data file (5821 levels, from the surface to 9.88 hPa) (Fig. 3a) to a processor merged and subsampled profile (278 levels, from the surface to 0.008 hPa) (Fig. 3b).
3.5 RTTOV and uncertainties
The radiosonde and model profiles, both on the processor vertical grid, and their respective surface parameters are passed to RTTOV for the calculation of the TOA Tb. RTTOV version 11.3, currently used by the GRUAN processor, is documented by Hocking et al. (2015).
The surface emissivity depends on the surface type. For land and sea ice, the processor uses a fixed value, 0.95 and 0.92, respectively. Those estimates are potentially far from the truth, but any bias introduced by fixed emissivity terms is expected to cancel out when the difference in simulated Tb is calculated. Note that RTTOV allows the use of the emissivity atlases over land and sea ice, but this option has not yet been investigated. Over sea, the surface emissivity is calculated by the RTTOV FAST Emissivity Modeling (FASTEM) version 5 (Kazumori and English, 2015). Although version 5 is the default version, this can be changed in the input attribute file. It is worth noting here that although the radiosonde may drift from above land to above sea (ice) (or the opposite), the surface type can only be of one kind. The land surface type is typically used as most radiosonde launch sites are well inside land masses. However, for the small island sites of La Réunion, Nauru, Manau, Ny-Ålesund, Graciosa, and Tenerife, the radiosonde is expected to rapidly drift over sea and therefore the sea surface type is used instead. The difference between sea and sea ice is controlled by the sea-ice mask used by the NWP model.
The viewing angle is set by default to nadir (0∘) for all simulations. However, different angles could potentially be used for the purpose of better comparisons with real satellite data, for example.
All simulations assume clear-sky scenes and use RTTOV direct mode (ignoring the scattering) with the cloud liquid water option off (data not available from GRUAN data file). It is acknowledged that this may introduce discrepancies in the comparison between model and radiosonde in situations in which the radiosonde encounters one or several cloud layers. The brightness temperatures calculated from the radiosonde data perturbed by the presence of clouds (e.g. peaks in the humidity profile and to a lesser extent in the temperature profile) will differ from those calculated from the model data that assume clear-sky conditions. Because the RS92-GDP does not provide a cloud flag, indirect screening may be required for fine comparisons. To that end, one can use the precipitable water column from the RS92-GDP metadata as a proxy for cloud and or assume the presence of cloud when the relative humidity exceeds a threshold value.
Finally, note that RTTOV interpolation mode (used to interpolate the input levels to the coefficient levels for the calculation of the atmospheric optical depth, and then back from the coefficient levels to the input levels for the calculation of the radiative transfer equation) uses the log-linear on weighting function mode as described by Hocking et al. (2015). This aims to avoid a known issue causing the oscillation of the temperature Jacobians.
It was observed that the interpolation of the model fields at the GRUAN launch site coordinates results in large discrepancies, especially affecting surface parameters (surface pressure and elevation) and the lower part of the profiles, when the local orography presents large variations at scales of the same order as the model grid resolution. The interpolation, using the weighted average of the four neighbouring grid points at a given forecast time may result in the model surface being below or above the actual GRUAN launch site surface. A typical example is the site at La Réunion where the radiosondes are launched from the Maïdo observatory at an altitude of 2200 m, compared to which the interpolation of the ECMWF model gives an altitude of 980 m and the interpolation of the Met Office model 0 m. In Lindenberg by comparison, the radiosondes are launched from the altitude of 103 m while both models estimate the altitude to be 57 m. To estimate the associated error, a set of dummy model profiles are generated with the surface pressure forced to that provided in the GRUAN metadata. If the model has a surface below that of the observations, the model profiles are linearly interpolated and cut at the observed surface pressure, and the surface parameters become those of the lowest level. If the model has a surface above that of the observations, the model profiles are linearly extrapolated to the observed surface pressure, and the model surface parameters become those of the new lowest level. The difference between the Tb calculated from those modified profiles and the Tb calculated from the original profiles provides an estimation of the associated error. This is referred to as u_surf_bt in the processor output.
Finally, the GRUAN uncertainties are propagated into radiance space. As described by Calbet et al. (2017), this can be achieved by multiplying the GRUAN profiles of uncertainty by the Jacobians derived by RTTOV from the GRUAN atmospheric profiles, or by applying the radiative transfer to the input atmospheric GRUAN profiles perturbed with their associated uncertainties. The GRUAN processor is designed to follow the second method although the first one will be further discussed in Sect. 5. In the processor, two sets of perturbed profiles are created, one containing the GRUAN profiles of temperature, pressure, and humidity, incremented by their respective total uncertainty (T+u_temp, P+u_press, and q+u_q), and one containing the GRUAN profiles decremented by their total uncertainty (T−u_temp, P−u_press, and q−u_q). The resulting brightness temperatures calculated by RTTOV based on those two sets of perturbed profiles, referred to as and , respectively, are compared to Tb, calculated with the unperturbed profiles, to estimate the associated uncertainty in radiance space. The greatest difference between and is given in output as u_gruan_bt. Note that the eight combinations of sign that this approach can allow have been tried during the test phase. The resulting uncertainty was not found to be significantly different from that obtained with and , but the processing time significantly increased. and were therefore retained as the best compromise.
It should be noted that the simplified nature of this approach, which applies a perturbation of constant sign in the vertical, ignores the complicated fluctuations that the propagation of uncertainty via a multiplication by the Jacobians would induce (see Sect. 5). Here, we assume that the GRUAN profiles of uncertainty used to perturb the atmospheric profiles are fully correlated at all levels. This assumption differs from the truth in that GRUAN total uncertainty consists of a root sum square of correlated and uncorrelated components (Dirksen et al., 2014). Nevertheless, assuming a fully correlated perturbation enables the estimation of the total GRUAN uncertainty upper bound in radiance space allowed by this approach. The lower bound, not addressed in the GRUAN processor, can be obtained by assuming the uncertainty profiles are completely uncorrelated and lies close to zero as demonstrated by Calbet et al. (2017).
Ideally, the correlated and uncorrelated components of GRUAN uncertainty should be treated separately with, for example, the Monte Carlo method described in the Guide to the Expression of Uncertainty in Measurement (GUM) (https://www.bipm.org/en/publications/guides/gum.html, last access: 2 January 2019). However, those components are not all independently available and it is currently not possible to differentiate them in the RS92-GDP. Note that the radiosonde (random and/or systematic) errors are not provided. Instead, the GRUAN algorithm corrects the systematic errors in the radiosonde measurements, acknowledging that the correction is not perfect and introduces an associated residual uncertainty (accounted for in the total uncertainty).
For completeness, perturbations to the surface parameters could be added to the total uncertainty budget in radiance space, but GRUAN does not provide uncertainties associated with these measurements. An alternative is discussed in Sect. 5.
3.6 Outputs
For each pair of collocated radiosonde and NWP model fields, the GRUAN processor generates two output files in netCDF format. The first file contains the model-related fields including, but not limited to, the profiles of temperature, humidity, and pressure on the processor vertical grid, the interpolation matrix W, the simulated brightness temperature, the temperature, humidity, and pressure Jacobians, and a quality control flag (qcflags). Note that for successful simulations, qcflags is equal to zero. The second file contains the GRUAN-related fields, including GRUAN atmospheric profiles and associated uncertainties on the processor vertical grid, the Jacobians, and the Tb and Tb uncertainties estimated from the perturbed GRUAN profiles (u_gruan_bt).
Both files also contain metadata documenting the GRUAN processor version number (here 6.2); the NWP model, model validity time, and model version number; the simulated satellite name, platform, and channel; the RTTOV version, RTTOV coefficient creation date, bias, and root mean square error (when available); and the metadata available from the original RS92-GDP.
Note that some GRUAN processor simulated brightness temperatures have been ingested into the GAIA-CLIM Virtual Observatory (http://gaia-clim.vo.eumetsat.int/, last access: 2 January 2019) for the purposes of visualisation, manipulation, and extraction of collocated GRUAN–NWP–satellite data.
For illustration purposes, 1 year of collocated profiles and simulated Tb are presented. The dataset corresponds to 1160 radiosondes launched from Lindenberg, Germany, in 2016, compared to the Met Office and ECMWF models. Tb values have been simulated at the Advanced Technology Microwave Sounder (ATMS) 22 channel frequencies, a microwave radiometer with sounding capability in the oxygen band (53–57 GHz), sensitive to tropospheric and lower-stratospheric temperature, and in the water vapour band (around 183 GHz), sensitive to mid- to upper-tropospheric humidity (Bormann et al., 2013).
The dataset is divided into two samples composed of daytime and night-time profiles. This is aimed at discriminating the GRUAN profiles affected by solar radiation, the dominant source of uncertainty according to Dirksen et al. (2014). All profiles with a solar zenith angle (calculated as a function of latitude, longitude, and UTC) smaller (greater) than 90∘ at launch time is considered daytime (night-time). Note that for a refined analysis, the whole profile (not just launch time) should be checked and only profiles with the sun below (or above) the horizon throughout should be used. Note that for simplicity, no cloud screening is applied in this case study. This caveat may, as suggested in the previous section, exacerbate the biases observed when comparing brightness temperature simulated from radiosonde profiles and from model fields. Future work dedicated to the in-depth analysis of model errors and uncertainties based on the processor outputs will address the impact of clouds on the simulations.
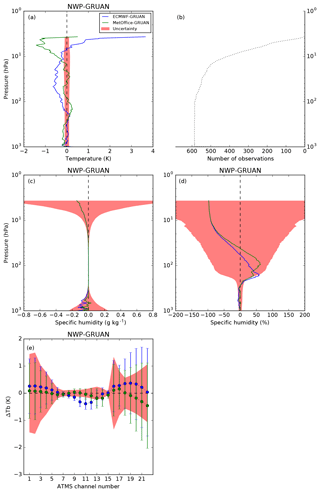
After screening, 573 pairs of GRUAN processor outputs are available in daytime and 587 in night-time for each model. The mean difference NWP–GRUAN in temperature, humidity, and simulated Tb is shown in Figs. 4 (daytime) and 5 (night-time) together with the number of available comparisons as a function of the pressure. Note that at pressures less than 10 hPa, the data sampling decreases rapidly as fewer balloons reach those levels. An arithmetic mean is used to average the uncertainty over the sampling according to Immler et al. (2010) (Eq. 4). For temperature and humidity, the GRUAN total uncertainty as provided in the RS92-GDP is used (the relative humidity uncertainty is converted into specific humidity uncertainty in the GRUAN processor), while the uncertainty in Tb shows the GRUAN uncertainties propagated in radiance space via the perturbation of the atmospheric profiles. Note that the model uncertainty and the uncertainty associated with the vertical interpolation are ignored in this section but addressed in Sect. 5.
It is important to note that both Met Office and ECMWF operationally assimilate the radiosonde profiles from the GCOS Upper Air Network (GUAN), which, in Lindenberg, are the same as the GRUAN profiles but without the specific GRUAN processing (and without uncertainty characterisation). Therefore, unlike the forecasts, the model analyses (T+0) are not completely independent from the observations. However, this is not expected to significantly affect the mean comparison as only about 5 % of the profiles fall in the first time window (i.e. interpolation between T+0 and T+3).
In Figs. 4 and 5, the main feature for ECMWF is a 0.5 K cold bias in the stratosphere (100–10 hPa), observed both day and night. This bias has also been detected by Shepherd et al. (2018) in the ERA5 reanalysis that is based on IFS cycle 41r2, the operational model in 2016. It is attributed to an excess of moisture transported into the lower stratosphere, which leads to a cold bias by radiative cooling. The model also presents a 50 %–75 % wet bias peaking between 200 and 100 hPa, slightly more pronounced during the day. This is consistent with the results from Ingleby (2017), who showed a similar behaviour for several kinds of radiosonde.
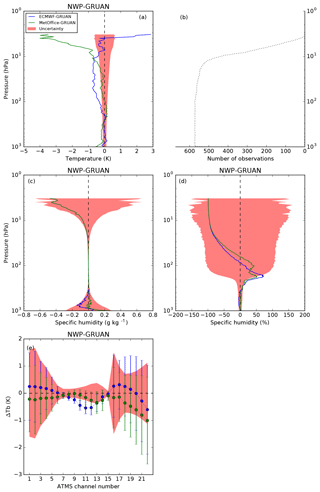
Figure 4Mean difference ECMWF–GRUAN (blue) and Met Office–GRUAN (green) calculated from 573 daytime collocations from Lindenberg in 2016. The temperature difference (a) is expressed in kelvin, the humidity difference is expressed in grams per kilogram (c) and in percentage (d), and the difference in simulated brightness temperatures for the 22 ATMS channels is expressed in kelvin (e) with the 1σ standard deviation (vertical bars). The red shading shows GRUAN uncertainty. The number of observations is shown as a function of the pressure (b).
The Met Office model presents a persistent 0.2 to 0.5 K cold bias at pressures greater than 300 hPa and a 0.25 K warm bias between 200 and 100 hPa seen at night-time only. This is consistent with Ingleby and Edwards (2015), who showed similar features in the comparison between radiosondes and the Met Office regional model covering the UK. The Met Office tropospheric humidity generally fits the radiosonde profiles well but presents a 50 %–60 % wet bias with a peculiar double peak at 200 and 100 hPa. A wet bias peaking at 300 hPa was already observed by Ingleby et al. (2013), the coarser vertical resolution used by the authors potentially explaining the different pressure level at which the bias is observed. However, the second maximum (at 100 hPa) seems to be a new feature that appears in 2015 and persists in 2017 (not shown). This remains unexplained to date.
In radiance space, it is important to distinguish between frequencies representative of the difference between NWP and GRUAN and those significantly affected by the surface and the mid-stratosphere to upper stratosphere where the GRUAN profiles are merged with the model. Hence, ATMS frequencies sensitive to the surface (23.8–54.4 and 88.2–165.5 GHz, channels 1–7 and 16–17, respectively) and to the upper stratosphere (57.29 ± 0.3222 ± 0.022–57.29 ± 0.3222 ± 0.0045 GHz, channels 13–15, respectively) should be considered with caution and not used for scientific applications. On the contrary, frequencies sensitive to the upper-tropospheric and lower-stratospheric temperature (peaking between 300 and 20 hPa) and to the mid-tropospheric humidity (peaking between 650 and 350 hPa) cover the same vertical domain as the information provided by GRUAN. For those frequencies, ATMS channel characteristics and mean Tb difference are provided in Table 1.
Table 1Mean difference NWP–GRUAN in simulated Tb for ECMWF () and Met Office ( and 1σ standard deviation for ATMS channels 8–12 and 18–22 at daytime and night-time.
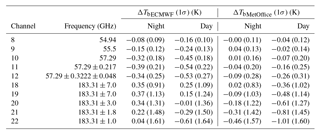
At frequencies sensitive to temperature (54–57 GHz, channels 8–12), hereafter referred to as temperature channels, the mean difference for ECMWF varies from −0.08 to −0.39 K at night, mostly outside GRUAN uncertainty (red shading, Fig. 5), reflecting the cold bias observed in the stratosphere. Note that a difference greater than GRUAN uncertainty does not mean a statistical disagreement since the uncertainty related to the model is unaccounted for (i.e. the total uncertainty of the comparison as expressed in Eq. (1) is larger than the GRUAN uncertainty alone). The difference is slightly larger in daytime (−0.16 to − 0.54 K). Similarly, the difference at frequencies sensitive to humidity (around 183 GHz, channels 18–22), hereafter referred to as humidity channels, varies from 0.04 to 0.37 K at night (−0.01 to −0.61 K during the day), within GRUAN uncertainty.
The mean difference in Tb for the Met Office is always found within GRUAN uncertainty and varies from −0.09 to 0.04 K during the night (−0.02 to −0.26 K in daytime) for the temperature channels and from −0.46 to 0.02 K during the night (−0.36 to −1.01 K in daytime) for the humidity channels.
The standard deviation of the differences is similar for both centres and does not vary much from day to night.
The previous section gives insights into the GRUAN uncertainty propagated in radiance space by the GRUAN processor. The approach offers a rapid but incomplete evaluation of the NWP–GRUAN comparison, but several aspects are overlooked in the final budget that for various reasons are not part of the internal processor processing. This includes
- (a)
the uncertainty associated with surface parameters, not provided in RS92-GDP and likely to change from station to station;
- (b)
the NWP model uncertainty, often expressed as a covariance matrix and used in the data assimilation process by the NWP centres, but not available in the input data files; and
- (c)
the uncertainty associated with the vertical interpolation operated by the processor for which estimation requires information on the last two points.
In this section, a mathematical framework is elaborated to estimate a robust uncertainty budget for the comparison between NWP fields and GRUAN observations, in radiance space, and statistically assess this comparison. This includes uncertainties in the GRUAN observations, in the vertical interpolation of the GRUAN processor, and in the model fields. Note that, as previously mentioned, any comparison to satellite radiances should also include other sources of uncertainty such as in the underlying radiative transfer models and cloud detection. For this study, we focus on the comparison to the Met Office model fields, but the same method could be applied to the comparison with ECMWF fields.
We define xrs as the radiosonde profiles and xm as the model profiles (temperature, humidity, and pressure, with a pressure coordinate). Note that xrs and xm are on different vertical grids. xrs is on the GRUAN processor vertical grid, composed of 278 levels, hereafter referred to as the fine grid (f), subsampled from the original GRUAN profiles (noting that with a ratio radiosonde pressure by processor pressure of less than 0.1 %, the subsampling uncertainty is assumed negligible). xm is on the model vertical grid, hereafter referred to as the coarse grid (c), as given in input.
Given H, the observation operator, we can express the simulated Tb as follows:
where W is the interpolation matrix.
Equations (15) and (16) can be further expanded as a function of the profiles' true value on the fine and coarse grids, hereafter and , respectively, and the errors associated with the radiosonde and the model fields, hereafter εrs and εm, as follows:
with defined as , where an expression for W∗, the pseudo-inverse of W, is given in Appendix B.
The comparison carried out in this study is in radiance space and the observation operator used to simulate the brightness temperatures is identical for both radiosonde and model field simulations. For these reasons, we consider the radiance space as our reference and ignore any errors associated with observation operator that would cancel out in the difference anyway since the errors associated with the observation operator are mainly systematic. Note that those errors need, however, to be taken into account if a simulated product is compared to real satellite observations.
We define the vertical interpolation error εint as
Equation (18) can be written as follows:
Given H, the Jacobian matrix provided by RTTOV and containing the partial derivatives of (i.e. the change in radiance, ∂y, for a change in the state vector, ∂x), Eqs. (17) and (20) can be approximated, assuming small errors, as follows:
Therefore, the NWP–GRUAN comparison in radiance space is expressed as follows:
Assuming a complete non-correlation between the interpolation error and those of the radiosonde and the model, the covariance of the difference is expressed as follows:
where E is the expectation operator. We can approximate Eq. (24) as
where , , and are the error covariance matrices of GRUAN measurements (on the fine grid), the forecast (on the coarse grid), and the vertical interpolation (on the fine grid), respectively, as described below.
We first define the GRUAN covariance matrix. GRUAN does not provide a full covariance matrix with the measurements; therefore is built as a diagonal matrix accounting for the different sources of uncertainty such as
where RT, Rq, and RP are diagonal matrices whose diagonals are the square of GRUAN profiles of total uncertainty for T, q (converted from relative humidity), and P, respectively, on the processor vertical grid; uskinT, uT2 m, uq2 m, and uP2 m the uncertainties associated with the surface parameters (i.e. skin temperature, 2 m temperature, 2 m humidity, and 2 m pressure) set to 0.3 K, 0.3 K, 0.04 RH, and 0.1 hPa, respectively (Sven Brickmann, DWD, private communication, 2016), estimated for the Lindenberg site. HT, Hq, and HP are the Jacobians of the temperature, humidity, and pressure profiles, respectively, and hskinT, hT2 m, hq2 m, and hP2 m are the Jacobians of the surface parameters.
RT, Rq, and RP are diagonal, which precludes a proper propagation of the correlation in radiance space. In this suboptimal case, , and by extension, Sδy, the covariance of the comparison, will not capture the most accurate representation of the uncertainty budget.
Then, we define the forecast error covariance matrix. For the purposes of this study, the forecast covariance matrix from the operational Met Office observation processing system, a one-dimensional variational analysis (1D-var) performed ahead of the main variational process, is used for . Alternatively, the forecast error covariance matrix can be estimated from an ensemble of NWP profiles as described in Appendix A.
Finally, we define the vertical interpolation covariance matrix. To estimate , the interpolation error must be quantified.
From Eq. (19) we have
where the random vector , representing the true state on the fine grid, is assumed to have mean , the (unknown) mean model forecast profile on the fine grid, and covariance , the covariance of in model space on the fine grid. It follows that we can express the covariance of the interpolation uncertainty as
Note that when the model grid coincides with the fine grid we have and Sint=0 as expected. Replacing W∗ by its form expressed in Appendix B, we obtain
Note that in practice (i.e. for numerical calculations) it is more convenient to use the form expressed in Eq. (28) to get as a symmetric and positive definite matrix.
This methodology has been applied to the 587 profiles of the night-time dataset described in the previous section. The covariances Sδy of each comparison as approximated in Eq. (25) have been averaged (arithmetic mean, hereafter ) and the square root of the diagonal. (i.e. the 1σ standard deviation of the comparison total uncertainty distribution) is shown in Fig. 6. In practice, we calculate Sδy as the sum of the covariance matrices of each variable: the surface measurement covariance (Ssurf_rs); the model surface covariance (Ssurf_m); the total humidity covariance (Sq_total); the total temperature covariance (ST_total); and the GRUAN pressure covariance (SP_rs). The square root of their diagonal is also shown in Fig. 6. In addition, Sq_total and ST_total can be further decomposed into the sum of the covariance matrices of each of their components: the GRUAN humidity and temperature covariance (Sq_rs and ST_rs); the model humidity and temperature covariance (Sq_m and ST_m); and the covariance of the vertical interpolation of the model humidity and temperature profiles (Sq_m_int and ST_m_int). The square root of their diagonal is also shown in Figs. 7 and 8.
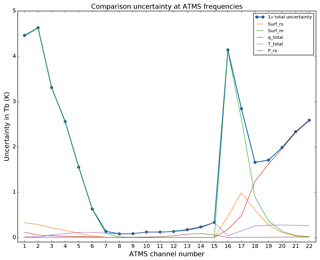
Figure 6The 1σ standard deviation of the total uncertainty distribution expressed as the square root of the diagonal of the mean comparison covariance (blue dots) and the square root of the diagonal of the components forming , namely, the GRUAN surface uncertainty (Surf_rs, orange), the model surface uncertainty (Surf_m, green), the humidity total uncertainty (q_total, red), the temperature total uncertainty (T_total, purple), and the GRUAN pressure uncertainty (P_rs, brown).
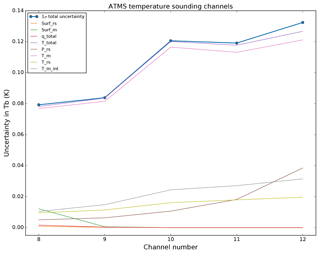
Figure 7Same as Fig. 6 but only for ATMS temperature upper-tropospheric and lower-stratospheric channels 8–12, with the square root of the diagonal of the components forming ST_total, namely, the GRUAN temperature uncertainty (T_rs, olive), the model temperature uncertainty (T_m, pink), and the model vertical interpolation uncertainty (T_m_int, grey).
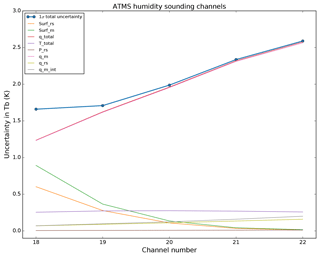
Figure 8Same as Fig. 6 but only for ATMS humidity tropospheric channels 18–22, with the square root of the diagonal of the components forming Sq_total, namely, the GRUAN humidity uncertainty (q_rs, olive), the model humidity uncertainty (q_m, pink), and the model vertical interpolation uncertainty (q_m_int, grey).
Note that on some occasions, the processor fine grid does not capture the lowermost or uppermost model levels, which caused missing values in W. The calculation has consequently been performed, for those cases, on the remaining levels of W. It is planned to refine the processor grid in the future version in order to avoid such missing data in the interpolation matrix.
As expected, the surface components of the total uncertainty are dominant at frequencies at which the radiance is sensitive to the surface (ATMS channels 1–7 and 16–17). Amongst them, the surface component from the model is the largest due to the low confidence in surface emission and properties. Channels with frequencies sensitive to temperature and humidity are dominated by the temperature and humidity total components, respectively.
The decomposition of the temperature and humidity total uncertainties in the temperature channels (Fig. 7) and in the humidity channels (Fig. 8), respectively, shows that, again, the model components are largely dominant. Note that for the highest peaking temperature channel (channel 12) the second largest uncertainty is the GRUAN pressure component. Also, the lowest peaking humidity channels (channels 18–19) are significantly affected by the surface uncertainty, although this may vary with the location and the water vapour burden, making those channels peak more or less high in the atmosphere and therefore more or less sensitive to the surface.
The total uncertainty ranges from 0.08 to 0.13 K for the temperature channels in Fig. 7 and from 1.6 to 2.5 K for the humidity channels in Fig. 8. Compared to the mean difference documented in Table 1, the night-time sampling satisfies the consistency requirement of Eq. (1) with k=1, noting that the σ term in Eq. (1) that should represent the uncertainty associated with the trilinear horizontal interpolation is currently unknown, although assumed small, and therefore ignored. Future work will be dedicated to the estimation of this σ term using a high-resolution regional model.
These preliminary results are in line with the uncertainty range provided by Loew et al. (2017). This should however be confirmed with the careful evaluation of multiple GRUAN sites over longer time periods, beyond the scope of this paper but planned to be addressed in the near future.
It is interesting to compare the GRUAN processor upper bound uncertainty, calculated assuming a complete correlation, i.e. u_gruan_bt, with the GRUAN contribution to . Ignoring the uncertainties associated with the surface parameters, the GRUAN contribution to can be calculated as the square root of the first three terms of Eq. (26). Figure 9 shows that u_gruan_bt is consistently 4 times larger than the 3σ standard deviation of the GRUAN contribution to at the frequencies of interest. It may indicate that the assumption of complete correlation in the uncertainty (i.e. the use of GRUAN total uncertainty as if correlated at all levels), associated with the calculation of the maximal total uncertainty in Tb, results in a large overestimation of the uncertainty in radiance space. In addition, it should be remembered that the use of diagonal matrices in Eq. (26) is suboptimal and may not capture the full extent of the uncertainty. The lack of explicit systematic and random errors associated with the radiosonde profiles and the lack of discretisation between correlated and uncorrelated uncertainty components in GRUAN products is also suboptimal. This stresses the need for the GRUAN community to provide proper covariance matrices, better-defined error profiles, and better discretisation of correlated and uncorrelated uncertainties. Finally, it is possible, although not likely, that a violation of the assumption of small uncertainties in Eqs. (21)–(22) could result in non-linear perturbations potentially causing the GRUAN contribution to to be underestimated.
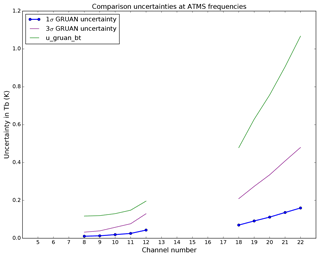
Figure 9The 1σ standard deviation of the uncertainty distribution from the GRUAN contribution to is shown in blue (dotted line). It is calculated as the square root of the first three terms of Eq. (26), i.e. . The 3σ standard deviation of the uncertainty distribution is shown in purple (solid line). u_gruan_bt, the GRUAN uncertainty propagated into radiance space by the GRUAN processor and averaged over the night-time sample, is shown in green (solid line).
Next, the overall agreement between the Met Office model and GRUAN, in radiance space, is assessed via a χ2 test. Here, a reduced χ2, hereafter , is estimated for each profile as follows:
where δyi is the NWP–GRUAN difference in Tb for the ith comparison, and is the mean comparison over the sample. The number of degrees of freedom c, in this context, is the number of channels regardless of any constraints as defined in Rodgers (2000) (Sect. 12.2).
Comparing calculated and theoretical will allow, in theory, the assessment and eventually revision of the uncertainty estimates used for the NWP model and GRUAN. Figure 10 shows the distribution of calculated for the night-time sampling (blue line) and how it compares to the theoretical estimated from random data of similar sampling size (green line). Dashed lines show the 95th percentile of each distribution. values beyond the theoretical 95th percentile line reflect the comparisons for which the model and GRUAN are significantly different. For this example, the 95th percentile of the calculated (blue dashed line) is 5 % larger than the theoretical one (green dashed line); i.e. about 10 % of the calculated values are greater than the theoretical 95th percentile threshold. This relatively good match between calculated and theoretical rules out the hypothesis of the violation of small uncertainties in Eqs. (21)–(22). However, it might be that one (or more) component of Sδy has been underestimated and could be revised until both 95th percentiles match. It is also possible that unforeseen sources of uncertainty have been unaccounted for in Eq. (25). In both cases, the increased total uncertainty will reduce the number of comparisons failing the test and reduce the difference between the calculated and theoretical 95th percentile threshold.
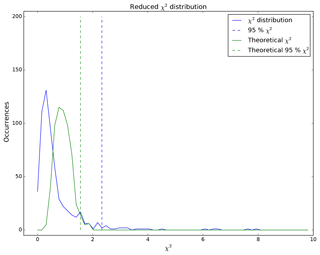
Figure 10Reduced χ2 distribution from the NWP–GRUAN night-time sampling (blue) and theoretical reduced χ2 estimated from a random sampling of equal size and equal degrees of freedom (blue). Dashed lines show the 95th percentile of each distribution.
A refined assessment using a larger sample spanning several years and several GRUAN sites will be addressed as part of future work, but is out of the scope of this study.
NWP models have demonstrated the ability to act as suitable reference comparators for the calibration and validation of satellite instruments. Model analysis and short-range forecast uncertainties are incrementally reduced by progressive improvements in data assimilation techniques and the ingestion of a large and growing number of observations from multiple sources. From the state of the art of NWP output fields, biases as small as a tenth of a kelvin can be highlighted in some satellite datasets. In addition, NWP models provide global fields, which allow for the evaluation of satellite data across the full dynamic range of the instrument. Yet model uncertainty estimates do not meet international metrological traceability standards as provided by other reference datasets, such as the GRUAN radiosondes.
In order to address the missing links in the traceability chain of model uncertainty, a collocation and radiance simulation tool (the GRUAN processor) has been developed in the framework of the GAIA-CLIM project. This allows us to quantify differences between GRUAN radiosonde profiles of well-defined uncertainties and NWP fields, in both observation and radiance space.
Based on the radiative transfer core capability of the radiance simulator developed and maintained by NWP SAF, the processor collocates model fields to GRUAN radiosonde profiles in space and time, then simulates top-of-atmosphere brightness temperatures for both datasets at frequencies used by satellite instruments, and propagates GRUAN uncertainties in radiance space. The details of the GRUAN processor have been described in this paper and a mathematical methodology aimed at assessing NWP–GRUAN comparisons in radiance space has been expounded.
For this study, a small sampling of 573 daytime and 587 night-time GRUAN radiosonde profiles from Lindenberg, Germany, in 2016, and matching NWP fields from the Met Office and ECMWF global models have been processed and analysed to demonstrate the GRUAN processor capability.
In the geophysical space of the radiosonde observations, the NWP–GRUAN comparison has highlighted 0.5 K cold biases located in the stratosphere of the ECMWF model and in the lower troposphere of the Met Office model. A wet bias ranging from 50 % to 75 % of the local specific humidity is visible in both models at a pressure of between 200 and 100 hPa.
In radiance space, the Met Office and ECMWF Tb are found to be within ±0.09 and ±0.39 K, respectively, of GRUAN night-time profiles (when GRUAN biases are minimal), at frequencies predominantly sensitive to temperature (54–57 GHz) in the vertical domain in which GRUAN radiosonde observations are available. Similarly, the Met Office and ECMWF Tb values are found to be within ±0.46 and ±0.37 K, respectively, of GRUAN night-time profiles at frequencies predominantly sensitive to humidity (around 183 GHz).
The propagation of GRUAN uncertainties in radiance space is performed in the GRUAN processor via perturbation of the temperature, humidity, and pressure profiles by plus and minus their total uncertainty as provided in the RS92-GDP data files. This process assumes a complete correlation of the uncertainties at all levels. This is a pessimistic assumption and the resulting uncertainty obtained in radiance space is therefore representative of a maximum uncertainty of the GRUAN component (the model uncertainty is not accounted for). The true GRUAN uncertainty in radiance space is smaller than that calculated as only a fraction of GRUAN total uncertainty (in observation space) is really correlated over the entire profile.
Independently from that maximum GRUAN uncertainty estimate, a rigorous estimation of the uncertainties in radiance space associated with the NWP–GRUAN difference is proposed in this study as a post-processing application based on the GRUAN processor outputs. The covariance of this difference, Sδy, is calculated as the sum of the GRUAN, model, and interpolation uncertainties propagated in radiance space.
Tested with the Met Office background error covariance, the NWP component of Sδy is found to be the dominant source of uncertainty. The total uncertainty of the difference ranges from 0.08 to 0.13 K at frequencies sensitive to temperature and from 1.6 to 2.5 K at frequencies sensitive to humidity, satisfying, on average, the consistency check (Eq. 1) for night-time profiles.
The GRUAN component of Sδy is found to be 4 times smaller (at 3σ) than the maximum GRUAN uncertainty estimated in the processor, demonstrating the large overestimation of the complete correlation assumption. However, it is worth stressing that in the absence of covariance information, error (random and systematic) characterisation, and discretisation between correlated and uncorrelated uncertainty components in GRUAN data files, the estimation of Sδy remains suboptimal.
The χ2 distribution calculated for the comparisons between model-based (Met Office) and GRUAN-based simulated Tb revealed that the number of significantly different comparisons is close to although slightly larger than that of the corresponding theoretical χ2 distribution. Implications are that either one or several components of Sδy are underestimated, or that a source of uncertainty has been overlooked.
The next step will be to process and analyse collocated profiles spanning several years and multiple GRUAN sites. This will provide a better, although incomplete, geographical distribution of model biases as well as their evolution in time. Away from the surface, NWP model biases are to first order a function of latitude and height and can usefully be studied for polar, mid-latitude, and tropical bands. For northern latitude bands, the NWP uncertainties can be studied by comparison with GRUAN observations, but for the tropics and southern latitudes, where there are few or no GRUAN data, these could to be supplemented with other high-quality radiosonde reports. The aim will be to provide a refined set of model uncertainty for selected frequencies spanning both microwave and infrared domains. Ultimately, the contribution from this work will help draw the full model uncertainty budget (composed of uncertainties in radiance space, radiative transfer modelling, scale mismatch, and cloud residual) for more robust assessment of satellite observations. Finally, the larger sampling will also ensure a more robust χ2 analysis and, if deemed necessary, help revise the model covariance matrices used in operation at the Met Office and ECMWF.
The quantitative estimate of errors and uncertainties in NWP models, for temperature, humidity, and radiance space, could aid in the interpretation of observation minus short-range forecast statistics for satellite instruments, for example by helping to identify whether biases in observation-minus-model background values could be due to systematic errors in the NWP model short-range forecasts. In future work, it is planned to use the GRUAN processor output to evaluate biases in observation-minus-model background statistics of satellite data.
GRUAN processor-based studies also have the potential to refine and improve bias correction schemes used in NWP centres by helping identify regions where NWP model biases are small as suggested by Eyre (2016). Similarly, the processing and inter-comparison of multiple radiosonde types can help determine which sets of observations could be used as anchors.
Finally, the GRUAN processor will also evolve with the evolution of RTTOV. For example, a parallel version of the processor is currently being tested with the ground-based fast radiative transfer model RTTOV (RTTOV-gb). RTTOV-gb is a modified version of RTTOV that allows for simulations of ground-based upward-looking microwave sensors (De Angelis et al., 2016). Model- and GRUAN-simulated Tb and propagated uncertainties are expected to help estimate the uncertainties in the microwave radiometer observations for which RTTOV-gb has been developed. It is also planned to upgrade the processor in order to support RTTOV 12 (Hocking et al., 2017). This upgrade will allow better handling of surface emissivity and give the option to output principal components used for the new generation of hyperspectral infrared sounders. Note that other fast radiative transfer models, such as the Community Radiative Transfer Model (CRTM), could potentially be tested with the GRUAN processor, although there is no immediate plan to do so.
For further information on the GRUAN processor source code and/or output availability, please contact the lead author (fabien.carminati@metoffice.gov.uk).
If the forecast error covariance matrix from the NWP forecast model used as input to the processor is not available, it can be determined from an ensemble of K NWP profiles, with K>N, where N is the number of vertical levels, such that
where K−1 gives the best estimate of the covariance of the population from which the sample K is drawn, and with X′ such as
where is the jth model profile of the K ensemble, and is the mean of the K profiles, both on the coarse model vertical grid.
The interpolation matrix W is not square and therefore its inverse cannot be calculated. Instead, a pseudo inverse, W∗, can be obtained using, for example, the weighted least-square estimate of (Rodgers, 2000). For that, we need to minimise
where, for the weight, we use the forecast error covariance matrix expressed on the fine grid, , since we interpolate the model profiles on that grid.
By taking the derivative with respect to and setting it to zero, we find
where
In order to find an expression for , we refer to , the forecast covariance matrix on the coarse model grid, to calculate the forecast error correlation matrix , on the coarse model grid. The correlation matrix is then reconditioned on the fine processor grid and referred to as , as explained below.
We define Σ, a diagonal matrix representing the square root of variance, as
Cm can be expressed as
We can then define as
However, Eq. (B6) does not guarantee that diagonal elements are equal to 1. This constraint needs to be imposed as
Given σm, a vector composed of the square root of the variance of εm variance, , is expressed as follows:
FC developed the GRUAN processor code, analysed the data, and prepared the paper with contributions from all co-authors. SM developed the mathematical framework presented in Sect. 5. BI and HL provided ECMWF datasets and helped with code design and data analyses. WB and SN helped with code design and data analyses. JH develops and manages RTTOV. AS developed the Radiance Simulator.
The authors declare that they have no conflict of interest.
This work and its contributors (Fabien Carminati, Stefano Migliorini, Bruce
Ingleby, Bill Bell, Heather Lawrence, and Stu Newman) were supported by the
European Union's Horizon 2020 research and innovation programme under the
GAIA-CLIM grant agreement no. 640276. We are grateful to John Eyre, Emma
Turner, and the referees for their comments and suggestions that helped us
improve the quality of our study.
Edited by: Ad
Stoffelen
Reviewed by: three anonymous referees
Agusti-Panareda, A., Vasiljevic, D., Beljaars, A., Bock, O., Guichard, F., Nuret, M., Garcia Mendez, A., Andersson, E., Bechtold, P., Fink, A., Hersbach, H., Lafore, J.-P., Ngamini, J.-B., Parker, D. J., Redelsperger, J.-L., and Tompkins, A. M.: Radiosonde humidity bias correction over the West African region for the special AMMA reanalysis at ECMWF, Q. J. Roy. Meteor. Soc., 135, 595–617, https://doi.org/10.1002/qj.396, 2009.
Auligné, T., McNally, A. P., and Dee, D. P.: Adaptive bias correction for satellite data in a numerical weather prediction system, Q. J. Roy. Meteor. Soc., 133, 631–642, https://doi.org/10.1002/qj.56, 2007.
Bauer, P., Thorpe, A., and Brunet, G.: The quiet revolution of numerical weather prediction, Nature, 525, 47–55, https://doi.org/10.1038/nature14956, 2015.
Bell, W., Candy, B., Atkinson, N., Hilton, F., Baker, N., Bormann, N., Kelly, G., Kazumori, M., Campbell, W. F., and Swadley, S. D.: The assimilation of SSMIS radiances in numerical weather prediction models, IEEE T. Geosci. Remote Sens., 46, 884–900, https://doi.org/10.1109/TGRS.2008.917335, 2008.
Bojinski, S., Verstraete, M., Peterson, T. C., Richter, C., Simmons, A., and Zemp, M.: The concept of essential climate variables in support of climate research, applications, and policy, B. Am. Meteorol. Soc., 95, 1431–1443, https://doi.org/10.1175/BAMS-D-13-00047.1, 2014.
Bonavita, M., Hólm, E. V., Isaksen, L., and Fisher, M.: The evolution of the ECMWF hybrid data assimilation system, Q. J. Roy. Meteor. Soc., 142, 287–303, https://doi.org/10.1002/qj.2652, 2016.
Bormann, N., Fouilloux, A., and Bell, W.: Evaluation and assimilation of ATMS data in the ECMWF system, J. Geophys. Res.-Atmos., 118, 12970–12980, https://doi.org/10.1002/2013JD020325, 2013.
Calbet, X., Peinado-Galan, N., Rípodas, P., Trent, T., Dirksen, R., and Sommer, M.: Consistency between GRUAN sondes, LBLRTM and IASI, Atmos. Meas. Tech., 10, 2323–2335, https://doi.org/10.5194/amt-10-2323-2017, 2017.
Courtier, P., Thépaut, J., and Hollingsworth, A.: A strategy for operational implementation of 4D-Var, using an incremental approach, Q. J. Roy. Meteor. Soc., 120, 1367–1387, https://doi.org/10.1002/qj.49712051912, 1994.
De Angelis, F., Cimini, D., Hocking, J., Martinet, P., and Kneifel, S.: RTTOV-gb – adapting the fast radiative transfer model RTTOV for the assimilation of ground-based microwave radiometer observations, Geosci. Model Dev., 9, 2721–2739, https://doi.org/10.5194/gmd-9-2721-2016, 2016.
Dee, D.: Variational bias correction of radiance data in the ECMWF system, in: Proc. of the ECMWF Workshop on Assimilation of High Spectral Resolution Sounders in NWP, 28, 97–112, available at: https://www.ecmwf.int/search/elibrary (last access: 2 January 2019), 2004.
Dirksen, R. J., Sommer, M., Immler, F. J., Hurst, D. F., Kivi, R., and Vömel, H.: Reference quality upper-air measurements: GRUAN data processing for the Vaisala RS92 radiosonde, Atmos. Meas. Tech., 7, 4463–4490, https://doi.org/10.5194/amt-7-4463-2014, 2014.
Eyre, J. R.: Observation bias correction schemes in data assimilation systems: a theoretical study of some of their properties, Q. J. Roy. Meteor. Soc., 142, 2284–2291, https://doi.org/10.1002/qj.2819, 2016.
Green, P., Gardiner, T., Medland, D., and Cimini, D.: Guide to Uncertainty in Measurement & its Nomenclature, GAIA-CLIM Deliverable D2.6, available at: http://www.gaia-clim.eu/ (last access: 2 January 2019), 2018.
Haseler, J.: Early-delivery suite, ECMWF Technical Memorandum No. 454, available at: https://www.ecmwf.int/search/elibrary (last access: 2 January 2019), 2004.
Hocking, J., Rayer, P., Rundle, D., Saunders, R., Matricardi, M., Geer, A., Brunel, P., and Vidot, J.: RTTOV v11 Users Guide, Tech. Rep. NWPSAF-MO-UD-028, EUMETSAT Satellite Application Facility on Numerical Weather Prediction (NWPSAF), available at: https://www.nwpsaf.eu/site/software/rttov/rttov-v11/ (last access: 2 January 2019), 2015.
Hocking, J., Rayer, P., Rundle, D., Saunders, R., Matricardi, M., Geer, A., Brunel, P., and Vidot, J.: RTTOV v12 Users Guide, Tech. Rep. NWPSAF-MO-UD-037, EUMETSAT Satellite Application Facility on Numerical Weather Prediction (NWPSAF), available at: https://www.nwpsaf.eu/site/software/rttov/documentation/ (last access: 2 January 2019), 2017.
Hollmann, R., Merchant, C. J., Saunders, R., Downy, C., Buchwitz, M., Cazenave, A., Chuvieco, E., Defourny, P., de Leeuw, G., Forsberg, R., Holzer-Popp, T., Paul, F., Sandven, S., Sathyendranath, S., van Roozendael, M., and Wagner, W.: The ESA climate change initiative: Satellite data records for essential climate variables, B. Am. Meteorol. Soc., 94, 1541–1552, https://doi.org/10.1175/BAMS-D-11-00254.1, 2013.
Hyland, R. W. and Wexler, A.: Formulation for the thermodynamic properties of the saturated phases of H2O from 173.15 K to 473.15 K, ASHRAE Trans., 89, 500–519, 1983.
Immler, F. J., Dykema, J., Gardiner, T., Whiteman, D. N., Thorne, P. W., and Vömel, H.: Reference Quality Upper-Air Measurements: guidance for developing GRUAN data products, Atmos. Meas. Tech., 3, 1217–1231, https://doi.org/10.5194/amt-3-1217-2010, 2010.
Ingleby, B.: An assessment of different radiosonde types 2015/2016, European Centre for Medium Range Weather Forecasts, available at: https://www.ecmwf.int/search/elibrary (last access: 2 January 2019), 2017.
Ingleby, B. and Edwards, D.: Changes to radiosonde reports and their processing for numerical weather prediction, Atmos. Sci. Lett., 16, 44–49, https://doi.org/10.1002/asl2.518, 2015.
Ingleby, B., Isaksen, L., Kral, T., Haiden, T., and Dahoui, M.: Improved use of atmospheric in situ data, ECMWF Newsletter, 155, 20–25, https://doi.org/10.21957/cf724bi05s, 2018.
Ingleby, N., Lorenc, A., Ngan, K., Rawlins, F., and Jackson, D.: Improved variational analyses using a nonlinear humidity control variable, Q. J. Roy. Meteor. Soc., 139, 1875–1887, https://doi.org/10.1002/qj.2073, 2013.
Joo, S., Eyre, J., and Marriott, R.: The impact of Metop and other satellite data within the Met Office global NWP system using an adjoint-based sensitivity method, Mon. Weather Rev., 141, 3331–3342, https://doi.org/10.1175/MWR-D-12-00232.1, 2013.
Kazumori, M. and English, S. J.: Use of the ocean surface wind direction signal in microwave radiance assimilation, Q. J. Roy. Meteor. Soc., 141, 1354–1375, https://doi.org/10.1002/qj.2445, 2015.
Leutbecher, M., Lock, S., Ollinaho, P., Lang, S. T., Balsamo, G., Bechtold, P., Bonavita, M., Christensen, H. M., Diamantakis, M., Dutra, E., English, S., Fisher, M., Forbes, R. M., Goddard, J., Haiden, T., Hogan, R. J., Juricke, S., Lawrence, H., MacLeod, D., Magnusson, L., Malardel, S., Massart, S., Sandu, I., Smolarkiewicz, P. K., Subramanian, A., Vitart, F., Wedi, N., and Weisheimer, A.: Stochastic representations of model uncertainties at ECMWF: state of the art and future vision, Q. J. Roy. Meteor. Soc., 143, 2315–2339, https://doi.org/10.1002/qj.3094, 2017.
Loew, A., Bell, W., Brocca, L., Bulgin, C. E., Burdanowitz, J., Calbet, X., Donner, R. V., Ghent, D., Gruber, A., Kaminski, T. and Kinzel, J., Klepp, C., Lambert, J. C., Schaepman-Strub, G., Schröder, M., and Verhoelst, T.: Validation practices for satellite based earth observation data across communities, Rev. Geophys., 55, 779–817, https://doi.org/10.1002/2017RG000562, 2017.
Lorenc, A. C., Ballard, S. P., Bell, R. S., Ingleby, N. B., Andrews, P. L., Barker, D. M., Bray, J. R., Clayton, A. M., Dalby, T., Li, D., Payne, T. J., and Saunders, F. W.: The Met. Office global three-dimensional variational data assimilation scheme, Q. J. Roy. Meteor. Soc., 126, 2991–3012, https://doi.org/10.1002/qj.49712657002, 2000.
Lu, Q. and Bell, W.: Characterizing channel center frequencies in AMSU-A and MSU microwave sounding instruments, J. Atmos. Ocean. Tech., 31, 1713–1732, https://doi.org/10.1175/JTECH-D-13-00136.1, 2014.
Lupu, C. and Geer, A. J.: Operational Implementation of RTTOV-11 in the IFS, ECMWF Tech. Memo. 748, available at: https://www.ecmwf.int/search/elibrary (last access: 2 January 2019), 2015.
Massonnet, F., Bellprat, O., Guemas, V., and Doblas-Reyes, F. J.: Using climate models to estimate the quality of global observational data sets, Science, 354, 452–455, https://doi.org/10.1126/science.aaf6369, 2016.
Paufler, P.: Landolt-Börnstein: Numerical data and functional relationships in science and technology, edited by: Madelung, O., Springer-Verlag Berlin, 23, 1360–1360, https://doi.org/10.1002/crat.2170231029, 1988.
Rawlins, F., Ballard, S., Bovis, K., Clayton, A., Li, D., Inverarity, G., Lorenc, A., and Payne, T.: The Met Office global four-dimensional variational data assimilation scheme, Q. J. Roy. Meteor. Soc., 133, 347–362, https://doi.org/10.1002/qj.32, 2007.
Rodgers, C. D.: Inverse methods for atmospheric sounding: theory and practice, World Scientific, Sect. 12.2, 2000.
Saunders, R., Matricardi, M., and Brunel, P.: An improved fast radiative transfer model for assimilation of satellite radiance observations, Q. J. Roy. Meteor. Soc., 125, 1407–1425, https://doi.org/10.1002/qj.1999.49712555615, 1999.
Saunders, R., Rayer, P., Blackmore, T., Matricardi, M., Bauer, P., and Salmond, D.: A new fast radiative transfer model-RTTOV-9, in: Proc. Joint 2007 EUMETSAT Meteorological Satellite Conference and the 15th Satellite Meteorology and Oceanography Conference of the American Meteorological Society, Amsterdam, The Netherlands, 24–28 September 2007, 2007.
Saunders, R., Hocking, J., Turner, E., Rayer, P., Rundle, D., Brunel, P., Vidot, J., Roquet, P., Matricardi, M., Geer, A., Bormann, N., and Lupu, C.: An update on the RTTOV fast radiative transfer model (currently at version 12), Geosci. Model Dev., 11, 2717–2737, https://doi.org/10.5194/gmd-11-2717-2018, 2018.
Shepherd, T. G., Polichtchouk, I., Hogan, R. J., and Simmons, A. J.: Report on Stratosphere Task Force, ECMWF Technical Memorandum, 824, available at: https://www.ecmwf.int/en/elibrary/18259-report-stratosphere-task-force (last access: 2 January 2019), 2018.
Simmons, A., Untch, A., Jakob, C., Kållberg, P., and Unden, P.: Stratospheric water vapour and tropical tropopause temperatures in ECMWF analyses and multi-year simulations, Q. J. Roy. Meteor. Soc., 125, 353–386, https://doi.org/10.1002/qj.49712555318, 1999.
Smith, A.: Radiance simulator v2.0 user guide, EUMETSAT Satellite Application Facility on Numerical Weather Prediction (NWPSAF), Tech. Rep. NWPSAF-MO-UD-040, available at: https://www.nwpsaf.eu/site/software/radiance-simulator/documentation/ (last access: 2 January 2019), 2014.
Sommer, M., Dirksen, R., and Rohden, C.: Brief Description of the RS92 GRUAN Data Product (RS92-GDP), Technical Document GRUAN-TD-4, available at: https://www.gruan.org/documentation/gruan/td/ (last access: 2 January 2019), 2016.
Thorne, P. W., Madonna, F., Schulz, J., Oakley, T., Ingleby, B., Rosoldi, M., Tramutola, E., Arola, A., Buschmann, M., Mikalsen, A. C., Davy, R., Voces, C., Kreher, K., De Maziere, M., and Pappalardo, G.: Making better sense of the mosaic of environmental measurement networks: a system-of-systems approach and quantitative assessment, Geosci. Instrum. Method. Data Syst., 6, 453–472, https://doi.org/10.5194/gi-6-453-2017, 2017.
Zeng, Y., Su, Z., Calvet, J. C., Manninen, T., Swinnen, E., Schulz, J., Roebeling, R., Poli, P., Tan, D., Riihelä, A., Tanis, C. M., Arslan, A. N., Obregon, A., Kaiser-Weiss, A., John, V. O., Timmermans, W., Timmermans, J., Kaspar, F., Gregow, H., Barbu, A. L., Fairbairn, D., Gelati, E., and Meurey, C.: Analysis of current validation practices in Europe for space-based climate data records of essential climate variables, Int. J. Appl. Earth Obs., 42, 150–161, https://doi.org/10.1016/j.jag.2015.06.006, 2015.
Zou, X., Wang, X., Weng, F., and Li, G.: Assessments of Chinese FengYun Microwave Temperature Sounder (MWTS) measure- ments for weather and climate applications, J. Atmos. Ocean. Tech., 28, 1206–1227, https://doi.org/10.1175/JTECH-D-11-00023.1, 2011.
- Abstract
- Copyright statement
- Introduction
- Datasets
- Processor design
- Data analysis illustration
- Comparison assessment
- Conclusion
- Data availability
- Appendix A: Forecast error covariance matrix estimation
- Appendix B: Interpolation matrix pseudo inverse
- Author contributions
- Competing interests
- Acknowledgements
- References
- Abstract
- Copyright statement
- Introduction
- Datasets
- Processor design
- Data analysis illustration
- Comparison assessment
- Conclusion
- Data availability
- Appendix A: Forecast error covariance matrix estimation
- Appendix B: Interpolation matrix pseudo inverse
- Author contributions
- Competing interests
- Acknowledgements
- References